Prognosis of Six-Month Glasgow Outcome Scale in Severe Traumatic Brain Injury Using Hospital Admission Characteristics, Injury Severity Characteristics, and Physiological Monitoring during the First Day Post-Injury

Abstract

Gold standard prognostic models for long-term outcome in patients with severe traumatic brain injury (TBI) use admission characteristics and are considered useful in some areas but not for clinical practice. In this study, we aimed to build prognostic models for 6-month Glasgow Outcome Score (GOS) in patients with severe TBI, combining baseline characteristics with physiological, treatment, and injury severity data collected during the first 24 h after injury. We used a training dataset of 472 TBI subjects and several data mining algorithms to predict the long-term neurological outcome. Performance of these algorithms was assessed in an independent (test) sample of 158 subjects. The least absolute shrinkage and selection operator (LASSO) led to the highest prediction accuracy (area under the receiving operating characteristic curve = 0.86) in the test set. The most important post-baseline predictor of GOS was the best motor Glasgow Coma Scale (GCS) recorded in the first day post-injury. The LASSO model containing the best motor GCS and baseline variables as predictors outperformed a model with baseline data only. TBI patient physiology of the first day-post-injury did not have a major contribution to patient prognosis six months after injury. In conclusion, 6-month GOS in patients with TBI can be predicted with good accuracy by the end of the first day post-injury, using hospital admission data and information on the best motor GCS achieved during those first 24 h post-injury. Passed the first day after injury, important physiological predictors could emerge from landmark analyses, leading to prediction models of higher accuracy than the one proposed in the current research.

Introduction

Traumatic brain injury (TBI) is a major cause of neurological disability and death worldwide. Deterioration in patients with TBI is primarily due to secondary brain injury such as hypoxia, energy dysfunction, and increased intracranial pressure (ICP). Secondary brain insults are often quantified in the acute in-hospital period, where major complications occur; therefore, they can carry important prognostic information.^1–3

Prognostic models of long-term neurological recovery and mortality currently considered gold standard were developed based on hospital admission characteristics.^4,5 For unfavorable Glasgow Outcome Scale (GOS), these models achieved good discriminatory ability in each other's development populations (area under the receiving operating characteristic curves [AUCs] between 0.77 and 0.80); however, in other external populations, their discriminatory ability was poor (AUCs ranging from 0.66 to 0.76).⁶ The difficulty in generalizing these models to other populations originates from injured populations that are very heterogeneous at the time of injury and cannot be fully characterized with admission hospital data only. The incorporation of secondary injuries that occur in the acute clinical phase in models purely based on baseline static information could improve characterization of TBI populations and therefore, outcome prediction.

Research efforts have been made to develop prognostic models based on post-baseline summarized insults. In general, studies have described subject-specific pathophysiological data using either simple measures such as mean, medians, standard deviations, and duration of insults,^7–10 or more comprehensive summary measures like the “dose” of secondary brain injury given by the area under the curve over a specific threshold^1,11,12 and entropy values.² However, models developed on this type of secondary injury features have not been useful for outcome prediction. Some models have been built on small sample sizes or for description purposes only and may fail to consider important predictors.^{1,2,7,8,10–12} One model built on a moderate sample size including many secondary injury features and important baseline predictors showed good discrimination ability. Nevertheless, it lacks external validation and could be biased due to the inclusion of features with no clinical meaning.³

The goal of this study is to develop prognostic models for long-term functional outcome after TBI, using hospital admission data, injury severity, and automated physiological data collected within the first 24 h after intensive care unit (ICU) admission. To characterize physiological changes over time, we consider about a thousand summary measures, including those used in previous smaller studies.^2,3,11–13 We hypothesize that secondary injury information collected early after injury can increase prognostic accuracy over current models based on admission characteristics only. The novelty of this study is that our models are built based on a database of patients with TBI and validated in a separate TBI population, making them more generalizable to other settings. In addition, this is the most comprehensive study to date of prognostic models in severe TBI using information until 24 h after injury (landmark analysis). We expect that our prognostic models will help improve management of TBI patients and provide more realistic expectations of outcomes.

Methods

Study population

Subjects with severe TBI were enrolled in one of several observational or clinical trial studies and admitted to the neurosurgical ICU of the Ben Taub General Hospital (BTGH) located in Houston, Texas, in two different time periods: between 1989 and 2000 (training set), or between 2006 and 2012 (test set). On hospital admission, demographic and clinical data were collected. In the ICU, physiological data such as ICP, mean arterial pressure (MAP), and oxygen saturation of arterial blood (SaO₂) were recorded by a monitor every 36 sec. In addition to automated recording of patient physiology, vital sign data were collected by ICU nurse practitioners hourly. Among other functional outcome measures, the GOS was measured at 6 months post-injury.

In this study, we were interested in building prognostic models for 6-month GOS,¹⁴ dichotomized in unfavorable (severe disability, vegetative, or dead) versus favorable (good recovery, moderate disability). The BTGH hospital admission and first day ICU data were used to build our models. Although in the original data the cohorts combined comprised 1239 patients, our population consisted of 630 TBI patients after excluding subjects who met the following exclusion criteria, in the order described: died within the first 24 h after injury or date of death could not be determined (n = 5); had gunshot wounds or unknown mechanism of injury (n = 157); had GOS missing 6 months after injury (n = 238); and had missing automated physiological data throughout the 24-h period or physiological data could not be recovered (n = 209).

Patients considered for this analysis were enrolled under informed consent from a legally authorized representative or an exception from informed consent mechanism, depending on each study Institutional Review Board protocol. The use of these data was approved by the Institutional Review Board of University of Texas Health Science Center at Houston (protocol HSC-SPH-16-0591).

Participating studies in the BTGH database

The observational studies conducted throughout the years 1989–2000 included studies of jugular venous oxygen saturation, brain tissue pO₂, cerebral blood flow and cerebral blood flow autoregulation, and microdialysis monitoring.^15–20 The inclusion criteria for these studies was motor GCS <6 on admission or within 48 h after injury, and age >14. The exclusion criteria were GCS 3 with fixed and dilated pupils and severe associated systemic injury.

A randomized trial of ICU management comparing a cerebral blood flow targeted management strategy to an intracranial pressure targeted management strategy was conducted between 1994 and 1997.²¹ The inclusion criteria for the trial was motor GCS <6 or deteriorated to motor GCS <6 within 48 h after injury, age >14, and admission within 12 h of injury. The exclusion criteria were GCS 3 with fixed and dilated pupils, contraindication to placement of jugular bulb catheter, severe associated systemic injury, and severe pre-existing disease.

A clinical trial conducted between 2006 and 2012 enrolled patients with motor GCS <6 after resuscitation within 6 h of injury. Exclusion criteria were GCS 3 with fixed and dilated pupils, penetrating trauma, pregnancy, life-threatening systemic injury, and severe pre-existing disease.²²

Except for the clinical trial conducted between 2006 and 2012 (the test set of our study), the rest of the studies did not exclude penetrating injuries.

Predictors of 6-month GOS

Several non-dynamic (baseline or static) and dynamic (longitudinal) predictors were considered during model building. Baseline predictors consisted of hospital admission variables and scores derived from these ones. Physiological, injury severity, and treatment variables recorded during the first 24 h after ICU admission were defined as dynamic predictors. A full list of dynamic covariates included in our models, the pre-processing and imputation of the physiological variables, and additional details can be found in the Supplementary Appendix 1 and Supplementary Appendix 2.

Model building, testing, and calibration

To build the 6-month GOS prognostic models, the data collected in the period 1989–2000 were used for model training (n = 472), and the data gathered between 2006 and 2012 for model testing (n = 158). In the training and test sets, 63% and 66% of the patients had unfavorable 6-month GOS, respectively. First, we computed the non-dynamic and dynamic predictors previously described for each subject and applied the least absolute shrinkage and selection operator (LASSO) to select a subset of most predictive variables. The LASSO penalizes the absolute magnitude of the coefficients in the logistic regression model and drops variables that do not contribute to making the model's prediction closer to the true response.²³ Additionally, LASSO helps to prevent overfitting of models and is often used for datasets where the number of predictive variables is much larger than the number of observations.

Second, the subset of features chosen by LASSO was used as input variables for different machine learning algorithms. Because in general there is not a single method that dominates all others in terms of classification performance, we applied various supervised learning algorithms on the training data and chose the one that gave the highest classification accuracy in the test set. The supervised learning algorithms considered were decision trees, random forests (RF), support vector machines, linear discriminant analysis (LDA), quadratic discriminant analysis, and logistic regression (LR).²⁴ We also used the shrunk LASSO coefficients from the selected model in the first step to make predictions. Some details about these algorithms can be found in the Supplementary Appendix 3. The AUC in the test set was used to determine model discrimination.

Statistical analysis

For the chosen model, we evaluated overall model performance using the scaled Brier score (the scaled Brier score of a perfect model is 0%). We also computed sensitivity, for specificities of 80%, 85%, and 90%. The rationale for setting high values of specificity is that a false diagnosis of a poor neurological outcome has more serious implications than erroneously predicting a favorable outcome.

The scale of continuous variables in the chosen model was assessed by testing the significance of spline terms in a restrictive cubic spline model. ²⁵ Model calibration was assessed with the Hosmer-Lemeshow (HL) statistic, calibration slope, and calibration-in-the-large. A good calibrated model should have a HL associated p value above 0.05, calibration-in-the-large close to 0, and a calibration slope close to 1.²⁶

Sensitivity analyses

Because the LASSO may not pick the most predictive covariates among highly correlated predictors, we also tried random forests for selection of the most important covariates from the full set of features. In addition, we modified the imputation method, pooling 1 h instead of 2 h of self-patient data to complete missing physiology. To assess temporal confounding (e.g., differences in populations heterogeneity), we mixed the two study cohorts, including different patients from the same period in training and test sets.

Results

Description of study population

Baseline characteristics of the training and test sets are summarized on Supplementary Appendix 4, Supplementary Table S4. Patients in the training and test sets had similar distributions for motor GCS, Pupil reactivity, hypotension, age, initial ICP, SAH, and epidural hematoma, but were significantly different with respect to the injury severity score (ISS; p < 0.001) and the Marshall CT scan classification (p < 0.001). ISS score was not associated with unfavorable GOS either in the training (p = 0.58) or in the test sets (p = 0.75). Marshall CT scan classification was significantly associated with unfavorable GOS in both the training (p = 0.02) and test sets (p < 0.001).

Two hundred and thirty-eight patients who had missing 6-month GOS could not be included in this study. Of these, patients who had recorded physiological data (n = 193) were not significantly different from patients with recorded 6-month GOS and physiological data (n = 630) with respect to many hospital admission variables, such as enrollment motor GCS (p = 0.15), age (p = 0.99), or pupillary reactivity (p = 0.18; Supplementary Appendix 4, Supplementary Table S5). However, the set who had recorded 6-month GOS had higher median ICP at baseline (median ICP = 14; IQR = 13), compared with those who had missing 6-month GOS median ICP = 11; interquartile range = 10; p = 0.001), and higher best motor GCS achieved in the first 24 h post-injury (p < 0.001).

Model building

We computed a total of 959 dynamic features and seven static features for all the patients in the training data. Because some of the baseline and dynamic features were not available or could not be computed for every patient, the training data were reduced to 431 patients. For features with missing data, we assessed their univariate association with the outcome, and excluded from the analysis those with p values greater than 0.25 (omitted 9 features). The LASSO model selection chose 35 important predictors of GOS. Important baseline predictors were the International Mission for Prognosis and Analysis of Clinical Trials in TBI (IMPACT) core model prognostic score of unfavorable outcome, presence of epidural hematoma (EDH), and the Marshall CT scan classification. Among the dynamic predictors, many variables corresponding to cluster membership, standard deviations, summary measures of correlation between MAP and ICP, cepstral coefficients, and the best motor Glasgow Coma Scale (GCS) achieved in the first 24 h post-injury were deemed important.

The LASSO model with shrunk coefficients achieved the highest classification accuracy among the methods, followed by RF, LR, and LDA; the LASSO AUC was equal to 0.85 in the test set (95% CI: 0.79–0.91), compared with 0.83 for RF, LR, and LDA. Performance of the top classification algorithms on the training and test sets is presented on Table 1. In addition, the LASSO model with baseline and post-baseline features performed significantly better in the test set compared with a model with baseline covariates only (AUC = 0.85 vs. 0.77; p = 0.01). To assess the contribution of the first 24 h post-injury physiology in predicting the 6-month outcome, we performed a LASSO model selection on the complete set of physiological and baseline features, excluding the best motor GCS. When we used the LASSO shrunk coefficients to assess model performance in the test set, the model with physiological and baseline data did not perform better than a model with baseline covariates only (AUC = 0.73 vs. AUC = 0.77, respectively). This indicates that the best motor GCS may be the most important post-baseline predictor of long-term functional outcome in patients with TBI when making predictions by the first day after injury.

Table 1.

Supervised Learning Algorithms with Best Performance on the Test Data

Methoda	AUCb in Training set (n = 431)	AUC in Test set (n = 158)
Least absolute shrinkage and selection operator (LASSO)	0.90	0.85
Random forests (RF)	0.94	0.83
Logistic regression (LR)	0.94	0.83
Linear discriminant analysis (LDA)	0.93	0.83

^aBaseline, post-baseline motor GCS, and post-baseline physiological variables were selected by the supervised learning classifiers.

^bAUC = Area under the receiving operating characteristic curve.

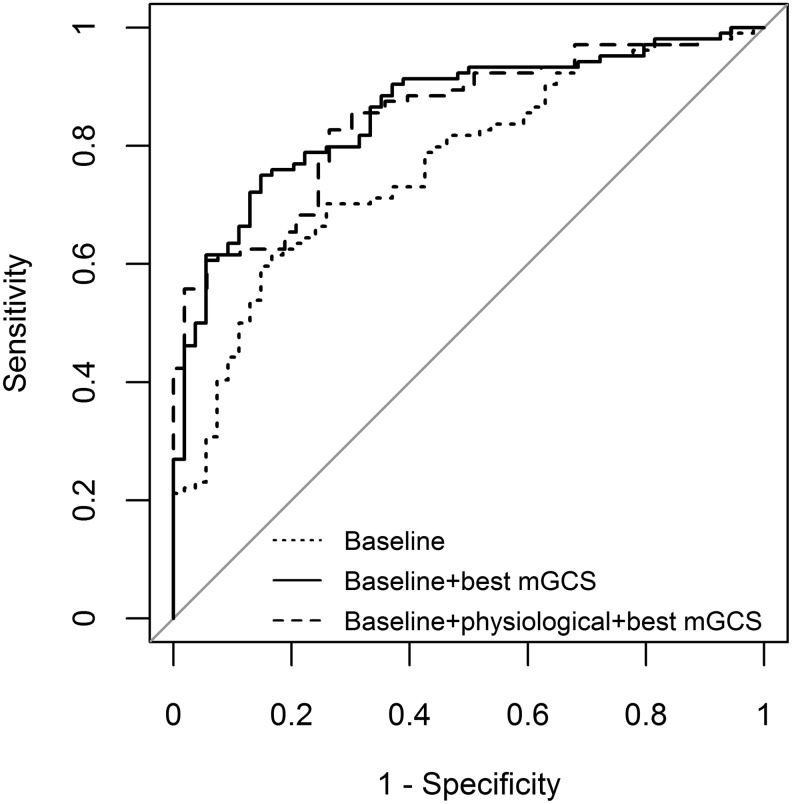
A LASSO model with baseline covariates and the best motor GCS had AUC = 86% of discrimination ability (95% CI: 0.80- 0.92) in the data used for testing. Hence, compared with a model containing several summary measures of physiological data in addition to the best motor GCS and baseline characteristics, this simpler model provides similar discrimination power on the test set and is less likely to overfit the training data. Receiver operating characteristics curves for the LASSO models previously described are presented on Figure 1.

FIG. 1.

Receiver operating characteristic curves for least absolute shrinkage and selection operator models built on different set of features. Best mGCS, best motor Glasgow Coma Scale.

Prognostic model based on best motor GCS and hospital admission data

The most parsimonious model with best performance on the test set contained the following covariates: presence of subarachnoid hemorrhage (SAH), EDH, IMPACT prognostic score of unfavorable outcome, the first 24 h best motor GCS, and Marshall CT scan classification. This model resulted of applying adaptive LASSO (ALASSO) to the model with baseline covariates and the best motor GCS selected by LASSO in the previous section. Adaptive LASSO was applied with the purpose of removing potential noise factors.²⁷ The AUC of this model was maintained at 86% (95% CI: 0.80- 0.92).

The ALASSO model fit the data well (HL p value = 0.52). Overall performance of this model given by the Brier scaled score was 38%. Calibration-in-the-large was −0.06 and the calibration slope was 1.10. For specificities of 80%, 85%, and 90%, the model correctly classified patients with unfavorable GOS, 80%, 75%, and 63% of the time, respectively. The equation of the proposed model for prediction of 6-month GOS is as follows:

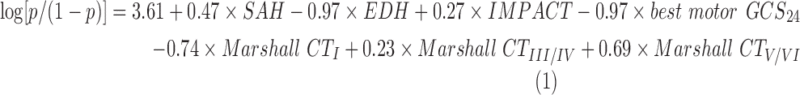where p is the probability of unfavorable 6-month GOS given the covariates of the model. For Marshall CT scan classification, the second category is set as the reference category. The coefficients of the proposed model (1) were obtained by fitting the model to the combined training and test sets.

Sensitivity analysis results

When we used a different model selection procedure than LASSO and a different imputation method, the trained data mining algorithms resulted in similar AUCs on the test set (not shown) compared with the ones obtained with our preferred methods. Using patients from different cohorts for model training also gave similar results, which indicates absence of temporal confounding.

Discussion

We aimed to build prognostic models for 6-month GOS in patients with TBI based on hospital admission characteristics and on injury severity, treatment, and physiological data collected during the first 24 h post-ICU admission. Our hypothesis was that secondary injury that occurs during the first day after injury would improve outcome prediction over models based on admission characteristics only. The hospital admission core model developed by the IMPACT group, based on age, motor score, and pupillary reactivity, achieved an AUC of 76% on the entire TBI population of this study.

A more comprehensive baseline model developed by this group, which included as predictors the variables from the core model in addition to presence of hypoxia or hypotension, Marshall CT scan classification, glucose, and hemoglobin (the lab model), achieved an AUC of 79% on our test set.⁴ The performance of the IMPACT lab model on the training set of this study could not be assessed due to the presence of missing data in hypoxia and laboratory variables. If our hypothesis was proven, significantly higher AUCs would lead to more reasonable expectations of neurological function recovery, making our models useful tools for clinical decision making. In this study, we used data of 431 patients to build the models, and an independent dataset of 158 patients for model testing. Patients in the training and test sought care at the same hospital but those in the test set were treated more recently. The rationale of using patients from two different time periods was to obtain a prediction model that could be more generalizable to future populations, which would be representative of current practices. The major contributor to prediction of poor neurological outcome was the best motor GCS within the first 24 h post ICU admission. When applied to the test set, a model containing baseline characteristics and the best motor GCS recorded during the first day post-injury had an AUC of 0.86 with a margin of error of 6%, indicating an estimate with good precision. In addition, this estimate is unbiased because it was obtained from a different sample than that of training, although further validation is needed using data from a different hospital.

The GCS post-baseline has been shown to be an important predictor of functional outcome in TBI. For instance, Lu and colleagues built a model for prediction of 6-month GOS of excellent discrimination (AUC = 96%, sensitivity = 83.5%, specificity = 80.73%), where the GCS measurements on Days 7 and 14 post-injury and the change in GCS from the emergency department to Day 14 were the most influential attributes.²⁸ In our model, when the best motor GCS was included in a LASSO model with baseline characteristics only, the AUC was 10% lower than in Lu and colleagues; this is likely due to the differential amount of follow-up used (24 h vs. 14 days). A much earlier prognostication may be necessary in this population of critically ill patients. Because early sedation and paralysis affect patient level of consciousness, the GCS or its components have not been generally included in prognostic models. However, the best GCS recorded or the change in GCS from enrollment provide a more accurate representation of clinical severity after injury.

In the past, prognostic models on functional outcomes in TBI patients that used physiological data over time had performances that range from acceptable² to good.^1,3 To our knowledge, the model with highest discrimination power was developed by Guiza and colleagues.³ By using physiological data of the first day after ICU admission, they built a model for 6-month GOS with an AUC equal to 0.87. They showed that dynamic physiology alone significantly improved outcome prediction (AUC = 0.68 with static attributes versus 0.87 with static and dynamic physiological data). Guiza and colleagues' findings contradict our study results, which indicate no added value of physiological data over hospital admission data. However, they used a smaller dataset of 160 patients for model development and a bootstrap technique to compute measures of performance on the same data. In addition, they computed summary measures like ICP-MAP correlation coefficients every 10 min in 24 h and first derivative of the correlation signal, which may not be entirely appropriate since a correlation in a specific 10-min time period lacks clinical significance. Further, it is unclear how they handled missing data problems. For all these reasons, the AUC they reported could be biased and unrealistically high. In our study, we computed the most important features according to Guiza and colleagues, except for the ones mentioned above, and 360 other features they did not consider. Further, we used a clinically-driven method of imputation, a larger sample for model building, and a separate population for testing. Consequently, our values of model performance are more robust and represent unbiased estimates of accuracy.

We showed that physiological data during the first 24 h post-injury did not carry valuable prognostic information on this population. However, the best motor GCS recorded provided important prognostic information independent of hospital admission characteristics. To our knowledge, this is the first study of 6-month GOS prediction in TBI patients based on a large (relative to past studies) sample size for model development and an independent sample for evaluation that uses post-baseline information (see Supplementary Appendix 4, Supplementary Table S6, for a comparison of our model and existing prognostic models for 6-month GOS). It would be worth exploring the predictive value of data collected in the ICU passing the first day after injury; important physiological predictors may emerge with longer follow-up. However, accuracy potentially gained with longer follow-up would be downweighed by extra bias associated with additional missing ICU data and timing to make major clinical decisions.

Author Disclosure Statement

No competing financial interests exist.

Supplementary Material

Supplementary Appendix S1

Supplementary Appendix S2

Supplementary Appendix S3

Supplementary Appendix S4

Supplementary Table S1

Supplementary Table S2

Supplementary Table S3

Supplementary Table S4

Supplementary Table S5

Supplementary Table S6