MULTIPLE IMPUTATION FOR BOUNDED VARIABLES

Abstract

Missing data are a common issue in statistical analyses. Multiple imputation is a technique that has been applied in countless research studies and has a strong theoretical basis. Most of the statistical literature on multiple imputation has focused on unbounded continuous variables, with mostly ad hoc remedies for variables with bounded support. These approaches can be unsatisfactory when applied to bounded variables as they can produce misleading inferences. In this paper, we propose a flexible quantile-based imputation model suitable for distributions defined over singly or doubly bounded intervals. Proper support of the imputed values is ensured by applying a family of transformations with singly or doubly bounded range. Simulation studies demonstrate that our method is able to deal with skewness, bimodality, and heteroscedasticity and has superior properties as compared to competing approaches, such as log-normal imputation and predictive mean matching. We demonstrate the application of the proposed imputation procedure by analysing data on mathematical development scores in children from the Millennium Cohort Study, UK. We also show a specific advantage of our methods using a small psychiatric dataset. Our methods are relevant in a number of fields, including education and psychology.

1. Introduction

Data on educational attainment of 5-year-old children in the UK were collected as part of the Millennium Cohort Study (MCS), a longitudinal study of British children born at the beginning of the twenty-first century (Smith and Joshi, 2002). Children’s achievement was assessed by means of questionnaires administered to their school teachers (Johnson, 2008). For cohort members attending schools in Wales, Scotland, and Northern Ireland, the Celtic Country Teacher Survey (CCTS) questionnaire was specifically developed to replicate the information collected by the Foundation Stage Profile in England, which sets the standards put forward by the Department for Education for the development, learning and care of children from birth to five. Here, we focus on the CCTS sample which consists of observations from the third sweep of the MCS for about seven thousand children residing in Wales, Scotland or Northern Ireland. The variable of interest is mathematical development (MD) total score measured over different assessment scales; it takes values on the bounded range (0, 27). The histogram of MD scores (Fig.1) shows a strong left skewness, characterised by a steep slope after the mid range of the support. Unfortunately, data on educational attainment was received for less than half of the cohort members.

Figure 1.

Histogram of mathematical development (MD) scores in the Millennium Cohort Study.

It is well known that including in the analysis only complete cases, i.e. cases that have been observed for all variables in the model, may have undesirable consequences depending on the missing data mechanism, the amount of missing information, and the variables affected by the missingness (Rubin, 1987; Little and Rubin, 2002). First, the results of complete-case analyses can be biased. Second, the cumulative effect of missing data in several variables often leads to the exclusion of a substantial proportion of the original sample, resulting in a serious loss of precision of the estimates and of power in detecting associations between variables. This clearly could have an impact on the validity of the conclusions drawn from a study.

Multiple imputation (MI) (Rubin, 1987) is a statistical technique for handling missing data and has received much attention by researchers because it is easy to understand and apply. Software implementations of MI are relatively recent (e.g. Royston and White, 2011, van Buuren and Groothuis-Oudshoorn, 2011). The application of MI is appropriate when the data are missing completely at random (MCAR) or missing at random (MAR). Under the MAR assumptions, the probability that the values are missing may depend on observed information, but not on the missing values themselves (Little and Rubin, 2002). In other words, the actual values of a missing variable do not have systematic differences between those who did and did not provided information, given the observed data. The imputation model plays an important role in the overall procedure as it provides the values that fill the blanks. Common modelling choices for the imputation of discrete variables are the binomial, multinomial, and Poisson distributions. For continuous variables as well as discrete variables that are treated as continuous for practical purposes, the predictive distribution is often assumed to be normal. The normal model, without further qualification, requires that:

1. the missing values can be arbitrarily small or arbitrarily large;

2. the conditional distribution of the variable with missing values is bell-shaped; and

3. the predictors of the missing values have a linear association with the missing values.

The normal distribution is by far the most commonly used even though a large number of variables do not conform to it. This is particularly true when a variable can take on only strictly positive values (singly bounded) or values constrained between lower and upper bounds (doubly bounded). Examples of singly bounded variables include measurements of length, weight and volume; examples of doubly bounded variables include psychometric scales, clinical scores, survey questionnaire items, and school grades. Other examples of doubly bounded variables in psychology and related areas are given by Smithson and Shou (2017). The probability of observing values near the bounds is often substantial (‘boundary modes’), which makes the application of standard normal imputation inappropriate because:

1. this may result in imputed values outside the admissible range (e.g. negative school grades);

2. the distribution is far from being bell-shaped (e.g. skewed, bimodal or J-shaped); and

3. so-called floor and ceiling effects, typical of bounded variables, may induce nonlinear relationships between variables.

There are particular analyses where having imputed values outside the admissible range of data will not bias results (e.g. estimating the mean or in some regression models). However, for many statistics this is not the case. For example, if the variance, scale, shape or conditional quantiles (Geraci, 2016a) were the parameter(s) of interest, their values could be biased by data not conforming to the range of admissible values.

The aim of this paper is to develop a novel MI strategy using transformation-based quantile models (Geraci and Jones, 2015). These models provide a natural and flexible solution to the problem of imputing continuous bounded variables. In Sect. 2, we review existing methods for imputing continuous non-normal missing data. In Sect. 3, we introduce our proposed methods, with additional details on computation and software in Online Resource 1. In Sect. 4, we evaluate the proposed methods as compared to common approaches that are used for imputing bounded variables via a simulation study (additional results are given in Online Resource 2). In Sect. 5, we demonstrate the advantages of our MI approach using real data examples. We conclude with final remarks in Sect. 6.

2. Methods for Imputation of Continuous Non-normal Variables

Several authors proposed solutions to the imputation of bounded variables. For example, van Buuren and Groothuis-Oudshoorn (2011) suggest replacing out-of-range imputations with the closest bound (which they call squeezing), that is, censoring. As we will show in a simulation study (Sect. 4), this approach can potentially bias subsequent inferences as it is unable to address the issue at its root (see also Rodwell et al., 2014). Another approach often followed is to first transform the variable being imputed (e.g. taking the log), then generate imputations on the transformed scale using a normal model, and finally apply the inverse transformation to these values (White et al., 2011). This approach too may fail to address the issues discussed above and may even perform worse than a complete-case analysis (Geraci, 2016a).

Predictive mean matching (PMM) (Little, 1988) is an attractive method that performs well in several non-standard situations (Morris et al., 2014; Lee and Carlin, 2017). It shares some of the properties of nonparametric imputation and other robust methods such as local residual draws, though it relies on parametric predictions. In PMM, the distribution of the resulting imputed values will often match that of the observed values since imputations are randomly chosen from complete observations (‘donors’) that are similar to the unit with the missing value. This can be of practical utility when in the presence of bounded support, non-normality, and nonlinearity (White et al., 2011). These are all features that characterise, for example, the distribution of MD scores and its relationship with important predictors in the MCS data (Mensah and Kiernan, 2010; Geraci and Jones, 2015). However, there are some potential drawbacks that may limit the suitability of PMM in some situations. To perform satisfactorily, PMM usually requires an adequate pool of donors. Moreover, if the unobserved values, conditional on the covariates, are believed to lie outside the observed range, then PMM will not be able to provide appropriate imputations (de Jong et al., 2016). Some of these approaches are discussed and compared by von Hippel (2013) and Rodwell et al. (2014) who considered censoring, truncating and transforming imputations under the assumption that the censored or truncated or transformed distribution is approximately normal (see also Lee and Carlin, 2017, for a simulation study using transformations). These studies showed that these methods work in a limited number of cases and for specific targets of the analysis; otherwise, they perform poorly. Further, confidence intervals from PMM have been shown to produce under-coverage of the mean of the complete data (Rodwell et al., 2014).

Some authors developed parametric MI methods for continuous non-normal data, with either singly or doubly bounded supports, including Tukey’s gh distribution (He and Raghunathan, 2006, 2012), beta and Weibull densities (Demirtas and Hedeker, 2008a), the generalised lambda distribution (Demirtas, 2009), and Fleishman’s power polynomials (Demirtas and Hedeker, 2008b). While these proposals can be used with non-normal data, none of them possesses simultaneously all the features we require in our study. For example, most of these alternatives are parametric (He and Raghunathan, 2006, 2012; Demirtas and Hedeker, 2008a, 2008b) and, while flexible, they lack the robustness enjoyed by quantile regression. Further, some of these methods (Demirtas and Hedeker, 2008a, 2008b) have been applied to univariate missing data only, under the assumption of MCAR. It is not known how these would perform under MAR assumptions. We surmise that an extension to a regression approach would be technically difficult since these methods rely on the estimation of several parameters which control the location, scale, and shape of the distribution. Such parameters would have to be modelled as functions of the covariates in order for MI to benefit from any related flexibility (usually only location is modelled through covariates). An exception is given by He and Raghunathan’s (2012) approach which extends previous work (He and Raghunathan, 2006) to multivariate continuous data. Although this approach can be applied to MAR data, it is clearly not appropriate when information about the missing values comes from discrete covariates as well. Finally, the evaluation of all these methods is hindered by the lack of software.

3. Methods

3.1. Multiple Imputation

Let Y = (Y₁, …, Y_q) be a vector of q random variables and let Y_−j denote the collection of q variables in Y except Y_j, j = 1, …, q. The goal is to make inference about an unknown quantity, say θ, using Y. In real applications, it is common that some of the components of Y may be incompletely observed. Let $Y^{\text{obs}}=\left(Y_1^{\text{obs}},\dots ,Y_q^{\text{obs}}\right)$ and $Y^{\text{mis}}=\left(Y_1^{\text{mis}},\dots ,Y_q^{\text{mis}}\right)$ denote the observed and missing parts of Y, respectively. Throughout the paper, we assume that the mechanism is either MCAR or MAR, that is, Pr(Y is missing|Y^mis, Y^obs) = Pr(Y is missing|Y^obs).

The basic idea in multiple imputation is to replace the missing values by multiple plausible predictions (van Buuren and Groothuis-Oudshoorn, 2011) drawn from the predictive distribution of each $Y_j^{\text{mis}}$. There are basically two strategies for drawing imputations, one based on the joint distribution of Y and one based on a sequence (chain) of conditional distributions for Y_j|Y_−j, commonly referred to as multivariate imputation by chained equations (MICE). The latter strategy is apposite when it is not possible, or very difficult, to specify a joint distribution for Y (for example, when Y contains both discrete and continuous variables). This is the situation we will consider throughout the paper. However, for the sake of simplicity and without loss of generality, we will illustrate the proposed methods for only one such conditional distribution, say, Y_q|Y_−q.

We then redefine Y_q ≡ Z and Y_−q ≡ X, where Z is a random variable with continuous cumulative distribution function (CDF) and X is a vector of q − 1 covariates that are informative about the conditional distribution F_Z|X. Also, suppose that only X is observed completely (we explain further below how the procedure works if this is not the case), while Z is observed for s subjects and missing for n − s subjects. Without loss of generality, we assume that the first s subjects are observed completely. That is, in a sample (z_i, x_i), i = 1, …, n, both X and Z are completely observed for i = 1, …, s, while X is completely observed and Z is missing for i = s + 1, …, n.

The basic idea of MI is to recover the missing information from the conditional distribution F_Z|X. The latter is estimated from the complete observations and a sample of imputations is drawn from ${\widehat{F}}_{Z|X}$. Under MAR assumptions, F_Z|X can be consistently estimated. MI works in three successive stages as schematically described below:

1. Randomly draw a sample of imputations using the predictive distributions ${\widehat{F}}_{Z|X}$ for units i = s + 1, …, n. Repeat M times and create M copies of the dataset. Note that, for a MI procedure to be proper (Rubin, 1987; Nielsen, 2003), the uncertainty related to the estimate ${\widehat{F}}_{Z|X}$ must be taken into account. In Bayesian normal imputation, this corresponds to sampling first from the posterior distributions of the parameters of F_Z|X, given their priors. Alternatively, one can use approximate Bayesian bootstrap (ABB) imputation (Rubin and Schenker, 1986) which consists in estimating ${\widehat{F}}_{Z|X}$ using a bootstrap sample of the observed data.

2. Analyse each of the M datasets and obtain M estimates of θ, the quantity of interest.

3. Take the average of such M estimates to produce one final estimate, for which the variance is estimated as a function of the within- and between-imputation variance.

If the variables in X too have missing values, then all missing values are first filled in by simple random sampling with replacement from the observed values (White et al., 2011), and the imputation step (1) above is applied to each incomplete variable by iterating over a sequence of conditional imputation models. The chain of conditional distributions is then run for a predefined number of Gibbs sampler’s iterations. Satisfactory performance is typically achieved with just 5 or 10 iterations (Van Buuren et al., 2006; van Buuren and Groothuis-Oudshoorn, 2011). For a detailed illustration of MICE and guidance on its application, see for example van Buuren and Groothuis-Oudshoorn (2011) and White et al. (2011).

Parametric approaches to the estimation of F_Z|X introduce assumptions about the shape of F. For continuous Z, it is common to assume normality. In this case, the imputer needs only to specify the functional form of the predictor. This can be, for example, the linear specification Z = α + x^⊤β + ϵ, where $ϵ~\mathcal{N}\left(0,{\sigma }^2\right)$. The imputations are then drawn from the conditional normal distribution Φ {(z − α* − x^⊤β*)/σ*}, where Φ denotes the standard normal distribution function. The parameters α*, β* and σ* represent sampled values from the posterior distributions of, respectively, α, β and σ (Bayesian imputation) or bootstrap estimates from the observed data (ABB imputation). Generating the imputations then reduces to drawing a sample from a uniformly distributed variate U and then applying the inverse transform sampling method to predict Z* given x, that is

$$Z^{*}={\alpha }^{*}+x^{\top }{\beta }^{*}+{\sigma }^{*}{\text{Φ}}^{-1}(U),$$ (1)

where Φ⁻¹ is the quantile function of the standard normal.

3.2. Bounded Variables and Quantile-Based Imputation

The focus of this paper is on continuous variables with bounded support. Let Z be a random variable with either a singly bounded support (a, ∞) or a doubly bounded support (a, b), where a and b are known real scalars. Without loss of generality, we consider the linearly transformed variable Z ≡ Z − a or Z ≡ (Z − a)/(b − a) with support (0, ∞) or (0, 1), respectively. We first motivate and sketch the basic idea and then describe each step of the MI procedure.

As mentioned previously, the use of the normal distribution to impute missing values for bounded variables is difficult in practice. We want to avoid introducing assumptions that may aggravate (rather than solve) the missing data problem. Therefore, we propose a semi-parametric approach where the estimate of F_Z|X, which is needed for imputing missing values in Z, is obtained via the estimation of its inverse, i.e. $F_{Z|X}^{-1}$.

Let us start by considering the pth quantile linear model

$$Q_{Z|X}(p)={\alpha }_p+x^{\top }{\beta }_p,0<p<1,$$ (2)

where $Q_{Z|X}\equiv F_{Z|X}^{-1}$ is the quantile function of Z conditional on X and $\left({\alpha }_p,{\mathit{\beta }}_p^{\top }\right)$ are q regression coefficients indexed by p. In a distribution-free framework (Koenker and Bassett, 1978), the estimation of α_p and β_p does not require assumptions about the shape of the error distribution. If model (2) is correctly specified, then α_p + x^⊤β_p is the pth quantile of Z conditional on X. For imputation purposes, one can use the inverse transform sampling

$$Z^{*}=Q_{Z|X}(U),$$ (3)

where U is standard uniform. In quantile-based imputation, the predictive distribution is not restricted to any particular parametric form (Muñoz and Rueda, 2009; Bottai and Zhen, 2013; Geraci, 2016a). This approach provides flexibility when normal assumptions are violated and no other parametric alternative is readily available. However, imputations obtained using Eq. (3) may still fall outside the admissible range. To address this problem, we propose using

$$Q_{h\left(Z;{\text{λ}}_p\right)|X}(p)={\alpha }_p+x^{\top }{\beta }_p,$$ (4)

where

$$h\left(Z;{\text{λ}}_p\right)=\{\begin{array}{ll}\frac{1}{2{\text{λ}}_p}\left[{\{g(Z)\}}^{{\text{λ}}_p}-\frac{1}{{\{g(Z)\}}^{{\text{λ}}_p}}\right]\hfill & \text{ if }{\text{λ}}_p\ne 0\hfill \\ \text{log}\{g(Z)\}\hfill & \text{ if }{\text{λ}}_p=0,\hfill \end{array}$$ (5)

and g(Z) is defined in Table 1. Transformation (5), referred to it as ‘Proposal I’ by Geraci and Jones (2015), is monotone and depends on the transformation parameter λ_p, which is specific to the quantile p. Transformation (5) applies to both singly and doubly bounded variables, i.e. $h:(0,\infty )\to ℝ$ or $h:(0,1)\to ℝ$, and comes into four forms depending on the domain of Z and on its symmetric or asymmetric shape (Table 1). Not only does this transformation have range $ℝ$ and an explicit inverse for values in its range, but it also shares the flexibility and parsimony of other well-known transformations (discussed further in Sect. 3.3).

Table 1.

Choices of g(Z) for generic transformation (5) depending on the domain of Z and on its symmetric or asymmetric shape.

Domain	Symmetric	Asymmetric
(0, ∞)	g(Z) = Z	g(Z) = log(1 + Z)
(0, 1)	g(Z) = Z/(1 − Z)	g(Z) = −log(1 − Z)

The value of λ_p selects one of the curves that belong to the Proposal I family. If Z is singly bounded, then h⁻¹ is convex for λ_p ≤ 1 and it approaches the exponential function for λ_p → 0; it is concave for λ_p > 1. If Z is doubly bounded, then h⁻¹ is S-shaped for any value of λ_p ≤ 1 and it approaches the logistic function for λ_p → 0. The asymmetric inverse h⁻¹ is also S-shaped, although asymmetrically, and it approaches the complementary log-log function for λ_p → 0. If λ_p is unknown, its value is estimated from the data by optimising the quantile regression objective function (see Online Resource 1). If prior knowledge about the shape of the transformation is available, then the value of λ_p can be fixed and the estimates of the parameters (α_p, β_p) will adjust accordingly to such constraint so that the predictions will still be optimal.

Since h is monotone, the equivariance property of quantiles applies, i.e.

$$Q_{Z|X}(p)=h^{-1}\left\{Q_{h\left(Z;{\text{λ}}_p\right)|X}(p);{\text{λ}}_p\right\}.$$ (6)

That is, we can apply the inverse transformation to recover the quantiles on the original scale. If the domain of Z is (a, ∞) or (a, b), then the imputation Z* = Q_Z|X (U) can be linearly mapped to its original domain, i.e. Z* ≡ Z* + a or Z* ≡ a + (b − a) Z*. Therefore, the back-transformation in (6) ensures, without any post hoc adjustment, that the imputations lie within the appropriate range. Note that the latter can be the theoretical range. This represents a valuable advantage of quantile-based imputation over PMM (of which we give a practical demonstration in Sect. 5.2). Finally, model (6) does not depend on the shape of the error distribution (either before or after transformation) and therefore applies to non-normal data. A special case of the imputation model (6) using a logistic transform has been previously suggested by Geraci (2016a). Note that a transformation-based approach would be invalid with standard mean regression since, in general, E(Z) ≠ h⁻¹ {E(h(Z))}. Yet, a common practice is, for example, to back-transform imputations obtained from a mean regression with log(Z) in the presence of skewness or boundary issues (a thorough simulation to investigate related issues is given by Rodwell et al., 2014).

Given these premises, we propose the following MI procedure:

1. Take a bootstrap sample $\left(z_i^B,x_i^B\right)$, i = 1, …, s, with replacement from those with complete data {(z_i, x_i) : i = 1, …, s}.

2. Take a sample u_k for k = s + 1, …, n from a standard uniform distribution and estimate the parameters ${\alpha }_{u_k}$, ${\beta }_{u_k}$ and ${\lambda }_{u_k}$ from

   $$Q_{h\left(Z;{\text{λ}}_{u_k}\right)|X}\left(u_k\right)={\alpha }_{u_k}+x^{\top }{\beta }_{u_k}$$

   using the bootstrap sample $\left(z_i^B,x_i^B\right)$, i = 1, …, s. This task requires obtaining n − s sets of estimates ${\alpha }_{u_k}^{*}$, ${\mathit{\beta }}_{u_k}^{*}$ and ${\text{λ}}_{u_k}^{*}$, one for each uniformly sampled quantile u_k.
3. Finally, obtain the back-transformed quantile-based imputations as

   $$z_k^{*}=h^{-1}\left\{{\alpha }_{u_k}^{*}+x_k^{\top }{\beta }_{u_k}^{*};{\text{λ}}_{u_k}^{*}\right\},$$

   k = s + 1, …, n. Linearly map $Z_k^{*}$ to its original domain as appropriate.

4. Repeat steps (1–3) for M times to obtain M imputations for each unit k = s + 1, …, n.

We would like to stress that the bootstrapping in step 1 above introduces the uncertainty associated with the parameters estimates in the imputation procedure (Rubin and Schenker, 1986). Our approach requires estimating as many sets of quantile-specific parameters as the number of missing values. Although this may seem an inconvenience from a computational point of view, this procedure is in fact very fast when the transformation parameter λ_p is given since it is sufficient to fit a linear quantile model as in Eq. (4) using standard linear programming algorithms (Koenker, 2005). Knowledge of the transformation parameter λ_p is unrealistic in most situations. If λ_p needs to be estimated along with α_p and β_p, computing time will, in general, increase. We therefore examined alternative computational strategies which are discussed in detail in Online Resource 1. The proposed methods are implemented in the R (R Core Team, 2016) package Qtools (Geraci, 2016b, 2017) for which sample code is offered in Online Resource 1. In particular, the sample code shows how the proposed imputation model can be embedded in a chain of imputation models with the R package mice (van Buuren and Groothuis-Oudshoorn, 2011) when several variables are incompletely observed. An approach based on chained equations is used also in Sect. 5.

3.3. Other Transformations for Bounded Variables

In principle, one can consider many transformations. Here, we give a brief overview of only those that have been already proposed in the quantile regression literature and that are appropriate for our purpose. Following our earlier remarks, the transformations should: (i) have appropriate range; (ii) be flexible enough to cover a wide spectrum of situations; (iii) be parsimonious to not excessively burden the estimation.

The Box–Cox transformation (Box and Cox, 1964) applies to singly bounded (strictly positive) variables and has been traditionally used to address the violation of the normal assumptions. This family of transformations has proved to be useful in the empirical determination of functional relationships in QR modelling (Powell, 1991; Buchinsky, 1995; Chamberlain, 1994; Mu and He, 2007). However, the range is still a singly bounded interval (except for λ_p = 0, i.e. the log transformation). This can be an issue when back transforming imputations, since quantiles based on the inverse of the Box–Cox transformation, namely

$$Q_{Z|X}(p)={\left\{{\text{λ}}_p\left({\alpha }_p+x^{\top }{\beta }_p\right)+1\right\}}^{\frac{1}{{\text{λ}}_p}},$$ (7)

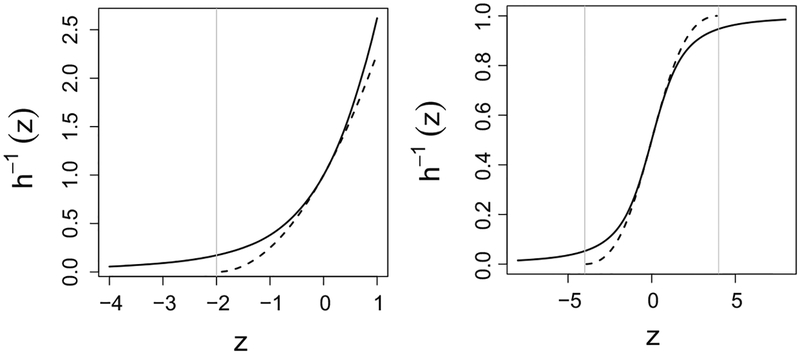
are not defined for λ_p(α_p + x^⊤ β_p) + 1 ≤ 0 when λ_p ≠ 0. If the Box–Cox transformation was used in the imputation procedure as described in the previous section, there would be a risk of having to censor all imputations such that ${\alpha }_{u_k}^{*}+x_k^{\top }{\beta }_{u_k}^{*}\le -1/{\text{λ}}_{u_k}^{*}$, which may occur with probability greater than zero for some data points. An illustration is given in Fig. 2, where the inverse transformations (6) and (7) are plotted for λ = 0.5. As shown in the plot, the Box–Cox transformation is not defined for values less than −2. This problem cannot be prevented using standard linear programming estimation ((Powell, 1991; Buchinsky, 1995; Chamberlain, 1994). However, it can be avoided using residual cusum process estimation (Mu and He, 2007), which computationally has been found to be considerably slow (Geraci and Jones, 2015).

Figure 2.

Left plot: Inverse of the Proposal I transformation for a singly bounded variable (solid line) and Box–Cox transformation (dashed line). Right plot: Inverse of the Proposal I transformation for a doubly bounded variable (solid line) and Aranda-Ordaz transformation (dashed line). The range boundaries of the Box-Cox and Aranda-Ordaz transformations are marked by vertical grey lines.

The Aranda-Ordaz (AO) symmetric and asymmetric transformations were originally proposed to generalise, respectively, the logit and complementary log–log link functions in binomial regression (Aranda-Ordaz, 1981). These have been recently applied to model conditional quantiles of doubly bounded outcomes (Dehbi et al., 2016). The symmetric AO family too suffers from boundary issues since the range of the transformation is still doubly bounded (except for λ_p = 0, i.e. the logit transformation). An illustration of the range problem of the symmetric AO is given in Fig. 2. The asymmetric AO transformation does have range $ℝ$, but we do not include it in our study as it is concave for all λ_p, thus reducing flexibility (Geraci and Jones, 2015).

Lack of appropriate range can cause considerable difficulties for the transformation-based quantile approach, see for example Fitzenberger et al. (2010). To improve over the Box–Cox and the symmetric Aranda-models, Geraci and Jones (2015) proposed the transformation in (5). The ‘Proposal II’ transformation of Geraci and Jones (2015) generalises (5) by including an additional parameter to model asymmetry. As the estimation of a two-parameter transformation would increase the computational burden in our imputation procedure, we do not consider it any further. See Geraci and Jones (2015) for a discussion on alternative, but less flexible transformations.

4. Simulation Study

We carried out a simulation study to assess the performance of the transformation-based QR imputation against commonly used approaches. The ultimate goal of this simulation is to study the impact an imputation model has on the location, scale and shape of the distribution of the imputed variable. This bias may, in turn, propagate to a particular analysis model and cause bias and lower efficiency in the estimators of the parameters of interest. Hence, we first assess the imputation methods in relation to their impact on the distribution of the imputed variable (Sect. 4.1), and then in relation to particular analysis models (i.e. logistic and linear regression models, Sect. 4.2).

Let Y = (Y₁, Y₂, Y₃, Y₄, Y₅) be the matrix of variables in our simulation, with Y₁ ~ U(1, 4), Y₂ ~ N(0, 1), (Y₃|Y₁ = y₁, Y₂ = y₂) ~ N(y₁ + y₂, 1), and Y₄ ~ U(0, 2). The variable Y₅ was generated according to the following models:

• (Model 1) Y₅ = V/(1+V), where V is generated as log(V) = −4+Y₁+Y₂+0.1Y₃+e₁,

• (Model 2) Y₅ = V/(1+V), where V is generated as log(V) = −4+Y₁+Y₂+0.1Y₃+Y₁e₁,

• (Model 3) Y₅ = e₂,

where e₁ ~ N(0, 1) and e₂|Y₄ ~ Beta(0.5, (Y₄ + 4)/10). Therefore, the variable Y₅ is doubly bounded on the unit interval.

We replicated R = 1000 datasets with sample size n ∈ {100, 300, 1000} for each of the three models above. At each replication, observations in the variable Y₅ were randomly deleted with probability

$$p=\frac{e^{1-\alpha V}}{0.2+e^{1-\alpha V}},$$

where V = Y₁ and α = 2 for Models 1 and 2, and V = Y₄ and α = 6 for Model 3.

We consider two different scenarios, one in which λ_p is given, and one in which λ_p is estimated from the data, and the following six imputation methods: normal imputation (LM), log-normal imputation (LMlog), predictive mean matching (PMM), linear quantile regression imputation (QR), and quantile regression imputation based on the symmetric (QRTs) and asymmetric (QRTa) transformation models. QRTs and QRTa were assessed either with λ_p = 0 or with unknown λ_p. The number of imputations M and the number of the Gibbs sampler’s iterations were both set to 5. We used the R packages mice (van Buuren and Groothuis-Oudshoorn, 2011) and Qtools (Geraci, 2016b, 2017). The latter makes use of linear programming algorithms from the quantreg package (Koenker, 2016). For the sake of brevity, we report the results for n = 300 only. Tables and figures for other sample sizes are given in Online Resource 2.

4.1. Assessing Imputation Methods in Relation to the Distribution of the Imputed Variable

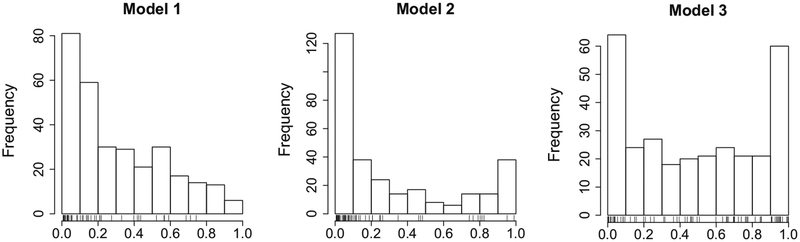
The performance of the imputation methods was first assessed in terms of the bias associated with the estimation of the CDF of Y₅ evaluated at six quantiles with expected probabilities $\mathcal{T}=\text{{}0.01,0.05,\text{0.25},\text{0.5},\text{0.75},\text{0.95}}$. Note that the variable Y₅ in Models 1 and 2 has quantiles that are linear on some transformed scale (Model 2 is heteroscedastic). The distribution of Y₅ in Model 3 is strongly bimodal and cannot be transformed to linearity. Figure 3 shows the histograms depicting the distribution of Y₅ for selected realisations from the different models. Instances of the distribution of missing values according to these MAR mechanisms are depicted by the rug plots in Fig. 3.

Figure 3.

Instances of the doubly bounded variable Y₅ generated under different models. Missing values are marked in the rug plot.

For each imputation method, we estimated ${\widehat{F}}^{(mr)}\left({\overline{q}}_{\tau }\right)$, where ${\widehat{F}}^{(mr)}$ is the empirical CDF (ECDF) of the mth imputed dataset for Y₅ within replication r and

$${\overline{q}}_{\tau }=\frac{1}{R}\sum _{r=1}^R{\widehat{q}}_{\tau }^{(r)},\text{ for }\tau \in \mathcal{T}\text{,}$$

is the τth ‘true’ quantile computed empirically as the average across replications of the sample quantiles ${\widehat{q}}_{\tau }^{(r)}$ from the full dataset. Subsequently, we calculated the relative percentage bias as

$$\frac{1}{R}\sum _{r=1}^R\frac{{\widehat{F}}^{(r)}\left({\overline{q}}_{\tau }\right)-\overline{F}\left({\overline{q}}_{\tau }\right)}{\overline{F}\left({\overline{q}}_{\tau }\right)}\cdot 100,$$

where ${\widehat{F}}^{(r)}\left({\overline{q}}_{\tau }\right)=1/M{\sum }_{m=1}^M{\widehat{F}}^{(mr)}\left({\overline{q}}_{\tau }\right)$ is the Rubin’s estimate of F and $\overline{F}$ is the ‘true’ CDF computed as the average across replications of the ECDFs for Y₅ from the full datasets.

Table 2 shows that, as expected, LM, LMlog and QR failed to produce imputations with appropriate range, as opposed to PMM and transformation-based quantile regression models which always generated imputations within the unit interval. In particular, the log-normal model prevents imputations from being negative but it cannot avoid yielding imputations above one. Notably, log-transforming the bimodal data generated from Model 3 even increased the number of invalid imputations as compared to LM.

Table 2.

Average number of imputations outside the unit interval for the linear model (LM), linear model with log transformation (LMlog) and linear quantile regression model (QR), along with average proportions of missing values for each simulated model. Averages are computed over 1000 replications.

Sample size	Imputation method			Proportion (%) of missing values
	LM	LMlog	QR
Model 1
100	22.9	1.6	18.5	16.9
300	68.1	4.9	55.4	17.2
1000	228.1	15.6	182.4	17.4
Model 2
100	26.3	9.6	10.7	17.3
300	75.9	27.1	24.8	17.5
1000	247.5	88.0	74.7	17.3
Model 3
100	20.8	28.0	10.9	22.4
300	55.8	82.0	17.5	22.3
1000	178.4	271.2	35.1	22.3

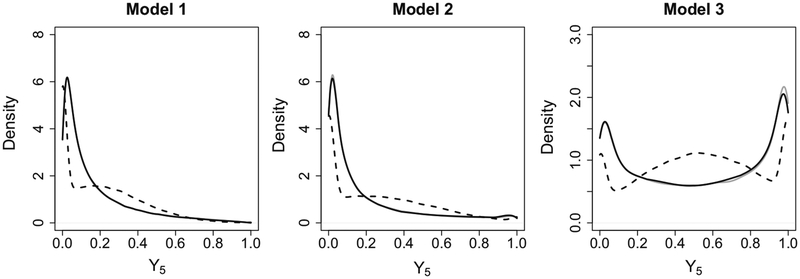
Figure 4 depicts the average estimated density obtained from the full datasets and from the datasets completed with LM and QRTs imputations. The values of out-of-range LM imputations were replaced with closest bounds as suggested by van Buuren and Groothuis-Oudshoorn (2011). While the empirical distribution resulting from the transformation-based QR model naturally mimics the target distribution, to the point that the two overlap, a post hoc constraint on imputations is obviously unable to remedy the misspecification of the distribution.

Figure 4.

Density of ‘true’ missing values in Y₅ (solid grey), density of censored imputations from a linear model (dashed black), and density of imputations from a symmetric transformation model (solid black). The solid lines are nearly indistinguishable as they overlap almost everywhere.

Table 3 shows that LM and QR were heavily biased near the boundaries of the support of Y₅ and performed even worse than the complete-case analysis (CC). The log transformation (LMlog) seemed to improve over the linear models but it was still biased. PMM and transformation-based imputation showed an advantage as compared to CC, LM and LMlog, though their performance was dependent on the data generating model. The bias for QRTs was, in general, smaller than or similar to that of the other approaches when data were generated from Models 1 and 2 and λ_p was fixed. This is not surprising since the symmetric transformation model is correctly specified for λ_p = 0. In contrast, the asymmetric model was overall more competitive under Model 3, and so was PMM. Similar results were obtained for transformation-based quantile imputation models under the assumption of unknown λ_p, except for a larger bias at the quantile 0.01 under Model 1.

Table 3.

Average relative bias (%) at different probabilities of the empirical cumulative distribution of Y₅ (n = 300) for the complete case analysis (CC), normal imputation (LM), log-normal imputation (LMlog), predictive mean matching (PMM), linear quantile regression imputation (QR), and imputation based on the symmetric (QRTs) and asymmetric (QRTa) transformed quantile regression models. The latter were fitted with either (1) known or (2) unknown λ_p.

	CC	LM	LMlog	PMM	QR	QRTs (1)	QRTa (1)	QRTs (2)	QRTa (2)
Model 1
0.01	−30.1	437.0	−34.5	−10.2	354.9	2.2	−11.6	23.0	18.8
0.05	−25.2	59.4	−18.9	−3.3	46.0	0.4	−7.3	11.4	2.2
0.25	−15.9	−4.6	0.5	−0.2	−4.6	0.1	−1.3	1.3	−0.3
0.5	−9.4	−4.4	2.1	0.0	−3.2	0.1	0.4	0.0	0.4
0.75	−4.5	−0.3	0.5	−0.0	−0.1	0.0	0.3	−0.3	0.1
0.95	−0.9	0.1	−0.3	−0.0	0.1	0.0	−0.0	−0.2	−0.1
Model 2
0.01	13.9	459.7	1.2	15.7	151.2	5.1	4.5	5.8	5.2
0.05	5.1	83.6	3.9	10.9	27.2	2.6	1.7	3.4	2.1
0.25	−5.5	−0.1	1.5	3.3	−1.2	0.0	−1.6	0.2	−1.5
0.5	−6.7	−6.6	−0.2	0.1	−3.1	−0.2	−1.1	−0.1	−1.1
0.75	−4.4	−0.5	−1.3	−0.7	−0.4	−0.1	0.0	−0.2	−0.0
0.95	−1.0	−0.1	−1.8	−0.2	0.0	−0.0	0.0	−0.0	−0.0
Model 3
0.01	1.6	109.7	−20.4	−0.6	15.2	4.5	3.5	−0.2	2.8
0.05	2.0	9.8	−10.9	−0.4	3.2	0.7	0.7	1.9	2.3
0.25	2.6	−7.9	11.8	0.5	0.7	0.1	−0.0	0.1	0.1
0.5	2.2	0.1	7.3	0.4	0.2	0.1	−0.1	−0.3	−0.0
0.75	1.7	3.2	0.7	0.5	0.0	0.3	0.1	0.3	0.1
0.95	0.7	−0.6	−4.0	0.3	−0.2	0.3	0.1	0.2	0.0

The simulations results for n = 100 and n = 1000 are reported in Online Resource 2 (Tables 1 and 6, respectively). For n = 100, there was a general worsening of the bias for all imputation methods, although to different extents. The bias for QRTs and QRTa on the lower 5% of the distribution of Y₅ was substantially higher than that for PMM, and indeed higher than that for CC and LMlog. This is not surprising since a relatively small sample with around 20% of missing can hardly provide enough information for accurately estimating tail quantiles of a linear model, let alone those of a nonlinear model. For n = 1000, the results were similar to those for n = 300.

4.2. Assessing Imputation Methods in Relation to the Analysis Model

In this Section, we study the differences in performance between the imputation methods for a particular analysis model. We therefore assessed the performance of LMlog, PMM, QRTs, and QRTa when θ is the regression parameter from either a logistic or a linear model. The reason for considering a logistic model follows from the common practice in psychology, education, epidemiology and related areas to apply cutoffs to continuous scores to classify individuals in separate groups.

In the first analysis, we considered a logistic regression on V ~ Bin(1, π), where $V=I_{Y_5<0.1}$, with the logit of the probability π = Pr(V = 1) defined as

$$\text{log}\frac{\pi }{1-\pi }={\theta }_0+{\theta }_1{Y}_1+{\theta }_2{Y}_2+{\theta }_3{Y}_3$$

under Models 1 and 2 or as

$$\text{log}\frac{\pi }{1-\pi }={\theta }_0+{\theta }_1{Y}_4$$

under Model 3.

In the second analysis, we considered a linear regression on V ~ N(μ, ω²), with V = Y₂ and μ = θ₀ + θ₁Y₁ + θ₂Y₃ + θ₃Y₅ under Models 1 and 2, or V = Y₄ and μ = θ₀ + θ₁Y₅ under Model 3.

The estimates ${\widehat{\theta }}_l^{(mr)}$, l = 0, 1, 2, 3, at each replication r were pooled across imputations

$${\widehat{\theta }}_l^{(r)}=\frac{1}{M}\sum _{m=1}^M{\widehat{\theta }}_l^{(mr)},$$

while standard errors were obtained from

$${\widehat{\sigma }}_l^{(r)}=\sqrt{{\widehat{\varphi }}_l^{(r)}+\left(1+\frac{1}{M}\right){\widehat{\psi }}_l^{(r)}},$$

where ${\widehat{\varphi }}_l^{(r)}=1/M{\sum }_{m=1}^M{\widehat{\varphi }}_l^{(mr)}$ is the average within-imputation variance, ${\widehat{\varphi }}_l^{(mr)}$ is the model’s estimated variance for ${\widehat{\theta }}_l^{(mr)}$, and ${\widehat{\psi }}_l^{(r)}=1/(M-1){\sum }_{m=1}^M{\left({\widehat{\theta }}_l^{(mr)}-{\widehat{\theta }}_l^{(r)}\right)}^2$ is the between-imputation variance. For each replication, we calculated the relative differences of the estimates ${\widehat{\theta }}_l^{(r)}$ and ${\widehat{\sigma }}_l^{(r)}$ as compared to those from the logistic regressions on the full datasets. The relative differences were averaged across replications. Finally, the ‘empirical’ coverage at the nominal level of 95% was calculated as the mean proportion of 95% confidence intervals that included the full dataset estimates.

In Table 4, CC, LMlog, PMM and QRT imputation are compared in relation to the estimates and standard errors from logistic regression. There is sign that PMM struggles with larger biases under more complex data generating scenarios (Models 2 and 3). Moreover, the variability associated with PMM, which is higher than the full-data variability as a natural consequence of the MI procedure, seems perhaps too high under the strongly nonlinear Model 3. This behaviour of PMM represents an interesting finding which we observed also in the real data analysis (Sect. 5.1). Coverage was not far from the nominal 95% in most cases (Table 5). The imputation based on a log-linear model performed poorly, with a rate of 83%. PMM showed signs of under-coverage at 91% in the third scenario, which seems to be a consequence of the larger bias. The simulations results for n = 100 and n = 1000 are reported in Online Resource 2 (Tables 2–3 and Tables 7–8, respectively). At n = 100 and n = 1000, the relative merits and demerits of each method were not much dissimilar from those at n = 300 except that, for the largest sample size, PMM showed a better coverage in the third scenario as a result of a substantially larger variability.

Table 4.

The first two columns show the pooled estimated coefficients and standard errors (SE) from the logistic regressions on $\mathrm{Pr}\left(I_{Y_5<0.1}\right)$ (n = 300) using the full datasets (FD). The remaining columns show the average relative differences (%) as compared to those from FD for the complete case analysis (CC), log-normal imputation (LMlog), predictive mean matching (PMM), and symmetric (QRTs) and asymmetric (QRTa) transformed quantile regression imputation models. The latter were fitted with either (1) known or (2) unknown λ_p.

	FD		CC		LMlog		PMM		QRTs (1)		QRTa (1)		QRTs (2)		QRTa (2)
	Est.	SE	Est.	SE	Est.	SE	Est.	SE	Est.	SE	Est.	SE	Est.	SE	Est.	SE
Model 1
θ0	3.3	0.6	1.0	24.0	2.3	22.0	0.0	21.1	0.2	21.2	−5.3	21.1	2.9	21.7	−3.4	21.7
θ1	−1.8	0.3	1.0	16.6	0.6	14.9	0.2	14.7	0.4	14.8	−4.0	14.0	2.0	15.2	−2.8	14.4
θ2	−1.8	0.3	1.3	14.6	−3.0	12.6	−0.0	13.4	0.4	13.5	−4.5	12.8	1.1	13.9	−4.1	13.0
θ3	−0.2	0.2	0.1	14.6	−2.6	13.9	−1.2	14.3	−1.4	13.7	−5.6	12.8	−0.3	14.1	−5.8	13.3
Model 2
θ0	1.1	0.4	−14.1	23.6	−6.5	22.7	6.4	27.4	−0.5	23.1	−13.8	22.8	1.1	23.5	−13.6	22.7
θ1	−0.6	0.2	−8.7	13.9	−4.3	13.5	4.9	16.4	0.4	14.7	−8.0	14.7	1.5	15.0	−7.8	14.4
θ2	−0.8	0.2	−7.6	9.5	−10.5	9.8	−8.0	10.0	−0.4	11.5	−4.9	11.0	−0.1	11.1	−5.0	10.9
θ3	−0.1	0.1	−10.2	10.3	−16.1	10.4	−12.2	11.5	−3.8	12.5	−8.9	11.5	−4.8	11.7	−9.7	11.9
Model 3
θ0	−1.5	0.3	0.4	49.5	−24.9	38.4	5.2	97.1	2.6	55.8	2.8	55.8	3.0	54.7	2.5	55.7
θ1	0.2	0.3	1.2	34.5	−159.2	28.5	29.6	70.5	15.2	39.3	16.6	39.3	17.8	38.3	14.5	39.2

Table 5.

Joint coverage at the nominal 95% level for the parameters of the logistic regressions on $\mathrm{Pr}\left(I_{Y_5<0.1}\right)$ (n = 300) for the complete-case analysis (CC), log-normal imputation (LMlog), predictive mean matching (PMM), and symmetric (QRTs) and asymmetric (QRTa) transformed quantile regression imputation models. The latter were fitted with either (1) known or (2) unknown λ_p.

	CC	LMlog	PMM	QRTs (1)	QRTa (1)	QRTs (2)	QRTa (2)
Model 1	94.7	97.2	95.5	97.5	96.1	97.5	97.0
Model 2	95.0	96.4	95.7	96.0	95.9	96.2	95.4
Model 3	94.8	83.4	91.3	93.2	93.4	92.9	92.8

In Table 6, the imputation methods are compared in relation to the estimates and standard errors from linear regression, while coverage is reported in Table 7. Of the three scenarios, the third seemed to be most challenging for all methods. In particular, CC and LMlog performed worst in terms of bias and coverage, followed by PMM which, as in the logistic regression analysis, showed some under-coverage. Analogous results were observed for n = 100 and n = 1000 (Tables 4–5 and Tables 9–10, respectively, in Online Resource 2).

Table 6.

The first two columns show the pooled estimated coefficients and standard errors (SE) from the linear regressions on Y₂ for Models 1 and 2 or Y₄ for Model 3 (n = 300) using the full datasets (FD). The remaining columns show the average relative differences (%) as compared to those from FD for the complete-case analysis (CC), log-normal imputation (LMlog), predictive mean matching (PMM), and symmetric (QRTs) and asymmetric (QRTa) transformed quantile regression imputation models. The latter were fitted with either (1) known or (2) unknown λ_p.

	FD		CC		LMlog		PMM		QRTs (1)		QRTa (1)		QRTs (2)		QRTa (2)
	Est.	SE	Est.	SE	Est.	SE	Est.	SE	Est.	SE	Est.	SE	Est.	SE	Est.	SE
Model 1
θ0	0.2	0.1	13.6	23.6	−5.0	9.9	−1.3	3.7	0.6	3.6	0.7	3.8	−3.6	5.2	0.3	4.3
θ1	1.9	0.2	−1.3	5.8	−10.5	59.3	−0.2	3.4	0.3	4.0	−0.7	4.9	−1.3	7.0	−1.1	5.4
θ2	−0.6	4.9 · 10−2	−0.2	14.2	−1.9	16.6	−0.1	3.5	0.1	3.4	0.3	3.7	−0.7	5.1	0.0	4.1
θ3	0.3	2.9 · 10−2	−1.8	9.9	4.8	17.6	0.2	2.3	−0.1	2.5	1.0	2.9	0.2	3.6	0.8	3.2
Model 2
θ0	1.8 · 10−2	0.1	−39.7	25.1	−223.0	3.7	−41.9	1.3	−15.2	0.7	−38.4	0.9	−19.1	0.8	−39.9	0.9
θ1	0.5	0.1	−9.1	5.0	−58.1	33.4	−4.6	5.4	−0.9	5.7	−3.2	5.9	−1.3	5.6	−3.4	5.8
θ2	−0.5	0.1	−1.2	15.5	−7.0	4.6	−0.7	1.1	−0.2	0.8	−0.5	0.9	−0.3	0.8	−0.5	0.9
θ3	0.5	2.9 · 10−2	0.6	10.1	3.8	5.4	0.5	0.9	0.1	0.8	0.4	0.8	0.1	0.9	0.4	0.8
Model 3
θ0	1.1	0.1	16.7	−5.0	−2.8	−22.5	−0.2	52.8	−0.0	28.8	0.2	30.7	0.3	31.2	0.2	30.8
θ1	−0.1	0.1	−29.0	−3.6	−58.8	−46.2	−10.7	69.1	−4.0	38.2	−0.1	40.2	1.3	40.8	0.1	40.4

Table 7.

Joint coverage at the nominal 95% level for the parameters of the linear regressions on Y₆ (n = 300) for the complete-case analysis (CC), log-normal imputation (LMlog), predictive mean matching (PMM), and symmetric (QRTs) and asymmetric (QRTa) transformed quantile regression imputation models. The latter were fitted with either (1) known or (2) unknown λ_p.

	CC	LMlog	PMM	QRTs (1)	QRTa (1)	QRTs (2)	QRTa (2)
Model 1	94.0	95.1	94.0	94.4	94.8	94.7	94.7
Model 2	94.8	83.3	95.2	95.0	95.1	94.9	95.0
Model 3	51.9	78.0	90.0	93.6	92.2	93.5	92.7

In conclusion, the proposed methods seem to have an advantage when the sample size is moderate to large, and the true generating model is strongly nonlinear.

5. Examples

5.1. Celtic Country Teacher Survey Data

In this section, we examine the CCTS data introduced previously. For imputation purposes, we considered the following variables: child’s MD score as calculated from the teacher’s questionnaire, child’s sex (binary; baseline: boy), maternal age at child’s birth (age.mother, binary; baseline: 30 years or less), mother’s ethnicity (ethnicity.mother, binary; baseline: white), number of children previously born alive to the mother (parity, binary; baseline: nulliparous), gestational age (gestational.age, binary; baseline: preterm, i.e. ≤ 37 weeks), relationship status of parents/carers (marital.status, binary; baseline: married or cohabiting), educational level of each parent (edu.mother and edu.father, binary; baseline: General Certificate of Secondary Education – GCSE – or higher), and household income category (four groups; baseline: less than 10,400 British pounds per annum). Data were abstracted for 7019 singletons. MD score had the highest proportion of missing values (54.3%), followed by father’s education (31.8%), income (9.3%), gestational age (2.3%), mother’s education (1.9%), ethnicity (1.7%), mother’s age at birth (1.5%), parity and sex (1.4%). Marital status was completely observed. A QR analysis of these data is given in Geraci and Jones (2015), while data for children living in England have been analysed by Mensah and Kiernan (2010) using Tobit regression. In both studies, incomplete observations were removed.

We imputed missing values (M = 5) using the package mice (van Buuren and Groothuis-Oudshoorn, 2011). Missing categorical values were imputed by means of dichotomous and polytomous logistic regression. Missing MD scores were imputed using either normal imputation (LM), or log-normal imputation (LMlog), or predictive mean matching (PMM), or quantile regression based on the symmetric transformation model (QRT). For the latter, the unknown transformation parameter was estimated as discussed in Online Resource 1. The columns of the matrix feeding the MICE algorithm were sorted in increasing amount of missingness (i.e. monotone visiting sequence) and the number of the Gibbs sampler’s iterations was set to 5.

The results were in line with our simulation study. LM and LMlog were not able to capture the shape of the observed distribution and produced imputations outside the admissible range (see Fig. 1 in Online Resource 2). This obviously represents a potential source of bias for an analysis based on the completed datasets obtained from these methods. In contrast, PMM and QRT performed remarkably well in terms of both preserving the shape of the distribution of MD scores and giving imputations within bounds.

Once the imputation procedure has been carried out, one can perform an analysis on each of the completed datasets and then pool the results using Rubin’s rules. By way of example, we considered a logistic model for the probability π = Pr (I_MD.score>22), i.e. the probability of achieving more than 80% of the total MD score. (Of course, a similar analysis could be performed on the probability of a low achievement.) The covariates were entered in the model as follows:

$$\begin{gathered} \text{log}\frac{\pi }{1-\pi }={\theta }_0+{\theta }_1\text{sex}+{\theta }_2\text{age.mother}+{\theta }_3\text{ethnicity.mother} \\ +{\theta }_4\text{parity}+{\theta }_5\text{gestational.age}+{\theta }_7\text{marital.status} \\ +{\theta }_8\text{edu.mother}+{\theta }_9\text{edu.father}+{\theta }_{10}{\text{income}}_{(10400-20800]} \\ +{\theta }_{11}{\text{income}}_{(20800-31200]}+{\theta }_{12}{\text{income}}_{(31200+]}. \end{gathered}$$

We are interested in comparing the results of the logistic regression analysis based on the LMlog, PMM, and QRT imputations. In Table 8, we report, for each method, the estimated regression coefficients and standard errors.

Table 8.

Estimated coefficients, standard errors (SE) and p values from the logistic regression analysis of the Celtic Country Teacher Survey data for the complete-case analysis (CC), log-normal imputation (LMlog), predictive mean matching (PMM), and imputation based on the transformed quantile regression model (QRT).

	CC		LMlog		PMM		QRT
	Est. (SE)	p-value	Est. (SE)	p-value	Est. (SE)	p-value	Est. (SE)	p-value
Intercept	0.45 (0.24)	0.059	0.00 (0.16)	0.994	0.41 (0.25)	0.156	0.51 (0.29)	0.138
Sex	0.17 (0.09)	0.066	0.20 (0.09)	0.070	0.32 (0.10)	0.014	0.26 (0.06)	< 0.001
Age.mother	0.21 (0.10)	0.033	0.06 (0.09)	0.527	0.08 (0.13)	0.551	0.19 (0.06)	0.002
Ethnicity.mother	0.19 (0.33)	0.575	−0.05 (0.27)	0.873	0.14 (0.23)	0.544	0.22 (0.22)	0.335
Parity	−0.23 (0.10)	0.016	−0.15 (0.08)	0.074	−0.15 (0.07)	0.058	−0.29 (0.07)	0.001
Gestational.age	−0.22 (0.19)	0.259	0.02 (0.13)	0.877	−0.12 (0.17)	0.503	−0.12 (0.20)	0.578
Marital.status	−2.15 (0.78)	0.006	−0.24 (0.09)	0.011	−0.17 (0.14)	0.261	−0.23 (0.18)	0.248
Edu.mother	−0.23 (0.15)	0.123	−0.28 (0.10)	0.016	−0.36 (0.15)	0.053	−0.36 (0.10)	0.004
Edu.father	−0.34 (0.12)	0.006	−0.29 (0.15)	0.109	−0.45 (0.08)	< 0.001	−0.43 (0.12)	0.008
Income (10400–20800]	0.38 (0.16)	0.015	0.32 (0.13)	0.029	0.30 (0.20)	0.185	0.32 (0.13)	0.029
Income (20800–31200]	0.55 (0.17)	0.001	0.40 (0.12)	0.002	0.38 (0.27)	0.215	0.45 (0.22)	0.082
Income (31200+]	0.81 (0.18)	< 0.001	0.59 (0.14)	0.001	0.64 (0.17)	0.004	0.65 (0.19)	0.008

According to the complete-case (CC) analysis, the probability of high (> 22) MD scores was larger for females, for children born to older mothers, and for those born to nulliparous mothers. Children in families with married or cohabiting parents, and parents with more advanced education and higher income, were also more likely to score higher in mathematical development. The large p values for ethnicity and gestational age provided evidence against a meaningful role of these two covariates. As compared to CC, the pooled coefficients based on LMlog imputations gave similar directions of the associations. However, the magnitudes of ${\widehat{\theta }}_0$ (intercept), ${\widehat{\theta }}_2$ (maternal age at child’s birth), and ${\widehat{\theta }}_6$ (marital status) were notably smaller and, in general, p values were larger.

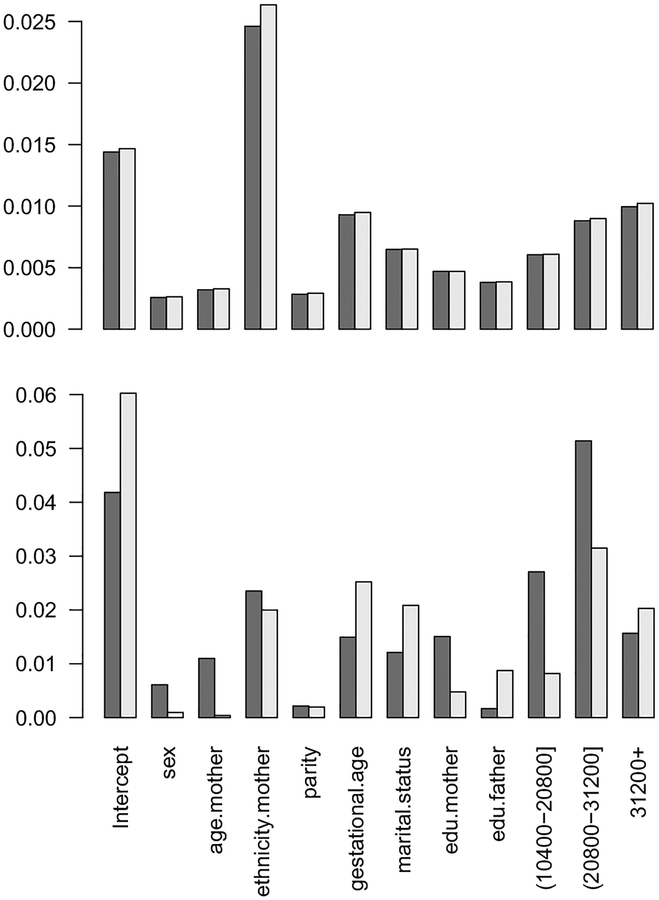
PMM and QRT seemed to be consistent in terms of the magnitude and direction of most estimates except for ${\widehat{\theta }}_2$ (maternal age), ${\widehat{\theta }}_3$ (mother’s ethnicity), and ${\widehat{\theta }}_4$ (parity) which were larger in magnitude for QRT. Also, there was a disagreement between PMM and QRT in relation to the statistical significance of the estimates, with occasionally larger standard errors and, consequently, larger p values for PMM. Previous studies (Machin and McNally, 2005; Kiernan and Mensah, 2009; Mensah and Kiernan, 2010) showed that maternal age, maternal education, and household income are important predictors of educational attainment. The results based on QRT agree with those findings. However, PMM leads to estimates whose practical and/or statistical significance suggests the opposite. Further investigation revealed that PMM had similar within-imputation variance as compared to QRT but relatively larger between-imputation variance for these variables (Fig. 5). Such results mirror our findings in Sect. 4.

Figure 5.

Barplots of the average within-imputation variance (top) and the between-imputation variance for predictive mean matching (dark grey) and transformation-based quantile regression (light grey) for the Celtic Country Teacher Survey data.

We conclude this section with a brief report on diagnostics. We ran the MICE algorithm with 5 imputations and 20 Gibbs sampler’s iterations to assess convergence over a longer stretch of iterations as suggested by van Buuren and Groothuis-Oudshoorn (2011). All the chains showed convergence already at the fifth iteration for all the imputation methods considered above. The results for MD scores are shown in Online Resource 2 (Figures 2 and 3).

5.2. Reisby’s Data on Depression Scores

In this section, we briefly give a demonstration of a specific advantage of our approach as compared to PMM when predictions are to be made on a theoretical (rather than observed) range. We considered data that were obtained in a psychiatric study described in Reisby et al. (1977). The aim of the study was to evaluate the longitudinal (over several weeks) relationship between imipramine and desipramine plasma levels and clinical response in 66 depressed inpatients. Subjects were rated with the Hamilton Depression Rating Scale (HDRS) whose theoretical range is 0 to 52 (Bech and Rafaelsen, 1980).

We had information on HDRS scores at baseline (week 0) and for 5 weekly follow-ups. There was a small number of missing values (5 at week 0, 3 at week 1, 1 at week 2, 1 at week 3, 3 at week 4, and 8 at week 5). The only complete covariate at our disposal was the sex of the patients.

For imputation, we considered the model

$$Q{h}_{\left({\text{HDRS}}_t;{\text{λ}}_p\right)|\text{HDRS}t-1,\text{sex}}(p)={\beta }_{0,p}+{\beta }_{1,p}{\text{HDRS}}_{t-1}+{\beta }_{2,p}\text{sex}$$

where h is the symmetric Proposal I transformation for doubly bounded variables, and HDRS_t, t = 1, …, 5, is the HDRS score at week t. This model implies that HDRS_t depends only on the previous measurement HDRS_t−1, a simplification which can be easily relaxed.

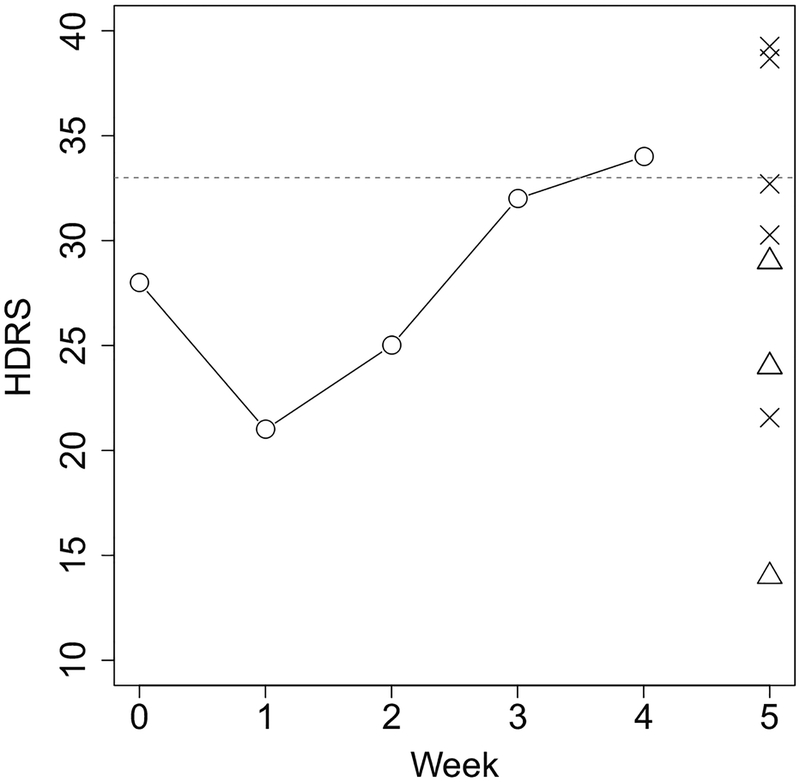
We report the results for one patient (ID 322) who had missing HDRS score at week 5. The observed values for this patient up to week 4 are shown in Fig. 6. Five imputed values at week 5 from our quantile-based approach and from PMM are marked with crosses and triangles, respectively. It is clear that this patient experienced an upward trend between baseline and the last observed follow-up. Our approach yielded imputations that, on average, were consistent with this trend. In contrast, the PMM imputations seemed to be excessively low given the temporal trajectory of this patient’s scores. This is not surprising since, at week 5, the upper bound of the observed scores for all 58 subjects was 33, with only 5 observations between 24 and 33. In other words, transformed quantile regression imputation allows for extrapolation outside the observed range, but within the theoretical range. The inability of PMM to deal with extrapolation as well as interpolation has been discussed by others (see for example de Jong et al., 2016).

Figure 6.

Hamilton Depression Rating Scale (HDRS) scores for subject with ID 322 in the Reisby’s dataset. Circles represent observed values, while imputations from transformation-based quantile regression and predictive mean matching are marked with, respectively, crosses and triangles. The horizontal dashed line marks the upper bound of the scores for all subjects observed at week 5.

6. Conclusion

We investigated the problem of missing values in bounded variables which seems to be underestimated in the statistical literature. In our simulation study, predictive mean matching proved to be competitive and represents a useful tool at the imputer’s disposal. However, our newly developed approach based on transformed quantile regression had some advantages over the other methods in selected scenarios. In particular, our method showed lower bias and smaller between-imputation variance. As compared to predictive mean matching, transformation-based quantile imputation is computationally more demanding, especially when the transformation parameter is estimated from the data. However, we introduced a novel gradient search algorithm for nonlinear estimation which showed good numerical stability and computing speed. Moreover, it is not guaranteed that the proposed imputation is proper (Nielsen, 2003), although simulation results suggest that our method has randomisation validity (Rubin, 1987, pp. 117–118). Finally, when the sample size is small, quantile-based imputation does not seem to bring appreciable benefits (or losses) as compared to other imputation methods, although it is still preferable to a complete-case analysis when the bounded variable is affected by MAR and is used as predictor.

Of course, since it is not possible to establish a ‘one-size-fits-all’ imputation approach, best practice suggests conducting sensitivity analyses. Having said that, we believe that multiple imputation approaches based on linear models with support over the real line, transformed mean regression and post hoc adjustments like censoring should be avoided altogether. The proposed methods can accommodate different distributions and boundary types and can be readily applied using the Qtools package in R.