Abstract
Selecting between competing Structural Equation Models (SEMs) is a common problem. Often selection is based on the chi square test statistic or other fit indices. In other areas of statistical research Bayesian information criteria are commonly used, but they are less frequently used with SEMs compared to other fit indices. This article examines several new and old Information Criteria (IC) that approximate Bayes Factors. We compare these IC measures to common fit indices in a simulation that includes the true and false models. In moderate to large samples, the IC measures outperform the fit indices. In a second simulation we only consider the IC measures and do not include the true model. In moderate to large samples the IC measures favor approximate models that only differ from the true model by having extra parameters. Overall, SPBIC, a new IC measure, performs well relative to the other IC measures.
Keywords: Bayes Factor, Structural Equation Models, BIC, Chi-Square Tests, Model Fit, Model Selection
1. Introduction
Structural equation models (SEMs) refer to a widely used general class of statistical models. SEMs are well-established in the social and behavioral sciences, and are diffusing to the health and natural sciences (e.g., Bentler and Stein 1992; Shipley 2000; Schnoll et al. 2004; Beran and Violato 2010). Key issues in the use of SEMs are determining the fit of the model to the data and comparing the relative fit of two or more models to the same data. An asymptotic chi-square distributed test statistic that tests whether a SEM exactly reproduces the covariance matrix of observed variables was the first test and index of model fit (Jöreskog 1969, 1973). However, given the approximate nature of most models and the enhanced statistical power that generally accompanies a large sample size, the chi-square test statistic routinely rejects models in large samples regardless of their merit as approximations to the underlying process. Starting with Tucker and Lewis (1973) and Jöreskog and Sörbom (1979), a variety of fit indices have been developed to supplement the chi-square test statistic (see Bollen and Long 1993). Controversy surrounds these alternative fit indices for several reasons. For example, the sampling distribution of a particular fit index is often not known. Additionally, sometimes the fit index tends to increase as sample size increases (Bollen 1989, 269–281). Finally, there is disagreement about the optimal cutoff values for a “well-fitting” model.
Researchers frequently use the Bayesian Information Criterion (BIC) to compare the fit of models in multiple regression, generalized linear models, and several other areas of statistical modeling (Raftery 1995). Yet despite this common use, the BIC has received little attention in the SEM literature. Cudeck and Browne (1983) and Bollen (1989) give only brief mention to Schwarz’s (1978) BIC as an approximation to the Bayes Factor. Raftery (1993, 1995) provides more discussion of the BIC in SEMs, as do Homburg (1991) and Haughton et al. (1997). However, compared to the RMSEA, CFI, or other fit indices, it is less common to see the BIC in applications of SEMs, despite its potential value in comparing the fit of competing models. It is known that asymptotically the BIC should choose the true model structure when it is included among the choices (e.g., Hannan and Quinn 1979), but this tells us little about how the BIC works in small to moderate sized samples. Furthermore, we know of no study that examines the BIC in SEM model selection when none of the candidate models is the true model, which is the most common situation in applied research.
The primary purpose of this article is to examine the performance of different Information Criteria (IC) based on Bayes Factors in model selection in SEM. We compare the BIC, the Haughton Bayesian Information Criterion (HBIC, see Haughton 1988), and two new IC measures: the Information Matrix-Based Information Criterion (IBIC) and the Scaled Unit Information Prior Bayesian Information Criterion (SPBIC, see Bollen et al. 2012). In the course of presenting the IBIC and SPBIC, we explain their potential use in choosing among models.1 Bollen et al. (2012) present the theoretical justifications for the IBIC and SPBIC, but they only examine them in a multiple regression context; no one has examined them in the context of SEMs. Our analysis is restricted to IC-based approximations to the Bayes Factor; we do not attempt a fully Bayesian analysis. In so doing, we follow the practice of the vast majority of social and behavioral scientists working with other types of statistical models beyond SEM.2
Our simulation has two parts: 1) when the true model is among the choices and 2) when all models are approximations. The first simulation compares the success of the BIC, HBIC, IBIC, SPBIC, and more common SEM fit indices in finding the true model across sample sizes ranging from 100 to 5000. Asymptotically, the BIC, HBIC, IBIC, and SPBIC should select the true model, but we do not know their behavior in small to moderate sample sizes. In addition, we have no information on which, if any of the IC measures, approach their asymptotic behavior more quickly. The second simulation addresses the behavior of the IC measures when the true model is not in the pool of models.
The next section introduces the SEM equations and assumptions and reviews the current methods of assessing SEM model fit. Following this is a section in which we present the Bayes Factor, the BIC, and the HBIC, IBIC, and SPBIC. We then describe our Monte Carlo simulation study that examines the behavior of various model selection criteria for a series of models that are either correct, underspecified, or overspecified. An empirical example then illustrates the IC measures in model selection. Finally, we conclude with a discussion of the implications of the results and recommendations for researchers.
2. Structural Equation Models and Fit Indices
SEMs have two primary components: a latent variable model and a measurement model. We write the latent variable model3 as:
| (1) |
The n vector is m × 1 and contains the m latent endogenous variables. The intercept terms are in the m × 1 vector of αη. The m × m coefficient matrix B gives the effect of the ηs on each other. The n latent exogenous variables are in the n × 1 vector ξ. The m × n coefficient matrix Γ contains the coefficients for ξ’s impact on the ηs. An m × 1 vector ζ contains the disturbances for each latent endogenous variable. We assume that E(ζ) = 0, COV (ζ, ξ) = 0, and we assume that the disturbance for each equation is homoscedastic and nonautocorrelated across cases, although the variances of ζs from different equations can differ and these ζs can correlate across equations. The m × m covariance matrix Σζζ has the variances of the ζs down the main diagonal and the across equation covariances of the ζs on the off-diagonal. The n × n covariance matrix of ξ is Σξξ.
The measurement model is:
| (2) |
| (3) |
The p × 1 vector y contains the indicators of the ηs. The p × m coefficient matrix Λy (the “factor loadings”) give the impact of the ηs on the ys. The unique factors or errors are in the p × 1 vector ε. We assume that E(ε) = 0 and COV(η, ε) = 0. The covariance matrix for the ε is Σεε. There are analogous definitions and assumptions for measurement Equation 3 for the q × 1 vector x. We assume that ζ, ε, and δ are uncorrelated with ξ and in most models these disturbances and errors are assumed to be uncorrelated among themselves, though the latter assumption is not essential.4 We also assume that the errors are homoscedastic and nonautocorrelated across cases.
In these models, the covariance matrix (Σ) and the mean vector (μ) are functions of the parameters of the model. These are the implied covariance matrix [Σ(θ)] and the implied mean vector [μ(θ)] where θ is a vector that contains all parameters of a model including coefficients, means, variances, and covariances. General expressions for Σ(θ) and μ(θ) are available in several sources (e.g., Bollen 1989) and by substituting the parameters that apply to a specific model the implied moments are available for this model. If a model is true, then:
| (4) |
and
| (5) |
The log likelihood of the maximum likelihood (ML) estimator, derived under the assumption that z, which is the combined vector for the data (x and y), comes from a multinormal distribution, is
| (6) |
where K is a constant that has no effect on the values of θ that maximize the log likelihood.
The chi-square test statistic derives from a likelihood ratio test of the hypothesized model to a saturated model where the covariance matrix and mean vector are exactly reproduced. The null hypothesis of the chi-square test is that Equations 4 and 5 hold exactly. In large samples, the likelihood ratio (LR) test statistic follows a chi-square distribution when the null hypothesis is true. Excess kurtosis can affect the test statistic, though there are various corrections that, among other things, address excess kurtosis (Satorra and Bentler 1988; Bollen and Stine 1992). In practice, the typical outcome of this test in large samples is rejection of the null hypothesis that represents the model. This often occurs even when corrections for excess kurtosis are made. At least part of the explanation is that the null hypothesis assumes exact fit whereas in practice we anticipate at least some inaccuracies in our modeling. The significant LR test simply reflects what we know: our model is at best an approximation. If the model is approximately correct and no other assumptions are violated, the large sample distribution of the test statistic is a noncentral chi-square distribution, its shape governed by a noncentrality parameter and the degrees of freedom (for example, see Cudeck and Browne 1983).
In response to the common rejection of the null hypothesis of perfect fit, researchers have proposed and used a variety of fit indices. The Incremental Fit Index (IFI, Bollen 1989), Comparative Fit Index (CFI, Bentler 1990), Tucker-Lewis Index (TLI, Tucker and Lewis 1973), Relative Noncentrality Index (RNI, Bentler 1990; McDonald and Marsh 1990), and Root Mean Squared Error of Approximation (RMSEA, Steiger and Lind 1980) are just a few of the many indices of fit that have been proposed. Though the popularity of each has waxed and waned, there are problems characterizing all or most of these. One is that there is ambiguity as to the proper cutoff value to signify that a model has an acceptable fit. Different authors recommend different standards of good fit and in nearly all cases the justification for cutoff values are not well founded. Second, the distributions of most of these fit indices are not given. Thus, with the exception of the RMSEA, confidence intervals for the fit indices are not provided. Third, the fit indices that are based on comparisons to a baseline model (e.g., TLI, IFI, RNI) can behave somewhat differently depending on the fitting function used to estimate a model (Sugawara and MacCallum 1993). This suggests that standards of fit should be adjusted depending on the fitting function employed. An additional problem is that the means of the sampling distributions of some measures tend to be larger in bigger samples than in smaller ones even if the identical model is fitted (e.g., Bollen and Long 1993). Thus, cutoff values for such indices might need to differ depending on the size of the sample.
Another set of issues arise when comparing competing models for the same data. If the competing models are nested, then a LR test that is asymptotically chi-square distributed is available. However, in such a case, the issue of statistical power in small samples remains. Furthermore, the LR test is not available for nonnested models. Finally, other factors such as excess kurtosis can impact the LR test. The situation is not made better by employing other fit indices. Though we can take the difference in the fit indices across two or more models, there is little guidance on what to consider as a sufficiently large difference to conclude that one model’s fit is better than another. In addition, the standards might need to vary depending on the estimator employed and the size of the sample for some of the fit indices. Nonnested models further complicate these comparisons since the rationale for direct comparisons of nonnested models for most of these fit indices is not well-developed.
This brief overview of the LR test and the other fit indices in use in SEMs reveals that there are drawbacks to the current methods of assessing the fit of models. It would be desirable to have a method to assess fit that worked for nested and nonnested models and that had a rationale in statistical theory. From a practical point of view, it is desirable to have a measure that is calculable using standard output from SEM software. In the next section, we examine the Bayes Factor and methods to approximate it that address these criteria.
3. Approximating Bayes Factors in SEMs
The Bayes Factor expresses the odds of observing a given set of data under one model versus an alternative model. For any two models 2 and 1, the Bayes Factor, B21, is the ratio of P(Y|Mk) for two different models, where P(Y|Mk) is the probability of the data Y given the model, Mk. More explicitly, the Bayes Factor, B21, is
| (7) |
Conceptually, the Bayes Factor is a relatively straightforward way to compare models, but it can be complex to compute.5 The marginal likelihoods must be calculated for the competing models. Following Bayes’ Theorem, the marginal likelihood (also known as the integrated likelihood) can be expressed as a weighted average of the likelihood of all possible parameter values under a given model.
| (8) |
where θk is vector of parameters of Mk, P(Y | θk, Mk) is the likelihood under Mk, and P(θk | Mk) is the prior distribution of θk.
Closed-form analytic expressions of the marginal likelihoods are difficult to obtain, and numeric integration is computationally intensive with high dimensional models. Approximation of this integral via the Laplace method and the use of modern computing technology help solve this problem. Technical details of the Laplace method can be found in many sources, including Kass and Raftery (1995). In brief, a second order Taylor expansion of the log P(Y|Mk) around the ML estimator leads to the expression in Equation 9, where is the log likelihood function (i.e., ), is the expected information matrix, dk is the dimension (number of parameters) of the model, and O(N−1/2) is the approximation error, and N is the sample size.
| (9) |
This equation forms the basis for several approximations to the Bayes Factor. Here we briefly present the equations for several approximations, including Schwarz’s BIC, Haughton’s BIC, IBIC, and SPBIC. Derivations and justifications for these equations can be found in Bollen et al. (2012). Here our goal is simply to present the final equations, show their relationships to each other, and explain how they can be calculated for SEM models using standard output from software.
The Standard Bayesian Information Criterion (BIC)
Schwarz’s (1978) BIC drops the second, third, and fifth terms of Equation 9, on the basis that in large samples, the first and fourth terms will dominate in the order of error. Ignoring these terms gives
| (10) |
If we multiply this by 2, the BIC for M2 and M1 is calculated as
| (11) |
In SEMs the usual chi-square test statistic is based on a likelihood ratio test of the hypothesized model (say M1) compared to the saturated model (say Ms). Setting the saturated model to M2 and the hypothesized model to M1, we can write the BIC in terms of the usual chi-square test statistic and its degrees of freedom (df) using equation (11) as
| (12) |
where Tml is the chi-square test statistic using the ML estimator and df is the corresponding degrees of freedom for the model.
An advantage of the BIC is that it does not require specification of priors and it is readily calculable from standard output of most statistical packages. In the case of SEMs, all that is needed are the chi-square test statistic (Tml) of the model, its degrees of freedom (df), and the sample size (N) to calculate it. In addition, using equation (12), a value of BIC greater than zero supports the saturated model over the hypothesized model whereas a negative BIC supports the hypothesized model (Raftery, 1995). Sometimes the BIC value is calculated without a comparison to a saturated or other model based on equation (10) . If this is done for all of the models to be compared, then the one with the lowest value is the best fitting model.
For reviews and critiques of the BIC see Winship (1999) and Weakliem (1999).
Haughton’s BIC (HBIC)
A variant on the BIC retains the third term of Equation 9 (Haughton 1988). We call this approximation the HBIC (Haughton labels it BIC*).
| (13) |
In comparing models M2 and M1 and multiplying by 2 this leads to
| (14) |
The HBIC form that compares the hypothesized model to the saturated model using the chi-square test statistic is
| (15) |
The HBIC as with the BIC is straightforward to calculate from the output of SEM programs and using a calculator.
The HBIC performed well in model selection in a simulation study for SEMs (Haughton et al. 1997). Though this IC measure retains more terms in the approximation than does the BIC, this is no guarantee that it is a better approximation of BIC in finite samples. Our simulations will explore this issue.
The Information Matrix-Based BIC (IBIC)
A recent article by Bollen et al. (2012) proposes IBIC, which retains additional terms from (9). The estimated expected information matrix is obtainable with many SEM packages (it can be computed as the inverse of the covariance matrix for parameter estimates). Taking advantage of this, we preserve the fifth term in Equation 9.6
For models M2 and M1 and multiplying by 2, the Information matrix based Bayesian Information Criterion (IBIC) is given by
| (16) |
The IBIC measure that compares the hypothesized model (M1) to the saturated (Ms) and makes use of the chi-square test statistic and its degrees of freedom is
| (17) |
As with the HBIC, we do not know whether the extra terms retained enhance the finite sample performance of the IBIC over the BIC. But we will look at this question in our simulation.
The Scaled Unit Information Prior BIC (SPBIC)
An alternative derivation of Schwarz’s BIC makes use of the prior distribution of θk. It is possible to arrive at Equation 10 by utilizing a unit information prior, which assumes that the prior has approximately the same information as the information contained in a single data point. Critics have argued that the unit information prior is too flat to reflect a realistic prior (Raftery 1999). This prior also penalizes complex models too heavily, making BIC overly conservative toward the null hypothesis (Weakliem 1999; Kuha 2004; Berger et al. 2006). Some researchers have proposed centering priors around the MLE of Mk. Alternatively, some researchers have proposed using some form of scaling of the prior by a predefined scale (see Kuha 2004). In fact, HBIC defined above can also be derived by scaling the prior by a predefined constant. More recently, Bollen et al. (2012) proposed a Scaled Unit Information Prior BIC (SPBIC). The SPBIC uses a normal prior centered at zero for the parameters in question. As stated above, the BIC has a variance scaled at the level of unit information. The SPBIC differs from the BIC in that it chooses the variance that maximizes the probability density at the ML estimates of the parameters. Bollen et al. (2012) provide complete details of the SPBIC derivation; we refer readers there for more information. The final analytical expression is as follows, where is the observed information matrix evaluated at and θ* is the prior mean for model k.
| (18) |
with SPBIC equal to
| (19) |
When comparing a hypothesized model (M1) to the saturated model (Ms) and making use of the likelihood ratio chi-square, we are led to
| (20) |
where ds is the number of parameters from the saturated model or the number of variances, covariances, and means of the observed variables, d1 is the number of parameters in the hypothesized model, and the other terms have already been defined. The observed information matrix is obtainable from the inverse of the covariance matrix of the parameter estimates when the covariance matrix is based on the observed information matrix (e.g., in Mplus or the sem package in R).
To evaluate this, we must use a prior mean, , for the kth model. One possibility is to put all parameters at zero (i.e., ). This seems reasonable for parameters that are coefficients (other than intercepts and means), but is less reasonable for variances, intercepts, means, and covariances that are not of central interest. Therefore, for the models we consider we set to zero for coefficients and keep the remaining parameters at their estimated values. The end result is that the only nonzero elements in the difference of are for the coefficients. If the saturated model is part of the comparison, we need to take a different approach because the parameters of the saturated model are only variances and covariances. If we were to set θ* to the sample variances and covariances, then the denominator in the top line of equation (20) would be zero and undefined. A simple way around this for the saturated model is to have the prior mean be the estimated variances for all observed variables and the prior means for the covariances set to zero. If means and intercepts are part of the model, then the saturated model could set the elements of θ* that correspond to the means equal to the sample means. This would prevent the zero in the denominator.
For more details on the calculation of the scaling factor (which is model dependent and thus leads to an empirical Bayes prior) and the derivation of the analytical expression below, see Bollen et al. (2012).7 The essential point for the practitioner is that the prior is implicit in the information and does not need to be explicitly calculated. All elements of the SPBIC formula are available from SEM software that uses the observed information matrix to calculate the asymptotic covariance matrix of parameter estimates (e.g., Mplus or the sem package in R). For a basic example of the steps in calculating SPBIC, as well as the other Bayes Factor approximations listed here, see the empirical example section.
Theoretically, in large samples we expect the IBIC and SPBIC to perform as well as the BIC or the HBIC. But we cannot easily know the finite sample behavior of these measures and whether one or the other has better performance in small to moderate samples. Homburg (1991) conducted a simulation study of the BIC and compared it to cross-validation techniques. His conclusion was that the BIC performed well in finding the true model for sample sizes greater than 200 and data from multinormal distributions. Haughton et al. (1997) analyzed the BIC, HBIC, and several fit indices. These authors simulate a three factor model with six indicators and compare minor variants on the true structure to determine how successful the Bayes Factor approximations and several fit indices are in selecting the true model. Their simulation results find that the Bayes Factor approximations as a group are superior to the p-value of the chi-square test and the other fit indices in correctly selecting the true generating model when the true model is among the choices. They find that HBIC does the best among the Bayes Factor approximations. Among the other fit indices and the chi-square p-value, the IFI and RNI have the best correct model selection percentages, though their success is lower than the Bayes Factor approximations.
The Homburg (1991) and Haughton et al. (1997) studies are valuable in several respects, not the least of which is their demonstration of the value of the IC measures. However, it is unclear whether their results extend beyond the models that they examined. Moreover, the structure of most of the models that Haughton et al. (1997) considered were quite similar to each other. The performance of the IC measures for models with very different structures is unknown. Finally, they did not look at the situation where the true model was not included among the possible models.
Our simulation analysis seeks to test the generality of the Homburg (1991) Haughton et al. (1997) results by looking at larger models with alternative models that range from mildly different to very different structures. In addition, we provide the first evidence on the performance of the IBIC and SPBIC in the selection of SEMs. Finally, we provide the first evidence on the performance of the IC measures when all models in the pool are approximations.
4. Simulation Study
As we mentioned in the introduction, our simulation has two parts. The first part compares the IC measures and a variety of fit indices in their ability to correctly select a true model from among other models. The second part of the simulation focuses on the IC measures and their behavior when choosing from a pool of models that excludes the true structure, that is, when all models are approximations. For both parts of the simulation we use models designed by Paxton et al. (2001), which has been the basis for several other simulation studies. They chose these models after reviewing a large number of empirical studies using SEM that appeared in several social and behavioral science journals and tried to capture key features of these models in the simulation model. Specifically, we focus on their models with few latent variables with a small to moderate number of indicators per factor.
This enables comparisons to the results for other fit indices that use the same design, but different fit indices. Standard SEM assumptions hold in these models: exogenous variables and disturbances come from normal distributions and the disturbances follow the assumptions presented in Section 2 above.
The underlying population model for the first simulation (SIM1) has a latent variable model with three latent variables linked in a chain.
The measurement model contains 9 observed variables, 3 of which crossload on more than one latent variable. Scaling is accomplished by fixing λ =1 for a single indicator loading on each latent variable
This true model is labeled M1. Panel (a) of Figure 1 is a path diagram of this true model. It is the model with both solid and dashed lines included and is equivalent to the model in the preceding equations. The population parameters for this model are as follows: primary factor loadings were set to a standardized value of .70 to represent a communality of 49%, while complex loadings were set to a standardized value of .21. Regression parameters among latent variables were set to a standardized value of .60, to represent multiple R2 of 36%. For an extended discussion of the rationale for the choice in parameter values see Paxton et al. (2001).
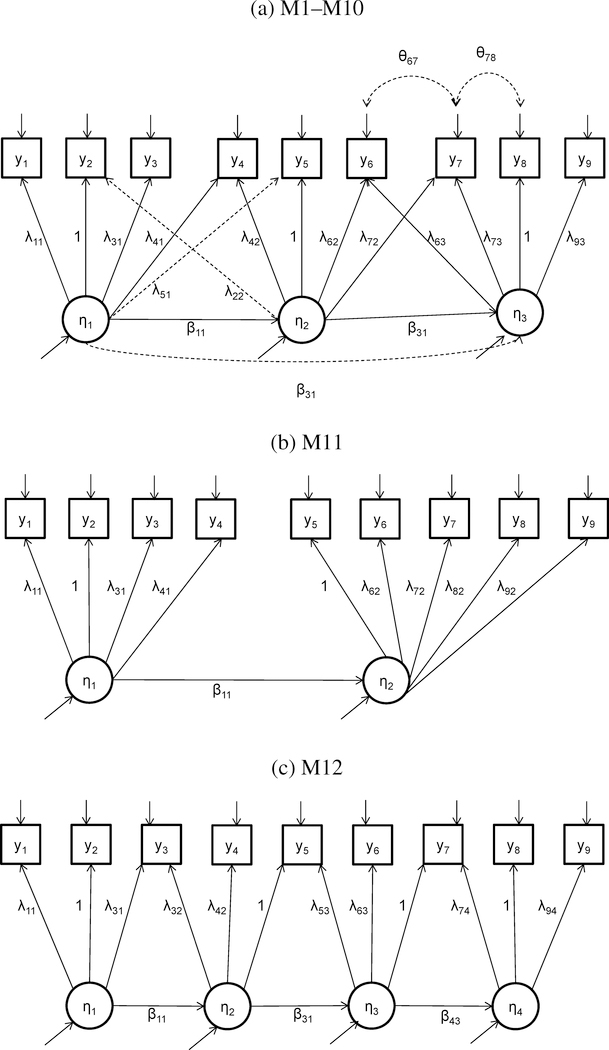
Figure 1:
Path Diagrams of the Models in SIM1
For each simulated data set, we fit a series of misspecified models, which are also depicted in Figure 1. This range of models tests the ability of the different fit statistics to detect a variety of common errors. Parameters were misspecified so as to introduce error into both the measurement and latent variable components of the models. Some of these errors corresponded to the true model (M1) with extra, unneeded parameters (M6, M8, M9); others dropped necessary parameters (M2, M3, M4, M10), some both added and dropped parameters (M5, M7), while some even changed the number of latent variables in the model (M11, M12). Figure 1, panels (b) and (c), represent these last two specifications. Table 1 lists these models with their modifications.
Table 1:
Fitted Models for SIM1
| Model | Description | # Par. | Dropped Parameters | Extra Parameters |
|---|---|---|---|---|
| Correct Model | ||||
| M1 | Correct model | 23 | ||
| Misspecified Measurement Models | ||||
| M2 | Drop 1 cross loading | 22 | λ41 | |
| M3 | Drop 2 cross loadings | 21 | λ41, λ72 | |
| M4 | Drop 3 cross loadings | 20 | λ41, λ72, λ63 | |
| M5 | Drop cross-loadings; add correlated errors | 22 | λ72, λ63 | θ67 |
| M6 | Correlated errors | 24 | θ67 | |
| M7 | Switch factor loadings | 23 | λ21, λ52 | λ51, λ22 |
| Misspecified Structural Models | ||||
| M8 | Add double-lagged effect | 24 | γ31 | |
| M9 | Add correlated errors and double-lagged effect | 25 | θ67, β31 | |
| M10 | No relations among η’s | 21 | β21, β32 | |
| M11 | Two latent variables (remove η3) | 19 | λ42, λ72, λ73, λ93, β32, ψ33 | λ82, λ92 |
| M12 | Four latent variables (add η4) | 24 | λ41, λ62, λ72, λ83, λ93 | λ32, λ53, λ74, λ94, β43, ψ44 |
The underlying population model for the second simulation (SIM2) uses a generating model that is identical to SIM1 in the latent variable model, but contains an additional two observed indicators for each latent variable. Parameter values were the same except for the addition of two measured variables per factor.
The misspecified models used in SIM2 are given in Table 2.
Table 2:
Fitted Models for SIM2
| Model | Description | # Par. | Dropped Parameters | Extra Parameters |
|---|---|---|---|---|
| Correct Model | ||||
| M1 | Correct model | 35 | ||
| Misspecified Measurement Models | ||||
| M2 | Drop 1 cross loading | 34 | λ61 | |
| M3 | Drop 2 cross loadings | 33 | λ61, λ11,2 | |
| M4 | Drop 3 cross loadings | 32 | λ61, λ11,2, λ10,3 | |
| M5 | Drop cross-loadings; add correlated errors | 34 | λ11,2, λ10,3 | θ10,11 |
| M6 | Correlated errors | 36 | θ10,11 | |
| M7 | Switch factor loadings | 35 | λ21, λ72 | λ71, λ22 |
| Misspecified Structural Models | ||||
| M8 | Add double-lagged effect | 36 | γ31 | |
| M9 | Add correlated errors and double-lagged effect | 37 | θ10,11, γ31 | |
| M10 | No relations among η’s | 33 | β21, β32 | |
| M11 | Two latent variables (remove η3) | 31 | λ62, λ10,3, λ11,3, λ13,3, λ14,3, λ15,3, β32, ψ33 | λ12,2, λ13,2, λ14,2, λ15,2 |
| M12 | Four latent variables (add η4) | 37 | λ61, λ92, λ10,2, λ11,2, λ13,3, λ14,3, λ15,3, | λ42, λ52, λ83, λ12,3, λ11,4, λ12,4, λ14,4, λ15,4, β43, ψ44 |
For each simulation we generated 1000 data sets with each of the following sample sizes: N = 100, N = 250, N = 500, N = 1000, and N = 5000. Note that, following standard practice, samples were discarded if they led to non-converging solutions, and new samples were drawn to replace the “bad” samples until a total of 1000 samples were drawn that had convergent solutions for each of the 12 fitted models.8 All data were generated in R and analyzed with the sem package (Fox 2006).9
4.1. Simulation Part I
In the first part of the simulation we include all of the models including the true one that generated the data. Our interest is in the ability of the different IC measures and fit indices to choose the true model among the 12 possibilities. The fit statistics included were the BIC, IBIC, SPBIC, HBIC, AIC, chi-square p-value, IFI, CFI, TLI, RNI, and RMSEA.
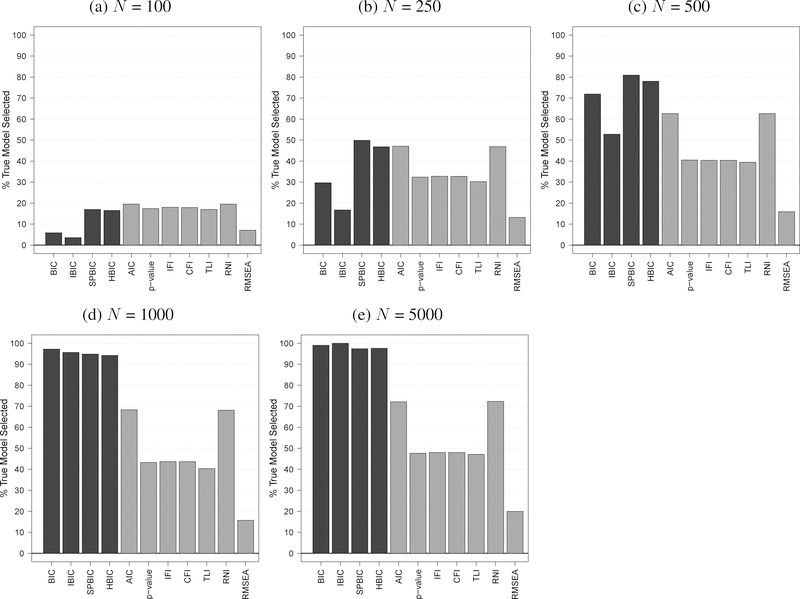
For each simulated data set we estimated all 12 models and calculated each fit index including the IC measures. We then determined whether the best fitting model in each sample was the true model. This was repeated for all replication samples at a given N. For the BIC, IBIC, SPBIC, HBIC, AIC, and RMSEA the model with the lowest value has the best fit.10 For all of the other fit indices, the highest value signifies the best fit. Figure 2 gives the percentage of samples for which the true model was chosen for a given fit measure and given sample size across the 1000 replications. These results are for the first underlying simulation model (SIM1).
Figure 2:
SIM1 Percentage Selections of the True Model
One clear result from these graphs is the dramatic improvement in the performance of the IC measures as the sample size grows. At the smallest N (100), success in choosing the true model among the 12 models was 20% or less. Choosing a model at random would have a success rate of roughly 8%, so the best of the IC measures (SPBIC, HBIC, AIC) are doing better than chance but the BIC and IBIC are not. In contrast, increasing the sample size to 250 has the best IC measures (SPBIC, HBIC, AIC) with success rates of over 40% with SPBIC the best at 50% and the IBIC and BIC once again coming in considerably lower. Starting at N = 500, the SPBIC and HBIC break away from the AIC with the SPBIC over 80% success in picking the true model. The BIC comes in next with about 70%, followed by the AIC at a little over 60% and the IBIC a little lower. With a large sample size of 1000 or 5000, all the IC measures except AIC approach 100% success in finding the true model. Among the IC measures the new SPBIC and the HBIC have the best overall performance across sample sizes.
For comparison purposes we also included other popular fit indices. At the smallest samples these fit indices perform roughly the same as the IC indices, but starting at an N of 500 the best IC measures are superior to these. Of these common fit indices, the RNI appears best, but its performance never gets much better than 70% success even at the largest sample sizes. The RMSEA overall has the lowest percentage success in choosing the true model from the pool of models.
When we turn to SIM2 which includes more indicators per latent variables, we find a rather interesting result (not shown to conserve space). At the same smaller sample size, all fit indices are more successful in choosing the true model than they were at the same N in SIM1. For instance, at N = 100 several of these measures are approaching a 40% success rate, something that we did not see until an N of 250 in SIM1. Starting at 250 we have the IC measures pulling away from the other fit indices with the AIC lagging behind the other IC measures. Again the SPBIC and HBIC have the best overall performance in choosing the correct model.
In sum, our simulation results find that there are differences in the finite sample behavior of the IC measures. The SPBIC and HBIC have the best overall performance, but in large samples all but the AIC among the IC measures have great success in locating the true model. We also find that the IC measures are generally superior to the other fit indices in finding the true model in larger sample sizes.
4.2. Simulation Part II
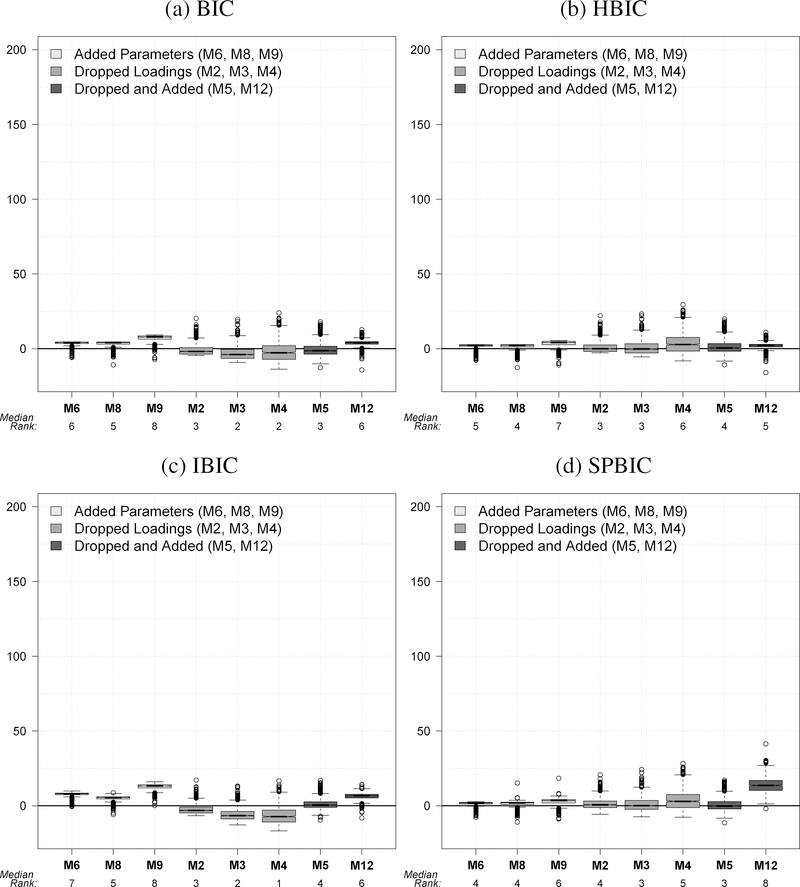
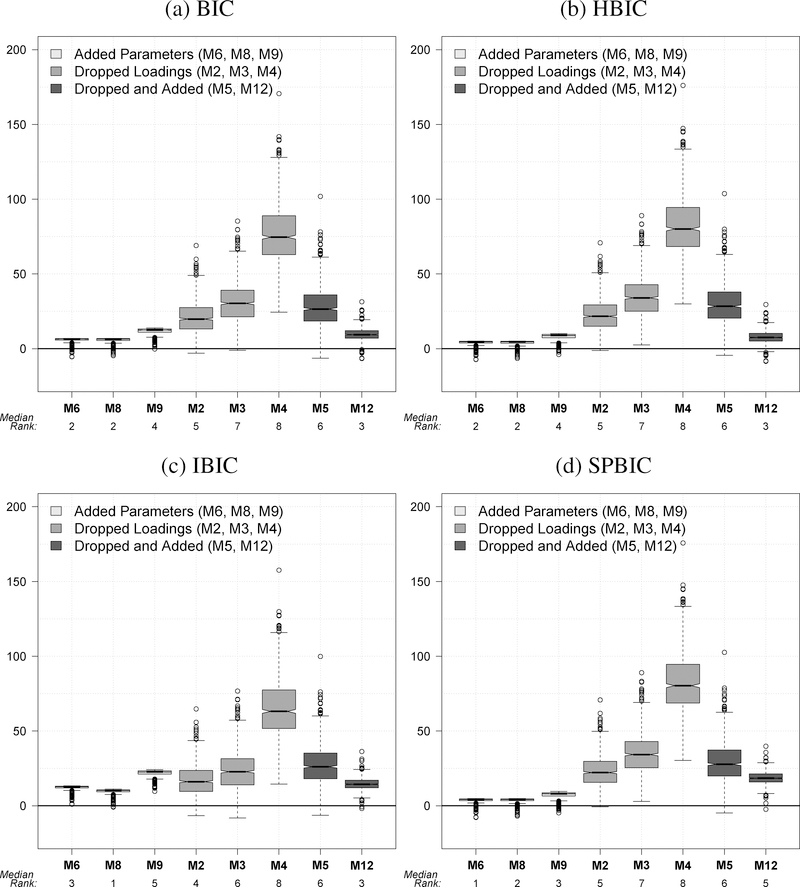
The second part of the simulation examines model selection when the true model is not among the choices. This reflects more realistic conditions in that we expect researchers to be using an approximate rather than the true structure in practice. We use the same simulation data as Part I, but we remove the true structure from among the choices resulting in 11 alternative models (rather than 12). We restrict our analysis to the IC measures, the primary focus of our article. Contrary to Part I, we cannot list the percentage of times the true model is selected because there is no true model among the choices. Instead, we provide tables that give the median value and Interquartile Range (IQR) for each IC measure for each model. Furthermore, we include the median rank in fit that each model has in each replication at the different sample sizes. Because this analysis generates a lot of tables, we only report three tables in the text for three sample sizes: 100, 500, and 1000 for SIM1. The tables for the remaining sample sizes are in the online appendix along with all of the tables for SIM2 (available at http://dvn.iq.harvard.edu/dvn/dv/jjharden). We also report box-and-whisker plots of the values of each IC measure for each of the 11 models in this section. The tables and figures give us comparative fit information. We can see which models tended to have better fit (lower IC values) than the others and whether this varied with sample size.
We roughly group the remaining 11 models into three categories. The first are models with extra parameters (M6, M8, M9). These are the true generating model with unnecessary parameters added to it. In other words, the extra parameters have a population value of zero. The second group are models with dropped parameters (M2, M3, M4). They are the true generating model with one or more parameters incorrectly removed (or set to zero). The third group is a mixture of extra and dropped parameters and includes cases with the wrong number of latent variables. Models M5, M7, M11, and M12 fall into this group. Finally, M10 is in its own group as a model in which only a β parameter is dropped.
Table 3 presents the results from SIM1 for N = 100. Each time through the simulation the IC measure is computed for all the models. Then the IC value for the true model is subtracted from each other model’s IC value. This makes the true model value equal to zero. Models that fit worse than the true model get positive values and those that fit better get negative values. Because lower values signify better fit, a negative median value in the table means that the median value on the particular IC measure signifies a better fit than the true model. A positive value represents a median value higher than the true model.
Table 3:
SIM1 Fit Statistic Quantiles and Median Ranks with No True Model (N = 100)
| Models: | Extra Parameters | Dropped Loadings | Dropped and Extra | Dropped β Only | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| M6 | M8 | M9 | M2 | M3 | M4 | M5 | M7 | M11 | M12 | M10 | ||
| BIC | ||||||||||||
| Median | 4.16 | 4.12 | 7.76 | −1.90 | −3.92 | −2.74 | −1.38 | 25.04 | 36.58 | 4.11 | 33.61 | |
| IQR | 1.06 | 1.43 | 2.29 | 4.36 | 6.10 | 9.13 | 5.25 | 13.81 | 21.37 | 1.73 | 17.55 | |
| Median Rank | 6 | 5 | 8 | 3 | 2 | 2 | 3 | 9 | 10 | 6 | 10 | |
| HBIC | ||||||||||||
| Median | 2.32 | 2.28 | 4.09 | −0.06 | −0.24 | 2.77 | 0.45 | 25.04 | 43.93 | 2.27 | 37.28 | |
| IQR | 1.06 | 1.43 | 2.29 | 4.36 | 6.10 | 9.13 | 5.25 | 13.81 | 21.37 | 1.73 | 17.55 | |
| Median Rank | 5 | 4 | 7 | 3 | 3 | 6 | 4 | 9 | 11 | 5 | 10 | |
| IBIC | ||||||||||||
| Median | 8.05 | 5.48 | 13.19 | −3.20 | −6.65 | −7.27 | 0.45 | 22.08 | 25.78 | 6.60 | 28.58 | |
| IQR | 0.95 | 1.42 | 2.17 | 3.93 | 5.04 | 8.07 | 3.69 | 12.87 | 18.56 | 2.47 | 17.26 | |
| Median Rank | 7 | 5 | 8 | 3 | 2 | 1 | 4 | 10 | 10 | 6 | 10 | |
| SPBIC | ||||||||||||
| Median | 1.88 | 2.00 | 3.35 | 0.57 | 0.05 | 2.95 | −0.15 | 27.46 | 46.20 | 13.59 | 32.71 | |
| IQR | 1.03 | 1.35 | 2.37 | 4.44 | 5.94 | 8.75 | 4.76 | 15.70 | 19.28 | 6.75 | 16.44 | |
| Median Rank | 4 | 4 | 6 | 4 | 3 | 5 | 3 | 9 | 11 | 8 | 10 | |
Note: Cells report median and interquartile range (IQR) values of the fit statistics across the simulations, with median model ranks below. Lower numbers indicate better fit.
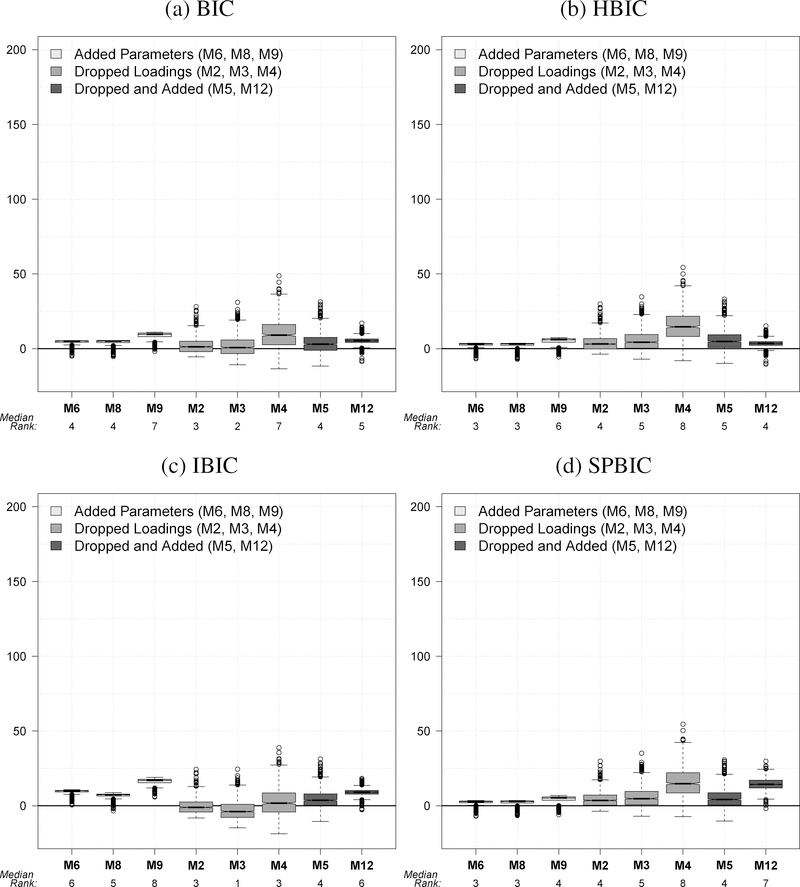
Several bad fitting models (M11, M10, M7) are evident across all of the IC measures when N is 100. For example, M11 has a median SPBIC of 46.20 and an IQR of 19.28. This is far from zero and the IQR suggests considerable variability. The median rank of 11 for M11 means that its central tendency was to be among the worst fitting models of the 11 considered. A similar pattern was found for the other IC measures for the three models M11, M10, and M7. M11 and M7 involve both dropped and added parameters where M10 only drops (sets to zero) the paths between two latent variables in the original (see Figures 1 and 2). Not all models with dropped parameters fare poorly with the IC measures. M2, M3, and M4 drop one, two, or three cross-loadings, respectively, yet the median for the BIC, HBIC, and IBIC are negative signifying a better median fit than the true model. Lower median ranks for many of these IC measures reflect their tendency to fare well in comparison to the remaining models. This tendency is weaker for SPBIC, whose median fit is close to the true model’s value of zero.
Contrast this with models M6, M8, and M9 all of which have extra, unnecessary parameters included. The median of all IC measures is positive which exhibits a small penalty for the extra parameters. The median rank of fit for these models and IC measures tends to be toward the middle (fifth to seventh). Considering that the model is correct except for the inclusion of unnecessary parameters, this implies that the IC measures are penalizing extra parameters more strongly than they are dropped parameters, at least at the smallest sample size (N = 100). M12, which has a mixture of dropped and excluded parameters through the introduction of an extra latent variable, comes in toward the middle of the rankings for the IC measures with the highest median ranking for SPBIC (median rank = 6). It also is worth noting that the smallest variability (IQR) of the IC measures occurs for the models that add unnecessary parameters (M6, M8, M9).
Increasing the sample size to 500 (Table 4) leads to a general pattern that is similar with some important differences. The fit of M11, M10, and M7 are even worse than they were with N = 100 and their fit is considerably worse than any of the other models. Another difference compared to N = 100 is that M2, M3, and M4, which drop factor loadings, no longer have negative median values of the IC measures that suggest a better fit than the true model. We might expect that an IC measure that favors parsimony to favor models like M2, M3, and M4. Though we saw this in the smallest sample, it is not evident in this moderate sized sample. The models M6, M8, and M9, which add unnecessary parameters, have positive values and the HBIC and SPBIC have low median ranks for these models. We also note that the models with the extra parameters have the smallest variability as they did with N = 100.
Table 4:
SIM1 Fit Statistic Quantiles and Median Ranks with No True Model (N = 500)
| Models: | Extra Parameters | Dropped Loadings | Dropped and Extra | Dropped β Only | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| M6 | M8 | M9 | M2 | M3 | M4 | M5 | M7 | M11 | M12 | M10 | ||
| BIC | ||||||||||||
| Median | 5.79 | 5.78 | 11.14 | 6.39 | 9.27 | 30.01 | 10.69 | 129.51 | 247.79 | 6.77 | 195.97 | |
| IQR | 1.18 | 1.23 | 2.20 | 9.58 | 12.20 | 19.36 | 12.32 | 33.77 | 49.74 | 3.37 | 41.10 | |
| Median Rank | 3 | 3 | 6 | 4 | 5 | 8 | 6 | 9 | 11 | 4 | 10 | |
| HBIC | ||||||||||||
| Median | 3.95 | 3.94 | 7.46 | 8.23 | 12.95 | 35.52 | 12.52 | 129.51 | 255.15 | 4.94 | 199.65 | |
| IQR | 1.18 | 1.23 | 2.20 | 9.58 | 12.20 | 19.36 | 12.32 | 33.77 | 49.74 | 3.37 | 41.10 | |
| Median Rank | 2 | 2 | 5 | 5 | 6 | 8 | 6 | 9 | 11 | 3 | 10 | |
| IBIC | ||||||||||||
| Median | 11.36 | 8.84 | 19.82 | 3.37 | 3.20 | 20.62 | 10.74 | 126.82 | 229.88 | 11.08 | 187.64 | |
| IQR | 1.14 | 1.12 | 2.15 | 9.31 | 12.02 | 18.76 | 11.61 | 33.33 | 48.66 | 3.20 | 41.04 | |
| Median Rank | 5 | 3 | 7 | 2 | 2 | 8 | 5 | 9 | 11 | 5 | 10 | |
| SPBIC | ||||||||||||
| Median | 3.51 | 3.62 | 6.64 | 8.75 | 13.40 | 35.74 | 12.00 | 132.26 | 257.60 | 16.00 | 195.53 | |
| IQR | 1.18 | 1.16 | 2.19 | 9.33 | 12.26 | 19.56 | 11.92 | 33.66 | 48.43 | 4.69 | 40.75 | |
| Median Rank | 2 | 2 | 3 | 4 | 6 | 8 | 5 | 9 | 11 | 6 | 10 | |
Note: Cells report median and interquartile range (IQR) values of the fit statistics across the simulations, with median model ranks below. Lower numbers indicate better fit.
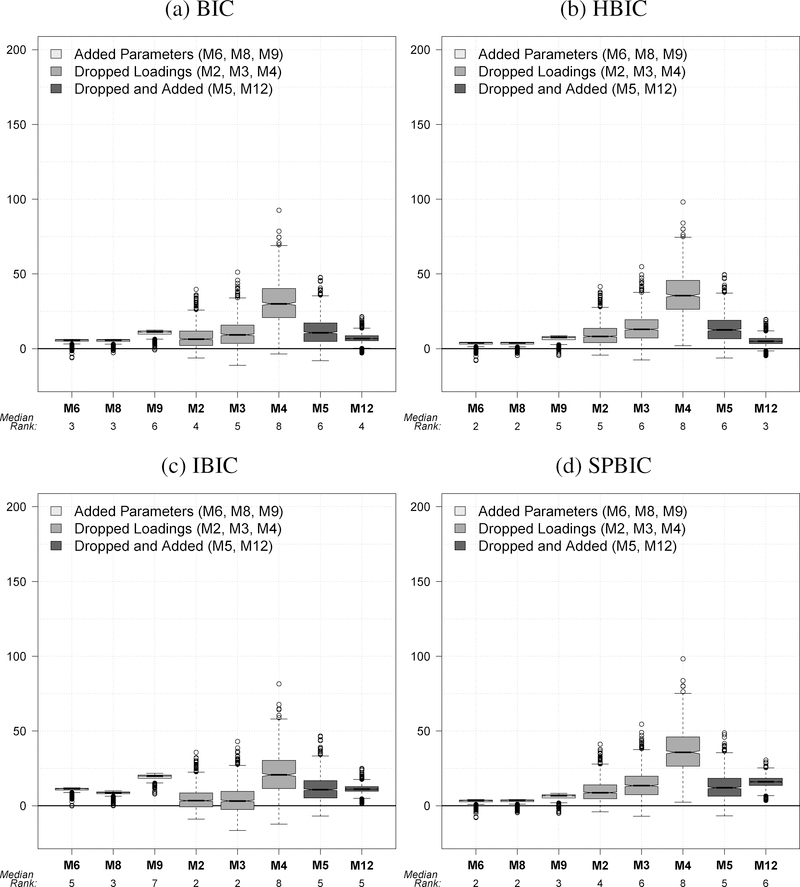
Table 5 gives our results for N = 1000. The results are quite similar to those for N = 500 with noticeably poorer fit for all but the models with the extra parameters (see the online appendix at http://dvn.iq.harvard.edu/dvn/dv/jjharden for N = 250 and 5000).
Table 5:
SIM1 Fit Statistic Quantiles and Median Ranks with No True Model (N = 1000)
| Models: | Extra Parameters | Dropped Loadings | Dropped and Extra | Dropped β Only | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| M6 | M8 | M9 | M2 | M3 | M4 | M5 | M7 | M11 | M12 | M10 | ||
| BIC | ||||||||||||
| Median | 6.47 | 6.43 | 12.44 | 19.82 | 30.30 | 74.58 | 26.53 | 262.62 | 515.62 | 9.34 | 405.62 | |
| IQR | 1.14 | 1.27 | 2.29 | 14.31 | 17.69 | 26.02 | 17.52 | 47.65 | 66.96 | 5.05 | 56.23 | |
| Median Rank | 2 | 2 | 4 | 5 | 7 | 8 | 6 | 9 | 11 | 3 | 10 | |
| HBIC | ||||||||||||
| Median | 4.64 | 4.59 | 8.76 | 21.66 | 33.97 | 80.09 | 28.36 | 262.62 | 522.97 | 7.50 | 409.29 | |
| IQR | 1.14 | 1.27 | 2.29 | 14.31 | 17.69 | 26.02 | 17.52 | 47.65 | 66.96 | 5.05 | 56.23 | |
| Median Rank | 2 | 2 | 4 | 5 | 7 | 8 | 6 | 9 | 11 | 3 | 10 | |
| IBIC | ||||||||||||
| Median | 12.75 | 10.23 | 22.55 | 16.10 | 22.75 | 63.11 | 26.08 | 259.65 | 494.72 | 14.38 | 395.90 | |
| IQR | 1.14 | 1.24 | 2.17 | 14.00 | 17.44 | 25.78 | 17.08 | 47.14 | 65.86 | 4.96 | 56.09 | |
| Median Rank | 3 | 1 | 5 | 4 | 6 | 8 | 6 | 9 | 11 | 3 | 10 | |
| SPBIC | ||||||||||||
| Median | 4.20 | 4.24 | 7.97 | 22.17 | 34.22 | 80.31 | 27.77 | 265.26 | 525.28 | 18.42 | 404.95 | |
| IQR | 1.12 | 1.24 | 2.20 | 14.06 | 17.53 | 25.93 | 17.41 | 46.66 | 66.46 | 5.40 | 55.43 | |
| Median Rank | 1 | 2 | 3 | 5 | 7 | 8 | 6 | 9 | 11 | 5 | 10 | |
Note: Cells report median and interquartile range (IQR) values of the fit statistics across the simulations, with median model ranks below. Lower numbers indicate better fit.
In Figures 3–6 we provide the box-and-whiskers plots for each IC measure for individual models for N = 100, 250, 500, and 1000. The figures differ from the tables in that the consistently worst fitting models, M11, M10, and M7, are omitted. We did this because their IC values were so high that to plot them in the figures would necessitate greatly expanding the maximum for the y-axis and make it hard to see the features of the IC measures for the other models which have better fit.
Figure 3:
SIM1 IC Box-and-Whisker Plots and Median Ranks with No True Model (N = 100). Box-and-Whisker plots represent each fit statistic for each model over the 1,000 simulations. Numbers below the model names represent the median rank of each fit statistic for each model over the 1000 simulations.
Figure 6:
SIM1 IC Box-and-Whisker Plots and Median Ranks with No True Model (N = 1000). Box-and-Whisker plots represent each fit statistic for each model over the 1,000 simulations. Numbers below the model names represent the median rank of each fit statistic for each model over the 1000 simulations.
These figures reinforce the impressions from the tables in displaying the small variability of the IC measures for the models with extra parameters (M6, M8, M9) and the increase in IC measures for the other models as sample size grows. As the sample size increases, the IC measures tend to favor the models that are correct except for extra parameters. What was not evident from the tables are the outlying values for the IC measures for the M2 to M5 models. Along with their greater variability in IC measures, they also have more generally high outlier values.
The SIM2 simulation adds more variables to the model, but otherwise is similar to the SIM1 models that we just reviewed. The online appendix has tables to summarize the median value, IQR, and median rank for each model across N = 100, 250, 500, 1000, and 5000 (available at http://dvn.iq.harvard.edu/dvn/dv/jjharden). SIM2 results are similar to those from SIM1 in that the IC measures favor the extra parameter models more as the sample size increases. However, one difference at the smallest sample size (N = 100) is that except for IBIC, the median IC measure values are nearly all positive for the models that drop factor loadings. In SIM1 they tended to be negative and hence favoring these trimmed structures over the true structure. That is not true here. Also the separation in IC measures for the three extra parameters models tends to be larger at the same sample size for SIM2 vs. SIM1. The trend toward favoring the true plus extra parameter models begins at lower sample sizes.
4.3. Simulation Summary
Taken all together, what do we learn from these results using approximate models and excludes the true model? One result is that given the choice of models that drop (set to zero) some parameters versus a model that is true but has extra parameters included, the IC measures tend to favor the extra parameter over the dropped parameters. This trend is most clear in the moderate to large sample sizes. The only evidence that we found for the IC measures tilting toward simpler models with dropped parameters occurred in the smallest sample (N = 100) and in the SIM1 design. Other than that there was not a trend toward choosing a model with fewer parameters.
What about the relative performance of the different IC measures? In Part I of the simulation study we found that SPBIC and HBIC had the best overall performance in choosing the true model, though the behavior of all IC measures was much more similar in larger samples. In Part II where the true model is not one of the choices, the criterion for best model is less apparent. If we believe that we are better off selecting a model that has all of the parameters in the generating model and its only misspecification is including extra parameters that are zero in the population, then we would favor IC measures that have such models with values closest to zero. The HBIC and SPBIC are generally better on this criterion than the BIC and IBIC, though there are not dramatic differences. Alternatively, suppose a researcher favors IC measures that choose parsimonious models that trim small effects. Here the evidence slightly favors the BIC and IBIC which have lower median values than the SPBIC and HBIC.11
5. Empirical Example
Next we turn to utilizing these IC measures in an applied setting. We use data drawn from the National Longitudinal Survey of Youth (NLSY) of Labor Market Experience to illustrate the IC measures calculations with SEM. Bollen and Curran (2004) consider five different longitudinal models of family income. They extracted a subsample of data consisting of N = 3912 individuals with complete data assessed at two year intervals from 1986 to 1994. The repeated measure was the square root of the respondent’s report of total net family income for the prior calendar year. The five longitudinal models considered are listed below (for details, see Bollen and Curran 2004).
Autoregressive: yit = αt + ρt,t−1yit−1 + ζit
Latent Growth Curve: yit = αi + βiλt + ζit
Autoregressive Latent Trajectory (ALT) with ρ free: yit = αi + βiλt + ρt,t−1yit−1 + ζit
ALT with ρ equal: yit = αi + βiλt + ρyit−1 + ζit
ALT with ρ zero and yi1 predetermined: yit = αi + βiλt + (0)yit−1 + ζit
Applied researchers are commonly confronted with several choices such as these when modeling data with SEMs. We illustrate the calculation of the IC measures employing the chi-square statistic that compares the hypothesized model to the saturated model. All the IC measures are computable with the following information: (1) the chi square test statistic (Tml), (2) the degrees of freedom (df), (3) the sample size (N), (4) the number of estimated parameters for the saturated (ds) and hypothesized (d1) models, (5) the expected or observed information matrix for the saturated [ or ] and hypothesized models [ or ], and (6) the parameter estimates ( and ). The BIC and HBIC only requires (1) to (3); the IBIC requires requires all but (4) and (6), and the SPBIC requires (1) to (6).12
The top half of Table 6 gives all of the necessary quantities for the five models presented in Bollen and Curran (2004). The lower half of Table 6 presents the IC measures using those quantities for each model. Note that all of the measures point to the ALT models as better fitting than the autoregressive and latent growth curve models. Among the three ALT models, the one with the autoregressive parameter free has the best fit for BIC, HBIC, and SPBIC. The IBIC points towards the ALT model with equal autoregressive parameters.
Table 6:
Computation of IC Measures for the Bollen and Curran (2004) Models
| Autoregressive | Latent Growth Curve | ALT ρ free | ALT ρ equal | ALT ρ zero | |
|---|---|---|---|---|---|
| Tml | 534.27 | 412.93 | 26.26 | 62.44 | 203.33 |
| N | 3912 | 3912 | 3912 | 3912 | 3912 |
| log(N) | 8.27 | 8.27 | 8.27 | 8.27 | 8.27 |
| 6.43 | 6.43 | 6.43 | 6.43 | 6.43 | |
| df | 6 | 10 | 3 | 6 | 7 |
| ds (SPBIC) | 20 (15) | 20(15) | 20 (15) | 20 (15) | 20 (15) |
| d1 (SPBIC) | 14 (9) | 10 (3) | 17 (10) | 14 (7) | 13 (6) |
| 134.89 | 134.89 | 134.89 | 134.89 | 134.89 | |
| 102.61 | 74.26 | 130.18 | 102.77 | 94.19 | |
| 195428707 | 195428707 | 195428707 | 195428707 | 195428707 | |
| 1137006314 | 180774515 | 214642815 | 251962808 | 189536063 | |
| BIC | 484.64 | 330.21 | 1.44* | 12.81 | 145.43 |
| HBIC | 495.67 | 348.59 | 6.95* | 23.83 | 158.29 |
| IBIC | 463.39 | 287.95 | 2.25 | −8.29* | 117.59 |
| SPBIC | 450.42 | 208.93 | −55.66* | −69.51 | 52.20 |
Note:
Fit statistic’s minimum value. Values for ds and d1 in parentheses are used in the computation of SPBIC. Discrepancies in computations may result from rounding error.
Recall that the IC measures are comparing fit to the saturated model. Though we do not know the true model, the IC measures point toward the ALT model, possibly with the free autoregressive parameter. Even though the BIC, HBIC, and SPBIC all point toward the ALT model with the autoregressive parameters free, only the SPBIC clearly points to this model over the saturated model in that it SPBIC takes a large negative value. According to Raftery (1995), a difference of less than 2 provides only weak evidence of a difference in model fit when using IC for model selection; a difference of greater than 10 is considered very strong evidence of superior fit (with the model with the smaller value being preferred).
6. Conclusions
As in any statistical analysis, a key issue in the use of SEMs is determining the fit of the model to the data and comparing the relative fit of two or more models to the same data. However, current practice with SEMs commonly employs methods that are problematic for several different reasons. For example, the asymptotic chi-square distributed test statistic that tests whether a SEM exactly reproduces the covariance matrix of observed variables routinely rejects models in large samples regardless of their possible merit as approximations to the underlying process. Several other fit indices have been developed in response, but those measures also have important problems: their sampling distributions are not commonly known, some tend to differ with sample size, and there is disagreement about the optimal cutoff values for a “well-fitting” model.
Analytic research tells us that the IC measures will choose the true model as the sample size goes to infinity. However, this does not tell us how the IC measures perform in finite samples or in the typical situation when the true model is not among the choices. One part of our article uses simulated data to examine the finite sample behavior of these IC measures and traditional fit indices when the true model is one of the options. We find that these IC measures are better at finding the true model than are other fit indices in our first simulation. The SPBIC and HBIC have the best overall performance among the IC measures, though in large samples all but AIC perform well. We also looked at model selection when all models are approximate. Here we found that in moderate to large samples all the IC measures favored the model that had the true structure with extra parameters. Other models with dropped only or a mixture of dropped and extra parameters did not fare as well, though models with dropped parameters with small values looked better than other remaining misspecifications. Of course, neither the ICs or any fit index eliminates the uncertainty of model selection. But, overall, our results suggest that researchers using SEM should take a closer look at these IC measures and their use in model selection.
Supplementary Material
Figure 4:
SIM1 IC Box-and-Whisker Plots and Median Ranks with No True Model (N = 250). Box-and-Whisker plots represent each fit statistic for each model over the 1,000 simulations. Numbers below the model names represent the median rank of each fit statistic for each model over the 1000 simulations.
Figure 5:
SIM1 IC Box-and-Whisker Plots and Median Ranks with No True Model (N = 500). Box-and-Whisker plots represent each fit statistic for each model over the 1,000 simulations. Numbers below the model names represent the median rank of each fit statistic for each model over the 1000 simulations.
Footnotes
The online appendix and complete replication materials for the analyses presented here are available at http://dvn.iq.harvard.edu/dvn/dv/jjharden.
A dedicated Bayesian statistician would prefer formal Bayesian analyses, by specifying explicit prior probabilities to develop actual Bayes Factors, which could then be compared to the various IC approximations. Though we recognize the value of this approach as an ideal, social and behavioral scientists in practice rarely work with prior distributions, but instead use IC based measures that do not require prior specifications for model selection. Our goal is to assess the accuracy of such IC measures for selecting the true model or the best approximation to the true model in SEM, an area that has received little attention, and with some IC measures that are new.
The latent variable model is also called the “structural equation.” Because the latent variable and measurement models both have structural parameters we prefer the term “latent variable model” to avoid this confusion.
We can modify the model to permit such correlations among the errors, but do not do so here.
Of course, advances in computational statistics over the last few decades has eased the burden of this complexity.
Note that this is very similar to Kashyap’s (1982) approximation (KBIC), which uses log(N) rather than . We compared KBIC to IBIC in our simulation study below and found that IBIC consistently outperformed KBIC, particularly at small sample sizes. Thus, the slightly greater complexity in IBIC appears to be worthwhile. See the online appendix for more details on this comparison (available at http://dvn.iq.harvard.edu/dvn/dv/jjharden).
Bollen et al. (2012) also discuss an alternative computation of SPBIC when . As ck = ∞, the prior variance goes to 0, so the prior distribution is a point mass at the mean, θ*. This case never occurs in the simulations or empirical example we discuss below so we do not discuss it further here. Such a case is less studied so that we would caution readers that we have too little experience with the SPBIC to know its behavior under these less common circumstances.
This was most problematic at small sample sizes for SIM1—at N = 100, 168 samples had to be discarded for nonconvergence. The respective SIM1 numbers at other sample sizes are: N = 250: 32, N = 500: 2, N = 1000: 1, and N = 5000: 0. The numbers for SIM2 are: N = 100: 27, N = 250: 3, N = 500: 1, N = 1000: 0, and N = 5000: 0.
The sem package uses the observed information matrix for the calculation of the asymptotic covariance matrix of the parameter estimates. This provides the output needed for the SPBIC (observed information matrix). The IBIC uses the expected information matrix, which is not available in the sem package in R. We used the observed information matrix in place of the expected information matrix. We did not anticipate much of a difference, but checked this issue in the following way. The expected information matrix is the expected value, or mean, of the observed information matrices. We computed the mean of the 1000 simulated observed information matrices for each model, then replaced each of those means as the expected information matrices for their respective models and reran SIM1, n = 100. If there were any differences between using the observed and expected information matrices, we would expect it at the smallest sample size of 100. The result was an IBIC performance value (true model selection %) within a percent or two to what we got using the observed information. Though we would not anticipate large differences in other cases, we would still recommend that the expected information matrix be used for IBIC when it is available.
Selecting the lowest value for the IC is an exact test that does not take into account the magnitude of the difference in the fit statistic from the next best-fitting model. Alternatively, following the guidelines of Raftery (1995), we could consider models with differences in fit of less than 2 as essentially tied. Relative performance of the various criteria was similar when we did so; therefore to simplify presentation we assess correct selection in terms of the exact selection based on lowest value.
Of course, we remind readers of the limitations of any simulation design and the need to replicate results under diverse conditions.
Nearly all SEM software provide all but the information matrices as part of standard output. Many packages permit output of the asymptotic covariance matrix of the parameter estimates. The inverse of this covariance matrix provides an estimate of the information matrix. Whether it is the expected or observed information matrix depends on the SEM software and the option used. The online supplementary materials include a R function that takes output from any software package and computes all of the IC measures.
References
- Bentler PM (1990). Comparative fit indexes in structural models. Psychological Bulletin, 107(2):238–246. [DOI] [PubMed] [Google Scholar]
- Bentler PM and Stein J (1992). Structural equation models in medical research. Statistical Methods in Medical Research, 1(2):159–181. [DOI] [PubMed] [Google Scholar]
- Beran TN and Violato C (2010). Structural equation modeling in medical research: A primer. BMC Research Notes, 3(1):267–277. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berger JO, Ray S, Visser I, Bayarri MJ, and Jang W (2006). Generalization of BIC. Technical report, University of North Carolina, Duke University, and SAMSI. [Google Scholar]
- Bollen KA (1989). Structural Equations with Latent Variables. John Wiley & Sons, New York. [Google Scholar]
- Bollen KA and Curran PJ (2004). Autoregressive latent trajectory (alt) models: A synthesis of two traditions. Sociological Methods & Research, 32(3):336–383. [Google Scholar]
- Bollen KA and Long JS (1993). Testing Structural Equation Models. Sage, Newbury Park, CA. [Google Scholar]
- Bollen KA, Ray S, Zavisca J, and Harden JJ (2012). A comparison of bayes factor approximation methods including two new methods. Sociological Methods & Research, 41(2):294–324. [Google Scholar]
- Bollen KA and Stine RA (1992). Bootstrapping goodness of fit measures in structural equation models. Sociological Methods & Research, 21(2):205–229. [Google Scholar]
- Cudeck R and Browne MW (1983). Cross-validation of covariance structures. Multivariate Behavioral Research, 18(2):147–167. [DOI] [PubMed] [Google Scholar]
- Fox J (2006). Structural equation modeling with the sem package in R. Structural Equation Modeling, 13(3):465–486. [Google Scholar]
- Hannan EJ and Quinn BG (1979). The determination of the order of an autoregression. Journal of the Royal Statistical Society. Series B (Methodological), 41(2):190–195. [Google Scholar]
- Haughton DMA (1988). On the choice of a model to fit data from an exponential family. The Annals of Statistics, 16(1):342–355. [Google Scholar]
- Haughton DMA, Oud JHL, and Jansen RARG (1997). Information and other criteria in structural equation model selection. Communications in Statistics, Part B - Simulation and Computation, 26(4):1477–1516. [Google Scholar]
- Homburg C (1991). Cross-validation and information criteria in causal modeling. Journal of Marketing Research, 28(2):137–144. [Google Scholar]
- Jöreskog K (1969). A general approach to confirmatory maximum likelihood factor analysis. Psychometrika, 34(2):183–202. [Google Scholar]
- Jöreskog K (1973). Analysis of Covariance Structures. Academic Press, New York. [Google Scholar]
- Jöreskog K and Sörbom D (1979). Advances in Factor Analysis and Structural Equation Models. Abt Books, Cambridge, MA. [Google Scholar]
- Kashyap RL (1982). Optimal choice of ar and ma parts in autoregressive moving average models. IEEE Transactions on Pattern Analysis and Machine Intelligence, 4(2):99–104. [DOI] [PubMed] [Google Scholar]
- Kass RE and Raftery AE (1995). Bayes factors. Journal of the American Statistical Association, 90(430):773–795. [Google Scholar]
- Kuha J (2004). AIC and BIC: Comparisons of Assumptions and Performance. Sociological Methods & Research, 33(2):188–229. [Google Scholar]
- McDonald RP and Marsh HW (1990). Choosing a multivariate model: Noncentrality and goodness of fit. Psychological Bulletin, 107(2):247–255. [Google Scholar]
- Paxton P, Curran PJ, Bollen KA, Kirby J, and Chen F (2001). Monte carlo experiments: Design and implementation. Structural Equation Modeling, 8(2):287–312. [Google Scholar]
- Raftery AE (1993). Bayesian model selection in structural equation models In Bollen KA and Long JS, editors, Testing Structural Equation Models, pages 163–180, Newbury Park, CA. Sage. [Google Scholar]
- Raftery AE (1995). Sociological Methodology, chapter Bayesian Model Selection in Social Research (with Discussion), pages 111–163. Blackwell, Cambridge, MA. [Google Scholar]
- Raftery AE (1999). Bayes factors and bic: Comment on a critique of the bayesian information criterion for model selection. Sociological Methods & Research, 27(3):411–427. [Google Scholar]
- Satorra A and Bentler PM (1988). Scaling corrections for chi-square statistics in covariance structure analysis In ASA 1988 Proceedings of the Business and Economic Statistics Section, pages 308–313, Alexandra, VA: American Statistical Association. [Google Scholar]
- Schnoll RA, Fang CY, and Manne SL (2004). The application of sem to behavioral research in oncology: Past accomplishments and future opportunities. Structural Equation Modeling, 11(4):583–614. [Google Scholar]
- Schwarz G (1978). Estimating the dimension of a model. Annals of Statistics, 6(2):461–464. [Google Scholar]
- Shipley B (2000). Cause and Correlation in Biology: A User’s Guide to Path Analysis, Structural Equations, and Causal Inference. Cambridge University Press, New York. [Google Scholar]
- Steiger JH and Lind JC (1980). Statistically based tests for the number of common factors Presented at the annual meeting of the Psychometric Society, Iowa City, IA. [Google Scholar]
- Sugawara HM and MacCallum RC (1993). Effect of estimation method on incremental fit indexes for covariance structure models. Applied Psychological Measurement, 17(4):365–377. [Google Scholar]
- Tucker LR and Lewis C (1973). A reliability coefficient for maximum likelihood factor analysis. Psychometrika, 38(1):1–10. [Google Scholar]
- Weakliem DL (1999). A Critique of the Bayesian Information Criterion for Model Selection. Sociological Methods & Research, 27(3):359–397. [Google Scholar]
- Winship C (1999). Editor’s Introduction to the Special Issue on the Bayesian Information Criterion. Sociological Methods & Research, 27(3):355–358. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.