Adaptable Mechanisms That Regulate the Contrast Response of Neurons in the Primate Lateral Geniculate Nucleus

Abstract

The response of the classical receptive field of visual neurons can be suppressed by stimuli that, when presented alone, cause no change in the discharge rate. This suppression reveals the presence of an extraclassical receptive field (ECRF). In recordings from the lateral geniculate nucleus (LGN) of a New World primate, the marmoset, we characterize the mechanisms that contribute to the ECRF by measuring their spatiotemporal tuning during prolonged exposure to a high-contrast grating (contrast adaptation). The ECRF was strongest in magnocellular cells, where contrast adaptation reduced suppression from the ECRF: adaptation of the ECRF transferred across spatial frequency, temporal frequency, and orientation, but not across space. This implies that the ECRF of LGN cells comprises multiple adaptable mechanisms, each broadly tuned but spatially localized, and consistent with a retinal origin. Signals from the ECRF saturated at high contrasts, and so adaptation of one part of the ECRF brought into its operating range signals from other parts of the visual field. Although the ECRF is adaptable, its major impact during contrast adaptation to a spatially extended pattern was to reduce visual response and hence reduce a neuron's susceptibility to contrast adaptation; in normal viewing, a major role of the ECRF might be to protect visual sensitivity in scenes dominated by high contrast.

Introduction

The contrast gain of many neurons in the visual pathway depends on the distribution of contrasts present in an image: gain is greatest when the overall contrast is low and least when contrast is high. This adaptive response can be explained by supposing that although a neuron's classical receptive field (CRF) (Barlow, 1953; Kuffler, 1953) provides a stable and approximately linear representation of image contrast, the output of the CRF is regulated by a fast acting “contrast gain control” (Shapley and Victor, 1979a; Bonin et al., 2005). In retina and dorsal lateral geniculate nucleus (LGN) of primate, contrast gain controls are more prominent in cells that are part of the magnocellular (M) pathway and much weaker in cells that are part of the parvocellular (P) pathway (Kaplan and Shapley, 1986; Benardete et al., 1992; Solomon et al., 2002, 2006; Alitto and Usrey, 2008).

Most models of the gain control suggest that it arises from many subunits, each sensitive to high spatial frequencies, the activity of which is rectified, pooled, and used to drive a suppressive mechanism (Shapley and Victor, 1979b; Bonin et al., 2005). The subunit pool is spread over a large region of the visual field, and so the gain control might be synonymous with the extraclassical receptive field (ECRF), a suppressive mechanism that envelops the CRF (Enroth-Cugell and Freeman, 1987; Jones et al., 2000; Felisberti and Derrington, 2001; Passaglia et al., 2001; Solomon et al., 2002; Bonin et al., 2005; Zaghloul et al., 2007). Recent work in retina suggests, however, that local and peripheral gain controls might operate through different mechanisms: whereas inhibitory signals from amacrine cells provide an ECRF from distal regions of visual space, contrast gain controls directly over the CRF might arise in the bipolar cells themselves (Rieke, 2001; Beaudoin et al., 2007; Zaghloul et al., 2007). Additionally, although neurons in LGN must inherit gain controls built in the retina (Cleland et al., 1983; Nolt et al., 2007; Alitto and Usrey, 2008), further gain controls might arise from interneurons within the LGN (Hubel and Wiesel, 1961; Levick et al., 1972; Nolt et al., 2007), or reflect feedback from the visual cortex (Sillito et al., 1993; Webb et al., 2005a; Nolt et al., 2007). Little is known about the functional properties of cortical neurons that provide feedback to the LGN, but it is likely that as with most cortical neurons, they are more selective than LGN neurons for the spatiotemporal structure of images (Briggs and Usrey, 2007).

We establish here the functional properties of LGN neurons during prolonged exposure to a modulated pattern; this experimental method is referred to in the literature as “habituation” or “contrast adaptation,” and we will refer to it as contrast adaptation. Contrast adaptation brings about a slow reduction in the responsivity of some retinal and LGN cells, and most neurons in visual cortex, that persists for several seconds after the removal of the adapting stimulus (Movshon and Lennie, 1979; Ohzawa et al., 1985; Sclar et al., 1985; Smirnakis et al., 1997; Brown and Masland, 2001; Chander and Chichilnisky, 2001; Baccus and Meister, 2002; Solomon et al., 2004; Duong and Freeman, 2007; Tailby et al., 2008). We distinguish the impact of this slow contrast adaptation from that of contrast gain controls, which provide a rapid regulation of responsivity. We will use the slow desensitization brought about in contrast adaptation to establish the contributions of different mechanisms to contrast gain control in the LGN.

Materials and Methods

Surgery.

Experiments were undertaken as part of a larger series on 10 adult male common marmosets (Callithrix jacchus jacchus), weighing between 300 and 400 g. All procedures conformed to the guidelines approved by Animal Ethics Committee of The University of Sydney. Each animal was initially sedated with an intramuscular injection of 12 mg/kg Alfaxan (Jurox) and 3 mg/kg diazepam (Roche). We then gave preoperative intramuscular injections of 0.2 mg/kg atropine (Pfizer), to reduce lung secretions, and 0.3 mg/kg dexamethasone (Maine Pharmaceuticals) to reduce inflammation. Subsequent surgery was performed under supplemental local anesthesia (2% Lignocaine; AstraZeneca Pharmaceuticals). A femoral vein was cannulated, the trachea was exposed, and an endotracheal tube was inserted. The head was placed in a stereotaxic frame, and a craniotomy was made over the right LGN.

Postsurgical anesthesia was maintained by continuous intravenous infusion of sufentanil citrate (4–12 μg/kg/h; Sufenta Forte; Janssen Cilag) in physiological solution (sodium lactate; Baxter International) with added dexamethasone (0.4 mg/kg/h; Mayne Pharma) and Synthamin 17 (225 mg/kg/h; Baxter International). The electrocardiogram and EEG were monitored continuously. Muscular paralysis was then induced and maintained by continuous infusion of pancuronium bromide (0.3 mg/kg/h; AstraZeneca Pharmaceuticals). The animal was artificially ventilated so as to keep end-tidal CO₂ near 33 mmHg. At any sign of the anesthesia becoming less effective, the dose of sufentanil citrate was increased. Rectal temperature was kept near 38°C with the use of a heating blanket. Additional antibiotic and anti-inflammatory cover was given daily by intramuscular injections of 25 mg of Noricillin and 0.1 mg of dexamethasone. The pupils were dilated with atropine sulfate, and the corneas were protected with high-permeability contact lenses that remained in place for the duration of the experiment. No artificial pupils were used. Supplementary lenses (with power determined by ophthalmoscopy, and subsequently adjusted to maximize the spatial resolution of P cells) were used to focus the eyes at a distance of 114 cm.

A small incision was made in the dura, and a guide tube containing the electrodes (single-electrode recordings: paralyene-coated tungsten, 5–10 MΩ; FHC; tetrode recordings: tetrodes, 2–5 MΩ; Thomas Recordings) was positioned in this. At the end of the experiment, the animal was given intravenous 500 mg/kg sodium pentobarbitone (Lethobarb; Verbac Australia) and perfused transcardially with 0.9% saline in 0.1 m phosphate buffer (PB), followed by a solution of 4% paraformaldehyde in PB. The brain was blocked and transferred to 30% sucrose in PB for cryoprotection. Coronal sections (50 μm) were cut on a freezing microtome and stained for Nissl substance. Electrode tracks were reconstructed from the positions of the lesions made during the experiment.

Visual stimuli and recording.

A front-silvered mirror was used to bring the receptive field onto the center of a calibrated cathode-ray-tube monitor (ViewSonic G810), refreshed at 100 Hz and viewed from 114 cm, at which distance it was 20° wide and 15° high. Visual stimuli were generated by a quad-processor Power Macintosh computer using custom software (EXPO; P. Lennie, University of Rochester, Rochester, NY); multiple independently controlled stimuli could be displayed simultaneously and were drawn using commands to OpenGL. The stimulus was usually a drifting sinusoidal grating presented within a circular window or annulus with hard edges; the remainder of the screen was held at the mean luminance (45 cd/m²). When making measurements, the stimuli in the set (one of which was always a blank screen) were presented in random order, each 5–10 times, in trials lasting 1 s. The analog signal from the electrodes was amplified, filtered, and sampled at 48 kHz by the same computer that generated the visual stimulus. Putative spikes were displayed on a monitor, and templates for discriminating spikes were constructed by analyzing multiple traces. The timing of waveforms that cohered to the template was recorded with an accuracy of 0.1 ms. Off-line analysis was performed using Matlab (MathWorks).

Cell identification.

For each cell, we determined the sign of response (ON, OFF), the tuning for temporal frequency and spatial frequency, and the contrast response. Along with the pattern of transitions between eye representations, and in two cases subsequent histological reconstructions, these measures were used to classify cells as part of the P or M pathway (Dreher et al., 1976; Derrington and Lennie, 1984; White et al., 2001). We usually used reverse correlation methods to establish the spatial location of the receptive field for subsequent experiments. Cells that could not be reliably classified as P or M, including those in which the receptive field received strong input from the short-wavelength sensitive (“blue”) cones, are not included in the following analyses. Receptive fields were located within 15° of the fovea. ON- and OFF-center cells were not distinguished by the impact of contrast adaptation and are pooled in what follows.

Measuring the impact of the ECRF.

We believe the CRF and ECRF overlap substantially in space. To determine the impact of the ECRF, we used a variant of masking: a small central patch of drifting grating was surrounded by an annulus of the same spatial frequency, which was slightly higher than that preferred by the neuron. The size of the central patch was that preferred by the neuron. The inner diameter of the annulus was chosen such that it produced strong suppression with a minimum modulation of the firing rate.

The central patch and concentric annulus were centered on the receptive field: the patch grating and annulus grating drifted in the same direction, at different temporal frequencies (5.5 and 8.3 Hz, respectively) (Bonds, 1989; Bonin et al., 2005). From the train of impulses discharged during each stimulus presentation, we extracted the amplitude of the Fourier component at the temporal frequency of the grating in the central patch. We are interested in the steady-state response, and so we discarded the first 0.15 s of response before subjecting the spike train to Fourier analysis. We use the annulus to stimulate the ECRF, rather than superimposing that grating on the central patch (Bonin et al., 2005), because we will use that spatial segregation to selectively adapt the ECRF. The different temporal frequencies of the two gratings ensure that any residual activation of the CRF by the annular grating does not interfere with the target measurements.

Contrast adaptation.

Measurements were made in control and adapted states for each of several stimulus manipulations. In each case, the adaptor was a drifting grating of maximum contrast, confined to either the central patch or the surrounding annulus, or present in both. Unless stated otherwise, the spatial frequency of the adaptor was the same as that of the test and drifted at 5–8 Hz. In making measurements during adaptation, each test grating was presented for 1 s, separated by a 3–4 s adaptation, after an initial adapting period of 30 s. In making control measurements, the adapting gratings were replaced with a uniform field of the mean luminance; control measurements were made before adaptation and again at least 3 min after the end of the adapting stimulus, during which time the screen was held at the mean luminance. The responses before and after adaptation were always of similar amplitude, so we combined these measurements to provide the “control” state.

Model.

Most of our stimuli are composed of central and annular gratings whose contrast was varied independently. To provide a robust description of adaptation, we considered a family of divisive models described in detail previously (Cavanaugh et al., 2002). We ignore response phase and concentrate on response amplitude. Any reasonable model needs to account for two major phenomena. First, it must provide for saturation in response as the contrast of the central patch increases. Second, it must allow the annular grating to modify that contrast response. As in most models of contrast gain control, the response amplitude (R) grows nonlinearly with contrast (c) of the central patch:

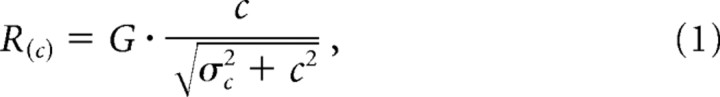where G is the response gain of the cell under study and σ_c is the inflection point of the contrast response; σ_c indicates the strength of signals from contrast gain controls activated by the central grating patch.

Models of suppression from the ECRF can be divided into two broad categories: in the contrast gain model, the presence of the annular grating changes only the denominator in Equation 1 (see also Bonin et al., 2005); in the response gain model, it changes the magnitude of the response gain term (G) in Equation 1. Although a full description of cell activity might require elements of both (Nolt et al., 2007), which we return to in Results, in the experiments here the response gain model provided good predictions. As we will show, increasing the contrast of the annulus did not always lead to increased suppression, so the model used here provides the capacity for saturation in the amount of suppression (Solomon et al., 2002). The amount of suppression (S) depends on the contrast of the annulus (s):

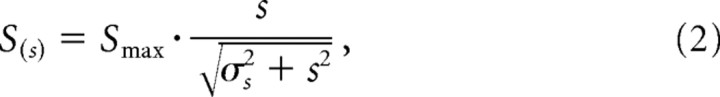where S_max is the maximum suppression. σ_s is the inflection point for the contrast response of suppression and therefore provides for saturation in the amount of suppression recruited by the annulus.

To implement the response gain model, we express the cell response gain, G in Equation (1), as a function of annulus contrast:

where K is the maximum gain. When we use the model to describe the responses to the central patch alone, the annulus contrast is zero and Equations 2–3 are irrelevant, so we estimated σ_c and G. Responses to the central test alone were often greater during adaptation to the annulus than in the control state, but we were interested in the impact of the annular adaptor on suppression evoked by that annulus. We therefore normalized the responses to that at zero annulus contrast, separately for each of the control and adapted states, so in each state the curve is determined by S_max and σ_s. In most cases, we wanted a simple metric with which to express the change in responses during adaptation. To do this, we fit the responses in the control and adapted state at the same time. To describe adaptation to the central patch, we allowed adaptation to change σ_c. To describe adaptation to the annulus, we allowed σ_s to change. In all cases, the fitting procedure (the function lsqnonlin provided by Matlab) minimized the square error between the predictions and the observed responses [here always the average Fourier component (F1) at the modulation frequency of the central patch]. The predictions were good, leaving, on average, <10% of the response variance unexplained (Carandini et al., 1997) and usually <5%.

Statistical tests.

Unless noted otherwise, we use a two-tailed, paired Student's t test to evaluate adaptation-induced changes in response. We usually characterize the percentage increase in the target variable; that is, if the variable increased during adaptation from 1 to 1.5, this would be an increase of 150%.

Results

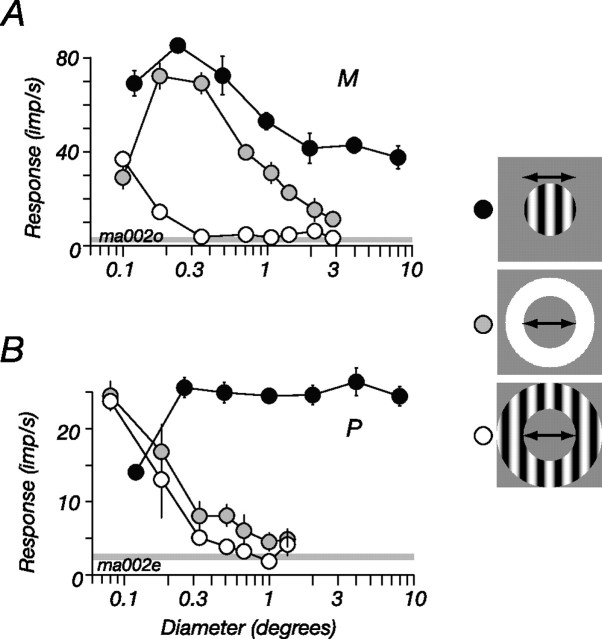
We distinguish two mechanisms in the receptive field of LGN cells: the CRF and the ECRF. The CRF is a linear mechanism whose activity can directly evoke action potentials in the neuron under study (Rodieck, 1965); the ECRF is a mechanism(s) whose activity modulates the responsivity of the CRF, usually by suppressing it. These two components of the receptive field overlap in space, but they can be substantially isolated with appropriate stimuli. This is shown for an M cell in Figure 1A, where we measured responses to gratings of high spatial frequency, windowed into circular patches or annuli. The gratings were of high enough spatial frequency that they were invisible to the “surround” component of the CRF. Small patches of drifting grating mainly recruit activity from the center mechanism of the CRF, and responses at first increased with patch size (Fig. 1, filled symbols), reflecting increasing activation of the CRF. Larger patches of grating activate both the CRF and the ECRF, and response at larger sizes therefore reflects the balance of activity in the two mechanisms: as the patch diameter increased from 0.4 to 2°, response halved.

Figure 1.

Spatial summation in P and M cells in marmoset LGN. A, M cell. B, P cell. Each curve plots the amplitude of response at the frequency of stimulation (F1). The filled symbols show responses to drifting gratings presented within a circular patch, the outer diameter of which was varied. The open symbols show responses to an annular patch of the same drifting grating, the inner diameter of which was varied. The shaded symbols show responses to an annulus that contained a uniform field modulated in time: the inner diameter of the annulus was varied. For both the P and M cell, the inner diameter of the annular grating had to be <0.5° to elicit a response, whereas the uniform annuli evoked responses at most inner diameters. For the P cell, responses to circular patches of drifting gratings rapidly increase with patch size and then asymptote. For the M cell, responses to the patches first increase with patch size, then decrease; this decrease (suppression) reveals the presence of an ECRF. Temporal frequency, 5 Hz; contrast, 0.5; spatial frequency, 2 cycles/° (A) or 3 cycles/° (B). In this and all subsequent figures, the error bars show ±1 SEM.

The reduction in response as patch diameter increased from 0.4 to 2° implies that suppression is being recruited from an ECRF, because when the inner diameter of an annular grating (Fig. 1, open symbols) spanned this same region, there was no modulation in the discharge rate of the M cell and therefore no activation of the CRF. Yet although the ECRF is larger than the CRF center, it might be no larger than the CRF surround (Bonin et al., 2005; Nolt et al., 2007): when measurements were made with an annulus that contained a uniform field modulated in time, a stimulus that lies within the bandpass of the CRF surround, it generated robust responses at most inner diameters (Fig. 1A, shaded symbols). In the following experiments, we used the tuning curves for patches and annuli (Fig. 1, open and filled symbols) to find for each cell the regions that preferentially drive the CRF or the ECRF: because the ECRF remains active at high spatial frequencies, we can use annular gratings to activate it without activating the CRF.

Although an ECRF can be revealed in P cells, it is generally much weaker (Fig. 1B), and it is therefore difficult to isolate. To illustrate this we estimated suppression from size tuning curves using a suppression index: 1 − (R_large/R_opt), where R_large is the response to a 10° diameter grating and R_opt is the response to a grating of optimal size. In 66 P cells, the mean suppression index was 0.29 (median, 0.27; SD, 0.16); in 69 M cells, the mean suppression index was 0.52 (median, 0.55; SD, 0.19) (Solomon et al., 2002, 2006; Alitto and Usrey, 2008).

Strong contrast adaptation in M cells of marmoset LGN

We first need to show that neurons in the marmoset LGN are susceptible to contrast adaptation. Previous work in macaque LGN shows that M cells are strongly desensitized by contrast adaptation and P cells less so (Solomon et al., 2004; Tailby et al., 2008). This is also the case in marmoset LGN. Figure 2, A and B, shows the impact of contrast adaptation on one P cell and one M cell; the adapting and test stimuli were gratings drifting at 5.5 Hz, confined to a small patch centered on the CRF. The size of this patch was the optimal for each cell, determined as in Figure 1. Contrast adaptation substantially reduces the response of the M cell at all stimulus contrasts. The response of the P cell is less affected by adaptation.

Figure 2.

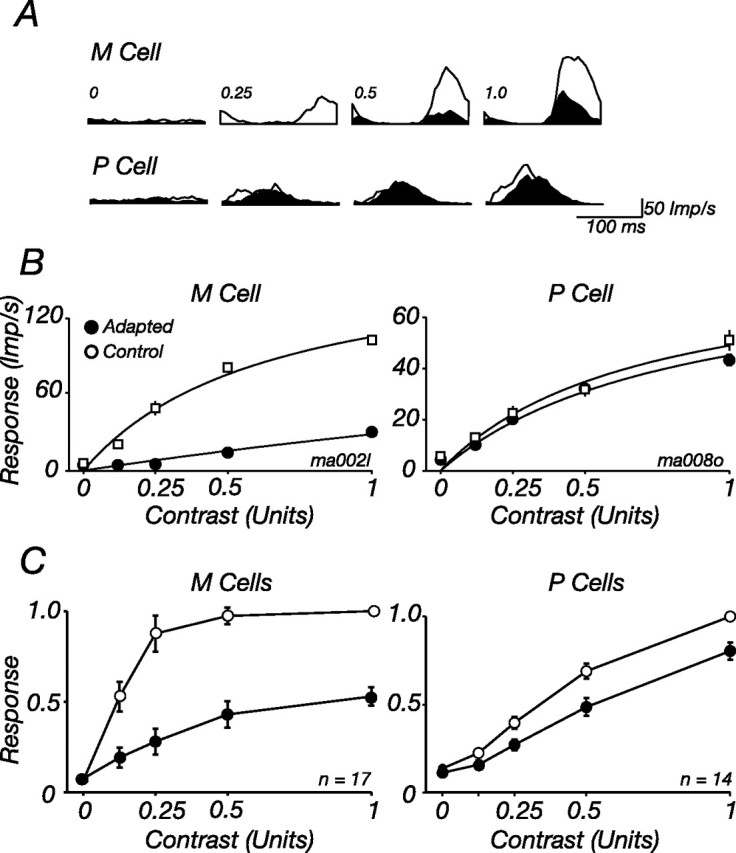
Contrast adaptation reduces the contrast sensitivity of M cells in marmoset LGN. A, Peristimulus time histograms (PSTHs) showing modulation of the discharge in response to a grating drifting at 5.5 Hz, sampled in 1 s epochs during adaptation to a high-contrast grating of optimal size and spatial frequency (shaded histograms, Adapted) or a blank screen (open histograms, Control). PSTHs are shown for four contrasts of the grating for one M cell (top) and one P cell (bottom). B, Response amplitude (F1) as a function of stimulus contrast, for tests presented during adaptation to a high-contrast grating (filled symbols) or blank screen (open symbols). The same cells as in A are shown. Solid lines show best-fitting predictions of Equations 1–3, where for each cell only σ_c was allowed to vary. Temporal frequency, 5.5 Hz; diameter, 0.5° (P cell) or 0.4° (M cell); spatial frequency, 3 cycles/° (P cell) or 3.2 cycles/° (M cell). C, Average for all M and P cells in our sample. (1 M cell was tested at different contrasts and is excluded from the plot). Responses of each cell were normalized to the maximum obtained in the control state before averaging.

To describe the impact of adaptation, we fitted a form of the Naka-Rushton model to the contrast response (Eq. 1; see Materials and Methods), allowing only contrast sensitivity (which is defined by the parameter σ_c) to vary between the control and adapted states. In M cells adaptation brought about a large reduction in contrast sensitivity (σ_c increased to 535% of its control value; SD, 200; n = 18). Adaptation had less effect on P cells, where it increased σ_c to 144% of its control value (SD, 132; n = 14). Figure 2C summarizes the impact of adaptation on M and P cells in our sample: for each cell, responses were normalized to the maximum obtained in the control state, and these normalized responses were averaged across cells.

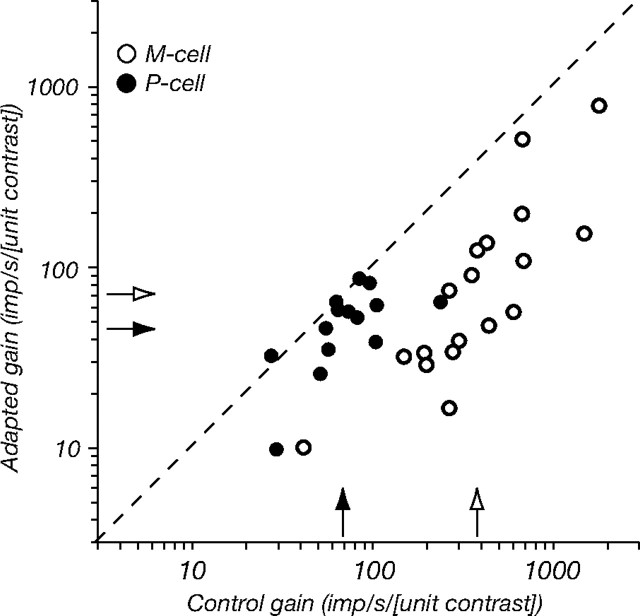
M cells respond more robustly to low-contrast gratings than do P cells, and this is reflected in the contrast response curve by a steeper slope at very low contrasts. This slope is the contrast gain, which has units of (imp/s/[unit contrast]) and can be estimated from Equation 1 as G/σ_c. Figure 3 compares contrast gain in the control and adapted states for all cells in our sample. Adaptation has such a large effect on M cells that whereas in the control state the contrast gain of M cells is fivefold greater than that of P cells, during adaptation it is only twice as great.

Figure 3.

Contrast adaptation reduces the difference in contrast gain of P and M cells. Contrast gain (obtained from Eq. 1: G/σ_c) of 14 P cells (filled symbols) and 18 M cells (open symbols) for gratings of optimal size and spatial frequency, in control conditions (abscissa) and during adaptation to a high-contrast grating of the same configuration (ordinate), is shown. Arrows on the ordinate and abscissa show the geometric mean contrast gain for P cells (filled arrows) and M cells (open arrows). In the control state, this average gain of M cells was 382 imps/s/[unit contrast], and in the adapted state it was 72. For P cells, these values were 72 and 45, respectively.

Impact of contrast adaptation covaries with response to the adapting stimulus

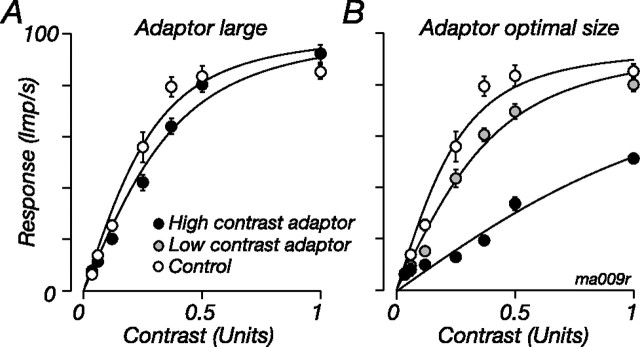
The reduction in the sensitivity of marmoset M cells that adaptation brings about is much greater than we reported for M cells in macaque LGN (where the average increase in σ_c was ∼180%) (Solomon et al., 2004). The work in macaque used large gratings (diameter, ∼8°) for the adaptor and test, whereas here the adapting and test gratings are confined to a small region over the receptive field (usually ∼0.5° in diameter). In most visual neurons, the impact of an adapting stimulus is proportional to the response it evokes (Barlow and Hill, 1963; for example, see Carandini et al., 1998; Sanchez-Vives et al., 2000; for review, see Kohn, 2007), so the adapting grating should have a greater impact when it is smaller in size, because it recruits less suppression from the ECRF and is therefore more effective at driving the cell. This is the case: for eight M cells, we measured contrast response during adaptation to large patches of drifting grating (diameter, 8°) and to patches of optimal size; the test stimulus was always the optimal size. Figure 4 shows for one M cell that when the adapting stimulus was large (and therefore not as effective a stimulus for the cell) (Fig. 4A, filled symbols), it increased σ_c from 0.36 to 0.47 (128% of control value). When the adapting stimulus was smaller and more effective (Fig. 4B, filled symbols), adaptation increased σ_c to 411% of control. Across the eight cells tested, large adaptors increased σ_c 171% (SD, 48) and smaller adaptors increased it 542% (SD, 127) of control.

Figure 4.

The impact of contrast adaptation depends on the size and contrast of the adapting grating. A, Contrast response for a patch of drifting grating of optimal diameter (0.3°) during adaptation to a patch of high-contrast grating of diameter 8° (filled symbols) or to a blank screen (open symbols). B, Same as A, but the adapting grating was smaller (diameter 0.3°) and of high contrast (contrast, 1.0; filled symbols) or low contrast (contrast, 0.2; shaded symbols). Solid lines show best-fitting predictions of Equations 1–3, where for each adaptor only σ_c was allowed to vary. Temporal frequency, 5.5 Hz; spatial frequency, 1.8 cycles/°. The low-contrast adaptor evoked 39.6 imp/s; the large high-contrast adaptor evoked 46.0 imp/s; the small high-contrast adaptor evoked 64.0 imp/s.

If response magnitude is an important variable in contrast adaptation, then adaptation should be much less when the adapting stimulus is small but of low contrast. In five M cells we compared the impact of adaptation for large adaptors of high contrast and for small adaptors of low contrast that drove the cell to a similar response. The results are shown for the cell in Figure 4B by the shaded symbols: small low-contrast adaptors induced a small change in the contrast response (σ_c increased to 151% of the control value), about that induced by a large high-contrast grating (Fig. 4A). Across the five cells tested, the small low-contrast adaptors and large high-contrast adaptors increased σ_c in a similar way (μ 141%, SD 24 vs μ 167%, SD 103; p = 0.59). Suppression therefore seems to exert its effect before the major site of contrast adaptation; if it is engaged, it reduces the impact of the adapting stimulus as if reducing the effective contrast of the adaptor.

The response of retinal and LGN cells depends on the temporal frequency of a drifting grating, so if the magnitude of adaptation is proportional to the response evoked by the adaptor, then it should depend on the temporal frequency of the adaptor. To test this, we measured the contrast response during adaptation to high or low temporal frequency (which evoke strong and weak responses, respectively); the adaptor was always small and of the same high spatial frequency as the test, and the test always drifted at 5.5 Hz. Adaptation was stronger when the adaptor drifted at high frequency [a 16 Hz adaptor increased σ_c to 934% of control (SD, 709; n = 12), much more than a 1 Hz adaptor (179%; SD, 221; n = 15) (see also Solomon et al., 2004). The impact of adaptation was always less pronounced in P cells: a 1 Hz adaptor increased σ_c to 103% (SD, 40; n = 10) and a 16 Hz adaptor increased σ_c to 131% (SD, 45; n = 12) of control.

The ECRF is desensitized in contrast adaptation

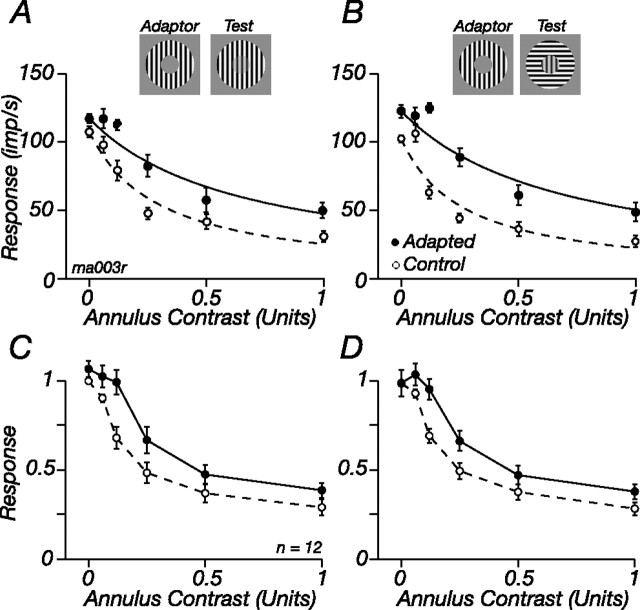
We now ask whether suppression from the ECRF can be reduced in contrast adaptation. To measure the contrast sensitivity of the ECRF, we concurrently presented a central test patch and surrounding annulus. Both were of the same high spatial frequency; the contrast of the central test was always 0.5 and that of the annulus varied. The responses of one M cell and one P cell (the same cells shown in Fig. 2) are shown by the open histograms (folded to one cycle of drift of the central test) in Figure 5A: as the contrast of the annular grating increased, the response to the test grating diminished, particularly in the M cell. We adapted the ECRF in the same way as above, except that this time the adapting gratings were confined to the annular region; during the adaptation phase, the central region was held at the mean luminance. The filled histograms in Figure 5A show the responses of the two cells during adaptation to the annular grating; at a given annulus contrast, response is higher, and suppression therefore weaker, during annular adaptation than during adaptation to a gray screen. The reduction in suppression was most pronounced at low contrasts of the annular grating.

Figure 5.

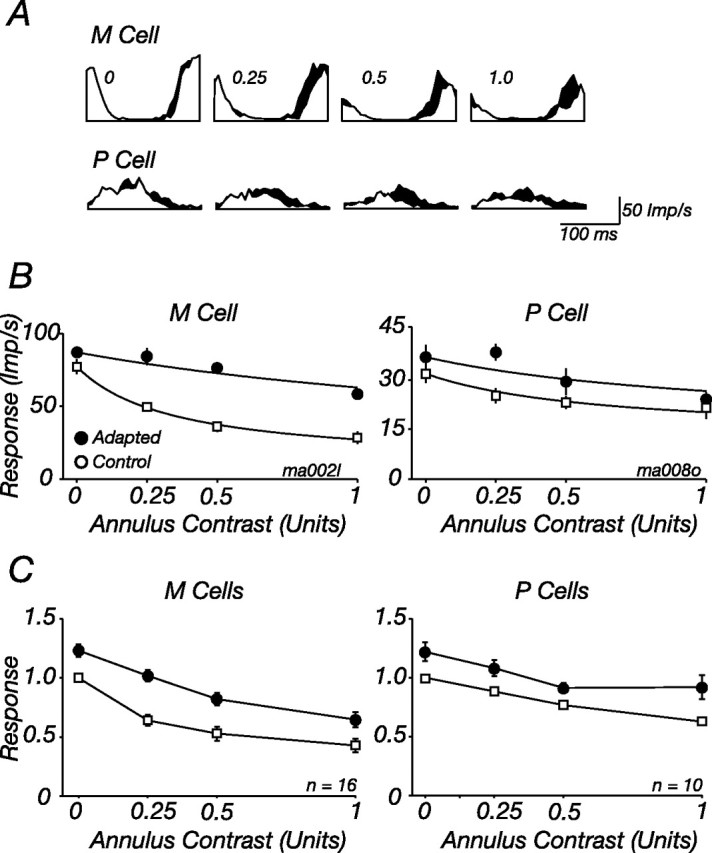
Contrast adaptation reduces suppression from the ECRF. A, Peristimulus time histograms (PSTHs) showing modulation of the discharge in response to a central patch of grating drifting at 5.5 Hz, in the presence of a surrounding annuli drifting at 8.3 Hz. Responses during adaptation to a high-contrast annulus grating (shaded histograms, Adapted) or a blank screen (open histograms, Control) are shown. PSTHs are shown for four contrasts of the annulus grating for one M cell (top) and one P cell (bottom). B, Response amplitude at the temporal frequency of the central patch (F1) as a function of annulus contrast, for tests presented during adaptation to a high-contrast annulus (filled symbols) or blank screen (open symbols). The same cells as in A, which are also shown in Figure 2, are shown. Solid lines show best-fitting predictions of Equations 1–3, where for each cell only σ_s was allowed to vary. Contrast of central patch, 0.5; diameter of central patch, 0.5° (P cell) or 0.4° (M cell); spatial frequency of central and annular patch, 3 cycles/° (P cell) or 3.2 cycles/° (M cell). C, Average for all M and P cells in our sample. (1 M cell was tested at different contrasts and is excluded from the plot). Responses of each cell were normalized to the maximum obtained in the control state before averaging.

Figure 5 shows that suppression from the ECRF is susceptible to contrast adaptation. Prolonged exposure to a high-contrast annulus reduces the suppression evoked by low-contrast annular gratings (including where annulus contrast was 0, a point we return to below), and this was more prominent in M cells than in P cells. To describe the change in suppression, we calculated metrics similar to those used above (see Materials and Methods); responses to the test are divided by the activity of the ECRF (Eq. 3), whose contrast–response is itself described by a Naka-Rushton function (Eq. 2). Adaptation was well described by a change in the contrast sensitivity of suppression (σ_s), such that adaptation to annuli drifting at 8 Hz reduced the contrast sensitivity of suppression (i.e., increased σ_s) to 273% of the control value (SD, 120; n = 14; three cells were omitted where fits explained <75% of the response variance).

Suppression in P cells is weaker than that in M cells (Figs. 1B, 5C), and it is therefore harder to measure changes in it. In 10 P cells where suppression was evident, we measured the impact of adaptation to annular gratings. Annular adaptation to gratings drifting at 8 Hz reduced the contrast sensitivity of this suppression, on average to 209% (SD, 161) of the control value. This reduction is less than that found in M cells, but not significantly so (p = 0.8, Student's t test).

As is done in Figure 2C, Figure 5C summarizes the impact of annular adaptation on the M and P cells in the sample: for each cell, responses were normalized to the maximum obtained in the control state, and these normalized responses were then averaged across cells. Annular adaptation reduced the contrast sensitivity of suppression in M cells and increased the response to the central test stimulus even when there was no stimulus in the annular region (we return to this later); there is less change in the contrast sensitivity of suppression in P cells, but across the range of annular contrasts responses increase.

Adaptable ECRF mechanisms show broad spatiotemporal sensitivity

If the LGN ECRF is built in a feedforward manner, without input from visual cortex, the spatiotemporal tuning of the mechanisms should be as broad as that of most retinal and LGN neurons, and so the impact of adaptation will transfer across orientation and spatial and temporal frequency (Solomon et al., 2004; Duong and Freeman, 2007). Conversely, if the ECRF is built on feedback from the visual cortex, the mechanisms providing it will be sharply tuned, and we expect that the impact of adaptation will depend on the relative configuration of the adaptor and test.

To determine the orientation tuning of the ECRF, we measured the contrast sensitivity of suppression for two sets of annular gratings, one of which was the same orientation, and drifted in the same direction, as the central test, and one of which was orthogonal to the central test; the test was usually a contrast of 0.25. In the unadapted state, the contrast sensitivity of suppression did not depend on the orientation of the annulus: the open symbols in Figure 6, A and B, show for one cell that the contrast sensitivity of suppression was the same at each orientation, and across the nine cells tested, there was no difference (p = 0.48) (Figs. 6C,D). To determine whether this broad tuning arose from pooling across narrowly tuned adaptable mechanisms, we then made the same measurements during adaptation to an annular grating of the same orientation as the central test. The impact of adaptation on suppression was characterized in the same way as above, allowing different parameters for each orientation of the annulus. The filled symbols in Figure 6 show that adaptation of the ECRF was not orientation selective: during adaptation, σ_s increased to 241% of control at the adapted orientation and to 253% at the unadapted orientation. Across the nine cells tested, adaptation increased σ_s at the adapted orientation 191% (SD, 60) and at the unadapted orientation 204% (SD, 85; p = 0.51). This suggests that the adaptable ECRF subunits are not tuned for orientation.

Figure 6.

Adaptation of the ECRF transfers across orientation. A, B, Response of an M cell to a central patch in the presence of annuli of the same orientation as that patch (A), or the orthogonal orientation (B), in the control state and during adaptation to an annulus of the same orientation as the patch. Central patch contrast, 0.5; diameter, 0.6°; spatial frequency, 0.8 cycles/°. C, D, Average response of 12 cells in the control state and during annular adaptation; the response of each cell was normalized to the maximum obtained in the control state before averaging. C, Test annuli at the same orientation as the patch and the adaptor. D, Test annuli orthogonal to the adaptor. Conventions are as in Figure 5B.

We measured the spatial frequency bandwidth of adaptable subunits in a different way. We were concerned that because annular gratings of low spatial frequency will robustly stimulate the classical surround, it might be difficult to disentangle the contribution of the classical surround and the ECRF to cell responses. We therefore measured spatial frequency tuning for a single, large patch of grating (diameter, 8°), before and during adaptation to an annular grating of high spatial frequency. The contrast of the test grating was usually 0.5. If the ECRF arises in subunits that are tuned to a narrow range of spatial frequencies, as are cortical neurons, then adaptation should only reduce suppression (i.e., increase response) in the vicinity of the adapted frequency. If instead the subunits of the ECRF are broadly tuned, as are most retinal and LGN neurons, adaptation should increase response across a broad range of frequencies.

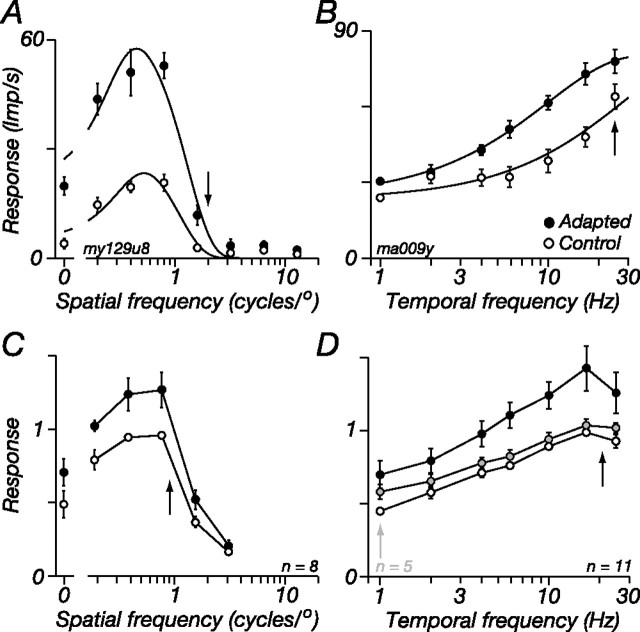
Figure 7A shows this test for one M cell: annular adaptation at high spatial frequencies increases response at all spatial frequencies of the test, and so the tuning curves in the adapted and control states resemble scaled versions of each other. In none of the cells tested did we see localized changes in response near the adapted frequency. To quantify this, we fit the classical difference-of-Gaussians model (Croner and Kaplan, 1995) to the frequency responses before and during adaptation, allowing all parameters to vary between states. This model does not incorporate an ECRF, so adaptation will be reflected in changes to the classical center and surround receptive field mechanisms. Adaptation had no effect on the space constants of the center or surround Gaussians so measured (adaptation reduced center size to 89.7%, SD 15.9, of its control value, and increased surround size to 117.4%, SD 20.9; p = 0.08 and 0.06, respectively); during adaptation, the volume of the center increased slightly more than the volume of the surround (center: to 129.2%; SD, 32.5 of control; surround: to 121.6%; SD, 22.4), but this was not significant (p = 0.35), so the shape of the spatial tuning curve is little changed by adaptation (Duong and Freeman, 2007). In 8 of the 11 cells tested in this way, the adapting spatial frequency was between 0.8 and 1.2 cycles/° (geometric mean, 0.95). To show how adaptation changed the spatial tuning of cells across our sample, Figure 7C shows the average responses of these cells (responses were normalized to the maximum achieved in the control state before averaging). Adaptation increases response across all spatial frequencies to which the cells responded.

Figure 7.

Adaptation of the ECRF transfers across spatial and temporal frequency. A, Response of an M cell as a function of spatial frequency for a large (diameter, 8°) patch of drifting grating, in the control state and during adaptation to an annular grating of high spatial frequency. Contrast, 0.2; temporal frequency, 5 Hz. B, Response of another M cell as a function of temporal frequency for a large patch of grating, in the control state and during adaptation to an annular grating of high temporal frequency. Contrast, 0.25; spatial frequency, 1 cycle/°. C, Average spatial frequency tuning curves of a subset of M cells where the annular adaptor was a grating of spatial frequency between 0.8 and 1 cycle/° (μ = 0.95; SD, 0.14). D, Average response of all M cells during adaptation to an annular grating of optimal spatial frequency, drifting at 16 or 25 Hz (n = 11; filled symbols). A subset (n = 5) was also tested during annular adaptation to a grating that drifted at 1 Hz (shaded symbols). The average control response (open symbols) of this subset could not be distinguished from the average response of all 11 cells and is omitted for clarity. Arrows show the adapting frequencies, which were 2 cycles/° and 8.3 Hz (A) or 1 cycle/° and 25 Hz (B). Smooth lines show the best predictions of the descriptive model described in Results. In C and D, the response of each cell was normalized to the maximum obtained in the control state before averaging.

In 11 M cells, we measured the transfer of ECRF adaptation across temporal frequency. The spatial frequency of the test grating was the preferred for the cell, 8° in diameter and usually a contrast of 0.5; the adaptor was an annular grating. The results of this experiment are shown for one M cell in Figure 7B: during ECRF adaptation to a 25 Hz annular grating response increases at all temporal frequencies. Figure 7D shows for all cells in our sample how adaptation to a high temporal frequency (25 Hz; black symbols) annulus changed response. For each curve, responses were normalized to the maximum achieved in the control state and averaged across cells. The highest temporal frequency that we could test was 25 Hz, and we could not characterize the impact of adaptation on the high-frequency limb of the temporal response curve. To determine the impact of adaptation on individual cells, we nevertheless fit a difference-of-exponentials function (Derrington and Lennie, 1984) to the responses and from this calculated (1) the lowest frequency at which response was half the maximum obtained and (2) the ratio of the maximum response to the response at the lowest frequency tested (which was 1 Hz). If adaptation to high-frequency annuli selectively increases the response to high frequencies, then the tuning curve should become more bandpass, and both these indices will increase. Neither index showed significant changes between the adapted and control states (p = 0.57 and p = 0.17, respectively), so the shape of the temporal tuning curve is little changed by adaptation to high temporal frequencies. In five cells we measured the impact of a low-frequency adaptor on the temporal response (1 Hz) (Fig. 7D, gray symbols). The low-frequency adaptor had much less of an effect on response than the high-frequency adaptor; its impact was generally the same at all temporal frequencies.

For some cells, we also measured the contrast response of the ECRF (as in Fig. 5) during adaptation to annuli of high or low temporal frequency; the test annulus always drifted at 8 Hz. An annular adaptor drifting at 16 Hz was more effective than one drifting at 1 Hz, with adaptation respectively increasing σ_s 322% (SD, 280; n = 7) and 157% (SD, 143; n = 9), consistent with the idea that although the temporal frequency tuning of the ECRF is broad, it is more sensitive to high frequencies than low frequencies (Bonin et al., 2005; Solomon et al., 2006).

In summary, adaptation to an annular grating elevates response across all spatial and temporal frequencies to which a cell responds. This, together with the absence of orientation selectivity of ECRF adaptation (Fig. 6), implies that the subunits of the ECRF are broadly responsive to spatiotemporal pattern.

The ECRF is composed of independently adaptable subunits

All models of ECRF suppression suppose that it arises in the output of many subunits whose outputs are rectified. These subunits might provide a direct suppressive input to the neuron under study, or their activity might first be pooled, providing an estimate of local contrast with which to regulate the sensitivity of the CRF (Shapley and Victor, 1979b; Shapley et al., 1981; Bonin et al., 2005; Webb et al., 2005a). If signals from the subunits are pooled, then this mechanism might be revealed in contrast adaptation: adaptation within subunits will be spatially specific, and adaptation after their pooling will not be.

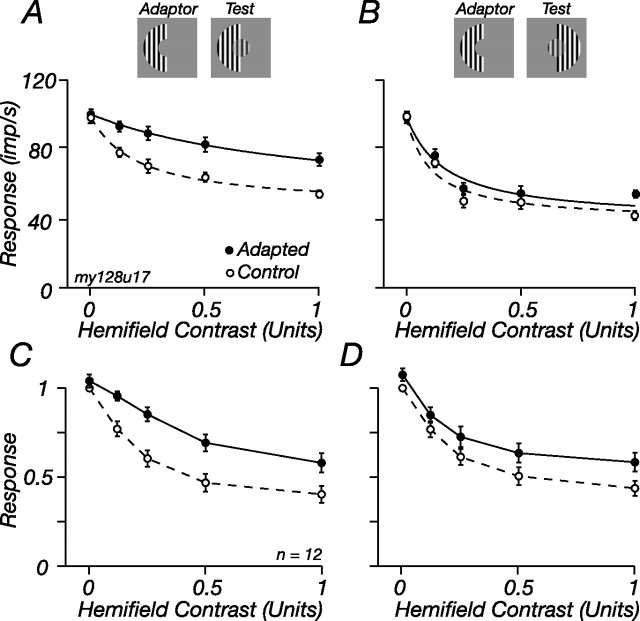
To determine the spatial specificity of adaptation, we divided the annulus into two equal hemifields and measured suppression from each hemifield before and during adaptation confined to one of them. Figure 8 shows that adaptation reduced suppression from the adapted side much more than it reduced suppression from the unadapted side. For the M cell in Figure 8, A and B, adaptation increased σ_s 442% in the adapted hemifield and 140% in the unadapted hemifield. Across the population of 12 M cells in which we made these measurements, σ_s in the adapted hemifield increased 347% (SD, 41), and in the unadapted hemifield it increased 174% (SD, 54; p < 0.001) (Fig. 8C,D). The small transfer of adaptation might imply that some adaptation occurs after integration of signals from the two sides, but it is also expected if there are subunits that span the adapted and control hemifields.

Figure 8.

Adaptable ECRF mechanisms are spatially localized. The response of an M cell to a central patch in the presence of varying contrasts of half an annulus (hemifield), in the control state (open symbols) and during adaptation to a high-contrast hemifield (filled symbols). A, Responses in the control and adapted state for the hemifield that was adapted. B, Same as in A, but for the unadapted hemifield. Central patch contrast, 0.5; diameter, 1°; spatial frequency, 1 cycle/°. C, D, Average response of 12 cells in the control state and during adaptation to an annular hemifield; the response of each cell was normalized before averaging. C, Test stimuli in the same hemifield as the adaptor. D, Test stimuli in the other hemifield. Conventions are as in Figure 5B.

Spatial summation of suppression and the impact of adaptation

So far we have described the impact of adaptation on the ECRF by a change in σ_s. This parameter is the inflection point of the ECRF contrast–response function: if the value of σ_s is sufficiently low, then suppression saturates at high contrasts. This might reflect saturation in the subunits themselves, or after summation of their signals (Webb et al., 2005a).

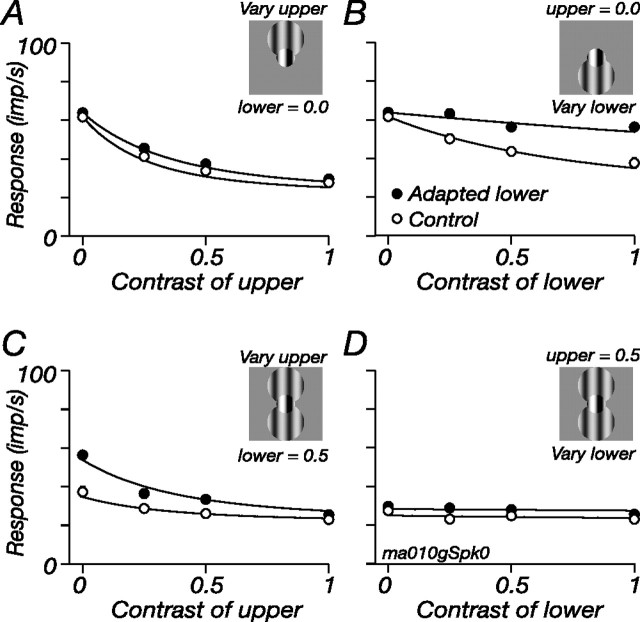
To test this, we determined how suppressive signals from different regions of the ECRF are combined. We constructed a tripartite stimulus, as shown in Figure 9. The central test region was defined in the usual way and was a contrast of 0.25. The ECRF stimulus was two patches of grating, one above (“upper”) and one below (“lower”) the test: the contrast of the upper and lower annular gratings varied independently. Figure 9 shows the resultant contrast response curves of one M cell. The open symbols show the responses in the control state, and the filled symbols show responses during adaptation to the lower patch, which we address below. The open symbols in Figure 9A show that the upper grating elicited robust suppression; when the same measurements were made in the presence of the lower grating (Fig. 9C), the upper grating provided only moderate additional suppression. Figure 9, B and D, shows similar measurements, but as a function of contrast in the lower grating: without an upper grating, the lower grating elicited strong suppression but added little if there was already a grating in the upper patch. All this is consistent with saturation in the ECRF after the pooling of its signals (Webb et al., 2005a).

Figure 9.

Pooled signals of adaptable ECRF subunits are subject to a compressive nonlinearity. For a full description of the figure, see Results. A central test grating (contrast, 0.25) abutted two discs whose contrast varied independently, the spatial arrangement of which is indicated by the insets. Each panel shows the modulated response at the frequency of stimulation of the central patch (5.5 Hz). A, C, Response as a function of the contrast of the grating in the upper disc. A, The lower disc was held at zero contrast. C, The lower disc was a drifting grating (8.3 Hz) of contrast 0.5. B, D, Response as a function of the contrast of the grating in the lower disc. B, The upper disc was held at zero contrast. D, The upper disc was a drifting grating of contrast 0.5. In all panels, the open symbols show responses in the control state, and filled symbols show responses during adaptation to a high-contrast grating confined to the lower disc. Lines show the predictions of the model described in Results (Eq. 4). Central patch diameter, 0.7°; disc diameters, 1.4°; spatial frequency of all gratings, 0.8 cycles/°.

Figure 9 confirms that the major site of contrast adaptation is before summation of ECRF signals across space (as in Fig. 8) and, furthermore, that adaptation might have little effect on the subsequent nonlinearity. The filled symbols in Figure 9 show response during adaptation to the lower patch. Figure 9B shows that adaptation reduced suppression from the lower patch; Figure 9A shows that suppression from the upper patch was unaffected; Figure 9C shows that when the lower patch was adapted, additional suppression could be accumulated from the upper patch; Figure 9D shows that the reverse is not the case: even during adaptation, the presence of a stimulus in the upper patch prohibited further suppression from the lower patch.

We quantified these observations by fitting the model: s in Equation 2 became the weighted sum of contrast in the upper and lower patches, such that:

where c_u and c_l are the contrasts of the upper and lower patches, respectively; w_l is the weight applied to the lower patch (constrained to be <1); and A_l describes the impact of adaptation on the effective contrast of the lower region (A_l was assigned a value of 1 in the control state). When the contrast over the upper and lower regions is the same, the model is the general one defined by Equations 1–3; in all experiments so far, the general model could explain adaptation equally well through changes in σ_s or changes in s (data not shown). Only with multiple stimuli over the ECRF could we distinguish changes in σ_s from changes in s.

We fit the model to the complete data set (a matrix of four contrasts of the lower annulus and four contrasts of the upper disk); for clarity, only some of the responses are shown in Figure 9. The smooth lines in Figure 9 show the predictions of the model, with only A_l allowed to vary with adaptation. In this cell and the other four M cells on which we made measurements, the model performed well, on average leaving 8.1% (SD, 3.5) of the response variance unexplained, using four parameters (K, σ_s, w_l, A_l) to describe 32 observations. The weights applied to the lower patch averaged 0.61, and adaptation required A_l to be, on average, 0.29 (i.e., the contrast over the lower region was approximately three times more effective in the control state than in the adapted state). Fits that allowed σ_s to vary (and constrained A_l to 1) did not perform as well, leaving, on average, 10.3% (SD, 4.6) of the variance unexplained, although this was not significantly worse than the fit of the model above (p = 0.2). In similar experiments not shown, we stimulated the ECRF with two abutting annular rings concentric around the central patch and made measurements before and during adaptation to the inner ring. In seven cells so tested, the impact of adaptation could also be well described by a change in the effective contrast over the inner ring, and these predictions were significantly better [leaving 9.0% (SD, 1.8) of the response variance unexplained] than those in which only σ_s was allowed to vary (12.6%; SD, 2.8; p < 0.001). We conclude that adaptation induces spatially localized changes of contrast sensitivity in subunits of the ECRF and that the output of these subunits is pooled before being subject to a compressive nonlinearity.

Adaptation reveals suppression from distal regions of the visual field

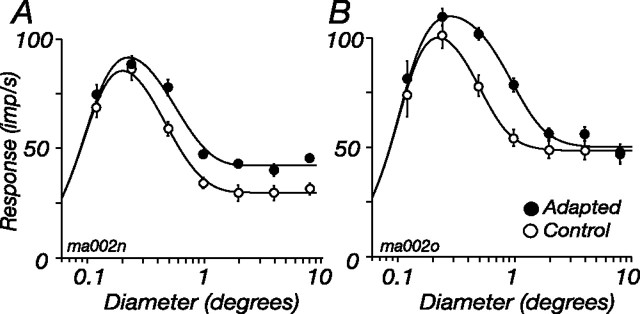
Spatial summation measured with patches of drifting grating, as in Figure 1, reflects the interaction of signals from the CRF and signals from the ECRF: small patches mainly drive the CRF, and larger patches recruit more of the ECRF. We expect that adaptation of the ECRF will change the shape of the spatial summation curves, increasing response to large patches. Yet adaptation might also change the area over which CRF or ECRF signals are accumulated (Pettet and Gilbert, 1992; DeAngelis et al., 1995), bringing about more complex changes in spatial summation. To determine how annular adaptation changes spatial summation, we measured responses to drifting gratings of varying diameter in the control state and during adaptation; the contrast of the grating was usually 0.5. Figure 10 shows the responses of two representative M cells; for both cells, annular adaptation increased response at larger patch sizes. For the cell in Figure 10A, the summation curves asymptote at different heights, but at the same diameter. The cell in Figure 10B appears to behave differently: the curves asymptote at the same response amplitude but different diameters.

Figure 10.

Adaptation of the ECRF changes spatial summation. Two examples showing how the tuning for the diameter of a patch of drifting grating is changed by adaptation to an annular grating are shown. A, M cell showing generalized increase of response at large patch diameters. B, M cell appearing to show a change in the area over which suppressive signals are gathered. Smooth lines show the best-fitting predictions of the model described in Results. Conventions are as in Figure 5B. Contrast, 0.5; temporal frequency, 5.5 Hz; spatial frequency, 3.2 cycles/° (A) or 2 cycles/° (B).

For the cell in Figure 10A, annular adaptation seems to reduce the strength of the ECRF without affecting the area over which it accumulates signals. For the cell in Figure 10B, in contrast, adaptation seems to increase the size of the ECRF (and concomitantly reduce its sensitivity, so the integrated volume of the ECRF is unchanged by adaptation). Rather than suppose multiple mechanisms, expressed differently in each cell, a single model can explain the response of both M cells in Figure 10. That is, adaptation only reduces the sensitivity of ECRF subunits. For cells in which the pooled signal of ECRF subunits is subject to a saturating nonlinearity (including the cell in Fig. 10B), adaptation brings more distal subunits of the ECRF into its operating range, and the size of the ECRF therefore appears to increase.

To determine whether this model can predict spatial summation curves obtained as in Figure 10, we fit a version of Equations 1–3 to each of the nine cells tested. Instead of contrast, which is fixed here, the input to the CRF (c in Eq. 1) was provided by a Gaussian over the two dimensions of space, and for each patch diameter we calculated the proportion of that Gaussian activated by the stimulus. The output of another larger Gaussian provided the input to the ECRF (s in Eq. 3); c and s are therefore the integrated volume of the CRF and ECRF, and these volumes increase with stimulus diameter. In making predictions, six parameters described the spatial summation curve: the characteristic radii of the CRF and ECRF Gaussians, the semisaturation constants (σ_c and σ_s), S_max, and K. These were all the same during control and adapted states. A seventh parameter scaled s during adaptation, by the same amount at all stimulus diameters. The smooth lines in Figure 10 show the predictions of the model. In these cells and the other seven tested, the predictions were very good, leaving, on average, 4.4% of response variance unexplained (SD, 4.3). [If all parameters were allowed to vary with adaptation, the model left 2.3% unexplained (SD, 2.0).]

Although we cannot rule out tightly linked reciprocal changes in the size and sensitivity of the ECRF, in the interests of parsimony we conclude that during adaptation the signals provided by the ECRF subunits are reduced, but that the area over which the subunits are pooled remains constant.

Relationship between the ECRF and other forms of contrast gain control

We now ask whether the ECRF is synonymous with the contrast gain control. That they are a single mechanism is explicit in the “contrast–gain” model, where the ECRF is the area over which contrast signals are summed to provide the denominator in Equation 1 (Bonin et al., 2005; Solomon et al., 2006; Nolt et al., 2007; Mante et al., 2008). In the response gain model we have used here, however, the ECRF vertically scales the CRF signal, which has already been passed through a contrast gain control (Eq. 1) (Rieke, 2001; Beaudoin et al., 2007). In this formulation, therefore, the ECRF is distinct from what is usually referred to as the contrast gain control. For single patches of grating that vary in size and contrast, the stimulus often used in recent work (Bonin et al., 2005; Solomon et al., 2006), the predictions of these two models are very similar (data not shown).

Some additional evidence for the response gain model of the ECRF is presented in Figure 11A–C: these show for two cells the contrast response for central test gratings, in the presence and absence of an annular grating. The major effect of the annular grating is to vertically scale the contrast–response to the central test (see similar data by Cavanaugh et al., 2002; Solomon et al., 2002; Webb et al., 2002). The best-fitting predictions of three different models are shown. The lines in Figure 11A show for the two cells the predictions of the standard contrast gain model, where the denominator in Equation 1 includes a weighted combination of the central and annular contrasts (Bonin et al., 2005), as follows:

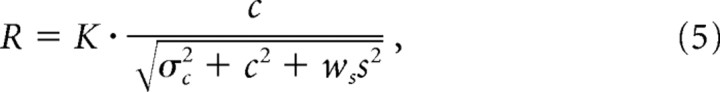where c is the contrast of central patch, s is the contrast of the annulus, and σ_c, w_s, and K are constants. The lines in Figure 11C show the predictions of the response gain model already described in Equations 1–3. The quality of the predictions returned by the two models is summarized by the open symbols in Figure 11D, which compare the percentage of response variance left unexplained by each model for the 22 M cells in our sample (the stars show the relevant values for the two example cells). Points above the line indicate cells in which the response gain model was better, and those below the line show cells in which the contrast gain model was better. In most cells, the quality of the predictions are very similar; for 5 of 22 cells, the response gain model provided much better predictions, and for 1 of 22 cells, the contrast gain model provided better predictions. This might be expected, because the response gain model includes an extra variable that allows for saturation in the signal from the annulus. To provide an equal fitting on which to compare the models, we provided a similar term for the contrast gain model (by replacing s in Eq. 5 with the expression in Eq. 2). The predictions of this modified contrast gain model are shown in Figure 11B; the cell in the left panels is the cell in which the modified model most improved the fits. The filled symbols in Figure 11D compare the predictions of the modified model and the response gain model. The modified model improved the predictions (the filled symbols are lower than their open pair), and 2 of 22 cells were much better fit by it than by the response gain model; nevertheless, as is shown in the right panel in Figure 11B, the contrast gain model remained incapable of predicting responses in 5 of 22 cells. We conclude that a major effect of the ECRF in LGN cells is to scale cell response, rather than effective image contrast, and its impact can therefore be quite different to the contrast gain control that lies over the CRF. Some of this difference is attributable to a saturating nonlinearity in the signals from the ECRF.

Figure 11.

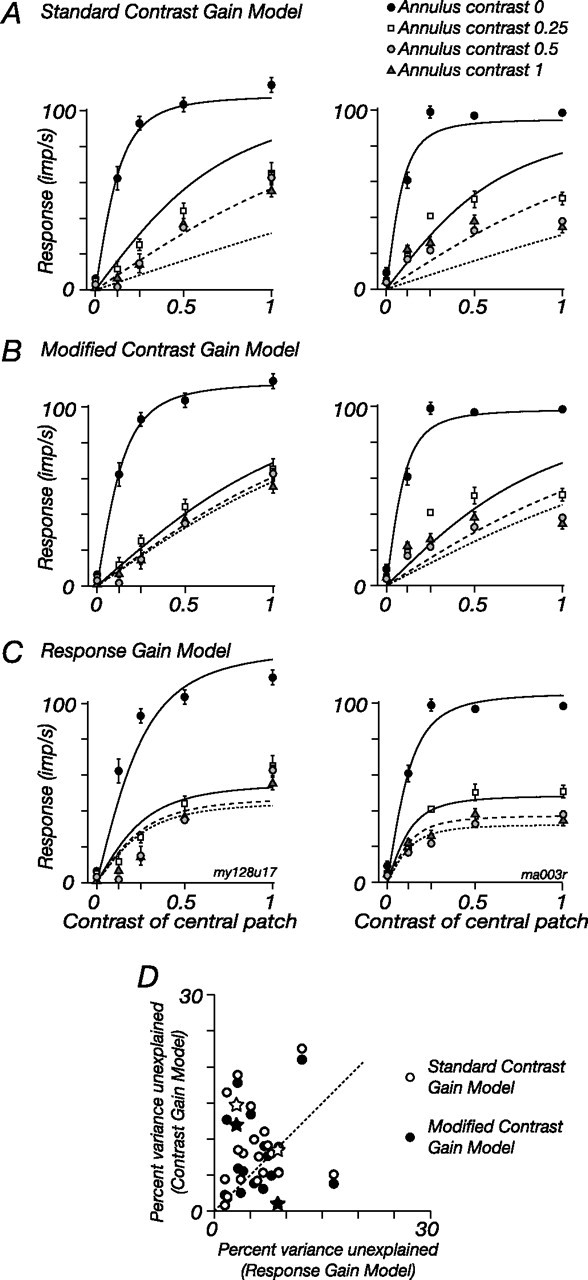
Comparison of contrast–gain and response–gain models of the ECRF. A, The left panels show the modulated response of one M cell, and the right panels show the response of a second M cell, at the drift frequency (5.5 Hz) of a central patch of sinusoidal grating. The central patch abutted an annular grating that drifted at 8.3 Hz. The four sets of data points in each panel show response as a function of the patch contrast, for each of four annulus contrasts. The lines show the predictions of the standard contrast gain model of the ECRF (Eq. 5 in Results). B, Same data as in A. The lines show the predictions of a modified contrast gain model, where the ECRF signal was subject to a compressive nonlinearity. C, Same data as in A and B. The lines show the predictions of the response gain model. D, The open symbols compare the response variance left unexplained by the response gain model (C) and the standard contrast gain model (A) for all cells (n = 22). The filled symbols compare the response gain model and the modified contrast gain model (B) for the same cells. The stars plot the cells shown in A–C.

Discussion

Our main findings are threefold. First, the ECRF of LGN neurons is susceptible to contrast adaptation; second, contrast adaptation of the ECRF transfers across a broad range of simple visual patterns but is predominantly localized in space; and third, how contrast adaptation is expressed in LGN neurons depends on the relative activation of the CRF and ECRF. In the following, we address how these experiments constrain models of the ECRF of LGN neurons and their implications for subsequent visual processing.

Construction of the ECRF

Our observations suggest that the ECRF of marmoset LGN neurons is constructed primarily from subcortical, rather than cortical, elements. By using contrast adaptation, we have shown that the ECRF is composed of multiple, independently adaptable subunits insensitive to orientation and broadly tuned for spatial and temporal frequency, properties characteristic of subcortical visual neurons. We expect that a cortical contribution to the ECRF would reveal itself as localized reductions in ECRF sensitivity around the orientation or spatiotemporal frequency of the adaptor, something we never observed. We think it is unlikely that anesthesia has masked the influence of cortical feedback: in macaque LGN, the strength of the ECRF is independent of anesthesia (Alitto and Usrey, 2008). We did not observe “S-potentials” in our LGN recordings, so we could not compare the response of retinal ganglion cells and their LGN targets during adaptation; all the properties of the adaptable ECRF subunits are consistent with a retinal origin, possibly augmented by interneurons in the LGN (Hubel and Wiesel, 1961; Levick et al., 1972; Nolt et al., 2007).

Some or all of the retinal ECRF must arise in amacrine cells. There are two potential mechanisms by which amacrine cells might suppress the firing of ganglion cells: through direct inhibitory input to the ganglion cells themselves, or by modifying the transmission of bipolar cell terminals (Cook and McReynolds, 1998; Taylor, 1999; Flores-Herr et al., 2001; Shields and Lukasiewicz, 2003; Beaudoin et al., 2007; Zaghloul et al., 2007). Some bipolar cell terminals adapt (Kim and Rieke, 2001; Manookin and Demb, 2006), and bipolar cells are the source of signals to amacrine cells, so bipolar cell adaptation might contribute to the adaptable ECRF subunits (Brown and Masland, 2001; Baccus and Meister, 2002). However, we do not know the size of the amacrine cells that provide the ECRF, or the collection area of the adaptable subunits, and it may well be that the major site of ECRF adaptation is in the amacrine cells.

Adaptable mechanisms within the ECRF

Adaptation of one subregion of the ECRF had its greatest impact on the sensitivity of that subregion but could also produce small (although reliable) reductions in the sensitivity of other subregions. In addition, responses to the central test were always higher during annular adaptation than during the control state (compare Fig. 5C), even when the inner border of the adapting annulus was 0.5° from the test (data not shown), suggesting that the adaptor desensitized a gain control underlying the central test. The change in response over the central test might reflect a reduction in a tonic suppressive mechanism, and not one that is driven by luminance contrast. We have checked this informally by doing the following: in M cells, we compared the mean rate (for a blank screen) before and during adaptation. Our experiments were not designed to precisely measure mean rate (in each condition, we usually measured ∼10 s of spike rate to a blank screen); nevertheless, as expected, adaptation to a grating in the central patch reduced the mean rate to 55.7% of the baseline rate [SD, 36.4; p < 0.0001; n = 18; baseline rate was 11.2 impulses/second (imp/s); SD, 9.5] (see also Solomon et al., 2004). Adaptation to the annulus did not significantly change the mean rate (it increased to 133.6% (SD, 114.3) of the baseline rate of 11.8 imp/s; SD, 15.7; n = 17; p = 0.39). We conclude that any tonic component of suppression is likely only weakly susceptible to contrast adaptation; increased response to the central patch during annular adaptation probably reflects desensitization of a gain control that spans the annulus and the central patch.

The dendritic fields of diffuse bipolar cells in marmoset retina are not large enough to accommodate this transfer (Luo et al., 1999), and this implies that some component of adaptation occurs after spatial pooling of bipolar cell signals, perhaps in amacrine cells (Baccus and Meister, 2002), whose signals might also be responsible for sublinear summation within the ECRF (Werblin and Copenhagen, 1974; Passaglia et al., 2001). Alternatively, the transfer may reflect additional adaptable mechanisms within the LGN.

Our observations do show that suppression from the ECRF occurs before the major site of contrast adaptation in the mechanisms that provide the CRF; if these adaptable CRF mechanisms are the bipolar cells, then a large part of the ECRF must arise in inputs to the bipolar cell terminals (Victor and Shapley, 1979). If the adaptable CRF reflects desensitization within the ganglion cell (Manookin and Demb, 2006), then the ECRF may act through modulation of bipolar cell terminals or direct inhibitory input onto the ganglion cell.

Functional implications

In V1 neurons of macaque, the ECRF seems to have two major sources: one is narrowly tuned for spatial form, dichoptic, very susceptible to contrast adaptation, and is probably built in cortex (Webb et al., 2005b). The other is broadly tuned, monocular, and less susceptible to adaptation. The properties of this “early” mechanism seem consistent with the LGN ECRF, and their expression in V1 may primarily reflect properties inherited from LGN neurons.

In LGN neurons the ECRF acts before contrast adaptation, and so a large high-contrast stimulus recruits less adaptation than a small stimulus of the same contrast. This leads to the following hypothesis: adapting stimuli over the CRF of cortical neurons (particularly those that get input from M cells) will transfer across orientation or spatial frequency when the adapting stimulus is small and therefore recruits substantial adaptation at subcortical levels. This might be the case: in recordings from cat and primate V1, adaptation can transfer from an adapting orientation to its orthogonal, even if the neuron is unresponsive to the adapting grating, but we do not know how this depends on the size of the adaptor (Sengpiel and Bonhoeffer, 2002; Dhruv et al., 2004; Crowder et al., 2006). We expect that in cortical neurons adaptation will be more selective for spatial form when the stimulus is larger, because a larger fraction of the adaptation should arise in cortical neurons.

Our measurements also show that the area over which the ECRF sums contrast signals depends on the spatial distribution of that contrast (see also Levitt and Lund, 2002). This nonlinearity makes it difficult to be certain of the size of the ECRF and thus to compare estimates of its size with anatomical structures (Angelucci et al., 2002), or the size of the CRF (Bonin et al., 2005; Solomon et al., 2006). For high-contrast, continuous images, regions near the CRF will dominate the ECRF, and for low-contrast or discontinuous images, more distal regions will have an impact.

Whereas contrast adaptation is useful for probing the organization of inputs to receptive fields, it is less clear that this slow form of sensitivity regulation is important in normal visual function. The contrast of photographs of natural scenes is generally quite low, and for most of these images the firing rate of most cells will also be low, so it is difficult to see a major contribution of fatigue over long time periods (Mante et al., 2008). Nevertheless, brief exposure to high contrasts can be sufficient to induce desensitization (Muller et al., 1999; Manookin and Demb, 2006), and this might be a reasonably frequent occurrence. Given the profound impact of adaptation to small gratings in M cells, one role of the ECRF might be to protect these highly sensitive neurons from fatigue in environments dominated by high contrast (O'Shea and Rowell, 1975).