Structure of Online Dating Markets in U.S. Cities

Abstract

We study the structure of heterosexual dating markets in the United States through an analysis of the interactions of several million users of a large online dating website, applying recently developed network analysis methods to the pattern of messages exchanged among users. Our analysis shows that the strongest driver of romantic interaction at the national level is simple geographic proximity, but at the local level, other demographic factors come into play. We find that dating markets in each city are partitioned into submarkets along lines of age and ethnicity. Sex ratio varies widely between submarkets, with younger submarkets having more men and fewer women than older ones. There is also a noticeable tendency for minorities, especially women, to be younger than the average in older submarkets, and our analysis reveals how this kind of racial stratification arises through the messaging decisions of both men and women. Our study illustrates how network techniques applied to online interactions can reveal the aggregate effects of individual behavior on social structure.

PATTERNS of romantic and sexual partnerships—who pairs with whom—have broad implications for health and society. For example, the level of assortative mating (the extent to which like pairs with like) has long been considered an indicator of societal openness (Glass 1954; Kalmijn 1991). Mating patterns also determine how wealth and resources are passed from one generation to another (Schwartz 2010; Breen and Salazar 2013), have implications for mental and physical health (Waldron, Hughes, and Brooks 1996; Smith and Christakis 2008), and shape sexual networks that drive the spread of sexually transmitted infections (Morris and Kretzschmar 1995; Liljeros et al. 2001).

There exists an extensive empirical and theoretical literature exploring the mechanisms behind patterns of romantic pairing (Kalmijn 1998; Schwartz 2013). In societies where people choose their own mates, it is widely accepted that romantic pairing is driven by the interplay between individuals’ preferences for partners and the composition of the pool of potential mates (Becker 1973; Mare 1991; Xie, Cheng, and Zhou 2015). The process can be modeled game theoretically as a market in which individuals aim to find the best match they can subject to the preferences of others (Gale and Shapley 1962; Roth and Sotomayor 1992). There is also a large body of empirical work that documents the relationship between observed partnering patterns and the supply of partners as reflected in the population composition of cities, regions, or countries (Blau, Blum, and Schwartz 1982; Lichter, LeClere, and McLaughlin 1991; South and Lloyd 1992a,b; Lichter, Anderson, and Hayward 1995; Angrist 2002; Blossfeld and Timm 2003; Guzzo 2006; Harknett 2008; Trent and South 2011).

These studies are limited, however, in what they can reveal about the structure of dating or marriage markets. One issue is that we typically do not have access to the actual population of available dating partners and must instead make do with proxies such as census data, obliging us to treat entire towns or cities as a single undifferentiated market. A more fundamental problem is that previous studies have only looked at extant partnerships and not the larger set of all courtship interactions among mate-seeking individuals. In order to properly study dating markets, one needs data on all courtship overtures that occur within the focal population: not only those that are successful and result in a partnership but also those that are rejected. As we show in this article, the complete set of such overtures forms a connected network whose structure can be analyzed to reveal key features of romantic markets.

Unfortunately, complete data on courtship interactions have been historically hard to come by because unrequited overtures are rarely documented. The few empirical studies that have directly observed courtship patterns have tended to focus narrowly on specific institutions, subpopulations, or geographic locations (Sprecher et al. 1984; Laumann et al. 2004), and relatively little is known about the empirical structure of romantic and sexual markets across the general population or how this structure varies from one locale to another.

The advent of online dating and its spectacular rise in popularity over the last two decades has, however, created a new opportunity to study courtship behaviors in unprecedented detail (Rosenfeld and Thomas 2012). Here we report on a quantitative study of the structure of adult romantic relationship markets in the United States using nationwide data on online-dating users and their behaviors. We combine activity data for millions of participants with recently developed network analysis methods to shed light on the features of relationship markets at the largest scales. There have been recent studies using early-stage patterns of online mate choice—who browses, contacts, or responds to whom—to shed light on individuals’ preferences for mates (Hitsch, Hortâsu, and Ariely 2010; Lewis 2013; Lin and Lundquist 2013; Bruch, Feinberg, and Lee 2016), but the work presented here goes beyond these studies to examine how individuals’ choices aggregate collectively to create structured relationship markets that strongly influence individuals’ dating experiences.

The data we analyze come from a popular US dating website with more than 4 million active users at the time of our study. Our analysis focuses on all (selfidentified) heterosexual, single men and women who sent or received at least one message on the site during the period of observation—January 1, 2014, to January 31, 2014—and who indicated that they were pursuing some form of romantic relationship (long-term dating, short-term dating, and/or sex). For each user, we have a range of self-reported personal characteristics along with time-stamped records of all messages exchanged on the site. It is the latter that are the primary focus of our analysis because it is the messaging patterns that reveal the aggregate demand for individuals within the market.

We quantify messaging patterns using methods of network analysis (Newman 2018). We examine the set of all reciprocal interactions between opposite-sex users, meaning pairs of individuals between whom at least one message was sent in each direction in the pair. Reciprocal interactions we take to be a signal of a baseline level of mutual interest between potential dating partners. Our primary focus is on understanding the division of the online-dating population into distinct submarkets: How does the market divide into subpopulations of daters, and how are those subpopulations characterized? We define submarkets as roughly self-contained groups of individuals within the network such that most reciprocal exchange of messages occurs within groups. This corresponds closely to the established concept of “community structure” in network theory, a community in this context being a tightly knit subgroup of individuals within a larger network. A number of sensitive techniques for the detection of network communities have been developed in recent years, and we employ a selection of those techniques here (Fortunato 2010). Technical details of the algorithmic methods used in our calculations are given in the supplementary materials.

Dating Markets Are Divided into Distinct Geographic Regions

For our first analysis, we examine community structure within the entire data set of all users of the website during the month of observation. A total of 15,302,512 reciprocal interactions took place during this period. We aggregate these interactions at the level of 3-digit zip codes—geographic regions used by the US Post Office—and count the number of interactions that take place between every pair of 3-digit zip codes. For instance, there were 75,686 reciprocal interactions between individuals in Manhattan and individuals in neighboring Brooklyn but only 2170 interactions between individuals in Manhattan and individuals in far-away San Francisco.

The result of this aggregation is a weighted network in which the nodes represent 3-digit zip code regions, and the weighted edges represent the number of interactions. We take this network and perform a standard community detection analysis on it using the modularity maximization method (see the supplementary materials and references [Blondel et al. 2004; Newman 2004]). The results for the lower 48 states are shown in map form in Figure 1.

Figure 1:

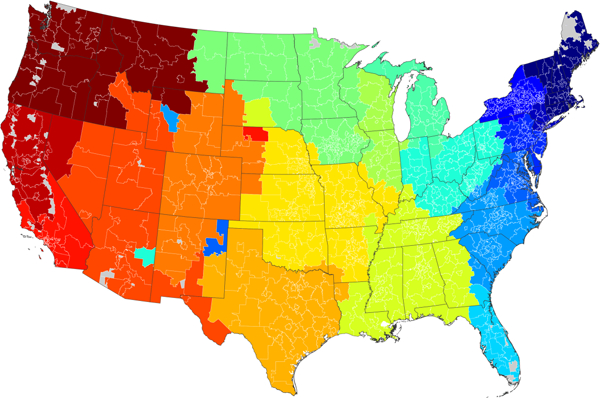
Division of the messaging network for the lower 48 states into 19 communities by modularity maximization using the Louvain algorithm (Blondel et al. 2004). Colors represent communities at the level of 3-digit zip codes. Gray regions are areas with no assigned zip code.

As the figure shows, the communities found in this nationwide network of messaging are tightly geographically circumscribed. Many of them appear to correspond to commonly accepted geographic divisions of the country: New England, the East Coast, the South, Texas, the Mountain West, Northern and Southern California, and so forth. In essence, it says that most people are interested in others who are in their own region of the country, which is reasonable. Few people living in New York will exchange messages with people in California if the primary goal is to arrange a face-to-face meeting with a possible romantic partner. This finding is consistent with recent work looking at friendship communities using Facebook data, which finds that incidence of friendship is strongly decreasing in geographic distance (Bailey et al. 2018).¹

Community structure in the broad, nationwide network of messaging thus appears to be dominated by geographic effects. Because our primary goal here is to observe and analyze more subtle demographic effects within dating markets, we need to factor out the gross influence of geography. Our approach for doing this is a simple one: We focus on subnetworks within individual cities. We choose cities as our basic unit of analysis because they are large enough to provide a population of significant size and at the same time small enough that travel distance between individuals will not be a deterrent to interaction. In the sections that follow, we perform a series of analyses on subsets of the data corresponding to four large cities: New York, Boston, Chicago, and Seattle. We define cities using the standard core-based statistical areas (CBSAs) for the corresponding metropolitan regions, except for New York, where the CBSA is large enough that there are clearly separate dating markets within it. For New York, therefore, we define our area of study more narrowly to be the five boroughs of Manhattan, the Bronx, Queens, Brooklyn, and Staten Island.

One can look at the analysis of Figure 1 as providing some justification for previous studies that focused on demographics within geographically localized communities. Although some mate pursuit does take place at longer distances, behaviors are substantially curtailed by geography, and demographic patterns of interest can be seen most clearly in smaller markets. Most prior studies do have the drawback of considering only the population as whole, however, and not specifically the population of mate seekers and of lacking, in most cases, direct data on dating and courtship interactions.

Dating Markets Are Demographically Stratified within Cities

We now turn our attention to the structure of dating markets within our four cities of New York, Boston, Chicago, and Seattle and particularly to community structure at the level of individual participants within these markets. The community structure in this case is more complex than the simple geographic effects we saw in Figure 1. Specifically, it displays a mix of so-called assortative and disassortative mixing (Newman 2003). For the heterosexual dating communities studied here, it is disassortative by gender, meaning most messages are between individuals of opposite sex, but assortative by various other characteristics, as we will see. It is the latter behavior on which we primarily focus, but our community detection calculations need to be sensitive to both in order to fully reveal the structure of the market. Here we make use of a powerful and flexible community detection method based on maximum-likelihood techniques, the expectation-maximization (EM) algorithm, and belief propagation (Decelle et al. 2011; Karrer and Newman 2011), which can sensitively and rapidly detect complex forms of structure in large networks. For details, see the supplementary materials.

Focusing again on networks of two-way message exchanges, we present in the following analyses the results of community divisions of each city network into four separate communities or submarkets (eight if you count men and women separately). We find that about 75 percent of all reciprocal interactions in our four cities are between individuals within the same submarket, indicating that the communities align well with the conventional definition: tightly knit groups with most interaction going on within groups. The choice to divide into four submarkets is to some extent arbitrary. We have repeated the analysis for other numbers of submarkets and find essentially similar patterns to those reported here (see the supplementary materials). The choice of four submarkets offers a good compromise between resolution of finer details and adequate statistical power within submarkets.

Figure 2 shows a variety of demographic features of the submarkets in the four cities. The most obvious defining feature of the submarkets is the age of their members, shown in Figure 2A. The youngest submarket, numbered 1 in each city, corresponds primarily to individuals in their early 20s, whereas submarkets 2 to 4 correspond to those in their upper 20s, 30s, and 40s and above, respectively. This pattern is consistent, with only minor variation, across the four cities. As the figure shows, there is a small but systematic difference in age between men and women across all submarkets: In every case, the men are older than the women, with a median age difference of 1 year and 7 months.

Figure 2:

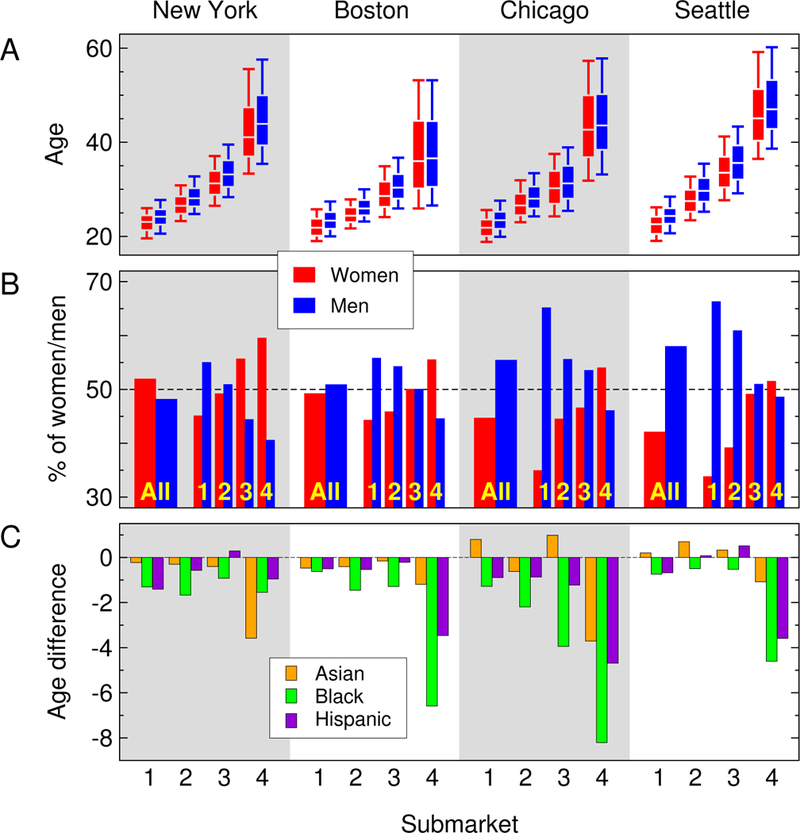
(A) Distribution of ages of men and women in each submarket in each of the four cities studied. Boxes indicate the 25th, 50th, and 75th percentiles; whiskers indicate the ninth and 91st percentiles. (B) Percentage of men and women in each submarket, and overall, for each city. (C) Average age of minority women in each submarket by ethnicity, measured relative to average age of white women in the same submarket. Units of analysis are users.

However, submarkets are not characterized by age alone. As Figure 2B shows, they also differ in male-to-female ratio, and here we see another consistent pattern: The younger submarkets tend to be male heavy, but the mix becomes progressively more female heavy in the older submarkets. There are a number of factors that may drive this pattern. Women’s first marriages are at a younger age on average than men’s (Qian and Preston 1993; Finer and Philbin 2014), which takes more women than men out of younger dating markets. Furthermore, because partnering of younger women with older men is more common than the reverse (Hernan, Berardo, and Berardo 1985; Hitsch et al. 2010), some older men may seek out younger partners, swelling the ranks of men in the younger submarkets. Conversely, some younger women may leave the youngest submarkets in search of older partners, depleting the supply of women. (This would also help explain the higher average age of men in each submarket.) The same behaviors also reduce the number of men in the older submarkets and increase the number of women. Depending on the overall population balance of the city, the end result can be a severe distortion of the sex ratio at the oldest or youngest ages. The youngest submarkets in Chicago and Seattle, for example, have almost two men for every woman.

An additional facet of the submarket structure, one that affects predominantly women, comes to light when we look at the balance of ethnicities. Figure 2C shows the mean age of minority women in each submarket broken down by ethnicity and measured, in this case, relative to the mean age of white women in the same submarket. The plot demonstrates a systematic tendency for minority women to be younger than their white counterparts within the same submarket. The effect is small in the younger submarkets but becomes more pronounced in the older ones. This is partly due to the fact that there are fewer black women than white women among the oldest users of the site (supplemental materials, Figure S4), but these compositional effects are not large enough to account for the pronounced age difference seen in Figure 2C. Studies of mate preferences of online daters have shown that black women are on average viewed by heterosexual men as less desirable partners than nonblack women (Fisman et al. 2008; Hitsch et al. 2010; Robnett and Feliciano 2011; Lin and Lundquist 2013), and the behavior seen in Figure 2C may reflect the aggregate outcome of such preferences at the submarket level. In Chicago’s oldest submarket, for instance, black women are more than eight years younger on average than white women, suggesting that men in that submarket are exchanging messages with black women who are substantially younger than the white women they exchange messages with.²

Dating Markets Reflect the Aggregated Choices of Individuals

Next we examine how the choices of men and women about whom to message differ across submarkets and by gender. Because men send more than 80 percent of first messages on the site, we focus on men’s first messages and women’s replies. Figure 3 shows the difference between the ages of men and the women they message, by submarket and race, in Chicago and New York, in the form of “heat maps.” (Similar figures for Boston and Seattle are shown in the supplementary materials.) The rows labeled “1st messages” show age difference in first messages, and the rows labeled “Replies” show the age difference in replies, with brighter colors corresponding to larger age differences. We see that in both Chicago and New York, the age differences between men and the women they message are approximately two to three times larger in the oldest submarket than in the youngest. This is consistent with previous work showing that men’s preferences for partners become more pronounced as they age (Skopek, Schmitz, and Blossfeld 2011).

Figure 3:

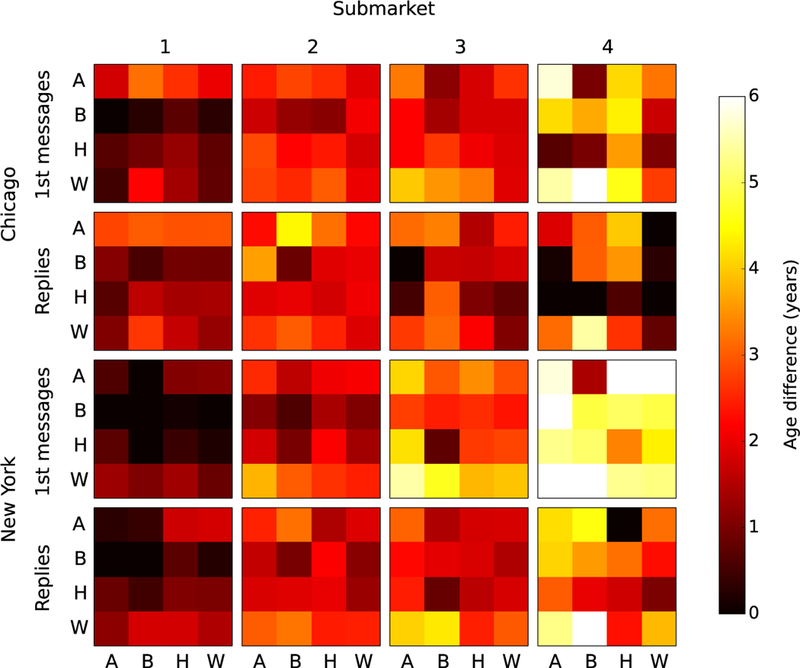
Mean difference in years between the age of men of varying races and the women they message in Chicago and New York by race of women and submarket. Race is coded as follows: A = Asian, B = Black, H = Hispanic, and W = White. The first two rows show the average age difference for all initial messages sent in Chicago and those that received a reply, respectively; and the bottom two rows show the same patterns for New York. In both cities, the age gap between men and their potential mates increases (lighter colors) as we move from younger to older submarkets. In addition, we see that black and white men in the oldest New York submarket pursue younger women, on average, than black and white men in the oldest Chicago submarket. However, unlike in Chicago, only Asian women are pursued by older black men in New York at substantially younger ages than their non-Asian counterparts. White men in the oldest submarket pursue both Asian and black women at younger ages compared to Hispanic and white women.

Figure 3 also sheds light on the behavioral mechanisms driving the racial stratification patterns we observed in Figure 2C. The top two rows of the figure for Chicago reveal that white men in older submarkets pursue minority women who are on average two or more years younger than the white women they message. This is especially pronounced in submarket 4, where the average age gap between white men and the minority women they write to is around five to six years compared to two years for white women. However, minority women tend not to reciprocate overtures from older white men, which is why the age gap in replies among minority and white women is not as pronounced. The one exception is for black women in Chicago: The average age gap in messages between these women and the white men they respond to is around 5.8 years. Thus, it is both how men pick the women they message and how women reply that drive the racial stratification we saw in Figure 2.

In New York, the messaging patterns look somewhat different from Chicago because New York men, despite being of similar age to their Chicago counterparts, pursue younger women on average. Black men in the oldest New York submarket write to women who are on average 4.5 years younger than they are, whereas for white men, the corresponding figure is 6.2 years. And although older white men in New York message younger black and Asian women than white women, the differences are slight: Women of all races in New York’s submarket 4 are being pursued at younger ages, so the racial difference is more attenuated. In other words, it’s not that black women in New York’s oldest submarket receive messages from younger men than black women in Chicago’s oldest submarket (i.e., men closer to their own age) but that white women in New York’s oldest submarket receive messages from older men than white women in Chicago’s oldest submarket. Overall, we see that men’s and women’s choices about who to message and respond to shape submarket structure differently in the two cities.

Additional features of interest in the submarket structure are revealed by an examination of messaging patterns within and between submarkets. For this analysis, we focus on initial contacts between individuals and on whether those contacts receive a reply Across all submarkets and cities, we find that 57 percent of first contacts are between users in the same submarket. The remaining 43 percent are between users in different submarkets, and the pattern of within- and between- group messages, depicted in Figure 4, shows a number of interesting regularities. The first and third rows of the figure show data for initial contacts made by men and women, respectively. The bright squares down the diagonal of each matrix represent the large fraction of within-group contacts. The darker squares off the diagonal show that users are sending a modest number of messages to the submarkets immediately older and younger than their own but very few messages to submarkets two or more steps away. One deviation from this pattern is visible in the messages sent by men in submarket 3 (the 30-somethings). Across all four of our cities, this group is the only one whose members send a majority of their messages to women in different submarkets from their own, the largest number going to women in the next youngest submarket, submarket 2 (mid-to-late 20s).

Figure 4:

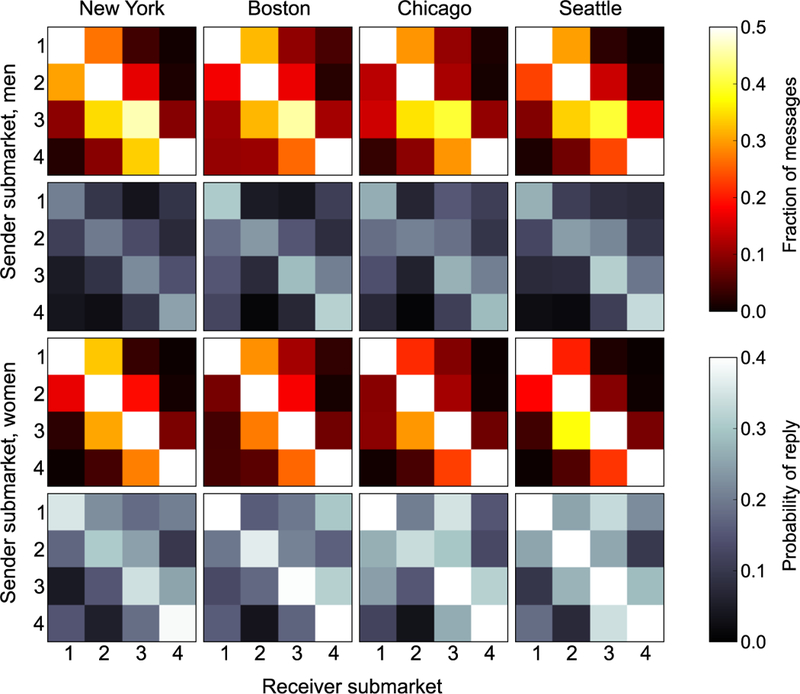
Fractions of messages sent, and fraction that receive a reply, for messages from men to women (top two rows) and women to men (bottom two rows) in each of the four cities studied. Brighter colors indicate larger numbers of messages.

The second and fourth rows of Figure 4 give the fraction of first messages that receive a reply—establishing a possible reciprocal interest between the individuals in question. Women’s replies to messages sent by men (second row) occur at a substantially lower rate than men’s replies to women (fourth row), which is likely a volume effect: Because women receive four times as many first messages as men, they can afford to be more selective in their replies. Again, across all cities and among both men and women, reply rates are highest within submarkets. Women receive replies more often when initiating contact with men in older submarkets compared to younger ones (which is consistent with prior studies), although there are some exceptions. Notice, for instance, that in all cities, women in the oldest submarket (submarket 4) are—surprisingly—more likely to receive a reply from men in the youngest submarket (submarket 1) than in the second youngest (submarket 2).

Discussion

The experience of mate selection is frequently described, both in popular discourse and the scientific literature, in the language of markets: An individual’s goal is to secure the best possible mate for themselves in the face of competition from others. However, we know little about the structure of these romantic markets in part for lack of appropriately detailed data. The advent and vigorous growth of the online dating industry in the last two decades provides a new source of data about courtship interactions on an unprecedented scale.

In this study, we have provided a first look at how network analysis techniques can reveal the structure of U.S. dating markets as evidenced by interactions on a popular dating website. Across the United States as a whole, we find that geography is the defining feature of national dating markets. Within cities, submarkets are defined by age as well as other demographic factors—most notably, race. We find that submarket structure is shaped by both first-messaging patterns and replies. Three-quarters of all reciprocated messages fall within submarkets, and only one-quarter fall between individuals in different submarkets. A larger fraction, about 43 percent, of all first messages are between different submarkets, which indicates that people do attempt to contact partners outside of their submarkets, but those attempts are often unsuccessful. Overall, our results reveal the aggregate implications of individuals’ mate choices and suggest that metropolitan areas are best characterized as a collection of geographically integrated but demographically distinct submarkets.

More generally, our study illustrates how state-of-the-art network science techniques can be applied to rich data from online interactions or administrative records to reveal subtle features of social structure. In recent years, the growing availability of search data from online sources has led to interest in how individuals’ choices reveal submarkets in other social domains (Piazzesi, Schneider, and Stroebel 2015; Rae 2015). As we have shown in the dating context, market outcomes reflect the choices made by actors on both sides (e.g., men and women in heterosexual dating markets, workers and firms in job markets). Our approach could straightforwardly be extended to look at structural features of housing or job markets, and we view this as a fruitful direction for future work.

Materials and Methods

Data

The data used as the starting point for our study come from one of the largest free dating sites in the United States and were collected in July 2014. The site does not market itself to any particular demographic group and attracts a diverse population of users whose makeup, in most locales, corresponds loosely to that of the general population. The site is known for its user-driven matching algorithm, which reduces the effect of site interference on users’ mate-choice behavior. The population of users is concentrated in coastal areas, although there are significant numbers of users in major Midwestern cities, such as Chicago. We restrict our analysis to active users, which we define to mean that they sent or received at least one message on the site during the observation period, which was January 1, 2014, to January 31, 2014. This eliminates a significant number of users who sign up and use the site but then become inactive or who sign up and never use it. We also remove from the data all users who identify as gay or bisexual (about 14 percent of the overall user base of the site) and those who indicate that they are not looking for romantic relationships. (People can indicate, for example, that they are only looking for friendship or activity partners.)

Community Detection

The primary technical tool employed in our analysis is community detection (Fortunato 2010), which takes a network of nodes and the connections, or edges, between them—users and messages in the present context—and divides it into tightly knit groups such that most edges fall within groups and few fall between. The most widely used method for community detection is modularity maximization (Newman 2004; Fortunato 2010), which makes use of the standard quality function known as modularity (Newman and Girvan 2004). This function, defined as the fraction of edges within groups minus the expected fraction of such edges if edges are placed at random, is large and positive for divisions of a network into good communities and small for poor divisions. Modularity maximization finds good communities by looking for the division with the largest modularity score. In our analysis of the complete, nationwide network of messages between active users, Figure 1, we make use of modularity maximization on the weighted network of conversations between users in different 3-digit zip codes. There are a range of practical methods for performing the maximization itself. In our calculations, we use the Louvain algorithm of Blondel et al. (2004), which is an iterative greedy algorithm that has been shown to give high-quality results with short run times (Yang, Algesheimer, and Tessone 2016). We use the implementation from the Gephi network analysis package, with the resolution parameter equal to 0.65, which results in the 19-community division shown in Figure 1.

Though it is fast and gives good results, modularity maximization is not ideal for the community analysis of our individual city networks. This is because, as explained, these networks contain both assortative and disassortative structure. Modularity maximization is normally capable only of detecting assortative structure. For this part of our analysis, therefore, we use an alternative community detection method based on the maximum-likelihood fitting of a generative, community-structured network model: the degree-corrected stochastic block model (Karrer and Newman 2011). In this approach, one defines a model that generates networks with community structure then fits that model to the observed network. The parameters of the best fit tell us which nodes of the network belong to which communities. More specifically, they give us the posterior probability that each node belongs to each community; in the final stage of the calculation, we assign every node to the community for which it has highest probability of membership. The fitting itself is performed using an EM algorithm, with the E-step carried out using belief propagation (Decelle et al. 2011). Technical details are given in the supplementary materials. Code is available upon request.