Abstract
Background
Vaccination history may confound estimates of influenza vaccine effectiveness (VE) when two conditions are present: (1) Influenza vaccination is associated with vaccination history and (2) vaccination modifies the risk of natural infection in the following seasons, either due to persisting vaccination immunity or due to lower previous risk of natural infection.
Methods
Analytic arguments are used to define conditions for confounding of VE estimates by vaccination history. Simulation studies, both with accurate and inaccurate assessment of current and previous vaccination status, are used to explore the potential magnitude of these biases when using different statistical models to address confounding by vaccination history.
Results
We found a potential for substantial bias of VE estimates by vaccination history if infection- and/or vaccination-derived immunity persisted from one season to the next and if vaccination uptake in individuals was seasonally correlated. Full adjustment by vaccination history, which is usually not feasible, resulted in unbiased VE estimates. Partial adjustment, i.e. only by prior season's vaccination status, significantly reduced confounding bias. Misclassification of vaccination status, which can also lead to substantial bias, interferes with the adjustment of VE estimates for vaccination history.
Conclusions
Confounding by vaccination history may bias VE estimates, but even partial adjustment by only the prior season's vaccination status substantially reduces confounding bias. Misclassification of vaccination status may compromise VE estimates and efforts to adjust for vaccination history.
Keywords: Influenza, Vaccine, Vaccine effectiveness, Vaccination history, Confounding, Test-negative study
1. Introduction
Seasonal influenza viruses, in particular influenza A viruses, rapidly evolve antigenically, forcing frequent reformulation of the seasonal vaccine components [1]. The closeness of the antigenic match between vaccine viruses and influenza viruses circulating in the human population affects vaccine effectiveness (VE) [2], which therefore needs to be assessed seasonally to inform public health policy and the formulation of next season's vaccine.
Natural influenza virus infection elicits an immune response that modifies susceptibility to influenza viruses, possibly for years [3]. Similarly, some protection due to seasonal influenza vaccination has been shown to persist beyond the season in which it was administered [4]. Vaccination history may thus, independently of current vaccination status, be associated with the risk of influenza infection. On the other hand, influenza vaccination status is associated with influenza vaccination history [5]. Sullivan et al. [6] pointed out that, therefore, VE estimates may be confounded by vaccination history. In addition, vaccination history might also act as effect modifier [16], [17].
Here, we develop a theoretical argument demonstrating how VE estimates may be confounded by vaccination history. We present results from a simulation study that explores the magnitude of the resulting bias in VE estimates under a range of assumptions. We also examine the effect of misclassification on the attempt to adjust VE estimates for confounding by vaccination history.
2. Theoretical considerations
2.1. Basic assumptions
Let represent influenza vaccination status for the season k years in the past from the current season, where denotes receipt of influenza vaccine before the start of the season k years in the past and represents being unvaccinated in that season. For simplicity, we let (vaccination status in current season) and is the vaccination history over the past seasons, preceding the season under investigation. Assuming that , i.e. a total of six seasons are considered, including the current season, a subject might have vaccination history , i.e. she/he was only vaccinated in the previous season.
Vaccination uptake is determined by a time-invariant personal trait that might be referred to as “health care-seeking behavior”, , here assumed to be categorical. We assume independence of vaccination uptake from infection and vaccination history, conditional on . A given level of may, e.g., be associated with a seasonal vaccination uptake probability of 75%.
The event of becoming infected with influenza virus in the current season is , remaining uninfected is and the influenza history up to the prior season is . Although seasonal risk of influenza is driven by an incidence process, that process will not be modeled, but will be given as a seasonal attack rate for those susceptible to infection.
Finally, we assume vaccination to act in an “all-or-none” manner [7] which means that susceptible subjects become, after vaccination, fully immune to the target agent with a given probability (=VE) or remain fully susceptible.
2.2. Vaccination history-associated bias in VE estimates from test-negative design studies
In the absence of confounding, VE is defined [8] as
| (1) |
Estimating and using a cohort study design would require a large study with expensive follow-up of study subjects to ensure capturing of all relevant events. A more economical approach is a case-control design, in which the risk ratio of interest is estimated using an odds ratio. For post-licensure studies of influenza VE, the test-negative variant of the case-control design is widely used [6], [9], [10], [11]. In a test-negative design (TND) study, subjects are enrolled based on a case definition, usually acute respiratory infection (ARI) or influenza-like illness (ILI). Cases are those who show evidence of influenza infection (=“test-positive”), usually from polymerase chain reaction-based tests; controls are those without such evidence (=“test-negative”). Under the assumption of an “all-or-none” vaccination effect, the “rare disease” assumption is not necessary for the odds ratio to be an unbiased estimator of the risk ratio [10].
Fig. 1 depicts a directed acyclic graph (DAG) [12] representation of a TND study of influenza VE: The influenza infection, , may cause a syndrome that fulfills a case definition, such as acute respiratory infection,. That syndrome may lead to study inclusion, , which also entails the administration of a diagnostic influenza test. The variable represents non-influenza etiologies of . Conditioning on the collider (study inclusion) opens the backdoor path
where the dashed line between and represents an undirected edge [6]. However, that backdoor path is blocked by also conditioning on the case definition . Two backdoor paths, however, remain open:
and
Fig. 1.
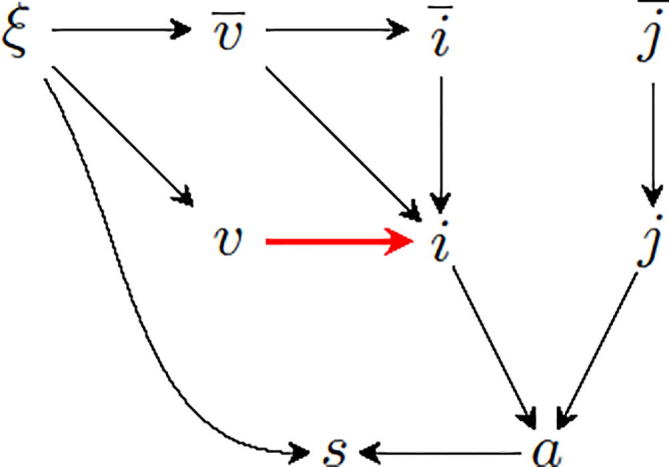
DAG representing a TND study of influenza VE. The bold red edge between vaccination (v) and influenza infection (i) represents the association of interest. See text for explanation.
These backdoor paths result in confounding by vaccination history, i.e
| (2) |
where is the true VE and is an estimate.
As both paths pass through , adjusting for vaccination history is sufficient (see Appendix A), such that, under usual regularity conditions, the odds ratio
| (3) |
equals the causal risk ratio and VE is
| (4) |
For notational convenience, the conditional terms and, representing study inclusion and fulfillment of the case definition, respectively, have been omitted from (3) and (4).
2.3. VE estimates adjusted for vaccination history
If VE is not affected by vaccination history (no effect modification), it could be estimated from TND data using the following logistic regression model:
| (5) |
where are dummy variables representing K distinct vaccination histories. Note that, for simplicity, we omit the term βc⋅x, which is the dot product of a covariate vector and the associated coefficient vector βc. The adjusted VE estimate is given by
| (6) |
If VE is modified by vaccination history, valid VE estimates could still be obtained by adding interaction terms between current vaccination and vaccination history to model (5) (see Online Supplement S1).
As the number of vaccination histories grows exponentially with the total number of seasons as , adjusting for the full vaccination history is, in most cases, unfeasible. Adjusting the analysis of current season's VE only by the vaccination status in the prior season can be considered as partial adjustment for vaccination history. The corresponding model is
| (7) |
The partially-adjusted VE estimate is obtained from (6).
2.4. Simulation study
The simulation model is described in detail in Online Supplement S2. Briefly, this is a discrete time (one season time steps) stochastic model. People of five different levels of “health care-seeking behavior” (), with their implied probabilities to get vaccinated each season and to seek medical care with acute respiratory infection (Online Supplement S2, Table S2.1). Influenza risk is determined by susceptibility to infection at the beginning of the season and the assumed seasonal attack rate. Susceptibility is a function of current and past vaccination status, infection history and the assumptions regarding vaccination- and infection-derived immunity carry-over. This is not a transmission model as seasonal attack rates are provided as an input to the simulation. This is also true for the seasonal attack rates of non-influenza acute respiratory illness. Subjects with acute respiratory illness (influenza or non-influenza) are recruited into a TND study and VE is estimated from the simulated study data as described below. This is typically repeated 10,000 times per parameter combination. The simulation was implemented in R [13] as were the analyses of the simulated data (see Online Supplement S2 and exemplary R code). We generated data from TND studies using different levels of season-to-season persistence of vaccine- and infection-derived immunity, and , respectively. This was modeled as probability of “all-or-none” immunity (see [7]) to persist from one season to the next. Persistence of immunity was therefore modeled as a proportion of subjects with infection- or vaccine-derived immunity in one season who remained immune in the following season. Persistence of vaccine-derived immunity was assumed to be always as strong as or weaker than infection derived immunity; this led to missing values in the subdiagonals of all figures representing simulation results. Finally, we assumed that immunity from either source did not wane during an influenza season and that no other covariates were present.
2.5. Data analysis
Simulated data sets were analyzed using the following logistic regression models:
-
1.
(model 1–unadjusted; VE estimate, see (6))
-
2.
(model 2–categorical), using dummy variables to represent a categorical variable encoding prior season's and current season's vaccination status: This will give rise to three effect estimates, with the unvaccinated (both in previous and current season) as reference category: VE for the newly vaccinated, VE for the previously vaccinated and effectiveness of previous season’s vaccination for preventing influenza illness in the current season:
| (8) |
Note that the comparison of the previously vaccinated with the never vaccinated is an invalid measure of current season’s VE because it is confounded by prior season’s vaccination.
-
3.
(model 3–partially adjusted; see also (7)); VE estimate, see (6).
-
4.
(model 4–partially adjusted with interaction); two VE estimates: One for those unvaccinated in prior season as in (6); one for those with prior vaccination:
2.6. Misclassification of current and prior vaccination status
It is well known that assessment of vaccination status is inaccurate, even if corroborated by vaccination registries or other data sources, in addition to self-report [14]. We therefore also generated data that was misclassified with respect to current and prior vaccination status (see Online Supplement S2), using sensitivity and specificity for both seasons. These numbers were analyzed like the original numbers using models 1, 2, 3 and 4. We also conducted a sensitivity analysis of misclassification of current and prior vaccination status, by varying both parameters independently from 80% to 98% and using a subset of the parameter values for vaccination- and infection-induced immunity carry-over and calculated crude (model 1) and partially vaccination history-adjusted (model 3) VE estimates (Online Supplement S5).
3. Simulation results
3.1. Vaccination status and history assessed with perfect accuracy
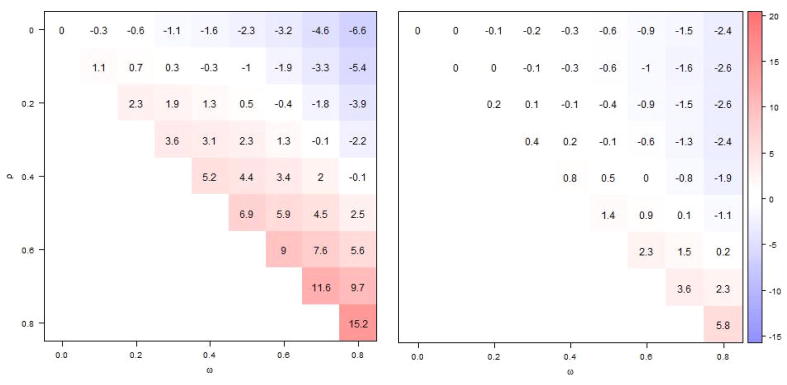
VE estimates that were unadjusted for vaccination history (model 1) were biased, unless neither vaccine- nor infection-derived immunity persisted or if negative and positive biases neutralized each other (Fig. 2, left panel). The stronger the carry-over of infection-derived immunity (larger ), the larger the bias towards too low values of VE. The opposite was true for longer persistence of vaccine-derived immunity (higher values of ) (Fig. 2, left panel). If VE estimates were partially adjusted for vaccination history by including in the past season’s vaccination status as covariate, biases were generally much reduced (Fig. 2, right panel). In rare instances, however, the unadjusted VE estimates fared better than the partially adjusted ones, e.g. with and .
Fig. 2.
Comparing absolute bias in VE estimates from model 1 (left panel), unadjusted for prior vaccination and model 3 (left panel), adjusted for prior season’s vaccination status with shades of blue indicating positive bias and shades of red negative bias. Displayed values are based on 10,000 simulations, for different levels of infection-derived (ω) and vaccine-derived (ρ) immunity carry-over (to next season). The true VE is 60% and current and prior season's vaccination status are measured with perfect accuracy.
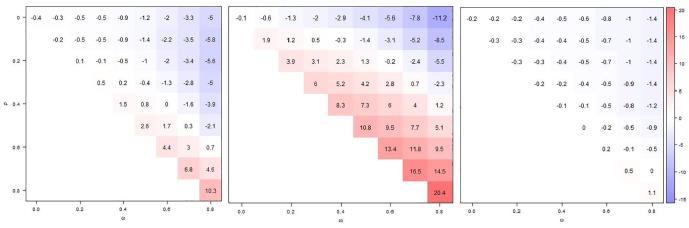
If VE was estimated such as to identify modification of VE by prior season’s vaccination status, despite the lack of such effect modification–-VE was assumed to be unaffected by prior vaccination–- estimates for the “newly vaccinated” (no vaccination in previous season) from both models 2 and 4 (VE estimates are mathematically identical) showed a pattern of bias similar to the unadjusted estimates, but somewhat less pronounced (Fig. 3, left panel). If VE for those vaccinated in the prior season was estimated by the use of a categorical vaccination status/history variable (model 2), massive bias resulted, similar to the unadjusted analysis, but even more pronounced (Fig. 3, middle panel). If, on the other hand, VE in that group was estimated using an interaction term between prior and current season’s vaccination status (; model 4), bias was largely eliminated (Fig. 3, right panel). In a study with 1000 cases and 2000 controls, differences in VE estimates by prior vaccination status would only rarely be statistically significant (Type I error), regardless of model, unless both vaccination- and infection-induced immunity persisted across seasons with high probability (Online Supplement S3, Fig. S3.1).
Fig. 3.
Comparing absolute bias in VE estimates from models 2 and 4 (estimates identical) for those without prior vaccination (left panel); from model 2 for those with prior vaccination (middle panel); and model 4 for those with prior vaccination (right panel). Displayed values are based on 10,000 simulations, for different levels of infection-derived (ω) and vaccine-derived (ρ) immunity carry-over (to next season). The true VE is 60% and current and prior season's vaccination status are measured with perfect accuracy.
Full adjustment for vaccination history (model 5) produced unbiased VE estimates (mean VE rounded to one digit always 60%—not shown).
3.2. Vaccination status and history assessed with imperfect accuracy
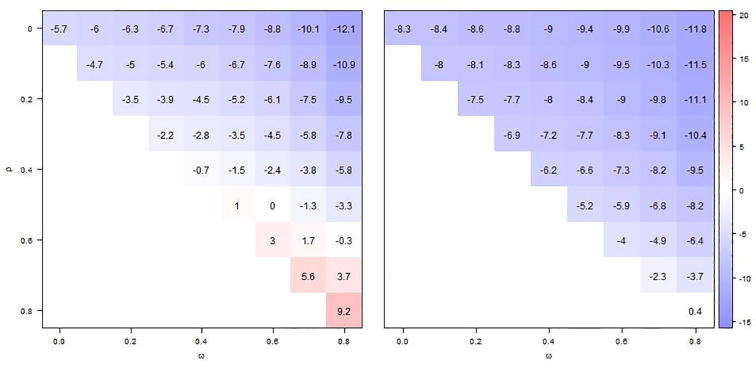
If both current and prior season's vaccination status were assessed with error (sensitivity, specificity ), mean VE estimates, regardless of model, were invariably lower than with accurate vaccination status assessment, rendering positive biases less positive or even negative and negative biases more pronounced (Fig. 4, Fig. 5). Partially adjusted VE estimates (model 3) maintained a weak positive bias only under the most extreme assumption of immunity persistence (Fig. 4, right panel).
Fig. 4.
Comparing absolute bias in VE estimates from model 1 (left panel), unadjusted for prior vaccination and model 3 (right panel), adjusted for prior season’s vaccination status with shades of blue indicating positive bias and shades of red negative bias. Displayed values are based on 10,000 simulations, for different levels of infection-derived (ω) and vaccine-derived (ρ) immunity carry-over (to next season). The true VE is 60% and current and prior season's vaccination status are measured with inaccuracy (sensitivity, σ = 95%, specificity ζ = 90%).
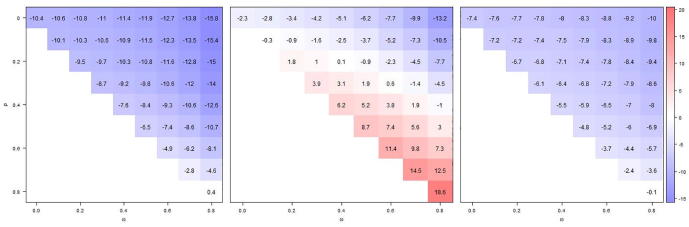
Fig. 5.
Comparing absolute bias in VE estimates from models 2 and 4 (estimates identical) for those without prior vaccination (left panel); from model 2 for those with prior vaccination (middle panel); and model 4 for those with prior vaccination (right panel). Displayed values are based on 10,000 simulations, for different levels of infection-derived (ω) and vaccine-derived (ρ) immunity carry-over (to next season). The true VE is 60% and current and prior season's vaccination status are measured with inaccuracy (sensitivity, σ = 95%, specificity ζ = 90%).
If the modification of VE by prior season was investigated (models 2 and 4) in the absence of such phenomenon and by using misclassified data, the VE in those not considered vaccinated in the previous season became negatively biased except for the strongest persistence of vaccination- and infection-derived immunity (; Fig. 5, left panel). Even though misclassification attenuated the bias in VE for the previously vaccinated, as estimated from model 2 (Fig. 5, middle panel), the difference with the VE in the previously unvaccinated was much more likely to be statistically significant (Type I error); if vaccination-derived immunity persisted from one season to the next in at least 60%, the probability to wrongly reject the null hypothesis of no repeat vaccination effect on VE was at least a third (Online Supplement S3, Fig. S3.2a). In contrast, VE in the previously vaccinated from model 4 was always negatively biased (Fig. 5, right panel), similar to the previously unvaccinated, and the Type I error probability was barely larger than without misclassification (Online Supplement S3, Fig. S3.2b).
3.3. Other scenarios
If both VE and influenza risk were seasonally variable and negatively correlated (the higher the VE, the lower the seasonal attack rate), similar patterns were seen as described for historically constant VE, but biases were generally about a third smaller (see Online Supplement S4, Fig. S4.1). The patterns were also similar when current season's VE was only 20% (see Online Supplement S4), even though bias increased substantially, in particular relative bias.
3.4. Sensitivity analysis of misclassification of vaccination status in current and prior season
For levels of sensitivity and specificity different from the default (sensitivity 95%, specificity 90%), biases were generally more negative with decreasing accuracy and more positive with increasing accuracy (Online Supplement S5, Figs. S5.1 and S5.2). Unadjusted VE estimates were biased low if accuracy was low, but could be low or high, depending on the levels of immunity carry-over, when accuracy was high (Fig. S5.1). Adjusted VE estimates were biased low with very few exceptions: Under high accuracy and highest immunity carry-over, they were weakly biased towards too high values.
4. Discussion
Vaccination history may be a confounder of influenza VE estimates. Using computer simulation we demonstrated that failure to control for vaccination history may cause nontrivial bias in VE estimates, anywhere from underestimation by 11 percentage points to overestimation by 25 percentage points, assuming a true VE of 60%. This corresponds to relative biases of −18% and 42%, respectively; with lower VE, the relative error was even larger (Online Supplement S4). The effect of carry-over of vaccine-derived immunity was generally larger than from infection-derived immunity because, by assumption, vaccination was much more common than infection. This reflects the current situation in the US and in some European countries [15]. Bias from vaccine-derived immunity is generally positive (towards too high values of VE) because the protective effect of prior vaccination is not separated from the effect of current season's vaccination. Bias from infection-derived immunity, on the other hand, is generally opposite in direction, because the protective effect of previous infection is not separated from the effect of currently being unvaccinated. The strength of these two effects will determine the net direction of the bias (Fig. 2, left panel).
Fully and accurately adjusting for vaccination history completely eliminates confounding by vaccination history (Fig. 1, Appendix A). As long as past influenza infection does not affect future vaccination uptake, adjustment for influenza infection history is unnecessary (see Appendix A). Even if past influenza illness were to affect the decision to become vaccinated in the future, it would be unnecessary to adjust for history of influenza infection—a virtually impossible task in the context of an observational study; adjustment for perceived influenza illness, regardless of whether laboratory-confirmed or not, would suffice. Unfortunately, as the number of possible vaccination history trajectories grows exponentially with the number of seasons considered, full adjustment for vaccination history is impractical. Restricting the considered time frame to only two or three seasons—resulting in manageable 2 and 4 distinct vaccination histories, respectively—may not be sufficient to capture the full immunological interplay between past vaccination and natural infection, but may offer a way to partially adjust for vaccination history. In our simulation study, partially adjusted VE estimates for most, if not all, settings were considerably less biased than unadjusted estimates (Fig. 2). If vaccination status was misclassified, VE estimates, whether adjusted or not, were considerably lower, resulting in more biases toward too low values (Fig. 4). The resulting bias in partially vaccination history–adjusted VE estimates was virtually always conservative (VE estimates too low) (Fig. 4, right panel). Comparing VE estimates partially adjusted for vaccination history (model 3) to unadjusted VE estimates (model 1) may indicate the potential importance of the problem: If these estimates are close, confounding by vaccination history likely is not a major issue. In all our simulations, under low confounding conditions (immunity persistence , with a true VE of 60%, the crude and adjusted VE were, on average, always within 5 percentage points, regardless of misclassification. Under high confounding conditions, however, that difference was never below 4 and as high as almost 10 percentage points (not shown).
Recently, numerous studies have examined the effect of repeat vaccinations on VE, mostly using data from two seasons and calculating VE for those vaccinated in both seasons, only in the current and only in the prior season, compared to those not vaccinated in either season, analogous to our model 2. We believe that this analysis is invalid for the VE of the previously vaccinated, due to confounding by vaccination history: Those having been vaccinated in the prior season have a different vaccination—and infection— history on average than the referent group (neither vaccinated in prior nor current season) and thus likely different susceptibility to influenza infection before vaccination. We therefore advise against this type of analysis. If modification of VE by prior season's vaccination status is suspected, interaction terms should be used instead (model 4; see online Supplement S1). Many of these studies were reviewed and meta-analyzed by Belongia et al. [16] and Ramsay et al. [17]. Both meta-analyses confirmed that, while most studies estimated a higher VE for those vaccinated only in the current season vs. those vaccinated in both seasons, especially for influenza A(H3N2) and influenza B, these differences were usually not statistically significant nor were the pooled differences. As we have shown, even in the absence of modification of VE by vaccination history, group-specific VE estimates may wrongly suggest effect modification (model 2, type I error).
In a recent study of seasonal VE during the 2016–17 season in the US [18] one of the main analyses investigated VE by prior season’s vaccination status (Table 4), also corresponding to our model 2 (categorical) analysis. This analysis was complemented by a supplemental analysis (supplemental Table) corresponding to our model 4, which we would classify as the more appropriate analysis because history of vaccination is—at least in part—adjusted for. The supplemental VE estimates for the previously vaccinated were consistently lower than those based on the categorical analysis. Interestingly, in our simulated studies, with no modification of VE by prior season’s vaccination status, VE estimates for those deemed vaccinated in the prior season (categorical model 2) were also mostly higher than for the previously unvaccinated and this was even more pronounced in the analyses of misclassified data (Fig. 3, Fig. 5, left and middle panel). On the other hand, there was little bias in the partially-adjusted VE estimates for the previously vaccinated (model 4, Fig. 3, Fig. 4, right panels) and, consequently, these estimates were typically lower than the categorical estimates, like in [18]. This seems to support the notion that the consistently identified lower VE in those previously vaccinated cannot be attributed to confounding by vaccination history, but more likely reflects an immunological phenomenon.
Misclassification of current and past vaccination status clearly is a major challenge for VE assessment in general [14], and for efforts to adjust for confounding by vaccination history in particular. The use of a misclassification correction method for vaccination status, e.g. using the method described by Greenland and Klinebaum [19], should be explored in future studies.
Our study suffers from several limitations. First, our simulation study, which explores the possible confounding bias by vaccination history is necessarily a simplification of reality and we ignored other important confounders. But even assuming that our simulation model is reasonable, the potential parameter space, most importantly regarding persistence of immunity from vaccination and/or infection, is too large for systematic exploration. We are therefore left with considerable uncertainty regarding the importance of confounding by vaccination history in real VE studies. The resulting bias could be more plausibly bounded using empirical evidence to inform the distribution of these parameters. Furthermore, we have treated influenza as an immunological entity. In reality, not only different influenza types and subtypes often co-circulate, but also different strains of individual types/sub-types. It is unclear how that might affect the relationship between influenza infection and vaccination in previous seasons and current influenza risk. Moreover, we have used an “all-or-none”, as opposed to a “leaky” [7], model of vaccination effect on susceptibility. Even though this does not affect our theoretical considerations, it is well-known that a “leaky” vaccination effect would change the interpretation of TND studies [6], [10], [20]. The impact of partial adjustment for vaccination history on VE estimates under a “leaky” model should be investigated by future studies. Finally, if test accuracy were to be associated with vaccination status, VE estimates would be even further compromised.
In summary, we have shown that confounding by vaccination history and inaccuracy of vaccination status assessment in TND VE studies, which are increasingly used to inform vaccine policy, can compromise VE estimates. Even partial adjustment, e.g. by vaccination status in one or two prior seasons, can substantially reduce confounding bias and improve the robustness of VE estimates and the conclusions derived therefrom, even though misclassification of current and past vaccination status may compromise efforts to adjust for it.
Declaration of interests
The authors declared that there is no conflict of interest.
Acknowledgements
The findings and conclusions in this report are those of the authors and do not necessarily represent the official position of the Centers for Disease Control and Prevention. We would like to thank Drs. Carrie Reed and Jerry Tokars, both Influenza Division, CDC for their helpful comments on the manuscript.
Footnotes
The findings and conclusions in this report are those of the authors and do not necessarily represent the views of the Centers for Disease Control and Prevention
Supplementary data to this article can be found online at https://doi.org/10.1016/j.jvacx.2019.100008.
Appendix A.
Confounding of VE by vaccination history
Let represent the vaccination and infection history, with being a specific history. The causal odds ratio of interest can then be written as
| (A.1) |
| (A.2) |
Only if
-
1.
(independence of vaccine uptake from vaccination and infection history) and
-
2.
(independence of infection risk from vaccination and infection history),
will the terms become and cancel out. The right-hand side of (A.2) then reduces to the marginal odds ratio
| (A.3) |
i.e. the odds ratio, and thus VE estimate, that is not adjusted for vaccination and infection history equals the causal odds ratio/VE estimate (A.1). If either of these conditions are not met, the odds ratio (A.3) will be confounded by vaccination and infection history.
Adjustment for vaccination history sufficient if vaccination status is independent of infection history
Separating into vaccination history and infection history , the causal odds ratio (A.1) becomes
| (A.4) |
If vaccination, conditional on vaccination history, is independent of infection history, i.e. , the terms in (A.4) become and cancel, reducing (A.4) to (3). Thus, adjusting for vaccination history, , without adjusting for infection history, , is sufficient to estimate VE, as long as there are no other sources of confounding and if, conditional on vaccination history, vaccination is independent of infection history.
Appendix B. Supplementary material
The following are the Supplementary data to this article:
References
- 1.Smith D.J., Lapedes A.S., de Jong J.C. Mapping the antigenic and genetic evolution of influenza virus. Science. 2004;305:371–376. doi: 10.1126/science.1097211. [DOI] [PubMed] [Google Scholar]
- 2.Belongia E.A., Kieke B.A., Donahue J.G., Greenlee R.T., Balish A., Foust A. Effectiveness of inactivated influenza vaccines varied substantially with antigenic match from the 2004–2005 season to the 2006–2007 season. J Infect Dis. 2009;199:159–167. doi: 10.1086/595861. [DOI] [PubMed] [Google Scholar]
- 3.Skowronski D.M., De Serres G., Crowcroft N.S. Association between the 2008–09 seasonal influenza vaccine and pandemic H1N1 illness during spring–summer 2009: four observational studies from Canada. PLoS Med. 2010;7:e1000258-e. doi: 10.1371/journal.pmed.1000258. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Petrie J.G., Ohmit S.E., Johnson E., Truscon R., Monto A.S. Persistence of antibodies to influenza hemagglutinin and neuraminidase following one or two years of influenza vaccination. J Infect Dis. 2015;212:1914–1922. doi: 10.1093/infdis/jiv313. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Hollmeyer H.G., Hayden F., Poland G., Buchholz U. Influenza vaccination of health care workers in hospitals—a review of studies on attitudes and predictors. Vaccine. 2009;27:3935–3944. doi: 10.1016/j.vaccine.2009.03.056. [DOI] [PubMed] [Google Scholar]
- 6.Sullivan S.G., Tchetgen Tchetgen E.J., Cowling B.J. Theoretical basis of the test-negative study design for assessment of influenza vaccine effectiveness. Am J Epidemiol. 2016;184:345–353. doi: 10.1093/aje/kww064. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Halloran M.E., Longini I.M., Jr, Struchiner C.J. Design and interpretation of vaccine field studies. Epidemiol Rev. 1999;21:73–88. doi: 10.1093/oxfordjournals.epirev.a017990. [DOI] [PubMed] [Google Scholar]
- 8.Orenstein W.A., Bernier R.H., Dondero T.J. Field evaluation of vaccine efficacy. Bull World Health Organ. 1985;63:1055-. [PMC free article] [PubMed] [Google Scholar]
- 9.Foppa I.M., Ferdinands J.M., Chaves S.S. The case test-negative design for studies of the effectiveness of influenza vaccine in inpatient settings. Int J Epidemiol. 2016;45:2052–2059. doi: 10.1093/ije/dyw022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Foppa I.M., Haber M., Ferdinands J.M., Shay D.K. The case test-negative design for studies of the effectiveness of influenza vaccine. Vaccine. 2013;31:3104–3109. doi: 10.1016/j.vaccine.2013.04.026. [DOI] [PubMed] [Google Scholar]
- 11.Haber M., An Q., Foppa I.M., Shay D.K., Ferdinands J.M., Orenstein W.A. A probability model for evaluating the bias and precision of influenza vaccine effectiveness estimates from case-control studies. Epidemiol Infect. 2015;143:1417–1426. doi: 10.1017/S0950268814002179. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Greenland S., Pearl J., Robins J.M. Causal diagrams for epidemiologic research. Epidemiology. 1999:37–48. [PubMed] [Google Scholar]
- 13.R Core Team . 2014. A language and environment for statistical computing. [Google Scholar]
- 14.Irving S.A., Donahue J.G., Shay D.K., Ellis-Coyle T.L., Belongia E.A. Evaluation of self-reported and registry-based influenza vaccination status in a Wisconsin cohort. Vaccine. 2009;27:6546–6549. doi: 10.1016/j.vaccine.2009.08.050. [DOI] [PubMed] [Google Scholar]
- 15.Mereckiene J., Cotter S., Nicoll A. 2014. Seasonal influenza immunisation in Europe. Overview of recommendations and vaccination coverage for three seasons: pre-pandemic (2008/09), pandemic (2009/10) and post-pandemic (2010/11) [DOI] [PubMed] [Google Scholar]
- 16.Belongia E.A., Skowronski D.M., McLean H.Q., Chambers C., Sundaram M.E., De Serres G. Repeated annual influenza vaccination and vaccine effectiveness: Review of evidence. Expert Rev Vaccines. 2017 doi: 10.1080/14760584.2017.1334554. [DOI] [PubMed] [Google Scholar]
- 17.Ramsay L.C., Buchan S.A., Stirling R.G. The impact of repeated vaccination on influenza vaccine effectiveness: a systematic review and meta-analysis. BMC Med. 2017;15:159-. doi: 10.1186/s12916-017-0919-0. [DOI] [PMC free article] [PubMed] [Google Scholar] [Retracted]
- 18.Flannery B., Chung J.R., Monto A.S. Influenza Vaccine Effectiveness in the United States during the 2016–2017 Season. Clin Infect Dis. 2018 doi: 10.1093/cid/ciy775. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Greenland S., Kleinbaum D.G. Correcting for misclassification in two-way tables and matched-pair studies. Int J Epidemiol. 1983;12:93–97. doi: 10.1093/ije/12.1.93. [DOI] [PubMed] [Google Scholar]
- 20.Lewnard J.A., Tedijanto C., Cowling B.J., Lipsitch M. Measurement of vaccine direct effects under the test-negative design. Am J Epidemiol. 2018 doi: 10.1093/aje/kwy163. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.