Generic Repeat Finder: A High-Sensitivity Tool for Genome-Wide De Novo Repeat Detection

Generic Repeat Finder, a tool for genome-wide de novo repeat detection, outperforms previous repeat detectors in sensitivity.

Abstract

Comprehensive and accurate annotation of the repeatome, including transposons, is critical for deepening our understanding of repeat origins, biogenesis, regulatory mechanisms, and roles. Here, we developed Generic Repeat Finder (GRF), a tool for genome-wide repeat detection based on fast, exhaustive numerical calculation algorithms integrated with optimized dynamic programming strategies. GRF sensitively identifies terminal inverted repeats (TIRs), terminal direct repeats (TDRs), and interspersed repeats that bear both inverted and direct repeats. GRF also detects DNA or RNA transposable elements characterized by these repeats in plant and animal genomes. For TIRs and TDRs, GRF identifies spacers in the middle and mismatches/insertions or deletions in terminal repeats, showing their alignment or base-pairing information. GRF helps improve the annotation for various DNA transposons and retrotransposons, such as miniature inverted-repeat transposable elements (MITEs), long terminal repeat (LTR) retrotransposons, and non-LTR retrotransposons, including long interspersed nuclear elements and short interspersed nuclear elements in plants. We used GRF to perform TIR/TDR, interspersed-repeat, and MITE detection in several species, including Arabidopsis (Arabidopsis thaliana), rice (Oryza sativa), and mouse (Mus musculus). As a generic bioinformatics tool in repeat finding implemented as a parallelized C++ program, GRF was faster and more sensitive than the existing inverted repeat/MITE detection tools based on numerical approaches (i.e. detectIR and detectMITE) in Arabidopsis and mouse. GRF is more sensitive than Inverted Repeat Finder in TIR detection, LTR_FINDER in short TDR detection (≤1,000 nt), and phRAIDER in interspersed repeat detection in Arabidopsis and rice. GRF is an open source available from Github.

It is estimated that the human (Homo sapiens) genome is composed of 50% to 70% repetitive sequences (i.e. repeatome) including tandem, inverted, and interspersed repeats (de Koning et al., 2011). Unfortunately, because of low accuracy in current repeat annotation methods, we still do not know much about the origins, compositions, structures, and biological relevance of these repetitive elements (de Koning et al., 2011; Padeken et al., 2015). Inverted repeats (IRs) are nucleotide sequences that can form self-complementary pairing between their two halves. Perfect IRs are also known as palindromes, and imperfect IRs contain nucleotide pairs that are not reversely complementary (i.e. mismatches in two arms), have gaps/indels in arms, or have a nonpalindromic spacer in the middle (Lilley, 1980; Smith, 2008). Terminal IRs (TIRs) are actually IRs with a spacer in the middle. IRs can form hairpins and cruciforms to serve as target sites for DNA- or RNA-binding proteins (Chasovskikh et al., 2005; Brázda et al., 2011). For example, some DNA-binding proteins have an IR arrangement for their two binding sites in DNAs (Strawbridge et al., 2010). In vivo, IRs as short as 14 nt demonstrate the ability to form hairpin structures (Nag and Petes, 1991). Cruciform formation requires IRs of ≥6 nt (Brázda et al., 2011). Poly(ADP-ribose) polymerase-1 is a ubiquitous DNA-binding protein responsible for many catalytic activities in cells that participate in regulation of chromatin structure, DNA methylation, and transcription (Lonskaya et al., 2005; Pelham et al., 2013). Using atomic force microscopy images, human poly(ADP-ribose) polymerase-1 has been shown to bind with the cruciform structure of a 106-nt IR in an Escherichia coli plasmid in vitro (Chasovskikh et al., 2005).

IRs can be transcribed into single- and double-stranded RNAs to participate in important biological processes such as RNA editing, microRNA (miRNA) and small interfering RNA biogenesis, gene silencing, and alternative splicing/polyadenylation (Melquist and Bender, 2004; Kawahara and Nishikura, 2006; Martinez-Contreras et al., 2006; Piriyapongsa and Jordan, 2007; Gentry and Meyer, 2013; Matzke and Mosher, 2014; Zhang et al., 2014). For example, the human miRNA gene has-mir-548 is derived from a transposable element (TE) that has a pair of 37-nt TIRs with a 6-nt internal sequence. When it transcribes into a single-stranded RNA, a highly stable hairpin loop can be formed, which is then recognized and processed by the protein machinery to generate a 22-nt mature miRNA (Piriyapongsa and Jordan, 2007). In plants, IRs have been shown to produce double-stranded RNAs that can be processed by DICER-LIKE enzymes to produce small interfering RNAs (21–24 nt in size; Zhang et al., 2014).

It is also well known that repeat sequences contribute to genome instability and are linked to many human diseases (Gordenin et al., 1993; La Spada and Taylor, 2010; Gu et al., 2015; Lee et al., 2015). For example, in prokaryotes, palindromic structures (e.g. GAATTC) are frequently recognized and cleaved by endonucleases, and short palindromes of ≤22 nt are generally more stable than longer ones (Muskens et al., 2000). In E. coli, in vitro constructions of perfect palindromes ≥30 nt are not stable (Leach and Stahl, 1983), and the addition of an ∼150-nt spacer into palindromes can enhance their stability (Muskens et al., 2000). In yeast (Saccharomyces cerevisiae), long IRs >100 nt without a spacer or with a short spacer are a threat to chromosome integrity (Zhang et al., 2013). In renal carcinoma, a type of kidney cancer, palindromic AT-rich IRs are thought to contribute to chromosomal translocation and rearrangement (Kato et al., 2014).

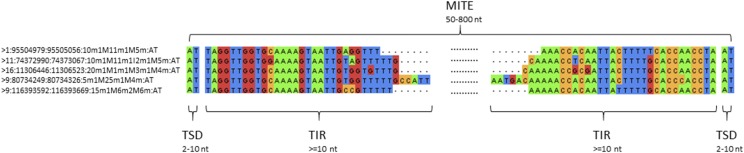
Among repetitive elements, TEs are a popular focus of research because more and more evidence supports the idea that they interact with epigenetic components to offer phenotypical plasticity for organisms and to enable a species to rapidly fine-tune phenotypic responses to changing environments (Gao et al., 2016; Rey et al., 2016). TEs are generally categorized into either retrotransposons or DNA transposons. Retrotransposons are often characterized by terminal direct repeats (TDRs; e.g. retrotransposons with long terminal repeats [LTRs]) or terminal inverted repeats (TIRs; e.g. DIRS-like elements [Poulter and Goodwin, 2005; Piednoël et al., 2011]); and some retrotransposons (e.g. long interspersed nuclear elements [LINEs] and short interspersed nuclear elements [SINEs]) are essentially interspersed repeats (Wicker et al., 2007). The terminal sequences of LTR retrotransposons range from ∼100 nt to >5,000 nt in size (Wicker et al., 2007). LINEs have a size of ∼6,000 nt (Ostertag and Kazazian, 2001; Sargurupremraj and Wjst, 2013). SINEs range from 50 nt to 500 nt in size (Sun et al., 2007). DNA transposons such as miniature inverted-repeat transposable elements (MITEs) are often characterized by TIRs (Wicker et al., 2007). As shown in Figure 1, a MITE (50–800 nt in size) in the human genome is composed of an internal sequence and the conserved flanking TIR pair (≥10 nt), and the whole MITE is flanked by a pair of direct repeats or target site duplication (TSD; 2–10 nt; Ye et al., 2016). In general, MITEs don’t encode proteins and cannot transpose by themselves. They usually locate in introns or intergenic regions (Wright et al., 2003; Lu et al., 2012) and have a copy number of ≥3 in genomes (Ye et al., 2016). Neither a TIR nor a TDR is necessarily equivalent to a TE, and TEs may have TIRs or TDRs in their sequences, but TIRs or TDRs are defined in terms of purely structural features. For example, in the Arabidopsis (Arabidopsis thaliana) genome, TTGTTCATCA ... TGATGAACAA (chromosome 2; strand, +; start, 1259356; end, 1259556) is a TIR but not annotated with any TE so far, and ATAGAGATCTA ... ATAGAGATCTA (chromosome 2; strand, +; start, 15818542; end, 15818606) is a TDR, but is not annotated with any TE element yet.

Figure 1.

The typical structure of a MITE. A MITE detected in the human genome is composed of an internal sequence and the conserved flanking TIR pair, and the whole MITE is flanked by a pair of TSDs. The whole length of a MITE varies from 50 to 800 nt. The TIR is usually ≥10 nt, and the TSD is usually 2 to 10 nt. At left is a list of the MITEs detected by GRF in the human genome, with the format: “chromosome:start:end:modified CIGAR:TSD”. The CIGAR string represents the base-pairing information of theTIRs. In our modified CIGAR string, which is different from the standard CIGAR, “m” indicates a reverse-complementary pair; “M” means unpaired or mismatch; “I” means insertion, and “D” means deletion.

Obviously, more comprehensive and accurate annotation of the repeatome, including transposons, will be critical for us to deepen our understanding of their origins, biogenesis, regulatory mechanisms, and roles in genome integrity, gene structures, and gene expression regulation. Unfortunately, current bioinformatics tools used in detecting repeats and transposons have obvious limitations and miss appropriate annotations of many repeats and transposons in genomes (Sreeskandarajan et al., 2014; Ye et al., 2014, 2016). Recently, using algorithms of numerical calculation-and-comparison that replace conventional string search-and-comparison, we developed three MATLAB tools (i.e. findIR [Sreeskandarajan et al., 2014], detectIR [Ye et al., 2014], and detectMITE [Ye et al., 2016]) to detect IRs and MITEs that are characterized by their TIRs. For instance, the numerical calculation-and-comparison method in detectIR and detectMITE uses a complex number scoring system to calculate the cumulative scores of each nucleotide and all subsequences of certain length for chromosomes efficiently using the vector operation (linear time); it then examines the cumulative scores of all subsequences to find pairs that are separated by a predefined distance and have an absolute value of the sum of cumulative scores of ≤2 (default), which allows at most one mismatch (no insertion or deletion [indel]) in the base complementarity of the minimum pair of TIRs. Thus, the candidate TIRs can be quickly detected. In contrast, the conventional string search-and-comparison method (without optimization) needs to compare each subsequence with all other subsequences of a chromosome to find the candidate pairs (reverse complementary pairs), and it has quadratic time complexity to find all TIR candidate pairs. Using these numerical calculation-and-comparison tools, we are able to detect many perfect IRs (or palindromes; Sreeskandarajan et al., 2014), imperfect IRs with or without spacers in the middle (Ye et al., 2014), and MITEs (Ye et al., 2016) that were missed by existing popular tools or databases.

However, the popular terminal-repeat (TR) detection tools such as Inverted Repeat Finder (IRF; Warburton et al., 2004), LTR_FINDER (Xu and Wang, 2007), detectIR (Ye et al., 2014), and detectMITE (Ye et al., 2016) cannot accurately detect TR pairs that bear indels. Moreover, there is no bioinformatics tool that utilizes numerical calculation algorithms for efficient, sensitive, and comprehensive detection of TDRs and interspersed repeats on a genome scale. Thus, we developed a new parallel C++ tool called Generic Repeat Finder (GRF) to solve these problems. Based on an algorithm that combines numeric calculation approaches with optimized dynamic programming strategies, GRF can identify TIRs, TDRs, and interspersed repeats bearing both inverted and direct repeats in genomes more sensitively and comprehensively. For TIRs and TDRs, GRF can detect spacers in the middle and mismatches/indels in TRs, and can show sequence alignment or base-pairing information of TRs. GRF can help improve the annotation for various DNA transposons or retrotransposons such as MITEs (characterized by TIRs), LTR retrotransposons (characterized by TDRs), and non-LTR retrotransposons, such as LINEs and SINEs (interspersed repeats). In this study, we performed short TIR and TDR (not exceeding 1,000 nt) detection to demonstrate the use of GRF. We also compared the performance and output of GRF in Arabidopsis and mouse (Mus musculus) with those of other popular repeat and TE detection tools, such as detectIR (Ye et al., 2014), detectMITE (Ye et al., 2016), IRF (Warburton et al., 2004), LTR_FINDER (Xu and Wang, 2007), Red (Girgis, 2015), and phRAIDER (Schaeffer et al., 2016). GRF is an open source tool (https://github.com/bioinfolabmu/GenericRepeatFinder).

RESULTS

Overview of Algorithms

TIR Detection

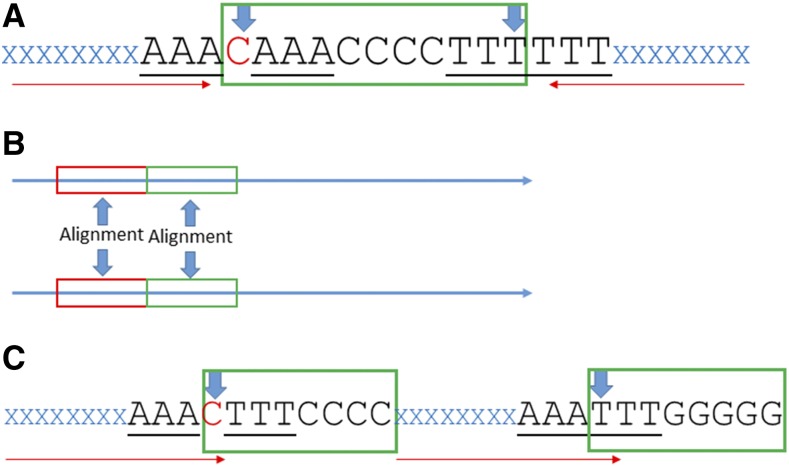
We assume that any TIR pair must bear a minimum of fragments without indels in the boundaries (seed regions). We used the following steps: (1) Use the complex number scoring system A = 1, T = −1, C = j, G = −j to calculate the cumulative score for each nucleotide of an entire chromosome. (2) Calculate the cumulative scores of all subsequences of certain length (e.g. 10 nt by default) for all chromosomes efficiently using the vector operation: C = V(l:n) – [0 V(1:n − l)] (Ye et al., 2014). (3) Examine the cumulative scores of all subsequences and find pairs (seed regions) that are separated by predefined distances and allow at most one mismatch (no indel) in the base complementarity of the minimum pair of TIRs. (4) Perform base-by-base verification for qualified pairs. (5) Inwardly extend the seed regions (minimum TIRs) according to base complementarity (Fig. 2A). To improve the efficiency of alignments for long sequences, a block-by-block alignment strategy was used with the assumption that a pair of TIRs should have a high similarity after reverse complementary transformation (Fig. 2B). (6) Remove redundant results. (7) Optionally, output a selection of high-quality IRs (i.e. length ratio of spacer/total IR sequence is ≤0.2) and long-stem IRs (i.e. the stem length is ≥100 nt).

Figure 2.

Major algorithm for TIR/TDR detection with indels. A, The base extension of inverted repeats. Blue “XXX...XXX” denotes the inverted repeats, and red arrows show the extension direction. The red “C” is the first unpaired base during base comparison. CAAACCCCTTT outlined by the green rectangle needs to be aligned with its reverse complementary part AAAGGGGTTTG. B, Block-by-block alignment. Here are two long sequences (>100 nt) shown by horizontal arrows. Red and green rectangles represent blocks (100 nt). The alignment of the sequences will be conducted first between two red blocks; if the end position of the best alignment is near the end of the red block, the alignment will continue between the green blocks. C, The base extension of direct repeats. Blue “XXX…XXX” denotes two direct repeats, and red arrows show the extension direction. The red “C” is the first unpaired base during base comparison. The sequences in the green rectangles are the parts that need alignment. CTTTCCCC will be aligned to TTTGGGGG.

TDR Detection

The algorithm of TDR detection is similar to TIR detection, except: (1) Seed regions are examined by identity instead of reverse complementarity and (2) during the seed region extension phase, the direction of base alignment is concurrent (Fig. 2C).

Interspersed repeat detection

(1) Use a new scoring system: A = (1, 0, 0, 0), T = (0, 1, 0, 0), C = (0, 0, 1, 0), G = (0, 0, 0, 1) to calculate cumulative scores for subsequences of certain length (e.g. 20 nt by default) for all chromosomes. (2) Filter out the scores of subsequences with low complexity. (3) Perform transformation to make sure each sequence and its reverse complementary sequence have the same score. (4) Group sequences with the same scores together using a hash table. (5) Find candidate repeats (seed regions) within each group by comparing nucleotide sequences. (6) In each repeat group, extend the seed regions by allowing mismatches in both upstream and downstream flanking regions. (7) Compare repeat copies with the consensus sequence in a group and remove the ones with more than the predefined number of mismatches. (8) Merge repeat groups with the same consensus sequences and remove redundant repeat copies in a merged group.

Genome-Wide Repeat Detection by GRF in Different Species

We used GRF to perform TIR/TDR, interspersed repeat, and MITE detection in Arabidopsis, rice (Oryza sativa), Physcomitrella patens, Populus trichocarpa, maize (Zea mays), Plasmodium falciparum, mouse, and humans (see “Materials and Methods”). We further filtered out TIRs/TDRs containing tandem repeats using Phobos (Leese et al., 2008; Mayer et al., 2010). We also filtered out TIRs with total sizes (including internal spacers) <80 nt and TDRs with TR sizes (one-side repeat size) <40 nt. The example of a TIR bearing an indel in CIGAR (Li et al., 2009), dot bracket notation (DBN), and alignment formats is shown in Supplemental Figure S1, A–C. Overall, the distributions of structures (i.e. perfect/imperfect TRs; with/without spacer), mismatches, indels, and sizes of TIRs and TDRs were similar in these species (Supplemental Figs. S2 and S3; Supplemental Tables S1 to S3). We used GRF to detect interspersed repeats in these species (see “Materials and Methods”), filtered out interspersed repeats containing tandem repeats using Phobos, and filtered out interspersed repeats with sizes <40 nt. The example of an interspersed repeat group with alignments against the consensus sequence is shown in Supplemental Figure S1D. Overall, the distributions of copy number and size of interspersed repeats in these species are similar (Supplemental Fig. S4; Supplemental Table S4). Interestingly, maize has many more interspersed repeats than mouse and human even though they have similar genome sizes (Supplemental Table S4). We also found that a small portion of the TIRs/TDRs (0.01–5.57%) were overlapped (see “Materials and Methods”) with interspersed repeats (Supplemental Table S5). We used GRF to detected MITE candidates in these species (see “Materials and Methods”) and CD-HIT (Fu et al., 2012) to cluster similar MITE candidates into MITE families. Overall, the distributions of structures, mismatches, indels, and sizes of MITEs are similar in these species (Supplemental Fig. S5; Supplemental Tables S1 to S3). Interestingly, rice and maize have more MITEs than other species (Supplemental Table S1). We also detected nested MITEs (i.e. small MITEs are included in large MITEs without overlapped TIRs, whose biological functions are not clear and need further study) and found 255 cases in rice, 2 cases in P. patens, 8 cases in P. trichocarpa, 973 cases in maize, 2 cases in human, and none in Arabidopsis, P. falciparum, and mouse. The summary of repeat detection results by GRF in different species is shown in Table 1. The performances including the runtime and memory consumption of TIR, TDR, interspersed repeat, and MITE candidate detection in different species using different parameters are shown in Supplemental Tables S6 and S7.

Table 1. Summary of repeat detection results by GRF (after phobos filtration) in different species.

Species	TIR	High-Quality IR	Long-Stem IR	TDR	MITE	Nested MITEs	Interspersed repeat
Arabidopsis	5,010,983	48,179	232	123,617	126	0	679,068
O. sativa	12,085,468	236,356	2,052	896,812	20,063	255	7,407,771
P. patens	28,322,280	380,058	518	291,698	751	2	10,866,199
P. trichocarpa	23,482,569	359,694	284	1,129,750	908	8	5,004,661
Z. mays	59,910,445	1,712,978	5,794	7,973,830	49,971	973	157,798,471
P. falciparum	4,529,681	46,067	0	127,944	35	0	56,580
M. musculus	79,262,280	874,188	4,180	3,743,729	1,619	0	42,073,336
H. sapiens	111,625,482	1,423,589	24,694	8,119,622	2,431	2	37,331,960

High-Quality and Long-Stem IRs in Different Species

We used GRF to detect high-quality (spacer/total IR length ratio ≤ 0.2) and long-stem IRs (stem ≥100 nt; the overall IR size might not be long) separately in Arabidopsis, rice, P. patens, P. trichocarpa, maize, P. falciparum, mouse and human (see “Materials and Methods”). The reasons we think low spacer/total IR length ratio is important for annotating high-quality IRs are as follows: (1) more complementary pairs will facilitate the formation of hairpins in single strand or cruciforms in double strand; (2) they tend to have higher integrity in terms of two-arm architecture with relatively smaller spacers; (3) they can be examined visually and easily for human validation of hairpin or cruciform structures; and (4) they can be used as a good reference to compare accuracy and comprehensiveness in IR detection among different tools. We further filtered out IRs containing tandem repeats using Phobos. Overall, the distributions of structures, mismatches, indels, and sizes of both high-quality IRs and long-stem IRs are similar in these species (Supplemental Figs. S6 and S7; Supplemental Tables S8 to S10). Interestingly, the number of high-quality IRs is much higher than that of long-stem IRs in these species (Supplemental Table S8).

Comparison of IR Detection between GRF and Other Tools

For IR detection, we compared GRF with other popular tools, such as detectIR (Ye et al., 2014) and IRF (Warburton et al., 2004). We also compared GRF and detectMITE (Ye et al., 2016) in detecting MITEs, which bear TIRs.

detectIR is a MATLAB tool for IR detection allowing spacers in the middle and mismatches/uncomplimentary pairs within two TIRs (stems), based on numeric calculation algorithms (Ye et al., 2014). We performed IR detection in Arabidopsis and mouse using both GRF and detectIR with compatible settings (see “Materials and Methods”), and compared their performances and outputs. In Arabidopsis, GRF (0.21 min and 0.81 gigabyte [GB] random access memory [RAM] with a single thread) was faster and consumed less memory than detectIR (5.50 min and 3.29 GB RAM with a single thread) and had the same 32,774 results. In mouse, GRF (5.34 min and 6.97 GB RAM with a single thread) was faster and consumed less memory than detectIR (48.65 min and 20.39 GB RAM with a single thread) and had the same 1,147,783 results. Clearly, when using similar parameters, GRF is much faster. However, GRF could achieve higher sensitivity in IR detection since it allows the presence of indels within stems whereas detectIR cannot. We found that in Arabidopsis, GRF (0.28 min and 0.81 GB RAM with a single thread) can detect 23,127 IRs with indels in stems that are missed by detectIR; in mouse, GRF (6.94 min and 6.97 GB RAM with a single thread) can detect 378,579 IRs with indels in stems that are missed by detectIR. These suggest that GRF is faster, more memory efficient, and more sensitive than detectIR due to the fact that GRF can detect TIRs bearing indels.

IRF is a popular tool for identifying approximate IRs (Warburton et al., 2004). It finds short fragments of paired repeats (seed regions) and then uses the alignment strategy to verify and extend the candidates (Warburton et al., 2004). To compare GRF and IRF, we generated simulated datasets of TIRs from protein-coding genes, noncoding genes, and intergenic sequences of Arabidopsis and mouse as the control sets and performed head-to-head comparisons between GRF and IRF. For each sequence type, we randomly selected 10,000 fragments of genomic sequences ranging from 0 to 1,000 nt in length as the spacers. For the positive sets (the TIR dataset), we used the first-order Markov model (Sarich et al., 2014) to generate a new random sequence as one TIR repeat arm (10–100 nt, 10–200 nt, 10–500 nt, 10–1,000 nt, and 10–2,000 nt), and added it to the 5′-end of the spacer with its reverse complementary sequence added to the 3′-end of the spacer. We also mutated the reverse complementary sequence to allow at most 10% errors including mismatches and indels. For the negative sets (the non-TIR dataset), two random sequences with the same lengths were added to both ends of the spacer. We used the positive and negative datasets as the inputs for comparison. If the detected TIR regions covered ≥90% of the simulated sequences at ends (i.e. true TIRs in the positive set or random sequences in the negative set), it was labeled as positive, otherwise as negative. As shown in Supplemental Table S11, GRF is more sensitive than IRF in TIR detection for Arabidopsis and mouse, with consistently higher sensitivity and specificity values. We also performed IR detection in Arabidopsis and rice genomes using both GRF and IRF with compatible settings and filtrations (see “Materials and Methods”) and compared their performances and outputs. In Arabidopsis, IRF took 0.49 h and 0.18 GB RAM with a single thread (no multithreading capability) to finish detection while GRF took 0.32 h and 1.42 GB RAM with 64 threads. In rice, IRF took 1.12 h and 0.25 GB RAM with a single thread to finish detection while GRF took 1.04 h and 2.12 GB RAM with 64 threads. Due to multithreading ability, it is possible for GRF to screen the genomes using less time. We downloaded the public transposon annotations of Arabidopsis from the Araport database (Cheng et al., 2016; https://www.araport.org/) that integrates homology approaches with manual curation (https://www.araport.org/download_file/TAIR10_genome_release/annotation/gff/transposons/README.transposons) and the public transposon annotations of rice from RAP-DB (Kawahara et al., 2013; Sakai et al., 2013; http://rapdb.dna.affrc.go.jp), extracted DNA transposon annotations with compatible sizes, and compared the GRF and IRF results with these annotations (see “Materials and Methods”). As shown in Supplemental Table S12, for TIR detection, GRF covers significantly more annotations than IRF in Arabidopsis (51.35% versus 3.2%), as well as in rice (46.81% versus 3.54%).

Based on numeric calculation algorithms (Ye et al., 2016), detectMITE is a MATLAB tool for MITE detection allowing mismatches in TIRs. We performed MITE candidate detection without further family clustering by CD-HIT (Fu et al., 2012) in Arabidopsis and mouse using both GRF and detectMITE (Ye et al., 2016) with compatible settings (see “Materials and Methods”) and compared their performances and outputs. In Arabidopsis, GRF (8.84 min and 0.60 GB RAM with four threads) was faster and consumed less memory than detectMITE (186.92 min and >10 GB RAM with four processes). Comparing the outputs, none of the unique results (32,742) of detectMITE (i.e. results detected by detectMITE but missed by GRF) was a qualified MITE candidate (i.e. minimum TIR length ≥10; AC/GT content ≥20%; no homopolymer or dinucleotide stretch of a length ≥8 in TIRs), but all unique results (228,678) of GRF (i.e. results detected by GRF but missed by detectMITE) were qualified (Supplemental Table S13). In mouse, GRF (1.29 h and 5.89 GB RAM with 16 threads) was faster and consumed less memory than detectMITE (53.39 h and >130 GB RAM with 16 processes). None of the unique results (550,074) of detectMITE was qualified, but all unique results (4,562,949) of GRF were qualified (Supplemental Table S13). These suggest that GRF is more sensitive, faster, and more memory efficient than detectMITE.

Comparison of TDR Detection between GRF and Other Tools

The intermediate detection results of some LTR retrotransposon detection tools, such as LTR_FINDER (Xu and Wang, 2007), are essentially TDRs. They can be used for comparison of TDR detection. Here, we compared GRF and modified LTR_FINDER (which outputs intermediate TDR results) in TDR detection. We also compared the GRF integrated hybrid approach (i.e. GRF + modified LTR_FINDER that takes TDRs from GRF as the input) with LTR_FINDER in LTR retrotransposon detection.

LTR_FINDER is a tool for de novo LTR retrotransposon detection (Xu and Wang, 2007) and does the following: (1) searches for all exactly matched string pairs in input sequences using a suffix-array algorithm (Ko and Aluru, 2005); (2) uses alignment strategy to combine short close repeat pairs into a longer pair (LTR candidate); and (3) filters LTR candidates and predicts LTR retrotransposons (Xu and Wang, 2007). We modified the source code of LTR_FINDER to output intermediate results (i.e. the genomic locations of LTR candidates) and generated simulated datasets of TDRs in Arabidopsis and mouse as the control sets to perform side-by-side comparisons between GRF and LTR_FINDER using the an approach similar to that described in the previous section. As shown in Supplemental Table S14, GRF is more sensitive than LTR_FINDER in TDR detection for Arabidopsis and mouse, with consistently higher sensitivity and specificity values. We also performed TDR detection in Arabidopsis and rice genomes using both GRF and LTR_FINDER with compatible settings and filtrations (see “Materials and Methods”) and compared their performance and output. In Arabidopsis, LTR_FINDER (0.25 h and 0.42 GB RAM with a single thread (no multithreading capability) was faster than GRF (0.60 h and 3.51 GB RAM with 64 threads). In rice, LTR_FINDER took 1.11 h and 0.59 GB RAM with a single thread while GRF took 1.06 h and 3.97 GB RAM with 64 threads. We extracted LTR transposon annotations with compatible sizes from the aforementioned public transposon annotations and compared the GRF and LTR_FINDER results with these annotations (see “Materials and Methods”). As shown in Supplemental Table S12, GRF covers more annotations than LTR_FINDER in Arabidopsis (0.79% versus 0.54%), and also in rice (0.89% versus 0.54%). Both GRF and LTR_FINDER have low coverage, probably because the extracted annotations of LTR transposons do not have well-defined TDR structures or long enough TDRs (i.e. ≥40 nt).

We also modified the source code of LTR_FINDER (Xu and Wang, 2007) to make it accept TDRs from GRF as the input for downstream transposon detection. Then we performed LTR retrotransposon detection in Arabidopsis and rice using both LTR_FINDER and the GRF integrated hybrid approach with compatible settings and compared their performances and outputs (see “Materials and Methods”). In both LTR_FINDER and the hybrid approach, we restricted the length of the LTR retrotransposon to 1,200–27,000 nt (default parameter of LTR_FINDER). We extracted the LTR transposon annotations with compatible sizes from the aforementioned public transposon annotations and compared the LTR_FINDER and hybrid approach results with these annotations (see “Materials and Methods”). Overall, the hybrid approach is much slower and consumes more memory than LTR_FINDER, because the TDR detection step in the hybrid approach has a very large search space (i.e. the distance between seed regions can range from 1,090 nt to 27,000 nt and indels are allowed). In Arabidopsis, LTR_FINDER covers 13.87% of the annotated LTR retrotransposons, whereas the hybrid approach covers 12.65% of the annotated LTR retrotransposons; in rice, LTR_FINDER covers 15.75% of the annotated LTR retrotransposons, whereas the hybrid approach covers 14.31% of the annotated LTR retrotransposons (Supplemental Table S15). These results suggest that the GRF integrated hybrid approach has lower sensitivity and performance than LTR_FINDER in LTR retrotransposon (1,200–27,000 nt) detection in Arabidopsis and rice. Clearly, GRF needs further improvement in long TDR detection.

Comparison of Interspersed Repeat Detection between GRF and Other Tools

Red is a fast and accurate tool for de novo repeat detection using machine learning methods (Girgis, 2015). It is reported (Girgis, 2015) that Red is much faster than popular repeat detection tools, such as RepeatScout (Price et al., 2005) and ReCon (Bao and Eddy, 2002), has a much lower false positive rate than WindowMasker (Morgulis et al., 2006), and is highly sensitive to both transposons and tandem repeats. phRAIDER is a de novo repeat element detection tool incorporating the PatternHunter spaced seed model (Schaeffer et al., 2016). It is reported (Schaeffer et al., 2016) to be much faster than RepeatScout (Price et al., 2005) with similar accuracy. Accordingly, we compared GRF with Red and phRAIDER for interspersed repeat detection.

We performed interspersed repeat detection in Arabidopsis and rice using both GRF and Red with compatible filtrations (see “Materials and Methods”) and compared their performances and outputs. In Arabidopsis, Red (5.44 min and 1.41 GB RAM with a single thread) was faster than GRF (20.03 min and 2.53 GB RAM with a single thread). In rice, Red (18.24 min and 2.86 GB RAM with a single thread) was faster than GRF (1.26 h and 8.57 GB RAM with a single thread). We extracted transposon annotations other than DNA or LTR transposons with compatible sizes from the aforementioned public transposon annotations and compared the GRF and Red results with these annotations (see “Materials and Methods”). As shown in Supplemental Table S12, GRF covers more annotations than Red in Arabidopsis (2.00% versus 0.21%), but fewer in rice (1.10% versus 6.96%). On the other hand, Red (1) does not cluster interspersed repeats into groups, whereas GRF does; (2) does not consider inverted interspersed repeats (i.e. interspersed repeats in opposite directions), whereas GRF does, because GRF reports the orientation of the entire repeats in a group so we know whether any two repeats in a group are in inverted orientation or not.

We performed interspersed repeat detection in Arabidopsis and rice using both GRF and phRAIDER with compatible settings and filtrations (see “Materials and Methods”) and compared their performances and outputs. In Arabidopsis, phRAIDER (13.17 s and 746.08 MB RAM with a single thread) was faster than GRF (20.03 min and 2.53 GB RAM with a single thread). In rice, phRAIDER (1.78 min and 5.40 GB RAM with a single thread) was faster than GRF (1.26 h and 8.57 GB RAM with a single thread). We extracted transposon annotations other than DNA or LTR transposons with compatible sizes from the aforementioned public transposon annotations and compared the GRF and phRAIDER results with these annotations (see “Materials and Methods”). As shown in Supplemental Table S12, GRF covers more annotations than phRAIDER in Arabidopsis (2.00% versus 0.01%), as well as in rice (1.10% versus 0.02%). These suggest that GRF is more sensitive than phRAIDER in interspersed repeat detection in Arabidopsis and rice. On the other hand, phRAIDER does not consider inverted interspersed repeats, but GRF does.

DISCUSSION

In TIR and TDR detection, our numeric approaches are faster than conventional string search-and-comparison approaches (Sreeskandarajan et al., 2014; Ye et al., 2014), because we calculate the cumulative scores of all pairs of subsequences (length = 10 by default) of a chromosome separated by a specific distance in linear time using efficient vector operations and narrow down the search space for TR candidates by limiting the cumulative scores. Thus, the number of sequences requiring base-by-base verification for complementarity is greatly reduced, and the seed regions (minimum TRs) can be quickly and exhaustively detected. In the extension of seed regions, mismatches/indels are allowed and the dynamic programing strategy optimized with block comparison is used to speed up alignment. The length of the seed region determines the sensitivity of the detection. The detection with a shorter seed region will be more sensitive but slower because it increases the number of sequences requiring base verification and alignment and vice versa. By default, the length of seed region is 10 nt, and users can adjust it according to their needs (minimum length = 5 nt). In TIR detection of Arabidopsis, the detection with seed length = 10 nt can cover 63.06% of the results from the detection with seed length = 5 nt but is ∼54× faster. In the extension of seed regions, we adopt a block-by-block alignment strategy (block size = 100 nt by default) to improve performance. Compared with the regular dynamic programing strategy, this strategy can achieve similar accuracy but is much faster. For instance, in TIR detection of Arabidopsis, block-by-block alignment can correctly detect >99.99% of the alignments that the regular dynamic programing strategy can detect but is 15.4 times faster. Users can increase the block size to achieve higher alignment accuracy. In interspersed repeat detection, we reduce the search space by clustering all subsequences (length = 20 nt by default) with the same cumulative scores into groups, and then verify repeat sequences within groups. In the verification process, we consider both direct and inverted interspersed repeats and provide the strand information in the output, which is not available in Red (Girgis, 2015) and phRAIDER (Schaeffer et al., 2016). Inverted interspersed repeats can be candidates for inverted SINEs, which have been shown to have negative effects on gene expression (Tajaddod et al., 2016). We also add OpenMP-assisted central processing unit parallelization in TR and interspersed repeat detection to reduce the runtime without largely increasing the memory consumption. In TIR, TDR, and interspersed repeat detection, some of the GRF outputs could be low-complexity sequences (e.g. ATATATATATATATAT). We provided scripts to filter out the outputs containing tandem repeats using Phobos. Users can adjust the parameters of Phobos and remove these low-complexity sequences using our scripts. In TIR detection, we allow users to select high-quality (based on the spacer/total IR sequence length ratio) and long-stem IRs as outputs, which can significantly reduce the size of outputs.

Compared with other numeric calculation-and-comparison-based tools (i.e. detectIR [Ye et al., 2014] and detectMITE [Ye et al., 2016]), GRF is faster, more memory efficient, and more sensitive (allowing indels in stems). Compared with other popular repeat detection tools, such as IRF (Warburton et al., 2004), LTR_FINDER (modified to output intermediate results; Xu and Wang, 2007), Red (Girgis, 2015), and phRAIDER (Schaeffer et al., 2016), GRF is more sensitive because the numeric approach can exhaustively search the seed regions in the genome and detect lots of putative results missed by the other detection methods, which is helpful in improving the current repeat and TE annotations. Our new approach to simulate TIRs/TDRs based on the first-order Markov model is useful in evaluating the accuracy of different TR detection tools in any species. For DNA transposon detection, we have implemented the MITE detection module based on the algorithm of detectMITE (Ye et al., 2016). Compared with detectMITE, GRF is faster and more sensitive and supports nested MITE detection. For LTR retrotransposon detection, GRF outputs TDRs as LTR candidates, and other tools, such as LTR_FINDER (Xu and Wang, 2007), can be used for downstream LTR identification and filtration. For non-LTR retrotransposons, such as LINEs and SINEs, GRF identifies many interspersed repeats missed by Red (Girgis, 2015) and phRAIDER (Schaeffer et al., 2016) for further filtration and verification. GRF covers more public transposon annotations than IRF (TIR detection), LTR_FINDER (modified to output intermediate results; TDR detection), and phRAIDER (interspersed repeat detection) in Arabidopsis and rice. In the future, it is possible to use high-throughput short reads to reduce the false negative of these tools in transposon detection (Kang et al., 2016). Other functions of GRF, such as showing the alignments of TIRs/TDRs/interspersed repeats and extracting sequences with specific lengths of spacers/TRs, can help biologists better understand and examine the results, and these functions are not available in the aforementioned repeat detection tools.

Obviously, future work is needed in GRF to improve its performance of long TIR/TDR detection (e.g. >1,000 nt) with indels and to allow gap openings in interspersed repeat detection due to the limitation of its current algorithm. For interspersed repeat detection, we can quickly locate the seed regions based on our current numeric algorithm, but allowing gaps in the extension phase of the seed regions is challenging for the following two reasons. First, the extension needs multiple sequence alignment (MSA), which is a heavy computational task. For N individual sequences, the naive method requires constructing the N-dimensional equivalent of the matrix formed in standard pairwise sequence alignment. The search space thus increases exponentially with increasing N and is also strongly dependent on sequence length. A naive MSA takes O(Length^N) time to produce. To find the global optimum for N sequences this way is an non-deterministic polynomial-complete problem (Wang and Jiang, 1994; Just, 2001; Elias, 2006). Even though there are different MSA algorithms to improve the alignment speed with high alignment correctness (Lipman et al., 1989; Edgar, 2004; Grasso and Lee, 2004; Collingridge and Kelly, 2012), MSA is still a challenging computational task in the bioinformatics community. If we have a large number of long sequences (e.g. n > 100; length >1,000 nt) that need MSA, it will take a long time to finish. Second, it is hard to determine when to stop the seed region extension, because we do not know how long the interspersed repeats could be. Nevertheless, we will be committed to improve GRF in the future so that it can allow indels in interspersed repeat detection.

CONCLUSION

In conclusion, GRF is a generic and sensitive tool for genome-wide repeat and TE detection. It not only can improve repeatome annotation of genomes but also can help deepen our understanding of the origins, structures, and biological relevance of repetitive elements. GRF needs further development to improve its performance of long TIR/TDR detection with indels and to allow gap openings in interspersed repeat detection.

MATERIALS AND METHODS

Algorithms and Design

TIR Detection

Based on the algorithm of detectMITE (Ye et al., 2016), which can detect IRs bearing spacers in the middle and mismatches in TRs, a new strategy was used that combines numerical calculation and dynamic programming approaches to allow indels in TR detection. It was assumed that any TIR pair must bear a minimum of fragments (default = 10 nt, adjustable as a parameter) without indels in their boundaries. The algorithm is as follows: (1) Use the complex number scoring system: A = 1, T = −1, C = j, G = −j to calculate the cumulative score for each nucleotide of an entire chromosome. For instance, the cumulative score for each nucleotide of the sequence AAATTTis (1, 2, 3, 2, 1, 0). (2) Calculate the cumulative scores of all subsequences of certain length (length = 10 by default) of a chromosome efficiently using the vector operation C = V(l:n) – [0 V(1:n − l)] (Ye et al., 2014). Here, l denotes the length of subsequences (I = 10, by default); n denotes the length of the chromosome; V denotes the cumulative scores of all nucleotides of the chromosome, obtained from step 1; C denotes the cumulative scores of all subsequences with length I. For instance, the cumulative scores of all subsequences (length = 4) of sequence AAATTT(i.e. AAAT, AATT, ATTT) = V(4:6) – [0 V(1:2)] = (2, 0, −2). (3) Examine the cumulative scores of all subsequences and find pairs that are separated by predefined distances (from 0 to 980 by the resettable default, limiting the total IR length to 20–1,000) and have the absolute value of the sum of cumulative scores ≤2 (default), which allows at most one mismatch (no indel) in the base complementarity of the minimum pair of TIRs. For instance, the absolute value of the sum of cumulative scores of AAAAAGCCCCCandGGGGGATTTTT= |(5 + 4j) + (−4 − 5j)| = 2, which are complementary TIRs (pairs) bearing one mismatch. (4) Perform base-by-base verification for qualified pairs; only sequences with true complementarity are kept and considered as seed regions. (5) Inwardly extend the seed regions according to base complementarity. If indels in TRs are not enabled, direct base-by-base comparisons will be used, and the inward extension will stop when the maximum number of mismatches (adjustable) is reached or all bases are compared, and the percentage of unpaired bases in the stem will be checked (at most 10% by default). If the stem does not satisfy the percentage requirement, the longest substem satisfying the percentage requirement will be reported. Otherwise, block-based dynamic programing approach will be used. In such cases, base-by-base comparisons are still used to find the first unpaired bases, and the Needleman-Wunsch algorithm (Needleman and Wunsch, 1970) is used to find the best alignment of the sequence between the unpaired bases against its reverse complementary bases (Fig. 2A). The best alignment must have the highest alignment score in all qualified alignments (i.e. alignments satisfying structure constraints such as the maximum number of mismatches/indels and maximum percentage of unpaired bases). To improve the efficiency of alignments for long sequences, a block-by-block alignment strategy is used with the assumption that a pair of TRs should have a high similarity after reverse complementary transformation (Fig. 2B). For short sequences with lengths ≤2 × block size (the default size is 100), regular base-by-base alignment is used. For the best alignment in the current block, if the length of aligned sequences is ≤0.8 * block size (default), the alignment procedure will stop and the end position of the best alignment will be returned. Otherwise, a new block will be created and the alignment will continue from the current end position. The detections of IRs with different distances between two seed regions including steps 3 to 5 can be performed in parallel. (6) Remove redundant results (i.e. small TRs that are part of LTRs) by making an index of positions of TRs in the chromosome. (7) Filter high-quality IRs (based on the spacer/total IR sequence length ratio; adjustable) and long-stem IRs.

TDR Detection

TDRs are a pair of direct repeats separated by a spacer. The algorithm of IR detection is modified and applied to TDR detection with the following differences. (1) After obtaining the cumulative scores of all subsequences of a chromosome, the absolute value of the difference of cumulative scores of each pair separated by a spacer is calculated, and the pairs with an absolute value of the difference ≤2 (default) are kept as the two seed regions. Further verification of the seed regions is based on base identity, allowing one mismatch. (2) During the seed region extension phase, the direction of base alignment is concurrent, and the inner sequence between two seed regions is aligned against the forward extended sequence with the same length (Fig. 2C).

Interspersed Repeat Detection

Interspersed repeats are identical or nearly identical DNA sequences that are spread out through the genome (Treangen and Salzberg, 2011). They are different from TR pairs and have two or more copies in different chromosomes and strands. The following numeric algorithm for interspersed repeat detection was developed. (1) Use a new scoring system, A = (1, 0, 0, 0), T = (0, 1, 0, 0), C = (0, 0, 1, 0), G = (0, 0, 0, 1), to calculate cumulative scores for subsequences (length = 20 nt by default) of all chromosomes. For instance, ATCGATCG has a cumulative score of (2, 2, 2, 2). (2) Filter out the scores of subsequences with low complexities (i.e. G/C or A/T content <20%, or Lempel-Zic complexity value <0.675; Han and Wessler, 2010; Ye et al., 2016), which might be tandem repeats. (3) Perform the following transformation to make sure each sequence and its reverse complementary sequence have the same score. For score (n_A, n_T, n_C, n_G), if n_A < n_T, swap n_A and n_T, and swap n_C and n_G; if n_A = n_T and n_C < n_G, swap n_C and n_G. (4) Group sequences with the same scores together using a hash table (linear time). (5) Find candidate repeats (seed regions) within each group by comparing nucleotide sequences. For every two repeats, if their sequences are the same or reverse complementary, they are grouped together and considered to be copies in the same repeat group. For each repeat group, the copy number must be ≥3 (by default). (6) In each repeat group, extend the seed regions allowing mismatches in both upstream and downstream flanking regions. In the extension phase, if ≥80% (default) of the sequences have the same base in one position, the base will be defined as a determined base; otherwise, it will be undetermined (marked as “N”). The extension will stop when the maximum number of undetermined bases (default = 1 in either direction) is reached, and a consensus sequence will be generated (including determined and undetermined bases). (7) Compare repeat copies with the consensus sequence in a group and remove the ones with more than two mismatches (adjustable default; excluding undetermined bases). (8) Merge repeat groups with the same consensus sequences and remove redundant repeat copies in a merged group. The copy number of a merged group must be ≥3 (by default). Steps 2, 3, 5, 6, and 7 can be performed in parallel.

Removing TIRs, TDRs, and Interspersed Repeats Containing Tandem Repeats (Optional)

Some of the detected TIRs, TDRs, or interspersed repeats could be low-complexity sequences (e.g. “ATATATATATATATAT” has a valid structure of IRs), and scripts in the GRF package were provided for users to filter out the output sequences containing tandem repeats using Phobos, a highly accurate tandem repeat search tool for complete genomes.

Implementation of GRF

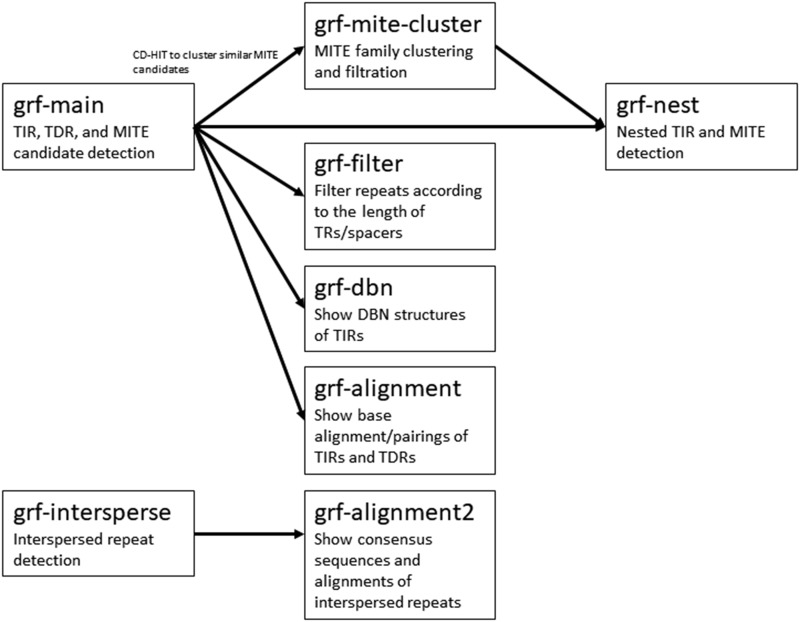
GRF was implemented with C++ and used OpenMP (Dagum and Menon, 1998) for CPU parallelization. GRF was tested on Ubuntu 14.04+ with g++ 4.9+. Inside the “bin” folder of the GRF package, the program grf-main is for TIR, TDR, and MITE candidate detection; grf-intersperse is for interspersed repeat detection; grf-mite-cluster is for MITE family clustering and filtration; grf-nest is for nested TIR/MITE detection; grf-dbn shows the DBN structures of TRs; grf-alignment shows the sequence alignment/pairing of TRs; grf-alignment2 shows the consensus sequences and alignments of interspersed repeats. grf-filter filters repeats according to the lengths of TRs and/or spacers. grf-main, grf-intersperse, and grf-mite-cluster are parallel programs. Users can adjust many parameters in TIR, TDR, interspersed repeat, and MITE detection (see “readme.txt” in the GRF package). The relationship of the programs in the GRF package is shown in Figure 3.

Figure 3.

The relationship flowchart of the component programs within the GRF package.

Other Useful Functions of GRF

Compared with existing numerical approach based tools that can only detect IRs (Sreeskandarajan et al., 2014; Ye et al., 2014) or MITEs (Ye et al., 2016), GFR has the following new functions: (1) adding more sequence structure constraints (i.e. the maximum number of mismatches/indels and maximum percentage of unpaired bases in TIRs/TDRs); (2) showing the base-pairing of TIRs in modified CIGAR (Li et al., 2009; “M” is for mismatch and “m” for match, instead of “m” for both match and mismatch, as in the standard CIGAR), DBN, and alignment formats; (3) showing the base identity of TDRs in modified CIGAR and alignment formats; (4) showing the consensus sequences and MSAs for interspersed repeats (in the consensus sequences, each base is the base with the highest frequency); (5) filtering repeats according to the lengths of TRs and/or spacers; (6) removing redundant TRs (i.e. small TRs that are part of large TRs) in the output; (7) detecting nested TIRs/MITEs.

Application of GRF in Transposon Detection

MITE (DNA Transposon) Detection

Additional modules were developed so that GRF can be used in genome-wide MITE detection directly. Since MITEs (50 to 800 nt) are characterized by TIRs, a TIR detection algorithm was first used to locate MITE candidates and then use specific structure constraints (Ye et al., 2016) to filter candidate sequences. The algorithm is as follows. (1) Find short TIR pairs (default length = 10; at most one mismatch allowed) separated by a distance (from 30 to 780 by default, limiting the total IR length from 50 to 800) using the numeric calculation approach. (2) Only keep the candidate pairs with TSDs (i.e. 2- to 10-nt direct repeats) in the flanking regions. (3) Extend the remaining TIR pairs allowing indels/mismatches. (4) Filter out candidate MITE sequences with low complexity (Ye et al., 2016) in TIR regions. (5) Cluster candidate MITEs into families according to sequence similarities by tools such as CD-HIT (Fu et al., 2012). (6) Filter out MITE families with the genome copy number <3 (default) and select the representative sequence for each family using the methods described in detectMITE (Ye et al., 2016). In addition, GRF can detect nested MITEs (i.e. small MITEs are included in large MITEs without overlapped TIRs), whose biological functions are not clear and need further study.

LTR Retrotransposon Detection

Since LTR retrotransposons are characterized by TDRs, the TDRs detected by GRF can be further filtered to predict LTR retrotransposons. Popular de novo LTR retrotransposon detection tools such as LTR_FINDER (Xu and Wang, 2007) and LTRharvest (Ellinghaus et al., 2008) can be modified and used as the downstream filtration tool. The source code of LTR_FINDER (included in the GRF package) was successfully modified to accept the TDRs detected by GRF as the input. LTR_FINDER can further adjust alignments, detect signals, and recognize important enzyme domains to produce reliable results (Xu and Wang, 2007). In this article, this new hybrid approach was compared with the original LTR_FINDER using public LTR retrotransposon annotations as the benchmark.

Genome-Wide Repeat Detection by GRF in Different Species

Genome sequences of Arabidopsis (Arabidopsis thaliana; TAIR10.31), Populus trichocarpa (JGI2.0), rice (Oryza sativa; IRGSP-1.0), maize (Zea mays; AGPv4), and Physcomitrella patens (ASM242v1) were downloaded from the Ensembl plant database (http://plants.ensembl.org/index.html); Plasmodium falciparum (ASM276v2) was downloaded from the National Center for Biotechnology Information database (https://www.ncbi.nlm.nih.gov/); and human (Homo sapiens; GRCh38 primary assembly) and mouse (Mus musculus; GRCm38 primary assembly) were downloaded from the Ensembl database (http://useast.ensembl.org/index.html; Yates et al., 2016). GRF was used for TIR/TDR, interspersed repeat, and MITE detection in our Ubuntu server (4x Intel Xeon E7-4870 2.40 GHz; 10C/20T; 512 GB RAM). For TIR/TDR detection, the following parameters were used in GRF: minimum TR length = 10 nt; distance between seed regions = 0–980 nt; seed region length = 10 nt; at most one mismatch was allowed in the seed region; at most 10% unpaired bases were allowed for TRs (no limit for the maximum number of mismatches or indels). “script/extract_tr.py” was used in the GRF package to extract the TRs (without spacers) in the TIR/TDR outputs, and Phobos (version 3.3.12; http://www.ruhr-uni-bochum.de/ecoevo/cm/cm_phobos.htm) was used with default parameters and output format “0” to detect tandem repeats in the extracted TRs. Then “script/filter.py” was used to filter out the TIRs/TDRs containing tandem repeats based on Phobos outputs. TIRs were further filtered out with total sizes (including internal spacer) <80 nt and TDRs with TR sizes (one-side repeat size) <40 nt.

For interspersed repeat detection, the following parameters were used in GRF: seed region length = 20 nt; minimum copy number = 3; maximum number of undetermined bases (in either direction) = 1; the minimum identity for a determined base in the consensus sequence = 80%; maximum number of mismatches for a repeat copy compared with the consensus sequence (excluding undetermined bases) = 2. “script/convert.py” was used to convert the interspersed repeat outputs to FASTA format, and Phobos (only accepting the FASTA file as input) was used to detect tandem repeats in the converted FASTA file. Then, “script/filter2.py” was used to filter out the interspersed repeats containing tandem repeats based on Phobos outputs and “script/format.py” was used to format the filtered results (each repeat group is separated by dashed lines). The interspersed repeats with copy number <3 were filtered out after Phobos filtration. Interspersed repeats with total sizes <40 nt were further filtered out.

For MITE detection, the following parameters were used in GRF: the distance between seed regions = 30–780 nt, and other settings were the same with TIR detection. For MITE family clustering, “cd-hit-est” was used in the CD-HIT package (version 4.6.8; Fu et al., 2012) with the following settings: (1) sequence identity threshold (“-c”) = 0.9 (default); (2) alignment coverage for the longer sequence (“-aL”) = 0.99 and length difference cutoff (“-s”) = 0.8. To detect high-quality IRs, in GRF (grf-main), “-r 0.2” was set, which means that maximum spacer/total IR sequence length ratio = 0.2; to detect long-stem IRs, “–min_tr 100” was set, which means that minimum TR length = 100 nt. To find the overlapped portion of TIR/TDR results and interspersed repeat results, each TIR/TDR result was examined, and if it is completely covered (from start to end) by any interspersed repeat detected by GRF, this TIR/TDR result will be considered to be covered by interspersed repeat results, and the same rule was used to examine each interspersed repeat result. The following optional parameters were also used to make another run of TIR and TDR detection to measure the performance of GRF: (1) minimum TR length = 40; (2) seed region length = 40; (3) maximum mismatch number in seed region = 4.

Comparison of IR Detection between GRF and detectIR

IR (total length = 22 nt including internal spacer) detection was performed allowing at most one mismatch in stems and at most two bases in the spacer in Arabidopsis and mouse using both GRF and detectIR. In detectIR, the module detectPerfectIR was used to detect perfect IRs with repeat length = 22 nt, and the module detectImperfectIR_S1.m was used to detect IRs allowing mismatches and gaps (spacers) with the following settings: (1) minimum and maximum sequence length = 22 nt; (2) maximum mismatch = 1; and (3) maximum gap (number of bases in the spacer) = 2. In GRF, the following compatible settings were used to detect perfect and imperfect IRs: (1) minimum TIR length = 10 nt; (2) seed region length = 10 nt; (3) maximum mismatch in the seed region = 1; (4) minimum and maximum distances between seed regions = 2; (5) maximum mismatch in TIR = 1; (6) maximum percentage of unpaired bases in TIRs = 100% (i.e. no requirement for the percentage of unpaired bases). IR (length = 22 nt) detection was also performed using GRF allowing at most one mismatch and one indel in stems and at most two bases in the spacer in Arabidopsis and mouse, and the results of GRF were compared with the results of detectIR obtained above. Here, in GRF, the following settings were used: (1) minimum seed region length = 5; (2) maximum number of indels = 1; (3) minimum and maximum distances between seed regions = 12; other settings were kept the same as in the previous run. In the comparison of outputs, any results from the two programs that have the same start and end positions were considered to be common results.

Comparison of IR Detection between GRF and IRF

In the comparisons of simulated data, the following compatible settings were used in IRF (version 3.07) and GRF. In IRF, (1) alignment scores were +1 (match), −1 (mismatch), and −2 (indel), for a minimum score of 8; (2) match probability = 80% and indel probability = 10%; (3) maximum stem length to report = 10,000 nt (this cannot be set to a smaller value); and (4) maximum loop length to report = 1,000 nt. In GRF, (1) alignment scores were +1 (match), −1 (mismatch), and −2 (indel); (2) minimum TIR length = 10 nt; (3) seed region length = 10 nt; (4) at most one mismatch was allowed in the seed region; (5) minimum distance between seed regions = 0 and maximum distance between seed regions was adjusted according to different TIR lengths in different runs of simulated data (i.e. maximum TR length of simulated TIRs = 100, 200, 500, 1,000, or 2,000 nt and maximum spacer length of simulated TIRs = 1,000 nt, so the corresponding maximum distance between seed regions is 1,180, 1,380, 1,980, 2,980, or 4,980 nt); (6) at most 10% unpaired bases are allowed in TIRs. IR detection was performed in Arabidopsis and rice using GRF and IRF with compatible settings. In IRF, the same settings were used as described previously in this section for IRF. In GRF, the same settings were used as described previously in this section except that the maximum distance between seed regions was set to 980 nt, which guaranteed that the maximum length of IRs was 1,000 nt. The results of GRF and IRF were filtered by total sequence length (80 to 1,000 nt), the results of IRF were filtered by the maximum percentage of unpaired bases in TIRs (10%), and tandem repeats were filtered out in GRF and IRF results using Phobos. The public transposon annotations of Arabidopsis were downloaded from the Araport database (https://www.araport.org/; Cheng et al., 2016), which integrates homology approaches with manual curation (see https://www.araport.org/download_file/TAIR10_genome_release/annotation/gff/transposons/README.transposons) and the public transposon annotations of rice were downloaded from RAP-DB (Kawahara et al., 2013; Sakai et al., 2013; http://rapdb.dna.affrc.go.jp), chromosomal DNA transposon annotations were extracted with sizes ranging from 80 to 1,000 nt, and the GRF and IRF results were compared with these public annotations. In the comparison of outputs, if the length of the overlapped part between an annotation and an output sequence from the selected tool (i.e. GRF or IRF) was ≥80% of the lengths of both the annotation and the output sequence, this annotation was considered as having been discovered by the selected tool.

Comparison of TDR Detection between GRF and LTR_FINDER

The source code of LTR_FINDER (version 1.0.6) was modified to output intermediate TDR results (i.e. the genomic locations of LTR candidates) for the comparison with GRF. In the comparisons of simulated data, the following compatible settings were used in LTR_FINDER and GRF. In LTR_FINDER, (1) alignment scores were +1 (match), −1 (mismatch), −2 (gap open), −2 (gap extension), and −2 (gap end); (2) minimum and maximum distances between 5′ and 3′ LTRs were 0 and 1,000 nt; (3) minimum length of LTR = 10 nt and maximum length of LTR was adjusted according to different TDR lengths in different runs of simulated data (i.e. maximum TR length of simulated TDRs = 100, 200, 500, 1,000, or 2,000 nt); (4) minimum length of exact match pair = 10 nt; and (5) threshold for joining new sequence in existed alignment = 0.9. In GRF, (1) alignment scores were +1 (match), −1 (mismatch), and −2 (gap); (2) seed region length = 10 nt; (3) at most one mismatch is allowed in the seed region; (4) the minimum TDR length = 10 nt; (5) minimum distance between seed regions = 0 and maximum distance between seed regions is adjusted according to different TDR lengths in different runs of simulated data (i.e. maximum TR length of simulated TDRs = 100, 200, 500, 1,000, or 2,000 nt and maximum spacer length of simulated TDRs = 1,000 nt, so the corresponding maximum distance between seed regions is 1,090, 1,190, 1,490, 1,990, or 2,990 nt); (6) at most 10% unpaired bases were allowed in TDRs. TDR detection was performed in Arabidopsis and rice genomes using GRF and LTR_FINDER (modified to output intermediate results) with compatible settings. In LTR_FINDER, the same settings as described above were used except that the maximum length of LTR was set to 500 nt and the maximum distance between 5′ and 3′ LTRs was set to 980. In GRF, the same settings were used as described previously in this section for GRF, except that the maximum distance between seed regions was set to 980 nt (default). The results of GRF and LTR_FINDER were filtered by the maximum total sequence length (1,000 nt) and minimum TR length (40 nt), and tandem repeats in GRF and LTR_FINDER results were filtered out using Phobos. The chromosomal LTR transposon annotations with sizes ranging from 80 to 1,000 nt were extracted from the aforementioned public transposon annotations and compared with the GRF and LTR_FINDER results with these annotations using the method described previously in section "Comparison of IR Detection between GRF and IRF".

Comparison of Interspersed Repeat Detection between GRF and Red

Interspersed repeat detection was performed in Arabidopsis and rice using both GRF and Red (version 05/22/2015) and their performances and outputs were compared. In Red, the default settings were used. In GRF, the following settings were used: (1) seed region length = 20 nt; (2) minimum copy number = 3; (3) maximum number of undetermined bases (in either direction) = 1; (4) minimum identity for a determined base in the consensus sequence = 80%; (5) maximum number of mismatches for a repeat copy compared with the consensus sequence (excluding undetermined bases) = 2. Output sequences containing tandem repeats in GRF and Red were filtered out using Phobos and output sequences <40 nt in length were filtered out. The chromosomal transposon annotations other than DNA or LTR transposons with sizes ≥40 nt were extracted from the aforementioned public transposon annotations, and the GRF and Red results were compared with these annotations using the method described previously in section "Comparison of IR Detection between GRF and IRF".

Comparison of Interspersed Repeat Detection between GRF and phRAIDER

Interspersed repeat detection was performed in Arabidopsis and rice using both GRF and phRAIDER (version 2.0) and their performances and outputs were compared. In GRF, the same settings were used as described in the previous section. In phRAIDER, the following settings were used: (1) minimum repeat length = 20 nt; (2) minimum number of repeats in a group = 3. Output sequences containing tandem repeats in GRF and phRAIDER were filtered out using Phobos and output sequences <40 nt in length were filtered out. The chromosomal transposon annotations other than DNA or LTR transposons with sizes ≥40 nt were extracted from the aforementioned public transposon annotations, and the GRF and phRAIDER results were compared with these annotations using the method described previously in section "Comparison of IR Detection between GRF and IRF".

Comparison of MITE Candidate Detection between GRF and detectMITE

MITE candidate detection was performed in Arabidopsis and mouse using both GRF and detectMITE (version 20160128) with the following settings: (1) MITE length ranged from 50 to 800 nt; (2) minimum TIR length = 10 nt; (3) at most one mismatch (no indel) was allowed in TIRs; (4) four threads (GRF)/processes (detectMITE) were used in Arabidopsis and 16 threads/processes were used in mouse. In detectMITE, the maximum number of paralleled processes was the same as the number of chromosomes of the input genome (i.e. 7 in Arabidopsis and 22 in mouse), so more threads/processes were not used in the two programs. In the comparison of outputs, any result from the two programs that had the same start and end positions was considered to be a common result.

Comparison of LTR Retrotransposon Detection between GRF Integrated Hybrid Approach and LTR_FINDER

The source code of LTR_FINDER (Xu and Wang, 2007) was modified to make it accept TDRs from GRF as the input for downstream transposon detection. The modified LTR_FINDER accepts TDRs from GRF as the LTR candidates (Xu and Wang, 2007) and performs further analysis including adjusting alignments, finding signals, and recognizing enzyme domains (Xu and Wang, 2007). LTR retrotransposon detection was performed in Arabidopsis and rice using both LTR_FINDER and the hybrid approach (GRF + modified LTR_FINDER that takes TDRs from GRF as the input). For the original LTR_FINDER, default settings were used: (1) alignment scores were +2 (match), −2 (mismatch), −3 (gap open), −1 (gap extension), −1 (gap end); (2) minimum and maximum distances between 5′ and 3′ LTRs = 1,000 nt and 20,000 nt, respectively; (3) minimum and maximum lengths of LTR = 100 nt and 3,500 nt, respectively; (4) minimum length of exact match pair = 20 nt; (5) threshold for joining new sequence in existing alignment = 0.7. For the hybrid approach, GRF was first used to find TDRs with the compatible settings: (1) alignment scores were +2 (match), −2 (mismatch), and −3 (indel); (2) seed region length = 10 nt; (3) at most one mismatch was allowed in the seed region; (4) minimum TDR length = 100 nt; (5) minimum and maximum distances between seed regions = 1,090 nt and 23,490 nt, respectively, which guaranteed that the minimum and maximum distances between the starts of 5′ and 3′ TRs were the same with LTR_FINDER (i.e. 1,100 nt and 23,500 nt, respectively); (6) at most 30% unpaired bases were allowed in TDRs. The output TDRs were then filtered using the length requirement from the original LTR_FINDER (TDR length, 100 to 3,500 nt; spacer length, 1,000 to 20,000 nt), and the modified LTR_FINDER with default settings for downstream analysis was used. For both approaches, the tRNA database in the LTR_FINDER package was used to find signals, and PS_SCAN (Gattiker et al., 2002) was used to find protein domains with a local copy of the PROSITE database (ftp://ftp.expasy.org/databases/prosite/prosite.dat). The chromosomal LTR transposon annotations with compatible sizes (i.e. 1,200 to 27,000 nt) were extracted from the aforementioned public transposon annotations, and the original LTR_FINDER and hybrid approach results were compared with these annotations using the method described previously.

Supplemental Data

The following supplemental materials are available.

• Supplemental Figure S1. Examples of output TIRs and interspersed repeats.

• Supplemental Figure S2. Density plots of sizes of different parts of TIRs in different species.

• Supplemental Figure S3. Density plots of sizes of different parts of TDRs in different species.

• Supplemental Figure S4. Density plots of copy numbers and sizes of interspersed repeats in different species.

• Supplemental Figure S5. Density plots of sizes of different parts of MITEs in different species.

• Supplemental Figure S6. Density plots of sizes of different parts of high-quality IRs in different species.

• Supplemental Figure S7. Density plots of sizes of different parts of long-stem TIRs in different species.

• Supplemental Table S1. Counts and percentages of TIRs, TDRs, and MITEs detected by GRF with different structures in different species.

• Supplemental Table S2. Distributions of mismatches and indels of TIRs, TDRs, and MITEs detected by GRF in different species.

• Supplemental Table S3. Size distributions of different components of TIRs, TDRs, and MITEs detected by GRF in different species.

• Supplemental Table S4. Results of interspersed repeat detection by GRF in different species.

• Supplemental Table S5. Numbers and percentages of the results that are the overlapped portions of detected TRs and interspersed repeats.

• Supplemental Table S6. Performances of TIR, TDR, interspersed repeat, and MITE candidate detection by GRF in different species using default parameters.

• Supplemental Table S7. Performances of TIR and TDR detection by GRF in different species using optional parameters.

• Supplemental Table S8. Counts and percentages of high-quality and long-stem IRs detected by GRF with different structures in different species.

• Supplemental Table S9. Distributions of mismatches and indels of high-quality and long-stem IRs detected by GRF in different species.

• Supplemental Table S10. Size distributions of different components of high-quality and long-stem IRs detected by GRF in different species.

• Supplemental Table S11. Comparisons of GRF and IRF in TIR detection using simulated datasets.

• Supplemental Table S12. Comparisons of GRF and other tools using transposon annotations.

• Supplemental Table S13. Comparison of MITE candidate detection between GRF and detectMITE in different species.

• Supplemental Table S14. Comparisons of GRF and LTR_FINDER in TDR detection using simulated datasets.

• Supplemental Table S15. Comparison of LTR retrotransposon detection between the hybrid approach and LTR_FINDER in Arabidopsis and rice.