Receptive Field Shift and Shrinkage in Macaque Middle Temporal Area through Attentional Gain Modulation

Abstract

Selective attention is the top-down mechanism to allocate neuronal processing resources to the most relevant subset of the information provided by an organism's sensors. Attentional selection of a spatial location modulates the spatial-tuning characteristics (i.e., the receptive fields of neurons in macaque visual cortex). These tuning changes include a shift of receptive field centers toward the focus of attention and a narrowing of the receptive field when the attentional focus is directed into the receptive field. Here, we report that when attention is directed into versus of receptive fields of neurons in the middle temporal visual area (area MT), the magnitude of the shift of the spatial-tuning functions is positively correlated with a narrowing of spatial tuning around the attentional focus. By developing and applying a general attentional gain model, we show that these nonmultiplicative attentional modulations of basic neuronal-tuning characteristics could be a direct consequence of a spatially distributed multiplicative interaction of a bell-shaped attentional spotlight with the spatially fined-grained sensory inputs of MT neurons. Additionally, the model lets us estimate the spatial spread of the attentional top-down signal impinging on visual cortex. Consistent with psychophysical reports, the estimated size of the “spotlight of attention” indicates a coarse spatial resolution of attention. These results illustrate how spatially specific nonmultiplicative attentional changes of neuronal-tuning functions can be the result of multiplicative gain modulation affecting sensory neurons in a widely distributed region in cortical space.

Introduction

Selective attention modulates sensory responses of neurons throughout the visual cortex (Treue, 2001; Reynolds and Chelazzi, 2004). Attention modulates neuronal responses based on spatial and feature selection (Treue and Martínez Trujillo, 1999; McAdams and Maunsell, 2000; Martínez-Trujillo and Treue, 2004; Bichot et al., 2005): it affects neuronal contrast response functions, possibly increasing apparent stimulus contrast (Reynolds et al., 2000; Martínez-Trujillo and Treue, 2002; Carrasco et al., 2004; Williford and Maunsell, 2006), scales the temporal integration functions of sensory inputs (Cook and Maunsell, 2004; Busse et al., 2008), and increases response selectivity of the neuronal population response (Martínez-Trujillo and Treue, 2004). These diverse effects of attention are generally consistent with attention modulating the gain of sensory neurons in visual cortex. However, it is still unclear how attentional gain interacts with sensory inputs to selectively shape neuronal responses: although strong evidence suggests that attention imposes a multiplicative modulation of the sensory response characteristics of neurons, various studies report nonmultiplicative changes of neuronal responses (Moran and Desimone, 1985; Chelazzi et al., 1993; Treue and Maunsell, 1996, 1999; Connor et al., 1997; Luck et al., 1997; Reynolds et al., 1999; Recanzone and Wurtz, 2000; Williford and Maunsell, 2006; Womelsdorf et al., 2006).

Such nonmultiplicative attentional effects are particularly apparent for the influence of attention on the spatial-tuning characteristics of neurons in extrastriate visual cortex. When attention is directed to different regions in space, neuronal receptive field (RF) centers in these areas shift toward the attended location and narrow the width of spatial responsivity (Connor et al., 1997; Womelsdorf et al., 2006), as originally predicted by Moran and Desimone (1985). This nonmultiplicative modulation of the center and width of spatial tuning stands in marked contrast to the multiplicative influence of attention on the tuning to features such as orientation or direction of motion of neurons in the same visual areas (McAdams and Maunsell, 1999; Treue and Martínez Trujillo, 1999; Martínez-Trujillo and Treue, 2004). For example, when attention is directed inside versus outside of the receptive fields of neurons in the middle temporal visual area (area MT), their bell-shaped motion-tuning functions do not change their center and width but are rather multiplicatively scaled by attention (Treue and Martínez Trujillo, 1999).

Here, we attempt to reconcile these contrasting effects of attention by investigating the influence of selective attention on the spatial-tuning functions of MT neurons. We find that attentional modulation of the center and the width of spatial tuning of MT neurons are correlated. We develop an attentional gain model that accounts for this correlation by assuming a bell-shaped spatial attentional spotlight imposing multiplicative spatial weighting on the sensory inputs of MT neurons. By using a Gaussian bell-shaped function, we exploit the fact that the result of a multiplicative interaction of two Gaussians still is a Gaussian. The model also allows us to reverse engineer the spatial distribution of the attentional influence on the neuronal population in area MT, predicting that a coarse resolution of spatial attention (i.e., a large spotlight of attention) underlies the spatially selective modulation of receptive fields in visual cortex.

Materials and Methods

Experimental setup and visual stimulus.

We recorded from 78 neurons in area MT of the visual cortex of two macaque monkeys (n = 57 and n = 21 cells in monkey R and D, respectively) in a spatial attention task and obtained high-resolution receptive field maps under several conditions of spatial attention (see below). Details of the methods and procedures have been provided previously (Treue and Maunsell, 1999; Womelsdorf et al., 2006). In short, recordings were done with tungsten electrodes (impedance, 1.0–4.0 MΩ; Frederick Haer) and cells isolated with a window discriminator (BAK Electronics or Plexon). Cells were localized in area MT by their physiological characteristics and the histological reconstruction of recording sites in monkey R. Access to MT was provided by a craniotomy and a recording chamber surgically implanted above the superior temporal sulcus of the left hemisphere. During the experiment, a custom computer program running on an Apple Macintosh PowerPC controlled stimulus presentation, and monitored and recorded eye positions and neuronal and behavioral responses. Eye positions were determined using a high-resolution, video-based eye-tracking system (ET49; Thomas Recording) with a sampling frequency of 230 Hz and were digitized and stored at 200 Hz.

We used, as stimuli, moving random dot patterns (RDPs) of small bright dots (density, 10 dots per deg²) plotted within a stationary circular aperture on a dark (0.7 cd/m²) computer monitor. Dots had an unlimited lifetime and were replotted at the opposite side of the aperture when they left the aperture during motion.

Experimental paradigm.

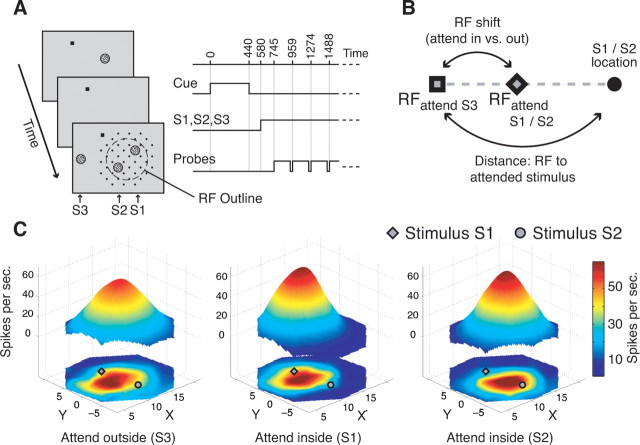
We used a spatial attention task illustrated in Figure 1A. A trial started once the animal foveated a small square presented on a computer screen. Then the cue, a stationary random dot pattern (with 19 cd/m² bright dots) was presented for 440 ms, and after a brief blank delay three moving RDPs were shown. Two of them (S1 and S2) were positioned within similarly activating regions within the receptive field of the isolated neuron and always at equal eccentricity, whereas the third RDP (S3) was presented outside the receptive field in the opposite hemifield. The task was to detect a small, transient (80 ms) change of the direction of motion of the stimulus at the cued location. Changes of this target stimulus and the distractors occurred at random times between 90 and 4090 ms after onset of S1, S2, and S3. Change times were drawn from a flat uniform distribution. During the sustained state of selective spatial attention, we obtained high-resolution receptive field maps by recording the responses to a probe stimulus of higher contrast (47 cd/m²) successively presented for 190 ms at the intersections of a dense virtual grid adjusted to cover the receptive field and its immediate surround. Potential probe positions that would have caused the probe to overlap S1 or S2 were not used (Fig. 1A). The sequence of probe positions was randomized for each trial. S1, S2, and S3 moved in the antipreferred direction of the neuron and were of intermediate contrast (19 cd/m2), whereas the probe stimulus moved in the preferred direction and had higher contrast (42 cd/m2). Temporal intervals in which no probe was shown (“virtual probe presentations”) were included in the succession of probe presentations to determine the baseline response (evoked by the two antipreferred stimuli in the RF). Our experimental design allowed us to map the receptive field during sustained states of selective attention to either of the stimuli inside the receptive field (attend-inside conditions) or to the stimulus outside the receptive field (attend-outside condition). For the current study, we performed for each neuron the two experimental comparisons of switching attention from outside the RF (S3) to either the one (S1) or the other (S2) stimulus inside the receptive field.

Figure 1.

Experimental protocol and illustration of receptive field maps. A, Experimental layout showing the succession of cue, target stimulus (S1, inside the receptive field outline; dashed circle), distractor stimuli (S2, inside receptive field; S3, outside receptive field), and the possible locations of the probe stimulus (black dots). B, Illustration of the calculation of receptive field shift (distance of the receptive fields in the attend outside and attend inside conditions) proportional to the distance of the receptive field (attend outside) to the attended stimulus position. C, Example receptive fields of a neuron while attention was directed outside the receptive field to S3 (left), inside the receptive field to stimulus S1 (middle), and to stimulus S2 (right). The bottom maps show spline-interpolated neuronal response profiles and the floating three-dimensional maps are the Gaussian fits used to describe the receptive field parameters. The example illustrates that responses to probes close to (far from) an attended stimulus in the receptive field were enhanced (reduced) compared with when attention was directed to S3.

Data analysis.

We quantified the spatial structure of neuronal receptive fields by using the average response to the probe beyond the baseline activity at each grid intersection in an interval from 60 to 200 ms after probe onset. The two-dimensional (2D) grid of neuronal firing rates in response to the probe was analyzed nonparametrically (by spline interpolation of the response surface), as well as parametrically by fitting the response profile with a two-dimensional Gaussian model of the form

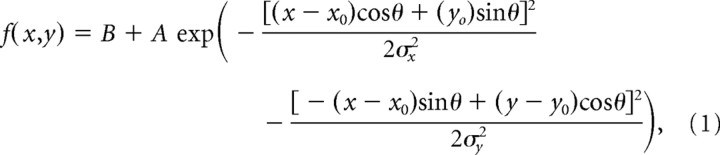with f (x, y) reflecting the response to the probe at spatial position (x, y) (x₀, y₀) being the receptive field center, θ the orientation of its main elliptical axis, and σ_x and σ_y the SDs of the two axes. This model has been successfully applied in previous studies to describe receptive fields of MT neurons (Raiguel et al., 1995; Britten and Heuer, 1999). The fitting was performed by minimizing the χ² value between model and data. For the spline-interpolated surface, we computed the receptive field center by determining as the center of mass of the area above one-half-maximum response and the size of the receptive field as the square root of that area. This definition is different from a threshold-based approach, in which the receptive field would be defined as the sum of all locations eliciting a response exceeding a particular threshold. When comparing receptive field sizes between conditions that show large differences in overall response gain, our measure would not result in a change in receptive field size but the latter definition would find size increases as more location exceed the threshold value. These differences do not play a sizeable role in our study because gain changes between attentional conditions were small compared with the changes in receptive field size observed.

Nevertheless, for every cell we also computed the number of probe positions that caused a response significantly (Wilcoxon rank sum test) exceeding a threshold. We used the square root of this number of effective probe locations as a measure of the receptive field size. We performed this analysis using two different threshold comparisons. In one analysis, we determined the size of the receptive field in the attend-in condition by testing for significant response increases attributable to the probe against responses during attend-in intervals in that no probe was presented (see above, virtual probe presentations). In the second analysis, we compared the same probe responses against the response to virtual probe presentations in the attend-out condition. In both analyses, the attend-out probe responses were compared against the virtual probe presentations in the attend-out condition. The second analysis is therefore sensitive to a general elevation of the baseline response in the attend-in condition and would show a receptive field increase under such conditions.

We evaluated the goodness of fit to the response profiles of the neurons in two steps. First, we removed fits that did not provide a better description of the response profile than the variability around the average response of the neuron by comparing the residuals to the global mean using the Kruskal–Wallis test. For neurons not exceeding the 95% significance level, the fitted receptive field surface represented the data not better than a surface based on the variability underlying the average activity level. In a second step we removed receptive field fits that strongly deviated (see below) in at least one of the free parameters with regard to those of all other receptive field fits [baseline, amplitude, center position, and σ (i.e., the average of the tuning width along the major and minor axis of the receptive field)]. We used an incremental procedure to eliminate those outliers by excluding fits from the final analysis in which any of the parameters exceeded 4 SDs of the overall variation in that parameter. This two-step procedure eliminated 24 of 119 pairs (20.2%) of the attend-in and attend-out condition (see Results).

We evaluated shifts of the receptive field center in the attend-in versus attend-out condition by treating the receptive field location in the attend-out condition as the reference position (RF_out). We calculated the distance of this reference position (1) to the receptive field center when attention was directed inside the receptive field (RF^attended) and (2) to the attended stimulus position inside the receptive field. We defined the receptive field shift as the distance between RF_out and RF^attended proportional to the distance between RF_out and the attended stimulus position inside the receptive field (compare Fig. 1B), defining positive (negative) shift values to be toward (away from) the attended stimulus. To quantify changes in the amplitude of the Gaussian (i.e., the maximal firing rate of the spline-interpolated surfaces) and size of the receptive fields, we computed the ratio of the values of the attend-in and attend-out conditions. All analysis and model calculations were done with Matlab (MathWorks).

Model.

We propose a spatial multiplicative model using modulatory attentional signals on feedforward sensory inputs. For simplicity of presentation, we restrict the model to one-dimensional space. Sensory feedforward spatial inputs are modeled with a Gaussian connectivity profile (x_R, receptive field center; A_R, amplitude; σ_R, size). Attention is acting multiplicatively on these connections and the model assumes a bell-shaped function of spatial attention. Here, we restrict the model to a Gaussian bell shape of the attentional spotlight with center (x_Att), amplitude (A_Att), and size (σ_Att). The spatial response profile of a neuron (the “output RF”) is the product of two functions, the receptive field profile of its input (“input RF”) multiplied by attention with the connectivity profile

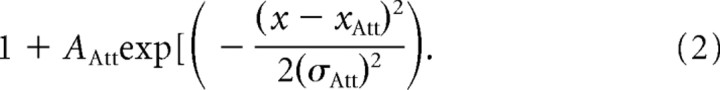When attention is weak (A_Att≪1), input and output receptive fields are very similar. When attention is strong (A_Att≫1), its influence has a Gaussian profile with a negligible baseline. Because the receptive field in the attended condition (RF^attended) is the result of a multiplication of the Gaussian input RF and the attentional Gaussian connectivity profile, we can calculate the parameters as follows:

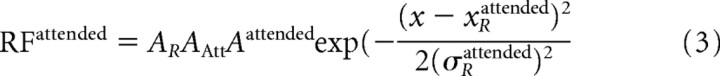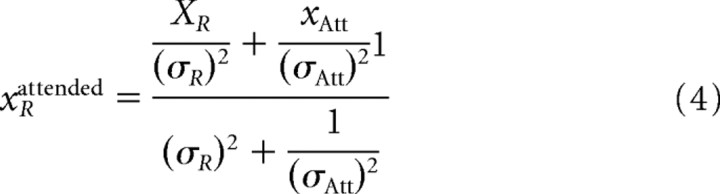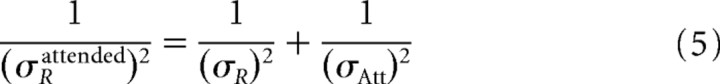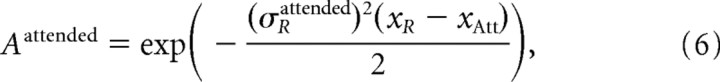with x corresponding to the spatial position of the sensory inputs and A_R and A_Att corresponding to the amplitudes of the receptive field and attention, respectively (see supplemental material for details, available at www.jneurosci.org). The proposed model makes no assumptions or predictions about the height of the various curves, as cortical normalization processes tend to keep the volume under the receptive field response surface constant (Croner and Kaplan, 1995) (i.e., create multiplicative changes to the receptive field amplitude without changing the location or width parameters). Our data are consistent with such a normalization process because they show the expected inverse correlation between the attentional influence on receptive field size and amplitude (for details, see supplemental material, supplemental Fig. 1, available at www.jneurosci.org). Although a complete model of cortical responses would have to include a normalization process, we did not incorporate it into our model for a lack of data that would constrain which of many possible implementations to include and because our focus, namely the influence of attention on receptive field size and position and their relationship, is unaffected by a multiplicative normalization.

Equation 4 represents the new receptive field center, and Equation 5 represents the new receptive field size. Note that the shift and shrinkage of the receptive fields with attention is calculated as (x_R^attended−x_R)/(x_Att−x_R) and σ_R^attended/σ_R, respectively. From these terms and Equations 4 and 5, the model predicts a fixed relationship of changes in receptive field center (“shift”) and changes in receptive field size (“shrinkage”) according to

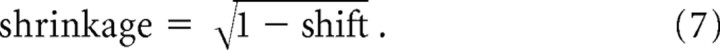This equation allows disregarding the width of the attentional influence and the receptive field size and position by representing the final result as the relationship between the observed receptive field parameter changes attributable to spatial attention.

In addition, knowing the location of attention and the size of the output RF with attention outside the receptive field, we can calculate the half-width of the spatial spread of the attentional influence σ_Att according to

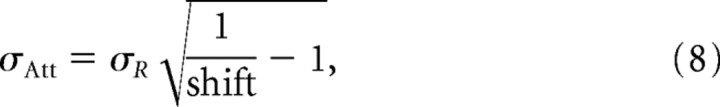as long as the model's prediction that RFs only shift toward the attentional center is correct.

Bootstrap confidence interval and Monte Carlo simulations.

Equation 7 describes the theoretical relationship between receptive field shift and shrinkage. The first statistical test we performed for comparing a given experimental receptive field shift–shrinkage value to the theoretical value was through bootstrapping the raw receptive field profiles in the attend-in and attend-out conditions and assessing the confidence interval of both shift and shrinkage (Efron and Tibshirani, 1993). To this end we bootstrapped the individual receptive fields before fitting and then restricted further extraction of the size and center values to those receptive fields of the bootstrap sample with an R² value above the median. These receptive fields were then used to calculate a random distribution (n = 1000) of receptive field shrinkage and shift for a given pair of receptive fields to obtain the 95% confidence range for that pair. This analysis tests whether a given single neuron data follow a theoretical behavior given the chosen experimental sampling of the 2D visual space and the observed variability.

In a second statistical approach, we computed the expected variability on the theoretical model predictions by performing a Monte Carlo simulation of repeated experimental measurements of a theoretical Gaussian receptive field profile modulated by a Gaussian-shaped attentional spotlight. We simulated the experimental mapping of the receptive fields in the attend-in and attend-out conditions by using the mean parameters across all experiments together with their variability. This statistical approach tests how much variability should be expected from a given theoretical model given the known experimental conditions. Therefore, it allows estimating the expected theoretical distribution of the data around the mean model predictions, and it allows testing if the data follow the theoretical model. The experimental setup and measurement procedure were simulated as follows: a virtual grid of 7 × 7° with a step size between adjacent points of 1° was chosen; receptive field centers and sizes in the attend-out condition were generated according to the experimental distribution (log₁₀ of sigma_out/“grid step size” = 0.20 ± 0.17; mean ± SD); position of the initial receptive field center with respect to the grid center was randomized (SD of 0.3 for a step size of 1.0); attention was centered with respect to the receptive field center (at 1 SD from the receptive field center plus the variability around this position from neuron to neuron, SD of 0.25); firing rate variability was included (log₁₀ of the SD over the mean rate, −0.10 ± 0.24); a background firing rate was added to the neuronal receptive field profile (1/10 of the maximal firing rate). For each of the 10,000 simulations of the experiment at a given shift value (from 1 up to 90% in steps of 1%), the attentional and initial receptive field parameters (center and size) were randomly drawn from the corresponding distributions and firing rate variability included. The resulting receptive field profiles in the attend-out and attend-in conditions were fitted like the experimental data. In each case we assessed the 99% expected variability attributable to these experimental conditions.

Eye position measurement.

Eye positions were measured with a high-resolution, video-based eye-tracking system (ET49; Thomas Recording) with a sampling frequency of 230 Hz and were digitized and stored at 200 Hz. To test for a potential systematic contribution of changes in eye positions between attention conditions to the receptive field changes, we calculated the average eye position difference between the attend-inside conditions and the attend-outside condition along the axis of the respective stimuli (i.e., along the axis from S1 to S3 or from S2 to S3). We found a very small difference of eye positions of only 0.009° (±0.004° SE) in the direction of the attended stimulus, which is far smaller than the difference in receptive field position between conditions (see below). These findings suggest that changes in eye position contributed marginally at best to changes in spatial neuronal sensitivity (cf. Womelsdorf et al., 2006).

Results

Determining the dataset of neuronal receptive fields pairs

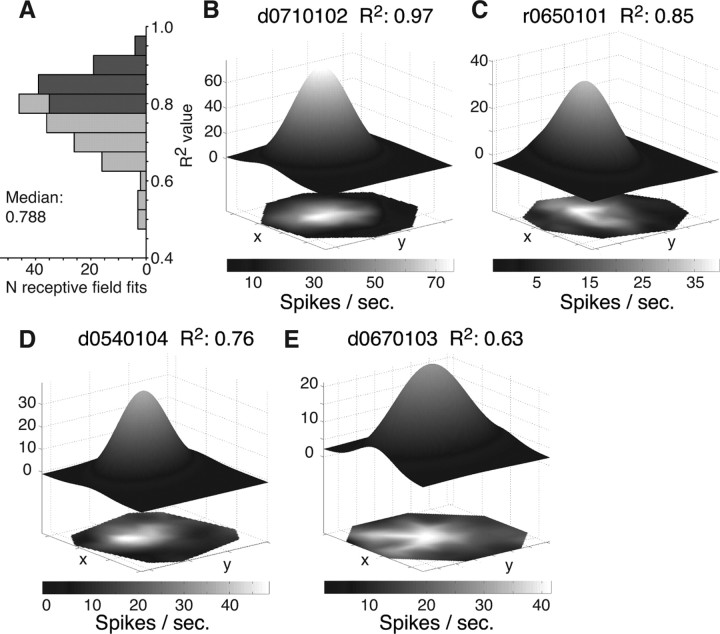
We mapped the receptive fields of 78 single neurons in area MT of two monkeys while they directed attention to one of two stimuli inside (attend-in condition) or to a stimulus outside (attend-out condition) the receptive field. For 64 neurons the receptive field of the attend-out and the receptive field of at least one of the two attend-in conditions could be fit by a two-dimensional Gaussian (Fig. 1C) (see Materials and Methods). To capture in detail the quality of the fits in the remaining 97 pairs of receptive fields (65 and 32 pairs from monkey R and D, respectively) in the attend-in and attend-out condition, we binned the R² values of the individual receptive field fits (Fig. 2A). The distribution of R² values (median, 0.788) demonstrates that the majority of the response profiles could be well modeled by a Gaussian profile despite the continuous presence of two antipreferred stimuli within the receptive field, limiting the sampling to regions outside of these stimuli. To exclude poor fits caused by nonoptimal spatial sampling from further analysis, we opted for a conservative inclusion criterion of the fits by focusing on those receptive field pairs, in which each fit exceeded the median R² value of 0.788 (n = 27 pairs). In the following, these pairs are termed the selected receptive field pairs. For comparison, we will also present results of all those remaining fitted pairs (n = 70), in which at least one receptive field fit showed an R² value below the median. Examples of fits with R² values above the median are presented in Figure 2, B and C, and example fits with an R² value below the median are shown in Figure 2, D and E. Moreover, to ease comparison with nonparametric analysis from previous studies, we additionally analyzed changes in receptive field parameters from the spline-interpolated receptive field profiles (Fig. 2B–E, bottom).

Figure 2.

Fitting MT receptive fields with a Gaussian profile. A, Distribution of R² values of the Gaussian fits to individual receptive fields in the different attentional conditions. Bar coloring indicates fits with an above-median (dark gray) and below-median (light gray) R² value. B–E, Examples of spline-interpolated (bottom, surfaces in two dimensions) and fitted (top, three-dimensional surfaces) receptive field profiles with an above-median R² value (B, C) and a below-median R² value (D, E).

Attentional effects on neuronal receptive fields

Across the population of receptive field pairs (monkey R, 65 pairs; monkey D, 32 pairs) we observed three effects: a shrinkage of the receptive fields and a moderate increase in the receptive field amplitude when attention was switched from outside to inside the receptive field. When attention was switched between the two locations inside the receptive field, we found a substantial shift in the location of receptive field center. Figure 3 shows the distribution of the three effects. Because the two monkeys each showed the same effects for the three modulations, we pooled the receptive field pairs for further analysis and illustration of results and give the individual monkeys' values below.

Figure 3.

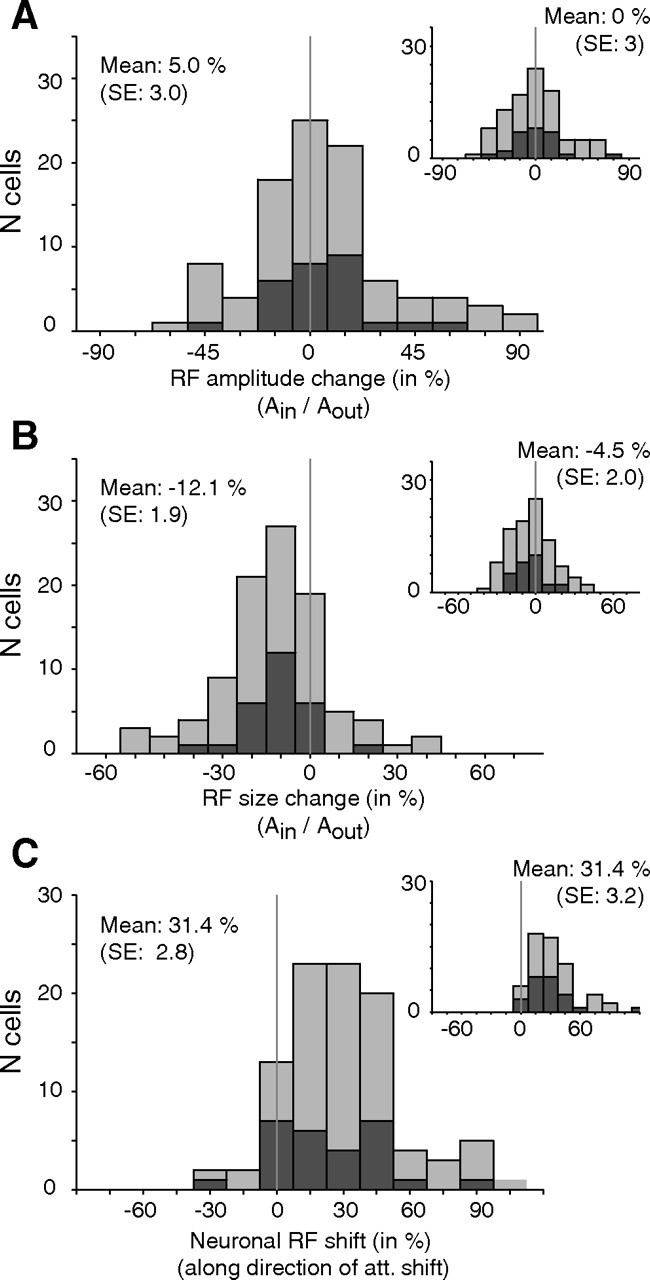
Neuronal receptive field modulation with attention inside versus outside the RF for 97 RF pairs (in each panel, mean and SE are computed across all 97 RF pairs). The dark gray colored bars indicate “selected” RF pairs [i.e., those pairs in which both RFs were fitted with above-median R² values (n = 27)]. A, Distribution of changes in RF amplitude between conditions (Gaussian-fitted RFs). The inset plot shows changes in amplitude (maximum response to the probe) extracted from the spline-interpolated RFs. B, Histogram of receptive field size changes with attention inside versus outside the receptive field. Values below zero indicate receptive field shrinkage. The inset shows the size changes when RF size is measured as the square root of the area above the one-half maximum response in the interpolated profile. C, Distribution of receptive field shifts parallel to the axis connecting the receptive field center when attention was directed to S3 and the target location in the paired condition when attention was directed into the receptive field (Fig. 1B, long arrow). Positive values signify shifts toward the attended stimulus inside the receptive field. The inset shows the RF shift distribution obtained from the nonparametric maps (with RF centers measured as the center of mass of the area at one-half-maximum response).

Figure 3A shows the distribution of the relative change in maximal response (receptive field amplitude) with attention inside versus outside the receptive field. For the 27 selected receptive field pairs (Fig. 3A, dark gray bars) the average neurons' peak response was 4.7% (±4% SE, n = 27) higher with attention inside versus outside the receptive field, but this effect failed to reach significance (p = 0.21, one sample t test). Similarly, the modulation of the peak response was not significant when all pairs of receptive field fits were considered (Fig. 3A, light plus dark gray bars) (mean: 5%, p > 0.14, n = 97; monkey R, 4.1 ± 4.3%; monkey D, 5.1 ± 2.2%) and when the modulation was based on the peak response obtained from the nonparametric analysis (mean, 0% for the selected pairs; 1% for all pairs) (Figure 3A, inset). The wide range of modulations of the receptive field amplitude might be partially attributable to the influence of a normalization process (see Materials and Methods) (see supplemental material, available at www.jneurosci.org).

Determining changes in receptive field size we observed a highly significant shrinkage of −11.2% (±2.3%, p < 0.001, one sample t test, n = 27) (Fig. 3B) with attention inside versus outside the receptive field for the selected pairs (for the entire sample, −12.1 ± 1.9%, n = 97; monkey R, −14.7 ± 2.5%; monkey D, −7.8 ± 2.6%). This shrinkage is significantly larger than obtained for the same sample with the nonparametric analysis (mean of −4.5%, n = 97) (Fig. 3B, inset) and compared with the −4.3% population average we reported previously based on a nonparametric analysis of all receptive field pairs (Womelsdorf et al., 2006), but even the shrinkage based on the nonparametric analysis was significant (p < 0.05, one sample t test). Note that the latter analysis used the square root of the area above the one-half maximum response to the probes compared using the σ parameter for the Gaussian-fitted response profiles. Because of the shrinkage of the receptive fields the increase in receptive field amplitude does not reflect an overall gain change as the neurons' responsiveness dropped for positions away from the center of the receptive field.

As a further nonparametric measure of receptive field size changes between the attend-in and attend-out conditions, we determined for every cell and for the selected cells the changes in receptive field size between the two conditions by determining the number of probe positions resulting in significant responses. Just like the results described above based on fitting the receptive field with a response surface, this measure also showed a significant shrinkage of receptive field size. For our complete cell population (n = 97), the shrinkage amounted to 8.7% (p < 0.001, one sample t test) in the first and 4.3% (p < 0.01) in the second analysis as described in Materials and Methods. For the selected cells (n = 27), the two corresponding shrinkages were 8.7% (p < 0.01) and 5.9% (p < 0.05), respectively.

Figure 3C shows the effect of attention on the receptive field positions. On average, receptive field centers for the selected pairs were shifted 25.3% (±4.6%, p < 0.001, one sample t test, n = 27) (Fig. 3C, dark gray bars) toward the stimulus inside the receptive field when it was attended compared with when attention was directed to the stimulus in the opposite hemifield. The average shift value for the entire sample (Fig. 3C, light and dark gray bars) of 31.4% (±2.8%, p < 0.001, one sample t test, n = 97; monkey R, 38 ± 3.6%; monkey D, 18 ± 2.8%) was not significantly larger. The 25.3 and 31.4% proportional shifts of receptive fields correspond to an average receptive field shift of 1.43 and 2.56° of visual angle, respectively. Similar average receptive field shifts were obtained for the interpolated maps (i.e., when the receptive field center was measured as the centroid of the area above the one-half-maximum response) (Fig. 3C, inset): on average, receptive fields shifted 27.9% for the selected dataset and 31.4% for the whole dateset (both, p < 0.001; one sample t tests).

Intriguingly, the shift of receptive fields toward the attended focus and the narrowing of the spatial tuning show a highly significant correlation (r = −0.55, p < 0.01) (Fig. 4C, red data points) (i.e., neurons with larger receptive field shifts toward the attended stimulus showed stronger receptive field shrinkage). The correlation of receptive field shift and shrinkage also holds for the entire sample of fitted receptive field pairs (r = −0.38, p < 0.001) (Fig. 4C, red plus gray data points), as well as for the RF shift and shrinkage correlation calculated on the basis of nonparametric receptive field profiles (r = −0.56, p < 0.01) (Fig. 4D, red data points).

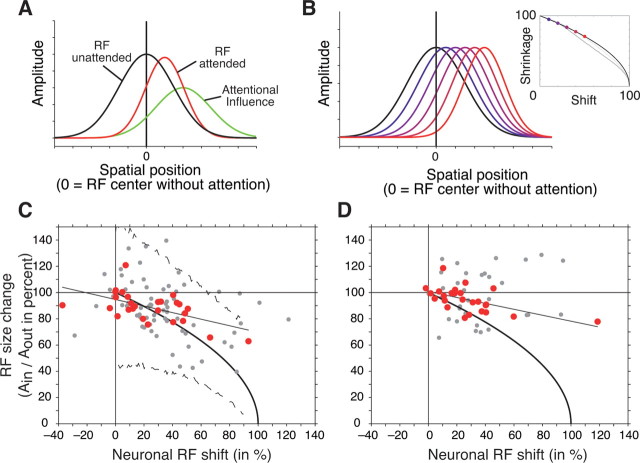
Figure 4.

Illustration of model assumptions and the model's fit to the neuronal data. A, The model predicts that the spatial response profile of a neuronal receptive field (here as one-dimensional Gaussians) with attention outside the receptive field (RF unattended, black line) interacts multiplicatively with a Gaussian-shaped attentional influence (green line). Multiplying these two Gaussians results in a narrower receptive field which is shifted toward the center of attention (RF attended, red line). B, Illustration of the predicted relationship of the extent of neuronal receptive field shift and receptive field shrinkage (Eq. 7). The stronger the shift of neuronal receptive fields [blue to red (left to right) Gaussian receptive field profiles] the stronger the receptive field shrinkage following Equation 7 and shown in the inset (blue to red dots). The black line in the inset illustrates the predicted shift and shrinkage relationship according to Equation 7, assuming a Gaussian-shaped receptive field and a Gaussian-shaped attentional spotlight. Gray lines show the prediction under the assumption of a cosine-shaped attentional spotlight together with receptive fields shaped as Gaussian (dark gray) or cosine functions (light gray). C, Scatter plot of the observed receptive field shrinkage (y-axis; 100% represents no size change) and receptive field shift (x-axis) for 27 pairs of receptive fields in the attend-in versus attend-out conditions that could be fit with an R² value above the median (red colored dots) and for the remaining 70 pairs (gray dots). The black line shows the linear regression, whereas the solid black curve indicates the relationship of receptive field shift and shrinkage predicted by the model. Dashed lines show the 99% confidence range expected for data points across all cells (based on the Monte Carlo simulation, see Materials and Methods). D, Same format as in C, but plotting the results based on the comparison of the nonparametric estimates of the receptive field center (center of mass) and size (square root area above one-half-maximum response).

Spatially selective gain modulation

The reported modulation of receptive field position and size by spatial attention reflects a nonmultiplicative change of the spatial-tuning characteristics of individual MT neurons. To test whether the observed findings nevertheless could be reconciled with a multiplicative attentional modulation, we created a general gain model assuming that attention multiplicatively modulates the spatial weighting of inputs to MT from a mosaic of cells with smaller receptive fields. By assuming that spatial attention is distributed with a Gaussian profile centered on the attended stimulus' location, the model creates MT receptive fields by the multiplicative interaction of the Gaussian-shaped input receptive field with the Gaussian-shaped input weights. Because multiplying two Gaussians results in a Gaussian, the MT receptive field profile with attention remains Gaussian shaped, with its width and center position being a function of the distance between the original two Gaussians and their respective widths (Fig. 4A).

The model predicts that receptive field shift and shrinkage are correlated such that receptive fields shrink with attention inside the receptive field proportional to $\sqrt{1-\text{RF}\text{shift}}$ (Fig. 4B) (see Materials and Methods) (i.e., a strong shift is accompanied by a strong shrinkage of receptive fields). Note that the predicted correlation of receptive field shift and shrinkage does not rely on the assumption of a Gaussian function for receptive fields and the attentional spotlight. Rather, a positive correlation of shift and shrinkage occurs for the interaction of other bell-shaped functions (e.g., cosine shapes) as well. Figure 4B (inset, gray curves) illustrates that this basic relationship is also predicted when assuming either a cosine-shaped attentional spotlight or a cosine shape for receptive fields and attentional spotlight. Different bell-shaped functions vary primarily in the predicted slope of the relationship of RF shift and shrinkage as one approaches RF shifts larger than ∼40%. We therefore restrict our analysis to the assumption of Gaussian receptive field shape and a Gaussian attentional spotlight, which has the advantage to allow for straightforward model equations (see Materials and Methods).

Figure 4C shows the observed correlation of receptive field shift and shrinkage along with the predicted correlation (solid black curve). For the selected receptive field pairs, 70.3% (19 of 27) (Fig. 4C, red dots) of the data points had a 95% confidence range overlapping with the model prediction. Considering the remaining 70 pairs (Fig. 4C, gray dots), the bootstrap analysis showed that 75.7% (53 of 70) of them significantly overlapped with the model prediction.

The bootstrap analysis provided a means to test whether individual data points can be accounted for by the model. In a second step, we viewed the issue from the perspective of the model and asked how likely it would have been to observe individual data points that correspond to the model prediction if we would have repeated the experiment with more neurons and similar experimental settings by means of a Monte Carlo simulation (see Materials and Methods). The dashed lines in Figure 4C show the resulting upper and lower statistical bounds (99% confidence level) of the variability of the shift–shrinkage relationship that is caused by the variability in our experimental design applied to a simulated theoretical experiment. These bounds show that 24 of the 27 selected points (88.9%) could be accounted for by the model (Fig. 4C, red dots). Considering the entire sample there were still 86.6% (84 of 97) of the observed shift–shrink relationships that are statistically expected with 99% confidence.

Prediction of attentional spread

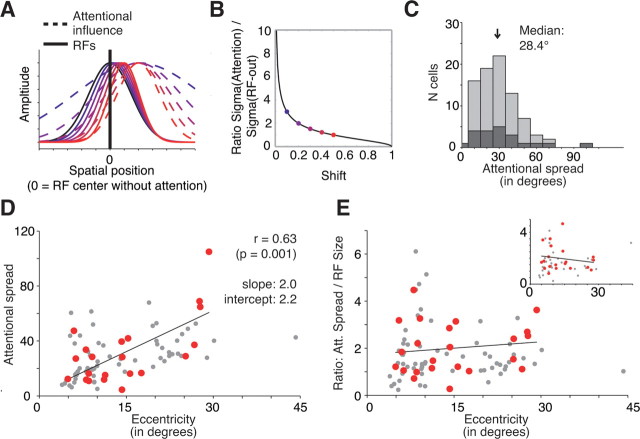
In addition to the ability to account for the observed relationship between receptive field shift and shrinkage, the model allows us to estimate the spatial spread of the attentional influence given the observed modulation of neuronal spatial tuning (compare Eq. 8). Figure 5A illustrates the predicted attentional spread underlying varying degrees of receptive field shifts and shrinkage, showing that narrower attentional width induces stronger modulation of receptive fields, that is, stronger shrinkage and shifts toward the attentional focus. The general relationship is presented in Figure 5B, which plots the ratio of estimated attentional spread and receptive field size as a function of the observed shift. Figure 5B demonstrates that for receptive field shifts smaller than ∼0.3, the attentional widths are expected to be far broader than the receptive field size. Note that the described relationship is valid only for receptive field shifts toward the attended position and not beyond it (i.e., only for shifts between 0 and 100%). Using this relationship, we estimated the attentional spread underlying each of the observed receptive field shifts (Fig. 5C,D). We observed a median full width of the attentional spread of 27.4° (mean, 28.4 ± 3.8°) for our sample of selected receptive fields (median size, 16.4°; mean full-width RF size, 18.6°) indicating that the attentional spread is on average ∼60% larger than the size of MT receptive fields.

Figure 5.

Model prediction and estimation of attentional spread underlying the observed shift and shrinkage of neuronal receptive fields. A, Given a fixed spatial center of attention, the model estimates a narrower attentional spread (blue to red, dashed Gaussians) and the stronger the receptive field is shifted toward the attentional focus (blue to red, solid Gaussians). B, Relationship between the expected RF shrinkage (when attention is shifted into the RF) as a function of the observed RF shift (Eq. 8, see Materials and Methods). C, Distribution of the attentional spread (full width) estimated based on the observed RF shifts. Dark/light gray bars represent the data from the selected/all RF pairs as in Figures 2–4. D, Scatter plot showing that the estimated attentional spread (y-axis) grows with an increasing eccentricity of the attentional focus (x-axis). The best-fitting linear regression has the form width of attentional spread, 2.0 × eccentricity + 2.2. Red dots represent the data from selected RF pairs, and gray dots represent the data from all RF pairs as in Figures 2–4. E, Same format as in D, but showing the lack of correlation between the ratio of attentional spreads to RF size with eccentricity of the neuron's RF.

In addition, there was a significant positive correlation of the width of the attentional influence with the eccentricity of the RFs (Fig. 5D, red data points) (r = 0.64, p < 0.001): attentional spread grows from ∼2.2° near the fovea to ∼60° at an eccentricity of 30° (regression intercept, 2.2; slope, 2.0°), indicating that the spotlight of attention increases linearly with eccentricity of attention. Note that the significant relationship of attentional spread and eccentricity also holds for the entire sample of fitted data points (r = 0.50, p < 0.001) (Fig. 5D, red plus gray data points).

To investigate a possible influence of receptive field size on the correlation of the estimated attentional spread with eccentricity we analyzed the ratio of attentional spread to receptive field size as a function of eccentricity. We found a constant ratio (Fig. 5E) (correlation: r = 0.13, p = 0.276; linear regression: intercept, 1.7; slope, 0.0). This result indicates that the attentional spotlight grows along with RF size across increasing eccentricity.

Moreover, this finding justifies to normalize RF maps with different RF size and from different eccentricities to derive a nonparametric estimation of the average attentional spotlight. A nonparametric estimation of the attentional profile and its relationship to RF size could provide additional support for the described modeling approach. Therefore, the individual RF profiles were rotated to have the abscissa along the S1–S2 axis and origin (0.0) at the center between the two stimuli S1 and S2. Then, the distance between adjacent probes along the S1–S2 axis were normalized to a unit grid step size. The resulting average RF maps for each attention condition (Fig. 6A–C) visualize our main finding that attention shifted RFs toward the attended stimulus, with the average RF in the attend-outside condition well-centered at the origin of the axes. According to the model, attention is acting multiplicatively on this RF profile in the attend outside condition. We can therefore estimate from these nonparametric average RF maps the average, normalized width of the attentional profile by taking the ratio of the RFs in the attend-inside to attend-outside condition. The resulting ratio maps are shown in Figure 6, D and E, and demonstrate an average attentional profile that is centered (“focused”) around the position of the corresponding attended stimuli (S1–S2). Importantly, the average size of the attentional profile in the ratio maps (square root of the area above one-half maximum) of 5.2 (attend S1 versus S3, 5.1; attend S2 versus S3, 5.3) was ∼60% bigger than the size of the average RF maps from the individual attention conditions (attend S1, 3.2; S2, 3.3; S3, 3.6). Thus, the results from this nonparametric analysis correspond closely to the average prediction of the parametric model, providing a very similar estimation of the attentional spread (relative to the RF size) underlying the RF shift and shrinkage.

Figure 6.

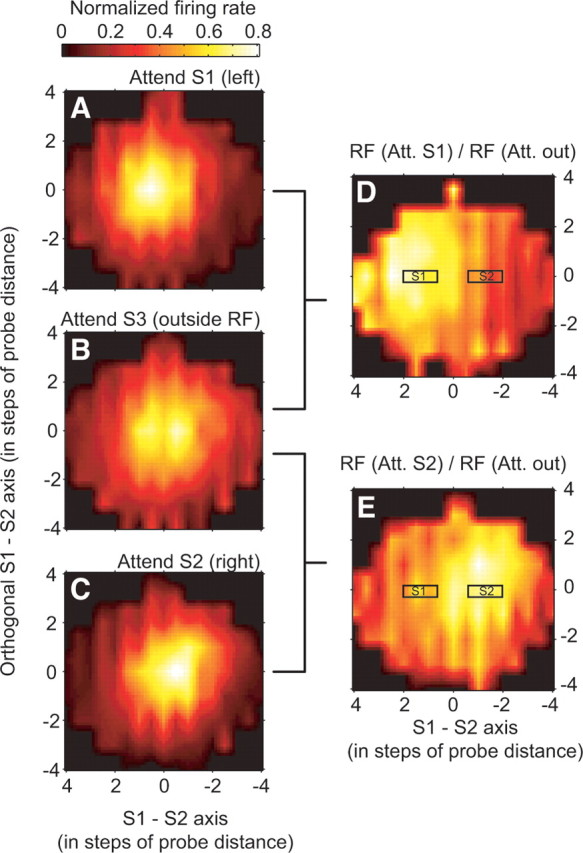
Average profiles of the nonparametric interpolated RF profiles of the three attentional conditions and derivation of an average, normalized attentional profile. A–C, Average RF when attention was directed to stimulus S1 inside the RF (A, to the left of 0/0), to stimulus S3 outside the RF (B), and to stimulus S2 inside the RF (C, to the right of 0/0). D, E, Average attentional effect illustrated as the ratio of the RF profiles of attend-S1-to-attend-S3 (D) and attend-S2-to-attend-S3 (E). The relative positions of stimulus S1 and S2 in the attentional maps are indicated by black rectangles (at positions of ±1, ±1.5, or 2 probe “steps” across cells, varying as a function of the chosen mapping grid for individual neuronal RFs). Maps were smoothed by linearly interpolation between adjacent data points in the plot.

Discussion

Our results document a correlation between the shift of MT receptive field centers and the concurrent shrinkage of their size when attention is relocated from a location far outside to a stimulus inside of the receptive field. This finding was evident in a nonparametric estimation of receptive field parameters as well as for a conservative selection of those receptive fields well fit by a bell-shaped (Gaussian) profile. We demonstrate how the nonmultiplicative effect of attention on position and size of MT receptive fields can be quantitatively accounted for by a general gain mechanism modulating the spatial weighting of sensory inputs to area MT neurons and assuming a bell shape spatial profile. The proposed gain model also allowed us to estimate the size of the “attentional spotlight” as to be ∼1.6 times larger than the receptive fields in MT and independent of eccentricity, and this finding helped to visualize the attentional profile acting on the RF inputs. This independency suggests that the minimal size of the attentional spotlight reflects the spatial spread of the feedforward input to area MT at a given eccentricity rather than being able to be adapted to stimuli smaller than the receptive field.

When attention is directed to a subregion of the receptive field of MT neurons the response to probe stimuli close to the attentional focus is enhanced whereas the response to distant probes is reduced (i.e., the receptive field of these neurons shift toward the attended position). This attentional attraction of spatial sensitivity reflects a nonmultiplicative change of a neuron's spatial-tuning curve. When attention is shifted between inside and outside the receptive field, we observed only a small (5%) nonsignificant change in the receptive field. Although this modulation is smaller than the ∼10% response modulation by spatial attention that was observed in MT in a previous study (Treue and Martínez Trujillo, 1999), this is most likely attributable to the use of the late, sustained response to stimuli in the previous study because attentional effects are known to be weak for the early components of neuronal responses to the appearance of stimuli and grow in the course of a trial when using hazard rates with a positive slope (Motter, 1994; Roelfsema et al., 1998; McAdams and Maunsell, 1999; Reynolds et al., 1999; Treue and Maunsell, 1999; Ghose and Maunsell, 2002).

Previous studies have shown response gain modulation when switching spatial attention from outside to inside a receptive field. This multiplicative modulation does not affect tuning preference or selectivity to features such as orientation and direction of motion in extrastriate visual areas such as MT and V4 (McAdams and Maunsell, 1999; Treue and Martínez Trujillo, 1999; Martínez-Trujillo and Treue, 2004). These observations stand in marked contrast to the highly nonmultiplicative attentional modulation of spatial tuning that we observed. We propose a gain model that resolves this apparent contradiction by suggesting that the attentional modulation of receptive fields in area MT is the result of a bell-shaped pattern of multiplicative modulation imposed onto the input to MT neurons. The ability of our model and other models (Olshausen et al., 1993; Reynolds et al., 1999; Compte and Wang, 2006) to simulate shifts and size changes of receptive fields shows that such nonmultiplicative effects can be created from multiplicative neuronal interactions.

This push/pull effect of attention on spatial tuning resembles the sharpening of direction tuning across the population of MT neurons reported previously (Martínez-Trujillo and Treue, 2004). That study reported a response increase for those neurons preferring directions close to the attended direction of motion and a response suppression for neurons tuned for nonattended directions in line with the feature-similarity gain model of attention (Treue and Martínez Trujillo, 1999). Despite these similarities, it should be pointed out that the two effects differ in critical aspects. First, in the population response to direction of motion, Martínez-Trujillo and Treue (2004) observed a linear decline of the multiplicative gain factor with increasing dissimilarity of the attended to the preferred direction of motion, although we report here that attentional modulation of the spatial tuning is brought about by a bell-shaped (e.g., Gaussian) spatial gain pattern. This difference in the modulation of spatial and feature selective responses is not surprising given the different characteristics of spatial and feature tuning: tuning selectivity for the direction of motion is similar in area MT and its input areas, indicating that MT neurons pool across input neurons with the same preferred direction (Simoncelli and Heeger, 1998). A feature-similarity gain modulation (Treue and Martínez Trujillo, 1999) can therefore be achieved by changing the overall gain of MT neurons directly or using the same factor across all its inputs. Spatial tuning however is far broader in MT than in its input areas. It is therefore created de novo from inputs to MT that differ in their preferred location, and this integration process can be specifically targeted by attentional mechanisms. This could be achieved with at least two approaches: the neurons in an earlier area (e.g., V1) with smaller receptive fields that provide the input to one MT neuron might already be multiplicatively modulated by attention. Alternatively, the receptive field shift and shrinkage could be due a specific pattern of multiplicative attentional modulations imposed onto the synaptic inputs of an MT neuron. In both cases, spatial attention would reshape the spatial sensitivity of MT neurons in a multiplicative way but with a gain that is locally adjusted according to a bell-shaped spatial weighting function.

The mechanistic explanation of the proposed multiplicative attentional gain model is closely related to the framework of gain fields that has been applied to neuronal responses throughout sensory cortex (Andersen et al., 1985; Salinas and Abbott, 1996, 2001; Salinas and Their, 2000; Salinas, 2004). Gain field architectures describe neuronal response characteristics to a sensory stimulus as an interaction with additional parameters such as, for example, eye position in the orbit and gaze direction (Brotchie et al., 1995), or describe a multiplicative interaction of different stimulus attributes (Peña and Konishi, 2001, 2004). Similar to gain fields, our proposed multiplicative model provides a general formalization of how the integration of sensory inputs is modulated by feedback connections (Olshausen et al., 1993; Salinas and Abbott, 1997). In the existing approaches, the multiplicative mechanisms had to be inferred from neural network simulations. In contrast, we provide a straightforward mathematical formalization of the model that allows investigating the integration of neuronal responses across visual cortex without taking recourse to simulations.

One notable prediction of the model is a broad spatial spread of the attentional influence underlying the observed modulation of spatial sensitivity in area MT. The estimated spread of the attentional influence was ∼2.2° at the fovea, increasing systematically by ∼2° every degree of eccentricity. Such a broad influence resonates with psychophysical studies that have proposed a coarse resolution of attention and an increase of the size of the spotlight of attention with eccentricity (Suzuki and Cavanagh, 1997; Intriligator and Cavanagh, 2001; Cutzu and Tsotsos, 2003; Tse et al., 2003). This finding could also explain that attention to regions just outside the receptive field of neurons in area V4 induces changes in the spatial sensitivity similar to the changes with attention inside the receptive field we report (Connor et al., 1997).

The proposed feedforward architecture is not the sole candidate to account for the observed findings. Previous attention models focusing on sensory cortex have emphasized the modulation of recurrent/lateral inhibitory interactions to enhance filtering of distracting visual information from access to higher visual area (Olshausen et al., 1993; Tsotsos et al., 1995; Reynolds and Desimone, 1999; Deco and Schürmann, 2000; Compte and Wang, 2006; Hamker and Zirnsak, 2006; Ardid et al., 2007; Buia and Tiesinga, 2008). Although models such as Reynolds and Desimone's (1999) implementation of the biased competition model (Desimone and Duncan, 1995) resemble the model proposed here, in that they involve spatially selective modulation, they were designed to account for the modulation of responses to multiple stimuli in the receptive field, rather than attentional effects on receptive field profiles. Those models, including ours, that propose multiplicative interactions of attention and sensory responses represent particularly parsimonious accounts of neuronal changes under different attentional conditions, without the need of assuming an attentional effect directly targeting inhibitory interactions among neurons.

The proposed gain model of attention suggests that multiplicative operations could reflect a general computational mechanism underlying selective modulation of sensory neuronal responses (see also Boynton, 2005; Ghose and Maunsell, 2008). This suggestion is supported by previous studies showing that single neurons are capable to combine excitatory and inhibitory inputs about sensory attributes multiplicatively (Gabbiani et al., 2002) and that multiplicative gain is capable to control the responsiveness of cortical neurons (Chance et al., 2002).

In summary, our observation of neuronal receptive field shifts toward and shrinkage around the focus of attention suggest that spatial attention acts like an attractor of spatial sensitivity. This nonmultiplicative modulation of the spatial-tuning characteristics of single neurons is consistent with a general multiplicative modulation impinging on the input of these neurons. Such an attentional gain has also been shown during feature-based attention (McAdams and Maunsell, 1999; Treue and Martínez Trujillo, 1999; Martínez-Trujillo and Treue, 2004; Maunsell and Treue, 2006), suggesting that both space-based and feature-based attentional selection of sensory inputs uses multiplicative modulations to create complex changes of neuronal responses in extrastriate cortex.