Adaptation Reduces Spike-Count Reliability, But Not Spike-Timing Precision, of Auditory Nerve Responses

Abstract

Sensory systems use adaptive coding mechanisms to filter redundant information from the environment to efficiently represent the external world. One such mechanism found in most sensory neurons is rate adaptation, defined as a reduction in firing rate in response to a constant stimulus. In auditory nerve, this form of adaptation is likely mediated by exhaustion of release-ready synaptic vesicles in the cochlear hair cell. To better understand how specific synaptic mechanisms limit neural coding strategies, we examined the trial-to-trial variability of auditory nerve responses during short-term rate-adaptation by measuring spike-timing precision and spike-count reliability. After adaptation, precision remained unchanged, whereas for all but the lowest-frequency fibers, reliability decreased. Modeling statistical properties of the hair cell–afferent fiber synapse suggested that the ability of one or a few vesicles to elicit an action potential reduces the inherent response variability expected from quantal neurotransmitter release, and thereby confers the observed count reliability at sound onset. However, with adaptation, depletion of the readily releasable pool of vesicles diminishes quantal content and antagonizes the postsynaptic enhancement of reliability. These findings imply that during the course of short-term adaptation, coding strategies that employ a rate code are constrained by increased neural noise because of vesicle depletion, whereas those that employ a temporal code are not.

Introduction

All sensory systems face the challenge of encoding an efficient representation of behaviorally relevant stimuli in the external world (Barlow, 1961). Adaptation is a common feature of sensory systems that yields an efficient sensory code by removing redundant information inherent in environmental cues (Barlow, 1961; Laughlin, 1989; Brenner et al., 2000; Fairhall et al., 2001). One specific form of adaptation is a decrease in a neuron's firing rate in response to a constant stimulus (Adrian and Zotterman, 1926). Possible roles for this rate adaptation in auditory neurons include enhancement of acoustic transients (Delgutte, 1980) and input–output gain control (Dean et al., 2005).

Sensory neurons encode information by using the number of spikes and/or the precise timing of these spikes, strategies referred to as rate and temporal coding, respectively. The distinction between these two codes is mostly heuristic because when the counting window is narrowed the two coding strategies converge. However, trial-to-trial response variability in either spike count or spike timing represents noise in the neural signal and can constrain the ability of neurons to efficiently transmit information (Rieke et al., 1997). Understanding the underlying cellular mechanisms that determine response variability in different sensory neurons promises insight into the limitations of neural coding.

The limitations of rate and temporal coding can be studied readily in the peripheral auditory system because both strategies are used to convey information about the acoustic environment. The tonotopic arrangement of hair cells and primary afferents allows sound frequency to be encoded using the number of spikes by a rate-place code. Alternatively, some sound frequencies can be encoded using the precise timing of spikes by phase-locking to the stimulus waveform (Kiang, 1965; Rose et al., 1967; Heinz et al., 2001). Furthermore, firing rate, synchronization, and phase cues can all encode changes in sound level (Kiang, 1965; Anderson et al., 1971; Johnson, 1980; Colburn et al., 2003). As in all other sensory systems, trial-to-trial variability in spike count and timing imposes limitations on discrimination performance (Heinz et al., 2001).

We examined the impact of rate-adaptation on the response variability of both spike timing (precision) and spike count (reliability) by comparing initial and adapted time epochs of single-unit responses recorded in the auditory nerve. In response to a constant stimulus, the firing rate of a cochlear neuron rapidly decreases to a maintained firing rate over a time course of tens of milliseconds (Kiang, 1965; Westerman and Smith, 1984; Crumling and Saunders, 2007). This rapid form of adaptation is likely mediated by exhaustion of release-ready synaptic vesicles in the cochlear hair cell (Furukawa et al., 1978; Moser and Beutner, 2000; Spassova et al., 2004). Furthermore, cochlear ganglion cells are not subject to any intrinsic neural feedback circuitry and their responses are statistically independent from each other (Johnson and Kiang, 1976). Thus, short-term adaptation in the peripheral auditory system provides the opportunity to study, independent of circuit properties, how specific synaptic mechanisms limit neural coding strategies.

Materials and Methods

Animal subjects

Hatchling white leghorn chickens (Gallus domesticus) were obtained from a commercial breeder (CBT, Cumberland, MD) and studied between 3 and 24 d of age. The University of Pennsylvania Institutional Animal Care and Use Committee approved the protocol for the treatment and maintenance of animals.

Surgical preparation

The surgical preparation has been described previously in detail (Saunders et al., 1996). Briefly, each animal was anesthetized with an intramuscular injection of a 25% solution of urethane at a dose of 0.01 ml/g of body weight. A tracheotomy was performed to maintain an open airway, and the left ear canal was excised to expose the tympanic membrane. Tissue over the calvarium was removed to reveal the posterior-lateral and superior surfaces. Application of dental cement secured the chick to a head holder. A 5 mm hole was made through the left posterior-lateral portion of the skull above the temporal bone to expose the inner bony layer. Then, a 1.5 mm hole was opened in the inner bony layer to reveal the endothelial lining of the lateral cochlear wall at the recessus tympani. The lining was gently pierced with a microdissecting pin and carefully retracted to reveal the medial wall of the cochlear duct. The cochlear nerve appeared as a white band within the cartilaginous wall.

Acoustic stimulation

Animals were tested in a double-walled, acoustically shielded chamber. The head holder was secured to a frame. A heating pad and direct current halogen lamp maintained body temperature at 41°C. A closed-field speaker [Beyer Dynamic (Hicksville, NY) earphone, model DT-48] stimulated the ear through a sound tube (10 cm long, 5 cm diameter). The sound tube was fitted with a 0.5 mm probe-tube microphone (Model ER-7; Etyomotic Research, Elk Grove Village, IL), which was placed ∼2 mm in front of the tympanic membrane. The second harmonic of the earphone was 60–74 dB below the fundamental across all tested frequencies. Output from the probe microphone was connected to the analyzer module of a frequency synthesizer (System One; Audio Precision, Beverton, OR) and converted to decibels relative to 20 μPa [decibels sound pressure level (dB SPL)]. The generator module of the synthesizer produced tonal and noise stimuli under computer control. An automatic calibration procedure achieved a constant sound intensity level of 100 dB SPL between 0.1 and 4.0 kHz. By adjusting the synthesizer output voltage, the earphone could present different sound intensity levels to the ear (Saunders et al., 1996).

Cochlear nerve recording

A borosilicate glass microelectrode (15–30 MΩ) filled with 3 m KCl was secured to a microdriver, inserted into scala tympani, and advanced in 1 μm steps. Electrical signals were amplified, fed to an oscilloscope, audio monitor, and level detector. A broadband noise search stimulus was used to detect isolated cochlear nerve units. The arrival times of action potentials of well isolated units were stored on hard disk with 10 μs resolution.

Unit characterization

Using 40 ms tone bursts, a tuning curve was constructed for each unit by recording the evoked discharge rate at different intensity-frequency combinations between 0 and 100 dB SPL and 0.1 and 6.0 kHz. From the tuning curve, the characteristic frequency (CF) and rate-level threshold at CF (CF-Th) were determined visually.

Experimental stimulus protocol

Cochlear nerve units were stimulated with repeated phase-locked 40 ms tone bursts (rise/fall time, 2.5 ms) at CF and +20 dB re CF-Th. A 400 ms silent interval between tone bursts allowed recovery of the cell from neural adaptation (Spassova et al., 2004). We defined the presentation of each tone burst as one trial. At least 200 trials were presented to each cell and the occurrence times of spikes on each trial were recorded.

Inclusion criteria for cells

The three inclusion criteria for this study are as follows.

Data sufficiency.

The analysis only included cells with at least 200 trials containing a total of at least 500 recorded action potentials. This ensured that a sufficient amount of spike data were available to determine the neural response variability of each cell.

Preparation health.

Only cells with a CF-Th <80 dB SPL were included. This ensured that the data set was not contaminated by recordings from damaged or unhealthy preparations. The cutoff of 80 dB SPL is 5 dB SPL higher than the highest threshold reported previously for healthy chicks (Saunders et al., 1996).

Data stationarity.

Successful interpretation of the analysis of response variability required that the neural responses arose from a stationary process (Rieke et al., 1997). Thus, only a subset of consecutive trials (data epochs) in which the mean spike count (firing rate) of the cell remained relatively stable were analyzed. The earliest 200 trial data epoch for which the mean spike count of any 10 trial block deviated <40% from the mean spike count of any other 10 trial block was selected. Cells that failed to exhibit a “stationary” 200 trial epoch were discarded from the analysis. This minimized confounding the analysis with possible changes in the physiological state of the cell, fidelity of the recording electrode, or spike detection. The first data epoch that met this criterion was selected rather than the epoch that was most stable to avoid selecting epochs that overestimated the reliability of the cell's response. However, even when data epochs and cells were not selected for stationarity, the major findings presented here remained the same.

Of the 145 cells for which 200 or more trials were recorded, only one cell was excluded for having <500 recorded spikes. Of the remaining 144 cells, nine were excluded for having thresholds >80 dB SPL. Finally, 50 cells failed the stationarity test, leaving a total of 85 cells that met the three inclusion criteria. These cells had a range of CFs from 0.12 to 3.25 kHz.

Selection of analysis window

Exclusion of the 5 ms associated with the rise and fall time of the stimulus limited the window of analysis for each trial to 35 ms. We also corrected for conduction time down the sound tube, which, based on its length, was 0.269 ms. This adjusted the 35 ms window so that it included only the time when the stimulus was present at the tympanic membrane at full intensity. The “group delay” that encompasses latencies caused by middle ear conduction, cochlear mechanics, the hair cell transduction mechanism, synaptic transmission, and neural conduction (Köppl, 1997) was not measured because it was beyond the scope of this study.

Event detection

The current analyses are event based, where one event was defined as the neural response to a single cycle of the sinusoidal acoustic stimulus. Therefore, the response was divided into a set of consecutive response events that were each one stimulus period long. The beginning and end points of these events were determined by calculating the mean phase angle of the response, which yielded a set of preferred response times (Goldberg and Brown, 1969). Each event was a cycle-long window centered on a preferred response time, as depicted by the large black circles in Figure 1A. Only events that fell fully within the 35 ms window were included. Partial events at the beginning or end of the window were not considered. In a small number of cells, the spike count during the initial events was unstable, perhaps because of an unaccounted-for group delay causing the analysis window to include events responding to the stimulus ramp. To minimize contamination by the stimulus ramp, the “first event” was defined as the first of the two earliest consecutive events for which the spike count of the subsequent event did not increase by 50%.

Figure 1.

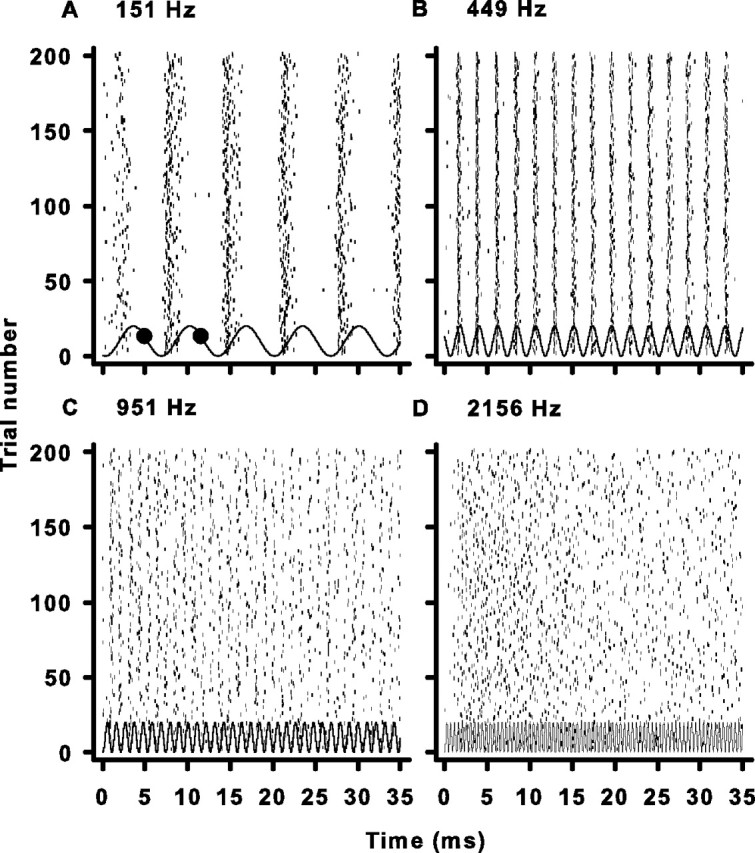
Examples of cochlear nerve responses to pure tones. A, Raster plot of the response of a single unit to multiple presentations of a pure tone at CF. The small dark ticks represent occurrences of spikes. The solid wavy line represents the pressure waveform of the pure tone stimulus at the tympanic membrane. The large black circles are the boundaries of the first event in the response (see Materials and Methods). The number at the top left of each panel is the CF and stimulus frequency. B–D, Same as A but for cells with progressively higher CFs.

Analysis of spike-timing precision

To obtain a measure of spike-timing variability (temporal jitter) the distribution of the first spike latency of each response event was examined (Berry et al., 1997; Uzzell and Chichilnisky, 2004). This temporal jitter was quantified as the SD (σ) of spike occurrence times in the event where only the first spike in each trial was included in the analysis. Thus, for each event, σ was calculated using the following equation.

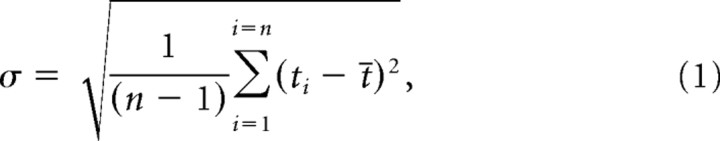where n equals the number of events that contain at least one spike, t_i a first spike occurrence time, and t̄ is the mean first spike occurrence time across all trials. Because spike data are discretely sampled in time, σ can be underestimated. For example, if all spikes occur in one bin, σ would be zero, when in fact some of those spikes may have occurred at different times within the bin. A conservative estimate then is to add a correction factor equal to half of the sampling bin size, which represents the case where half the observations occur on one side of the bin whereas the rest occur on the other (Rokem et al., 2006). Because the sampling bin was 10 μs, the correction factor was only 5 μs and was added to all estimates of σ. For each cell, the mean temporal jitter across all response events was calculated. Furthermore, to compare initial and adapted states, the mean temporal jitter of events that fell fully within the first 10 ms (initial) and the last 10 ms (adapted) of the response was measured. The initial epoch was the first 10 ms that started at the beginning of the first response event. The adapted epoch was the latest 10 ms window that started at the same phase as the initial one. In addition, the most central 10 ms window that started at the same phase was analyzed. For the purposes of this study, a decrease in spike-time precision was defined as an increase in temporal jitter.

The temporal jitter of spike times was measured on a cycle-by-cycle basis. Implicit in this calculation of spike-timing variability was the assumption that temporal coding in the auditory nerve is characterized by regular spike intervals corresponding to the stimulus period, and that the regularity of these intervals is directly related to the ability to phase lock. The measure of temporal jitter was based on the SD of spike times calculated directly from the neural response. Previous reports of the variability in spike times in the auditory nerve have relied on temporal dispersion, a measure that assumes a rectangular (Hill et al., 1989; Köppl, 1997) or Gaussian (Paolini et al., 2001) distribution of spike times and that is derived from the vector strength (synchronization index). We compared temporal jitter to temporal dispersion based on a Gaussian distribution (Paolini et al., 2001) and found a significant difference (paired t test, p = 1.93 × 10⁻⁸). Temporal dispersion was on average 2% smaller and, thus, tended to slightly overestimate precision (data not shown). Thus, temporal jitter captures the variability in spike-timing without assumption in a way that is comparable with other auditory nerve studies as well as similar studies in other sensory systems (Berry et al., 1997; Uzzell and Chichilnisky, 2004).

Analysis of spike-count reliability

The variability in spike count was defined as the variance of spike count (ν) divided by the mean spike count (μ) over 200 trials for windows that were T = 10 ms long. This yielded the Fano factor (FF) (Fano, 1947):

The window, T, was slid by Δt = 10 μs increments (the sampling resolution) across the 35 ms stimulus duration to obtain the FF for each starting time, t. The mean FF for each neuron was calculated across all values of t as well as the FF of the first 10 ms (initial) and the last 10 ms (adapted) window. Starting with the initial and adapted windows at the same phase controlled for possible periodic variations in the FF. In addition to the first and last 10 ms, the middle 10 ms window was analyzed. All three time epochs were identical to those selected in the spike-timing analysis. For the purposes of this study, a decrease in spike-count reliability was defined as an increase in the FF.

We equate variability in spike count with neural noise that constrains the ability of cochlear neurons to transmit information via a rate code. However, variability can be measured on different time scales and the time scale chosen imposes an experimenter's assumption as to how messages are decoded in downstream areas. Furthermore, there is probably more than one relevant time scale with which the CNS decodes auditory information. In measuring the FF, a counting window of 10 ms was chosen. This interval is not meant to suggest that 10 ms is the temporal integration window of the CNS. Rather, it was selected because it was larger than the stimulus cycle period of any pure tone generated in this study, and therefore there was always at least one cycle of data on which to base the FF calculation. It is also a time window that has been used in a number of other studies (de Ruyter van Steveninck et al., 1997; Buracas et al., 1998; Uzzell and Chichilnisky, 2004; Schaette et al., 2005) and allows comparison of present results with those in other sensory systems. We also calculated FF using different counting windows ranging from 1 to 35 ms (data not shown) and the resulting mean FF values were stable in the 5–35 ms range. At shorter durations, the FF increased and approached one, consistent with previous findings that report Poisson statistics for very short counting windows (Teich et al., 1990).

Error estimation

In measuring the variability of spike counts and times, we are interested in the variability of the true underlying response statistics. Because experimental data are finite, the current measures only estimate the true variability. Therefore, bootstrap procedures were used to estimate the errors in σ, μ, ν, and FF. Synthetic data sets were generated from the estimated spike-timing and -count probability distributions (Kass et al., 2005; Schaette et al., 2005). For each estimate of σ from the real data, 1000 synthetic data sets were generated with the same number of observations as the real data set. From these, the associated σ values were calculated. The SD of these 1000 synthetic σ values was taken as the estimation error for σ. An analogous procedure was performed for error estimates of μ, ν, and FF using spike-count distributions, also with 1000 samples.

Synchronization hypothesis testing

Temporal jitter was measured from the first spike times in analysis windows that were the length of a stimulus cycle period. Thus, even for a response event in which spike timing was random within a cycle (i.e., the distribution of spike times is uniform), the temporal jitter would equal $\sqrt{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$12$}\right.}$ or ∼0.28 of the stimulus period. This can be derived by evaluating the integral for the variance (Eq. 3) over a stimulus period and taking its square root:

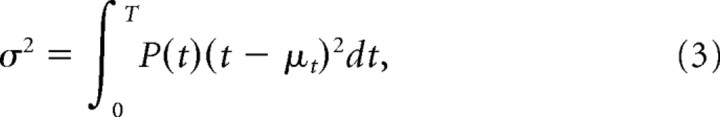where for a uniform probability distribution over the time window, T, P(t) = 1/T, and its mean, μ_t = T/2.

In a finite data set, a response event that has no synchronization or phase preference could yield a σ less than the derived theoretical one. Thus, for each event, spike times from an unsynchronized, uniform distribution were simulated. The number of spikes was matched to the number used to calculate the measured σ for that event. Finally, the σ of the simulated spike times was calculated and the process repeated 1000 times. Thus, an estimate of the probability that a “non-phase-locked” event would generate spike times with σ equal to or less than the measured value was obtained. If p < 0.05, the event was considered significantly phase locked and, therefore, the temporal jitter value was considered reflective of actual spike-timing precision and not just a result of measurement noise.

Poisson hypothesis testing

The firing rate of cochlear neurons responding to constant pure tones is time-varying such that it is higher at preferred stimulus phases and at the beginning of the stimulus because of phase locking and neural adaptation, respectively. If the probability of a spike occurring at a given time depended only on the instantaneous firing rate at that time and not the occurrence of any other spikes, the neural response would be described as a Poisson process (Rieke et al., 1997). This would be the most random process possible for a given instantaneous firing rate function. The FF of a Poisson process is always 1 regardless of the location or length of the counting window, although the converse is not necessarily true: an FF of 1 does not mean a process is Poisson. Because estimates of FF are from finite data and may deviate from 1 even if the data were generated by a Poisson process, we tested whether a Poisson process could have generated an FF equal to or less than the measured FF. To test this null hypothesis, spike data were simulated for each cell in which the probability of a spike occurrence was equal to the instantaneous firing rate as derived from the cell's peristimulus time histogram (DeWeese et al., 2003). For each cell, 200 trials of data were generated and the FF calculated at each time point. The process was repeated 1000 times and used to calculate the probability that the simulated FF value at each time point equaled or fell below the measured value. The measured FF was considered to be significantly lower than that possible from a Poisson process if the probability p was <0.05.

Statistical analysis of means

The σ and FF were measured for cells with different CFs and at three different 10 ms time windows during adaptation. To test the statistical significance of changes in the dependent variables σ and FF caused by changes in CF or time window, the cells were divided into four logarithmically spaced frequency bins (123–278 Hz; 279–631 Hz; 632–1432 Hz; 1433–3247 Hz). A two-way repeated-measures (one repeated factor) ANOVA was undertaken for each dependent variable with CF and time window as factors. If effects were significant, paired comparison post hoc Tukey tests were run. Because both ANOVAs revealed significant effects, reported p values were taken from comparisons made with the post hoc tests.

Modeling statistical properties of the hair cell-afferent fiber synapse

The properties of a synapse adhering to binomial statistics are described by the mean number of vesicles released or quantal content (Eq. 4), the variance of the quantal content (Eq. 5), and, finally, the Fano factor (Eq. 6).

where N equals the number of releasable vesicles and p_vesicle is the average release probability. Furthermore, the probability of any given number of vesicles being released is defined by Equation 7:

where x is the number of vesicles released.

In our preparation, we cannot measure directly quantal content because the single-unit recordings report only suprathreshold responses. However, hair cell–afferent fiber synapses possess a unique attribute such that a single vesicle is sufficient to elicit a postsynaptic action potential (Siegel, 1992; Glowatzki and Fuchs, 2002). This so-called “uniquantal” nature of the hair cell-afferent fiber synapse is presumably mediated by a low-threshold afferent fiber. The postsynaptic fiber should, in theory, report all synaptic responses with a spike except for the failures when no vesicles are released (x = 0) or when the fiber is refractory. Thus, an analogous set of statistical parameters can be derived to predict the expected spiking responses from the single-unit recordings. By evaluating p_x when x = 0 for any hypothetical number of releasable vesicles, an apparent spike probability of (1 − p_{x = 0}) is obtained where all but the failures lead to a spike. Substituting this apparent spike probability into the basic binominal descriptors of Equations 4–6 yields the mean number of spikes (Eq. 8), the variance of the number of spikes (Eq. 9), and, finally, the Fano factor (Eq. 10):

The simple binomial description of vesicle release suggests that FF_vesicle should be independent of N (Eq. 6). However, the statistics of predicted spiking behavior suggest that FF_spike does depend on N (Eqs. 7, 10). These relationships were considered for a brief counting window such that only one spike or less was expected to occur. If longer windows, such as the 10 ms window used in the data analysis, were modeled to allow multiple independent release events, then FF_vesicle and FF_spike would remain as defined by Equations 6 and 10. However, because the model does not include refractoriness, it provides an upper bound to FF_spike as negative temporal correlations between spikes that arise from refractoriness would reduce FF_spike (Young and Barta, 1986; Berry and Meister, 1998).

Results

Patterns of chick auditory nerve discharge

We recorded the spike discharge times in vivo from chick (Gallus domesticus) auditory nerve units during repeated identical pure tone stimulation at the CF of each neuron. Four representative examples of spike firing patterns from cells with CFs of 151, 449, 951, and 2156 Hz are shown in Figure 1. The raster plots demonstrate a clear temporal relationship between the sinusoidal acoustic stimulus and the discharge of the nerve cell. At low frequencies, it is particularly obvious that spikes occur at a preferred phase of the stimulus cycle, a phenomenon commonly referred to as phase-locking (Rose et al., 1967). With increasing characteristic frequency, the temporal structure of the response degrades (Fig. 1, compare A, D) as the stimulus cycle shortens, a finding that is consistent with previous studies in chickens and other species (Kiang, 1965; Rose et al., 1967; Palmer and Russell, 1986; Hillery and Narins, 1987; Köppl, 1997; Furman et al., 2006). These temporal responses patterns are typical of the rest of the units in this study.

The raster plots of the two higher-frequency cells (Fig. 1C,D) exhibit a visually noticeable reduction in the number of spikes occurring during the latter part of the stimulus duration. This reduction in firing rate is indicative of a second well known phenomenon, that of short-term adaptation (Kiang, 1965; Westerman and Smith, 1984). In chick auditory nerve, the average time constant of adaptation is 19 ms, but is much more pronounced in higher CF cells (Fig. 1, compare A,B with C,D), where the time constants of adaptation can be four times faster (Crumling and Saunders, 2007).

Spike-timing precision improves with increasing CF

An extraordinary feature of the peripheral auditory system is its ability to generate precisely timed spikes that are phase locked to the acoustic stimulus waveform (Kiang, 1965; Rose et al., 1967; Köppl, 1997). The temporal precision of auditory nerve responses from trial to trial has usually been measured using temporal dispersion, a quantity that is derived from the vector strength of the response (Goldberg and Brown, 1969) by assuming a rectangular or Gaussian distribution of spike occurrence times on each stimulus cycle (Hill et al., 1989; Köppl, 1997; Paolini et al., 2001). To avoid an assumption about the shape of the distribution, we measured the variability in spike timing on each stimulus cycle as the SD in spike times (temporal jitter; σ) obtained directly from the neural data.

In the same four cells as in Figure 1, σ of individual events tended to be distributed around a fairly stable mean value for a given CF (Fig. 2). Furthermore, temporal jitter decreased as CF increased from a mean value of 429 μs at 151 Hz to 107 μs at 2156 Hz. This increase in temporal precision seemed counter-intuitive to the observation that in this preparation, phase locking degrades with increased CF (Fukui et al., 2006; Furman et al., 2006). However, classical measures of phase locking are with respect to phase and can be misleading with respect to time. Because the length of the stimulus period decreases with increasing CF, even a poorly phase-locked response from a high-frequency cell can be temporally precise.

Figure 2.

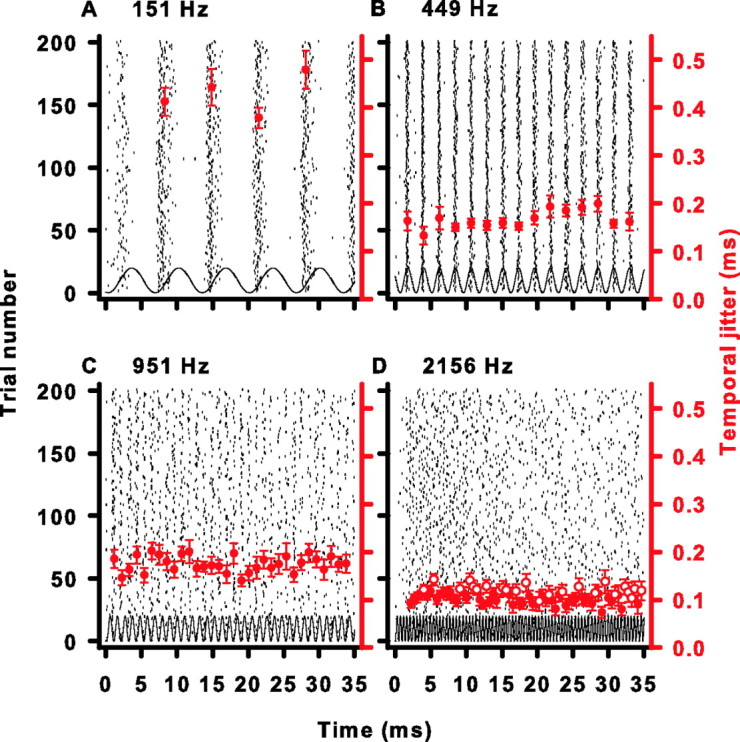
Temporal jitter in four cells during adaptation. A, Same raster plot as in Figure 1A. Large filled red circles are the temporal jitter of an event with a duration of one stimulus cycle period centered around the symbol. Error bars are SDs of the temporal jitter estimates as determined by a bootstrap procedure (see Materials and Methods). B–D, Same as in A but for the same cells as in Figure 1B–D. Large open red circles are events whose temporal jitter does not vary significantly from the temporal jitter generated by an unsynchronized response as tested by a Monte Carlo simulation (see Materials and Methods).

It is possible, given a finite data sample, to measure a very precise temporal jitter during the course of a brief stimulus cycle period that arises from random non-phase-locked responses. We used a Monte Carlo procedure, which generated simulated unsynchronized data (see Materials and Methods) to test whether the observed σ of individual events deviated significantly from σ attributed to unsynchronized or random firing during a comparable stimulus period. The open red circles in Figure 2D identify response events with temporal jitters that are not different from the temporal jitter of an unsynchronized or randomly firing neuron (see Materials and Methods). Rather than reflecting an absolute upper frequency limit to phase-locking, these marked events probably reflect an inability to measure small deviations from uniformity because of measurement noise in a finite data sample.

We calculated a mean σ for each neuron by averaging across all individual observed events. The mean temporal jitter as a function of CF declines from low to high frequencies and ranges from 576 μs down to 79 μs (Fig. 3), and is consistent with a previous study in chick that measured temporal jitter across CF (Fukui et al., 2006). The curved solid line on Figure 3 represents the temporal jitter that an unsynchronized neuron yields from the cycle-long window analysis. This corresponds to the stimulus period multiplied by $\sqrt{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$12$}\right.}$ (for derivation, see Materials and Methods). Note that all σ values lie below this line, suggesting that all neurons fired with a temporal precision that was better than unsynchronized. However, the red data points represent responses from which the mean σ contains >5% individual events that were not significantly different from an unsynchronized response as determined by the Monte Carlo procedure. Nevertheless, even in the cell with the smallest number of synchronized events, 22% of the events were significantly synchronized, demonstrating that some phase locking was measurable at all frequencies studied. Thus, even at frequencies up to 3 kHz, chick auditory nerve cells can track the acoustic waveform. These data demonstrated an increase in precision at higher frequencies. However, the experiments do not address whether this increase was caused by faster modulations in the stimulus waveform, tonotopic specializations in the hair cell-afferent fiber synapse, or an increase in the effect of refractoriness caused by shortened interspike intervals.

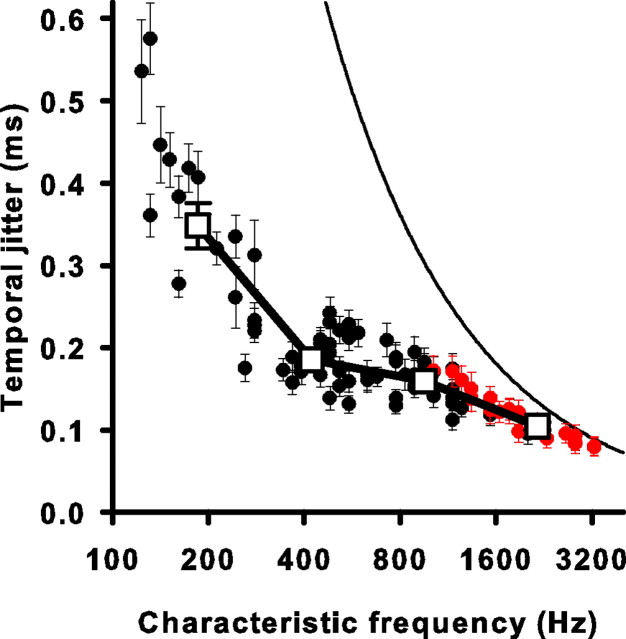
Figure 3.

Spike-timing precision improves with higher CF. The mean temporal jitter of all events is plotted for each cell as a function of CF (circles). Error bars are the average SD of the temporal jitter estimate as determined by a bootstrap procedure (see Materials and Methods). Red circles represent units for which >5% of events had temporal jitters that could have been generated by an unsynchronized event with 5% probability, as tested by a Monte Carlo simulation (see Materials and Methods). Open squares represent averaged data for four logarithmically spaced frequency ranges. Error bars are the SEs of the mean. The solid curved line is the temporal jitter expected for an unsynchronized event resulting from using an analysis window that is one stimulus cycle long. It is equal to the square root of 1/12 divided by the CF (for derivation, see Materials and Methods).

Spike-timing precision does not degrade during neural adaptation

The ability of a cochlear neuron to fire with temporal precision could degrade with duration of stimulation, especially if presynaptic mechanisms responsible for spike-rate adaptation also contribute to the timing of neurotransmitter release. We tested the effect of duration of stimulation on temporal precision of auditory nerve responses by comparing the mean temporal jitter of events that occurred in the initial 10 ms of the response with the mean temporal jitter of those that occurred in the adapted or last 10 ms of the response. We also analyzed the middle 10 ms of the response. Only events that fit completely in these 10 ms epochs were included. When we compared initial and adapted σ as a function of CF (Fig. 4), there was no significant difference between the temporal jitter of the initial and adapted periods at any frequency (p > 0.16). Thus, on the time scale of short-term adaptation, auditory nerve spike-timing precision remained unchanged. This suggests that the critical signaling steps leading to neurotransmission at the hair cell-afferent fiber synapse are not temporally degraded during adaptation.

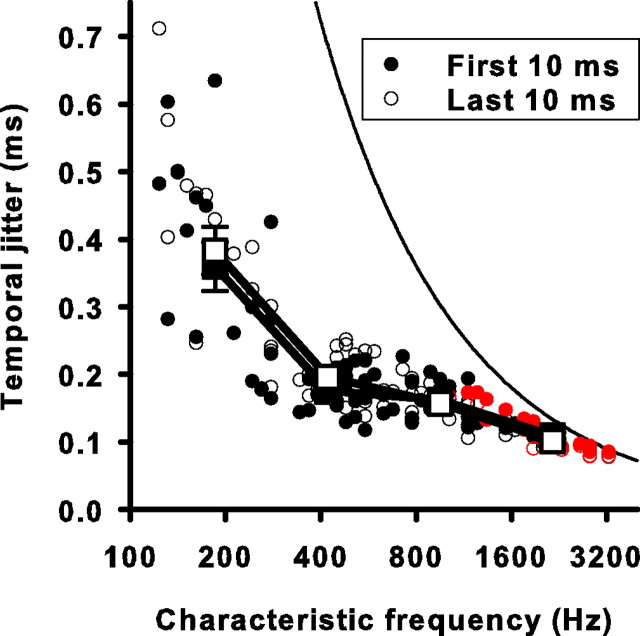
Figure 4.

Temporal jitter is unaffected by short-term adaptation at all CFs studied. The mean temporal jitter for the first (filled circles) and last (open circles) 10 ms of the response of each unit is plotted against the CF. Error bars for single units are left out for the sake of clarity and are on the same order as those for Figure 3. Red circles represent 10 ms windows for which >5% of events had temporal jitters that could have been produced by an unsynchronized event with 5% probability as tested by a Monte Carlo simulation (see Materials and Methods). Square symbols are averaged data for four frequency ranges (same ranges as Fig. 3). The solid curved line is the temporal jitter expected for an unsynchronized event resulting from using an analysis window that is one stimulus cycle long. It is equal to the square root of 1/12 divided by the CF (for derivation, see Materials and Methods).

Auditory nerve responses are reliable

Variability in the number of spikes occurring in response to identical repeated stimuli is one indicator of the reliability of a neural response. We calculated the mean (μ) and variance (ν) of the spike count in a 10 ms window across 200 trials for each cell. The window was moved across the 35 ms stimulus duration in 10 μs steps starting at the beginning of the first event with μ and ν calculated at each step. Figure 5 shows the relationship between the mean spike count and its variance for the four representative units from Figure 1. The auditory nerve responses can approach the theoretical minimum variance for any given mean spike count. This minimum variance is depicted by the solid scalloped curves in Figures 5 and 6, and is described by ν_min = f(1 − f), where f is the fractional difference between the mean spike count and its nearest integer value (de Ruyter van Steveninck et al., 1997). The low-frequency cell with a CF of 151 Hz (Fig. 5A) as well as all 10 ms windows observed for all cells with CFs of 278 Hz or less (Fig. 6, red dots) approach this maximal reliability. Similar minimal variance is also observed for cells in the frequency band between 279 and 631 Hz, but to a somewhat lesser degree (Figs. 5B, 6, green dots). At higher frequencies, the spike-count variance continues to deviate from its theoretical minimum (Figs. 5C,D, 6, yellow and blue dots).

Figure 5.

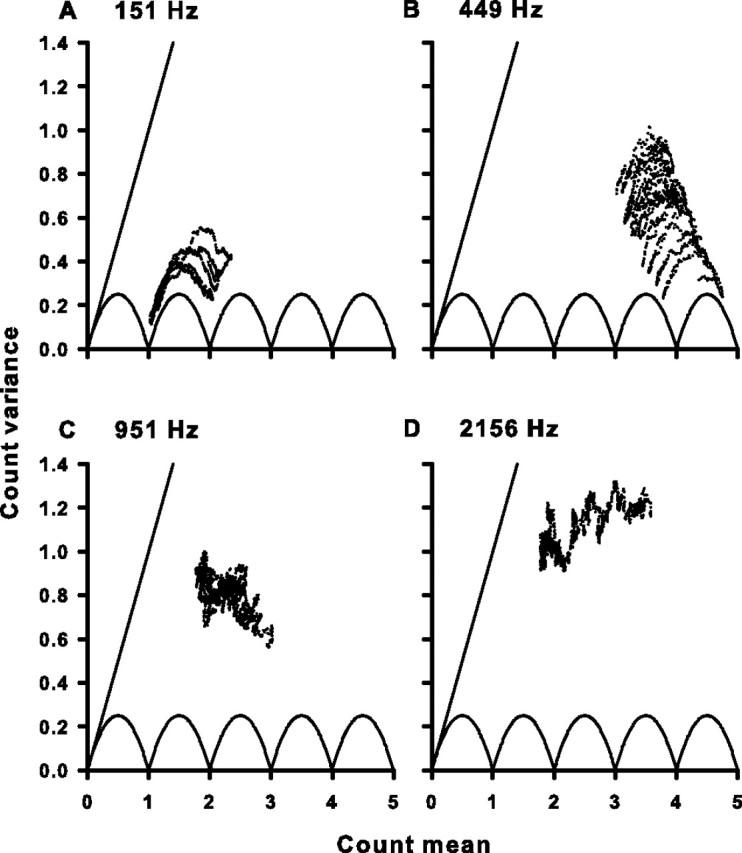
Variance and mean of the spike count for four cells. A, The spike-count variance plotted as a function of the spike-count mean for the same cell as in Figure 1A. Each dot represents the variance and mean for one 10 ms window of the response as the window slides in 10 μs steps across the whole response window. The solid scalloped line is the minimum variance possible for a given spike-count mean. The solid straight line is the unity line and represents the variance expected for a Poisson process at each mean. The number at the top left of the panel is the CF and stimulus frequency. B–D, Same as in A, but for the same cells as in Figure 1B–D.

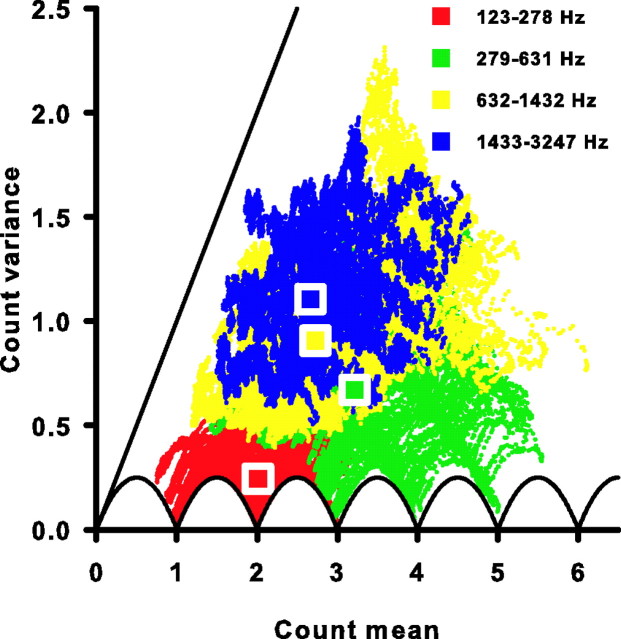
Figure 6.

All cells have sub-Poisson spike-count variance. The spike-count variance is plotted against the spike-count mean for all 10 ms windows of all 85 cells studied (colored symbols). Each color represents a different frequency range (top right key). The solid scalloped line is the minimum variance possible for a given spike-count mean. The solid straight line is the unity line and represents the variance expected for a Poisson process at each mean. Square symbols are plotted at the mean of the count mean and count variance for each frequency range.

Although the variability of the nerve responses varied greatly, all cells examined (Fig. 5, 6) demonstrate a mean spike count that is greater than its variance as all data points lie below the unity line. A unity relationship exists between the mean spike count and its variance if the probability of a spike occurring at one time is independent of the occurrence of spikes at any other time, as would be expected from a Poisson stochastic point process (Rieke et al., 1997). Thus, the sub-Poisson relationship between the auditory nerve's mean spike count and its variance suggested that these data are not consistent with a simple Poisson spike generation mechanism, even one with a time-varying firing rate. Instead there must be temporal correlations between spikes, such as those caused by refractoriness (Teich and Khanna, 1985; Young and Barta, 1986; Berry and Meister, 1998). This sub-Poisson reliability can be advantageous for neurons using a rate code. The temporal correlations can reduce the variability of temporal patterns and, hence, are also advantageous to neurons using a temporal code.

Spike-count reliability decreases with increasing CF

Another useful metric of spike reliability in neural systems is the Fano factor. The FF is defined as the ratio of the spike-count variance over the mean spike count, and represents a normalized variance indicating how reliably a spike count can be estimated from a time window that contains several spikes on average (Teich and Khanna, 1985; Zador, 1998). It provides a convenient measure for comparing spike reliability between cells that have different mean firing rates. We calculated a mean FF for each cell by averaging the FFs calculated from successive 10 ms windows covering the entire stimulus duration and found that FF increased systematically from low- to high-CF cells ranging from 0.03 to 0.59 (Fig. 7A). The increase in FF with CF might be attributable to a decreased mean spike count (μ), an increased spike-count variance (ν), or both. We examined mean μ and ν as a function of CF (Fig. 7B,C). On average, μ increases from 1.97 spikes (per 10 ms) at the lowest frequencies to 3.21 spikes, where it remains constant or decreases slightly at frequencies higher than 400 Hz. Thus, changes in μ do not account for the increase in FF. However, changes in ν do, as ν showed a systematic increase across CF similar to that found for FF (Fig. 7A,C).

Figure 7.

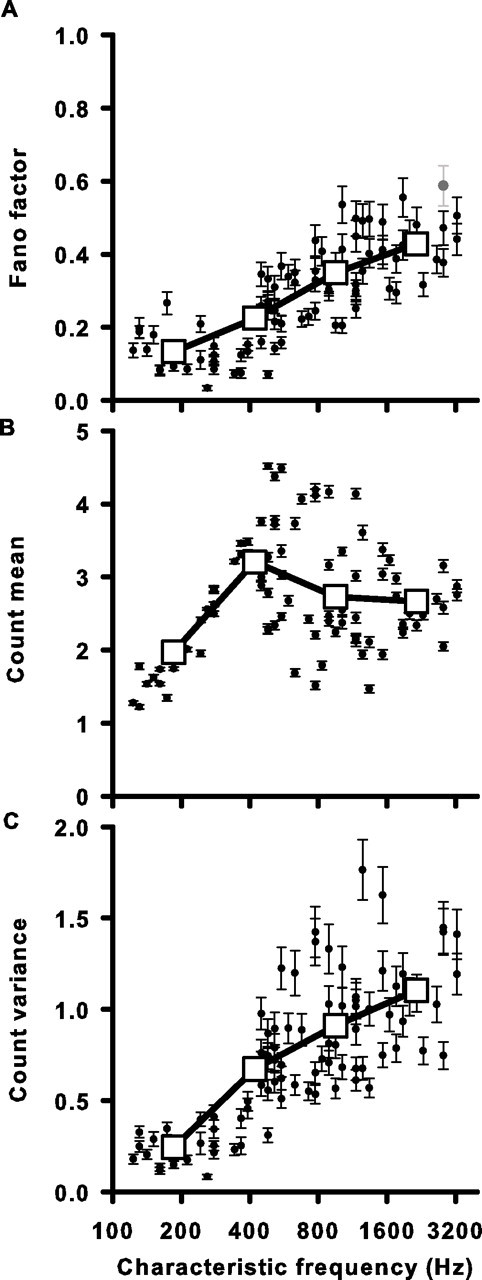
Spike-count reliability decreases with higher CF. A, The mean Fano factor (spike-count variance/mean) for each unit plotted against CF. Filled circles are the average FF for all 10 ms windows in the cell's response. The single gray circle is a unit for which >5% of the 10 ms windows had measured FF values that did not vary significantly from an FF generated by a Poisson process with the same instantaneous firing rate function. This was tested using a Monte Carlo simulation (see Materials and Methods). B, Spike-count mean as a function of CF. C, Spike-count variance as a function of CF. Error bars represent the average SD of the count mean, variance, and FF for all 10 ms windows in the cell's response as determined by a bootstrap procedure (see Materials and Methods). Large open squares represent the data binned into four frequency ranges and averaged (same ranges as Fig. 6). The SEM is smaller than the square symbol size in all cases.

For a Poisson spike-generating process described solely by its instantaneous firing rate, the mean spike count equals its variance and, thus, FF = 1. All of our measured FF values fell below 1, consistent with sub-Poisson behavior. Because the measured FF values were only estimates of the true spike-count variability, we were concerned that measured FF values could indeed be generated by a Poisson process with the same instantaneous firing rate function as our cells (see Materials and Methods). In only one cell could a Poisson process have generated any of our measured FFs (with >5% probability) and this was only true for 7.54% of the 10 ms windows analyzed in that cell (Fig. 7A, gray symbol). Thus, essentially all cells examined were significantly more reliable in their firing than what would be expected from a Poisson process. However, as CF increased, cells became less reliable as they faced increased neural noise in the form of a relative increase in spike-count variance. This constrains their ability to transmit information via both a rate code, because spike count was more variable, and a temporal code, because responses were becoming more Poisson-like.

Spike-count reliability decreases after neural adaptation

Does short-term rate adaptation influence the reliability of spike counts? It is unknown whether the variability in spike counts undergoes changes on a similar time scale as the mean spike count. Thus, we compared the variability in spike counts between the beginning and end of the stimulus. Figure 8 shows how FF, μ, and ν vary with duration of stimulation for one representative unit (CF, 2156 Hz; same unit as in Fig. 1D). The FF increases gradually and is clearly higher by the last 10 ms window than the first. For the particular cell in Figure 8, the change in FF is predominantly caused by the decrease in μ because ν stays relatively constant. To quantify the impact of adaptation on spike reliability, we compared for each cell the initial FF to the adapted FF.

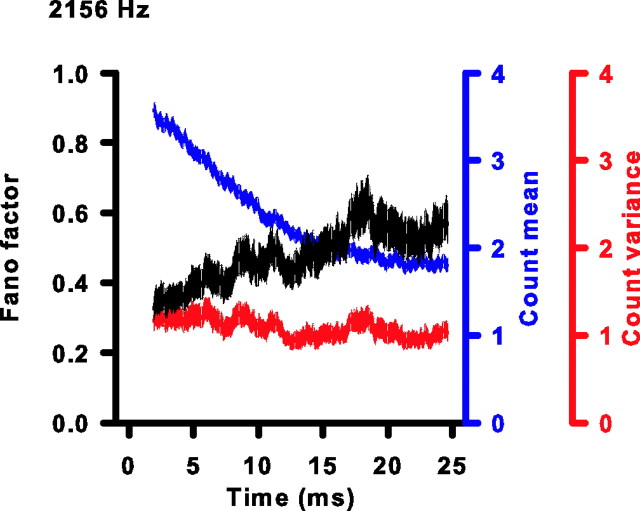
Figure 8.

FF increases during short-term adaptation. The Fano factor (black), spike-count mean (blue), and spike-count variance (red) plotted as a function of duration of stimulation for the same cell as in Figure 1D. The thickness of each curve is the SD of the estimated parameter at each time as determined by a bootstrap procedure (see Materials and Methods). The number at the top left of the figure is the CF and stimulus frequency.

The comparison of FFs between initial and adapted epochs is plotted as a function of CF in Figure 9A. In addition, we also analyzed the middle 10 ms window of the response. There was a significant increase in FF after adaptation except in the lowest frequency range, where there was no significant increase (initial FF, 0.10 ± 0.02; middle FF, 0.11 ± 0.02; adapted FF, 0.14 ± 0.02; p = 0.105). In the highest frequency range, FF more than doubled (initial FF, 0.26 ± 0.01; middle FF, 0.43 ± 0.02; adapted FF, 0.53 ± 0.03; p < 0.001). To understand better the CF-dependent effect on FF during adaptation, we examined whether the effect was simply caused by a decrease in μ associated with short-term rate adaptation or caused by an increase in ν, or both. We compared the initial and adapted μ and ν as a function of CF (Fig. 9B,C). As CF increased, adaptation also increased, as measured by a decrease in μ with duration of stimulation. This was consistent with previous findings (Crumling and Saunders, 2007). The adapted spike-count variance, ν, was only slightly higher than the initial ν and was not significantly different at the lowest frequency range (Fig. 9C) (p = 0.53). The increase in FF with duration of stimulation seen at all but the lowest CFs was due, therefore, to a decrease in μ and not an increase in ν. This suggested that the mechanism responsible for short-term rate adaptation does not decrease spike-count variance proportionally to the mean firing rate, and results in decreased response reliability.

Figure 9.

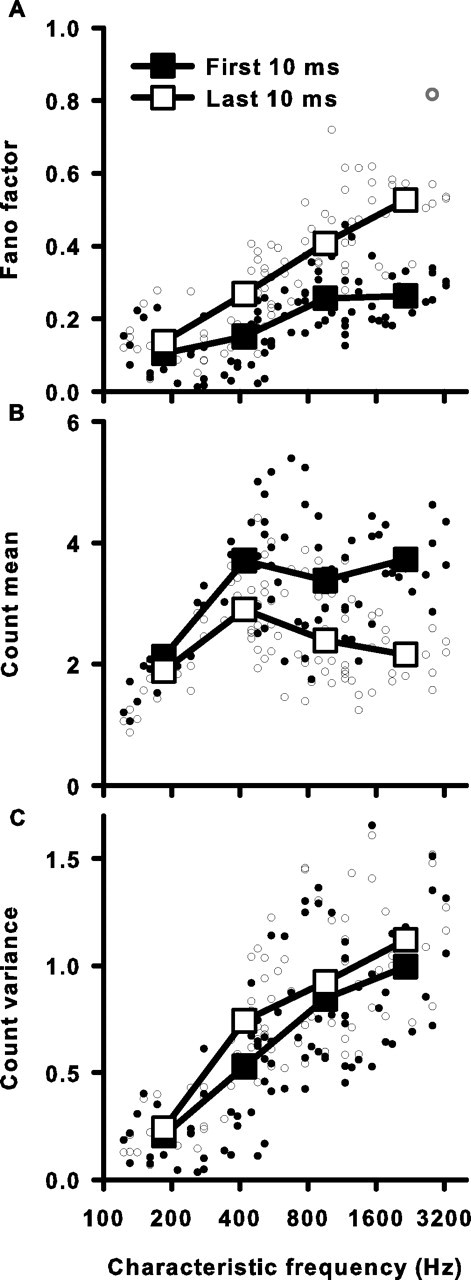
Spike-count reliability decreases during short-term adaptation for all but the lowest frequency cells. A, Fano factor for the first (filled circles) and last (open circles) 10 ms window of a single cell's response as a function of CF. Error bars for single units are left out for the sake of clarity and are on the same order as those for Figure 7. The single open gray circle represents a cell with an adapted FF value that did not vary significantly from the FF generated by a Poisson process with the same instantaneous firing rate function as tested by a Monte Carlo simulation (see Materials and Methods). Large square symbols are averages for four frequency ranges (same ranges as in Fig. 6). All SEs are smaller than the symbol size. B, Spike-count mean of the first and last 10 ms as a function of CF. C, Spike-count variance of the first and last 10 ms as a function of CF.

Possible mechanisms underlying changes in spike reliability

Adaptation in the peripheral auditory system has been attributed to a depletion of the readily releasable pool of synaptic vesicles (Moser and Beutner, 2000; Spassova et al., 2004). In terms of a binomial statistical model, adaptation has been attributed to a decrease in N, the number of releasable vesicles, rather than a change in p_vesicle, the average probability of vesicle release (Furukawa et al., 1978). For a binomial process, the FF is independent of N and proportional to (1 − p_vesicle) (Eq. 6). Because it is impossible to measure quantal transmitter release in the intact preparation, we used a binomial statistical model of the hair cell–afferent fiber synapse to better interpret our single-unit data in terms of the underlying properties of vesicle release. A unique response property of this synapse allows us to make a simplifying assumption about the relationship between vesicle release and spike generation (see Materials and Methods).

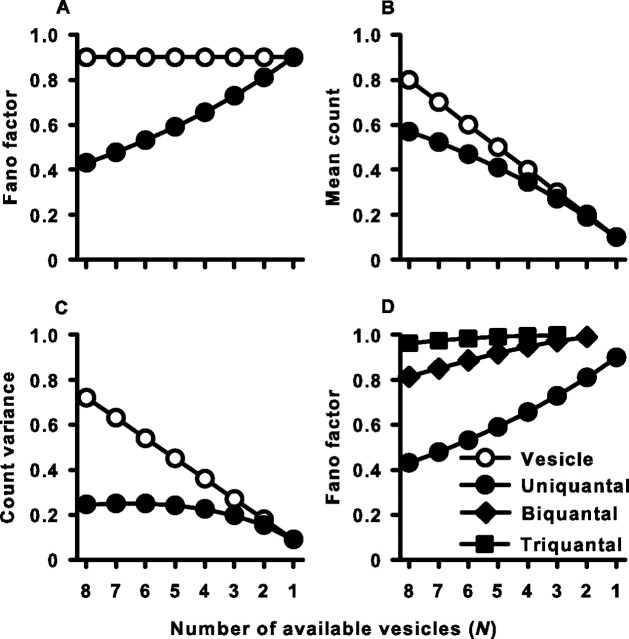
We used Equations 6–10 to examine the theoretical count, variance, and FF of both vesicles released and spikes generated during adaptation that result from a fixed probability of release (p_vesicle), and a progressive decrease in the available number of vesicles (N). Both the model vesicle count and spike count decay with N as expected during adaptation (Fig. 10B). However, whereas the variance of the vesicle count decays proportionally with the mean vesicle count, the spike-count variance is essentially constant during adaptation (Fig. 10C) and results in the increase in spike-count FF (Fig. 10A). This contrasts with the vesicle-count FF, which remained constant across adaptation as expected from a binomial process for which N, but not p_vesicle, is changing. This same basic relationship between modeled counts, variances, and FFs was observed for both vesicles and spikes across a whole range of release probabilities tested from 0.05 to 0.5 (data not shown).

Figure 10.

Vesicle depletion reduces spike-count reliability. Vesicle- and spike-count statistics were predicted from a model. Transmitter release was modeled as a binomial process with N available vesicles, each with release probability, p_vesicle = 0.1. Spike generation required ≥1 (uniquantal), ≥2 (biquantal), or ≥3 (triquantal) released vesicles. Parameters in all panels are plotted as a function of adaptation, simulated by a decrease in N. A, Fano factor of vesicle and spike count for the uniquantal case. B, Mean vesicle and spike count for the uniquantal case. C, Vesicle- and spike-count variance for the uniquantal case. D, Fano factor of spike count for the uniquantal, biquantal, and triquantal cases.

It was also necessary to rule out the possibility that all of the initial suppression of FF was caused by our choice of a brief counting window, which limits the response to one spike or less, rather than our assumption about the uniquantal nature of synaptic transmission. Thus, given the same brief counting window, we examined the impact on FF of increasing the number of vesicles required for spike generation, defined as x + 1 (Fig. 10D). In all cases, as N diminished, FF increased toward (1 − p_x). However, the most dramatic effects of spike-count “regularization” were seen when only one vesicle was required to trigger an action potential and support a role for the uniquantal nature of hair cell–afferent fiber synaptic transmission.

The results of the spike output from this simple model recapitulate the experimental observations reported here. The experimental spike-count FF increased during adaptation because of a failure of the spike-count variance to scale with the mean spike count. We suggest that the ability of one or a few quanta to trigger a postsynaptic action potential forces reliability onto the afferent fiber synapse at the onset of the stimulus because all vesicle release events are read out as single spike events.

Discussion

The response properties of a cochlear neuron change during the course of a constant stimulus presumably as an adaptive coding mechanism (Fig. 1). Therefore, to better understand the noise constraints on possible adaptive coding mechanisms, we compared changes in the response variability of both the spike timing (σ) and the spike count (FF) during the course of pure-tone stimulation. We found that the reliability of spike counts decreased during adaptation except at the lowest frequencies, whereas the precision of spike timing remained unchanged (Figs. 4, 9). A statistical model of synaptic function suggested that the ability of one or a few vesicles to elicit an action potential reduces the inherent response variability expected from quantal neurotransmitter release to confer count reliability at sound onset. However, with adaptation, depletion of the readily releasable pool of vesicles diminishes quantal content and antagonizes the postsynaptic enhancement of reliability (Fig. 10).

Spike-timing precision

The precision of spike timing was unchanged during adaptation (Figs. 2, 4), meaning that action potentials occurred with the same level of synchronization to the stimulus waveform. At conventional synapses, sustained repetitive stimulation can cause an increase in asynchronous transmitter release and a decrease in synchronous transmitter release, most likely caused by calcium accumulation (Cummings et al., 1996; Jensen et al., 1999, 2000; Lu and Trussell, 2000; Hagler and Goda, 2001; David and Barrett, 2003; Kirischuk and Grantyn, 2003). Calcium might be expected to accumulate in the hair cell in response to a sustained pure tone. However, the hair cell possesses several specializations that ensure rapid calcium entry and removal. These include rapidly activating and deactivating voltage-gated calcium channels (Lewis and Hudspeth, 1983; Beutner and Moser, 2001; Spassova et al., 2001), fast mobile calcium buffers (Roberts, 1993; Edmonds et al., 2000; Heller et al., 2002), as well as potent calcium pumps to extrude calcium from the cytoplasm (Dumont et al., 2001). The current observation that cochlear neurons maintain precise spike-timing during sustained stimulation is consistent with the maintenance of a rapid and highly regulated calcium signal in the hair cell.

Spike-count reliability

Stochastic processes are hypothesized to underlie the generation of spike trains (Del Castillo and Katz, 1954; Perkel et al., 1967). Discharge patterns recorded from a variety of sensory systems, including auditory nerve, exhibit predominantly sub-Poisson statistics manifest by FFs less than one for time windows on the order of tens of milliseconds, suggesting reliable, nonrandom spike discharges (Teich and Khanna, 1985; Young and Barta, 1986; Berry et al., 1997; de Ruyter van Steveninck et al., 1997; DeWeese et al., 2003; Schaette et al., 2005). This is in contrast to the predominantly supra-Poisson statistics observed with longer counting windows (Teich et al., 1990; Lowen and Teich, 1992; Kelly et al., 1996). Over the counting window analyzed in this study, all auditory nerve fibers responded with sub-Poisson spike-count reliability (Figs. 5, 6). However, the reliability degraded during adaptation.

The increase in the spike-count FF with adaptation results from the failure of the spike-count variance to scale with the mean spike count (Figs. 8, 9). Scaling would be expected if the binomial statistics of synaptic vesicle release were solely responsible for neuronal discharge patterns (Eq. 6). So what constrains the variance and regularizes spike count? One source of spike-count regularization at this synapse is the low threshold of the postsynaptic afferent fiber. The uniquantal hypothesis (Geisler, 1981) states that a single quantum of neurotransmitter release is sufficient to trigger a postsynaptic action potential at the hair cell-afferent fiber synapse. Although the release of transmitter from the hair cell is often multivesicular, direct recordings have demonstrated that only one or two vesicles are sufficient to elicit a suprathreshold response postsynaptically (Siegel, 1992; Glowatzki and Fuchs, 2002). Such an easily saturated spiking mechanism has the potential to limit spike count dramatically and decrease the variance of the synapse's output, even if a binomial process is underlying the release of synaptic vesicles. This prediction is supported by our model, which predicted spiking behavior based on binomial release statistics and a saturating spiking mechanism (Fig. 10).

Another possible source of spike-count regularization in our experimental data is refractoriness, which can limit the number of spikes that occur during a stimulus (Gray, 1967; Gaumond et al., 1983; Johnson and Swami, 1983). Refractoriness regularizes temporal patterns of spikes in retina (Berry and Meister, 1998) and is also known to reduce the FF of auditory nerve responses (Young and Barta, 1986). During adaptation, the spike rate declines and results in a longer average interspike interval. In theory, this leads to spikes that occur in a less refractory state. Unfortunately, the current experiments do not allow us to assess the contribution of this second postsynaptic mechanism on reliability.

Not all cells exhibited a decrease in reliability with adaptation. FF undergoes smaller changes at lower frequencies (Fig. 9A). Interestingly, at progressively lower frequencies, the time course of spike-rate adaptation slows (Crumling and Saunders, 2007). Thus, over 35 ms, there is a smaller change in the mean spike count (Fig. 9B). Because slower adaptation presumably reflects less vesicle pool depletion, the smaller change in FF is consistent with the model finding that postsynaptic enhancement of reliability dominates when more vesicles are available (Fig. 10A). We would also expect a smaller influence of refractoriness at low CFs, where many interspike intervals are longer.

Possible consequences of adaptation on auditory coding

Different sensory systems have evolved different mechanisms to help ensure that only the most relevant environmental information is encoded. Rate adaptation improves the efficiency and reduces redundancy of neural coding by expending fewer spikes when encoding a sustained stimulus, presumably because most of the important stimulus features are rapidly encoded during the onset (Barlow, 1961). Although the decreased firing rate reduces the information capacity of the neuron (Rieke et al., 1997), it is possible to minimize information loss if neural noise in the form of spike-timing and -count trial-to-trial variability is minimized. This is especially important in early sensory relays whose primary function may be to provide relatively unfiltered information efficiently to the CNS. Here, however, we found that one form of neural noise, spike-count variability, increased during adaptation in the auditory nerve. This implies that rate coding becomes noisier during adaptation and that it would therefore be a more reliable strategy at stimulus onset.

The natural acoustic environment is made up of mostly transients, not constant stimuli. Therefore, what role does adaptation play in a peripheral auditory system subjected to a dynamic world? Rate adaptation has been proposed to enhance the encoding of sound transients (Delgutte, 1980). Interestingly, adaptation occurs on a fast time scale of tens of milliseconds, an interval similar to that of behaviorally relevant sound components. For example, maternal calls that are behaviorally relevant to the chick include individual components as short as 10–100 ms (Collias and Joos, 1953). Thus, short-term rate adaptation may indeed be effective in reducing the redundancy of behaviorally relevant acoustic signals, but perhaps at the expense of rate code information after the onset of sound components.

Rate adaptation also is proposed to play a role in adaptive rescaling of the sensory input–output function in both the visual system (Laughlin, 1989) and higher auditory centers (Dean et al., 2005). By rescaling its output to match the stimulus statistics of the immediate environment, an organism can use a limited set of neuronal responses to encode a larger ensemble of sensory conditions. In auditory nerve, rate-level functions to pure tones shift to higher sound levels after the addition of a simultaneous background noise (Costalupes et al., 1984). Most of this shift has been attributed to cochlear suppression from frequencies surrounding the CF of a neuron. However, if a tone at CF precedes the pure tone, a similar albeit smaller shift is observed, suggesting that rate-adaptation can also contribute to rescaling of the rate-level function (Gibson et al., 1985). This adaptation-induced shift results in a decrease in the maximum firing rate, which our findings suggest would be coupled with a decrease in firing-rate reliability. Therefore, although adaptation could in theory extend the range of sound levels that are encoded by a single neuron, it would do so at the cost of decreased discrimination performance when using a rate code strategy.

In contrast to reliability, spike-timing precision, which helps convey frequency, phase (Rose et al., 1967), and intensity (Anderson et al., 1971; Johnson, 1980; Colburn et al., 2003) information remained intact during rate adaptation. The resilience of temporal precision in the face of a constant pure tone re-enforces the importance of temporal fine structure coding by the avian auditory system. We predict that this emphasis on maintenance of spike timing during adaptation extends to more dynamic and naturalistic sound environments. Although different species have evolved to hear in different soundscapes, many exhibit rate adaptation on the same time scale as the chick (Kiang, 1965; Westerman and Smith, 1984), which is likely mediated by vesicle pool depletion (Furukawa et al., 1978; Moser and Beutner, 2000). Our data suggest that this vesicle depletion reduces spike-count reliability, but not temporal precision. Thus, cellular mechanisms conserved across species may impose common limitations on neural coding.