Perceptual Learning Directs Auditory Cortical Map Reorganization through Top-Down Influences

Abstract

The primary sensory cortex is positioned at a confluence of bottom-up dedicated sensory inputs and top-down inputs related to higher-order sensory features, attentional state, and behavioral reinforcement. We tested whether topographic map plasticity in the adult primary auditory cortex and a secondary auditory area, the suprarhinal auditory field, was controlled by the statistics of bottom-up sensory inputs or by top-down task-dependent influences. Rats were trained to attend to independent parameters, either frequency or intensity, within an identical set of auditory stimuli, allowing us to vary task demands while holding the bottom-up sensory inputs constant. We observed a clear double-dissociation in map plasticity in both cortical fields. Rats trained to attend to frequency cues exhibited an expanded representation of the target frequency range within the tonotopic map but no change in sound intensity encoding compared with controls. Rats trained to attend to intensity cues expressed an increased proportion of nonmonotonic intensity response profiles preferentially tuned to the target intensity range but no change in tonotopic map organization relative to controls. The degree of topographic map plasticity within the task-relevant stimulus dimension was correlated with the degree of perceptual learning for rats in both tasks. These data suggest that enduring receptive field plasticity in the adult auditory cortex may be shaped by task-specific top-down inputs that interact with bottom-up sensory inputs and reinforcement-based neuromodulator release. Top-down inputs might confer the selectivity necessary to modify a single feature representation without affecting other spatially organized feature representations embedded within the same neural circuitry.

Introduction

The spatial distributions of sensory receptors in the skin, retina, and cochlea are preserved in mosaics of topographically organized two-dimensional maps that tile the cerebral cortex. During critical periods of development, cortical maps are dynamically maintained to allocate larger representational areas to sensory inputs with the greatest relative strengths. Thus, restricting sensory inputs to a single eye or a limited region of the skin or cochlea during an early period of postnatal life produces an expansion of the territory of the region within the map (Wiesel and Hubel, 1963; Simons and Land, 1987; Zhang et al., 2001). In this regard, cortical map plasticity observed in early development is dominated by a “bottom-up” process in the sense that the representational area is dictated by the patterns of afferent sensory inputs impinging on cortical neurons with minimal dependence on the animal's state of attention or motivation.

Topographic maps in the primary somatosensory and auditory cortex remain plastic through adulthood (for review, see Feldman and Brecht, 2005; Ohl and Scheich, 2005). Here we ask, to what extent is plasticity in adult sensory maps controlled by bottom-up sensory input statistics or, alternatively, by “top-down” factors such as the animal's attentional state or task demands? Psychophysical studies have shown that perceptual improvements are specific to the stimulus features used in the task (Karni and Sagi, 1991; Ahissar and Hochstein, 1997; Irvine et al., 2000; Hawkey et al., 2004; Fitzgerald and Wright, 2005), but also to stimulus features to which the subjects are asked to attend (Ahissar and Hochstein, 1993). The neural correlates of top-down control over perceptual learning have remained contentious. Results from human imaging and psychophysical experiments suggest that the effects of perceptual learning in early sensory fields is primarily governed by bottom-up inputs (Watanabe et al., 2001, 2002; Petkov et al., 2004), whereas direct physiological evidence from single-unit recordings in awake animals suggests that task demands can influence neural responses as early as the primary sensory cortex (Ahissar et al., 1992; Sakurai, 1994; Crist et al., 2001; Schoups et al., 2001; Li et al., 2004; Fritz et al., 2005). Task-dependent influences on receptive fields in the primary sensory cortex have only been observed in awake animals and, even then, have only been observed to last for short periods of time. Studies that investigate long-term effects of conditioning on adult cortical map and/or their constituent receptive field organization have generally claimed that receptive field plasticity reflects the pattern of bottom-up sensory inputs and their relationship to reinforcement-based neuromodulator release (Ji et al., 2001; Kilgard et al., 2001, 2002; Weinberger, 2004; Yan and Zhang, 2005). Our understanding of the relative contribution of bottom-up and top-down signals to adult cortical plasticity has remained clouded, however, because nearly every conditioning study has imposed varying attentional demands on subjects presented with varying sensory inputs.

The present study attempts to disambiguate the contribution of these two signals to learning-induced plasticity of cortical maps. Rats assigned to a frequency recognition (FR) or loudness recognition (LR) task were presented with the same set of auditory stimuli but learned that only one feature, frequency or intensity, was relevant to the demands of the task. The arrangement of sensory stimuli, behavioral reinforcement, and task demands allowed us to formulate a set of mutually exclusive hypotheses: if bottom-up factors direct cortical map plasticity, we predicted that both groups would exhibit similar cortical map changes because the bottom-up inputs were identical. If top-down factors guided cortical map plasticity, we predicted that cortical map plasticity would be restricted to the stimulus domain that was relevant to the task demands. We formulated a secondary hypothesis based on a set of perceptual learning studies that found top-down effects restricted to higher cortical areas and bottom-up effects dominant in lower cortical areas (Watanabe et al., 2002; Petkov et al., 2004). We recorded from the primary auditory cortex (AI) and the suprarhinal auditory field (SRAF), a secondary and putatively higher auditory field, with the expectation that reorganization in SRAF would be more strongly influenced by task demands, whereas plasticity in AI would most likely reflect the pattern of bottom-up sensory inputs.

Materials and Methods

Subjects.

Nineteen adult female Sprague Dawley rats (age, 14–18 weeks) were used in the study. The rats were assigned to the FR (n = 6), LR (n = 6), or naive control (n = 7) groups. Recordings were obtained from AI and SRAF in FR and LR rats after improvements in task performance reached asymptote and were compared with recordings in age-matched naive control rats. In the FR group, four rats yielded recordings from both AI and SRAF; we recorded from AI only in one rat and from SRAF only in one rat. In the LR group, we recorded from both AI and SRAF in five rats and AI only in one rat. In the control group, we recorded from both AI and SRAF in one rat, recorded from AI only in three rats, and recorded from SRAF only in three rats.

Multiunit responses to tone pips and white-noise bursts were obtained from a total of 1828 recording sites. We recorded a total of 892 acceptable tuning curve files from tone-pip stimuli in AI (FR, 278; LR, 349; control, 265) and a total of 936 in SRAF (FR, 342; LR, 292; control, 302). We obtained a total of 809 acceptable rate-level function (RLF) files in AI (FR, 215; LR, 337; control, 257) and a total of 824 in SRAF (FR, 269; LR, 274; control, 281).

Behavioral training.

Rats assigned to the FR and LR groups were trained to identify a target auditory stimulus from a set of distracter auditory stimuli. The auditory stimuli consisted of 150 ms tone pips (10 ms linear ramps) of variable frequency and intensity. Rats assigned to the FR task were rewarded for making a “Go” response shortly after the presentation of a 4987 Hz tone at any intensity. Rats assigned to the LR task were rewarded for making a Go response shortly after the presentation of a 35 dB sound pressure level (SPL) tone at any frequency. Training was performed in an acoustically transparent operant training chamber (20 × 20 × 18 cm, length × width × height) contained within a sound-attenuated chamber. Input and output devices (photobeam detector, food dispenser, sound card, house light) and software were manufactured by Med Associates (Georgia, VT). The frequency and intensity values of all tones used in the FR and LR tasks were drawn from the same set of possible values (Table 1). The rats were shaped in three phases. During phase A, rats were trained to make a nose poke response to obtain a food reward. During phase B, rats were trained to make a nose poke only after presentation of an auditory stimulus (5 kHz at 35 dB SPL). During phase C, rats were conditioned to make discriminative responses to the target stimulus and not to a limited set of non-target stimuli. Rats were advanced to the actual training program (levels 1–6) once their performance in phase C was clearly under stimulus control. Once rats were working within the actual training program, they began each day on level 1.

Table 1.

Tone frequencies and intensities used in the auditory recognition task

Phase Aa
Phase B
Frequency	4987*
Loudness	35**
Phase C
Frequency	1600	4987*	15,542
Loudness	35**	55	75
Level 1
Frequency	1600	2825	4987*	8803	15,542	27,437
Loudness	35**	45	55	65	75	80
Level 2
Frequency	1950	3121	4987*	7981	12,771	20,435
Loudness	35**	43	51	59	67	75
Level 3
Frequency	2370	3438	4987*	7234	10,494	15,215
Loudness	35**	41	47	53	59	65
Level 4
Frequency	2885	3794	4987*	6557	8622	11,335
Loudness	35**	39	43	47	51	55
Level 5
Frequency	3515	4190	4987*	5944	7085	8440
Loudness	35**	37	39	41	43	45
Level 6
Frequency	4275	4619	4987*	5388	5821	6285
Loudness	35**	36	37	38	39	40

Frequency values are in hertz (Hz), and Loudness values are in decibel sound pressure level (dB SPL). For each trial, the tone frequency and intensity were selected independently and randomly from the list corresponding to the current difficulty level. For any specific level, the probability that any of the six frequencies and intensities will be selected is equal. The asterisks indicate target stimuli for the FR (*) and LR (**) tasks.

^aGo response rewarded without auditory stimuli.

A single behavioral trial was defined as the length of time between the onsets of two successive tones. The intertrial interval was selected at random from a range of 3–9 s. A rat's behavioral state at any point in time could be classified as either Go or “NoGo.” Rats were in the Go state when the photobeam was interrupted. All other states were considered NoGo. For a given trial, the rat could elicit one of five reinforcement states. The first four states were given by the combinations of responses (Go or NoGo) and stimulus properties (target or non-target). Go responses within 3 s of a target were scored as a hit, and a failure to respond within this time window was scored as a miss. A Go response within 3 s of a non-target stimulus was scored as a false positive, and the absence of a response was scored as a withhold. The fifth state, false alarm, was defined as a Go response that occurs >3 s after stimulus presentation. A hit triggered delivery of a food pellet (45 mg; BioServe, Frenchtown, NJ). A miss, false positive, and a false alarm initiated a 5 s “time-out” period during which time the house lights were turned off and no stimuli were presented. A withhold did not produce a reward or a time out.

Trials were grouped into blocks of 50. At the conclusion of each block, a target response ratio (number of hits/number of target trials), a non-target response ratio (number of false positives/number of non-target trials), and a false alarm ratio (number of false alarms/number of trials) were calculated. For the FR task, if the target response ratio was >90% and the non-target response ratio was <20% the task difficulty was increased by one level (unless the rat was working on stimulus level 6). The stimulus level difficulty was reduced by one level if any of those criteria were not met (unless the rat was working on stimulus level 1). For the LR task, the target response ratio criterion was set to 80% and the non-target response ratio was set to 30%. This difference in criteria adjusted for the fact that the LR task was inherently more difficult and ensured that rats in both tasks were moving through the levels (and therefore experiencing equivalent stimuli) at comparable rates.

At the conclusion of training, each day of behavioral performance underwent an additional quality control. If the rat was inattentive (target response ratios <50%) or hyperactive (false alarm ratios >15%) over a block of 50 trials, the block was discarded. The rats worked for an average of 1200 acceptable trials per day. Less than 5% of the blocks met the criteria set for inattentive or hyperactive behavior. Psychometric functions and stimulus target recognition thresholds were calculated for each training session by plotting the percentage of Go responses as a function of the stimulus frequency and intensity. The frequency difference (FR rats) or intensity difference (LR rats) at which a Go response was made 50% of the time was defined as the target recognition threshold. We elected to use 50% Go probability as the recognition threshold because it corresponded to the indecision point, the stimulus difference at which the rat was equally likely to make a false positive response as it was to make a withhold response.

Learning curves were reconstructed by plotting the change in recognition threshold over the course of training. Learning curves generally exhibited an initial negative slope corresponding to periods of greater perceptual learning, followed by a relatively flat period that indicated a plateau in target recognition threshold. The behavioral asymptote was defined as the transition point between these two phases of learning. Because single animal learning curves are inherently noisy, we first defined a set of “stable minimum” values that included only threshold values that were preceded and followed by values that differed by <15%. The minimum value from this set was defined as the minimum recognition threshold, and the earliest training session that was within 15% of the minimum recognition threshold was defined as the behavioral asymptote. This approach allowed us to distinguish stable improvements in recognition threshold from ostensibly spurious threshold values (e.g., session 5 in Fig. 2C and session 8 in Fig. 2D).

Figure 2.

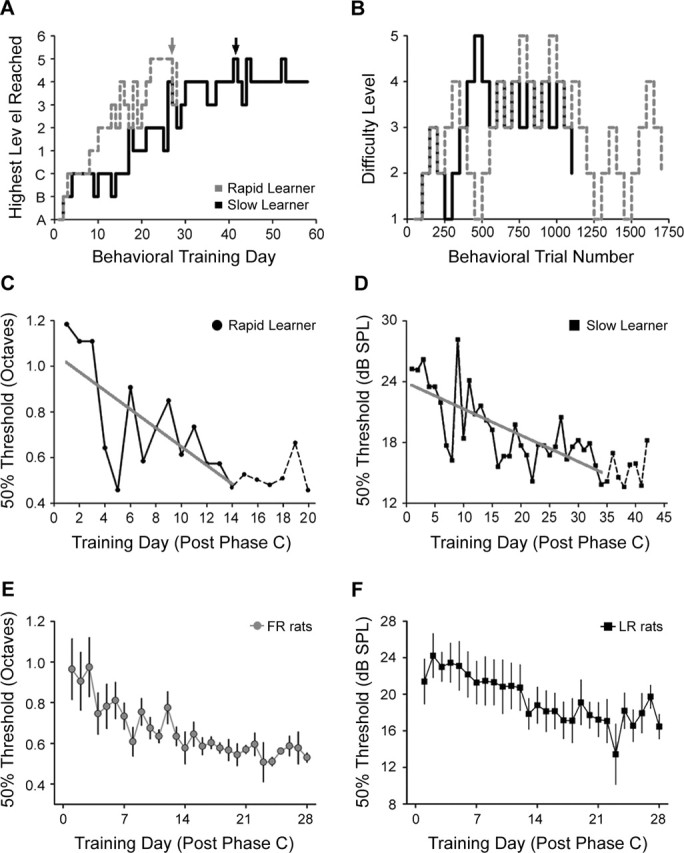
Documentation of perceptual learning in the auditory recognition task. A, The highest training phase reached on an individual day of training is shown across the entire training period for one rat in the FR task categorized as a rapid learner (dashed gray line) and one rat in the LR task classified as a slow learner (solid black line). The description of auditory stimuli used in each phase is provided in Table 1. B, Task performance for the same rats shown in A obtained from a single day of training (indicated by black and gray arrows in A) is shown to illustrate the adaptive tracking protocol. C, D, Fifty percent recognition thresholds plotted across each training day for the same rapid learning rat (C) and slow learning rat (D). Changes in the recognition threshold between the first day of training until performance reached an asymptotic level were fit with a linear regression (thick gray line), and the slope of the regression line was defined as the slope of the learning curve. Dashed lines indicate post-asymptotic training days that were not included in the slope calculation. E, F, Target recognition threshold values (mean ± SE) across the first 28 d of training for all rats in the FR (E) and LR (F) tasks.

We elected to use 35 dB SPL as the target intensity rather than an intermediate intensity that would have been more equivalent to the intermediate target frequency used in the FR task for two reasons. First, in AI of the rat, unlike the cat or bat, the vast majority of neurons are maximally responsive to sound intensities >70 dB SPL (Phillips and Kelly, 1989; Doron et al., 2002; Polley et al., 2004). To test our hypothesis that significantly more neurons would become maximally responsive to the target intensity as a result of LR training, it seemed most reasonable to choose a target intensity that was most different from the normally preferred intensity, yet still audible across all frequencies used in the task. We concluded that 35 dB SPL met these opposing demands reasonably well. Second, even with the distracter intensities made as different from the target intensity as possible, performance on the LR task was still slightly worse overall than performance on the FR task. Although we cannot be absolutely certain why this difference occurred, it seems reasonable to assume that (1) because the distance between the rat's head and the speaker was not fixed, the absolute sound level impinging on the ears for a stimulus of fixed intensity was not constant and/or (2) even if the sound level reaching the ear for a stimulus of fixed intensity was constant, the subjective perception of loudness would vary between pure tones of different frequencies (Robinson and Dadson, 1956). Thus, we selected a 35 dB SPL target because it would have the greatest hypothesized effect on the neural encoding of sound intensity relative to controls and because it would be perceptually easier to recognize the highest or lowest absolute sound level within a set, rather than an intermediate value.

Electrophysiological recording procedure.

The rats were anesthetized with sodium pentobarbital (50 mg/kg, followed by 10–15 mg/kg supplements as needed), the auditory cortex was surgically exposed, and multiunit activity was recorded with tungsten microelectrodes (1–2 MΩ; FHC, Bowdoinham, ME). AI was defined based on short latency (8–20 ms) evoked onset responses in the most dorsal auditory field containing a complete tonotopic gradient running at ∼15° relative to the horizontal plane. The center of SRAF is located in cortical area TE3 ∼2 mm ventral to the center of AI and 0.5 mm dorsal to the rhinal fissure [the area named VAAF in the study by Kalatsky et al. (2005)]. SRAF has a clearly organized tonotopic gradient running approximately orthogonal to the horizontal plane. SRAF is separated from AI by an intermediate field, VAF, which abuts the dorsal border of SRAF and the ventral border of AI. Pure tone tuning curves in SRAF are typically broader than those observed in AI at sound intensities near threshold (e.g., Q14), and onset response latencies are 4 ms longer, on average, than AI neurons (D. B. Polley, unpublished observations).

Recording sites (20–35 per mm²; 150–250 μm separation between recording sites) were evenly distributed across AI and SRAF while avoiding blood vessels. A typical map of either field could be delineated from 60 to 100 individual penetrations, of which 45–80 sites might be sufficiently tuned to be included in the map and the remainder used to define map borders or unresponsive regions. At every penetration site, the recording microelectrode was lowered orthogonal to the pial surface to a depth of 450–550 μm (layers 3/4), where robust stimulus-driven responses were most readily recorded. Frequency–intensity response areas were reconstructed by presenting 60 pure-tone frequencies (1–30 kHz, 20 ms duration, 5 ms raised cosine ramps) at 11 sound intensities (0–70 dB SPL, 7 dB SPL increments) to the contralateral ear using a calibrated sound delivery and recording system (Tucker-Davis Technologies, Alachua, FL).

Analysis of electrophysiological responses.

Characteristic frequency (CF) was defined for each tuning curve as the frequency that evoked a response at threshold. Cortical recruitment functions were calculated by determining the polygonal area associated with a single penetration within the map and then calculating the range of sound frequencies that elicited a response from that site at each of the 11 sound intensities. The area of all polygons activated by a tone of a specific frequency and intensity was then summed and expressed as a percentage of the total map area. Tuning curve bandwidth was defined at 14 and 42 dB SPL above threshold and was expressed as a Q-factor value (CF/bandwidth).

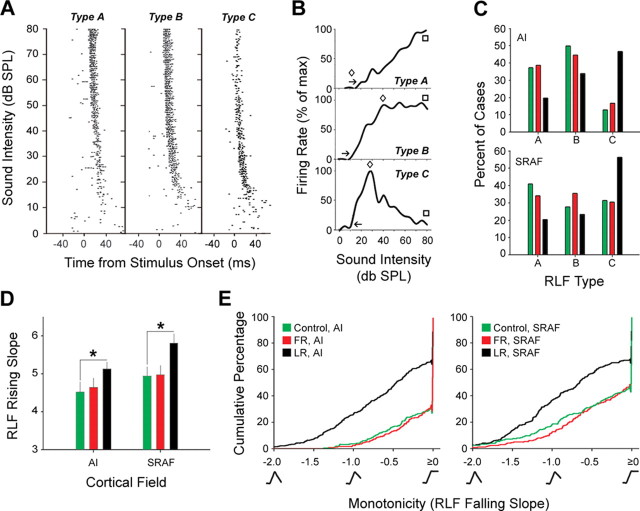
RLFs were constructed by presenting white-noise bursts (150 ms duration, 5 ms raised cosine ramps) at 17 intensities ranging from 0 to 80 dB SPL in 5 dB SPL increments. Each intensity was presented 20 times in a pseudorandom order. At each site, the spontaneous firing rate collected during the 100 ms before stimulus onset was subtracted from the stimulus onset response (mean duration of the onset response ± SD, 21.44 ± 10.68 ms). Each RLF was normalized to its maximum firing rate, and the following measures (defined below) were derived according to the method outlined by Schreiner et al. (1992): (1) minimum response threshold; (2) transition point; (3) best level; (4) slope of the RLF between the minimum response threshold and the transition point; and (5) monotonicity. If the spike rate remained at zero for two consecutive sound levels, all sound levels less than or equal to the greater of the two levels were considered subthreshold. The minimum response threshold was defined as the first sound level in the suprathreshold region of the RLF (see Fig. 7B, arrow). In many cases, the RLF consisted of a fast-growing low-intensity portion and a saturated or decreasing response function at higher sound intensities. The transition point was defined as the lowest suprathreshold intensity at which the firing rate failed to increase by at least 10% (mean change in firing rate: pre-threshold, 38%; post-threshold, −5.9%) (see Fig. 7B, diamond). The best level was defined as the sound level that evoked the greatest magnitude response. Monotonicity was defined as the slope of the RLF between the transition point and the highest sound level estimated by a linear regression analysis. In the event that the RLF increased linearly above the minimum response threshold (e.g., type A in Fig. 7B) and a transition point could not be determined, a linear regression analysis was performed on all sound levels above threshold. In both cases, the slope of the regression function was used as a quantitative measure of monotonicity, whereby a negative slope corresponded to a nonmonotonic response and a slope of zero or greater corresponded to a monotonic response function. A minimum of five sound intensity values, including the transition point, had to be included in the linear regression analysis or a monotonicity value was not determined for that recording site. Less than 3% of recording sites were excluded for this reason. RLFs were classified as type A, B, or C (see Fig. 7C) according to the following criterion: functions without a transition point (diamond) were considered type A, functions with falling slopes less than −0.5 were considered type C, and all other functions were classified as type B. Tessellated maps were generated by defining the Cartesian coordinates, CF, and best level for each penetration site and applying the voronoi function in Matlab (Mathworks, Natick, MA). All analyses were performed blind to experimental condition.

Figure 7.

Task-specific restructuring of receptive fields for sound intensity. A, Example raster plots illustrate three representative types of neural responses to white-noise bursts of varying intensity: monotonically increasing (type A), saturating (type B), and nonmonotonic (type C). Each dot represents the occurrence of an action potential. B, RLFs correspond to the raster plots shown in A. The minimum response threshold, transition point, and response at highest intensity are indicated by the arrows, diamonds, and squares, respectively. C, Frequency of occurrence for type A, B, and C RLFs in AI and SRAF for control (green), FR (red), and LR (black) rats. The color scheme applies for all subsequent panels. D, Mean ± SE slope of RLF rising phase (between the arrow and diamond in B). The asterisks indicate statistically significant differences obtained with an unpaired t test (p < 0.05). E, Cumulative percentage plots illustrate shifts in the distribution of monotonicity values (slope of the RLF between the diamond and square in B) in AI (left) and SRAF (right).

Results

Stimulus statistics in the auditory recognition task

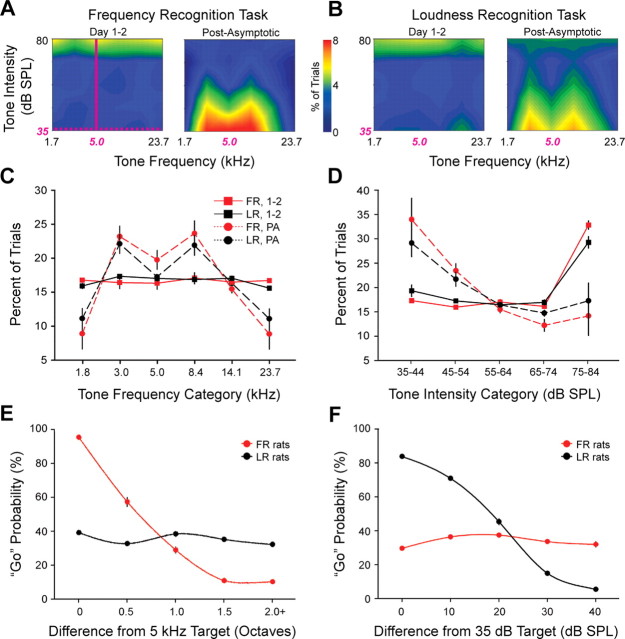
Adult rats were trained to perform an auditory recognition task. The rats were assigned to FR or LR tasks and were presented with isolated tones of variable frequency and intensity. FR rats were rewarded for breaking a photo beam with their snout (Go response) after the presentation of a 5 kHz tone at any intensity (Fig. 1A, solid magenta line). LR rats were rewarded for making a Go response after presentation of a 35 dB SPL tone at any frequency (Fig. 1A, dashed magenta line). The arrangement of stimulus presentation and reinforcement scheduling highlights two essential features of this experimental design. First, the FR and LR tasks used statistically similar sets of sensory stimuli from the first day of behavioral shaping until the last day of training (Fig. 1A–D). The complete set of tone frequencies and intensities used throughout behavioral training is shown in Table 1. The rats were not cued to attend to either frequency or intensity but learned to attend to the task-relevant acoustic feature solely through trial and error. A statistical analysis confirmed that tone frequency (Fig. 1C) and intensity (Fig. 1D) distributions were statistically inseparable between LR and FR rats throughout all phases of training (ANOVA; p > 0.09 for all comparisons). Second, we used an adaptive tracking procedure to adjust task difficulty such that rats in both groups would consistently produce the correct behavioral responses on 70–80% of the trials. Rats learned to make a Go response for food reward (phase A) within 1 d. In all subsequent phases of training, rats were rewarded for making a Go response after the target stimulus only. The task became increasingly difficult as rats became more proficient. Task difficulty was increased either by adding non-target distracter stimuli (phase C) or making the distracter stimuli more similar to the target stimuli (levels 1–6). Thus, tone frequencies were initially distributed across a broad range of frequencies spanning 1.6–28 kHz but became significantly more focused around the 5 kHz target frequency once behavioral performance reached asymptote (repeated-measures ANOVA interaction term; p < 0.025 for FR and LR tone frequency distributions) (Fig. 1C). Similarly, tone intensities were initially distributed across a broad range spanning 35–80 dB SPL but became significantly more clustered around 35 dB SPL throughout the post-asymptotic behavioral period (repeated-measures ANOVA interaction term; p < 0.005 for FR and LR tone intensity distributions) (Fig. 1D). By the time task improvement had reached a plateau, rats were typically working on higher task levels (e.g., levels 3–5) but rarely performed accurately enough to reach level 6. Consequently, the distribution of tone frequencies illustrated in Figure 1C shifts from flat to “M-shaped,” because the distribution of non-target distracter frequencies have decreased in the frequency ranges furthest from the target and are most commonly drawn from frequency ranges flanking the target frequency range. Had rats been able to consistently perform the task at level 6, the non-target distracter intensities and frequencies would have been drawn almost entirely from the target frequency (5 kHz ± 0.375 octaves) and intensity (35–44 dB SPL) category.

Figure 1.

Stimulus statistics and behavioral performance for the auditory recognition task. A, B, Distribution of tone frequencies and intensities presented in training days 1–2 and all post-asymptotic training sessions in FR (A) and LR (B) rats. Any tone falling along the dashed horizontal line served as a target stimulus for the LR task. Any tone falling along the solid vertical line was a target stimulus for the FR task. C, D, Frequencies (C) and intensities (D) presented in each behavioral trial are compared between FR (red) and LR (black) rats on days 1–2 (squares) and post-asymptotic (PA) days (circles). Tone frequency categories (C) are ¾-octave-wide bins centered on the frequency value shown. E, F, Behavioral performance as a function of tone frequency (E) and tone intensity (F) during the post-asymptotic training sessions for all rats trained in the FR (red) and LR (black) tasks. All values shown are mean ± SE.

Based on psychometric functions, we were able to determine that rats could selectively attend to either frequency or intensity. Accordingly, the probability of making a Go response in the FR task was strictly determined by tone frequency and was not influenced by tone intensity (Fig. 1E). Conversely, the probability of making a Go response in the LR task was exclusively determined by tone intensity and was independent of tone frequency (Fig. 1F). The psychometric functions shown in Figure 1, E and F, were reconstructed from training sessions after behavioral performance had reached asymptote. It is important to note, therefore, that rats in both groups continued to attend only to the task-relevant stimulus dimension even when the range of stimuli in the task-irrelevant stimulus dimension became increasingly restricted.

Perceptual learning in the auditory recognition task

The rate of progression to more difficult levels of training and final recognition threshold values varied between individual rats. Examples of an FR-trained rat that learned the task rapidly and an LR-trained rat that learned the task more slowly are shown in Figure 2A–D to illustrate the range of learning aptitudes. Both rats progressed to advanced levels of the task, albeit at different rates (Fig. 2A). An example of all stimulus sets presented on a single day of training is shown for both rats in Figure 2B. Once individual rats completed shaping phase C, they began each day of training thereafter on level 1 and were advanced to higher training levels based on their response accuracy. The target recognition threshold (stimulus difference at which the correct response was made 50% of the time) decreased over the course of training for each rat (Fig. 2C–F). Target recognition thresholds typically decreased to an asymptotic level 2–6 weeks after completing shaping phase C (Fig. 2C,D). The change in recognition threshold from the first day of training on difficulty level 1 up to the point of asymptotic performance was fit with a linear regression (Fig. 2C,D, thick gray line). The slope of the linear fit was used to indicate the overall degree of perceptual learning and is compared with the extent of physiological plasticity described below (Fig. 6). We observed a significant decrease in target recognition thresholds over the first 4 weeks of training measured for all rats in the FR task (one-way, repeated-measures ANOVA; F = 3.17, p < 0.0005) (Fig. 2E) and LR task (one-way, repeated-measures ANOVA; F = 2.86, p < 0.001) (Fig. 2F).

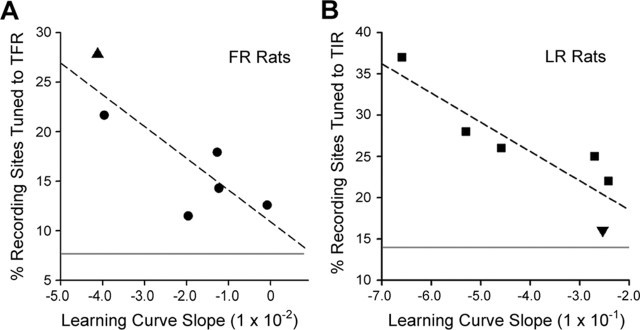
Figure 6.

The percentage of recording sites tuned to the task-relevant stimulus feature is correlated with the degree of perceptual learning. A, Percentage of AI and SRAF recording sites tuned to the trained frequency range (TFR) in each FR-trained rat. B, Percentage of AI and SRAF recording sites tuned to the trained intensity range (TIR) in each LR-trained rat. The linear fit for each data set is represented by the dashed line. The upward triangle data point (A) and downward triangle data point (B) correspond to the rapid-learning FR rat and slow-learning LR rat, respectively, in Figure 2A–D. Solid gray lines represents the mean percentage of recording sites tuned to the TFR (A) and TIR (B) in control rats.

Cortical map plasticity in the frequency domain

Topographically ordered maps for sound frequency in field AI and SRAF are shown in Figure 3, A and B. The centers and selectivity of sound frequency tuning curves were defined for each recording site as the CF and as bandwidths of the tuning curve at various sound levels above threshold. Note that the CF gradient in AI progresses from high to low along an anteroposterior axis, whereas the CF gradient in SRAF runs from high to low along a dorsoventral gradient.

Figure 3.

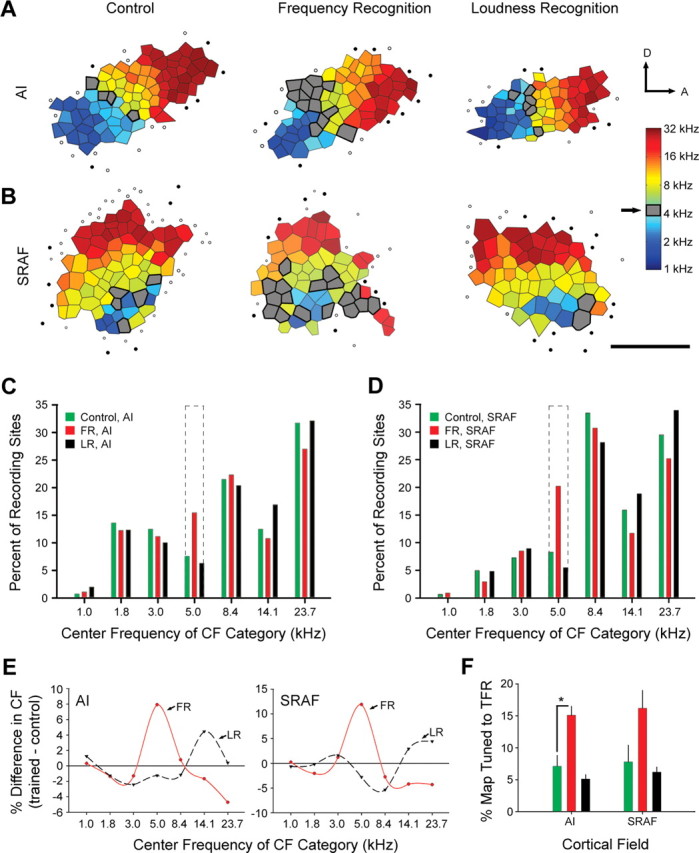
Task-specific reorganization of cortical maps in the frequency domain. A, B, Representative tonotopic maps from AI (A) and SRAF (B) were delineated with fine-grain microelectrode mapping. The color of each polygon in the tessellated map represents the CF associated with neurons located in the middle cortical layers at that position in the map. Gray shaded polygons indicate recording sites with CF values within the trained frequency range (5 kHz ± 0.375 octaves). Filled circles indicate unresponsive sites. Open circles represent sites with sound-driven responses that did not meet the criteria for inclusion in AI or SRAF. Scale bar, 1 mm. The arrows indicate dorsal (D) and anterior (A) orientations. C, D, Distribution of CF values in AI (C) and SRAF (D) for all recordings obtained in control (green), FR-trained (red), and LR-trained (black) rats. Dashed lines indicate the trained frequency range. E, Difference functions were calculated by subtracting the CF distribution in control rats from FR-trained (solid red) and LR-trained (dashed black) CF distributions. Zero values (solid black line) indicate no difference relative to controls. Tone frequency categories (C–E) are ¾-octave-wide bins centered on the frequency value shown. F, Mean ± SE percentage of map area with CF values in the trained frequency range (TFR). The asterisk indicates a statistically significant difference obtained with an unpaired t test (p < 0.05).

Rats trained in the FR, but not LR, task displayed a pronounced expansion of cortical sites with CFs at or near the 5 kHz (5 kHz ± 0.375 octaves) target frequency compared with controls (Fig. 3A,B, gray shaded polygons). The distribution of CF values over the entire population of recording sites in each group was quantified by categorizing CF values into seven ¾-octave-wide bins (Fig. 3C,D). The percentage of AI recording sites with CF values in the trained frequency range (5 kHz ± 0.375 octaves) (Fig. 3C, dotted lines) doubled in FR rats compared with controls (15.5 vs 7.5%; χ² = 8.3; p < 0.005) (Fig. 3C) but was essentially unchanged in LR rats compared with controls (6.3%; χ² = 0.37; p = 0.55). Similarly, the percentage of SRAF recording sites with CF values within the trained frequency range was 2.5 times greater in rats trained in the FR task than in control rats (20.2 vs 8.3%; χ² = 18.2; p < 5 × 10⁻⁵) (Fig. 3D) but was not significantly changed in LR rats compared with controls (5.5%; χ² = 1.8; p = 0.18). Plotting the same data as difference functions demonstrates that FR training induced a specific increase in CF values at the trained frequency range in both AI and SRAF, whereas LR training did not change the CF distribution in any consistent manner compared with controls (Fig. 3E). Alternatively, one can measure tonotopic map plasticity by calculating the map area tuned to the trained frequency range and expressing that value as a percentage of the total map area. The relative area of the map tuned to the trained frequency range in AI was significantly increased after FR, but not LR, training compared with control (15.1 ± 1.4% vs 7.1 ± 1.7%; t = 3.58; p < 0.01) (Fig. 3F). We also observed an expansion of the relative area of SRAF tuned to the trained frequency in FR rats compared with control (16.2 ± 2.8% vs 7.8 ± 2.6%), but this trend did not reach statistical significance (Mann–Whitney U test; p = 0.05) (Fig. 3F).

Cortical map plasticity in the intensity domain

Although the spatial distribution of best level, the sound level that evoked the highest firing rate, was not arranged into a topographically organized gradient, recording sites with similar best-level values tended to cluster in contiguous areas of the map (Fig. 4A,B). A qualitative comparison of the same representative maps shown in Figure 3, A and B, demonstrates a strikingly different trend when examined for the best level rather than CF. Rats trained in the LR task exhibited a pronounced increase in cortical sites with best-level values in the trained intensity range (35 ± 5 dB SPL, blue sites), whereas AI maps for sound intensity in FR and control rats are dominated by sites that preferred sound intensities close to 80 dB SPL (Fig. 4A). We also observed a preponderance of sites in SRAF of LR rats tuned to the trained intensity range, although the difference was not as striking as AI because there was an overall increase in the number of cortical sites that preferred low to intermediate sound levels in both FR and control rats in this field (Fig. 4B).

Figure 4.

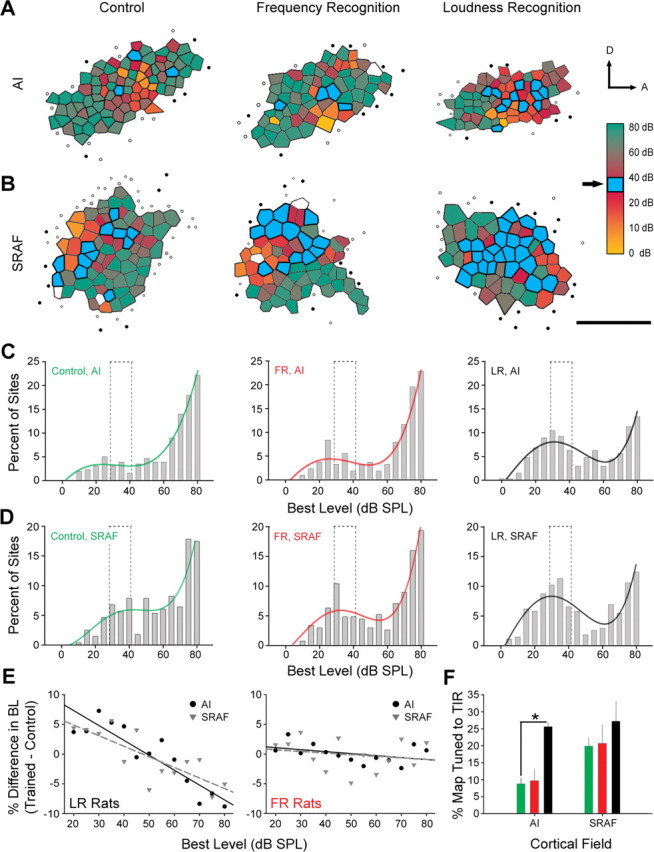
Task-specific reorganization of cortical maps in the intensity domain. A, B, Representation of sound intensity in AI (A) and SRAF (B) are created using the same conventions as in Figure 2, except that the color within each polygon indicates the best level for neurons at that recording site, rather than CF. Empty polygons indicate recording sites where a best level could not be determined because responses were poorly driven by white-noise bursts. Blue shaded polygons indicate recording sites with best-level values in the trained intensity rage (35 ± 5 dB SPL). The arrows indicate dorsal (D) and anterior (A) orientations. C, D, Distribution of best-level values in AI (C) and SRAF (D). The dotted line indicates the trained intensity range. Each distribution is fit with a fourth-degree polynomial function (colored lines) to illustrate the shape of the distribution. E, Difference functions were calculated by subtracting the best-level distribution values in control rats from the best-level distribution values in LR-trained (left) and FR-trained (right) rats. Solid and dashed lines represent linear fits of the difference values for AI (solid black) and SRAF (dashed gray). Flat slopes indicate no difference relative to control. F, Mean ± SE percentage of map area tuned to the trained intensity range (TIR) in control (green), FR-trained (red), and LR-trained (black) rats. The asterisk indicates a statistically significant difference obtained with an unpaired t test (p < 0.05).

The distributions of best-level values in AI are strongly skewed toward high sound intensities in control and FR-trained rats and are not different from one another [Kolmogorov–Smirnov (KS) test; p = 0.59], whereas the best-level distribution in LR-trained rats was clearly bimodal with a second peak centered within the trained intensity range (KS test; LR vs control, p < 1 × 10⁻⁶) (Fig. 4C). Similarly, best-level distributions in SRAF were similar between control and FR-trained rats (KS test; p = 0.26) but were significantly shifted toward lower sound intensities in LR-trained rats (KS test; LR vs control, p < 1 × 10⁻⁶) (Fig. 4D). Difference functions were calculated for LR and FR-trained rats relative to controls. The slopes of the linear regression lines applied to the LR–control function (AI, −1.5; SRAF, −1.07) were substantially more negative than the regression line slopes in the FR–control function (AI, −0.2; SRAF, −0.16), indicating that LR, but not FR, training decreased the percentage of sites tuned to 60–80 dB SPL and increased the percentage of sites tuned to 20–40 dB SPL (Fig. 4E). Accordingly, the relative area of the AI map tuned to the trained intensity range nearly tripled in LR-trained rats compared with control rats (25.6 ± 1.3% vs 8.8 ± 1.8%; t = 7.72; p < 0.0001) (Fig. 4F) but was unchanged in FR-trained rats (9.7 ± 3.3%). There was a similar trend in SRAF, but the difference between LR-trained rats and control was not significant (t = 1.14; p = 0.32).

Best-level measurements were obtained with white-noise bursts rather than pure tones presented at the CF for each recording site because of the extensive amount of time required to delineate the complete maps of AI and/or SRAF (mapping both fields in a single rat typically required >30 h). It is possible, however, to obtain a rough estimate for changes in the cortical representation of tone intensity by analyzing the multiunit responses to the tonal stimuli used to generate the tuning curves. Although the best level was arguably a more sensitive assay for training effects in the intensity domain because it was defined by spike rate (analog) rather than by categorizing a recording site as responsive or not responsive to a specific tone frequency/intensity combination (binary), analysis of cortical recruitment functions allowed us to determine whether plasticity in the intensity domain was differentially expressed between different frequency ranges in LR rats. Cortical recruitment functions are essentially the converse of tuning curve bandwidth measurements; rather than measure the range of frequencies to which the neuron(s) was responsive, we measured the percentage of total map area activated by a pure tone at a specific frequency and intensity. Cortical recruitment functions for each tone frequency were grouped into the same seven ¾-octave-wide categories and compared between LR and control rats in AI and SRAF.

For the majority of tone frequency categories, we observed a group-by-intensity interaction such that low-intensity tones activated a greater area of the map and higher intensity tones activated a smaller area of the map in LR rats compared with controls in both cortical fields (Fig. 5). A significant group-by-intensity interaction term was observed with a mixed-design ANOVA for 1.8, 3.0, 5.0, 14.1, and 23.7 kHz frequency categories in AI (F > 2.4 and p < 0.02 for each comparison) (Fig. 5A,B) and for 1.0, 1.8, 3.0, and 5.0 kHz frequency categories in SRAF (F > 3.5 and p < 0.005 for each comparison) (Fig. 5C,D). This relationship was effectively captured by subtracting the values obtained in control rats from LR rats and plotting the difference function (Fig. 5E,F). This effect was consistent with best-level measurements obtained with white-noise bursts; LR rats exhibited fewer recording sites that were preferentially responsive to high-intensity stimuli and a greater number of sites that were most responsive to low-intensity stimuli (Fig. 4C–E) and extends on this observation by demonstrating that this effect was primarily frequency independent.

Figure 5.

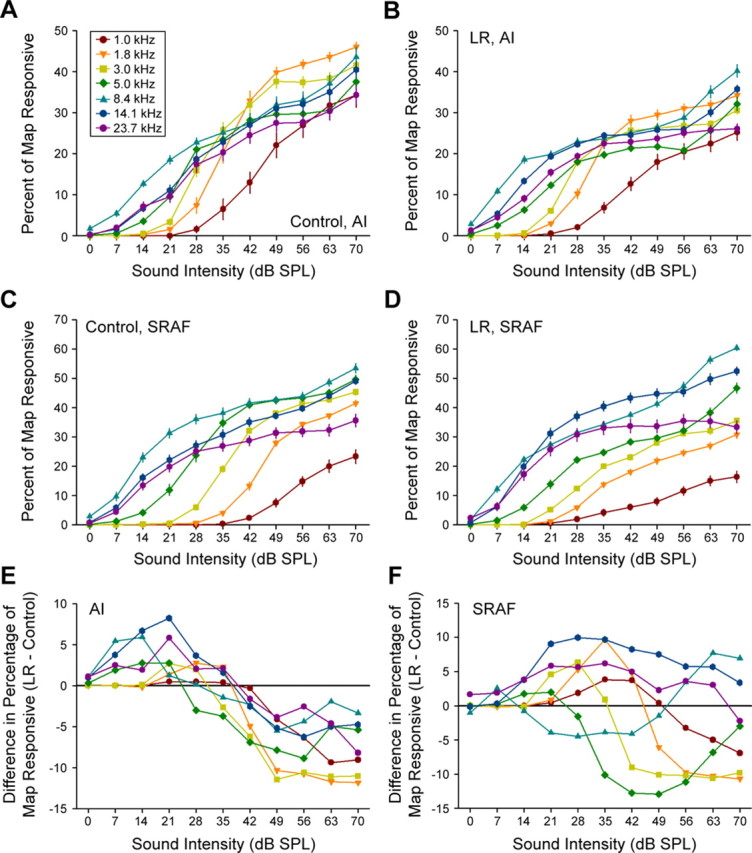
Plasticity in cortical recruitment functions. A–D, Mean ± SE percentage of the cortical map area activated by tones grouped into seven frequency categories in control (A, C) and LR (B, D) rats for AI (A, B) and SRAF (C, D). E, F, Difference functions (LR minus control) for all frequencies in AI (E) and SRAF (F). Zero values (solid black lines) indicate no difference relative to controls.

The relationship between cortical map changes and behavioral threshold

To further underscore the specific relationship between topographic map plasticity and perceptual learning, we also found that the degree of topographic map plasticity within the task-relevant stimulus dimension for an individual rat was correlated with the extent of that rat's improvement in the perceptual learning task (Fig. 6). Perceptual learning was quantified by fitting the decrease in target recognition threshold with a linear regression (as illustrated in Fig. 2C,D). The negativity of the regression slope, essentially a combined indicator of the learning rate and the degree of threshold change, was used as a single metric for task improvement. In FR rats, the slope of the learning curve was significantly correlated with the percentage of AI and SRAF sites with CF values in the trained frequency range (r = −0.81; p < 0.05) (Fig. 6A) but was not correlated with the percentage of sites with best-level values in the trained intensity range (r = 0.45; p = 0.44). Conversely, the slope of the learning curve in LR rats was significantly correlated with the percentage of AI and SRAF sites with best-level values within the trained intensity range (r = −0.89; p < 0.05) (Fig. 6B) but was not correlated with the percentage of sites with CF values in the trained frequency range (r = −0.02; p = 0.96). In the event that maps of both AI and SRAF were obtained in a single rat (n = 5 LR; n = 4 FR), the percentage of sites with values in the trained frequency or intensity range were averaged so that a single value could be calculated for each rat. The learning curve slope values in LR rats were greater than FR rats by ∼1 order of magnitude, but this does not indicate that LR rats showed significantly greater learning overall. This difference is strictly attributable to the fact that decibel and frequency are different units of measurement and comparing the slope values between them is meaningless. As shown in Figure 2, E and F, target recognition threshold decreased to ∼66% of its original value for both groups. It is also worth noting that significant correlations were only observed for either group using the specific combination of learning curve slope relative to the percentage of recording sites with CF or best-level values in the trained frequency or trained intensity range. Significant correlations were not observed using any other combination of behavioral learning index or physiological plasticity measure or when comparisons were restricted to AI or SRAF only.

A straightforward test for the bottom-up versus top-down hypothesis is to determine whether cortical sites co-opted into the expanded representation of the attended target dimension also belonged to the representation of the unattended target dimension (in other words, whether the gray shaded sites in Fig. 3, A and B, are also the blue shaded sites in Fig, 4, A and B). Because the FR and LR tasks used identical sets of tone pips that became increasingly focused around the target frequency and trained intensity, the bottom-up model would predict that cortical sites preferentially responsive to one target stimulus would be plastically modified to be preferentially responsive to the other. The top-down model, in contrast, would predict that individual sites within the map could become incorporated into the attended target stimulus representation without being incorporated into the unattended target stimulus representation. Our data strongly support a top-down model. Rats trained in the FR task exhibited approximately twice the number of AI and SRAF sites tuned to the trained frequency range compared with controls. Of these sites, however, only 1% was also tuned to the trained intensity range. Similarly, rats trained in the LR task had more than twice the number of AI and SRAF sites tuned to the trained intensity range compared with controls, but only 2% of these sites were also tuned to the trained frequency range. Receptive fields tuned to both target dimensions were equally rare in control rats, amounting to <1%.

Effects of training on receptive field bandwidth

We also analyzed receptive field tuning specificity as a neural correlate of perceptual learning and determined that sharpening of the receptive fields for sound intensity and sound frequency were related to the demands of the LR, but not FR, task. Intensity receptive fields were determined at each recording site by measuring the firing rate evoked by the presentation of a white-noise burst played across a range of sound levels spanning 0–80 dB SPL. These functions, commonly called RLFs, could be classified as monotonically increasing (Fig. 7A, left), saturating (Fig. 7A, middle), or nonmonotonic (Fig. 7A, right). The shapes of the RLF corresponding to each response type are a first approximation of the filter function of that site, or receptive field, for sound intensity (Fig. 7B). RLFs recorded in AI of control and FR-trained rats were most commonly monotonically increasing (type A) or saturating high-pass (type B) filters with only 10–15% exhibiting nonmonotonic (type C) RLFs. There was a more equal distribution of each response type in SRAF of FR and control rats (Fig. 7C). In contrast, approximately one-half of the RLFs recorded from rats trained in the LR task were nonmonotonic (47 and 56% for AI and SRAF, respectively) (Fig. 7C). Receptive field selectivity for sound intensity was quantified by measuring the slopes of the rising and falling phases of the RLFs. For both AI and SRAF, the initial increase in firing rate between the threshold and transition point (RLF slope between the arrow and diamond in Fig. 7B) occurred more rapidly in LR-trained rats compared with controls (AI: t = 2.03, p < 0.05; SRAF: t = 2.36, p < 0.05) but was unchanged between FR-trained rats and controls (Fig. 7D). The percentage of sites that decreased their firing rate across higher sound intensities (RLF slope between the diamond and square in Fig. 7B) was significantly greater in LR-trained rats compared with controls (KS tests; p < 1 × 10⁻⁶ for AI and SRAF), but the distributions were unchanged between FR-trained rats and controls (KS tests; p = 0.95 and p = 0.32 for AI and SRAF, respectively) (Fig. 7E). Collectively, the rising and falling slopes of the RLFs were significantly steeper in LR rats compared with FR rats and controls, demonstrating that in addition to becoming preferentially responsive to the trained intensity range, receptive fields in LR rats became more narrowly tuned to a restricted range of sound intensities.

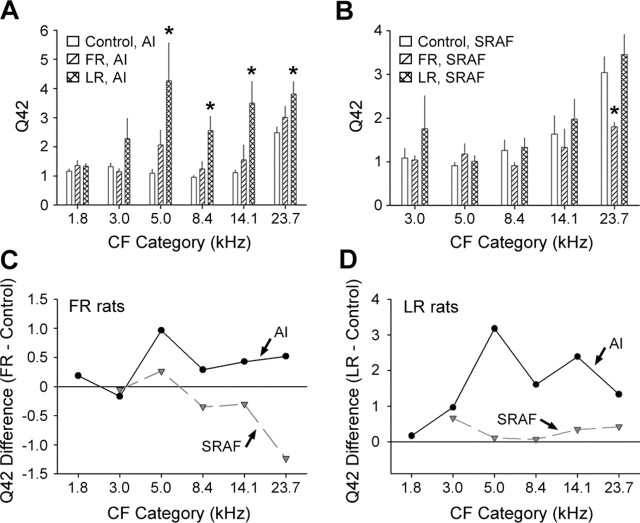
Tuning curve bandwidth, measured as Q-factor, was used to assay breadth of tuning in the frequency domain. We did not find any significant differences in tuning curve bandwidth measured 14 dB SPL above threshold in FR versus control rats (t = 1.54; p = 0.13) or LR versus control rats (t = 1.28; p = 0.2). We did, however, observe that tuning curves were significantly narrower 42 dB SPL above threshold in LR versus control rats (Q42 = 2.69 ± 0.17 vs 1.69 ± 0.1 for LR and control, respectively; t = 5.0; p < 5 × 10⁻⁶) but not between FR and control rats (Q42 = 1.52 ± 0.09 for FR rats; t = 1.28; p = 0.2). Q42 was then measured as a function of cortical field and CF category to better determine where these effects were most strongly expressed (Fig. 8). We found that tuning curves were significantly narrower for CF categories 4–7 in AI (t > 2.43 and p < 0.025 for all comparisons) but were not significantly different in SRAF for any CF category (Fig. 8A,D). An increase in Q42 value in LR rats could be a predictable consequence of the aforementioned observation that unit discharge rate became increasingly nonmonotonic to stimuli of increasing intensity. To affirm that the narrowing of tuning curve bandwidth in LR rats is essentially an epiphenomena of plasticity in the intensity domain, we made independent comparisons of Q42 values in AI of control rats to Q42 values from nonmonotonic recording sites in AI of LR rats (type C) and to the monotonic recording sites in AI of LR rats (types A and B). We found that Q42 values were significantly higher in CF categories 5–7 when the sample of AI recording sites in LR rats was restricted to nonmonotonic responses (t > 2.5 and p < 0.025 for all comparisons). Q42 values in the trained frequency range were also greater in LR rats compared with controls, but this difference was not statistically significant after the Bonferroni correction (t = 2.7; p = 0.04). Importantly, we did not observe any significant differences in Q42 for CF category 4, 5, 6, or 7 when the comparison was made with AI recording sites with monotonic RLFs (t < 1.8 and p > 0.08 for all comparisons).

Figure 8.

Task-specific changes in tuning curve bandwidth. A, B, Q-factor (mean ± SE) measured 42 dB above threshold for recording sites in control (open bars), FR (diagonal hatched bars), and LR (crosshatched bars) rats for AI (A) and SRAF (B). Higher Q42 values represent narrower tuning curve bandwidths. The asterisks indicate statistically significant differences compared with control values (p < 0.025). C, D, The same data are represented as difference functions (trained rat values minus control values) to highlight changes between FR versus control (C) rats and LR versus control (D) rats in AI (solid black lines) and SRAF (dashed gray lines). Zero values (solid black lines in C and D) indicate no difference relative to controls. Tone frequency categories are ¾-octave-wide bins centered on the frequency value shown.

Comparing Q42 values in FR rats with controls revealed a trend for narrower tuning within the trained frequency range in AI (Q42 = 2.06 ± 0.52 vs 1.09 ± 0.13 for FR and control, respectively) (Fig. 8A,C), but this difference was not close to reaching statistical significance after the Bonferroni adjustment for multiple comparisons (t = 1.8; p = 0.08). The only difference in Q42 observed between FR rats and controls was a significant increase in tuning curve bandwidth among neurons with the highest-frequency CFs in SRAF (t = 3.17; p < 0.005) (Fig. 8B,C). It should be noted that Q42 could not be calculated for any recording site with a minimum response threshold >28 dB SPL because of the fact that tone pips were presented at a maximum of 70 dB SPL. This excluded all recording sites with CF values falling within category 1 in AI and all category 1 and 2 recording sites in SRAF, amounting to 11% of recording sites overall.

Comparison of three descriptive models for cortical map plasticity

In the present study, the terms “bottom-up” and “top-down” refer to two ends of a theoretical continuum that describes the relative weight of environmental sensory signals versus internal cognitive signals for driving adult cortical map changes. The extreme position of the bottom-up model holds that adult cortical plasticity is exclusively determined by the sensory stimulus statistics; internal factors such as arousal and attention have no bearing on plastic changes. Numerous studies have disproved this hypothesis by demonstrating that adult animals passively exposed to auditory stimuli that have no behavioral significance do not exhibit enduring auditory receptive field plasticity (Recanzone et al., 1993; Bao et al., 2004; Polley et al., 2004; Rutkowski and Weinberger, 2005). Conversely, altering the levels of internal signals alone via electrical stimulation of neuromodulatory nuclei without temporally paired auditory stimuli does not induce any measurable receptive field plasticity (Bakin and Weinberger, 1996). Plasticity in adult cortical maps therefore must arise from an interaction between internal cognitive variables and external sensory signals.

We defined three hypothetical models to describe how sensory inputs and internal signals could have interacted to shape the specific features of cortical map reorganization observed in the present study. Figure 9 presents difference functions for CF (Fig. 9A) and best-level distributions in LR- and FR-trained rats relative to controls for each of the three models and for the actual data. The maximum change values indicate CF or best-level ranges that would be over-represented relative to controls, the minimum values indicate CF or best-level values that would be under-represented relative to controls, and a value of zero indicates no difference relative to controls. The stimulus statistics model holds that changes in CF and best-level distributions should change to reflect the sensory stimulus statistics encountered throughout a period of elevated arousal or attention. According to the stimulus statistics model (Fig. 9A,B, top row), CF and best-level distributions should mirror the statistical distribution of tone frequencies and intensities experienced throughout the post-asymptotic behavioral period. The reward-based model predicts that CF and best-level distributions will shift to preferentially represent the intensity and frequency of tones that precede rewarded trials, regardless of which property is relevant to the task demands. We calculated the relative probability that each tone frequency and intensity was presented during a rewarded trial throughout the post-asymptotic training sessions for each rat and estimated the cortical map changes that would preferentially represent those stimuli (Fig. 9A,B, second row). The task-relevant model also states that cortical map changes will be specific to the stimuli encountered in rewarded trials but adds the stipulation that these changes will be expressed in the task-relevant stimulus dimension only (Fig. 9A,B, third row).

Figure 9.

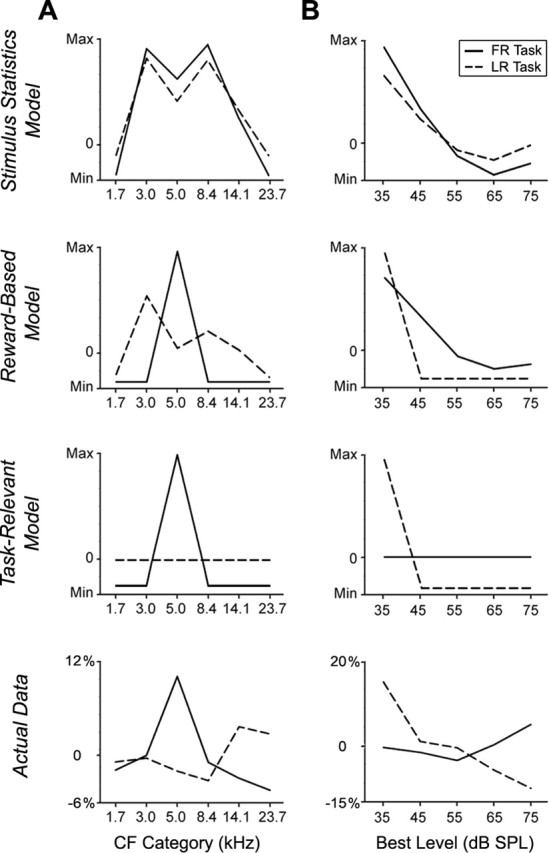
Cortical map reorganization best explained by a model limited to task-relevant stimulus features. Line plots depict differences in the CF distributions (A) and best-level distributions (B) in FR-trained rats (solid lines) and LR-trained rats (dashed lines) relative to controls (value = trained − control). The first three rows present predicted changes in CF and best-level distributions based on overall stimulus statistics encountered in the task (top row), the stimulus statistics that precede rewarded trials only (second row), and stimulus statistics limited to the attended stimulus dimension (third row). The predicted changes for the FR and LR groups are compared with the actual changes in CF and best-level distributions in the bottom row. The CF and best-level categories are identical to those used in Figure 1. The actual data shown in the bottom reflect mean values pooled from AI and SRAF (shown individually in Figs. 3c–e, 4c–e). Max, Maximum; Min, minimum.

The actual data for CF and best-level distributions were pooled for all recording sites in AI and SRAF and compared with the predictions of each of the three models (Fig. 9A,B, bottom row). As described in Figures 3 and 4, rats trained in the FR task exhibited a specific over-representation of CF values near 5 kHz but no consistent change in best-level values relative to controls. Conversely, rats trained in the LR task exhibited an over-representation of best-level values near 35 dB SPL but no consistent change in CF values relative to controls. The stimulus statistics model failed to predict this double dissociation and incorrectly predicted that CF values flanking the trained frequency range would be most over-represented relative to controls. The reward-based model correctly predicted the plasticity observed in the attended stimulus dimension but incorrectly predicted that the covariance introduced in the irrelevant stimulus domain (i.e., the increased percentage of soft tones for FR rats and the increased percentage of mid-frequency tones for LR rats) would also affect CF and best-level distributions (Fig. 9A,B, second row). Of the three models, the task-relevant model most closely predicted the observed physiological plasticity. It correctly predicted that rats trained in the FR task will have an over-representation of the CF values near 5 kHz and LR rats will have an over-representation of best level values close to 35 dB SPL. Although the physiological data in the task-irrelevant domain (Fig. 9A, third row, dashed line, 9B, third row, solid line) were not as flat as the task-relevant model predicted, the actual values were either at zero (and therefore equivalent to control) or close to zero, and of the three models, the task-relevant model clearly came closest to predicting the actual data in the unattended stimulus domain.

Discussion

Rats were trained to selectively attend to either the frequency or intensity of auditory stimuli that varied in both dimensions. Rats in both groups progressively improved in their ability to correctly recognize the target frequency or intensity amid sets of increasingly similar distracter stimuli. Electrophysiological recordings performed at the conclusion of training revealed plasticity in AI and SRAF expressed in the task-relevant stimulus dimension only. Rats trained in the FR task exhibited a significantly greater proportion of recording sites with CF values in the trained frequency range and an expansion of the relative AI map area tuned to the trained frequency range compared with LR rats and controls. Rats trained in the LR task had an increased proportion of recording sites in AI and SRAF with best-level values in the trained intensity range and an expansion of the relative AI map area preferentially tuned to the trained intensity range compared with FR rats and controls. LR training also increased the steepness of the rising and falling RLF slopes, creating a substantially increased percentage of recording sites that were tuned to a restricted range of sound intensities compared with the monotonic high-pass RLFs observed most commonly in FR rats and controls. Significantly enhanced responses for sound intensities below the trained intensity range (i.e., 7–28 dB SPL) were also observed in cortical recruitment function and best-level measurements in LR-trained rats compared with FR-trained and control rats. The 35 dB SPL target intensity was measured with a calibrated microphone positioned beneath the speaker at a distance approximating the rat's typical head position. As such, 35 dB SPL represents the idealized sound level that would reach the ear for the target intensity, but depending on the exact distance and position of the rat's ear relative to the speaker, the actual sound level impinging on the ear could be slightly less, but not likely more, than 35 dB SPL. We speculate that enhanced responses to lower sound intensity stimuli therefore reflects the fact that the actual sound level reaching the ear for rewarded trials could be skewed toward lower intensities.

The complete functional architecture of a single auditory cortical field arises from a “lattice” of independent maps that code for sound frequency, bandwidth, intensity, and bianaural interaction type (for review, see Schreiner, 1998). Receptive field reorganization in the auditory cortex resulting from associative learning protocols is similarly multifaceted; animals conditioned to make discriminations in pitch-modulated stimuli demonstrate receptive field plasticity in the spectral domain (Recanzone et al., 1993; Blake et al., 2002; Fritz et al., 2003; Rutkowski and Weinberger, 2005; Witte and Kipke, 2005), animals trained to discriminate changes in envelope modulation rate exhibit plasticity in the temporal domain (Beitel et al., 2003; Bao et al., 2004), and animals trained to discriminate changes in intensity-modulated stimuli express plasticity in the intensity domain (Polley et al., 2004). The present results extend on these studies by demonstrating that the domain of receptive field reorganization (spectral, temporal, or intensive) is not necessarily reflective of the type of stimuli that animals are presented with in the learning task. Rather, plasticity of maps and constituent receptive fields may represent the functional state that allowed the animal to best solve the challenges of the sensory discrimination task regardless of the specific properties of the bottom-up sensory inputs. The results of this study also demonstrate that maps embedded within the same neural circuits can reorganize independently without disturbing one another. In this framework, top-down control mechanisms might enable the cortical network to operate selectively on one component of a complex sensory signal in which basic sensory attributes (e.g., sound location and sound intensity) covary.

Our experiments required the use of lengthy fine-grained microelectode mapping procedures. Plasticity in the resultant maps therefore reflects accumulated physiological changes induced by training that can be assayed under anesthesia. Although our study speaks most strongly to more enduring modifications of cortical networks that result from extensive perceptual training, it would be valuable to understand whether auditory cortical plasticity that results from rapid conditioning protocols such as fear conditioning or neuromodulatory pairing might also be influenced by top-down mechanisms (for review, see Kilgard et al., 2002; Suga and Ma, 2003; Weinberger, 2004). Ultimately, procedures that characterize plasticity using real-time awake recording methods might reveal top-down mechanisms that allow the cortex to switch between different flexible states of information processing according to rapidly changing environmental demands (Edeline et al., 1993; Ohl and Scheich, 1997; Ohl et al., 2001; Fritz et al., 2003, 2005).

Our interest in mapping SRAF, a secondary and putatively higher auditory field, to supplement recordings from AI was inspired by a set of perceptual learning studies in the visual (Watanabe et al., 2002) and auditory (Petkov et al., 2004) systems that describe task-related modulations restricted to higher cortical fields. Based on these studies, we reasoned that task-dependent plasticity might be expressed most strongly in SRAF, whereas plasticity in AI, if observed at all, might predominantly reflect bottom-up influences. We were surprised to find that plasticity in AI was equally pronounced and, for some response properties, even more pronounced than that seen in SRAF. Expansion of the relative map area dedicated to the trained frequency range (Fig. 3F) and trained intensity range (Fig. 4F) was observed in AI but not in SRAF. Similarly, differences in tuning curve bandwidth changes and cortical recruitment functions were observed in AI of LR-trained rats but not in SRAF. In summary, task-dependent reorganization was observed in both fields, but plasticity in AI was equivalent to or more pronounced than what was observed in SRAF. These observations suggest that task-dependent plasticity may be expressed at lower levels of the cortical hierarchy with more extensive periods of perceptual training and/or the hierarchical organization of auditory cortical fields in the rat is far less elaborated than the hierarchical organization in the human cortex and therefore may be less susceptible to differential expression of task-dependent modulations.

Seitz and Watanabe (2005) have recently proposed that early cortical fields may contribute to perceptual learning by improving processing of sensory stimuli that bear a consistent temporal relationship to reinforcement signals. According to this view, the cortical network is agnostic to whether a particular stimulus feature is relevant to the task; receptive fields for all stimulus features that are consistently paired with reinforcement (i.e., inputs from neuromodulatory nuclei) will undergo reorganization. Our experiments attempted to address this issue by introducing covariance between the task-relevant and task-irrelevant sensory features. Despite the fact that the stimuli paired with reward in both the FR and LR tasks became increasingly focused on soft mid-frequency tones, plasticity was only observed in the task-relevant stimulus domain. This observation suggests that models for cortical plasticity based solely on temporally paired inputs from neuromodulatory nuclei and sensory inputs might be incomplete and that top-down inputs from sources such as the prefrontal cortex, parietal cortex, or higher auditory areas might also play an important role.

This conclusion must be tempered, however, by two caveats. First, the stimulus properties in the task-irrelevant domain did not exactly covary with the stimulus properties in the task-relevant domain. The frequencies or intensities associated with reward in the task-irrelevant domain were substantially restricted by the time behavior reached asymptote but were not constant. Second, the covariance became progressively more pronounced as performance improved. The predicted plasticity for each model was derived from stimuli presented once the rats had reached an asymptotic level of task performance. We reasoned that the stimuli presented during this period of training would have the greatest impact on the physiological plasticity recorded at the conclusion of training. It is possible, however, that the plasticity documented at the end of training might also have been shaped by earlier phases of training when the distributions of frequencies and intensities used for the training stimuli were still broad (Fig. 1C,D, dashed lines). It will be worthwhile, in future studies, to identify the relative contribution of early versus late stages of training.

Nevertheless, these data propose a testable alternative to the model put forth by Seitz and Watanabe (2005). Rather than explain perceptual enhancement and/or physiological plasticity solely as a temporal interaction between sensory and reinforcement signals, we propose that plasticity is restricted to the task-relevant domain only if stimuli in the task-irrelevant domain interfere with the ability to solve the task. In our study and several others that find physiological plasticity restricted to the task-relevant stimulus dimension (Schoups et al., 2001; Li et al., 2004), the task-irrelevant stimulus inputs must be actively suppressed to best solve the task, whereas the task-irrelevant stimuli do not necessarily compromise the subject's ability to solve the task in the studies by Petkov et al. (2004) or Watanabe et al. (2001, 2002). The same is true of a recent study published by Rutkowski and Weinberger (2005) that describes an expansion in the relative area of the AI tonotopic map preferentially responsive to the target frequency but also to low-frequency sounds emitted by the reward delivery mechanism. In this case, as with the studies by Watanabe et al. (2001, 2002), the sounds emitted by the reward delivery system were temporally paired with reward and irrelevant to the task demands but did not interfere with the rat's ability to recognize the target stimulus. In the event that non-target stimuli are both irrelevant and competitive, top-down inputs may limit receptive field reorganization only to the stimuli that contribute the most information about the occurrence of upcoming unconditioned stimuli. A reorganizational scheme that increases the neural resources (e.g., map area or receptive field bandwidth) allocated to the conditioned stimuli that most effectively predict unconditioned stimuli and limits neural resources that represent redundant or irrelevant stimuli would be optimized from the standpoint of information processing (Gallistel, 2003).

Although some questions remain concerning the role of attention and task-relevant inputs, it is abundantly clear from the present data, psychophysical data (Seitz and Watanabe, 2003), and previous studies investigating the neural correlates of conditioned responses (Diamond and Weinberger, 1986; Edeline et al., 1993; Recanzone et al., 1993; Rutkowski and Weinberger, 2005) that the neural plasticity accompanying perceptual learning is specific to sensory inputs that reliably predict behaviorally reinforcing events. Engaging animals in challenging behavioral tasks is known to increase levels of dopamine, acetylcholine, and norepinephrine in the cerebral cortex (Usher et al., 1999; Himmelheber et al., 2000; Schultz, 2000; Dalley et al., 2001). It is important to note that the increased presence of these neuromodulators does not temporarily reinstate a critical period-like process in which the functional organization of the adult sensory cortex can once again be shaped by the overall sensory input statistics. Plasticity in adult cortical networks that accompanies perceptual learning is likely to be shaped by an interaction between sensory inputs, neuromodulator release, and top-down influences from higher sensory areas or association cortices.