Role of the Neurogranin Concentrated in Spines in the Induction of Long-Term Potentiation

Abstract

Synaptic plasticity in CA1 hippocampal neurons depends on Ca²⁺ elevation and the resulting activation of calmodulin-dependent enzymes. Induction of long-term depression (LTD) depends on calcineurin, whereas long-term potentiation (LTP) depends on Ca²⁺/calmodulin-dependent protein kinase II (CaMKII). The concentration of calmodulin in neurons is considerably less than the total concentration of the apocalmodulin-binding proteins neurogranin and GAP-43, resulting in a low level of free calmodulin in the resting state. Neurogranin is highly concentrated in dendritic spines. To elucidate the role of neurogranin in synaptic plasticity, we constructed a computational model with emphasis on the interaction of calmodulin with neurogranin, calcineurin, and CaMKII. The model shows how the Ca²⁺ transients that occur during LTD or LTP induction affect calmodulin and how the resulting activation of calcineurin and CaMKII affects AMPA receptor-mediated transmission. In the model, knockout of neurogranin strongly diminishes the LTP induced by a single 100 Hz, 1 s tetanus and slightly enhances LTD, in accord with experimental data. Our simulations show that exchange of calmodulin between a spine and its parent dendrite is limited. Therefore, inducing LTP with a short tetanus requires calmodulin stored in spines in the form of rapidly dissociating calmodulin–neurogranin complexes.

Introduction

Synapses undergo bidirectional modifications that are thought to underlie learning and memory. Long-term potentiation (LTP) is typically induced by 100 Hz, 1 s tetanic stimulation. In contrast, many minutes of 1 Hz stimulation are generally used to induce long-term depression (LTD). It has been established that elevation of postsynaptic Ca²⁺ concentration within specific ranges is necessary for induction of LTP and LTD. Two Ca²⁺/calmodulin (CaM)-dependent enzymes play especially prominent roles in these processes at the CA1 hippocampal synapses that have served as a model system for the study of bidirectional plasticity. Ca²⁺/CaM-dependent protein kinase II (CaMKII) is required for induction of LTP, whereas the Ca²⁺/CaM-dependent protein phosphatase calcineurin (CaN) is required for LTD (Malenka and Bear, 2004).

Recently, it has become clear that the total concentration of CaM in cells is much less than the total concentration of its targets and only a small fraction of CaM is free (Persechini and Stemmer, 2002; Tran et al., 2003). Under resting conditions, the free apocalmodulin (apoCaM) concentration is low, because neurons contain proteins that bind apoCaM. The main postsynaptic binding protein is neurogranin (Ng; also termed RC3), whereas the major presynaptic binding protein is GAP-43 (also termed neuromodulin or P-57). Ng (Baudier et al., 1991) is a neuron-specific protein that is enriched in the cortex and hippocampus (Represa et al., 1990; Gerendasy and Sutcliffe, 1997). It has been shown that Ng appears at the same time as CaMKII-dependent LTP, during the third week postnatally (Represa et al., 1990; Yasuda et al., 2003). Ng has a much higher than average concentration in dendritic spines (Watson et al., 1992; NeunerJehle et al., 1996).

Several studies have been conducted to elucidate the role of Ng in synaptic plasticity. Injection of antibodies to Ng into hippocampal CA1 pyramidal cells prevented induction of LTP in these neurons (Fedorov et al., 1995). In agreement with this finding, knockout of Ng resulted in a large decrease in the LTP induced by a single 100 Hz, 1 s tetanus, whereas LTD was slightly enhanced (Huang et al., 2004). Quite different effects were reported by Krucker et al. (2002), probably because in the latter case, the Ng gene was replaced with a construct that retained an N-terminal peptide of Ng.

Two points of view exist regarding the role of Ng and GAP-43 in neurons. According to one view, these species act as cache of CaM that enhance local time-dependent activation of Ca²⁺/CaM-dependent enzymes in response to elevations of [Ca²⁺] (Cimler et al., 1985; Gerendasy and Sutcliffe, 1997; Prichard et al., 1999). The other view is that they homeostatically constrain Ca²⁺/CaM-mediated signaling (Slemmon and Martzen, 1994; Gerendasy, 1999; Krucker et al., 2002).

Here, we present a computational study of the dependence of NMDA receptor-dependent plasticity on the Ng control of CaM availability. Our results account for the observed effects of Ng knockout on LTP and LTD and provide an explanation of the need for a high Ng concentration in spines.

Materials and Methods

Basic structure of the model.

Several mathematical models of bidirectional plasticity have been published (Castellani et al., 2001; Shouval et al., 2002; d’Alcantara et al., 2003). However, these models do not attempt to account for the change in the number of postsynaptic AMPA receptors (AMPARs) as a mechanism of synaptic plasticity. They also use stationary elevations of [Ca²⁺] during induction of synaptic plasticity instead of pulsatile Ca²⁺ patterns, which result from synaptic stimulation. Other models have dealt with the dynamics of the CaMKII/protein phosphatase 1 (PP1) system during LTP (Lisman and Goldring, 1988; Coomber, 1998; Bhalla and Iyengar, 1999; Holmes, 2000; Zhabotinsky, 2000; Kubota and Bower, 2001; Lisman and Zhabotinsky, 2001). Recently, Hayer and Bhalla (2005) have published a set of models to study a role of bistability in synaptic plasticity. They took into account trafficking of AMPARs and CaMKII and used pulsatile Ca²⁺ patterns to induce transitions between the stable states. Results of these models have been taken into account during development of our model. In the model, we consider the change in number of postsynaptic AMPARs as a major mechanism of synaptic plasticity and use Ca²⁺ pulses (Sabatini et al., 2002) as the input signals in our model.

CaM was explicitly included in one previous model of bidirectional plasticity (d’Alcantara et al., 2003) and in models of the system CaMKII/PP1 (Coomber, 1998; Holmes, 2000; Kubota and Bower, 2001). In all of these models, either the total concentration of CaM was approximately one order of magnitude higher than the concentrations of CaMKII and CaN or the concentration of free CaM was kept constant. However, the total concentration of CaM is considerably lower than the sum of concentrations of Ng, GAP-43, CaMKII, and CaN (see below), and the concentration of free CaM may thus vary during calcium transients, a feature that is reflected in our model.

It is widely accepted that the amplitude of the EPSP depends on the synaptic content of AMPARs, which increases after activation of CaMKII and decreases with activation of PP1 (Malenka and Bear, 2004). Evidence shows that the interplay of CaMKII and the CaN-controlled PP1 is responsible for the induction of bidirectional plasticity at CA3–CA1 synapses (Mulkey et al., 1994; Malenka and Nicoll, 1999). These experimental findings form the basis for our simplified model of the postsynaptic component of LTP and LTD.

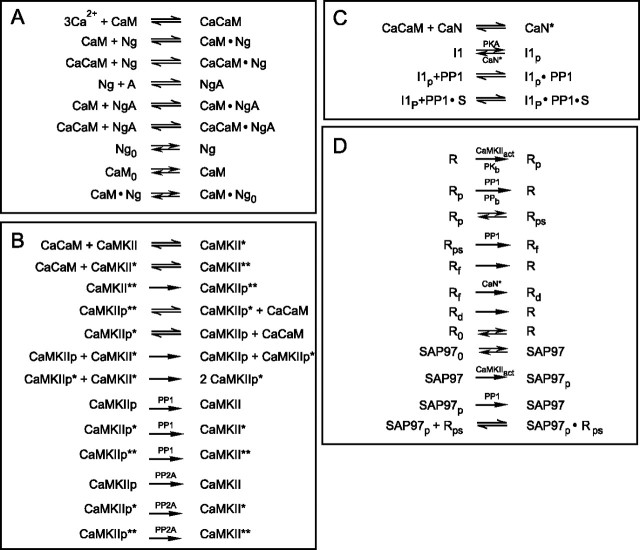
Our model consists of four blocks (Fig. 1). Block A (Fig. 1A) deals with Ca²⁺ binding to CaM and the interactions of Ng and CaM. We account for exchange of Ng, CaM, and the NgCaM complex between the spine and the parent dendrite and accumulation of Ng in spines as a result of its binding to an anchor localized there. Block B (Fig. 1B) includes the Ca/CaM activation of CaMKII, autophosphorylation of CaMKII, and its dephosphorylation by PP1 and protein phosphatase 2A (PP2A). Block C (Fig. 1C) presents a model of the CaN/PP1 cascade. Block D (Fig. 1D) deals with the phosphorylation-controlled trafficking and retention of the postsynaptic AMPARs.

Figure 1.

Block scheme of the model. A, Interactions of Ng, apoCaM, and CaCaM; exchange of Ng, CaM, and the CaM·Ng complex between the spine and parent dendrite; and accumulation of Ng in the spine; A is the Ng anchor. B, Activation of CaMKII by CaCaM, autophosphorylation of CaMKII, and dephosphorylation of CaMKIIP by PP1 and PP2A. C, Activation of CaN and control of PP1 by PKA and CaN via I1. D, Phosphorylation of the AMPAR·Sg complex (R) and SAP97 (SAP) by CaMKII and their dephosphorylation by PP1. Mass-action law reactions are shown by simple arrows, and enzymatic reactions are indicated by enzyme abbreviations above or below the arrows.

Interactions and exchange of CaM and Ng.

We use the Hill approximation to model Ca²⁺ binding to CaM. The Hill approximation is a convenient tool that is frequently used for phenomenological description of experimental data. It approximates cooperative stepwise binding of multiple identical ligands with a one-step simultaneous binding of several ligands. Therefore, it replaces multiple complexes of a protein with ligands with a single “average” complex. We use the Hill approximation with n = 3 and [Ca²⁺]₅₀ = 10.0 μΜ (Persechini et al., 1996), because it was shown that Ca²⁺ activation of both CaN and CaMKII at a constant concentration of CaM is well approximated in this way (Stemmer and Klee, 1994; Bradshaw et al., 2003). In what follows, we designate the (Ca²⁺)₃CaM complex as CaCaM.

The total concentration of CaM in neurons is ∼10 μm (Egrie et al., 1977; Kakiuchi et al., 1982; Rodriguez-Medina et al., 1998). At low [Ca²⁺], most of the CaM is bound to Ng and GAP-43. According to Huang et al. (2004) the concentration of Ng in the hippocampus is 1.9 μg/mg protein. Taking brain protein content as 8% yields an average concentration of Ng in neurons of ∼20 μm. Punctate staining of Ng is indicative of a much higher than average concentration in dendritic spines (Watson et al., 1992; NeunerJehle et al., 1996). GAP-43 is ∼0.5% of total protein in the brain (Cimler et al., 1985), which gives an average concentration of ∼18 μm. It is enriched in the axonal growth cones (Skene et al., 1986) and arbors (Aigner et al., 1995). The dissociation constant of the CaM·Ng complex is ∼5 μm according to Huang et al. (2000) and 1 μm according to preliminary data of T. R. Gaertner and M. N. Waxham (personal communication). The K_d for CaM–GAP-43 is ∼3 μm according to Alexander et al. (1987). There is indirect evidence that Ng preferentially binds apoCaM (Gerendasy et al., 1994; Huang et al., 2000). On the other hand, there is no difference in the affinity of GAP-43 toward apoCaM and Ca²⁺/CaM (Alexander et al., 1987). In our simulations, affinities of CaM and CaCaM to Ng are taken to be equal if not stated otherwise.

We have set the total concentrations of both Ng and GAP-43 in the neuron to 20 μm and the total concentration of CaM to 10 μm. We have studied the effect of varying the dissociation constants of the CaM·Ng and CaM·GAP-43 complexes from 1.0–5.0 μm, always keeping them equal. We infer from the fact that Ng is highly concentrated in spines (Watson et al., 1992; NeunerJehle et al., 1996) that there are anchors for Ng. In the model, we assume a single anchor A, which binds Ng with a moderate affinity in spines, dendrites, and cell body. A high concentration of A in the spine is responsible for a high level of bound Ng in the form Ng·A complex.

To model formation of CaCaM, we have taken from the full scheme of complex formation, which includes Ca²⁺, CaM, and Ng, only the simplest kinetic pathway that consisted of dissociation of the CaM·Ng complex and binding of Ca²⁺ to CaM. However, the existence of a large pool of CaM·Ng in the spine suggests that direct binding of Ca²⁺ to this complex can be a significant pathway for CaCaM formation at high Ca²⁺ elevations during induction of LTP. To check the importance of this pathway, we included binding of Ca²⁺ to the CaM·Ng complex leading to immediate formation of CaCaM and free Ng in our model. We assigned the largest rate constants permitted by the principle of detailed balance and by the diffusion limit on the reaction rates between proteins to the added reaction. Then we repeated the simulations, the results of which are displayed in Figure 4. The new reaction added only 5% to the maximum concentration of CaCaM obtained with the original model. Activation of CaMKII was essentially unchanged.

Figure 4.

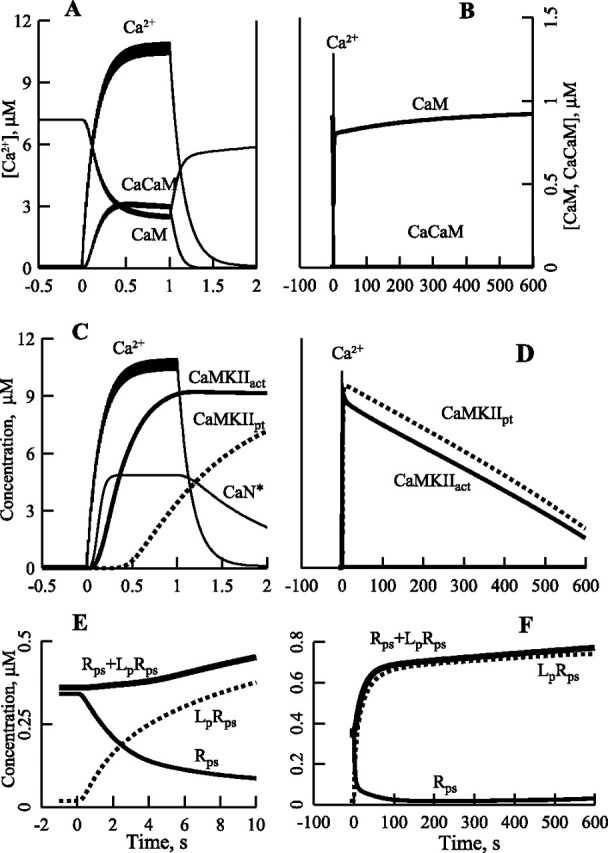
Kinetics of Ca²⁺, calmodulin, (Ca²⁺)₃CaM, and activation of CaN, CaMKII, autophosphorylation of CaMKII, and phosphorylation of the AMPA receptor–stargazin complex during and after 100 Hz, 1 s stimulation. A, B, Kinetics of Ca²⁺, CaM, and CaCaM. C, Kinetics of Ca²⁺, CaN*, total activated CaMKII (CaMKII_act), and total autophosphorylated CaMKII (CaMKII_pt). D, Autophosphorylation of CaMKII is responsible for a prolonged activation of CaMKII. E, F, Kinetics of R_ps, L_pR_ps and R_ps + L_pR_ps, L_p is SAP97_p.

We account for diffusional exchange of CaM, Ng, and the CaM·Ng complex between the spine and the parent dendrite. The total concentrations of CaM, Ng, and GAP-43 and their dissociation constants determine the concentration of free CaM (CaM₀) in dendrites and the cell body. The total concentration of A in the neuron determines the level of free Ng (Ng₀) and consequently the concentration of the free CaM·Ng complex (CaM·Ng₀) in dendrites and the cell body. The model deals with a typical synapse, which belongs to a small population of synapses involved in homosynaptic plasticity events, whereas the parent dendrite is considered to be at basal conditions.

CaCaM activation, autophosphorylation, and dephosphorylation of CaMKII.

We use [CaCaM]₅₀ for CaMKII (50 nm) and for T286-autophosphorylated CaMKII (0.05 nm) as rounded experimental values (Hudmon and Schulman, 2002). To simplify our model, we neglect the holoenzyme structure of CaMKII and use concentrations of CaMKII subunits in various states as variables in the model. We model the first step of autophosphorylation at T286 after the binding of two CaCaM as a monomolecular reaction because this is an intraholoenzyme reaction (Hudmon and Schulman, 2002). To preserve the autocatalytic kinetics of the CaMKII autophosphorylation, we treat autophosphorylation of partially phosphorylated CaMKII as a bimolecular reaction between autophosphorylated (CaMKIIp) and nonphosphorylated, CaCaM-activated (CaMKII*) subunits of CaMKII. We ran parallel simulations with this lumped model of CaMKII autophosphorylation and a model that accounts for the real structure of the CaMKII holoenzyme (Miller et al., 2005). Comparison of results from these two models shows that the lumped model properly simulates the macroscopic kinetics of CaMKII autophosphorylation in the presence of protein phosphatases. We treat the spine as a single compartment and all the CaMKII as a soluble enzyme. Both PP1 and PP2A dephosphorylate soluble CaMKIIp (Strack et al., 1997).

CaCaM activation of CaN and control of PP1 by protein kinase A and CaN via inhibitor-1.

We take [CaCaM]₅₀ for CaN (10 nm) as a rounded experimental value (Stemmer and Klee, 1994). Activity of PP1 is controlled by CaN and protein kinase A (PKA) via inhibitor I (I1), PKA phosphorylates I1, and CaN dephosphorylates it (Mulkey et al., 1994). Phosphorylated I1 (I1P) deactivates PP1 with K_I = 1 nm (Endo et al., 1996).

Phosphorylation-controlled traffic and retention of AMPARs.

To simulate the effects of Ng on bidirectional plasticity (Huang et al., 2004), it is necessary to have a model of NMDA receptor-dependent early LTP and LTD. Because the change in the number of postsynaptic AMPARs is a principal mechanism of synaptic plasticity at CA1 excitatory synapses (Malenka and Bear, 2004), we consider it the only mechanism in our simplified model.

There are three known species that participate in trafficking and retention of AMPARs and are substrates of the CaMKII–CaN/PP1 system. The first is the GluR1 subunit of AMPAR. Esteban et al. (2003) have shown that phosphorylation of S845 in the C-tail of GluR1 by PKA and activity of CaMKII are necessary for delivery of GluR1 to the postsynaptic membrane. Lee et al. (2003) have shown that LTD is abolished and LTP is dramatically reduced in GluR1 double mutant, S831A, S845A mice. In our simplified model, activity of PKA is assumed to be constant.

The second species is stargazin (Sg), a transmembrane protein that binds AMPARs via its extracellular N-domain (Chen et al., 2000). AMPARs are localized to synapses through direct binding of the cytosolic C-tail of Sg to the first two PDZ [postsynaptic density-95 (PSD-95)/Discs large/zona occludens-1] domains of synaptic PSD-95 (Schnell et al., 2002). Phosphorylation of the C-tail of Sg by CaMKII is required for synaptic delivery of AMPARs (Tomita et al., 2005). It was shown that overexpression of PSD-95 mimics and occludes LTP (Stein et al., 2003; Ehrlich and Malinow, 2004). These data strongly suggest that CaMKII-phosphorylated Sg forms stable complexes with both GluR1 and PSD-95.

The third species is synapse-associated protein-97 (SAP97). Because the PDZ ligand of GluR1 is necessary for LTP (Hayashi et al., 2000) and PSD-95 is not known to bind directly to GluR1, one must assume that another PDZ domain containing an anchor protein must participate in LTP. SAP97 is the only such protein known to bind GluR1 directly (Leonard et al., 1998). Besides, it has been shown that binding of glutamate to GluR1 causes its dissociation from Sg (Tomita et al., 2004); therefore, an additional anchor is needed to maintain GluR1 in the postsynaptic position during synaptic activity. It was suggested that the complex of SAP97 with protein 4.1N binds GluR1 and postsynaptic F-actin (Lisman and Zhabotinsky, 2001) creating such an additional anchor. SAP97 concentrates at the PSD of asymmetric synapses (Valtschanoff et al., 2000; Rumbaugh et al., 2003), and its presence increases the number of synaptic AMPARs (Rumbaugh et al., 2003). Overexpression of SAP97 drives GluR1 to synapses, potentiates AMPAR-related EPSCs, and occludes LTP (Nakagawa et al., 2004). Finally, Mauceri et al. (2004) have shown that CaMKII phosphorylation of SAP97 at S39 results in its delivery to synapses.

The exact role of each of the above processes remains unclear, and it is therefore not possible to build a definitive model at this time. Therefore, we have chosen a minimal scheme that we hope captures the flavor of what actually takes place. We emphasize that our goal here is not to verify the events that occur in these expression processes but merely to develop a plausible scheme of the early steps in induction of LTD and LTP that are dependent on CaCaM. On the other hand, we have chosen to make the expression processes quite specific, setting the basis for future work that deals specifically with these reactions.

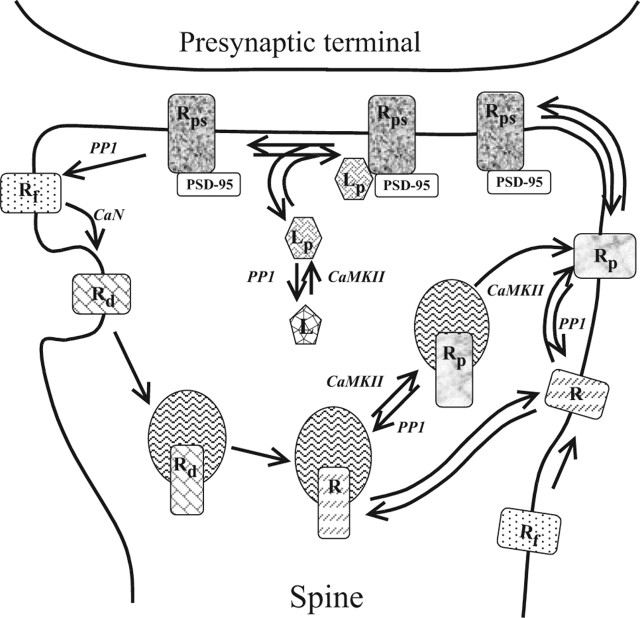
It has been shown that Sg and the GluR1-containing AMPAR form a stable complex (Vandenberghe et al., 2005). We neglect dissociation of this complex and consider it an “effective” AMPAR that undergoes trafficking and participates in transmission. The precise roles of the two serines in the C-tail of GluR1 and multiple phosphorylated sites in the C-tail of Sg are not known. Therefore, we represent them as a single phosphorylated site in this simplified model. Figure 2 presents the major processes involved in our model. The nonphosphorylated form of the complex AMPAR·Sg, designated R in Figures 1D and 2, cycles between the exstrasynaptic membrane and spine endosomes (Mack et al., 2001). Phosphorylation of R by CaMKII results in formation of R_p and its delivery to the extrasynaptic plasma membrane (Park et al., 2004). Then R_p diffuses to the postsynaptic membrane, where it can bind PSD-95 with high affinity. Such synaptic R_p is designated R_ps. Dephosphorylation of R_p or R_ps results in their endocytosis. Endocytosis of the dephosphorylated form of R_ps (designated R_f) results in two forms of internalized AMPARs. Ca²⁺-independent endocytosis results in R, whereas Ca²⁺-dependent endocytosis activated by CaN (Beattie et al., 2000) produces a nonphosphorylatable form, R_d, that slowly converts to R. SAP97, designated L, is also phosphorylated by CaMKII, and the resulting L_p can bind R_ps, forming a complex, L_pR_ps, that is protected from dephosphorylation. The model also includes exchange of R and L between the spine and the parent dendrite. In the model, the amplitude of the EPSP is assumed to be proportional to the concentration of postsynaptic R_i (i.e., to the sum of the concentrations of R_ps and L_pR_ps).

Figure 2.

Traffic and postsynaptic retention of AMPARs dependent on GluR1, Sg, and SAP97. R is the nonphosphorylated form of the AMPAR·Sg complex formed via the GluR1–Sg interaction, R_p is the exstrasynaptic phosphorylated form, R_ps is synaptic R_p, R_f is the immediate product of R_ps dephosphorylation, and R_d is a nonphosphorylable form, which slowly converts to R; L is SAP97, and L_p is phosphorylated L.

Selection of parameters of the model.

Some parameters of the model are well determined; these are the majority of the total concentrations of species and the dissociation and rate constants relevant to the Ca²⁺/CaM-dependent activation of CaN and CaMKII. On the other hand, there are no direct data on the rates of phosphorylation and dephosphorylation of AMPAR, Sg, and SAP97. We initially chose values of the rate constants of these reactions by analogy with the known values for reactions with different substrates. Then we varied these values until we obtained a point in the parametric space that produced reasonable agreement with the experimentally obtained frequency–response curves [Huang et al. (2004), their Fig. 5E]; the deviations of the calculated values from the experimental values were <25% of the latter (see our Fig. 6). In the neighborhood of this point, variation of the rate constants for phosphorylation and dephosphorylation of AMPAR, Sg, and SAP97 up to 50% does not result in significant changes in the plasticity outcomes. In what follows, we did not change these rate constants while varying parameters responsible for the control of free CaM. We did not try to fit the simulations precisely to the experimental data because we used a simplified model. We used rounded values of the experimentally determined concentrations and rate constants.

Figure 6.

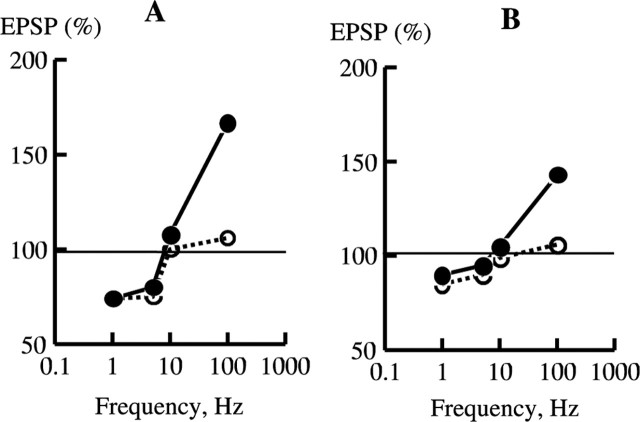
Simulation of frequency–response curves from Huang et al. (2004). A, Frequency–response curves plotted from data taken at 60 min from the curves shown in Figure 5. B, Experimental curves plotted according to data from Huang et al. (2004). WT, •; KO, ○.

The results presented in Figures 3–6 for the wild type (WT) have been obtained with a single set of parameters, which we call the basic set and which are given in the supplemental material (available at www.jneurosci.org). All changes of specific parameters are indicated in the relevant figures, tables, and text.

Figure 3.

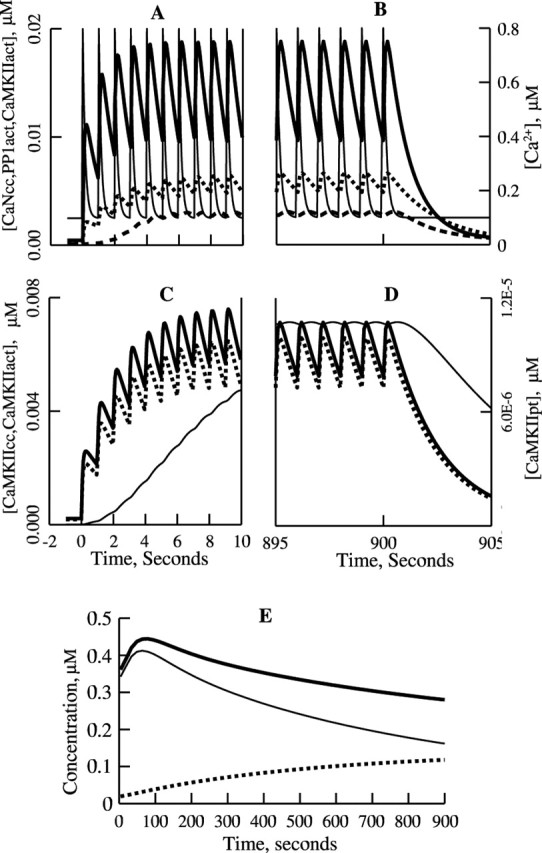
Simulated kinetics of activation of CaN, PP1, and CaMKII, autophosphorylation of CaMKII, and phosphorylation of the AMPAR complex during (A, C) and immediately after (B, D) 1 Hz, 15 min stimulation. A, B, Kinetics of CaN bound to CaCaM (CaN*; —), active PP1 (PP1_act; —▪—), and active CaMKII (CaMKII_act; — —) shown together with the Ca²⁺ pulses (—). C, D, Absence of autophosphorylation of CaMKII; CaMKII bound to CaCaM (CaMKII_cc; —), CaMKII_act (— —), and autophosphorylated CaMKII (CaMKII_pt; —). E, Kinetics of the postsynaptic AMPAR·Sg complexes: R_ps (—), L_pR_ps (— —), and R_ps + L_pR_ps (—).

Figure 5.

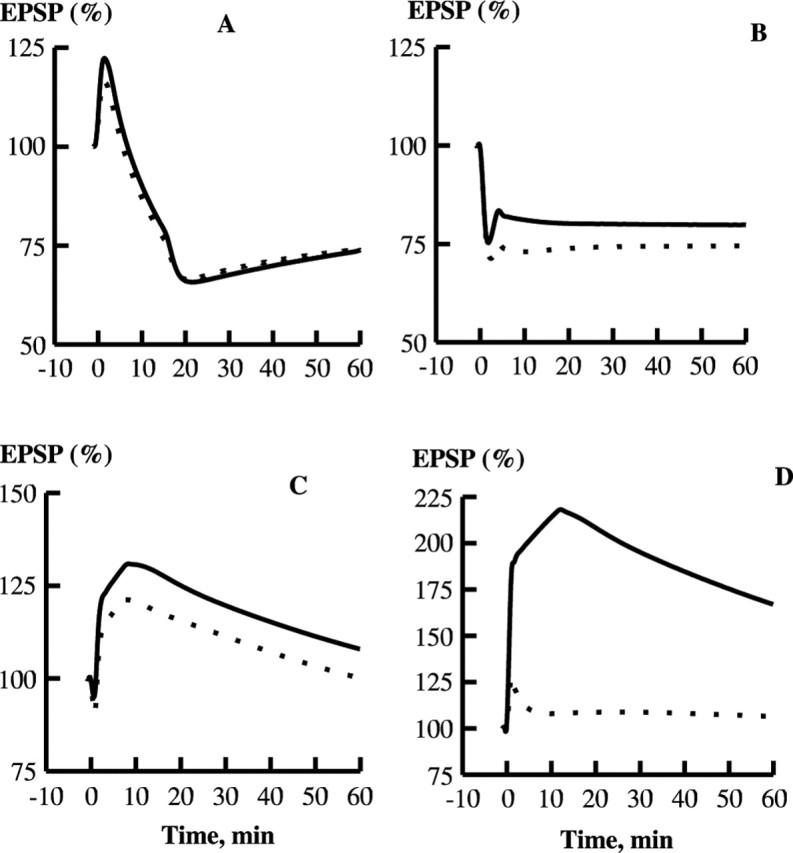
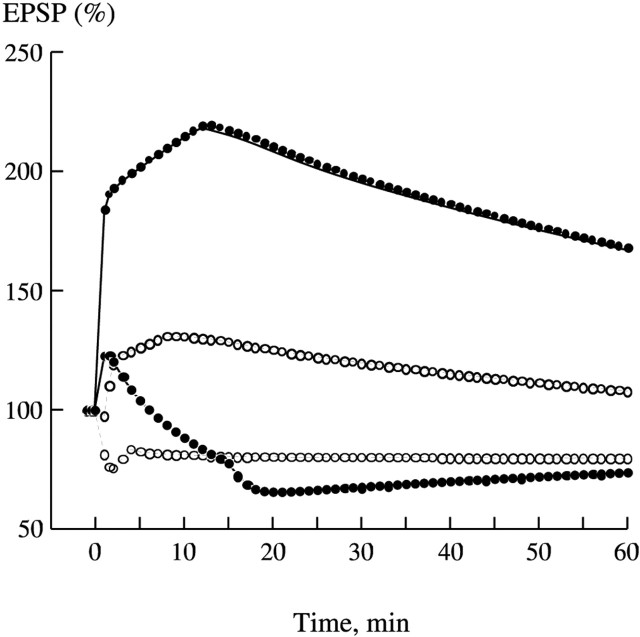
Effect of Ng on LTP and LTD in the model. A, Kinetics of EPSP in response to 1 Hz, 15 min stimulation, at 60 min after the start of stimulation. WT, 74% of the basal transmission; Ng KO, 74% of the basal transmission. B, Response to 5 Hz, 3 min stimulation. WT, 80%; Ng KO, 75%. C, Response to 10 Hz, 90 s stimulation. WT, 108%; Ng KO, 100%. D, Response to 100 Hz, 1 s stimulation. WT, 167%; Ng KO, 106%. WT, (—); Ng KO, (- - -).

The detailed model.

The detailed schemes of all reactions and transport processes, differential equations, and parameters are given in the supplemental material (available at www.jneurosci.org). In our model, all concentrations are calculated as molar quantities of the molecules divided by the spine volume. This includes AMPARs, because only their C-tails, which are in the cytoplasm, participate in the reactions of our model.

Input signals.

The input signals in our model are the postsynaptic Ca²⁺ elevations resulting from synaptic activation of the NMDA receptors. A single Ca²⁺ pulse rises instantaneously to an amplitude of 0.7 μm and decays with a characteristic time constant of 0.15 s (Sabatini et al., 2002). We use simple summation of the Ca²⁺ pulse trains (Helmchen et al., 1996) in modeling induction of plasticity with the single frequency train protocols (Sabatini et al., 2002). For 100 Hz tetanic stimulation, this results in a maximum elevation of [Ca²⁺] of ∼10 μm. If we take into account the fact that depolarization during the 100 Hz tetanic stimulation will lead to an increase in the Ca²⁺ entry per stimulus pulse, we reach a maximum Ca²⁺ concentration close to 30 μm, the level measured experimentally (Petrozzino et al., 1995). However, incorporating this effect makes no difference in our simulations, because CaMKII is already saturated by [Ca²⁺] at ∼10 μm.

Software.

We use the XPPAUT software (Ermentrout, 2002) for the simulations.

Results

In our model, all reactions occur inside the spine of a typical synapse, which belongs to a small population of synapses that undergo homosynaptic plasticity, whereas the parent dendrite and the entire neuron remain at basal conditions. In the model, the total average concentrations of CaM (10 μm), Ng (20 μm), and GAP-43 (20 μm) determine the uniform concentration of free CaM (0.9 μm) throughout all compartments of the neuron at rest. On the other hand, Ng and its complexes with CaM are distributed non-uniformly in the neuron. Ng is predominantly a cytosolic protein but is found in smaller amounts in membrane-enriched microsomes and synaptosomes (Watson et al., 1994). It is distributed throughout the perikaryal and dendritic cytoplasm but found in specific locations in granular form. Punctate Ng is found mostly in dendritic spines (Watson et al., 1992; NeunerJehle et al., 1996), where it is often closely associated with the PSD (Watson et al., 1994). Granular labeling is also found at the membranes of mitochondria and trans-Golgi vesicles (NeunerJehle et al., 1996). The simplest explanation of the high accumulation of Ng at specific locations is that these sites contain anchors for Ng. Using the yeast two-hybrid screen, Prichard et al. (1999) have shown that CaM binds to Ng in vivo and is the only Ng-interacting protein isolated from brain cDNA libraries. This could mean that the anchors should have considerably lower affinity for Ng than does CaM. This conforms to the suggestion that Ng may only be loosely associated with the PSD (Watson et al., 1994). To accumulate a large amount of Ng in a spine, one needs a rather high concentration of such low-affinity anchors there. Our model reflects the fact that the concentration of Ng in spines is much higher than the average concentration throughout the neuron. We also assume that the granular form contains a large fraction of the total Ng in the neuron, leaving the concentration of its free diffusible form rather low. With our basic set of parameters, the concentration of Ng bound in the spine is 113.7 μm and that of its diffusible form is 1.0 μm. In what follows, we show that these concentrations can be varied by one order of magnitude without a significant effect on the amplitude of LTP.

Kinetics of enzymes and the postsynaptic AMPARs during induction of synaptic plasticity

We first studied how key species behave during and after induction of synaptic plasticity. We started with the response of the model to 1 Hz, 15 min stimulation, the protocol often used for induction of LTD. Figure 3 shows how the concentrations of Ca²⁺, the activated enzymes, and the postsynaptic AMPAR populations vary during the induction period (the onset of this period is in the left panels, and the end is in the right panels). The amplitude of Ca²⁺ pulses is 0.7 μm (see Materials and Methods), and there is a negligible increase in the stationary component of [Ca²⁺] because of the pulse summation (Helmchen et al., 1996) over the induction period (Fig. 3A,B). The concentration of free CaM is equal to 0.9 μm at rest and during stimulation with precision better than 0.01%. The concentration of free CaCaM is 0.9 pm at rest and reaches 0.25 nm at the end of stimulation; the concentration of CaMNg is 0.23 μm at rest and during stimulation, and that of CaCaMNg is 0.23 pm at rest and reaches 0.64 pm during stimulation. The time course of enzyme activation by CaCaM during LTD induction is shown in Figure 3, A and B. The transitional period of activation of CaN lasts ∼7 s, after which stationary oscillations of [CaN*] ([CaCaM·CaN]) occur in the range of 10–20 nm; PP1 is activated in parallel, but oscillations of its concentration are negligible. On the other hand, CaMKII, the total concentration of which is double that of CaN, is much less activated. Figure 3, C and D, which shows activation of CaMKII on a larger scale, reveals that autophosphorylation of CaMKII is practically absent. Figure 3E shows the concentrations of the postsynaptic receptors. One can see a strong decrease in the concentration of the postsynaptic AMPARs not bound to SAP97, R_ps, and a considerable increase in the concentration of AMPAR·SAP97 complexes, L_pR_ps. As a result, the sum of concentrations of R_ps and L_pR_ps decreases, leading to the synaptic depression shown in Figure 5A.

We next examined how CaN and CaMKII become activated during the 100 Hz, 1 s tetanic stimulation usually used to induce LTP. Because the relaxation time of [Ca²⁺] decline is 0.15 s, the tetanus leads to buildup of free intraspinal [Ca²⁺] to ∼10 μm. This large rise in [Ca²⁺] drives the concentration of CaCaM from nanomolar levels to ∼0.4 μm with a characteristic time of 150 ms, whereas CaM drops approximately threefold during the tetanus. After the end of stimulation, the concentrations of CaM and CaCaM quickly return to their basal values (Fig. 4A,B). Figure 4, C and D, shows the time course of enzyme activations. During the initial period of Ca²⁺ elevation, CaCaM binds to CaN. After saturation of CaN, CaCaM binding to CaMKII becomes noticeable. Autophosphorylation of CaMKII, which is initiated by the binding of two CaCaM, is delayed even more. Once autophosphorylated, the activity of CaMKII persists for ∼10 min after the tetanus, slowly decreasing because of dephosphorylation by PP2A (Fig. 4D). This prolonged activity is essential for induction of LTP. Finally, Figure 4, D and F, demonstrates that an increase in concentration of L_pR_ps is the cause of rise of the total concentration of postsynaptic receptors, [R_ps] + [L_pR_ps], that is responsible for the synaptic potentation shown in Figure 5D.

Effect of Ng on bidirectional plasticity

Huang et al. (2004) showed that knockout of Ng greatly reduces the LTP induced with a 100 Hz, 1 s tetanus and slightly enhances LTD. We explored the effects of deletion of Ng in our model.

First, we needed to adjust the amplitudes of the Ca²⁺ transient in Ng knock-out (KO) to take into account the finding that the amplitude of Ca²⁺ transients in proximal dendrites during 100 and 5 Hz stimulation is approximately twofold lower in Ng (−/−) compared with WT (Huang et al., 2004). Therefore, in simulations of the Ng KO, we used an amplitude of single Ca²⁺ pulses in spines crease in to 0.5 μm, in semiquantitative accord with Huang et al. (2004). It should be noted that when we explored the effect of this parameter change in separate simulations, we found that it had small but significant effects on the plasticity induced by low-frequency stimulation but almost no effect on the 100 Hz-induced LTP (data not shown).

Then we simulated the Huang et al. (2004) experiments on bidirectional plasticity in the wild-type and Ng KO mice. Figure 5 demonstrates the development of synaptic plasticity in our model with the basic set of parameters in normal and Ng KO conditions. Figure 5A displays LTD in WT and KO after 1 Hz, 15 min stimulation, and Figure 5B shows LTD induced with a 5 Hz, 3 min train. Figure 5C demonstrates responses induced with a 10 Hz, 90 s train, and Figure 5D shows LTP in the wild-type and Ng KO synapses after induction with a single 100 Hz, 1 s train. Tables 1 and 2 show concentrations of the principal species in the spine at rest, immediately, and 60 min after 1, 5, 10, and 100 Hz stimulation in WT and 100 Hz stimulation in KO.

Table 1.

Concentrations (μm/L) of the principal species in the spine at rest, immediately, and 60 min after 1, 5, 10 Hz stimulation in WT

Species	t = 0	1 Hz		5 Hz		10 Hz
		t = 900a	t = 3600	t = 180a	t = 3600	t = 90a	t = 3600
Ca2+	0.10	0.80	0.10	1.0	0.10	0.10	0.10
CaM	0.90	0.90	0.90	0.89	0.90	0.92	0.90
CaCaM	9.0 × 10−7	2.5 × 10−4	9.0 × 10−7	6.0 × 10−4	9.0 × 10−7	9.9 × 10−7	9.0 × 10−7
Ng	0.77	0.77	0.77	0.77	0.77	0.77	0.77
CaM·Ng	0.23	0.23	0.23	0.23	0.23	0.23	0.23
CaCaM·Ng	2.3 × 10−7	6.4 × 10−7	2.3 × 10−7	2.8 × 10−5	2.3 × 10−7	2.5 × 10−7	2.3 × 10−7
CaN*	4.5 × 10−4	9.6 × 10−3	4.5 × 10−4	0.13	4.5 × 10−	5.0 × 10−4	4.5 × 10−4
PP1act	9.0 × 10−5	2.7 × 10−3	9.0 × 10−5	2.8 × 10−2	9.0 × 10−5	1.0 × 10−4	9.0 × 10−5
CaMKIIact	1.8 × 10−4	4.9 × 10−3	1.8 × 10−4	0.41	1.8 × 10−4	3.3 × 10−3	1.8 × 10−4
R	0.30	3.5 × 10−2	0.19	4.8 × 10−4	0.17	6.4 × 10−3	0.18
Rp	6.9 × 10−2	3.7 × 10−2	4.2 × 10−2	2.2 × 10−2	3.8 × 10−2	4.6 × 10−3	4.1 × 10−2
Rps	0.34	0.16	0.21	3.3 × 10−2	0.19	2.3 × 10−2	0.20
SAP97p·Rps	1.9 × 10−2	0.12	5.8 × 10−2	0.25	0.10	0.49	0.18
Rd	0.18	0.73	0.69	0.88	0.80	0.78	0.71
Rf	2.0 × 10−4	5.3 × 10−4	1.2 × 10−4	1.4 × 10−4	5.7 × 10−5	7.1 × 10−6	4.4 × 10−5
SAP97	0.70	0.61	0.69	0.44	0.69	0.32	0.68
SAP97p	5.6 × 10−6	1.3 × 10−4	5.7 × 10−6	8.1 × 10−3	5.8 × 10−6	4.8 × 10−5	6.0 × 10−6

^aEnd of stimulation.

Table 2.

Concentrations (μm/L) of the principal species in the spine at rest, immediately, and 60 min after 100 Hz stimulation in WT and KO

Species	WT			KO
	t = 0	t = 1a	t = 3600	t = 0	t = 1a	t = 3600
Ca2+	0.10	11	0.10	0.10	7.8	0.10
CaM	0.90	0.30	0.90	2.0	1.5 × 10−2	2.0
CaCaM	9.0 × 10−7	0.38	9.0 × 10−7	2.0 × 10−6	6.8 × 10−3	2.0 × 10−6
Ng	0.77	0.81	0.77	0.00	0.00	0.00
CaM·Ng	0.23	8.7 × 10−2	0.23	0.00	0.00	0.00
CaCaM·Ng	2.3 × 10−7	0.10	2.3 × 10−7	0.00	0.00	0.00
CaN*	4.5 × 10−4	4.9	4.5 × 10−4	1.0 × 10−3	1.8	1.0 × 10−3
PP1act	9.0 × 10−5	0.16	9.0 × 10−5	2.0 × 10−4	0.13	2.0 × 10−4
CaMKIIact	1.8 × 10−4	9.1	1.8 × 10−4	4.0 × 10−4	0.63	4.0 × 10−4
R	0.30	3.8 × 10−4	0.24	0.30	1.3 × 10−2	0.27
Rp	6.9 × 10−2	0.35	5.7 × 10−2	7.9 × 10−2	0.34	7.2 × 10−2
Rps	0.34	0.28	0.28	0.39	0.37	0.36
SAP97p·Rps	1.9 × 10−2	8.9 × 10−2	0.32	4.8 × 10−2	6.2 × 10−2	0.11
Rd	0.18	0.19	0.27	0.78	0.80	0.88
Rf	2.0 × 10−4	8.2 × 10−5	1.1 × 10−4	3.9 × 10−4	3.4 × 10−4	3.4 × 10−4
SAP97	0.70	0.26	0.66	0.70	0.63	0.69
SAP97p	5.6 × 10−6	0.10	6.1 × 10−6	1.2 × 10−5	1.7 × 10−2	1.3 × 10−5

^aEnd of stimulation.

The kinetics of EPSP shown in Figure 5 mainly demonstrate reasonable agreement with the results obtained by Huang et al. (2004), taking into account that their experiment presents the field EPSPs, and we simulate the postsynaptic responses, which are measured by intracellular recording in the experiment. One significant discrepancy is the response to 10 Hz stimulation. In this case, our simulations show that after stimulation, a moderate potentiation occurs that is followed by a decrease in the EPSP, whereas the experiment demonstrates a slow increase in the EPSP after short-term depression. This discrepancy is most likely because of the great simplification of our model (e.g., omission of the effects of the GluR2/GluR3 subunits and PKC).

Figure 6A shows the frequency-dependent curves of bidirectional plasticity for WT and Ng KO constructed from the points in Figure 5 taken at t = 60 min. Figure 6B shows the corresponding experimental curves taken from the data of Huang et al. (2004). The simulations are in reasonable agreement with the experimental data. The Ng KO produces a very large drop in LTP induced with the 100 Hz protocol and a much smaller decrease at lower frequencies of stimulation. As in the experiments, the points in our simulations that determine the frequency-dependence curve in KO are shifted downward from those in WT.

We note that the summed concentration of postsynaptic AMPARs ([R_ps] + [L_p R_ps]) is 0.36 μm in WT and 0.39 μm in Ng KO in the resting state. Thus, the basal transmission in Ng KO is 108% of that in WT.

Model sensitivity to variation of parameters controlling availability of CaM

Having obtained the results shown in Figures 4 and 5, we next studied the sensitivity of the model to variations of the parameters that affect the concentrations of free and bound CaM in spines. Those include the dissociation constants of the CaM·Ng and CaCaM·Ng complexes, the concentration of Ng capable of diffusion in cytoplasm, and the rate of exchange of CaM, Ng, and CaM·Ng complex between the spine and the parent dendrite.

The dissociation constant of the CaM·Ng complex is 5 μm (Huang et al., 2000), and K_d for CaM·GAP-43 is ∼3 μm (Alexander et al., 1987). Data on the affinity Ng for Ca²⁺/CaM are controversial. Experimental results on the retention of Ng in affinity columns indicated a much higher affinity of Ng to apoCaM compared with Ca²⁺/CaM. However, release of Ng from the CaM–Sepharose columns was achieved with a buffer containing 3 mm CaCl₂ (Baudier et al., 1991) and 6 mm CaCl₂ (Huang et al., 2000), and the gel filtration chromatography that showed dissociation of the Ca²⁺/CaM·Ng complex used 1.2 mm CaCl₂ (Huang et al., 1993). The circular dichroism spectra showing absence of the Ca²⁺/CaM·Ng complex formation have been obtained with 5 mm Ca²⁺ (Gerendasy et al., 1995). On the other hand, from the titration curves in a study by Gerendasy et al. (1994) (Fig. 3E), one can estimate K_d of ∼2 μm with EGTA (2 mm) and ∼3 μm in the presence of CaCl₂ (2 mm), which is a significant but not drastic difference. All of these data have been obtained at [Ca²⁺] one to two orders of magnitude higher than both the K_d for the Ca²⁺/CaM complex and the Ca²⁺ elevations during induction of LTP. Neither one of these studies explicitly presents the K_d for the Ca²⁺/CaM·Ng complex.

Because Alexander et al. (1987) showed that there was no difference in the affinity of GAP-43 for apoCaM and Ca²⁺/CaM and the published data indicate a close resemblance of interactions of Ng and GAP-43 with CaM (Gerendasy et al., 1995), we set the dissociation constants of CaM·Ng and CaCaM·Ng to be equal in our basic set of parameters and chose the value of K_d to be 3 μm. After reproducing the experimental frequency-dependence curves, we checked the effect of the uncertainty in absolute values of K_d on the results. Table 3 shows that similar results are obtained with the dissociation constants of the CaM·Ng and CaCaM·Ng complexes, both equal to 1.0, 3.0, or 5.0 μm. It is therefore clear that plasticity does not significantly depend on the value of the affinity of Ng to CaM and CaCaM in this range, when those affinities are equal.

Table 3.

Weak dependence of plasticity on equal dissociation constants, K_d, of the CaM·Ng and CaCaM·Ng complexes

Kd (μm)a	100 Hz	10 Hz	5 Hz	1 Hz
1.0	169	108	69	78
3.0	167	108	80	74
5.0	165	108	84	73
Ng KO	106	100	75	74

Data are EPSPs (percentage) at 60 min after the start of stimulation.

^aOther parameters are from the basic set (see supplemental material, available at www.jneurosci.org).

We next checked to what extent uncertainty about the affinity of CaCaM to Ng is important for understanding plasticity. Figure 7 shows that there is practically no difference in plasticity between cases when the affinity of CaCaM to Ng is negligible or equal to that of CaM. This result is easy to understand, because Ng cannot compete for CaCaM with CaMKII and CaN.

Figure 7.

Synaptic plasticity depends weakly on affinity of Ng to (Ca²⁺)₃CaM. LTD induced by 1 Hz, 15 min; 5 Hz, 3 min; and 10 Hz, 1.5 min protocols is practically indistinguishable whether affinity of (Ca²⁺)₃CaM for Ng is negligible or crease in to that of apoCaM. LTP induced by a 100 Hz, 1 s protocol is slightly higher when Ng does not bind (Ca²⁺)₃CaM. The curves appear in the following order (from bottom to top) after 20 min: 1, 5, 10, and 100 Hz stimulation. The lines correspond to K_d = 3 μm, and the circles correspond to 1/K_d = 0.

We know the total concentration of Ng, Ng₀, in the neuron but have no information on the concentration of Ng capable of diffusion in cytoplasm and exchange between spines and the parent dendrites. In Table 4, we examine the plasticity obtained with our basic set of parameters when the concentration of exchangeable Ng, Ng*, which is the sum of the concentrations of Ng and the CaM·Ng complex in the parent dendrite, is varied between 0.1 and 10.0 μm. These data show that there are no drastic differences in results, demonstrating that plasticity depends only weakly on the concentration of exchangeable Ng.

Table 4.

Moderate dependence of plasticity on the total concentration of exchangeable Ng, Ng* = [Ng]₀ + [CaM·Ng]₀

Ng* (μm)a	100 Hz	10 Hz	5 Hz	1 Hz
0.1	143	107	78	74
1.0	167	108	80	74
3.0	165	108	89	71
10.0	164	108	93	68

Data are EPSPs (percentage) at 60 min after the start of stimulation. Concentration of CaMNg₀can be calculated with the following equation: CaMNg₀ = CaM₀Ng*/(K_d + Ng*) = 0.9Ng*/(3.0 + Ng*), CaM₀ = 0.9 μm and [CaCaM] = 0.9 pm in the spine at rest and in the dendrite.

^aOther parameters are from the basic set (see supplemental material, available at www.jneurosci.org).

Another important question is how strongly the exchange of CaM between the spine and the parent dendrite affects synaptic plasticity. It has been shown previously that exchange of Ca²⁺ ions (Sabatini et al., 2002; Noguchi et al., 2005) and photoactivatable GFP (Bloodgood and Sabatini, 2005) between spines and the parent dendrites is limited. Figure 8 shows that in WT, plasticity is nearly independent of the rate of the spine–dendrite exchange of CaM, Ng, and CaM·Ng complex when the rate constant is varied three orders of magnitude from 0.01–10 s⁻¹. In the simulated KO, the dependence is negligible for 1 Hz stimulation (Fig. 8A), whereas LTD induced with the 5 Hz stimulation is slightly stronger when exchange is low (Fig. 8B), and 10 Hz stimulation does not significantly affect plasticity at any rate of exchange (Fig. 8C). However, the exchange rate strongly affects LTP induced with the 100 Hz, 1 s protocol, which decreases only moderately in the Ng KO when the rate constant is 10 s⁻¹, whereas LTP practically disappears when this rate is 0.01 s⁻¹ (Fig. 8D). These results show that induction of LTP does not depend on the spine–dendrite exchange of CaM if CaM is stored in spines as the CaM·Ng complex. On the other hand, our simulations show that a moderate exchange exists on the level around our basic value because the Ng KO does not eliminate completely the 100 Hz-induced LTP in the experiment.

Figure 8.

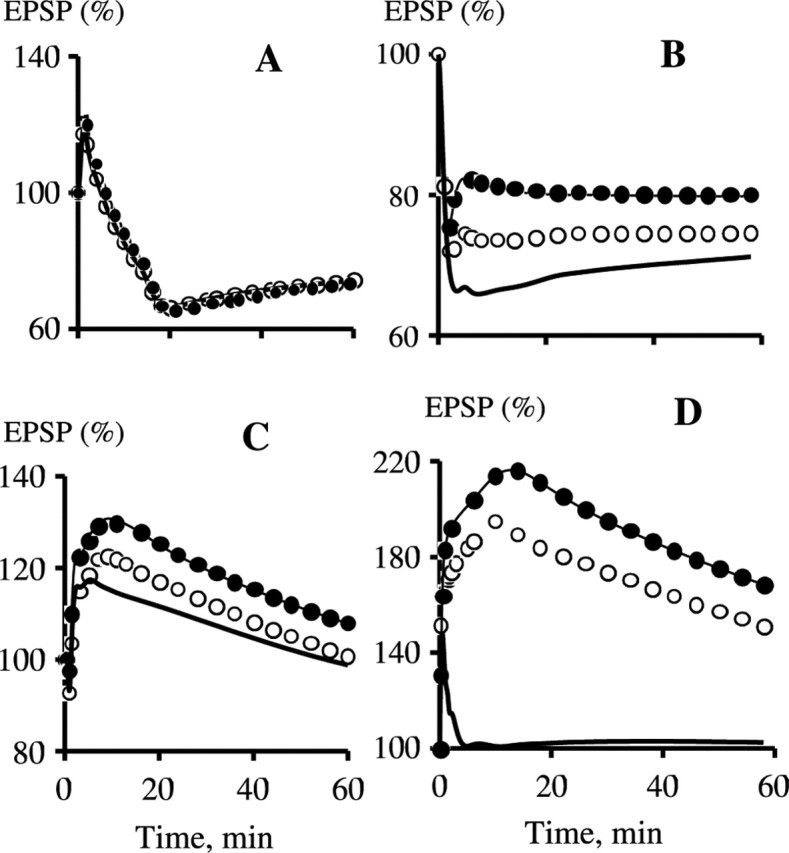
The spine–dendrite rate of exchange of CaM, Ng, and the CaM·Ng complex does not affect plasticity in WT. However, a high exchange rate could salvage LTP in KO. A, Kinetics of EPSP in response to 1 Hz, 15 min stimulation. B, Response to 5 Hz, 3 min stimulation. C, Response to 10 Hz, 90 s stimulation. D, Response to 100 Hz, 1 s stimulation. The curve designations are as follows: WT, the exchange rate constant (k), equals 10.0 s⁻¹ (•); WT, k = 0.01 s⁻¹ (—); KO, k = 10.0 s⁻¹ (○); KO, k = 0.01 s⁻¹ (—).

It has been shown that the concentration of Ng is high in dendritic spines (Watson et al., 1992; NeunerJehle et al., 1996). However, there is no experimental estimate of this concentration. Therefore, we need to determine how its variation affects synaptic plasticity. We varied the concentration of Ng stored in the spine and examined the effect on LTP induced by 100 Hz, 1 s stimulation. Our simulations show that LTP decreases from 167% to 151% if the concentration of the CaM·Ng complex stored in the spine drops 10-fold from ∼114 to 11.4 μm and to 139% when it decreases to 5.7 μm. However, the amplitude of the EPSP is 97% of the basal level if this concentration is 0. This demonstrates that LTP induced by a 100 Hz, 1 s tetanus depends moderately on the amount of CaM stored in spines if this amount is above a certain level, but LTP vanishes if stored CaM is absent.

Here, we show that the parameters that control the availability of CaM can be varied within rather wide ranges without strong effects on induction of bidirectional plasticity in our model. According to our simulations, exchange of CaM between spines and the parent dendrites is rather limited. Because of this, CaM stored in spines is necessary for induction of LTP by short tetanic stimulation.

On the lack of effect of Ng KO on late LTP

Whereas the early LTP induced by a single 100 Hz, 1 s tetanus is drastically reduced by Ng KO, the late LTP induced by three consecutive 100 Hz, 1 s tetani separated by 10 min intervals is not affected significantly by this KO (Pak et al., 2000). These data may cast doubt on the importance of Ng for induction of LTP. In our model, LTP induced by three consecutive 100 Hz, 1 s tetani with 10 min intervals is strongly diminished in the Ng KO compared with WT (data not shown). This is a clear discrepancy from the experiment. We suggest the following explanation for this discrepancy.

It has been shown that late LTP induced with multiple tetani separated by 5–10 min intervals is strongly dependent on PKA. Moreover, late LTP can be induced by direct activation of PKA (Frey et al., 1993) and, in the latter case, needs minimal Ca²⁺ signaling via NMDA receptors (Otmakhov et al., 2004). Strong activation of PKA leads to considerable inhibition of PP1, resulting in the decrease in [Ca²⁺] needed for activation of CaMKII (Blitzer et al., 1998). We suggest that long inter-tetani intervals result in substantial activation of PKA and inhibition of PP1, which with normal Ca²⁺ signaling diminish the dependence of CaMKII activation on CaM and, consequently, the dependence of LTP on Ng. This mechanism is beyond the scope of our model.

Late LTP can also be induced with much shorter protocols (Nguyen and Kandel, 1997). Moreover, its induction with multiple 100 Hz, 1 s tetani separated by 20 or 3 s intervals produces a form of long-lasting LTP that is independent of PKA (Scharf et al., 2002; Woo et al., 2003). It is likely that, in PKA-independent, long-lasting LTP, PP1 is not sufficiently suppressed and proper activation of CaMKII needs substantial amounts of CaM. If this is true, our model predicts that the amplitude of such LTP will be strongly reduced in the Ng KO, because in our simulations, the amplitude of LTP induced with three 100 Hz, 1 s tetani separated by 20 or 3 s intervals is strongly reduced in the Ng KO compared with WT (data not shown).

Discussion

Role of Ng in induction of LTP and LTD

We have sought to elucidate the role of Ng in induction of bidirectional plasticity. It was shown previously that disrupting CaM binding to Ng by injection of antibodies to Ng into CA1 pyramidal cells prevented induction of LTP by two 100 Hz, 1 s tetani separated by a 2 min interval (Fedorov et al., 1995). Later, Huang et al. (2004) showed that knockout of Ng strongly reduces the LTP induced by a single100 Hz, 1 s tetanus, whereas weakly affecting plasticity induced by lower frequencies. Together with the demonstration that Ng accumulates at high concentrations in dendritic spines (Watson et al., 1992; NeunerJehle et al., 1996), these data favor the idea that Ng forms a cache of CaM in spines, which is needed for induction of LTP with short tetani.

To reach a better understanding of the role of Ng in synaptic plasticity and to check the above idea, we have developed a mathematical model of the postsynaptic component of long-term bidirectional plasticity, which uses changes in the number of postsynaptic AMPARs as the mechanism of plasticity. This is the first model of the bidirectional plasticity that uses as the input signals the postsynaptic Ca²⁺ elevations formed by trains of Ca²⁺ pulses generated by synaptic activation of NMDA receptors (Petrozzino et al., 1995; Sabatini et al., 2002). The model reproduces with good accuracy the frequency-dependent curves obtained in the experiment by Huang et al. (2004).

Our simulations indicate that exchange of CaM between spines and the parent dendrites is too slow to provide enough CaM for sufficient activation of CaMKII by short Ca²⁺ signals. As a result, elimination of the CaM storage in spines drastically diminishes LTP induced with a 100 Hz, 1 s tetanus.

Our model predicts that the S36A mutation, which prevents PKC phosphorylation of Ng by PKC, will not affect synaptic plasticity, whereas the S36D mutation, which imitates phosphorylation, will reduce LTP the same way that KO does. We also predict that the PKA-independent, long-lasting LTP induced by multiple tetani separated by 20 or 3 s intervals (Scharf et al., 2002; Woo et al., 2003) will be strongly reduced in the Ng KO.

Our model is in agreement with the data of Huang et al. (2004) but not with results obtained by Krucker et al. (2002). Consequently, we need to discuss contradictions between these two experimental studies of the effects of knockout of Ng on bidirectional plasticity. In the knockout studied by Huang et al. (2004), LTP was strongly reduced, whereas LTD was slightly enhanced, resulting in a downshift of the frequency-dependence curve (Fig. 6B). In contrast, this curve was shifted upward in the knockout studied by Krucker et al. (2002), where LTD was absent and LTP was strongly enhanced. One may suggest that the effects found by Krucker et al. (2002) were attributable to overexpression of the N-terminal peptide of Ng, which was not involved in binding CaM. We can compare the outcomes of elimination of Ng as a CaM ligand suggested by the Krucker et al. (2002) phenomenological scheme and our model.

In both the Krucker et al. (2002) scheme and our model, Ng KO leads to elevation of free CaM. Krucker et al. (2002) suggested that in Ng-deficient neurons, the background activity leads to depression of basal transmission to such an extent that subsequent low-frequency stimulation produces LTP. Contrary to their suggestion, basal transmission is elevated in the Ng KO in our model, and low-frequency stimulation produces slightly enhanced LTD compared with WT. Krucker et al. (2002) suggested that phosphorylation of Ng by PKC, which prevents binding of CaM, should shift the Bienenstock–Cooper–Munro sliding threshold between LTD and LTP (Bienenstock et al., 1982) in favor of LTP. Our simulations lead to the opposite conclusion that preliminary phosphorylation of Ng, which is equivalent to removal of Ng as a CaM ligand, will result in suppression of LTP. This is in accord with experimental findings that previous activation of PKC prevents induction of LTP (Stanton, 1995). Moreover, Hsu et al. (2000) have shown that transient removal of extracellular Mg²⁺ shifts the frequency–response curve downward, suppressing LTP and enhancing LTD, and that this effect is blocked by a selective PKC inhibitor.

Justification of the model

Molecular mechanisms involved in synaptic plasticity are complex (Malenka and Bear, 2004). To understand how the system works, one needs an intricate diagram of the network of participating reactions and transport processes. But this is not enough. Because synaptic plasticity is a highly dynamic phenomenon, concentrations of participating species and rates of processes play a crucial role. Therefore, a dynamic model is needed for full understanding.

We have presented here a simplified model of transduction, and the limitations of this model warrant discussion. In the model, the phosphorylation and dephosphorylation of the AMPAR·Sg complex, which lead to trafficking and retention of AMPARs, are assumed to be rate determining. Because of that assumption, detailed mechanisms of processes involved in trafficking, such as diffusion, endocytosis and exocytosis are not included in the model explicitly.

Because the requirement of kinases and phosphatases for plasticity is well established, long-term elevations of the relevant protein kinase or phosphatase activities have been suggested as mechanisms of maintenance, and some experimental evidence to support these mechanisms has been found (Lisman and Zhabotinsky, 2001; Morishita et al., 2001). However, plausible molecular mechanisms of such long-term elevations are quite complex and include multiple protein–protein interactions. Because mechanisms of maintenance play a secondary role in this study, we suggest other plausible mechanisms of maintenance, which allow a simpler description. To simulate maintenance of early LTP, we assume that critical phosphorylated sites in the Sg·GluR1·SAP97complex formed during induction of LTP are protected from phosphatase activity. Such protection via complex formation is known in the literature. A relevant example is the protection of CaMKII autophosphorylated at T286 from PP2A when CaMKII is bound to the PSD (Strack et al., 1997; Yoshimura et al., 1999). Maintenance of protein synthesis-independent LTD is attributable to slow recycling of actively internalized AMPARs.

Although we have chosen perhaps the simplest among the multiple plausible mechanisms of maintenance of LTP and LTD, we believe that our results on the role of Ng and limited CaM in induction of LTD and LTP will not change significantly in more detailed models that incorporate multiple mechanisms of expression and maintenance of LTD and LTP.

In our simplified model, the induced trafficking of AMPARs takes place within the spine, and we neglect trafficking via more complex routes that include the dendritic membrane. A consensus exists that the trafficking consists of two major steps: exchange between the synaptic and extrasynaptic membranes and endo/exocytosis from or to the extrasynaptic membrane (Malinow and Malenka, 2002). However, the extrasynaptic membrane can belong to the spine, to the parent dendrite, or to both. It has been shown that endocytosis takes place in both spines and dendrites (Blanpied et al., 2002). On the other hand, only insertion of GluR1 into the dendritic plasma membrane has been demonstrated (Maletic-Savatic et al., 1998; Park et al., 2004), suggesting that it is the primary site of exocytosis. However, Mack et al. (2001) have shown that although in young mice (postnatal day 14) GluR1 is located in dendrites and spines, in older mice (postnatal day 42), the majority of GluR1 is concentrated in spines. This observation points to spines as the probable main source of fast delivery of GluR1-containing AMPARs during LTP, justifying our simplification.

In conclusion, we have developed a mathematical model of the postsynaptic component of bidirectional plasticity, which uses realistic Ca²⁺ transients as the input signals and changes in the number of the AMPARs as the mechanism of expression. The model reproduces with good accuracy the experimental data on the effect of the Ng KO on bidirectional plasticity. Significant variations of the model parameters do not affect the overall agreement of the simulations with the experimental data. Our model demonstrates that for induction of LTP with short tetani, high Ca²⁺ elevations must be combined with CaM stored in spines in the form of rapidly dissociating CaM·Ng complexes.