Abstract
Multi-decadal surface temperature changes may be forced by natural as well as anthropogenic factors, or arise unforced from the climate system. Distinguishing these factors is essential for estimating sensitivity to multiple climatic forcings and the amplitude of the unforced variability. Here we present 2,000-year-long global mean temperature reconstructions using seven different statistical methods that draw from a global collection of temperature-sensitive paleoclimate records. Our reconstructions display synchronous multi-decadal temperature fluctuations, which are coherent with one another and with fully forced CMIP5 millennial model simulations across the Common Era. The most significant attribution of pre-industrial (1300-1800 CE) variability at multi-decadal timescales is to volcanic aerosol forcing. Reconstructions and simulations qualitatively agree on the amplitude of the unforced global mean multi-decadal temperature variability, thereby increasing confidence in future projections of climate change on these timescales. The largest warming trends at timescales of 20 years and longer occur during the second half of the 20th century, highlighting the unusual character of the warming in recent decades.
Arising from both natural forcing and unforced internal variability in the climate system, decadal- to multi-decadal surface temperature variations will continue to be superimposed on the anthropogenic global warming trend [1–7], affecting estimates of transient climate response to individual forcings and regional climate change [8]. Therefore, knowledge of multi-decadal global mean surface temperature (GMST) fluctuations, as well as their relative magnitude compared to that of the projected long-term warming trend, is of crucial importance for understanding future climate change [9, 10].
Global and regional-scale multi-decadal temperature variability (MDV) was found to be under- or over-estimated in climate simulations of the recent past [11–13]. Some multi-centennial to millennial-scale assessments of paleoclimate observations and simulations suggest that temperature variability at multi-decadal and lower frequencies is underestimated by CMIP5 [14] models [15, 16], contrasting with other evidence that suggests models contain realistic amplitudes of MDV [17, 18]. Global networks of instrumental observations extend back to 1850 at best [19], which is too short to fully characterize MDV and its driving forces and evaluate the simulated MDV amplitude [20]. Estimating the relative contributions of various climate forcings, and assessing the ability of climate models to accurately simulate observed climate phenomena, requires a far longer perspective [10].
Over the Common Era (CE, the past 2,000 years), paleoclimate proxy-based observations of temperature and climate forcings are available at up to sub-annual resolution and covering much of the globe [21]. Reconstructed GMST over the full CE provides context for recent warming, and offers an opportunity to benchmark the ability of climate models to simulate MDV and to study the planetary energy balance and other key aspects of the climate system. Most previous large-scale millennial-long temperature reconstructions have highlighted the extraordinary rate and magnitude of the warming in recent decades [1]. However, there are considerable discrepancies among the reconstructions in the amplitude, and partly also the timing, of past temperature fluctuations at inter-annual to multi-centennial time-scales [1, 22]. The extent to which the differences can be attributed to different reconstruction methodologies relative to different paleoclimate proxy networks is presently unclear, although both have been shown to strongly influence temperature reconstructions [23]. The recently updated compilation of temperature-sensitive records in a community-vetted, quality-controlled database [21] provides an opportunity to improve the reconstruction of GMST for the CE. Despite much innovative work in this area [22, 24], there have been few coordinated efforts to reconstruct global temperatures using a consistent experimental framework [23].
Here, we use seven different statistical methods to reconstruct GMST over the past 2,000 years (1-2000 CE; Tab. 1). The methods range from a basic composite-plus-scaling (CPS) and regression-based techniques (PCR, M08) frequently used in past reconstructions, to newer linear methods (OIE, BHM) and techniques that account for nonlinear relations between proxy values and temperature (PAI), or combine information from proxy data and climate models (DA). All procedures use the same input dataset (Ref. 21, Supplementary Fig. 1) and the same calibration dataset for the reconstruction target, the infilled version [25] of HadCRUT4 [19]. For each method, a 1000-member ensemble of reconstructions is generated, allowing a probabilistic assessment of uncertainties. Further details on each method, such as the various approaches used to generate the reconstruction ensembles and the ability to include low-resolution records, are provided in the Methods.
Table 1. Overview of the reconstruction methods and data-model comparison.
“Refs” indicate key References. “Annual proxies only” indicates whether a method only incorporates proxy data of annual or higher resolution. The last two columns present the variance ratios and correlations between multi-decadal (30-200 year bandpass filtered) models and data, respectively, over the period 1300-2000 (Fig. 2). Ensemble medians are provided for each reconstruction method and 2.5th and 97.5th percentiles in square brackets. Percentage of ensemble members with correlations larger than expected from noise in parenthesis. Details see Methods. Unfiltered data and results for each model simulation are shown in Supplementary Tables 1-3.
| Refs | Annual resolved proxies only | model/data variance ratios | model vs. data correlations | |
|---|---|---|---|---|
| Composite plus scaling (CPS) | 26, 27 | yes | 0.96 [0.39, 2.49] | 0.64 [0.44, 0.80] (99.6%) |
| Principal component regression (PCR) | 27, 28 | yes | 1.01 [0.39, 2.65] | 0.60 [0.38, 0.77] (99.4%) |
| Optimal information extraction (OIE) | 29 | no | 1.13 [0.48, 3.02] | 0.61 [0.43, 0.83] (99.5%) |
| Regularized errors in variables (M08) | 26 | no | 1.01 [0.41, 2.59] | 0.65 [0.49, 0.79] (99.8%) |
| Pairwise comparison (PAI) | 30 | no | 0.63 [0.25, 1.65] | 0.63 [0.43, 0.79] (99.7%) |
| Bayesian hierarchical model (BHM) | 31 | yes | 1.12 [0.47, 2.91] | 0.53 [0.37, 0.66] (98.9%) |
| Offline data assimilation (DA) | 32 | yes | 1.15 [0.44, 3.02] | 0.62 [0.40, 0.86] (99.6%) |
Temperature history of the Common Era
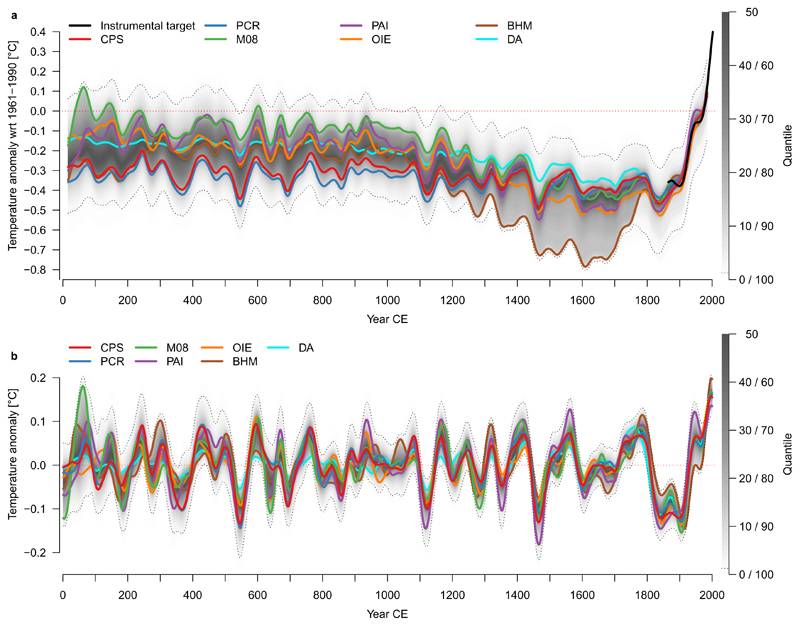
The temperature evolutions reconstructed by the seven methods (Fig. 1a) exhibit the major features of previous reconstructions over the CE [1]. All reconstructions show that the GMST during the first millennium CE was warmer than during the second millennium (excluding the 20th century). All reconstructions show a significant cooling trend prior to 1850 CE (Methods), followed by a rapid industrial-era warming. The warmest 10-year (30-year, 50-year) period of the past two millennia falls within the second half of the 20th century in 94% (89%, 84%) of ensemble members. The most pronounced difference between the reconstructions produced by the different methods is the amplitude of the pre-industrial multi-centennial cooling trend, manifesting in a temperature difference of about 0.5°C between the warmest (DA method) and the coldest (BHM method) estimates around 1600 CE.
Figure 1. Global mean surface temperature history over the Common Era.
a, Colored lines: 30-year low-pass filtered ensemble medians for the individual reconstruction methods. Gray shading: quantiles of all reconstruction ensemble members from all seven methods; the 2.5th and 97.5th percentiles are indicated with black dotted lines. Black: instrumental data [25] 1850–2017. b, Same as (a) but for 30- to 200-year bandpass filtered ensemble; instrumental data not shown.
Methods that are implemented to include proxy records of lower-than-annual resolution (Tab. 1 and Methods) yield systematically larger pre-industrial cooling trends, on average −0.23°C/ka [−0.31, −0.11] (ensemble median [2.5th percentile, 97.5th percentile]), compared to the other methods (−0.09°C/ka [−0.27, 0.02]).
The uncertainties for all reconstruction methods increase back in time and are particularly large prior to medieval times (Supplementary Fig. 3), owing to the decreasing number of input proxy data (Supplementary Fig. 1) and associated change in the observing network. The magnitude of uncertainties varies among the reconstructions depending on the method-specific approach to generate the reconstruction ensemble (Methods).
In the currently available database, many paleoclimate archives are seasonally biased [22, 33, 34] (SM section S3) and the relative seasonal representation varies over time. The majority of the included tree-ring records are detrended for removal of biological age effects by methods that cannot capture centennial to multi-centennial scale temperature variability [35, 36]. This problem likely manifests itself more back in time [22], and may result in an underestimation of low-frequency variability especially during the first millennium CE [37]. On the other hand, marine low-resolution records seem to overestimate the true variance [38]. Many of the paleoclimate records also have a mixed and, presumably, non-linear response to temperature and hydroclimate [39, 40] that is likely not stable over time [41].
Whereas multi-centennial to millennial-scale trends differ among the GMST reconstruction methods [22, 42, 43] (Fig. 1a), multi-decadal fluctuations are more similar (Fig. 1b). Removing the centennial-scale trend reveals remarkably coherent MDV with narrower confidence ranges across reconstruction techniques (Fig. 1b), suggesting a more robust result across methods.
Multi-decadal variability and response to forcing
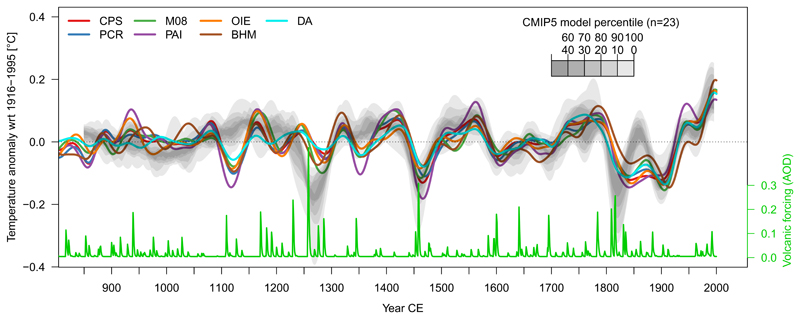
To explore the influence of the major known climate forcings on multi-decadal GMST, we compared an ensemble of 23 CMIP5 climate model simulations (Methods) with each of the temperature reconstructions. We find strong reconstruction–model agreement over the past millennium (Fig. 2) in both the timing and magnitude of multi-decadal (30-200 year bandbass filtered) GMST variance: The median model/data variance ratio across all reconstruction and model ensemble members is 1.01 and close to one for the individual reconstruction methods (Tab. 1). Multi-decadal data-model coherence is substantially larger than expected by chance (Tab. 1, Methods).
Figure 2. Multi-decadal temperature variability in reconstructions and models and volcanic forcing over the past millennium.
Colored lines: Ensemble median reconstruction from the different methods, 30- to 200-year bandpass filtered. Gray shading: model simulation percentiles. Green: volcanic forcing [59].
Warm anomalies around 1320, 1420, 1560 and 1780, cold anomalies around 1260, 1450 and 1820 and the periods of reduced variability during the overall cold 17th century and the relatively warm 11th century are captured by both the reconstructions and simulations. These similarities between reconstructions and models suggest a dominant influence of external forcing on multi-decadal GMST variability.
The data-model agreement is particularly strong between 1300 and 1800. The weaker agreement prior to 1300 might mainly be explained by the reduced quality of volcanic forcing estimates used in CMIP5 during this period [44], for example the 1109 CE eruption, which is followed by a clear GMST cooling (Fig. 2), is missing in the forcing datasets [45, 46] used for these CMIP5 simulations (Supplementary Fig. 20b). The apparent data-model mismatch in the 19th century is caused by the difference in response to the 1809 and 1815 eruptions, which is probably overestimated by the CMIP5 model simulations [47] (Supplementary Fig. 19).
To quantitatively evaluate the GMST response to external forcings in the reconstructions compared to model simulations, we apply a formal detection and attribution (D&A) analysis [48–50]. D&A analysis uses robust linear regression of reconstructed GMST on unforced, single and cumulatively-forced simulated GMST. The regression coefficients (scaling factors) may be interpreted as the extent to which reconstructed variability is explained by candidate unforced and forced responses. For the D&A analysis, we choose the period 1300–1800 CE, for which the anthropogenic forcing is negligible, and for which the uncertainties in the forcings, simulations and reconstructions are relatively small and time invariant compared to earlier centuries [21, 44, 50] (Fig. 2).
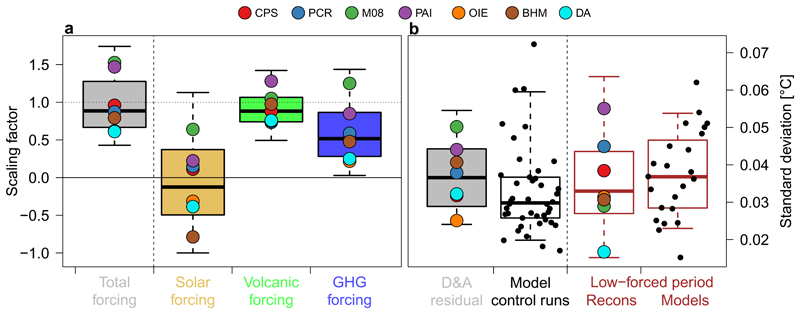
For all reconstruction methods, the D&A scaling factors are significantly above zero when performing the D&A analysis on multi-decadal time-scales and using fully forced model simulations (Fig. 3a, left; details see Methods). This means that the influence of external forcing on GMST variance is detectable in the simulations. The full ensemble median of the scaling factors (0.89) is close to unity and in four of the seven reconstruction methods (CPS, PCR, PAI and BHM), the 90% range of scaling factors does encompass unity, indicating a consistent response to total external forcing in models and reconstructions. This result is robust for single model (CESM-CAM5 [51]) and multi-model ensembles (Supplementary Fig. 7).
Figure 3. Pre-industrial forcing response and magnitude of unforced MDV.
a Multi-decadal detection and attribution scaling factors over 1300–1800 CE for the CESM1-CAM5 model based on differently forced runs. Gray box-whisker plot: D&A experiment using fully forced runs. Golden, green and blue box-whisker plots: multivariate experiment combining runs with solar forcing only, volcanic forcing only and GHG forcing only. Circles represent the individual reconstruction methods (median). b Estimates of unforced natural variability based on the D&A regression residuals of the full-forcing experiment (gray), the standard deviation in pre-industrial control simulations (black) and reconstruction and model standard deviation during the period of low external forcing variability 850-1100 (brown; details see Methods). Boxes represent the interquartile range, whiskers the 90% range. Black points represent the individual model simulations.
To disentangle the influence of different forcing factors, we repeat the D&A analysis by simultaneously regressing the ensemble means of three different CESM-LME model experiments (volcanic, solar and greenhouse gas (GHG) only) onto the reconstructions (eq. 2 in Methods). Choosing combinations of model experiments which account for different forcings allows us to estimate the relative contribution associated with each forcing (Fig. 3a, right). Results show that solar forcing is not detectable at multi-decadal time-scales in the reconstructions (scaling factors not significantly above zero), but volcanic and GHG forcing responses are consistent in pre-industrial, multi-decadal reconstructions and simulations [52]. Volcanic forcing has scaling factors very close to one confirming the agreement illustrated in Fig. 2. A weak relationship between solar forcing and GMST is confirmed by cross-wavelet analysis (Supplementary Fig. 16), suggesting that solar variability as presently reconstructed cannot account for GMST variability over the Common Era, although it has been detected on multi-decadal time scales regionally [53, 54] as well as over the NH on multi-centennial timescales [54].
The residuals of the D&A analysis can be used to quantitatively estimate the magnitude of internal unforced MDV in the reconstructions (Methods). The residuals of the “total forcing” D&A analysis (Fig 3a, leftmost box-whisker plot) are shown in Fig 3b, and they are interpretable as the unforced variability in the actual climate system after the linear response to total forcing simulations is removed. This estimate of the unforced variability in the actual climate system is consistent with the variability in pre-industrial control simulations (Fig.3b, left two box-whisker plots): 99% of estimates based on the D&A residuals are within the 95% range of control simulations. Also, the interquartile range of all possible paired comparisons encompasses zero (Supplementary Fig. 8).
Differences in the estimates from the two lines of evidence may arise from both random and systematic uncertainties in both reconstructions and simulations [55] (eq. 2 in Methods). Reconstruction uncertainties include underestimation of the reconstructed variance due to sparse observations, temporal smoothing, integration or seasonal bias, structural data model error, and large observational errors [43, 56–58]. Simulation uncertainties arise from errors in amplitude or timing of estimated radiative forcings [59], incorrect timescale of the simulated responses to forcing [60], and underestimation of the forced and unforced response because of incomplete representation of processes in the actual climate system [61].
To evaluate the likelihood of these biases influencing these results, we can compare the variability in reconstructions and model simulations for the Medieval “quiet” period [62] for external radiative forcing (850-1100 CE), which is independent from the period used for D&A (Fig. 3b, rightmost two box-whisker plots). This analysis suggests that there is no significant difference between reconstructed and simulated unforced variability (Methods). Our analysis does not confirm earlier findings of models underestimating internal MDV [15, 27]. Rather, it suggests that current models are able to realistically simulate the relative magnitudes of the externally and internally forced GMST on multi-decadal time scales.
Long-term context of the recent warming rates
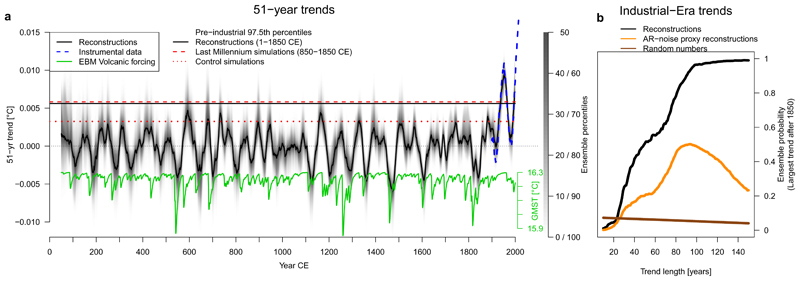
To place recent warming rates into a long-term context, we calculate 51-year running GMST trends from the unfiltered reconstructions (Fig. 4a). The different reconstruction methods agree on the magnitudes of multi-decadal trends over the CE, as shown by the narrow uncertainty range in Fig. 4a.
Figure 4. Multi-decadal temperature trends over the Common Era.
a, 51-year trends in reconstructions (black, ensemble percentiles shaded) and instrumental data [25] (blue dashed), with temperature response to volcanic forcing [59] based on a Energy Balance Model (green, see Methods). For the trends, the years on the horizontal axis represent the end-year of the 51-year trends. Horizontal lines denote pre-industrial 97.5th percentiles in reconstructions (black), models (red dashed) and pre-industrial control runs (red dotted), including all ensemble members and years. b, Ensemble probability of largest trend occurring after 1850 CE as a function of trend length. Black: reconstructions; orange: reconstructions using noise-proxies; brown: random numbers.
Energy balance model (EBM, green line in Fig. 4; Supplementary Figs. 14-15) simulations with volcanic forcing [59, 63] suggest a multi-decadal temperature response to secular frequency and amplitude variations in the forcing (Supplementary Figs. 12-13), which is qualitatively consistent with reconstructions. The fractional multi-decadal variance increases with increasing frequency of volcanic eruptions (Supplementary Fig. 15). Volcanic eruptions are found to coincide with strong multi-decadal cooling trends in both reconstructions and model simulations [64], and this is then followed by an increased probability of strong warming trends, due to the the recovery from the volcanic cooling (Fig. 4a and Supplementary Figs. 9-13). Both the cooling and subsequent warming trends are found to occur much more frequently than would be expected by chance.
Reconstructions and models yield practically identical values for the upper range of pre-industrial temperature trends (horizontal lines in Fig. 4a), again suggesting that climate models are skillful in simulating the natural range of multi-decadal GMST variability.
Of the reconstruction ensemble members, 79% have the largest 51-year trend within the 20th century, which includes two distinct periods of large trends. The first reflects the Early Twentieth Century Warming [65], which was shown to originate from a combination of forcings, including anthropogenic, and internal multi-decadal variability of the climate system [3]. The second reflects the modern period of strong warming, which extends from the mid-1970s to today. The temperature trends during these two industrial-era periods are outside the range of pre-industrial variability, even more so when compared with control runs, in which strong warming trends after volcanic cooling do not occur (dashed red line in Fig. 4a). All instrumental 51-year trends starting 1948 (and ending 1998) or later exceed the 99th percentile of reconstructed pre-industrial 51-year trends.
The extraordinary rate of the industrial-era temperature increase is evident on time scales longer than approximately 20 years (Fig. 4b), for which the probabilities of the occurrence of the largest trends greatly exceed the values expected from chance alone, using random noise predictors with realistic memory properties (Methods).
In addition to using a variety of reconstruction methods, we assessed the robustness of our analysis of multi-decadal GMST variability and trends using a range of sensitivity tests, including reconstructions based on detrended calibration and different realizations of noise proxies, adjustments for variance changes back in time, and different calibration periods and proxy subsets. Our inferences on the multi-decadal GMST variability for the Common Era are robust to all these permutations (Supplementary Figs. 17-20). Nevertheless, we cannot rule out biases due to errors in the individual proxy records and the unequal spatio-temporal distribution of proxy data (Supplementary Fig. 1). Warm-season-sensitive records from the Northern Hemisphere high and mid latitudes dominate the collection of proxy records [21], thus our results may be biased towards this region and season, although these effects are reduced by using the global mean (Supplementary Section S3). The coherency across reconstruction methods nevertheless suggests reduced sensitivity of the results to methodological choices compared to earlier attempts [23], perhaps in large part because of the use of the largest database of temperature-sensitive proxy data yet assembled [21]. With respect to the forced climate simulations, independent uncertainties include the specification of long-time-scale physical processes, relatively poorly known slowly varying forcings, and representation of grid and sub-grid scale processes [66]. That the reconstructions presented here are coherently phased and of similar amplitude to CMIP5 simulated MDV suggests improved confidence in both these sources of information.
Agreement on both the timing and amplitude of GMST variability across the reconstruction and simulation ensembles suggests that some aspect of the observed multi-decadal variability is externally forced, principally by changes in the frequency and amplitude of volcanic forcing over the pre-industrial past millennium [38, 52, 67] and anthropogenic GHGs and aerosols thereafter [68] (Supplementary Fig. 7c). Furthermore, we find that estimates of the unforced variability from reconstructions and simulations span similar ranges with independent uncertainties. Our results suggest that multi-model ensemble projections for the near term produce reasonable estimates of the spread in global mean temperature change associated with both forced and unforced MDV, further justifying the use of such models as basis for regional- to global-scale simulations [69] and studies of associated societal impact, adaptation and resilience [70].
Methods
Input data and pre-processing
Paleoclimate observations
We use version 2.0.0 of the global PAGES 2k temperature proxy data collection [21]. For the reconstructions presented in the main text, we use the subset of records selected based on regional temperature screening and accounting for false discovery rates (R-FDR subset [21]). This screening reduces the total number of records from 692 to 257 but increases the GMST reconstruction skill for most methods and skill metrics. A comparison of reconstructions and evaluation statistics of the full versus screened networks is provided in Supplementary Fig. 17. Of the screened proxy records, 210 are annually resolved and are included by all reconstruction methods. Sub-annually resolved time series (29 records) were averaged over the April to March annual window. The 47 records with lower-than-annual resolution are only included by the M08, OIE and PAI methods (see below). Although none of the methods explicitly consider age uncertainties, the impact of age uncertainty on reconstructions can be estimated by sampling from a set of age ensembles for each of the age-uncertain records (e.g. Ref. 71). However, only a subset (15%) of the age-uncertain records in the version 2.0.0 of the PAGES 2k database include age ensembles or the requisite geochronological data to generate new age ensembles. Consequently, full consideration of age uncertainty is outside the scope of this research; nevertheless, this likely has minimal impacts on the reconstructions, as the final proxy network mainly consists of records with very small to negligible age uncertainties (81% tree or coral archives).
Instrumental observations
We use the Cowtan and Way [25] global mean temperature dataset, which is based on a kriging-interpolated version of HadCRUT4 [19]. We use an annual average based on the Apr-Mar window representing the "tropical year", which has the advantage of not interrupting the growing season of trees in both the Northern and Southern Hemispheres.
Experiment overview and settings
The time window 1850–2000 CE was used for calibration. For evaluation, we ran a second experiment calibrating over 1916–1995 CE and validating over 1881–1915 CE. Evaluation graphs are provided in the SM, Section S2. Results based on this shorter calibration period, which encompasses a period of significantly improved spatio-temporal coverage with instrumental and proxy data, are presented in the SM (Supplementary Fig. 17). All reconstruction methods generated an ensemble of 1000 GMST reconstructions, which were used for uncertainty quantification.
Reconstruction methods
Details on each method are provided in the following subsections. Table 1 summarizes some key aspects and references for the methods. Methodological constraints required some minor adaptations to the experimental setup for some techniques. These are as follows: CPS, PCR, BHM and DA include only annually and more finely resolved proxy records. CPS and PCR exclude records with more than 33% missing values and infill the remaining missing values over the calibration period. DA generates GMST from a spatially resolved temperature reconstruction. Multiple approaches to weighting the different reconstruction methods to generate a best estimate GMST time series are presented and discussed in the SM (Section S4).
Composite plus scaling (CPS)
Composite plus scaling is one of the most basic methods for quantitative climate index reconstruction, and has been applied widely for local to global reconstructions of temperature and other variables [26,72–75]. CPS generates reconstructions using two steps: First, the proxy records are converted into a single time series (composite) by calculating a weighted mean. Second, this composite is scaled to the mean and standard deviation of the reconstruction target over the calibration period. Here, we use a similar implementation of CPS as Ref. 27: The proxies are weighted by their non-detrended correlation with the GMST reconstruction target over the calibration period. A nested approach is applied, such that each year’s CPS reconstruction is based on a calibration using all proxies that are available in that year. To quantify uncertainties, for each member of the 1000-member ensemble, several key parameters are resampled:
10% of proxy records are withheld from calibration.
The weight of each proxy record (target correlation r) is multiplied by a factor between 1/1.5 and 1.5. In contrast to other studies (e.g. Ref. 76), we do not perturb r with an exponent but use a factor centered at 1 to ensure that the reconstruction ensemble is centered around a reconstruction using non-perturbed weighting.
In addition, each ensemble member is perturbed with red noise having the same standard deviation and AR(1) (first-order autoregression) coefficient as its residuals from the reconstruction target over the calibration period. We use an AR(1) model because the short length of time available for model fitting and evaluation does not allow for a reliable estimate of coefficients for higher-order and more complex models. Furthermore, CPS residuals only exhibit significant autocorrelation at lag 1 (not shown). Thus, the total uncertainty expressed by the ensemble spread is based on both parameter and calibration uncertainty [77]. For a detailed discussion of this ensemble approach refer to Refs 27, 77.
As for many linear methods, CPS is prone to variance losses in the reconstructions and a bias towards zero. Both the bias and reconstruction variance are directly related to the correlation of the proxies with the reconstruction target [22]. CPS is computationally efficient and the quality (e.g. in terms of skill measures) of its results is often comparable to more advanced (and often more expensive and parameter-dependent) methods (e.g. figures in this paper and Refs 27, 77, 78).
For proxy records with lower-than-annual nominal resolution, the correlations with the instrumental target have considerably reduced degrees of freedom. Furthermore many of these records are not interpolated to a value for each year in the PAGES 2k database v2.0.0, thus cannot be directly used for CPS. We therefore use only records with a median resolution ("ResMed" variable in the PAGES 2k proxy database) not exceeding 1. Furthermore, we only use records with a maximum of 1/3 of missing data within the calibration interval. This yields a total of 210 proxy records within the R-FDR screened subset. Missing data in the calibration window (2.23%) are infilled using DINEOF [79].
Principal component regression (PCR)
Principal component regression is a linear method, and, along with CPS and RegEM (see below), one of the most commonly used methods to reconstruct climate indices and fields over the Common Era [22, 24, 74, 80, 81]. PCR reduces the dimensionality of the proxy matrix by using only a certain number of its principal components as predictors in the regression. PCR has similar advantages and deficiencies as CPS. There is a large literature describing potential issues of the method and its parameter choices [22, 24, 57, 82–86].
Here, we use the nested PCR approach originally presented by Ref. 28 and implemented in many reconstructions of regional to hemispheric climate [27, 78, 87–91]. Our implementation is similar to Ref. 27; we use ordinary least squares to generate nested 1000-member ensemble reconstructions. We use identical parameters and input data as described for CPS above with a few exceptions: As additional parameter perturbation, principal components are truncated so that they explain between 40% and 90% of the total variance in the proxy matrix. Similar to the weighing in CPS, each proxy record is multiplied by a factor between 1/1.5 and 1.5 to perturb its weight within the PCA routine. Prior to this variance adjustment, all records are scaled to a mean of zero and unit variance over their common period of overlap.
Regularized expectation maximization (M08)
The core of the regularized errors-in-variables approach [26] is the regularized expectation maximization (RegEM [92]) algorithm with truncated total least squares (TTLS) regression [93]. The reconstruction by Ref. 26 (hereaftet M08) is the most widely used GMST reconstruction over the CE in the recent literature [26, 43, 78, 85, 94, 95], and has been much criticized [22]. Here we use the M08 implementation of RegEM to allow a direct comparison. Compared with other methods used herein, the most distinctive feature is a hybrid process to decompose two levels with high/low frequency bands of the reconstructions using the RegEM method with the TTLS regression. Thus, the method is able to combine low- and high-frequency proxies. The instrumental and gridded April to March average temperatures [25] were interpolated using the RegEM method to cover the whole period (1850–2000 CE) and used to calculate the regional properties of each record, e.g. the correlation coefficient between the proxy record and the regional and instrumental data during the calibration period.
The uncertainty in the original M08 method was calculated using the standard deviation of instrumental data during the calibration period and the correlation coefficient between the proxy reconstruction and instrumental data during the evaluation period [26]. Here, we adapted the uncertainty estimation to the ensemble reconstruction by perturbing each ensemble member with red noise of the same standard deviation and AR(1) coefficient as the residuals of the reconstruction during the evaluation period [27, 77].
Pairwise comparison (PAI)
Pairwise comparison is a nonlinear method [30] that allows proxy records with different temporal resolution to be combined. It has been used in a number of continental-scale temperature reconstructions [30, 77, 96]. PAI generates a non-linear, but monotonically increasing function to reconstruct climate by performing pairwise comparisons of the proxy records. The order of successive data points in each proxy time series is compared and the relative agreement of this ordering for all proxies is then calculated. The strength of this agreement is then used to predict temporal changes in the target climatic variable. Similar to CPS, PAI generates a unitless composite based on the pairwise comparisons. In contrast to CPS, which makes use of target correlations to generate the composite, the composite derived by PAI is fully independent of the reconstruction target. Therefore, careful proxy selection is important for PAI to yield skillful results. The composite is scaled to the reconstruction target over the calibration interval. Reconstruction ensembles are generated by calculating bootstraps, resampling the proxy records and adding noise to the target data. A detailed description of the method is provided in Ref. 30. Here we use the same parameters as in Ref. 96.
The key advantage of PAI compared to most other currently used methods is its ability to combine high- and low-resolution proxy datasets, including records with irregular temporal resolution or those that do not cover the calibration period.
Optimal information extraction (OIE)
The optimal information extraction (OIE) method was derived from the CPS method, and developed with several versions inspired by the local (LOC) method [97], a Bayesian framework (BARCAST) [98], the generalized likelihood uncertainty estimation method [99, 100] and the ensemble reconstructions [27].
We use version 2.0 of the OIE method, which was developed to reconstruct the GMST by combining previously published reconstructions (four Northern Hemisphere reconstructions with annual resolution and covering the past two millennia [26,101–103] and a Southern Hemisphere ensemble reconstruction [27] using direct and indirect regression, which generated a reconstruction through four steps. First, we matched the variance of each proxy record using the previous hemispheric reconstructions. Second, we averaged the matched records to generate a composited proxy record, which is like the CPS method to weight and average the screened records to a composited record. Third, we regressed the composite using the E-LOC method [94], which set the regression coefficients as random variables within the ranges of the direct and indirect regressions, and the regression coefficients were determined using the generalized likelihood uncertainty estimation method [99, 100]. Finally, the uncertainty is expressed as the ensemble spread, in which each ensemble member is perturbed with red noise having the same standard deviation and AR(1) coefficient calculated from the residuals of the reconstruction in step three [27, 77].
Bayesian hierarchical model (BHM)
The Bayesian hierarchical model, defined in Ref. 31, is based on two ingredients: (1a) a model of the GMST (T) that depends on external forcing and additive noise; and (1b) a model of the proxy signal (RP) as linearly dependent on T, with additive noise. Specifically:
| (1a) |
| (1b) |
where t is time (1-2000 CE) and:
RPt: "Reduced Proxy" series that captures the common signal of the entire proxy dataset. It is constructed through a Lasso Regression [104] between proxies with similar temporal availability and the observed anomalies [25] during the calibration period. This procedure is repeated over eight, 250-year nests with different temporal availability of proxies, and the fitted values obtained for each case are combined in a single series. The number of records that were used in each nest vary between 21 (earliest nest) and 199 (latest nest).
Tt: temperature anomalies series.
St: time series of solar irradiance computed from SATIRE-H [105].
Vt: transformed volcanic forcing from Easy Volcanic Aerosol (EVA) dataset [44, 106, 107]
Ct: transformed greenhouse-gas concentrations taken from the Coupled Model Inter-comparison Project (CMIP6) [108]
ηt and ϵt: zero-mean, unit-variance stationary stochastic processes and σP and σT are constant variance parameters.
This method proceeds by regressing a linear combination of the PAGES 2k data onto global temperature, and modeling the latter as depending on external forcings. All model parameters are assumed random, and their prior distributions are updated through a combination of Gibbs sampling and the Metropolis-Hastings algorithm. This allows us to estimate the latent variable Tt together with all the parameters of the model and thus to obtain samples of its joint posterior distribution given the set of proxy records. In addition, this procedure allows us to obtain prediction intervals for all the parameters and the latent variable of the model. We also considered a particular case of the model where all the external forcings Ct, Vt and St are zero. In this way, the reconstruction of the latent variable was performed using information from the proxies only. For this particular case we defined ηt to be white noise and ϵt to be an AR(1) process. In the case where the external forcings are not null, both ηt and ηt are Gaussian white noise processes.
Data assimilation (DA)
Data assimilation fuses proxy observations and climate model output to reconstruct multiple climate fields, while leveraging GCM physics. The DA procedures used in this study were developed for the Last Millennium Reanalysis (LMR) project [32, 109]. LMR’s DA method reconstructs full fields rather than just global mean temperature, and it holds advantages over competing methods such as linear regression, both frequentist and Bayesian [32]. Because it uses pre-computed output from a climate model, this approach is known as “offline” data assimilation. Offline assimilation enables vast improvements in computational cost with modest loss of reconstruction skill [110, 111]. The DA code used in this paper is adapted from an intermediate version of the code being developed in the LMR project.
The DA results in this study use information from two sources: the PAGES 2k v2.0.0 proxy network [21] and the NCAR Community Climate System Model version 4 (CCSM4) last millennium simulation [112]. The proxy records provide the temporal variations related to climate at specific locations while the model results quantify the covariances between different fields and locations in the climate system. In other words, proxies provide temporal variations while the model covariances spread this information over space and to other climate fields in a dynamically consistent way.
The DA methodology works by first drawing 200 random years from the output of the CCSM4 last millennium simulation. This collection of climate states represents an initial guess of the climate before any assimilation takes place, and is referred to as the model “prior”. This prior is initially the same for every year of the reconstruction. The DA method gets no information about temporal changes from the model, and DA also has no knowledge of when given forcings are present in the climate system. It is therefore worthwhile to compare forced responses in the model and the DA reconstruction as we do in Figs. 2-4.
To relate proxy observations to the model states, proxy system models [40] (PSMs) must be used. While the LMR framework allows for non-linear PSMs, recent work shows that linear PSMs help safeguard against GCM biases [113], which can be sizable. For tree-ring widths, which can be sensitive to temperature, moisture, or both, we use a bivariate linear regression to relate ring width to temperature (HadCRUT4 [19], spatially interpolated via kriging [25]) and moisture (precipitation from the Global Precipitation Climatology Centre [114]). For all other proxy types, we use a univariate linear regression to the temperature data set alone.
Using these relationships, an initial estimate of each proxy value is computed from the prior. For every year, the difference between each proxy estimate and the actual proxy observation is computed, and a Kalman filter is used to update the climate state so that these differences are reduced. Because the climate system is updated using the model covariances quantified in the prior, the end result is a dynamically consistent estimate of the climate system informed by the proxy data. To be used in this assimilation, PAGES 2k v2.0.0 records need to exhibit annual (or better) resolution, as well as at least 25 years of overlap with the instrumental datasets to calibrate the PSMs. For the primary experiment, which uses the R-FDR screened proxies, 229 records were assimilated, consisting of 134 trees, 68 corals or sclerosponges, 21 glacier ice cores, 5 lake sediments, and 1 bivalve.
Model simulations used
We use the last millennium runs of the following CMIP5 model simulations. BCC-CSM [115], CCSM4 [112], MPI_ESM_P (members 1-3) [116–118], CSIROMk3L-1-2 [119], GISS-E2-R (members 121, 124 and 127) [120], HadCM3 [50], CESM_1 (members 1-13) [51], yielding an ensemble of 23 simulations. Internal variability was generated from 29 CMIP5 pre-industrial control simulations of length 499−1198 years, giving 21427 years of internal variability (same models as before plus ACCESS1, BNU-ESM, CanESM2, CMCC-CM, CNRM-CM5, FGOALS (g2, s2), FIO-ESM, GFDL (2G, 2M), HadGEM2, INMCM4, IPSL-CM5A-LR, MRI-CGCM3 and NorESM1). All simulations were aggregated annually by April–March GMST and filtered in the same way as the reconstructions.
Post-processing for figures
To generate anomalies for a given reference period, we subtract the temporal average of each method’s ensemble mean over this period from all ensemble members of this method. For low- and band-pass filtering, we use butterworth filters from the R-package signal.
Pre-industrial trends
Significance of the linear pre-industrial trends of the unfiltered ensemble median reconstructions for all methods is tested using Mann-Kendall test (n = 1850, two-tailed) and block bootstrapping (tsboot() function in R, 100-year blocks) over the period 0-1850. Both tests yield significant (α = 0.05) negative trends for all reconstruction methods.
Multi-decadal GMST and Data-model agreement (Tab. 1 and Fig. 2)
Multi-decadal GMST variability is analyzed by applying a 30-200 year bandpass butterworth filter to all data. See Supplementary Fig. 18 for an alternative of Fig. 2 using a 20-100 year bandwidth. To account for the very high autocorrelation strongly reducing degrees of freedom, and non-normal distributions in the 30-200 year bandpass filtered reconstruction and model data, we test the significance of data model-coherence by comparison with random noise time series. We generate a red noise time series for each reconstruction and model ensemble member with the same AR(1) coefficient as the corresponding reconstruction or model data. These noise time series are then subjected to the 30-200 year bandpass filter and correlated to each other as is done for the reconstructions and models. The percentage of data vs. model correlations that exceed the noise-based correlations are provided in Tab. 1. The data-model comparisons are calculated over the 1300-2000 period, where uncertainties in all datasets are relatively low (see text).
Detection and Attribution (Fig. 3)
To determine the extent of forced variability in the reconstructions, a total least squares (TLS) regression of the fingerprint of external forcings on the reconstructions was performed. A given temperature reconstruction Y (t) decomposes into a linear combination of the m fingerprints Xi(t) for the climatic response to external forcings, and the internal variability ν0(t):
| (2) |
Each fingerprint Xi(t), given by a model simulation, has its own implementation of internal variability νi(t) which is decreased by averaging over an ensemble of multiple simulations.
To determine the scaling factors βi we perform a TLS regression, accounting for the presence of noise in both regressor and regressand. Such a regression is commonly solved using a regularized optimal detection approach which was introduced by Ref. 121, building on earlier work by Ref. 48. Optimisation focuses the regression on features of the forced signal which are most distinct from internal variability. Here, we choose not to optimize the signal and instead carry out a simpler non-optimised regression, following Ref. 50. As described in Ref. 48, the scaling factors and the noise-reduced fingerprints and reconstructions can be calculated, using a singular-value decomposition (SVD). Where these are defined as:
| (3) |
| (4) |
| (5) |
To account for the uncertainty due to internal variability, we calculate a range of 1000 scaling factors per reconstruction by superimposing random slices of internal variability sampled from pre-industrial control simulations on the columns of . Thus we obtain a distribution of 106 scaling factors per reconstruction method and fingerprint, accounting for uncertainty from both reconstruction method and internal variability. The effect of a forcing is said to be detectable if a scaling factor to that forcing is found to be significantly greater than zero. A difference in response to forcing in the model simulations and in the reconstructions is found if the estimated 90% scaling factor confidence interval does not encompass one.
Two different analyses are carried out. The first regresses model simulations with all forcings onto the reconstructions over the time period 1300–1800. This tests whether the response to external forcings is detectable (Fig. 3a, left). For this we use the ensemble mean of the 13 CESM-LME simulations. Our results are robust to using the CESM model only or the full multi-model mean of all 23 simulations (Supplementary Fig. 7). The second analysis uses a linear combination of the fingerprints of volcanic forcing, solar forcing and greenhouse gas forcings, which were generated from the ensemble mean of CESM-LME simulations, regressed onto the reconstructions. This analysis disentangles the forced response into these three different causes (Fig. 3a, right).
The smallest eigen value of the SVD can be used as an estimate of the sum-of-squares residual of the regression, which is compared, in figure 3b, to the model internal variability calculated as the standard deviation of the 500-year slices of pre-industrial control simulations. As a further estimate of unforced multi-decadal GMST variability, we use the 30-200 year band-pass filtered reconstructions and model simulations during the period 850-1100 (brown boxplots in Fig. 3b), which reflects a “quiet” period of relatively little forcing activity (i.e. few large volcanic eruptions and relatively constant solar forcing, see also Ref. 62).
To test the consistency of estimates of the unforced variance (Fig. 3b, left, right), we apply the following procedures: We first quantify the fraction of estimates based on the D&A residuals that lies within the confidence range of the estimate from control simulations. Note that the estimates based on the D&A residuals represent the “true” observed variability, so should be distributed about the true value. In contrast, each control simulation reflects one possible realization of internal variability, which may be different from the “real” sample. Thus, a difference in the medians between the two estimates does not necessarily reflect an inconsistency, but can arise from internal variability alone. However, the estimates from the observed situation should be within the confidence range of estimates from the control runs. This is indeed the case for 98.7% of estimates from the D&A residuals (n1 = 7000), which are within the 5%-95% range of control run estimates (n2 = 43). Second, we calculate all possible comparisons (subtractions) between estimates from the D&A and control runs (n = n1 * n2 = 301, 000). To assess consistency of the lines of evidence, we test if the confidence range of these comparisons encompasses zero. Supplementary Fig. 8 (top) shows that it does, and in fact the value of zero is within the interquartile range of estimates.
The same observation is also valid for the right hand side of Fig.3b, indicating consistency between the estimates of unforced variability from reconstructions and simulations within the Medieval Quiet Period between 850-1100 CE (Supplementary Fig. 8, bottom). This is confirmed by a Kruskal-Wallis non-parametric test [122] for difference of medians. Such non-parametric procedures may be sensitive to violation of the assumption of independence both within and between samples from populations. For the comparison of reconstructions and simulations for the Medieval Quiet Period, we expect that the largest non-independence stems from the definition of the period chosen. We therefore apply two different sensitivity tests: block-bootstrapping the period chosen, and bootstrapping the test statistic itself. Both sensitivity tests suggest that the inference is stable to sampling partly independent periods within the Medieval Quiet Period for the comparison.
Multi-decadal Trends (Fig. 4)
51-year running linear GMST trends are calculated for each ensemble member of the inter-annual (unfiltered) reconstructions. Trend values are allocated to the year at the end of each 51-year period. The ensemble median across all 7000 multi-method ensemble members (seven methods methods with a 1000-member ensemble for each method) of each overlapping trend is displayed as black line in Fig. 4a. The upper range of natural variability in these multi-decadal trends is estimated using the 97.5th percentile across all trends and ensemble members between 1–1850 CE. For the model simulations, the corresponding 97.5th percentile is calculated back to the first year, where all simulations have data (850 CE) and for the control simulations across their respective period of data availability. Instrumental trends are calculated from the reconstruction target time series between 1850–2017 CE.
For Fig. 4b, the running linear trends are calculated for lengths between n = 10 and n = 150 years for all 7000 ensemble members. The fraction of ensemble members, for which the center year of the largest n-year trend over the CE falls into the post-1850 period is displayed. AR-noise proxy reconstructions shown in Fig. 4b are generated as follows: For each proxy record, a random noise time series with the same AR spectrum as the real proxy time series is generated using the hosking.sim() function in R. Each noise time series is truncated to have the same length as the corresponding real proxy record. PCR, CPS and PAI reconstructions are then generated using these noise time series as input data, but the same parameters and target data as the real proxy reconstructions. Note that these noise proxies mimic the full AR spectrum of the real proxies, but the resulting noise proxies are uncorrelated to each other. Alternative results based on cross-correlated AR(1) noise-proxies confirm our findings and are presented in Supplementary Fig. 20. The random numbers (brown line) are calculated by simply dividing the number of trend segments falling entirely within 1850–2000 (e.g. 140 for 10-year trends) by the number of trends within the full 2,000-year reconstruction period (1990 for 10-year trends). This number decreases with increasing trend length.
Energy Balance model (Fig. 4)
The temporal evolution of the Earths global energy balance is computed by solving the ordinary differential equation (ODE) [63]
| (6) |
where C is the effective heat capacity of the system, set here to c = 9.01· 108 [Jm−2K−1] corresponding to an upper ocean box. The effective incoming radiation is reduced by the albedo (α = 0.3) and depends on the incoming solar flux Q = S0/4+ΔF, with S0 the solar constant (here: S0 =1365Wm−2) and ΔF a stochastic forcing term. The longwave outgoing radiation term is given by the product of the Stefan-Boltzmann constant σB = 5.67108 Wm−2K−4, and an emissivity term ϵ = 0.6 with the fourth power of the system’s temperature.
The heat capacity C is that of a 1m2 surface oceanic box, computed as f · ρ · c · h, with f = 0.7 scaling for the approximate ocean area fraction of the planet, ρ the density of water, c the specific heat capacity of water and h as depth of the box. For a fixed value of Q, the ODE solution describes the system’s convergence to an equilibrium state. However, in a simplified experiment, volcanic perturbations can also be considered disturbances in the energy balance, modeled by a radiative forcing anomaly relative to the equilibrium state, ΔF.
| (7) |
We obtain ΔF (all=CO2+solar+volcanic, volcanic) from the forcing reconstructions [60], translating original values values to effective radiative forcing [1, 123] to W/m2. Specifically for the aerosol optical depth (AOD), we use −25W/m2 per 1 unit AOD [1]. We run the EBM for two different forcing combinations: Volcanic only (Fig. 4 and Supplementary Fig. 14) and all = CO2 + solar + volcanic (Supplementary Fig. 14). The EBM response for both forcing scenarios shows consistent multi-decadal variability (Supplementary Fig. 14). The EBM also demonstrates that with an increase of the frequency of volcanic events, the relative proportion of variance in the multi-decadal to centennial band increases (Supplementary Fig. 15).
Data availability
The paleotemperature records (PAGES 2k v.2.0.0) used for all reconstructions are at www.ncdc.noaa.gov/paleo/study/21171. CMIP5 model runs are at: http://pcmdi9.llnl.gov/. The primary outcomes for this study, including the temperature reconstructions for each method and the data used to construct the key figures including external forcing datasets used herein, model GMST and the screened input proxy data matrix, are available through the World Data Service (NOAA) Paleoclimatology (https://www.ncdc.noaa.gov/paleo/study/26872) and Figshare (doi: 10.6084/m9.figshare.c.4507043)
Code availability
The code to generate the Figures is available along with the data in the repository listed above under Data availability.
Supplementary Material
Acknowledgements
This is a contribution to the PAGES 2k Network. Past Global Changes (PAGES) is supported by the US National Science Foundation and the Swiss Academy of Sciences. PAGES 2k Consortium members are acknowledged for providing input proxy data. Some calculations were run on the Ubelix cluster of the University of Bern. Sami Hanhijärvi provided the PaiCO code. Martin Grosjean, Steven J. Phipps and Johannes Werner provided inputs at different stages of the project. R.N. is supported by the Swiss NSF grant PZ00P2_154802. K.R. is funded by DFG grant no. RE3994-2/1. S.B. acknowledges funding from the European Union (project 787574). F.S. is funded by NSFC (41877440; 41430531; 41690114). A.S. was supported by NERC under the Belmont forum, Grant PacMedy (NE/P006752/1)
Footnotes
Author contributions R.N. coordinated the project. R.N. and J.E.G. provided and generated input data. R.N. (PCR, CPS, PAI), F.S. (OIE, M08), M.P.E (DA) and L.A.B (BHM) and developed and performed GMST reconstructions. R.N., K.R. and M.N.E. analyzed reconstruction results. L.L. and A.S. performed the D&A analysis. F.Z. calculated the solar cross-wavelet analysis. K.R. performed the EBM analyses. J.F. and V.V. contributed to other data analysis. R.N. made the figures. R.N., D.S.K., M.N.E. and K.R. wrote the paper. L.A.B., S.B., J.E.G., M.P.E., M.N.E., J.F., G.J.H., B.J.H., D.S.K., F.C.L., R.N., N.M., K.R., A.S., F.S. and L.vG designed the study, discussed the results and contributed to the writing.
Competing Interests The authors declare that they have no competing interests.
References
- [1].Masson-Delmotte V, et al. Information from Paleoclimate Archives. Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; 2013. pp. 383–464. [Google Scholar]
- [2].Abram NJ, et al. Early onset of industrial-era warming across the oceans and continents. Nature. 2016;536:411–418. doi: 10.1038/nature19082. [DOI] [PubMed] [Google Scholar]
- [3].Hegerl GC, Stefan Brönnimann, Andrew Schurer, Tim Cowan. The early 20th century warming: Anomalies, causes, and consequences. Wiley Interdisciplinary Reviews: Climate Change. 2018;9:e522. doi: 10.1002/wcc.522. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Medhaug I, Stolpe MB, Fischer EM, Knutti R. Reconciling controversies about the ‘global warming hiatus’. Nature. 2017;545:41–47. doi: 10.1038/nature22315. [DOI] [PubMed] [Google Scholar]
- [5].Deser C, Phillips A. An overview of decadal-scale sea surface temperature variability in the observational record. PAGES Magazine. 2017;25:2–6. [Google Scholar]
- [6].Keenlyside NS, Latif M, Jungclaus J, Kornblueh L, Roeckner E. Advancing decadal-scale climate prediction in the North Atlantic sector. Nature. 2008;453:84–88. doi: 10.1038/nature06921. [DOI] [PubMed] [Google Scholar]
- [7].Stott PA, et al. External Control of 20th Century Temperature by Natural and Anthropogenic Forcings. Science. 2000;290:2133–2137. doi: 10.1126/science.290.5499.2133. [DOI] [PubMed] [Google Scholar]
- [8].Deser C, Knutti R, Solomon S, Phillips AS. Communication of the role of natural variability in future North American climate. Nature Climate Change. 2012;2:775–779. [Google Scholar]
- [9].Hawkins E, Sutton R. The Potential to Narrow Uncertainty in Regional Climate Predictions. Bulletin of the American Meteorological Society. 2009;90:1095–1108. [Google Scholar]
- [10].Cassou C, et al. Decadal Climate Variability and Predictability: Challenges and Opportunities. Bulletin of the American Meteorological Society. 2018;99:479–490. [Google Scholar]
- [11].Santer BD, et al. Causes of differences in model and satellite tropospheric warming rates. Nature Geoscience. 2017;10:478–485. [Google Scholar]
- [12].Henley BJ, et al. Spatial and temporal agreement in climate model simulations of the Interdecadal Pacific Oscillation. Environmental Research Letters. 2017;12:044011. [Google Scholar]
- [13].Kajtar JB, et al. Global Mean Surface Temperature Response to Large-Scale Patterns of Variability in Observations and CMIP5. Geophysical Research Letters. 2019;46:2232–2241. [Google Scholar]
- [14].Taylor KE, Stouffer RJ, Meehl GA. An Overview of CMIP5 and the Experiment Design. Bulletin of the American Meteorological Society. 2012;93:485–498. [Google Scholar]
- [15].Laepple T, Huybers P. Ocean surface temperature variability: Large model–data differences at decadal and longer periods. Proceedings of the National Academy of Sciences. 2014;111:16682–16687. doi: 10.1073/pnas.1412077111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16].Rehfeld K, Münch T, Ho SL, Laepple T. Global patterns of declining temperature variability from the Last Glacial Maximum to the Holocene. Nature. 2018;554:356–359. doi: 10.1038/nature25454. [DOI] [PubMed] [Google Scholar]
- [17].Zhu F, et al. Climate models can correctly simulate the continuum of global-average temperature variability. Proceedings of the National Academy of Sciences. 2019;116:8728–8733. doi: 10.1073/pnas.1809959116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18].Ding Y, et al. Ocean response to volcanic eruptions in Coupled Model Intercomparison Project 5 simulations. Journal of Geophysical Research: Oceans. 2014;119:5622–5637. [Google Scholar]
- [19].Morice CP, Kennedy JJ, Rayner NA, Jones PD. Quantifying uncertainties in global and regional temperature change using an ensemble of observational estimates: The HadCRUT4 data set. Journal of Geophysical Research. 2012;117:D08101. [Google Scholar]
- [20].Meehl GA, et al. Decadal Prediction. Bulletin of the American Meteorological Society. 2009;90:1467–1486. [Google Scholar]
- [21].PAGES2k Consortium. A global multiproxy database for temperature reconstructions of the Common Era. Scientific Data. 2017;4 doi: 10.1038/sdata.2017.88. sdata201788. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [22].Christiansen B, Ljungqvist FC. Challenges and perspectives for large-scale temperature reconstructions of the past two millennia. Reviews of Geophysics. 2017;55:40–96. [Google Scholar]
- [23].Wang J, Emile-Geay J, Guillot D, McKay NP, Rajaratnam B. Fragility of reconstructed temperature patterns over the Common Era: Implications for model evaluation. Geophysical Research Letters. 2015;42:7162–7170. [Google Scholar]
- [24].Smerdon JE, Pollack HN. Reconstructing Earth’s surface temperature over the past 2000 years: the science behind the headlines. Wiley Interdisciplinary Reviews: Climate Change. 2016;7:746–771. [Google Scholar]
- [25].Cowtan K, Way RG. Coverage bias in the HadCRUT4 temperature series and its impact on recent temperature trends. Quarterly Journal of the Royal Meteorological Society. 2014;140:1935–1944. [Google Scholar]
- [26].Mann ME, et al. Proxy-based reconstructions of hemispheric and global surface temperature variations over the past two millennia. Proceedings of the National Academy of Sciences. 2008;105:13252–13257. doi: 10.1073/pnas.0805721105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [27].Neukom R, et al. Inter-hemispheric temperature variability over the past millennium. Nature Clim Change. 2014;4:362–367. [Google Scholar]
- [28].Luterbacher J, et al. Reconstruction of sea level pressure fields over the Eastern North Atlantic and Europe back to 1500. Climate Dynamics. 2002;18:545–561. [Google Scholar]
- [29].Shi F, Zhao S, Guo Z, Goosse H, Yin Q. Multi-proxy reconstructions of May–September precipitation field in China over the past 500 years. Clim Past. 2017;13:1919–1938. [Google Scholar]
- [30].Hanhijärvi S, Tingley MP, Korhola A. Pairwise comparisons to reconstruct mean temperature in the Arctic Atlantic Region over the last 2,000 years. Climate Dynamics. 2013;41:2039–2060. [Google Scholar]
- [31].Barboza L, Li B, Tingley MP, Viens FG. Reconstructing past temperatures from natural proxies and estimated climate forcings using short- and long-memory models. The Annals of Applied Statistics. 2014;8:1966–2001. [Google Scholar]
- [32].Hakim GJ, et al. The last millennium climate reanalysis project: Framework and first results. Journal of Geophysical Research: Atmospheres. 2016;121:6745–6764. [Google Scholar]
- [33].Rehfeld K, Trachsel M, Telford RJ, Laepple T. Assessing performance and seasonal bias of pollen-based climate reconstructions in a perfect model world. Clim Past. 2016;12:2255–2270. [Google Scholar]
- [34].Ljungqvist FC, Krusic PJ, Brattström G, Sundqvist HS. Northern Hemisphere temperature patterns in the last 12 centuries. Climate of the Past. 2012;8:227–249. [Google Scholar]
- [35].Esper J, et al. Ranking of tree-ring based temperature reconstructions of the past millennium. Quaternary Science Reviews. 2016;145:134–151. [Google Scholar]
- [36].Esper J, Cook ER, Krusic PJ, Peters K, Schweingruber FH. Tests of the RCS method for preserving low-frequency variability in long tree-ring chronologies. Tree-Ring Research. 2003;59:81–98. ISI:000232004100003. [Google Scholar]
- [37].Klippel L, George SS, Büntgen U, Krusic PJ, Esper J. Differing pre-industrial cooling trends between tree-rings and lower-resolution temperature proxies. Climate of the Past Discussions. 2019:1–21. [Google Scholar]
- [38].McGregor HV, et al. Robust global ocean cooling trend for the pre-industrial Common Era. Nature Geoscience. 2015;8:671–677. [Google Scholar]
- [39].George S. An overview of tree-ring width records across the Northern Hemisphere. Quaternary Science Reviews. 2014;95:132–150. [Google Scholar]
- [40].Evans M, Tolwinski-Ward S, Thompson D, Anchukaitis K. Applications of proxy system modeling in high resolution paleoclimatology. Quaternary Science Reviews. 2013;76:16–28. [Google Scholar]
- [41].Babst F, et al. Twentieth century redistribution in climatic drivers of global tree growth. Science Advances. 2019;5:eaat4313. doi: 10.1126/sciadv.aat4313. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [42].Smerdon JE. Climate models as a test bed for climate reconstruction methods: pseudoproxy experiments. Wiley Interdisciplinary Reviews: Climate Change. 2012;3:63–77. [Google Scholar]
- [43].Wang J, Emile-Geay J, Guillot D, Smerdon JE, Rajaratnam B. Evaluating climate field reconstruction techniques using improved emulations of real-world conditions. Climate of the Past. 2014;10:1–19. [Google Scholar]
- [44].Toohey M, Sigl M. Volcanic stratospheric sulfur injections and aerosol optical depth from 500 BCE to 1900 CE. Earth System Science Data. 2017;9:809–831. [Google Scholar]
- [45].Crowley TJ, Unterman MB. Technical details concerning development of a 1200 yr proxy index for global volcanism. Earth System Science Data. 2013;5:187–197. [Google Scholar]
- [46].Gao C, Robock A, Ammann C. Volcanic forcing of climate over the past 1500 years: An improved ice core-based index for climate models. Journal of Geophysical Research. 2008;113:D23111. [Google Scholar]
- [47].Marotzke J, Forster PM. Forcing, feedback and internal variability in global temperature trends. Nature. 2015;517:565–570. doi: 10.1038/nature14117. [DOI] [PubMed] [Google Scholar]
- [48].Allen MR, Stott PA. Estimating signal amplitudes in optimal fingerprinting, part I: theory. Climate Dynamics. 2003;21:477–491. [Google Scholar]
- [49].Bindoff NL, et al. Detection and Attribution of Climate Change: from Global to Regional. In: Stocker TF, et al., editors. Climate Change 2013 - The Physical Science Basis. Cambridge University Press; Cambridge: 2013. pp. 867–952. [Google Scholar]
- [50].Schurer AP, Hegerl GC, Mann ME, Tett SFB, Phipps SJ. Separating Forced from Chaotic Climate Variability over the Past Millennium. Journal of Climate. 2013;26:6954–6973. [Google Scholar]
- [51].Otto-Bliesner BL, et al. Climate Variability and Change since 850 CE: An Ensemble Approach with the Community Earth System Model. Bulletin of the American Meteorological Society. 2016;97:735–754. [Google Scholar]
- [52].Schurer AP, Tett SFB, Hegerl GC. Small influence of solar variability on climate over the past millennium. Nature Geoscience. 2013;7:104–108. [Google Scholar]
- [53].Taricco C, Mancuso S, Ljungqvist FC, Alessio S, Ghil M. Multispectral analysis of Northern Hemisphere temperature records over the last five millennia. Climate Dynamics. 2015;45:83–104. [Google Scholar]
- [54].Anchukaitis KJ, et al. Last millennium Northern Hemisphere summer temperatures from tree rings: Part II, spatially resolved reconstructions. Quaternary Science Reviews. 2017;163:1–22. [Google Scholar]
- [55].PAGES2k-PMIP3 group. Continental-scale temperature variability in PMIP3 simulations and PAGES 2k regional temperature reconstructions over the past millennium. Clim Past. 2015;11:1673–1699. [Google Scholar]
- [56].Frost C, Thompson SG. Correcting for regression dilution bias: comparison of methods for a single predictor variable. Journal of the Royal Statistical Society: Series A (Statistics in Society) 2000;163:173–189. [Google Scholar]
- [57].von Storch H. Reconstructing Past Climate from Noisy Data. Science. 2004;306:679–682. doi: 10.1126/science.1096109. [DOI] [PubMed] [Google Scholar]
- [58].Neukom R, Schurer AP, Steiger NJ, Hegerl GC. Possible causes of data model discrepancy in the temperature history of the last Millennium. Scientific Reports. 2018;8:7572. doi: 10.1038/s41598-018-25862-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [59].Sigl M, et al. Timing and climate forcing of volcanic eruptions for the past 2,500 years. Nature. 2015;523:543–549. doi: 10.1038/nature14565. [DOI] [PubMed] [Google Scholar]
- [60].Jungclaus JH, et al. The PMIP4 contribution to CMIP6 – Part 3: The last millennium, scientific objective, and experimental design for the PMIP4 past1000 simulations. Geosci Model Dev. 2017;10:4005–4033. [Google Scholar]
- [61].Diffenbaugh NS, Pal JS, Trapp RJ, Giorgi F. Fine-scale processes regulate the response of extreme events to global climate change. Proc Natl Acad Sci. 2005;104(44):15774–15778. doi: 10.1073/pnas.0506042102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [62].Bradley RS, Wanner H, Diaz HF. The Medieval Quiet Period. The Holocene. 2016;26:990–993. [Google Scholar]
- [63].Goosse H. Climate System Dynamics and Modelling. Cambridge University Press; New York: 2015. [Google Scholar]
- [64].Miller GH, et al. Abrupt onset of the Little Ice Age triggered by volcanism and sustained by sea-ice/ocean feedbacks. Geophysical Research Letters. 2012;39:L02708. [Google Scholar]
- [65].Brönnimann S. Early twentieth-century warming. Nature Geoscience. 2009;2:735–736. [Google Scholar]
- [66].Flato G, et al. Evaluation of Climate Models. In: Stocker T, et al., editors. Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge, United Kingdom and New York, NY, USA: Cambridge University Press; 2013. pp. 741–866. [Google Scholar]
- [67].Atwood AR, Wu E, Frierson DMW, Battisti DS, Sachs JP. Quantifying Climate Forcings and Feedbacks over the Last Millennium in the CMIP5–PMIP3 Models. Journal of Climate. 2016;29:1161–1178. [Google Scholar]
- [68].IPCC. Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge, United Kingdom and New York, NY, USA: Cambridge University Press; 2013. [Google Scholar]
- [69].Giorgi F, Gao X-J. Regional earth system modeling: review and future directions. Atmospheric and Oceanic Science Letters. 2018;11:189–197. [Google Scholar]
- [70].Seneviratne SI, et al. The many possible climates from the Paris Agreement’s aim of 1.5 degree C warming. Nature. 2018;558:41–49. doi: 10.1038/s41586-018-0181-4. [DOI] [PubMed] [Google Scholar]
- [71].Marcott SA, Shakun JD, Clark PU, Mix AC. A Reconstruction of Regional and Global Temperature for the Past 11,300 Years. Science. 2013;339:1198–1201. doi: 10.1126/science.1228026. [DOI] [PubMed] [Google Scholar]
- [72].Bradley RS, Jonest PD. ’Little Ice Age’ summer temperature variations: their nature and relevance to recent global warming trends. The Holocene. 1993;3:367–376. [Google Scholar]
- [73].Mann ME, Rutherford S, Wahl E, Ammann C. Testing the fidelity of methods used in proxy-based reconstructions of past climate. Journal of Climate. 2005;18 [Google Scholar]
- [74].Jones P, et al. High-resolution palaeoclimatology of the last millennium: a review of current status and future prospects. The Holocene. 2009;19:3–49. [Google Scholar]
- [75].Ljungqvist FC. A New Reconstruction of Temperature Variability in the Extra-Tropical Northern Hemisphere During the Last Two Millennia. Geografiska Annaler: Series A, Physical Geography. 2010;92:339–351. [Google Scholar]
- [76].Cook ER, et al. Asian Monsoon Failure and Megadrought During the Last Millennium. Science. 2010;328:486–489. doi: 10.1126/science.1185188. [DOI] [PubMed] [Google Scholar]
- [77].Gergis J, Neukom R, Gallant AJE, Karoly DJ. Australasian Temperature Reconstructions Spanning the Last Millennium. Journal of Climate. 2016;29:5365–5392. [Google Scholar]
- [78].Neukom R, et al. Multiproxy summer and winter surface air temperature field reconstructions for southern South America covering the past centuries. Climate Dynamics. 2011;37:35–51. [Google Scholar]
- [79].Taylor MH, Losch M, Wenzel M, Schröter J. On the Sensitivity of Field Reconstruction and Prediction Using Empirical Orthogonal Functions Derived from Gappy Data. Journal of Climate. 2013;26:9194–9205. [Google Scholar]
- [80].Mann ME, Bradley RS, Hughes MK. Global-scale temperature patterns and climate forcing over the past six centuries. Nature. 1998;392:779–787. [Google Scholar]
- [81].Luterbacher J, Dietrich D, Xoplaki E, Grosjean M, Wanner H. European seasonal and annual temperature variability, trends, and extremes since 1500. Science. 2004;303:1499–1503. doi: 10.1126/science.1093877. ISI:000220000100036. [DOI] [PubMed] [Google Scholar]
- [82].National Research Council (U.S.) Surface temperature reconstructions for the last 2,000 years. National Academies Press; Washington, DC: 2006. [Google Scholar]
- [83].Ammann CM, Wahl ER. The importance of the geophysical context in statistical evaluations of climate reconstruction procedures. Climatic Change. 2007;85:71–88. [Google Scholar]
- [84].Wahl ER, Ammann CM. Robustness of the Mann, Bradley, Hughes reconstruction of Northern Hemisphere surface temperatures: Examination of criticisms based on the nature and processing of proxy climate evidence. Climatic Change. 2007;85:33–69. [Google Scholar]
- [85].McShane BB, Wyner AJ. A statistical analysis of multiple temperature proxies: Are reconstructions of surface temperatures over the last 1000 years reliable? The Annals of Applied Statistics. 2011;5:5–44. [Google Scholar]
- [86].Wahl ER, Smerdon JE. Comparative performance of paleoclimate field and index reconstructions derived from climate proxies and noise-only predictors. Geophysical Research Letters. 2012;39 [Google Scholar]
- [87].Xoplaki E. European spring and autumn temperature variability and change of extremes over the last half millennium. Geophysical Research Letters. 2005;32:L15713. [Google Scholar]
- [88].Pauling A, Luterbacher J, Casty C, Wanner H. Five hundred years of gridded high-resolution precipitation reconstructions over Europe and the connection to large-scale circulation. Climate Dynamics. 2006;26:387–405. [Google Scholar]
- [89].Küttel M, et al. The importance of ship log data: reconstructing North Atlantic, European and Mediterranean sea level pressure fields back to 1750. Climate Dynamics. 2010;34:1115–1128. [Google Scholar]
- [90].Neukom R, et al. Multi-centennial summer and winter precipitation variability in southern South America. Geophysical Research Letters. 2010;37:L14708. [Google Scholar]
- [91].Wang J, et al. Internal and external forcing of multidecadal Atlantic climate variability over the past 1,200 years. Nature Geoscience. 2017;10:512–517. [Google Scholar]
- [92].Schneider T. Analysis of incomplete climate data: Estimation of mean values and covariance matrices and imputation of missing values. Journal of Climate. 2001;14 [Google Scholar]
- [93].Fierro R, Golub G, Hansen P, O’Leary D. Regularization by Truncated Total Least Squares. SIAM Journal on Scientific Computing. 1997;18:1223–1241. [Google Scholar]
- [94].Shi F, Yang B, Gunten LV. Preliminary multiproxy surface air temperature field reconstruction for China over the past millennium. Science China Earth Sciences. 2012;55:2058–2067. [Google Scholar]
- [95].Emile-Geay J, Cobb KM, Mann ME, Wittenberg AT. Estimating Central Equatorial Pacific SST Variability over the Past Millennium. Part I: Methodology and Validation. Journal of Climate. 2013;26:2302–2328. [Google Scholar]
- [96].PAGES2k Consortium. Continental-scale temperature variability during the past two millennia. Nature Geoscience. 2013;6:339–346. [Google Scholar]
- [97].Christiansen B, Ljungqvist FC. Reconstruction of the Extratropical NH Mean Temperature over the Last Millennium with a Method that Preserves Low-Frequency Variability. Journal of Climate. 2011;24:6013–6034. [Google Scholar]
- [98].Tingley MP, Huybers P. A Bayesian Algorithm for Reconstructing Climate Anomalies in Space and Time. Part II: Comparison with the Regularized Expectation–Maximization Algorithm. Journal of Climate. 2010;23:2782–2800. [Google Scholar]
- [99].Wang Z, et al. Human-induced erosion has offset one-third of carbon emissions from land cover change. Nature Climate Change. 2017;7:345–349. [Google Scholar]
- [100].Blasone R-S, et al. Generalized likelihood uncertainty estimation (GLUE) using adaptive Markov Chain Monte Carlo sampling. Advances in Water Resources. 2008;31:630–648. [Google Scholar]
- [101].Christiansen B, Ljungqvist FC. The extra-tropical Northern Hemisphere temperature in the last two millennia: reconstructions of low-frequency variability. Climate of the Past. 2012;8:765–786. [Google Scholar]
- [102].Moberg A, Sonechkin DM, Holmgren K, Datsenko NM, Karlén W. Highly variable Northern Hemisphere temperatures reconstructed from low- and high-resolution proxy data. Nature. 2005;433:613–617. doi: 10.1038/nature03265. [DOI] [PubMed] [Google Scholar]
- [103].Shi F, et al. Reconstruction of the Northern Hemisphere annual temperature change over the Common Era derived from tree rings. Quaternary Sciences. 2015;35:1051–1063. [Google Scholar]
- [104].Tibshirani R. Regression Shrinkage and Selection via the Lasso. Journal of the Royal Statistical Society. Series B (Methodological) 1996;58:267–288. [Google Scholar]
- [105].Vieira LEA, Solanki SK, Krivova NA, Usoskin I. Evolution of the solar irradiance during the Holocene. Astronomy & Astrophysics. 2011;531:A6. [Google Scholar]
- [106].Toohey M, Stevens B, Schmidt H, Timmreck C. Easy Volcanic Aerosol (EVA v1.0): an idealized forcing generator for climate simulations. Geosci Model Dev. 2016;9:4049–4070. [Google Scholar]
- [107].Thomason L, et al. Stratospheric Aerosol Data Set (SADS Version 2) Prospectus. Geosci Model Dev. in review. [Google Scholar]
- [108].Meinshausen M, et al. Historical greenhouse gas concentrations for climate modelling (CMIP6) Geosci Model Dev. 2017;10:2057–2116. [Google Scholar]
- [109].Emile-Geay J, Erb MP, Hakim GJ, Steig EJ, Noone DC. Climate dynamics with the Last Millennium Reanalysis. PAGES Magazine. 2017;25:162. [Google Scholar]
- [110].Steiger NJ, Hakim GJ, Steig EJ, Battisti DS, Roe GH. Assimilation of Time-Averaged Pseudo-proxies for Climate Reconstruction. Journal of Climate. 2014;27:426–441. [Google Scholar]
- [111].Acevedo W, Fallah B, Reich S, Cubasch U. Assimilation of pseudo-tree-ring-width observations into an atmospheric general circulation model. Clim Past. 2017;13:545–557. [Google Scholar]
- [112].Landrum L, et al. Last Millennium Climate and Its Variability in CCSM4. Journal of Climate. 2013;26:1085–1111. [Google Scholar]
- [113].Dee SG, Steiger NJ, Emile-Geay J, Hakim GJ. On the utility of proxy system models for estimating climate states over the common era. Journal of Advances in Modeling Earth Systems. 2016;8:1164–1179. [Google Scholar]
- [114].Becker A, et al. A description of the global land-surface precipitation data products of the Global Precipitation Climatology Centre with sample applications including centennial (trend) analysis from 1901–present. Earth System Science Data. 2013;5:71–99. [Google Scholar]
- [115].Xiao-Ge X, Tong-Wen W, Jie Z. Introduction of CMIP5 Experiments Carried out with the Climate System Models of Beijing Climate Center. Advances in Climate Change Research. 2013;4:41–49. [Google Scholar]
- [116].Jungclaus JH, et al. Characteristics of the ocean simulations in the Max Planck Institute Ocean Model (MPIOM) the ocean component of the MPI-Earth system model. Journal of Advances in Modeling Earth Systems. 2013;5:422–446. [Google Scholar]
- [117].Giorgetta MA, et al. Climate and carbon cycle changes from 1850 to 2100 in MPI-ESM simulations for the Coupled Model Intercomparison Project phase 5. Journal of Advances in Modeling Earth Systems. 2013;5:572–597. [Google Scholar]
- [118].Jungclaus J, et al. CMIP5 simulations of the Max Planck Institute for Meteorology (MPI-M) based on the MPI-ESM-P model: The past1000 experiment, served by ESGF. 2012 [Google Scholar]
- [119].Phipps SJ, et al. The CSIRO Mk3l climate system model version 1.0 – Part 2: Response to external forcings. Geosci Model Dev. 2012;5:649–682. [Google Scholar]
- [120].Schmidt GA, et al. Present-day atmospheric simulations using GISS ModelE: Comparison to in situ, satellite, and reanalysis data. Journal of Climate. 2006;19:153–192. [Google Scholar]
- [121].Ribes A, Planton S, Terray L. Application of regularised optimal fingerprinting to attribution. Part I: method, properties and idealised analysis. Climate Dynamics. 2013;41:2817–2836. [Google Scholar]
- [122].Kruskal WH, Wallis WA. Use of Ranks in One-Criterion Variance Analysis. Journal of the American Statistical Association. 1952;47:583–621. [Google Scholar]
- [123].Myhre G, Highwood EJ, Shine KP, Stordal F. New estimates of radiative forcing due to well mixed greenhouse gases. Geophysical Research Letters. 1998;25:2715–2718. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The paleotemperature records (PAGES 2k v.2.0.0) used for all reconstructions are at www.ncdc.noaa.gov/paleo/study/21171. CMIP5 model runs are at: http://pcmdi9.llnl.gov/. The primary outcomes for this study, including the temperature reconstructions for each method and the data used to construct the key figures including external forcing datasets used herein, model GMST and the screened input proxy data matrix, are available through the World Data Service (NOAA) Paleoclimatology (https://www.ncdc.noaa.gov/paleo/study/26872) and Figshare (doi: 10.6084/m9.figshare.c.4507043)