Toward Leveraging Human Connectomic Data in Large Consortia: Generalizability of fMRI-Based Brain Graphs Across Sites, Sessions, and Paradigms

Abstract

While graph theoretical modeling has dramatically advanced our understanding of complex brain systems, the feasibility of aggregating connectomic data in large imaging consortia remains unclear. Here, using a battery of cognitive, emotional and resting fMRI paradigms, we investigated the generalizability of functional connectomic measures across sites and sessions. Our results revealed overall fair to excellent reliability for a majority of measures during both rest and tasks, in particular for those quantifying connectivity strength, network segregation and network integration. Processing schemes such as node definition and global signal regression (GSR) significantly affected resulting reliability, with higher reliability detected for the Power atlas (vs. AAL atlas) and data without GSR. While network diagnostics for default-mode and sensori-motor systems were consistently reliable independently of paradigm, those for higher-order cognitive systems were reliable predominantly when challenged by task. In addition, based on our present sample and after accounting for observed reliability, satisfactory statistical power can be achieved in multisite research with sample size of approximately 250 when the effect size is moderate or larger. Our findings provide empirical evidence for the generalizability of brain functional graphs in large consortia, and encourage the aggregation of connectomic measures using multisite and multisession data.

Introduction

Since its debut in the last decade (Sporns et al. 2005), the study of functional interactions in the human connectome has become an increasingly appealing research frontier in neuroscience. The brain connectome is typically modeled using graph theoretical methods, which decompose the functional architecture of the brain into a large set of nodes and interconnecting edges (Bullmore and Bassett 2011). This approach has greatly advanced our understanding of the functional organization of the brain, bringing valuable insights into the topological characteristics of brain systems (Power et al. 2011) and variations therein related to neural development (Fair et al. 2009), aging (Meunier et al. 2009) and clinical brain disorders (Buckner et al. 2009; Lynall et al. 2010; Cao et al. 2016).

We are now in the era of “big data,” where large research consortia have been established around the world and hundreds or thousands of imaging scans could potentially be pooled to pursue questions that can only be addressed with large sample sizes (Biswal et al. 2010). Such applications include ascertaining genetic determinants of brain network structure (Richiardi et al. 2015) or elucidating patterns in brain network architecture predictive of low-incidence disease among individuals at risk (Cao et al. 2016). However, while moderate to high test–retest reliability of brain graph properties has been demonstrated in both resting state (Braun et al. 2012; Cao et al. 2014; Termenon et al. 2016) and active tasks (Cao et al. 2014; Wang et al. 2017) using data acquired at a single site, it remains unclear whether the increased sample size associated with pooling data collected across different sites is offset by attenuated reliability of network analysis measures in relation to statistical power. Previous work has shown relatively good predictability of connectome-based measures for neuropsychiatric disorders such as autism using multisite data (Abraham et al. 2017), suggesting larger participant-related variance compared with site-related variance in connectomic studies. Despite this, the reliability of the connectomic measures in a multisite setting has not been explicitly explored. The utility of data fusion in connectomics research will be constrained by the answer to this question.

Here, using the data from the North American Prodrome Longitudinal Study (NAPLS) consortium (Addington et al. 2012), we sought to examine the feasibility of aggregating multisite, multisession functional magnetic resonance imaging (fMRI) data in the study of brain graphs. In this work, 8 subjects were scanned twice (on consecutive days) at each of the 8 study sites across the United States and Canada using a battery of 5 fMRI paradigms including 4 cognitive tasks and a resting state scan. This unique sample allows us to probe the question of whether it is feasible (i.e., achieving acceptable levels of reliability) to aggregate fMRI data acquired from multiple sites and sessions and to determine which approach to aggregating such data maximizes reliability. Generalizability theory was used to quantify reliability of graph theoretical metrics, first for the full 8-site, 2-session study, and then for the circumstance in which a given subject is scanned once on one site drawn randomly from the set of all available sites (i.e., paralleling the design of the typical cohort study in which scans from a single session are pooled across multiple sites). We compared reliability of graph theoretical metrics across different fMRI paradigms and data processing schemes and isolated the most reliable nodes in the brain for each paradigm. We also estimated the required sample size to achieve satisfactory statistical power in a multisite study and investigated the effects of 2 data pooling methods (“merging raw data” and “merging results”) on the reliability of the resulting brain graphs. The results of this study provide evidence for the feasibility, sample size, and optimal method for pooling large sets of graph theoretical measures in large consortia.

Methods

Subjects

A sample of 8 healthy traveling subjects (age 26.9 ± 4.3 years, 4 males) was included as part of the NAPLS-2 consortium (Addington et al. 2012). The consortium comprises 8 study sites across the United States and Canada: Emory University, Harvard University, University of Calgary, University of California Los Angeles (UCLA), University of California San Diego (UCSD), University of North Carolina Chapel Hill (UNC), Yale University, and Zucker Hillside Hospital (ZHH). Each site recruited one subject and the participants traveled to each of the 8 sites in a counterbalanced order. At each site, subjects were scanned twice on 2 consecutive days with the same fMRI paradigms, resulting in a total of 128 scans (8 subjects × 8 sites × 2 days) for each paradigm. All scans were completed within a period of 2 months, during which time no changes were made to the MRI scanners at each site.

All participants received the Structured Clinical Interview for Diagnostic and Statistical Manual of Mental Disorders (DSM-IV-TR (First et al. 2002)) and Structured Interview for Prodromal Syndromes (McGlashan et al. 2001), and were excluded if they met the criteria for psychiatric disorders or prodromal syndromes. Other exclusion criteria included a prior history of neurological or psychiatric disorders, substance dependency in the last 6 months, IQ < 70 (assessed by the Wechsler Abbreviated Scale of Intelligence (Wechsler 1999)) and the presence of a first-degree relative with mental illness. All subjects provided informed consent for the study protocols approved by the institutional review boards at each site.

Experimental Paradigms

The NAPLS-2 consortium included a battery of 5 paradigms targeting functional domains of interest in cognitive neuroscience: a verbal working memory paradigm (hereafter WM paradigm), a paired-associates encoding paradigm for episodic memory (hereafter EM encoding paradigm), a paired-associates retrieval paradigm for episodic memory (hereafter EM retrieval paradigm), an emotional face matching paradigm (hereafter FM paradigm) and a resting-state paradigm (hereafter RS paradigm). These paradigms have been described in detail in previous studies (Forsyth et al. 2014; Gee et al. 2015; Noble et al. 2016) but are summarized briefly below.

The WM paradigm is a block-designed Sternberg-style task where subjects viewed a set of uppercase consonants (each set displayed for 2 s, followed by a fixation cross for 3 s). After each set, a lowercase probe appeared and the participants were instructed to indicate if the probe matched any of the consonants from the previous set by pressing designated buttons. Four conditions were presented in the task targeting 4 working memory loads with 3, 5, 7, and 9 consonants in the target sets. Each load comprised a total of 12 trials with 50% matched trials. The resting-state fixation blocks were interspersed throughout the task to provide a baseline. The entire task lasted for 9 min (184 whole-brain volumes).

The EM encoding task used an event-related paradigm where subjects were presented a series of semantically unrelated word pairs for objects from 12 different categories (e.g., animals, transportations, food, etc.) and colored picture pairs depicting each word. During each trial, participants were asked to imagine the 2 objects interacting together and then pressed a button once a salient relationship had been built between the 2 words. Each trial was displayed for 4 s and followed by a jittered interstimulus interval between 0.5 and 6 s. In the active baseline condition, subjects were presented by a series of 1-digit number pairs and colored squared pairs. Participants were asked to sum up the 2 numbers and press a button once the summation had been calculated. The paradigm consisted of 32 encoding trials and 24 baseline trials and lasted for 8.3 min (250 whole-brain volumes).

The EM retrieval paradigm followed directly after the EM encoding task. In this task, a pair of words was presented on the screen on each trial and subjects were asked to indicate whether the given word pair had been presented during the encoding paradigm by ranking their confidence level. The retrieval paradigm consisted of 64 trials where 50% had been presented during encoding task. In the active baseline condition, participants were instructed to press the button corresponding to a confidence level presented on the screen. The retrieval run lasted for 7.3 min (219 whole-brain volumes).

The FM task consisted of 2 consecutive identical runs on each day. Each run comprised 5 conditions where subjects viewed a set of emotional faces or geometric shapes. In the face matching condition, participants were instructed to choose which of the 2 faces shown on the screen presented the same emotion as a target face. In the face labeling condition, subjects were asked to choose which of the 2 labels (e.g., angry, scared, surprised, and happy) depicted a target face. In the gender matching condition, subjects needed to select which of the 2 faces on the screen was the same gender as a target face. In the gender labeling condition, participants selected which gender label (i.e., male or female) corresponded to a target face. In the shape matching condition, participants were asked to match 2 corresponding geometric shapes. Each block lasted for 50 s with 10 trials. The entire task was performed in 2 separate runs with 5.5 min (132 whole-brain volumes) each.

RS is a 5-min eyes-open paradigm (154 whole-brain volumes) where subjects were asked to lay still in the scanner, relax, gaze at a fixation cross, and not engage in any particular mental activity. After the scan, investigators confirmed with the participants that they had not fallen asleep in the scanner.

To ensure successful manipulation of active tasks, we checked task response rates for each scan. The scans with a response rate < 50% were excluded for data analysis. This resulted in exclusion of a total of 2 scans for the EM encoding paradigm. In addition, for each of the WM, EM encoding, EM retrieval, and FM tasks, 1 scan was unusable due to technical artifacts, and 1 scan for the EM encoding paradigm did not complete successfully. These data were also excluded from analysis.

Data Acquisition

Imaging data were acquired from 8 3 T MR scanners with 3 different machine models. Specifically, Siemens Trio scanners were used at Emory, Harvard, UCLA, UNC and Yale, GE HDx scanners were used at UCSD and ZHH, and a GE Discovery scanner was used at Calgary. The Siemens sites employed a 12-channel head coil and the GE sites employed an 8-channel head coil. fMRI scans were performed by using gradient-recalled-echo echo-planar imaging (GRE-EPI) sequences with identical parameters at all 8 sites: (1) WM paradigm: TR/TE 2500/30 ms, 77° flip angle, 30 4-mm slices, 1 mm gap, 220 mm FOV; (2) EM encoding and retrieval paradigms: TR/TE 2000/30 ms, 77° flip angle, 30 4-mm slices, 1 mm gap, 220 mm FOV; (3) FM paradigm: TR/TE 2500/30 ms, 77° flip angle, 30 4-mm slices, 1 mm gap, 220 mm FOV; (4) RS paradigm: TR/TE 2000/30 ms, 77° flip angle, 30 4-mm slices, 1-mm gap, 220-mm FOV. In addition, we also acquired high-resolution T1-weighted images for each participant with the following sequence: (1) Siemens scanners: magnetization-prepared rapid acquisition gradient-echo (MPRAGE) sequence with 256 mm × 240 mm × 176 mm FOV, TR/TE 2300/2.91 ms, 9° flip angle; and (2) GE scanners: spoiled gradient recalled-echo (SPGR) sequence with 260 mm FOV, TR/TE 7.0/minimum full ms, 8° flip angle.

Data Preprocessing

Data preprocessing followed the standard procedures implemented in the Statistical Parametric Mapping software (SPM8, http://www.fil.ion.ucl.ac.uk/spm/software/spm8/). The same preprocessing pipelines were used for each paradigm. In brief, all fMRI images were slice-time corrected to the first slices of each run, realigned for head motion, registered to the individual T1-weighted structural images, and spatially normalized to the Montreal Neurological Institute (MNI) template with a resampled voxel size of 2 × 2 × 2 mm³. Finally, the normalized images were spatially smoothed with an 8 mm full-width at half-maximum (FWHM) Gaussian kernel.

All preprocessed images were then examined for head motion. Specifically, we quantified frame-wise displacements (FD) for each subject in each run based on the previous definition (Power et al. 2012). The scans with an average FD ⩾ 0.5 mm were shown to have a pronounced within-subject effect on connectivity (Power et al. 2012) and thus were discarded. This resulted in the exclusion of 1 scan for the EM encoding task, 1 scan for the EM retrieval task, and 2 scans for the FM task. As a consequence, the final number of scans included for further network analysis were 127 for the WM paradigm, 123 for the EM encoding paradigm, 126 for the EM retrieval paradigm, and 125 for the FM paradigm.

Given the fact that the time series for WM, EM encoding and EM retrieval tasks were much longer than that for resting state than that during resting state, this discrepancy would confound the direct comparisons of the derived reliability estimates between paradigms. To achieve a matched amount of data, we only used the first 154 time points in these tasks for further analysis, which equaled the total number of time points in resting state.

Construction of Brain Graphs

Overview of Brain Graph Analysis

Our brain graph analysis followed closely with the approaches reported in the literature (Bullmore and Sporns 2009; Bullmore and Bassett 2011; Cao et al. 2014, 2016, 2017; Gu et al. 2017) and aimed to cover several different graph construction schemes. Particularly, nodes and edges are 2 fundamental elements in the construction of brain networks. The definitions of nodes and edges differ in the literature in terms of different brain atlases and different connection weights. While brain graphs derived from distinct processing schemes are qualitatively similar (Wang et al. 2009; Zalesky et al. 2010; Lord et al. 2016) and thus might all be valid in the study of human connectomes, the comparative reliability of different schemes in the context of multisite, multisession studies is unclear. In addition, whether to perform global signal regression (GSR) during data processing is still an open question and the reliability for this processing step has not been established (Murphy and Fox 2017). Here, we focused our analysis on 2 widely used brain atlases (the AAL atlas (Tzourio-Mazoyer et al. 2002) and the Power atlas (Power et al. 2011)), 2 types of graphs (binary graph and weighted graph) and 2 processing strategies (with GSR and without GSR). Consequently, 8 different graph models were constructed for each scan in our data: AAL binary graph with/without GSR, AAL weighted graph with/without GSR, power binary graph with/without GSR and power weighted graph with/without GSR. Figure 1 provides a diagram describing the graph construction procedures.

Figure 1.

Diagram of the overall analysis pipeline in the study (see Methods for details).

Node Definition

We used 2 different node definitions (1 anatomy-based and 1 function-based) to construct brain graphs, in order to investigate how different atlases would influence the results. The anatomically based definition was given by the AAL atlas consisting of 90 nodes based on cortical gyri and subcortical nuclei (Tzourio-Mazoyer et al. 2002), and the functionally based definition was given by the Power atlas with 264 nodes based on meta-analyses of task and rest data (Power et al. 2011). Notably, the Power atlas does not include nodes in the bilateral hippocampus, bilateral amygdala and bilateral ventral striatum. Since these regions are of particular interest in cognitive and clinical neuroscience, we additionally included these nodes based on previously published coordinates from meta-analyses (Spreng et al. 2009; Liu et al. 2011; Sabatinelli et al. 2011), thereby increasing the total number of nodes to 270 (one node per region and hemisphere). This expanded Power atlas has also been used in the previous research (Cao et al. 2014, 2017; Braun et al. 2015).

Noise Correction

The mean time series for each node in both atlases were then extracted from the preprocessed images. The extracted time series were then corrected for the mean effects of task conditions (for task data), white matter and cerebrospinal fluid signals, and the 24 head motion parameters (i.e., the 6 rigid-body parameters generated from the realignment step, their first derivatives, and the squares of these 12 parameters (Satterthwaite et al. 2013; Power et al. 2014)). To assess the effect of GSR on brain graph reliability, all measures were calculated both with and without GSR. The residual time series were then temporally filtered (task data: 0.008 Hz high pass, rest data: 0.008–0.1 Hz band pass) to account for scanner noises.

Edge Definition and Network Thresholding

The corrected and filtered time series were subsequently used to build a 90 × 90 (AAL atlas) or 270 × 270 (Power atlas) pairwise correlation matrix for each scan using Pearson correlations. The derived correlation matrices were further thresholded into 50 densities ranging from 0.01 to 0.50 with an increment interval of 0.01. At each density, only the connections with correlation coefficients higher than the given threshold were kept as true internode connections in the matrices. The density range was based on common practice in the literature and on empirical data where small-world networks are present within the range (Achard and Bullmore 2007; Cao et al. 2014, 2016). Afterwards, edges in binary networks were defined by assigning a value of 1 to the connections that survived a given threshold, and edges in weighted networks were given as the original correlation coefficients of the survived connections. For both binary and weighted networks, a value of 0 was assigned to the connections that did not survive a given threshold. As a result, 8 adjacency matrices were generated for each scan: 90 × 90 binary matrix with/without GSR, 90 × 90 weighted matrix with/without GSR, 270 × 270 binary matrix with/without GSR, and 270 × 270 weighted matrix with/without GSR. Graph theory based brain network measures were subsequently calculated from these derived matrices.

Graph Theoretical Measures for Connectomics

We computed a series of graph-based connectomic measures that are commonly reported in the literature evaluating the network connectivity strength, network segregation and integration, small-world and modular structures, assortative and hierarchical organizations, and nodal centrality. These measures can be generally divided into 2 categories: global measures and local measures. The global measures quantify the characteristics of the brain as an entity, as follows:

• Mean connectivity: mean of all elements in the correlation matrix.

• Small-worldness: an index assessing the combination of network segregation (clustering) and network integration (path length).

• Transitivity: normalized global metric of network clustering.

• Characteristic path length: average shortest path length between all pairs of nodes in the network.

• Global efficiency: average inverse of shortest path length between all pairs of nodes in the network.

• Modularity: degree to which the network can be divided into nonoverlapping communities.

• Number of modules: number of communities the network can be divided into.

• Assortativity: tendency for nodes to be connected with other nodes of the same or similar degree.

• Hierarchy: power law relationship between degree and clustering coefficients for all nodes in the network.

Accordingly, the local measures quantify the properties of each network node, including:

• Node strength: mean connectivity of a given node.

• Node diversity: variance of connectivity of a given node.

• Node degree: number of links connected to a given node.

• Clustering coefficient: proportion of node’s neighbors that are also neighbors of each other.

• Node path length: average path length between a given node and all other nodes in the network.

• Local efficiency: inverse of shortest path length for a given node.

• Betweenness centrality: fraction of shortest paths in the network that pass through a given node.

• Within-module degree: local degree of a given node in its own module relative to other nodes.

• Participation coefficient: ability of a given node in connecting different modules relative to connecting its own module.

All measures were computed using the Brain Connectivity Toolbox (BCT) (https://sites.google.com/site/bctnet/). For a more detailed description of these graph theoretical measures, please refer to the previous publications (Bullmore and Sporns 2009; Rubinov and Sporns 2010; Bullmore and Bassett 2011). Of note, the computations for small-worldness and modular partitions were based on 100 network randomizations, and Louvain greedy algorithm was used for the optimization of modularity quality function Q (with resolution parameter γ = 1) (Newman 2006; Blondel et al. 2008). After computation, all derived connectomic measures were averaged across all densities to ensure that results were not biased by a single threshold.

Assessment of Reliability Using Generalizability Theory

Generalizability Theory

The generalizability theory is an extension of the classical test theory which typically uses intraclass correlation coefficients (ICC) as index of reliability (Shrout and Fleiss 1979; Barch and Mathalon 2011; Cao et al. 2014). Unlike classical test theory, generalizability theory pinpoints the source of different systematic and random variances by decomposing the total variance into different facets of measurement (Shavelson and Webb 1991; Barch and Mathalon 2011). Here, the total variance in each of the outcome measures (σ²(Xpsd)) was decomposed into (1) the participant-related variance σ²(p), (2) the scan site-related variance σ²(s), (3) the session-related variance σ²(d), (4) their 2-way interactions σ²(ps), σ²(pd), σ²(sd), and (5) their 3-way interaction and random error σ²(psd,e) (Shavelson and Webb 1991; Noble et al. 2016).

$$\begin{array}{cc}{\sigma }^2\left(Xpsd\right)& ={\sigma }^2\left(p\right)+{\sigma }^2\left(s\right)+{\sigma }^2\left(d\right)+{\sigma }^2\left(ps\right)\\ & +{\sigma }^2\left(pd\right)+{\sigma }^2\left(sd\right)+{\sigma }^2\left(psd,e\right)\end{array}$$

Reliability was subsequently quantified using the D-coefficient (ϕ), which in essence measures the proportion of participant-related variance over the total variance, thus evaluating the absolute agreement of the target measure (analogous to ICC(2,1) in classical test theory (Shavelson and Webb 1991)).

$$\varphi =\frac{{\sigma }^2(p)}{{\sigma }^2\left(p\right)+\frac{{\sigma }^2(s)}{n(s)}+\frac{{\sigma }^2(d)}{n(d)}+\frac{{\sigma }^2(\mathit{ps})}{n(s)}+\frac{{\sigma }^2(\mathit{pd})}{n(d)}+\frac{{\sigma }^2(\mathit{sd})}{n\left(s\right)\ast n(d)}+\frac{{\sigma }^2(\mathit{psd},e)}{n\left(s\right)\ast n(d)}}$$

where, n(i) represents the number of levels in factor, i. According to established criteria (Shrout and Fleiss 1979; Cao et al. 2014; Forsyth et al. 2014), the D-coefficients can be interpreted as follows: poor reliability (<0.4), fair reliability (0.4–0.59), good reliability (0.6–0.74), and excellent reliability (>0.74).

Generalizability theory can be applied to 2 types of studies, namely, the generalizability study (G-study) and the decision study (D-study). In the G-study, the reliability coefficients are estimated based on the facets and their levels in the studied sample (here n(s) = 8, n(d) = 2)(Shavelson and Webb 1991; Forsyth et al. 2014), while in the D-study, the researchers define the universe they would like to generalize into, which may contain some or all of the facets and levels in the overall universe of observations (Shavelson and Webb 1991; Noble et al. 2016). Since in a neuroimaging consortium, a “nested” design is commonly used whereby each participant is scanned once only at one site and different subjects could be scanned on any number of different scanners, the expected site- and session-related variances would be higher than those in a “crossed” design as used in this study (Lakes and Hoyt 2009). We therefore recomputed the reliability coefficients to generalize our results to n(s) = 1 and n(d) = 1, which correspond to the expected reliability in a “nested” design with distinct subjects between sites and sessions.

Statistics

We performed both G- and D-studies on each of the examined graph properties. For each study, the measurement variances were decomposed using a 3-way analysis of variance (ANOVA) model, where graph properties were entered as dependent variables and subject, site and session were entered as random-effect factors. The estimated variances for each factor were then subjected to the reliability coefficients formula, and D-coefficients for each of the graph properties were calculated. This procedure was repeated for each processing scheme and each paradigm.

We then used the resulting coefficients to explore several scientifically interesting questions. In particular, we asked (1) whether there would be significant reliability differences between global and local properties; (2) whether different node and edge definitions (i.e., AAL binary, AAL weighted, Power binary, Power weighted) would result in differences in reliability measures; (3) whether GSR would significant affect reliability; and (4) whether different fMRI paradigms (i.e., WM, EM encoding, EM retrieval, FM, RS) would generate different reliability. Here, a mixed model was employed to answer these questions, where reliability measures for each property were given as the dependent variable, processing schemes (node and edge definitions, GSR strategies) were given as fixed-effect within-subject factors and fMRI paradigm as random-effect within-subject factor, and property type (global and local) was set as a fixed-effect between-subject factor. The main effects for each of the factors were then estimated.

Given the interdependency nature of graph measures, the reliability estimates derived from these measures are also likely to be dependent on each other. As a result, we further performed a more strict statistical comparison of the reliability measures after controlling for dependency of the observations. This was done by entering the prewhitened reliability values into the mixed model described above. The results from this analysis were also reported.

Node-Wise Reliability in D-Study

Given the fact that the D-study yielded significantly lower mean reliability than the G-study (see Results), particularly for measures of nodal centrality (i.e., degree, betweenness, within-module degree, and participation coefficient), we further probed the reliability of centrality measures for each node in the context of D-study, in order to ascertain the most reliable nodes in the brain in different paradigms. Here, we only utilized Power atlas and weighted networks without GSR to maximize reliability and minimize confounds, since other processing schemes were shown to be significantly less reliable (see Results). The reliability computation followed the same procedure as described above.

Comparison of Statistical Power Between Multisite and Single-Site Studies

Although performing a multisite study provides the opportunity to increase sample size and to generalize results cross sites, it would also likely lead to power loss since it introduces additional site-related variance which is not explicitly modeled in single-site studies. For this reason, we further estimated the minimal sample size that is required for a multisite study to achieve comparable power to that of a single-site study. As described above, the multisite reliability was obtained in the D-study context where both n(s) and n(d) equal to one. For single-site reliability, the D coefficients of all examined measures were recalculated for each of the 8 sites. For each site (16 scans with 8 subjects and 2 sessions), 3 variance components were considered: subject, session and subject × session. The reliability coefficients were computed in terms of these 3 components and then averaged across all 8 sites. By this procedure we acquired empirical estimates evaluating the reliability for a single-site study (Cannon et al. 2017, 2018).

In the situation of perfect reliability (r = 1), the effect size of measurement equals its “true” effect size. However, the effect size attenuates when the reliability of measurement decreases. Therefore, low reliability would bias the “true” effect size of the measurement and in turn lead to power loss (Cohen 1988). Here, we calculated the empirical effect sizes for all graph measures based on their reliability coefficients in the multisite and single-site study contexts. We considered a set of “true” effect sizes ranging from 0.3 to 0.9 (interval of 0.2) to mimic different levels of effect size in a case–control study (small: 0.3; medium: 0.5; large: 0.7; very large: 0.9 (Cohen 1988)). The effect sizes for each measure were computed according to Cohen’s formula (Cohen 1988):

$$\mathit{ES}\left(m\right)=E{S}^{\prime }\left(m\right)\mathrm{\times }\sqrt{\mathit{rel}(m)}$$

where ES′(m) is the “true” effect size of the given measurement, rel(m) is the reliability of the measurement, and ES(m) is the derived effect size under that reliability estimate.

The power estimations were performed using the R statistical power analysis toolbox pwr (https://cran.r-project.org/web/packages/pwr/index.html). Here, for each of the “true” effect sizes, we calculated statistical power across a range of sample sizes for both multisite and single-site studies. This generated a set of functions depicting the relationship between statistical power and sample size for both studies and thus provided the information on the optimal sample sizes for each measure in a multisite study context.

Comparison of Different Data Aggregation Approaches

We further addressed another practical question: at which level should we aggregate data from separate runs of a paradigm? For example, one could merge the outcomes by computing the connectomic measures for each scan run separately and then averaging the derived measures from multiple runs (Anderson et al. 2011). Alternatively, one could merge the original data by concatenating time series from multiple runs and then computing the connectomic measures from the concatenated time series (Laumann et al. 2015). We refer the former as the “merging results” approach and the latter as the “merging raw data” approach. Previous research has shown that concatenation of time series using single-session data dramatically decreases reliability (Cao et al. 2014), suggesting that “merging raw data” may not be an optimal choice for data aggregation. However, by using single-session data, splitting and concatenation of time series would also lead to the decrease of number of time points, bringing difficulty in the interpretation of the observed reliability changes. Therefore, it would be important to investigate whether the same reliability results apply to data concatenation by using scans from multiple sites and/or sessions. Since concatenation of multiple scans would dramatically increase the number of time points and thus potentially benefit reliability, any reliability reductions in the context of merged data would be most likely due to the concatenation method itself.

Here, we aimed to give a direct comparison of reliability measures derived from “merging results” and “merging raw data” approaches, in order to inform a superior data aggregation approach in a multisite, multisession study. The FM task used in this study offered an opportunity to explicitly investigate this question since it comprised 2 consecutive identical runs on each scan day (5.5 min each, see text above). Here, by “merging raw data” the preprocessed time series of both runs were concatenated and brain graph measures were computed from the concatenated time series (i.e., 11 min). In contrast, by “merging results” the graph measures were computed for each run separately and then averaged to acquire the mean measures for both runs. We subsequently calculated the reliability coefficients for the resulting measures from both approaches. A repeated-measures ANOVA model was employed to compare the reliability differences between these 2 approaches and single session, with the processing approach as within-subject factor and reliability measures as dependent variable.

Results

Brain Graph Reliability for Each Paradigm

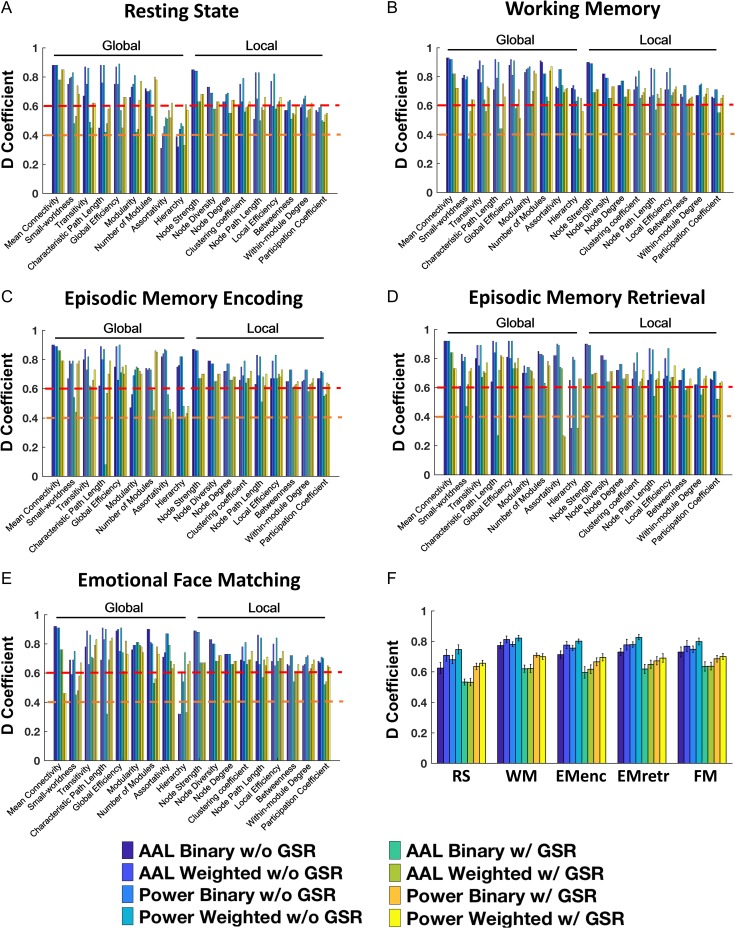
Overall, in the context of the 8-site, 2-session study (G-study), we observed fair to excellent reliability for almost all computed measures in all paradigms, regardless of processing scheme (Fig. 2A–E). The only exceptions for this were measures of assortativity and hierarchy during resting state, episodic memory retrieval and emotional face matching, 2 second-order metrics that showed poor to excellent reliability depending on processing scheme (0.26 < ϕ < 0.82). Among the remainder, the most reliable measures were mean connectivity (0.46 < ϕ < 0.93 for all schemes), transitivity (0.45 < ϕ < 0.91 for all schemes), global efficiency (0.45 < ϕ < 0.92 for all schemes), and node strength (0.63 < ϕ < 0.90 for all schemes). In addition, small-worldness, local efficiency, path length, clustering coefficient, and modularity also showed excellent reliability when using the Power atlas and weighted networks without GSR (0.74 < ϕ < 0.91) (Tables S4, S6, S8, S10, S12).

Figure 2.

Reliability for examined graph properties, paradigms and processing schemes in the G study context, wherein N_sites = 8 and N_sessions = 2 (A: resting state; B: working memory; C: episodic memory encoding; D: episodic memory retrieval; E: emotional face matching). (F) The statistical comparison between different paradigms and schemes by averaging all graph properties. The orange dashed lines indicate the level of fair reliability (⩾0.4) and the red dashed lines indicate the level of good reliability (⩾0.6).

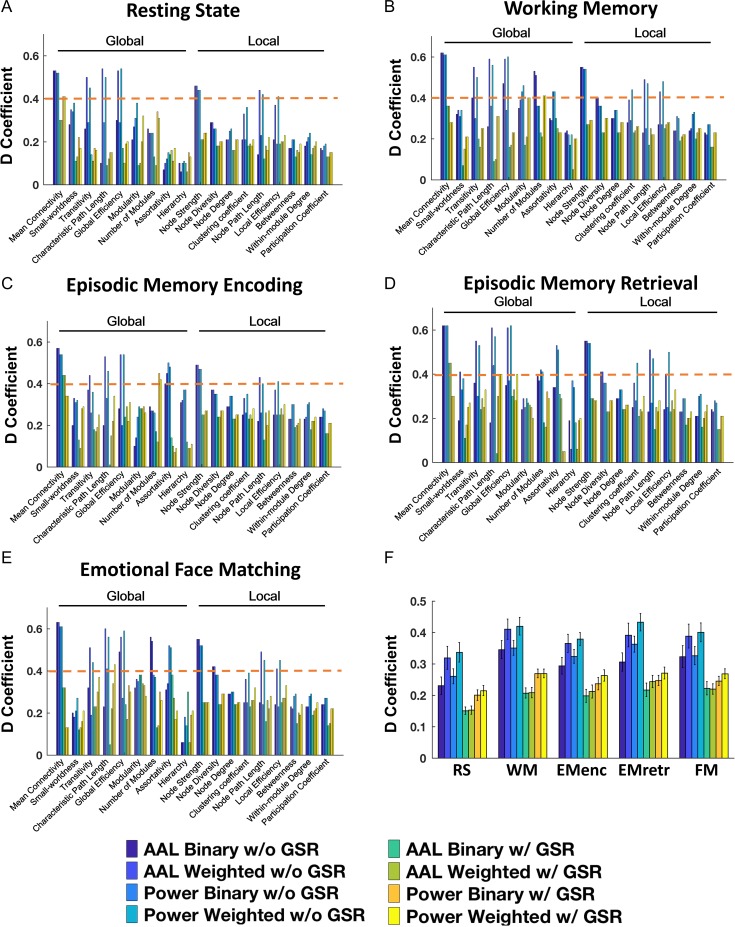
In the D-study with N_sites = 1 and N_sessions = 1, we found dramatically reduced reliability compared with G-study, particularly when analyzed with binary networks (0.06 < ϕ < 0.62 for all paradigms, Fig. 3A–E) and with GSR (0.01 < ϕ < 0.45 for all paradigms). Nevertheless, a few measures still showed fair to good reliability across all paradigms and across both atlases, though only for weighted networks without GSR. These included measures assessing network connectivity strength (e.g., mean connectivity, node strength, 0.44 < ϕ < 0.64 for all paradigms) and network segregation and integration (e.g., path length, efficiency, transitivity, 0.44 < ϕ < 0.62 for all paradigms) (Tables S5, S7, S9, S11, S13). Other measures, such as number of modules, also reached fair reliability in the working memory, episodic memory retrieval and emotional face matching tasks (0.36 < ϕ < 0.54). Together, these findings suggest that measures of network connectivity and network segregation and integration are the most reliable measures in human functional connectomics, even when pooling data in which different subjects are scanned once on different scanners.

Figure 3.

Reliability for examined graph properties, paradigms and processing schemes in the D study context, wherein N_sites = 1 and N_sessions = 1, simulating the design of the typical “big data” application involving pooling of data from different scanning sites (A: resting state; B: working memory; C: episodic memory encoding; D: episodic memory retrieval; E: emotional face matching). (F) The statistical comparison between different paradigms and schemes by averaging all graph properties. The orange dashed lines indicate the level of fair reliability (⩾0.4).

Reliability Comparisons Between Paradigms, Processing Schemes, and Property Types

For both G- and D-studies using original reliability data, the results revealed that fMRI paradigm (P < 0.001), node definition (F > 30.94, P < 0.001), edge definition (F > 24.01, P < 0.001) and GSR (F > 297.68, P < 0.001) all significantly influenced resulting reliability (Figs 2F, 3F). Specifically, graph measures computed from all examined tasks showed higher reliability than those from resting state (P_Bonferroni < 0.001). The Power atlas and weighted networks had higher reliability than the AAL atlas (P < 0.001) and binary networks (P < 0.001). Moreover, significantly higher reliability was observed for data without GSR compared with those with GSR (P < 0.001). In contrast, property type (global and local) did not show significant effect on reliability coefficients (F < 0.51, P > 0.49), suggesting that global and local properties are equally reliable.

After accounting for interdependency of the observations, we found that there were no longer significant differences between different paradigms and network types (P > 0.08). However, significant differences remained between measures with GSR and those without GSR (F > 20.60, P < 0.001), and between those based on the AAL atlas and those based on the Power atlas (F > 5.03, P < 0.03), suggesting that the effects of GSR and brain atlas on graph reliability are robust and less affected by the inherent dependency of the data structure.

Variance Components of Functional Graph Measures

Here we report the results of variance isolation derived from the Power weighted networks without GSR, since this scheme in general yielded the highest reliability. Overall, for all properties in all paradigms, the 3 largest variance components were participant, participant × site and participant × site × session (Figs S1–S5). These 3 components together accounted for more than 80% of the total variance for almost all properties. In contrast, session-related variance was the smallest, less than 1% of the total variance for most properties. In addition, site-related variance was much smaller (2–17 times) than participant-related variance for the vast majority of properties.

For resting state, the proportion of variance attributed to participant ranged between 4% and 50%, with the highest proportion in relation to global efficiency and lowest in relation to within-module degree. For cognitive tasks, the participant variance ranged between 4% and 59%. Here, the properties with the highest participant-related variance were mean connectivity and node strength, which accounted for about 60% of the total variance for all tasks. Other properties with high participant-related variance included measures of network segregation and integration (path length, transitivity, clustering coefficient, efficiency) and node diversity, which in general accounted for around 50% of the total variance for each task. In contrast, participant-related variance represented a low proportion (less than 40% of the total) for measures of small-worldness, modularity, hierarchy and nodal centrality (degree, betweenness, within-module degree, participation coefficient). These results suggest that graph properties evaluating network segregation and integration are more trait-related measures, while those evaluating small-world organization, modular structure, and centrality are more state-related measures.

Node-Wise Reliability in D-Study

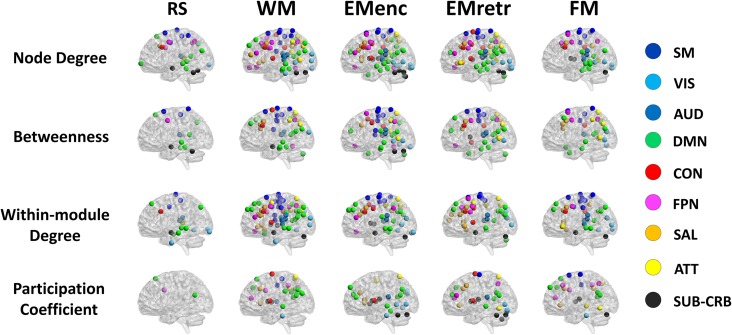
We found that examined tasks had considerably more reliable nodes than resting state for all centrality measures (Fig. 4). While assigning nodes into 9 well-established systems as previously reported (sensori-motor, visual, auditory, default-mode, cingulo-opercular, frontoparietal, salience, attention, subcorticocerebellar (Power et al. 2011)), the reliable nodes (ϕ > 0.40) mainly mapped to the frontoparietal system (e.g., superior, middle and inferior frontal gyri, and inferior parietal lobules), cingulo-opercular system (e.g., superior frontal gyrus, middle cingulate cortex, supramarginal gyrus, and rolandic operculum), salience system (e.g., anterior cingulate cortex, insula, supramarginal gyrus, and middle frontal gyrus), attention system (e.g., inferior frontal gyrus, superior and inferior parietal lobule, precuneous, and middle temporal gyrus), as well as the default-mode system (e.g., medial frontal cortex, precuneous, and middle temporal gyrus), visual system (e.g., middle occipital gyri, lingual gyrus, and fusiform gyrus), and sensori-motor system (e.g., precentral gyrus, postcentral gyrus, supplementary motor area, and paracentral lobule) (Fig. 4 and Table S14).

Figure 4.

The most reliable nodes in terms of nodal centrality measures in the D study context, wherein N_sites = 1 and N_sessions = 1. Nodes were allocated into 9 predefined functional systems according to Power et al. Note that the default-mode and sensori-motor systems showed high reliability in both resting state and cognitive tasks, while the higher-order systems (frontoparietal, cingulo-opercular, attention, salience) were predominantly reliable in cognitive tasks. RS = resting state; WM = working memory; EMenc = episodic memory encoding; EMretr = episodic memory retrieval; FM = emotional face matching.

In contrast to the results for task paradigms, the resting state data in general showed fewer reliable nodes. Here, the reliable nodes were mainly distributed in the default-mode system (e.g., medial frontal cortex, precuneous, and middle temporal gyrus) and sensori-motor system (e.g., precentral gyrus, postcentral gyrus, supplementary motor area, and paracentral lobule) (Table S14). Notably, these systems were part of the reliable systems found in the task paradigms, suggesting that the reliability distribution of nodal centrality consists of a set of systems that is independent of active tasks and another set of systems that is reliable only when tasks are presented.

Comparison of Statistical Power in Multisite Versus Single-Site Studies

The reliabilities of all connectomic measures were substantially higher in the single-site study compared with the multisite study context. Similar to the multisite study, measures of connectivity strength, network segregation and integration had highest reliability of all measures in the single-site study. In addition, measures of hierarchy, modular structure, node diversity and centrality were considerably more reliable in the single-site study than in the multisite study (Table S15).

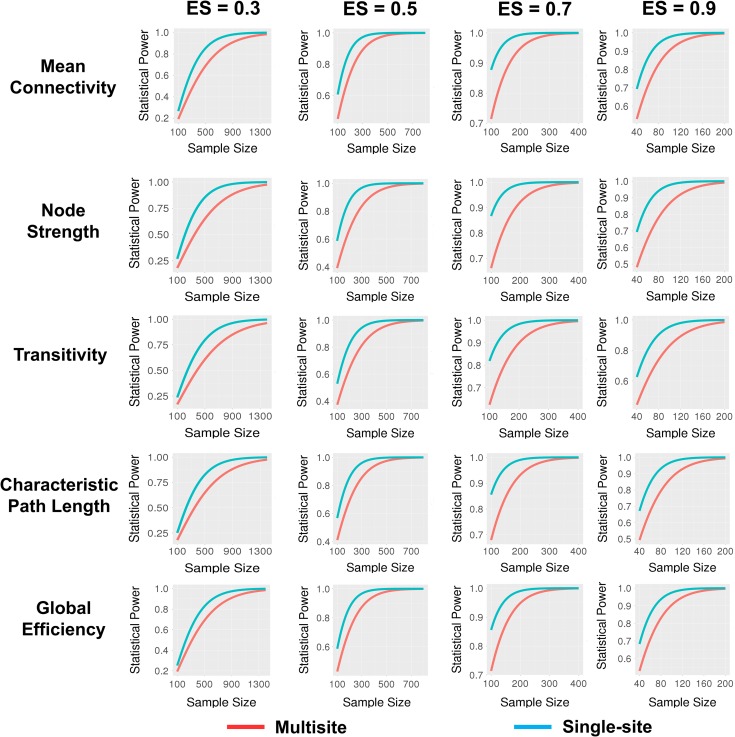
The power analysis revealed that with a small effect size (d = 0.3), the sample size needed for an adequate level of power (≥0.8) in multisite studies (approximately 700–1400) was much larger than that in single-site studies (less than 600 subjects) (Figs 5 and S8). With an increase of effect size, the sample size required to achieve adequate power was dramatically decreased, as was the difference in sample size needed for multisite and single site studies to have equivalently high power. In multisite studies, for the most reliable measures including network connectivity, network segregation and integration, only 250–300 subjects in total were needed to detect a medium effect (d = 0.5), only 100– 150 to detect a large effect (d = 0.7), and only <100 to detect a very large effect (d = 0.9) (Fig. 5). In contrast, for relatively less reliable measures such as hierarchy and nodal centrality, a total sample size of > 150 was required even with a very large effect size (d = 0.9) (Fig. S6). In single-site studies, a total sample size of 275 is sufficient to detect a medium effect and sample size of 100 to detect a large effect for all examined properties.

Figure 5.

Statistical power as a function of total sample size across multiple effect sizes for 5 selected connectomic measures. The red lines represent power for multisite studies while the blue lines represent power for single-site studies, based on Cohen’s d for 2-tailed contrast of 2 independent groups at α = 0.05. The effect sizes have been adjusted downward for observed reliabilities of each connectomic measure in the multisite and single-site contexts, respectively.

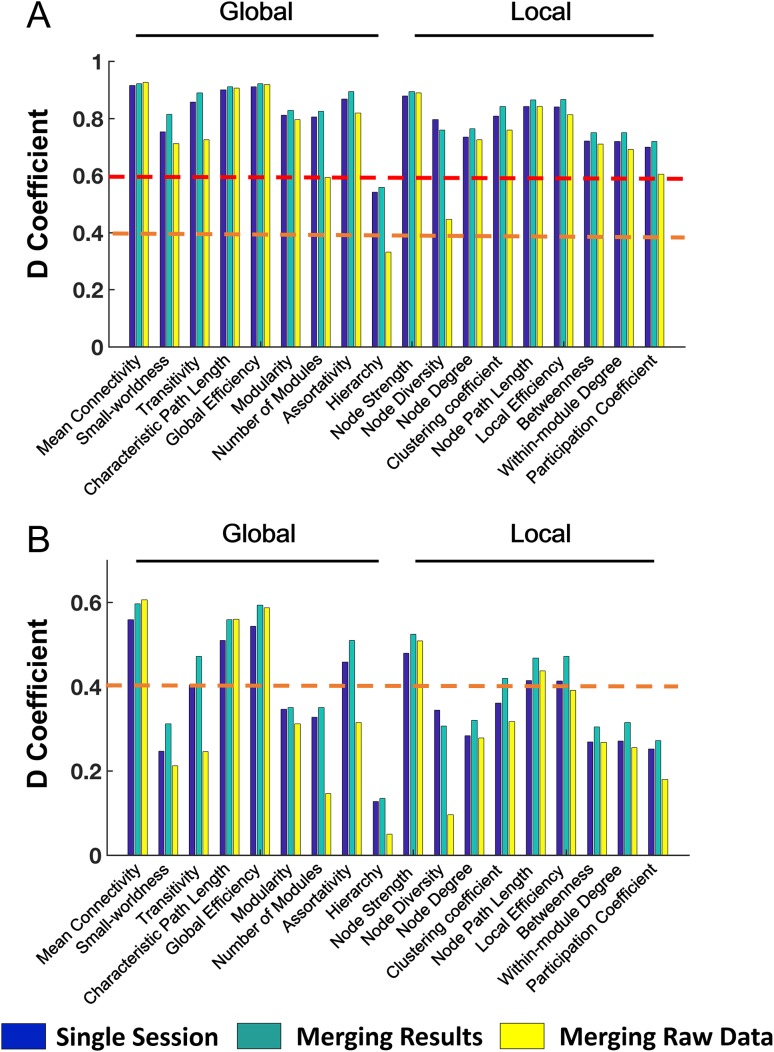
Comparison of Data Pooling Methods

By merging results from both runs, reliability of all studied graph measures increased compared with those derived from a single scan (Fig. 6). In contrast, the “merging raw data” approach reduced reliability for almost all measures. A direct comparison between the 2 methods demonstrated a significant difference in graph reliability, where the “merging results” approach yielded a significantly higher reliability than a single run (F > 20.91, P < 0.001) and the “merging raw data” approach (F > 16.30, P < 0.001) in both G- and D-studies. These results remained significant after prewhitening of the reliability data (F > 10.15, P < 0.005). Moreover, graph measures derived from single run showed significantly higher reliability than those derived from the “merging raw data” approach in both G- and D-studies (F > 5,40, P < 0.03), although only without prewhitening. These results support the superiority of using a “merging results” approach in data aggregation in the study of human functional connectomes.

Figure 6.

Reliability comparison of 2 data aggregation approaches (A: G study; B: D study). The “merging results” approach (i.e., averaging properties across sessions) was associated with significantly higher reliability compared with those from single session, while the “merging raw data” approach (i.e., concatenation of time series from both sessions) had significantly reduced reliability. The orange dashed lines indicate the level of fair reliability (⩾0.4) and the red dashed lines indicate the level of good reliability (⩾0.6).

Discussion

This study investigated a fundamental question in human functional connectomics research: how feasible is it to aggregate multisite fMRI data in large consortia? Our results demonstrated that (1) the connectomic measures derived from different sites and sessions showed generally fair to good reliability, particularly for measures of connectivity strength, network segregation, and network integration; (2) choice of parcellation scheme significantly influenced reliability, with networks constructed from the Power atlas significantly more reliable than those constructed from the AAL atlas; (3) application of GSR remarkably reduced reliability of connectomic measures; (4) while network diagnostics for some primary functional systems were consistently reliable independently of paradigm, those for higher-order cognitive systems were reliable predominantly when challenged by task; (5) a total sample size of 250 participants or more was likely to be sufficient for multisite case–control studies if the effect size of group differences is at least moderate (≥0.5); and (6) different data aggregation approaches yielded different reliabilities, with the “merging results” approach higher than the “merging raw data” approach. These results provide empirical evidence for the feasibility of pooling large sets of functional data in human connectomics research and offer guidelines for sample size, data analytic approaches, and aggregation methods that equate with adequate levels of reliability and statistical power.

Overall Reliability of Functional Graph Measures

Using our multisite, multisession data, we found that the vast majority of functional connectomic measures were reasonably reliable during both resting state and cognitive tasks. This finding is in line with previous studies using test–retest data, where fair to excellent test–retest reliability have been shown for functional graph metrics in various fMRI paradigms, including resting state (Braun et al. 2012; Cao et al. 2014; Welton et al. 2015; Termenon et al. 2016), working memory (Cao et al. 2014), emotional face matching (Cao et al. 2014), attentional control (Telesford et al. 2010), and natural viewing (Wang et al. 2017). These prior publications and our present data suggest that graph theory based connectomic measures are associated with overall high between-subject variance and relatively lower within-subject variance. Indeed, our analyses revealed that subject-related variance was one of the largest components for almost all examined properties in all paradigms. In contrast, within-subject variance such as scan site- and session-related variance, were found to be much smaller than subject-related variance, suggesting the feasibility of using these measures in the study of human functional connectomes in large consortia. Notably, 2 other relatively large components were the subject × site and subject × site × session interactions. This pattern is also consistent with previous findings in brain activity measures during working memory (Forsyth et al. 2014) and emotional face matching (Gee et al. 2015), suggesting that many fMRI measures are sensitive to factors such as subject alertness, diurnal variations, situational distractions, and variations in head placement, among others (Meyer et al. 2016). Because these factors were not controlled in our traveling subjects study, and indeed are difficult to homogenize across sites and time, the reliability coefficients presented here likely represent a lower bound estimate of reliability (i.e., theoretically higher reliabilities would be obtained with greater standardization of time of day, head positioning, and subject alertness).

Interestingly, some of the examined graph properties were associated with particularly high proportions of subject-related variance during the cognitive tasks, including measures of connectivity strength (e.g., mean connectivity and node strength), network segregation (e.g., clustering coefficient and transitivity) and network integration (e.g., path length and global/local efficiency). For each of these measures, approximately 50–60% of the total variance was attributed to subjects, indicating that subject-related variance was larger than any other components. Since a similar finding has also been reported in the previous test–retest studies (Telesford et al. 2010; Cao et al. 2014; Termenon et al. 2016), these results suggest that graph properties for connectivity strength, network segregation and network integration are particularly robust across scan sites and scan sessions and are thus possibly reflective of stable, participant-specific features of brain organization. In contrast, measures assessing the small-world and modular structures (e.g., small-worldness, modularity, number of modules) and nodal centrality (e.g., degree, betweenness, within-module degree, and participation coefficient) had in general equal proportions of subject-related and error-related components, suggesting that these measures are to a greater degree sensitive to within-subject factors and thus potentially more state-related. Prior work has shown that measures of network segregation and integration are highly heritable (Smit et al. 2008; Fornito et al. 2011), while measures of small-world and modular structures are dynamic during different behavioral and cognitive states such as finger tapping (Bassett et al. 2006), motor learning (Bassett et al. 2011, 2015) and memory (Braun et al. 2015). These findings converge with our results in suggesting that trait- and state-related characteristics of brain functional systems may be captured by different graph based connectomic measures.

Effects of Processing Schemes on Reliability

Our study found significant effects of processing scheme on the detected reliability. Specifically, networks constructed from the Power atlas were more reliable than those from the AAL atlas. This is consistent with the finding in a prior study where the Power atlas also showed better reliability than the AAL atlas in terms of test–retest reliability (Cao et al. 2014). Two factors may plausibly account for this. First, the number of nodes in the Power atlas is 3 times as large as that in the AAL atlas. Since atlas size has been shown to be quantitatively influence resulting graph measures (Wang et al. 2009; Zalesky et al. 2010), this effect may also translate to their reliabilities. Second, compared with the AAL atlas, the Power atlas represents a finer definition of functionally separated units derived from the meta-analysis of a large set of imaging data. As a result, networks constructed from the Power atlas may better pertain to the task paradigms used in the study and thus show higher reliability.

Apart from node definition, GSR has shown to have a significant effect on graph reliability. Here, our result is parallel to a previous study showing lower test–retest reliability of hub distributions with GSR (Liao et al. 2013). These findings are particularly interesting since the validity of GSR has been much discussed in the literature (Liu et al. 2017; Murphy and Fox 2017). Arguably, GSR is one of the most effective approaches available to control for head motion related artifacts (Power et al. 2012, 2014; Satterthwaite et al. 2013; Yan et al. 2013). However, global signal also incorporates nonartifactual sources such as postsynaptic spiking (Scholvinck et al. 2010) and brain glucose metabolism (Thompson et al. 2016), and may potentially help to increase diagnostic specificity for certain mental disorders such as schizophrenia (Yang et al. 2014). In addition, while effectively controlling for motion-related artifacts, the GSR step can also introduce spurious anticorrelations (Murphy et al. 2009) and distance-dependent artifact (Ciric et al. 2017) to the data. As a result, the decreased reliability associated with GSR may be attributable to the removal of reliable neural information from the signal and/or the introduction of additional noise into the analysis. Another interpretation, from an opposite point of view is that, head motion is usually highly reliable within subjects (Couvy-Duchesne et al. 2014; Zeng et al. 2014) which could potentially contribute to greater reliability of graph metrics if they are influenced by movement. This possibility would suggest a reliability–accuracy trade-off for brain connectomic measures, where reducing motion artifacts could attenuate reliability but increase accuracy for outcomes. Taken together, these results suggest that a more comprehensive evaluation of effect of GSR is still warranted in future work.

Reliable Nodes in Rest and Tasks

Across both resting state and the implemented tasks, the reliable nodes were predominantly distributed in the default-mode and sensori-motor systems. This result is highly parallel to the results of a recent study using the Human Connectome Project (HCP) test–retest data (Termenon et al. 2016), where the same distribution was reported for resting state. Interestingly, both systems serve as the primary functional systems in the human brain. The default-mode network is involved in brain’s resting state and becomes active when individuals are focused on internal thoughts (Buckner et al. 2008). The sensori-motor system may relate to the motor response during active tasks and the sensation of environmental changes during resting state. The functionality of these systems makes them plausible to be more robust than other systems independent of fMRI paradigms.

Besides the above systems, the cognitive tasks also showed high reliability for nodes in the frontoparietal system, cingulo-opercular system, salience system and attention system. Notably, these systems are pivotal to human cognitive functions such as memory (Prabhakaran et al. 2000; McNab and Klingberg 2008), emotional processing (Phillips et al. 2003) and executive functioning (Niendam et al. 2012), and are strongly associated with the memory–emotion task battery used in this study (Forsyth et al. 2014; Gee et al. 2015). Together, these findings suggest that the cognitive tasks would increase the reliability of the multimodal cognitive systems, while the primary functional systems are consistently robust through different brain states/imaging paradigms.

Statistical Power for Multisite and Single-Site Studies

Although a considerably larger sample size is required to compensate for power loss in a multisite study when the effect size is small, with medium to large effects, sample sizes required for adequate to excellent power are in the range typical of consortium studies, particularly for measures with relatively high multisite reliability (i.e., connectivity strength, network segregation and integration). Interestingly, a recently study using simulated data found that approximately 120 subjects per group are sufficient to yield satisfying power for network connectivity measures in multisite studies (Dansereau et al. 2017), which is quantitatively similar to the estimated sample size in our study. Since a total sample size larger than 200 subjects is increasingly common in large consortia, studies using data from these consortia are likely to be reasonably well-powered.

Effects of Data Pooling Methods on Reliability

By comparing 2 data pooling approaches, we found that “merging results” is associated with significantly better reliability of brain graph measures compared with the “merging raw data” approach. This result is consistent with previous work using single-session data that also revealed a significant decrease of graph reliability by the chopping and concatenation of fMRI time series (Cao et al. 2014). Notably, our current finding was derived from the concatenation of data from 2 identical runs, which increased the total number of time points by a factor of 2. Considering this, the reliability change reported here is most likely induced by the “concatenation” approach itself rather than the loss of data points. While speculative, the poor performance of “concatenation” approach may relate to the modification of the fundamental characteristics of original fMRI series such as signal frequency, which renders the concatenated signals particularly sensitive to physiological noise and other artifacts (Gavrilescu et al. 2008). In contrast, the average of graph properties computed from separate runs significantly increased reliability. This result is intuitive since the mean calculation of multirun data statistically reduces run-specific noise and thus boosts reliability. Another explanation here is that these 2 merging approaches would lead to different treatment of session-related variance, a factor that may affect the outcome reliabilities.

Limitations

We acknowledge several limitations for our study. First, although we have constructed brain networks with several different processing schemes in this work, the choice of other processing schemes such as the preprocessing parameters (Braun et al. 2012), filter frequency (Deuker et al. 2009; Braun et al. 2012), and selected thresholds (Schwarz and McGonigle 2011; Termenon et al. 2016) may still influence reliability. Second, while we have provided data on a set of fMRI experiments evaluating memory, emotion and resting functions of the brain, all findings reported in this study are nevertheless influenced by the specific paradigms, scan parameters, subjects and data processing methods used here, and it is possible that these results may not be able to generalize to other tasks, protocols, processing methods, and populations. Third, our reliability study was based on a crossed design where each subject was evaluated at all of the different sites across 2 sessions. This is different from a more commonly used nested design in which different subjects are evaluated on different scanners. We sought to generalize our results to mimic this situation using the D-study extension, where we were essentially modeling how well one scan randomly sampled from among the set of 16 scans available for each subject reflects their “true” score for each graph property. Fourth, the single-site reliability was estimated by averaging reliability measures across different sites, which implicitly treated site as a fixed-effect factor (Westfall et al. 2016). This was different from our multisite analysis where site was treated as a random-effect factor. Fifth, the total number of time points for the paradigms used in this study (particularly resting state) are generally small, which limits the possibility of exploring the reliability of graph measures in longer scan sessions. Our results suggest that reliability may not benefit from simply concatenating multiple sessions of fMRI data, at least for the face matching paradigm used here. However, it is still an open question whether further increase of fMRI data (e.g., concatenation of series from more than 2 sessions, and extension of scan length for each session) would compensate for the reliability penalty caused by the concatenation method. Sixth, the sample size in our study was relatively small. Although this traveling subject sample is one of the largest to date, future studies with larger samples assessing between-site reliability are still warranted. In addition, much of the work regarding within-site reliability could be performed using larger public datasets such as the HCP (Van Essen et al. 2013), the 1000 Connectome Project (Biswal et al. 2010) and the Healthy Brain Network Serial Scanning Initiative (’Connor et al. 2017). Seventh, our findings were based on 2 commonly used brain atlases which we have chosen to be representative of structural and functional atlases, respectively. However, given the large number of atlases available in the literature (Craddock et al. 2012) and given that no single atlas seems to be qualitatively superior than others (Arslan et al. 2017), it would be important to test the generalizability of connectomic findings across different atlases and to test the effect of parcel numbers on the reliability measures. Eighth, while we argue that single-site studies possess larger power than multisite studies (and tested this using empirical data), we urge the readers to note that the increased power in single-site studies is likely at the cost of higher false positive rate compared with multisite studies. In other words, results from single-site studies likely reflect idiosyncratic site-specific effects that do not necessarily generalize to other sites (Westfall et al. 2016). Last but not least, although our work reported here mainly focused on reliability, it is important to note that reliability is not the only criterion for the guidance of method/measurement selection in a multisite setting. Other measures such as sensitivity and specificity are equally important, and these need to be tested in future work.

Conclusions

In conclusion, using fMRI data and a traveling subject sample, our study presented evidence for the generalizability of human connectomic measures across sites and sessions and for the feasibility of pooling large set of brain network data for both resting state and active tasks. While our findings generally encourage the use of multisite, multisession scans to promote power in functional connectomics research, future work is still required to replicate these findings and to test the generalizability of these results.

Funding

Gifts from the Staglin Music Festival for Mental Health and the International Mental Health Research Organization and by National Institute of Health grants (U01 MH081902 to T.D.C.), (P50 MH066286 to C.E.B.), (U01 MH081857 to B.A.C.), (U01 MH82022 to S.W.W.), (U01 MH066134 to J.A.), (U01 MH081944 to K.S.C.), (R01 U01 MH066069 to D.O.P.), (R01 MH076989 to D.H.M.), (U01 MH081928 to L.J.S.), and (U01 MH081988 to E.F.W.).