Three Dimensional Pose Estimation for Laboratory Mouse From Monocular Images

Abstract

Video-based activity and behavior analysis for mice has garnered wide attention in biomedical research. Animal facilities hold large numbers of mice housed in ‘home-cages’ densely stored within ventilated racks. Automated analysis of mice activity in their home-cages can provide a new set of sensitive measures for detecting abnormalities and time-resolved deviation from baseline behavior. Large scale monitoring in animal facilities requires minimal footprint hardware that integrates seamlessly with the ventilated racks. Compactness of hardware imposes use of fisheye lenses positioned in close proximity to the cage. In this paper, we propose a systematic approach to accurately estimate the 3D pose of the mouse from single monocular fisheye-distorted images. Our approach employs a novel adaptation of a structured forest algorithm. We benchmark our algorithm against existing methods. We demonstrate the utility of the pose estimates in predicting mouse behavior in continuous video.

I. Introduction

Vision systems have greatly impacted animal-based research [1]–[3]. Researchers in various disciplines have relied on the precise and detailed measures afforded by automated vision systems to formulate and/or validate research hypotheses [4]–[6]. Vision systems have been used to quantify activity and behavior for many model organisms [6], [7]. Many commercial and academic systems target mice which, due to their small size and ease of use including relative ease for sophisticated genetic manipulation, are the most frequently characterized and used mammals in biomedical research [8]. Despite the availability of video monitoring systems for mice, automated behavioral analysis has yet to be deployed on a large scale. Generally speaking, only a minute fraction, if at all, of the mice under experiment at any particular institution are profiled automatically via vision systems, leaving hidden a wealth of information critical to research and well-being of the animals. Large scale use of vision systems will not only reveal data critical to researchers, it can also profoundly transform the corresponding animal care and health assessment. When there are hundreds or thousands of cages in one institution, monitoring of animal health and activity is infrequent, of limited measures, and rather subjective. Automating assessment of research mice in animal vivaria would increase efficiency and reduce bias (e.g., due to fatigue or drift [9]).

A. Target problem

One major impediment to wider use of vision systems in research institutions is the lack of integration of video monitoring systems with the typical housing for mice in the animal vivaria. Animal facilities utilize ventilated cage-racks to achieve high-density housing while maintaining consistent and controlled microenvironments in each individually ventilated cage (Figure 1). Wide use of vision systems is contingent on availability of minimal footprint hardware with seamless integration in ventilated racks. Salem et al. [10] reported on the first video-based hardware design specifically targeted for use in cage-racks. This system integrates into the ventilated rack without modification to the cages or racks nor alteration to animal husbandry procedures. The resulting video poses processing challenges as mouse appearance exhibits large variations induced by the nonlinearity of fisheye lenses exacerbated by lens placement in very close proximity to the cage. While the authors compute simple motion measures to demonstrate the utility of the system, they leave largely unsolved the problem of accurate action analysis of the mouse in video produced by the system. Providing a method for pose estimation and behavior detection in compact video systems introduced by [10] would result in a complete solution that could potentially revolutionize animal care and animal-based research. Continual in-rack automated monitoring can identify events of interest to animal care personnel as well as researchers including birth and death events. Automated detection of abnormalities in behavior patterns can also lead to early detection of illness, which can in turn be quickly treated or managed. Perhaps most impactful to research is the utility of continuous video-based automated detection of behavior in phenotyping and disease progression studies, characterizing animal models, and profiling social behavior [1], [7], [11], [12].

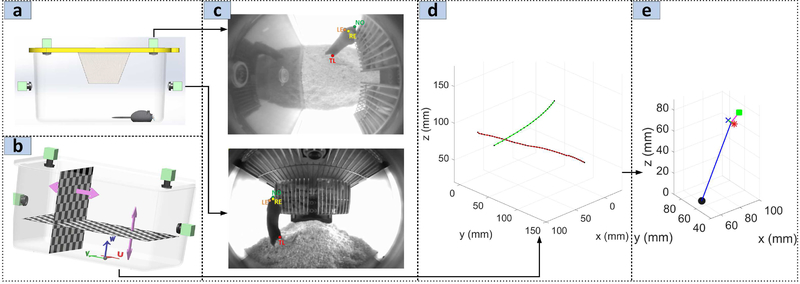
Fig. 1.

(a) Typical animal vivarium cage-racks and the compact video acquisition system installed in the rack. (b) A close-up of the acquisition unit along with a 3D CAD drawing to highlight the close placement of the fisheye lens cameras to the cage. (c) An example image acquired by the system and the corresponding 3D pose estimate obtained from the image through the methods described in this work. The stick-figure is keyed as follows: the black circle denotes the tail, the blue × denotes the left-ear, the red * denotes right-ear, and the green square denotes the nose.

B. Challenges

Deriving meaningful activity and behavior measures for scalable compact systems, such as the one in [10], is hindered by the challenging optical configuration compounded by the high defomability and near featurelessness of the target. The majority of work in the field of pose estimation assumes scaled orthography [13]. The assumption is violated in systems, such as the one described in [10], suited for scalable use in animal vivaria. The nonlinearities introduced by the fisheye lens and the proximity of the lens to the arena render the common methods used in pose estimation inapplicable, without major revision, to the videos produced by the systems of interest. Furthermore, even if a 2D image pose estimate were obtained using existing methods, the physical meaning of the estimate would be unclear due to the ambiguity in relation between 2D image coordinates and 3D physical coordinates in the recording setups of interest. In particular, it would be difficult to infer actual physical motion that is quantifiable in terms useful for biomedical researchers (e.g., distance traveled by mouse in mm or distance in mm of mouse nose from objects of interest in the cage) from the 2D pose estimate obtained for the distorted mouse image. The distortion in the image would also preclude easy application of established structure from motion methods [14] to the problem. Lastly, established methods such as [15], [16] use parts detectors and affinity maps which would be expected to have superior performance with humans over mice, due to the extent of visible articulation in the target.

C. Motivation

A practical solution would be to estimate the pose in 3D on a coordinate system defined relative to the cage. A per-frame pose estimate would be critical for accurate action analysis: Pose estimates immediately yield position and posture information, while the temporal evolution of the 3D pose estimates yields activity and behavior measures. However, as mentioned earlier, the current state of the art in pose estimation does not target (or is of limited applicability to) the problem at hand. Hence, in what follows is a systematic approach to obtaining accurate 3D pose estimates from compact video systems, such as [10], [17], that integrate in vivaria racks.

D. Summary of work

We propose a systemic approach to 3D pose estimation of mice applicable in compact systems aimed for large scale monitoring in animal vivaria. The methods described capitalize on the constrained recording environment to overcome challenges posed by the optical configuration as well as the high deformability and near featurelessness of the target. As opposed to pose estimation in the wild, many strong assumptions can be made and leveraged including target count, target appearance, illumination consistency, static arena (i.e., cage) size and features, and fixed camera placement. We outline means of construction of a unique training set for mouse key-points (Figure 1) to estimate the 3D pose of the mouse in each frame using a novel adaptation of a structured forest algorithm [18]. To our knowledge, we are the first to produce a 3D pose estimate (i.e., 3D physical coordinates of mouse keypoints) for the mouse from a monocular image in conventional video. We show that our 3D pose estimation algorithm yields greater accuracy when compared to two other methods. We use a rich manually annotated mouse behavior dataset to demonstrate that our single-image pose estimates can be used to accurately predict behavior in continuous video. This work extends our initial work on 3D position [17] and pose estimation [19], [20]. In particular, we introduce a novel pose-indexed features based ensemble model for the structured forest that reduces error rates by approximately 8% compared to those reported in [20]. Furthermore, we introduce a new behavior annotation training set and develop a behavior detection model based on 3-D pose estimates produces by the structured forest.

E. Contributions

Our contributions are:

• 3D mouse pose estimation method from single fisheye-lens distorted images. In all previous works, the pose parameters are defined in 2D image domain. We, however, use a novel structured-forest implementation to directly estimate 3D coordinates of the mouse key-points.

• A viable algorithmic path suited for scalable mouse-ethology vision systems. The methods outlined in our manuscript target compact systems that integrate with existing animal vivaria racks with minimal or no change to the racks. All previous works are based on systems that are not suited for densely populated ventilated racks, and hence allow assumptions (e.g., scaled orthography, image-domain pose) that might not hold in scalable systems.

• Behavior detection method using 3D pose estimates. Earlier works have shown the utility of 2D pose parameters in generating discriminant trajectory features for behavior detection in continuous video [5], [21]. We extend the prior art to 3D and extract features from the 3D pose estimates for use in behavior detection.

• Rich data sets of manually annotated video with mouse key-points and mouse behavior. The training sets are available on the website (scorhe.nih.gov) to encourage further contributions to the field.

F. Outline

Our manuscript is organized as follows. In section II, we review the state of the art in pose estimation and behavior detection for laboratory mice. In Section III, we describe the dataset used for the 3D pose estimation task. Section IV describes our adaptation of the structured forests algorithm [18] to the 3D pose estimation problem. Section V describes the methods used for behavior detection including our extension of trajectory features to those obtained from the 3D pose estimates. The results of the 3D pose estimation algorithm are presented in Section VI and compared to other methods. Section VI also presents the results of the behavior detection methods. The manuscript ends with discussion and conclusions.

II. Related Work

The majority of the work in pose and behavior detection is done for human subjects [15], [16], [22]. Automated analysis of mice activity and behavior has attracted commercial and academic interest over the past two decades [1], [6], [9], [11]. Hardware designs employ sensors [23], [24], conventional video [11], thermal imaging [25], and, more recently, depth imaging [26]. Video-based hardware systems for home-cage monitoring employed in academic works are typically simple prototypes and ad hoc setups with standard lens cameras positioned at a sufficient distance away from the side of the cage to capture full view of the cage (e.g., [12]). Some setups are based on overhead cameras [3], [21]. Neither placement, however, is suited for scalability due to space constraints, as well as cage and rack obstructions, in high-density ventilated housing [27]. Commercial hardware systems include Noldus [28] and CleverSys [29]. Desired output from automated analysis methods include position and pose estimation [3], [30]–[32], detection of predefined behaviors [12], [33], [34], and profiling social interactions [3], [21], [30]. Popular tools for automated ethology of mice and other animals are summarized in [1], [2]. We limit our review to video-based methods for mice home-cage monitoring.

A. Pose estimation methods

One sought output of automated analysis is a per-frame pose estimate, which can be used for motion analysis. We use ‘pose’ to refer to the posture and/or position of the mouse. Two defining components of pose estimation are the pose representation (i.e., pose parameters) and pose estimation/detection method. We review the literature works with respect to these two components. It is noted that in all the works reviewed, a segmentation step is applied first to isolate foreground pixels, with [21] being the exception.

a). Pose representation

The simplest representation of the mouse is by its binary silhouette centroid or its bounding box [21], [32]. A common pose representation is the ellipse and is used by [3], [33], [35]. Oriented ellipses, i.e., with one end of the ellipse aligned with the anterior of the mouse, are used in [26], [36], [37] and the commercial Ethovision package by Noldus [28]. More elaborate pose representations are employed in Branson and Belongie [31] and de Chaumont et al. [30]. In [31], an ellipse is used as a coarse pose which then guides estimation for more refined pose consisting of twelve manually constructed deformable 2D contour templates that are assumed to be representative of the mouse postures. de Chaumont et al. [30] model the mouse as a head, belly, and neck, with corresponding constrained displacements between each part. Each part is represented by a 2D articulated rigid body model.

b). Pose estimation/detection

For pose detection, Burgos-Artizzu et al. [21] use a trained detector [38] to estimate the bounding box of the mouse without the intermediate step of segmentation. Segmentation followed by an identity detection method is used in [32]. The centroid of the segmented foreground is then used for tracking. A more elaborate cascaded pose regression method [36], [39] is used in [26], [37]. Ohayon et al. [3] fit the foreground binary pixels to a 2D Gaussian Mixture Model (GMM) via Expectation Maximization (EM). Branson and Belongie [31] use a multiblob tracker for the ellipse detection and particle-filter contour tracker for contour refinement. de Chaumont et al. [30] use the foreground binary mask and edges for initial alignment and mean-shift processes drive the physics engine for refinements.

III. Training set

We seek to estimate the 3D position of four key-points on the mouse: tail (tl), left-ear (le), right-ear (re), and nose (no). Hence, the mouse pose ϕ is defined by the position of the landmarks, i.e., $\varphi =\left[{\gamma }_{tl},{\gamma }_{l-e},{\gamma }_{r-e},{\gamma }_{no}\right]$, where γ = (u, v, w) is the 3D position defined relative to a right-handed Cartesian coordinate system with origin at the center of the cage floor as shown in Figure 2b. Employing supervised learning algorithms for the 3D pose estimation task requires the availability of ground-truth ϕ_i for each image I_i, i ϵ {1,…,N} in the training set consisting of N samples. Obtaining ϕ_i strictly from I_i is not feasible due to mouse deformability and the non-standard optical configuration. To enable construction of I_i, overhead cameras were integrated and synchronized with the side view cameras as shown in Figure 2a. The overhead cameras are also fitted with fisheye lenses so as to be integrated in the cage with almost no impact on the view of the cage as seen by the side camera (e.g., no need to remove cage lid or cage wire-bar). The overhead cameras are strictly used for video acquisition related to building training sets, and are not utilized at runtime. In what follows we describe the different components required to build the ground-truth dataset, define a suitable pose representation, and assess annotation and 3D reconstruction consistency. The latter is used to define a pose distance measure to evaluate the quality of the estimates.

Fig. 2.

(a) 3D CAD illustrating the video acquisition unit augmented with overhead cameras enabling synchronized stereo acquisition. (b) Cartesian coordinate definition for cage with origin at the center of the cage floor. Each checkerboard pattern grid is moved at known increments to generate the image-to-physical coordinates lookup tables. (c) Example manual annotation of the key-points from top and side camera. (d) Reconstruction of the nose 3D position using the lookup tables ${\mathcal{C}}^{I-P}$. The red line is due to the nose annotation in the side camera image while the green line is due to the top camera annotation. The black dots in each line show the actual 3D points comprising the set {γ} corresponding to each annotated image position. (e) The 3D reconstructed ground-truth pose

A. Image-to-physical and physical-to-image coordinates mappings

With images from two orthogonal cameras, the 3-D position of a key-point annotated in both images can be recovered. While standard camera calibration and stereo vision methods used in 3D reconstruction are well known, extending the methods to work for the challenging optical configuration at hand is not a trivial task. Instead, we capitalize on the practical constraints (e.g., fixed cage size, fixed camera placement) of the scalable recording system design. Namely, we use checkerboard pattern grids, as shown in Figure 2b, to construct a lookup table ${\mathcal{C}}^{I-P}$ indexed by image pixel location σ such that the entry ${\mathcal{C}}^{I-P}\left(\sigma \right)$ in the table returns {γ}, a discrete set of physical points within the cage volume that project onto pixel σ. The accuracy and resolution with which ${\mathcal{C}}^{I-P}\left(\sigma \right)$ is populated can be set by the user. In our case, we use precision cut acrylic to accurately mount a rigid grid and move it in increments of 12.7mm. We use linear interpolation to get 2.54mm grid resolution. Armed with $C_S^{I-P}$ and $C_T^{I-P}$, the side and top camera lookup tables respectively, recovering the 3D position of a key-point annotated in the side view image at location σ_S and the top view image at σ_T is straightforward as shown in Figure 2c–d. The 3D position is computed as the intersection of the set of 3D points $\left\{{\gamma }_S\right\}={\mathcal{C}}_S^{I-P}\left({\sigma }_S\right)$ and the set $\left\{{\gamma }_T\right\}={\mathcal{C}}_T^{I-P}\left({\sigma }_T\right)$. Using the described methodolgy for reconstruction, the measured reconstruction error for the region of the lower half of the cage volume was 2.05mm. For the upper half of the cage, the reconstruction error was 6.59mm. It is noted that the vast majority of the mouse time is spent on the cage-floor, i.e., the lower half of the cage.

We note that other components of the 3D pose estimation algorithm require computation of the image pixel location σ in the side camera image corresponding to a physical point γ. We reorder the content of ${\mathcal{C}}_S^{I-P}$ to generate another lookup table ${\mathcal{C}}_S^{P-I}$ indexed by 3D physical location γ. ${\mathcal{C}}_S^{P-I}(\gamma )$ then gives the image pixel location σ to which γ projects.

Another component of the 3D pose estimation algorithm requires defining fixed pre-specified ‘anchor’ points in 3D physical corrdinates corresponding to each image pixel position. A mapping $\mathcal{M}$ is generated that associates with each 2D image point σ a 3D reference ‘anchor’ point ${\gamma }_{\sigma }=\mathcal{M}(\sigma )$. The fixed mapping $\mathcal{M}$ is utilized in defining 3D translation-tolerant pose representations as will be described in Section III–C. To describe the generation of the mapping $\mathcal{M}$, we first note that for each image coordinate σ, the earlier described lookup table ${\mathcal{C}}^{I-P}(\sigma )$ supplies a set of points {γ_σ} in 3D physical space that map to pixel location σ. The reference 3D ‘anchor’ position is chosen from the point set {γ_σ} (i.e., in physical space) which projects onto the 2D image point σ. Therefore, we define an image-to-physical coordinate mapping $\mathcal{M}(\sigma )$ that assigns to each image pixel σ a 3D position $\left({\mathcal{M}}_u(\sigma ),{\mathcal{M}}_v(\sigma ),{\mathcal{M}}_w(\sigma )\right)$ in the same Cartesian coordinates system on which the 3D pose is defined. Specifying $\mathcal{M}$ fully involves choosing a specific point from the set {γ} by applying an arbitrary constraint. Figure 3 pictorially shows the mappings ${\mathcal{M}}_u$, ${\mathcal{M}}_v$, and ${\mathcal{M}}_w$. Mainly, for all pixels with 3D points set intersecting the cage-floor, we choose the initial mapping by constraining w to lie in the cage-floor plane. For all the pixels with 3D points set intersecting the food basket, the initial mapping is chosen to be the basket plane. Likewise the ceiling plane is chosen for all pixels having lines intersecting the ceiling. Lastly, the cage side-wall planes are chosen for pixels with lines intersecting the side-walls.

Fig. 3.

The initial image-to-physical coordinates mappings applied to the ellipse-fit endpoint (marked by ×) for an example image. The 3D tail position of the mouse is represented relative to the (u, v, w) obtained through ${\mathcal{M}}_u$, ${\mathcal{M}}_v$, ${\mathcal{M}}_w$ respectively. The images are 240 × 320 pixels. The ranges of cage physical coordinates are u ∈ [−76mm, 76mm], v ∈ [−150mm, 150mm], w ∈ [0,178mm].

B. Image annotations and 3D pose reconstruction

The key-points are marked in both orthogonal views as shown in Figure 2. Approximately 90,000 frames were manually annotated to account for the large variation in appearance due to the hardware configuration and mouse posture. A separate set of 1,100 frames were annotated to be used for testing. Recovering the 3D position of each key-point is straightforward using the lookup tables ${\mathcal{C}}_S^{I-P}$ and ${\mathcal{C}}_T^{I-P}$ described above. We note that methods such as Structure from Motion (SfM) [40] could have been employed to semi-automate the generation of the training set.

C. Pose Representation

In 2D landmark estimation tasks, the landmarks are expressed in relative terms rather than absolute image pixel locations. Typically, the landmarks are expressed as relative offsets from the object detection window. Such a representation achieves scale and translation invariance. For the 3D pose estimation problem at hand, we seek to define θ, a translation-tolerant pose representation derived from ϕ. Similar to ϕ, $\theta =\left[{\theta }_{tl},{\theta }_{l-e},{\theta }_{r-e},{\theta }_{no}\right]$, where the subscripts correspond to tail, left-ear, right-ear, and nose respectively. Two steps are taken to compute θ. First, the ears and nose are represented as 3D offsets relative to the tail point, i.e., ${\theta }_{\{l-e,r-e,no\}}={\varphi }_{\{l-e,r-e,no\}}-{\varphi }_{tl}$. Referencing the landmarks to the tail point gives a similar representation in pose-space to similar mouse postures. Hence a mouse with an elevated bipedal stance, for example, would have the same representation of θ_l–e, θ_r–e, θ_no regardless of tail position. The second step addresses the representation of the tail point itself. Similar to 2D pose representation, we use a 2D image point within the detection window to establish a reference for the tail in order to achieve a translation-tolerant representation for the tail. However, the 2D image point cannot be used directly, rather we use the 3D ‘anchor’ point associated with the 2D image position as described in Section III–A. Specifically, the tail is expressed relative to $\mathcal{M}\left({\sigma }_a\right)$, where σ_a is chosen based on the binary silhouette of the mouse. Namely, σ_a is the foreground ellipse fit major axis endpoint closest to the lower left corner of the image, as shown in Figure 3. The binary silhouette is obtained by thresholding a segmentation map returned by a trained classifier. The classifier is trained on images where mouse pixels were annotated manually as described in [17]. For each image I, the segmentation map S is thresholded to produce a binary silhouette B. The statistics of the binary silhouette (ellipse-fit parameters, ellipse axes end points, bounding box, eccentricity, major axis to minor axis length ratio, and area) are computed. Of the computed statistics, σ_a, the ellipse-fit major axis endpoint is used to obtain the 3D ‘anchor’ as described above. Overall,

$$\theta =\left[{\varphi }_{tl}-\mathcal{M}\left({\sigma }_a\right),{\varphi }_{\{l-e,r-e,no\}}-{\varphi }_{tl}\right]$$ (1)

As seen in (1), the definition of θ expresses the key-points of the mouse (other than the tail) relative to the tail coordinates ϕ_tl = (u_tl, v_tl, w_tl).

D. Annotation Consistency

To assess the consistency of annotations and establish a meaningful measure for evaluating estimation accuracy, a set of ~ 6, 500 frames was annotated by two different trained annotators. The redundant annotations are used to define a distance metric, as proposed in [36], which equalizes the error from each pose parameter by weighing it with the inverse of its variance as observed in the redundant annotations. The distance measure between two poses θ¹ and θ² is

$$\begin{gathered} d\left({\theta }^1,{\theta }^2\right)=\sqrt{\frac{1}{D}\sum _{i=1}^D\frac{1}{var(\theta (i))}{\left(\Vert {\theta }^1(i)-{\theta }^2(i)\Vert \right)}^2} \\ i\in \{1,\cdots ,D\} \end{gathered}$$ (2)

where D is the number of pose parameters. The var(θ(i)) term in (2) refers to the variance in the i^th pose parameter distance between two human annotators. The distance measure in Eqn (2) weighs the error contribution of each parameter by the observed variance in the redundant annotations, hence equalizing the error from each parameter and providing a direct comparison between our method and human annotators. Following [36], we define a normalized distance threshold d_thr for a successful estimate. d_thr is set to be such that the normalized distance for 99% of the redundantly annotated frames falls below d_thr. So if the estimation output has a normalized distance (i.e., that computed via Eqn (2)) exceeding d_thr, then it is considered a failed estimate. Using the redundant annotations, d_thr was computed to be 3.77mm.

IV. 3D pose estimation

We first review standard decision forests as well as the extension by Dollár and Zitnick [18] to structured output spaces, after which we describe our adaptation of the method to structured pose estimation.

A. Standard decision forests and structured forests

A quick review of standard decision forests [41] and structured forests [18] helps set terminology and mathematical notation for the forthcoming sections. For consistency, the review herein closely follows the work on which we are expanding [18]. For a training set $\mathcal{S}:\{\mathcal{X},\mathcal{Y}\}$, a binary decision tree $f_t(x),x\in \mathcal{X}$ is a partition of the input feature space into regions storing an assigned output prediction $\widehat{y}=g\left(\left\{y_k\right\}\right)$ where $\left\{y_k\right\}\in \mathcal{Y}$ are the output labels falling in the regions having input feature vectors $\left\{x_k\right\}\in \mathcal{X}$. Each node in the tree defining a partition is referred to as a split or internal node, whereas the terminal node representing the region containing the prediction $\widehat{y}$ is referred to as leaf node. The partitioning is done in a recursive manner until criteria on the information content of the node or the depth of the tree is met, thereby reaching a leaf node, wherein a prediction g(·) is stored. A decision forest $\mathcal{F}$ is a collection of T separately trained trees f_t(x), t ∈ {1,...,T} along with an ensemble model that produces a prediction ${\widehat{y}}_F=\mathcal{E}\left({\widehat{y}}_t\right)$, t ∈ {1,…,T} from all the individual tree predictions ${\widehat{y}}_t$. The main tasks in training a forest are training each individual tree and defining a suitable prediction aggregation model, i.e. defining $\mathcal{E}(\cdot )$. Training each tree entails finding an optimal node split for each internal node and defining a prediction model for each leaf node, i.e., a suitable $\widehat{y}$. The split node function is obtained by maximizing an information gain criterion. The standard information gain relies on defining an information measure function H. For classification, it is common to define H as the Shannon entropy, Gini impurity, or the twoing criterion. For single-variate regression, a common H is one that minimizes variance of the child nodes.

Realizing the challenge of defining an information gain criterion for structured output spaces, Dollár and Zitnick [18] map the output space to discrete labels. The mapping would be defined such that similar structured labels are assigned the same discrete label. The information gain is then computed for the discrete classes, rather than the structured labels themselves, using the standard information gain criteria along with standard H used in classification training task. The mapping is used to train the split functions at each internal node. The structured labels arriving at each node, however, are stored and propagated until a leaf node is reached. A prediction model for each leaf node, and an ensemble model for the whole forest would then be formulated based on the stored structured labels. The success of this elegant solution is contingent upon finding an effective mapping from structured labels space to discrete labels, i.e., $\mathcal{Y}\to \mathcal{C}$, such that each label $y\in \mathcal{Y}$ is mapped to a discrete label $c\in \mathcal{C}$, where $\mathcal{C}=\{1,\dots ,k\}$. Given that measuring similarity for structured labels might not be well defined, [18] employed an intermediate mapping $\mathrm{\Pi }:\mathcal{Y}\to \mathcal{Z}$ such that $\mathcal{Z}$ is a space on which similarity can be measured by computing Euclidean distance. A discretization maping $\mathcal{Z}\to \mathcal{C}$ is then used to assign class identities.

B. Structured forests for 3D pose estimation

Our goal is to estimate the 3D pose of the mouse from a single camera, where pose is defined as the 3D coordinates of a set of key-points. We here propose a 3D pose estimation method which relies on the structured forest framework to estimate the 3D coordinates of key-points of the mouse while capitalizing on the underlying structure of these coordinates. Our method adapts the structured forest in [18] to the regression task such that each tree in the forest produces a pose- proposal (i.e., a full set of pose parameters). We propose a novel ensemble model $\mathcal{E}(\cdot )$ to select the single ‘best’ pose-proposal. Our ensemble model employs a single-variate regression model trained to estimate a distance measure between each pose-proposal and the ‘ground-truth’ pose (although unavailable at test-time) relying on pose-indexed features similar to those introduced and used in [36], [42]. The overall method, therefore, employs a two-layer composite statistical learning model. The first layer is a structured forest adapted to produce pose-proposals. The second is a standard regression forest used to chose the best pose-proposal. Each learning model will have its own training set. For clarity and distinction, we refer to the structured forest as $\mathcal{F}$ and the standard regression forest employed in the ensemble model as $\mathcal{E}$. For $\mathcal{F}$, (x, y) will denote a training sample pair composed of feature vector x and target output y. For $\mathcal{E}$, $\left(x^{\mathcal{E}},y^{\mathcal{E}}\right)$ will be used to denote its training sample feature vector and corresponding target output.

In the subsections that follow, we detail the key components for setting up and training structured forest to accomplish the pose-estimation task. Namely, we define: the input feature space $\mathcal{X}$, the mapping function Π, the discretization mapping $\mathcal{Z}\to \mathcal{C}$, the leaf node prediction model g(·), and the ensemble model $\mathcal{E}(\cdot )$.

1). Input Feature Space

Each training sample (x, y) is composed of a set of input features $x\in \mathcal{X}$ derived from the image of the mouse having ground-truth pose $y\in \mathcal{Y}$, where y in our case has been referred to as θ as in Eqn (1). Recall that images are first segmented, as described in section III–C, to identify the binary silhouette of the mouse. The features are derived both from the binary silhouette and the intensity image, more specifically the foreground bounding box region of the intensity image.

We utilize pixel look-up, gradient, and HOG features similar to those in [18]. However, as opposed to drawing features from a fixed size image patch, the features positions are chosen as offsets within the foreground binary silhouette bounding box. Furthermore, we augment our feature vector with the binary silhouette statistics described in III-C. In human pose estimation methods, intensity-value based features are not desirable due to the lack of robustness to illumination changes. However, given the constrained environment (e.g., consistent coat color of mice and fully controlled illumination in the system), intensity-value based features have been shown to be reliable and discriminative [36]. For purposes of comparison, we also use gradient and HOG features from the pixel-to-pixel registered feature channels as described in [38].

2). Intermediate mapping function

One key component of the structured forest approach is the mapping Π from the structured labels to an intermediate space on which dissimilarity can be measured. To generate the intermediate mapping, first a binary string representation, b, of the pose θ is generated. The binary string generation is controlled by two hyper-parameters. The first hyper-parameter is the length, l, of the string. The second is a binary indicator to choose one of two methods, either ‘fixed’ or ‘adaptive’, for assigning bit depth l_d to each pose parameter θ(d). In the ‘fixed’ method, each pose parameter θ(d) is mapped to $l_d=\frac{l}{D}$, where D = 12 is the total number of pose parameters. In the ‘adaptive’ method, the observed dynamic range of each pose parameter in the training set reaching the node is first computed. The number of bits assigned to parameter d is proportional to its range r(d) in the training set, namely $l_d=l\times r(d)/{\sum }_{i=1}^{D}r(i)$. If the variance of a parameter falls below a certain empirically set threshold, the parameter is not represented in the string, i.e. the l_d corresponding to the parameter is set to zero. Once the number of bits for each parameter has been set, we seek to represent parameter θ(d) with a b_d bit string of length l_d. To generate the binary sequence for θ(d), the full range of the parameter in the N training samples arriving at the node is computed as r(d) = max_iθ_i(d) – min_iθ_i(d), i ∈ 1,…,N. The range r(d) is uniformly partitioned into b_d bins. If θ_i(d), falls in the k^th range bin, the k^th bit in b_d is set. Once all the parameters are represented in binary strings, the binary representations for each parameter are concatenated to form the initial z vector. Mathematically, the mapping Π generating z is then defined as $\mathrm{\Pi }={\bigvee }_{d=1}^D{b}_d(\theta (d))$, where $\bigvee$ denotes concatenation and b_d(θ(d)) is the binary string representation of the d^th parameter of θ.

3). Discretization mapping

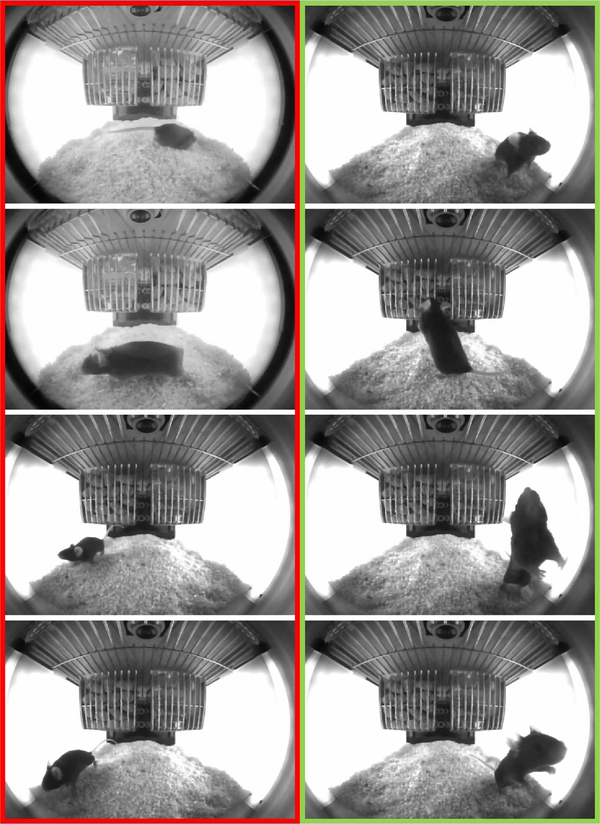
The goal of intermediate mapping function is to allow for discrete label assignments to the structured output labels, such that similar $y’\mathrm{s}\in \mathcal{Y}$ are assigned the same class label $c\in \mathcal{C}$, where $\mathcal{C}=\{1,\dots ,k\}$. We set k = 2 and follow the same two approaches (K-means and PCA) as in [18] to obtain a discrete label assignments for the set of y’s (i.e., θ’s) at each node. Figure 4 shows the output of the discretizing function on a sample set of poses.

Fig. 4.

Example output of the discretization function. The function was applied to eight randomly chosen poses. The red (left-column) and green (right-column) outlines group the images for which the poses received the same class label by discretization function. The results are intuitive as all the poses in which the mouse nose was at greater elevation are grouped together.

We note that the discretization mapping as described in the original structured forest work [18] was needed in order to define a distance metric for similarity between image patches. In our case, however, the Euclidean distance can be used directly to measure similarity between poses since pose is defined as landmark positions in Euclidean space. Therefore, clustering on poses can be done directly without the intermediate discretization mapping step. The intermediate mapping, however, does offer two added benefits: more control of the clustering afforded by the adaptive bit depth, and the denoising of pose parameters resulting from the binning operation when generating the binary string. In the Experiments section (Section VI), we compare the performance of the structured forest in which the intermediate mapping was used to an implementation where class label assignment is done via direct clustering (i.e., without employing an intermediate mapping).

4). Leaf node prediction model

Each leaf node stores a pose-proposal θ, i.e., a full set of pose parameters. In [18], the leaf node prediction is set to be the label y_m whose z_m is the medoid of all z_m’s at the node. Although we experimented with different approaches, we chose to retain the same leaf node prediction model as in [18]. Hence, our leaf node prediction is the pose whose z_m is the medoid.

5). Ensemble model

A feature vector x_n derived, as described in Section IV–B1, from a novel image I_n and applied to a T-tree structred forest produces T pose proposals y_j, j ∈ {1,…,T}, i.e., one proposal from each of the T trees. In this work, we define an ensemble model to choose the ‘best’ pose proposal $\widehat{y}$ out of the T pose proposals y_j’s. The best pose $\widehat{y}$ is chosen based on its estimated distance to ground-truth pose $y_n^{gt}$, i.e., if $y_n^{gt}$ were known, $\widehat{y}=y_i$, $i=\arg {\min }_{j}d(y_j,y_n^{gt})$, where d(·) is defined in Eqn (2). Clearly, the ground-truth pose $y_n^{gt}$ for the mouse in the test image I_n is not known, as indeed it is the quantity to be estimated. However, we utilize the training set consisting of images I_m and their known ground-truth poses y_m to model the correlation between image appearance and the actual distance d(y, y_m) of an arbitrary pose proposal y from the ground-truth pose y_m. Namely, for a pose-proposal y_j generated for image I_m, we train a model to estimate the distance $\widehat{d}(y_j,y_m^{gt})$. The distance estimate $\widehat{d}(y_j,y_m^{gt})$ is marked with a caret to indicate that indeed it is an estimate as opposed to the actual distance $d(y_j,y_m^{gt})$ computed when $y_m^{gt}$ is known. The model to produce $\widehat{d}$ is trained using image features $x_j^{\mathcal{E}}$, where the superscript $\mathcal{E}$ emphasizes that the features are derived for the ensemble model task, and the subscript j denotes the pose-indexed nature of the features, i.e., the dependence of the feature values on the pose-proposal y_j. In training, each image feature vector $x_j^{\mathcal{E}}$ computed for pose y_j is paired with output target value $d(y_j,y_m^{gt})$, i.e., the actual distance between pose proposal y_j and the ground-truth pose $y_m^{gt}$ (which is available for the training set images). In test-time, i.e., when the ground-truth pose is not available, for each pose proposal y_j, a feature vector $x_j^{\mathcal{E}}$ is formed and an estimate of $\widehat{d}(y_j,y^{gt})$ is obtained based on the learned correlation between $x^{\mathcal{E}}$ and y^gt in the training set. Hence, the proposed ensemble model employs a regression model that produces an estimate ${\widehat{d}}_j$ for each pose proposal y_j relying on feature vector $x_j^{\mathcal{E}}$ which is mainly composed of pose-indexed features. The pose proposal with the lowest distance estimate is chosen to be the output predicted pose $\widehat{y}$.

Given that the ensemble model $\mathcal{E}$ employs a regression model trained in a supervised learning framework, the three main tasks to fully specify $\mathcal{E}$ are to specify 1) the learning method, 2) the input features $x^{\mathcal{E}}$, and 3) the target output $y^{\mathcal{E}}$. Note that the superscript $\mathcal{E}$ is used to distinguish the feature vectors and the target output values used in the ensemble model from x and y described in Section IV–B1 used to trained the structured forest.

We chose to use standard single-variate regression forests (Section IV–A) as the learning method for out distance estimation task, as the output target is a single variable: the distance estimate. Hence our ensemble model $\mathcal{E}$ relies on a standard regression forest to supply a distance estimate for each pose-proposal. Each training sample for the regression forest comprises a set $\left(x^{\mathcal{E}},y^{\mathcal{E}}\right)$ where $x^{\mathcal{E}}=q(I,\varphi )$ are the features derived from image I with features indexed by pose ϕ, and $y^{\mathcal{E}}$ is the distance between pose ϕ and the ground-truth pose ϕ^gt associated with image I, i.e., $y^{\mathcal{E}}=d\left(\varphi ,{\varphi }^{gt}\right)$. In what follows, we thoroughly describe the method for generating training samples $\left(x^{\mathcal{E}},y^{\mathcal{E}}\right)$ used to train $\mathcal{E}$’s regression model.

Generating $y^{\mathcal{E}}$’s: The images used to train the ensemble model regression forest are I_m, m ∈ {1,…,M}. Each I_m has an associated ground-truth pose ${\varphi }_m^{gt}$. One training sample in the training set is that due to the ground-truth pose itself. Namely, $x_m^{\mathcal{E}}$ would be the vector derived from image I_m with features indexed by ground-truth pose ${\varphi }_m^{gt}$. The corresponding distance would be $y_m^{\mathcal{E}}=d({\varphi }_m^{gt},{\varphi }_m^{gt})=0$. Clearly, however, if we limit ourselves to the ground-truth samples, the training set will have no variety in pose deviations, and hence distance, from the ground-truth pose. We can inject variety in the pose-distances by generating poses ${\widehat{\varphi }}_{j,m}$ which deviate from the ground-truth pose ϕ_m. We generate P poses ${\widehat{\varphi }}_{j,m},j\in \{1,\dots ,P\}$ each of which will have distance $y_{j,m}^{\mathcal{E}}=d({\widehat{\varphi }}_{j,m},{\varphi }_m^{gt})$ from the ground-truth pose. Generating the poses ${\widehat{\varphi }}_{j,m}$ could be done by randomly perturbing the ground-truth pose ${\varphi }_m^{gt}$ similar in concept to the training set augmentation procedures described in [36], [39]. However, we utilize the fact that a P-tree pose-estimation structured forest can be trained to readily yield P pose proposals. Namely, we train a P-tree structured forest F′ using the training set $(I_m,{\varphi }_m^{gt})$, m ∈ {1,…, M} which is a randomly chosen subset of the full annotated set described in Section III, i.e., M < N. Each tree in F′ produces a pose proposal ${\widehat{\varphi }}_{j,m}$. Once F′ is trained, each image I_m in the training set is fed into F′. F′ produces (P − 1) proposals ${\widehat{\varphi }}_{j,m}$. The distance $y_{j,m}^{\mathcal{E}}=d({\widehat{\varphi }}_{j,m},{\varphi }_m^{gt})$ is computed. The feature vector $x_{j,m}^{\mathcal{E}}=q(I,{\widehat{\varphi }}_{j,m})$ is also computed. The pair $(x_{j,m}^{\mathcal{E}},y_{j,m}^{\mathcal{E}})$ is entered into the training set for the ensemble model $\mathcal{E}$ regression forest. As noted earlier, the ground-truth pose ${\varphi }_m^{gt}$ itself also contributes a sample, i.e. $(x_{gt,m}^{\mathcal{E}},0)$. Hence, each image and ground-truth annotation pair $(I_m,{\varphi }_m^{gt})$ contribute a total of P + 1 samples for $\mathcal{E}$’s regression model training set.

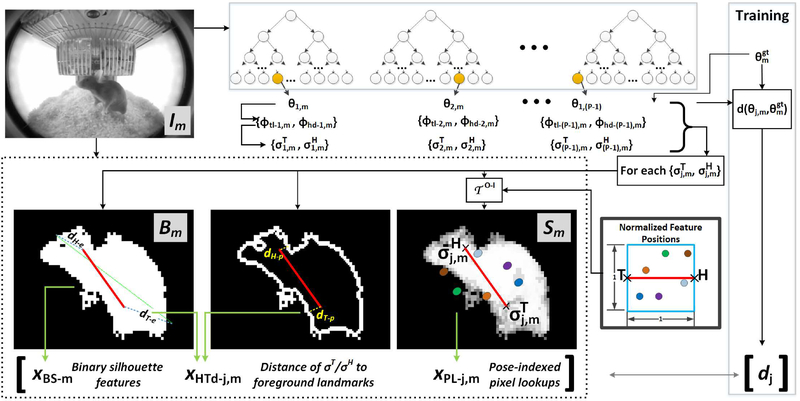
Generating $x^{\mathcal{E}}$’s: Recall that each image in the training set I_m, m ∈ {1,…,M} has a corresponding segmentation map S_m generated as described in Section III–C as well as a binary silhouette image B_m obtained by thresholding S_m. The feature vector $x_{j,m}^{\mathcal{E}}$ paired with $y_{j,m}^{\mathcal{E}}$ is composed of three sets of features derived from B_m and S_m. Namely, $x_{j,m}^{\mathcal{E}}=[x_{BS-m}^{\mathcal{E}},x_{PL-j,m}^{\mathcal{E}},x_{HTd-j,m}^{\mathcal{E}}].x_{BS-m}^{\mathcal{E}}$ are the binary silhouette statistics obtained from B_m as described in Section III–C. $x_{PL-j,m}^{\mathcal{E}}$ and $x_{HTd-j,m}^{\mathcal{E}}$ are pose-indexed features. The subscript j in $x_{PL-j,m}^{\mathcal{E}}$ and $x_{HTd-j,m}^{\mathcal{E}}$ indicates the dependence of the features on pose ${\widehat{\varphi }}_{j,m}$. The pose-indexed features are derived from the images S_m and B_m. In order to derive image features that are dependent on the 3D pose ${\widehat{\varphi }}_{j,m}$, the pose is projected onto the images S_m and B_m utilizing the mapping ${\mathcal{C}}_S^{P-I}$. For simplicity, rather than projecting all four key-points in ${\widehat{\varphi }}_{j,m}$, we limit the projection to two points. The first point is the 3D tail point. The second point, to which we refer as the ‘head’ point, is computed in 3D as the Euclidean mean of the two ears and the nose points. We use ${\sigma }_{j,m}^T$ to refer to the 2D image position returned by ${\mathcal{C}}_S^{P-I}$ for the 3D tail point in ${\widehat{\varphi }}_{j,m}$, while ${\sigma }_{j,m}^H$ is used to refer to the 2D image position corresponding to the 3D head point. In what follows, we describe in detail the content of the feature vectors $x_{PL-j,m}^{\mathcal{E}}$ and $x_{HTd-j,m}^{\mathcal{E}}$. For less cluttered notation, we leave out the subscripts j, m.

The set of features $x_{HTd}^{\mathcal{E}}$ derived from the binary silhouette image B_m constitute thirteen distance-based measurements made between the projected points (σ^H, σ^T) and the binary silhouette B_m. The first element of $x_{HTd}^{\mathcal{E}}$ is the Euclidean distance between σ^H and σ^T normalized by the binary silhouette major axis length, i.e. $x_{HTd}^{\mathcal{E}}(1)=\frac{\Vert {\sigma }^H-{\sigma }^T\Vert }{l_{maj}}$, where l_maj denotes the major axis length. The second element of $x_{HTd}^{\mathcal{E}}$ is the minimum distance between σ^T and the binary silhouette. Namely, the distance between σ^T and each point comprising the binary silhouette in B_m is computed and the minimum distance is assigned to $x_{HTd}^{\mathcal{E}}(2)$. The third element is the minimum distance between σ^H and the binary silhouette. The fourth and fifth elements are obtained by normalizing the second and third elements by l_maj, i.e. $x_{HTd}^{\mathcal{E}}(4)=\frac{x_{HTd}^{\mathcal{E}}(2)}{l_{maj}}$, $x_{HTd}^{\mathcal{E}}(5)=\frac{x_{HTd}^{\mathcal{E}}(3)}{l_{maj}}$. The sixth element is the minimum distance between σ^T and the perimeter pixels of the binary silhouette. The seventh element is the minimum distance between σ^H and the perimeter pixels of the binary silhouette. The eighth and ninth elements are the sixth and seventh elements normarlized by l_maj respectively. To compute the remaining elements of $x_{HTd}^{\mathcal{E}}$, a pairing of the binary silhouette major axis endpoints with {σ^H, σ^T} is chosen such that the overall distance between the two paired sets is minimized. The tenth element is then computed as the distance between σ^T and the major axis endpoint with which it was paired. The eleventh element is the distance between σ^H and the major axis endpoint with which it was paired. Lastly, the twelfth and thirteenth elements are the tenth and eleventh normalized by l_maj respectively.

The set of features comprising $x_{PL}^{\mathcal{E}}$ consist of pose-indexed pixel lookups from the segmentation map S_m. The position of the pixels are defined relative to the tail/head points. Namely, during training a set of normalized position offsets $\left\{o^N=\left(o_w^N,o_h^N\right)\right\},o_w\in [0.5-r,0.5+r],o_h\in [-r,r]$ are randomly chosen on a Cartesian coordinate system where (0, 0) corresponds to σ^T and (0, 1) point corresponds to σ^H. To compute $x_{PL}^{\mathcal{E}}$, a 2D similarity transformation ${\mathcal{T}}^{N-I}$ is computed between the normalized offsets space and the image head/tail points. The computed transformation is applied to the set of offsets {o^N} to generate the image positions $\left\{o^I=\left(o_w^I,o_h^I\right)\right\}$ of the pixels. $x_{PL}^{\mathcal{E}}$ is then populated with the values of the segmentation map at the image locations {o^I}, i.e. S_m({o^I}). Figure 5 graphically illustrates the main components of the training and testing procedures for $\mathcal{E}$.

Fig. 5.

A graphical illustration of the procedure of generating the feature vector used in the ensemble model. The image is fed to the structured forest. The resulting proposals are projected onto the segmentation map. The solid red line shows an example projection for one pose-proposal though different proposals will have different projections. Aside from the binary silhouette features, head/tail distance measures are computed along with pose-indexed pixel lookups. During training, the target value is the computed distance for each pose proposal from the ground-truth pose. Also during training, the ground-truth pose is used as a training sample with a distance of 0.

V. Behavior detection

One problem of great interest in video analysis is that of identifying bouts of predefined behaviors [43]. Video-based detection of pre-defined behaviors for mice has attracted wide attention from the scientific community as it serves as an effective tool to non-invasively measure well-being, social-interaction, and phenotypical changes [11], [12], [44]. Classification models utilize spatio-temporal features and/or trajectory features [21]. In what follows, we describe the dataset, the trajectory features, and the intensity-based features used in training a behavior detection model. We train multi-class boosting classifiers [45] based on trajectory features and, in Section VI, compare the results to classifiers trained on intensity features.

A. Dataset

We sought to identify six behaviors of interest to scientists and researchers. The behaviors are: walking, drinking, unsupported rearing, supported rearing, climbing, and foraging. An ‘other’ label is given to a frame which the mouse is engaged in a behavior that does not fall under any of the aforementioned six categories. Hence, the dataset has seven labeled categories. The dataset is divided into a training set and a test set. Table I details the annotated frames counts for all seven categories.

TABLE I.

Behavior annotations - training and testing datasets

Behavior Label	Training samples	Test Samples
drinking	11,901	876
walking	17,235	768
rearing (u)	15,036	876
rearing (s)	21,674	1,172
climbing	76,224	3,536
foraging	6,862	655
other	81,057	2,346

B. Trajectory features

Trajectory features are generated from a lower dimensional representation of the pose estimates. Namely, the pose estimates are reduced to two 3D points: the 3D position of tail ϕ_tl = (u_tl, v_tl, w_tl) and the 3D position of ‘head’ ϕ_hd = (u_hd, v_hd, w_hd). ϕ_hd is defined, similar to sect IV–B5, as the Euclidean mean of the positions of the ears and nose. Our trajectory features closely follow the work of Burgos-Artizzu et al. [21]. In [21], however, features were derived from the image centroids of two mice. The trajectory features included each mouse’ position, velocity, and acceleration, the distance between the two mice, and the movement direction of each mouse. Our adaptation of the trajectory features generates 29 measures based on the 3D head/tail positions of the mouse. The features include: 3D position of tail, 3D position of head, tail-to-head distance ||ϕ_hd −ϕ_tl||, interframe change in the tail-to-head distance, the pitch between head and tail $\alpha ={\tan }^{-1}\left(\frac{v_{hd}-v_{tl}}{u_{hd}-u_{tl}}\right)$, the yaw between head and tail $\beta ={\cos }^{-1}\left(\frac{w_{hd}-w_{tl}}{\Vert {\varphi }_{hd}-{\varphi }_{tl}\Vert }\right)$, the interframe change in α, the interframe change in β, tail velocity, head velocity, velocity of 3D centroid (i.e., mean of ϕ_hd, ϕ_tl positions), tail acceleration, head acceleration, and centroid acceleration. Using a 15 frame time-window, we compute the same weak trajectory features introduced by Burgos-Artizzu et al. [21].

C. Intensity-based features

Our intensity feature are also derived from a 15-frame time window centered at the current frame. The overall feature vector for the center frame is the concatenation of 15 feature vectors one from each frame in the time window. Each frame’s feature vector is comprised of three types of features. The first set of features are the binary silhouette statistics for the foreground object in the frame. The second set is intensity image pixel lookup values computed in the same fashion as was done in the structured forest pose estimation task. As described in section IV–B1, the positions of the pixels are randomly chosen during training as offsets relative to the binary silhouette bounding box. The third set of features incorporates optical flow information. For each frame in the time-window, optical flow is computed relative to the subsequent frame. An optical flow magnitude ‘image’ pixel-to-pixel registered with the intensity image is formed. The optical flow features constitute pixel lookups from the magnitude image. The positions of the pixels are also randomly chosen during training as offsets relative to an enclosing bounding box. The enclsoing bounding box, however, is the box enclosing both frames’ binary silhouette bounding boxes.

VI. Experiments

In this section, we assess the performance of both the 3D pose estimation algorithm and behavior detection methods. For the 3D pose estimation, first we evaluate the accuracy of the models as a function of training parameters. Namely, we investigate the effect of the parameters of (1) the intermediate mapping function, (2) discretization mapping, (3) ensemble model, (4) feature choice, and, lastly, we also investigate (5) general structured forest parameters. Second, we analyze the estimation results and identify the reasons for estimation failures. Third, we compare our structured forest implementation to other methods. For the behavior detection, we provide a qualitative assessment of the potential for use of the per-frame pose estimates in detecting behavior in continuous video. Namely, we compare the accuracy of the behavior classifier trained on intensity-based features to a classifier trained solely on 3D trajectory features. We also report on the increased detection accuracy resulting from supplementing the intensity features with the 3D trajectory features.

A. Model parameters sweeps

The accuracy of the 3D pose estimation structured forest implementation is dependent on the choice of model parameters. We investigate the effect of four sets of parameters on accuracy: The intermediate mapping, the discretization mapping, the ensemble model, feaure choice, and the general model parameters. The models are applied to the test set described in III-B. We report on the failure rate as well as the mean distance for all the successful estimates. The sweeps performed are described below.

1). Intermediate mapping parameters

In section IV–B2, we describe two variables that control the generation of the binary string representation of the pose parameters, which is subsequently used to assign a discrete class label to each pose. We sweep over the string length l for both ‘fixed’ and ‘adaptive’ bit assignment. The results of the sweeps are shown in Table II, where the string length l is expressed in multiples of D = 12, the number of pose parameters. The bolded entry in the table is the optimal parameter choice used in the final implementation.

TABLE II.

Intermediate mapping - string length sweep

	Failure Rate (%)	Success mean d	Failure Rate (%)	Success mean d
l	adaptive		fixed
1 × D	68.2	2.64	68.8	2.64
3 × D	31.4	2.00	30.5	2.04
5 × D	24.9	2.04	29.4	2.04
7 × D	29.3	2.00	30.2	2.00
9 × D	28.0	1.99	28.7	2.04

2). Discretization mapping parameters

Once the binary string is generated and reduced in dimensionality by PCA, two methods can be used to cluster the samples for class label assignment. The first, as per section IV–B3, is for the class label to be based on the sign of the projection on the principal component. The second is k-means. The results are shown in Table III. We also show in Table III the results of using direct clustering on poses foregoing the intermediate mapping.

TABLE III.

Discretization mapping sweeps

	Failure Rate (%)	Success mean d	Failure Rate (%)	Success mean d
method	Clustering with Π		Clustering w/out Π
PCA	24.9	2.04	35.0	2.15
K-means	31.0	2.04	32.5	2.13

3). Ensemble model parameters

The ensemble model $\mathcal{E}$ utilizes a regression model trained to predict a pose proposal’s distance from ‘true’ pose. As per section IV–B5, for each ground-truth pose ϕ_n a set of P pose proposals ${\widehat{\varphi }}_i,i\in \{1,\dots ,P\}$ are generated using a structured forest ${\mathcal{F}}^{\prime }$. In our implementation, ${\mathcal{F}}^{\prime }$ has P = 24 trees and was trained using a subset obtained by randomly discarding half of the samples in the full training set. The main parameter for building $\mathcal{E}$’s regression model is the pose-indexed features offset radius r, described in Section IV–B5. Table IV shows the results of sweeping over r.

TABLE IV.

Ensemble Model - Feature position offset radius sweep

Offset radius r	0.3	0.4	0.5	0.6	0.7
Failure Rate (%)	26.6	27.7	24.9	26.8	28.7
Success mean d	2.08	2.09	2.04	2.06	2.04

To highlight the gain in performance due to utilization of pose-indexed features, we carry out two tests. In the first, we eliminate x_PL from the feature vector. The failure rate increases from 24.9% to 30.6%. In the second test we replace x_PL with pixel lookups that are not pose-indexed but rather taken at randomly chosen pre-specified offsets relative to the detection window. These features are similar to the pixel lookup features described in section IV–B1 but are taken from S_n rather than I_n. The ‘static’ features (i.e., as opposed to pose-indexed features) caused the failure rate to increase to 29.2% from 24.9%.

Lastly, we report that our ensemble model produces results that are far more accurate that standard ensemble models. Namely, if we use the medoid, as proposed in [18], the failure rate is 40.7%. When using more traditional methods, such as the mean and median, the failure rates are 42.4% and 33.2% respectively. We note, however, that using mean and median of each pose parameter produces poses that are not guaranteed to be plausible physically.

4). Feature choice

To investigate the robustness of the raw intensity based features, we run experiments in which the feature vector is augmented with gradient and HOG features. When the feature vector was augmented with gradient features, the failure rate increased slightly from 24.9% to 26.6%. With inclusion of HOG features, the performance was further degraded and the failure rates went up approximately 8% to 32.7%. These experiments prove that raw intensity features are more robust for the task at hand.

5). General forest parameters

The last set of sweeps involved general forest parameters as well as training set size. We sweep over the number of trees in the structured forest, noting that increasing the number of trees in the forest reduces the number of samples used to train each tree. The results are shown in Table V. We sweep over the size of the training sets. The size of the training set is reduced by discarding a randomly chosen subset of the whole set. When the full set was used, the failure rate of 24.9% was at its lowest. The failure rate went up to 29.8% when the structured forest was trained with 0.8 of the training samples and 33.9% when 0.4 of the training samples were used. The distance distribution for the optimal model is shown in Figure VI-C2.

TABLE V.

Structured forest parameters - Tree count

Tree count	4	8	16	24	32	64
Failure Rate (%)	37.0	31.8	24.9	31.6	28.0	30.9
Success mean d	2.12	2.06	2.04	2.02	2.09	1.97

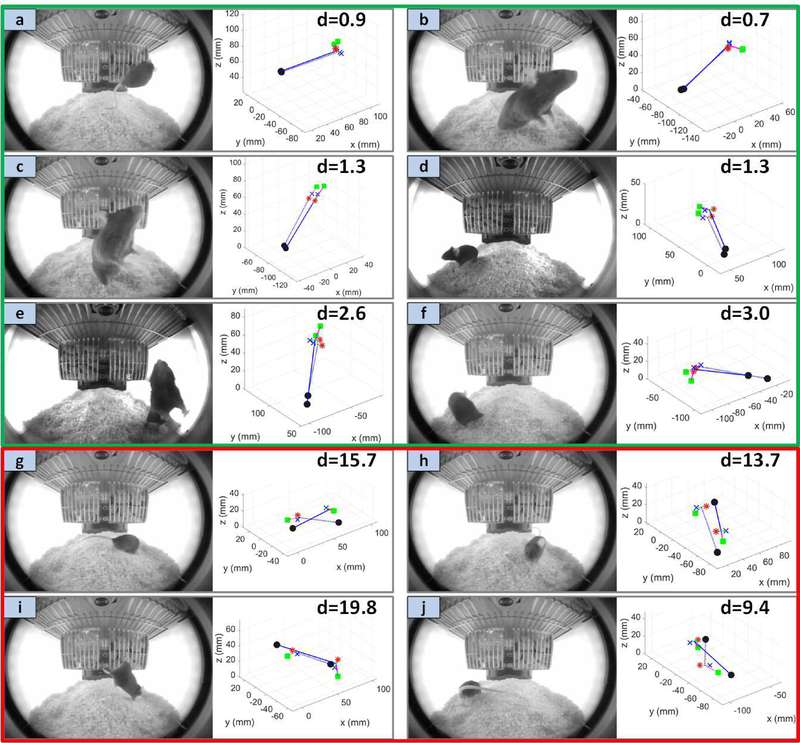
B. Analysis of estimation results

Figure 7 shows ten example pose estimates, six successful ones (Figure 7a–f) and four failed estimates (Figure 7g–j). The shown successful estimates were chosen to illustrate the deviation from ground-truth for a range of distances within the success threshold. The failure cases were chosen to highlight the typical reasons for failure. In Figure 7g–i, the predicted pose has ~ 180° reversal relative to the ground-truth. In Figure 7g, the mouse is the furthest it could be from the camera and has its head completely occluded by the rest of the body. The example in Figure 7h exhibits a large degree of self occlusion due to the mouse orientation and proximity to the lens. In Figure 7i the mouse is in a novel pose (i.e., descending from the basket). The closest pose in feature space is the one to which it was wrongly assigned, namely the more commonly observed pose in which the mouse is on its hind legs with its forearms against the basket. Lastly, Figure 7j illustrates a failure case due to the strong occlusion of the silhouette by the tail.

Fig. 7.

Example successful estimates (a)-(f) and failed estimates (g)-(h). The solid stick-figure is the ground-truth pose while the dashed stick-figure is the pose estimate.

C. Comparison to other methods

In this section we compare the results of our proposed algorithm to two methods. The first method is an adaptation of a state-of-the-art 2D pose estimation algorithm. The second is Deep Neural Networks. The distance distribution for both methods are shown in Figure VI-C2.

1). Three dimensional Cascaded Pose Regression

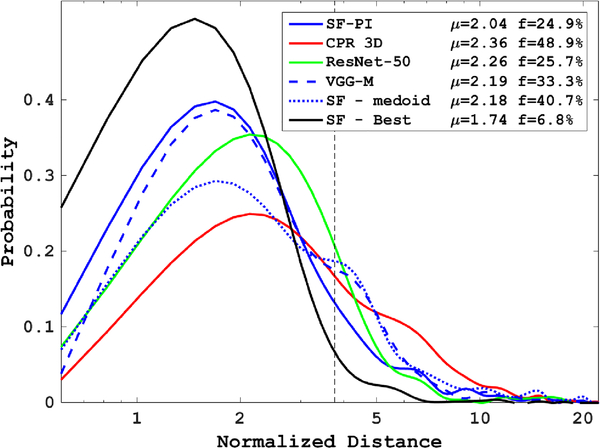
We compare our structured forest method to an established structured pose estimation algorithm. The Cascaded Pose Regression (CPR) algorithm [36] and its variants [39], [42] have produced state-of-the-art results in the 2D landmark estimation problem. The CPR algorithm has also achieved success when applied to 2D mouse pose estimation [26], [36]. We have adapted and optimized the CPR algorithm to the 3D mouse pose estimation task using the same training set described in this paper. For the details of our 3D CPR implementation, the reader is referred to [19]. The parameters of the method were modified to reduce the failure rate to 48.9%, a ~ 3% improvement over what was reported in [19]. Clearly, the structured forest method produces estimates with 24% lower failure rates than the 3D CPR.

2). Deep Neural Networks

Considering the large number of training examples at disposal, for completeness we also compare our approach against Deep Learning techniques. We first considered state-of-the-art human pose estimation approaches such as HourGlass [16] or OpenPose [15]. However, these approaches are designed to deal with multiple objects and articulated poses estimated directly from 2D image locations. Their final output is an ensemble of 2D image part detectors, very different from what is required for our task, which consists of estimating directly 3D absolute coordinates from two synchronized views of a single, easily detectable object. Therefore, we instead adapted two more “universal” Convolutional Neural Networks (CNN) state-of-the-art architectures which have been proven to work well on a wide range of tasks: VGG-M [46] and ResNet-50 [47]. Benchmarking both ensures that different choices of convolutional blocks types, normalization and network depth are tested. The CNNs were first trained using ImageNet (downloading pre-trained models available online), then fine-tuned using our 90K training images and finally applied to our test set. To adapt them to our task, some design and image handling changes had to be made. The first convolutional layer was changed to work on two channels (our two synchronized views) instead of three (single RGB image). The final Fully Connected layer was changed to have 12 outputs (each predicting the location of one keypoint in 3D). During fine-tuning, a L2 loss was used between the 12 predicted positions and ground-truth. Ground-truth locations were previously normalized using known cage dimensions so that 3D positions always in the range [−1, +1], greatly helping convergence compared to using absolute positions. Both image views were fed to the network after performing background subtraction (background was computed as the average of all training images). This achieves zero-mean input and helps the network instantly locate the foreground pixels (the mouse), similar to what achieved by our mouse segmenter. DropOut [48] was used in the final layers of VGG-M, while BatchNorm normalization [49] was used on ResNet-50 throughout. Both networks were trained with minibatch gradient descent using adam optimizer [50] and early-stopping conditions to avoid overfitting (stopping when no further improvement was observed on the test set during 5 epochs). The VGG-M implementation has a failure rate of 33.3%, while the ResNet-50 implementation has a failure rate of 25.7%. The distance distributions for both implementations are shown in Figure VI-C2.

D. Behavior detection

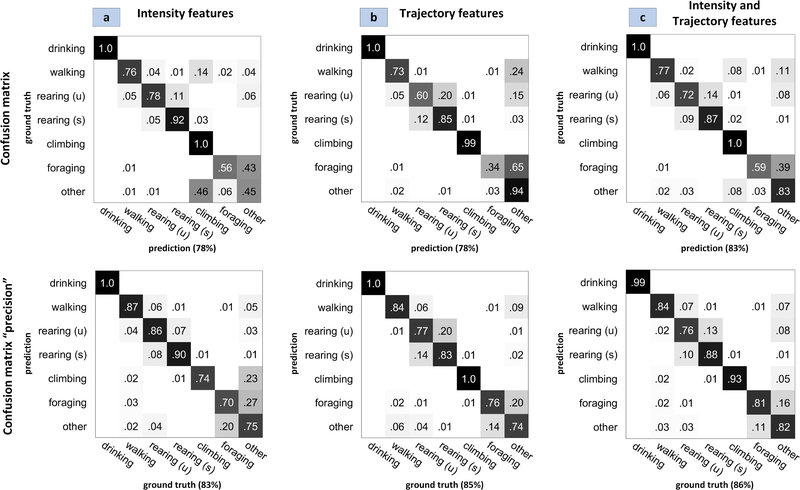
We qualitatively assess our pose-estimation method by designing three different behavior classifiers: a classifier based on trajectory features only, a classifier based on spatial and spatio-temporal intensity features, and lastly a classifier trained on both trajectory features as well as intensity based features. The optimal structured forest pose estimation model was used to generate pose estimates for all frames in the training set video clips. Trajectory features were derived from the pose estimates as described in V. Similarily intensity features were derived from the videos as described in V. Three different REBEL classifiers [45] were built. The test set was applied to all three classifiers. To compare the results, we use the diagnostics introduced by [51] for multiclass behavior detection problems. For each classifier we compute two matrices: the conventional confusion matrix which measure the recall of each class and the ‘precision’ confusion matrix which measures precision for each class. The matrices along with the diagonal mean are shown in Figure 8. It is clear from the results that, despite a 24.9% failure rate in pose estimation, the classifier based on trajectory features derived from our estimates parallels the accuracy of the intensity-features-based classifier (78% vs 78%) and has better precision (85% vs 83%). Furthermore, when the trajectory features are combined with the intensity features the resulting classifier has a 5% gain in recall (83% vs 78) and 3% gain in precision (86% vs 83%) over the classifier trained solely on intensity-features.

Fig. 8.

Confusion matrices and ‘precision’ confusion matrices for behavior detection model based on intensity features only (a) trajectory features only (b) and both sets of features (c). For each matrix, the mean of its diagonal is also shown.

VII. Discussion and Conclusion

We have proposed a systematic approach for 3D mouse pose estimation in compact, fisheye-lens based, vision systems. The structured forest algorithm employed in our solution preserves the structural relationships between the pose landmarks. Paired with the unique ensemble model, the structured forest implementation seems to overcome the challenges presented by the optical configuration as well as the deformability of the mouse. Furthermore, the predicted pose is by construction physically plausible, which is not guaranteed for the other 3D estimation methods to which we compared our implementation. In particular, we note that a maximum of only 25% of the estimates produced by the DNN implementations were plausible (e.g., preserving distance between ears and distance between nose and ears). We believe that the success of the two-layered approach (i.e., structured forest followed by pose-indexed-features-based ensemble model) is tied to the target’s properties. on one hand, the mouse is deformable and nearly featureless. on the other hand, the number of pose configurations of the mouse is limited (e.g., as compared to a human). Because of the more limited pose-space for the mouse coupled with the inherent ambiguity in pose, it makes sense to use the structured forest to generate a set of plausible pose configurations. The ensemble model then employs the finer pose-indexed features to select from the limited set of plausible poses. our novel ensemble model is superior to conventional ensemble models employing mean, median, or medoid as demonstrated in the Section VI–A3. The superiority in performance is attributed to the fact that the selection of the pose is guided by pose-indexed image features, as opposed to conventional methods where image features are not employed in the computation of the final output pose.

Our method is not only the first reported to estimate 3D mouse pose from conventional video, but tackles the additional challenges of estimation from a single image (i.e., with no temporal context) and the unique optical configuration required for systems suited for scalability in animal vivaria. Accurate per-frame 3D pose estimates constitute a very informative measure of mouse activity and behavior. We have further demonstrated the utility of the pose-estimates in behavior analysis by accurately identifying predefined behavior bouts in continuous video based on novel 3D trajectory features derived form the temporal evolution of the 3D poses.

The work presented estimates the 3D pose in a single image without consideration to temporal constraints. The accuracy of the algorithm will likely improve by incorporating a temporal consistency model. While our novel ensemble model greatly improved the selection of the best proposal over standard methods, Figure 6 shows that there remains better pose proposals to be chosen from the pool of proposals produced by the structured forest. Imposing temporal constraints can improve the selection of best pose. One advantage of our method is that several pose proposals are produced at each time step. Methods that merge pose proposals across time and space, such as [37], can be employed to further reduce the error rate. Additional accuracy in the pose estimates will very likely translate to improvements in the accuracy of the trajectory-features-based behavior detection model. Overall, the proposed approach is a step in the direction of ubiquity of vision systems in animal vivaria, transforming animal care and revealing large-scale experimental data for researchers in various disciplines.

Fig. 6.

Distance distributions for the test set comparing the proposed structured forest implementation with the pose-indexed features based ensemble model (SF-PI), to the CPR 3D implementation as well as the standard regression forests (RF) implementation. Also shown is the distance distribution for an ensemble model used in [18] in which the medoid of all proposals is the chosen prediction (SF-medoid), rather than the ensemble model described in section IV–B5. We also show the distance distribution for the best proposal (SF-Best) prior to applying the ensemble model, i.e. the pose proposal having the minimum distance to the ground-truth.