Implementation and Validation of a Three-dimensional Cardiac Motion Estimation Network

Abstract

Purpose

To describe an unsupervised three-dimensional cardiac motion estimation network (CarMEN) for deformable motion estimation from two-dimensional cine MR images.

Materials and Methods

A function was implemented using CarMEN, a convolutional neural network that takes two three-dimensional input volumes and outputs a motion field. A smoothness constraint was imposed on the field by regularizing the Frobenius norm of its Jacobian matrix. CarMEN was trained and tested with data from 150 cardiac patients who underwent MRI examinations and was validated on synthetic (n = 100) and pediatric (n = 33) datasets. CarMEN was compared to five state-of-the-art nonrigid body registration methods by using several performance metrics, including Dice similarity coefficient (DSC) and end-point error.

Results

On the synthetic dataset, CarMEN achieved a median DSC of 0.85, which was higher than all five methods (minimum–maximum median [or MMM], 0.67–0.84; P < .001), and a median end-point error of 1.7, which was lower than (MMM, 2.1–2.7; P < .001) or similar to (MMM, 1.6–1.7; P > .05) all other techniques. On the real datasets, CarMEN achieved a median DSC of 0.73 for Automated Cardiac Diagnosis Challenge data, which was higher than (MMM, 0.33; P < .0001) or similar to (MMM, 0.72–0.75; P > .05) all other methods, and a median DSC of 0.77 for pediatric data, which was higher than (MMM, 0.71–0.76; P < .0001) or similar to (MMM, 0.77–0.78; P > .05) all other methods. All P values were derived from pairwise testing. For all other metrics, CarMEN achieved better accuracy on all datasets than all other techniques except for one, which had the worst motion estimation accuracy.

Conclusion

The proposed deep learning–based approach for three-dimensional cardiac motion estimation allowed the derivation of a motion model that balances motion characterization and image registration accuracy and achieved motion estimation accuracy comparable to or better than that of several state-of-the-art image registration algorithms.

© RSNA, 2019

Supplemental material is available for this article.

Summary

A deep learning–based three-dimensional nonrigid body motion estimation technique based on cine MR images was implemented; the method was validated against five state-of-the-art nonrigid body registration methods by using several image and motion metrics.

Key Points

• ■ An unsupervised three-dimensional cardiac motion estimation network (CarMEN) based on cine MR images achieved motion accuracy comparable to or better than five state-of-the-art nonrigid body registration methods.

• ■ This method substantially improves and streamlines cardiac motion estimation with potentially important technical and diagnostic implications.

Introduction

Characterizing the motion of the heart using noninvasive imaging techniques such as MRI is challenging but potentially very important. On the technical side, this information could be used to improve the quality of the MRI data acquired by using cardiac gating techniques (1) or to minimize the unwanted effects of motion on the PET data acquired simultaneously in integrated PET/MRI scanners (2). From a more clinical perspective, detailed knowledge of the complex three-dimensional motion of the heart during the cardiac cycle (eg, myocardial velocity, strain, etc) would inform us about its mechanical status (eg, left ventricle dyssynchrony, wall motion hypokinesis, etc), with potential diagnostic implications.

Ideally, the motion estimates should be obtained from MRI sequences that are routinely used for clinical purposes, such as cine MRI. Although this breath-hold sequence allows the acquisition of data corresponding to each specific time point in the cardiac cycle (ie, systole, diastole, etc), characterizing the three-dimensional motion of the whole heart from these images is challenging because the tissue intensity is relatively homogeneous and morphologic details to facilitate the temporal correspondence search are limited. Furthermore, because a cine MRI volume in a time frame is technically a two-dimensional stack of independently acquired sections, rather than an actual three-dimensional volume where the whole heart is simultaneously acquired, out-of-plane motion during the cardiac cycle makes the derivation of three-dimensional estimates challenging. To date, various methods have been proposed to derive motion estimates from cine MRI, including optical flow and registration methods (3,4) and techniques based on feature tracking (5). Although each solution has specific merits and limitations, a parameter-free, rapid, and robust method for cine MRI–based motion estimation is still unavailable.

Alternatively, motion estimation can be recast as a data-driven learning task (6–18), which reduces processing times drastically because trained methods can quickly compute motion estimates from new data by using the learned parameters without the need of case-specific optimization (15,17). Recent work on MRI brain image registration has demonstrated the advantage of allowing real-world data to guide the efficient representation of motion through a structured training process while operating orders of magnitude faster (17). For more complex cardiac applications, Qin et al (19) have proposed a learning-based joint motion estimation and segmentation method for cardiac MRI. However, this method has only been validated on two-dimensional sections.

We present an unsupervised three-dimensional cardiac motion estimation network (CarMEN) for deformable motion modeling from two-dimensional cine MR volumes. Our aims were to train, test, and validate CarMEN by using real and synthetic data from adult and pediatric participants, and to compare its accuracy to that of several popular state-of-the-art registration packages in the presence of out-of-plane three-dimensional movement, acquisition artifacts, and pathologic changes. We hypothesized that CarMEN would achieve better accuracy compared with all other registration techniques. Although we used the method to register cardiac cine MR images here, CarMEN is in principle broadly applicable to other cardiac image registration tasks.

Materials and Methods

Datasets

Three datasets were used in this study (see Appendix E1 [supplement] for a full description). The Automated Cardiac Diagnosis Challenge dataset (20) was used for training and testing CarMEN. This dataset consisting of cine MR images and corresponding segmentations was obtained from 150 participants divided evenly into five subgroups: healthy participants, patients with myocardial infarction, patients with dilated cardiomyopathy, patients with hypertrophic cardiomyopathy, and patients with abnormal right ventricle. All image frames were resampled to a grid of 256 × 256 × 16 with resolution of 1.5 × 1.5 × 5 mm³. Preprocessing steps included manually centering the images about the center of the left ventricle and cropping the resulting images to the size 80 × 80 × 16. For each subgroup with 30 participants, 20 were randomly chosen for training and the remaining 10 were used for testing, leaving 100 participants for training and 50 participants for testing.

The second dataset consisted of synthetic cine MRI data that enabled us to validate the trained network model on data with known ground-truth motion and tissue segmentation. We used the established extended cardiac-torso, or XCAT (21), phantom software to generate three-dimensional anatomy masks at multiple time frames with size 80 × 80 × 16 and average resolution set to 1.5 × 1.5 × 5 mm³. We used the XCAT extension, MRXCAT (22), to simulate the MR acquisitions on the anatomy masks. Each simulation consisted of three frames approximately at diastole, middiastole, and systole. Motion estimate predictions were made for diastole-middiastole and diastole-systole input pairs.

Finally, a pediatric dataset of 33 participants consisting of cine MR images and expert-provided segmentations was used to assess how CarMEN generalizes to unseen datasets (23). Most of the participants displayed a variety of heart abnormalities such as cardiomyopathy, aortic regurgitation, enlarged ventricles, and ischemia, providing a realistic and challenging performance benchmark. Preprocessing steps included centering, cropping, and zero padding the sections such that the size of the images was 80 × 80 × 16.

CarMEN Architecture

In standard three-dimensional image registration formulation, a moving image M: 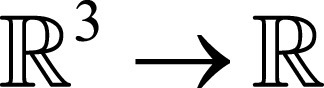is registered onto a fixed image F: 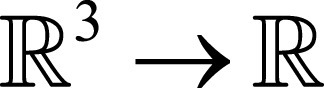, yielding the motion estimates ø: 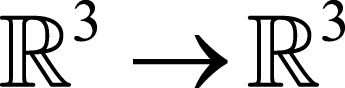, which characterizes the motion from F to M (ie, they represent the backward mapping). Most existing registration algorithms iteratively estimate ø based on solving:

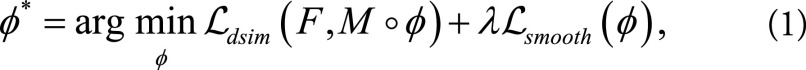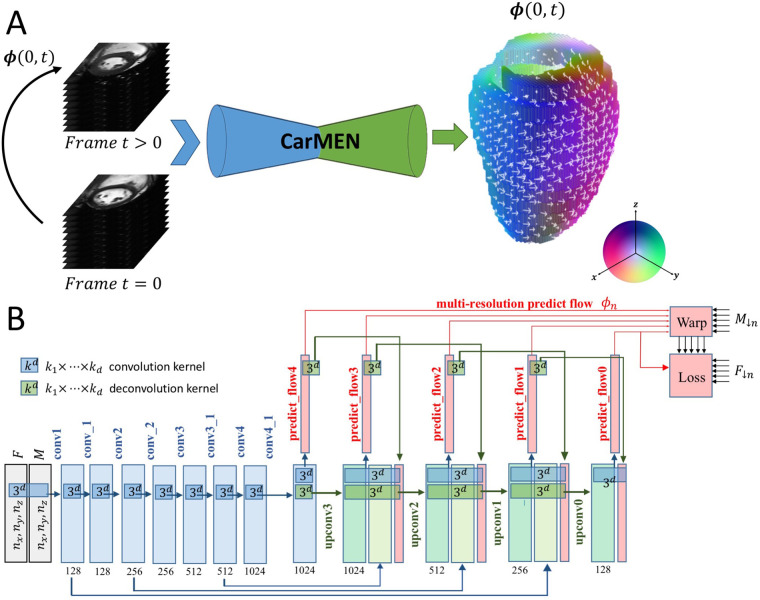
where L_dsim measures the image dissimilarity between 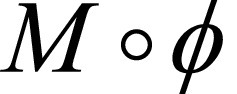and F, the regularization term L_smooth enforces smoothness in ø, and λ is the regularization parameter. Here we instead modeled a function g (F,M) = ø by using a convolutional neural network architecture (Fig 1). The input to the network was a pair of cine MRI volumes F and M of size 80 × 80 × 16 that were used to derive the multiresolution motion estimates. F corresponds to a frame at diastole and M to a frame later in the cardiac cycle. The input images were concatenated into a two-channel three-dimensional image. The network has eight convolutional layers with stride of two in three of them and a leaky rectified linear unit nonlinearity after each layer. Convolutional filter sizes were 3 × 3 × 3 for all layers. The number of feature maps increases in the deeper layers, roughly doubling every second layer with a stride of two. The refinement section has four “upconvolutional” layers consisting of unpooling followed by convolution. We applied the upconvolution to feature maps and concatenated it with corresponding feature maps from the contractive part of the network and an upsampled coarser motion prediction. Each step increases the resolution twice, and a convolutional filter of 3 × 3 × 3 is used to generate a coarse prediction. This was repeated five times, resulting in a predicted estimate in the final layer for which the resolution is equal to that of the input. The output of the network is an 80 × 80 × 16 × 3 tensor, representing the required voxelwise deformation in the x, y, z directions. The multiresolution predicted motion was then used to warp the moving image, also at multiple resolutions, to the fixed image space by using linear interpolation. This was performed through a spatial transform layer within the convolutional neural network. This step was akin to a multiresolution pyramid strategy used in conventional optimization techniques to improve the capture range and robustness of the registration (24). The network loss function used was the dissimilarity function L_dsim combined with a regularization term L_smooth that regularizes the full-resolution motion estimates (see Equation 1). L_dsim was defined as the standard mean absolute difference and

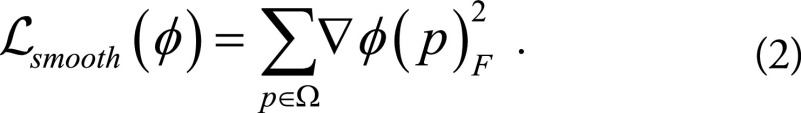Figure 1:

Image shows cardiac motion estimation network (CarMEN) architecture. A, Pair of two-dimensional stacks of cine MR images corresponding to two time points enable CarMEN to generate motion estimates ø (0, t), where t can range from 0 to T, the number of frames acquired. Each motion vector was color coded with red, green, and blue scheme as indicated. During training, diastole frame was maintained (t = 0) as fixed (F) stack and moving (M) stack varied with frames at later time point in cardiac cycle (t > 0). Once trained, CarMEN can generate motion estimates for specific input pair (eg, diastole to systole) or sequence of inputs covering entire cardiac cycle. B, Input stacks F and M are concatenated into two-channel three-dimensional volume. 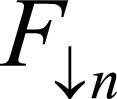and 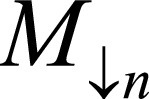denote F,M downsample by 2ⁿ, where n = 0,…,4. Network generates estimates ø_n at multiple resolutions that are used to warp multiresolution moving images. Loss function penalizes absolute difference between 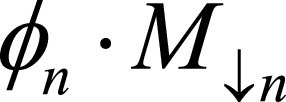and and 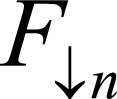regularizes ø_n.

The derivative ø was approximated by finite differences by applying the one-dimensional filter [-1,1] to ø along each dimension by convolution. We implemented CarMEN in TensorFlow (version 1.6; Google, Mountain View, Calif) and incorporated the regularization functional by using basic TensorFlow convolutional operations (see Appendix E1 [supplement] for architecture and training motivation).

Training and Testing

A sample is defined as a pair of image frames at diastole and at a later time point in the cardiac cycle; therefore, a single participant with 26 time frames corresponds to 25 samples. We trained CarMEN with 2512 samples from 100 participants of the Automated Cardiac Diagnosis Challenge training set (see Appendix E1 [supplement]), using minibatches of 10 image pairs. Data augmentation included random z-axis rotations and x, y, z translations. A step decay learning rate schedule initialized at 1 × 10⁻⁴ and reduced by half every 10 epochs was used. The regularization parameter λ was set to 1 × 10⁻⁷. The network was trained for 100 epochs, each epoch corresponding to one complete pass through the 2512 samples. To reduce overfitting of the network to one particular anatomy or image property, the 2512 samples were randomized at the beginning of each epoch (ie, each batch was made up of different participants and different cardiac phases). Once trained, CarMEN was tested by using the Automated Cardiac Diagnosis Challenge testing set with 1310 samples from 50 other patients. Next, we further tested the network on two other separate datasets: 200 samples from 100 simulations and 627 samples from 33 participants of the pediatric dataset (see Appendix E1 [supplement]). The training time was 4 hours and motion estimates for a single test input pair were generated in 9 seconds.

Evaluation

Obtaining the dense ground-truth motion estimates for the real testing data is not feasible because many motion fields can yield similar-looking warped images. Hence, an advantage of using synthetic data to validate our method is that we have the ground-truth motion and can therefore evaluate the motion estimates by directly comparing them to the simulated (yet realistic) cardiac motion. The ground-truth segmentation of the tissues in these data is also completely accurate; therefore, metrics such as the Dice similarity coefficient (DSC) are more indicative of the registration accuracy. Furthermore, although the most common measures to measure image similarity are mean squared error and peak signal-to-noise ratio because they are fast and easy to implement, they correlate poorly with registration quality as perceived by a human observer (25). To address this limitation, we also evaluated our method by using the multiscale structural similarity index metric, a state-of-the-art metric that accounts for changes in local structure and correlates with the sensitivity of the human visual system (26). We also measured the normalized cross-correlation because it is less sensitive to linear changes in the MRI signal intensity in the compared images.

To compute the DSC on the left ventricle, the left ventricle myocardium was segmented by warping the expert-provided segmentation M_mask using the predicted motion ø = g_θ (F,M). If the estimates ø represent accurate anatomic correspondences, then we expect the regions in F_mask and M_mask (ø) corresponding to the same anatomic structure to overlap well (ie, a DSC score of 1 indicates the left ventricle structures are identical). The accuracy of the motion estimates was evaluated by using the end-point error, or EPE, defined as the Euclidean distance between the predicted registration field ø and the ground truth ø^*,

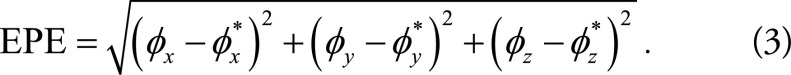In practice, we use the average end-point error value for all voxels in the left ventricle.

We evaluated the performance of CarMEN by comparing its performance to that of five state-of-the-art methods: two B-spline approaches with the Insight Segmentation and Registration Toolkit, or ITK, package (https://www.itk.org) (27,28); a B-spline Elastix variation (29); a mass-preserving approach termed Vampire (30); and the Diffeomorphic Demons, or dDemons, algorithm (31) (see Appendix E1 [supplement] for implementation details).

Statistical Analysis

Data were treated as nonparametric and presented as median and interquartile range (IQR) and compared by using two-sided Wilcoxon signed-rank tests. Statistical analysis was performed in Python (version 2.7; Python Software Foundation, Wilmington, Del; https://www.python.org). A two-sided P < .001 was considered to indicate statistical significance. All P values reported in the next sections refer to comparisons between an optimization-based method and CarMEN.

Results

The Table and Figure 2 show the performance of CarMEN on the three separate datasets relative to other optimized state-of-the-art registration methods. For the Automated Cardiac Diagnosis Challenge test dataset, for each of the 50 test participants, only the samples corresponding to images whose first frame is at diastole and second frame at systole were used because only those samples had expert-provided segmentations. For the pediatric and synthetic validation data, segmentations are available for the whole cardiac cycle; therefore, all participants and frames were included, and we report the average results of all frames.

Metrics Comparison

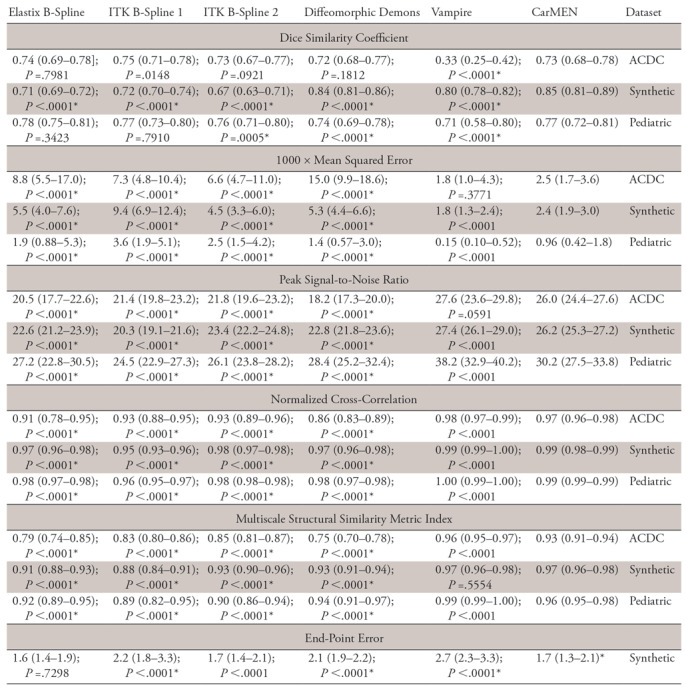
Note.—Data are medians, with interquartile ranges in parentheses. Included are the Automated Cardiac Diagnosis Challenge (ACDC), pediatric, and synthetic datasets. For all datasets, image metrics included the Dice similarity coefficient (DCS), mean squared error (MSE), peak signal-to-noise ratio (PSNR), normalized cross-correlation (NCC), and the multiscale structural similarity metric index (MS-SSIM). Motion estimates on the synthetic dataset are compared against the ground truth by using the average end-point error (EPE). Low MSE and EPE values are considered good, whereas high values of PSNR, NCC, and MS-SSIM are better. P values are relative to the method and were obtained by using two-sided Wilcoxon signed-rank tests. ITK = Insight Segmentation and Registration Toolkit.

*Indicates that cardiac motion estimation network (CarMEN) significantly outperformed (P < .001) metric of another method.

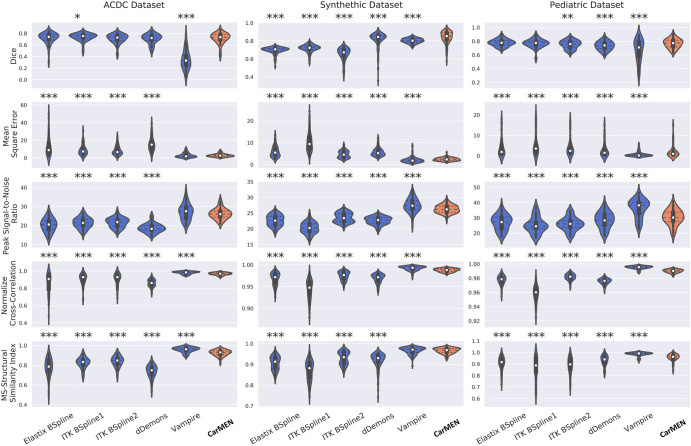
Figure 2:

Image shows image registration results on three datasets measured through five different image similarity metrics and represented with nonparametric violin plots. Violin plots are essentially mirrored density plots. Low mean squared error values are considered good, whereas high values of all other metrics are better. P values are relative to method and were obtained by using two-sided Wilcoxon signed-rank tests. * = P < .05, ** = P < .001; *** = P < .0001. ACDC = Automated Cardiac Diagnosis Challenge, CarMEN = cardiac motion estimation network, dDemons = Diffeomorphic Demons, ITK = Insight Segmentation and Registration Toolkit, MS = multiscale.

Automated Cardiac Diagnosis Challenge Dataset

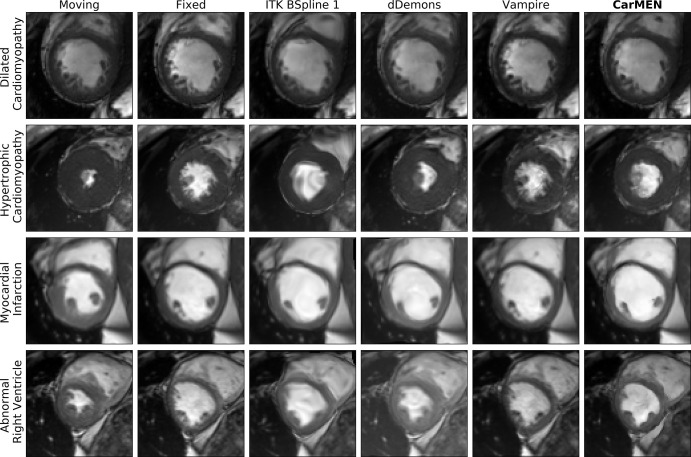
CarMEN and Vampire showed significantly (P < .001; n = 50) better performance relative to the other four state-of-the-art methods on all the metrics except for the DSC. However, there was no significant difference between the DSCs obtained across all methods and CarMEN except for Vampire, which had a significantly lower DSC (median, 0.33 [IQR, 0.25–0.42] vs 0.73 [IQR, 0.68–0.78]). Relative to CarMEN, Vampire had a significantly higher normalized cross-correlation (0.98 [IQR, 0.97–0.99] vs 0.97 [IQR, 0.96–0.98]) and multiscale structural similarity index metric (0.96 [IQR, 0.95–0.97] vs 0.93 [IQR, 0.91–0.94]). There was no significant difference in the mean squared error and peak signal-to-noise ratio metrics. Representative images of the four patient groups for a B-spline method, dDemons, Vampire, and CarMEN are shown in Figure 3. Different sections from base to apex are shown in Figure E5 (supplement). Except for Vampire, all optimization-based methods performed worse in patients with hypertrophic cardiomyopathy at visual inspection, in some instances resulting in unrealistic anatomies. In contrast, although only 20% of the training data consisted of this patient group, CarMEN successfully achieved a better registration with the exception of some outliers (see Fig E4 [supplement]). An example of how CarMEN may be used for motion-based cardiac assessment is shown in Figure 4.

Figure 3:

Image shows Automated Cardiac Diagnosis Challenge dataset. Cardiac motion estimation network (CarMEN) outperforms optimization-based methods across four pathologic subgroups. First and second columns correspond to heart at systole and diastole, accordingly. Moving image at systole is warped to diastole position by using predicted registration field for each method. dDemons = Diffeomorphic Demons, ITK = Insight Segmentation and Registration Toolkit.

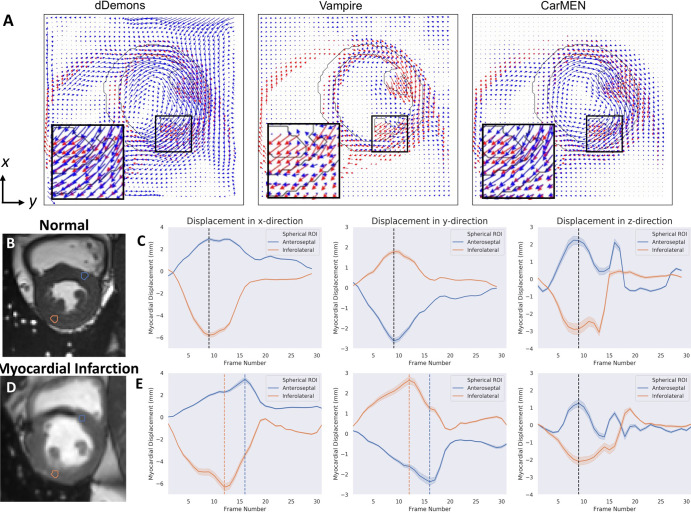
Figure 4:

A, Representative images of synthetic motion estimate in-plane components. Predicted estimates (blue) are compared with ground truth (red). B-E, Example of assessment of left ventricle dyssynchrony with cardiac motion estimation network (CarMEN) in, B, C, a healthy individual and, D,E, a patient with myocardial infarction. B, Cardiac MR image in short-axis orientation. Sample spherical volumes are placed at anteroseptal (AS) and inferolateral (IL) walls near base. C, Corresponding displacement graphs show absence of left ventricle dyssynchrony as both AS and IL walls reach peak displacement simultaneously (black dotted lines). D, E, In a patient with myocardial infarction, IL wall reaches peak displacement four frames earlier (orange dotted lines) relative to AS wall (blue dotted lines) corresponding to approximately 120 msec for frame resolution of 30 msec. This difference may indicate left ventricle dyssynchrony related to infarcted tissue in septal wall. dDemons = Diffeomorphic Demons, ROI = region of interest.

Synthetic Dataset

The Table, Figure 2, and Figure 5 show the performance of the network on the synthetic dataset. CarMEN had a significantly (P < .001; n = 200) higher DSC (0.85 [IQR, 0.81–0.89]) relative to all the other methods. CarMEN and Vampire showed significantly better performance relative to the other four methods on all other metrics. Relative to CarMEN, Vampire had a significantly lower 1000 × mean squared error (1.8 [IQR, 1.3–2.4] vs 2.4 [IQR, 1.9–3.0]), and a significantly higher peak signal-to-noise ratio (27.4 [IQR, 26.1–29.0] vs 26.2 [IQR, 25.3–27.2]) and normalized cross-correlation (0.99 [IQR, 0.99–1.00] vs 0.99 [IQR, 0.98–0.99]). There was no significant difference in the multiscale structural similarity index metric. The image metric distributions of Elastix and ITK B-spline 2 were mostly bimodal, each peak in the distributions corresponding to data at the diastole and systole positions (see Fig 2). Figure 5 shows the accuracy of the three-dimensional motion estimates. CarMEN had a significantly lower average end-point error (1.7 [IQR, 1.3–2.1]) relative to Vampire (2.7 [IQR, 2.3–3.3]), ITK B-spline 1 (2.2 [IQR, 1.8–3.3]), and dDemons (2.1 [IQR, 1.9–2.2]). There was no significant difference in the end-point error between CarMEN and Elastix B-spline. A comparison of the estimated motion and the ground truth can be seen in Figure 4, A. Separate DSC (Fig E6 [supplement]) and end-point error (Fig E7 [supplement]) figures show the results for middiastole and systole separately.

Figure 5:

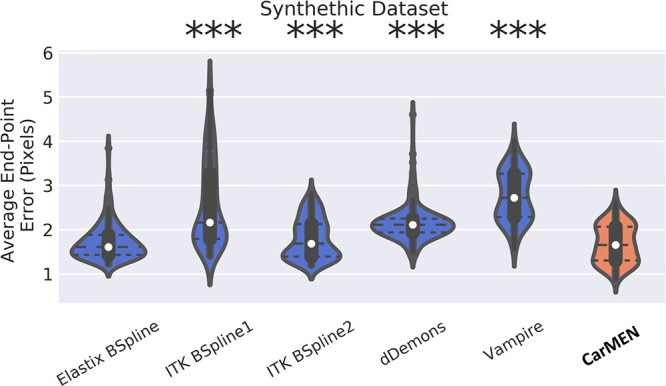
Image shows synthetic dataset. Cardiac motion estimation network (CarMEN) has lower or similar transformation error relative to optimization-based methods. Predicted registration field for each method is compared against ground truth by using average end-point error and they are represented with nonparametric violin plots. Violin plots are essentially mirrored density plots. Each method is compared against CarMEN by using two-sided Wilcoxon signed-rank tests. * = P < .05, ** = P < .001; *** = P < .0001. dDemons = Diffeomorphic Demons, ITK = Insight Segmentation and Registration Toolkit.

Pediatric Dataset

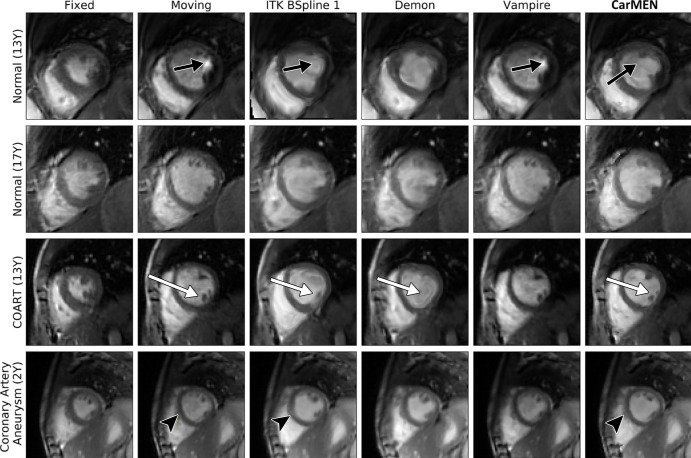
On the pediatric dataset, CarMEN and Vampire showed significantly (P < .001; n = 627) better performance relative to the other four state-of-the-art methods for all the metrics except the DSC. CarMEN has a significantly higher DSC (0.77 [IQR, 0.72–0.81]) relative to Vampire (0.71 [IQR, 0.58–0.80]), dDemons (0.74 [IQR, 0.69–0.78]), and ITK B-Spline 2 (0.76 [IQR, 0.71–0.80]). There was no significant difference in the DSC between CarMEN and the other two methods. Relative to CarMEN, Vampire had a significantly lower 1000 × mean squared error (0.15 [IQR, 0.1–0.52] vs 0.96 [IQR, 0.42–1.8]), higher peak signal-to-noise ratio (38.2 [IQR, 32.9–40.2] vs 30.2 [IQR, 27.5–33.8]), higher normalized cross-correlation (1.00 [IQR, 0.99–1.0] vs 0.99 [IQR, 0.98–0.99]), and higher multiscale structural similarity index metric (0.99 [IQR, 0.99–1.0] vs 0.96 [IQR, 0.95–0.98]). Representative images of various patient groups are shown in Figure 6. A common feature of some optimization-based methods is the disappearance of the papillary muscles in the warped images. In contrast, these structures are better visualized in most of the images obtained with our method (Fig 6, white arrows). CarMEN is also more robust to acquisition artifacts (Fig 6, black arrows), and better preserves anatomic features (Fig 6, arrowheads). Movie 1 (supplement) of the motion fields is provided as a sample.

Figure 6:

Image shows pediatric dataset. Cardiac motion estimation network (CarMEN) outperforms optimization-based methods across various subgroups and ages. First and second columns correspond to heart at systole and diastole, accordingly. Moving image at systole is warped to diastole position by using predicted motion estimates for each method. Two healthy participants and two patients are shown. CarMEN is more robust to image artifacts relative to optimization methods such as Insight Segmentation and Registration Toolkit (ITK) BSpline 1 and Vampire (black arrows). Papillary muscles disappear in some optimization-based methods but are preserved by proposed method (white arrows). CarMEN does a better job at preserving anatomy relative to ITK BSpline 1 (arrowheads). COART = coarctation of the aorta.

Movie 1.

Download video file ^{(2.3MB, mp4)}

Pediatric Dataset. The motion estimates for multiple points in the cardiac cycle for two state-of-the-art methods and CarMEN are shown. While the ground-truth motion for this real dataset is not known, the motion Vampire motion estimates yield physiollogically inaccuarte motion fields. On the other hand, the ITK B-Spline method and CarMEN yield more feasible motion estimates. In contrast to the ITK estimates, CarMEN generates zero motion outside the heart.

Discussion

By reframing the nonrigid three-dimensional cardiac motion estimation problem as an unsupervised learning task, we achieved better accuracy relative to several state-of-the-art methods, especially under abnormal conditions such as hypertrophic cardiomyopathy.

On real data, CarMEN and Vampire showed significantly better performance relative to all other methods on all image metrics except the DSC. Comparing the two, Vampire performed better than did CarMEN in several metrics, although Vampire had the lowest DSC among all methods. In contrast, CarMEN had an equal or better DSC relative to the other techniques. Our results on the synthetic dataset show that Vampire has the highest motion estimate error despite having good performance on image metrics. This result is also demonstrated in Figure 4, in which CarMEN-derived motion estimates on the synthetic dataset show better agreement with the ground truth. Thus, although Vampire produces visually accurate registrations, because warped and reference images look almost identical, the motion fields produced are largely inaccurate. The opposite is observed for Elastix B-spline and B-spline 1, both with lower motion estimate errors but decreased image registration accuracy. The bimodal distribution in the image metrics of these methods implies they have variable performance for small and large motion amplitude, the error being higher in the latter case. In contrast, CarMEN has a mostly normal distribution for all metrics. These results confirm that our method achieves a better registration accuracy while maintaining a lower or similar motion estimate error. Thus, given the challenging problem of nonrigid three-dimensional motion estimation from cine MRI data, our method learns a motion model that balances image similarity and motion estimate accuracy.

At visual inspection, we found CarMEN to be reliable across multiple patient subgroups including patients with hypertrophic cardiomyopathy, and also capable of preserving fine-detailed pathologic features present in patients with myocardial infarction. These performance features are essential to assess the mechanical status of the heart because participants with pathologic features as described here often present with abnormal wall motion. In contrast, most other methods were unable to handle highly abnormal left ventricular anatomy. We note that the real datasets used here originated from different institutions, were acquired with two types of scanners (Siemens Healthineers, Erlangen, Germany; GE Healthcare, Waukesha, Wis), and came from distinct patient populations. This flexibility is important because merely having good performance on a single test set does not guarantee good performance in predicting the values for future inputs from a different dataset due to possible overfitting to the training sampling space (eg, scanner, site, population). As shown in the representative images, our method better handles off-section three-dimensional movement, is more robust to acquisition artifacts, and better preserves abnormal anatomic information (ie, it does not overfit to a healthy heart). This robustness suggests others could use CarMEN with little to no fine-tuning. A potential application of CarMEN toward estimating left ventricle dyssynchrony was also shown in Figure 4.

Our study had several limitations. Our training dataset was not fully independent as we drew 2512 samples from 100 participants. To prevent CarMEN from overfitting to any particular participant or cardiac phase, we ensured each training batch was made up of different participants and different phases and that standard data augmentation techniques were applied. By testing and validating CarMEN on similar (ie, Automated Cardiac Diagnosis Challenge test set) and different (ie, pediatric validation set) data, we have demonstrated it did not memorize any particular anatomy or phase and that it instead learned a general model of cardiac anatomy and motion. Furthermore, its good performance on the pediatric dataset suggests we had a sufficient number of independent samples to prevent overfitting. Another limitation was that the use of cardiac MRI data acquired during multiple breath holds, as is routine for cine MRI, could also lead to section misalignments due to differences between breath-hold positions. Although accounting for these differences was beyond the scope of our work, a novel learning-based solution for automatic intersection motion detection and correction recently proposed by Tarroni et al (32) could be incorporated as a preprocessing step. In fact, although the current implementation of CarMEN is semiautomated due to the required manual centering and cropping of the left ventricle, automatic convolutional neural network–based techniques exist to automate this process (33). However, cropping could potentially limit motion compensated reconstructions where motion estimates for the entire field of view are needed. A potential solution is to use dual-gating techniques to first correct for respiratory motion such that the final images consist of only cardiac motion. Another constraint related to characterizing the three-dimensional motion from two-dimensional stacks of cine images is that the breath-hold acquisition could limit the suitability of CarMEN to correct PET data because it is known to affect cardiac motion. In contrast, PET data are acquired during free breathing and also inherently three-dimensional. A potential solution to both these limitations is to implement instead a novel three-dimensional free-breathing cardiac MRI acquisition technique that corrects the large affine and even nonlinear transformations due to respiratory motion (34) while maintaining excellent functional parameter agreement with those from a conventional cine protocol (35). In future work, cardiac motion derived from specialized MRI sequences (eg, tagged MRI) could be used as prior knowledge to improve the accuracy of the motion estimates.

In conclusion, we have proposed an unsupervised learning–based approach for deformable three-dimensional cardiac MR image registration. Our method learns a motion model that balances image similarity and motion estimation accuracy. We validated our approach comprehensively on three datasets and demonstrated higher motion estimation and registration accuracy relative to several popular state-of-the-art image registration methods.