Automated Sequence Design of 3D Polyhedral Wireframe DNA Origami with Honeycomb Edges

Abstract

3D polyhedral wireframe DNA nanoparticles (DNA-NPs) fabricated using scaffolded DNA origami offer complete and independent control over NP size, structure, and asymmetric functionalization on the 10–100 nm scale. However, the complex DNA sequence design needed for the synthesis of these versatile DNA-NPs has limited their widespread use to date. While the automated sequence design algorithms DAEDALUS and vHelix-BSCOR apply to DNA-NPs synthesized using either uniformly dual or hybrid single-dual duplex edges, respectively, these DNA-NPs are relatively compliant mechanically and are therefore of limited utility for some applications. Further, these algorithms are incapable of handling DNA-NP edge designs composed of more than two duplexes, which are needed to enhance DNA-NP mechanical stiffness. As an alternative, here we introduce the scaffolded DNA origami sequence design algorithm TALOS, which is a generalized procedure for the fully automated design of wireframe 3D polyhedra composed of edges of any cross section with an even number of duplexes, and apply it to DNA-NPs composed uniformly of single honeycomb edges. We also introduce a multiway vertex design that enables the fabrication of DNA-NPs with arbitrary edge lengths and vertex angles and apply it to synthesize a highly asymmetric origami object. Sequence designs are demonstrated to fold robustly into target DNA-NP shapes with high folding efficiency and structural fidelity that is verified using single particle cryo-electron microscopy and 3D reconstruction. In order to test its generality, we apply TALOS to design an in silico library of over 200 DNA-NPs of distinct symmetries and sizes, and for broad impact, we also provide the software as open source for the generation of custom NP designs.

Graphical Abstract

DNA is a versatile construction material that enables the fabrication of complex 2D^1–6 and 3D nanoscale materials^2,3,7–15 with applications in molecular computing,^16–19 light harvesting, metallic nanowire and nanoparticle (NP) casting,^24–28 and hierarchical materials.^29–32 Scaffolded DNA origami is a particularly powerful approach for synthesizing discrete objects of monodisperse chemical and geometric composition.¹ By virtually threading a long single-stranded DNA “scaffold strand” through each base pair in the target object and designing complementary oligonucleotide “staple strands” assuming Watson–Crick base pairing, thermal annealing in folding buffer results in the formation of self-assembled objects of predefined chemical, structural, and mechanical properties.^1,8,9,33

Wireframe DNA origami is one class of scaffolded DNA origami objects with particular versatility in its ability to program nearly any polyhedral 2D^3,4,6 or 3D^3,11,12 geometry. In this approach, each edge of the wireframe structure may in principle consist of one, two, or a multitude of duplexes that are interconnected via single-and double-stranded (DX) DNA crossover motifs, with edges merging at multiway junctions (vertices).^3,34,35 Despite their theoretical capacity to be applied to nearly any 2D or 3D geometry, the complexity of the DNA sequence design needed to fold such objects has limited their broad use. Specifically, the presence of numerous multiway junctions renders the manual scaffold routing and complementary staple design needed for wireframe assemblies extremely challenging, even for experts, compared with rectilinear objects that are quite commonly programmed semimanually using the software caDNAno.³⁶

While automated sequence design procedures exist for 2D^4,6 and 3D^11,12 wireframe geometries composed of up to two duplexes per edge, these assemblies are also limited in their mechanical stiffness. An alternative, commonly used design strategy to increase mechanical stiffness in structured nucleic acid assemblies is the six-helix bundle (6HB),³⁷ in which DNA duplexes are organized on a honeycomb lattice. As expected, 6HBs have been shown to have significantly increased mechanical stiffness with respect to isolated duplexes,^38,39 with up to a 66-fold increase in persistence length in 12 mM MgCl₂ salt,⁴⁰ which suggests that crossovers rigidly interconnect duplexes so that their cross section behaves as a homogeneous mechanical beam.^40–42 In addition, 6HBs are biologically more resistant to nucleases because of their larger cross section.^43,44 However, the complexity of the scaffold routing and staple sequence design needed to fabricate these objects have been limiting, with only several wireframe 6HB DNA-NPs reported,^43,45–47 despite numerous important applications in metallic patterning^32,46,47 and therapeutics.^43–45 In addition, published 6HB DNA-NP design strategies have been limited to using only single-instead of multilayer scaffold linkages between each wireframe edge, possibly further limiting their mechanical stiffness and stability. And while conversion of DNA to inorganic materials⁴⁸ or introducing chemical cross-linking⁴⁹ increases origami mechanical stiffness for applications in materials science, biological applications often require DNA origami objects to be used in their native, or near-native, state.^45,50–52

The previously published sequence design algorithms vHelix-BSCOR⁴ and PERDIX⁶ for 2D and vHelix-BSCOR¹¹ and DAEDALUS¹² for 3D wireframe scaffolded DNA origami have enabled the facile design of arbitrary 2D and 3D wireframe geometries, but each procedure is constrained to use a maximum of two duplexes per edge. While vHelix-BSCOR^4,11 and DAEDALUS¹² are fundamentally limited to using two duplexes per edge, PERDIX⁶ introduced a dual-graph approach that generalizes the solution to the scaffold routing problem that allows for any even number of duplexes per edge, in addition to arbitrary edge lengths, vertex degrees, and vertex angles in 2D⁶ and 3D, as demonstrated here for 6HB-based 3D wireframe polyhedra.

This algorithm, called TALOS (Three-dimensional, Algorithmically-generated Library of DNA Origami Shapes), enables the fully automated, top-down sequence design of polyhedral 6HB DNA-NPs with enhanced mechanical stiffness compared with previously published approaches^11,12 and also offers control over the distribution of staple lengths. To further enhance 6HB DNA-NP stiffness beyond previous designs that employed only a single-vertex scaffold crossover between each pair of neighboring edges (“flat vertex”; FV),^{32,43,45–47} we also introduce a three-way vertex crossover or “mitered vertex” (MV) motif. This motif is realized by extending the duplexes within individual vertices in order to ensure that every duplex within each honeycomb wireframe edge is connected to another duplex in a neighboring wireframe edge. Importantly, akin to the 2D implementation of PERDIX,⁶ the MV design motif enables DNA-NPs to consist of arbitrary edge lengths and vertex angles, which cannot be realized with other 3D polyhedral DNA origami sequence design algorithms.^11,12

We validate TALOS experimentally for both vertex types (FV/MV) using folding assays, transmission electron microscopy (TEM), and single particle cryo-electron microscopy (cryo-EM) and 3D reconstruction. Results demonstrate high yield of formation of origami objects and high structural fidelity at the nanometer scale. While direct experimental measurement of the relative mechanical stiffness offered by the MV design compared with the conventional FV design is beyond the scope of the current work, molecular dynamics (MD) simulations offer theoretical evidence for the relative increase in DNA-NP stiffness for the MV design. Finally, in order to test the generality of our sequence design procedure, we apply it to generate an in silico library of 240 DNA-NPs ranging from 10 to 200 nm in size, with explicit control over the distributions of staple lengths, which may be limited by chemical modifications or other synthetic constraints. For broad dissemination of our approach, TALOS is provided both as standalone open-source software (library of 240 DNA-NPs and TALOS software package) and as a simple web interface (http://talos-dna-origami.org) for custom DNA-NP design.

RESULTS AND DISCUSSION

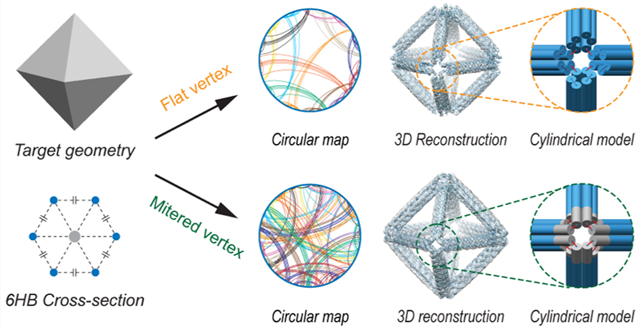
Any target 3D polyhedron can be defined by its 2D enclosing polyhedral surface, which may be represented by the set of edges and vertices that constitute the equivalent wireframe model. To specify the target wireframe geometry, standard polyhedron file formats can be used to define the spatial coordinates of all vertices and polygonal faces, which are equivalently defined by their enclosing edges and boundary vertices. For the current application, this wireframe geometry is used to define the target DNA-based molecular geometry to render, with each edge in the node-edge network consisting of the 6HB motif (Figures 1, S1, and S2).³⁷ If instead of a discrete polyhedron the target geometry is a smooth, continuous 3D geometry, then standard meshing and discretization procedures may be used to convert it to a representative wireframe model, as commonly performed, for example, in computer-aided visualization and finite element analysis.⁵³

Figure 1.

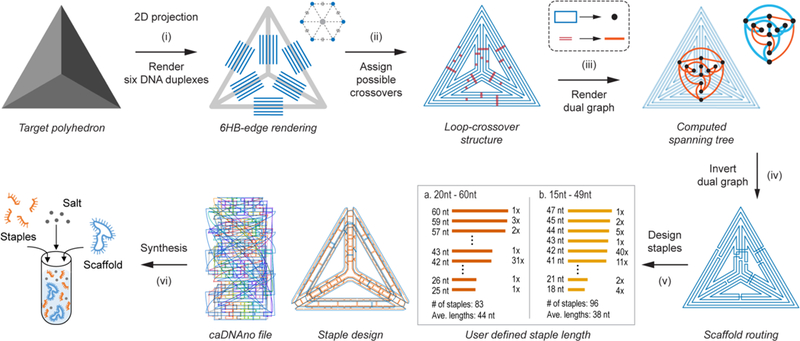
Overview of the top-down sequence design procedure TALOS for scaffolded 6HB DNA-NPs. The arbitrary target geometry is based on a polyhedral mesh, with discretized line segments (step (i)) to represent six DNA duplexes per wireframe edge with the endpoints joined (step (ii)) to form closed loops with geometrically allowable scaffold double crossovers between them. The dual graph of the loop–crossover structure is obtained (step (iii)) by converting each closed scaffold loop to a node and connecting each possible scaffold double crossover to an edge. The minimum spanning tree of the dual graph was then determined and inverted (step (iv)), defining the DNA scaffold routing. On the basis of the user-defined staple length (for this example, 20 to 60 nt (a) and 15 to 49 nt (b)), staple sequences generated (step (v)) by the algorithm were used with the input scaffold to synthesize (step (vi)) the 3D DNA-NP in one-pot thermal annealing.

Scaffold Routing.

In order to route the single-stranded scaffold throughout the entire target DNA origami object, a node-edge graph representation of the complete 6HB DNA-NP must be defined for either the FV or MV case. In this representation, a node-edge graph consists of nodes representing the scaffold crossing between each wireframe edge at the vertex and graph edges representing every DNA duplex along each wireframe edge. To construct this node-edge graph, each target wireframe edge, irrespective of vertex type, is first replaced with six disconnected line segments on a honeycomb lattice centered on the original wireframe edge (Figures 1(i), S1a–e, and S2a, representative of DNA duplexes in the final structure).⁶ This 6HB geometry forms three duplex layers: an “inner” layer closest to the NP center, a “middle” layer, and an “outer” layer away from the center of the structure. In the FV case, the nearest two line segments (depending on the layer shown in Figures S3 and S4) from neighboring edges are connected to form a new graph node, representing the wireframe edge-to-edge scaffold crossing (Figure S1e,f), with these segments scaled to multiples of 21 bp, as required by the natural helicity of B-form DNA.³⁴ The remaining four line segments of each wireframe edge connected to a neighboring line segment in the same wireframe edge, forming a new graph node representing the scaffold crossing at the FV (Figures S3 and S4).

In the case of the MV, the ends of each line segment constituting a DNA duplex are extended to the points of steric hindrances based on B-form DNA geometry. Once extended, nearest neighbor segments between each wireframe edge are connected to generate a new node, which are representative of scaffold crossings between wireframe edges and thereby form three scaffold crossings between the edges in the final object (Figure S2a,b). Thus, in both the FV and MV designs, all line segments are connected to two other segments and are part of a closed circuit (“loop”; Figures S1f and S2b). This constitutes the graph representation of the 6HB DNA-NP without crossovers.

With this graph representation constructed, we next determine the scaffold crossover positions (Figure S5) to route the scaffold around the entire object by using the loop–crossover structure previously defined in the 2D PERDIX algorithm⁶ but modified it to allow for connecting wireframe edges in 3D and across honeycomb layers. Briefly, this is accomplished by identifying all crossover locations between any two duplexes based on the natural helical twist of B-form DNA (Figures 1(ii), S1g,h, and S2c,d). The loop–crossover structure is then converted into its dual graph (Figures 1 (iii), S1i, and S2e),⁶ with each closed loop becoming a node and each possible crossover connecting two loops becoming an edge joining the two respective nodes. The minimum spanning tree of this dual graph is then calculated (Figures S1j and S2f) using Prim’s algorithm with the members of this tree (blue in the inset panel of Figure 1 (iii)) corresponding to the subset of crossovers needed to complete an Eulerian circuit. The spanning tree is then inverted back to the loop-crossover structure, which now only contains the crossovers that satisfy an Eulerian circuit (Figures 1(iv), S1k,i, and S2g,h).⁶ The minimum spanning tree from the dual graph additionally yields the order in which the scaffold traverses each vertex. This dual-graph algorithm generalizes to any routing composed of an even number of duplexes per wireframe edge, unlike our lab’s previously published direct spanning tree approach.¹²

As in the 2D PERDIX algorithm, the MV design presented here allows for the generation of objects with arbitrary edge length and not constrained to 21-bp multiples. This is accomplished when converting from the loop–crossover structure to the final model, where unpaired scaffold nucleotides are introduced to accommodate 5′- and 3′-end misalignment between every two neighboring connected duplexes at each vertex based on the natural B-form helicity of DNA and the distance between the two duplexes, as performed previously.⁶

Staple Design.

With the scaffold routing completed, staple sequences for folding the DNA-NP can be determined. Staples are assigned by generating the complementary sequences to the scaffold and routing through all permissible staple crossovers (see Supplementary Methods as well as Figures 1(v), S1m, S2i, and S5).³⁶ As a result of the routing, a subset of these staples form closed loops and are therefore nicked at the centers of their longest continuous double-stranded DNA domains to allow for linear oligonucleotide synthesis. Each staple is further divided to be within user-defined lengths (ranging from 20 to 60 nt by default, see Figures S5–S7) while maximizing the number of continuous 14-nt duplex domains across all staples, which is known to improve 6HB assembly yields (Figures S8–S18 and Tables S1–S4).^54,55

Poly-T stretches are used within vertex staples to covalently bridge two neighboring wireframe edges, with the length of each poly-T stretch determined based on the distance between the centroids of the two terminal duplex nucleotides, as implemented previously.⁶ In addition, in the MV case, staple design patterns are generated that allow for the necessary extensions of DNA duplexes at each vertex.

The final structure is then converted into a 3D atomic model for visualization and downstream modeling using MD and other approaches (Figures S19–S36), and a caDNAno (*.json) file is generated for manual base editing and staple functionalization (Figures S37–S45). This generalized solution for scaffold routing applies to 3D object generation of any even number of duplexes organized on a honeycomb lattice edge, although determining the precise staple routing for such objects becomes increasingly complex as the number of duplexes increases and is therefore left for future work.

Folding Validation.

To evaluate the generality and robustness of our automatic design procedure, we used it to generate scaffold routings and staple sequence designs for DNA-NPs of different 6HB edge lengths, vertex junction numbers, vertex angles, and vertex types (Tables S5–S17). As a result of their simpler design, conventional, single-edge-to-edge crossing FV DNA-NPs were analyzed first (Table S6). Particle folding was optimized based on salt and staple concentrations and annealing times to determine a protocol that maximized band resolution in agarose gel mobility shift assays (Figures S46–S50) and maximized yield of particle self-assembly, as judged by TEM (Figures S51–S54) for the 6HB DNA-NP. Optimal folding conditions were found to be consistent with previously published results⁸ and subsequently used for folding prior to 3D structural characterization using cryo-EM reconstruction.

Three tetrahedra of 42-bp (14.3 nm), 63-bp (21.4 nm), and 84-bp (28.6 nm) edge lengths were first used to evaluate the FV design based on an object composed purely of three-way junctions. Four-way and five-way junction objects were additionally evaluated using a regular octahedron of 84-bp edge length and a pentagonal bipyramid of 42-bp edge length (Figures 2a–c and S51–S57). Circular maps showing distinct domains of the scaffold connected by individual staples were generated to illustrate the complexity of scaffold folding that clearly benefits from our fully automated algorithm (Figure 2a). Both agarose gel electrophoretic mobility analysis and TEM indicated that particles were well-folded and monodisperse (Figures 2b, S48, and S51–S54). Cryo-EM was then used (Figures 2c and S55–S57) to visualize the particles flash-frozen from room temperature in their 3D state, further validating anticipated geometries and monodispersities.

Figure 2.

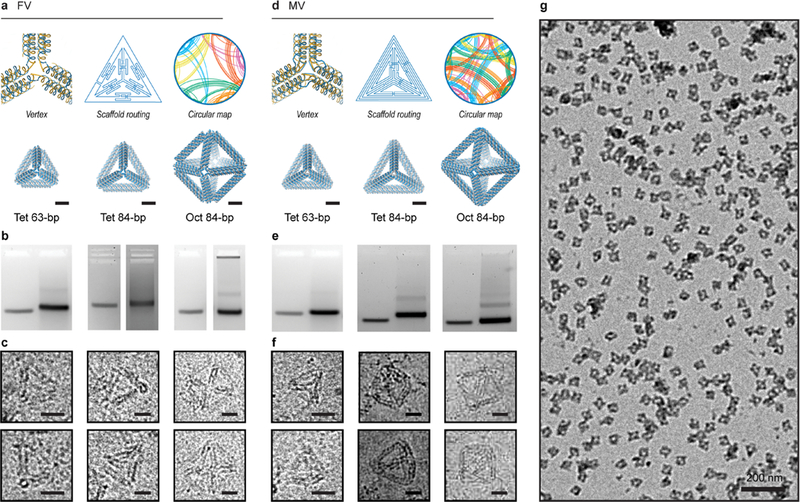
Validation of 6HB DNA-NP origami objects synthesized using TALOS sequence designs. (a–c) In the FV case, the routed structure is generated such that each wireframe edge is connected covalently to its neighboring edges by one scaffold and staple crossing. A circular map is rendered, in which the outer circle representing the scaffold has points assigned in the center of each double-stranded DNA domain with staple connections between regions rendered as lines traversing the circle (see also Figures S14–S18). Characterization of folding for FV tetrahedra of 63-bp and 84-bp edge lengths and an FV octahedron of 84-bp edge length with agarose gel mobility shift assays ((b); uncropped gel images in Figure S48) and cryo-EM (c). (d–f) In the MV case, the routed structure is generated such that each wireframe edge is connected covalently to its neighboring edges by three scaffold and staple crossings. Characterization of folding for MV tetrahedra of 63- and 84-bp edge lengths and an MV octahedron of 84-bp edge length with agarose gel mobility shift assays ((e); uncropped gel images in Figure S48) and cryo-EM (f). (g) Wide-field TEM micrograph shows monodisperse MV octahedra of 84-bp edge length (see also Figures S51–S64). Scale bars are 5 nm in atomic models and 20 nm in cryo-EM and 200 nm in the wide-field TEM.

We evaluated the MV design by synthesizing three distinct regular tetrahedra (42-, 63-, and 84-bp edge lengths) and a regular octahedron of 84-bp edge length (Figures 2d–f and S58–S64). The circular maps for the MV designs further illustrated their increased sequence design complexity with respect to the FV designs, solved by TALOS. Agarose gel shift assays showed a clear shift compared with the M13 ssDNA scaffold band in all cases (Figures 2e and S48). Mono-dispersities and sizes of DNA-NPs in solution were characterized using dynamic light scattering (Movies S1 and S2), further demonstrating that DNA-NPs were largely monomeric (Figure S49). Thermal stabilities of the DNA-NPs were characterized using melting curve analysis, which revealed that both FV- and MV-type objects have similar melting temperatures near 68–70 °C (Figure S50). To further characterize self-assembly, each object was visualized using cryo-EM (Figures 2f and S60–S64), showing DNA-NPs with anticipated target geometries. Wide-field view imaging using TEM showed in each case that DNA-NPs were also well-folded and monodisperse (Figure 2g).

Single Particle Cryo-EM and 3D Reconstruction.

To investigate the quality of the atomic structural predictions generated by TALOS, four DNA-NPs of 84-bp edge length representing both FV and MV designs and two distinct geometries were reconstructed in 3D using single-particle cryo-EM analysis. FV tetrahedral (Figures 3a, S65, and Movie S3) and octahedral (Figures 3b, S66, and Movie S4) particles were selected for class averaging and reconstructed to 21 and 18 Å resolution, respectively. The FV tetrahedron showed a lack of electron density at each vertex, as expected, but also showed a notable 3° twist at each vertex with 0.79 correlation with the atomic model. The electron density map for the octahedron showed no detectable twist, in contrast to the dual-helix edge octahedron reported previously.¹² The electron density aligned with the atomic model with a correlation of 0.83 and, like the tetrahedron, lacked electron density in the regions corresponding to the absence of a DNA duplex in this FV design.

Figure 3.

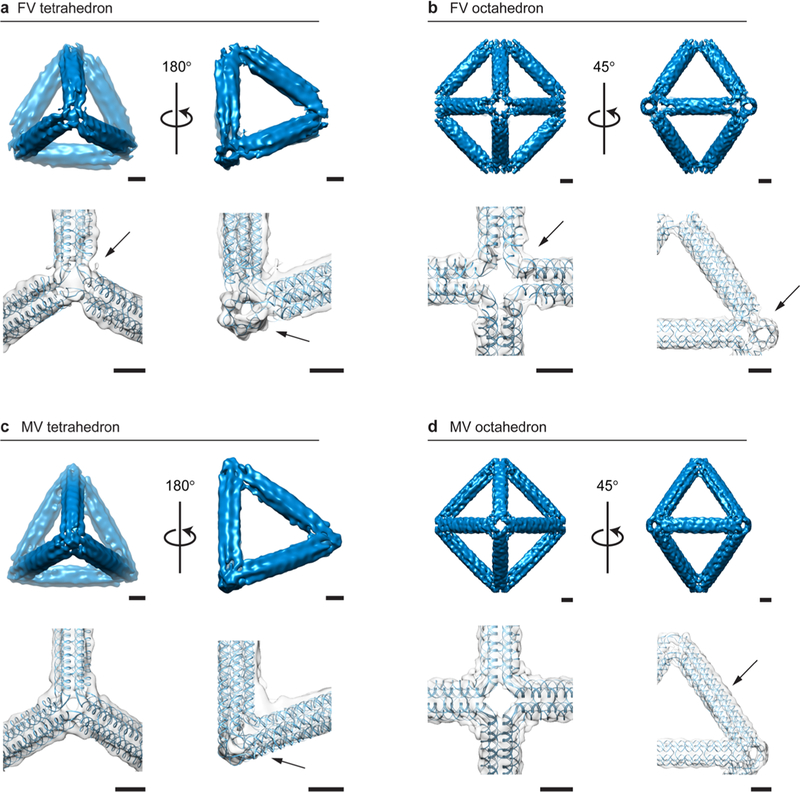
3D characterization of 6HB DNA-NPs using cryo-EM reconstructions compared with predicted atomic models. (a) The FV tetrahedron of 84-bp edge length shows straight edges with a distinctive FV type and a 3° left-handed twist visible at each vertex, with a clear signature of a 6HB along the edge (arrow). (b) The FV octahedron of 84-bp edge length has straight edges and regular programmed vertices with characteristic open vertices and no detectable deviation along the edge compared to the atomic model, with a clear signature of a 6HB along the edge (arrow). (c) The MV tetrahedron of 84-bp edge length shows the characteristic programmed electron-dense vertex (arrow). (d) The MV octahedron of 84-bp edge length has straight edges and electron-dense vertices with approximately a 1 nm deviation along the edge from the predicted atomic model (arrow). Scale bars are 5 nm.

To test the design fidelity of MV DNA-NPs, tetrahedral (Figures 3c, S68, S69, and Movie S5) and octahedral (Figures 3d, S70, and Movie S6) particles of 84-bp edge lengths were frozen to grids, and individual particles were selected for class averaging and particle reconstruction, yielding resolutions of 25 and 15 Å, respectively. In each case, the electron density agreed well with the atomic model, including the density for the three-way MVs, with a total correlation of 0.82 for the tetrahedron and the octahedron. The vertex twist was absent in all cases in the MV forms of the tetrahedron and octahedron, likely because of the close packing of free duplex ends at juxtaposed edges within individual multiway junctions. The resolution obtained from these reconstructions is on the same order as the DX-tile wireframe origami previously reported (18–21 Å)¹² and the periphery of a densely packed, asymmetric pointer object (14 Å).⁵⁶ We speculate that resolution is limited by the assumption of particle symmetry that is imposed during reconstruction, which is required because of the challenges associated with distinguishing distinct particle orientations algorithmically. Atomic-level thermal fluctuations frozen-in prior to single-particle imaging may additionally limit the maximum resolution obtainable for this class of objects.

Molecular Dynamics Characterization of DNA-NP Flexibility.

In order to gain further insight into the differences in the overall mechanical stiffness of the FV versus MV DNA-NPs, MD was used to simulate the conformational dynamics of regular tetrahedra of 42-bp edge length (Figure 4a,b and Movies S7, S8, and S9) and also compared with a DX-edge variant of the same edge length.^12,57 The root-mean-square deviation (RMSD) of each DNA-NP from its ground-state geometry illustrates the magnitude of thermal fluctuations for each type of vertex design (Figures 4c and S71). The FV DNA-NP exhibited similar flexibility to the DX-edge DNA-NP, where both were more flexible than the corresponding MV variant. Specifically, total RMSD values were 11.9 ± 0.6 and 11.0 ± 0.9 Å for the FV and DX DNA-NPs, respectively, versus 9.5 ± 0.6 Å for the MV design. The observed conformational flexibility of the FV DNA-NP design results in part due to the unconstrained ends of the outer 6HB duplexes, which exhibited significant dynamical motion compared with the overall structure. This is in contrast with the MV DNA-NP, in which the middle and outer duplexes exhibited relatively lower conformational flexibility due to their sterically and covalently constrained terminal ends. To further investigate local conformational dynamics, the root-mean-square fluctuation (RMSF) of each atom was calculated. This analysis highlighted regions of significantly enhanced conformational flexibility near the vertices, as visualized in red in Figure 4d. Importantly, the middle and outer duplexes in the MV design are longer than the inner duplexes, thus generating 24 additional double crossovers in the structure, thereby likely increasing overall mechanical stiffness compared with FV counterparts. The MVs also contain a 3-fold increase in edge-to-edge crossings at each vertex, likely further contributing to the suppressed conformational fluctuations observed (Figure 4d). As expected, suppressed overall edge bending and vertex twisting of the FV and MV DNA-NPs was observed with respect to the DX DNA-NP design (Figures S72–S75),^12,57 which is likely a result of the overall enhanced mechanical stiffness of the 6HB edge itself.⁴⁰ Importantly, the conformational dynamics in response to thermal fluctuations probed here only offers a lower bound on the enhanced mechanical stiffness of the MV DNA-NP design with respect to its FV counterpart. Large-scale, nonlinear deformations using an active probe such as atomic force microscopy would be needed to reveal the full extent of the enhanced mechanical stiffness offered by this alternative vertex design.⁴⁸

Figure 4.

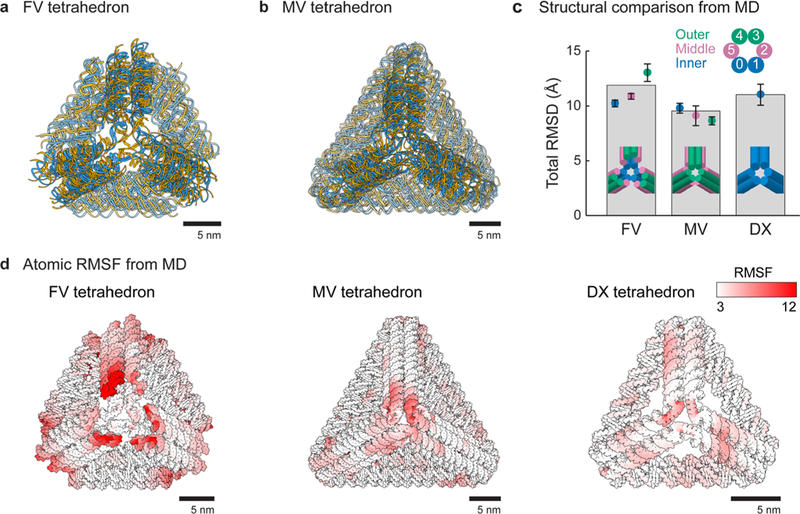
Molecular dynamics simulations of tetrahedra. (a,b) Superposition of molecular dynamics snapshots of FV (a) and MV (b) tetrahedra of 42-bp edge length at 0, 100, and 200 ns. Initial atomic models were generated by TALOS. (c) Total RMSD of all nucleic acid atoms based on the ground-state atomic model generated by TALOS. The FV and DX tetrahedra of 42-bp edge lengths show additional dynamical motion due to vertex fluctuations compared with the MV design. (d) All-atom RMSFs were calculated for the FV, MV, and DX tetrahedra over the 200 ns simulation and mapped as a white-to-red color gradient on each of the structures.

In Silico DNA-NP Library Generation.

To evaluate the generality of TALOS for application to a broad set of polyhedral geometries, we applied it generate the sequence design of all Platonic solids that have equal edge lengths, angles, and vertex junction numbers, as well as more complex geometries including Archimedean solids with unequal vertex angles, Johnson solids that include heterogeneity in vertex junction numbers, and Catalan solids that have unequal edge lengths (Figures S19–S31). Out of these 40 distinct geometric families, 28 (FV) and 32 (MV) DNA-NPs required scaffolds longer than the 7249-nt M13mp18 (Table S5), for which the remaining sequences were generated using 8064 nt,⁸ recombinant phage sequences up to 31 274 nt,⁵⁸ or a random sequence.

Because each duplex of the wireframe edge is independently extended to meet its neighboring-edge duplex in the MV design, asymmetric polyhedra with arbitrary edge lengths and vertex angles can also be generated using this design strategy. Two such examples are an asymmetric tetrahedron (Figure 5c, left) and a twisted triangular prism (Figure 5c, right). The asymmetric tetrahedron was designed with 42-bp, 69-bp, 103-bp, and 130-bp edge lengths, with the angle between each two edges on every vertex different due to the incongruence of each triangular face (Figure S76a). Folding of the asymmetric tetrahedron was validated by agarose gel mobility shift and TEM (Figure S76b,c). As an extension of the arbitrary vertex angle of the asymmetric tetrahedron, a twisted triangular prism was additionally designed with a 30° right-handed twist between the triangular top and bottom faces of the prism, with edge-to-edge angles of 60, 89, and 111° (Figure 5c), with the individual duplex extensions at the vertex generated to constrain these angles.

Figure 5.

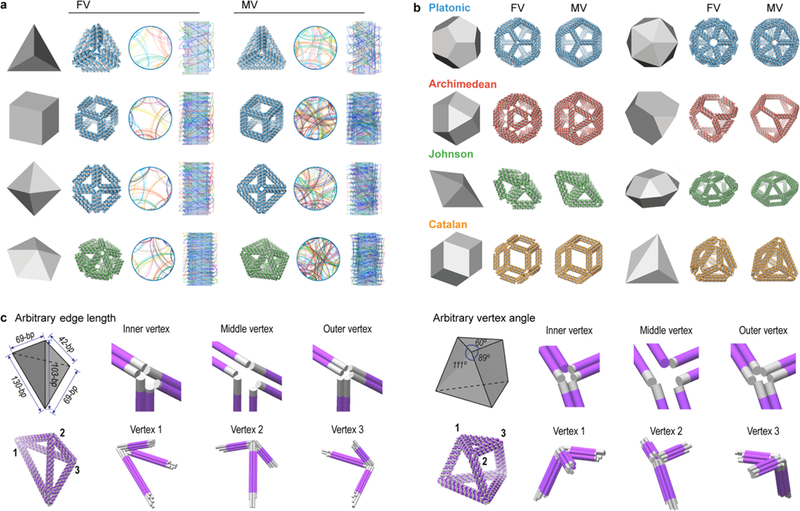
Fully automatic sequence design of diverse scaffolded 6HB DNA-NPs. (a) 3D representations of geometric models as input to the algorithm with associated 3D atomic models and circular map of the DNA-NPs for a tetrahedron, cube, octahedron, and pentagonal bipyramid using the automatic scaffold routing and sequence design procedure for the FV and MV cases. (b) 3D representations of geometric and atomic models for two Platonic-, Archimedean-, Johnson-, and Catalan-type geometries, with additional DNA-NPs shown in Figures S19–S31. All DNA-NPs in panels (a) and (b) have a minimum 42-bp edge length, and the required scaffold lengths are shown in Table S5. (c) The generality of the MV design for arbitrary edge length and arbitrary vertex angle with a fully asymmetric tetrahedron (left) and a twisted triangular prism (right). For both objects, the inner, middle, and outer layers of helices are shown with helical extensions shown in gray and vertices zoomed-in to show the 6HB extensions (gray) to achieve the modeled angles. Individual particles are not shown to scale.

CONCLUSIONS

Taken together, the preceding examples illustrate the capabilities of our procedure to fully automate complex scaffold routing and staple design for diverse polyhedral 3D geometries based on top-down geometric specification alone (Figure 5). While the folding of each DNA-NP would need to be validated experimentally prior to its use in applications, here we have provided the in silico-produced staple sequences for 240 DNA-NP geometries (Library of 240 Particles) that could serve as a platform for future library generation of diverse DNA-NP geometries for self-assembly of hierarchical NP-based materials.^46,59 Lastly the dual-graph procedure employed may also be further generalized to employ alternative multihelix edge types^8,10,32,54 as well as possibly the incorporation of insertions and deletions to program curvature and twist.⁹

METHODS

Top-Down Sequence Design.

TALOS (Three-dimensional, Algorithmically generated Library of DNA Origami Shapes) is available for use as open-source software (http://github.com/lcbb/talos ) and online at http://talos-dna-origami.org. Additional details can be found in the Supporting Information and documentation provided with the software.

Materials.

Full length single-stranded M13 was purchased from Guild BioSciences (Dublin, OH). Oligonucleotides were purchased from Integrated DNA Technologies (Coralville, IA), typically in 96-well plate format brought up to 200 nM concentration in nuclease-free water. Each staple (20 μL) was combined in equal volumes to obtaining an equimolar staple mix. Tris-acetate-EDTA (TAE, 10×), MgCl₂ hexahydrate, and NaCl were purchased from Sigma-Aldrich (St. Louis, MO).

DNA Nanoparticle Assembly.

DNA-NPs were folded in a solution of 20 nM scaffold, 600 nM staples, 1× TAE, 100 mM NaCl, and 14 mM MgCl₂ and annealed over the course of 22 h (95 °C for 5 min, 85 °C down to 76 °C for 5 min/°C, 75 °C down to 30 °C for 13.75 min/0.5 °C, 29 °C down to 25 °C for 10 min/°C, followed by 15 min at 37 °C) on a Bio-Rad T100 thermocycler (Hercules, CA). Folding was initially checked by agarose gel mobility shift assays. Folded sample (20 μL) was combined with 4 μL of 6× loading buffer (NEB) and loaded to a 2% agarose gel with 1× TAE and 12.5 mM MgCl₂ and 1× SybrSafe (ThermoFisher, Waltham, MA). Each gel was run at 90 V for 5 min followed by 65 V for 2–4 h in 1× TAE with 12.5 mM MgCl₂. Gels were run in an ice-chilled water bath. Gels were then visualized under blue light.

Folded DNA-NPs were purified from staples and folding buffer by the use of buffer exchange via spin filter concentrator columns with MWCO = 100 kDa cleaned with nuclease-free water. DNA-NPs were exchanged into buffer composed of 1× TAE with 100 mM NaCl and 12 mM MgCl₂ by centrifugation at 3000 rpm for 40 min at 25 °C, diluted approximately 10-fold, and reconcentrated a total of six times. For TEM, the final DNA-NP concentration was approximately 10 nM, while for cryo-EM the final DNA-NP concentration was approximately 100 nM. For TEM, samples were floated to the Formvar surface and stained by 2% uranyl formate with 25 mM NaOH. Negative stained TEM images were captured using a Thermo-Fisher FEI Tecnai Spirit Transmission Electron Microscope (Waltham, MA) set to 120 kV potential.

Cryo-EM Data Collection and Single-Particle Image Processing.

Freshly concentrated DNA nanostructure solution (3 μL) was applied onto the glow-discharged 200-mesh Quantifoil 2/1 grid, blotted for three seconds, and rapidly frozen in liquid ethane using a FEI Vitrobot Mark IV (Hillsboro, OR). All grids were screened on a JEOL JEM2200FS cryo-electron microscope (Peabody, MA) or a FEI Talos Arctica cryo-electron microscope operated at 200 kV and then imaged in the JEOL 3200 cryo-electron microscope or in a FEI Titan Krios cryo-electron microscope. Micrographs were recorded with a Gatan K2 Summit direct electron detector in counting mode, where each image is composed of 32 individual frames with an exposure time of 8 s and a total dose of ~40 electrons per Ų. A total of 96 images for the FV tetrahedron of 84-bp edge length, 119 images for the MV tetrahedron of 84-bp edge length, 724 images for the FV octahedron of 84-bp edge length, 657 images for octahedron with MV, and 662 images for the MV tetrahedron of 63-bp edge length were collected with a defocus range of ~1.5–4 μm. All the images were motion-corrected using MotionCor2.⁶⁰ Single-particle image processing and 3D reconstruction was performed using the image processing software package EMAN2.⁶¹ All particles were picked manually by e2boxer.py in EMAN2. The initial models generated by TALOS software were low-pass-filtered to 60 Å to avoid model bias. The following steps were performed as previously described.¹² A total of 1669 particles for the FV tetrahedron of 84-bp edge length, 1092 particles for the MV tetrahedron of 84-bp edge length, 3308 particles for the FV octahedron of 84-bp edge length, 5705 particles for MV octahedron, and 2511 particles for the MV tetrahedron of 63-bp edge length were used for final refinement, applying tetrahedral, tetrahedral, octahedral, octahedral, and tetrahedral symmetries, respectively. Resolutions for the final maps were estimated using the 0.143 criterion of the Fourier shell correlation (FSC) curve without any mask. A Gaussian low-pass filter was applied to the final 3D maps displayed in the UCSF Chimera software package.⁶² Correlation of each map with its corresponding atomic model is calculated by the UCSF Chimera fitmap function.

All-Atom Molecular Dynamics Simulations.

All-atom MD simulations were performed for tetrahedra of 42-bp edge length to compare the stability and dynamical motion of the FV versus MV design as well as the DX-edge design. The PDB files for the initial atomic coordinates of the FV and MV DNA-NP were generated using the TALOS algorithm, and the initial atomic coordinates of the DX DNA-NP were generated using the DAEDALUS algorithm.¹² All-atom systems were solvated in TIP3P water⁶³ with explicit Mg²⁺ and Cl⁻ ions added to neutralize DNA charges and to set the ion concentration to 12 mM, consistent with the experimental conditions. The all-atom system sizes for the fully solvated DNA-NP were 1.2 × 10⁶ (DX), 2.2 × 10⁶ (FV), and 3.3 × 10⁶ (MV) atoms, with the DNA alone comprising 3.4 × 10⁴ (DX), 9.9 × 10⁴ (FV), and 1.4 × 10⁵ (MV) atoms. The MD simulations were performed with the program NAMD2,⁶⁴ the CHARMM36 force field,⁶⁵ and Allnér Mg²⁺ parameters,⁶⁶ with an integration time step of 2 fs and periodic boundary conditions applied to an orthogonal simulation cell. The van der Waals energies were calculated with a 12 Å cutoff, a switching function applied from 10 to 12 Å, and a 14 Å pair list distance. The Particle Mesh Ewald (PME) method⁶⁷ was used to calculate full electrostatics with a maximum grid point spacing of 1 Å. Full electrostatic forces were computed every two time steps (every 4 fs), and nonbonded forces were calculated at each time step (2 fs). Equilibration and production simulations were performed in the NpT ensemble using the Nosé–Hoover Langevin piston method⁶⁸ for pressure control with an oscillation period of 200 fs and a damping time of 100 fs. Langevin forces were applied to all heavy atoms for temperature control (300 K) with coupling coefficients of 5 ps⁻¹. All hydrogen atoms were constrained to their equilibrium lengths during the simulations and atomic coordinates were recorded every 1 ps for downstream analysis of coordinate trajectories. Prior to production MD, solvent and ions were allowed to equilibrate for 1 ns, while the nucleic acid atoms were spatially constrained. For production MD, the DNA-NPs were run for 200 ns.

Analysis of 6HB Flexibility from MD Trajectories.

Atomic coordinates for tetrahedra of 42-bp edge length (FV and MV and DX edge) were extracted from production MD simulations every 1 ns. First, at each sampled time point, the atomic coordinates were superposed onto the reference geometric coordinates (t = 0 ns) by global minimization of the RMSD of the sampled atomic coordinates with respect to these reference coordinates. The total RMSD of all atoms was calculated as well as local RMSD values for inner, middle, and outer duplexes in the 6HB DNA-NPs. As a result of an equilibration time of approximately 50 ns, the total RMSD was calculated from the average of three separate bins of 50 ns (50–100, 100–150, and 150–200 ns). Superposition of atomic coordinates and RMSD calculations were performed using the Python package ProDy.⁶⁶ This software package was also used to calculate the RMSF values of all atomic coordinates averaged over the production MD simulations for each tetrahedron of 42-bp edge length.

Supplementary Material

Movie S9

MD Simulation – MV tetrahedron of 42-bp edge length

Movie S1

Nanosight – MV tetrahedron of 84-bp edge length

Movie S2

Nanosight – MV octahedron of 84-bp edge length

Movie S3

3D Reconstruction – FV tetrahedron of 84-bp edge length

Movie S4

3D Reconstruction – FV octahedron of 84-bp edge length

Movie S5

3D Reconstruction – MV tetrahedron of 84-bp edge length

Movie S6

3D Reconstruction – MV octahedron of 84-bp edge length

Movie S7

MD Simulation – DX tetrahedron of 42-bp edge length

Movie S8

MD Simulation – FV tetrahedron of 42-bp edge length