Abstract
The molecular structure of alkali metal rosmarinates was studied in comparison to rosmarinic acid using FT-IR, FT-Raman, 1H and 13C NMR spectroscopy, as well as density functional theory (DFT) calculations. The B3LYP/6-311+G(d,p) method was used to calculate optimized geometrical structures of studied compounds, atomic charges, dipole moments, energies, as well as the wavenumbers and intensities of the bands in vibrational and NMR spectra. Theoretical parameters were compared to experimental data. Antioxidant activity was determined using two spectrophotometric methods: (i) Assessing the ability to scavenge 1,1-diphenyl-2-picrylhydrazyl (DPPH) stable radical and (ii) assay of antioxidant power of ferric ions reducing (FRAP). The linear correlations were found between HOMO–LUMO (highest occupied molecular orbital–lowest unoccupied molecular orbital) energy gap and the reducing power expressed as FRAP (R = 0.77) as well as between IC50 values (the ability of quenching DPPH radicals) and Δνas-s(COO) in IR spectra (differences between asymmetric and symmetric stretching vibrations bands) (R = 0.99). Photochemical properties of studied compounds were also evaluated. The influence of alkali metal on the electronic system of the rosmarinic acid molecule was discussed.
Keywords: rosmarinates, IR, Raman, NMR, DPPH, FRAP, DFT calculations
1. Introduction
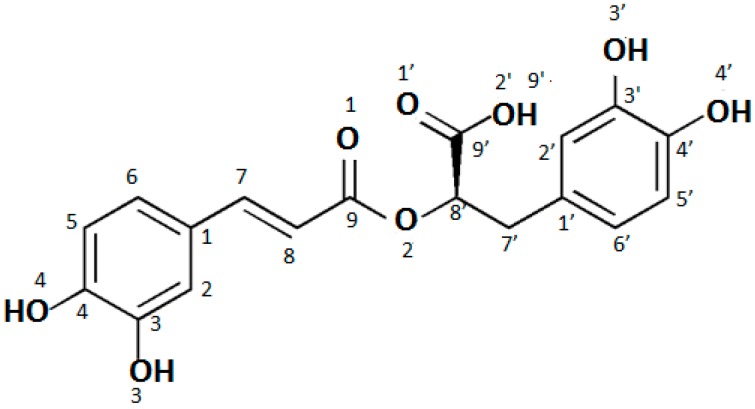
Rosmarinic acid is a naturally occurring bioactive compound. It is commonly found in plants such as rosemary, sage, lemon balm, oregano, lavender, mint, and savory [1,2,3,4]. The name of this compound comes from the plant from which rosmarinic acid was isolated for the first time (in 1958) [5]. Its structure was established as an ester of caffeic acid and 3,4-dihydroxyphenyllactic acid. The molecule of rosmarinic acid contains carboxylic group, two aromatic rings A and A’ with the ortho-catechol structures, the unsaturated C=C bond, and the ester moiety (Figure 1) [6,7]. Such a molecular structure entails specific properties of this compound. Rosmarinic acid has a lot of interesting biological activities. Its antioxidant activity is stronger than that of vitamin E [8] and it is the highest in the series of hydroxycinnamic acid derivatives: Rosmarinic acid > chlorogenic acid > caffeic acid > ferulic acid > coumaric acid [9,10]. The antimicrobial activity was also studied. Rosmarinic acid showed inhibitory and bactericidal exerts against some pathogenic bacteria, e.g., Staphylococcus epidermidis, Staphylococcus lugdunensis, Stenotrophomonas maltophilia, Enterococcus faecalis, Pseudomonas aeruginosa, Corynebacterium, Mycobacterium smegmatis, and Staphylococcus warneri [1]. The antiviral, antiallergic, neuroprotective, antiinflammatory, anti-HIV, and antitumor effects of rosmarinic acid were described in the literature [1,11]. According to Venkatachalam et al. [12] rosmarinic acid may be used as a potent chemopreventive agent in rat colon cancer. Kim et al. [1] reported that it might inhibit the metastasis of colorectal carcinoma. Properties [1,3], biosynthetic pathway [1,5], and the determination of rosmarinic acid in plant extracts [2,13,14] have already been described in the literature. Data concerning the molecular structure of rosmarinic acid [7,8] and its antioxidant activity [9,10] are also available, but there is no information about alkali metal rosmarinates. The influence of metal ions on the structure parameters as well as some physical, chemical, and biological properties of biological active molecules were previously studied by our team [15,16,17,18].
Figure 1.
Numbering of atoms in rosmarinic acid molecule.
The aim of this paper is a spectroscopic study on molecular structure and antioxidant activity of alkali metal rosmarinates in comparison to rosmarinic acid. Obtained results are compared with theoretical data obtained by density functional theory (DFT) calculations.
2. Results and Discussion
2.1. Calculations
The density functional theory (DFT) calculations were performed using the Gaussian 09 [19] program running on PC computer and Gauss View [20] molecular visualization program. To calculate optimized geometrical structure of studied compounds the Lee-Yang-Parr Becke’s three parameter hybrid functional method (B3LYP) with 6-311+G(d,p) basis set was used. The optimized molecular geometry was characterized as minimum in the energy by the absence of imaginary wavenumbers.
The calculated lengths of the bonds and size of the angles of the optimized molecules of rosmarinic acid (RA) as well as lithium (RA-Li), sodium (RA-Na), and potassium (RA-K) rosmarinates are shown in Table 1. Results obtained for rosmarinic acid molecule were compared with calculated and experimental data found in the literature [7,21]. Good linear correlation was obtained for theoretical as well as experimental data. Correlation coefficients received for bonds’ lengths equal R = 0.9996 and 0.9997, respectively. Regarding the angles between bonds appropriate values are 0.9941 for the calculated and 0.9786 for the experimental one. Exemplary correlations are shown in Figure S1.
Table 1.
The distances between atoms (Å) and the angles between bonds (°) in rosmarinic acid and its lithium, sodium, and potassium salt molecules calculated using B3LYP/6-311+G(d.p).
| Atom Numbers 1 | Rosmarinic Acid (RA) | RA-Li | RA-Na | RA-K | |||
|---|---|---|---|---|---|---|---|
| Exp. [7] | Calc. [7] | Calc. [21] | |||||
| The Distances between Atoms/Å 2 | |||||||
| C1-C2 | 1.395 | 1.411 | 1.393 | 1.407 | 1.407 | 1.407 | 1.407 |
| C2-C3 | 1.377 | 1.385 | 1.392 | 1.383 | 1.384 | 1.384 | 1.384 |
| C3-C4 | 1.384 | 1.407 | 1.412 | 1.406 | 1.406 | 1.406 | 1.405 |
| C4-C5 | 1.386 | 1.396 | 1.383 | 1.388 | 1.388 | 1.387 | 1.387 |
| C5-C6 | 1.372 | 1.390 | 1.413 | 1.393 | 1.392 | 1.393 | 1.393 |
| C1-C6 | 1.391 | 1.407 | 1.406 | 1.403 | 1.403 | 1.402 | 1.402 |
| C1-C7 | 1.462 | 1.457 | 1.457 | 1.459 | 1.461 | 1.462 | 1.462 |
| C7-C8 | 1.317 | 1.348 | 1.350 | 1.344 | 1.343 | 1.342 | 1.342 |
| C8-C9 | 1.459 | 1.469 | 1.469 | 1.470 | 1.475 | 1.477 | 1.478 |
| C9-O1 | 1.210 | 1.219 | 1.218 | 1.210 | 1.211 | 1.212 | 1.213 |
| C9-O2 | 1.327 | 1.363 | 1.365 | 1.367 | 1.358 | 1.354 | 1.350 |
| O2-C8′ | 1.442 | 1.428 | 1.427 | 1.434 | 1.438 | 1.441 | |
| C1′-C2′ | 1.405 | 1.405 | 1.400 | 1.400 | 1.401 | 1.400 | |
| C2′-C3′ | 1.390 | 1.388 | 1.388 | 1.388 | 1.388 | 1.388 | |
| C3′-C4′ | 1.405 | 1.406 | 1.401 | 1.400 | 1.400 | 1.400 | |
| C4′-C5′ | 1.392 | 1.391 | 1.389 | 1.389 | 1.389 | 1.389 | |
| C5′-C6′ | 1.397 | 1.397 | 1.394 | 1.394 | 1.395 | 1.395 | |
| C1′-C6′ | 1.399 | 1.397 | 1.397 | 1.397 | 1.397 | ||
| C1′-C7′ | 1.517 | 1.514 | 1.512 | 1.512 | 1.512 | 1.512 | |
| C7′-C8′ | 1.544 | 1.546 | 1.541 | 1.538 | 1.536 | 1.535 | |
| C8′-C9′ | 1.532 | 1.524 | 1.528 | 1.532 | 1.541 | 1.544 | |
| C9′-O1′ | 1.209 | 1.206 | 1.201 | 1.263 | 1.259 | 1.257 | |
| C9′-O2′ | 1.351 | 1.358 | 1.354 | 1.270 | 1.266 | 1.264 | |
| O2′-H/M | 0.972 | 0.969 | 1.863 | 2.217 | 2.531 | ||
| C3-O3 | 1.374 | 1.357 | 1.357 | 1.362 | 1.363 | 1.363 | 1.363 |
| O3-H3 | 0.820 | 0.970 | 0.973 | 0.966 | 0.966 | 0.966 | 0.966 |
| C4-O4 | 1.358 | 1.357 | 1.376 | 1.372 | 1.374 | 1.375 | 1.375 |
| O4-H4 | 0.820 | 0.965 | 0.969 | 0.963 | 0.962 | 0.962 | 0.962 |
| O4-H3 | 2.124 | 2.112 | 2.152 | 2.152 | 2.151 | 2.151 | |
| C3′-O3′ | 1.379 | 1.379 | 1.379 | 1.380 | 1.381 | 1.381 | |
| O3′-H3′ | 0.965 | 0.969 | 0.962 | 0.962 | 0.962 | 0.962 | |
| C4′-O4′ | 1.364 | 1.364 | 1.364 | 1.366 | 1.366 | 1.367 | |
| O4′-H4′ | 0.969 | 0.973 | 0.966 | 0.966 | 0.966 | 0.966 | |
| O3′-H4′ | 2.130 | 2.124 | 2.155 | 2.154 | 2.153 | 2.153 | |
| The Angles/° | |||||||
| C1-C2-C3 | 121.3 | 120.9 | 120.90 | 120.93 | 120.94 | 120.97 | |
| C2-C3-C4 | 119.8 | 120.3 | 119.69 | 119.72 | 119.73 | 119.73 | |
| C3-C4-C5 | 119.4 | 119.3 | 120.22 | 120.18 | 120.16 | 120.15 | |
| C4-C5-C6 | 120.6 | 120.3 | 119.77 | 119.78 | 119.79 | 119.79 | |
| C5-C6-C1 | 120.7 | 121.1 | 120.93 | 120.97 | 120.98 | 120.99 | |
| C2-C1-C6 | 118.1 | 118.1 | 118.49 | 118.42 | 118.40 | 118.37 | |
| C1-C7-C8 | 128.6 | 128.1 | 127.82 | 127.86 | 127.76 | 127.74 | |
| C7-C8-C9 | 121.5 | 119.8 | 120.28 | 120.44 | 120.60 | 120.71 | |
| C8-C9-O1 | 126.4 | 126.86 | 126.18 | 125.83 | 125.63 | ||
| O1-C9-O2 | 122.8 | 122.63 | 123.38 | 123.84 | 123.97 | ||
| C1′-C2′-C3′ | 120.58 | 120.65 | 120.66 | 120.70 | |||
| C2′-C3′-C4′ | 120.64 | 120.67 | 120.71 | 120.71 | |||
| C3′-C4′-C5′ | 119.09 | 119.05 | 119.03 | 119.02 | |||
| C4′-C5′-C6′ | 120.16 | 120.16 | 120.15 | 120.16 | |||
| C5′-C6′-C1′ | 121.11 | 121.18 | 121.26 | 121.26 | |||
| C2′-C1′-C6′ | 118.43 | 118.29 | 118.20 | 118.16 | |||
| C1′-C7′-C8′ | 113.35 | 113.82 | 114.03 | 114.32 | |||
| C7′-C8′-C9′ | 110.67 | 110.73 | 111.22 | 110.86 | |||
| C8′-C9′-O1′ | 125.2 | 126.17 | 120.90 | 119.69 | 119.23 | ||
| O1′-C9′-O2′ | 123.1 | 123.58 | 122.17 | 124.79 | 125.67 | ||
| C9′-O2′-H/M | 105.9 | 107.41 | 82.26 | 87.08 | 89.48 | ||
| C9′-O1′-H/M | 54.55 | 82.31 | 87.23 | 89.83 | |||
1 the numbering of atoms according to Figure 1; 2 1 Å = 10−10 m.
Analysis of the obtained data shows that salt is formed by the substitution of the alkali metal ion in place of the hydrogen cation in the carboxyl group of the rosmarinic acid molecule, since the biggest alternations were found within this group. The bond length between the O2′-H/M atoms in the salt molecules increases in comparison to the rosmarinic acid molecule from 0.894 Å to 1.562 Å (the numbering of atoms in the acid molecule is shown in Figure 1). Much smaller changes were noted in the bonds of C9′-O1′ (the increase by 0.056–0.062 Å) and C9′-O2′ (the decrease by 0.084–0.088 Å). In this way, these bonds in the COO group in salt molecules are almost equal. The lengths of bonds C9–O2, O2–C8′, and C8′-C9 change only by 0.004–0.017 Å. The remaining bonds in the studied molecules do not change at all. The size of the angles in the salt molecules also change a little compared to the acid molecule with the exception of the carboxyl group. The biggest changes were observed for C9′-O1′-H/M (the increase by 27.76–35.28°) and C9′-O2′-H/M (the decrease by 17.93–25.15°) angles. Much smaller changes were observed for the O1′-C9′-C8′ (the decrease by 6.94°), O1′-C9′-O2′ (2.09°) and C1′-C7′-C8′ (the increase by 0.97°) angles. The changes of angles around carbonyl group are about 1.2–1.3°. Other angles change only slightly (0.01–0.27°). This indicates, that the cation of metal is substituted instead of the hydrogen atom in the carboxyl group.
The lengths of bonds within the hydroxyl groups practically do not change in the series: RA → RA-Li → RA-Na → RA-K. On the other hand, the presence of weak intramolecular hydrogen bonds between the ortho-position hydroxyl groups should be noted. The bonds in acid molecule are similar to those in its salts molecules, so it is difficult to say, on this basis, which molecules will have stronger antioxidant properties, acid whether its salts. Antioxidant action of phenolic compound is based on free radical quenching. The free radical scavenging mechanism depends on hydrogen atom transfer (HAT), a single electron transfer (SET), or the combination of both HAT and SET, which may be described as ArOH → ArO• + e− + H+ [21]. Thus, antioxidant activity depends on (i) H-abstraction and (ii) stability of the formed free radical. Cao et al. [21] studied the geometry structures of ground state of rosmarinic acid and its free radicals formed on O3, O4, O3′, and O4′ atoms. They found that stronger intramolecular hydrogen bonds (1.97–1.98 Å) are in more radical form than in the ground state of acid molecule, which stabilizes the free radical forms and makes the abstraction of hydrogen atom from the hydroxyl group occur easily. The ability to create resonance semiquinone even quinone structures additionally results in the stability of the radicals.
By comparing two aromatic rings in studied molecules, it was found that the ring A’ has more equalized bonds lengths (ΔC′C′ = 0.013 ) than the A ring (ΔCC = 0.023 ) in acid as well as in salt molecules. This conclusion is confirmed when one compares the differentiation of angles. In the case of angles in the aromatic rings the variation in the size of the angles in the salt molecules (2.38° < ΔCCC < 2.55° and 2.55° < ΔC′C′C′ < 2.62°) is greater than in rosmarinic acid molecule (ΔCCC = 2.21° and ΔC′C′C′ = 2.40°). This is also visible in the values of aromaticity indices (Table 2) [22,23,24]. The ring A has probably more disturbed aromaticity because of the resonance semiquinone structures. On the other hand, A’ ring aromaticity is higher in salts molecules than in rosmarinic acid molecule, perhaps for the reason that the symmetry of the molecules increase.
Table 2.
Values of dipole moment, energy as well as aromaticity indices calculated using B3LYP/6-311+G(d.p) method for rosmarinic acid and its lithium, sodium, and potassium salts.
| Rosmarinic Acid | Rosmarinates | |||
|---|---|---|---|---|
| RA-Li | RA-Na | RA-K | ||
| Energy/Hartree 1 | −1297.1 | −1304.7 | −1459.5 | −1897.1 |
| Energy variation ΔE 2/kJ/mol | −7351.4 | −3675.7 | −3675.7 | |
| Dipole moment/Debye (D) 3 | 4.480 | 6.736 | 8.457 | 10.207 |
| Aromaticity indices [22,23,24] | ||||
| HOMA 4 Ring A | 0.9576 | 0.9580 | 0.9587 | 0.9576 |
| HOMA Ring A’ | 0.9828 | 0.9849 | 0.9840 | 0.9840 |
| I6 5 Ring A | 92.0475 | 92.2489 | 92.1176 | 92.0475 |
| I6 Ring A’ | 96.2393 | 96.6195 | 96.4861 | 96.4861 |
| Aj 6 Ring A | 0.9897 | 0.9902 | 0.9899 | 0.9897 |
| Aj Ring A’ | 0.9977 | 0.9981 | 0.9980 | 0.9980 |
| BAC 7 Ring A | 0.8588 | 0.8628 | 0.8608 | 0.8588 |
| BAC Ring A’ | 0.9313 | 0.9405 | 0.9385 | 0.9385 |
1 Hartree = 2625.5 kJ/mol; 2 ΔE = 2E(RA − M) + E(H2) − 2E(M) − 2E(RA); 3 1 D = 3.3356∙10−30 C∙m; 4 HOMA—Harmonic Oscillator Model of Aromaticity; 5 I6—Bird’s Index; 6 Aj—Julg’s Index; 7 BAC-Bond Alternation Coefficient.
The values of dipole moment, energy, and aromatic indices calculated for rosmarinic acid and its lithium, sodium, and potassium salts are shown in Table 2. The dipole moment values of rosmarinic acid and its salt molecules increase in the series: Rosmarinic acid < Li < Na < K salt. It indicates that polarity of studied compounds increase. The absolute energy of the tested molecules decreases in the same series. The values of the energy variation (ΔE) associated to the substitution reaction of the carboxylic hydrogen atom by an alkali metal atom have been calculated and included in Table 2.
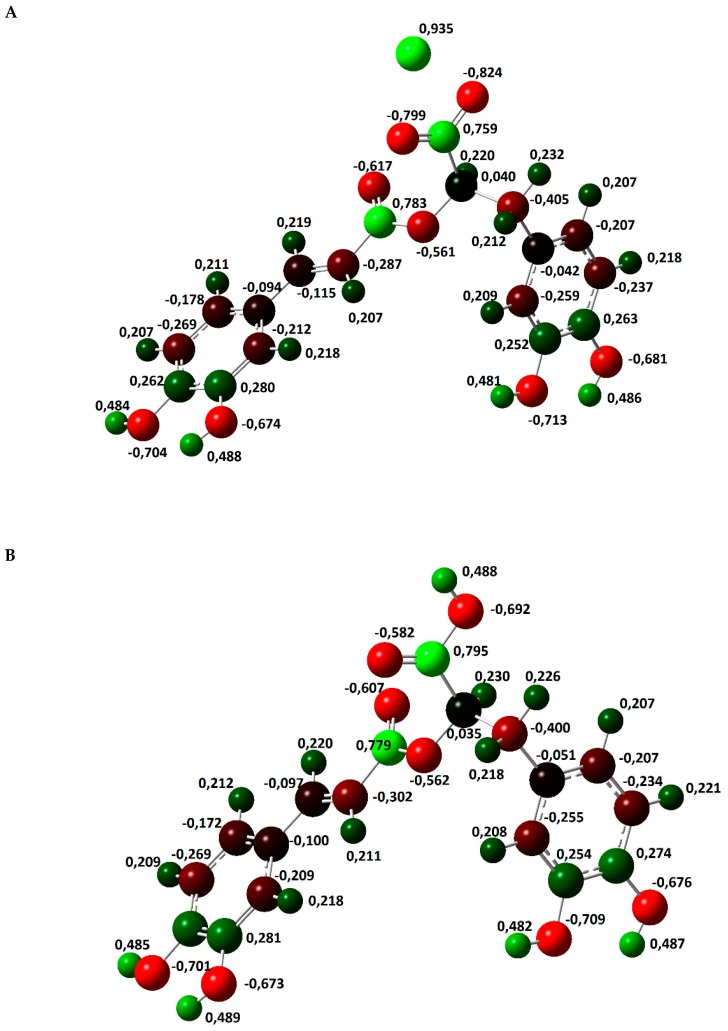
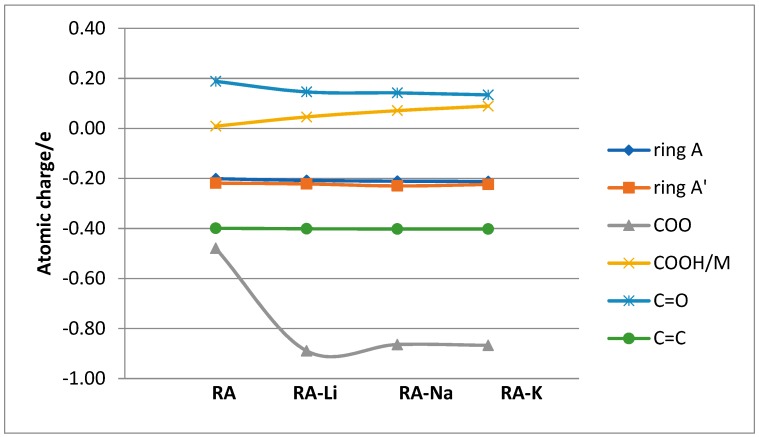
The atomic charge distribution in studied molecules was calculated by the natural bond orbital method (NBO) using B3LYP/6-311+G(d,p). Data obtained for rosmarinic acid and its sodium salt are presented in Figure 2. In the case of lithium and potassium rosmarinates, the values of atomic charges are very similar to sodium salt. The atomic charges on most of the atoms in molecules of a lithium and potassium salts only slightly differ relative to the sodium rosmarinate molecule, they are in the range 0.000–0.007e. The exception are oxygen atoms of carboxylate group: O1′ (−0.813, −0.799 and −0.803e), O2′(−0.836, −0.824 and −0.822), as well as alkali metal ion (0.935, 0.935, and 0.956 e, for RA-Li, RA-Na, and RA-K, respectively). Systematic changes in the series: RA > RA-Li > RA-Na > RA-K is noted for atomic charges of C7, C8, and O1 atoms. When it comes to comparing salt molecules with an acid molecule, the largest changes are observed for H9′/M atom (atomic charge increases by 0.468e. In the case of O1′ and O2′ atoms, negative atomic charges significantly increase for lithium salts (by 0.231 and 0.144e, respectively) in comparison to acid, but in the Li > Na > K salts series they slightly decrease (0.014 and 0.012e). Much smaller changes (0.037e) in the series RA > RA-Li > RA-Na > RA-K occur for the charges on C9′ atom of carboxylate group. The summary charges calculated for the aromatic rings, double bond, and carbonyl and carboxylic/carboxylate groups were calculated and are shown in Figure 3. In summary, the biggest changes in comparison to acid molecule are observed for COO group. However, very good linear correlation was found between the summary charge calculated for the COOH/M group and electron affinity, the ionic potential, and the atomic radius of the hydrogen/metal atom. Corresponding correlation coefficients are 0.9998, 0.9918, and 0.9891, respectively.
Figure 2.
Optimized molecular structures of rosmarinic acid (B) and its sodium salt (A) as well as atomic charges.
Figure 3.
The atomic charges calculated for chosen groups of studied molecules.
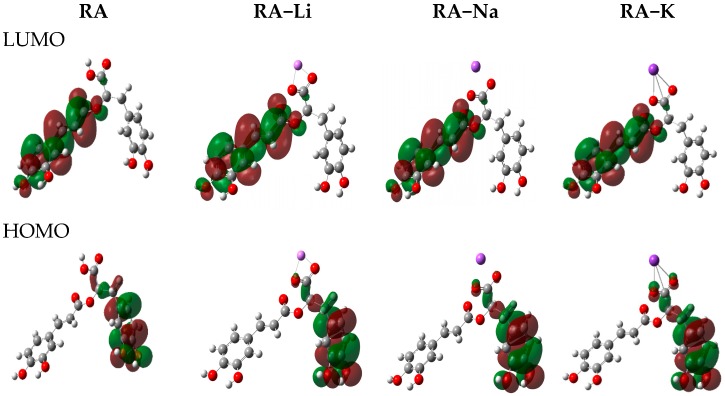
The frontier orbital energies are the important parameters of the molecular electron structure. The highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO) energies as well as other general reactivity descriptors [25,26,27,28] such as ionization potential (I), electron affinity (A), electronegativity (χ), chemical hardness (η), softness (s), chemical potential (μ), electrophilicity (ω), and nucleophilicity (N) indexes calculated on the basis of the HOMO and LUMO orbital’s energy are gathered in Table 3. Reactivity descriptors were calculated as follows: I = −EHOMO; A = −ELUMO; χ = (I + A/2); η = (I − A)/2; s = 1/2η; μ = −(I + A)/2; ω = μ2/2η; N = EHOMO(nuclefil)−EHOMO(TCNE) (nucleofilicity index N is referred to tetracyanoethylene TCE [28). The highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO) play an important role for predicting the charge transfer within the molecule, chemical reactivity, bioactivity, and stability of the compound [25,29]. The higher the HOMO energy is, the stronger electron donor molecule is, while LUMO energy reflects the ability to accept the electron. The distribution of HOMO electron density in a phenolic molecule may qualitatively indicate the active site of scavenging free radicals, because the reaction of H-abstraction is associated with the transfer of electron [21]. The HOMO and LUMO electron densities for rosmarinic acid and its lithium, sodium, and potassium salts are shown in Figure 4. The HOMO electron density in both acid and its salt molecules is mainly distributed over carbon atoms in A’ ring and O3′, O4′ oxygen atoms of ortho-hydroxyl groups, which can donate electrons easily during the H-abstraction. The LUMO electron density is distributed over ring A, double bond, carbonyl and carboxylic groups forming a conjugating system. This is beneficial for electron scattering and has some effects on free radicals such as O2− [21]. The HOMO-LUMO energy gap is a useful descriptor of chemical and biological activity of molecules. The smaller gap value is, the more chemically active the molecule is, and it is termed a soft molecule. The HOMO-LUMO gap values decrease in the following order: RA-Li > RA-Na > RA-K > RA, indicating the increase in the reactivity of studied molecules in above series. In this way rosmarinic acid should be chemically more active then salts molecules. The electrophilic or nucleophilic index is related to molecule ability to exchange electron density during a reaction [30,31]. The electron affinity, electronegativity and electrophilicity indexes decrease in series: rosmarinic acid > its lithium > sodium > potassium salts, while the values of chemical potential increase in the above series. The ionization potential decreases in order RA-Li > RA > RA-Na > RA-K, whereas the values of nucleophilicity increase in the above series. It indicates that the sodium and potassium salts have higher electron transfer ability than rosmarinic acid.
Table 3.
Energy of HOMO/LUMO orbitals and other reactivity descriptors.
| Molecular Descriptor | RA | RA-Li | RA-Na | RA-K |
|---|---|---|---|---|
| HOMO energy/eV | −5.774 | −5.788 | −5.641 | −5.558 |
| LUMO energy/eV | −2.170 | −1.871 | −1.746 | −1.698 |
| HOMO-LUMO energy gap/eV | 3.604 | 3.917 | 3.894 | 3.860 |
| Electron affinity (A)/eV | 2.170 | 1.871 | 1.746 | 1.698 |
| Ionization potential (I)/eV | 5.774 | 5.788 | 5.641 | 5.558 |
| Chemical hardness (η)/eV | 1.802 | 1.959 | 1.947 | 1.930 |
| Chemical softness (s)/eV | 0.277 | 0.255 | 0.257 | 0.259 |
| Chemical potential (μ)/eV | −3.972 | −3.830 | −3.693 | −3.628 |
| Electronegativity (χ)/eV | 3.972 | 3.830 | 3.693 | 3.628 |
| Electrophilicity index (ω)/eV | 4.378 | 3.744 | 3.503 | 3.410 |
| Nucleophilicity index (N)/eV | 3.713 | 3.699 | 3.847 | 3.930 |
I = −EHOMO; A = −ELUMO; χ = (I + A/2); η = (I − A)/2; s = 1/2η; μ = −(I + A)/2; ω = μ2/2η; N = EHOMO(nuclefil) − EHOMO(TCE); TCE−tetracyanoethylene.
Figure 4.
The HOMO/LUMO (highest occupied molecular orbital/lowest unoccupied molecular orbital) electron densities in molecules of studied compounds.
The wavenumbers and intensities of bands in vibrational spectra for the optimized structures of rosmarinic acid and its lithium, sodium, and potassium salt molecules were also calculated and presented in Table 4.
Table 4.
Calculated wavenumbers (cm−1) and intensities (Int) of bands in rosmarinic acid and its lithium, sodium and potassium salts spectra.
| Rosmarinic Acid | Lithium Rosmarinate | Sodium Rosmarinate | Potassium Rosmarinate | Assignment * | |||||
|---|---|---|---|---|---|---|---|---|---|
| cm−1 | Int | cm−1 | Int | cm−1 | Int | cm−1 | Int | ||
| 3851 | 70.0 | 3852 | 64.1 | 3849 | 63.5 | 3852 | 65.0 | νOH | |
| 3846 | 144.8 | 3844 | 140.8 | 3848 | 149.5 | 3849 | 135.4 | νOH | |
| 3793 | 115.9 | 3796 | 34.3 | 3796 | 97.1 | 3795 | 104.4 | νOH | |
| 3792 | 116.2 | 3791 | 206.6 | 3794 | 130.2 | 3794 | 119.8 | νOH | |
| 3759 | 93.2 | νOHCOOH | |||||||
| 3165; 3159 | 7.5; 16.1 | 3167; 3157 | 7.7; 15.0 | 3173; 3157 | 3.0; 19.4 | 3166; 3156 | 7.3; 18.6 | νCH | 20a |
| 3098 | 11.6 | 3102 | 12.3 | 3117 | 1.0 | 3100 | 13.5 | νasCH2 | |
| 3047 | 16.7 | 3044 | 28.9 | 3044 | 28.9 | 3041 | 17.6 | νsCH2 | |
| 1832 | 298.1 | νC=O | |||||||
| 1765 | 251.4 | 1761 | 224.5 | 1754 | 207.5 | 1752 | 215.2 | νC=O | |
| 1678 | 267.7 | 1683 | 221.3 | 1683 | 142.0 | 1682 | 199.4 | νC=C | |
| 1656; 1650 | 23.2; 205.6 | 1659; 1649 | 25.1; 109.4 | 1655; 1649 | 24.2; 169.1 | 1657; 1652 | 19.4; 94.8 | νCC | 8a |
| 1646; 1632 | 23.3; 47.8 | 1645; 1634 | 20.2; 48.2 | 1645; 1631 | 31.36; 43.6 | 1646; 1633 | 21.4; 46.4 | νCC. νC=C | 8b |
| 1589 | 496.8 | 1593 | 413.0 | 1617 | 507.7 | νasCOO | |||
| 1556; 1542 | 128.7; 252.8 | 1558; 1542 | 140.1; 287.3 | 1552; 1541 | 107.3; 280.4 | 1555; 1541 | 130.6; 247.9 | νCC | 19a |
| 1499; 1475 | 27.9; 64.7 | 1498; 1478 | 16.4; 13.0 | 1498; 1474 | 18.6; 57.6 | 1497; 1474 | 13.8; 68.6 | βOH. νCC | 19b |
| 1487 | 5.2 | 1495 | 10.6 | 1486 | 8.2 | 1486 | 7.8 | δsCH2 | |
| 1452 | 309.2 | 1428 | 335.1 | 1413 | 271.5 | νsCOO | |||
| 1396; 1390 | 21.6; 11.2 | 1393; 1389 | 24.6; 8.8 | 1391; 1388 | 33.6; 7.2 | 1394; 1389 | 36.3; 16.9 | νCC, βCHC=C | 14 |
| 1364 | 9.0 | 1362 | 3.2 | 1360 | 4.2 | 1358 | 5.6 | ωCH2 | |
| 1353; 1351 | 59.4; 51.1 | 1351; 1345 | 104.9; 34.7 | 1353; 1350 | 62.3; 37.9 | 1350; 1349 | 104.3; 38.4 | νCC. βOH | |
| 1344 | 89.9 | 1339 | 87.0 | 1339 | 14.9 | 1333 | 86.7 | ωCH2. βCHc=c | |
| 1334 | 142.6 | 1332 | 126.7 | 1333 | 138.3 | 1330 | 150.1 | νC-OHar. βOH, νCC | |
| 1324 | 36.4 | βOH | |||||||
| 1311; 1301 | 166.2; 358.2 | 1313; 1301 | 126.5; 409.5 | 1308; 1302 | 175.8; 236.6 | 1308; 1299 | 163.5; 404.3 | βCH. νC-O | 13 |
| 1214; 1213 | 49.7; 64.0 | 1214; 1211 | 55.8; 44.2 | 1214; 1209 | 43.6; 77.5 | 1215; 1212 | 58.9; 67.6 | βCH. βOH | 18b |
| 1186 | 27.7 | 1184 | 142.2 | 1184 | 242.4 | 1187 | 411.9 | βCHc=c. βCH | |
| 1171; 1166 | 24.2; 352.8 | 1176; 1169 | 95.4; 256.7 | 1177; 1169 | 28.2; 58.4 | 1177; 1170 | 24.8; 64.2 | βCH. βOH | 18a |
| 1124; 1123 | 271.4; 288.0 | 1124; 1121 | 293.8; 98.6 | 1138; 1129 | 168.4; 144.2 | 1123; 1122 | 247.4; 144.7 | βCH. βOH | |
| 1082 | 296.5 | 1085 | 144.1 | 1082 | 119.2 | 1083 | 100.9 | νsCOO | |
| 1021 | 28.8 | 1019 | 30.8 | 1018 | 31.6 | 1018 | 30.4 | γCHc=c | |
| 949; 931 | 2.1; 2.7 | 948; 930 | 0.4; 3.0 | 957; 929 | 3.7; 2.9 | 946; 928 | 3.7; 3.1 | γCH | 17a |
| 892 | 0.5 | 894 | 1.5 | 896 | 0.5 | 895 | 1.9 | γCH. γCHc=c | |
| 879 | 18.6 | 871 | 9.6 | 877 | 27.6 | 872 | 11.5 | ρCH2. αCCC | |
| 829; 810 | 13.5; 46.8 | 825; 808 | 27.5; 44.9 | 836; 808 | 8.8; 29.2 | 821; 807 | 34.1; 40.1 | γCH | 10a |
| 785; 771 | 13.6; 3.9 | 798; 787 | 7.1; 11.8 | 795; 782 | 19.0; 8.7 | 791; 785 | 13.5; 9.4 | αCCC | 12 |
| 753 | 6.3 | 771 | 24.4 | 748 | 14.4 | βsCOO | |||
| 745 | 3.3 | γC=O. γCH | |||||||
| 738 | 26.8 | 738 | 13.3 | 735 | 7.0 | γsCOO. γCH | |||
| 710; 706 | 13.1; 0.6 | 708; 701 | 1.2; 30.4 | 720; 704 | 3.2; 0.4 | 719; 708 | 11.4; 2.3 | φCC, γCHc=c | 4 |
| 582 | 62.2 | γOH | |||||||
| 578 | 27.9 | 565 | 3.9 | 588 | 2.4 | βasCOO | |||
| 530; 520 | 31.8; 22.4 | 526; 520 | 50.4; 4.9 | 528; 507 | 78.5; 8.7 | 524; 505 | 34.7; 10.4 | αCCC | 6a |
| 496 | 26.6 | 503 | 2.1 | 507 | 8.7 | 505 | 10.4 | αCCC | 6b |
| 467; 449 | 12.8; 0.1 | 466; 448 | 1.2; 4.3 | 466; 449 | 6.7; 0.1 | 469; 449 | 13.7; 0.1 | φCC | 16b |
* fundamental modes of the phenyl ring are numbered according to Varsányi [32]; s—strong; m—medium; w—weak; v—very; sh—shoulder; ν: stretching; β: in plane deformations; γ: out of plane deformations; δ: scissoring; α: the aromatic ring in-plane bending modes; φ: the aromatic ring out-of-plane ones; τ—bending off the plane-twisting; ω—bending off the plane-fan; ρ—bending in the plane-swinging.
2.2. Vibrational Spectra
Experimental data of IR and Raman spectra of rosmarinic acid and its alkali metal salts are gathered in Table 5 and visualized in Figure 5. The assignment of bands is based on the literature, quantum-mechanical calculations, and personal experience. The bands are numbered along with the notation used by Varsányi [32].
Table 5.
The wavenumbers (cm−1) and intensities (Int) of vibrational spectra of alkali metal rosmarinates.
| Rosmarinic Acid | Lithium Rosmarinate | Sodium Rosmarinate | Potassium Rosmarinate | Rubidium Rosmarinate | Cesium Rosmarinate | Assignment * | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| IR | R | IR | R | IR | R | IR | R | IR | R | IR | R | ||
| 3519 m | νOH | ||||||||||||
| 3456 s | νOH | ||||||||||||
| 3399 s | νOH | ||||||||||||
| 3313 m | νOH | ||||||||||||
| 2974 w | 2964 vw | 2952 w | 2965 vw | 2963 vw | 2966 w | 2963 w | νCH | 20a | |||||
| 2933 w | 2946 w | 2927 w | 2927 vw | 2931 w | 2931 vw | 2925 w | 2928 vw | 2933 vw | νasCH2 | ||||
| 2857 w | 2854 w | 2854 vw | 2855 w | 2857 vw | 2857 vw | 2857 vw | νsCH2 | ||||||
| 1726 s | 1727 w | νC=O | |||||||||||
| 1708 vs | 1708 m | νC=O | |||||||||||
| 1645 w | 1646 s | 1687 s | 1687 m | 1687 s | 1690 m | 1692 s | 1692 m | 1692 s | 1692 m | 1692 s | 1690 m | νC=C | |
| 1617 s | 1619 vs | 1632 sh | 1627 sh | 1631 sh | 1627 sh | 1630 sh | 1629 sh | 1627 sh | 1627 sh | 1629 sh | 1629 s | νCC | 8a |
| 1609 sh | νCC. νC=C | 8b | |||||||||||
| 1600 vs | 1606 vs | 1599 vs | 1608 vs | 1598 vs | 1606 vs | 1602 vs | 1606 vs | 1595 vs | 1606 vs | νasCOO | |||
| 1521 s | 1525 w | 1522 s | 1523 vw | 1522 s | 1525 w | 1522 s | 1527 w | 1522 s | 1527 w | 1521 s | 1517 w | νCC | 19a |
| 1464 w | 1478 w | 1445 m | 1444 w | 1446 m | 1447 w | 1446 m | 1448 w | 1446 m | 1447 w | 1446 m | 1447 w | βOH. νCC | 19b |
| 1446 w | δsCH2 | ||||||||||||
| 1412 m | 1407 vw | 1405 m | 1403 m | 1413 w | 1399 sh | 1407 vw | 1402 m | 1417 w | νsCOO | ||||
| 1350 m | 1384 w | 1385 m | 1385 m | 1378 w | 1381 w | νCC | 14 | ||||||
| 1362 m | 1365 vw | 1362 w | 1366 vw | 1362 sh | 1353 w | 1362 m | 1355 w | 1362 sh | 1349 w | νCC. βOH | |||
| 1307 m | 1316 w | ωCH2. βCHc=c | |||||||||||
| 1286 s | 1293 w | νC-O. τCH2. βOH | |||||||||||
| 1260 s | 1275 w | 1265 vs | 1264 m | 1262 vs | 1264 m | 1260 vs | 1266 m | 1262 vs | 1260 m | 1262 vs | 1266 m | νC-OHar. βOH | |
| 1232 s | 1244 w | ωCH2 | |||||||||||
| 1183 s | 1193 w | 1180 s | 1183 sh | 1177 s | 1190 sh | 1177 s | 1184 sh | 1177 s | βCH. νC-O | 13 | |||
| 1154 s | 1154 m | 1161 s | 1164 m | 1161 s | 1162 m | 1160 s | 1164 m | 1161 s | 1162 m | 1161 s | 1164 m | βCH. βOH | 18b |
| 1115 m | 1114 w | 1116 m | 1122 w | 1116 m | 1118 w | 1116 m | 1118 w | 1116 s | 1118 w | 1116 s | 1118 w | βCH. βOH | 18a |
| 1076 m | 1077 vw | 1069 w | 1068 w | 1069 w | 1069 w | 1069 w | 1073 w | 1071 m | 1073 vw | 1067 m | 1075 w | βCHc=c. βCH | |
| 1034 w | 1041 vw | 1032 w | 1033 vw | 1032 w | 1037 w | 1027 vw | 1034 w | 1037 vw | βCH. βOH | ||||
| 981 sh | γCHc=c | ||||||||||||
| 973 m | 972 vw | 976 m | 981 w | 974 m | 975 m | 974 m | 979 w | 976 m | 977 w | 976 m | 979 w | γCH | 17a |
| 916 vw | 917 w | νOHCOOH | |||||||||||
| 851 w | 852 w | 853 m | 853 w | 853 w | 853 w | 853 m | 857 w | 854 m | 857 w | 854 m | 861 w | γCH. γCHc=c | 5 |
| 819 m | 807 w | 810 m | 813 w | 810 m | 805 vw | 810 m | 813 w | 812 m | 813 w | 812 m | 811 w | γCH | 10a |
| 790 w | 792 w | βC=O | |||||||||||
| 782 w | 783 w | 788 w | 782 w | 788 w | 782 w | 784 w | 783 w | 786 w | 782 w | 786 w | αCCC | 12 | |
| 682 w | γC=O. γCH | ||||||||||||
| 642 m | 641 w | γOHar | |||||||||||
| 736 vw | 751 w | 735 vw | 742 vw | 738 vw | 738 w | 738 vs | 730 w | 728 w | βsCOO | ||||
| 594 w | 715 vw | 718 vw | 718 vw | 722 w | 717 vw | 724 w | 719 vw | 718 vw | 718 vw | 713 vw | γsCOO. γCH | ||
| 593 w | 597 w | 592 w | 591 w | 591 w | 597 vw | 592 w | 589 w | 592 w | 597 w | αCCC | 6a | ||
| 565 w | 568 w | 564 vw | 564 vw | 570 vw | 574 vw | 573 vw | 563 vw | 568 vw | βasCOO | ||||
| 531 w | 526 vw | 525 w | 524 vw | 521 w | 524 vw | 521 w | 526 vw | 523 w | 522 w | 521 w | 526 w | αCCC | 6b |
| 465 w | 458 w | 448 w | 454 w | 456 w | 456 w | 454 w | 455 w | 456 vw | 457 w | φCC | 16b | ||
* Fundamental modes of the phenyl ring are numbered according to Varsányi [32]; s—strong; m—medium; w—weak; v—very; sh—shoulder; ν: stretching; β: in plane deformations; γ: out of plane deformations; δ: scissoring; α: the aromatic ring in-plane bending modes; φ: the aromatic ring out-of-plane ones; τ—bending off the plane-twisting; ω—bending off the plane-fan; ρ—bending in the plane-swinging.
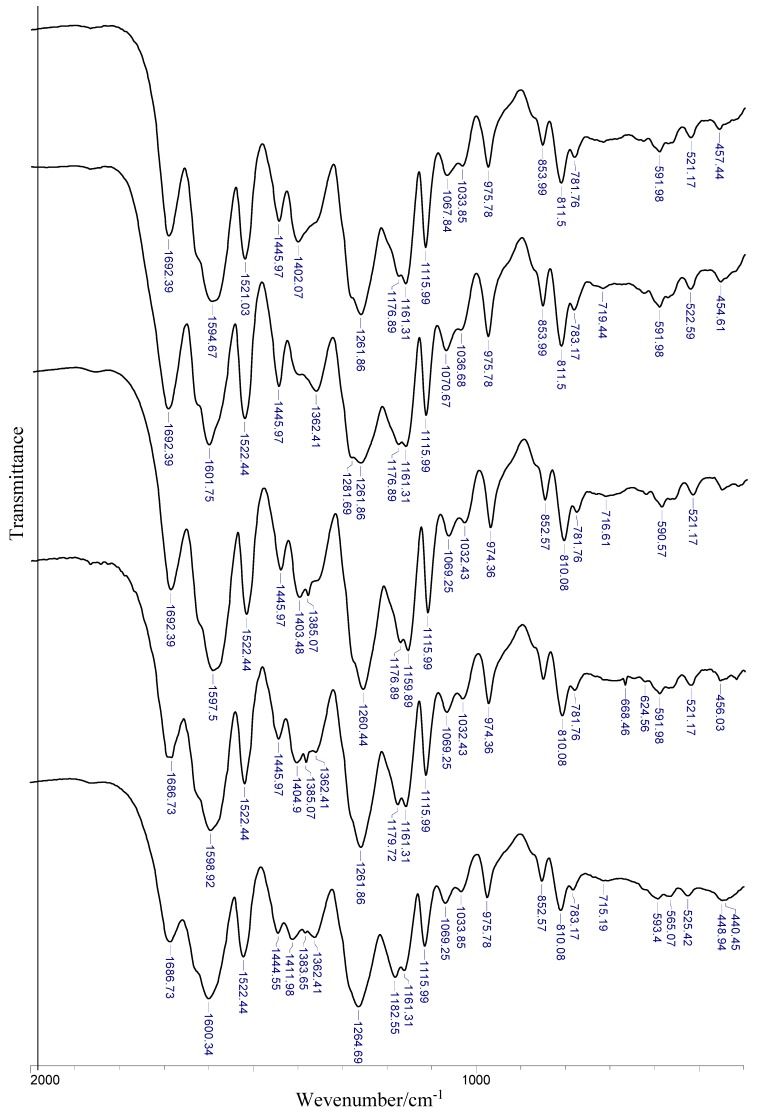
Figure 5.
Experimental vibrational spectra of Li, Na, K, Rb, and Cs rosmarinates (shown from bottom to top).
In the IR spectrum of rosmarinic acid, there is a very intense band originating from the stretching vibration of the carboxyl group νC=O at 1708 cm−1, while in Raman there are two bands of νC=O at 1708 and 1727 cm−1 (weak and medium intensity, respectively). In the rosmarinic acid spectrum the bands associated with in plane βC=O at 790 cm−1 (IR) and 792 cm−1 (Raman) as well as out of plane γC=O at 682 cm−1 (IR) deformations are observed. Some bands are connected with vibrations of hydroxyl groups, they are weak and of medium intensity bands coming from the stretching vibrations νOH at 3419, 3456 and 3399 cm−1 (IR) and deformations βOH at 1478 cm−1 and γOH at 917 cm−1 (Raman). In addition, a number of bands associated with vibrations of the aromatic ring can be seen in the ligand spectrum.
The substitution of the alkali metal atom in place of the hydrogen atom in the carboxylic group causes the disappearance of some characteristic for acid bands in the salt spectra, i.e., the bands coming from stretching and deformation vibrations of carboxylic group. Instead, there are very intense bands derived from the asymmetric stretching vibrations of carboxylate anion νas(COO−) lying in the range 1608–1606 cm−1 (Raman) and 1600–1598 cm−1 (IR) and symmetrical stretching vibration bands νs(COO−) in the range 141–1403 cm−1 (IR spectra). The less intense bands derived from symmetrical in plane deformations βs(COO−) appear at 738–736 cm−1 in IR spectra (751–728 cm−1. In Raman) and asymmetrical deformations βas(COO−) in the range 565–564 cm−1 (IR) and 573–568 cm−1 (Raman) as well as out of plane deformations γs(COO−) bands (715–718 and 724–713 cm−1, respectively in IR and Raman spectra). There are also low-intensity bands in Raman spectra, for example bands of symmetrical stretching vibrations νs(COO−) in the range 1417–1407 cm−1. The Raman spectra of alkali metal rosmarinates show a decrease in the wavenumbers and a reduction in the intensity of the bands coming from the vibrations of the aromatic ring, e.g., νas(CH2), β(CH), 19b (βOH, νCC), 16b (ϕCC), and 6b (αCCC) in comparison to the acid spectrum. In addition, the wavenumbers of some bands change regularly in the series of Li → Cs salts. The bands of βs(COO−) in Raman spectra, νs(COO−) and νas(COO−) in IR spectra are shifted to lower wavenumbers in Li > Na > K > Rb > Cs rosmarinates series but the bands of β(CH) deformation in the range 1075–1068 cm−1 and 5 (γCH) in Raman spectra show an increasing tendency in the above series. However a systematic decrease of the wavenumbers of the bands of asymmetric and symmetric stretching vibrations of carboxylate anions in the IR spectra was observed in the Li > Na > K > Rb > Cs salt series, the values of difference Δν = νas(COO−) − νs(COO−) increase in the order: Li > Cs > Na > K > Rb, correspondingly 188, 193, 194, 195, and 203 cm−1. It indicates an increasing share of metal-oxygen ionic binding.
The very good linear correlation was observed between the values of wavenumbers of chosen bands (νs(COO), βs(COO), β(CH), 5) and the parameters characterizing metals, i.e., electronegativity, atomic radius, electron affinity, and ionic potential (defined as the ratio of the ion charge to its radius). For electronegativity, ionic potential, and atomic radius, high correlation coefficients (0.875–0.987) were obtained. In addition, it was found that the wavenumbers of νs(COO−) band very well linearly correlates with the lengths of bonds (C9′-O1′ and C9′-O2′) and sizes of angles (O1′-C9′-O2′, C9′-O1′-M and C9′-O1′-M) of carboxyl group (correlation coefficients are in the range 0.991–0.999).
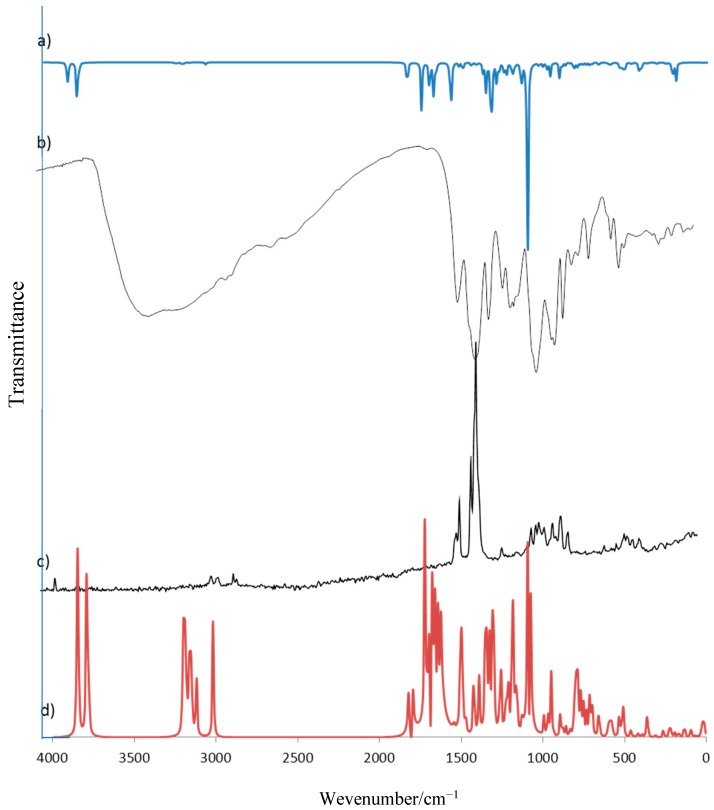
Experimental data have been compared to calculated wavenumbers and the good linear correlation is found (correlation coefficient R = 0.998, 0.999, 0.998, and 0.999, respectively for RA, RA-Li, RA-Na, and RA-K). Experimental and calculated vibrational spectra are presented exemplary for rosmarinic acid in Figure 6.
Figure 6.
Experimental and calculated vibrational spectra of rosmarinic acid: FT-IR (a,b) and Raman (c,d).
2.3. NMR Spectra
The experimental and theoretical chemical shifts of protons and carbons in NMR spectra of rosmarinic acid and its alkali metal salts in DMSO saturated solution are gathered in Table 6. Literature data [8] of experimentally obtained chemical shifts in 13C and 1H NMR spectra of rosmarinic acid are also presented. The good correlation between literature and the obtained data in this work is found (R = 0.999 for 13C as well as 1H NMR).
Table 6.
The experimental and theoretical (6-311+G(d.p)) chemical shifts (δ/ppm) of protons and carbons in NMR spectra of rosmarinic acid and its alkali metal salts in DMSO solutions.
| Rosmarinic acid | Rosmarinates | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Atom * | Exp. | Calc. | RA-Li | RA-Na | RA-K | RA-Rb | RA-Cs | ||||
| [8] | Exp. | Calc. | Exp. | Calc. | Exp. | Calc. | Exp. | Exp. | |||
| C1 | 127.6 | 125.36 | 132.75 | 125.48 | 132.86 | 125.48 | 133.07 | 125.45 | 133.20 | 125.45 | 125.41 |
| C2 | 114.5 | 113.26 | 115.54 | 114.73 | 115.47 | 114.73 | 115.19 | 114.68 | 114.88 | 114.21 | 114.62 |
| C3 | 146.8 | 145.93 | 150.95 | 146.07 | 151.38 | 146.00 | 151.19 | 146.09 | 150.95 | 145.88 | 146.15 |
| C4 | 149.7 | 148.63 | 153.46 | 148.86 | 153.02 | 148.73 | 152.75 | 148.73 | 152.25 | 148.71 | 148.85 |
| C5 | 116.2 | 116.70 | 117.72 | 116.81 | 118.13 | 116.70 | 118.08 | 116.70 | 117.76 | 116.73 | 116.77 |
| C6 | 123.1 | 121.58 | 132.56 | 120.90 | 131.59 | 120.82 | 131.45 | 120.57 | 131.20 | 121.05 | 120.58 |
| C7 | 147.6 | 144.94 | 156.96 | 144.47 | 154.15 | 144.39 | 152.48 | 144.39 | 153.42 | 144.93 | 144.47 |
| C8 | 115.2 | 115.40 | 113.42 | 115.58 | 116.60 | 115.49 | 117.16 | 115.47 | 116.75 | 115.50 | 115.54 |
| C9 | 168.5 | 165.92 | 171.03 | 166.33 | 170.56 | 166.30 | 170.56 | 166.32 | 170.39 | 166.16 | 166.38 |
| C1′ | 129.4 | 127.29 | 132.45 | 129.87 | 137.31 | 129.83 | 138.78 | 129.88 | 139.68 | 128.99 | 129.88 |
| C2′ | 117.5 | 115.77 | 119.00 | 116.17 | 119.55 | 116.06 | 118.98 | 116.00 | 119.11 | 116.03 | 116.04 |
| C3′ | 146.1 | 145.60 | 149.36 | 145.05 | 148.07 | 144.98 | 147.81 | 144.98 | 147.56 | 144.97 | 145.03 |
| C4′ | 145.2 | 144.02 | 150.28 | 143.71 | 148.58 | 143.63 | 148.13 | 143.61 | 148.28 | 143.78 | 143.66 |
| C5 | 116.5 | 114.90 | 119.00 | 115.17 | 119.10 | 115.11 | 119.10 | 115.23 | 118.83 | 115.16 | 115.29 |
| C6′ | 121.8 | 120.04 | 127.96 | 119.75 | 126.75 | 119.67 | 126.49 | 119.60 | 126.38 | 119.80 | 119.62 |
| C7′ | 37.9 | 36.11 | 41.07 | 37.23 | 35.83 | 37.25 | 36.02 | 37.26 | 35.83 | 36.84 | 37.25 |
| C8′ | 74.8 | 72.82 | 144.95 | 75.93 | 144.37 | 75.95 | 143.79 | 76.11 | 144.91 | 74.89 | 76.21 |
| C9′ | 167.4 | 170.83 | 165.08 | 172.88 | 183.49 | 173.07 | 179.28 | 172.51 | 175.57 | 172.11 | 172.52 |
| H2 | 6.88 | 7.06 | 7.65 | 7.05 | 7.65 | 7.05 | 7.61 | 7.05 | 7.50 | 7.06 | 7.06 |
| H3 | 9.64 | 5.47 | 5.41 | 5.35 | 5.30 | ||||||
| H4 | 8.79 | 4.99 | 4.86 | 4.84 | 4.91 | ||||||
| H5 | 6.61 | 6.77 | 7.00 | 6.76 | 6.95 | 6.76 | 6.98 | 6.74 | 7.03 | 6.76 | 6.74 |
| H6 | 6.79 | 7.01 | 7.03 | 6.92 | 7.04 | 6.92 | 7.05 | 6.90 | 6.96 | 6.95 | 6.90 |
| H7 | 7.39 | 7.47 | 7.74 | 7.38 | 7.98 | 7.38 | 7.84 | 7.38 | 7.73 | 7.41 | 7.39 |
| H8 | 6.11 | 6.24 | 6.54 | 6.19 | 6.42 | 6.19 | 6.40 | 6.18 | 6.38 | 6.21 | 6.19 |
| H2′ | 6.59 | 6.68 | 7.03 | 6.69 | 6.85 | 6.68 | 6.81 | 6.68 | 6.76 | 6.68 | 6.68 |
| H3′ | 8.73 | 4.50 | 4.35 | 4.30 | 4.30 | ||||||
| H4′ | 9.16 | 5.27 | 5.17 | 5.06 | 4.98 | ||||||
| H5′ | 6.54 | 6.64 | 6.97 | 6.61 | 6.97 | 6.61 | 6.96 | 6.60 | 6.94 | 6.62 | 6.60 |
| H6′ | 6.47 | 6.53 | 7.05 | 6.50 | 6.91 | 6.50 | 7.02 | 6.49 | 7.00 | 6.51 | 6.49 |
| H7′ | 2.85 | 2.99 | 4.34 | 3.05 | 4.81 | 3.03 | 4.83 | 3.01 | 4.10 | 3.02 | 3.00 |
| H7′’ | 2.93 | 2.90 | 3.56 | 2.77 | 4.30 | 2.78 | 4.24 | 2.77 | 5.31 | 2.81 | 2.77 |
| H8′ | 5.03 | 5.03 | 4.90 | 4.89 | 4.86 | 4.93 | 4.85 | ||||
| H9′ | 12.99 | 5.96 | |||||||||
* the numbering of atoms according to Figure 1.
The good linear correlation is also obtained between our experimental and calculated data connecting NMR spectra obtained for rosmarinic acid and its lithium, sodium, and potassium salts is obtained. The correlation coefficients equal 0.857, 0.879, 0.880 and 0.874 for 13C NMR, for 1H NMR corresponding values are: 0.987, 0.976, 0.979, and 0.938.
In 13C NMR spectra there are peaks connecting carbons of aromatic rings (C1–C6) and (C1′-C6′), the double bond (C7–C8), the ester group C9 and carboxyl group C9′. 13C NMR spectra of rosmarinic acid and its alkali metal salts shows the highest values of chemical shifts for C9′ carbon atom (170.8–173.1 ppm), slightly lower values of chemical shifts are observed for C9 atom (165.9–166.3 ppm). The chemical shifts observed for C3, C4, and C3′, C4′ atoms (the places of hydroxy groups substitution) as well as for C7 atom (of double bond) are in the range 143.7–148.9 ppm. The lowest chemical shift is observed for C7′ atom of CH2 group (36.1–37.3ppm). The chemical shifts for C8′ carbon atom are 72.8–76.2 ppm. The highest changes in salt spectra in comparison to acid spectrum is noted for C8′ and C1′ (127.3–129.9 ppm) carbon atoms. The increase in chemical shifts in salts spectra in comparison to acid spectrum is observed in the case of C2, C9, C1′, C2′, C7′, C8′, and C9′ atoms. In comparison, a decrease is noted for C6, C7, C3′, and C4′ atoms. There are no regular changes in the series of alkali metal rosmarinates in the experimental 13C NMR spectra. In theoretical spectra the decrease in chemical shifts is noted for C2, C3, C4, C5, C6, C9, C3′, C5′, C6′, and C9′, but only an increase for C1 and C1′ atoms.
In calculated 1H NMR spectra of rosmarinic acid and its alkali metal salts the chemical shifts for H3, H4, and H3′, H4′ protons are in the range 4.3–5.5 ppm. The signals for above atoms in experimental spectrum of acid are in the range 8.7–9.6 ppm, but in salts spectra corresponding signals are not found. The phenolic proton signals is usually a sharp singlet in the range of 7.5–4.0 ppm. The presence of two groups relative to each other in the ortho position strongly influences the chemical shift of phenolic protons (signals are in the range of 12–10 ppm). This is due to the formation of intramolecular hydrogen bonds [33]. In calculated spectra, the peak assigned for H9′ proton of carboxylic group occurs at 6.0 ppm, whereas in experimental spectra it is found at 13.0 ppm. Similar results were obtained in our previous investigations [27]. In experimental 1H NMR spectra of rosmarinates, the decrease in chemical shifts in comparison to acid spectrum is observed in the case of H6, H7, H8, H5′, H6′, H7′, and H8′ protons, while the increase is only noted for H7′. In theoretical spectra the decrease is observed for H3, H4, H3′, H4′, H8, H2′, H5′, and H6′ protons, and the increase for H7″ and H7 atoms. When it comes to comparing spectra of alkali metal rosmarinates, in experimental spectra, only slight changes are noted, while in theoretical spectra, the decrease in the series Li > Na > K salts is observed for the most protons, the increasing tendency is only observed for H7′.
The linear correlation was found between chemical shifts of C9′ atom in experimental NMR spectra and some metal parameters such as electronegativity (R = 0.773), ionic potential (0.766), atomic radius (0.762), and electron affinity (0.708).
2.4. Antioxidant Activity
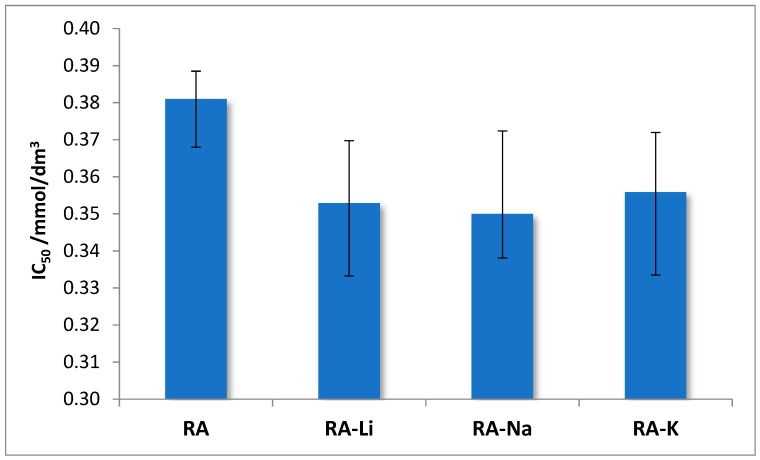
The antioxidant properties of rosmarinic acid and its salts with lithium, sodium, and potassium were examined. To assess the antioxidant activity, two methods were used that consist of (i) scavenging of free, stable DPPH* radicals and (ii) reduction of Fe3+ ions (FRAP method). The obtained results connecting the DPPH radical scavenging activity of studied compounds are expressed as IC50. The lower IC50 value, the better DPPH radical neutralizing properties represented by the test samples. Studies show that alkali metal rosmarinates have better antioxidant properties than rosmarinic acid, IC50 values obtained for salts are very similar (Figure 7).
Figure 7.
The IC50 values obtained in DPPH analysis for rosmarinic acid (RA) and its lithium, sodium, and potassium salts.
The clear linear correlation was found between differences of wavenumbers Δνas-s(COO) in IR spectra and IC50 values (effective concentration of the solution required to decrease the initial DPPH radicals by 50%). The correlation coefficient equals 0.989.
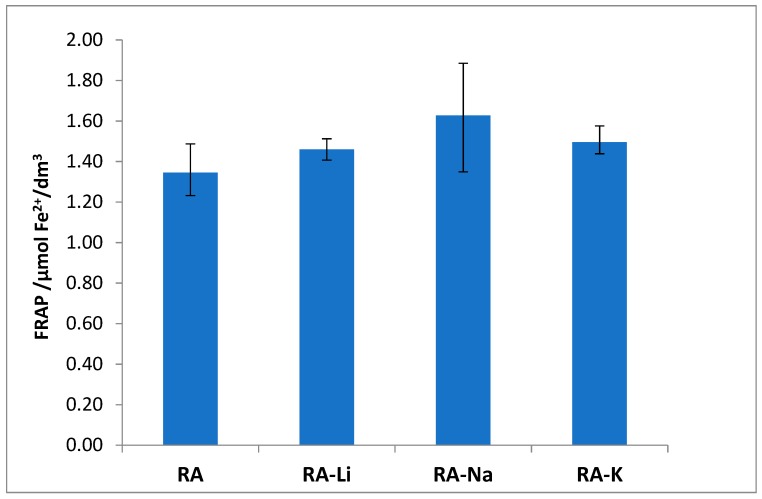
The studied salts have also higher ability to Fe3+ reduction than rosmarinic acid (Figure 8), and among them the sodium rosmarinate shows the highest antioxidant activity.
Figure 8.
Reducing power of the rosmarinic acid (RA) and its lithium, sodium, and potassium salts evaluated by FRAP (Fe3+ ion reduction capability) assay.
The antioxidant properties expressed through the Fe3+ ion reduction capability (FRAP method) linear correlate with the values of HOMO-LUMO energy gap. The correlation coefficient equals 0.7666.
2.5. Photochemical Properties
The results of kinetics studies of direct photolysis of rosmarinic acid and its salts are collected in Table 7. The first order kinetics model was assumed. Based on the obtained results, it could be stated that rosmarinic acid salts, as well as it alone, are photoresistant substances. The half times of the process are in the range 14.4 h (for rosmarinic acid) to 5.3 h (for sodium rosmarinate). This observation is in good agreement with literature data [34]. The 5 h exposition of the trans-RA solution in THF to the daylight resulted in lowering of its content by 2.5%. After a period of one month of continuous exposure to light, a loss of 22.3% of the amount of RA was found [34]. It was stated that under influence of light aphoto-isomerization process occurred and cis-RA is the only product of degradation [34]. A slight increase in pH values for rosmarinic acid and its salts solutions were observed after 2 h of irradiation with the exception of cesium and lithium rosmarinates (decrease).
Table 7.
The results of kinetics studies of photolysis of direct rosmarinic acid and its alkali metal salts.
| Substance | k1/min−1 | t1/22/min | t1/2/h | pH before Irradiation | pH after Irradiation |
|---|---|---|---|---|---|
| RA-Cs | 1.7 10−3 | 408 | 6.8 | 6.50 | 6.25 |
| RA-Rb | 0.9 10−3 | 770 | 12.8 | 5.09 | 5.49 |
| RA-K | 1.0 10−3 | 693 | 11.6 | 6.18 | 6.36 |
| RA-Na | 2.2 10−3 | 315 | 5.3 | 6.09 | 6.17 |
| RA-Li | 1.3 10−3 | 533 | 8.9 | 6.52 | 6.24 |
| RA | 0.8 10−3 | 866 | 14.4 | 4.23 | 4.92 |
1 k—rate constant; 2 t1/2—half time of the process.
The linear correlation between reaction rates and energy gap between HOMO and LUMO levels are observed in the series RA → RA-Li → RA-Na (R = 0.730).
3. Experimental Section
Materials and Methods
The alkali metal salts of rosmarinic acid were prepared by mixing in a 1:1 stoichiometric ratio mixture of rosmarinic acid and the standard solution of appropriate hydroxide with a concentration of 0.1 mol/L. The obtained mixture was dissolved in an ultrasonic bath. The water was evaporated in a water bath. The obtained precipitates were dried at 105 °C for 24 h. Rosmarinic acid, hydrochloric acid, sodium carbonate, as well as lithium, sodium, potassium, rubidium, and cesium hydroxides were from Sigma-Aldrich.
FT-IR and FT-Raman spectra of rosmarinic acid and synthesized salts were performed by method of pressing the sample within KBr. The spectra were recorded in the range of 400–4000 cm−1 at a resolution of 4 cm−1.
The NMR spectra of DMSO saturated solution were recorded with the NMR AC 200 F, Bruker unit at room temperature. TMS was used as an internal reference.
The determination of antioxidant activity was done by measuring the ability to quench the synthetic DPPH (1,1-diphenyl-2-picrylhydrazyl) radical by a modified Brand-Williams method [35]. For this purpose, the aqueous solutions of the tested compounds at the appropriate concentrations were prepared. Then, 0.05 mL of each sample was added to 2.5 mL of a methanolic solution of DPPH (absorbance is approx. 1.0). The samples were incubated in a dark at room temperature for 30 min. Absorbance of solutions was measured at λ = 515 nm against the blind test. All measurements were made in six replications. The percentage of the reduction of DPPH radical after incubation with the test solutions with reference to the control sample was calculated from the below equation:
where A0—absorbance of control sample and AS—absorbance of tested sample. The results were expressed as inhibitory concentration at 50% (IC50), which is the concentration of the test solution for achieving 50% of the radical scavenging capacity.
The determination of the ability to reduce iron in Fe3+-TPTZ complex (ferric-2,4,6-tripyridyl−s-triazine) into the Fe2+−TPTZ complex by the test compounds was made according to the FRAP method described by Benzie and Strain [36]. 0.05 mL of the samples was added to 2.5 mL FRAP reagent and incubated at room temperature for 15 min and then the absorbance of the solution was measured at λ = 596 nm and converted to the μmol Fe2+/L based on a comparison of absorbance values of samples with absorbance of Fe2+ standard measured under the same conditions. The FRAP reagent was prepared by mixing acetate buffer (pH 3.6), TPTZ (0.01 M), and FeCl3 (0.02 M) in a 10:1:1 ration, respectively.
To determine the antioxidant capacity of studied compounds following reagents were used: DPPH and FeCl3 from Sigma Aldrich; TPZZ from Fluka; methanol from Merck; HCl, CH3COONa from Chempur.
Evaluation of photochemical properties of rosmarincic acid and its salts was done as follows. A 50 mL working solution of currently studied solution at the concentration 20 µg/mL was subjected to the irradiation in a solar light simulator chamber SUNTEST CPS+, ATLAS USA equipped with a xenon lamp emitting radiation in the 300–800 nm range with an intensity of 500 Wm−2 for two hours. Illumination was stopped every 15 min, 2 mL of solution were taken and absorption spectrum was recorded. The absorbance changes were read at 324 nm as an analytical wavelength. All applied for photochemical experiments solutions were prepared by dissolving of the appropriate weighted mass of the studied substance in 100 mL of MiliQ water. All samples tested were prepared in triplicate.
Quantum mechanical calculations for rosmarinic acid and its salts molecules were made using the B3LYP method with the 6-311+(d,p) basis set and the GAUSSIAN 09 package of programs [19] running on a PC computer. Visualization of calculated parameters was performed by GaussView molecular visualization program [20]. The optimized molecular geometry was characterized as minimum in the energy by the absence of imaginary wavenumbers. To make quantity evaluation of aromaticity various indexes were calculated: AJ: normalized function of variance of bond lengths in the perimeter of the molecule; BAC: bond alternation coefficient; HOMA: abbreviation from Harmonic Oscillator Model of Aromaticity (HOMA = 1 − EN − GEO); GEO: geometric contribution to the aromaticity; EN: energetic contribution to the aromaticity; I6: Bird’s indice, which describes the geometric contribution to the aromaticity. The values of energy, dipole moment, atomic charges, general reactivity descriptors, as well as the wavenumbers and intensities of bands in vibrational spectra were calculated.
4. Conclusions
Spectroscopic study on alkali metal rosmarinates in comparison to rosmarinic acid molecule has been presented. The molecular structure has been determined using DFT calculation as well as the experimental spectroscopic techniques. Analysis of the obtained data shows that salt is formed by the substitution of alkali metal atom instead of the hydrogen atom in the carboxyl group, since the biggest changes in alkali metal rosmarinates in comparison to acid molecule regarding bond lengths, size of angles, and atomic charges were found. The substitution of the alkali metal atom in place of the hydrogen atom in the carboxylic group was confirmed by experimental as well as calculated vibrational spectra. The disappearance of some characteristic for acid bands in the salt spectra, i.e., the bands coming from stretching and deformation vibrations of carboxylic group was observed. In the IR or Raman spectra, the systematic decrease or increase of the wavenumbers of the bands not only of carboxylate anion was observed in Li → Na → K → Rb → Cs rosmarinates series. The increase in Δν = νas(COO−) − νs(COO−) difference in the above series indicates an increasing share of metal-oxygen ionic binding.
The very good linear correlation was observed between the values of wavenumbers of some bands in IR and Raman spectra and the parameters characterizing metals. The linear correlations were obtained for electronegativity, ionic potential, and atomic radius (correlation coefficients are in the range 0.88–0.99). In addition, it was found that the wavenumbers of νs(COO−) vibrations band very well-linearly correlate with the lengths of bonds and size of angles of the carboxyl group (0.99 < R < 1.00).
A very good linear correlation was found between the summary charge calculated for the COOH/M group and electron affinity, the ionic potential and the atomic radius of the hydrogen/metal atom (0.99 < R < 1.00).
The dipole moment values of rosmarinic acid and its salts molecules increase in the series: Rosmarinic acid < Li < Na < K salt, it follows that the polarity of studied compounds increase. The HOMO-LUMO energy gap is useful descriptors of chemical and biological activity of molecule. The smaller is gap value, the more chemically active the molecule is. Presented data in this manuscript show that rosmarinic acid should be chemically more active than salt molecules, while in the series of salts, the reactivity increases. Whereas the study on antioxidant activity of rosmarinic acid and its alkali metal salts indicate that alkali metal rosmarinates are better antioxidants than rosmarinic acid, the highest antioxidant properties have been found for sodium salt.
The antioxidant properties expressed through the Fe3+ ion reduction capability (FRAP method) linear correlate with the values of HOMO-LUMO energy gap (R = 0.77). On the other hand, IC50 values indicate the ability of quenching DPPH radicals correlate very well with Δνas-s(COO) in IR spectra (R = 0.99).
On the basis of the photochemical tests it was found that the rosmarinic acid and its alkali metal salts are photoresistant substances. The linear correlation between reaction rates and energy gap between HOMO and LUMO levels are observed in the series RA → RA-Li → RA-Na (R = 0.73).
Supplementary Materials
The following are available online, Figure S1: The correlation between calculated and literature data of bonds lengths and angles.
Author Contributions
Conceptualization, R.Ś. and W.L.; Investigation, R.Ś., G.Ś. and J.K.; Methodology, R.Ś., G.Ś., E.R. and J.K.; Writing—original draft, E.R. and J.K.; Writing—review & editing, E.R., R.Ś., W.L. and J.K.; Supervision, R.Ś. and W.L.
Funding
The project was funded by the National Science Center on the basis on the decision number 2015/17/B/NZ9/03581.
Conflicts of Interest
The authors declare no conflict of interest.
Footnotes
Sample Availability: Not available.
References
- 1.Kim G.D., Park Y.S., Jim Y.H., Park C.S. Production and applications of rosmarinic acid and structurally related compounds. Appl. Microbiol. Biotechnol. 2015;99:2083–2092. doi: 10.1007/s00253-015-6395-6. [DOI] [PubMed] [Google Scholar]
- 2.Berhow M.A., Rayford W.E., Vaughn S.F., Palmquist D., Tisserat B. Quantification of Rosmarinic Acid Levels by near Infrared Spectroscopy in Laboratory Culture Grown Spearmint Plantlets. J. Near. Infrared Spectrosc. 2008;16:99–104. doi: 10.1255/jnirs.769. [DOI] [Google Scholar]
- 3.Danaf N.A., Melhem R.A., Assaf K.I., Nau W.M., Patra D. Photophysical properties of neutral and dissociated forms of rosmarinic acid. J. Luminesc. 2016;175:50–56. doi: 10.1016/j.jlumin.2016.02.011. [DOI] [Google Scholar]
- 4.Shekarchi M., Hajimehdipoor H., Saeidnia S., Gohari A.R., Hamedani M.P. Comparative study of rosmarinic acid content in some plants of Labiatae family. Pharmacog. Mag. 2012;8:37–41. doi: 10.4103/0973-1296.93316. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Petersena M., Simmonds M.S. Rosmarinic acid. Phytochemistry. 2003;62:121–125. doi: 10.1016/S0031-9422(02)00513-7. [DOI] [PubMed] [Google Scholar]
- 6.Taguchi R., Hatayama K., Takahashi T., Hayashi T., Sato Y., Sato D., Ohta K., Nakano H., Seki C., Endo Y., et al. Structure-activity relations of rosmarinic acid derivatives for the amyloid β aggregation inhibition and antioxidant properties. Eur. J. Med. Chem. 2017;138:1066–1075. doi: 10.1016/j.ejmech.2017.07.026. [DOI] [PubMed] [Google Scholar]
- 7.Mariappan G., Sundaraganesan N., Manoharan S. Experimental and theoretical spectroscopic studies of anticancer drug rosmarinic acid using HF and density functional theory. Spectrochim. Acta A. 2012;97:340–351. doi: 10.1016/j.saa.2012.06.011. [DOI] [PubMed] [Google Scholar]
- 8.Akoury E. Isolation and Structural Elucidation of Rosmarinic Acid by Nuclear Magnetic Resonance Spectroscopy. Am. Res. J. Chem. 2017;1:17–23. doi: 10.21694/2577-5898.17003. [DOI] [Google Scholar]
- 9.Fadel O., El Kirat K., Morandat S. The natural antioxidant rosmarinic acid spontaneously penetrates membranes to inhibit lipid peroxidation in situ. Biochim. Biophys. Acta. 2011;1808:2973–2980. doi: 10.1016/j.bbamem.2011.08.011. [DOI] [PubMed] [Google Scholar]
- 10.Generalić Mekinić I., Skroza D., Ljubenkov I., Šimat V., Smole Možina S., Katalinić V. In vitro Antioxidant and Antibacterial Activity of Lamiaceae Phenolic Extracts. Food Technol. Biotechnol. 2014;52:119–127. [Google Scholar]
- 11.Sánchez-Campillo M., Gabaldon J.A., Castillo J., Benavente-García O., Del Baño M.J., Alcaraz M., Vicente V., Alvarez N., Lozano J.A. Rosmarinic acid, a photo-protective agent against UV and other ionizing radiations. Food Chem. Toxicol. 2009;47:386–392. doi: 10.1016/j.fct.2008.11.026. [DOI] [PubMed] [Google Scholar]
- 12.Venkatachalam K., Gunasekaran S., Namasivayam N. Biochemical and molecular mechanisms underlying the chemopreventive efficacy of rosmarinic acid in a rat colon cancer. Eur. J. Pharmacol. 2016;791:37–50. doi: 10.1016/j.ejphar.2016.07.051. [DOI] [PubMed] [Google Scholar]
- 13.Stehfest K., Boese M., Kerns G., Piry A., Wilhelm C. Fourier transform infrared spectroscopy as a new tool to determine rosmarinic acid in situ. J. Plant Physiol. 2004;161:151–156. doi: 10.1078/0176-1617-01099. [DOI] [PubMed] [Google Scholar]
- 14.Öztürk M., Duru M.E., İnce B., Harmandar M., Topçu G. A new rapid spectrophotometric method to determine the rosmarinic acid level in plant extracts. Food Chem. 2010;123:1352–1356. doi: 10.1016/j.foodchem.2010.06.021. [DOI] [Google Scholar]
- 15.Samsonowicz M., Świsłocka R., Regulska E., Lewandowski W. Experimental (FT-IR, FT-Raman, 1H, 13C NMR) and theoretical study of alkali metal 2-aminobenzoates. J. Mol. Struct. 2008;887:220–228. doi: 10.1016/j.molstruc.2007.11.041. [DOI] [Google Scholar]
- 16.Regulska E., Kalinowska M., Wojtulewski S., Korczak A., Sienkiewicz-Gromek J., Rzączyńska Z., Świsłocka R., Lewandowski W. Theoretical (in B3LYP/6-3111++G** level), spectroscopic (FT-IR, FT-Raman) and thermogravimetric studies of gentisic acid and sodium, copper(II) and cadmium(II) gentisates. Spectrochim. Acta A. 2014;132:713–725. doi: 10.1016/j.saa.2014.04.191. [DOI] [PubMed] [Google Scholar]
- 17.Samsonowicz M., Kowczyk-Sadowy M., Regulska E., Lewandowski W. Molecular structure and spectroscopic analysis of homovanillic acid and its sodium salt-NMR, FT-IR and DFT studies. Spectrochim Acta A. 2014;118:1068–1074. doi: 10.1016/j.saa.2013.09.123. [DOI] [PubMed] [Google Scholar]
- 18.Kowczyk-Sadowy M., Świsłocka R., Lewandowska H., Piekut J., Lewandowski W. Spectroscopic (FT-IR, FT-Raman, 1H-and 13C-NMR), Theoretical and Microbiological Study of trans o-Coumaric Acid and Alkali Metal o-Coumarates. Molecules. 2015;20:3146–3169. doi: 10.3390/molecules20023146. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Frisch M.J., Trucks G., Schlegel H.B., Scuseria G.E., Robb M.A., Cheeseman J.R., Scalmani G., Barone V., Mennucci B., Petersson G.A., et al. Gaussian 09W, Revision, E.01. Gaussian Inc.; Wallingford, CT, USA: 2009. [Google Scholar]
- 20.Dennington R., II, Keith T., Millam J., Eppinnett K., Hovell W.L., Gilliland R. GaussView, version 5.0.9. Semichem, Inc.; Shawnee Mission, KS, USA: 2009. [Google Scholar]
- 21.Cao H., Cheng W.-X., Li C., Pan X.-L., Xie X.-G., Li T.-H. DFT study on the antioxidant activity of rosmarinic acid. J. Mol. Struct. Theochem. 2005;719:177–183. doi: 10.1016/j.theochem.2005.01.029. [DOI] [Google Scholar]
- 22.Julg A., Francis P. Recherches sur la géométrie de quelques hydrocarbures non-alternants: Son influence sur les énergies de transition, une nouvelle définition de l’aromaticité. Theor. Chim Acta. 1967;7:249–259. doi: 10.1007/BF00527311. [DOI] [Google Scholar]
- 23.Bird C.W. A new aromaticity index and its application to five-membered ring heterocycles. Tetrahedron. 1985;41:1409–1414. doi: 10.1016/S0040-4020(01)96543-3. [DOI] [Google Scholar]
- 24.Krygowski T.M., Stępień B.T., Cyrański M.K. How the Substituent Effect Influences π-Electron Delocalisation in the Ring of Reactants in the Reaction Defining the Hammett Substituent Constants σm and σp. Int. J. Mol. Sci. 2005;6:45–51. doi: 10.3390/i6010045. [DOI] [Google Scholar]
- 25.Fukui K. Role of frontier orbitals in chemical reactions. Science. 1982;218:747–754. doi: 10.1126/science.218.4574.747. [DOI] [PubMed] [Google Scholar]
- 26.Parr R.G., Szentpály L.V., Liu S. Electrophilicity Index. J. Am. Chem. Soc. 1999;121:1922–1924. doi: 10.1021/ja983494x. [DOI] [Google Scholar]
- 27.Samsonowicz M., Regulska E., Kowczyk-Sadowy M., Butarewicz A., Lewandowski W. The study on molecular structure and microbiological activity of alkali metal 3-hydroxyphenylycetates. J. Mol. Struct. 2017;1146:755–765. doi: 10.1016/j.molstruc.2017.06.052. [DOI] [Google Scholar]
- 28.Samsonowicz M., Regulska E., Świsłocka R., Butarewicz A. Molecular structure and microbiological activity of alkali metal 3,4-dihydroxyphenylacetates. J. Saudi Chem. Soc. 2018;22:896–907. doi: 10.1016/j.jscs.2018.01.009. [DOI] [Google Scholar]
- 29.Samsonowicz M. Molecular structure of phenyl-and phenoxyacetic acids-Spectroscopic and theoretical study. Spectrochim. Acta A. 2014;118:1086–1097. doi: 10.1016/j.saa.2013.09.127. [DOI] [PubMed] [Google Scholar]
- 30.Domingo L.R., Perez P., Saez J.A. Understanding the local reactivity in polar organic reactions through electrophilic and nucleophilic Parr functions. RSC Adv. 2013;3:1486–1494. doi: 10.1039/C2RA22886F. [DOI] [Google Scholar]
- 31.Domingo L.R., Chamorro E., Perez P. Understanding the reactivity of captodative ethylenes in polar cycloaddition reactions. A theoretical study. J. Org. Chem. 2008;73:4615–4624. doi: 10.1021/jo800572a. [DOI] [PubMed] [Google Scholar]
- 32.Varsányi G., Kovner M.A., Láng L. Assignments for Vibrational Spectra of 700 Benzene Derivatives. Akademiai Kiado; Budapest, Hungary: 1973. [Google Scholar]
- 33.Silverstein R.M., Webster F.X., Kiemle D.J. Spectrometric Identification of Organic Compounds. J. Chem. Educ. 1962;39:546. doi: 10.1021/ed039p546. [DOI] [Google Scholar]
- 34.Razboršek M.I. Stability studies on trans-Rosmarinic acid and GC–MS analysis of its degradation product. J. Pharm. Biomed. Anal. 2011;55:1010–1016. doi: 10.1016/j.jpba.2011.04.003. [DOI] [PubMed] [Google Scholar]
- 35.Brand-Williams W., Cuvelier M.E., Berset C. Use of a free radical method to evaluate antioxidant activity. Food Sci. Technol. 1995;28:25–30. doi: 10.1016/S0023-6438(95)80008-5. [DOI] [Google Scholar]
- 36.Benzie I.F., Strain J.J. The Ferric Reducing Ability of Plasma (FRAP) as a Measure of “Antioxidant Power”: The FRAP Assay. Anal Biochem. 1996;239:70–76. doi: 10.1006/abio.1996.0292. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.