Abstract
Absolute quantification of PET brain imaging requires the measurement of an arterial input function (AIF), typically obtained invasively via an arterial cannulation. We present an approach to automatically calculate an image-derived input function (IDIF) and cerebral metabolic rates of glucose (CMRGlc) from the [18F]FDG PET data using an integrated PET/MRI system. Ten healthy controls underwent test–retest dynamic [18F]FDG-PET/MRI examinations. The imaging protocol consisted of a 60-min PET list-mode acquisition together with a time-of-flight MR angiography scan for segmenting the carotid arteries and intermittent MR navigators to monitor subject movement. AIFs were collected as the reference standard. Attenuation correction was performed using a separate low-dose CT scan. Assessment of the percentage difference between area-under-the-curve of IDIF and AIF yielded values within ±5%. Similar test–retest variability was seen between AIFs (9 ± 8) % and the IDIFs (9 ± 7) %. Absolute percentage difference between CMRGlc values obtained from AIF and IDIF across all examinations and selected brain regions was 3.2% (interquartile range: (2.4–4.3) %, maximum < 10%). High test–retest intravariability was observed between CMRGlc values obtained from AIF (14%) and IDIF (17%). The proposed approach provides an IDIF, which can be effectively used in lieu of AIF.
Keywords: Brain imaging, cerebral metabolic rates, [18F]FDG, integrated PET/MRI, image-derived input function
Introduction
In the last decade, combined PET/CT demonstrated the added value of anato-metabolic imaging1 in patient management, mainly in oncology.1,2 With the advent of combined PET/MR imaging, we witness a similar paradigm shift in managing patients with neurological disorders.3 Specifically, fully integrated PET/MRI bodes well for the prospect of finally realizing the promise of absolute quantification of PET data in clinical routine. This migration from semi-quantitative measures to full quantification is highly desirable as it has the potential to improve the diagnostic value of molecular imaging.4 To this end, routine quantification will depend on the development of automated approaches to provide clinicians with absolute quantitative values, in the same way as with standardized uptake values (SUVs) today.5
Absolute quantification in PET studies of the brain requires the knowledge of an input function (IF). In research studies, an arterial input function (AIF) can be obtained using arterial cannulation and collection of blood samples at regularly timed intervals. However, this approach is untenable for clinical routine. As a result, clinical brain studies currently apply a semi-quantitative approach based on SUVs, which lacks an absolute physiological scale. In the past, extraction of an IDIF for PET brain studies proved to be a challenge, given the presence of partial volume effects (PVEs)6,7 and involuntary subject motion.6,8
Various methodological approaches have been proposed to calculate an accurate IDIF, thereby accounting for the factors above. These methods can be classified into three categories: (1) PET-only,9–19 (2) standalone PET and MRI,20–25 and (3) combined PET/MRI.26–29 Most of the PET-only methods mandate the measurement of venous samples from a second venous line to avoid errors in IDIF originating from spill-in and spill-out effects occurring at late time points.6,30 On the other hand, standalone PET- and MR-based methods are subject to logistical challenges and a sheer amount of post-processing required. A fully integrated PET/MRI addresses the main challenges for the determination of an accurate IDIF in a clinical setting, such as delineation of the internal carotid arteries20,26,27 and motion correction of dynamic PET frames using MR navigators.31
Here, we introduce an MR-driven approach that allows for an automated calculation of IDIF using the synergistic information from an integrated PET/MRI. The calculated IDIF then allows for the non-invasive determination of brain metabolic rate of glucose (CMRGlc). Specifically, we employ an automated vessel segmentation algorithm and a PVC method, which accounts for the radial and circumferential variability of the PET tracer distribution around the vessel. Our objective was to establish an automated workflow for the absolute quantification of [18F]FDG-PET/MRI brain data for clinical routine that is validated against the reference standard (AIF).
Materials and methods
Ten healthy adults ((27 ± 7) years, (70 ± 10) kg, 5 males and 5 females) were included in this study. The study was approved by the Ethics Committee of the Medical University of Vienna (EK1960/2014) and was performed in accordance with the Declaration of Helsinki (1964), including current revisions. Subjects were confirmed to be healthy based on medical history, physical examinations and vital signs. Written informed consent was obtained from all subjects prior to the examinations.
Imaging protocol
All subjects underwent test–retest PET/MRI brain examinations on a fully integrated PET/MRI system (Siemens Biograph mMR). All examinations were performed in the afternoon, with subjects at rest with their eyes open. Moreover, no specific task was performed by the subject. The average time difference between the two examinations was (17 ± 44) days. Prior to each scan, a venous line was established for the injection of the [18F]FDG tracer and an arterial line was established in the contralateral arm for blood sampling. A head and neck coil was used in order to ensure a high signal-to-noise ratio of the MR imaging. Foam cushions were placed inside the MR head coil to minimize involuntary head movement.
The integrated PET/MR imaging protocol included a 3D time-of-flight MR angiography (TOF-MRA) sequence to image the internal carotid arteries with the following parameters: 0.5 × 0.5 × 1 mm3 voxel size, TE = 3.6 ms, TR = 21 ms, 25° flip angle, 228 × 384 matrix, 220 slices and an acquisition time of 6 min. The field-of-view of the TOF-MRA extended from the circle of Willis (CoW) to 10 slices below the branching point of the internal and external carotid arteries (ECAs). Subsequently, subjects were injected with [18F]FDG ((352 ± 66) MBq, 5.18 MBq/kg) intravenously as a slow bolus over 40 s. At the start of the injection, a 60-min list mode PET data acquisition was initiated and blood samples (1mL each) were obtained from the radial artery using a varying time schedule (24 × 5 s, 1 × 60 s, 1 × 120 s, 1 × 300 s, 1 × 600 s, 2 × 1200 s post injection) (Supplementary Figure 1). The blood sampling was done manually using vacuum test tubes via an arterial cannula fitted with an adapter. Prior to every arterial sample, the line was flushed with 5 mL sodium chloride solution to prevent clotting and sampling stagnant blood. To avoid dilution of the actual sample, a 1 mL of discard was drawn followed by the sampling of arterial blood sample. Whole-blood radioactivity concentrations were measured using a gamma counter (PerkinElmer, 2480 Automatic Gamma counter, Wizard23). To obtain the AIF, whole blood samples were centrifuged to separate the plasma component, followed by the measurement of radioactivity in the plasma. The measured whole blood and plasma tracer concentrations were used to calculate the dynamic plasma-to-blood ratio for each subject. This ratio was then used to convert the blood-IDIF to plasma-IDIF. Arterial sample concentrations were measured at instantaneous time-points, whereas the IDIF concentrations were measured at PET mid-scan time-points. In order to match the instantaneous blood sampling times with the PET mid-scan time, the AIF was interpolated into discrete time segments of 1 s length using a Piecewise Cubic Hermite Interpolating Polynomial.
To monitor head motion, MR navigators were used throughout the dynamic PET acquisition using the following parameters: 2D EPI 3.0 × 3.0 × 3.0 mm3 voxels, 64 × 64 matrix, 36 slices, TE 30 ms, TR 3000 ms. Navigator volumes were obtained at fixed time intervals: 0, 2.5, 5, 7.5, 10, 14, 17, 21, 26, 33, 38, 42, 44 and 50.5 min post injection. Following the PET/MRI examination, the subjects were moved to a PET/CT system (Biograph TruPoint64, Siemens Healthcare, USA), where a low-dose CT scan (120 kVp, 50 mAs) of the brain was acquired solely for the purpose of attenuation correction (AC).32,33
The PET list mode data were re-binned into a dynamic frame sequence (24 × 5 s, 1 × 60 s, 1 × 120 s, 1 × 300 s, 1 × 600 s, 2 × 1200 s post injection) and each PET frame was reconstructed (Siemens e7 tools) into a 344 × 344 × 127 matrix (voxel size 2.08 × 2.08 × 2.03 mm3) using the ordinary Poisson ordered subset expectation maximization (OP-OSEM) 3D algorithm (3 iterations, 21 subsets, 2 mm Gaussian filter). Scatter correction along with a CT-AC was applied to all PET data.34 To perform the CT-AC, the low-dose CT scan was co-registered to the T1-MPRAGE sequence (RS-1, Supplementary Figure 1) and a bilinear scaling31 was applied to convert the low-dose CT image to a CT-AC map.
Automated ICA segmentation
Data from the 3D TOF-MRA sequence were used to extract the ICA. To obtain the IDIF, the petrous region of the ICA was chosen as the volume-of-interest (VOI). Image segmentation was performed in three steps:
Extraction of the carotid vasculature
A combination of histogram-based quantile thresholding35,36 and automatic seeded region growing was used to extract the entire carotid vasculature (CV) (Supplementary Figure 2). The intensity corresponding to the 0.987 quantile of the gray value distribution was chosen as the optimum threshold value following an iterative optimization procedure using the TOF-MRA datasets. To remove residual contributions of the peripheral fat, an automated seed region growing was performed with a connectedness constraint, yielding only the CV (Supplementary Figure 2).
Extraction of the ICA
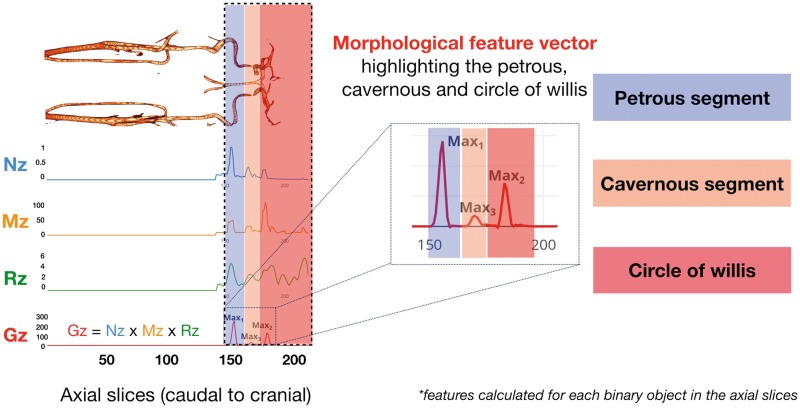
The obtained CV consists of the ICA, ECAs and the CoW (Supplementary Figure 2). The ICA was obtained by removing the CoW first, followed by the pruning of ECA. The CoW is superior to the cavernous segment and can be removed once the cavernous segment in the vasculature is localized. This was determined based on a morphological feature vector (Gz), which characterizes the shape of the vascular tree (Figure 1). This feature curve was calculated only for the intracranial segment of the TOF-MRA volume as only segmentation of the petrous part of the ICA was of interest. The morphological feature curve incorporates features, such as mean intensity, major axis length, ellipticity as well as the orientation of vessel segments present in the transaxial slices (Figure 1). The axial slice containing the structure with an orientation of 90° to the vessel denotes the location of the cavernous segment of the ICA, thus, allowing for the removal of the CoW. Moreover, the ICA and ECA arise from a common carotid artery, and therefore the localization of the branching point is key to the pruning of the smaller vessel (ECA), thus, leaving the ICA as the only remaining structure.
Figure 1.
Segmentation of the carotid vasculature (CV) features such as normalized mean intensity (Nz), major axis length (Mz) and ratio of major to minor axis length (Rz) were calculated and combined to produce a morphological feature vector (Gz), to highlight elliptical structures. The global maxima, Max1 of Gz (blue), corresponds to the petrous segment, while Max2 and Max3 correspond to the floor of circle of Willis (red) and cavernous (orange).
Segmentation of the petrous region of the ICA
This segmentation was done based on the classification of ICA by Gibo et al.37 The feature curve in Figure 1 highlights elliptical structures in the image as prominent peaks. Accordingly, the petrous segment was identified as the structure with the highest peak. These steps resulted in a petrous mask (Pmask), which was later used to extract the IDIF from the dynamic PET frames.
PET motion correction and alignment with TOF-MRA
To achieve the spatial correspondence between the PET frames and the MR-derived petrous masks, a post-reconstruction motion correction was employed. MR navigators interleaved between MR clinical sequences were used to monitor subject head motion (Supplementary Figure 1). The MR navigator acquired at the start of the PET acquisition (Nav-0, t = 0) was considered as the reference volume and all subsequent navigators were rigidly co-registered to Nav-0 (SPM 12, Wellcome Trust Center for Neuroimaging, UCL) to obtain the motion vectors. The resulting motion profile consisted of six parameters (three translations and three rotations; Figure 2). In early PET frames with low tracer activity, MR based motion correction was implemented. Temporal matching of MR navigators with PET frames was achieved using the least time difference between the PET frame mid-scan times and the navigator acquisition times. (Figure 3(a)). Eventually, transformation matrices obtained from the early MR navigators (<10 min) with respect to the reference MR navigator will be applied to Pmask, thus, generating multiple resliced Pmask VOIs.
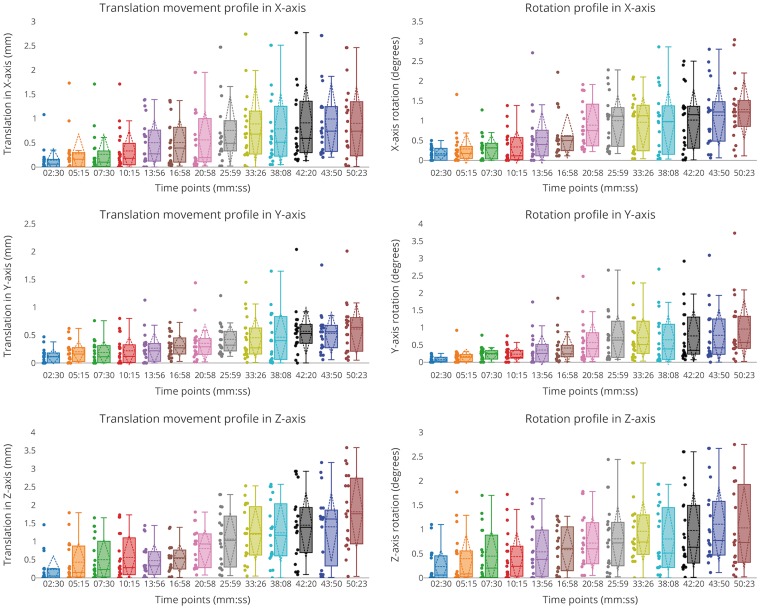
Figure 2.
Translation (left) and rotation (right) profiles in each axis with respect to examination time (Supplementary Figure 1) for 20 datasets. Subject motion (translation and rotation) increased with time and subject translation was prominent in the z-axis. It is seen that the motion was minimal during the first 10 min of the scan (maximum translation < 2 mm, average rotation < 1 and maximum rotation < 2°).
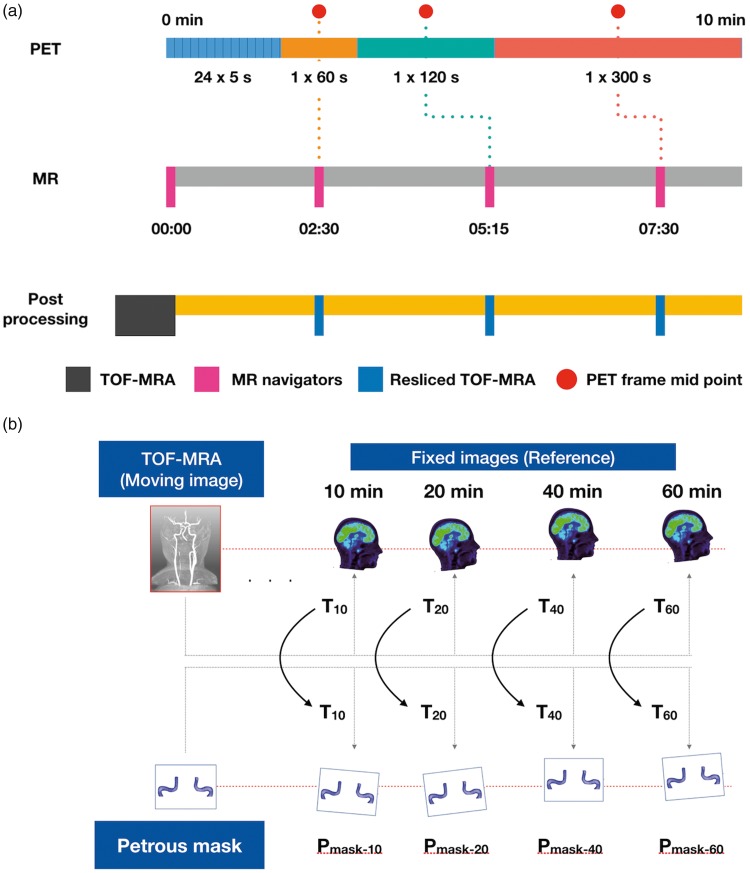
Figure 3.
(a) Use of MR navigator-based motion correction, in early PET frames (<10 min). Each MR navigator is assigned to a PET frame based on the time difference between the PET frame midpoint (PFM, red) and MR navigator's acquisition time (AT). Lower the time difference between PFM and AT, higher the probability of assigning the MR navigator to the respecting PET frame. The MR navigator acquired at start of the PET acquisition (time = 00:00) is considered as the reference volume (RV) and all other MR navigators (02:30, 05:15, 07:30) are registered to RV. The transformation matrices obtained from the process are transferred to the 3D TOF-MRA or Pmask, to achieve spatial correspondence to the PET frames. (b)Motion vectors (Tn) were obtained by co-registering the TOF-MRA with the late dynamic PET frames (>10 min) and then applied to the petrous mask (Pmask-n) to achieve spatial correspondence with the late dynamic PET frames.
Subsequently, spatial correspondence between the petrous mask and the PET data (>10 min) was achieved in a multi-step process using SPM 12 (Figure 3(b)). First, transformation matrices (T10–60) were derived from rigid inter-modality co-registration (Normalized mutual information) of the TOF-MRA data and the late PET frames (10 min, 20 min, 40 min and 60 min). Second, these matrices (T10-60) were applied to the petrous mask (Pmask). The alignment was confirmed visually using AMIDE 1.0.5 (AMIDE's a Medical Image Data Examiner38) without the need for further post-processing.
As a part of quality control, MR navigators acquired after 10 min were used to check for intra-frame motion within the individual late PET image volumes (1 × 10 min, 2 × 20 min frames). Here, motion vectors never exceeded 1 mm in any direction (Supplementary Table 1), thus, indicating no prominent intra-frame motion.
Partial volume correction
Correction of PVE was performed using a modified version of the Mueller-Gaertner method (MGM),39 with the extension of accounting for radial and circumferential variability of the activity in the petrous segment's background. Calculation of the true ICA tracer concentration entails first the removal of variable background activity that spilled into the target region (spill-in correction) followed by correction of activity loss in the target region (spill-out correction) caused by the convolution of true activity distribution by the system's PSF. This procedure mandates the knowledge of both the PSF and the nature of the background activity distribution (Supplementary Figure 3).
In order to determine the PSF corresponding to the applied acquisition protocol, a 1-mL syringe (diameter 4.7 mm, cylinder length 57 mm) was filled with about 75 MBq of [18F]FDG and placed axially in the system in approximately the same off-center position (∼50 mm) as the presumed position of the ICA. Data were acquired and reconstructed using the same protocol as used in the subjects. Subsequently, a modeled profile (using a step function with a height corresponding to the tracer concentration in the syringe at the start of the PET scans) was convolved with a 3D Gaussian PSF and compared to the measured trans-axial profile. The FWHM of the PSF was incremented in 0.5 mm steps. The convolved model function that best approximated the measured profile defined the FWHM of the PSF corresponding with our protocol. The FWHM of the PSF for the PET/MR system in use (Biograph mMR) was found to be (6.0 ± 0.4) mm.
To obtain an initial estimate of background activity, the spill-out zone (Spout) was defined by convolving Pmaski (i – indicates the PET frame, with ‘i’ varying from 1 to 30) with the derived PSF of the PET system (Figure 4(a)). An initial background mantel (Bmaski) was defined 10 mm radially from the edges of the SPout (Figure 4(a)). To account for circumferential differences in background activity (Figure 4(b)), the tracer concentration in the ring-like structure was segmented into 20 background regions (Bmaskij) by applying Otsu thresholding40 and scaled with the corresponding median activity (Bij) sampled from the PET frame. This allowed for the calculation of an initial estimate of ICAi using equation(2), assuming that the area between each Bmaskij and the ICA wall contains a constant tracer concentration equal to the Bij values determined at the periphery.
| (1) |
| (2) |
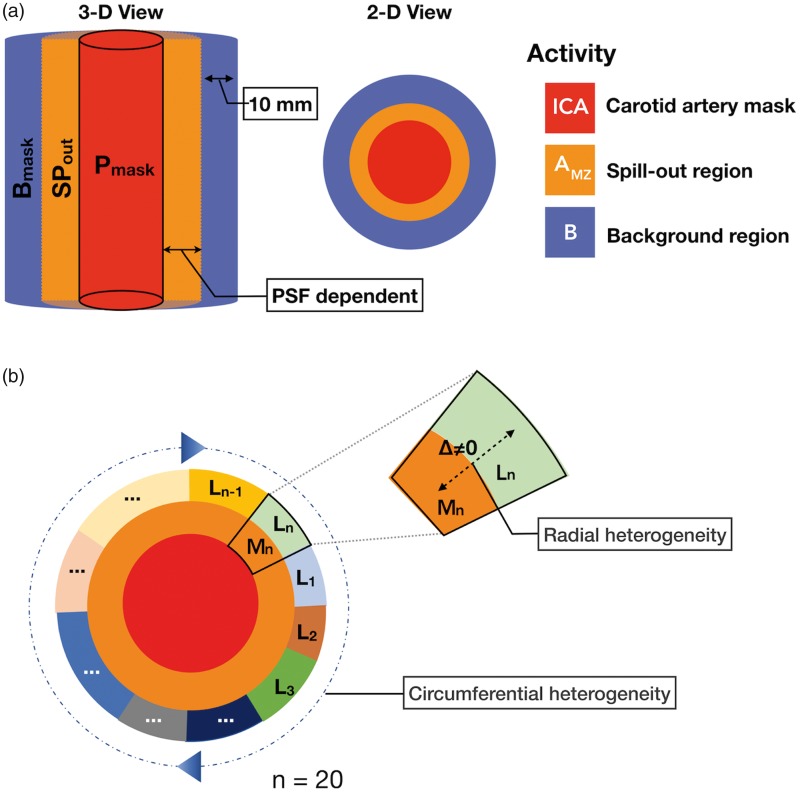
Figure 4.
(a)Spill-in correction: automatic delineation of a spill-out region (SPout, orange), defined by convolving the petrous mask (Pmask, red) with the PSF (FWHM-6.00 mm), and a background region (purple) of 10 mm (∼ 5 voxels) thickness defined from the edges of the spill-out region. (b) The circumferential heterogeneity of petrous segment (red) is graphically represented by labels (L1−n) with different colors, where n = 20. The radial heterogeneity is depicted using the sector-n, where the activity, Mn in the spill-out zone/mixed-zone (orange) is not the same as the activity, Ln in the background region (green).
Radial variability in the area between Bmaskij and ICA wall was addressed as follows. Initially, for each of the Bmaskij regions, a mixed zone (MZij) was defined, which includes the area between the ICA (Pmask) and Bmaskij (Figure 4(b)). The true tracer concentration in MZij (denoted AMZij) was then modelled as
| (3) |
where PETMZij is the observed tracer concentration in MZij and SPin, the spill-in factor. Subsequently, the set of background regions was tested for radial homogeneity by calculating the differences between AMZij and Bij. If AMZij was found to be within 3% of Bij (equivalent to | Bij – AMZij | < 0.03 Bj), it was assumed that radial uniformity was met for that particular background segment. Otherwise, a new estimate of ICA was derived iteratively until equation (2) was satisfied:
| (4) |
| (5) |
where αij is the observed spill-out contribution in the mixed zone MZij originating from the true ICA tracer concentration.
Here, the difference between the observed (αij) and modeled (ICA × SPout) ICA spill-out contribution in MZij was minimized for the whole set of mixed zones (MZij, j = 1,…20). The resulting ICA value was adjusted for maximum agreement of radial profiles in the mixed zone, thus, accounting for radial inhomogeneity. This procedure was repeated for all PET frames, to generate a partial volume corrected IDIF. Supplementary Figure 4 summarizes the radial and circumferential variability in a real case scenario.
Post-processing of the IDIF
Following MoCo and PVC, the IDIF was interpolated with a step length of 1 s to match the blood sampling times and was corrected for multiple effects. First, a plasma IDIF was derived based on the individual plasma-to-blood ratios obtained from sampled arterial blood of the study subjects. Second, the IDIF was scaled using the cross-calibration factor between the PET/MR and the on-site gamma counter. Third, the delay between the AIF and the IDIF was corrected by shifting the IDIF curve to match the arrival times of the AIF. Finally, due to the difference in sampling location (ICA for IDIF and radial arteries for AIF), a mono-exponential dispersion function with a tau value of 5 s41,42 was convolved with the IDIF to mimic the dispersion effects. Since the AIF is considered as the reference standard, all the corrections were applied to the IDIF for an unbiased comparison with the AIF.
Assessment of IDIF-derived metabolic rate of glucose
To assess agreement between the IDIF and AIF, the area-under-the-curve (AUC) derived from both curves was used. Specifically, disparities between the AUC measurements were assessed based on the percentage AUC difference (%DiffAUC) calculated as
| (6) |
Absolute percentage AUC differences were calculated across all studies as well as pair-wise between test and re-test acquisitions.
Finally, cerebral metabolic rate of glucose (CMRGlc) maps were calculated (PMOD 3.802, PMOD Technologies, Zurich, Switzerland) using the standard rate constant approach43 (lumped constant, LC = 0.6561). Absolute percentage differences between regional CMRGlc values for whole brain and in six pre-selected large regions of the brain (cerebellum, brainstem, anterior cingulate cortex, thalamus, corpus callosum and superior frontal cortex) from the Hammersmith atlas were determined using AIF and IDIF. All comparisons were performed in a non-parametric manner, using the median difference, the interquartile range and the extremes. In order to determine whether regions are affected differentially using the IDIF, a rank-sum test was performed among all regions.
Test–retest variability for both the IFs was assessed by calculating the absolute mean % difference, after normalizing the IFs to the respective injected dose and body weight (SUV). Similarly, test–retest variability was assessed by calculating the absolute median % difference for the CMRGlc values (whole brain and four random regions – insula, caudate, mid-frontal gyrus and superior frontal gyrus) obtained from both IFs
Results
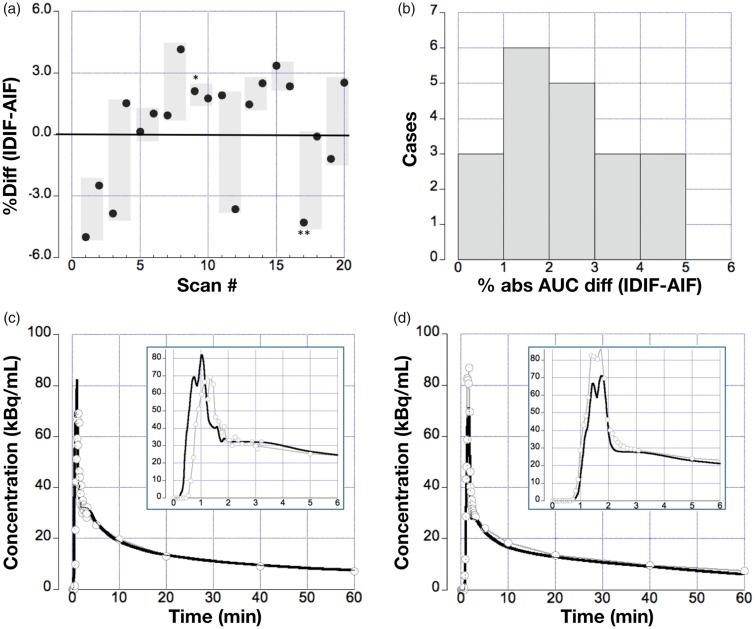
Assessment of the percentage difference between all AUCs using the IDIF and AIF yielded values within ±5% (Figure 5(a)), with a median absolute difference of 2.5% (interquartile range (IQR) = 2%–4%). Figure 5(b) shows the histogram of the absolute percent differences, indicating that 14/20 (70%) of the IDIF curves were found to be within 3% of the reference standard (AIF). The remaining 30% displayed a somewhat larger AUC difference in the range of 3%–5%. Moreover, 2/3 of all percent differences were determined to be positive, indicating a trend towards a possible overestimation of the AUC using the IDIF. The representative time-activity curves emphasizing the relationship between arterial blood samples and the IDIF are shown for a case with AUC difference <3% (Figure 5(c)) and for a case with AUC difference ∼4% (Figure 5(d)).
Table 1.
Demographics of the 10 healthy controls.
| Subject ID | Gender | Age (y) | Weight (kg) | Date |
FDG Activity (MBq) |
Blood glucose (mmol/L) |
|||
|---|---|---|---|---|---|---|---|---|---|
| Test | Retest | Test | Retest | Test | Retest | ||||
| HC002 | M | 23 | 75 | 06-06-2016 | 14-07-2016 | 217 | 371 | 4.55 | 5.72 |
| HC003 | F | 24 | 55 | 08-06-2016 | 09-11-2016 | 229 | 288 | 4.33 | 4.73 |
| HC004 | M | 28 | 74 | 11-07-2016 | 26-09-2016 | 384 | 367 | 4.88 | 5.49 |
| HC006 | F | 22 | 69 | 12-09-2016 | 07-11-2016 | 365 | 355 | 5.11 | 5.22 |
| HC007 | F | 22 | 56 | 14-09-2016 | 28-09-2016 | 292 | 292 | 5.38 | 5.61 |
| HC009 | F | 42 | 63 | 23-11-2016 | 05-12-2016 | 330 | 324 | 5.11 | 5.83 |
| HC010 | F | 20 | 65 | 07-12-2016 | 19-12-2016 | 337 | 338 | 5.11 | 5.55 |
| HC012 | M | 36 | 92 | 23-01-2017 | 13-02-2017 | 493 | 476 | 6.32 | 6.05 |
| HC013 | M | 24 | 70 | 15-02-2017 | 27-02-2017 | 350 | 363 | 5.05 | 5.16 |
| HC014 | M | 25 | 80 | 27-03-2017 | 29-03-2017 | 422 | 364 | 4.61 | 5.88 |
Figure 5.
(a) The panel displays the %-differences for all 20 scans (points); the shaded areas depict the difference range for test/retest scans obtained in the same subject. IDIF curves obtained from subject #5 (HC004 test, denoted as *) and #9 (HC007 test, denoted as **) are displayed in (c) and (d). Percent (%) differences between AUCs obtained from AIF (gray with circles) and IDIF (black) were calculated (b). Histogram displaying the distribution of absolute % AUC differences, 70% of the AUCs differ by <3% with the remaining curves differing by <5%. (c) IDIF obtained in subject #5: (HC004 test Table 1) with a good agreement between IDIF and AIF. (d) Example IDIF obtained from subject #9 (HC007 test) with a limited (tail area) agreement between IDIF and AIF.
Supplementary Figure 5 depicts the range of the AUCs for AIF (46.2 ± 7.6), IDIF with PVC (46.4 ± 8.1) and IDIF without PVC (35.7 ± 7). Supplementary Figure 6 shows the test–retest variability in the IFs, both AIF and IDIF showed similar variability with an absolute mean % difference (test–retest) of 9 ± 8% and 9 ± 7%.
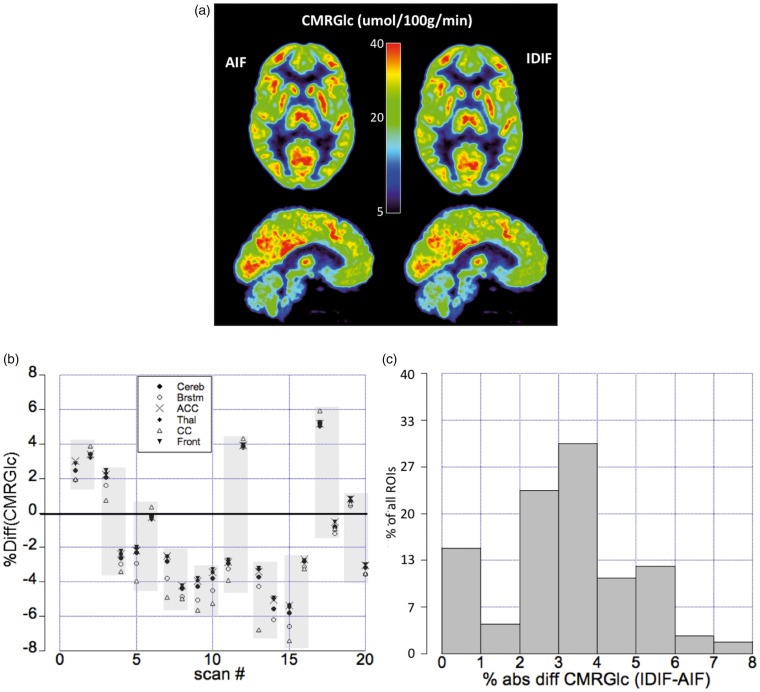
Figure 6(a) shows an example of a parametric image based on AIF and IDIF for a subject (HC014 retest) with 3% overestimation by IDIF. The whole brain CMRGlc values derived from AIF was found to be (mean ± SD = 32 ± 6, median ± IQR = 31 ± 9) umol/100 g/min and for IDIF (mean ± SD = 32 ± 6, median ± IQR = 29 ± 9) umol/100 g/min (Supplementary Figure 10). Absolute median % difference between CMRGlc values obtained using the AIF and IDIF for the whole brain was found to be 3.9%, with an interquartile range of 2.4%–5.4%. And for the six regions, the absolute mean % difference was determined as 3.2%, with an interquartile range of 2.4%–4.3% and a maximum difference of <10%. Figure 6(b) shows the %-differences with respect to CMRGlc values derived using the two IFs. Comparison of Figures 5(c) and 6(b) indicates an inverse relationship between the percentage difference in AUCs and CMRGlc.
Figure 6.
(a) Transaxial (top row) and sagittal (bottom row) images representing CMRGlc derived using the AIF (left) and the IDIF (right) for a subject with a 3% AUC overestimation by IDIF. Images show excellent agreement in absolute CMRGlc values. (b)Relative %-differences for six reference regions (cerebellum, brainstem, anterior cingulate cortex, thalamus, corpus callosum and superior frontal cortex) in all 20 scans. The shaded areas depict test/retest scans obtained in the same subject. (c)Histogram depicting the % absolute differences in CMRGlc values derived using the IDIF and the AIF. The graph shows a maximum for difference values in the range of 2–4%, with 85% of all differences laying within 5%.
Figure 6(c) shows the corresponding histogram, indicating that the most frequently observed differences are in the range of 2%–4%, with 85% of all differences being <5%. In all six-preselected brain regions, the CMRGlc values obtained from AIF and IDIF showed no significant difference.
The test–retest variability between AIF based CMRGlc and IDIF based CMRGlc is shown in Supplementary Figure 7. For both the IFs, CMRGlc obtained from the four regions during the retest were higher when compared to test, along with a reduction in variance during the retest. In general, retest AIF CMRGlc values were 14% higher (14% higher for insula, mid-frontal gyrus, superior frontal gyrus and 22 % higher for caudate) when compared to the test values, indicating a high intra-variability. A similar tendency was seen in retest IDIF CMRGlc values as well, with a 17% increase (12% higher for insula, 18% for caudate, 17% for mid-frontal gyrus and 16% for superior frontal gyrus) when compared to test values.
The absolute % relative difference between test and retest whole-brain CMRGlc values (Supplementary Figure 11) was found to be 14 ± 8% for AIF (with median ± IQR = 15 ± 16%) and 15 ± 10% for IDIF (with median ± IQR = 14 ± 17%).
Discussion
We present a clinically viable automated MR-driven approach to extracting an IDIF for the non-invasive determination of CMRGlc images using an integrated [18F]FDG-PET/MRI protocol. The approach is based on the accurate and automated extraction of an IDIF based on the combined acquisition of PET and MR data. It was validated against the reference standard of AIF. In the context of the automated IDIF calculation, a multi-factorial partial volume correction is required. Therefore, the directional and radial variability of the background region (Figure 4(b)) must be considered for an accurate correction of the spillover effects. This procedure also mandates the knowledge of the system's PSF for a given tracer and image reconstruction protocol. Any PVC must be preceded by motion correction. Our study shows that the above requirements can be effectively addressed by employing an integrated PET/MRI protocol followed by an automated post-processing pipeline.
Traditionally IDIF has been extracted from two different segments of the ICA: (1) the petrous region24–27,29,44–46 or (2) the cervical region.20,47 We believe that the petrous region is preferable, as it represents a rigid structure due to its placement inside the petrous canal. In contrast, the cervical segment is more elastic and prone to deformation. Since rigid transformations were used to achieve spatial correspondence between the TOF-MRA and the PET frames, the petrous region was chosen for derivation of the IDIF. The aforementioned segmentation algorithm was successful in defining the ICA irrespective of the subject-specific cerebral vasculature (Supplementary Figure 1). Moreover, due to its modular nature, the proposed algorithm can be easily modified for other FOV acquisitions (cervical and cavernous segments). The optimum quantile value of 0.987 may change based on the quality of TOF-MRA volumes. Decreasing the quantile value will result in higher inclusion of peripheral fat, whereas an increase will result in eroded segmentation of the carotid arteries. Care should be taken in choosing an optimum quantile value as the pre-segmentation of the carotid arteries is dependent on the chosen quantile value.
The ICA has a variable background both in radial and circumferential direction. Circumferential variability is due to the presence of cortical structures with different amount of tracer accumulation around the target region, whereas radial variability is related to the sampling of the background region (Figure 4(a) and (b)). Due to the spillover of ICA activity into the neighboring background tissue, an estimate of the circumferentially dependent background tracer concentration must be obtained at a distance from the ICA where the ICA spillover can be ignored. In most implementations, this is achieved by sampling background tracer concentration at a distance where ICA tracer concentration contributes <3% to the local tracer concentration. Of note, this approach cannot account for radial changes, as the tracer concentration sampled in such a way might not be representative for the background concentration directly adjacent to the vessel wall (Supplementary Figure 4).
The importance to account for radial and circumferential variability has not been fully appreciated in previous region-based PVC methods. Rousset et al.48 derived a closed solution for PVC using a geometric transfer matrix, which relates a vector of observed activities to a vector of true (PVC-corrected) activities. This linear equation system can be solved for the true activities by matrix inversion; however, the accuracy of such a solution strongly depends on the degree of ill-conditioning of the transfer matrix and, in addition to a large computational effort, might lead to unstable estimates of the corrected activities.
Obviously, the complexity of such a correction is dependent on the number of tissues believed to have different functional properties, i.e. the number and shape of homogenous regions that contribute to the PVE in each image voxel. Various investigators proposed the definition of such regions based on a combination of information from a high-resolution anatomical (e.g. MRI) and a functional (PET) image using wavelet decomposition.49,50 Our approach is similar to these methods in that it uses functionally homogenous background regions to correct for PVEs at one specific target region (ICA). Furthermore, it is accurate and computationally efficient for determining an IDIF by avoiding complex mathematical overhead by iteratively adjusting the activity in the target region so that it becomes consistent with the observed activity in the mixed zone. Although our approach is less ambitious than the general solution presented by Roussett et al., we believe that it is fitting for determining an IDIF that can be readily implemented in clinical applications.
The proposed PVC method requires the knowledge of PSF of the PET system. Since PSF varies with factors such as image reconstruction parameters and the type of tracer, a dedicated PSF measurement for the specific PET system and protocol is recommended.
Since all corrections are applied to a relatively small region, determination of an IDIF is highly sensitive to local misregistration arising from involuntary patient motion (Supplementary Figure 8). In a combined PET/MR system, MR navigator sequences can be used to derive high-temporal-resolution motion estimates along with the PET emission scan.31 The resulting motion vectors can be then applied to the VOI to account for motion between frames, therefore, avoiding PET image resampling. In the current protocol, MR navigators were acquired with a reasonably fast temporal sampling rate (∼2 min temporal separation between navigator), during the early phase of the scan (<10 min), thereby offering the possibility to perform motion correction using the motion fields from the MR navigators. However, due to the constraints of clinical sequences during the subsequent 50 min, MR navigators were acquired with low-temporal sampling rate (∼4–5 min temporal separation between every navigator). Therefore, a PET-MRI NMI-based co-registration was preferred, instead of using the motion fields from the late navigators (>10 min). Since MR navigators are acquired in a relatively short time duration (∼5 s), there is an increased probability that the motion vectors captured by these navigators are not representative of the average motion occurring during a 5-min time frame. While post-reconstruction motion correction approaches yield satisfactory results, simultaneously acquired PET and MR data offer the possibility of an “on-the-fly” motion correction, in which the motion vector is used to rebin the PET coincidence data, so that subject motion is addressed on a very basic line-of-response (LOR) level. Several pilot approaches have been proposed to incorporate on-the-fly motion correction schemes,51 yet implementation of these methods proved to be challenging due to the necessity of recalculating both normalization factors and random estimates.
Apart from comparing the CMRGlc images from the AIF and IDIF to determine the accuracy of the IDIF methodology, it is informative to compare the IFs by using metrics such as AUC. In the context of the standard rate constant approach, the AUC of the IF represents the total amount of tracer that is available to the tissue, while the metabolic rate encodes the relationship between the amount of tracer available for uptake and the actual tissue uptake. Therefore, demonstration of similarity by comparing the AUCs of AIF and IDIF provides a reasonable quality check to assess the accurateness of the method.
Analysis of AIF-derived AUC differences obtained from test/retest scans showed no significant correlation between the AUC differences and the length of time separating the two acquisitions (R2 = 0.03). These results suggest that time effects are most likely not responsible for the observed differences in IDIF-derived AUCs determined for the test/retest studies. A high test-retest variability ( < 20%) was seen in regional CMRGlc obtained from both the IFs (Supplementary Figure 7). A regional analysis of CMRGlc was chosen, as studies in the past have indicated the possibility of different brain regions exhibiting different amount of metabolic variability.52,53 However, it has been hypothesized that this relatively high amount of regional variability is due to changes in the physiological state of the subject across time.54–57
A current limitation of our study in view of a fully automation of the workflow is the need for a separate low-dose CT scan for CT-AC, which, for brain research, still is assumed a “silver standard.”34 Various accurate brain MR-based attenuation correction (MR-AC) methods58 have been proposed in the recent years and there is now guarded optimism in the field that, at least for the brain, MR-AC will soon be clinically feasible.32,33 However, the impact of these methods with respect to the derivation of an accurate IDIF still needs to be investigated. In our current study, the observed motion was minimal (maximum translation < 2.0 mm and maximum rotation < 2.0°, Figure 2) for all subjects during the first 10 min of the study. Therefore, no motion correction was performed for the early PET frames (<10 min). Though, a practical MR navigator-based motion correction approach31 was implemented (Figure 3(a)) to handle prominent motion for early PET frames (>2 mm), the performance of the method still needs to be evaluated. In our current implementation, stationary attenuation maps were used to perform AC, as motion magnitudes were minimal. However, such an approach might not be optimal in a clinical scenario where motion can be prominent. Since, CT-AC map misalignments can affect the quantification of the IDIF, the use of motion corrected CT-AC maps to reconstruct clinical PET data is advisable.
Finally, the calculation of CMRGlc was based on the standard rate constant approach since this study was performed with healthy volunteers. Though the use of standard rate constants might be less accurate than the application of kinetic modeling in case of pathology, the simplified approach might be better suited for clinical routine. Furthermore, when adopting our approach for the clinic, the obtained blood IDIF needs to be converted to plasma IDIF by using the hematocrit measured from the venous blood. However, it has been shown that the hematocrit values obtained from venous blood are ∼3% higher than those obtained from arterial blood59 and this difference must be considered during the conversion. In our study, we used the individual dynamic plasma to whole blood ratio to derive the plasma-IDIF. The mean (±SD) of this ratio derived from our study group (n = 20) was found to be 1.06 ± 0.01 (Supplementary Figure 9). Therefore, in future [18]FDG studies without arterial blood samples, we intend to apply a scaling factor of 1.06 to convert the blood-IDIF to plasma-IDIF.
As discussed earlier, most PET-based methods9–19 require blood samples for scaling the IDIF, while the stand-alone PET/CT and MR-based methods20–22 suffer logistic and co-registration issues. Integrated PET/MR-based IDIF methods,27,60 apart from providing logistic advantage, have shown to be promising in addressing the challenges associated with the calculation of IDIF. Our method extends the previous PET/MR approaches, by introducing an FOV independent robust petrous segmentation algorithm, MR navigator-based motion monitoring and a PVC algorithm, which accounts for circumferential and radial homogeneity for spill-in correction.
Conclusion
We have developed a computational framework to automatically calculate an IDIF for the absolute quantification of [18F]FDG PET brain data using a fully integrated PET/MRI system. Calculations of the IDIF and the CMRGlc parameters have been shown to correspond well to the values derived from the invasive AIF, thus, attesting to the concept of non-invasive absolute quantification of [18F]FDG PET imaging of the brain in combined PET/MRI studies.
Supplemental Material
Supplemental material for Towards quantitative [18F]FDG-PET/MRI of the brain: Automated MR-driven calculation of an image-derived input function for the non-invasive determination of cerebral glucose metabolic rates by Lalith KS Sundar, Otto Muzik, Lucas Rischka, Andreas Hahn, Ivo Rausch, Rupert Lanzenberger, Marius Hienert, Eva-Maria Klebermass, Frank-Günther Füchsel, Marcus Hacker, Magdalena Pilz, Ekaterina Pataraia, Tatjana Traub-Weidinger and Thomas Beyer in Journal of Cerebral Blood Flow & Metabolism
Acknowledgements
We would like to thank Johannes Jungwirth for recruitment of the study subjects, Daniela Senn and Julia Kesselbacher for providing continuous support in scanning the subjects. We express our gratitude to Markus Diemling and Martin Bauer for providing us technical assistance during the course of the study. Finally, we would like to thank Alexander Hammers, for sharing his experience with CMRGlc test-retest variability.
Funding
The author(s) disclosed receipt of the following financial support for the research, authorship, and/or publication of this article: This work was supported by the Austrian Science Foundation KLI482-B31. Lucas Rischka is recipient of a DOC Fellowship of the Austrian Academy of Sciences at the Department of Psychiatry and Psychotherapy, Medical University of Vienna.
Declaration of conflicting interests
The author(s) declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.
Authors' contributions
LK and OM contributed to analysis and interpretation of data along with drafting, revising and final approval of the manuscript. TTW, EP and MP contributed to data acquisition, followed by revision and approval of the manuscript. LR, AH, MH1, IR, RL, FGF and EMK made substantial contribution with data analysis, along with revision and approval of the manuscript. MH2 contributed with revising and approving the manuscript. TB contributed with study concept, design and revised the manuscript critically and approved the final version.
Supplementary material
Supplementary material for this paper can be found at the journal website: http://journals.sagepub.com/home/jcb
References
- 1.Wahl RL, Quint LE, Cieslak RD, et al. ‘Anatometabolic’ tumor imaging: fusion of FDG PET with CT or MRI to localize foci of increased activity. J Nucl Med 1993; 34: 1190–1197. [PubMed] [Google Scholar]
- 2.Czernin J, Allen-Auerbach M, Nathanson D, et al. PET/CT in oncology: current status and perspectives. Curr Radiol Rep 2013; 1: 177–190. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Drzezga A, Barthel H, Minoshima S, et al. Potential clinical applications of PET/MR imaging in neurodegenerative diseases. J Nucl Med 2014; 55: 47S–55S. [DOI] [PubMed] [Google Scholar]
- 4.Lammertsma AA. Forward to the past: the case for quantitative PET imaging. J Nucl Med 2017; 58: 1019–1024. [DOI] [PubMed] [Google Scholar]
- 5.Keyes JW. SUV: standard uptake or silly useless value?. J Nucl Med 1995; 36: 1836–1839. [PubMed] [Google Scholar]
- 6.Zanotti-Fregonara P, Chen K, Liow J-S, et al. Image-derived input function for brain PET studies: many challenges and few opportunities. J Cereb Blood Flow Metab 2011; 31: 1986–1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Krejza J, Arkuszewski M, Kasner SE, et al. Carotid artery diameter in men and women and the relation to body and neck size. Stroke 2006; 37: 1103–1105. [DOI] [PubMed] [Google Scholar]
- 8.Zanotti-Fregonara P, Liow J-S, Comtat C, et al. Image-derived input function in PET brain studies. Nucl Med Commun 2012; 33: 982–989. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Mourik JEM, Lubberink M, Klumpers UMH, et al. Partial volume corrected image derived input functions for dynamic PET brain studies: methodology and validation for [11C]flumazenil. Neuroimage 2008; 39: 1041–1050. [DOI] [PubMed] [Google Scholar]
- 10.Mourik JEM, Lubberink M, Schuitemaker A, et al. Image-derived input functions for PET brain studies. Eur J Nucl Med Mol Imaging 2009; 36: 463–471. [DOI] [PubMed] [Google Scholar]
- 11.Zhou S, Chen K, Reiman EM, et al. A method for generating image-derived input function in quantitative 18F-FDG PET study based on the monotonicity of the input and output function curve. Nucl Med Commun 2012; 33: 362–370. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Wahl LM, Asselin MC, Nahmias C. Regions of interest in the venous sinuses as input functions for quantitative PET. J Nucl Med 1999; 40: 1666–75. [PubMed] [Google Scholar]
- 13.Guo H, Renaut R, Chen K, et al. Clustering huge data sets for parametric PET imaging. Biosystems 2003; 71: 81–92. [DOI] [PubMed] [Google Scholar]
- 14.Fang Y-H, Kao T, Liu R-S, et al. Estimating the input function non-invasively for FDG-PET quantification with multiple linear regression analysis: simulation and verification with in vivo data. Eur J Nucl Med Mol Imaging 2004; 31: 692–702. [DOI] [PubMed] [Google Scholar]
- 15.Liptrot M, Adams KH, Martiny L, et al. Cluster analysis in kinetic modelling of the brain: a noninvasive alternative to arterial sampling. Neuroimage 2004; 21: 483–493. [DOI] [PubMed] [Google Scholar]
- 16.Naganawa M, Kimura Y, Ishii K, et al. Extraction of a plasma time-activity curve from dynamic brain PET images based on independent component analysis. IEEE Trans Biomed Eng 2005; 52: 201–210. [DOI] [PubMed] [Google Scholar]
- 17.Su Y, Shoghi KI. Single-input–dual-output modeling of image-based input function estimation. Mol Imaging Biol 2010; 12: 286–294. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Lyoo CH, Zanotti-Fregonara P, Zoghbi SS, et al. Image-derived input function derived from a supervised clustering algorithm: methodology and validation in a clinical protocol using [11C](R)-rolipram. PLoS One 2014; 9: e89101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Simončič U, Zanotti-Fregonara P. Image-derived input function with factor analysis and a-priori information. Nucl Med Commun 2015; 36: 187–193. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Sari H, Erlandsson K, Law I, et al. Estimation of an image derived input function with MR-defined carotid arteries in FDG-PET human studies using a novel partial volume correction method. J Cereb Blood Flow Metab 2017; 37: 1398–1409. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Litton JE. Input function in PET brain studies using MR-defined arteries. J Comput Assist Tomogr 1997; 21: 907–909. [DOI] [PubMed] [Google Scholar]
- 22.Fung EK, Carson RE. Cerebral blood flow with [15 O]water PET studies using an image-derived input function and MR-defined carotid centerlines. Phys Med Biol 2013; 58: 1903–1923. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Jaszczak RJ. The early years of single photon emission computed tomography (SPECT): an anthology of selected reminiscences. Phys Med Biol 2006; 51: R99–R115. [DOI] [PubMed] [Google Scholar]
- 24.Su Y, Arbelaez AM, Benzinger TL, et al. Noninvasive estimation of the arterial input function in positron emission tomography imaging of cerebral blood flow. J Cereb Blood Flow Metab 2013; 33: 115–121. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Su Y, Blazey TM, Snyder AZ, et al. Quantitative amyloid imaging using image-derived arterial input function. PLoS One 2015; 10: e0122920. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Jochimsen TH, Zeisig V, Schulz J, et al. Fully automated calculation of image-derived input function in simultaneous PET/MRI in a sheep model. EJNMMI Phys 2016; 3: 2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Khalighi MM, Deller TW, Fan AP, et al. Image-derived input function estimation on a TOF-enabled PET/MR for cerebral blood flow mapping. J Cereb Blood Flow Metab 2018; 38: 126–135. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Da Silva NA, Herzog H, Weirich C, et al. Image-derived input function obtained in a 3TMR-brainPET. Nucl Instruments Methods Phys Res Sect A Accel Spectrometers, Detect Assoc Equip 2013; 702: 22–25. [Google Scholar]
- 29.Su Y, Vlassenko AG, Couture LE, et al. Quantitative hemodynamic PET imaging using image-derived arterial input function and a PET/MR hybrid scanner. J Cereb Blood Flow Metab 2017; 37: 1435–1446. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Zanotti-Fregonara P, Fadaili EM, Maroy R, et al. Comparison of Eight methods for the estimation of the image-derived input function in dynamic [18 F]-FDG PET human brain studies. J Cereb Blood Flow Metab 2009; 29: 1825–1835. [DOI] [PubMed] [Google Scholar]
- 31.Keller SH, Hansen CC, Hansen CC, et al. Motion correction in simultaneous PET/MR brain imaging using sparsely sampled MR navigators: a clinically feasible tool. EJNMMI Phys 2015; 2: 14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Bailey DL, Pichler BJ, Gückel B, et al. Combined PET/MRI: global warming – summary report of the 6th international workshop on PET/MRI, March 27–29, 2017, Tübingen, Germany. Mol Imaging Biol 2018; 20: 4–20. [DOI] [PMC free article] [PubMed]
- 33.Ladefoged CN, Law I, Anazodo U, et al. A multi-centre evaluation of eleven clinically feasible brain PET/MRI attenuation correction techniques using a large cohort of patients. Neuroimage 2017; 147: 346–359. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Carney JPJ, Townsend DW, Rappoport V, et al. Method for transforming CT images for attenuation correction in PET/CT imaging. Med Phys 2006; 33: 976–983. [DOI] [PubMed] [Google Scholar]
- 35.Shih FY. Image processing and pattern recognition: fundamentals and techniques. John Wiley & Sons, 2010. Hoboken, New Jersey.
- 36.Teutsch M. Moving object detection and segmentation for remote aerial video surveillance. KIT Scientific Publishing 2010. Karlsruhe, Germany.
- 37.Gibo H, Lenkey C, Rhoton AL. Microsurgical anatomy of the supraclinoid portion of the internal carotid artery. J Neurosurg 1981; 55: 560–574. [DOI] [PubMed] [Google Scholar]
- 38.Loening AM, Gambhir SS. AMIDE: a free software tool for multimodality medical image analysis. Mol Imaging 2003; 2: 131–137. [DOI] [PubMed] [Google Scholar]
- 39.Müller-Gärtner HW, Links JM, Prince JL, et al. Measurement of radiotracer concentration in brain gray matter using positron emission tomography: MRI-based correction for partial volume effects. J Cereb Blood Flow Metab 1992; 12: 571–583. [DOI] [PubMed] [Google Scholar]
- 40.Otsu N. A Threshold selection method from gray-level histograms. IEEE Trans Syst Man Cybern 1979; 9: 62–66. [Google Scholar]
- 41.Iida H, Miura S, Shoji Y, et al. Noninvasive quantitation of cerebral blood flow using oxygen-15-water and a dual-PET system. J Nucl Med 1998; 39: 1789–1798. [PubMed] [Google Scholar]
- 42.Iida H, Kanno I, Miura S, et al. Error analysis of a quantitative cerebral blood flow measurement using H2(15)O autoradiography and positron emission tomography, with respect to the dispersion of the input function. J Cereb Blood Flow Metab 1986; 6: 536–545. [DOI] [PubMed] [Google Scholar]
- 43.Phelps ME, Huang SC, Hoffman EJ, et al. Tomographic measurement of local cerebral glucose metabolic rate in humans with (F-18)2-fluoro-2-deoxy-D-glucose: validation of method. Ann Neurol 1979; 6: 371–388. [DOI] [PubMed] [Google Scholar]
- 44.Mourik JEM, van Velden FHP, Lubberink M, et al. Image derived input functions for dynamic High Resolution Research Tomograph PET brain studies. Neuroimage 2008; 43: 676–686. [DOI] [PubMed] [Google Scholar]
- 45.Mourik JEM, Lubberink M, Schuitemaker A, et al. Image-derived input functions for PET brain studies. Eur J Nucl Med Mol Imaging 2009; 36: 463–471. [DOI] [PubMed] [Google Scholar]
- 46.Mourik JEM, Lubberink M, Lammertsma AA, et al. Image derived input functions: effects of motion on tracer kinetic analyses. Mol Imaging Biol 2011; 13: 25–31. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Fung EK, Carson RE. Cerebral blood flow with [15O]water PET studies using an image-derived input function and MR-defined carotid centerlines. Phys Med Biol 2013; 58: 1903–1923. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Rousset OG, Ma Y, Evans AC. Correction for partial volume effects in PET: principle and validation. J Nucl Med 1998; 39: 904–911. [PubMed] [Google Scholar]
- 49.Boussion N, Hatt M, Reilhac A, et al. Fully automated partial volume correction in PET based on a wavelet approach without the use of anatomical information. In: IEEE nuclear science symposium conference record, Oct 23, 2007, pp.2812–2816. Honolulu, HI, USA: IEEE.
- 50.Le Pogam A, Hatt M, Descourt P, et al. Evaluation of a 3D local multiresolution algorithm for the correction of partial volume effects in positron emission tomography. Med Phys 2011; 38: 4920–4923. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Catana C, Benner T, van der Kouwe A, et al. MRI-Assisted PET motion correction for neurologic studies in an integrated MR-PET scanner. J Nucl Med 2011; 52: 154–161. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Camargo EE, Szabo Z, Links JM, et al. The influence of biological and technical factors on the variability of global and regional brain metabolism of 2-[18F]fluoro-2-deoxy-D-glucose. J Cereb Blood Flow Metab 1992; 12: 281–290. [DOI] [PubMed] [Google Scholar]
- 53.Schaefer SM, Abercrombie HC, Lindgren KA, et al. Six-month test-retest reliability of MRI-defined PET measures of regional cerebral glucose metabolic rate in selected subcortical structures. Hum Brain Mapp 2000; 10: 1–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Brooks RA, Di Chiro G, Zukerberg BW. Test-retest studies of cerebral glucose metabolism using fluorine-18 deoxyglucose: validation of method. J Nucl Med 1987; 28: 53–59. [PubMed] [Google Scholar]
- 55.Duara R, Gross-Glenn K, Barker WW, et al. Behavioral activation and the variability of cerebral glucose metabolic measurements. J Cereb Blood Flow Metab 1987; 7: 266–271. [DOI] [PubMed] [Google Scholar]
- 56.Gur RC, Gur RE, Resnick SM, et al. The effect of anxiety on cortical cerebral blood flow and metabolism. J Cereb Blood Flow Metab 1987; 7: 173–177. [DOI] [PubMed] [Google Scholar]
- 57.Stapleton JM, Morgan MJ, Liu X, et al. Cerebral glucose utilization is reduced in second test session. J Cereb Blood Flow Metab 1997; 17: 704–712. [DOI] [PubMed] [Google Scholar]
- 58.Ladefoged CN, Benoit D, Law I, et al. Region specific optimization of continuous linear attenuation coefficients based on UTE (RESOLUTE): application to PET/MR brain imaging optimized MLAA for quantitative non-TOF PET/MR of the brain emission-based estimation of lung attenuation coefficients. Phys Med Biol 2015; 60: 8047–8065. [DOI] [PubMed] [Google Scholar]
- 59.Mokken FC, Van Der Waart FJM, Henny CP, et al. Differences in peripheral arterial and venous hemorheologic parameters. Ann Hematol 1996; 73: 135–137. [DOI] [PubMed] [Google Scholar]
- 60.Jochimsen TH, Zeisig V, Schulz J, et al. Fully automated calculation of image-derived input function in simultaneous PET/MRI in a sheep model. EJNMMI Phys 2016; 3: 2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Wu HM, Bergsneider M, Huang SC, et al. Measurement of the global lumped constant for 2-deoxy-2-[18F]fluoro-D-glucose in normal human brain using [15O]water and 2-deoxy-2-[18F]fluoro-D-glucose positron emission tomography imaging. A method with validation based on multiple methodologies. Mol Imaging Biol 2003; 5: 32–41. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplemental material for Towards quantitative [18F]FDG-PET/MRI of the brain: Automated MR-driven calculation of an image-derived input function for the non-invasive determination of cerebral glucose metabolic rates by Lalith KS Sundar, Otto Muzik, Lucas Rischka, Andreas Hahn, Ivo Rausch, Rupert Lanzenberger, Marius Hienert, Eva-Maria Klebermass, Frank-Günther Füchsel, Marcus Hacker, Magdalena Pilz, Ekaterina Pataraia, Tatjana Traub-Weidinger and Thomas Beyer in Journal of Cerebral Blood Flow & Metabolism