Simultaneous Improvement in the Precision, Accuracy, and Robustness of Label-free Proteome Quantification by Optimizing Data Manipulation Chains

High-quality label-free proteome quantification (LFQ) is valuable for clinical and pharmaceutical studies yet remains extremely challenging despite technical advances. Particularly, fluctuating precision, limited robustness, and compromised accuracy are known issues. Here, we described and validated a new strategy enabling the discovery of the LFQs of simultaneously enhanced precision, robustness, and accuracy from thousands of LFQ manipulation chains. In the proof-of-concept study, this strategy showed superior ability in identifying well-performing LFQs. An online tool incorporating this novel strategy was also developed.

Graphical Abstract

Highlights

• High-quality LFQ is valuable technique yet remains extremely challenging.

• Fluctuating precision, limited robustness, and compromised accuracy are known issues.

• We proposed a strategy collectively improving LFQ precision, robustness, and accuracy.

• An online tool incorporating this novel strategy was also developed.

Abstract

The label-free proteome quantification (LFQ) is multistep workflow collectively defined by quantification tools and subsequent data manipulation methods that has been extensively applied in current biomedical, agricultural, and environmental studies. Despite recent advances, in-depth and high-quality quantification remains extremely challenging and requires the optimization of LFQs by comparatively evaluating their performance. However, the evaluation results using different criteria (precision, accuracy, and robustness) vary greatly, and the huge number of potential LFQs becomes one of the bottlenecks in comprehensively optimizing proteome quantification. In this study, a novel strategy, enabling the discovery of the LFQs of simultaneously enhanced performance from thousands of workflows (integrating 18 quantification tools with 3,128 manipulation chains), was therefore proposed. First, the feasibility of achieving simultaneous improvement in the precision, accuracy, and robustness of LFQ was systematically assessed by collectively optimizing its multistep manipulation chains. Second, based on a variety of benchmark datasets acquired by various quantification measurements of different modes of acquisition, this novel strategy successfully identified a number of manipulation chains that simultaneously improved the performance across multiple criteria. Finally, to further enhance proteome quantification and discover the LFQs of optimal performance, an online tool (https://idrblab.org/anpela/) enabling collective performance assessment (from multiple perspectives) of the entire LFQ workflow was developed. This study confirmed the feasibility of achieving simultaneous improvement in precision, accuracy, and robustness. The novel strategy proposed and validated in this study together with the online tool might provide useful guidance for the research field requiring the mass-spectrometry-based LFQ technique.

Mass-spectrometry (MS)-based proteomics have emerged as one of the most powerful techniques to detect the correlation of complex molecular network rewiring with biological phenotypes (1), identify the human protein interactome (2), discover novel therapeutic targets (3), and characterize new protein therapeutics (4). Compared with qualitative proteomics, the quantitative MS-based proteomics is distinguished by its ability to give detailed level of protein intensities and can thus provide a more complete picture of cellular process and enable network-centered study (5). Among the approaches currently available for quantifying proteins, the label-free proteome quantification (LFQ)¹ shows unique advantages in (a) the simultaneous discovery of proteins without the labor-intensive and costly procedures of stable isotope labeling (6), (b) the capacity to process the large sample cohort (6, 7), and (c) its applicability to samples from any source (5, 8). Due to its distinguishing features above, the LFQ has become increasingly important in and has been extensively applied to a broad range of research fields, such as system biology (9), drug discovery (3), and agricultural (10), medical (11), and environmental (12) sciences.

However, in-depth and high-quality quantification remains extremely challenging despite recent advances in LFQ technique (13). The challenges include snowballing missing values (14), fluctuating precision (15), limited robustness (16), and compromised accuracy (6), among others. On one hand, a variety of powerful quantification tools integrating novel alignment and feature generation methods have been constructed to maximally fill in missing blanks and elevate the reproducibility of LFQ (17–19). On the other hand, many computational algorithms have been proposed to minimize the instrumental and experimental fluctuations (5), enhance the stability of the identified candidate markers (20), and reduce the extremely large dynamic range of the protein abundance (21). Specifically, ≥18 quantification software tools and ≥3 transformation, ≥18 pretreatment, and ≥7 missing-value imputation methods have been proposed and sequentially integrated into the quantification workflow to overcome the above challenges to the extent possible (supplemental Table S1). Recent investigation has revealed that the quality of LFQ relies heavily on the selection of tools or methods and, in turn, greatly affects the retrieval of reliable biological interpretation from the proteomic data (6). Therefore, it is essential to evaluate the correctness and further optimize the qualities of LFQs by comparatively benchmarking their performance (22).

To date, several studies have been conducted to evaluate the performance variations in quantification tools by assessing the number of proteins quantified (23, 24), the number of missing values produced (24), and the precision (25) or accuracy (26). Some well-performing tools are thus identified based on the criterion adopted by each study, but their identification results vary greatly (PEAKS and Progenesis were found to perform well in quantifying proteins (23) and reproducing missing values (24), respectively; OpenMS and MaxQuant were discovered superior in quantification precision (23) and accuracy (25, 26), respectively). These findings indicate significant variations among the evaluation results by different criteria. Moreover, the performance of seven normalization methods has been assessed using the quantification precision (27). However, the random, comprehensive, and sequential integration of all quantification tools, transformation, pretreatment, and imputation methods can result in thousands of potential LFQs (supplemental Table S1). The multiplicity and complexity therefore become one of the bottlenecks in the comprehensive assessment of all potential LFQs.

Precision (28) and robustness (29) are two well-established criteria for assessing the quality of LFQs that should be collectively considered to not only reduce proteome variations among replicates but also elevate consistency among the different lists of identified markers (24, 27). In the meantime, it was also necessary to consider both the quantification precision (28) and the deviations of spiked proteins from their expected abundance ratio (quantification accuracy (6)) for current proteomic analyses (27, 28). Due to the variation in the assessment results by different criteria and the vast number of potential LFQs (discussed in the previous paragraph), it is essential to assess the feasibility of identifying the LFQs that simultaneously enhance the precision, accuracy, and robustness and to design novel strategy for “thoroughly” evaluating (6, 24, 30) and collectively optimizing the performance of LFQs. Ideally, an additional tool with the unique functions of performance assessments (discussed in the preceding) should be constructed to facilitate current proteomic analyses. However, no such study has been conducted yet.

Herein, the feasibility of achieving simultaneous improvements in the precision, accuracy, and robustness of an LFQ was systematically assessed by collectively optimizing its multistep analyzing chain, and a new strategy was proposed by scanning quantification tools and all possible combinations of data manipulation chains. Based on the representative benchmark data acquired using different quantification measurements, this strategy successfully identified a number of data manipulation chains with simultaneous enhancement of performance in terms of multiple criteria. To facilitate proteome quantifications and discover the LFQs of the optimal performance, an online tool enabling collective performance assessment was developed.

MATERIALS AND METHODS

The Modes of Acquisition and Their Corresponding Quantification Tools Studied in This Work

The LFQ specified in this study was a multistep workflow that included the data preprocessing by various quantification tools and subsequent data manipulation chains. There were ≥18 quantification tools popular in current proteomics research, the majority of which were especially designed for preprocessing the data acquired by specific mode of acquisition (data-dependent (DDA) and data-independent (DIA) acquisitions). For the DDA mode, there were two quantification measurements: peak intensity and spectral counting (31), and the measurement sequential window acquisition of all theoretical mass spectra (SWATH-MS) belonged to the DIA mode (32). As described in supplemental Table S1, only two quantification tools (MaxQuant and MFPaQ) were capable of preprocessing the data of multiple quantification measurements. The subsequent data manipulation chain included a sequential process of three steps: transformation, pretreatment, and missing-value imputation (supplemental Table S1). Overall, the LFQ analyzed here is a multistep workflow collectively defined by sequential integration of quantification tools, transformation, pretreatment, and missing-value imputation methods.

Constructing the Manipulation Chains by Sequentially Integrating the Manipulation Methods

To the best of our knowledge, there were ≥3 transformation, ≥18 pretreatment (2 centering, 4 scaling, and 12 normalization methods), and ≥7 missing-value imputation methods sequentially integrated to construct a multistep (three-step in general and five-step in detail) manipulation chain. In particular, the 28 methods in the manipulation chain included three transformation: Box-Cox, LOG, and VSN; 18 pretreatment: (two centering: mean and median; four scaling: auto, Pareto, vast, and range; and 12 normalization: mean, median, MAD, TIC, cyclic Loess, linear baseline scaling, RLR, LOWESS, EigenMS, PQN, quantile, and TMM); and seven imputation: background, BPCA, censored, KNN, LLS, SVD, and zero. As a transformation method integrating with subsequent normalization technique, the VSN was unique in determining data-dependent transformation parameters by having a built-in transformation. For the convenience of the discussions in this study, each manipulation method was abbreviated by a three-letter code as shown in Table I. Within a particular step, if none of the method was used, a three-letter code, NON, was applied to indicate the nonapplication of any method in this step. The representative application of the manipulation methods in current proteomics was systematically reviewed and provided in supplemental Table S1.

Table I. Various manipulation methods including 3 transformation, 18 pretreatment (2 centering, 4 scaling, and 12 normalization methods), and 7 imputation methods together with their purpose of data manipulation and/or corresponding statistical/biological assumptions. All manipulation methods were abbreviated using three-letter code. As a transformation method integrating with subsequent normalization technique, the VSN determined data-dependent transformation parameters by having a built-in transformation (47, 79).

Classes	Abb.	Manipulation Method	Purpose/Assumption of the Manipulation Method
Transformation	BOX	Box-Cox Transformation	Making asymmetric data fulfill the normality assumption in a regression model by converting the protein abundances into a more symmetric distribution (80).
	LOG	Log Transformation	Converting the distribution of ratios of abundance values of proteins into a more symmetric (almost normal distribution) and minimizing the effect of proteins with extreme abundance (39).
	VSN	Variance Stabilization Normalization	Having a built-in transformation (47) and making individual observations more directly comparable (81); assuming that most of the proteins across different samples are not differentially expressed (81).
Pretreatment
Centering	MEC	Mean-Centering	Converting all the intensities to fluctuations around zero instead of around the mean of the protein intensities; assuming all proteins are equally important (35).
	MDC	Median-Centering	Making all the intensities to fluctuations around zero instead of around the median of the protein intensities; assuming all proteins are equally important (35).
Scaling	ATO	Auto Scaling	Adjusting each protein abundance for systematic variance using the standard deviation of each protein of all samples as scaling factor (82); assuming all proteins are equally important (35).
	PAR	Pareto Scaling	Scaling each protein abundance for systematic variance using the square root of the standard deviation of each protein of all samples as scaling factor (83); assuming all proteins are equally important (35).
	VAS	Vast Scaling	Adjusting each protein abundance for systematic variance using the coefficient of variation of each protein of all samples as scaling factor (84); assuming all proteins are equally important (35).
	RAN	Range Scaling	Scaling each protein abundance for systematic variance using the abundance range of each protein of all samples as scaling factor (85); assuming all proteins are equally important (35).
Normalization	MEA	Mean Normalization	Ensuring the protein abundance values from all studied samples directly comparable with each other (86); assuming the mean level of the protein abundance is constant for all samples (27).
	MED	Median Normalization	Making the protein intensities from all individual samples directly comparable with each other (27, 86); assuming the median level of the protein abundance is constant for all samples (36).
	MAD	Median Absolute Deviation	Ensuring the comparability of protein intensities among all samples (86); assuming the median level of the protein abundance and the spread of abundances are the same in all samples (37).
	TIC	Total Ion Current	Making the protein intensities from all samples directly comparable with each other (86); assuming the total area under the protein abundance curve is constant among samples (38).
	CYC	Cyclic Loess	Assuming that the intensities of the vast majority of the proteins are not changed in control and case groups (33, 87) and the systematic bias is nonlinearly dependent on the protein abundances (27).
	LIN	Linear Baseline Scaling	Assuming that the abundances of the majority of the proteins in samples are unchanged under the studied condition (33, 88) and the systematic bias is linearly dependent on the protein intensities (39).
	RLR	Robust Linear Regression	Assuming that the intensities of the majority of the proteins are not changed in control and case groups (87, 88) and the systematic bias is linearly dependent on the magnitude of protein abundances (27).
	LOW	Locally Weighted Scatterplot Smoothing	Assuming that the abundances of the majority of the proteins are unchanged under the studies circumstances (40, 87) and the systematic bias is nonlinearly dependent on the protein intensities (40).
	EIG	EigenMS	Overcoming the problems caused by the heterogeneity in the protein intensities of studied samples (43, 89); Does not require any assumption about the relative strength of signals due to each source of variation (43).
	PQN	Probabilistic Quotient Normalization	Ensuring the comparability of protein intensities among all samples (86); assuming that the majority of the protein intensities does not vary for the studied classes (41).
	QUA	Quantile Normalization	Making the protein intensities from all samples directly comparable with each other (86); assuming that the majority of protein intensity signals are unchanged among samples (40).
	TMM	Trimmed Mean of M Values	Ensuring the protein abundance values from all studied samples directly comparable with each other (86); assuming the majority of proteins are not differentially expressed between control and case groups (42).
Imputation	BAK	Background Imputation	Assuming that the protein values are missing because of having small concentrations in the sample and thus cannot be detected during the MS run (27).
	BPC	Bayesian Principal Component Imputation	Imputing based on the variational Bayesian framework that does not force orthogonality between the principal components (90).
	CEN	Censored Imputation	Imputing the lowest intensity values in the dataset by assuming that the missing of protein values is because of being below detection capacity (27).
	KNN	K-nearest Neighbor Imputation	Finding k most similar proteins (k-nearest neighbors) and using a weighted average over these k proteins to estimate the missing protein values (27, 91).
	LLS	Local Least Squares Imputation	Representing a studied protein that has missing values as a linear combination of a number of proteins similar to this particular protein (92).
	SVD	Singular Value Decomposition	Applying this imputation method to the data to obtain sets of mutually orthogonal expression patterns of all proteins in the data (91).
	ZER	Zero Imputation	Imputing the missing intensities of the studied proteins by directly replacing these missing values with a number of zeros (27).

Moreover, the manipulation methods were reported as based on their own statistical assumption about the data, which might make them inappropriate for manipulating some proteomic data (33, 34). Therefore, the corresponding statistical/biological assumption and purpose of data manipulation of methods in each step were systematically reviewed and are provided in Table I. Taking pretreatment methods as the example, there were generally three types of assumptions: (A-α) all proteins were assumed to be equally important, which was required by the appropriate application of both centering and scaling methods (35); (A-β) the level of protein abundance was assumed to be constant among all samples, which was a priori assumption for some normalization methods, including MEA, MED, MAD, and TIC (27, 36–38); and (A-γ) the intensities of the vast majority of the proteins were assumed to be unchanged under the studied conditions, which was demanded by some other normalization methods such as CYC, LIN, LOW, PQN, QUA, RLR, and TMM (27, 39–42). Among 12 normalization methods, the EIG was the only one with no priori assumption about the relative strength of signals due to each source of variation (43). It is important to emphasize that due to the distinct assumptions, some methods may be fundamentally inappropriate for certain datasets and cannot be assessed in this study (33, 34). Therefore, before any performance assessment in the Discussion section of this study, the nature of the studied dataset was first analyzed and whether the method's assumption held for these data was then discussed. Moreover, in the online tool developed for proteomic quantification and performance assessment, a default setting for confirming whether the method's assumption held for the analyzed dataset is provided in both the online and the local versions of the constructed tool.

Based on the preanalyses on the nature of the studied dataset and its obedience toward the method's assumption, 28 manipulation methods were screened, and only the ones with their assumption held for studied datasets were kept for the subsequent assessments based on performance. Theoretically, a random, comprehensive, and sequential integration of 27 methods (excluding VSN) could result in 3,120 manipulation chains of five steps (2 × 3×5 × 13 × 8 = 3,120, taking noncentering, nonscaling, nonnormalization, and nonimputation into account, which have been widely adopted in previous publications (44–46)). Transformation was reported to be essential prior to the downstream analysis in any proteomic study (47); nontransformation was thus not allowed in both the analyses of this study and the online tool. Moreover, because the VSN was unique in having a built-in transformation and subsequent normalization technique, it should not combine with other transformation or pretreatment methods and could only be combined with imputation. These combinations therefore resulted in eight additional manipulation chains. As a result, there were 3,128 potential manipulation chains, and detailed descriptions of all manipulation methods can be found in Supplementary Methods.

Multiple Criteria for Assessing the Performance of a Given Data Manipulation Chain

Several well-established and widely adopted criteria in current proteomics were collected in this study for ensuring a systematic performance assessment of a given data manipulation chain. Three criteria (precision, robustness, and accuracy) were used for quantitative assessment, while two others (classification capacity and differential abundance analysis in proteomics) were employed as qualitative evaluation. A description of these criteria, together with their corresponding metrics, can be found in Supplementary Methods.

(a) Precision Measuring the Reduction in Proteome Variation among Replicates

The quantification precision of the LFQ was profoundly affected by different modes of acquisition, various types of software for preprocessing raw proteomic data, and diverse methods for data manipulation, which could be evaluated by the pooled intragroup median absolute deviation (PMAD) of the protein intensities among replicates (6, 48). PMAD reflected LFQ's ability to reduce the variation among replicates and thus enhance technical reproducibility (28). Lower PMAD denoted more thorough removal of experimentally induced noise and indicated better precision of the corresponding LFQ and manipulation chain (15).

(b) Robustness among Different Sets of Protein Biomarkers Identified from Different Datasets

The robustness of the biomarker discovery from proteomic data was usually assessed by the popular metric: consistency score, which calculated the level of reproducibility among the different lists of biomarkers identified from the different partitions of the studied dataset (16, 29). A higher consistency score value indicated the more robust results in the biomarker discovery (29). Herein, the studied datasets were randomly sampled 50 times to generate multiple subdatasets. Then, each protein was ranked based on its statistical significance measured by q-value and fold change. Third, the top-ranked proteins in each subdataset were selected as markers. Finally, a consistency score was calculated based on its reported and well-established equation (16).

(c) Accuracy Assessing the Deviation of Spiked Proteins from Their Expected Abundance Ratio

To adjust/validate the quantification accuracy of LFQs, additional experimental data (e.g. spiked proteins) were created and applied as the golden references (6, 48), and the expected log fold changes (logFCs) for both the spiked and background proteins were essential for assessing quantification accuracy (the expected logFC for the background proteins should equal to zero) (24). Herein, the logFCs of protein intensities for both spiked and background proteins between distinct sample groups were first calculated. Then, the mean squared error was applied to assess the level of correspondence between the quantification and the expected logFC. The performance could be reflected by how well the quantification logFCs corresponded to the expected values using the references (24). The deviations in both quantification and expected logFCs would be zero with the minimized deviation (24).

(d) Qualitative Criteria for Assessing the Performance of Data Manipulation Chain

The qualitative criteria frequently adopted by previous report and applied in this study for assessing LFQ's performance included the LFQ's (1) classification capacity between distinct groups (49) and (2) differential abundance analysis in proteomics based on reproducibility optimization (50). On one hand, an appropriate manipulation chain was expected to retain or even enlarge the variation in proteomic data between distinct sample groups (49, 51), and a heatmap hierarchically clustering samples based on their protein abundances was thus used as an effective measure for assessing LFQ's classification capacity (49). On the other hand, to avoid overfitting/confounding, the distribution of p values of protein intensities between distinct sample groups should be examined using differential abundance analysis in proteomics (50) (ideally, one expected an uniform distribution for the bulk of nondifferentially expressed proteins, with a peak in the interval of [0.00, 0.05] corresponding to proteins with differential intensity (50)), and a volcano plot coloring proteins by differential intensity was thus drawn to depict the total number of the proteins of differential abundance (24). In the OMIC (any research field of biological study ending in -omics such as genomics, transcriptomics, proteomics or metabolomics) study exploring the mechanism underlying complex processes, a limited number of the proteins of differential abundance might lead to false discovery (52). Thus, to assess LFQ's classification capacity, the number of protein intensities in each sample was first reduced by feature selection. First, the differential significance of each protein between distinct sample groups measured by adjusted p value was calculated using the reproducibility-optimized test statistic (ROTS) package (53); then, the significant features (adjusted p value <0.05) were selected for subsequent heatmap analyses. Then, the proteins (rows) and samples (columns) were clustered based on their similarity in the profile of protein abundances. A corresponding process was described by a previous report (49). Moreover, to conduct differential abundance analysis in proteomics, differential significance of protein intensities between distinct sample groups measured by p value was first calculated using ROTS in R package (54). Then, the distribution of p values was visualized by histogram; skewed distribution might indicate overfitting/confounding in the studied manipulation chain (55).

Optimizing the Performance of Manipulation Chain by Assessing from Multiple Perspectives

Each criterion made the performance assessment possible from its own perspective, and the combination of multiple criteria could thus ensure the comprehensive evaluation of a given manipulation chain. On one hand, quantification precision and robustness were collectively considered to evaluate the performance of chain on the proteomic datasets acquired by either DDA or DIA. On the other hand, precision and accuracy were evaluated for DDA-based or DIA-based proteomic datasets. Moreover, an online tool was developed to provide the performance assessment from quantitative and qualitative perspectives (all criteria described in previous sections could be simultaneously evaluated). To optimize the performance of LFQ, potential manipulation chains with suitable assumptions appropriate to the studied datasets were systematically scanned, and the chains top-ranked by single or multiple criteria were identified as demonstrating the optimal performance.

Identification of the Well-Performing Manipulation Chains Using Hierarchical Clustering

PMAD values, consistency scores, or deviations from the expected abundance ratio of manipulation chains across different benchmark datasets (preprocessed by different quantification tools) were first calculated. Hierarchical clustering of the chains with calculable results of all benchmarks was conducted to identify the chains consistently performing well across all benchmarks. Particularly, the PMAD values, consistency scores, or deviations from the expected abundance ratio of a given chain among N sets of benchmark data were used to construct N-dimensional vectors. Then, hierarchical clustering was adopted to investigate the relationship among these vectors, and therefore among the corresponding chains. Manhattan distance was adopted to measure the distance between any two vectors (56). To view the hierarchical tree among chains, the tree generator iTOL was used to generate and display the tree structure (57).

Diverse and Representative Benchmark Datasets Collected for the Analyses in This Study

In total, 58 benchmark datasets from 11 studies were collected and applied to evaluate the performance of manipulation chains. As shown in Table II, the first study provided the peak intensity proteome data based on the cerebrospinal fluids from 10 Alzheimer's disease patients and 10 nondemented controls (23). There were five proteomic benchmark datasets (preprocessed by five quantification tools: DecyderMS, MaxQuant, OpenMS, PEAKS, and Sieve) in this study. The second study described a spectral-counting-based controlled, spiked proteomic data for which the ground truth of variant protein was known (58). Particularly, 48 UPS1 proteins were spiked into the yeast lysate with five different concentrations (0.5, 5, 12.5, 25, and 50 fmol/μg), and the samples were preprocessed using four quantification tools: IRMa-hEIDI, MaxQuant, MFPaQ, and Scaffold. For each tool, a random combination of five concentrations resulted in 10 datasets with two distinct concentrations. As a result, 40 datasets in total were collected for four quantification tools. The proteomics datasets of the third through fifth studies (59–61) were acquired by the DDA (peak intensity) technique and quantified by MaxQuant. Meanwhile, the datasets from the sixth through eighth studies (54, 62, 63) were acquired by DDA (peak intensity) technique and quantified by Progenesis. These six studies therefore resulted in six benchmark datasets. The ninth study gave one peak intensity proteomic dataset with six purified proteins spiked with two distinct concentrations (64), which was quantified by OpenMS. The 10th study provided the SWATH-MS-based DIA dataset containing 20 samples of wild-type mouse and 20 knock-in mice expressing GRB2 (29), which was preprocessed by OpenSWATH. Finally, the last study described SWATH-MS-based DIA data of two distinct mixture groups (three mixtures of 30% yeast versus 5% Escherichia coli and another three mixtures of 15% yeast versus 20% E. coli) (6). There were five benchmark datasets (preprocessed by five quantification tools: DIA-Umpire, Skyline, OpenSWATH, PeakView, and Spectronaut) in this study.

Table II. Detailed information of the studied benchmarks (ordered by their appearances in “Results and Discussion”). Three types of assumptions held for these benchmarks: (A-α) all proteins are equally important; (A-β) the level of protein abundance is constant among all samples; (A-γ) the intensities of the majority of the proteins are not changed under the studied conditions. The assumption A-α held for all benchmarks, while both assumption A-β and A-γ could not hold for the datasets of the fourth study. The corresponding quantification measurements and applied quantification software tool(s) were also provided.

No.	Benchmark Studies	PRIDE or Other IDs	Description of Benchmark Study	Assumption Held	No. of Proteins	Quantification Measurement (Applied Quantification Tools)
1	PLoS One 11: e0150672, 2016	Shevchenko	10 Alzheimer's disease patients 10 nondemented controls	A-α, A-β, A-γ	4,967	Peak Intensity (DecyderMS, MaxQuant, OpenMS, PEAKS, Sieve)
2	Data Brief 6:286–294, 2015	PXD001819	48 UPS1 proteins spiked into the yeast lysate with five concentrations	A-α, A-β, A-γ	752	Spectral Counting (IRMa-hEIDI, MaxQuant, MFPaQ, Scaffold)
3	Nat. Commun.	PXD002882	21 Crohn's disease patients	A-α, A-β, A-γ	4,169	Peak Intensity (MaxQuant)
	7:13419, 2016		10 healthy individuals
4	Cell Host Microbe	PXD006129	14 western-style diet mice	A-α, A-β, A-γ	3,243	Peak Intensity (MaxQuant)
	23:27–40, 2018		14 chow-fed mice
5	Microbiome	PXD006224	60 metabolic-phase fecal samples	A-α, A-β, A-γ	9,761	Peak Intensity (MaxQuant)
	5:144, 2017		24 equilibrium-phase fecal samples
6	Proteomics	PXD002885	8 hESC fresh cells in protocol A	A-α, A-β, A-γ	198	Peak Intensity (Progenesis)
	16:2937–2944, 2016		8 hESC fresh cells in protocol C
7	J. Proteome Res. 11:4118–4126, 2015	PXD002099	48 UPS1 proteins spiked with distinct concentrations (2 vs 50 fmol/μl)	A-α, A-β, A-γ	1,442	Peak Intensity (Progenesis)
8	J. Proteome Res. 9:761–776, 2010	CPTAC-ST6	48 UPS1 proteins spiked with distinct concentrations (0.25 vs 20 fmol/μl)	A-α, A-β, A-γ	1,570	Peak Intensity (Progenesis)
9	J. Proteome Res. 16:2964–2974, 2017	PXD006336	6 purified proteins spiked with distinct concentrations (sample group 1 vs 2)	A-α, A-β, A-γ	22,719	Peak Intensity (OpenMS)
10	Cell Rep.	PXD003972	20 wild type mouse samples	A-α, A-β, A-γ	901	SWATH-MS (OpenSWATH)
	18:3219–3226, 2017		20 knock-in mice expressing GRB2
11	Nat. Biotechnol. 34:1130–1136, 2016	PXD002952	3 mixtures of 30% yeast vs 5% E. coli 3 mixtures of 15% yeast vs 20% E. coli	A-α	5,731	SWATH-MS (DIA-Umpire, Skyline, OpenSWATH, PeakView, Spectronaut)

RESULTS AND DISCUSSION

Dependence of Quantification Precision on the Selection of Multistep Manipulation Chain

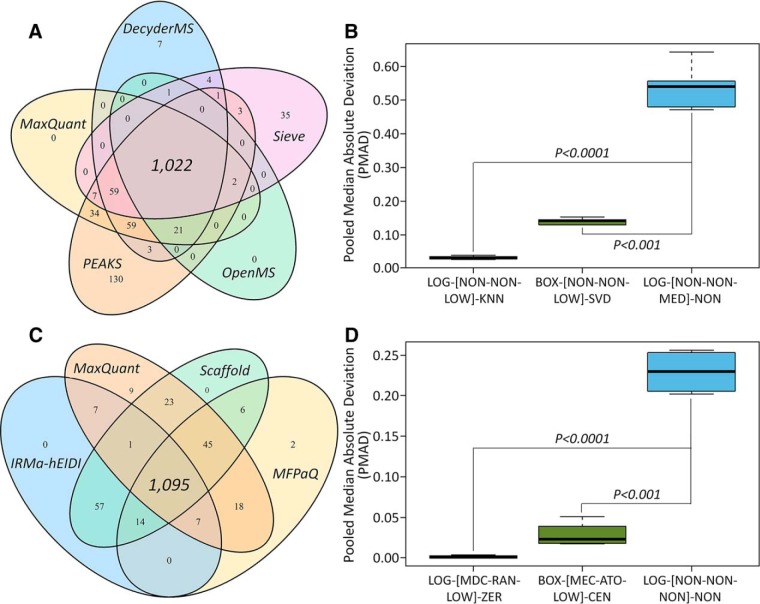
The LFQ precision measured by the pooled intragroup median absolute deviation (PMAD) across replicate groups was widely adopted as an effective measurement of quantification performance (28). To assess the level of dependence of precision on the multistep manipulation chains, two benchmark datasets acquired by either peak intensity or spectral counting were first collected from study 1 (23) and study 2 (58) of Table II. Then, the precision of these datasets was improved by the collective optimization of the multistep manipulation chains. As shown on the left side of Table III, the precision of representative chains for peak intensity benchmark (Table II, study 1) varied greatly (PMADs were from 0.0558 to 3.9600). Based on the precision levels defined by PMAD values (superior: <0.14 (6), good: 0.14∼0.3 (65), fair: 0.3∼0.7 (66), and poor: >0.7 (66)), the chain adopted by the original study (23) to manipulate the collected dataset (LOG-[NON-NON-MED]-NON, the first line in Table III highlighted in gray) performed consistently “fair” across five quantification tools (PMADs from 0.4708 to 0.6430). Clearly, some chains performed better than the one used in original study (with the LOG-[MEC-RAN-PQN]-BPC performing “superior” for all quantification tools). Similarly, the precision of the representative chains for spectral counting dataset (Table II, study 2 of distinct concentrations: 12.5 versus 25 fmol/μg of the spiked UPS1 protein) is provided in supplemental Table S2. As reported in the original study (58) of this dataset, only log transformation was used (the first line in supplemental Table S2, highlighted in gray color), and it performed consistently “good” across four quantification tools. Still, the precision of some chains was found to surpass that of the original one (with LOG-[MDC-RAN-EIG]-KNN performing “superior” across all quantification software tools).

Table III. The level of dependence of precision and robustness on the selection of manipulation chains assessed based on the benchmark dataset of the first study in Table I (23). These studied LFQs were collectively defined by five quantification tools and eight representative manipulation chains. As reported in original study (23), the log transformation together with median normalization were applied before any subsequent analysis, which defined the manipulation chain of that study as LOG-[NON-NON-MED]-NON (highlighted in gray background). The precision levels were defined by the PMAD values (superior: <0.14, good: 0.14∼0.3, fair: 0.3∼0.7, and poor: >0.7), and the robustness levels were assigned by the ranking of consistency scores (high: top 20%, medium: 20∼50%, and low: bottom 50%). Each manipulation method within an LFQ was abbreviated by a three-letter code that was systematically defined in Table I.

Representative Chains for Data Manipulation	Precision: Reproducibility among technical replicates (PMAD)					Robustness: Rank of manipulation chains by consistency scores
	DecyderMS	MaxQuant	PEAKS	OpenMS	Sieve	DecyderMS	MaxQuant	PEAKS	OpenMS	Sieve
LOG-[NON-NON-MED]-NON	5.56E−01 (Fair)	5.41E−01 (Fair)	6.43E−01 (Fair)	4.80E−01 (Fair)	4.71E−01 (Fair)	457 (High)	358 (High)	369 (High)	313 (High)	687 (Medium)
LOG-[MDC-RAN-EIG]-KNN	1.31E−01 (Superior)	1.40E−01 (Superior)	1.33E−01 (Superior)	1.33E−01 (Superior)	1.20E−01 (Superior)	176 (High)	120 (High)	104 (High)	163 (High)	122 (High)
LOG-[MEC-NON-EIG]-BAK	6.45E−01 (Fair)	7.41E−01 (Poor)	7.85E−01 (Poor)	8.04E−01 (Poor)	4.06E−01 (Fair)	193 (High)	387 (High)	1,421 (Low)	936 (Medium)	75 (High)
LOG-[MEC-RAN-PQN]-CEN	1.64E−01 (Good)	1.94E−01 (Good)	2.64E−01 (Good)	4.64E−01 (Fair)	5.76E−02 (Superior)	1,409 (Low)	1,744 (Low)	1,879 (Low)	1,489 (Low)	2,152 (Low)
LOG-[MEC-RAN-PQN]-BPC	8.19E−02 (Superior)	8.38E−02 (Superior)	8.78E−02 (Superior)	8.41E−02 (Superior)	5.58E−02 (Superior)	2,239 (Low)	2,290 (Low)	2,319 (Low)	2,239 (Low)	2,298 (Low)
BOX-[MDC-PAR-EIG]-ZER	2.61E+00 (Poor)	3.02E+00 (Poor)	2.00E+00 (Poor)	2.74E+00 (Poor)	3.96E+00 (Poor)	174 (High)	138 (High)	278 (High)	228 (High)	2 (High)
BOX-[MEC-RAN-NON]-KNN	2.23E−01 (Good)	2.29E−01 (Good)	2.23E−01 (Good)	2.25E−01 (Good)	2.19E−01 (Good)	474 (High)	473 (High)	379 (High)	451 (High)	332 (High)
BOX-[MEC-ATO-RLR]-BPC	1.64E+00 (Poor)	1.24E+00 (Poor)	1.49E+00 (Poor)	1.46E+00 (Poor)	1.10E+00 (Poor)	2,210 (Low)	2,203 (Low)	2,237 (Low)	2,032 (Low)	2,341 (Low)

Based on the preanalyses on the nature of the studied datasets and their obedience toward the assumption of manipulation methods, all methods were appropriate for manipulating the datasets of Table II, studies 1 and 2. On one hand, comprehensive evaluation of the precision of 3,128 potential manipulation chains for study 1 (peak intensity) found that >1,000 chains (for each quantification tool) demonstrated an enhanced precision compared with the one (LOG-[NON-NON-MED]-NON) adopted by the original study (23). As shown in Fig. 1A, 1,022 chains with a consistently better precision than LOG-[NON-NON-MED]-NON for all quantification tools were identified. Ten example chains with substantially enhanced precision are provided in supplemental Table S3 (the significant differences in precision between the original chain and example one can be found in Fig. 1B). On the other hand, for study 2 of distinct concentrations (12.5 versus 25 fmol/μg) of the spiked UPS1 proteins (spectral counting), the evaluation of precision of >3,000 potential chains identified 1,095 (Fig. 1C) as performing consistently better than the one adopted in the original report (58). Supplemental Table S4 provides the example chains of greatly enhanced precision, and the significant differences in precision between the original chain and the example ones can also be observed in Fig. 1D for this spectral-counting-based benchmark. All in all, these findings indicate that the precision was highly dependent on the multistep manipulation chain, and a comprehensive assessment can facilitate the discovery of the well-performing chains.

Fig. 1.

Comprehensive assessment of precision of 3,128 potential manipulation chains and comparison to the chains successfully adopted by previous studies (23, 58). On one hand, a log transformation together with the median normalization were applied before any analysis in the Table II, study 1 (23), which defined manipulation chain of that study as LOG-[NON-NON-MED]-NON. (A) The Venn diagram illustrating the number of chains (combined with five quantification tools) performing better in precision than LOG-[NON-NON-MED]-NON. (B) Significant difference in precision between LOG-[NON-NON-MED]-NON and two example chains. On the other hand, only log transformation was used to manipulate the spectral counting data from Table II, study 2 (58), the manipulation chain of which could therefore be defined as LOG-[NON-NON-NON]-NON. (C) The Venn diagram showing the number of chains (combined with four quantification tools) performing better than the chain adopted by the original study (LOG-[NON-NON-NON]-NON). (D) The significant differences were observed between LOG-[NON-NON-NON]-NON and two example chains (LOG-[MDC-RAN-LOW]-ZER and BOX-[MEC-ATO-LOW]-CEN). Each manipulation method within a chain was abbreviated by a three-letter code that was defined in Table I.

The identification of the well-performing chains was conducted in previous sections based on the datasets quantified by various tools for a single experiment. However, each tool might generate the dataset of a tool-specific property, which could result in different chains appropriate for each tool. In other words, it would be essential to assess the dependences of the well-performing chains on different tools. Thus, a variety of datasets from multiple experiments but quantified by the same tool were collected. Particularly, eight tools for DDA-based proteomics (MFPaQ, MaxQuant, OpenMS, PEAKs, Progenesis QI, Proteios S.E., Scaffold, and Thermo Proteome Discoverer) were first searched in the PRoteomics IDEntifications (PRIDE) database (67). Then, several criteria were applied to guarantee the availability and processability of the collected raw proteomic data, which included (1) label-free quantification, (2) complete set of raw data files, and (3) clear descriptions on sample groups. The application of these criteria on PRIDE datasets further yielded three quantification tools with multiple (≥2) datasets, which included MaxQuant, OpenMS, and Progenesis. Third, eight benchmarks of these three tools (three benchmarks for both MaxQuant and Progenesis; two benchmarks for OpenMS) were collected for the subsequent analyses (Table II, study 1 and studies 3–9).

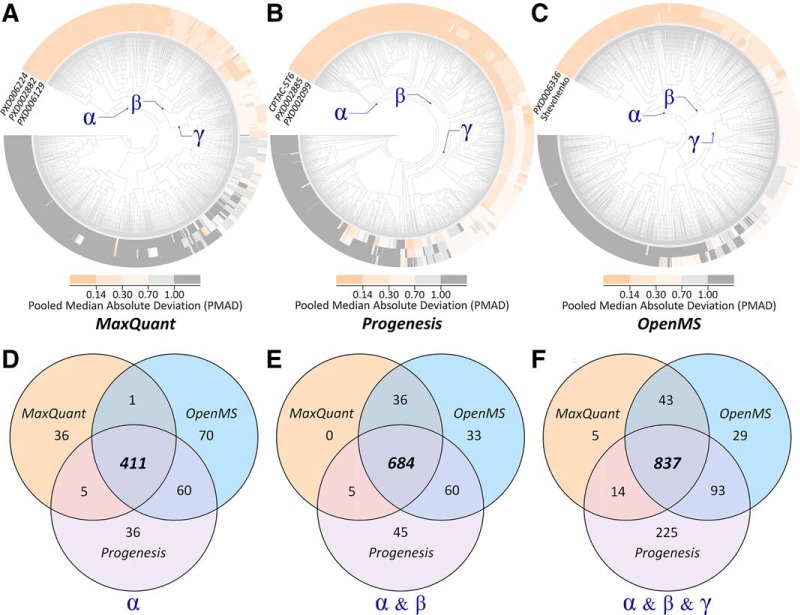
Based on the eight sets of data, the dependence of well-performing manipulation chains on the selection of quantification tool was assessed using the precision of >3,000 chains. As shown in Fig. 2, the clustering analyses among chains across multiple datasets were done for MaxQuant (Fig. 2A), Progenesis (Fig. 2B), and OpenMS (Fig. 2C). Second, three neighboring partitions of varied performance were identified, which included partition α containing the chains of consistently superior precision (PMADs <0.14) across multiple datasets, partition β including the chain of good precision (PMADs <0.3) across multiple datasets, and partition γ consisting of the chains of fair precision (PMADs <0.7) for multiple datasets. Finally, the Venn diagrams showing the manipulation chains shared by different quantification tools or demonstrating tool-specific characteristics were provided for the chains within partition α (Fig. 2D), partition α and β (Fig. 2E), and partition α and β and γ (Fig. 2F). As demonstrated, the majority of these well-performing chains were shared by all quantification tools, while there were still dozens of chains performing well only for a single tool. Moreover, the number of chains performing well for both OpenMS and Progenesis was much larger than that for both MaxQuant and Progenesis or for both MaxQuant and Progenesis.

Fig. 2.

The dependence of well-performing manipulation chains on the selection of quantification tool comprehensively assessed by the precision of 3,128 potential chains. First, the clustering analyses among manipulation chains across multiple datasets were conducted for three quantification tools: (A) MaxQuant, (B) Progenesis, and (C) OpenMS. Then, three neighboring partitions of varied performance were identified, which included partition αcontaining the chains of consistently superior precision (PMADs <0.14) across multiple datasets, partition βincluding the chain of good precision (PMADs <0.3) across multiple datasets, partition γ consisting of the chains of fair precision (PMADs <0.7) for multiple datasets. Finally, the Venn diagrams showing the chains shared by multiple tools or demonstrating tool-specific characteristics were provided for the chains within (D) partition α, (E) partition α and β, and (F) partition α and β and γ.

Inconsistency among the Quantification Performance Assessed from Multiple Perspectives

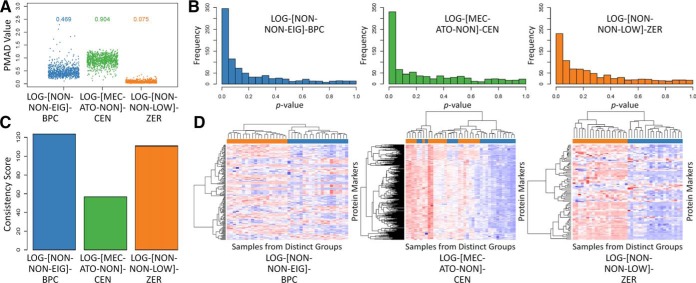
Besides precision (28), several other criteria could be used to assess the performance of LFQ (24), which include: the quantification accuracy (6) and robustness (29), classification capacity (49), and differential abundance analysis (50). Given the huge amount of potential manipulation chains and complicated nature of the studied datasets, the level of consistency among the performance assessed by different criteria was essential for proteomic quantification. Thus, the benchmark dataset (Table II, study 10 (29)) acquired using SWATH-MS was collected, and the quantification performance of three example chains (as illustrated in Fig. 3) were assessed by multiple criteria. Particularly, due to the lack of spiked proteins in the collected dataset, the performance of the example chains were assessed only by four criteria: precision (Fig. 3A), differential abundance analysis (Fig. 3B), robustness (Fig. 3C), and classification capacity (Fig. 3D). As illustrated, the performance of the different chains evaluated by the same criterion varied greatly, and there was substantial inconsistency among the performance of a given chain assessed using different criteria. For example, LOG-[MEC-ATO-NON]-CEN performed the worst in precision (Fig. 3A) but was top-ranked for differential abundance analysis (Fig. 3B).

Fig. 3.

The performance of three representative manipulation chains (LOG-[NON-NON-EIG]-BPC, LOG-[MEC-ATO-NON]-CEN and LOG-[NON-NON-LOW]-ZER) assessed by multiple criteria: (A) precision, (B) differential abundance analysis, (C) robustness, and (D) classification capacity. Each manipulation method within a chain was abbreviated by a three-letter code that was defined in Table I.

The inconsistency among the quantification performance assessed by multiple criteria can also be found in Table III. For all quantification tools, the precision of LOG-[MEC-RAN-PQN]-BPC was “superior,” but its robustness was always “low. Similarly, as shown in supplemental Table S2, the precision of BOX-[NON-VAS-EIG]-BAK was consistently “poor”, but its accuracy was always “high”. However, the chains performing well under both criteria could also be found (e.g. the LOG-[MDC-RAN-EIG]-KNN performed well under both precision and robustness in Table III). Moreover, as shown in supplemental Fig. S1, some chains (e.g. BOX-[NON-PAR-TIC]-KNN) performed consistently well across all criteria, while others (e.g. BOX-[MEC-VAS-PQN]-BAK) always lacked quantification capacities under multiple criteria. Because these criteria complement one another, a collective consideration of them may lead to simultaneous improvement in precision, accuracy, or robustness. In other words, a collective optimization of LFQ based on the assessment of >3,000 chains may facilitate the discovery of well-performing LFQs.

Simultaneously Enhancing Precision and Accuracy of Data Manipulation by Chain Optimization

(1) For the Proteomic Data Acquired by Data-Independent Acquisition (DIA)

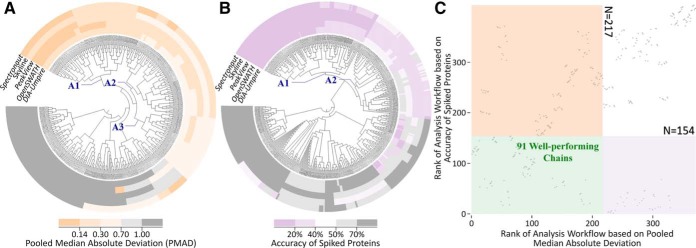
As one of the most advanced DIA techniques, the SWATH-MS-based proteomics was recently applied to provide more comprehensive detection and accurate quantitation of proteins compared with the traditional technique (68). In order to identify the LFQs of the simultaneously improved quantification precision and accuracy, five DIA-based benchmarks of Table II, study 11 (6), preprocessed by five quantification tools (DIA-Umpire, OpenSWATH, PeakView, Skyline, and Spectronaut), were collected to reveal the difference in precision and accuracy among various chains. By analyzing the nature of the five studied datasets and their obedience toward the assumption of the manipulation methods shown in Table I, all normalization methods (excluding EIG) and VSN transformation were inappropriate to manipulate studied data because (1) the level of protein abundance could not be assumed as constant among all studied samples and (2) the intensities of the vast majority of proteins could not be assumed as unchanged. In other words, because both assumptions (A-β and A-γ) could not hold for the studied datasets, the methods based on these assumptions were fundamentally inappropriate for the datasets and were excluded from the >3,000 potential chains. As a result, clustering analysis was used to identify the relationships among the performance of the remaining 480 potential manipulation chains. As illustrated in Fig. 4A, quantification precision of the majority of these 480 chains was consistent across five quantification tools, and the chains within partition A (A1, A2, and A3) performed consistently well across five quantification tools. Similar to precision, the accuracy of most chains were also consistent across these tools (Fig. 4B), and the chains within partition A (A1 and A2) performed consistently well across five tools. Based on the above assessments by two criteria, Fig. 4C provided the ranks of each manipulation chain (indicated by gray dot) collectively defined by precision (horizontal axis) and accuracy (vertical axis). The pink, violet, and green regions indicate the chains of good precision (partition A in Fig. 4A), good accuracy (partition A in Fig. 4B), and good performance for both precision and accuracy, respectively. This finding revealed the feasibility of identifying the chains of simultaneously improved precision and accuracy, which was known as the key issue for SWATH-MS-based quantitative proteomics (69). Moreover, there were 91 manipulation chains (within the green region of Fig. 4C) identified as well-performing under both criteria (precision and accuracy). The analysis on the distribution of the manipulation methods in these 91 chains could facilitate the discovery of the chains suitable for SWATH-MS-based proteomics.

Fig. 4.

The strategy proposed in this study to discover the manipulation chains of simultaneously improved precision and accuracy based on the benchmarks from Table II, study 11. First, clustering analyses among chains across five quantification tools were conducted for (A) precision and (B) accuracy. Second, a two-dimensional scatter plot (C) was drawn to show the ranks of each manipulation chain (represented by a gray dot) collectively determined by precision (horizontal axis) and accuracy (vertical axis). The pink, violet, and green areas in C denoted the chains of good precision (A1+A2+A3 in A), good accuracy (A1+A2 in B), and good performance for both, respectively. As a result, 91 chains (within the green region of C) were found to perform well under both criteria (precision and accuracy).

Therefore, the distributions of manipulation methods in the identified chains were systematically analyzed. As shown in Fig. 5, 63 out of 91 (69.2%) chains were based on LOG transformation, and the remaining adopted BOX transformation. On one hand, two centering methods (MEC and MDC) and the noncentering (NON) showed equal chance to combine with LOG, which denoted that the selection of different centering methods (even noncentering) could hardly influence LFQ's performance when combining with LOG. On the other hand, only NON was in combination with BOX transformation, which indicated that BOX did not prefer to combine with any centering approach under this circumstance. Among four scaling methods together with the nonscaling (NON), only two (RAN and NON) were suitable for combining with LOG. If RAN was applied, the EIG normalization together with the nonnormalization (NON) became the ones of good performance. Moreover, the combinations of BOX-ATO and BOX-RAN were found equally suitable for quantifying this SWATH-MS dataset, and the EIG normalization and NON were still found to perform well. When the vast majority of the proteins were differentially expressed between distinct sample groups, EIG was reported to be not only effective in reducing the intragroup variations (good precision) but also suitable for normalizing the data of spiked proteins (good accuracy) (27), which was consistent with the finding of this study. For seven imputation methods together with the nonimputation (NON), they showed equal chance within those 91 chains, which indicated that the selection of different imputation (even NON) had nothing to do with the quantification performance in this situation.

Fig. 5.

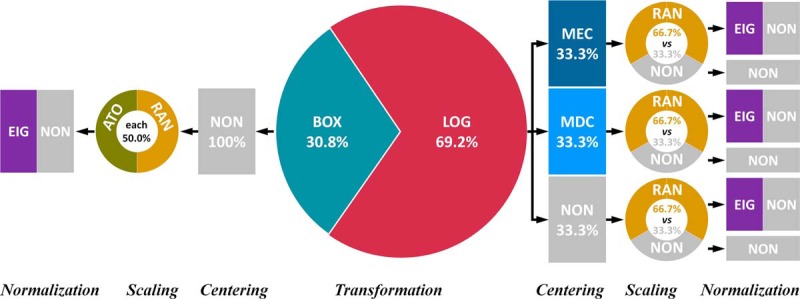
The distribution of manipulation methods in 91 well-performing chains identified based on five DIA-based datasets from Table II, study 11. The manipulation method was abbreviated by three-letter code that was defined in Table I. For the seven imputation methods together with the nonimputation (NON), they demonstrated the exactly equal chances within the 91 well-performing chains, which showed that the selection of different imputation methods (even NON) had nothing to do with the performance under this circumstance. Therefore, the imputation methods were not displayed in this distribution. All normalization methods together with VSN transformation were found inappropriate for manipulating the five DIA-based benchmarks, and the assumptions of these methods did not hold for the studied dataset.

(2) For the Proteomic Data Acquired by DDA

For DDA-based proteomics, it was also necessary to consider both quantification precision and accuracy (27, 28). Therefore, four DDA-based benchmark datasets from Table II, study 2 of distinct concentrations (12.5 versus 25 fmol/μg) of spiked UPS1 protein (58), preprocessed by four quantification tools (IRMa-hEIDI, MaxQuant, MFPaQ, and Scaffold), were collected to uncover the difference in both precision and accuracy among manipulation chains. Based on the preanalyses on the nature of the four studied datasets and their obedience toward the assumption of manipulation methods, all methods were appropriate to manipulate these benchmarks in the first place. Then, the clustering analysis was used to reveal the relationship among the performance of 3,128 chains. Similar to Fig. 4, these chains of consistently good performance in precision and accuracy were partitioned into a clustered area (A1, A2, and A3) in supplemental Fig. S2A and another clustered area (A1 and A2) in supplemental Fig. S2B, respectively. The regions in supplemental Fig. S2C colored in pink, violet, and green indicate the chains of good precision (areas of A1, A2, and A3 in supplemental Fig. S2A), good accuracy (areas of A1 and A2 in supplemental Fig. S2B), and good performance in precision and accuracy, respectively. The red dot in supplemental Fig. S2C denotes the chain used in the original study (58), which was among those identified 728 chains of consistently good performance. However, hundreds of chains were identified as performing better than the original one in both precision and accuracy (shown in the lower left corner of supplemental Fig. S2C). Besides the four benchmarks analyzed previously, there were nine additional benchmarks of the distinct concentrations of the spiked UPS1 proteins (58). Herein, these nine benchmarks were analyzed using the same strategy discussed previously, and nine sets of manipulation chains performing well in both precision and accuracy were identified (supplemental Figs. S3–S11). Together with the first benchmark dataset of 12.5 versus 25 fmol/μg, the intersection of 10 sets of well-performing chains led to 133 chains well-performing under both criteria (precision and accuracy).

Moreover, a systematic analysis on the distributions of manipulation methods in the identified 133 chains was also conducted. As shown in supplemental Fig. S12, 84 out of the 133 (63.2%) identified chains were based on LOG transformation, and the remaining used BOX transformation. When combining with LOG, TMM was the only normalization method performing well under both precision and accuracy. Two centering methods (MEC and MDC) and the noncentering (NON) showed equal chances to combine with LOG-scaling-normalization, which indicated that the selection of different centering methods (even noncentering) could hardly influence the quantification performance in this situation, but the centering would be accompanied by different scaling methods (PAR, RAN, and NON were suitable for all centering). When combining with BOX, TMM, QUA, and TIC normalization stood out from all normalization methods. Only noncentering was integrated with BOX transformation, which demonstrated that BOX did not prefer to combine with any centering method under this circumstance. To the best of our knowledge, the TIC, TMM, and QUA have been frequently applied for normalizing the spectral-counting-based proteomic datasets (42, 70–72). Moreover, a comprehensive literature search in PubMed by combining the name of the remaining normalization methods with “spectral counting” and “proteomics” resulted in few publications, which may indicate the incapability of these methods in simultaneously improving precision and accuracy. For seven imputation methods together with nonimputation (NON), they showed exactly equal chances within those 133 well-performing chains, which denoted that the selection of different imputation methods (even NON) still had nothing to do with the performance in this situation.

Collectively Improving Precision and Robustness of Data Manipulation by Chain Optimization

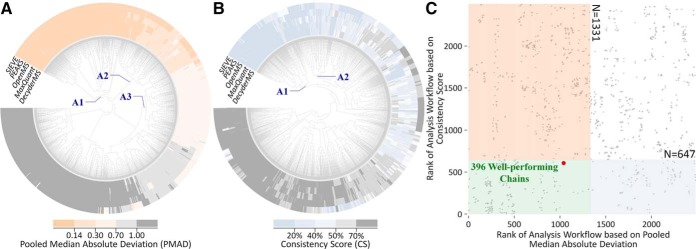
Precision (28) and robustness (29) (with distinct underlying theory) are two well-established criteria for assessing manipulation chain's performance. Particularly, both criteria should be collectively considered not only to reduce proteome variations among replicates but also to enhance consistencies among different lists of identified biomarkers (24, 27). In this study, five proteomic benchmark datasets from Table II, study 1 (23), preprocessed by various quantification tools (DecyderMS, MaxQuant, OpenMS, PEAKS, and Sieve), were first collected to reveal the difference in both precision and robustness among the chains. Based on the preanalysis on the nature of these five studied datasets and their obedience toward the assumption of manipulation methods, all methods were appropriate for manipulating the datasets in the first place. Then, clustering analysis was conducted to discover the relation among the performance of different chains. As shown in Fig. 6A, the precision of the majority of >3,000 chains were consistent among quantification tools, and the chains within partition A (A1, A2, and A3) performed consistently well in five tools. Similar to precision, the robustness of most manipulation chains was consistent for five tools (Fig. 6B), and the chains in partition A (A1 and A2) performed consistently well across five different tools. Based on the preceding evaluation from two perspectives, Fig. 6C illustrates the ranks of each chain (represented by a gray dot) collectively determined by precision (horizontal axis) and robustness (vertical axis). Pink, blue, and green regions in Fig. 6C indicate those chains of good precision (partition A in Fig. 6A), good robustness (partition A in Fig. 6B), and good performance for both precision and robustness, respectively. Moreover, the red dot in Fig. 6C denotes the chain adopted in the original study (23), which was among the identified 396 chains of consistently good performance. However, hundreds of chains were also discovered to perform better than the original one in both precision and accuracy (shown in the lower left corner of Fig. 6C). This finding reveals the feasibility of identifying the manipulation chains of collective enhancements in precision and robustness, which is essential for current proteomics (24, 27).

Fig. 6.

The strategy proposed in this study to discover the manipulation chains of simultaneously improved precision and robustness based on benchmarks collected from Table II, study 1. First, clustering analysis among manipulation chains across five quantification tools was conducted for (A) precision and (B) robustness. Second, a two-dimensional scatter plot (C) was drawn to provide the ranks of each chain (represented by gray dot) collectively determined by precision (horizontal axis) and robustness (vertical axis). The pink, blue, and green areas in C indicated the chains of good precision (A1+A2+A3 in A), good robustness (A1+A2 in B), and good performance for both precision and robustness, respectively. As a result, 396 chains (within the green area of C) were found to perform well under both criteria (precision and robustness).

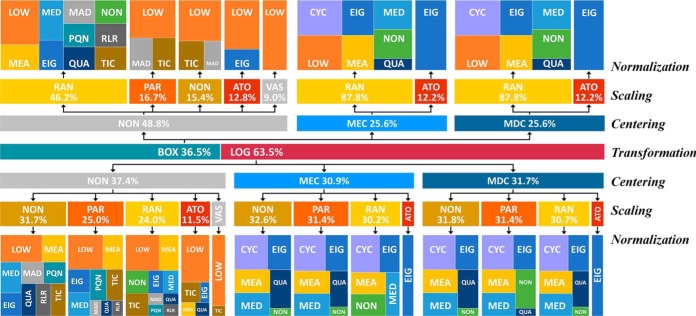
Furthermore, the analysis on the distribution of manipulation methods in those identified 396 chains was conducted. As illustrated in Fig. 7, 251 out of these 396 (63.5%) identified chains were based on LOG transformation, and the remaining used BOX transformation. If the centering methods (MEC/MDC) were applied, both RAN and ATO scaling showed great chance of good performance, and PAR scaling together with the nonscaling (NON) demonstrated high chance of good performance when combining with LOG. For normalization, several methods showed great chance of good performance, including CYC, EIG, MED, MEA, QUA, and sometimes LOW. If noncentering was applied, all scaling methods had the chance of good performance, and the normalization methods showing a good performance included LOW, MEA, EIG, TIC, and MAD. Similar to the previous discussion, seven imputation methods together with the nonimputation (NON) showed a similar chance within 396 well-performing chains, which indicated that the selection of different imputation methods (even NON) might have little impact on the performance in this situation. As a transformation method integrating the normalization technique, VSN performed well under this circumstance regardless of the selection of imputation methods (even NON).

Fig. 7.

The distribution of manipulation methods in the 396 well-performing chains identified based on the datasets from Table II, study 1. The manipulation methods were abbreviated by three-letter codes (defined in Table I). For the seven imputation methods together with the nonimputation (NON), they showed similar chances within those 396 chains, which indicated that the selection of different imputation methods (even the NON) may have slight influence on the performance under this circumstance. Therefore, the imputation methods were not displayed in this distribution.

Development of an Online Tool for Proteomic Quantification and Performance Assessment

Because the underlying theories of multiple criteria were distinct from each other, a collective consideration of the quantification precision, accuracy, and robustness as well as qualitative criteria could achieve the most comprehensive assessment and were reported to be essential for modern proteomic research (24, 27). However, because of the dataset-dependent nature of performance assessment and the lack of suitable datasets for assessing the feasibility of the proposed strategy, a powerful tool for proteomics quantification and performance assessment was urgently needed. So far, several LFQ-relevant tools have been available and popular in proteome quantification (supplemental Table S5). Gmine (73) and Perseus (74) integrated various manipulation methods in their quantification process, but no performance assessment function was provided. LFQbench (6) and msCompare (75) were recognized for evaluating the performance of three to five tools. The Normalyzer (28), SPANS (76), and GiaPronto (77) were distinguished as able to assess one to eight pretreatment methods. Because a typical LFQ combined both quantification tool and manipulation method, any assessment focusing solely on the tool or the method could not fully reflect the overall performance of LFQ. Moreover, none of these tools could systematically assess the performance (as highly recommended by the previous studies (24, 27)) based on multiple criteria of distinct underlying theories. Because the performance of given LFQs was susceptible to the studied dataset (78), it was essential to find the most appropriate tool together with a manipulation chain for particular datasets. However, it was challenging to perform such discovery as there were large numbers of potential workflows and the multifaceted nature of the evaluation criteria.

Therefore, a web-based tool (official site: https://idrblab.org/anpela/; mirror sites: http://idrblab.cn/anpela/, http://idrb.zju.edu.cn/anpela/) was developed as the first tool enabling the performance assessment of the entire LFQ manipulation chain (collectively assessed by five well-established criteria) in this study. This tool not only automatically detects the diverse formats of data generated by all quantification tools but also provides the most complete set of manipulation methods among available web-based and standalone tools (supplemental Table S5). Due to its unique abilities in discovering well-performing chains, performing assessment from multiple perspectives, and validating quantification accuracy based on spiked proteins, it has great application potentials for any proteomic studies requiring LFQ technique. This online tool can be readily accessed by users with no login requirement and is freely accessible using a variety of popular web browsers such as Google Chrome, Mozilla Firefox, Safari, and Internet Explorer (10 or later), and the procedures for using this online tool are fully illustrated and documented in its online tutorial.

Due to the tremendous computational workload required for assessing >3,000 chains, it is extremely time- and resource-consuming to make this comprehensive assessment service online. Therefore, an alternative way of enabling the evaluation on a user's local computer was provided as standalone software, which can be downloaded from both the official and mirror sites and provides the same sets of assessment metrics and plots as that of the online version. The exemplar input and output files can be downloaded together with the source code of this standalone tool. The installation and configuration of R environment together with a number of packages required before running the tool are provided in the User Manual (downloadable from its website), which can help the users to get familiar with this tool as soon as possible.

CONCLUSION

Based on the in-depth analyses in this study, some common trends in the identified well-performing chains were discovered, which might give recommendation for researchers in relevant fields. As shown in Figs. 2A-2C, although there were manipulation chains dependent heavily on the studied datasets (great variations in the colors of PMAD), >50% of the analyzed chains showed a consistent precision (the same colors of PMAD) across multiple datasets. These results indicate that there were manipulation chains performing consistently well/badly regardless of the analyzed datasets. Similarly, as provided in Figs. 4A and 4B, although there were chains dependent on the applied software tools (variations in the branch colors), many studied chains gave consistent performance (the same branch colors) across multiple software tools. These results denoted that, similar to various datasets, there were manipulation chains performing consistently well/badly regardless of the applied software tools. Moreover, the well-performing manipulation chains identified for DIA and DDA datasets were shown in Fig. 5 and supplemental Fig. S12, respectively. As shown, although there were some common features between the identified manipulation methods, there were great variations in these figures. These results denoted that the well-performing methods also depended on the acquisition methods. Based on the preceding analyses, variations could be frequently induced by different datasets, various acquisition methods, and diverse software tools, which made it extremely essential to develop tool for both proteomic quantification and comprehensive performance assessment. Thus, a tool was developed to enable the performance assessments of the entire data manipulation chain (collectively assessed by five well-established criteria) in this study. This online tool not only automatically detected the diverse formats of data generated by quantification tools but also provided the most complete set of manipulation methods among all available web-based and standalone tools.

DATA AVAILABILITY

The mass spectrometry proteomics data were previously published (see Table II) and have been deposited to the ProteomeXchange Consortium via the PRIDE partner repository with the data set identifiers PXD001819, PXD002882, PXD006129, PXD006224, PXD002885, PXD002099, PXD006336, PXD003972 and PXD002952.