A comparison of the transport kinetics of glycine transporter 1 and glycine transporter 2

Erdem et al. compare the kinetics of the SLC6 family glycine transporters GlyT1 and GlyT2. Though the two transporters are rate-limited by distinct reaction steps, they both display high transport capacity, with the kinetics of GlyT1 sufficient to supply extracellular glycine to the NMDA receptor.

Abstract

Transporters of the solute carrier 6 (SLC6) family translocate their cognate substrate together with Na⁺ and Cl⁻. Detailed kinetic models exist for the transporters of GABA (GAT1/SLC6A1) and the monoamines dopamine (DAT/SLC6A3) and serotonin (SERT/SLC6A4). Here, we posited that the transport cycle of individual SLC6 transporters reflects the physiological requirements they operate under. We tested this hypothesis by analyzing the transport cycle of glycine transporter 1 (GlyT1/SLC6A9) and glycine transporter 2 (GlyT2/SLC6A5). GlyT2 is the only SLC6 family member known to translocate glycine, Na⁺, and Cl⁻ in a 1:3:1 stoichiometry. We analyzed partial reactions in real time by electrophysiological recordings. Contrary to monoamine transporters, both GlyTs were found to have a high transport capacity driven by rapid return of the empty transporter after release of Cl⁻ on the intracellular side. Rapid cycling of both GlyTs was further supported by highly cooperative binding of cosubstrate ions and substrate such that their forward transport mode was maintained even under conditions of elevated intracellular Na⁺ or Cl⁻. The most important differences in the transport cycle of GlyT1 and GlyT2 arose from the kinetics of charge movement and the resulting voltage-dependent rate-limiting reactions: the kinetics of GlyT1 were governed by transition of the substrate-bound transporter from outward- to inward-facing conformations, whereas the kinetics of GlyT2 were governed by Na⁺ binding (or a related conformational change). Kinetic modeling showed that the kinetics of GlyT1 are ideally suited for supplying the extracellular glycine levels required for NMDA receptor activation.

Introduction

Glycine is an amino acid neurotransmitter that elicits both neuronal inhibition and excitation in the central nervous system. In neurons of the adult mammalian brain, ionotropic glycine receptors are inhibitory, because they support Cl⁻ influx and subsequent cellular hyperpolarization. Glycine is excitatory by acting as a coagonist of N-methyl-D-aspartate receptors (NMDARs; Johnson and Ascher, 1987). Glycinergic neurotransmission is terminated by clearance of glycine from the extracellular space (Johnston and Iversen, 1971). This is achieved by two glycine transporter subtypes: glycine transporter 1 (GlyT1) and glycine transporter 2 (GlyT2; Guastella et al., 1992; Liu et al., 1993; Kim et al., 1994). GlyT1 is predominantly expressed in astrocytes, and it is thought to regulate the glycine concentration in the vicinity of NMDARs. This concept was originally proposed based on the observation that coexpression of GlyT1 modulated the function of NMDARs in oocytes (Supplisson and Bergman, 1997) and in neurons (Bergeron et al., 1998). In contrast, GlyT2 is expressed in glycine-releasing neurons in the spinal cord and in the brain stem, where it drives the reuptake of glycine into presynaptic terminals (Liu et al., 1993). GlyT2-dependent influx of glycine does not only clear the synapse but also replenishes vesicular stores. Inactivating mutations in GlyT2 phenocopy mutations in inhibitory glycine receptors A and B and lead to hyperekplexia/startle disease (Carta et al., 2012; Giménez et al., 2012), because the inhibitory tone provided by glycine is absent. This highlights the importance of GlyT2 in maintaining presynaptic vesicular glycine stores.

The GlyTs belong to the solute carrier 6 (SLC6) family of transporters. Both subtypes harness the energy stored in the transmembrane-concentration gradients of Na⁺ and Cl⁻ to transport glycine against an opposing gradient. Their stoichiometry has been elucidated and is 2 Na⁺/1 Cl⁻/1 glycine and 3 Na⁺/1 Cl⁻/1 glycine for GlyT1/SLC6A9 and GlyT2/SLC6A5, respectively (López-Corcuera et al., 1998; Roux and Supplisson, 2000). Both GlyTs carry a positive net charge through the membrane upon glycine transport. Thus, in cells expressing GlyTs, glycine gives rise to transport-associated currents, which can be measured by voltage clamp recordings. An analysis of these currents allows for extracting information on the transport cycle provided that solutions are rapidly exchanged. In fact, by using this technique, comprehensive models have been developed for the transporters for dopamine (DAT/SLC6A3; Erreger et al., 2008) and serotonin (SERT/SLC6A4; Schicker et al., 2012). This has allowed for interrogating the transport cycle to understand how the monoamine transporters operate, how they switch between transport modes, and how (co)substrates, inhibitors, and allosteric modulators impinge on the transport cycle (Bulling et al., 2012; Li et al., 2015; Hasenhuetl et al., 2016, 2018; Bhat et al., 2017; Kern et al., 2017). It is safe to assume that the transport cycle of all SLC6 transporters is comprised of similar partial reactions. However, it is likely that the kinetic decision points differ: transporters, for instance, have to cope with different membrane potentials depending on whether they operate in neurons or glial cells. In addition, monoamine transporters and GlyTs are on different branches of the SLC6 family tree (Bröer and Gether, 2012). Here, we explored the transport cycles of GlyT1 and GlyT2. The underlying hypothesis posits that GlyT1 and GlyT2 differ in rate-limiting partial reactions and their voltage dependence, which reflects their adaption to distinct physiological environments. The analysis confirmed the working hypothesis and revealed that the transport cycles of GlyT1 and GlyT2 have distinct rate-limiting steps, which are differentially affected by membrane voltage. These dissimilarities between GlyT1 and GlyT2 were recapitulated in kinetic models, which allowed for rationalizing the impact of the different operating modes on synaptic glycine levels.

Materials and methods

Cell culture

Cercopithecus aethiops SV40-transformed kidney (Cos-7) cells were obtained from American Type Culture Collection (ATCC CRL-1651) and cultured in Dulbecco’s modified Eagle’s medium containing 10% fetal bovine serum. The cells were passaged every 2–4 d. For electrophysiological experiments, the cells were seeded into 35-mm dishes. Once confluent, they were transfected with a plasmid encoding N-terminally GFP-tagged hGlyT1b or hGlyT2a, respectively; the cDNAs of hGlyT1b in eGFP-C-1 and hGlyT2b in pcDNA3.1(+)-N-eGFP were bought from Genscript. The transfection was performed with jetPRIME (0.8 µg DNA/dish) according to the manufacturer’s protocol. On the following day, the cells were seeded at low density into poly-D-lysine–coated dishes. Current recordings were conducted 16–24 h after seeding.

Electrophysiology

Substrate-induced currents were recorded in the whole-cell patch clamp configuration. Unless otherwise stated, the external solution consisted of 140 mM NaCl, 2.5 mM CaCl₂, 2 mM MgCl₂, 20 mM glucose, and 10 mM HEPES, pH adjusted with NaOH to pH 7.4. The internal solution consisted of 5.9 mM NaCl, 1 mM CaCl₂, 0.7 mM MgCl₂, 10 mM EGTA, 10 mM HEPES, and 133 mM K-gluconate, pH adjusted with potassium hydroxide (KOH) to pH 7.2. Experiments with varying external Na⁺ concentrations were conducted with solutions obtained by mixing the external solution with Na⁺-free solution (substituted and pH adjusted with NMDG) at the appropriate ratios. Similarly, for experiments that required different Cl⁻ concentrations, these were adjusted by mixing the external solution with Cl⁻-free solution (substituted withmethanesulfonic acid, pH-adjusted with NaOH) at the desired ratios. In some experiments, potassium was omitted from the internal solution and replaced with NMDG. Renderings in the figures show the employed extra- and intracellular ionic compositions. Substrate was used at a concentration of 1 mM unless stated otherwise.

Currents were recorded at room temperature (20–24°C) using an Axopatch 200B amplifier and pClamp 10.2 software (MDS Analytical Technologies). Current traces were filtered at 1 kHz and digitized at 10 kHz using a Digidata 1440A (MDS Analytical Technologies). Drugs were applied using an Octaflow II system (ALA Scientific Instruments), which permits complete solution exchange around the cells within 50 ms. Current amplitudes in response to glycine application were quantified using Clampfit 10.2 software. Passive holding currents were subtracted, and the traces were filtered using a 100-Hz digital Gaussian low-pass filter.

Uptake

Cos-7 cells were transiently transfected with hGlyT1b or hGlyT2a. Cells were seeded into poly-D-lysine–coated wells (2–3 ⋅ 10⁴ cells/well) of 96-well plates 24 h before the experiment. On the day of the experiment, the medium was aspirated, and the wells were washed with 0.1 ml of external solution (same composition as outlined above for patch clamp experiments) containing the concentration of Cl⁻ indicated in the pertinent figure. The uptake was initiated by adding 50 µl of 0.1 µM [³H]glycine (50 Ci/mmol) in the corresponding external solution and allowed to proceed for 15 min at room temperature. Thereafter, the cells were rapidly rinsed with an ice-cold external solution and subsequently lysed in 1% SDS. The released radioactivity was quantified by liquid scintillation counting. Preliminary experiments verified that uptake of [³H]glycine was linear with time for >20 min. Nonspecific uptake was determined in the presence of 1 mM and 10 mM cold glycine for hGlyT1b and hGlyT2a, respectively.

Modeling

Kinetic models for GlyT1 and GlyT2, respectively, were built to account for the data (cf. Fig. 7). Time-dependent changes in state occupancies were evaluated by numerical integration of the resulting system of differential equations using Systems Biology Toolbox (Schmidt and Jirstrand, 2006) and MATLAB 2015a (MathWorks). The voltage dependence of individual rates was modeled according to Läuger (1991) assuming a symmetric barrier as

$$k_{ij}= k_{ij}^0\text{exp}(-z_{Qi,j}FV/2RT),$$ (1)

with F = 96485 with C · mol⁻¹ R = 8.314 JK⁻¹mol⁻¹, V as the membrane voltage in volts, T = 293°K, and k^ij0 are the rates at 0 mV. We calculated coupled membrane currents in response to substrate application as

$$I=(-F{\displaystyle \sum }{z}_{Q,ij}(p_i{k}_{ij}-p_j{k}_{ji}))NC/N_A,$$ (2)

with z_Q,ij as the net charge transferred during the transition, NC as the number of transporters set to 10 ⋅ 10⁶ and N_A as 6.022 ⋅ 10²³. The extra- and intracellular ion concentrations were set to the values used in patch clamp experiments. The noninstantaneous onset of substrate in the patch clamp experiments was accounted for by modeling the substrate application as an exponential rise with a time constant of 10 ms.

Figure 7.

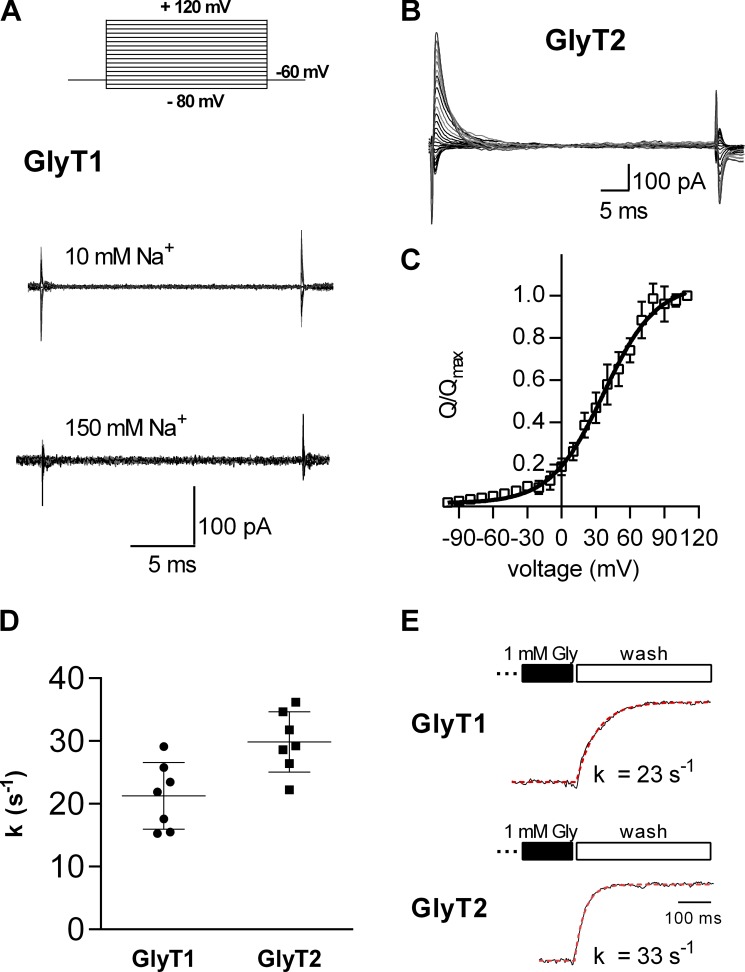
Transporter associated transient elicited by voltage jumps. (A) Protocol used to elicit transient transporter currents. Cells were held at −60 mV and stepped for 30 to 50 ms to voltages between −80 mV and +120 mV. The shown current traces in A and B are the subtraction of currents recorded in absence and in the presence of 1 mM glycine. GlyT1 did not feature transient currents in presence of 10 mM (A, upper trace) or 150 mM external Na⁺ (A, lower trace). However, transient currents were detected in GlyT2 in the presence of 150 mM Na⁺ (B). (C) The Q was plotted as a function of voltage (n = 6 for each data point). The data points in the graph are the Qs normalized to the corresponding largest charge (Q_max) at saturating voltages. The data were fit to a Boltzmann equation (black solid line). The potential at which half of the charge had moved (V_0.5) and the valence estimated by the fit were 36.7 ± 3.1 mV and 1.05 ± 0.12, respectively. The current decays at +30 mV were fit to a monoexponential function, and the estimated time constant was 5 ± 1.6 ms (n = 5). (D) Summary of seven experiments, each showing the deactivation rate (k) upon glycine washout for both GlyT1 and GlyT2. These data were obtained using a setup that allowed for rapid solution removal. Measurements were performed using standard internal and external solutions at a holding potential of −60 mV. Error bars in C and D represent SD. (E) Representative traces showing current deactivation upon washout of glycine for both GlyT1 and GlyT2, respectively. The deactivation rate k was used to approximate the turnover rate. It was determined by fitting the current decay to a monoexponential function.

Online supplemental material

Fig. S1 presents a full scheme of the transport cycle of GlyT1. Fig. S2 presents a full scheme of the transport cycle of GlyT2. Table S1 presents the reactions and rate constants of GlyT1. Table S2 presents the reactions and rate constants of GlyT2.

Results

Rapid application of glycine evokes an inwardly directed peak current through GlyT1 but not through GlyT2

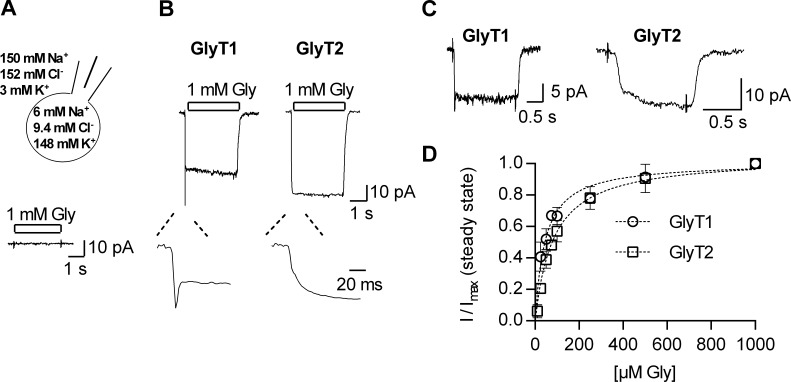
We recorded currents evoked by glycine in the whole-cell patch clamp configuration by relying on a rapid application system. This allowed for exchange of the solution surrounding the cell within 50 ms (Boehm, 1999). Cos-7 cells were selected because glycine did not elicit any appreciable current in untransfected cells (Fig. 1 A). Fig. 1 B shows representative traces of a current through GlyT1 (left panel) and GlyT2 (right panel), both recorded at −60 mV and induced by the application of 1 mM glycine. Consistent with previous reports, glycine evoked a steady current through both GlyT1 and GlyT2, which deactivated upon glycine removal (Supplisson and Bergman, 1997; López-Corcuera et al., 1998; Roux and Supplisson, 2000). In addition, we also observed an initial peak current in GlyT1 expressing cells on glycine application (inset, left panel), which was absent in cells expressing GlyT2 (inset, right panel). To the best of our knowledge, this initial current through GlyT1 has not been described previously. It was inwardly directed and subject to monoexponential decay with a time constant in the range of 10 ms. The detectability of this event was contingent on rapid solution exchange, because the peak current was absent when we reduced the flow rate of our perfusion device (data not shown). The peak current by GlyT1 also depended on the applied glycine concentration: It became clearly discernable from the steady current only at glycine concentrations above 25 µM. This is evident from the representative traces shown in Fig. 1 C, where application of 25 µM glycine onto a cell expressing GlyT1 resulted in a peak current (left panel of Fig. 1 C), but this was not seen in cells harboring GlyT2 (right panel of Fig. 1 C). The amplitude of the steady-state current also depended on the concentration of glycine. In Fig. 1 D, we show the amplitudes of steady currents through GlyT1 and GlyT2, which were elicited by increasing glycine concentrations and normalized to the current recorded at 1 mM glycine. Both curves were adequately described by the equation for a saturation hyperbola. Half-maximal effective concentration (EC₅₀) values of 44.7 ± 2.4 µM and 83.5 ± 5 µM were estimated for GlyT1 and GlyT2, respectively, by curvilinear regression. These values are in good agreement with those of earlier reports (Aubrey et al., 2000; Ju et al., 2004; Wiles et al., 2006).

Figure 1.

Glycine-induced currents through GlyT1 and GlyT2. (A) Top: Cell scheme indicating the intra- and extracellular ion compositions used in the experiments. Bottom: Recording of an untransfected Cos-7 cell challenged with 1 mM glycine. (B) Typical currents evoked on application of 1 mM glycine, recorded from transiently transfected Cos-7 cells held at −60 mV. The left and the right panels show a current through GlyT1 and GlyT2, respectively. The insets are magnifications of the initial period following the application of glycine. GlyT1 features an inwardly directed peak current, which is absent in the current carried by GlyT2. (C) Currents evoked on application of 25 µM glycine in cells expressing GlyT1 or GlyT2. Error bars represent SD. (D) Glycine concentration dependence of the steady current amplitude of GlyT1 (open circles) and GlyT2 (open rectangles; n = 4–7). The current amplitudes were normalized to the corresponding current at 1 mM glycine (I/I_max). The data points were fit to saturation hyperbolas (indicated as dashed lines). The estimated EC₅₀ values for current induction were 43.4 ± 2.2 µM for GlyT1 and 76 ± 5.3 µM for GlyT2.

Voltage dependence of steady and peak current amplitudes

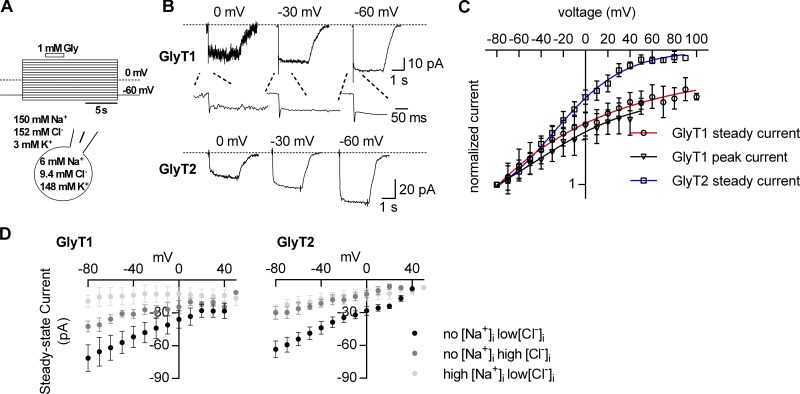
GlyTs operate in cells, which undergo changes in membrane potential. The transport cycles of the GlyTs harbor electrogenic partial reactions. Changes in voltage impinge on these reactions, which can impede normal operation in the forward transport mode. For instance, Na⁺ dissociation from the inward-facing conformation of SERT is voltage-dependent. In the absence of intracellular K⁺ and at potentials more positive than −20 mV, this puts a brake on the transport cycle of SERT. However, subsequent intracellular K⁺ binding remedies this problem: K⁺ binding is also voltage-dependent and cancels voltage-dependent Na⁺ binding. This helps maintain a constant turnover rate over the range of physiological voltages (Hasenhuetl et al., 2016). There is no evidence for countertransport of K⁺ by GlyTs. Hence, it is not clear how the transport cycle of GlyTs copes with the membrane potential. We addressed this question by exploring the voltage dependence of currents through GlyTs and their dependence on intra- and extracellular concentrations of ions. We relied on a fast perfusion system to determine the current–voltage relation of both peak current and the steady-state current through GlyT1: Glycine-induced currents were recorded at voltages ranging from −80 mV to +80 mV. The protocol is illustrated in Fig. 2 A: Cos-7 cells were held at the indicated voltages for a time period of 15 s. During each episode, 1 mM glycine was applied for 3 s. The same protocol was also used to assess the voltage dependence of the steady current through GlyT2. Fig. 2 B shows traces of the resulting currents carried by GlyT1 (upper panel) and GlyT2 (lower panel), which were recorded at 0 mV, −30 mV, and −60 mV. It is obvious from these recordings that the noise was generally larger at 0 mV than at −60 mV. The current–voltage relation was assessed by plotting the current amplitudes as a function of voltage (Fig. 2 C): Both the steady-state and the peak currents were normalized to the corresponding largest currents at −80 mV. The steady-state current amplitudes of GlyT1 and GlyT2 were evaluated up to voltages of +80 mV. In contrast, the analysis of the peak current by GlyT1 was precluded by excessive noise at potentials above +40 mV. Regardless of this limitation, it is clear from Fig. 2 C that the current–voltage relation of both the steady-state currents and the peak current of GlyT1 was only linear in the negative voltage range; at potentials −10 mV or greater, there was a deviation from linearity. As a consequence, the amplitude of the steady-state current through GlyT1 remained substantial up to voltages as positive as +80 mV. We also note that the voltage dependence of the peak current by GlyT1 was very similar to the voltage dependence of its steady current. In contrast, the current–voltage relation for GlyT2 remained essentially linear up to +40 mV. At voltages more positive than +40 mV, the current through GlyT2 was suppressed.

Figure 2.

Voltage dependence of currents through GlyT1 and GlyT2. (A) Voltage protocol used to elicit glycine-induced currents through GlyT1 and GlyT2, respectively. Cells were held at the indicated voltages for 15 s (voltage range: −80 to +80 mV). During each episode, 1 mM glycine was applied to the cell for 3 s. The cell scheme indicates the intra- and extracellular ion compositions used in B and C. (B) Sample traces of currents through GlyT1 (upper panel) and GlyT2 (lower panel) elicited on application of 1 mM glycine when recorded at 0 mV, −30 mV, and −60 mV, respectively. The insets shown in the upper panel are magnifications of the initial period following the application of glycine. (C) Current–voltage relation of the steady-state currents through GlyT1 (open circles) and GlyT2 (open rectangles) and the peak current through GlyT1 (open triangles; n = 10–18). The data points were fit to a Boltzmann equation. The fits are indicated as blue, red, and black solid lines. (D) Voltage dependence of currents induced by 1 mM glycine measured under the following conditions: (1) no Na⁺ low Cl⁻ (1 mM), (2) no Na⁺ high Cl⁻ (150 mM), and (3) high Na⁺ low Cl⁻ (150 mM Na⁺, 1 mM Cl⁻). The left panel shows data of GlyT1 (n = 5). The right panel shows data of GlyT2 (n = 5–7). Either 150 mM intracellular Cl⁻ or 150 mM intracellular Na⁺ suppressed the currents of both subtypes in the explored voltage range (−80 mV to +40 mV). Error bars in C and D represent SD.

Ion dependence of steady current amplitudes

The driving force of the transport cycle is provided by the ionic gradients. In SERT, elevation of intracellular Na⁺ eliminates the forward cycle mode and thus switches the transporter into the exchange mode; in contrast, intracellular Cl⁻ is immaterial to the transport cycle (Hasenhuetl et al., 2016). It is not clear how intracellular Na⁺ and Cl⁻ affect the partial reactions required for completion of the transport cycle of GlyTs. We compared the effect of having no and high intracellular Na⁺ (i.e., 150 mM) on the amplitude of the steady-state current carried by the GlyTs. In these experiments, we kept the intracellular Cl⁻ concentration constant at 1 mM. In GlyT1-expressing cells, the average steady-state current amplitude at 150 mM intracellular Na⁺ was ∼25% at −80 mV of that measured in the absence. As is evident from Fig. 2 D (left panel), high intracellular Na⁺ uniformly suppressed the steady current over the explored voltage range (i.e., −80 mV to +40 mV). Similarly, raising the intracellular Na⁺ concentration to 150 mM in cells expressing GlyT2 reduced the steady-state current by ∼60% at −80 mV, and the currents were uniformly reduced at all voltages (Fig. 2 D, right panel).

We also investigated the effect of cytosolic Cl⁻ on the currents carried by GlyT1 and GlyT2. In these measurements we omitted intracellular Na⁺ and compared the effect of 1 mM and 150 mM intracellular Cl⁻, respectively, on the glycine-induced steady current by the GlyTs. Similar to the suppression seen with high intracellular Na⁺, raising the intracellular Cl⁻ concentration to 150 mM reduced the steady current amplitude. The current amplitude at 150 mM intracellular Cl⁻ was ∼60% at −80 mV of that observed in the presence of 1 mM intracellular Cl⁻ in the case of GlyT1 and 40% at −80 mV in the case of GlyT2 (Fig. 2 D, right panel). In the explored voltage range, high intracellular Cl⁻ uniformly suppressed the steady currents of both subtypes.

Raising the intracellular concentration of either Na⁺ or Cl⁻ is predicted to reduce the steady-state current through the GlyTs, because Na⁺ and Cl⁻ are cosubstrates: A cotransported ion must dissociate into the cytosol to allow for the return of the empty transporter to the outward-facing conformation. At a high intracellular concentration, the cosubstrate is expected to rebind to the inward-facing transporter. This must slow down substrate transport and reduce the amplitude of the steady current. On the contrary, it was surprising that neither 150 mM Na⁺ nor 150 mM Cl⁻ intracellularly sufficed to produce full inhibition of the current. We note that 150 mM NaCl suffices to fully block the current through other SLC6 transporters, i.e., SERT and DAT (Erreger et al., 2008; Hasenhuetl et al., 2016). Full current blockage at high intracellular Na⁺ is a prediction of the alternate access model in a sodium-coupled transporter. We therefore infer that in the case of GlyT1 and GlyT2, 150 mM NaCl is too low a concentration to fully occupy the Na⁺ and/or the Cl⁻ binding site at the inward-facing transporters. To reach full current block, a higher intracellular NaCl concentration is apparently required (presumably >1 M NaCl). However, due to technical limitations, we cannot test concentrations >150 mM NaCl. Regardless of this limitation, these data indicate that the affinity of Na⁺ and of Cl⁻ for the inward-facing state (Ti) of both GlyT1 and GlyT2 is lower than their affinity for the outward-facing conformation.

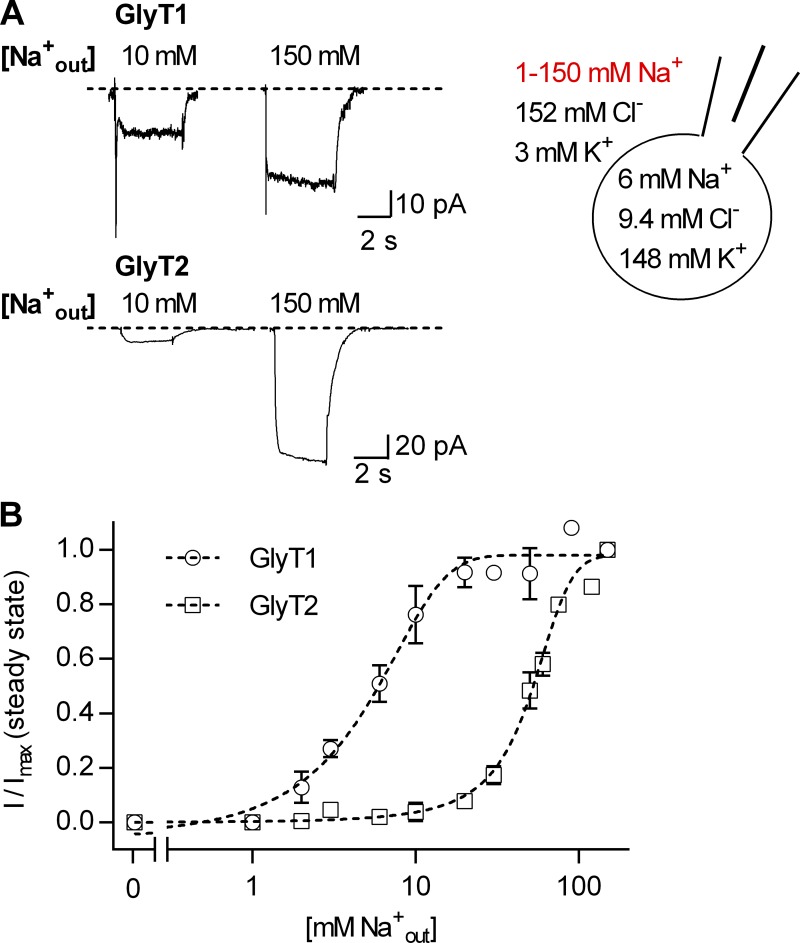
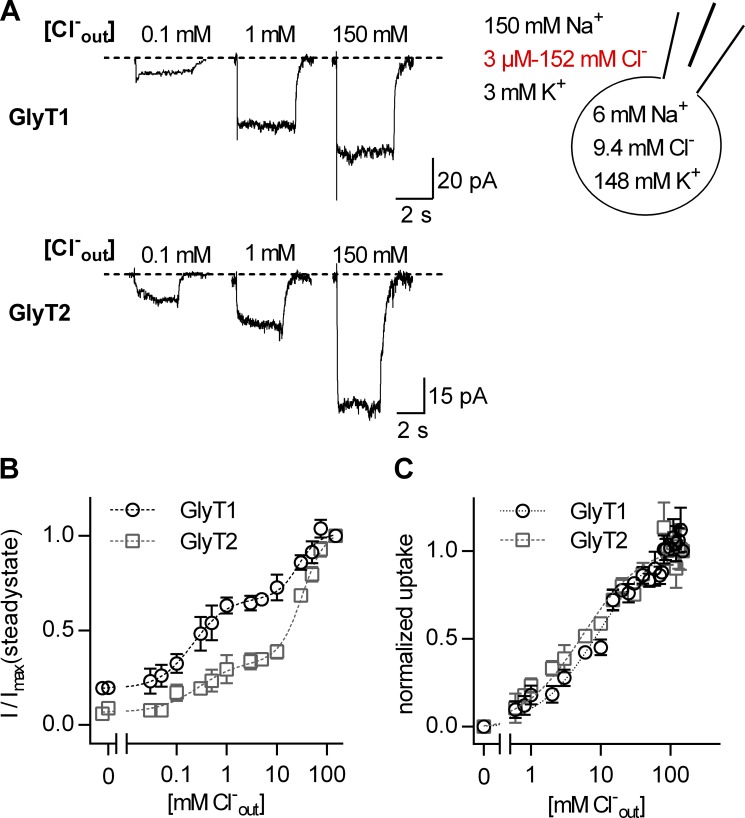
To test the latter, we determined the affinity of Na⁺ and of Cl⁻ for the outward-facing state (To) by examining the dependence of the steady-state current amplitude of GlyT1 and GlyT2 on the extracellular concentration of the cosubstrate Na⁺ and Cl⁻. Fig. 3 A shows representative traces of currents by GlyT1 and GlyT2, which were elicited at −60 mV by 1 mM glycine in the presence of 10 mM and 150 mM extracellular Na⁺ and at constant concentration of extracellular Cl⁻ (i.e., 152 mM). There wasn't any detectable current in the nominal absence of extracellular Na⁺. With increasing Na⁺ concentrations, the steady current amplitude of both GlyTs rose until a maximum was reached at around 100 mM Na⁺ (Fig. 3 B). The data were adequately fit by a Hill equation, and the fit yielded an EC₅₀ of 5.58 ± 0.2 mM and a Hill coefficient of 1.85 ± 0.11 for GlyT1, and an EC₅₀ of 51 mM ± 0.92 and a Hill coefficient of 3.12 ± 0.19 for GlyT2. The Hill coefficients were consistent with the established stoichiometry of GlyT1 and GlyT2: 2 Na⁺ and 3 Na⁺ ions, respectively, are translocated with one molecule of glycine. The chloride dependence is summarized in Fig. 4: Fig. 4 A depicts representative traces of currents, which were elicited at −60 mV by 1 mM glycine in the presence of 0.1 mM, 1 mM, and 150 mM extracellular Cl⁻ and at 150 mM external Na⁺. The concentration–response curves are shown in Fig. 4 B: With increasing Cl⁻ concentrations, the current amplitude rose in a nonmonotonous manner. To adequately fit the data, it was necessary to employ the equation for a biphasic concentration–response curve. The fit provided two affinity estimates for Cl⁻. The EC₅₀ values of the high- and low-affinity component were 0.21 ± 0.04 mM and 26.4 ± 3.6 mM for GlyT1, respectively, and 0.28 ± 0.1 mM and 32.1 ± 1.8 mM for GlyT2, respectively. We envisage two alternative explanations to account for the biphasic concentration dependence: Either there are two populations of the transporters featuring different Cl⁻ affinities, or there is an additional allosteric chloride binding site (of low affinity), which, upon Cl⁻ binding, leads to acceleration of the transport cycle. It is difficult, however, to design an experiment that can distinguish between these two possibilities. We note that Antonov et al. (2005) provide indirect evidence for an internal allosteric Cl⁻ binding site.

Figure 3.

Dependence of currents through GlyT1 and GlyT2 on extracellular Na⁺. (A) Representative current traces evoked by 1 mM glycine in the presence of 10 mM and 150 mM extracellular Na⁺. The upper panel shows currents through GlyT1, the lower panel currents through GlyT2. The cell scheme shows the intra- and extracellular ion composition used in the displayed experiments. The varying extracellular Na⁺ concentrations are indicated in red. (B) Dependence of the steady current amplitude on the concentration of extracellular Na⁺. Open circles are the normalized average current amplitudes of GlyT1. Open rectangles are the normalized average current amplitudes of GlyT2. The currents were normalized to corresponding largest current at 150 mM extracellular Na⁺. The data were fit to the Hill equation (dashed lines), and the fits yielded an EC₅₀ of 5.58 ± 0.2 mM and a Hill coefficient of 1.85 ± 0.11 for GlyT1 and an EC₅₀ of 51 mM ± 0.92 and a Hill coefficient of 3.12 ± 0.19 for GlyT2 (n = 3–5 for each point). The axis break divides the abscissa into a linear and a logarithmic scale. Error bars represent SD.

Figure 4.

Dependence of currents through GlyT1 and GlyT2 on extracellular Cl⁻. (A) Sample currents evoked by 1 mM glycine in the presence of 0.1 mM, 1 mM, and 150 mM extracellular Cl⁻ through GlyT1 (upper panel) and GlyT2 (lower panel). The cell scheme shows the intra- and extracellular ion compositions used in the displayed experiments. The varying extracellular Cl⁻ concentrations are indicated in red. (B) The dependence of the steady current amplitude on the concentration of extracellular Cl⁻ for GlyT1 (open circles) and for GlyT2 (open rectangles). The currents were normalized to the corresponding current at 150 mM extracellular Cl⁻. The data points were fit to a biphasic dose response curve (dashed lines, n = 4 each concentration). The EC₅₀ values of the high- and low-affinity components were 0.21 ± 0.05 mM and 26.4 ± 3.6 mM for GlyT1, respectively, and 0.28 ± 0.1 mM and 32.1 ± 1.8 mM for GlyT2, respectively. (C) Dependence of [³H]glycine uptake on extracellular Cl⁻, normalized to uptake at 150 mM Cl⁻ (n = 3 for each concentration). A fit to a one-site binding model (dashed lines) yielded EC₅₀ of 5.5 ± 0.6 for GlyT1 and 2.4 ± 0.2 mM for GlyT2. The axis breaks in B and C divide the abscissae into linear and logarithmic scales. Error bars in B and C represent SD.

In the absence of Cl⁻, we observed robust glycine-induced currents, which were larger in GlyT1- than in GlyT2-expressing cells (Fig. 4 B). This was surprising: The results of previous studies suggested that the currents of both GlyTs are fully coupled to the transport of glycine (Roux and Supplisson, 2000). This predicts that the amplitude of the steady current and the amount of glycine uptake are equivalent measures. Accordingly, we measured uptake of radiolabeled glycine into Cos-7 cells expressing GlyT1 or GlyT2 in the presence of different extracellular Cl⁻ concentrations (Fig. 4 C). In contrast to the amplitudes of the steady currents, the dependence of glycine uptake on Cl⁻ was monophasic. The fits yielded EC₅₀ values of 5.5 ± 0.6 mM for GlyT1 and 2.4 ± 0.2 mM for GlyT2. Moreover, there wasn't any glycine uptake in the nominal absence of extracellular Cl⁻. The latter suggests that the GlyTs carry uncoupled currents in the absence of Cl⁻.

Cooperative binding of cosubstrates and glycine

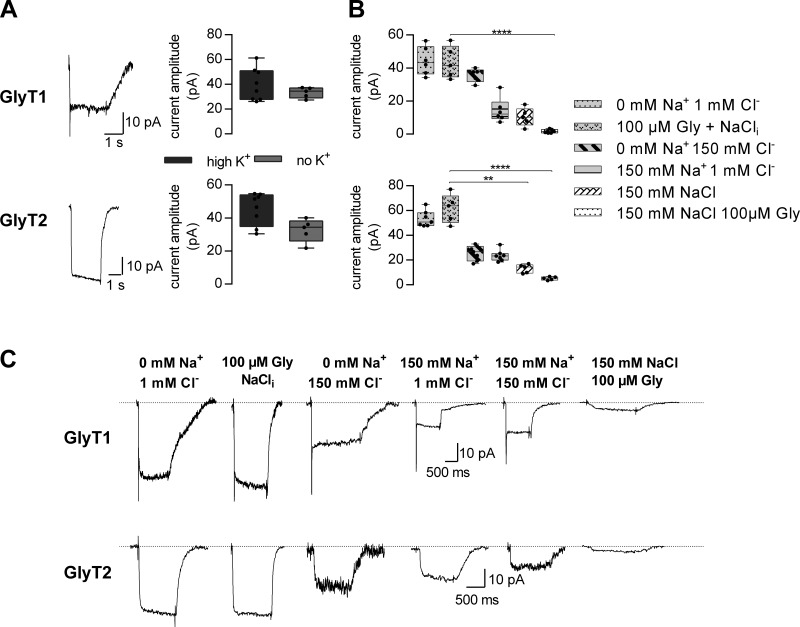
Taken together, the results shown in Figs. 2, 3, and 4 suggest that in both GlyTs, the affinities of the cosubstrate ions are lower on the intra- than on the extracellular side. This observation is difficult to reconcile with the principle of microscopic reversibility: In a kinetic cycle, the product of the rates in one direction must equal the product of the rates in the opposite direction. This cannot be easily enforced if all ion affinities are higher for the outward-facing conformation than for Tis. We therefore surmised that this peculiarity resulted from a modulatory action of intracellular K⁺. We explored this conjecture by examining the effect of intracellular K⁺ on currents carried by the two GlyT subtypes. Fig. 5 A shows a comparison of the amplitudes of currents induced by 1 mM glycine in the presence and absence of 150 mM cytosolic K⁺. This manipulation did not affect the current amplitudes in any significant way, nor did it result in a change in current kinetics (see current traces in the left panel of Fig. 5 A). This lack of effect rejects the hypothesis that intracellular K⁺ interacts with the GlyTs.

Figure 5.

The effect of intracellular ions on currents carried by GlyT1 and GlyT2. (A) Sample traces of currents through GlyT1 (upper trace) and GlyT2 (lower trace), induced by the application of 1 mM glycine. The displayed currents were recorded at −60 mV in the absence of intracellular K⁺. The box plots show the comparison of current amplitudes in presence of 150 mM intracellular K⁺ and in absence thereof (n = 6–8). Omission of intracellular K⁺ did not change the current amplitude of GlyT1 (upper right panel) and GlyT2 (lower right panel) significantly (P = 0.49, Mann–Whitney U test). (B) Comparison of current amplitudes for the indicated intracellular conditions at −60 mV (n = 5–7 for each GlyT1 and GlyT2). In the case of GlyT1, there was significant current suppression in the presence of 150 mM intracellular Cl⁻, Na⁺, and 100 µM glycine. In the case of GlyT2, there was significant current inhibition in the presence of 150 mM intracellular Cl⁻ and Na⁺ (1) without and (2) with 100 µM glycine (Kruskal–Wallis test, Dunn’s post hoc test). Error bars in A and B represent SD. (C) Sample traces of currents by GlyT1 (upper panel) and GlyT2 (lower panel) in the presence of the indicated intracellular concentrations of Na⁺, Cl⁻, and glycine (Gly). NaCl_i is the standard internal solution described in experimental procedures. ***, P ≤ 0.01; ****, P ≤ 0.001 (Kruskal–Wallis test, Dunn's post hoc test).

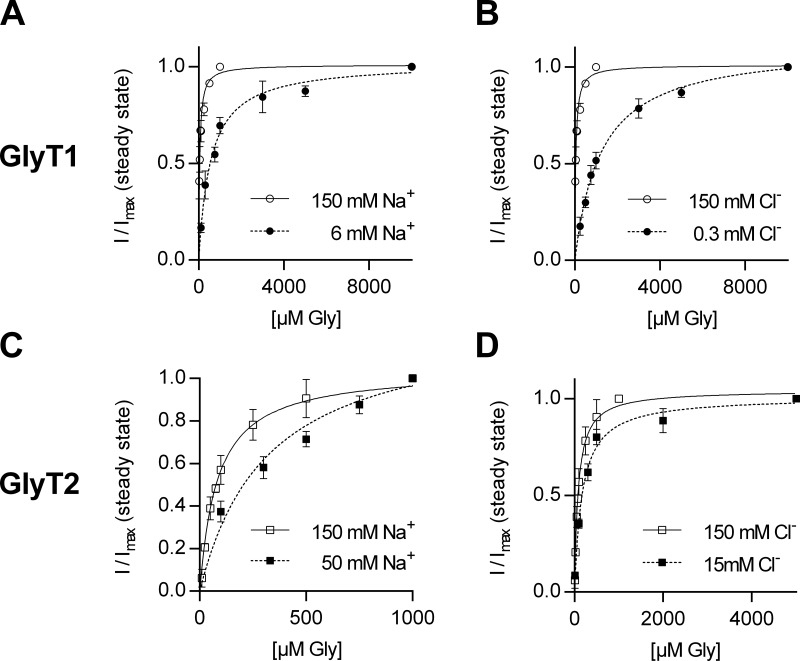
As an alternative explanation, we posited that the observed asymmetry in intra- and extracellular cosubstrate affinities was accounted for by cooperative binding of Na⁺, Cl⁻, and glycine to GlyTs. That is, each ligand binds to the transporter with low affinity when alone but with high affinity upon complex formation. If true, differences in affinity are not pertinent to the side of titration but due to a difference in transporter states that the ions bind to. In this model, the recordings of current suppression by cytosolic Cl⁻ and Na⁺ interrogated states from which glycine had already dissociated (as shown in Fig. 2 D): Accordingly, these affinity estimates for ions are to glycine-free states. In contrast, the protocols used in Fig. 3 and Fig. 4 measured the corresponding affinities for glycine-bound states. We verified this hypothesis by comparing the extent of current suppression by intracellular Na⁺ or Cl⁻ (150 mM each) and their combination in the absence and presence of intracellular glycine (100 µM): The pertinent representative traces are shown in Fig. 5 B; Fig. 5 C provides a summary of the average current amplitudes from five to seven recordings. It is evident that the current elicited by superfusing cells, which had been clamped at −60 mV, with 1 mM glycine was largest, if intracellular Na⁺ and Cl⁻ were low. Solely increasing intracellular glycine (i.e., to 100 µM) did not result in a reduced current amplitude (Fig. 5 B, second set of traces in Fig. 5 C). The current progressively decreased with high intracellular Cl⁻, high intracellular Na⁺, and their combination (Fig. 5 C). On average, the current reduction was more pronounced in the presence of both 150 mM Cl⁻ and Na⁺, but the remaining current amplitudes were still substantial. However, the current was almost fully suppressed if glycine (100 µM) was also added to the internal solution in the presence of high Na⁺ and high Cl⁻. The data in Fig. 5 C are thus consistent with the hypothesis that cosubstrates and substrate bind to the glycine transporter subtypes in a cooperative manner. Corroborating evidence comes from additional experiments, where we investigated the concentration dependence of the steady current on glycine at lower extracellular Na⁺ and Cl⁻ concentrations, respectively. For both GlyT isoforms, we chose a Cl⁻ and Na⁺ concentration at which the half-maximal response with 1 mM glycine was obtained, i.e., 6 mM Na⁺ and 0.3 mM Cl⁻ for GlyT1 and 50 mM Na⁺ and 15 mM Cl⁻ for GlyT2, and monitored the current amplitude at increasing glycine concentrations. Fig. 6 shows the summary of these experiments. It is evident that there was a significant right shift, which is consistent with the hypothesis that substrate and the cosubstrates bind in a cooperative manner.

Figure 6.

Steady currents as a function of glycine concentration in presence of a lower external Na⁺ and Cl⁻ concentration, respectively. (A and B) GlyT1 current amplitudes in response to increasing glycine concentrations at 6 mM Na⁺ (A) and 0.3 mM Cl⁻ (B); we obtained K_m values of 556.5 µM at 6 mM Na⁺ (99% confidence interval [CI_99%] = 440.5–672.5 µM) and of 1.2 mM at 0.3 mM Cl⁻ (CI_99% = 1.08–1.38 mM; n = 4–6). In comparison, the K_m was 44.74 µM (CI_99% = 38.2–51.3 µM) at 150 mM NaCl. (C and D) Current amplitudes of GlyT2 in response to increasing glycine concentrations in presence of 50 mM Na⁺ (C) and 15 mM Cl⁻ (D); K_m values were 319.7 µM at 50 mM Na⁺ (CI_99% = 207.4–432.1) and 172.3 µM at 15 mM Cl⁻ (CI_99% = 128.7–215.9; n = 3–5), compared with 150 mM NaCl: K_m = 83.5 mM (CI_99% = 70.1–96.9). All data points were normalized to the current at the highest glycine concentration. Error bars in all panels represent SD.

Na⁺ binding to the outward-facing conformation is voltage-dependent in GlyT2-expressing cells but not in GlyT1-expressing cells

Voltage jumps trigger transient currents through ion-coupled transporters of different families, e.g., sodium-glucose transporter 1 (Panayotova-Heiermann et al., 1995) and the SLC6 family member γ-aminobutyric acid transporter 1 (GAT1; Mager et al., 1993). These currents are contingent on the presence of extracellular Na⁺ and eliminated by the copresence of substrate. Their detection requires canceling of large displacement currents elicited by voltage jumps. This is achieved by subtracting currents, which are elicited by voltage jumps in transporter-expressing cells in the presence of the substrate from those recorded in its absence. Such displacement currents are seen in both the presence and absence of substrate. In contrast, the transient current is inhibited by substrate. Hence, the subtraction allows for isolating the transient current. We used this approach to examine the Na⁺-induced transient currents through GlyTs: Voltage jumps (illustrated in the inset of Fig. 7 A) did not induce any appreciable transporter-associated currents in Cos-7 cells expressing GlyT1 (lower traces in Fig. 7 A). However, transient currents were readily detectable in Cos-7 cells harboring GlyT2 (traces in Fig. 7 B). To rule out the possibility that transient currents in GlyT1 were not detected due to strong binding of Na⁺ ions, we performed the same experiment in the presence of extracellular 10 mM Na⁺ (upper traces in Fig. 7 A). We also did not detect any transient currents under these conditions.

In Fig. 7 C, normalized charge (Q; i.e., area under the currents) was plotted as a function of voltage. The resulting charge–voltage relation had a sigmoidal shape, as is expected for a reaction during which a charge is moved in response to a change in the electric field of the membrane. The data were fitted to a Boltzmann equation, which yielded an estimate of the potential at which half of the charge had moved and an estimate of the valence associated to this process (i.e., 1.05). These transient currents by GlyT2 were absent when Na⁺ was removed from the bath solution (data not shown). The transient currents on voltage jumps allowed for estimating the number of GlyT2 transporters expressed at the surface of the cell from which the current was recorded. For this, the Q was determined at a potential at which Q had saturated. Q was then divided by the elementary charge. Because the estimated valence was ∼1, this division is expected to give the number of transporters at the plasma membrane. According to this analysis, on average, 9.5 ⋅ 10⁶ ± 1.7 ⋅ 10⁶ (n = 7) GlyT2 transporters were expressed on the surface of a Cos-7 cell. This information was used to calculate the turnover rate of GlyT2: the turnover rate is the number of charges/second carried by the steady current divided by two (each cycle transports two net charges through the membrane) and by the number of transporters. The estimated turnover rate was approximately 15 s⁻¹. This rate is in good agreement with that reported by others (Supplisson and Roux, 2002). Importantly, it provides an upper limit for the rates of the partial reactions in the transport cycle, because a partial reaction cannot be slower than the overall turnover rate.

We also estimated the turnover rate of GlyT1 and GlyT2 by another approach, which relied on recordings of current deactivation upon substrate removal. The deactivation rate allows for extracting the turnover rate based on the following considerations: Upon substrate removal, the transporters, which have just entered the transport cycle, must complete this cycle for the current to fully vanish. However, this measure may somewhat overestimate the turnover rate, because those transporters, which have entered the transport cycle, already dwell in states subsequent to the initial reactions in the transport cycle. Hence, they do not have to undergo the full cycle to return to the outward-facing conformation. In Fig. 7, we show the summary of recordings of current decay rates (i.e., deactivation rate) upon removal of (external) substrate (Fig. 7, D and E). Based on these current decays, we estimate GlyT1 and GlyT2 to have turnover rates of ∼21 s⁻¹ and 30 s⁻¹, respectively. The turnover rate estimate for GlyT2 is in reasonable agreement with that estimated by the approach delineated above.

Kinetic models of GlyT1 and GlyT2

Kinetic models can be used to rigorously test hypothetical mechanisms: When implemented into a kinetic model, a seemingly plausible mechanism may fail to emulate experimental observations within the boundaries of realistic parameter values. In this case, the hypothetical mechanism must be rejected, and the reaction scheme must be revised. Here, we built kinetic models for the GlyTs to find plausible explanations for our experimental observations (see Figs. S1 and S2). The reaction schemes for GlyT1 (Fig. S1) and GlyT2 (Fig. S2) were constrained by the following boundary conditions: (1) parsimony, i.e., we used the minimum number of states to emulate our findings, and we assumed symmetry (we explicitly posit that the inward- and the outward-facing conformations do not differ in their association and dissociation rates for substrate and cosubstrates and that the Tos- and Tis are equally stable); (2) microscopic reversibility, i.e., in any closed loop, the product of the reaction rates in one direction must equal those in the opposite direction; and (3) the requirement to account for all experimental findings with a single set of parameter values. We note that microscopic reversibility combined with simultaneous emulation of all observations imposes a very powerful constraint. In fact, it allows for only a very limited variation in parameter values (i.e., any change in the reaction scheme affects all possible loops and all synthetic data).

The experimental data supplied apparent affinities for substrate and cosubstrates, the turnover rate of the transport cycle, the deactivation rate upon substrate removal, the flipping rate of GlyT1, and the valences of the voltage-dependent reactions, which must yield the stoichiometry of the reaction when summed. In addition, the model is constrained by the voltage-dependent nature of several partial reactions: Voltage affects, for instance, the conversion of the substrate bound outward to the inward-facing conformation in GlyT1; in GlyT2, sodium binding to the To is voltage dependent. In both GlyT1 and GlyT2, the steady current is a strongly dependent on voltage, but the I-V curves differ.

The schemes shown in Fig. 8 A are simplified versions of the models, which highlight rate-limiting and voltage-dependent reactions. The voltage-dependent reactions are specified by their associated valences. We stress, for instance, that assigning a valence of 1.0 to the transition of GlyT1 from the outward to the inward state produces a slope of the peak current, which is steeper than observed. We interrogated these models to understand (1) the presence of a substrate-induced peak current in GlyT1 and its absence in GlyT2, and, conversely, (2) the voltage-induced peak current in GlyT2 and its absence in GlyT1, and (3) the cooperative nature of substrate and cosubstrate binding.

Figure 8.

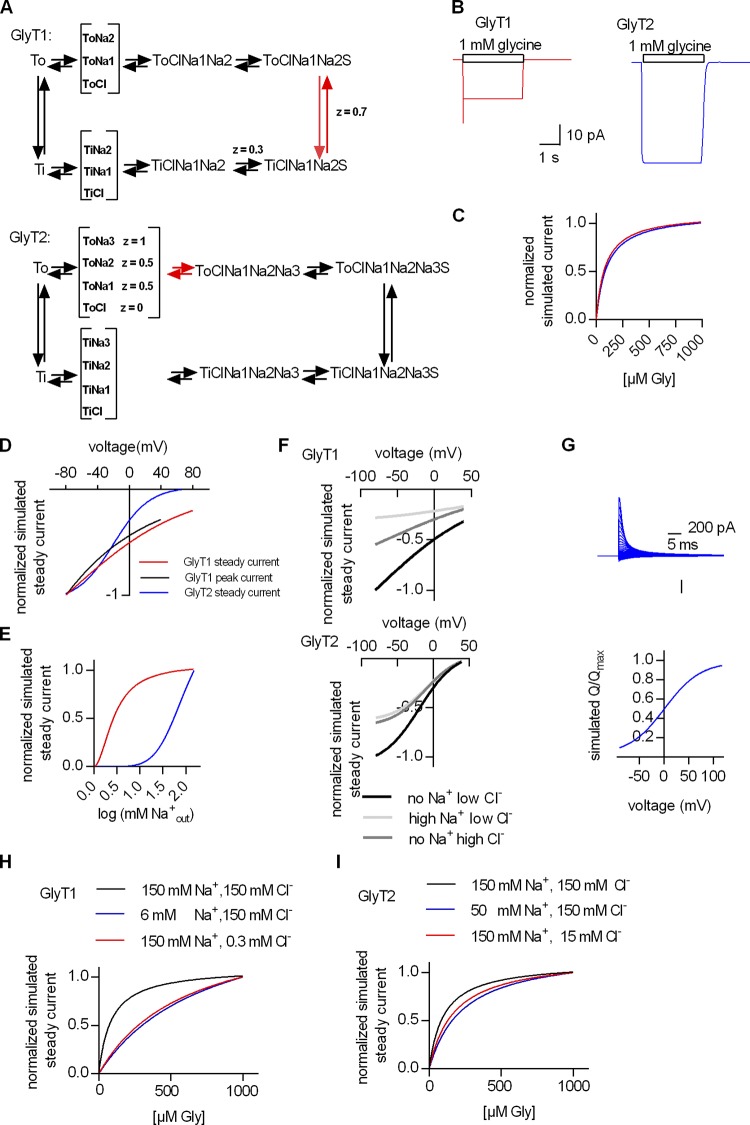
Kinetic model of the transport cycles of GlyT1 and GlyT2. (A) Simplified representation of the kinetic schema of GlyT1 (upper panel) and GlyT2 (lower panel). z, valence. The reaction arrows in red indicate the rate-limiting transitions. For incorporation of cooperative binding of cosubstrates and substrate, it was necessary to allow for random order binding. Because the number of states in a random order binding schema is 2 × (2^{number of ligands}), the resulting models became quite complex (for a full description of the model, see supplemental figures and Tables S1 and S2, respectively). (B) Simulated currents of GlyT1 and GlyT2, respectively. (C) Simulated dependence of the steady current through GlyT1 and GlyT2 on the concentration of extracellular glycine. (D) Simulated voltage dependence of the steady and the peak current through GlyT1 and the steady current through GlyT2. (E) Simulated dependence of the steady current amplitude of GlyT1 and GlyT2 on the extracellular Na⁺ concentration. (F) Simulated dependence of the steady current amplitude of GlyT1 (upper panel) and GlyT2 (lower panel) on intracellular Cl⁻ and Na⁺, respectively, calculated for voltages ranging from −80 mV to +40 mV. The concentrations used intracellularly were (1) no Na⁺ low Cl⁻ (1 mM), (2) high Na⁺ low Cl⁻ (150 mM Na⁺, 1 mM Cl⁻), and (3) no Na⁺ high Cl⁻ (150 mM). (G) Simulated transient current on voltage jump (upper panel) in GlyT2 and the QV relation thereof (lower panel). (H) Simulated dependence of the steady current of GlyT1 in the presence of extracellular 150 mM Na⁺, 150 mM Cl⁻ (black line), 6 mM Na⁺, 150 mM Cl⁻ (blue line), and 150 mM Na⁺, 0.3 mM Cl⁻ (red line). (I) Simulated dependence of the steady current of GlyT2 in the presence of extracellular 150 mM Na⁺, 150 mM Cl⁻ (black line), 50 mM Na⁺, 150 mM Cl⁻ (blue line), and 150 mM Na⁺, 15 mM Cl⁻ (red line).

The models faithfully reproduce the substrate-induced currents, i.e., there is both a peak and steady current in GlyT1, but GlyT2 only carries a steady current when challenged with glycine (compare synthetic traces in Fig. 8 B and recorded traces in Fig. 1 B). Similarly, the models also reproduce the hyperbolic saturation curve for substrate, if cosubstrates are not limiting (compare Fig. 8 C and Fig. 1 D). Thus, the emulated currents confirmed the assignments of valences to distinct steps. This was confirmed by examining the synthetic current–voltage relations: Their slopes depend on the magnitude of the assigned valences. It is evident from a comparison of Fig. 8 C and Fig. 2 C that the model captures the essential features of each individual transporter. Most importantly, the voltage dependence of the peak current can only be emulated under a very restricted set of parameters. Conversely, the absence of the peak current in GlyT2 is contingent on placing the electrogenic transition late in the cycle. This was confirmed by interrogating the model of GlyT2 and examining the output of emulated voltage-dependent transient currents through GlyT2: The synthetic currents in Fig. 8 G recapitulate the data shown in Fig. 7, B and C, provided that the following boundary conditions are met: (1) Na⁺ is initially bound to the To before the application of substrate, and (2) Na⁺ binding is electrogenic. Thus, the modeling exercise confirms that the absence of the peak current in GlyT2 is due to forebound sodium and that the electrogenic reaction represents sodium binding to the outward state upon completion of the transport cycle.

As an internal control, we also recapitulated the apparent affinity of Na⁺ and the slope of the Na⁺ curves (compare Fig. 8 E and Fig. 3 B). Raising the internal concentrations of cosubstrates offers an insight into the cooperative nature of substrate and cosubstrate binding: There is only a modest inhibition of the steady current over the entire voltage range (Fig. 8 F). This synthetic dataset, which recapitulates the experimental data shown in Fig. 2 F, can only be produced by our models by assuming cooperative binding of substrate and cosubstrates. This conjecture was further confirmed by emulating saturation curves for substrate at different concentrations of extracellular sodium and chloride (Fig. 8, H and I): The data shown in Fig. 6, A and B were only reproduced by posting strong cooperative binding in GlyT1, i.e., the reciprocal affinity of substrate and cosubstrate to GlyT1 increases 50-fold. In contrast, while still substantial, this cooperativity factor (Coop) is less pronounced in GlyT2. The reciprocal effect on the dissociation rate is captured by positing a Coop of 8 (compare Fig. 8 I and Fig. 6, C and D). Cooperative binding requires a random order of binding or a mixed scheme of random and sequential binding. Hence, the models must account for many states (see Figs. S1 and S2). In SLC transporters, these are actually supported by structural studies. More than eight distinct conformations, for instance, have been solved in the bacterial betaine transporter BetP, and 12 are posited for completion of the transport cycle (Perez et al., 2014). Accordingly, we emphasize that the large number of states in the models of GlyT1 and GlyT2 are a necessity rather than an overparameterization. More importantly, the models have explanatory power, because they allow for rationalizing the differences between GlyT1 and GlyT2.

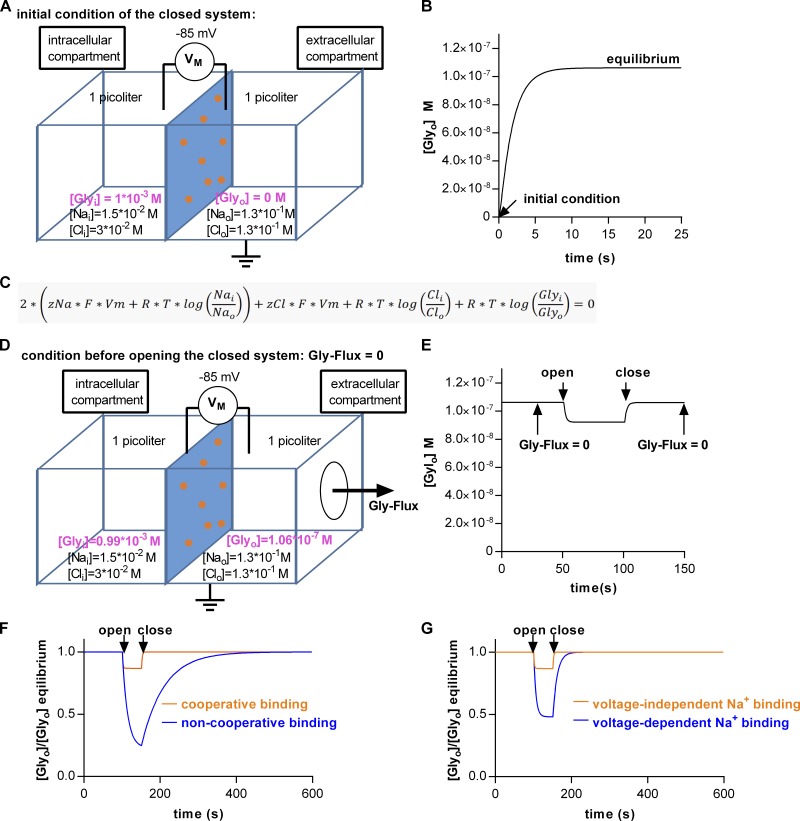
Both cooperativity and electrogenic binding have repercussions on the extracellular concentration of glycine, which can be maintained at steady state in an open system. The kinetic models allow for predicting the intra- and extracellular glycine concentration. We explored the impact of transport kinetics on the level of the extra- and intracellular glycine concentrations by simulating the situation within a hypothetical neuron or glial cell and in the extracellular milieu surrounding this cell. Our model is comprised of two compartments (one intra- and one extracellular), separated by an impermeable membrane containing 10⁶ units of GlyT1 (Fig. 9 A). For the simulation, we assumed that all glycine was initially contained in the intracellular compartment (i.e., 1 mM; Supplisson and Roux, 2002) and that the volume of the intra- and extracellular compartment was 1 pl (Sitte et al., 2001). The intracellular Na⁺ and Cl⁻ concentrations and the membrane potential, which we selected, correspond to those reported for astrocytes (Rose and Ransom, 1996; Bekar and Walz, 1999; Parpura and Verkhratsky, 2012). The model predicts a net flow of glycine into the extracellular compartment as a result of active cycling of the transporters: Fig. 9 B shows the time-dependent increase in the extracellular glycine concentration as it approaches equilibrium. The extracellular concentration, which is achieved (0.1 µM), corresponds to the threshold concentration, where glycine acts as a coagonist on NMDA receptors (Kleckner and Dingledine, 1988). Importantly, the level of extra- and intracellular glycine concentration at equilibrium matches precisely the prediction of the equation in Fig. 9 C, which describes the electrochemical potential of a secondary active transporter operating with the stoichiometry of GlyT1. It is to be expected that the prediction and the simulation are in agreement: The system must run into the equilibrium predefined by the thermodynamic equation because of its closed nature and because the incorporated kinetic model implicitly assumes a loss-free energetic coupling between Na⁺, Cl⁻, and glycine. However, on inspection of the equation, it becomes clear that in a closed system, the intra- and extracellular neurotransmitter concentrations at equilibrium are fully determined by the stoichiometry of the transporter. Conversely, this implies that, at steady state, the kinetics of the transporter and changes thereof must remain inconsequential. However, this only applies to a closed system: In an open system, the kinetics of a transporter ought to play a pivotal role in shaping the extra- and intracellular glycine concentrations. We mimicked an open system by creating a hole in the extracellular compartment (Fig. 9 D). Glycine flux through this conceptual hole represents glycine escape by diffusion or glycine uptake into adjacent cells. Thus, the open system resembles the situation in vivo more closely. Upon opening of the system, the extracellular glycine concentration drops to a value below the one predicted by the thermodynamic equation (Fig. 9 E). However, upon subsequent closure, the extracellular glycine concentration rapidly returns to this value (Fig. 9 E).

Figure 9.

Simulated intra- and extracellular glycine concentrations in and around a cell containing GlyT1. (A) A closed system comprised of two compartments (intra- and extracellular) separated by a membrane (indicated in blue). The membrane was assumed to contain 10⁶ units of GlyT1 (orange spots). The volume of each compartment and the membrane potential (V_M) were set to 1 pl and −85 mV, respectively. The initial intracellular Na⁺, Cl⁻, and glycine concentrations were 15 mM, 30 mM, and 1 mM, respectively. The initial extracellular Na⁺, Cl⁻, and glycine concentrations were 130 mM, 130 mM, and 0 mM, respectively. (B) Glycine concentration in the extracellular compartment plotted as a function of time. At time point 0, the simulation was started (i.e., extracellular glycine = 0). Upon active cycling, the extracellular glycine concentration ramped up to ∼0.1 mM—reaching equilibrium. (C) Equation for the electrochemical potential of a transporter adhering to GlyT1 stoichiometry. (D) The closed system shown in A was opened: The conceptual hole in the extracellular compartment allowed for glycine escape. (E) The extracellular glycine concentration as a function of time. At the indicated time point (i.e., 50 s), the hole was opened. This led to a drop in the extracellular glycine concentration. Upon closure (Gly-Flux = 0) at 100 s, the glycine concentration in the extracellular compartment returned to the thermodynamically permitted maximum. (F) Extracellular glycine concentration assuming cooperative (orange trace) and noncooperative (blue trace) substrate and cosubstrate binding. Plotted is the ratio of the concentration predicted by the kinetic model and the concentration predicted by the equation in C as a function of time. A value of 1 indicates thermodynamic equilibrium. (G) Extracellular glycine concentration assuming voltage-independent (orange trace) and voltage-dependent (blue trace) Na⁺ binding to the outward-facing conformation of GlyT1.

In Fig. 9, F and G, we tested how specific kinetic properties of GlyT1 shape the concentration profile in an open system. In Fig. 9 F, we show how the simulated extracellular concentration changes, if we assume that GlyT1 had (orange trace) or had not (blue trace) bound substrate and cosubstrates in a cooperative manner. Cooperative binding accelerates transport, both in the forward and the reverse directions, and it is therefore expected to clamp the extracellular concentration to a value close to the energetically permitted maximum. Similarly, the model allows for exploring the impact of voltage-dependent partial reactions. Our recordings showed that, in GlyT1, the voltage-dependent step was the conformational rearrangement, which converts the substrate-bound To into the substrate-bound Ti. In Fig. 9 G, we assigned the voltage dependence to a different partial reaction in the transport cycle (i.e., to Na⁺ binding to the To). The simulation showed a substantial drop in the extracellular concentration of glycine in an open system and a delayed return to the equilibrium upon closure of the system (blue line in Fig. 9 G). It is important to point out that, by changing this assignment, we did not alter transport stoichiometry, and thus this manipulation solely affected transport kinetics. Our simulations imply that voltage-dependent binding of Na⁺ to GlyT1 hampers the ability of the transporter to clamp the extracellular concentration to the thermodynamically permitted maximum. The simulations in Fig. 9 highlight the importance of transport kinetics. If the membrane potential of the glycine-containing cell is allowed to depolarize to −20 mV, the extracellular glycine concentration rises to 4 µM (data not shown), which suggests that the dynamic range of the glycine binding site of the NMDA receptor (EC₅₀ = 0.67 µM; Kleckner and Dingledine, 1988) can be covered by GlyT1.

Discussion

All SLC6 transporters operate by an alternating access mechanism. Electrophysiological recordings have allowed for interrogating the transport cycle of SLC6 transporters by providing real-time measurements of partial reactions. Detailed kinetic models have been developed using the rate constants, which were extracted from these recordings, for the transport cycle of GAT1 (Hilgemann and Lu, 1999), DAT (Erreger et al., 2008), and SERT (Schicker et al., 2012; Hasenhuetl et al., 2016, 2018). These models highlight the variations in the underlying alternating access mechanism, which presumably reflect the adaptation of a given transporter to the constraints imposed by physiological requirements. GAT1 and SERT, for instance, differ substantially in turnover rates, in intracellular handling of chloride, and in the role of intracellular potassium (Hilgemann and Lu, 1999; Bicho and Grewer, 2005; Hasenhuetl et al., 2018). In the present study, we analyzed the partial reactions in both GlyT1 and GlyT2, which bind substrate and cosubstrates, translocate these across the membrane, release them into the cytosol, and return in the empty state. This allowed us to generate comprehensive kinetic models of the transport cycles, which highlight the common features of and important differences between GlyT1 and GlyT2. The salient shared properties are as follows: Contrary to monoamine transporters, (1) both GlyTs have a high transport capacity—e.g., for GlyT2, we estimated a turnover rate of 15 s⁻¹—and (2) release Cl⁻ on the intracellular side. Specifically, we found that Cl⁻ dissociation into the cytosol was necessary for the return of the empty transporter to the outward-facing conformation. This is a key signature of a true cosubstrate. In contrast, SERT does not rely on chloride release to complete the transport cycle (Hasenhuetl et al., 2016). The return step of SERT is contingent on binding and countertransport of K⁺, which is immaterial to GlyT1 and GlyT2. Finally, (3) both GlyTs bind and unbind cosubstrates and substrate in a highly cooperative manner, a kinetic feature which—in combination with the rapid return step—supports a high transport velocity even under conditions of elevated intracellular Na⁺ or Cl⁻. We also identified kinetic differences between the GlyTs. Although Na⁺ binding occurs in both GlyTs before glycine binding, in GlyT1, most of the charge moved when glycine bound to the transporter; that is, the electrogenic event is within the transition event of the transporter from the outward-facing to the Ti (visible through the peak current). In comparison, in GlyT2, the majority of the charge moved after glycine had already dissociated into the cytosol: The electrogenic component is not within the transition event but much later, in the next round of Na⁺ binding of GlyT2. As this delayed event is not synchronized, it is buried within the steady current and hence there is no peak component. Importantly, the voltage-dependent reactions were also rate limiting for glycine transport, but they were located at different points in the transport cycle. The slowest reaction in the kinetic cycle of GlyT1 is the conversion of the substrate-bound transporter from the outward- to the inward-facing conformation. In contrast, it is Na⁺ binding or a related conformational change before extracellular glycine binding that is rate-limiting for GlyT2. Thus, the comparison of the transport cycles of the monoamine transporters (DAT and SERT), GAT1, GlyT1, and GlyT2 indicates that the evolution of SLC6 transporters is driven by the need not only to accommodate different substrates in the binding pocket but also to meet additional requirements imposed by physiological circumstances in which the transporters operate. These adaptations allow for coping with wide differences in extracellular substrate concentrations (reflecting volume vs. wiring transmission), membrane potential, and ion gradients.

The kinetic cycle of a transporter is a closed loop of partial reactions (Patlak, 1957; Läuger, 1991). Because glycine transport is associated with the movement of net charge, a subset of these partial reactions must be voltage dependent (Grewer et al., 2013). Transporters that have entered the transport cycle produce a current. This current is transient if the transporters are synchronized, and it is transformed into a steady current upon their gradual desynchronization. While the steady current reports on all electrogenic transitions in the transport cycle, transient currents only report on a subset. Here, we explored two transient current types, one evoked on rapid application of substrate and one on voltage jumps. The former was present in GlyT1- but absent in GlyT2-expressing cells; for the latter, the opposite was true. The absence of the substrate-induced peak current in cells expressing GlyT2 can be rationalized as follows: At physiological extracellular Na⁺ concentrations essentially all transporters adopt the outward-facing conformation. This primes them for synchronous entry into the transport cycle upon glycine application. Electrogenic reactions are expected to produce a peak current if they occur immediately after glycine binding (i.e., when the transporters are still synchronized). Conversely, if the first electrogenic transition, which follows glycine binding, occurs later in the transport cycle, the transporters may have already been desynchronized before undergoing this reaction. This accounts for the absence of substrate-induced peak current in cells expressing GlyT2. The transient current on voltage jump presumably reports on voltage-dependent Na⁺ binding to the outward-facing conformation of GlyT2 (López-Corcuera et al., 1998). This conjecture is supported by the observation that this current was absent when Na⁺ was omitted from the bath solution. In agreement with a previous report, we only found transient currents in cells expressing GlyT2 (López-Corcuera et al., 1998), suggesting that Na⁺ binding to the outward-facing conformation of GlyT1 is a voltage-independent reaction. In this context, it is worth noting that a previous report documented transient currents on voltage jumps when GlyT1 was expressed in Xenopus laevis oocytes (Cherubino et al., 2010). We are confident, however, that this current does not exist in Cos-7 cells. Although we do not know the reason for this discrepancy, we note that the SERT transporter also features a large transient current when expressed in X. laevis oocytes (Mager et al., 1994), which is absent in mammalian cells (Burtscher et al., 2018).

The steady current corresponds to the sum of all electrogenic reactions in the transport cycle. Nevertheless, the voltage dependence of the steady current is dominated by the voltage dependence of the rate-limiting reaction(s). The peak current through GlyT1 reflects the conformational rearrangement, which carries substrate and cosubstrates through the membrane electric field. Our recordings demonstrated a comparable voltage dependence of the peak current and the steady current. Hence, we conclude that this conformational transition underlying translocation of the substrate and cosubstrates is rate-limiting. In contrast, binding of Na⁺ to the outward-facing conformation (or a related conformational change) is most likely the rate-limiting step in the transport cycle of GlyT2. This conclusion is based on the following observations: The decay rate of the transient current on voltage jump was sufficiently slow, and its voltage dependence matched that of the steady current in the positive voltage range (compare Fig. 2 C and Fig. 7 B). However, our data also suggest that at more negative potentials, a different reaction must be rate-limiting.

An important consequence of voltage-dependent binding is an affinity change with voltage. Our recordings showed that at +50 mV, the inward steady current through GlyT2 is greatly reduced (cf. Fig. 2 C). We examined the consequence of voltage jumps on the area under the curve of the traces shown in Fig. 7 B: It is evident from this analysis that jumps from a negative voltage (where Na⁺ is bound) to positive voltages strip progressively larger amounts of charge from the cellular population of transporters (Fig. 7 C). This shows that a voltage jump to a positive potential induces Na⁺ dissociation. Therefore, we conclude that the affinity for Na⁺ is progressively reduced at positive voltages. Despite the presence of 150 mM internal Na⁺, the curve in Fig. 7 C reaches a plateau, indicating no appreciable occupancy of the Na⁺ binding sites at voltages exceeding +90 mV. Accordingly, the majority of binding sites must remain vacant even in the presence of 150 mM extracellular Na⁺. However, Na⁺ binding to the To is a prerequisite for progression through the transport cycle. This explains the observed suppression of the steady currents through GlyT2 at potentials more positive than +50 mV. A recent study explored the putative third Na⁺ binding site of GlyT2 by site-directed mutagenesis: The voltage dependence of the steady current through GlyT2-G650M was comparable to that of GlyT1 (Benito-Muñoz et al., 2018). Our kinetic model links the arrest of the transport cycle at positive potentials to electrogenic Na⁺ binding. Because this arrest is abolished in a GlyT2 mutant with a compromised Na3 site, it is reasonable to posit that Na⁺ binding to the Na3 site accounts for the majority of the charge elicited by voltage jumps. This interpretation is in line with the distal location of the Na3 site in homology structures of GlyT2 (Benito-Muñoz et al., 2018). The Na⁺ ion must travel from an extracellular starting point through a substantial fraction of the membrane electric field to reach the Na3 site. This movement is therefore expected to produce a transient current upon voltage jumps. In addition, it can plausibly represent a rate-limiting step, if accessibility of the Na3 site is restricted.

Kinetic models provide valuable mechanistic insights into the logic of substrate translocation; however, they are subject to criticism, because they require a large collection of states and hence many parameters. For the sake of parsimony, kinetic models of coupled transporters usually posit a sequential binding order of cosubstrates and substrate, because a sequential scheme allows for emulating experimental observations with a minimal number of states and reaction rates (Zhang et al., 2007; Erreger et al., 2008; Bulling et al., 2012; Schicker et al., 2012). For instance, in SERT, experimental data suggested a random rather than a sequential binding order of cosubstrate and substrate (Humphreys et al., 1994). However, it was possible to emulate many experimental observations by positing the more parsimonious sequential binding scheme (Bulling et al., 2012; Schicker et al., 2012). Yet this parsimonious kinetic model failed when challenged with datasets in which a cosubstrate was removed from the intra- or extracellular solution or when tasked with explaining the action of amphetamines on the transport cycle of SERT (Hasenhuetl et al., 2018). Thus, it was necessary to expand the model by positing random and cooperative binding. In the case of the GlyTs, parsimonious sequential binding models fail to explain key experimental observations, i.e., the fact that raising intracellular sodium and chloride does not arrest the transport (compare Fig. 5) and the dependence of the apparent substrate affinity on the concentration of cosubstrate ions (compare Fig. 6). While developing the kinetic model, we examined the possible reaction schemes and the parameter space. The observed cooperativity can be accounted for by a kinetic model, which employs a fully random order binding scheme or a mixed scheme of random and sequential binding, which both render the kinetic model more complex (i.e., increase in the number of states and reaction rates). For GlyT1, a fully random model was necessary to emulate the experimental observations. For GylT2, we selected a reaction scheme, which relied on a mixed scheme, because it was more parsimonious. In this context, it is worth mentioning that it is possible to differentiate between a random and a mixed reaction order where the substrate binds exclusively in the final step (Lolkema and Slotboom, 2019). This can be achieved by supplying cosubstrate ions and subsequently challenging with substrate. In a mixed scheme, the Hill coefficients for cosubstrate increase with substrate concentration, while in a fully random binding order, the Hill coefficient remains constant. Unfortunately, because of the limiting size of the recorded currents, this analysis is not technically feasible in the case of GlyTs. At low glycine concentrations, the currents are too small, and hence the Hill coefficient cannot be determined with adequate precision. Our experiments revealed that the Coop required for modeling of GlyT1 is substantially larger than those calculated for SERT: In SERT, the Coops for individual substrates covered the range of 1 to 10 (Hasenhuetl et al., 2018). In GlyT1, a Coop of 50 is required to account for the cosubstrate-dependent shift in glycine affinity. In contrast, GlyT2 operates with comparable glycine affinity but a lower affinity for sodium; therefore, the effect of cooperative substrate and cosubstrate binding is less pronounced, and the experimental data can be emulated with a Coop of 8. The difference in cooperativity is important, because transport velocity in both the forward and reverse modes is linked to rapid formation and disassembly of the ternary complex (of transporter, substrate, and cosubstrates). If cooperativity is eliminated, GlyT1 fails to maintain extracellular glycine in an open system (compare Fig. 9 F). The high cooperativity of GlyT1 allows the transport to operate in a fully reverse mode: In the substrate- and cosubstrate-loaded states, the transporter can only release sodium and chloride on the extracellular side and proceed in the transport cycle if there is a pronounced drop in affinity due to cooperativity. In contrast, SERT and other monoamine transporters can only mediate substrate efflux by entering into the exchange mode (Sitte and Freissmuth, 2015). We stress that this specific feature of GlyT1 cannot be achieved by altering the rates of conformational transitions between inward and outward states. In addition, the rates of conformational transitions are constrained by the experimental data: They can be extracted from the transient currents, e.g., the inward flipping rate of GlyT1 is accessible for the decay rate of the peak current, yielding a rate of 70 s⁻¹. Similarly, the outward flipping rate is constrained by the current–voltage relation, which dictates that the outward flipping rate is faster than the inward flipping rate, and the deactivation rate of the steady current. Our models posit symmetry, i.e., that the rates for each individual reaction are the same in both directions. This assumption is justified by parsimony to avoid overparametrization. We acknowledge that these models have limitations, but they faithfully reproduce the full set of experimental data and allow for a number of insights. The most salient feature is to show that GlyT1 can switch rapidly between the forward and reverse modes. This affords regulation of the extracellular glycine concentration in an open system (compare Fig. 9, F and G). The model predicts that the extracellular glycine concentration rises from 0.1 µM to 4 µM if a GlyT1 expressing astrocyte is allowed to depolarize to −20 mV. Thus, the dynamic range of the glycine binding site of the NMDA receptor (EC₅₀ = 0.67 µM; Kleckner and Dingledine, 1988) can be covered by GlyT1. Based on these observations, it is evident that the kinetic features of GlyT1 allow the transporter to supply extracellular glycine to support activation of NMDA receptors (Johnson and Ascher, 1987; Kleckner and Dingledine, 1988). In contrast, both, the transport stoichiometry and the kinetics of the transport cycle render GlyT2 unsuitable for maintaining extracellular glycine levels. Human GlyT1 and GlyT2 share only ∼50% sequence identity. Vertebrate GlyT1 and GlyT2 are thought to originate from an ancestral deuterostome GlyT1-like glycine transporter (Shpak et al., 2014). We conclude that the evolutionary divergence of GlyT1 and GlyT2 was also driven by physiological requirements, which dictated tuning of both stoichiometry and kinetics. This adaptation shaped the transport cycle and resulted in major differences in those partial reactions, which became voltage dependent and/or rate limiting.