Myosin lever arm orientation in muscle determined with high angular resolution using bifunctional spin labels

High-resolution structural information is invaluable for understanding muscle function. Savich et al. use bifunctional spin labeling to determine the orientation of the myosin lever arm in muscle fibers at high resolution under ambient conditions, augmenting previous insights obtained from fluorescence and EM.

Abstract

Despite advances in x-ray crystallography, cryo-electron microscopy (cryo-EM), and fluorescence polarization, none of these techniques provide high-resolution structural information about the myosin light chain domain (LCD; lever arm) under ambient conditions in vertebrate muscle. Here, we measure the orientation of LCD elements in demembranated muscle fibers by electron paramagnetic resonance (EPR) using a bifunctional spin label (BSL) with an angular resolution of 4°. To achieve stereoselective site-directed labeling with BSL, we engineered a pair of cysteines in the myosin regulatory light chain (RLC), either on helix E or helix B, which are roughly parallel or perpendicular to the myosin lever arm, respectively. By exchanging BSL-labeled RLC onto oriented muscle fibers, we obtain EPR spectra from which the angular distributions of BSL, and thus the lever arm, can be determined with high resolution relative to the muscle fiber axis. In the absence of ATP (rigor), each of the two labeled helices exhibits both ordered (σ ∼9–11°) and disordered (σ > 38°) populations. Using these angles to determine the orientation of the lever arm (LCD combined with converter subdomain), we observe that the oriented population corresponds to a lever arm that is perpendicular to the muscle fiber axis and that the addition of ATP in the absence of Ca²⁺ (inducing relaxation) shifts the orientation to a much more disordered orientational distribution. Although the detected orientation of the myosin light chain lever arm is ∼33° different than predicted from a standard “lever arm down” model based on cryo-EM of actin decorated with isolated myosin heads, it is compatible with, and thus augments and clarifies, fluorescence polarization, x-ray interference, and EM data obtained from muscle fibers. These results establish feasibility for high-resolution detection of myosin LCD rotation during muscle contraction.

Introduction

Muscle contraction is a process in which the nanometer-sized force-bearing elements of myosin contribute to macroscopic contraction of the tissue. Despite recent technical advances in cryo-electron microscopy (cryo-EM; Taylor et al., 2019) and x-ray crystallography (Brown et al., 2011; Robert-Paganin et al., 2018), important structural details of the force generation mechanism by myosin remain unclear. The essential light chain (ELC) and regulatory light chain (RLC) are members of the calmodulin (CaM) superfamily and by binding to the IQ1 and IQ2 motifs on an α-helical segment of the myosin heavy chain, they form the relatively rigid light chain domain. Together with the myosin converter subdomain, the light chain domain acts as a lever arm for producing force and movement. Either due to structural flexibility of this complex or to sample inhomogeneity, the above methods have not definitively determined the structure of the vertebrate myosin lever arm, even in the simplest biochemical state, rigor (no ATP).

In addition, none of the above-mentioned structural techniques provide structural information under ambient conditions (not vitrified or crystallized) in vertebrate muscle fibers. Fluorescence polarization does not have this limitation and has been used to provide orientational information about the ELC (Knowles et al., 2008) and RLC (Brack et al., 2004; Romano et al., 2012; Fusi et al., 2015) in skinned fibers. However, fluorescence polarization has low angular resolution, even when it combines data from multiple labeling sites, using maximum entropy (ME) analysis (Zannoni, 1988).

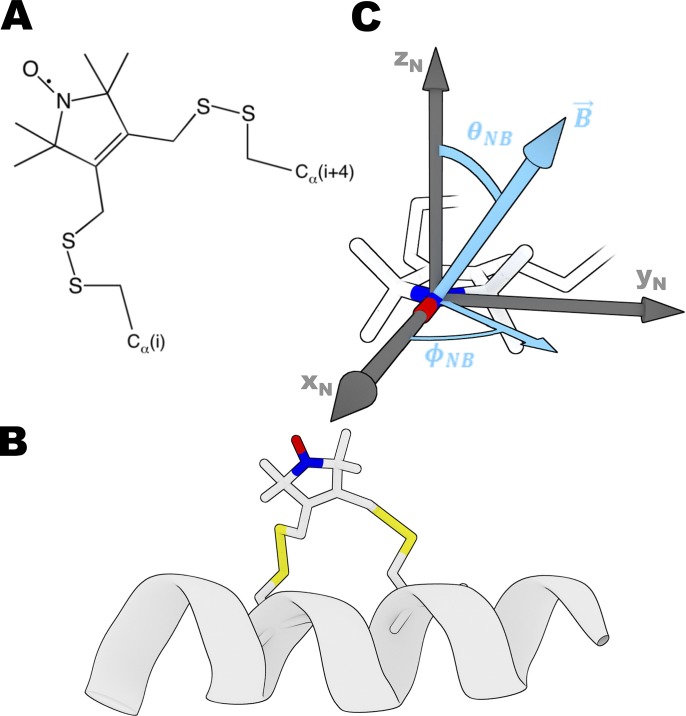
Electron paramagnetic resonance (EPR) of nitroxide spin labels offers high orientational resolution (1–5°) under physiological conditions in skinned fibers, providing a potential solution to the above limitations (Thomas and Cooke, 1980; Cooke et al., 1982; Fajer et al., 1986, 1988; Arata, 1990; Hambly et al., 1991, 1992; Zhao et al., 1996; Thomas et al., 2009; Nogara et al., 2016). The sensitivity of the EPR spectrum to the angle between the nitroxide π orbital (z_N axis in Fig. 1 B) and the magnetic field B (light blue arrow in Fig. 1 B) and to the rate and amplitude of rotational motion provides high-resolution information about the orientation and rotational dynamics of a spin label relative to the magnetic field. It has been shown that a deuterated spin label can increase the angular resolution of EPR (Fajer, 1994a,b), but monofunctional (flexible) attachment of the label produces ambiguity concerning orientation of the protein structural elements.

Figure 1.

The bifunctional spin label (BSL). (A) Chemical structure of BSL reacted with two cysteine residues. (B) BSL bound stereospecifically to an α-helix at positions i and i + 4. (C) Angles that define the orientation of the nitroxide (defined by axes x_N, y_N, and z_N) relative to the applied magnetic field B; these angles directly determine the high-resolution orientation dependence of the EPR spectrum. Coordinates of BSL are from Binder et al., 2018 (Preprint).

The bifunctional spin label (BSL; Fig. 1) provides rigid and stereospecific attachment of the probe to an α-helix (Wilcox et al., 1990; Fleissner et al., 2011; Sahu et al., 2017), thus providing unambiguous information about helix orientation, distance, and rotational motion (Arata et al., 2003; Rayes et al., 2011; Thompson et al., 2015; Binder et al., 2018 Preprint). Specifically, as demonstrated previously in applications to actin-bound Dictyostelium discoideum myosin S1, the angular resolution of BSL stereospecifically immobilized on helices of the catalytic domain was ∼1° (Binder et al., 2015). Due to increasing interest in thick filament muscle regulation, it is important to study both the actin-attached and actin-detached states of myosin with BSL’s high angular resolution, since orientation of the lever arm in multiple biochemical states in contracting muscle remains ambiguous (Irving, 2017).

In the present study, we exchanged BSL-labeled RLC onto the myosin lever arm in permeabilized rabbit muscle fibers and measured the orientation of helices in the N- and C-lobes in the absence of nucleotide (rigor) and in the presence of ATP (relaxation).

Materials and methods

Protein and muscle fiber preparations

Wild-type rabbit skeletal RLC (skRLC) insert (UniProtKB entry MLRS_RABIT; P02608) was obtained from Genscript. Wild-type chicken gizzard smooth muscle RLC (smRLC) insert was as in Mello and Thomas (2012). Mutants of skRLC and smRLC were obtained using a Q5 site-directed mutagenesis kit (New England BioLabs) and a pET3a vector. Constructs were verified via sequencing at University of Minnesota Genomics Center. Purified plasmid (ZymoPURE Plasmid Miniprep kit) was transformed into BL-21AI strain of Escherichia coli. Protein was expressed and prepared via inclusion body purification (Nelson et al., 2005). Endogenous cysteines were replaced by alanines, and a dicysteine BSL labeling motif was introduced for each construct on helix B (D53C-A57C) and helix E (G103C-V107C) in skRLC and (D56C-S60C) in smRLC. Skinned rabbit psoas muscle fiber bundles were dissected, permeabilized, and stored in fiber storage buffer (Prochniewicz et al., 2008) plus 4 mM dithiothreitol (DTT). Heavy meromyosin (HMM; the double-headed soluble myosin fragment) was purified from rabbit skeletal muscle (Muretta et al., 2015).

Preparation of BSL–RLC

Each dicysteine RLC mutant in labeling buffer (30 mM Tris, 50 mM KCl, and 3 mM MgCl₂, pH 7.5) was incubated at 4°C with 5 mM DTT for 1 h to ensure reduction of engineered cysteine residues before labeling. DTT was removed using Zeba Spin desalting columns (Thermo Scientific), and RLC was incubated at 4°C for 1 h in fivefold molar excess of bifunctional 3,4-bis-(methanethiosulfonylmethyl)-2,2,5,5-tetramethyl-2,5-dihydro-1H-pyrrol-1-yloxy spin label (BSL; B485940; Toronto Research Chemicals). The covalent disulfide double bond between BSL and the α-helix backbone produces bifunctional stereospecific attachment under this labeling condition (Fig. S2 of Binder et al., 2015). Following incubation, excess spin label was removed and the protein was exchanged into rigor buffer (25 mM imidazole, 10 mM EGTA, 100.3 mM KPr, and 1.5 MgAc₂, pH 7.1) using Zeba Spin desalting columns. Labeling efficiency (spin labels attached per protein) was determined to be >80% based on double integration of EPR spectra. Mass spectrometry (performed on Agilent 7200B quadrupole time-of-flight gas chromatography-mass spectrometry) shifted unlabeled populations by 228 g/mol (SD = 2 g/mol, n = 5), as predicted for the label’s molecular weight in bidentate attachment (228 g/mol). No monodentate peaks were observed (308 g/mol molecular weight increase) upon labeling, confirming that BSL strongly favors dicysteine attachment.

BSL–RLC exchange onto HMM and decoration of fibers with BSL–RLC–HMM

BSL-labeled RLC was exchanged onto HMM (Muretta et al., 2015) by combining the two proteins (3:1 RLC:HMM, mol/mol) in 50 mM Tris, pH 7.5, 120 mM KCl, 12 mM EDTA. Samples were incubated for 10 min at 30°C, followed by addition of 12 mM MgCl₂ and incubation on ice for 15 min. Free RLC was subsequently removed using Amicon Ultra Centrifugal Filters, 0.5 ml, 50 K MWCO (EMD Millipore), and finally, samples were exchanged into rigor buffer. Actin in fiber bundles was decorated with the resulting BSL–RLC–HMM complex by circulating protein samples through a 25 µl glass capillary (Drummond Scientific) containing a tied fiber bundle.

BSL–RLC exchange into permeabilized fibers

Glycerinated rabbit psoas fibers were dissected into bundles, ranging from 0.3 to 0.5 mm in diameter and 3–5 cm in length and were tied at each end using surgical silk. The tied fiber bundles were then held in place at a fixed length within a 25-µl glass capillary (Drummond Scientific), with the ends of the sutures affixed to the capillary using short sections of silicone tubing. Buffer exchange was accomplished with a Masterflex C/L peristaltic pump (Cole-Parmer) at the flow rate of 0.5 ml/min. Spin-labeled RLC constructs were exchanged onto permeabilized fibers as described previously (Mello and Thomas, 2012), except that the concentration of DTT in the wash before data acquisition was 0.5 mM instead of 30 mM. TnC was reconstituted during a 1-h incubation at 4°C. Rabbit skeletal TnC was purchased from Life Diagnostics. It was shown previously that this exchange and reconstitution protocol is complete (>90% reconstitution for both RLC and TnC) and has no significant effect on function, as measured by Ca-dependent myofibrillar MgATPase assays (Mello and Thomas, 2012). Rigor and relaxation solutions used during acquisition were as described previously (Fusi et al., 2015). Ionic strength and pH during acquisition were maintained at 150 mM and 7.1, respectively.

EPR spectroscopy

EPR was performed on a Bruker EleXsys E500 X-band spectrometer (9.6 GHz). Spectra of BSL–RLC and BSL–RLC–HMM were acquired in the ER4122 SHQ spherical resonator. Parallel and perpendicular field experiments on fiber bundles were performed in TM₁₁₀ 4103TMA and TE₁₀₂ 4104OR-R resonators, respectively. Minced fiber measurements were performed in a quartz flat cell in the TE₁₀₂ 4104OR-R cavity. Sample temperature was set to 4°C in all experiments. Sweep width was 120 G with 1,024 points per spectrum. The center magnetic field (B_c) was set according to B_c = v/2.803 MHz/G. Conversion time and time constant were 20.48 ms. Modulation amplitude and microwave power were 1–2 G and 2–20 mW, depending on the resonator.

Data analysis

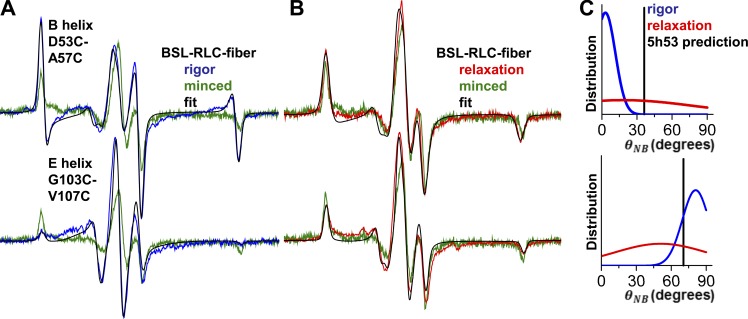
EPR spectra were background subtracted, normalized by dividing by the second integral, and analyzed as described previously to determine the angular distribution of spin labels relative to the muscle fiber axis, assuming the rigid limit regimen due to the immobilization granted by the BSL spin label (Binder et al., 2015). Magnetic tensor values (g and T, defining the orientational dependence of the spectrum) were determined from completely disordered samples (minced fibers). The angular distribution was fit to Gaussian functions for both angles θ_NB and ϕ_NB (Fig. 1 C), with SDs σ_θ and σ_φ. Sensitivity of EPR to θ_NB in systems with axial symmetry (as in oriented muscle fibers) is considerably greater than the sensitivity to ϕ_NB, so we focus on θ_NB values for molecular modeling. Confidence intervals were determined from the cumulative distribution function, comparing the ratio of the residual sum of squares of each fit with that of the best fit.

Molecular modeling

Angle measurements derived from atomistic models were calculated using custom extensions written for Visual Molecular Dynamics 1.9.3 (Humphrey et al., 1996). Minimization of models was performed using SciPy and NumPy packages of Python. Structure images were rendered using Blender, version 2.79 (Blender Foundation).

Online supplemental material

Fig. S1 shows EPR data on BSL–RLC–fiber in rigor, BSL–RLC–fiber in relaxation, and BSL–RLC–HMM–fiber in rigor (black). Fig. S2 shows the cumulative distribution function of the F-ratio distribution for the key parameters in the present paper. Fig. S3 indicates the effect of AMPPNP on the oriented BSL-RLC–fiber labeled on the B helix. For contextualizing our method with other techniques, we show Fig. S4 with ME distributions from bifunctional rhodamine (BR) experiments (Romano et al., 2012; Fusi et al., 2015) and Fig. S5 with lower 50-kD domain alignment of our model (Fig. 6) with a typical 7-nm resolution model of the Z-ward head of the lead bridge derived from insect flight muscle tomography (PDB accession number 1O18, chain J; Chen et al., 2002). Table S1 summarizes orientational parameters corresponding to Fig. S1. Equations that are referenced in the supplemental material are included in sections “EPR equations” and “ME equations.”

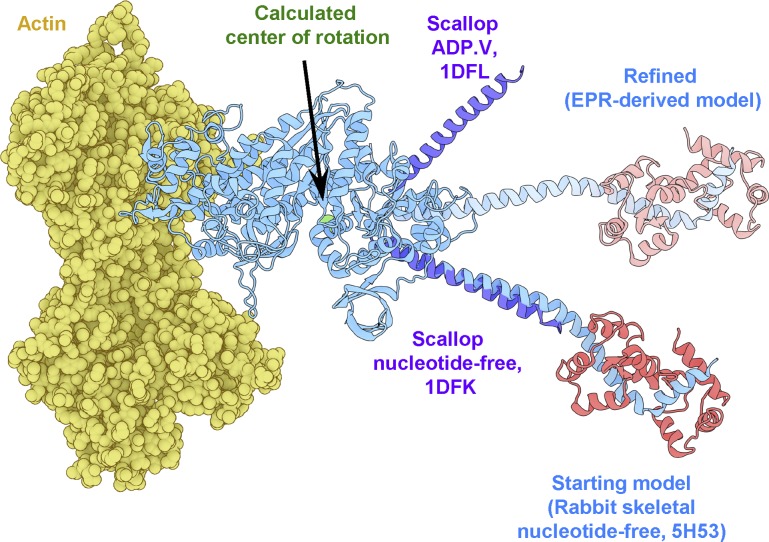
Figure 6.

Refinement of the rigor actomyosin model. In blue is the initial model of skeletal myosin attached to actin (yellow) with RLC in red (5H53). Catalytic domains of myosin in other states were aligned with the catalytic domain of 5H53 to find the plane of lever arm rotation (purple), 1DFL and 1DFK (Houdusse et al., 2000). The center of rotation is denoted by a green sphere. In pale blue is the lever arm orientation derived from EPR-derived orientations of helices B and E on the RLC (pale red).

Results

EPR spectra of BSL–RLC in muscle fiber bundles

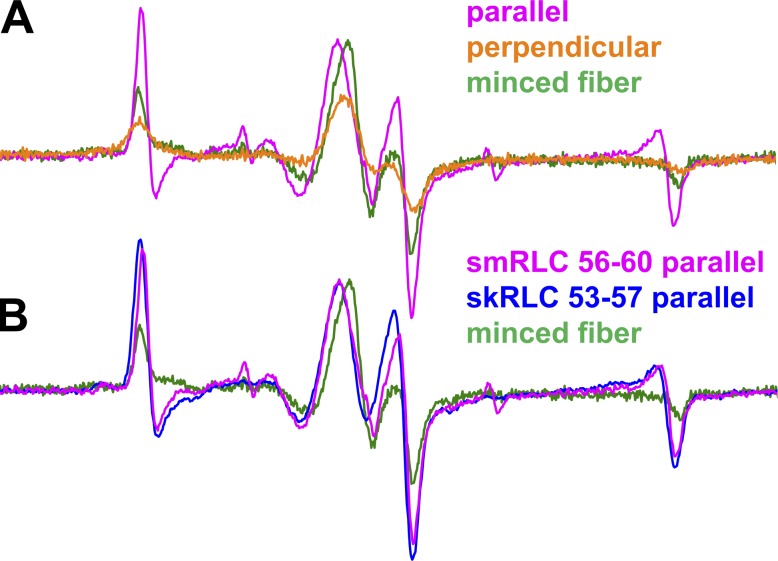
We performed three types of EPR experiments on muscle fiber bundles with the muscle fiber axes (1) parallel or (2) perpendicular to the applied magnetic field or (3) randomly oriented due to mincing, thus eliminating orientation dependence. The parallel spectrum line shape (Fig. 2 A, magenta) typically shows the greatest difference from that of the minced fiber (Fig. 2 A, green). Hereafter, we plot EPR data as derivative of absorbtion as a function of magnetic field. The perpendicular experiment is also sensitive to orientation (Fig. 2 A, orange), but apparent disorder is caused by the helical symmetry of the actomyosin complex about the muscle fiber axis. Therefore, we focus on the parallel spectra compared with spectra of minced fibers.

Figure 2.

The EPR spectra of oriented BSL-RLC muscle fibers. (A) The effect of changing fiber orientation on EPR spectrum for smRLC helix B (56–60). (B) The parallel field experiment on helix B of skRLC and smRLC homologues labeled at equivalent sites. Field sweep is 120 G.

Our previous work on myosin in skeletal fiber bundles and HMM involved smRLC from chicken gizzard (Mello and Thomas, 2012; Muretta et al., 2015). Here, we extend this to the skRLC homologue. Fig. 2 B shows that θ_NB orientations of smRLC and skRLC are hardly distinguishable, which is consistent with fluorescence polarization experiments (Romano et al., 2012). Therefore, to maximize the physiological relevance of our work, we focus on skRLC.

We measured EPR spectra in solution (randomly oriented) of isolated BSL–RLC or BSL exchanged onto HMM to determine rotational dynamics. In randomly oriented samples (e.g., proteins in solution or minced fibers), the rotational correlation time (characteristic time for diffusive rotation by one radian) of the spin label was calculated from

$${\tau }_R=a{\left[1-\left(\frac{T_{\parallel }^{\text{'}}}{T_{\parallel }}\right)\right]}^b,$$

where $2T_{\parallel }^{\text{'}}$ is the splitting between the low- and high-field features of the observed spectrum (Fig. 3) and $2T_{\parallel }$ is the rigid-limit splitting (69–71 G, depending on local polarity), with a = 5.4 × 10⁻¹⁰ s and b = −1.36 (Goldman et al., 1972). Exchanging BSL–RLC (mol wt 19,000 g/mol) onto HMM (mol wt 350,000 g/mol) leads to $2T_{\parallel }^{\text{'}}$ = 70.6 G (SD = 0.2 G, n = 4; Fig. 3, black), indicating rigid immobilization of the probe on the nanosecond timescale. We conclude that BSL is rigidly immobilized when bifunctionally attached to RLC, consistent with the rigid immobilization seen previously with BSL attached to other proteins (Her et al., 2018).

Figure 3.

EPR spectra of BSL–RLC (blue) and BSL–RLC–HMM (black) in solution (randomly oriented). Structural models show RLC in gray and myosin heavy chain in blue. The position of the label is depicted by red spheres on the B helix (orange) of the N-lobe and the E helix (magenta) of the C-lobe (PDB accession number 5H53; Fujii and Namba, 2017). Vertical bars indicate the positions of outer peaks of the HMM spectra, which indicate a lack of submicrosecond rotational motion. Field sweep is 100 G.

Orientation of probes in fiber bundles

Following the RLC-fiber exchange protocol, we performed EPR measurements on helices B and E (Fig. 4). With a single Gaussian-oriented component, the B helix in the N-lobe was fit by (θ_NB,B, σ_θ,B) = (4 ± 4°, 9 ± 3°), and the E helix in the C-lobe was fit by (θ_NB,E, σ_θ,E) = (81 ± 4°, 11 ± 3°) (Fig. 4 C, blue). 95% confidence intervals are depicted by horizontal lines in Fig. S2.

Figure 4.

EPR resolves the angular distributions of BSL-RLC in rigor and relaxation. EPR of BSL-RLC-fiber in (A) rigor (blue) and (B) relaxation (red). Fits are in black, and minced fiber data (randomly oriented control) are green. Field sweep is 100 G. The ${\theta }_{NB}>0^{\circ }$ distribution in C for the nucleotide-free (blue, first component) and ATP-bound (red, single component) state is derived from corresponding helices. Vertical bars represent predicted angles from the PDB accession number 5H53 model.

The addition of ATP, inducing relaxation, produces spectra that are very similar to those of minced fibers (compare red and green in Fig. 4 B). Fitting these spectra with a single Gaussian component resulted in σ_θ,B ≈ 60° and σ_θ,E ≈ 40°. This degree of disorder is consistent with RLC–RLC distance measurements performed by double electron–electron resonance on smooth muscle myosin filaments labeled with a monofunctional spin label (Vileno et al., 2011), where it was observed that probes on the N-lobe exhibited greater disorder than on the C-lobe. Previous fluorescence polarization experiments also show substantial orientational disorder in relaxation at 4°C (Fusi et al., 2015), consistent with our results.

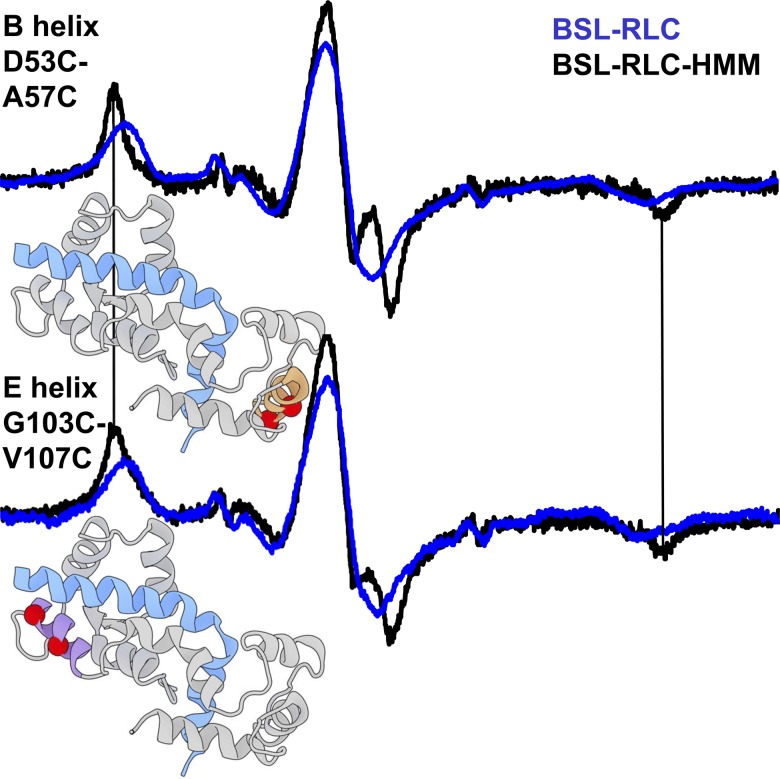
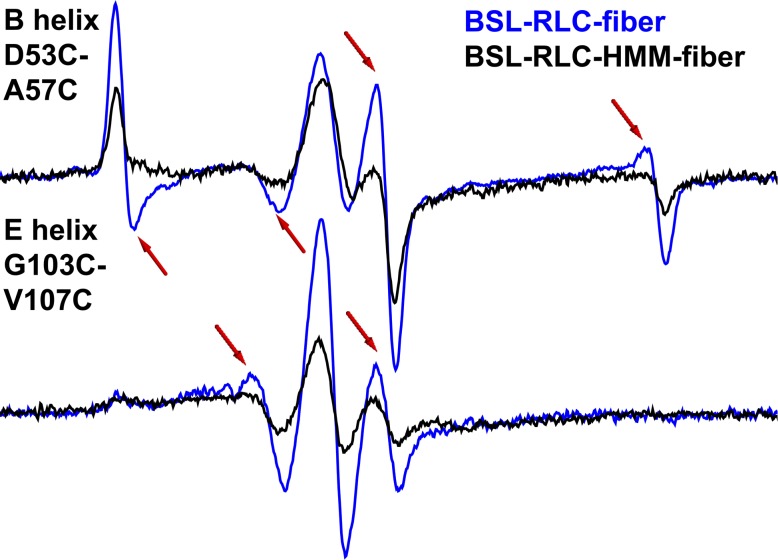
Probes are much less oriented in BSL–RLC–HMM-decorated fibers

To ensure that the measured orientation in a fiber bundle stems from RLC stereospecifically bound to the IQ2 domain of the actin-attached myosin, we exchanged BSL–RLC onto HMM and then decorated a fiber bundle with BSL–RLC–HMM. The spectrum of the E helix in this experiment is similar to that of the BSL–RLC–fiber (Fig. 5, bottom, Table S1), except that the mole fraction of the oriented component is less (about half). The spectrum of the B helix is also less ordered (compare blue and black, Fig. 5, top; Table S1). In both cases, disorder increases when myosin is cut at the HMM–light meromyosin junction. The greater disorder of the B helix is consistent with its more distal location (compared with the E helix) on the lever arm near the flexible hook. For both the E and B helices, the orientation of BSL–RLC is greater for the labeled fiber bundle (Fig. 5; Table S1) than for HMM. We conclude that BSL–RLC labeling of the lever arm must be at least as specific in intact fibers as in HMM-decorated fibers.

Figure 5.

EPR spectra of BSL–RLC–HMM–fiber (black) and BSL–RLC–fiber (blue) in parallel orientation. Arrows indicate the most prominent spectral features of the oriented component. Field sweep is 100 G.

Previously published FRET experiments, with a donor on the E helix of RLC bound to HMM and an acceptor bound to the active site, produced a well-defined donor–acceptor distance, implying stereospecificity of RLC on the IQ2 domain. Biochemically initiated kinetic steps in the ATPase cycle, with labeling sites on exchanged RLC and the catalytic domain, lead to 25–30% FRET changes during ATP cycling, consistent with a stereospecific population of RLC bound during lever arm transitions (Muretta et al., 2015; Rohde et al., 2017). Nonspecific binding of RLC to demembranated fibers can obscure the measurement of orientation or lead to an inconclusive data interpretation. The RLC–fiber exchange protocol that was used in the present study yields <15% of nonspecifically bound RLC (Mello and Thomas, 2012).

To interpret these results in terms of the movement of the lever arm, we performed molecular modeling of the actin-attached state in the absence of nucleotide, combining the orientational distributions from both B and E helices (Fig. 4 C, blue).

Model of a lever arm in a nucleotide-free state

Having determined orientational distributions of BSL on the B and E helices of the RLC, we sought to compare those measurements with established atomic models of the actomyosin complex. We began with a recent cryo-EM structure derived from rabbit skeletal muscle (PDB accession number 5H53; Fujii and Namba, 2017), which used the squid PDB 3I5G (Yang et al., 2007) crystal structure for docking and refinement of myosin coordinates. Coordinates for BSL were obtained from a crystal structure of the label bound to a helix in T4 lysozyme (Fleissner et al., 2011). The presence of unresolved EM density in the above-mentioned reference suggests a small population of an alternative conformation. We used a refined conformation of BSL that was obtained from global analysis of orientational EPR data and double electron–electron resonance data (Binder et al., 2018 Preprint). BSL was modeled onto both of our RLC sites by alignment of backbone atoms, and a θ_NB value was subsequently calculated from the model for each label, with the model’s actin filament axis assumed to be parallel to the external magnetic field (as it would be in a parallel-oriented fiber experiment). Initial results gave poor agreement with the orientational distribution centers derived from our EPR data: θ_NB for helix B was 37.1° (difference of +33.1°), and θ_NB for helix E was 70.4° (difference of −10.6°; Fig. 5 C, blue).

This initial result was not surprising, as (a) the myosin captured in the 5H53 structure was not resolved in the lever arm domain, and (b) the structure is of fast-frozen decorated myosin S1 (single headed). It is likely that lever arm would have a different orientation than measured in our EPR experiments with double-headed BSL–RLC–HMM–fiber and BSL–RLC–fiber under ambient conditions in a demembranated fiber bundle. Therefore, we sought to determine the orientation of the myosin lever arm that is most consistent with the EPR data.

We began by aligning additional myosin S1 structures to our actomyosin model, choosing several structures solved in various biochemical states with different lever arm orientations (Houdusse et al., 2000; Himmel et al., 2002; Fig. 6). Next, we used an established method to calculate a vector corresponding to the lever arm helix in each structure (Enkhbayar et al., 2008) and subsequently found the approximate center of rotation for the lever arm by calculating the average point of nearest convergence for all vectors (Fig. 6). Next, we applied a series of arbitrary 3-D rotations about that defined center to the portion of our model comprising the lever arm, RLC, and attached labels. After each transformation, we calculated new θ_NB values from the model and assessed their deviation from the corresponding EPR-derived measurements. Minimizing these deviations by least-squares optimization, we obtained a new orientation of the lever arm that is most compatible with our experimental findings (Fig. 6).

The structure depicted in (Fig. 6) represents the solution that renders the smallest possible perturbation on our initial cryo-EM–based model. The minimal rotation relative to the starting structure is parameterized by Euler angles α = 0°, β = −33.2°, and γ = +3.3°, in the model’s global coordinate space using the ZYZ convention (as in the Supplemental material of Binder et al., 2018 Preprint). The small magnitude of both α and γ indicate minimal azimuthal rotation relative to the actin axis, which was oriented along the global z axis in our model. While the β value indicates a significant change in the lever arm tilt relative to actin, it is striking to observe that this EPR-informed solution falls within the same rotational plane as the lever arms in other atomic structures of S1 (Fig. 6).

We also applied the above procedure to a structure of a postrigor (actin-binding cleft is open, since it does not bind actin) chicken skeletal myosin (PDB accession number 2MYS). In the 2MYS model, our labeling sites correspond to E49C-A53C and G99C-V103C. The search for an EPR-compatible rotation of the lever arm converged on a configuration with α = 0°, β = −48.7°, and γ = +20.2°. The rotation is axial and azimuthal and required more drastic adjustments than were rendered on PDB 5H53. Hence, the smallest structural adjustment of the lever arm accommodating our data are a rotation α = 0°, β = −33.2°, and γ = +3.3°, which brings the 5H53 lever arm to a more perpendicular orientation (Fig. 6).

Discussion

Summary of results

We used BSL to determine the orientation of specific structural elements of skeletal muscle myosin. We studied BSL-labeled fiber bundles in three configurations: parallel to the magnetic field, perpendicular to the magnetic field, and minced (randomly oriented; Fig. 2 A). We found that smRLC, used in previous studies (Mello and Thomas, 2012), reports a similar orientation compared with skRLC, which is consistent with BR fluorescence polarization data (Romano et al., 2012).

BSL has been shown to adopt a stereospecific conformation on α-helices on the myosin motor domain, based on a combination of EPR on oriented muscle fibers and double electron–electron resonance on actomyosin in solution (Binder et al., 2015, 2018 Preprint). That work supports the orientation of BSL on α-helices of RLC, as determined in the present study. While future studies will be conducted to define more rigorously the level of stereospecific binding after exchange and the level of functional effects due to the exchange of native RLC with BSL-labeled RLC, in the present study, we found that BSL is immobilized when bound to helices B and E on RLC in HMM (Fig. 3) and that in the fiber, orientation is ordered in rigor but disordered by ATP (Fig. 4), consistent with previous studies of myosin orientation in muscle (Cooke et al., 1982; Romano et al., 2012).

Since our angular predictions for demembranated fiber bundles did not agree with S1 5H53 cryo-EM model data, we found a minimum rotation of the myosin lever arm of the most recent rigor actomyosin model that brings it into agreement with our angular parameters (Fig. 6). That model places myosin’s lever arm almost perpendicular to the fiber axis. A key result of the present study is a method to resolve the oriented components of myosin beyond the motor domain in a muscle fiber under ambient conditions, with high angular resolution (Table S1). The model in Fig. 6 was constructed under the assumption that the lever arm behaves as a rigid body in rigor. This assumption is less likely to be valid in other biochemical states, such as relaxation and contraction.

The N-lobe of RLC is less immobilized than the C-lobe in HMM

The fact that we see a significant difference in the mole fractions of the oriented/disordered components between the helices deserves attention. Previous work demonstrated stereospecific BSL attachment (Binder et al., 2018 Preprint) and circular dichroism data on CaM labeled with BSL did not show a significant change in secondary structure compared with wild-type CaM (Her et al., 2018). Although spin-counting and mass-spectrometry data before RLC exchange in this study suggest complete bifunctional labeling, the reversible chemistry of the disulfide bonds leaves room for the possibility of partial disruption of stereospecifically attached labels after RLC exchange on a site-by-site basis.

We hypothesize that the actual difference in the oriented mole fraction is mostly caused by the N-lobe being more disordered when it is conjugated on the IQ2 domain. Indeed, as a member of the CaM superfamily, RLC shares the following property: the C-lobe interacts strongly with the N-terminal part of the IQ2 motif in a “semiopen” conformation, while the N-lobe is in an “open” confirmation and interacts with the hook more weakly (Heissler and Sellers, 2014). This is consistent with our observation of more disorder in the B helix in rigor.

While the orientational distributions of the E helix in the indirectly labeled BSL–RLC–HMM–fiber are similar to that of the directly labeled BSL–RLC–fiber (Fig. 5, bottom; and Table S1), the B helix is much less ordered in the HMM-labeled fiber (Fig. 5, top). We hypothesize that this behavior is observed because the N-lobe is adjacent to the distal HMM free end. This is consistent with two RLC crystal structures of sea scallop catch muscle, where the two structures were identical in the C-lobe region, but differed in the N-lobe, implying a less immobilized domain with a highly conserved glycine acting as a hinge on the D helix (Brown et al., 2011).

Comparison with fluorescence polarization data

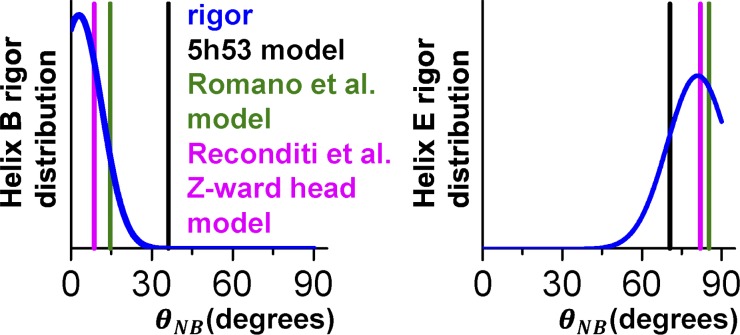
To contextualize our modeling results, we made comparisons with recent fluorescence polarization measurements (Romano et al., 2012). In that work, the lever axis was defined as a vector joining the α-carbons of Cys707 and Lys843 of the 2MYS model. The hook axis is a vector joining the midpoints between Phe836/Ile838 and Met832/Leu834. The orientation of the lever arm was characterized by β (the angle between the lever axis and actin) and γ (rotation of the hook axis around the lever axis). Romano et al. (2012) reported a ME distribution centered at (β, γ) ≈ (105°, 40°). By setting (β, γ) of 2MYS with BSL probes attached to E49C-A53C and G99C-V103C, we directly compared these two methods. The above-mentioned rotation (β, γ) results in θ_NB values of 14.6° and 85.3° for the B and E helices, respectively. Thus, the result of Romano et al. (2012) lies within the confidence interval of our method for the E helix, whereas the orientation of the B helix differs from ours by 10.3° (Fig. 7). Even though fluorescence polarization experiments are versatile in measuring changes of orientation with high temporal resolution, the ME distribution is a low-resolution approximation of the angular distribution, so the difference in 10.3° between our results and those of Romano et al. (2012) could be attributed to multiple factors. Indeed, examining the ME results for BR (whose dipole is roughly parallel to the attached helix axis) located on helix B and helix E yields measurements of helix orientation that are virtually indistinguishable (Fig. S4). EPR of BSL on these same helices clearly resolves them (Fig. 7), including mole fractions of distinct populations (Table S1), illustrating EPR’s superior orientational resolution over fluorescence polarization.

Figure 7.

Comparison of the probe angular distributions measured by EPR and other methods. Spectra of BSL–RLC–fiber in rigor (blue) with a prediction derived from S1 cryo-EM 5H53 model (black), BR fluorescence polarization on skinned fibers (green), and Z-ward head of the double-head model derived from x-ray interference experiment on fibers (magenta).

Conversely, a disadvantage of our EPR approach is that it has lower sensitivity than fluorescence and thus requires the use of fiber bundles 0.3–0.5 mm in diameter, making it challenging to induce uniform Ca²⁺ activation for force measurement during contraction to establish function after RLC exchange. While previous work has established that the RLC exchange protocol used here restores function to physiological levels (Szczesna et al., 1996; Roopnarine, 2003; Mello and Thomas, 2012), the functional effects of BSL labeling were not quantified here. We propose that this limitation can be overcome in future studies by using high-field EPR, where parallel single-fiber studies are feasible (Nesmelov and Thomas, 2010). Nevertheless, the large disorienting effect of ATP indicates the physiological relevance of the present studies.

Myosin lever arm orientation in rigor

Previous EPR measurements with monofunctional labels showed ≥30° lever arm rotation during isometric contraction in scallop muscle (Baker et al., 1998) and ≥13° lever arm rotation between the rigor and pPDM state (SH1 and SH2 thiols are cross-linked, weakly attached state with the reaction product trapped in the active site) in rabbit muscle (Mello and Thomas, 2012). In both studies, the lack of stereospecific labeling results in an underdetermined measurement of lever arm orientation in different biochemical states.

A key conclusion of the present study, that the ordered lever arms occupy a more perpendicular state in the post–power stroke state in rigor muscle than in the conventional lever arm down model (based primarily on crystal structures or cryo-EM involving myosin fragments), is consistent with other structural studies of muscle fibers.

Crystal structures and cryo-EM on myosin fragments yield similar orientation of the lever arm helix to 5H53 as it is seen from lower 50-kD alignment (PDB accession numbers 5W1A, Drosophila melanogaster skeletal myosin II; 1SR6, scallop [Risal et al., 2004]; 4PD3, rigor-like human nonmuscle myosin IIB [Münnich et al., 2014]; and 5JLH, human cytoplasmic myosin IIC bound to actin [von der Ecken et al., 2016]). EM tomography on highly ordered insect flight muscle differs from the abovementioned models. Tomograms from Schmitz et al. (1996) and Chen et al. (2002) show populations of cross-bridges with a more perpendicular lever arm orientation than is predicted by 5H53. A perpendicular conformation of the myosin lever arm was found in two types of cross-bridges, termed the “lead bridge” and “rear bridge.” The lead bridge is a double-headed cross-bridge in a myac layer (longitudinal section containing a single layer of alternating actin and myosin filaments). The myosin molecule that is closer to M-line (M-ward lead bridge head) is fitted by a “lever arm down” model (tilt angle 151 ± 11°). The myosin molecule that is closer to the Z-disk, however (Z-ward lead bridge head), has a tilt angle of 98 ± 2.3°. The rear bridge is a single-headed cross-bridge with a lever arm tilt of 106 ± 12°. Our EPR-derived model (Fig. 6) is compatible with either of these approximately perpendicular orientations. A characteristic property of the rear bridge EM density is that it disappears under nucleotide addition (e.g., AMPPNP; Schmitz et al., 1996). The addition of 5 mM AMPPNP, however, does not change the angular distribution in our case (Fig. S3). Thus, the population of oriented lever arms that we observe might correspond to a structure resembling the Z-ward heads of the lead bridge. Comparing our results further, even though the azimuthal angles of the lever arms of the lead bridge Z-ward heads were different from our model (Fig. 6), the apparent axial position of the lever arm helix in the models generated from the tomograms (PDB accession numbers 1M8Q, 1MVW, 1O18, 1O19, 1O1A, 1O1B, 1O1C, 1O1D, 1O1E, 1O1F, and 1O1G) resembles the perpendicular orientation of our prediction. In Fig. S5, we show a characteristic comparison of our model and a Z-ward head of the lead bridge (PDB accession number 1O18, chain J), which was done by aligning lower 50-kD domain. It is apparent that even in highly ordered insect flight muscle, a significant degree of disorder is present. In the EM tomography analysis, group averaging was performed over self-similar motifs. This method prevents averaging out of ordered populations in a sample with a high degree of heterogeneity. Similarly, EPR spectra are highly sensitive to ordered populations, even when they are sparsely populated.

X-ray interference of a frog muscle fiber in rigor was analyzed in the context of two-headed cross-bridge attachment (Reconditi et al., 2003), using the same lever arm axis definition as in the BR studies (Romano et al., 2012). Analysis yielded two angles: 127° for the M-ward head and 92° for a Z-ward head. BSL probes modeled on RLC of 2MYS at positions E49C-A53C and G99C-V103C had angular parameters of θ_NB,B = 8.6°, θ_NB,E = 82.0° in the Z-ward head configuration (Fig. 7, magenta). These are much closer to our experimental values for θ_NB than those derived from the M-ward head configuration (θ_NB,B = 34.8°, θ_NB,E = 88.7°). Due to the mismatch between periodicities of thick and thin filaments, it is likely that a significant fraction of heads bind to actin in a nonoptimal orientation in vertebrate muscle. We hypothesize that the Z-ward head is more ordered than the M-ward head, consistent with reports that the BR experiments in rigor detect a single oriented component (Brack et al., 2004; Romano et al., 2012; Fusi et al., 2015).

Previous FRET studies on fast skeletal muscle with the A2 ELC isoform are consistent with a perpendicular lever arm orientation in rigor (Guhathakurta et al., 2015), as observed more directly in the present study by EPR. Applying our approach to cardiac muscle fibers might shed additional light on this hypothesis, since cardiac muscle has only the A1 ELC isoform.

Conclusion

We used stereospecific labeling of RLC at two distinct sites to determine the orientation of the lever arm of actin-attached myosin in skinned skeletal muscle fibers in rigor. Two populations were observed simultaneously, both ordered and disordered, with the ordered population representing a lever arm that is perpendicular to the muscle fiber axis. This orientation, determined in muscle fibers at ambient temperature, differs by 33° from the lever arm down orientation determined from cryo-EM on isolated myosin heads bound to actin. Relaxation (addition of ATP in the absence of Ca) produced substantial angular disorder. These results have a profound effect on models of muscle force generation, and future experiments under other physiological conditions have the potential to provide a more direct link between muscle physiology and structural biology.