Random formation of G-quadruplexes in human telomere overhangs leads to a kinetic folding pattern with targetable vacant G-tracts

Abstract

G-quadruplexes formed in the 3′ telomere overhang (~200 nucleotides) have shown to regulate biological functions of human telomeres. The mechanism governing the population pattern of multiple telomeric G-quadruplexes is yet to be elucidated inside the telomeric overhang in a time window shorter than thermodynamic equilibrium. Using a single-molecule force ramping assay, we quantified G-quadruplex populations in telomere overhangs in a full physiological range of 99 to 291 nucleotides. We found that G-quadruplexes randomly form in these overhangs within seconds, which leads to a population governed by a kinetic, rather than thermodynamic, folding pattern. The kinetic folding gives rise to vacant G-tracts between G-quadruplexes. By targeting these vacant G-tracts using complementary DNA fragments, we demonstrated that binding to the telomeric G-quadruplexes becomes more efficient and specific for telomestatin derivatives.

GRAPHICAL ABSTRACT

Introduction

Telomeres in eukaryotic cells contain Guanine(G)-rich single-stranded 3ʹ overhangs (1). The overhangs participate in the formation of T-loop and shelterin to protect chromosomes (2, 3). They also serve as a substrate for housekeeping enzymes such as telomerase for chromosomal maintenance (4). The average length of the 3ʹ telomere overhang ranges from 100–300 nucleotides (nts) in different human cells (5). The G-rich tandem repeats in the 3′ human telomeric overhang have a consensus sequence of 5′-GGGTTA (6). Both in vitro and intracellular investigations have shown G-quadruplexes can form in these tandem repeats (7, 8). G-quadruplexes are four-stranded structures formed by a stack of G-quartets, which have a co-planar arrangement of four guanines held together by Hoogsteen hydrogen bonding (7, 9). The G-quadruplex in the 3′ overhang of the telomere has shown to inhibit telomerase, an enzyme overexpressed in most of the cancer cells (10). Thus, elucidating the mechanism of G-quadruplex populations in telomere regions becomes critical to understand their interactions with telomerase and associated proteins, which may lead to new approaches to fight against cancer.

Current investigations mostly focus on the shortest single-stranded telomere sequence, (GGGTTA)_n=4, in which only one G-quadruplex can form. Given that overhangs can be as long as n=66 repeats (11), it is necessary to explore the G-quadruplex populations in longer telomere overhangs. On the other hand, critical cellular processes, such as the rate of telomere shortening (12, 13), are likely regulated by G-quadruplexes in the overhang (14, 15). Therefore, it is of pivotal importance to elucidate the effect of overhang length on the G-quadruplex populations. However, preparation of DNA fragments with tandem repeats becomes exceedingly difficult when many guanines are present in the sequence. The situation is aggravated as large quantities of DNA are needed in conventional assays such as NMR and CD (7, 16). Another challenge arises from the fact that multiple folded species are present in longer fragments (15, 17, 18), which presents a convoluted matrix for ensemble average techniques. As a result, only scattered G-quadruplex investigations have been carried out for telomere fragments with n>4 (18–24). In these experiments, it has been reported that G-quadruplexes are arranged in a “beads-on-a-string” model without quadruplex-quadruplex-interactions (20, 21). Contradictory findings, however, have shown that negative cooperativity exists among three G-quadruplexes inside a fragment with 12 G-rich repeats (n=12, or 12G) (25).

Most of these investigations are focused on the thermodynamic equilibrium condition that is achieved after hours of incubation (22, 25, 26). Inside cells, the time window for the formation and dissolution of G-quadruplexes can be seconds or below (27, 28). Such a discrepancy necessitates the reexamination of the telomeric G-quadruplex population in a physiologically relevant time window of seconds instead of hours. The primary focus of this work is to understand the mechanism governing the population pattern of G-quadruplexes in a full physiological range of telomere overhangs (n ≤ 48) on a biologically relevant time scale.

To deconvolute different species formed in long telomere overhangs, we employed single-molecule force ramping assays in individual telomere fragments ranging from n=4 (or 4G) to n=48 (or 48G) TTAGGG repeats, the latter of which (n=48) represents the longer end of the human telomeric overhang spectrum. We observed that G-quadruplex is randomly formed inside long telomere overhangs within seconds, resulting in a population pattern governed by a kinetic pathway. Such a pathway precludes the maximal formation of G-quadruplex units, a thermodynamically favored scenario. With increasing overhang length, G-quadruplex shows reduced formation probability, in agreement with the simulation that assumes the random (kinetic) formation of G-quadruplexes. This kinetic formation leads to multiple vacant G-tracts between neighboring G-quadruplexes. To confirm the presence of these vacant G-tracts, we conjugated a G-quadruplex ligand, L2H2–6OTD (29), with a DNA sequence complementary to the vacant G-tracts (5′-CCCTAA). We found this conjugate has significantly increased binding affinity to the G-quadruplex in the longest telomere overhang, 48G. Our work not only revealed fundamental mechanism governing the G-quadruplex population pattern in the full-length telomere overhangs within a biologically relevant time scale, but also opens a new door to design more efficient G-quadruplex ligands by targeting the DNA flanking the G-quadruplex structures.

Materials and Methods

Materials

DNA oligomers were purchased from Integrated DNA Technologies (www.idtdna.com) and further purified by 10% denaturing PAGE gel and stored at −20 °C. All the enzymes required for the preparation of DNA constructs were purchased from NEB (www.neb.com). The polystyrene beads coated with streptavidin or anti-digoxigenin for the single-molecule experiments were purchased from Spherotech (Lake Forest, IL). All chemicals were purchased from VWR (Radnor, Pennsylvania) with purity >98%.

Preparation of DNA Construct

DNA constructs containing 4 and 8 G-tracts (see Table S1 for sequences) for single-molecule mechanical unfolding experiments were synthesized using protocols described elsewhere (30). Briefly, a DNA construct containing a single-stranded DNA oligomer with a sequence of 5′-(TTAGGG)₄ or 5′-(TTAGGG)₈ was sandwiched between the 2028 bp and 2690 bp dsDNA handles. These handles have terminal biotin and digoxigenin modifications which allow tethering of the DNA molecule between the streptavidin and the digoxigenin antibody coated polystyrene beads, respectively.

The DNA constructs for longer telomere fragments (12G to 48G) were synthesized using dynamic splint ligation method, a strategy developed in our lab(21) for the synthesis of commercially unavailable long ssDNA with tandem G-rich repeats. Briefly, each single-stranded DNA sequence of interest was first ligated to the 2028 bp and 2690 bp dsDNA handles separately. The two ligated products were brought together by a splint DNA and ligated using T4 DNA ligase. To increase the efficiency of ligation, we introduced a thermal cycle (with an upper limit of 40 °C) to shuffle the splint bound to the DNA repeats to the desired position for the ligation. The optimal ratio between the splint and template DNA fragments was determined when enough splint DNA was present to cover all the G-tracts (21).

Single-Molecule Mechanical Unfolding Experiments

The single molecule investigation was carried out in a home-built laser tweezers instrument for which the detailed description has been reported previously (31). All the experiments, unless specified otherwise, were carried out in a 10 mM Tris/100 mM KCl buffer at pH 7.4 and 23 °C. The digoxigenin and biotin labelled DNA construct was immobilized onto a 2.10 μm polystyrene bead coated with anti-digoxigenin via digoxigenin−anti-digoxigenin antibody interaction. The DNA immobilized bead and the streptavidin coated bead were trapped by two laser foci separately and the DNA construct was then tethered between these two beads (Figure 1A). The tethered DNA was stretched at a constant loading rate of 5.5 pN/s until it reached just below the plateau force (maximum 65 pN) and relaxed to 0 pN at the same rate by moving one of the trapped beads. The beads were allowed to incubate at zero pN for 30 seconds between adjacent pulling cycles to ensure maximal refolding (18). The force−extension (F−X) curves were recorded at 1 KHz using LabVIEW 8.2 programs (National Instruments Corp., Austin, TX).

Figure 1:

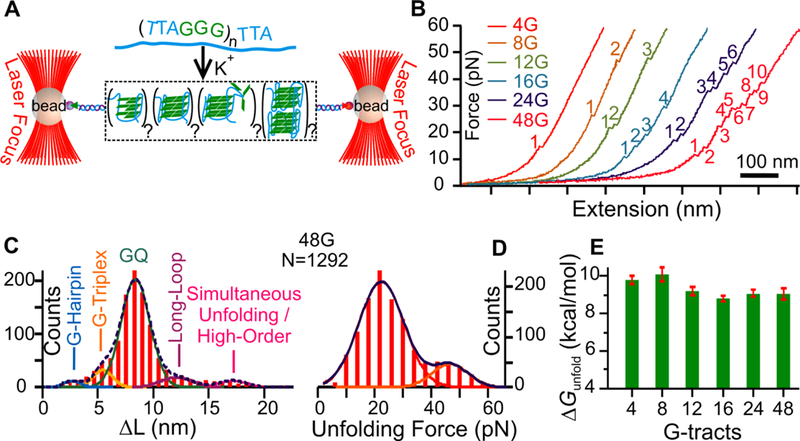
Single-molecule analyses of telomere overhangs in a 10 mM Tris buffer supplemented with 100 mM K⁺ at pH 7.4. (A) Experimental setup for single-molecule unfolding experiments. A single-stranded telomere sequence is sandwiched between a biotinylated 2028 handle and a digoxigenin labelled 2690 handle. The two handles are tethered between streptavidin and anti-digoxigenin coated beads, which are optically tapped in separate laser foci. (B) Force - Extension curves observed by moving one of the optically trapped beads away from another. The sudden rupture events (denoted with numbers) in each curve represent unfolding’s of the structures. (C) Change-in-contour-length (ΔL) histogram of the 48G construct consisting of 48 G-tracts. Folded species are resolved using multi-peak Gaussian fitting and identified by the length of the folded nucleotides in each structure. See Figure S2 for detailed calculation and Figure S3 for ΔL histograms of folded species in the 4G to 24G constructs. (D) Unfolding force histograms of the structures formed in the 48G construct. See Figure S3 for unfolding force histograms of the 4G to 24G constructs. Curves represent Gaussian fittings. (E) Change in the free energy of unfolding (ΔG_unfold) calculated from deconvoluted G-quadruplex populations in the 4G, 8G, 12G, 16G, 24G, and 48G telomere constructs. See Materials and Methods for detailed deconvolution and ΔG_unfold calculation. Compared to the 4G and 8G constructs, ΔG_unfold of the G-quadruplexes in the 12G-48G is decreased about 1 kcal/mol.

Data Analysis: Change in Extension

The change in extension (Δx) at a particular force (F) was calculated as the extension difference between the stretching and the relaxing traces. The resulting Δx at this force was then converted to the change in contour length (ΔL) using the following wormlike-chain (WLC) model (32),

$$\Delta x/\Delta L=1-1/2{\left(k_{B}T/FP\right)}^{1/2}+F/S$$ Equation 1

where k_B is the Boltzmann constant, T is the absolute temperature, P is the persistent length of dsDNA (50.8 nm) (33) and S is the stretching modulus (1243 pN) (33).

Data Analysis: Average Formation of Secondary Structures

The average number of secondary structures formed in different constructs (P) was calculated according to the formula,

$$P=\frac{N}{N_T}$$ Equation 2

where N is the number of unfolded events observed in a total of N_T force-extension (F-X) curves.

The percentage of G-quadruplex and other intermediates formed among secondary structures in a construct was determined through multi-peak Gaussian fitting on the ΔL population shown in Figure 1C using Igor Pro (WaveMetrics, Portland, OR) software.

Data Analysis: Calculation for Thermodynamically Favored Folding

The probability for the maximally (thermodynamically) allowed secondary structures formed in telomere overhang (Th_max) was calculated by the following equation,

$$T{h}_{max}=x^n+\left(1-x^n\right)\times x^{n-1}+(1-(x^n+\left(1-x^n\right)\times x^{n-1}))\times x^{n-2}+$$ Equation 3

where n is the maximum number of G-quadruplexes without vacant G-tract in between, x is the average formation probability of the G-quadruplex (0.86) observed in the 4G construct capable of forming only one G-quadruplex.

Kinetically Favored Folding: Statistical Calculation

Kinetically favored folding was calculated based on the assumption that the formation of G-quadruplex in the telomere sequence is a random process. For example, in a telomere sequence consisting of 8 G-tracts (the 8G construct, Figure S4), two G-quadruplexes can form in the first and the last four consecutive G-tracts, respectively, whereas only one G-quadruplex can fold in the G-tracts 2–5, 3–6, or 4–7. There is also a possibility of forming one G-quadruplex in the first four or the last four G-tracts without forming a second G-quadruplex. All the statistical possibilities of forming G-quadruplex in different length of telomere sequence were computed using a Matlab program (Supporting Information) and reported in Table S3.

Difference between Experimentally Observed Folding Patterns and Those Predicted by Thermodynamic or Kinetic Pathway

The deviation between the experimentally observed folding pattern and that predicted from thermodynamic or kinetic folding pathway (Figure 2A–C) was quantified using the root mean square deviation (RMSD) calculated from the cumulative histograms,

$$RMSD=\sqrt{\frac{\sum {\left(E_i-X_i\right)}^2}{n}}$$ Equation 4

here E_i and X_i represent the probabilities of the i^th bins in the cumulative frequency histograms of the features observed from the experiments and those calculated from the thermodynamic or the kinetic model, respectively; n is the total number of the bins.

Figure 2:

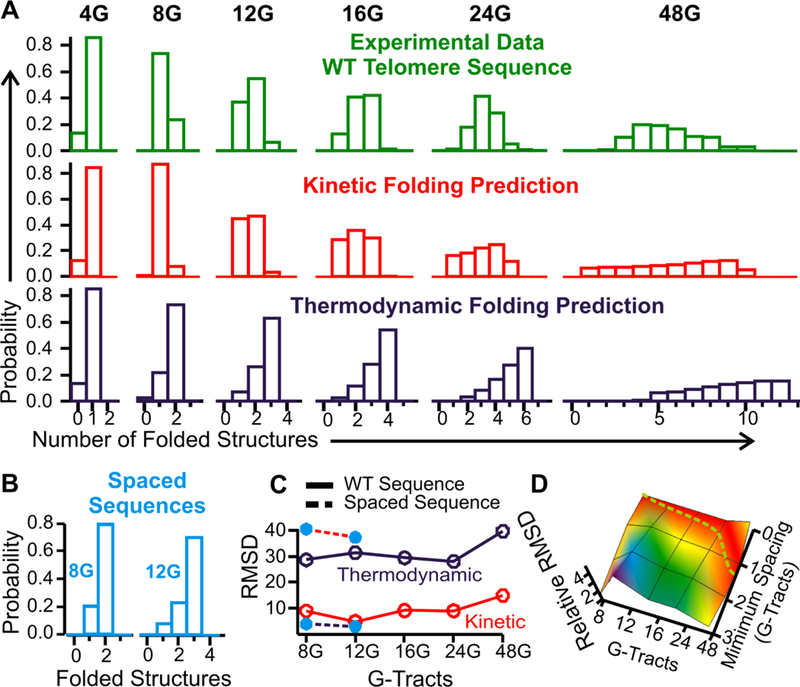
Population pattern of folded structures in telomere overhangs. (A) Comparison of experimentally observed G-quadruplex population pattern (green) with that simulated from kinetic (random formation, red) or thermodynamic (dark blue) pattern. (B) Experimentally observed folding patterns for the 8G and 12G telomere sequences in which each G-quadruplex forming sequence is dispersed by 24-nt thymine-rich fragments (spaced sequences). (C) RMSD deviation between experimental pattern and that obtained from the kinetic (red) or thermodynamic (dark blue) models. Wild-type sequences are represented by solid lines with open circles and the spaced sequences are depicted with dotted lines with filled circles (cyan). (D) Relative RMSD between experimental population pattern and the kinetic population patterns that incorporate different spacing between neighboring G-quadruplexes (See Figure S6 for simulated kinetic population patterns without and with various minimum spacing between two G-quadruplexes in the 4G to 48G constructs). The dotted green trace represents the minimum spacing required for the 4G to 48G overhangs. The spacing becomes obvious when the overhang is longer than the 24G.

Calculation of Vacant G-tracts

Number of free (vacant) G-tracts (V_GT) that do not participate in the secondary structure formation is calculated from the observed folded structures using the equation,

$$V_{GT}=T_{GT}-\frac{N}{N_T}\left(F_{GH}\times 2+F_{GT}\times 3+F_{GQ}\times 4+F_{MF}\times 5+F_{HO}\times 8\right)$$ Equation 5

where T_GT is the total number of G-tracts for a given telomere overhang construct (T_GT =24 for the 24 G construct), N is the number of the unfolded events observed in a total of N_T force-extension (F-X) curves. F_GH, F_GT, F_GQ, F_MF, and F_HO represent the fractions of G-hairpin, G-triplex, G-quadruplex, misfolded G-quadruplex, and higher-order structures, respectively. They were determined from the multi-peak fitting of the ΔL histogram in a given telomere construct (Figures 1C & S3A). The numbers 2, 3, 4, 5, and 8 represent the number of participating G-tracts in the G-hairpin (17), G-triplex (34), G-quadruplex (7), misfolded G-quadruplex (35), and higher-order structures (36), respectively.

Calculation of the Change in Free Energy of Unfolding (ΔG_unfold)

The stretching and relaxing force–extension curves were used to calculate the change in free energy (ΔG_unfold) associated with the unfolding of the individual G-quadruplexes according to the Jarzynski equality for non-equilibrium systems (37),

$$\Delta G_{unfold}=-k_{B}Tln{\sum }_{i=1}^N\frac{1}{N}{e}^{-\frac{W_i}{k_{B}T}}$$ Equation 6

where N is the number of unfolding events and W_i is the non-equilibrium work done for unfolding each structure.

Prior to the determination of the ΔG_unfold for individual G-quadruplexes using equation 6, G-quadruplex population was deconvoluted from the partially folded structures (G-hairpin and G-triplex), misfolded species, and higher order structures. First, the percentage population for each species in a construct was determined using multi-peak Gaussian fitting of ΔL histograms (Figures 1C and S3A). The overlapping regions between any two populations were then randomly assigned to each of the population according to the ratio between the two species in each bin of a particular ΔL histogram (38).

Calculation of Ligand Bound Population and Dissociation Constant (K_d)

The unfolding force for each structure was recorded in individual F-X curves and a force histogram was plotted for all the DNA constructs with or without ligands (Figures S9–S13). We observed a two-Gaussian distribution in the presence of ligand. The area underneath the peak with a higher unfolding force increased with the ligand concentration (Figures S9–S13), indicating that the higher-force population corresponds to the ligand-bound G-quadruplex (39). Both ligand-bound and ligand-free populations were deconvoluted from the unfolding force histograms according to two-peak Gaussian functions. For the 24G and 48G constructs, there was a small fraction of the population in the high force region even in the absence of the ligand. When ligand-bound fractions were calculated for DNA constructs, these small fractions were subtracted from the overall bound fraction using Equation 7.

$$\%Boun{d}_{LC=X}=\frac{Count{s}_{P1,LC=X}}{Count{s}_{0,LC=X}}\times 100\%-\left\{\frac{Count{s}_{P0,LC=0}}{Count{s}_{P1,LC=0}}\times Count{s}_{P0,LC=X}\right\}\times 100\%$$ Equation 7

here %Bound_LC=X is the percentage of bound fraction at X nM or 0 nM ligand concentration, Counts_P1, Counts_P0 and Counts₀ are the cumulative counts of the bound fraction, the unbound fraction, and the overall count, respectively, from the rupture force histograms.

The ligand-bound population not unfolded in the force range of 0–65 pN was calculated from the shift of each F-X curve relative to the expected curve, in which all structures were unfolded (40).

A binding curve was then constructed by plotting the bound fractions of G-quadruplex against ligand concentrations. The dissociation constant (K_d) for each system was retrieved by fitting the binding curve with a Langmuir isotherm for single binding site,

$$Bound\%=\frac{\max \times \left[Conc\right]}{K_d+\left[Conc\right]}$$ Equation 8

where Bound% is the percentage of G-quadruplex bound to a ligand, max is the saturation percentage of the ligand-bound G-quadruplex, and [Conc] is the ligand concentration.

Ligand Binding Experiment

To carry out the ligand binding experiment, we incubated the telomeric construct in a 10 mM Tris buffer (pH 7.4) that contains 100 mM KCl and a ligand of desired concentration. Before each mechanical pulling experiment, the molecule is allowed to rest under zero tension with constant influx of a buffer that contains the desired ligand with fixed concentration. The single-molecule tethers were stretched at a constant loading rate of 5.5 pN/s till just below the 65 pN plateau. The same loading rate was used to relax the construct to the zero force. Then the molecule was subjected to a constant flow of buffer containing the desired ligand with fixed concentration for 30 seconds to allow complete refolding and binding of the ligand. This extension-relaxation-incubation cycle was repeated until the tether was broken between two optically trapped beads.

Click Reaction to synthesize DNA-Ligand conjugates

To 8 μL of 2 mM terminal alkyne modified DNA in water, 2 μL of 100 mM L2H2–6OTD-azide ligand (see SI for synthesis) in DMSO was added. To this mixture, 3 μL of freshly prepared solution containing 0.1 M CuBr and 0.1M TBTA in a 1:2 ratio in 3:1 DMSO/t-BuOH was added. This reaction was carried out overnight. The completion of the reaction was confirmed through 14% native gel shift assay. The DNA conjugated with the telomestatin derivative migrated more slowly towards the positively charged electrode due to the reduced charge density on the DNA-ligand conjugate (Figure 4B). The conjugated DNA was extracted from the gel and the concentration was determined using UV absorption at 260 nm. The molar extinction coefficient was the sum of those of the DNA and the ligand at 260 nm.

Figure 4:

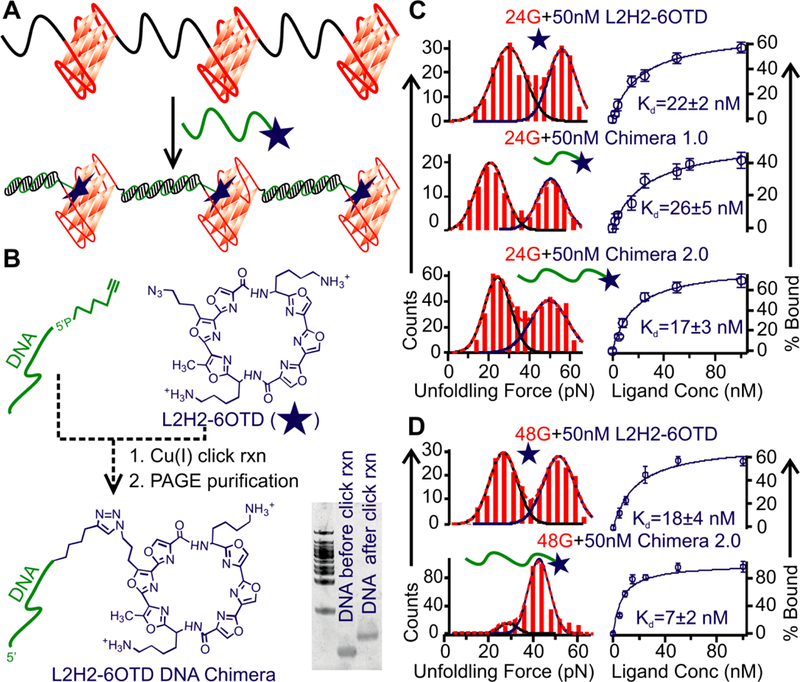
Recognition of vacant G-tracts. (A) Schematic of the binding of chimera ligands to telomere G-quadruplexes. The vacant G-tracts hybridize to the DNA fragment in the chimera ligand, which facilitates the binding of the telomestatin derivative (L2H2–6OTD) to the G-quadruplex. (B) Synthesis of the chimeric ligand using click reaction. The gel shift depicts successful ligation between the DNA and the L2H2–6OTD. (C) Bindings of 50 nM L2H2–6OTD monomer, Chimera 1.0 (with 9-nt complementary DNA) and Chimera 2.0 (with 15-nt complementary DNA) ligands to the 24G telomere overhang. Rupture force histograms depict ligand-bound high-force population and ligand-free low-force population. Based on the fraction of ligand-bound G-quadruplex, binding curves are shown to the right. (D) Rupture force histograms (left) and binding curves (right) for the 48G telomere construct in the presence of the pure ligand L2H2–6OTD (top) and the Chimera 2.0 (bottom). With respect to the 24G construct, binding is significantly increased for the Chimera 2.0 over the L2H2–6OTD ligand in the 48G construct.

Results and Discussion

Folded Species in the 4G−48G Telomere Overhangs

To overcome the difficulties in the deconvolution of different species in long telomere overhangs encountered by ensemble average techniques, we employed single-molecule force ramping assays in optical tweezers instrument (Figure 1A). We mechanically unfold and refold DNA secondary structures formed in human telomeric fragments, 5′-(TTAGGG)_n, where n = 4 (4G), 8 (8G), 12 (12G), 16 (16G), 24 (24G) and 48 (48G). Preparation of the 48G construct is challenging as it contains 291 guanine-rich nucleotides that are not commercially available. We used a divide-and-conquer strategy to prepare the entire construct by piecing together four 12G fragments using dynamic splitting ligation developed in our lab previously (21) (Figure S1). The 4G−48G constructs can form maxima of 1, 2, 3, 4, 6 and 12 G-quadruplex units, respectively. The secondary structures present in the telomere sequence will unfold when the force experienced by the structure exceeds its mechanical stability. Unfolding of these structures was manifested by a sudden change in the extension or force in a force−extension (F−X) curve (see Figure 1B for F−X curves of the 4G, 8G, 12G, 16G, 24G and 48G constructs). The size of folded structures was measured by the change-in-contour length (ΔL, Figure 1C) while the mechanical stability of the structure was depicted by the rupture force (F_rupture, Figure 1D) at which the unfolding occurred. To allow complete unfolding of all structures in the telomeric fragments, all F−X curves were recorded up to 60 pN before relaxing to 0 pN to refold DNA structures within a 30-second incubation period.

The ΔL for the unfolding events was plotted in a histogram (Figures 1C and S3) from which different populations were deconvoluted. We observed that G-quadruplex is the predominant species (85%, 83%, 86%, 85%, 82%, and 79% for the 4G, 8G, 12G, 16G, 24G, and 48G constructs, respectively), followed by the G-triplex population. Misfolded species with long loops (18, 35) and G-hairpin structures (17) are only present in telomere sequences longer than 24G (>144 nts, Figure S3; see Table S2 for population percentages of all folded structures in the telomere sequences).

We evaluated the change in the free energy of unfolding (ΔG_unfold) for the G-quadruplex in the 4G to 48G constructs.

After G-quadruplexes were deconvoluted from ΔL histograms (see Data Analysis in Materials and Methods), ΔG_unfold was calculated from the unfolding work by the Jarzynski equality for non-equilibrium systems (Equation 6). We observed that ΔG_unfold values for G-quadruplexes showed a decreasing trend with the length of the telomere overhang (Figure 1E, ΔG_unfold values are 9.8±0.2, 10.1±0.4, 9.2±0.2, 8.7±0.1 9.1±0.2, and 9.0±0.3 kcal/mol, for the 4G, 8G, 12G, 16G, 24G, and 48G constructs, respectively). It is noteworthy that compared to the shorter telomere overhang (4G and 8G), G-quadruplexes become ~1 kcal/mol less stable in overhangs longer than the 8G. Given that multiple G-quadruplexes form in longer overhangs (Figure 2A), it suggests the existence of negative cooperativity likely due to the electrostatic repulsion between G-quadruplexes, which is consistent with previous finding (25).

Kinetic Folding Pattern for Randomly Formed G-quadruplexes in Telomere Overhangs

Previous reports found that after hours of incubation, maximal number of G-quadruplexes was formed in telomere overhangs longer than the 4G (20, 22, 25, 26). In such a case, free energy minimum is reached by maximizing the enthalpic contribution from the Hoogsteen bonds inside G-quadruplexes. However, the maximal number of G-quadruplexes is not favored entropically since all G-tracts must fold into G-quadruplexes with much reduced degree of freedom. In the simplest case of the 8G construct that contains 8 G-tracts, there is only one arrangement that leads to the thermodynamically favored formation of two side-by-side G-quadruplexes (each G-quadruplex requires four tandem G-tracts). By contrast, random formation of one G-quadruplex is three times more likely to occur (Figure S4). This leads to an overall faster, or kinetically favored, formation of the G-quadruplex population that is thermodynamically disfavored. To evaluate whether G-quadruplex population follows the kinetic or the thermodynamic pathway in our force ramping experiments, we used an incubation time of 30 seconds. Previous single molecule investigations have shown this incubation time corresponds to the half-life of G-quadruplexes in 4G-8G telomeric overhangs (15). During experiments, we did not observe any refolding of telomeric G-quadruplex structures when the tether was under tension, even at low forces in comparison to structures such as hairpins. The tethers were incubated for 30s under zero tension to allow full refolding of G-quadruplexes before next pulling cycle. The 30s was estimated from the previous finding on G-quadruplexes with various lengths to reach maximal folding (see Figure 5 in reference (18)). We also evaluated longer incubation times. Out of five traces incubated for 120s and 300s, the percentage of features observed for the 24G construct (320 %) was similar to that collected during the 30s incubation (319%), confirming the 30s window is sufficient to reach a steady state. Within this 30s time frame, we analyzed the distribution pattern of folded features in each force-extension curve up to 60 pN at which almost all species should unfold (Figure 2A). Compared to previous reports in which hours of incubations were used to reach a thermodynamic equilibrium of G-quadruplex populations (22, 25), the maximal number of G-quadruplexes expected in a thermodynamic pathway (see Equation 3 and Figure 2A bottom panel) was not observed for most of the telomere overhangs longer than the 4G in our 30s experiments (Figure 2A top panel).

Rather, the experimental distribution pattern agrees well with the simulation based on the kinetic model (see Materials and Methods and Figure 2A middle panel). To quantify the difference between the experimental observation and the kinetic or the thermodynamic model, we calculated weighted Root Mean Square Deviation (RMSD, see Materials and Methods). Indeed, the experimental G-quadruplex distribution pattern agrees significantly better with the kinetic rather than the thermodynamic model (Figure 2C).

To confirm this finding, we designed a control experiment using DNA constructs with two and three G-quadruplex forming sequences (see the ‘8G-Spaced’ and the ‘12G-Spaced’ sequences in Table S1) in which each G-quadruplex is sequestered by 24-nt thymine-rich spacers. Due to the long spacers (41), the G-quadruplexes formed within separated G-rich regions are expected to behave independently. Therefore, the folding pattern of G-quadruplexes in these spaced sequences should follow the thermodynamic model. This prediction was exactly observed in Figure 2B&C, confirming that G-quadruplexes fold at random locations in the wild-type telomere overhangs. In addition, we calculated the average numbers of the structure formation (see Equation 2) from the experimental data in both wild-type and spaced telomere constructs, as well as those from the kinetic folding simulation and the thermodynamic folding model (Figure 3A). The striking agreement of the structural formation in the wild-type telomere sequence (solid green) and the kinetic folding simulation (dotted red) reaffirms that the G-quadruplex folding pattern in telomere overhangs predominantly follows a kinetic folding pathway.

Figure 3:

Vacant G-tracts in telomere overhangs. (A) Comparison of experimentally observed formation (see Materials and Methods for detailed calculation) of folded structures (green) with that calculated by the simulation using the thermodynamic (dark blue) or kinetic (red) model. Cyan trace represents the experimental observation on the 8G and 12G constructs that contain 24-nt thymine rich spacer sequence between two neighboring G-quadruplex forming sequences. Red asterisk represents the formation of secondary structures in the 48G calculated from the simulation without minimum spacers. (B) The average vacant G-tracts per structure in the 8G-48G constructs. Dotted trace is a linear fitting to guide eyes.

We constructed a free energy diagram to rationalize that the kinetic folding is preferred over the thermodynamic in an exemplary 12G construct (Scheme 1). In the thermodynamic folding (blue), three G-quadruplexes are formed eventually, which represents the maximal possibility of G-quadruplex formation in this construct. This provides the biggest driving force in the change in free energy (ΔG_{thermodynamic} = 27.6 kcal/mol). In all other cases in which G-quadruplexes are randomly formed (red), a maximum of 2 G-quadruplexes can be formed (ΔG_{kinetic, max} = 18.4 kcal/mol). Although not favored thermodynamically, the kinetic folding of a G-quadruplex is twice more likely to occur during the folding of the first or the second G-quadruplex, which leads to reduced apparent activation energy on the order of k_BTln2 (0.41 kcal/mol) in each case (see Figure S8 for details). Once the 12G (or other overhang) construct adopts a kinetic folding path, it cannot return to the thermodynamic path without unfolding the G-quadruplex trapped kinetically. Such an escape is not likely during the physiologically relevant time scale given the slow unfolding kinetics of a telomeric G-quadruplex at zero force (1.3 – 0.0003 s⁻¹ dependent on the geometry of the unfolding) (42).

Scheme 1.

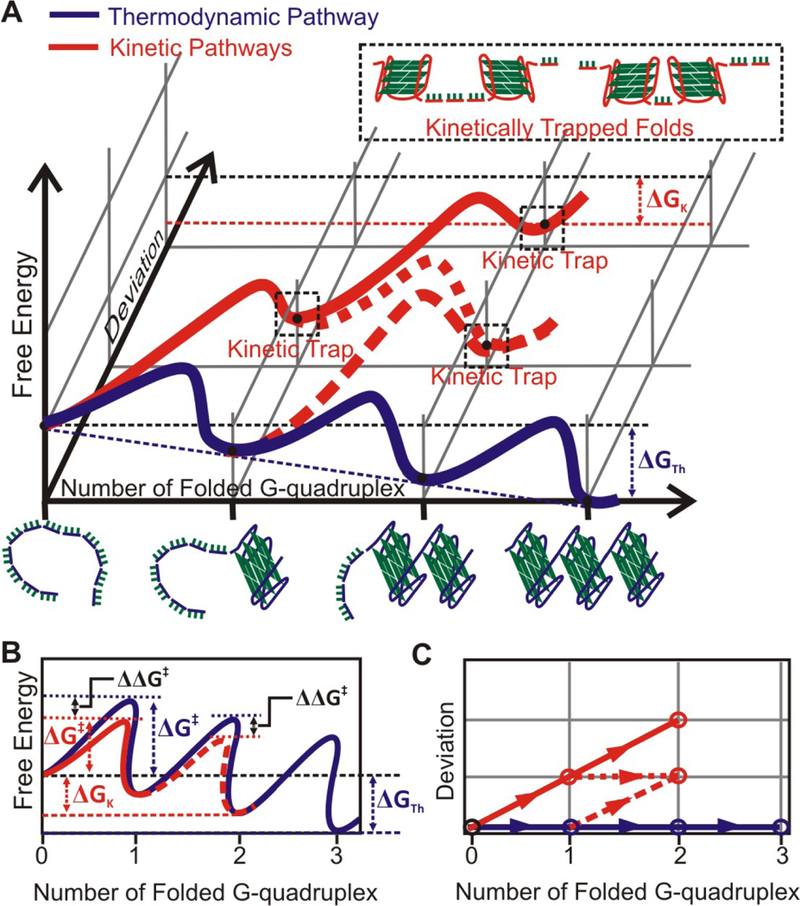
Free energy diagram for the folding of G-quadruplexes in the telomere 12G overhang. The thermodynamic folding (blue) involves sequential formation of all 3 G-quadruplexes. The change in free energy of folding (ΔG_fold) is estimated from Jarzynski equality (see Eqn 6), whereas the activation energy of folding (ΔG^†_fold) and the activation distance (x^†) are obtained from the fitting of the rupture force histogram using Dudko model(58) (Figure S7). For kinetic folding model, different pathways for the folding of one G-quadruplex are combined into an ensemble trajectory with an apparent ΔG^†_{fold,apparent} about 0.41 kcal/mol lower than that of the thermodynamic model (see Figure S8 for details). Folding of the two G-quadruplexes is treated similarly in the kinetic model. (A) 3D free energy diagram (drawing not to scale, see Figure S7 for actual values). The y axis depicts the deviation steps from the thermodynamic folding path. (B) Projection of the 3D diagram on the plane of free-energy vs reaction coordinate. (C) Projection of the 3D diagram on the plane of reaction coordinate vs deviation steps.

Vacant G-tracts between G-quadruplexes

Deviations, however, exist between experimental and kinetic folding patterns, especially in long telomere overhangs (Figures 2A and 3A). One explanation for such deviations is the presence of the G-quadruplex – G-quadruplex repulsion, which is likely due to the high charge density of folded G-quadruplex structures (see below). To account for this, we introduced minimum spacing (in units of vacant G-tracts) between two quadruplexes in a modified simulation (Figures S5 & S6). The newly simulated results fit the kinetic model even better (Figures 2D and 3A). From the RMSD deviation between the simulated and the experimentally observed folding patterns, we found that the minimum spacing increases with the length of the telomeric overhang (Figure S6). From each F-X curve, we also evaluated the number of structures formed in a specific telomere overhang. This allowed us to estimate the number of G-tracts involved in the folded structures and the vacant G-tracts in various telomere overhangs (Equation 5). Significantly, we found that the longer the overhang, the more (or the longer) the vacant G-tracts (Figure 3B). This finding qualitatively agrees with the simulated data for the minimum spacing discussed above (Figures 2D and S6).

Close inspection on the vacant G-tracts reveals that in the 48G construct, the average length of vacant G-tracts is 4.5 per structure formed (Figure 3B), which is long enough for the formation of another G-quadruplex (requires a minimum of 4 G-tracts). The fact that this G-quadruplex is not formed in the vacant G-tracts can be ascribed to the electrostatic repulsion between closely packed G-quadruplexes with high charge densities. It has been found that for charged spheres such a G-quadruplex, counterion condensation does not occur (43) to screen the electrostatic interactions as expected for linear polyelectrolytes (44, 45). In overhangs shorter than the 48G, it has fewer tendencies to form multiple G-quadruplexes due to the length of the overhang, as well as the kinetic folding mechanism (Figure 2A). Therefore, it becomes rare to inhibit the formation of the middle G-quadruplex due to the electrostatic repulsion from the two flanking G-quadruplexes. In addition, in shorter overhangs, the two ends of each overhang become more significant with respect to the overall length. As a result, G-quadruplexes have a better chance to form closer to one of the terminals with reduced repulsions. Experimentally, the electrostatic repulsion is consistent with the finding that G-quadruplex becomes less stable with smaller ΔG_unfold in longer overhangs (Figure 1E).

Targetable Vacant G-tracts

To confirm the presence of vacant G-tracts between neighboring G-quadruplexes, we designed G-quadruplex ligands that can target these vacant tracts (Figure 4A). In this strategy, we applied Cu(I) catalyzed click chemistry reaction (46) to attach a DNA fragment, 5′- TAA-(CCCTAA)_n=1,2 to the L2H2–6OTD (29), a telomestatin derivative known to bind many G-quadruplex conformations (47) (see Materials and Methods and Figure 4B for preparation). Since the 5′-CCCTAA sequence is complementary to that in the vacant G-tracts, hybridization should occur between the DNA fragment and the vacant G-tracts in the telomere overhang. As a result, the L2H2–6OTD moiety in the ligand chimera becomes closer to the G-quadruplex, leading to a proximity effect that strengthens the binding of the conjugate to the G-quadruplex in the telomere overhang (Figure 4A). The binding of a ligand to the G-quadruplex is expected to increase the mechanical stability of the G-quadruplex (39), which is manifested as the high-force population in unfolding force histograms. This allows the evaluation of the binding efficiencies (ligand-bound fraction and the dissociation constant K_d, see Materials and Methods) between the 24G construct and the ligands conjugated with the 9-nt (5′-TAACCCTAA, Chimera 1.0) or the 15-nt (5′-TAACCCTAACCCTAA, Chimera 2.0) fragments (Figure 4C).

Comparison of the bindings in the 24G revealed no significant difference between the Chimera 1.0 (K_d=26 ± 5 nM, Figure 4C) and the pure ligand (L2H2–6OTD, K_d=22 ± 2 nM). This can be rationalized by the fact that the hybridization between the 9-nt DNA in the Chimera 1.0 and the vacant G-tracts is not strong at room temperature (melting temperature of the hybridization: 24 °C).

Hybridization of longer complementary sequences helps to strengthen the binding (48). Indeed, at 50 nM, we observed that the Chimera 2.0 ligand has a significantly higher ligand-bound G-quadruplex fraction (62 ± 5.3 %) compared to the Chimera 1.0 (48 ± 5.8 %). However, comparison of the K_d values among the Chimera 2.0 (K_d = 17 ± 3 nM, Figure 4C), the Chimera 1.0 (K_d = 26 ± 5 nM), and the pure ligand (K_d = 22 ± 2 nM), did not show drastically improved binding for the Chimera 2.0. This can be ascribed to the fact that vacant G-tracts in the 24G construct may not be long enough to hybridize with the 15-nt C-rich nucleotides in the Chimera 2.0. As the 48G construct is expected to contain more (or longer) vacant G-tracts (Figures 2D, S6, and 4B), we evaluated the binding efficiency of the Chimera 2.0 in the 48G construct (Figure S11). As expected, 50 nM Chimera 2.0 binds to the G-quadruplexes in the 48G construct with a dramatic increase in the binding fraction (95.2 ± 5.2 %) compared to the L2H2–6OTD (57.5 ± 4.4 %) (Figure 4D). Consistent with this, the dissociation constant for the Chimera 2.0 (7 ± 2 nM) was also significantly smaller than the L2H2–6OTD (18 ± 4 nM). These results not only confirmed the presence of vacant G-tracts in telomere overhangs, but also supported the finding that these vacant G-tracts increase with the overhang length (Figure 3B).

It is notable that previous thermodynamic investigations do not reveal the presence of vacant G-tracts (22, 24, 25), which can be ascribed to the slow reannealing conditions (in hours) used in these experiments. The formation of vacant G-tracts observed here was within physiologically relevant time scale of seconds. It has been shown that single-stranded telomeric overhang helps to assemble shelterin complex (3, 49) or recruit telomerase (50). The vacant G-tracts are therefore expected to mediate these important functions. The vacant G-tracts are also expected to help specific targeting of telomere G-quadruplexes. Binding of specific G-quadruplexes remains a challenge in the field (40, 48, 51, 52). Recent analysis has revealed that 716,310 potential G-quadruplex forming sites in the human genome, especially in the telomeres and promoter regions (53). Most small-molecule ligands developed so far use generic interactions such as π-π stacking and electrostatic attraction to bind to G-quadruplexes (54, 55). These mechanisms will lead to non-specific binding of small molecules to G-quadruplexes in various regions of the genome, resulting in altered gene expressions and unfavorable side-effects. Targeting vacant G-tracts using complementary DNA (48), PNA (56), or LNA (57) fragments can serve a new way to increase the specificity in the binding of telomere G-quadruplexes.

Conclusions

In summary, by investigating G-quadruplex formation in the full-range of telomere overhangs, we found G-quadruplexes form randomly in the telomere overhang, resulting in a kinetically driven population pattern within a physiologically accessible time frame. Neighboring G-quadruplexes are dispersed by vacant G-tracts, whose length or occurrence increases with the length of telomere overhang. These vacant G-tracts between G-quadruplexes can be utilized as anchors to attract telomere G-quadruplex ligands with much increased binding efficiency.