Joint analysis of heterogeneous single-cell RNA-seq dataset collections

Abstract

Single-cell RNA-seq is being increasingly applied in complex study designs, commonly spanning multiple individuals, conditions, or tissues. Analysis of such heterogeneous collections requires a way of identifying recurrent cell subpopulations. We developed Conos, an approach that relies on multiple plausible inter-sample mappings to construct a global graph connecting all measured cells. The graph enables identification of recurrent cell clusters and propagation of information between datasets in multi-sample or atlas-scale collections.

Progress of scRNA-seq techniques has enabled individual groups to measure dozens of samples, often in complex designs incorporating treatment / control sets, disease and normal pathology, or multiple tissues. Consortium efforts are underway to generate atlases of single-cell datasets covering diverse biological contexts with thousands of samples^{1, 2}. Joint consideration of such panels poses technical and conceptual analysis challenges, necessitating new methods and re-consideration of the aims. In contrast to the traditional batch correction problem, where inter-sample variation can be treated as a technical artifact that needs to be controlled for^{3, 4}, the panels can include systematically different samples, with some of the datasets lacking any shared cell subpopulations. Recent alignment methods^{5, 6}, while significantly more flexible, were designed to align relatively small sample panels with modest compositional variation. We therefore set out to develop an approach for analyzing and navigating large heterogeneous sample collections.

We reasoned that a unified graph representation could capture likely relationships between cells in different samples, and that statistical analysis of such a joint graph can identify subpopulations across different samples (Figure 1a). To construct the joint graph, Conos (Clustering On Network Of Samples) performs pairwise alignments of individual samples, identifying plausible inter-sample cell-cell correspondence (inter-sample edges). Such mappings are error-prone, as inter-sample variation cannot be usually modeled or constrained. Across many pair-wise comparisons, however, the recurrent subpopulations of cells will tend to map to each other, forming clique-like communities within the joint graph that can be identified over the background noise of spurious edges (Figure 1a). Conos also adds low-weight edges connecting neighboring cells within the individual samples, as a weak prior for preserving local neighborhoods of cells in each sample. The plausible mapping between a pair of samples is established using mutual nearest-neighbor (mNN) mapping in reduced expression space^{5, 6}. We evaluated spaces capturing common variation across two or more samples, including common principal component analysis⁷ (CPCA), joint non-negative matrix factorization, and higher order generalized singular value decomposition⁸.

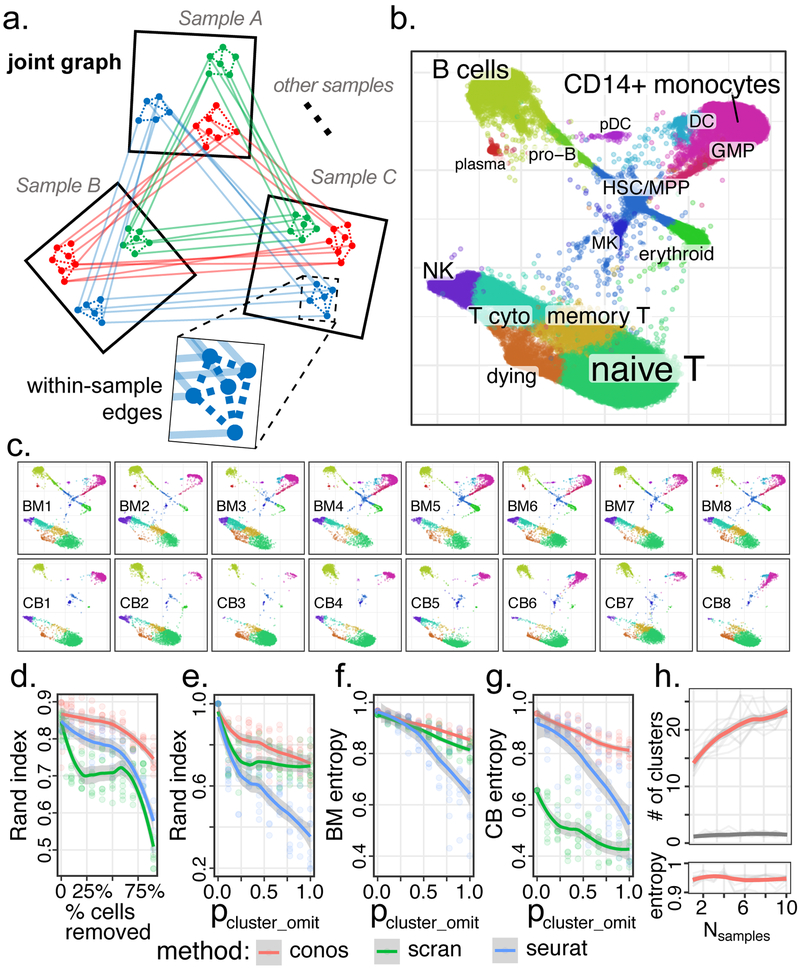
Figure 1. Joint graph is an effective strategy for assembling diverse scRNA-seq dataset collections.

a. Conos builds joint graph by comparing all pairs of datasets. Reduced space (e.g. CPCA) is determined for each pair and the putative inter-sample edges are established using mutual-nearest neighbor mapping. Low-weight within-sample edges are also included in the graph. Subpopulations of cells recurrent within the dataset collection form clique-like communities of inter-sample edges within the joint graph.

b. Joint graph combining eight human bone marrow and eight cord blood datasets is visualized using largeVis embedding.

c. Visualization of each individual sample on the joint embedding.

d. Adjusted Rand index (y-axis) is shown as a function of the fraction of cells omitted from the datasets (x-axis) relative to the full dataset for different joint clustering approaches. Conos shows improved stability of subpopulation detection even for small numbers of cells.

e. Stability of the subpopulation detection is shown for increasing amount of heterogeneity between datasets. Adjusted Rand index is shown for increasing probability of random subpopulation omission from individual datasets (x-axis, see Methods).

f,g. Mixing of different bone marrow (h) and cord blood (i) datasets within the identified subpopulations is quantified using normalized average cluster entropy (see Methods).

h. The power to detect cell subpopulations increases with the size of the collection. The number of stable clusters (y axis, see Methods) detected in a collection of human bone marrow samples (red curve) increases as more samples are added to the collection (x-axis), while maintaining high level of sample mixing (high average cluster entropy) within each cluster. In contrast, addition of randomized expression datasets (grey) does not result in such increase.

d-h: Mean across n=10 random replicates is shown for each point, with shading marking the 95% confidence band.

We first applied Conos to a collection of sixteen scRNA-seq samples of human bone marrow and cord blood from the Human Cell Atlas². Projection of the resulting joint graph separated all major subpopulations (Figure 1b, Supp. Figure 1), with the detected joint cell clusters connecting the corresponding subpopulations across the entire collection. While the individual samples were well-mixed within the joint graph, the systematic difference in the composition of the two tissues was also apparent (Figure 1c). To quantify robustness and sensitivity we perturbed the full dataset to decrease signal or increase heterogeneity between samples. Examining recovery of the original subpopulations identified by each method under decreasing numbers of cells (Figure 1d) or under decreasing magnitude of subpopulation-specific expression signatures (Supp. Figure 1e), we find that CPCA shows optimal performance, significantly outperforming earlier methods. Conos performance remained robust under parameter perturbations (Supp. Note 1), and even with simple pairwise alignment strategies (e.g. nearest neighbor mapping based on simple gene correlation; Supp. Figure 1). We have applied Conos to re-analyze a number of recently published complex datasets^9-12, in all cases joining corresponding annotated subpopulations across different samples and tissues (Supp. Figures 2-7).

Modern experimental designs are likely to combine distinct classes of samples within the panels, such as sets of disease samples and healthy controls, or multiple tissues from different individuals. We simulated increasing heterogeneity of a panel by omitting increasing number of random clusters from samples, and evaluating the method’s ability to recover originally detected subpopulations (Figure 1e). Conos showed higher robustness compared to other methods. Furthermore, Conos was able to sustain uniform mixing (i.e. high entropy) of cells from different samples among the identified joint clusters even under high sample heterogeneity, where some of the samples shared few or no cell subpopulations (Figure 1f,g). Community detection on a joint graph shows high sensitivity, for instance enabling Conos to detect subpopulations that may be represented by only a single cell in a given sample (Supp. Figure 1f). More importantly, the sensitivity of the proposed approach increases as more samples are added to the panel (Figure 1h), suggesting that larger collections of scRNA-seq samples will reveal more subtle recurrent cell subpopulations.

Consideration of diverse sample panels requires one to re-examine the aims of integration. While for homogeneous panels, the aim is to identify a set of clusters that appear in nearly every sample, this is not the case for panels with distinct classes of samples. For example, for a panel containing both tumor and adjacent normal samples¹², it would not be desirable to lump tumor cells with any normal tissue subpopulations, even though the cluster of tumor cells would be restricted to a subset of samples (e.g. Supp. Figure 5). In a more nuanced scenario, the clustering may separate tumor-associated CD4⁺ T cells from their counter-parts in the healthy tissues⁹, picking up persistent biological difference in their state (Figure 2a-d). However, for annotating major cell types, a unified cluster of CD4⁺ T cells across all samples would be more appropriate. Graph communities can be viewed as a hierarchical clustering of cells, and in that way the difference between separating or joining tissue-specific subgroups of CD4⁺ T cells is equivalent to cutting the hierarchy at different levels (Figure 2d,e, Supp. Figure 5). Overall, lower cuts will yield higher resolution of subpopulations, but will also decrease cluster breadth – the average fraction of samples in which a cluster appears. As the balance between the desired resolution and breadth will depend on the question being posed by the investigator, Conos incorporates an interactive tool to explore the hierarchical community structures (Supp. Figure 8). For the situations when higher degree of mixing between samples is desired, Conos implements an option to increase “alignment strength” by sampling cell-cell edges from neighborhoods of higher radii and rebalancing edge weights (see Methods). Adjustment of this continuous “alignment strength” parameter and the optional edge weight rebalancing based on the sample type enables higher mixing at expense of resolution (Supp. Figure 9).

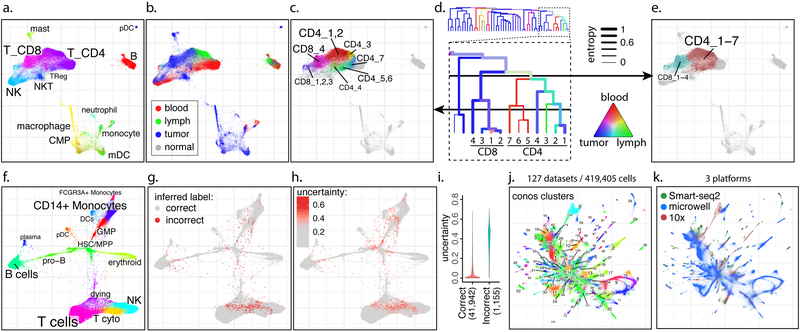
Figure 2. Examples of analyses using joint graphs.

a-e. Trade-off between cluster resolution and sample breadth. Joint graph is shown for n=15 samples from eight breast cancer patients⁹ (a). The distribution of source tissues (b). A fragment of the subpopulation hierarchy is shown for T cells subsets (d), with color of the branches showing tissue composition, and width showing normalized sample entropy (higher entropy corresponds to more samples contributing to the branch). Depending on the level, a cut of the cluster hierarchy can yield more granular but tissue-specific clusters (c) or less granular clusters that incorporate more tissues and samples (e).

f-i. Propagation of cell annotation labels. Joint embedding of bone marrow samples from n=8 patients is shown (f). The annotations were erased from all but one sample, and propagated back to the entire dataset. Positions of the incorrectly propagated labels (g). Uncertainty of propagation, reported by Conos (h). Reported uncertainty of correctly and incorrectly propagated labels (i).

j-k. Conos integration of the Tabula Muris¹ and Han et al.¹⁶ mouse atlases. Joint graph of the 127 datasets is, with colors and numbers marking top-level joint clusters (j) or scRNA-seq platforms (k).

Joint graph can be used to map properties between samples by simulating the diffusion process. For instance, one can propagate discrete cell annotation labels to datasets that have not yet been annotated (Figure 2f). On the bone marrow example, Conos propagates labels from one dataset to the other seven with 97% accuracy (Figure 2g). The diffusion propagation keeps track of uncertainty, and almost all of the misclassified cells were reported to have high uncertainty of the labels (Figure 2h,i). Similarly, diffusion of gene expression magnitudes provides a way of deriving common expression space (Supp. Figure 10). Such “corrected” expression values are often estimated by the existing batch correction or alignment methods. We contend that the utility of such “corrected” expression values will be mostly limited to visualization. Once the appropriate clustering of cells is established, we expect follow up analyses to focus on the expression variation among samples. This includes cell type-specific analysis of expression differences between groups of samples, or variation within groups. Corrected expression values specifically attenuate differences between samples, and would lead to inflated significance estimates in comparisons of different cell subpopulations. Instead, Conos reformulates the differential expression tests as comparisons of in silico bulk RNA-seq measurements¹³ that can be delegated to common differential expression software^14,15, providing convenience routines for the common differential tests.

Overall, our results demonstrate that integration of single-cell collections into a unified graph representation provides effective means for integrative analysis, including subpopulation identification, differential expression or annotation. Compared to existing methods, Conos implementation shows improved stability and sensitivity, particularly notable on heterogeneous sample panels, such as multi-tissue / multi-patient clinical study designs. This robustness allows Conos to wire together very diverse collections of samples, such as organism-scale atlases where most of the samples will have few or no cell types in common. For example, we re-analyzed Tabula Muris mouse atlas¹, combining 48 datasets covering different mouse tissues (Supp. Figures 11-13), and further combined it with another atlas by Han et al.¹⁶ (Figure 2j,k). The resulting joint graph integrated a total of 127 individual datasets, containing 419,405 cells, and was effective at identifying common cell populations across samples measuring diverse tissues, as well as overcoming the differences of the three different scRNA-seq platforms utilized (Supp. Figures 14-18). The approach is fast, particularly when using a simpler PCA space (Supp. Figure 19). Conos can also be applied other molecular modalities. As an example, we used Conos to assemble mouse single-cell chromatin accessibility atlas^{17, 18}, as well integrate accessibility and scRNA-seq data (Supp. Note 2). We hope that the presented approach will enable other research groups to effectively interpret single-cell RNA-seq collections in complex experimental designs.

Online Methods

Overview of the approach.

Conos processing can be divided into several key phases. During the phase I, each individual dataset in the sample panel is filtered and normalized using standard packages for single-dataset processing: pagoda2 or Seurat. Specifically, Conos relies on these methods to perform cell filtering, library size normalization, identification of overdispersed genes, and in case of pagoda2 - variance normalization. Conos is robust to variations in the normalization procedures, but it is recommended that all of the datasets would be processed uniformly. During phase II, Conos performs pairwise comparisons of the datasets in the panel to establish initial, error-prone, mapping between cells of different datasets. These inter-sample edges are then combined with lower-weight intra-sample edges during phase III – joint graph construction. The joint graph is then used for downstream analysis, including community detection, label propagation, etc.

Pairwise dataset alignments (phase II).

Initial inter-sample edges between a given pair of datasets i and j was established based on a choice of 1) rotation space, and 2) neighbor mapping strategy (nearest neighbor or mutual nearest neighbor). For each dataset, a set of overdispersed (hypervariable) genes (gⁱ, g^j) was determined using pagoda2 (by default n.odgenes=2000 top overdispersed genes were used), and a union of overdispersed genes from both datasets was taken, limiting the genes to those for which the data was available in both datasets: g = [gⁱ ∪ g^j] ∩ Gⁱ ∩ G^j, where Gⁱ and G^j are the full gene sets for the two datasets. Subsequent analysis was carried out on matrices Mⁱ and M^j, with columns corresponding to genes g, and rows corresponding to the cells in each dataset. The entries of each matrix were taken to be the variance-normalized expression magnitudes determined by pagoda2 (normalized expression magnitudes are used if pre-processing was performed by Seurat).

The reduced projection matrices Rⁱ and R^j were obtained according to the space used: For CPCA and JNMF, these corresponded to projections onto the corresponding common/joint components (30 components, by default). For PCA space, PCs (30 by default) were determined independently for Mⁱ and M^j, with Rⁱ and R^j then determined by projecting the cells of each dataset onto a joint (i.e. 60-dimensional) space of both sets of PCs. For gene space, Rⁱ and R^j were taken to be the matrices Mⁱ and M^j themselves.

Cell-cell similarity between cells k and l was determined as w_kl = max(r_kl,0), where r_kl is the Pearson linear correlation between the k-th row of Mⁱ and l-th row of M^j. An alternative L2 distance was implemented as $w_{kl}=\text{exp}\left(-\frac{\Vert M_k^i-M_l^j{\Vert }_2}{\sigma }\right)$, where the default scaling constant σ = 10⁵.

Joint graph (phase III).

For a given sample collection, the nodes of the joint graph G correspond to all of the cells included in the collection, connected by a combination of inter- and intra-sample edges. The inter-sample edges were determined as mutual nearest neighbors (mNN, default) or plain nearest neighbors (NN), with the weight w_kl. Neighborhood size k=15 was used by default. Intra-sample edges for each dataset i connected each cell to k_self (default k_self = 5) cells within the dataset i using weights w_kl = c_self · r_kl within the reduced space Rⁱ as determined by the projection of the cells onto the top PCs of Mⁱ. The constant c_self = 0.1 was used to reduce the contribution of the intra-sample edges relative to the inter-sample edges.For the visualization purposes, joint graphs were laid out in two dimensions using largeVis algorithm, varying parameter alpha between 0.5 and 2.5 depending on the complexity of the dataset.

Joint clustering.

Joint clusters were determined as communities of the joint graph G, using standard community detection methods. By default, walktrap.communities algorithm implemented by the igraph package was used, with step=20. Louvain clustering implemented by igraph::multilevel.communities method provided much faster performance, but lacked hierarchical output. Implementation of the Leiden community detection method with the resolution parameter was adapted from https://github.com/vtraag/leidenalg.

Alignment strength.

By default, Conos aims to preserve biological variation by keeping track of cell-cell distances using edge weights, and treating all comparisons in a symmetric way. In some cases, however, the user may want to force greater degree of alignment (mixing) of the datasets. This results in a trade-off between resolution (ability to resolve finer subpopulation) and mixing of samples (Supp. Figure 9). To provide such a control we added k₁ parameter, which allows to increase the nearest neighbor search radii. k₁ is initially used instead of k during mNN-graph construction. Then, the edges are pared down to reduce maximal degree of the graph vertices close to k, making the graph less dense and more regular. The following greedy procedure is used:

1. Vertices are ordered from the highest to the lowest degree.

2. For each vertex, edges are ordered by the degree of their target vertices (high to low).

3. Algorithm iterates through the vertices and corresponding edges, removing an edge if the degrees of its both incident vertices are larger than a specific cut-off k₀.

As this is a greedy algorithm, to achieve more uniform reduction Conos runs the procedure iteratively, reducing k₀ from k₁ to k using logarithmic grid of three steps. We also observed that even with very large k₁ (when trying to force alignment of very distant cells), some vertices have too few nearest neighbors with positive correlation r_kl. To prevent that, weight calculation can be changed from w_kl = max(r_kl, 0) to w_kl = 1 + r_kl (using cor.base=2 argument; by default cor.base value will be increased towards 2 automatically when increasing k₁). To provide a user-friendly way to control k₁ we also implemented an alignment strength parameter α (alignment.strength), such that k₁ = α²K_max, where K_max is the maximal number of total cells among the samples in the panel. Thus, α varies from 0 to 1, where 0 (default) corresponds to the alignment with no additional edges, and 1 corresponds to a full (non-informative) alignment with uniform edge placement over graph.

Rebalancing of edge weights.

In many experimental designs, samples can be classified by an extraneous factor, such as patient group (e.g. healthy vs. disease), or protocol (e.g. Smart-seq2 vs. 10x Chromium). As discussed in the manuscript, such systematic differences should typically lead to hierarchically-defined factor-specific subclusters within each major subpopulation. However, in some cases, the user may want to explicitly force alignment across such factors. To implement such control, we added an optional step, which balances weights of the edges connecting cells from samples belonging to the same or different values of the factor. This is achieved by minimizing of the following function:

$$\sum _{l=1}^{N_{\mathit{factors}}}\sum _{s=1}^{N_{\mathit{cells}}}\mid \frac{\sum _{\mathit{t}\in {\mathrm{adj}}_l(s){\mathit{W}}_{\mathit{st}}}}{\sum _{\mathit{t}\in \mathrm{adj}(s){\mathit{W}}_{\mathit{st}}}}-\frac{1}{{\mathit{N}}_{\mathit{factors}}^s}\mid ,$$

where N_factors is the total number of factor levels; N_cells is the total number of cells in the dataset; adj(s) is the set of cells adjacent to the cell s; adj_l (s) is the set of cells adjacent to s and belonging to the factor level l; w_st is the weight of the edge between cells s and $t;N_{\mathit{factors}}^s$ is the number of different factors among cells connected to s. The minimization is performed using a the two-step procedure. The first step estimates the imbalance ratio for a cell s and a factor level $l:u_{sl}=N_{\mathit{factors}}^s\frac{{\sum }_{\mathit{t}\in {\mathrm{adj}}_l(s)}{w}_{st}}{{\sum }_{\mathit{t}\in \mathrm{adj}(s)}^{qqqqq}{w}_{st}}$. The second step updates the edge weights as $w_{st}=\frac{w_{st}}{\sqrt{u_{s{l}_t}{u}_{t{l}_s}}}$, where l_c denotes the factor level of the cell c. This procedure is repeated 50 times, which does not guarantee convergence, but allows to reduce the loss function by several orders of magnitude in a reasonable time. Such optimization preserves the ratios of the edge weights $\forall \frac{w_{sj}}{w_{si}}:l_i=l_j$, varying only the weight ratios between the edges connecting cells with different factor levels. Further prioritization of the edges connecting samples from different factor levels can be gained using same.factor.downweight parameter (which, when set below the default value of 1 will reduce the weight of edges connecting cells of the same factor level). Edge rebalancing procedure can also be applied without an extraneous grouping of samples by assigning each sample to its own factor level.

Label and value propagation.

Propagation of both labels and expression magnitudes was treated as a general problem of information propagation between graph vertices. Graph vertices can have multiple labels, either continuous or discrete. Such labels can be affected by biases or different kinds of noise. Assuming that adjacent vertices on the graph have similar labels, we can reduce this noise using iterative diffusion process on the joint graph. For continuous labels the diffusion process was implemented as follows:

1. At the beginning of an iteration, each vertex has a label L_i ; An edge between vertices i and j has weight w_i,j and length d_i,j = 1 – w_i,j (see phases II and III for info about weight estimation).

2. During the iteration, for each label we update its value with ${L_i}^{\prime }=\frac{{\sum }_{j\in ad{j}_i}{v}_{i,j^{\ast }}{L}_j}{{\sum }_{j\in ad{j}_i}{v}_{i,j}}$, where v_i,j = exp(−a(d_i,j + b)), a and b are hyper-parameters of the algorithm (default values a = 10, b=0.5 were used). The set adj_i includes all vertices adjacent to i, including vertex i(w_i,i = 1).

3. The iterations are carried out until one of the two conditions are met: i) a maximum allowed number of iterations is reached (default 15), or the infinity norm of difference between the two labelings (max_i∣L_i′ – L_i∣) falls below a minimal threshold (default 0.005).

Considering each gene as a continuous label, Conos uses this diffusion process to correct gene expression matrices and bring all of the datasets into a “common” expression space. We note that a single iteration of the diffusion process with parameter a=0 is equivalent summing of expression over adjacent cells, which is a common approach for noise correction in scRNA-seq data.

For discrete labels, the implementation tracked label uncertainty, with the diffusion process being used to estimate posterior probability of each label for each vertex. This was performed by running diffusions on the probability distribution of the labels:

1. Posterior distribution of possible labels was kept for each vertex. The starting state for the labeled vertices was set so that the probability of the true label is set to 1, with the probability of other values set to 0. For the unlabeled vertices, all of the values were initially set to 0.

2. On these distributions we simultaneously simulate the diffusion process for each component of the distribution (i.e. for each label). After each diffusion step, the values of the posterior distributions were re-normalized so that the sum of the label probabilities was equal to 1.

Diffusion of discrete values was used for the cell annotation propagation results (Figure 2f-h). In the figures, the uncertainty of the labeling was evaluated as 1 – max_i(p_i).

Benchmark design.

Quantitative performance of different methods shown in Figure 1 and Supp. Figure 1 relied on the same general design, where each method m was ran on a full dataset to obtain clustering C^m. The full dataset was then gradually perturbed to pose a more challenging problem, and the ability of different methods to recover their corresponding original clustering C^m was measured. Such procedure aims to place different methods on equal footing, and make use of realistic data (as opposed to synthetic). Details of different benchmarks are given below:

• Cell subsampling benchmark (Figure 1e). HCA BM+CB 3k dataset containing a total of 16 samples was used (see below for dataset details). A percentage of cells p_removed ∈ [0, 80%] (x-axis) was randomly sampled and removed from each dataset in the collection. For each value of p_removed, a total of 10 replicates of dataset perturbation were generated. To assess performance, adjusted Rand index (y axis) was calculated relative to the first replicate with p_removed = 0. A smoothed mean for each method and the corresponding 95% confidence band is shown on the Figure 1e were calculated using igraph::geom_smooth() method. Note that all of the examined methods show certain level of instability to negligible perturbations of the dataset (such as shuffling of the cell order in the matrix, or removal of a single cell). As datasets sampled with p_removed = 0 shuffled the order of the cells, the adjusted Rand index value at p_removed = 0 is below 1.

• Cell mixing benchmark (Supp. Figure 1e). HCA BM+CB 3k dataset was used. For each dataset i, background expression vector bⁱ was determined for each gene g as $b_g^i=N_g^i$, where $N_g^i$ is the total number of molecules of gene g detected in the dataset i. A perturbed dataset with a mixing proportion p_mix ∈ [0,1] was generated for each cell by iterating through each molecule of the cell, keeping the original molecule with a probability 1 – p_mix, or alternatively (with probability p_mix) replacing it with a molecule randomly sampled from the background profile bⁱ. This way datasets generated with p_mix = 0 are equivalent to the original data, whereas p_mix = 1 yields datasets where each cell is a random sampling of the background, and any cell subpopulations would be impossible to discern.

• Cluster dropping benchmark (Figure 1f-h). To simulate increasing compositional variability between the samples, cells belonging to a cluster c ∈ C^m were omitted with a probability p_omit. The sampling procedure was carried out independently for each dataset, so that different clusters were dropped from different datasets (increasing compositional variability). To guarantee a minimal dataset size, a total of 5 clusters were sampled this way in each dataset. Under such procedure, p_omit = 0 maintains the full original dataset, whereas p_omit = 1 maximizes inter-sample compositional differences.

  The degree to which the cells from the different samples were mixed within the resulting clusters was quantified using normalized relative entropy, weighted by the cluster size:

  $$1-\frac{\sum _{k=1}^{n_{\mathit{clust}}}{s}_{k}KL(f_k,F)}{\log (n_{\mathit{samples}})\sum _{k=1}^{n_{\mathit{clust}}}{s}_k}$$

  where f_k is a vector giving the number of cells from each sample in a cluster k, KL(f_k, F) is the empirical KL divergence (relative entropy) between the f_k and the total number of cells in each dataset F (calculated using KL.empirical from entropy package in R), s_k is the total number of cells in a cluster k, n_clust is the number of clusters detected by the method on a current realization of the dataset, and n_samples is the total number of samples in the panel. As we expected to observe systematic composition differences between bone marrow (BM) and cord blood (CB), the normalized entropy was assessed separately for BM and CB cells (Figure 1g and 1h, respectively).

• Number of stable clusters (Figure 1i). To assess how the number of stable clusters changes with the increasing size of the sample panel, we assembled a larger panel of samples covering the same tissue (HCA BM+10x BM dataset). Ten randomized “series” were constructed, with each series starting with two randomly chosen datasets, and then adding one dataset per step up to a maximum of 10 available datasets (sampling without replacement was used to construct the series). As community detection algorithms rely on heuristics such as maximization of modularity, we evaluated the number of stably detectable clusters as a number of independent subtrees in the hierarchy returned by the walktrap.community algorithm. A stable subtree was determined as a subtree containing at least 30 cells that can be detected under a 10% cell subsampling perturbation (see below) with the Jaccard coefficient to the best matching subtree above 0.8. To evaluate these stability properties, for each run additional 10 subsampling runs were made omitting 10% of the cells of the sample and rerunning walktrap.community to generate the perturbed trees based on which the Jaccard coefficient was calculated.

• Sensitivity to individual cells (Supp. Figure 1f). To evaluate how well different methods are able to pick up rare cells in the dataset, we simulated rare cell occurrences by randomly choosing a single sample in the panel, choosing a random joint cluster c ∈ C^m that occurs within that dataset, and then leaving only one randomly selected cell from that cluster c within that sample. HCA BM+CB 1k panel was used, containing 16 samples. A total of 16 × 5 × 5 = 400 perturbed panels were generated, sampling five different clusters c from each of the 16 datasets, with five different random choices of the retained cell being made. In evaluating the performance, the remaining cell from the cluster c was scored as correctly classified if it was assigned to a cluster to which other cells of a cluster c were most commonly assigned.

• Control of alignment strength (Supp. Figure 9). To evaluate the effectiveness of the optional alignment strength and edge weight rebalancing parameters, we used an example of the human pancreas islets datasets (Dataset 10) from 10x Chromium, inDrops and Smart-Seq2 protocols. Individual samples were separated according to the provided annotations, and normalized using Pagoda2 with parameters nPcs=100 and n.odgenes=1000. Pagoda2 objects were aligned using Conos with PCA space (k=30, k.self=5, cor.base=2). For each value of the alignment strength parameter (α ∈ [0.0, 0.1, 0.2, 0.3, 0.5, 1.0]), the analyses were run with and without edge weight balancing. Because cell type annotation for Smart-Seq2 protocol was not available, Conos label propagation procedure was used to label these cells (Supp. Figure 9a; label transfer was performed using alignment generated using default Conos parameters, i.e. α = 0.0 and no edge weight balancing).

  For each combination of the alignment strength and edge balancing parameters we obtained a joint graph, representing the dataset alignment. For each such graph G_i we then estimated a value of the resolution parameter R_i of Leiden clustering, which yields approximately 100 clusters of size ≥ 10 cells. Then, for each G_i we ran Leiden clustering while varying the resolution parameter on a uniform grid between 0.1 and R_i with 15 intermediate points. For each of the resulting clusterings, we then estimated the normalized relative entropy against the protocol factor (Supp. Figure 9b). Finally, as a visual check, we visualized the embeddings of the graphs using largeVis (Supp. Figure 9c).

• Assessment of runtime performance. Suppl. Figure 19 shows runtime CPU and memory requirements of Conos under two different scenarios: i) cell subsampling benchmark detailed above, and ii) integration of increasing number of datasets. The later was done by taking an increasing number of random 1k cell draws from the first HCA BM dataset, combining up to a 100 such simulated datasets. Memory usage was approximated based on the total size of the session (which may not account for transient spikes of memory usage). We note that while the current implementation performs O(N²) comparisons between samples N, the overall runtime, especially in PCA space, is fast enough to allow for integration of hundreds of datasets. Simple schemes to reduce runtime and memory requirements can be devised for very large collections, such as limiting pairwise alignments to a certain random fraction of all possible comparisons. Performance was assessed a cluster of nodes equipped with Xeon E5-2XXX family CPUs, using 12 cores per process.

Implementation of other methods.

Conos performance was compared with the two previously published methods, configured in the following way:

• Seurat package was installed from CRAN (v2.3.4). The pre-processing and dataset alignment was ran as recommended in the tutorial: http://satijalab.org/seurat/immune_alignment.html . The results presented use default resolution. Using alternative resolution parameters (0.6, 1.4) did not affect the performance significantly.

• The mNN approach by Haghverdi et al. was ran by installing scran package from CRAN (v 1.6.9). Hypervariable genes for each dataset were determined according to the tutorial. To enable execution on large datasets within the available memory constraints, the number of hypervariable genes was limited to the top 2000 genes (same number as used for Conos), based on the sum rank of genes across dataset-specific hypervariable gene lists. To determine joint clustering, an approach analogous to Conos was used: k-nearest neighbor graph (k=30) was constructed based on the 30 top PCs of the adjusted expression values, and igraph::walktrap.community method was used to identify cell clusters. Using alternative number of genes (1000, 3000) and components (20,50) did not affect the performance significantly.

To enable large-scale benchmarking, the number of common space components estimated by Conos and the two methods above was limited to 20.

Data availability and dataset-specific analysis details.

1. Human Cell Atlas (HCA) bone marrow and cord blood was downloaded from the HCA portal (https://preview.data.humancellatlas.org/). The dataset represents a relatively uniform collection of data on well-studied tissues, making it particularly suitable for benchmarking purposes. To reduce calculation times in benchmark evaluations, we took a random subset of the cells from lane1 of each dataset. 3000 cells per sample were used by default (HCA BM+CB 3k datasets). A smaller, 1000 cell dataset (HCA BM+CB 1k) was used for the more extensive sensitivity analysis (Supp. Figure 1f).

2. For Figure 1i, we combined HCA BM samples with two samples (“Frozen BMMCs Healthy Donors 1 and 2”) downloaded from 10x Genomics (https://www.10xgenomics.com/resources/datasets/). This was done to extend the number of samples (x axis in Figure 1i).

3. Azizi et al. data on breast cancer was downloaded from GEO (GSE114725) as a count matrix, together with the provided annotations. In showing the plots (Figure 2, Supp. Figure 4) the annotations were simplified to collapse patient-specific populations and omit smaller subpopulation distinctions. To demonstrate applicability to different levels of data fragmentation, the dataset was re-analyzed by combining either 8 patients, 15 patient+tissue combinations, or 53 patient+tissue+replicate combinations. The dataset provides a good example of a clinically-oriented panel with both tissue and patient-level heterogeneity.

4. Lambretchs et al. molecular count data and annotations on the lung cancer were downloaded from ArrayExpress (E-MTAB-6149, E-MTAB-6653). The dataset provides an example of a more typical case-control design of a clinically-oriented panel.

5. Guo et al. molecular count data and annotations non-small-cell lung cancer were downloaded from GEO (GSE99254). The dataset serves as an example of a heterogeneous clinically-oriented panel, with limited complexity and number of cells in some of the samples.

6. Puram et al. molecular count data and annotations on head-and-neck cancer were downloaded from GEO (GSE103322). Similar to Guo et al, the dataset provides an example of a collection with challenging complexity and cell number variation in a clinically-oriented panel.

7. Human cortex comparison. The datasets were included as an example of integration of distinct nuclei-based protocols.

   • Count matrix for Hoghe et al. bioRxiv 2018 was downloaded from downloaded from http://celltypes.brain-map.org/rnaseq.
   • Lake et al. count matrix was downloaded from GEO (GSE97930).

8. Tabula Muris mouse data was downloaded from https://tabula-muris.ds.czbiohub.org/. Only cells with at least 1000 molecules were analyzed. A total of 48 datasets were combined.

9. Mouse cell atlas by Han et al. and the relevant annotations were downloaded from http://bis.zju.edu.cn/MCA/. Cell line datasets were excluded.

10. Human pancreas islets data from different platforms, used to demonstrate alignment between different platforms and illustrate mixing controls (Supp. Figure 9) was taken from the following sources:

    • 10x Chromium platform data were taken from the publication Xin et al.¹⁹ and downloaded from GEO (GSE114297). Normalized count matrices were used.
    • inDrops platform data were taken from the publication of Baron et al.²⁰ and downloaded from GEO (GSE84133). Only human data (4 samples) was used. Normalized count matrices were used.
    • Smart-seq2 platform data were taken from the publication of Segerstolpe et al.²¹ with count matrices downloaded from ArrayExpress (E-MTAB-5061). Only data from healthy patients (6 samples) were used.
11. For the demonstration of ATAC-seq alignment, and alignment between ATAC-seq and RNA-seq (Supp. Note 2), the following datasets were used:

    • sci-ATAC data from Cusanovich et al.¹⁷ was downloaded from the authors website (http://atlas.gs.washington.edu/mouse-atac/). Author-provided accessibility scores were used as gene-level input to Conos.
    • sci-CAR data from Cao et al.¹⁸ was downloaded from GEO (GSE117089). To increase coverage, the cells were aggregated into groups of 10 based on transcriptional similarity (see Supp. Note 2 for details)

Code availability.

Conos is implemented as an R package with C++ optimizations, and is available on GitHub (https://github.com/hms-dbmi/conos) under the GPL-3 open source license. Analysis scripts and intermediate data representations used for the preparation of the manuscript can be found on the author’s website (http://pklab.med.harvard.edu/peterk/conos/).