Instrumental Variable Approach to Estimating the Scalar-on-Function Regression Model with Measurement Error with Application to Energy Expenditure Assessment in Childhood Obesity

Summary

Wearable device technology allows continuous monitoring of biological markers and thereby enables study of time-dependent relationships. For example, in this paper, we are interested in the impact of daily energy expenditure over a period of time on subsequent progression toward obesity among children. Data from these devices appear as either sparsely or densely observed functional data and methods of functional regression are often used for their statistical analyses. We study the scalar-on-function regression model with imprecisely measured values of the predictor function. In this setting, we have a scalar-valued response and a function-valued covariate that are both collected at a single time period. We propose a generalized method of moments-based approach for estimation while an instrumental variable belonging in the same time space as the imprecisely measured covariate is used for model identification. Additionally, no distributional assumptions regarding the measurement errors are assumed, while complex covariance structures are allowed for the measurement errors in the implementation of our proposed methods. We demonstrate that our proposed estimator is L₂ consistent and enjoys the optimal rate of convergence for univariate nonparametric functions. In a simulation study, we illustrate that ignoring measurement error leads to biased estimations of the functional coefficient. The simulation studies also confirm our ability to consistently estimate the function-valued coefficient when compared to approaches that ignore potential measurement errors. Our proposed methods are applied to our motivating example to assess the impact of baseline levels of energy expenditure on BMI among elementary school-aged children.

1 |. MOTIVATING EXAMPLE

It is estimated that about 20% of the U.S. child population suffer from obesity and the percentage of childhood obesity has more than tripled in the last 40 years¹. The consequences of childhood obesity include reduced healthy physiological, behavioral and psychological development during childhood. Obesity in children and adolescents also leads to adverse health outcomes such as type 2 diabetes and cardiovascular diseases in adulthood. To combat this epidemic, targeted environmental and behavioral school-based interventions designed to increase physical activity among school-aged children have gained widespread interest. Examples of these school-based interventions include activity permissive learning environments and the use of stand-biased desks in classrooms^2,3,4,5.

In a recent study, stand-biased desks were introduced to a Texas school district as a means of increasing school day physical activity. A research question of interest was to quantify the association between daily energy expenditure and subsequent progression toward obesity among children. The children were given accelerometer armbands to approximate their daily energy expenditure. Since the levels of true daily energy expenditure is not directly observable, it is calculated as a function of the observed physical activity behavior from the devices. In this manuscript, we assume that the objective measures of energy expenditure obtained from physical activity monitors are prone to measurement error and develop a method of analysis that calibrates the measurement error and is easily applicable for assessing the effects of daily energy expenditure on 18-month change in BMI.

Technological advances on wearable or implantable devices enable continuous monitoring of biological markers resulting in complex data designed to answer scientific questions such as questions related to energy expenditure levels obtained from activity monitors^{6,7,8,9,10,11}. The resulting data appear as either sparsely or densely observed functional data and techniques for functional data analysis are often used for their statistical analyses^12,13. Functional data analysis focuses on the analysis of infinite dimensional data that appear as curves, trajectories, shapes or images^12,13. Methods developed for functional data analysis are based on extensions of ideas from multivariate analysis, nonparametric regression, functional analysis, dimension reduction techniques and square integrable processes^14,12.

In determining the role of energy expenditure in obesity development among children, we consider the linear scalar-on-function regression model with a scalar-valued outcome Y and an imprecisely observed function-valued covariate, X(t). In this setting, X(t) is a latent function-valued covariate that is not directly observable. Instead, it is unbiasedly measured by W(t) prone to some measurement error. Linear scalar-on-function regression models extend classical regression methods to allow function-valued covariates with scalar-valued outcomes in regression settings and many statistical methods have been proposed to estimate the model^{15,16,17,18,13,12,19,20} when the covariate is measured with negligible error.

When functional data are contaminated with errors, measurement errors were often treated as additional error terms associated with the function-valued responses. For example,²¹ considered nonparametric estimation of longitudinal data where the responses were longitudinally observed and contaminated with errors. Under independence error structures for the measurement errors, scatter plot smoothing methods were used to estimate the mean and covariance functions of the response curves²¹.²² provided methods for nonparametric estimation of response curves contaminated by random noise. The mean functions were estimated through the use of B-splines and functional principal component analysis. While²² discussed the presence of measurement errors under independent realizations from a random process, the measurement errors considered were associated with random response curves.²³ assumed uncorrelated error structures and provided Gaussian and generalized shrinkage estimates for the functional principal components scores to improve the variance of the errors associated with the function-valued responses prone to errors.²⁴ considered measurement error in the functional smooth random-effects model where the responses were curves with vector-valued covariates. The error process considered were random errors associated with the response curves and the model was estimated through quasi-score estimating equations²⁴.²⁵ proposed a nonparametric approach for the analyses of sparsely observed longitudinal data using functional principal component analyses in the presence of measurement errors. However, the measurement errors considered were errors associated with the observed responses²⁵.

Most work addressing measurement error in functional data have treated these errors as additional error terms in the models as discussed above. To our knowledge, there is limited research on functional regression models when the functional covariate is contaminated with measurement error. A common practice in the literature is to pre-smooth each contaminated functional covariate, then use the smoothed curves to build and estimate regression models. However, our simulation studies show that the pre-smoothing step does not correct the attenuation bias in regression coefficient estimation caused by measurement error and it has similar numerical performances as the naive estimator which uses the contaminated functional covariate directly without any pre-smoothing. Similar findings were also discussed in²⁶. More recently, some authors have considered treating these error terms as classical measurement errors. These recent developments^27,26,28 extend methods for addressing measurement errors in linear regression models to functional regression settings. Using the smoothing spline mixed model to estimate the measurement error variance,²⁷ developed a two-stage nonparametric regression calibration method for the partial functional linear model. The method proposed in²⁷ relies on the assumption that the measurement errors are independent and identically distributed normal random variables. However, in practice, the measurement errors from the same curve can be correlated and not necessarily follow the normal distribution.²⁶ provided a simulation-extrapolation approach for addressing imprecisely observed function-valued covariates with scalar outcomes. The authors allowed correlated measurement error structures, but required its covariance structure to be of a pre-determined parametric form. We recently developed methods for reducing measurement error biases associated with function-valued covariates prone to measurement error in regression models involving multiple function-valued outcomes²⁸. We estimated the model parameters using the EM algorithm, while functional principal components were used to estimate the variance of the classical measurement error.

In this paper, we propose a different approach to incorporate measurement errors and allow unspecified error structures. A function-valued instrumental variable belonging in the same parameter space as X(t) is used for model identification, and the generalized method of moments-based approach is proposed to consistently estimate the functional coefficient, β(t), in the presence of functional measurement errors. Our proposed method for functional measurement errors do not treat the imprecisely observed function-valued covariate as longitudinal or time series data. Rather, we consider the functional covariate as a single function that is used to estimate a latent variable such as true energy expenditure. Under our newly developed methods, estimation of the measurement error covariance is not required for parameter estimation. To the best of our knowledge, the use of function-valued instrumental variables in the functional linear regression model is novel. We illustrate the impacts of measurement error and covariance structures on the estimated parameters through simulation studies. With the increasing use of wearable or activity monitoring devices to study biological phenomenon in biomedical research, it is critical that statistical methods that allow their accurate and unbiased assessments be developed.

The rest of the paper is organized as follows. Our proposed methodology is introduced and described in Section 2. We provide relevant asymptotic results in Section 3; while the simulation results and the application to our motivating example are provided in Sections 4 and 5, respectively. Finally, discussions and concluding remarks are provided in Sections 5.2 and 6, respectively.

2 |. MODELS

Let (Y, X) be a pair of scalar-valued random variable and a random function assumed to be square integrable and defined on [0, 1] such that X = {X(t), t ∈ [0,1]}. The scalar-on-function regression model with a mis-measured functional covariate for the i^th subject is

$$Y_i=\underset{0}{\overset{1}{\int }}\beta (t)X_i(t)dt+{\epsilon }_i,$$ (1)

$$W_i\left(t\right)=X_i\left(t\right)+U_i\left(t\right),$$ (2)

where β(t) is an unknown functional coefficient. The X_i(t) is a function-valued covariate that is not directly observable but measured by W_i(t). The W_i(t)’s serve as unbiased measures for X_i(t) subjected to measurement errors U_i(t) that are possibly correlated over time. For notation simplicity, we leave out the intercept α in (2) and assume both response Y_i and functional covariate X_i are centered with $\sum _{i=1}^n{Y}_i=0$ and $\sum _{i=1}^n{X}_i(t)=0$ for t ∈ [0, 1].

We first approximate β(t) in (1) using polynomial splines and write $\beta (t)\approx \sum _{k=1}^{K_n}{\gamma }_k{b}_k(t)$ where ${\left\{{\gamma }_k\right\}}_{k=1}^{K_n}$ are unknown spline coefficients, while ${\left\{b_k(t)\right\}}_{k=1}^{K_n}$ are a set of spline basis functions on [0,1]. In this manuscript, B-spline basis functions are used due to their flexibility and computational efficiency. These basis functions can be efficiently constructed using the Cox-De Boor recursion formula²⁹. In the spline approximation provided above, the number of basis, K_n, is allowed to increase with the sample size and the corresponding spline functions provide better approximations for larger sample sizes. For large n, K_n is often chosen to be large enough to reasonably approximate the patterns in β(t). In subsection 4.2, we propose a data driven method to automatically select K_n for finite samples.

Following the spline approximations, Model (1) becomes

$$Y_i\approx \sum _{k=1}^{K_n}{\gamma }_k\underset{0}{\overset{1}{\int }}{X}_i(t)b_k(t)dt+{\epsilon }_i.$$ (3)

Let $X_{ik}=\underset{0}{\overset{1}{\int }}{X}_i(t)b_k(t)dt,W_{ik}=\underset{0}{\overset{1}{\int }}{W}_i(t)b_k(t)dt$, and $U_{ik}=\underset{0}{\overset{1}{\int }}{U}_i(t)b_k(t)dt$. The measurement error model in (2) becomes W_ik = X_ik + U_ik and the full model is re-written as

$$Y_i\approx \sum _{k=1}^{K_n}{\gamma }_k{X}_{ik}+{\epsilon }_i$$ (4)

$$W_{ik}=X_{ik}+U_{ik}k=1,\dots ,K_n,$$ (5)

where $\left\{U_{i1},\dots ,U_{i{K}_n}\right\}$ are correlated errors. Under this representation, the proposed model reduces to a variation of multivariable linear regression model with measurement errors. However, the main difference is that the number of linear covariates in (4) and (5) is not fixed, instead it increases with the sample size.

2.1 |. Instrumental variables

The presence of measurement errors in predictor variables of regression models renders the model unidentifiable without additional information³⁰. Such additional information can come in the form of replicates of W(t), assumption of a known covariance function of the measurement error Σ_UU, or the presence of instrumental variables for X(t) in the data. An instrumental variable is a variable that is correlated with X(t) but is, uncorrelated with U(t). The presence of an instrumental variable for X(t) in the data allows for consistent estimation of β(t) when X(t) is subjected to error. While the use of instrumental variables has been well studied in generalized linear regression models with measurement errors^{31,30,32,33,34,35,36,37}, use of instrumental variables in functional linear regression settings with measurement errors are limited.³⁸ considered the use of instrumental variables in scalar on function regression when X(t) is endogenous (i.e. corr{X(t), ε} ≠ 0). Using a function-valued instrumental variable, the authors extended the generalized method of moments approach to high dimensional settings to estimate the function-valued model parameter. While our proposed models also consider scalar on function regression, the current application focuses on the case where X(t) is imprecisely observed, rather than it being an endogenous covariate.²⁶ estimated the covariance matrix of the measurement error in the scalar on function models by treating the function-valued covariate as longitudinal data. In our proposed methods, we do not consider X(t) longitudinal. Rather, it is considered a function obtained at one time point to describe a latent variable or a true covariate. In this paper, an instrumental variable approach is proposed for model identifiability while generalized method of moments is used to consistently estimate β(t).

For i = 1, …, n, let ${\left\{M_i(t)\right\}}_{i=1}^n$ be a function-valued instrumental variable observed for the i^th individual. Assume ${\left\{M_i(t)\right\}}_{i=1}^n$ are independent across subjects with {M_i(t)} independent of {M_j(t)}, for i ≠ j. Also, cov {M_i(t), U_i(s)} = 0 and cov {M_i(t), ε_i} = 0 for any t, s ∈ [0,1], while {M_i(t)} is correlated with {X_i(t)}. The independence assumption between M_i(t) and U_i(s) is often referred to as instrument exogeneity across time. While a strong assumption, this condition cannot be directly tested or assessed since U_i(t) is unobserved. Therefore, theoretical considerations regarding the application are often used in the selection of an instrumental variable in practice.

In addition to equations (1) and (2), we add the model equation for the instrumental variable as M_i(t) = δX_i(t) + ω_i(t), for some constant δ ≠ 0 and a mean zero error {ω_i(t)}, which is uncorrelated with {X_i(t)}. While M_i(t) is correlated with X_i(t), it is not necessarily an unbiased measure for X_i(t). We reformulate our final model below with all the assumptions

$$Y_i=\underset{0}{\overset{1}{\int }}\beta (t)X_i(t)dt+{\epsilon }_i$$ (6)

$$W_i\left(t\right)=X_i\left(t\right)+U_i\left(t\right),$$ (7)

$$M_i(t)=\delta X_i(t)+{\omega }_i(t),$$ (8)

where E(ε_i) = 0, E{U_i(t)} = 0 and E{ω_i(t)} = 0. In addition, we assume cov{X_i(t), ε_i} = 0, cov {M_i(t),ε_i} = 0, cov {M_i(t), U_i(s)} = 0, for t, s ∈ [0,1] and i = 1, ⋯ , n. Our methodology is described next.

2.2 |. Proposed method for estimating the functional coefficient

Let $M_{ik}={\int }_0^1 M_i(t)b_k(t)dt$, for k = 1, …, K_n, and $M_i={\left(M_{i1},\dots ,M_{i{K}_n}\right)}^T$. Then one has

$$cov\left(Y_i,M_i\right)\approx cov\left(X_i,M_i\right)\mathit{\gamma },$$ (9)

$$cov\left(W_i,M_i\right)=cov\left(X_i,M_i\right),$$ (10)

where $\mathit{\gamma }={\left({\gamma }_1,\dots ,{\gamma }_{K_n}\right)}^{\text{T}}$. Therefore,

$$cov{\left(W_i,M_i\right)}^{T}cov\left(Y_i,M_i\right)\approx cov{\left(W_i,M_i\right)}^{T}cov\left(W_i,M_i\right)\mathit{\gamma }$$ (11)

$$\mathit{\gamma }\approx {\left[cov{\left(W_i,M_i\right)}^{T}cov\left(W_i,M_i\right)\right]}^{-1}cov{\left(W_i,M_i\right)}^{T}cov\left(Y_i,M_i\right),$$ (12)

and the unknown coefficients γ can be estimated by

$$\widehat{\mathbf{\gamma }}={\left({\Omega }_{WM}^T{\Omega }_{WM}\right)}^{-1}{\Omega }_{WM}^T{\Omega }_{MY},$$ (13)

where Ω_WM and Ω_MY are sample estimates of cov(W_i, M_i) and cov(Y_i, M_i) respectively, defined as

$${\Omega }_{WM}=\frac{1}{n}\sum _{i=1}^n\widetilde{W_i}{\tilde{M}}_i^T,$$ (14)

$${\Omega }_{MY}=\frac{1}{n}\sum _{i=1}^n{\tilde{M}}_i{\tilde{Y}}_i^T,$$ (15)

and ${\tilde{M}}_i$, ${\tilde{Y}}_i$ and $\widetilde{W_i}$, are centered variables, each with a sample mean of zero. When M_i and W_i, are of the same dimension, and Ω_MW is an invertible square matrix, then $\widehat{\mathit{\gamma }}$ is reduced to $\widehat{\mathit{\gamma }}={\left({\Omega }_{MW}\right)}^{-1}{\Omega }_{MY}$. As a result, for any t ∈ [0, l], the estimator of the regression coefficient function is defined as

$$\widehat{\beta }(t)=\sum _{k=1}^{K_n}{\widehat{\gamma }}_k{b}_k(t).$$ (16)

The proposed $\widehat{\beta }(t)$ is a generalized method of moments based estimator. While no distributional assumptions are required for U_i(t), the estimation of β(t) depends on the assumption that an instrument, M_i(t), exists in the data. Additionally, estimation of the covariance matrix for the measurement error is not required for the successful implementation of our proposed methodology. Under current functional data methodology, a naive estimator of β(t) would be based on W_i(t) and Y_i with W_i(t) being treated as the true value for X_i(t). Simulation studies in Section 4 show that failure to account for potential measurement errors can substantially bias the results. The strength of our $\widehat{\beta }(t)$ is that while X_i(t) might not be directly observed, estimation of its effect on the response is based on its unbiased measure as well as additional information provided in the data in the form of M_i(t).

3 |. ASYMPTOTIC PROPERTIES

In this section, we establish the L₂ consistency of $\widehat{\beta }(t)$. We summarize the needed assumptions as follows:

1. We assume (Y_i, X_i(t), W_i(t), M_i(t), t ∈ [0, l]) for i = 1, …, n are independent with the same distribution as (Y, X(t), W(t), M(t), t ∈ [0, l]).

2. The instrument variable M = {M(t), t ∈ [0, l]} is uncorrelated with regression error ϵ and the measurement error U = {U(t), t ∈ [0, l]} with cov{M(t), ϵ} = 0 and cov{M(t), U(s)} = 0 for any s, t ∈ [0, l].

3. The latent functional covariate X = {X(t), t ∈ [0, 1]} is independent of the regression error ϵ with cov{X(t), ϵ} = 0 for t ∈ [0, l], but is correlated with instrument variable M. Let Σ_XM (t, s) = cov{X (t), M (s)}. We assume that for any positive functions h₁, h₂, h₃, h₄, there exist constants λ₁, λ₂ > 0 such that

   $${\lambda }_1\le \frac{\int \cdots \int h_1(t){\Sigma }_{XM}(t,s)h_2(s)h_3\left(t^{\prime }\right){\Sigma }_{XM}\left(t^{\prime },s^{\prime }\right)h_4\left(s^{\prime }\right)dtdsd{t}^{\prime }d{s}^{\prime }}{\int h_1(t)h_2(t)dt\int h_3\left(t^{\prime }\right)h_4\left(t^{\prime }\right)d{t}^{\prime }}\le {\lambda }_2.$$

4. We assume sup_t [E |M (t)|^l + E |W (t)|^l + E |U (t)|^l] < +∞ for some sufficiently large l > 0.

5. The variance of the error term ${\sigma }_{\epsilon }^2=\mathbb{E}\left({\epsilon }^2\right)$ is bounded.

6. We assume Σ_XX (t, s) = Cov {X (t), X (s)}, Σ_MM (t, s) = Cov {M (t), M (s)}, Σ_UU (t, s) = Cov {U (t), U (s)} are all positive definite bivariate functions and there exist positive constants λ₁ and λ₂ such that for any positive functions a₁ (t), a₂ (t) ∈ L²[0, 1],

   $$\begin{gathered} {\lambda }_1\int a_1(t)a_2(t)dt\le \iint a_1(t){\Sigma }_{MM}(t,s)a_2(s)dtds\le {\lambda }_2\int a_1(t)a_2(t)dt, \\ {\lambda }_1\int a_1(t)a_2(t)dt\le \iint a_1(t){\Sigma }_{UU}(t,s)a_2(s)dtds\le {\lambda }_2\int a_1(t)a_2(t)dt. \end{gathered}$$

7. The coefficient function β(t) is (p + 1)-times continuously differentiable with β(t) ∈ ℂ^p+1[0, 1].

8. The number of knots $N_n⩆n^{1/(2p+3)}$ and interior knots $k_1,\dots ,k_{N_n}$ satisfy that

   $$\frac{{\text{min}}_{j\in \left\{1,\dots ,N_n\right\}}|k_{j+1}-k_j|}{{\text{max}}_{j\in \left\{1,\dots ,N_n\right\}}|k_{j+1}-k_j|}>c$$

   for some constant c > 0.

Assumptions (A1), (A4)-(A5) and (A7)-(A8) are standard in polynomial spline regression literature. Similar assumptions were also used in^39,40,41. Assumption (A3) requires that {X(t)} and {M(t)} be correlated and {M(t)} contains information about {X(t)}. Assumption (A3) fails if {X (t)} and {M (t)} are independent of each other with Σ_XM (t, s) = 0 for all t, s ∈ [0, 1]. This is required to guarantee the invertibility of the matrix in (13) and the proposed generalized method of moments estimator to be well defined. Assumption (A6) implies that the covariance functions of random processes {X(t)}, {M(t)} and {W(t)} all are positive definite.

Theorem 1.

Under assumptions (A1)-(A8), the coefficient function estimator $\widehat{\beta }(t)$ in (16) is L₂–consistent with

$$\Vert \widehat{\beta }(t)-\beta (t){\Vert }_2=O_p\left(\frac{1}{N_n^{p+1}}+\sqrt{\frac{N_n}{n}}\right),$$

where ||·||₂ is the functional L₂ norm.

Theorem 1 establishes the L₂ rate of consistency for $\widehat{\beta }(t)$ in the presence of measurement errors. Our asymptotic result is comparable to the rate of convergence results given in⁴² and⁴³ when the functional covariates are measured without errors. Here we assume the functional covariates are observed continuously. As argued in⁴³, the rate of convergence obtained in Theorem 1 does not change when the functional covariates are observed discretely at a sequence of grid points, provided that the maximum distance between any neighboring grid points converges to zero sufficiently quickly. The proof of our asymptotic results are provided in the Appendix.

4 |. SIMULATION

In this section, we discuss our simulation results and describe the tuning parameter selection.

4.1 |. Simulation Results

We now describe our simulation experiments and study the numerical performance of our proposed methodology. All data in our simulations were independently generated from the functional linear regression model

$$Y=\underset{0}{\overset{1}{\int }}\beta (t)X(t)dt+\epsilon ,$$

where we consider two forms for β(t) with β₁ (t) = sin (2πt) and β₂(t) = sin(π(8(t−.5))/2)/(1+(2(8(t−.5))²)(sign(t−.5)+1)), and sign(a) = 1 and sign(−a) = −1, for a > 0. We only present the result for the case β₁(t) and defer the simulation results for β₂(t) in the Supplementary Material. The regression errors, ε, were simulated independently and follow a N (0, σ²). While the observable functional covariate X (t) = sin (2πt) + ε_X (t), where ε_X(t) denotes a mean zero Gaussian process with constant marginal variance ${\sigma }_X^2$ and cor{ε_X(t₁), ε_X(t₂)} = ρ_X for any t₁ ≠ t₂. We generated the observed functional covariate W (t) = X (t)+u (t) and the instrumental variable M (t) = X (t)+ ω (t) where errors u (t) and ω (t) are also mean zero Gaussian processes with constant marginal variances ${\sigma }_u^2$ and ${\sigma }_{\omega }^2$, and correlations ρ_u and ρ_M respectively. All the error terms were generated to be independent of each other. In all our simulations, the number of replications considered were n_r = 1000. For the methods described in this section, the number of knots were selected using a tailored cross-validation approach as discussed in Section 4.2.

Since we only report the results for β₁(t), we will simply use β(t) and drop the subscript. Let ${\widehat{\beta }}^r(t)$ be the estimator of β(t) in r^th replication and $\overline{\beta }(t)=\frac{1}{n_r}\sum _{l=1}^{n_r}{\widehat{\beta }}^r(t)$. Let ${\left\{t_l\right\}}_l^{n_{grid}}$ be a sequence of equally spaced grid points on (0, l) to evaluate the performance of proposed estimator. We define the averaged squared bias of $\widehat{\beta }(t)$ as

$$ABia{s}^2(\widehat{\beta })=\frac{1}{n_{grid}}\sum _{l=1}^{n_{grid}}{\left\{\overline{\beta }\left(t_l\right)-\beta \left(t_l\right)\right\}}^2,$$

the averaged sample variance as

$$Avar(\widehat{\beta })=\frac{1}{n_r}\sum _{r=1}^{n_r}\frac{1}{n_{grid}}\sum _{l=1}^{n_{gstd}}{\left\{{\widehat{\beta }}^r\left(t_l\right)-\overline{\beta }\left(t_l\right)\right\}}^2,$$

and averaged integrated mean square error as

$$AIMSE(\widehat{\beta })=ABia{s}^2(\widehat{\beta })+Avar(\widehat{\beta }).$$

We first generated data with σ = 1, σ_X = 4, σ_u = 4, σ_ω = 1, ρ_X = ρ_u = ρ_M = 0 and four different sample sizes n = l00, 200, 500, l000. We estimated the regression coefficient function using the proposed methodology. However, the matrix inversion in the definition of the proposed method of moments estimator can be unstable. Therefore, we adopted the small sample modification³⁰ to improve the finite sample performance of our proposed method. In addition to our approach, four additional approaches were also considered for estimating β in the simulation studies. In the first scenario, we assumed X(t) was observed and ${\widehat{\beta }}_X$ was estimated by regressing {Y_i} on {X_ik} directly in Equation (4). The second estimator, ${\widehat{\beta }}_W$, ignored the measurement error and estimated the spline coefficients by regressing {Y_i} on {W_ik} instead. The third estimator ${\widehat{\beta }}_{WRS}$ is a variant of the second approach and obtained using individually pre-smoothed ${\widehat{W}}_i$ based on polynomial splines regression. The fourth estimator, ${\widehat{\beta }}_{WS}$, is obtained by pre-smoothing each W_i using smoothing spline approach instead. Note that ${\widehat{\beta }}_X$ was not available in the real data analysis. However, it served as a benchmark to assess the performance of our estimator in the simulation studies. The naive estimators, ${\widehat{\beta }}_W$, ${\widehat{\beta }}_{WRS}$, ${\widehat{\beta }}_{WS}$, ignored the measurement error in the data. The estimator ${\widehat{\beta }}_{IV}$ was obtained using our proposed instrumental variable based method.

Table 1 reports the ABias², Avar and AIMSE values for different estimators. For our proposed instrumental variable based estimator, ${\widehat{\beta }}_{IV}$, we clearly see that ABias², Avar and AIMSE all decrease with increasing sample sizes, supporting our asymptotic convergence result. Furthermore, the biases of ${\widehat{\beta }}_X$ and ${\widehat{\beta }}_{IV}$ are similar and much smaller than the bias of ${\widehat{\beta }}_W$. Furthermore, the bias of ${\widehat{\beta }}_W$ was non-ignorable even when the sample size was increased to l000. This suggests that failure to account for measurement error can lead to biased estimation of the functional coefficient. In addition, similar to ${\widehat{\beta }}_W$, both ${\widehat{\beta }}_{WRS}$ and ${\widehat{\beta }}_{WS}$ have non-ignorable bias, which indicates that pre-smoothing step does not take care the attenuation bias. Comparing Avar, ${\widehat{\beta }}_W$ had the smallest sample variance due to larger variability in W and the fact that the variance of regression coefficient is inversely related to the variability in the covariates. Our proposed method of moment estimator ${\widehat{\beta }}_{IV}$ had the largest sample variance due to variability in both W and M. However, for relatively large sample sizes (n=500, or 1000), the proposed ${\widehat{\beta }}_{IV}$ had better overall performance than all the approaches based on W with smaller AIMSE values.

TABLE 1.

This table assesses the impact of sample sizes on the estimators. It reports the averaged squared bias (ABias²), averaged sample variance (Avar) and averaged integrated mean squared error (AIMSE) for different sample sizes n. The response error is assumed to follow Normal distribution. The true parameter function is β₁(t).

	${\widehat{\beta }}_X$
n	ABias2	Avar	AIMSE
100	0.0017	0.1764	0.1781
200	0.0011	0.0864	0.0875
500	0.0001	0.0408	0.0408
1000	0.0000	0.0198	0.0199
	${\widehat{\beta }}_W$
n	ABias2	Avar	AIMSE
100	0.0394	0.1121	0.1515
200	0.0400	0.0534	0.0934
500	0.0392	0.0246	0.0638
1000	0.0394	0.0121	0.0515
	${\widehat{\beta }}_{WRS}$
n	ABias2	Avar	AIMSE
100	0.0393	0.1117	0.1510
200	0.0400	0.0538	0.0938
500	0.0392	0.0247	0.0638
1000	0.0393	0.0122	0.0515
	${\widehat{\beta }}_{WS}$
n	ABias2	Avar	AIMSE
100	0.0145	0.3806	0.3951
200	0.0149	0.1676	0.1825
500	0.0144	0.0867	0.1011
1000	0.0147	0.0448	0.0595
	${\widehat{\beta }}_{IV}$
n	ABias2	Avar	AIMSE
100	0.0017	0.2144	0.2161
200	0.0011	0.1044	0.1055
500	0.0001	0.0497	0.0498
1000	0.0000	0.0244	0.0245

To investigate the performance of the proposed estimator when the response Y_i follows a non-normal distribution, we now allow the regression error ε have a non-symmetric distribution centered at 0. Namely, the regression errors are independently and identically simulated from a Gamma(1.0, l.5) and then shifted to have mean 0. We report the simulation result in Table 2. Although, the approaches based on W tend to have smaller AIMSEs for smaller sample sizes, our approach tend to do comparably well for sample size 500 and dominates for large sample size (1000) in term of AIMSE. Our approach (${\widehat{\beta }}_{IV}$) along with ${\widehat{\beta }}_X$ also have have very low bias. Again, the naive approaches ${\widehat{\beta }}_W$, ${\widehat{\beta }}_{WRS}$ and ${\widehat{\beta }}_{WS}$ preform poorly and have non-diminishing biases.

TABLE 2.

This table assesses the impact of sample sizes on the estimators. It reports the averaged squared bias (ABias²), averaged sample variance (Avar) and averaged integrated mean squared error (AIMSE) for different sample sizes n. The response error is assumed to have a Gamma(1, 1.5) distribution, where Gamma(α, β) denotes a distribution with mean αβ. The true parameter function is β₁(t).

	${\widehat{\beta }}_X$
n	ABias2	Avar	AIMSE
100	0.0009	0.3963	0.3972
200	0.0014	0.1887	0.1901
500	0.0001	0.0895	0.0895
1000	0.0000	0.0438	0.0438
	${\widehat{\beta }}_W$
n	ABias2	Avar	AIMSE
100	0.0380	0.2301	0.2681
200	0.0395	0.1078	0.1474
500	0.0390	0.0519	0.0909
1000	0.0391	0.0252	0.0642
	${\widehat{\beta }}_{WRS}$
n	ABias2	Avar	AIMSE
100	0.0380	0.2306	0.2686
200	0.0395	0.1079	0.1474
500	0.0389	0.0520	0.0910
1000	0.0391	0.0254	0.0645
	${\widehat{\beta }}_{WS}$
n	ABias2	Avar	AIMSE
100	0.0140	1.0100	1.0241
200	0.0145	0.3434	0.3579
500	0.0148	0.1974	0.2121
1000	0.0145	0.0941	0.1086
	${\widehat{\beta }}_{IV}$
n	ABias2	Avar	AIMSE
100	0.0012	0.4335	0.4346
200	0.0013	0.2122	0.2135
500	0.0001	0.1012	0.1013
1000	0.0001	0.0496	0.0497

We now assess how the size of error terms of u(t) and W(t) affect the proposed estimation method. For ρ_X = ρ_u = ρ_M = 0, σ = 1, σ_X = 4, n = 500, we consider different combinations of (σ_u, σ_ω) with potential values of σ_u, σ_ω ranging from 0.5, l, 4 to l6. Thus, the signal to noise ratio in the measurement error and instrumental variable equation were 8, 4, 1 or 0.25. Table 3 summarizes our simulation results from the various set-ups. We found that increasing the error sizes associated with either the measurement error or the instrumental variable lead to larger AIMSEs. In addition, the error in the instrumental variable had a larger effect on the accuracy of our estimated β(t) when compared to the impact of the measurement errors. We also note that the AIMSEs for (σ_u = 1, σ_ω = 16) was more than four times larger than those for (σ_u = 16, σ_ω = 1). Although the naive and IV approaches tended to perform comparably for smaller values of σ_u, our IV approach dominates the naive approaches for larger measurement error and β_s has the worse performance. But changes in the IV error variance have little effect on the AIMSE estimates for the naive approaches since IVs are completely ignored in the naive estimation. Therefore, it is not surprising naive approaches have smaller AIMSEs than our IV approach. We report the performance of the naive estimator in Section S.2 of the supplementary Material.

TABLE 3.

Impacts of varying magnitudes of measurement error and instrumental variable variance on our proposed estimator. The averaged squared bias (ABias²), averaged sample variance (Avar) and averaged integrated mean squared error (AIMSE) of $\widehat{\beta }$ for sample size n = 500.

σω = 1				σu = 1
σu	ABias2	Avar	AIMSE	σω	ABias2	Avar	AIMSE
0.5	0.0001	0.0506	0.0507	0.50	0.0001	0.0488	0.0489
1	0.0001	0.0504	0.0505	1.00	0.0001	0.0504	0.0505
4	0.0001	0.0497	0.0498	4.00	0.0001	0.0794	0.0795
16	0.0028	0.1070	0.1097	16.00	0.0003	0.4784	0.4787

We are also interested in investigating the impact of the correlation in the error terms affect on our estimated coefficient. To do this, we simulated data with σ = 1, σ_X = σ_u = 4, σ_ω = 1 and n = 500, under varying degrees of correlations in ε_X(t), u(t), and W(t) with ρ_X, ρ_u, ρ_ω = 0, 0.25, 0.5 or 0.75, corresponding to none to strong correlation in the error terms. Table 4 indicates that larger correlation in ε_X(t) lead to larger AIMSEs and less accurate estimate of the coefficient function, due to increased multi-collinearlity in predictor variables. However, correlations in the measurement error u(t) and instrument error W(t) have less impact on the coefficient function estimation. This is due to the fact that these errors are independent of each other and of the covariate X(t). Similar to ${\widehat{\beta }}_X$, the degree of correlation in X(t) is more relevant for the performance of our proposed estimator.

TABLE 4.

The impact of correlation structures on the parameter estimates. The averaged squared bias (ABias²), averaged sample variance (Avar) and averaged integrated mean squared error (AIMSE) of $\widehat{\beta }$ for sample size n = 500.

		ρX			ρu			ρM
	0	0.25	0.5	0.75	0.25	0.5	0.75	0.25	0.5	0.75
ABias2	0.0001	0.0001	0.0002	0.0003	0.0001	0.0001	0.0001	0.0001	0.0001	0.0001
Avar	0.0497	0.0540	0.0775	0.1521	0.0485	0.0483	0.0482	0.0552	0.0603	0.0652
AIMSE	0.0498	0.0541	0.0776	0.1524	0.0486	0.0484	0.0483	0.0553	0.0604	0.0653

4.2 |. Tuning parameter selection

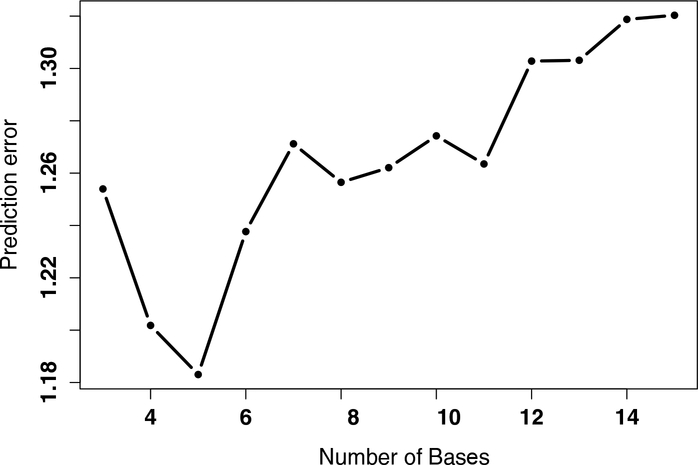
Our proposed method requires specification of the number of bases beforehand by the practitioner. In non-parametric settings, selection of the number of basis functions amounts to a model selection problem. Additionally, it is well known that model selection in measurement error settings are complex⁴⁴. In this manuscript, we provide an approach based on a 5-fold cross- validation for the selection of the number of basis functions. For each choice of possible number of bases, the original data set is divided into 5 non-overlapping subsets. The model parameters are then estimated repeatedly by excluding one of the subsets of the original data under each estimation. The mean prediction error of the fitted model, using W(t) in lieu of X(t), is estimated based on each data subset withheld, averaging over the 5 data subsets. Subsequently, the number of basis functions associated with the smallest mean prediction error is selected as the number of bases. Plots of the estimated mean prediction error for the function considered in our simulation studies were obtained. As an example, we plotted the prediction errors for one simulation run with sample size n = 500. Based on this plot, the number of bases selected was 5, see Figure 1.

FIGURE 1.

Plots of the estimated mean prediction error for the function considered in our simulation studies.

5 |. APPLICATION

In this section, we describe the application of our methods to the motivating example. Students enrolled in the study were followed over an eighteen month period. The study design was a cluster randomized trial where teachers within three schools in the College Station Independent School District were randomly assigned to receive either the treatment (stand-biased desks) or control (traditional desks)⁵. The data contain measurements obtained at baseline and at the beginning of each semester over two academic years. An objective of the study was to investigate the relationship between energy expenditure behavior at baseline and the 18-month change in body mass index (BMI) from baseline among the students. Thus, an outcome of interest was the difference or change in BMI values from baseline to 18 months post follow up. The count of steps represents the number of steps taken over a given period of time and is an indicator of a subject’s physical activity levels. Current guidelines for recommended daily physical activity levels are based on the duration of time spent in either moderate or vigorous intensity activity levels and number of steps per day^{7,45,46,47,48}. For example,⁴⁷ indicated that activity levels of 12,000 steps/day and 15,000 steps/day for boys and girls, respectively were recommended for maintenance of healthy body composition for children between the ages of 6–12 years. While daily energy expenditure is defined as the total number of calories or energy used by the body to perform daily bodily functions.

In our application, energy expenditure and step counts were both collected per minute from the SenseWear Armband® (Body-Media, Pittsburgh, PA) among the 374 children enrolled in the study who wore accelerometers while in school for one week at baseline. The children’s body weight, height, age, and sex were all collected at baseline, while their BMI’s were calculated at the beginning of each semester over the study period. True daily energy expenditure behavior, X(t), was considered the latent covariate. The surrogate measure for X(t) was the energy expenditure taken per hour obtained from the device, W(t). Step counts measured by the device was treated as the instrumental variable in this application, M(t). We assume that cov{X(t), M(t)} ≠ 0 and cov{M(t), U(t)} = 0. Justification of the use of instrumental variables is challenging in practice. However, an instrumental variable may be based on a separate independent measure of X(t). In our application, both M(t) and W(t) were obtained from the same device. But their measured or calculated measures were obtained separately. The SenseWear Armband® obtained the step count based on a 3-axis accelerometer and pattern recognition. While the calculation of total energy expenditure was based on heat flux, skin temperature, galvanic skin response, and anthropometrics⁴⁹. A description of the final analytic sample is provided in Table 5.

TABLE 5.

Descriptive statistics for the study sample at baseline (n=255). “Other”=Asians/Native Americans, EE= energy expenditure, s.d.=standard deviation.

Variable	Mean(s.d.)/ N(%)
BMI at baseline (kg/m2)	17.40(2.98)
BMI in Spring Year 2 (kg/m2)	17.55(3.18)
Average Step Counts/hour	13.16(11.51)
Average EE (kcal/hour)	1.2(0.41)
Age (years)	8.79(0.76)
Whites	174(68.24 %)
Blacks	34(13.33 %)
Hispanics	25(9.80 %)
Other	22(8.63 %)
Boys	132(51.76 %)
Girls	123(48.24 %)
Treatment	148(58.04 %)
Control	107(41.96 %)

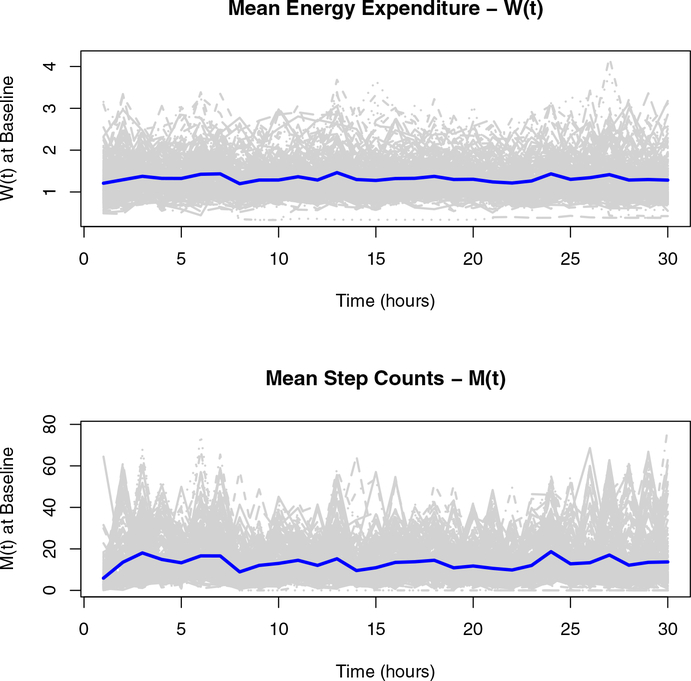
To assess impacts of energy expenditure obtained at baseline on the difference in BMI values among the enrolled students, we first assumed that both W and M were discretely observed on a time interval [0, T]. On average, the students wore the devices for six hours on each school day during the week it was worn at baseline. Since the accelerometry data were collected per minute, we combined all the data for the week the device was worn and averaged all the minute-level data collected within the week to hourly-level data to reduce any potential noise associated with the data collection. Figure 2 provides the plot of W_i(t) and M_i(t) against time for all subjects included in the study. The grey lines illustrate the individual trajectories while the blue solid line is the smoothed mean for the observed energy expenditure and step counts among all the subjects.

FIGURE 2.

Plots of observed energy expenditure {W (t)} and mean step counts {M (t)} vs. time for all subjects at baseline from our motivating example. The figure confirms that the relationship between W(t) with time is nonlinear. In this setting W(t) is assumed to be an unbiased measure of X(t), while M(t) is an instrumental variable for X(t).

Two sets of analyses were performed to illustrate our developed methods. We first assessed the relationship between energy expenditure and BMI at baseline. The second analysis involved investigating the impact of energy expenditure at baseline on changes in BMI values at 18 months follow up. Due to loss of follow up or missing data, 255 and 156 students contributed to the baseline and the 18-month follow up analyses, respectively.

The average BMI values at baseline was 17.4 kg/m²(SD = 2.98) and 17.6 kg/m²(SD = 3.2) during the spring semester of the second academic year. The mean step counts per hour at baseline was 13.16 (SD = 11.5) and the mean energy expenditure at baseline was 1.21 kcal/hour (SD = 0.41), while the average age of the children at baseline was 7.9 years (SD = 0.80). About n = 174(68.24%) were whites, blacks n = 34(13.33%), Hispanics n = 25(9.8%) and others n = 22(8.63%). See Table 5 for additional details.

5.1 |. Results

5.1.1 |. Impacts of error-free covariates on outcomes

The error free covariates collected from the study include the student’s school, teacher, ethnicity, grade, age, gender and treatment assignment group. To adjust for these error free covariates as well as the cluster randomized setting of the study design, we first performed random effects analyses of the error free covariates against the outcomes. A random intercept for the nested effects of teachers nested within schools was included in the models. We also fitted a random effect term for both schools and teachers nested within schools, however, the models failed to converge. The error free adjusted residuals were subsequently obtained from the regression fits from the mixed effects model with the random intercept term for teacher within school.

Two sets of mixed effects analyses were performed. The first analysis focused on BMI at baseline as the outcome. The second analysis focused on 18-month change in BMI from baseline as the outcome. The results from the error free analyses of both the baseline and follow up data are included in Table 6. Overall, we found that age had a significant impact on the BMI values at both baseline and at 18 months post baseline (p < 0.0001 and p = 0.04). Additionally, there were statistically significant differences in the race effect when we compared the differences in BMI between students from ethnically minority populations (blacks and Hispanics) to the white students at both baseline and follow up (p < 0.0001). Specifically, we found that after controlling for all other covariates included in the model, the BMI values for the black and Hispanic students were 0.08 and 0.06 higher on average than the BMI values for the white students at baseline. While at follow-up, we found the BMI values for the black and Hispanic students to be 0.06 and 0.03 higher on average than the BMI values for the study students after controlling for age, school, teacher, baseline levels of BMI, and treatment assignment. No statistically significant difference was observed between the other race category when compared to the white students included in the study at baseline and follow up (p = 0.15 and p = 0.07). There were also no differences in the average BMI values between the schools, teachers, grades, and treatments at both baseline and follow up (p > 0.05).

TABLE 6.

Results from the mixed effects analyses. “Baseline Model” is the mixed effects analysis of the error free covariates on BMI at baseline. “Follow up Model” is the mixed effects analysis of the error free covariates on BMI at 18 months, adjusting for BMI at baseline. The analyses of the error-free covariates adjusted for both the cluster randomized design of the study and the error-free covariates on the outcomes. Random intercepts were included in both models for teachers nested within schools.

Baseline Model				Follow up Model
Effect	Estimate	S.E.	P-value	Effect	Estimate	S.E.	P-value
Intercept	2.53	0.15	< 0.0001	Intercept	−0.03	0.06	0.62
Age	0.03	0.004	< 0.0001	Age	−0.005	0.002	0.04
School 1 vs. School 3	−0.08	0.11	0.46	School 1 vs. School 3	−0.07	0.06	0.29
School 2 vs. School 3	−0.06	0.26	0.83	School 2 vs. School 3	−0.18	0.16	0.30
Teacher	0.003	0.02	0.87	Teacher	0.01	0.01	0.28
Grade 2 vs. Grade 4	−0.003	0.14	0.98	Grade 2 vs. Grade 3	0.04	0.05	0.44
Grade 3 vs. Grade 4	0.005	0.11	0.97	Log BMI at baseline	1.02	0.007	< 0.0001
Black vs. White	0.08	0.006	< 0.0001	Black vs. White	0.06	0.004	< 0.0001
Hispanic vs. White	0.06	0.006	< 0.0001	Hispanic vs. White	0.03	0.004	< 0.0001
Other vs. White	0.01	0.006	0.15	Other vs. White	−0.006	0.003	0.07
Girls vs. Boys	−0.02	0.003	< 0.0001	Girls vs. Boys	−0.001	0.002	0.73
Treatment vs. Control	0.02	0.06	0.77	Treatment vs. Control	−0.04	0.03	0.28
Teacher(School)	0.01	0.003	0.003	Teacher(School)	0.001	0.0003	0.03
Residual	0.02	0.0003	< 0.0001	Residual	0.004	0.0001	< 0.0001

5.1.2 |. Impact of baseline levels of energy expenditure on BMI

Residuals obtained from the mixed effects assessments of the impacts of the error free covariates on the outcomes at were obtained from the baseline and follow up analyses the following model

$$E\left[Y_{ijk}|b_{k(j)}\right]=Z_{ijk}^{\text{T}}{\beta }_z+b_{k(j)}+{ϵ}_{ik(j)}$$

where ${ϵ}_{ik(j)}~\mathcal{N}\left(0,{\sigma }_w^2\right)$, $b_{k(j)}~\mathcal{N}\left(0,{\sigma }_b^2\right)Y_{ijk}=\left(\text{log}\left({\text{BMI}}_{Spring16}\right)\right)$, Z_ijk =(log(BMI_Fall14) ethnicity, grade, age, gender, treatment, teacher, school)^⊤, i = 1, …,157 students, j = 1, …,3 schools, k = 1, …,8 teachers (nested within schools). These residuals were subsequently used as the outcomes in our measurement error models. Thus, the outcome assessing the effects of energy expenditure on BMI were the error free and cluster randomized design adjusted residuals for the baseline measures of BMI for the first analyses and for the difference between BMI obtained at baseline and the BMI obtained at end of the study for the second analyses. Six knots were used in the application, while nonparametric bootstraps were used for computing the 95% point-wise confidence intervals for $\widehat{\beta (t)}$.

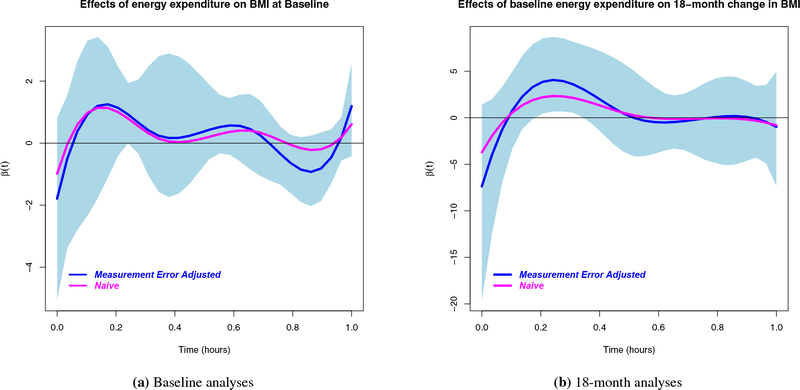
We provide the results from the baseline analyses and the follow up analyses in Figure 3. Plots of the estimated functional coefficient and the estimated 95% point-wise confidence intervals are provided in the figure. For assessments of the impact of energy expenditure on BMI at baseline, the bootstrap confidence intervals did not contain the zero line completely, indicating that the functional coefficient was not zero across the whole time space. Similarly, in determining the impacts of baseline measures of energy expenditure on the 18-month change in BMI over the study period, the estimated bootstrap confidence intervals did not contain the zero line completely. Because the function-valued coefficient was not completely zero across time, there was some statistical evidence of a relationship between baseline measures of energy expenditure and BMI values obtained at a future time, such as 18 months post baseline. Additionally, the relationship observed depended on both the level of energy expenditure and time.

FIGURE 3.

Plots of measurement error adjusted and naive estimates of β(t) at baseline and also at 18 months. In (a), we estimate the effects of energy expenditure on BMI at baseline and in (b) we obtain plots of the effects of energy expenditure on 18-month change in BMI for the students included in our motivating example. The shaded regions are the 95% point-wise Bootstrap confidence intervals, the blue line represents measurement error adjusted coefficients, while the pink line is the naive estimator that ignores potential measurement error.

5.1.3 |. Impact of measurement error on the analyses

In addition to our method of moments-based instrumental variable estimator, we also obtained naive estimators of the effects of energy expenditure on BMI see Figure 3. As illustrated in both sets of analyses, the approaches obtained without accounting for measurement error appeared notably different from the estimators obtained from the instrumental variable based approaches. Based on Figure 3, the impacts of measurement error on both sets of analyses depended on time. While it is well known in simple linear regression models that the effects of measurement on estimation is to attenuate its effects towards zero, its impact in this functional linear regression setting is more complex. For both sets of analyses, we found that the measurement error adjusted function-valued coefficients tended to be larger than the naive coefficient. However, the naive estimate of β(t) at baseline was found to be larger than the measurement error adjusted at the beginning and the end of the observational period.

5.2 |. Discussion

⁵⁰ recently studied the relationship between baseline energy expenditure and the three-year change in BMI among 182 five to ten year old children with overweight and obesity health conditions in Australia. Using regression analysis and change in BMI Z-scores, the authors concluded that baseline measures of energy expenditure significantly impacted the three-year change in BMI among the children. However, our current results indicated that baseline levels of energy expenditure did have some statistically significant relationships on the future body weights among children, however, these impacts depended on activity levels and the time of activity.

In this manuscript, we developed an instrumental variable approach for addressing potential measurement errors associated with function-valued covariates in scalar on function regression models. The developed methods can be used for assessments of the impacts of data collected on biological markers obtained repeatedly over a dense time space on health outcomes. A limitation of our current approach is that the instrumental variable must be collected on the same time period as the unbiased measure for the true covariate. Thus, the developed methods are applicable for devices that collect data on multiple biological markers over the same time period.

Our current approach does not allow inclusion of random effects of error-free covariates directly into (1) to account for cluster randomized or impacts of demographics. Some future work in this area include accounting for multi-level designs as well allowing the inclusion of error free covariates. Finally, the current methods are based on assessing impacts of energy expenditure on health outcomes using mean regression methods. It will be interesting to discover how accounting for measurement errors associated with function-valued covariates work in model settings that permit robust modeling of BMI such as quantile regression or other generalized robust model settings.

6 |. CONCLUSION

We studied the scalar on function regression model with measurement error. In this setting, we considered a scalar valued outcome with a functional covariate that was corrupted by measurement error. Most existing methods either implicitly assume the measurement errors are independent over time, or the measurement error covariance is known or can be estimated. However, the measurement errors are likely to be correlated over time. In addition, the measurement error variances are never known and estimates are seldom available. In this paper, we took advantage of the additional information provided in an instrument variable and developed a generalized methods of moments-based approach to identify and consistently estimate the functional regression coefficient. To our knowledge, it is the first in the literature to use instrument variable approach to address the measurement error problem in the scalar on function regression model. Using B-spline basis expansions, we re-parameterized the functional linear regression model to a multiple linear regression model with measurement error. The function-valued coefficient was estimated by first identifying the model using a function-valued instrumental variable observed on the same time space as the surrogate measure, while the generalized methods of moments approach was used for estimation. The proposed methodology was motivated by a childhood obesity study focused on assessing the relationship between energy expenditure and subsequent progression to obesity among elementary school-aged children. We successfully applied our proposed model to conclude that the estimated association between baseline measures of energy expenditure and the 18-month change in BMI was sometimes significant. This association indicated that school programs and policies that increase physical activity among students might have some beneficial impact. In an effort to combat childhood obesity, physical activity policies within school are implemented to encourage more physical activity behavior among children. Our developed methods improves on the current statistical approaches used to evaluate the effectiveness of such policies.

Finally, our simulation studies indicated the importance of accounting for measurement errors when a function-valued covariate in functional linear regression model is suspected to be imprecisely observed. Failure to account for the measurement errors can lead to severely biased estimates.

APPENDIX.

A SKETCH OF TECHNICAL ARGUMENTS

We denote the B-spline basis of degree p on [0, 1] as ${\left\{b_k(t)\right\}}_{k=1}^{K_n}$. For notational convenience, we use a scaled B-spline basis in the proof, which is defined as $B_k(t)=\sqrt{N_n}{b}_k(t)$ for k = 1, …,K_n. With some abuse of notation, we still denote $X_{ik}=\underset{0}{\overset{1}{\int }}{B}_k(t)X_i(t)dt,W_{ik}=\underset{0}{\overset{1}{\int }}{B}_k(t)W_i(t)dt,u_{ik}=\underset{0}{\overset{1}{\int }}{B}_k(t)u_i(t)dt$ for the scaled B-spline basis for simplicity.

By²⁹, there exists a set of coefficients ${\mathit{\gamma }}^{*}={\left({\gamma }_1^{*},\dots ,{\gamma }_{K_n}^{*}\right)}^T$ and a spline function ${\beta }_n^{*}(t)=\sum _{k=1}^{K_n}{\gamma }_k^{*}{B}_k(t)$ such that $\underset{t}{\text{sup}}|\beta (t)-{\beta }_n^{*}(t)|\le c{N}_n^{-(p+1)}$ for some constant c > 0. Let $Q_n(t)=\beta (t)-{\beta }_n^{*}(t)$. Then one can write

$$\begin{gathered} Y={\alpha }_0+\underset{0}{\overset{1}{\int }}\beta (t)X(t)dt+\epsilon ={\alpha }_0+\underset{0}{\overset{1}{\int }}\left\{{\beta }_n^{*}(t)+Q_n(t)\right\}X(t)dt+\epsilon \\ ={\alpha }_0+{\sum }_{k=1}^{K_n}{\gamma }_k^{*}{X}_k+\underset{0}{\overset{1}{\int }}{Q}_n(t)X(t)dt+\epsilon . \end{gathered}$$

Therefore,

$$\begin{gathered} \widehat{\mathit{\gamma }}-{\mathit{\gamma }}^{*}={\left({\Omega }_{WM}^{\top }{\Omega }_{WM}\right)}^{-1}{\Omega }_{WM}^{\top }{\Omega }_{MY}-{\mathit{\gamma }}^{*} \\ ={\left({\Omega }_{WM}^{\top }{\Omega }_{WM}\right)}^{-1}{\Omega }_{WM}^{\top }\left\{\left({\Omega }_{WM}-{\Omega }_{UM}\right){\mathit{\gamma }}^{*}+{\Omega }_{\epsilon M}+{\Omega }_{QM}\right\}-{\mathit{\gamma }}^{*} \\ ={\left({\Omega }_{WM}^{\top }{\Omega }_{WM}\right)}^{-1}{\Omega }_{WM}^{\top }\left(-{\Omega }_{UM}{\mathit{\gamma }}^{*}+{\Omega }_{\epsilon M}+{\Omega }_{QM}\right), \end{gathered}$$

where ${\Omega }_{UM}=\frac{1}{n}\sum _{i=1}^n{\tilde{U}}_i{\tilde{M}}_t^T,{\Omega }_{\epsilon M}=\frac{1}{n}\sum _{i=1}^n{\tilde{\epsilon }}_i{\tilde{M}}_i,{\Omega }_{QM}=\frac{1}{n}\sum _{i=1}^n{\tilde{Q}}_{ni}{\tilde{M}}_i$ and ${\tilde{U}}_i,{\tilde{\epsilon }}_i,{\tilde{Q}}_{ni}$ are centered versions of $U_i={\left(u_{i1},\dots ,u_{i{K}_n}\right)}^T$, ε_i, and $Q_{ni}=\underset{0}{\overset{1}{\int }}{Q}_n(t)X_i(t)dt$ respectively. Thus, by Lemma 1 in supplementary materials included in the Web Appendix, there exists a constant c > 0, such that

$$\begin{gathered} \Vert \widehat{\beta }(t)-{\beta }_n^{*}(t){\Vert }^2=\Vert {\sum }_{j=1}^{K_n}\left({\widehat{\gamma }}_j-{\gamma }_j^{*}\right)B_j(t){\Vert }^2\le c\Vert \widehat{\mathit{\gamma }}-{\mathit{\gamma }}^{*}{\Vert }^2 \\ =c\Vert {\left({\Omega }_{WM}^{\top }{\Omega }_{WM}\right)}^{-1}{\Omega }_{WM}^{\top }\left(-{\Omega }_{UM}{\mathit{\gamma }}^{*}+{\Omega }_{\epsilon M}+{\Omega }_{QM}\right){\Vert }^2 \\ =c{\left(-{\Omega }_{UM}{\mathit{\gamma }}^{*}+{\Omega }_{\epsilon M}+{\Omega }_{OM}\right)}^{\top }{\Omega }_{WM}{\left({\Omega }_{WM}^{\top }{\Omega }_{WM}\right)}^{-2}\times {\Omega }_{WM}^{\top }\left(-{\Omega }_{UM}{\mathit{\gamma }}^{*}+{\Omega }_{\epsilon M}+{\Omega }_{QM}\right) \end{gathered}$$

By Lemma 4 in the Web Appendix, there exist c,C > 0 such that

$$\begin{gathered} \Vert \widehat{\beta }(t)-{\beta }_n^{*}(t){\Vert }^2\le c{\left(-{\Omega }_{UM}{\mathit{\gamma }}^{*}+{\Omega }_{\epsilon M}+{\Omega }_{QM}\right)}^{\top }\left(-{\Omega }_{UM}{\mathit{\gamma }}^{*}+{\Omega }_{\epsilon M}+{\Omega }_{QM}\right) \\ \le C\left({\mathit{\gamma }}^{*\top }{\Omega }_{UM}^{\top }{\Omega }_{UM}{\mathit{\gamma }}^{*}+{\Omega }_{\epsilon M}^{\top }{\Omega }_{\epsilon M}+{\Omega }_{QM}^{\top }{\Omega }_{QM}\right). \end{gathered}$$

By Lemmas 2,3,6 in the Web Appendix, one has $\Vert \widehat{\beta }(t)-{\beta }_n^{*}(t){\Vert }^2=O_P\left(N_n/n\right)+O_P\left(N_n/n\right)+O_P\left(N_n^{-(2p+1)}\right)=O_P\left(N_n/n+N_n^{-(2p+1)}\right)$.

Finally, an error decomposition gives that

$$\begin{gathered} \Vert \widehat{\beta }(t)-\beta (t){\Vert }^2\le \Vert \widehat{\beta }(t)-{\beta }^{*}(t){\Vert }^2+\Vert {\beta }^{*}(t)-\beta (t){\Vert }^2 \\ =O_P\left(N_n/n+N_n^{-(2p+1)}\right)+O_P\left(N_n^{-(2p+2)}\right) \\ =O_P\left(N_n/n+N_n^{-(2p+1)}\right)\square . \end{gathered}$$