Abstract
Swarming colonies of the light-responsive bacteria Serratia marcescens grown on agar exhibit robust fluctuating large-scale flows that include arrayed vortices, jets and sinuous streamers. We study the immobilization and quenching of these collective flows when the moving swarm is exposed to intense wide-spectrum light with a substantial ultraviolet component. We map the emergent response of the swarm to light in terms of two parameters—light intensity and duration of exposure—and identify the conditions under which collective motility is impacted. For small exposure times and/or low intensities, we find collective motility to be negligibly affected. Increasing exposure times and/or intensity to higher values suppresses collective motility but only temporarily. Terminating exposure allows bacteria to recover and eventually reestablish collective flows similar to that seen in unexposed swarms. For long exposure times or at high intensities, exposed bacteria become paralysed and form aligned, jammed regions where macroscopic speeds reduce to zero. The effective size of the quenched region increases with time and saturates to approximately the extent of the illuminated region. Post-exposure, active bacteria dislodge immotile bacteria; initial dissolution rates are strongly dependent on duration of exposure. Based on our experimental observations, we propose a minimal Brownian dynamics model to examine the escape of exposed bacteria from the region of exposure. Our results complement studies on planktonic bacteria, inform models of patterning in gradated illumination and provide a starting point for the study of specific wavelengths on swarming bacteria.
Keywords: bacterial swarms, active jamming, light response of bacteria, active matter
1. Introduction
Swarming motility is a flagella-based mode of bacterial surface migration that is widespread in both Gram-positive and Gram-negative bacteria [1–8]. Swarming is typically initiated when free-swimming or planktonic bacteria grown in fluids are transferred to soft wet agar gels [5]. The transfer triggers a change in phenotype; individual cells become significantly elongated and the number of flagella increases, sometimes to 10–100 [1,7]. At high densities, the highly motile expanding colony develops complex, long-range intermittent collective flow features that involve multiple bacteria travelling in rafts or flock-like clusters. Collective speeds are typically high near the edge of the expanding colony and decrease away from the propagating edge [2,4,5,9] as one moves towards the centre of the colony. Studies demonstrate that swarming confers multiple benefits including enhanced colonization of environments and elevated resistance to antibiotics [10–12]. Swarming is also found to be co-regulated with virulence, and also implicated in infectiousness and fitness of pathogenic bacterial species [3,7].
Healthy bacteria sense spatio-temporally distributed cues, continuously process these inputs and transduce them to variations in motility and other responses [1,4,9,13]. Single bacteria are observed to respond to chemical and mechanical stimuli by modulating and controlling the molecular motors underlying flagellar motion [14–18]. Intense light with wavelengths in the range 290–530 nm encompassing the ultraviolet (UV) range is known to trigger changes in the motility of planktonic chemotactic bacteria [19–21]. Prolonged exposure to high-intensity light results in progressively slow swimming with paralysis occurring eventually [19,20] due to irreversible motor damage. Striking variations in motility associated with modulated functioning of the MotA–MotB pair and FliG comprising the rotary motor complex in the flagella are also observed in chemotactic bacteria. The net result is a change in the swimming gait—specifically, tumble length and tumble frequency [15,17]—as for instance seen in Escherichia coli and Streptococcus [20,22].
Connecting and relating single-cell responses to collective response when bacteria are subject to variations and changes in environmental factors remains a topic of active research. Here, we report on the effects of an environmental stimulus bacteria usually encounter—wide-spectrum light with significant UV components. Exposure to light is known to inhibit cell growth and induce gene damage [23] in marine organisms including alphaproto-bacteria and bacterioplankton [24], airborne bacteria [25], as well in bacterial biofilms [26,27]. Irradiation of surfaces using blue light and phototherapy that activates endogenous or exogenous photosensitizers [13,28–30] has been shown to sterilize and disinfect bacteria-laden surfaces and swarming bacteria. Intense light is also known to promote wound healing [29,31] with visible light recently approved to treat bacterial infections such as acne [32]. Consequently, from a medical perspective, light treatments employing UV-A, UV-B and UV-C radiation are emerging as attractive alternatives to antibiotic treatment of pathogenic bacteria. Given the timeliness of light treatments, understanding the connection between motility, infectiousness and light exposure is thus particularly important and motivates the studies presented in this article.
The layout of this paper is as follows. In collectively moving swarms, individual self-propelling cells are influenced by steric and hydrodynamic interactions with their neighbours [4–6,33–35]. These interactions result in complex structural and flow features including fluctuating regions of high vorticity and streamers. As a point of departure, we first discuss features of unexposed bacterial swarms—the base state. Following this, we report and analyse the drastic variations in mobility that ensue when localized regions of the swarm are exposed to wide-spectrum light. Using two independently tuned parameters—the light intensity and duration of exposure—we identify the conditions under which motility is affected or quenched significantly. Interestingly, this adverse impact on motility may be either reversible or irreversible. For low intensities or short exposure times, bacteria recover their motility and reestablish collective flows when exposure is terminated. For long exposures or high intensity light, actively generated collective motion ceases slowly and the passive region grows with time extending eventually to the scale of the light field. As quenching progresses, the dense multiple domains of immotile cells that form hinder the penetration of unexposed bacteria into the region. Active bacteria are thus prevented from entering the exposed region thereby localizing the damage in the colony. Post-exposure, swarming cells penetrate the previously quenched domain, dislodge and then convect immobile bacteria away. We find that the dissolution rate is strongly dependent on the duration of light exposure.
To complement our experiments and investigate how exposed bacterial clusters may be able to escape the illuminated region before being rendered immotile, we analyse an agent-based Brownian dynamics model that incorporates the effects of self-propulsion, thermal noise and light exposure acting in tandem. We deduce that variations in bacterial spreading distances may arise in a population of cells featuring a distribution of self-propulsion speeds. Subpopulations of bacteria corresponding to the fast cells may escape from the exposed region. Taken together, our experimental observations and computational results suggest that exposure time is as important as light intensity in determining the fate of exposed swarms.
2. Experimental methods
Here, we provide a summary of the experimental methods and protocols used. Details can be found in electronic supplementary material, §1.1–1.3. Swarms of Serratia marcesens (strain ATCC 274, Manassas, VA) were grown on agar substrates prepared by dissolving 1 wt% Bacto Tryptone, 0.5 wt% yeast extract, 0.5 wt% NaCl and 0.6 wt% Bacto Agar in deionized water. Melted agar was poured into petri dishes, and 2 wt% of glucose solution (25 wt%) was added. Bacteria were then inoculated on solidified agar plates and incubated at 34°C. Colonies formed and grew outward from the inoculation site. Swarms were imaged 12–16 h after inoculation.
We used an inverted microscope (Nikon, Eclipse Ti-U) to image bacteria with the free surface facing down. Depending on the experiment either a Nikon 10× (NA = 0.3) or a Nikon 20× (NA = 0.45) objective was used. Images were gathered at 30 frames per second (fps) with a Sony XCD-SX90 camera or at 60 fps and 125 fps with a Photron Fastcam SA1.1 camera. Videos of the swarm were analysed with particle image velocimetry (PIV) techniques (PIVLab [36]) to extract bacterial velocity fields. PIV-based techniques determine velocity fields by calculating local spatial correlations between successive images. Here, PIV yields the bacterial velocity fields directly (averaged over a few bacteria) and not the velocity field of the ambient fluid. We sampled the velocity field at 3 μm spatial intervals in the images, checking the frame rate for accurate resolution. We analysed the results using in-house adaptations of freely available object-oriented Python language. Structural features of the bio-swarm such as local alignment of bacterial packs and orientation were analysed using the Orientation J and Directionality plugins [37,38] in ImageJ (https://imagej.net/Directionality).
To mimic the exposure of bacteria to naturally occurring wide-spectrum light, we used a mercury vapour lamp as our light source (electronic supplementary material, figure S1 and §1). Standard epifluorescence optical components with the optical light path passing through the objective were used to focus the light on the swarm. The bare unfiltered maximum intensity (measured at 535 nm) of the lamp I0 was reduced to lower, filtered (maximum) intensities I using graded neutral density filters. Since both I0 and I depend on the objective, care was taken to calibrate the incident intensity carefully. Using a spectrophotometer (Thorlabs, PM100D), we measured maximum intensities I0 = 980 mW cm−2 (at 535 nm) for the 10× and I0 = 3100 mW cm−2 (at 535 nm) for the 20× objectives. Variations in the intensity of incident light were small—this was done by checking the incident intensity on a blank slide.
3. Results and discussion
3.1. Base state prior to exposure
To study and quantify properties of the base unexposed swarming state, images of unexposed swarms were analysed and statistics of the collective flows observed were extracted using PIV. We sampled the velocity field at 3 μm spatial intervals, between images taken at 60 or 125 fps. Since the algorithm we used is based on direct Fourier transform correlations, we used multiple passes and window sizes. The initial passes used large interrogation windows for better signal-to-noise ratio and more robust cross correlation. The interrogation window sizes decreased with each pass to increase the vector resolution. The window sizes used finally in our analysis corresponded to 64, 32, and 8 pixels or 21, 11 and 2.5 μm, allowing us to detect bacteria speeds of approximately 50 μm s−1.
The spatial correlation function Cv(Δr) and the temporal correlation Ct(Δt) of the velocity fields were then calculated using
| 3.1 |
and
| 3.2 |
respectively, where the brackets denote averages over reference positions r0 and times t0. As a representative statistic of the swarms, the probability distribution function p(v) of bacterial speeds based on the PIV-measured bacterial speeds v in a region of area 400 μm2 and at a distance 100 μm from the edge of the expanding colony shows a peak at 18 μm s−1, an expectation value ≈28 μm s−1 and a tail that extends to 100 μm s−1 [33]. The advancing front of the swarm is approximately 3 μm s−1.
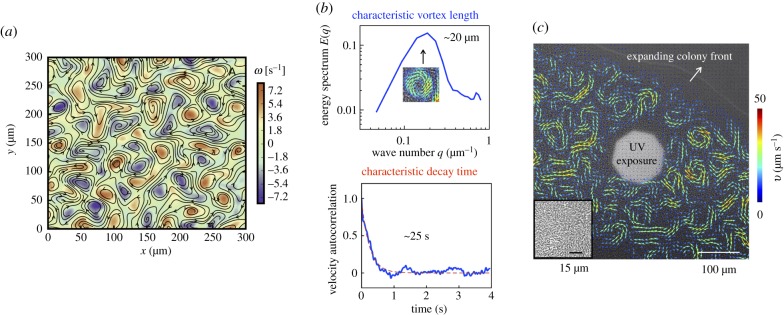
The collective flows feature intermittently arrayed vortices interspersed with streaming flock-like structures (figure 1a,b). Extracting the value of Δr at which the correlation function first crosses zero (figure 1b), we estimate vortex sizes λc ≈ 20 μm. For Δr less than a vortex length, the bacterial velocities are correlated positively, Cr > 0. As Δr increases, the function Cr decays crossing zero and then stays negative for 21 μm < Δr < 32 μm. Thus we anticipate neighbouring vortices to be anti-correlated with opposite vorticity (counterclockwise and clockwise). For Δr > 32 μm, velocity fields become progressively uncorrelated and Cr → 0 again. Examining the temporal correlation function and fitting the data to a single exponential of the form Ct(Δt) = exp(− t/τ) (figure 1b), we estimated the typical lifetime of a vortex τ ≈ 0.25 s.
Figure 1.
Characteristics of swarming and expanding colony. (a) Far from the edge of the swarm, the active flows show intense vortical patterns: colour here indicates strength of the vorticity fields ω(x, y). Overlaid on this colour map are velocity vectors obtained by PIV. We observe clockwise and counter-clockwise vortices that are arrayed and form periodically. Additionally, we observe interspersed streaming and flocking flows. (b) Combining computed spatial and temporal correlations of the swarming base state (before exposure to light) with analysis of the energy spectra, we deduce that vortical structures are correlated over characteristic lengths ≈20 μm and over characteristic times ≈0.25 s. (c) Snapshot of a Serratia marcescens colony on an agar substrate, during exposure to high-intensity light from a mercury-arc lamp. PIV-derived velocity fields are overlaid in colour. Swarming motion is pronounced approximately 50 μm from the expanding colony front. The inset shows pre-exposure bacterial alignment ≈150 μm from the colony front. (Online version in colour.)
We are unable to directly measure the thickness of the swarming layer. Based on previous work on Serratia [21], we expect this thickness to vary slowly with distance from the leading edge. This expectation is consistent with electronic supplementary material, movie S1, where the thickness in the near vicinity of the expanding edge is likely less than a monolayer. Studies on other bacteria (specifically E. coli [39]) suggest that swarming on agar substrates occurs in a thin layer of nearly uniform thickness close to the leading edge; far from this cells can form multi-layered regions.
3.2. Reversible and irreversible quenching of collective motility
To illuminate the swarm with a defined incident beam, we used the epifluorescence set-up; an octagonal-shaped light iris (aperture) was used to adjust the size of the illuminated region. Figure 1c is a snapshot of the expanding colony, a region of which (white area) is exposed. The swarm is expanding from left to right as indicated. Bacteria swim in a thin layer above the agar substrate (inset). Overlaid on the image in figure 1c are bacterial velocity fields gathered from PIV; the image is taken after 80 s of exposure. Outside of the exposed region, the velocity field exhibits long-range collective flows. Unexposed bacteria move fastest approximately 100–400 μm from the colony edge. By contrast, inside the exposed region, the bacterial motility is significantly impaired. This is evident in electronic supplementary material, movies S2(a) and S2(b); as swarming bacteria are exposed to light, they slow down and are eventually trapped within the exposed region. This feature is also reflected in the trajectories of the small tracer-like particles as they slow down and eventually stop moving when trapped among the passive bacteria. The interphase boundary between the exposed (passive) domain and the unexposed (active) part of the swarm features strong vortices, jets and streamers, extending up to just a few micrometres away from the exposed domain.
The response of bacteria to light depends on the wavelength, intensity, duration of the light and the presence of photo-sensitizers in the surrounding medium [13,26–30]. These studies also found that high intensity light greater than 200 mW cm−2 at wavelengths 390–530 nm can lead to increased tumbling, followed by slow swimming and eventually irreversible paralysis. Experiments with Bacillus subtilis demonstrate that photosensitizers can reversibly or irreversibly affect collective motility. It has been hypothesized that the paralysis is due to flagellar motor damage caused by photosensitizing flavins and dyes that are present in growth media.
Consistent with these previous experiments, we found that when a macroscopically large region of swarming Serratia marcescens was exposed to light, passivation was not immediate and in fact was sometimes even reversible. Yet for sufficiently large light intensities and exposure times, bacteria were permanently passivated. To examine this response in detail, we systematically explored two features of the response to wide-spectrum light: (i) the reversible versus irreversible nature of the bacterial response and (ii) the effects of exposure time and light intensities on the growth rate of the passivated domain during exposure and the dissolution rate following termination of exposure.
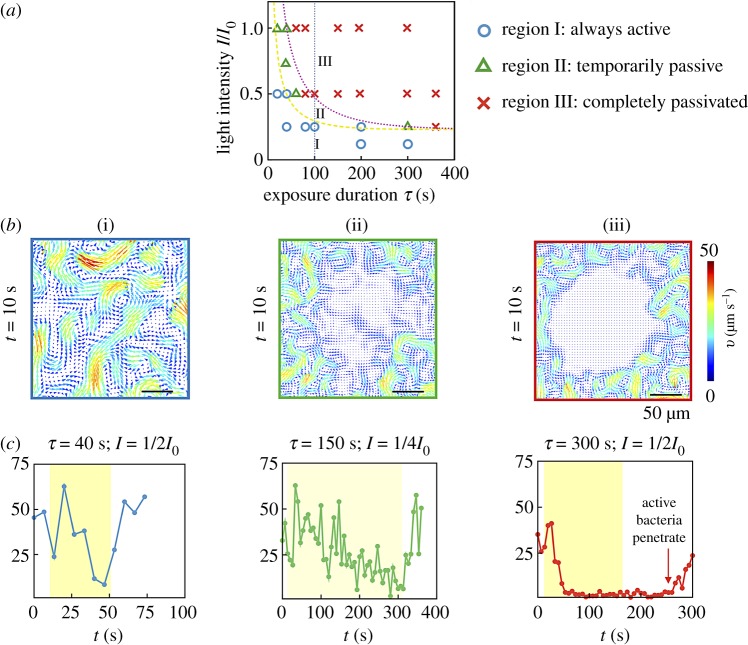
Figure 2 illustrates the three modes of the collective bacterial response to light: exposed cells either (i) retain mobility with negligible effects, (ii) transiently stop moving and then regain motility at the single cell and collective level (reversible) or (iii) permanently stop moving (irreversible). This classification was based on averages obtained from time-dependent swarm velocity fields. The observed phase behaviour was mapped onto a phase diagram in terms of exposure time τ and light intensity I (varied from the bare value I0 using neutral density filters) as variables. For sufficiently small exposure times (τ ∼ 20–40 s) and intensities (I < 220 mW, at 535 nm), exposed cells remain always active. Conversely, for large exposure times (τ > 60 s) and sufficiently high intensities (I > 220 mW, at 535 nm), the bacteria are permanently passive (over the duration of the experiment). Between these two phases lies the temporarily passive, reversible case.
Figure 2.
Phase space for collective motility after exposure. (a) Changes in flow features of swarming Serratia marcescens—relative to the unexposed base state—depend strongly on intensity and duration of light exposure. We use a wide spectrum mercury lamp (bare intensity I0 = 980 mW cm−2 at 535 nm) with filters to selectively expose regions of the swarm to a filtered maximum intensity I. Experiments were conducted a minimum of three times per condition, and the resultant phase behaviour was observed to be robust. From subsequent PIV analysis, we classify the response into one of three types: (I) always active, (II) temporarily passive and (III) always passive. The yellow (dashed) and pink (dotted) curves are phase boundaries (equation (3.3)) consistent with a lower threshold in intensity for irreversible response. (b) Velocity fields taken 10 s post-exposure are shown for each phase. Colours reflect speed with the arrows denoting polar orientation. Collective motility of temporarily immobile bacteria is recovered in approximately 15 s past exposure. (c) We plot the average speed of the swarm in the central region, highlighted by the box in (b) for times encompassing pre-exposure, exposure (yellow band) and post-exposure. Pre-exposure, the average swarm speed fluctuates between 25 and 50 μm s−1. For case (I), the bacteria briefly slow down during exposure, but recover in 6 s. In (II), the swarm speed approaches zero during exposure and recovers in 12 s. In (III), the collective swarm speed drops to very low values (close to zero) and remains steady. The data for the PIV were sampled at 60 fps, we only show around four points for every 25 s for clarity. For light intensities that fall within region (II) of the phase plot, it is likely that some bacteria are more impaired mobility-wise than others due to the natural variations in resistance to light-induced damage. We see no evidence from our videos of bacteria re-animated by the swarm when they are in the fully passivated region (region III). The averaged speed remains consistently zero until the active region (phase) starts to convect the paralysed bacteria away. Here, τ is the time of exposure and I is the intensity. (Online version in colour.)
The differences between the three collective motility regimes are highlighted in figure 2b,c; these show PIV-derived velocity fields taken 10 s past exposure (figure 2b) and the average bacterial speed 〈vc〉 in the exposed region over time (figure 2c). Here, 〈vc〉 is the average speed of the velocity fields in a 22 × 22 μm2 area, located at the centre of the exposed region. In case (i), exposed cells remain motile and continue to exhibit long-range collective motions; the speed decreases but does not fully reach zero during exposure. The speed recovers to pre-exposure levels approximately 5 s after exposure. In case (ii), bacteria stop moving during exposure, yet spontaneously start moving again ∼1–10 s after the light is switched off. The cell speed 〈vc〉 takes longer to recover to pre-exposure levels than case (i), and the recovery occurs heterogeneously with cells moving within the temporally quiescent region (figure 2b, tile ii). In case (iii), cells stop moving during exposure and do not regain their motility afterward for the whole duration of the experiment (20–300 s). Unlike case (ii), cells in the exposed region here do not spontaneously regain their motility (figure 2b, tile iii). In this case, the passive domain evolves solely due to its interaction with the active swarm at its boundary (electronic supplementary material, movies S3 and S4). The active swarm convects passive bacteria away from the boundary and the passive phase is dismantled entirely; the speed 〈vc〉 eventually increases (figure 2c, tile iii) as the swarm recaptures the quenched area.
Responses qualitatively similar to these have been observed earlier in studies on E. coli and S. typhimurium [19]. Specifically, prolonged exposure to unfiltered light in both bacterial species resulted in constant tumbling, and eventual paralysis. S. typhimurium was found to responds instantaneously to exposure with recovery of normal motility in 2 s or less upon cessation of exposure provided the duration of exposure was less than 5 s. Bacterial E. coli cells recovered normal motility in 1–10 s after cessation of exposure. Sustained exposure that ultimately results in paralysis was however found to be irreversible (with no recovery of motility even after 15 min) for both species. Our experimental results encapsulated in figure 2 show that collective motility in swarming Serratia marcescens exhibits similar responses to light exposure.
The boundaries separating the three regimes in the phase-plot shown in figure 2a can be quantified by hypothesizing the existence of a lower threshold for the intensity Imin below which bacteria are not affected. Inspecting the data, we deduce that these boundaries do not correspond to a single or unique value of the light dosage (intensity multiplied by exposure time) or net power. To interpret figure 2a, we propose a simple fit that takes into account the presence of a time scale controlling collective response to light that results in either temporary ( = τtemp) or permanent ( = τperm) passivation following:
| 3.3 |
Fitting yields (A, Imin, τtemp) = (0.2, 0.23, 62) for the yellow (dashed) curve and (A, Imin, τperm) = (0.33, 0.23, 100) for the pink (dotted) curve. The bare (unfiltered, maximum) intensity I0 = 980 mW cm−2 at 535 nm. As expected, τtemp < τperm. The variation in A reflects the fact that our experiments do not probe the τ → 0 limit. We emphasize that the form of equation (3.3) was chosen since it provides a minimal analytical form that still allows for discrimination between incomplete and complete paralysis while still respecting a possible limiting threshold for intensity (at the density corresponding to the experiments). The term /τ multiplying the exponential term allowed us to obtain the same value of Imin for both responses. Additional studies are required to compare critical intensities and time scales obtained from (3.3) and corresponding values for planktonic isolated swimming bacteria.
The recovery of collective motility when sustained exposure is not maintained has significant implications. While isolated bacteria can reorient by run and tumble movements, motility driven by close bacteria–bacteria interactions dominates in a swarm. In patterned or localized light fields, fast cells have a higher chance of escaping the exposure region before they become completely paralysed. Slowly moving cells however can end up exposed to light for longer times and, also—in the process—be easily aligned and hindered by already paralysed cells.
3.3. Form and growth of the quenched region
To determine the extent of the quenched domain and thereby quantify its form and growth, we next determined the location and shape of the boundary separating the passive and active domains. We used two threshold-based methods: the first used image intensity fluctuations [40,41] obtained from raw images and the second used PIV-derived velocity fields computed from the raw data. Our experiments were (unless stated otherwise) conducted at a filtered intensity of 3100 mW cm−2 (measured at 535 nm); exposure time τ was varied from 10 to 300 s.
3.3.1. Boundary of the quenched region
The first method to extract the boundary of the quenched region was based on analysis of point-wise fluctuations of the spatially varying intensity field
| 3.4 |
where I*(r, t) is the two-dimensional image intensity at pixel position r and Δt is the time step. To reduce noise in the system arising from effects such as pixel resolution, short-range fluctuations and background light fluctuations, we first filtered the pixel-wise values of |ΔI*(r, t, Δt)| by smoothing over 3 × 3 μm2 areas. We then varied Δt to obtain temporally resolved domains. We found that using Δt = 0.1 s, which corresponds to the time taken by a Serratia cell swimming at 50 μm s−1 to move roughly a body distance (5 μm) provided good results; variations in Δt around this value (0.05 s < Δt < 0.3 s) resulted in only small variations in results. As seen in figure 3, intensity fluctuations allow us to identify and distinguish two domains, the quenched domain where values of |ΔI*| are relatively small and the motile domain where |ΔI*| are relatively large. Thresholding |ΔI*| then yields the locus of points that defines the boundary of the active and passive phases. In the second method, the boundary position was obtained from coarse-grained spatially averaged bacterial velocity fields from PIV (figure 3b); the exact boundary was subsequently identified and fixed using a threshold criterion [33]. The locations of the active and passive domains, as well as their relative sizes such as area, match between the two methods, although the intensity fluctuation-based method identifies smaller features of the boundary compared to the PIV-based method.
Figure 3.
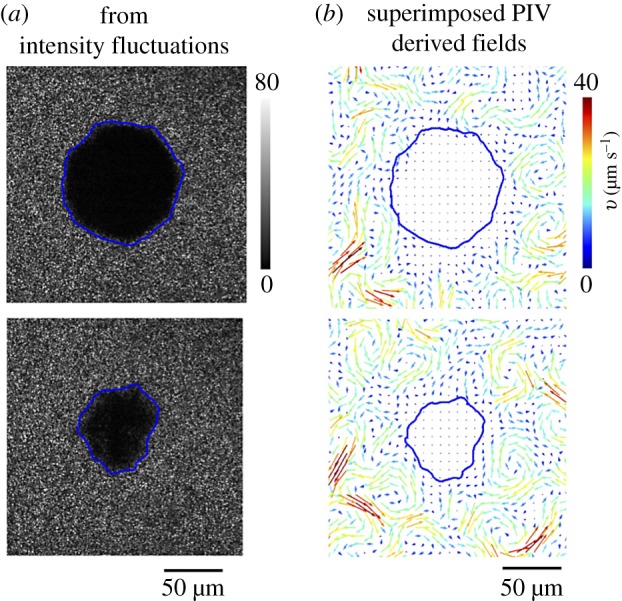
Thresholding using intensity fluctuation fields. (a) We calculated the intensity fluctuation difference map |I*(r, t + Δt) − I*(r, t)|, here with Δt = 0.1 s. Intensity fluctuations are low (black) in the regions where the swarm is not moving. Suitably thresholding the result allows us to identify the boundary position (blue curve). The quenched (black blob) phase shrinks with time as is observed by examining the extent of the region at t = 1 s (top) and t = 40 s (bottom) as measured post-exposure. The exposure duration τ = 80 s and intensity (at 535 nm) was 3 W cm−2. (b) Thresholding of PIV-derived velocity (speed) fields confirms the boundary location obtained from the intensity fluctuation maps. The diffuse boundary may also be located using phase field approaches [33,42]. (Online version in colour.)
The metrics just described capture complementary aspects of the swarm’s motility: the intensity fluctuations are a scalar measure of density fluctuations and PIV yields vectorial velocity fields that quantify instantaneous polarity fields. In summary, simple thresholding using the intensity fluctuations and/or PIV-derived velocity fields, yields physically meaningful boundary positions that separate the quenched region from the swarm. This approach can be formalized using phase-field approaches in order to extract the location and width of the interface [33,42].
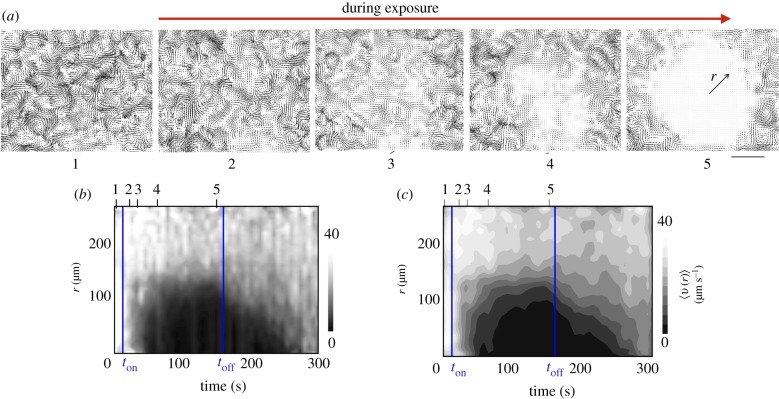
Figure 4a illustrates the manner in which we used PIV-derived velocity fields to study the dynamics of the quenching process. In the swarming state, the motion of Serratia marcescens clusters may be decoupled into a mean velocity (approximate velocity of the swarm front) and a diffusion-like term dependent on features of the collective coherent structures given by approximately where ℓcc is the length scale of the collective structure and τcc is its lifetime. For a suspension without collective flow features, it is reasonable to expect that the quenching process starts where the light intensity is maximum—i.e. at r = 0. When the light source is switched on, the collective flow features result in significant spatial variations with clusters slowing down non-uniformly (figure 4a; electronic supplementary material, figure S3). The PIV-derived velocity fields emphasize this; bacteria slow down forming fragmented and partially passivated sub-domains (electronic supplementary material, movies S2(a) and S2(b)). After a period of time, these fragmented domains combine into a large quenched domain. The time delay observed in going from the temporarily passive to fully immotile state is a consequence of interplay between the static light field, the dynamic motions of the bacteria and interactions arising from the close-packed nature of the swarm. An integral part of this process involves bacterial clusters slowing down as they experience increasingly jammed environments with local flocks aligning.
Figure 4.
Thresholding using PIV-derived fields allows for analysis of the evolution of the quenched region. (a) PIV-derived bacterial velocity fields before (tile 1) and during (tiles 2–5) light exposure. We note from tile (5) that as the exposure is continued, the paralysing effects persist only a short distance into the active unexposed region as evident from the vortical structures seen near the edge. (b) The azimuthally averaged velocity 〈v〉(r) shown as a colour map highlights the creation of an immotile quenched domain within the exposed region. When the light is switched off, the active bacteria from the unexposed regions penetrate into the quenched domain, eroding it away. The filtered maximum intensity =500 mW cm−2. We note the brief lag after the light is switched on (the lag here being ton), the gradual increase and (possible subsequent saturation) to a finite size as t → toff and the rapid erosion and mixing with the grey interphase region t > toff. (c) Using averaging filters that effectively smooth the fields in (b) yields less resolved fields. Note the difference in the manner intensities are plotted on the bars shown on the right of (b) and (c). (Online version in colour.)
3.3.2. Averaging to obtain radially dependent fields
A convenient way to view the quenching process is to think of this as one where actively generated energy of the swarm is lost or degraded as the bacterial collective velocities die down. The rate at which the quenched region forms then depends on the rate at which this actively generated energy is lost. If the mean propagation speed of the swarm front is ignored, the fluctuating swarm velocities, v, can be treated as time-varying fields with a zero mean that encode information about the energy content of the swarm. Averaging over time scales long enough to encompass multiple vortex and streamer lifetimes, and then averaging azimuthally about the polar angle in the swarming plane, will provide a radially dependent scalar field 〈|v|〉 whose intensity is a direct measure of activity. In the process we lose information about structural asymmetries and irregularities inherent to the quenched domain as well as variations in motility inside the domain.
Just as we previously used a cut-off value as a threshold criterion to define a two-dimensional boundary, we can apply a similar procedure to the reduced radial field to determine the mean radius of the quenched region. This procedure can be applied to either the averaged intensity maps or the averaged speed field; here we present results for the latter. In line with this interpretation, we coarse-grained the PIV-derived velocity fields to obtain radially dependent speed profiles. The temporal variations of the azimuthally averaged bacterial speeds 〈v〉(r, t) with r as measured from the centre of the illuminated region from the PIV-derived two-dimensional fields, for the experiment shown in figure 4a, are plotted in figure 4b,c. Quenched domains appear as dark regions characterized by negligibly low speeds. After the initial lag time tlag, the extent of the quenched domain is observed to increase steadily with time t before eventually saturating at large time due to the finite extent of the illuminated region. When the light is turned off, active bacteria penetrate the passive phase, convect passive bacteria away and in approximately 100 s post-exposure recapture the illuminated domain.
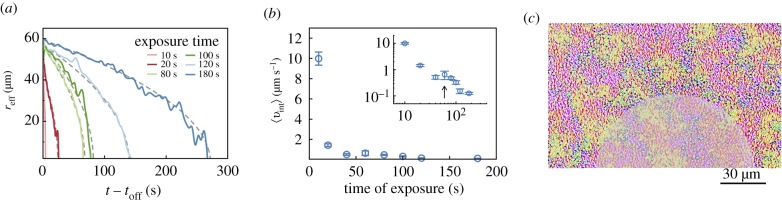
Focusing on reduced speed contours of the kind shown in figure 4b,c, we found that a cut-off value 〈v〉 ≈ 10 μm s−1 yielded meaningful values of the boundary separating the quenched (lower mean speeds) from the active (larger mean speeds) region. The radial extent of the quenched domain thus obtained is shown in figure 5a.1 Variations in the radial extent are a consequence of asymmetric formation of the passive domain. The results shown represent an average of three experiments.
Figure 5.
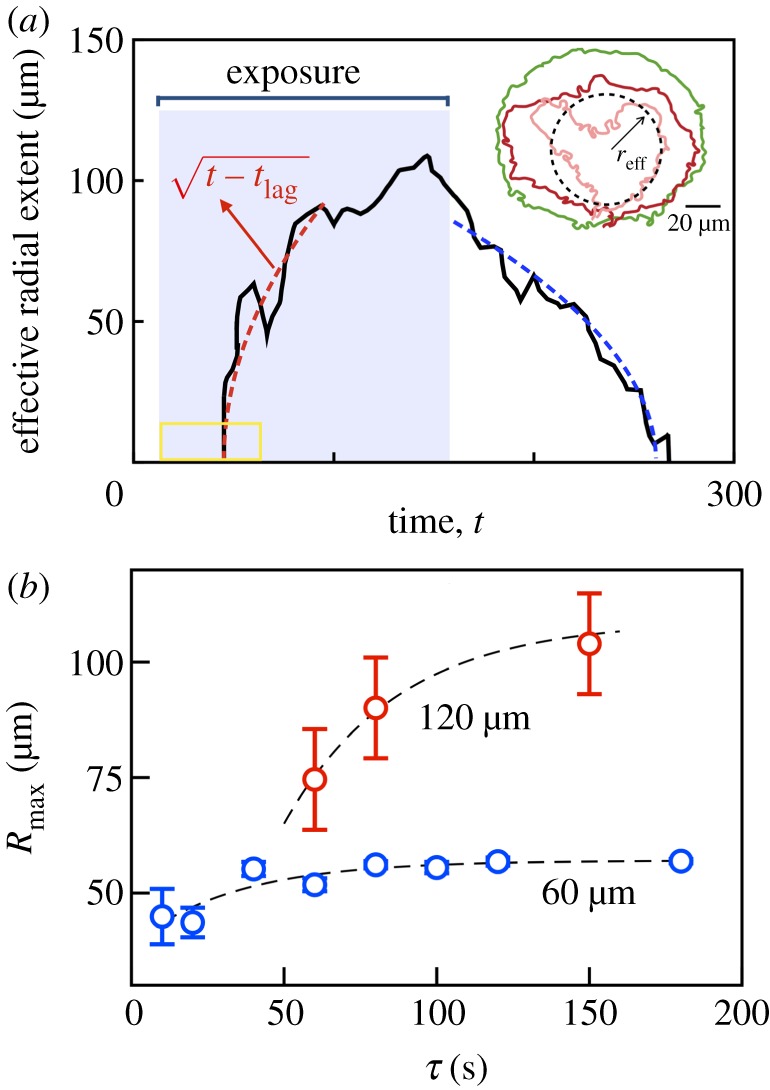
Growth, shape and dissolution of the quenched domain. (a) Inset: two-dimensional interface boundaries at various instants in time obtained from thresholding the ΔI (x, y) fields but prior to azimuthal averaging. Pink, red and green curves correspond to exposure times of 10, 20 and 100 s (aperture size 60 μm, 20× objective). These shapes yield effective radii of quenched region that are consistent with values obtained from PIV data based first on thresholding using a cutoff 〈v〉 = 10 μm s−1 and subsequent azimuthal averaging (not shown). (a) Using a larger aperture size and longer exposure time allows us to probe the dynamics of growth in more detail. The effective radius as identified by taking thresholding the averaged PIV data is shown. The effective radius of the quenched region grows during exposure (lag time tlag ≈ 50 s) and asymptotes to a constant as long as the light source remains on. For comparison, a square root dependence is shown as the red dashed curve. Post-exposure, the effective radius decreases to zero in finite time. The aperture size is 120 μm. (b) The maximum extent Rmax ≡ reff(t = toff) increases with exposure duration τ and asymptotes to constant values. (Online version in colour.)
Revisiting the interpretation of the quenching process as one where energy is extracted, it is interesting to compare the light-driven quench with a two-phase moving interface problem—the one-dimensional freezing of a domain due to a heat sink at the origin—where the interface follows a square root dependence in time (electronic supplementary material, §II). For comparison, in figure 5a, we plot the function with ton being the time when the light source is turned on and tlag being the lag time.
3.4. Exposure time and spatial extent of quenched domain
Next, we examined how varying the time of exposure while keeping the size of the illuminated region fixed changes the spatio-temporal dynamics of the quenching process. Aiming to obtain an upper bound on the size of the swarming domain that is impacted, we chose to use intensity fluctuation fields rather than the PIV-derived velocity fields to analyse the data and identify the interface boundary. To adjust the viewing window, the 60 μm aperture experiments were conducted with the 20× objective and the 120 μm aperture experiments with the 10× objective. We took into account the higher value for the intensity for the 60 μm aperture case at 20×. Both these corresponded to bacterial response ending in the completely passive regime (region III in figure 2a).
Figure 5b is a plot of the average radial size of the quenched domain obtained from four experiments with corresponding standard deviation shown as error bars. We conclude that Rmax ≡ reff(t = toff) increases with exposure duration τ and asymptotes to a constant that is less than the aperture size (≈58 μm for 60 μm aperture, ≈109 μm for 120 μm aperture). The disparity between the maximum radius of the quenched region and the aperture size is a consequence of the finite thickness over which the speed profile transitions from the active (large) value to the passive (nearly zero) value.
3.5. Caging and jamming in quenched region
Also shown in figure 5a is the rate at which the quenched domain erodes when exposure is terminated. We found that the dissolution time taken by the active swarm to completely penetrate the quenched region and convect the paralysed bacteria away was strongly dependent on size of the swarm (set by the aperture) as well as on the duration of illumination τ. To understand why this may be so, we examined movies of the dissolution process. Electronic supplementary material, movies S4 and S5 illustrate the dynamics of small tracer particles as they encounter the moving interface. We find that these tracers behave as trapped/caged particles—they do not move until they are dislodged by the active swarm.
Recognizing that quenched bacterial clusters may behave similarly, we examined the structure and alignment of bacterial clusters in both the active and the quenched phases using the DirectionalJ and OrientationJ plugins that are a part of the open source software ImageJ. These plugins calculate directional derivatives of the gradient in image features of a specified region of interest, obtain the direction along which these derivatives are maximized, and finally compute the structure tensor. The structure tensor provides eigenvalues and eigenvectors that characterize the alignment direction, degree of alignment and degree of coherence. Qualitatively, the orientation is visualized as a false-colour image with coloured domains with domains of the same colour indicating similarly aligned bacteria and intensity quantifying degree of coherence. Structural information such as size of coherently arrayed structures and length scales over which structural features are correlated when combined with PIV data provides a complete picture of how the moving active phase erodes the passive quenched region and the evolution of the interface.
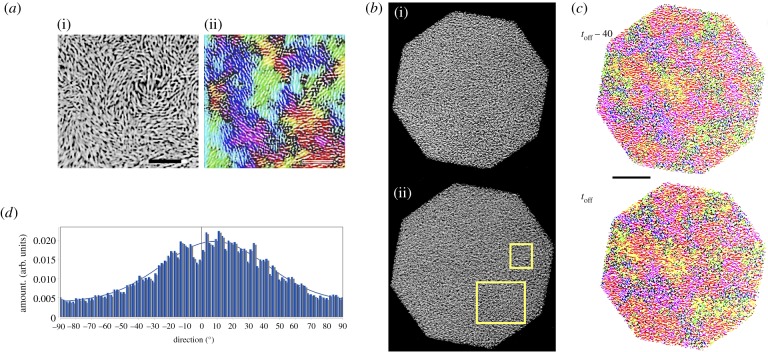
Analysis of images obtained during the quenching process for the case where bacteria end up irreversibly quenched (figure 6) reveals that (i) multiple structurally heterogeneous domains spanning sizes as large as 15–20 μm exist in both the active and quenched regions, (ii) bacteria in these quenched domains are densely packed, (iii) while each sub-domain is aligned in a preferred direction, as a whole a wide distribution of sizes and orientations are observed, and finally (iii) there is evidence of slight changes in alignment during the final stages of quenching. It is known that dense suspensions of passive non-propelling nematic rods can align with time due to thermally driven Brownian diffusion. Supported by electronic supplementary material, movies, figure S3, and figures 5 and 6, we hypothesize that the passivated bacteria indeed behave as passive nematic rods with increasing alignment as τ increases. Examination of the size of the aligned regions and the fact that adjacent regions may be aligned differently with only slow rearrangements at large exposure times suggests strongly that bacterial clusters end up in caged and jammed configurations. This possibly results from (i) aligning due to motility contrasts during the initial part of the quenching process, (ii) steric interactions that enhance this effect and (iii) collective flows that persist initially during quenching.2
Figure 6.
(a) (i) Close-up of a region in the unexposed active phase (scale bar 15 μm) illustrating aligned regions. These features are highlighted when analysing this image using the Orientation J plugin in ImageJ. The false colour rendering obtained shown in (ii) shows domains with distinctly co-aligned bacteria. Coloured regions indicate regions with closely matching alignment (orientation). Higher intensity of the same colour indicates a smaller dispersion along the common direction of orientation. Characteristic length scales here are slightly smaller than that obtained from PIV-based velocity correlation length scales shown in figure 1b. (b) Contrast-adjusted images of the quenched region (octagonal aperture, size 120 μm). Image (i) correspond to the structure at time toff − 40 s while image (ii) is the structure at time toff just when the light source is turned off. (c) Analysis of these images using the ImageJ plugin Orientation J reveals the presence of distinct regions where quenched bacteria are aligned in a similar manner. Closer examination of the regions highlighted in the white rectangles reveals that domains can have a distribution of sizes and orientations, are tightly packed, and do not undergo significant changes once quenched. At the same time, the slight differences in the size and shape of the domains suggest that slow processes including thermally driven (Brownian motion related) realignment may occur over long time scales (scale bar in black 20 μm). (d) The orientational distribution in degrees (−π/2 ≤ θ ≤ π/2) of structures in the complete region within the octagonal area in (b(ii)) as detected by the ImageJ plugin Directionality (https://imagej.net/Directionality). Images with completely isotropic content yield a flat histogram. We see a distribution of angles and the peak of the Gaussian fit that accounts for periodicity (blue curve) is close to zero (goodness of the fit =0.95). Combined with (c(i),(ii)), these observations support the hypothesis that the quenched region comprises distinct, multiple, tightly packed domains of aligned bacteria. Each domain has a different mean alignment. (Online version in colour.)
3.6. Spatial extent of illumination and duration of exposure are both important
As seen in figure 5a, post-exposure, active bacteria invade and disrupt immotile bacteria. The size of the eroding region follows roughly a square root dependence with time until complete dissolution (blue dashed curve). In our active, far-from equilibrium system, the passive domain is eroded by single bacteria–bacteria interactions (displacements originating from steric and self-propulsive mechanisms) as well as by collective highly non-equilibrium flow structures that form near the surface. Elucidating the origin of this scaling requires a consideration of the coupling between interface shape, interface speed and interface flow fields [33]. The time to complete dissolution, as expected, increases with exposure time as plotted in figure 7a. We also measured the initial boundary dissolution speed by calculating 〈vint〉 = (reff(toff) − reff(toff + Δt))/Δt, where Δt = 10 s. We find that 〈vint〉 varies significantly with exposure time—as shown in figure 7b—decreasing from 10 to 0.1 μm s−1 as τ increases from 10 to 300 s. The decrease in speed is not monotonic, rather we observe a peak (inset) that is not ascribable to experimental variations.
Figure 7.
(a) The effective extent of the quenched, passive domain decreases over time t at rates that depend on the exposure duration τ. Longer exposure times prolong erosion by the active swarming bacteria, increasing the time it takes for the passive phase to disappear (at time t0). For each τ, the effective size reff follows (grey dashed curves) with t0(τ) being the time for complete dissolution. All the points here correspond to the irreversibly quenched regime. (b) The average initial dissolution velocity 〈vint〉 decreases significantly with τ. Data are the average calculated from four experiments with standard deviation as error bars (intensity ≈3 W cm−2). (c) False colour image of the orientational map of bacterial clusters obtained by analysis with ImageJ plugin Orientation J (https://imagej.net/Directionality). The aperture used is the 60 μm aperture (effective total span-wise size of 120 μm) and exposure time τ = 180 s. The snapshot analysed is the image obtained 10 s after the light source is switched off. Each colour denotes a similarly oriented cluster of bacteria as identified by the Orientation J plugin. We observe clusters in the quenched region (shown overlaid as the translucent region) and penetration of moving (active) bacteria clusters into the previously exposed region. The intensity of the colour is a measure of the closeness of orientation. Structural information on orientation and the size of coherent structures when combined with PIV gives us a complete picture of how the moving active phase erodes the passive quenched region and the evolution of the interface [33]. (Online version in colour.)
Combining our observations (summarized in figures 6 and 7a,b) with the qualitative structural information gleaned from figure 7c, we hypothesize that for long exposure times or high intensities, as the exposed bacteria are slowly paralysed and slow down, they form jammed, highly aligned domains. The larger the extent of alignment and size of the domain, the more they resist erosion and thus result in longer times to complete dissolution and slower initial dissolution rates. The aperture size that sets the length scale of the light exposure is as important as the duration of exposure, τ.
4. Escape of bacteria from the light
Our experimental set-up was suited to study the dynamics of the interphase region and the flows in its vicinity. It is known that high aspect ratio densely packed passive polar rods can organize into ordered states through thermal motions augmented by additional steric interactions [43] or other weakly aligning interactions [44]. Here, the slowing of individual bacteria, the resultant disruption of motility at the collective level and further orienting affects of local (shearing) flows may allow the mechanisms operating in the passive case to also influence the formation of aligned phases we observe in figures 6a–c and 7c. A natural question to then ask is whether small sub-domains of bacteria can escape from the illuminated region before they become completely immobilized. Intuitively, one expects slower bacteria or slower clusters to be trapped; however, since the large-scale complex flows are collective, convective effects could set paralysed bacteria in motion.
Our experiments unfortunately do not offer the resolution to answer this question. To complement our experiments, we therefore propose and analyse an agent-based Brownian dynamics model.
4.1. Minimal model for a test cell
Our aim here is to investigate the competition between propulsion speed and light-induced jamming that underlies ability of a test cell (mimicking a real cell cluster) to escape from the illuminated region. To do this, we work within the framework of an extended Langevin dynamics model. We analyse the spatio-temporal dynamics of a test cell cluster moving in the x–y plane with velocity v0p with p = cosθ ex + sinθ ey being the unit vector denoting the instantaneous direction of motion. The cell motion has both deterministic (self-propulsion) and stochastic components (rotational and translational diffusion).
To keep the model simple, we assume that (a) test cells undergo over-damped Langevin dynamics with dissipation coming from viscous Stokes drag, (b) cell diffusivities are modified from the bare (thermal noise dictated) equilibrium values by a multiplicative factor term that depends on time and (c) consistent with the non-equilibrium active setting, the diffusivities could (but not necessarily) correspond to different temperatures. Thus, the random terms that impact the translational (ηT) and rotational (ηR) motion of the test cell satisfy
| 4.1 |
and
| 4.2 |
with the time-dependent factors F(t) and G(t) incorporating the slow deactivation of the self-propelling, diffusing particle; δ is the Kronecker delta function while I is the identity tensor in two dimensions.
In our simulations, the test cell moves in a light field with spatially dependent intensity Φ(r) of extent RL. To next specify the functions F(t) and G(t) in equations (4.1) and (4.2), we turn to our experimental results and also to previous studies on Bacillus subtilis [30]. Experiments show that as bacterial cells become sluggish, the tendency to form flowing flocks and large packs reduces. The overall reduction in cluster size and a less ordered motion within individual clusters give rise to slightly decreased correlation lengths. Guided by these previous studies and our experiments, we assume that light exposure increases the tumbling frequency and the rotational diffusion coefficient. As the test cell moves among its deactivating neighbours, its translational diffusion is hindered due to crowding and alignment effects (indirect effects of light exposure). Note that clusters may also experience anisotropic translational diffusivities due to the different environments perpendicular and normal to the propulsion direction. Treating the anisotropy in diffusion coefficients as secondary to the fact that the diffusion slows down, we choose the approximate forms
| 4.3 |
and
| 4.4 |
with the two independent dimensionless parameters and characterizing the light-induced deactivation process.
To make progress, we work in time scaled by the rotational diffusion coefficient of a single test cell and lengths scaled by . Note that τc is the time scale over which the test cell velocities are correlated. Decomposing the extended Langevin equations (electronic supplementary material, §III) in terms of the Cartesian components of the cell (x, y) and orientation in terms of the polar angle θ (u·ex = cosθ), we derive the discrete, stochastic time-stepper yielding the location and orientation of the test cell
| 4.5 |
| 4.6 |
| 4.7 |
Here, and are normally distributed random variables with mean 0 and standard deviation 1. The random variable is similarly chosen from a normal distribution and allows the test cell to possibly undergo large reorientations. The index n + 1 is associated with time instant tn+1 = tn + Δt and is the (dimensionless) Peclet number. The Peclet number is a useful measure of activity. For small Peclet number, cell motions are correlated for distances much more than their size, exhibiting active displacements that deviate from their innate Brownian motion. In the limit of zero Peclet number, the particles behave as Brownian particles with no effects of their innate activity. Swarming bacteria provide a model system for very large activity levels and hence moderate to high Peclet number.
Equations (4.5)–(4.7) constitute a first-order Euler–Maruyama scheme. For simplicity, we have also ignored direct changes to the self-propulsion speed.
4.2. Role of exposure time and propulsion speed
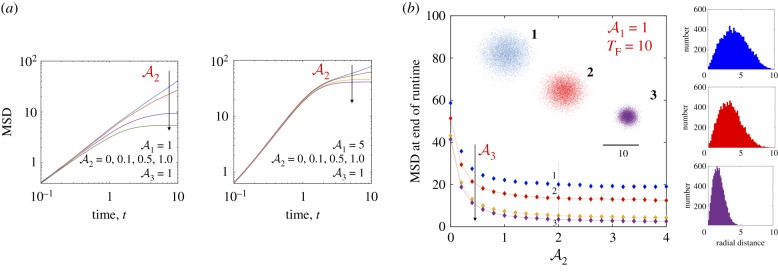
We evolved equations (4.3)–(4.7) in time for two illumination modalities. The first is uniform unbounded light field with Φ(r) = 1 and RL = ∞. The second case we considered was a localized field and zero elsewhere. We chose Δt ∈ (10−3 − 10−4). The effect of negative was also explored for the sake of completeness. Figures 8 and 9 summarize our findings on the effects of self-propulsion and bounded light field on the dynamics of 104 independent test cells.
Figure 8.
Dynamics of self-propelled and diffusing particles (N = 104) interacting with a constant, unbounded light field (Φ(r) = 1, RL = ∞). Light exposure modifies the translational and rotational diffusivities, but not the self-propulsion speed. Cells are released at the origin r = 0 and trajectories integrated for a dimensionless time interval TF = 10 with Δt ∈ (4 × 10−4, 10−3). (a) When the cell speed is held constant, examination of the ensemble averaged MSD(t) shows trajectories becoming denser and compact yielding a plateau in the MSD corresponding to localization and paralysis of the particles. Changes in rotational diffusivities are required for this to happen since the self-propulsion speed is assumed to be constant; this effect is exacerbated as becomes larger. Note that as increases, the longer the particles typically travel before exposure effects dominate. (b) MSD (t = TF) as a function of for various values of (from top to bottom: 0.1, 0.5, 1 and 2) with . Consistent with (a), we observe saturation for . The inset shows the (x, y) locations of the particles for parameters corresponding to points 1, 2 and 3 marked on the plot at TF = 10. Examination of the corresponding number distribution plots (right tiles) shows the peak shifting to lower values of radial distance r, and significant changes to the tail end of the distribution function. Since the light field is unbounded, all particles are eventually affected. For particles with low Peclet number (low activity), the exposure time determines how far they can travel before becoming deactivated. (Online version in colour.)
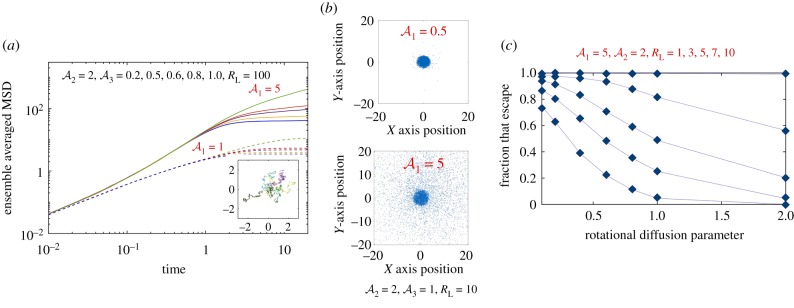
Figure 9.
Effects of an imposed (dimensionless) length scale RL using a finite extent light field and zero elsewhere. We integrate trajectories of 104 particles using Δt = 4 × 10−4 up to final times TF. (a) First effects of finite light extent. The dimensionless MSD is shown as a function of time for RL = 100. Solid curves are results for while dashed curves are for . We see that as increases from 0.2 to 1.0, MSD saturates rapidly. Inset: sample trajectories for for 0 ≤ t ≤ 20 demonstrating localization for t > 6. (b) Decreasing RL from 100 to 10 brings out the role of Peclet number in enabling escape. We show cell positions at t = TF = 10 (note that cells outside of this domain are not shown). (c) The fraction of 104 trajectories that start at r = 0 and are located at r > RL at T = 10. Note that some of these trajectories reenter the domain in the simulation. Curves are shown as a function of the rotation diffusion parameter . (Online version in colour.)
4.3. Spatial effects on deactivation
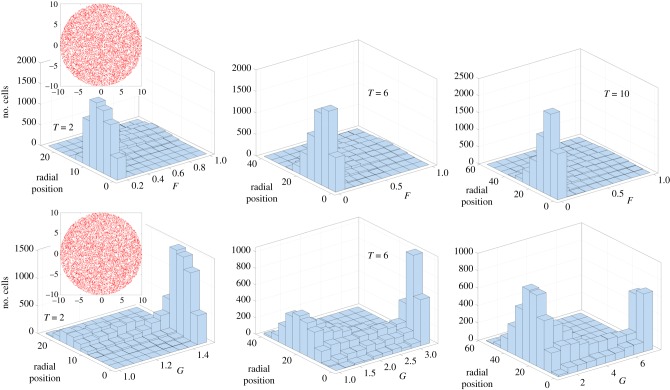
Even when cell–cell interactions are negligible (negligible aligning effects), the light-induced changes to single-cell motility can induce patterns in the quenched region and possibly result in fast particles trapped/caged by slow particles. To investigate if such a process can indeed occur, we followed the evolution of 104 cells distributed uniformly within a circle of radius RL = 10 with each starting off with diffusivities F = 1 and G = 1. As time progresses, these non-interacting test cells self propel and diffuse but at different rates depending on the light intensity, time and position. Figure 10 shows the results of a single realization. Here , and . We track each cell for various periods of time, and then plot a histogram that shows the spatial distribution of cells with specific values of F(t) and G(t). Note that the cells can diffuse and move out of the lighted region; and some of these cells that escape the light can move back into the lighted region. We observe that particles starting at the same point at t = 0 can develop spatio-temporally patterned F(t) and G(t) fields; more so, if we compare particles that start at different points in space at t = 0. Specifically, particles may be considered trapped if F(t) ≪ 1 and G(t) ≫ 1. In general increasing or accelerates this process while increasing reduces the effect.
Figure 10.
Histogram and spatio-temporal distributions of 104 test cells that start within the illuminated region of extent RL = 10. Here , and . The density of cells is constant at t = 0 (top and bottom, red dots) and each cell starts with values F = 1 and G = 1. We track F(t) and G(t) of the ensemble of cells as a function of time and plot the distribution in terms of cell numbers at three time instances T = 2, 6 and 10. These are not ensemble averaged results and represent just one specific realization; nonetheless, we expect these results to be illustrative of the spatial heterogeneities that develop due to light-mediated effects on the diffusion coefficients. (Online version in colour.)
Finally, we also investigated how test cells may escape the illuminated region when they start at values away from the centre. Without loss of generalization—due to the radial symmetry of the incident light field—equations (4.3)–(4.7) were solved with the initial condition x(0) = R0 < RL and y(0) = 0. Trajectories were tracked until a final (dimensionless) time τ; thus in this way both finite light extent as well as finite exposure time were investigated. The average first escape time (conditional average) of test particles that reach RL for times t ≤ τ was then calculated. The result was then studied as a function of τ. Between 104 and 106 trajectories were computed with particles starting from each fixed point R0 with other parameters held constant. For each trajectory, whenever a simulated particle reaches the light field threshold radius RL or the maximum time is reached, the simulation of that particle ends. Only the particles that escape light field within the time limit are considered. The average escape time is the sum of the escape time of all particles that escaped divided by the total number of particles that escaped. Figure 11 summarizes our results for simulations with 104 cells started at R0 = RL/2, where RL = 10. We explored the effects of and on the escape time for the three windows τ = 10, 20 and 30. Note that higher values of τ enable more particles to escape but the mean escape time correspondingly increases.
Figure 11.
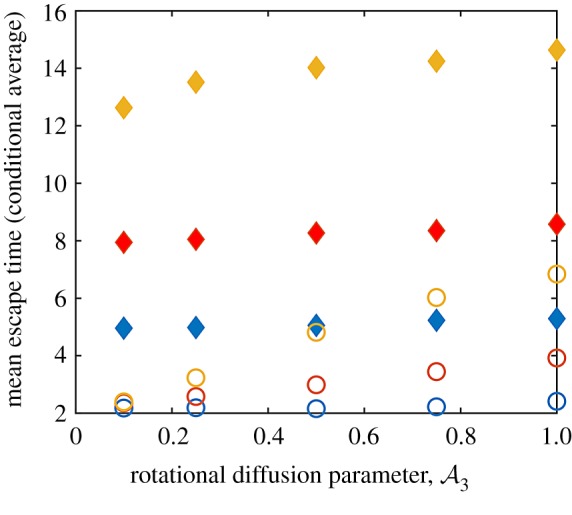
The relationship between , exposure time τ and the escape time for particles that start off-centre. Here the initial conditions are X(0) = 5 and Y(0) = 0 and integrations are conducted for a time window (in dimensionless terms) τ. Whenever a simulated cell reaches the edge of the illuminated region—a circle with radius RL = 10 centred at the origin—the simulation of that particle ends and the time taken by the cell to reach the edge is noted. Cells that remain within the illuminated region are not considered. The (conditional) escape time is then calculated. Unfilled circles correspond to and filled diamonds to . In terms of colours, blue data points are for τ = 10, red data points are for τ = 20 and yellow data points correspond to τ = 50. N = 104, Δt = 10−3, τ = (10, 20, 50) and . (Online version in colour.)
Taken together, figures 8–11 and electronic supplementary material, figure S4, suggest that were one to simulate many non-interacting test cells starting at various points of space, the spatio-temporal pattern of deactivation combined with any intercell variations in will impact the ultimate fate of the cell. Variations in bacterial spreading distances may arise in a realistic population of cells featuring a distribution of self-propulsion speeds. Subpopulations of bacteria corresponding to the fastest moving cells may escape from the exposed region. While these results provide a start, a careful consideration of aligning and hydrodynamic interactions is required to fully explore the manner in which semi-paralysed and resistant cells in the quenched region may escape the light.
5. Summary and perspectives
Previous work has highlighted the effect of light exposure—especially that of UV light—on biomolecular and biochemical mechanisms underlying propulsion in free swimming planktonic bacteria. Here, we presented work that complements these single-cell experiments by analysing the effects of light exposure on collective motility in swarming Serratia marcescens. In the absence of exposure, the swarming bacteria exhibit collective flows with significant intermittent vorticity and streaming motions [33]. When exposed to wide-spectrum light, collective motility in the swarm can be severely impacted depending on two critical parameters—light intensity and duration of exposure. At low exposure levels, swarms are unaffected by light and maintain long-range collective motions. For sufficiently intense exposures, bacteria are rendered immobile and paralysed, an effect that is either reversible or irreversible, depending on the exposure level. For long exposure times or at high intensities, exposed bacteria become paralysed and form aligned and jammed clusters. The effective size of the quenched region increases with time and saturates to slightly less than the extent of the illuminated region. We observe that the quenched phase with irreversible impairment of motility occurs for beyond a critical value of illumination power and requires a minimum exposure time. Post-exposure, active bacteria dislodge exposed bacteria from these caged configurations with initial dissolution rates strongly dependent on duration of exposure.
Small regions of immobile bacteria can block space accessible to swarms and trap motile bacteria thus preventing them from escaping the light. Bacterial populations in nature typically feature cells with a distribution of properties. This raises the possibility that the subpopulations of exposed bacteria corresponding to the fastest moving cells that are predisposed to UV resistance may escape from the exposed region. Reestablishing collective motility, and upon subsequent cell division, these cells may trigger the emergence of resistant strains. Our experiments also suggest that activity combined with effects of Brownian noise could lead to enhanced alignment of neighbouring cells. Thus, fast-moving cells could sometimes surprisingly end up in jamming states. We thus propose that the role of motility is subtler than is evident at first sight and that exposure time is as important as light intensity in determining the rate at which the quenched domain is eroded by active bacteria.
A natural extension of our experiments would be to systematically isolate the effects of light on properties controlling swarm survival and swarm virulence such as cell–cell interactions—as well as active/passive cell–particle interactions [45]. Experiments using filters that allow for studies of wavelength-dependent immobilization at the single-cell level and at the collective level will provide significant insight in this regard. Detailed agent-based Brownian dynamics simulations that account for the steric interactions and hydrodynamic interactions will both guide as well as aid in the interpretation of these experiments.
Supplementary Material
Supplementary Material
Supplementary Material
Supplementary Material
Supplementary Material
Supplementary Material
Acknowledgements
We would like to thank an anonymous reviewer for the suggestion to use the ImageJ plugin Directional J.
Endnotes
An equivalent metric can be obtained from intensity fluctuations rather than from PIV. Tracing un-averaged boundary positions from the image intensity fluctuations |ΔI*|, we estimated the effective size of the quenched region. Comparing results, we found that the calculated extent of the quenched region obtained from using the velocity field is approximately 5–10 μm less than that obtained from using the intensity fluctuation fields. This difference is attributed to differences between the variables being averaged (density fluctuations versus velocity fields). The inset in figure 5a illustrates the asymmetry and extent of boundaries thus obtained.
We also observe aligning behaviour in mixtures of motile and immotile bacteria grown on agar under non-swarming conditions. When multiple moving bacteria encounter stuck or sluggish bacteria, they orient and form aligned flocks (clusters) that either push through the obstacle displacing it or move around it.
Data accessibility
Relevant data are available from the authors upon request.
Authors' contributions
A.G., A.E.P. and P.E.A. conceived the study. A.E.P. performed the experiments. A.G. and A.E.P. analysed the data and wrote the manuscript. A.G. designed the simulation. J.Y. performed simulations of the model and analysed the results. All authors approve the submission.
Competing interests
We declare we have no competing interests.
Funding
A.E.P. was supported by an NSF Graduate Research Fellowship. P.E.A. acknowledges funds from NSF-DMR-1104705 and NSF-CBET-1437482. A.G. acknowledges funds from UC 2018 Senate CORE Award from the University of California, Merced.
References
- 1.Alberti L, Harshey RM. 1990. Differentiation of Serratia marcescens 274 into swimmer and swarmer cells. J. Bacteriol. 172, 4322–4328. ( 10.1128/jb.172.8.4322-4328.1990) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Harshey RM. 2003. Bacterial motility on a surface: many ways to a common goal. Annu. Rev. Microbiol. 57, 249–273. ( 10.1146/annurev.micro.57.030502.091014) [DOI] [PubMed] [Google Scholar]
- 3.Verstraeten N. 2008. Living on a surface: swarming and biofilm formation. Trends Microbiol. 16, 496–506. ( 10.1016/j.tim.2008.07.004) [DOI] [PubMed] [Google Scholar]
- 4.Copeland MF, Weibel DB. 2009. Bacterial swarming: a model system for studying dynamic self-assembly. Soft Matter 5, 1174–1187. ( 10.1039/b812146j) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Darnton NC, Turner L, Rojevsky S, Berg HC. 2010. Dynamics of bacterial swarming. Biophys. J. 98, 2082–2090. ( 10.1016/j.bpj.2010.01.053) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Turner L, Zhang R, Darnton NC, Berg HC. 2010. Visualization of flagella during bacterial swarming. J. Bacteriol. 192, 3259–3267. ( 10.1128/JB.00083-10) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Kearns DB. 2010. A field guide to bacterial swarming motility. Nat. Rev. Microbiol. 8, 634–644. ( 10.1038/nrmicro2405) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Harshey RM, Patridge JD. 2015. Shelter in a swarm. J. Mol. Biol. 427, 3683–3694. ( 10.1016/j.jmb.2015.07.025) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Steager EB, Kim CB, Kim MG. 2008. Dynamics of pattern formation in bacterial swarms. Phys. Fluids 20, 073601 ( 10.1063/1.2953245) [DOI] [Google Scholar]
- 10.Butler MT, Wang Q, Harshey RM. 2010. Cell density and mobility protect swarming bacteria against antibiotics. Proc. Natl Acad. Sci. USA 8, 3776–3781. ( 10.1073/pnas.0910934107) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Roth D, Finkelshtein A, Ingham C, Helman Y, Sirota-Madi A, Brodsky L, Ben-Jacob E. 2013. Identification and characterization of a highly motile and antibiotic refractory subpopulation involved in the expansion of swarming colonies of Paenibacillus vortex. Environ. Microbiol. 15, 2532–2544. ( 10.1111/1462-2920.12160) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Lai S, Trembley J, Deziel E. 2009. Swarming motility: a multicellular behaviour conferring antimicrobial resistance. Environ. Microbiol. 11, 126–136. ( 10.1111/j.1462-2920.2008.01747.x) [DOI] [PubMed] [Google Scholar]
- 13.Chen C, Liu S, Shi X, Chate H, Wu Y. 2017. Weak synchronization and large-scale collective oscillation in dense bacterial suspensions. Nature 542, 210–214. ( 10.1038/nature20817) [DOI] [PubMed] [Google Scholar]
- 14.Berg HC, Brown DA. 1972. Chemotaxis in Escherichia coli analysed by three-dimensional tracking. Nature 239, 500–504. ( 10.1038/239500a0) [DOI] [PubMed] [Google Scholar]
- 15.Berg HC. 2008. E. coli in motion. Berlin, Germany: Springer. [Google Scholar]
- 16.Wadhams GH, Armitage JP. 2004. Making sense of it all: bacterial chemotaxis. Nat. Rev. Mol. Cell Biol. 5, 1024–1037. ( 10.1038/nrm1524) [DOI] [PubMed] [Google Scholar]
- 17.Berg HC, Anderson RA. 1973. Bacteria swim by rotating their flagellar filaments. Nature 245, 380–382. ( 10.1038/245380a0) [DOI] [PubMed] [Google Scholar]
- 18.Patteson AE, Gopinath A, Goulian M, Arratia PE. 2015. Running and tumbling with E. coli in polymeric solutions. Sci. Rep. 5, 15761 ( 10.1038/srep15761) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Taylor BL, Koshland DE Jr. 1975. Intrinsic and extrinsic light responses of Salmonella typhimurium and Escherichia coli. J. Bacteriol. 123, 557–569. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Wright S, Walia B, Parkinson JS, Khan S. 2006. Differential activation of Escherichia coli chemoreceptors by blue-light stimuli. J. Bacteriol. 188, 3961–3971. ( 10.1128/JB.00149-06) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Steager E, Kim C-B, Patel J, Bith S, Naik C, Reber L, Kim MJ. 2007. Control of microfabricated structures powered by flagellated bacteria using phototaxis. Appl. Phys. Lett. 90, 263901 ( 10.1063/1.2752721) [DOI] [Google Scholar]
- 22.Conley MP, Berg HC. 1984. Chemical modification of Streptococcus flagellar motors. J. Bacteriol. 158, 832–843. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Kodoth V, Jones M. 2015. http://medicalmate.gr/img/cms/UVC, 1.
- 24.Alonso-Saez L, Gasol JM, Lefort T, Hofer J, Sommaruga R. 2006. Effect of natural sunlight on bacterial activity and differential sensitivity of natural bacterioplankton groups in northwestern Mediterranean coastal waters. Appl. Environ. Microbiol. 72, 5806–5813. ( 10.1128/AEM.00597-06) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Sharp DG. 1940. The effects of ultraviolet light on bacteria suspended in air. J. Bacteriol. 39, 535. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Said MB, Khefacha S, Maalej L, Daly I, Hassen A. 2011. Effect of ultraviolet, electromagnetic radiation subtype C (UV-C) dose on biofilm formation by Pseudomonas aeruginosa. Afr. J. Microbiol. Res. 5, 4353–4358. ( 10.5897/ajmr11.449) [DOI] [Google Scholar]
- 27.Li B, Logan BE. 2005. The impact of ultraviolet light on bacterial adhesion to glass and metal oxide-coated surface. Colloids Surf. B Biointerfaces 41, 153–161. ( 10.1016/j.colsurfb.2004.12.001) [DOI] [PubMed] [Google Scholar]
- 28.Abana CM. et al. 2017. Characterization of blue light irradiation effects on pathogenic and nonpathogenic Escherichia coli. Microbiologyopen 6, e00466 ( 10.1002/mbo3.466) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Dai T, Vrahas MS, Murray CK, Hamblin MR. 2012. Ultraviolet C irradiation: an alternative antimicrobial approach to localized infections? Expert Rev. Anti Infect. Ther. 10, 185–195. ( 10.1586/eri.11.166) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Lu S, Bi W, Wu X, Xing B, Yeow EKL. 2013. Loss of collective motion in swarming bacteria undergoing stress. Phys. Rev. Lett. 111, 208101 ( 10.1103/PhysRevLett.111.208101) [DOI] [PubMed] [Google Scholar]
- 31.Dai T. et al. 2013. Blue light rescues mice from potentially fatal Pseudomonas aeruginosa burn infection: efficacy, safety, and mechanism of action. Antimicrob. Agents Chemother. 57, 1238–1245. ( 10.1128/AAC.01652-12) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Pei S, Inamadar AC, Adya KA, Tsoukas MM. 2015. Light-based therapies in acne treatment. Indian Dermatol. Online J. 6, 145 ( 10.4103/2229-5178.156379) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Patteson AE, Gopinath A, Arratia PE. 2018. The propagation of active-passive interfaces in bacterial swarms. Nat. Commun. 9, 5373 ( 10.1038/s41467-018-07781-y) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Patteson AE, Gopinath A, Arratia PE. 2016. Active colloids in complex fluids. Curr. Opin. Colloid Interface Sci. 21, 86–96. ( 10.1016/j.cocis.2016.01.001) [DOI] [Google Scholar]
- 35.Bensity S, Ben-Jacob E, Ariel G, Be’er A. 2015. Antibiotic-induced anomalous statistics of collective bacterial swarming. Phys. Rev. Lett. 114, 018105 ( 10.1103/PhysRevLett.114.018105) [DOI] [PubMed] [Google Scholar]
- 36.Thielicke W, Stamhuis E. 2014. PIVlab—towards user-friendly, affordable and accurate digital particle image velocimetry in MATLAB. J. Open Res. Softw. 2, 1 ( 10.5334/jors.bl) [DOI] [Google Scholar]
- 37.Rezakhaniha R, Agianniotis A, Schrauwen JTC, Griffa A, Sage D, Bouten CVC, van de Vosse FN, Unser M, Stergiopulos N. 2012. Experimental investigation of collagen waviness and orientation in the arterial adventitia using confocal laser scanning microscopy. Biomech. Model. Mechanobiol. 11, 461–473. ( 10.1007/s10237-011-0325-z) [DOI] [PubMed] [Google Scholar]
- 38.Duclos G, Garcia S, Yevicka HG, Silberzan P. 2014. Perfect nematic order in confined monolayers of spindle-shaped cells. Soft Matter 10, 2346–2353. ( 10.1039/C3SM52323C) [DOI] [PubMed] [Google Scholar]
- 39.Wu Y, Berg HC. 2011. Water reservoir maintained by cell growth fuels the spreading of a bacterial swarm. Proc. Natl Acad. Sci. USA 109, 4128–4133. ( 10.1073/pnas.1118238109) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Volpe G, Gigan S. 2014. Simulation of the active Brownian motion of a microswimmer. Am. J. Phys. 82, 659–664. ( 10.1119/1.4870398) [DOI] [Google Scholar]
- 41.Wilson LG, Martinez VA, Schwarz-Linek J, Tailleur J, Bryant G, Pusey PN, Poon WCK. 2011. Differential dynamic microscopy of bacterial motility. Phys. Rev. Lett. 106, 018101 ( 10.1103/PhysRevLett.106.018101) [DOI] [PubMed] [Google Scholar]
- 42.Gopinath A, Armstrong RC, Brown RA. 2006. Second order sharp-interface and thin-interface asymptotic analyses and error minimization for phase-field descriptions of two-sided dilute binary alloy solidification. J. Cryst. Growth 291, 272–289. ( 10.1016/j.jcrysgro.2006.03.001) [DOI] [Google Scholar]
- 43.Gopinath A, Armstrong RC, Brown RA. 2004. Observations on the eigenspectrum of the linearized Doi equation with application to numerical simulations of liquid crystal suspensions. J. Chem. Phys. 121, 6093–6094. ( 10.1063/1.1785148) [DOI] [PubMed] [Google Scholar]
- 44.Gopinath A, Mahadevan L, Armstrong RC. 2006. Transitions to nematic states in homogeneous suspensions of high aspect ratio magnetic rods. Phys. Fluids 18, 028102 ( 10.1063/1.2167811) [DOI] [Google Scholar]
- 45.Patteson AE, Gopinath A, Purohit PK, Arratia PE. 2016. Particle diffusion in active fluids is non-monotonic in size. Soft Matter 12, 2365–2372. ( 10.1039/C5SM02800K) [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Relevant data are available from the authors upon request.