Mononuclear Manganese(III) Superoxo Complexes: Synthesis, Characterization, and Reactivity

Abstract

Metal–superoxo species are typically proposed as key intermediates in the catalytic cycle of dioxygen activation by metalloenzymes involving different transition metal cofactors. In this regard, while a series of Fe–, Co–, and Ni–superoxo complexes have been reported to date, well-defined Mn–superoxo complexes remain rather rare. Herein, we report two mononuclear Mn^III–superoxo species, Mn(BDPP)(O₂^•–) (2, H₂BDPP = 2,6-bis((2-(S)-diphenylhydroxylmethyl-1-pyrrolidinyl)methyl)pyridine) and Mn(BDP^BrP)(O₂^•–) (2′, H₂BDP^BrP = 2,6-bis((2-(S)-di(4-bromo)phenylhydroxyl-methyl-1-pyrrolidinyl)methyl)pyridine), synthesized by bubbling O₂ into solutions of their Mn^II precursors, Mn(BDPP) (1) and Mn(BDP^BrP) (1′), at −80 °C. A combined spectroscopic (resonance Raman and electron paramagnetic resonance (EPR) spectroscopy) and computational study evidence that both complexes contain a high-spin Mn^III center (S_Mn = 2) antiferromagnetically coupled to a superoxo radical ligand (S_OO• = 1/2), yielding an overall S = 3/2 ground state. Complexes 2 and 2′ were shown to be capable of abstracting a H atom from 2,2,6,6-tetramethyl-1-hydroxypiperidine (TEMPO-H) to form Mn^III–hydroperoxo species, Mn(BDPP)(OOH) (5) and Mn(BDP^BrP)(OOH) (5′). Complexes 5 and 5′ can be independently prepared by the reactions of the isolated Mn^III-aqua complexes, [Mn(BDPP)(H₂O)]OTf (6) and [Mn(BDP^BrP)(H₂O)]OTf (6′), with H₂O₂ in the presence of NEt₃. The parallel-mode EPR measurements established a high-spin S = 2 ground state for 5 and 5′.

Short abstract

Two mononuclear Mn^III−superoxo complexes, synthesized by bubbling O₂ into solutions of their Mn^II precursors at −80 °C and well-characterized spectroscopically and computationally, were shown to be capable of abstracting a H atom from TEMPO-H to form Mn^III−hydroperoxo species.

Introduction

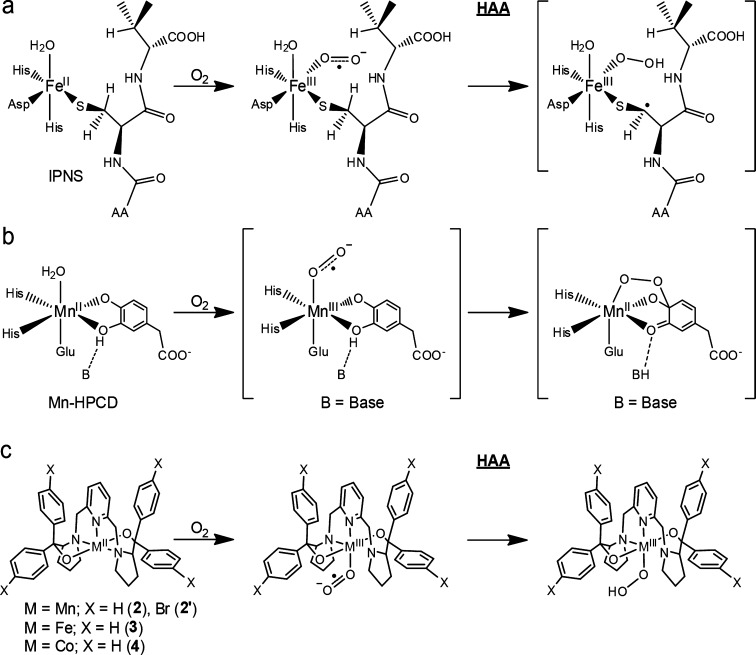
Functionalization of organic compounds using O₂, a green oxidant, represents an essential process in nature.¹ Despite having favorable thermodynamic driving forces, direct substrate oxygenations usually have to traverse high kinetic barriers arising from the triplet-to-singlet spin inversion of O₂.¹ Nature has developed a diverse array of enzymes that contain transition metal cofactors to activate O₂; thus, metalloenzyme-catalyzed reactions typically proceed with unrivaled efficiencies under ambient conditions. The majority of O₂-activating wild-type enzymes utilize Fe and Cu in their active sites, whereas a few of them feature Mn and Ni. To the best of our knowledge, none of them incorporates Co. Catechol dioxygenases play a pivotal role in the global carbon cycle because they catalyze cleavage of aromatic rings and hence reclaim large quantities of carbon sequestered in ubiquitous aromatic compounds in nature.² Two forms of homoprotocatechuate 2,3-dioxygenases with the respective active-site metal ions being Fe^II and Mn^II have been isolated, namely, Fe-HPCD from Brevibacterium fuscum(3) and Mn-MndD from Arthrobacter globiformis.⁴ Surprisingly, the native enzymes, Fe-HPCD and Mn-MndD, and their artificial variants, Mn-HPCD, Fe-MndD, and Co-HPCD, generated by reconstituting the native enzymes with nonphysiological metal ions, all exhibit comparable catalytic activity.⁵ Therefore, it has long been believed that transition-metal-catalyzed oxidative transformations share common mechanistic features, in which O₂ initially binds to a reduced metal center to form an oxidized metal–superoxo species, which functions as the reagent to perform subsequent chemistry.⁶ Isopenicillin N synthase (IPNS), an iron-dependent nonheme enzyme, which catalyzes formation of isopenicillin N en route to a number of important antibacterial drugs,⁷ serves as a prototypical example for the proposed mechanism. O₂ association at the Fe^II center in IPNS has been experimentally shown to yield a Fe^III–superoxo intermediate, which initiates hydrogen atom abstraction (HAA) to generate presumably a hydroperoxo species (Scheme 1a).⁸

Scheme 1. Mechanism of Dioxygen Activation by (a) IPNS, (b) Mn-HPCD, and (c) Model Complexes Supported by a BDPP^2– or BDP^BrP^2– Ligand.

Notably, Fe^III– and Co^III–superoxo species were detected in the His200Asn mutant of Fe-HPCD and Co-HPCD in the turnover of an electron-poor substrate, 4-nitocatechol.⁹ Upon mixing of O₂ to Mn-HPCD, two intermediates were trapped and characterized by electron paramagnetic resonance (EPR) spectroscopy. They were assigned to a Mn^III ion coordinated by an unidentified radical, assumed to be a superoxo, and a Mn^II–alkylperoxo species (Scheme 1b), but the conclusive evidence remains elusive.¹⁰ Furthermore, Mn^III–superoxo intermediates have been invoked in a series of Mn-catalyzed chemical transformations on the basis of the measurements using mass spectrometry,¹¹ and the existence of the putative Mn–superoxo species was postulated by investigations using low-temperature absorption spectroscopy¹² and reactivity studies.¹³

In addition to several synthetic nonheme Fe^III– and Co^III–superoxo models,¹⁴⁻¹⁸ a Mn^III–superoxo complex, [Mn^III(O₂)(OH₂)L]²⁺ (L = [5,11,17,23-tetrakis(trimethylammonium)-25,26,27,28-tetrahydroxylcalix[4]arene)]), has been crystallographically characterized to feature an unusual linear Mn–O₂ arrangement.¹⁹ Its electronic structure has been probed by EPR and resonance Raman (rR) spectroscopy, and [Mn^III(O₂)(OH₂)L]²⁺ was shown to exhibit catalytic reactivity toward alkene epoxidation. Unexpectedly, the determined Mn^III–O₂ bond distance (2.444 Å) is considerably longer than that of the trans Mn–OH₂ bond (2.210 Å). Notably, the Mn^III–O bond lengths found for Mn–(O₂), Mn–OOR, and Mn–OR (R = H, Me, Ph, Ph-^pNO₂) species range from 1.832 to 1.901 Å (Table S1). Therefore, more work on well-defined Mn^III–superoxo complexes remains highly desirable due to the important roles played by such species in chemistry and biology.

Our earlier work reported synthesis and reactivity of nonheme Fe^III– and Co^III–superoxo complexes, Fe(BDPP)(O₂^•–) (3) and Co(BDPP)(O₂^•–) (4) (H₂BDPP = 2,6-bis((2-(S)-diphenylhydroxylmethyl-1-pyrrolidinyl)methyl)pyridine).^14,16 Complexes 3 and 4 were synthesized by oxygenating the corresponding divalent metal precursors and found to be capable of performing HAA reactions (Scheme 1c). The aforementioned mechanistic hypothesis for O₂ activation prompted us to test the accessibility of the Mn^III–superoxo congeners via the same reaction route. To this end, we herein present the synthesis of two well-defined Mn^III–superoxo species and their spectroscopic characterizations as well as reactivity studies.

Results and Disscussion

Synthesis and Characterization of Mn^III–Superoxo Complexes

Bubbling O₂ into THF or CH₂Cl₂ solutions of Mn(BDPP) (1) and Mn(BDP^BrP) (1′) (H₂BDP^BrP = 2,6-bis((2-(S)-di(4-bromo)phenylhydroxyl-methyl-1-pyrrolidinyl)methyl)pyridine) at −80 °C results in a color change from pale yellow to deep yellow, due to the growth of three absorption bands at 370, 450, and 740 nm (Figures S4 and 1). This observation hints at the formation of Mn–O₂ adducts, Mn(BDPP)(O₂^•–) (2) and Mn(BDP^BrP)(O₂^•–) (2′). Our repeated attempts to obtain single crystals of 2 and 2′ were foiled due to their gradual decomposition even at −80 °C.

Figure 1.

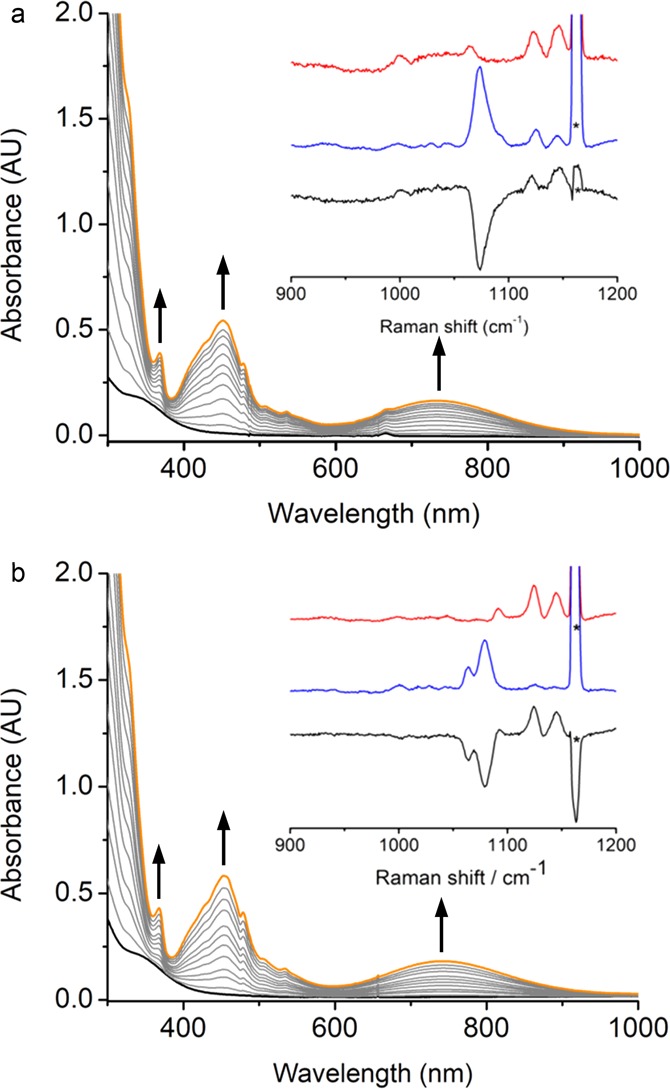
UV–vis spectra change for formation of (a) 2 and (b) 2′. Complex 2 or 2′ (orange) from a reaction of 1 or 1′ (black, 0.4 mM) with O₂ in THF at −80 °C. Inset: rR spectra of 2 or 2′ (7.5 mM) in CH₂Cl₂ (λ_ex 457 nm, 10 mW, 77 K; red line: 2-¹⁶O or 2′-¹⁶O, blue line: 2-¹⁸O or 2′-¹⁸O, black line: difference spectrum 2-¹⁶O – 2-¹⁸O or 2′-¹⁶O – 2′-¹⁸O). Asterisks denote solvent peaks.

The rR spectra (λ_ex at 457 nm) of 2-¹⁶O in CH₂Cl₂ reveal a Fermi doublet at 1125 and 1145 cm^–1 (1135 cm^–1 on average; see the inset in Figure 1a), which shifts to 1073 cm^–1 upon ¹⁸O substitution (99 atom %). The signals at 1125 and 1145 cm^–1 in the 2-¹⁸O rR spectrum originate from trace ¹⁶O₂ contamination presumably coming from air during the sample preparation. The observed isotope shifts (62 cm^–1) are close to the value for a diatomic O–O bond stretching mode (ν_O–O) estimated by Hooke’s law. In the case of 2′, its ¹⁶O rR spectrum (the inset in Figure 1b) also shows a doublet with exactly the same frequencies as those detected for 2-¹⁶O. Interestingly, its ¹⁸O rR spectrum also demonstrates a different doublet at 1064 and 1078 cm^–1. The relative intensities of the two peaks of a given doublet measured for 2′-¹⁶O or 2′-¹⁸O are different, which essentially rules out the possibility that there exists two isomers for 2′. On the basis of these observations, we attributed the two peaks observed for 2′-¹⁶O and 2′-¹⁸O to Fermi doublets. For the related Fe– and Cu–superoxo complexes, Fermi doublets arising from O–O stretching vibrations were typically found for either ¹⁶O or ¹⁸O samples,^15b,20a but detection of both ¹⁶O and ¹⁸O Fermi doublets has been reported for a structurally characterized diiron(III)-μ-1,2-peroxo complex.^20b The O–O stretching frequencies detected for 2 and 2′ closely match those reported for well-characterized metal–superoxo complexes (Table 1), thereby evidencing that 2 and 2′ accommodate a superoxo ligand.

Table 1. O–O Stretching Frequencies of Mononuclear Metal Superoxo Complexes^a.

complex	ν(16O–16O), cm–1	ν(18O–18O), cm–1	Δν(O–O), cm–1	ref
2	1125, 1145	1073	62	this work
2′	1125, 1145	1064, 1078	61	this work
[MnIIIL(O2•–)(H2O)](PF6)2	1124	1035	89	(19)
3	1125	1062	63	(14)
4	1135	1070	65	(16)
[FeIII(TAML)(η2-O2•–)]2–	1260	1183	77	(15)
FeIII(TpMe2)(LPh)(O2•–)	1168	1090	78	(17)
CoIII(TpMe2)(LPh)(η1-O2•–)	1150	1090	60	(17)
CoIII(salen)(py)(O2•–)	1144	1082	62	(18)
[CuII(TMG3tren)(η1-O2•–)]+	1117	1059	58	(21)
[CuII(6-pivTPA)(O2•–)]+	1130	1067	63	(22)
[CrIII (14-TMC)(η1-O2•–)(Cl)]+	1170	1104	66	(23)

^aL = 5,11,17,23-tetrakis(trimethylammonium)-25,26,27,28-tetrahydroxycalix[4]arene; TAML = 3,3,6,6,9,9-hexametyl-2,5,7,10-tetraoxo-3,5,6,7,9,10-hexahydro-2H-benzo[e][1,4,7,10]tetraazacyclotridecine-1,4,8,11-tetraide; Tp^Me2 = hydro-tris(3,5-dimethylpyrazolyl)borate; L^Ph = bis(2-N-methylimizadolyl)methylphenylborate; salen = N,N′-ethylene-bis(salicylideneiminato); TMG₃tren = 1,1,1-tris(1-tetramethylguanidino)]ethyl)amine); 6-pivTPA = (6-pivaloyl-amidopyridyl-2-methyl)bis(6-methylpyridyl-2-methyl)amine; 14-TMC = 1,4,8,11-tetramethyl-1,4,8,11-tetraazacyclo-tetradecane.

In the following, we focus our discussion on 2′ because it has higher stability and solubility than those of 2 in MeTHF, and we summarize similar results of 2 in the Supporting Information. The X-band EPR spectrum of 2′ in MeTHF at 6.3 K (Figure 2) is typical for near-axial quartet systems with a sizable axial zero-field splitting D and marginal rhombicity E/D (|2D| ≫ 0.3 cm^–1, and E/D ≈ 0). Specifically, the resonances of g_eff,⊥ ≈ 4 and g_eff,|| ≈ 2 originate from the transition within its M_S ≈ ± 1/2 Kramers doublet. Consequently, the weak sextet around 115 mT can be attributed to the edge of the intra-Kramers doublet spectrum (g_eff,|| ≈ 6 and g_eff,⊥ → 0) for the M_S ≈ ± 3/2 levels. The nicely resolved six lines at the g_eff,|| ≈ 2 and 6 and g_eff,⊥ ≈ 4 regions are due to the hyperfine coupling with ⁵⁵ Mn (I = 5/2). From the relative intensity of the g_eff ≈ 4 and 6 signals, the effective splitting 2D′ (D′ = 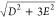of the quartet ground state was estimated to be −10.4(5) cm^–1 (see the inset in Figure 2).

Figure 2.

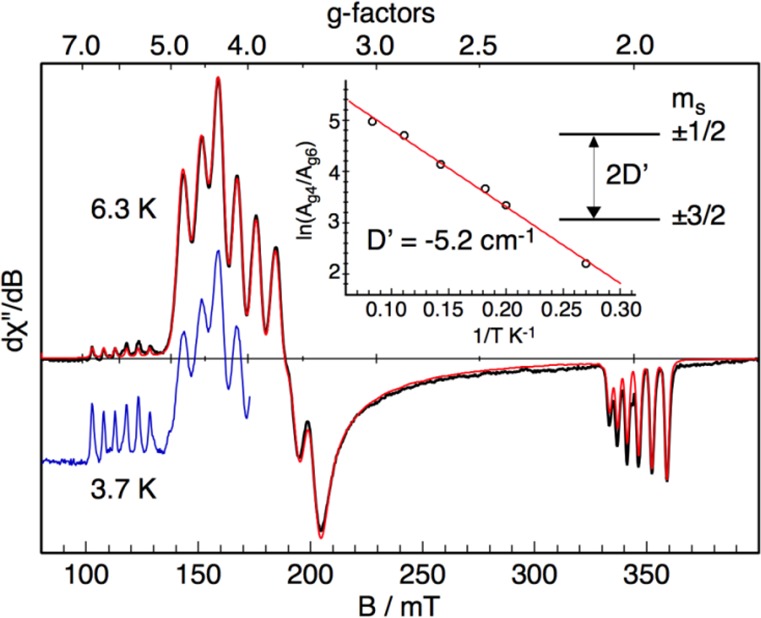
X-band EPR spectra of 2′ (2 mM) recorded at 6.3 K (black) and at 3.7 K (blue), and the simulation for 6.3 K (red). The simulation yields the following parameters: g_iso = 1.997(10), D = −5.2(5) cm^–1, E/D = 0.03(1), and |A_x,y,z| = 234(10), 225(10), and 142(10) MHz. Note that the sign of the A values cannot determined experimentally. The inset shows the logarithm of the intensity ratio of the derivative signals g_eff ≈ 4 and g_eff ≈ 6 as a function of inverse temperature and a fit with the corresponding Boltzmann function (red line). Frequency 9.63595 GHz, power 0.2 mW, modulation 100 kHz/0.75 mT.

The experimental EPR spectra of 2′ can be nicely fitted by using a usual spin-Hamiltonian for S = 3/2:

in which g is the intrinsic g matrix and A is the magnetic hyperfine coupling matrix. Double integration of the spectrum revealed nearly quantitative conversion of 1′ to 2′ in a yield of 96 (10)%.

The spectroscopic investigations suggest that 2′ is best formulated as a high-spin Mn^III ion (S_Mn = 2) bound to a O₂^•− radical (S_OO• = 1/2) in an antiferromagnetic fashion yielding an overall quartet ground state (S = 3/2). As we will elaborate below, the exchange interaction in 2′ is in the strong coupling regime. The intrinsic D_Mn and A_Mn values of the Mn^III center in 2′ can be obtained from the effective D and A values determined experimentally for the total spin S = 3/2 ground state by using the relation D = (7/5)D_Mn and A = (6/5)A_Mn.²⁴ The resulting intrinsic values, D_Mn = −3.7 cm^–1 and A_Mn.iso = 167 MHz, fall into the range typically measured for distorted octahedral Mn^III complexes.²⁵ In contrast, an alternative formulation of 2′ as a high-spin Mn^IV complex (S_Mn = 3/2) can be safely ruled out, because well-characterized six-coordinate S = 3/2 Mn^IV compounds rarely feature negative D values and the magnitude of D never exceed 3 cm^–1, whereas negative D values are rather common for high-spin Mn^III complexes in elongated octahedral environments.²⁶ Experimentally, no signals that can be attributed to S = 5/2 have been observed up to 40 K, above which the fast relaxation induces significant line broadening of the EPR spectrum. Therefore, the exchange coupling constant between the high-spin Mn^III center and the superoxo ligand cannot be determined accurately.

Conversion of Mn^III–Superoxo Complexes to Mn^III–Hydroperoxo Complexes

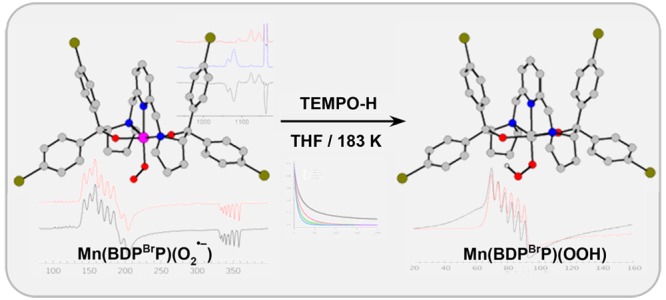
Treating 2 and 2′ with 10 equiv of TEMPO-H in THF at −90 °C resulted in an exponential decay of their signature bands (Figures S7 and 3) and nearly quantitative yields of TEMPO radical (86% for 2, Figure S8; 93% for 2′, Figure S9). Our previous work showed that the reaction of the related Fe^III- and Co^III–superoxo complexes (3 and 4) with H-donor, DHA or TEMPO-H, produced the corresponding hydroperoxo species;^14,16 we thus surmised the products of the similar reactions with 2 and 2′ to be Mn^III–hydroperoxo species, Mn(BDPP)(OOH) (5) and Mn(BDP^BrP)(OOH) (5′). Treating the resulting solutions containing 5 and 5′ with HOTf followed by NaI allowed us to determine the yields of H₂O₂ to be 83% and 81%, respectively (Figures S11b and S12b).²⁷ The final products (Figures S11a and S12a) obtained by the acidified solution of 5 and 5′ were identified as Mn^III-aqua complexes, [Mn(BDPP)(H₂O)]OTf (6) and [Mn(BDP^BrP)(H₂O)]OTf (6′), which were characterized by X-ray crystallography (Figure 4). More importantly, complexes 5 and 5′ can be directly synthesized from the reactions of 6 and 6′ with an excess amount of a 2:1 mixture of H₂O₂ and NEt₃ in THF at −90 °C as monitored by electronic spectroscopy. As shown in Figures S13 and 5, upon addition of the mixture of H₂O₂ and NEt₃, the characteristic absorptions of 6 and 6′ at 460 and 600 nm gradually vanished along with the steady growth of those of 5 and 5′. Our repeated attempts to obtain the O–O vibrational frequencies of 5 and 5′ from rR measurements failed, largely because 5 and 5′ have no intense chromophores in the usual UV–vis region (Figure 3) and the intensity of the O–O stretching signal is too low to be readily detected.

Figure 3.

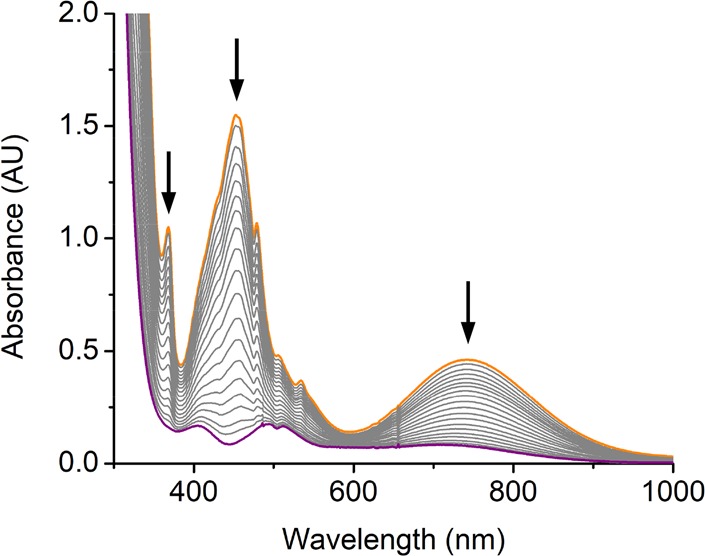
UV–vis spectra change monitored from the reaction of 2′ (orange line, 1 mM) with 10 equiv of TEMPO-H in THF at −90 °C. The purple line represents Mn(BDP^BrP)(OOH) (5′) with four absorption bands at 410, 495, 515, and 720 nm.

Figure 4.

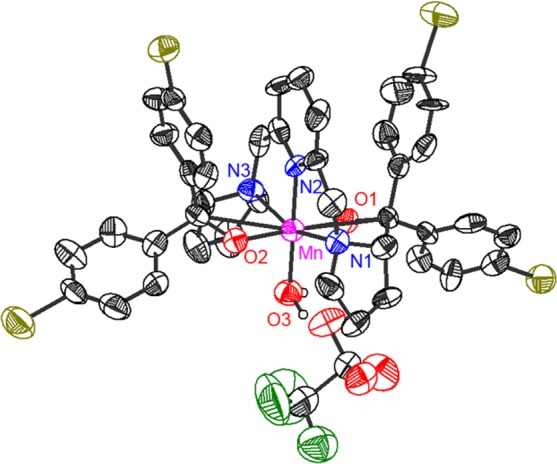
ORTEP presentation of [Mn(BDP^BrP)(H₂O)]OTf (6′). Hydrogen atoms are omitted for clarity. The Mn^III center of 6′ possesses an octahedral coordination environment. The important bond distances and angles of 6′ are as follows: Mn–N₁ = 2.248(7) Å, Mn–N₂ = 2.069(7) Å, Mn–N₃ = 2.255(7) Å, Mn–O₁ = 1.861(5) Å, Mn–O₂ = 1.881(5) Å, Mn–O₃ = 2.023(5) Å; ∠N₁–Mn–N₂ = 77.7(3)°, ∠N₂–Mn–N₃ = 79.1(3)°, ∠N₁–Mn–O₃ = 101.5(3)°, ∠N₃–Mn–O₃ = 101.7(3)°, ∠O₁–Mn–N₂ = 90.7(3)°, ∠O₂–Mn–N₂ = 91.3(2)°, ∠O₁–Mn–O₃ = 90.5(2)°, ∠O₂–Mn–O₃ = 87.5(2)°.

Figure 5.

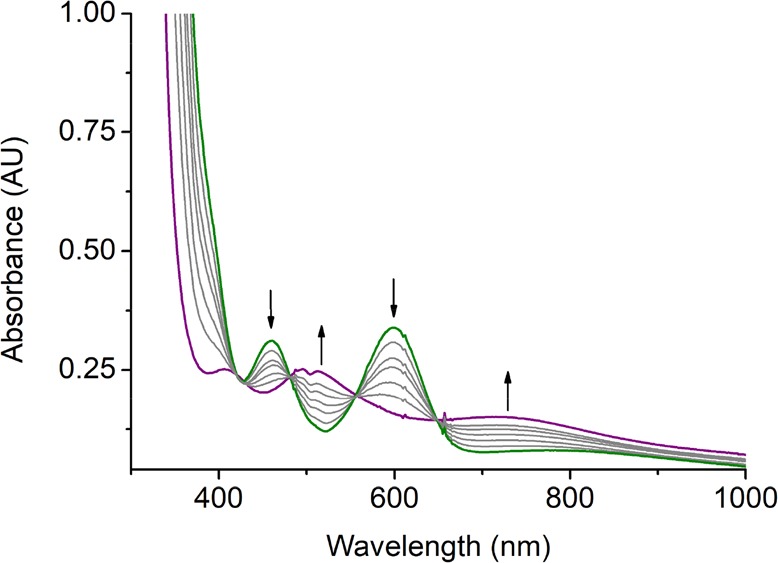
UV–vis spectra change monitored from the reaction of [Mn(BDP^BrP)(H₂O)]OTf (6′) (green line, 1 mM) with an excess amount of a 2:1 mixture of H₂O₂ and NEt₃ in THF at −90 °C. The purple line represents Mn(BDP^BrP)(OOH) (5′).

Figure 6 depicts a parallel-mode X-band EPR spectrum of 5′ in MeTHF at 10 K. Complex 5′ shows a six-line hyperfine pattern at g ∼ 8 that stems from the transition within the |2^±⟩ non-Kramers doublet of an S = 2 spin manifold, thus indicating that 5′ contains a high-spin Mn^III center. Its intensity declines with the temperature; hence, 5′ possesses a negative D value. The fit of the intensity variation as a function of temperature gives D = −3.6(5) cm^–1. The resonance condition for this parallel-mode signal is ℏν = , where δ_±2 ≈ 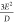, ℏν is the microwave quanta, and θ is the angle between the magnetic field (B) and the z-axis of the D tensor. Moreover, its intensity is proportional to 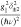. Thus, one cannot simultaneously determine g_|| and δ_±2 values accurately. During the simulation of the EPR spectrum, we therefore only allowed E/D to vary while fixing D to −3.6 cm^–1 and g_iso to 2, the typical g value often found for related high-spin Mn^III complexes.²⁸ A satisfactory simulation yields the following parameters, E/D = 0.09(1) and |A_z| = 119(10) MHz. The broad underlying feature starting from ca. 60 mT is tentatively assigned to a high-spin Mn^III decay product since its relative intensity is dependent on the preparation. The onset of the signal at ca. 150 mT originates from small amount of O₂ in the solution.

Figure 6.

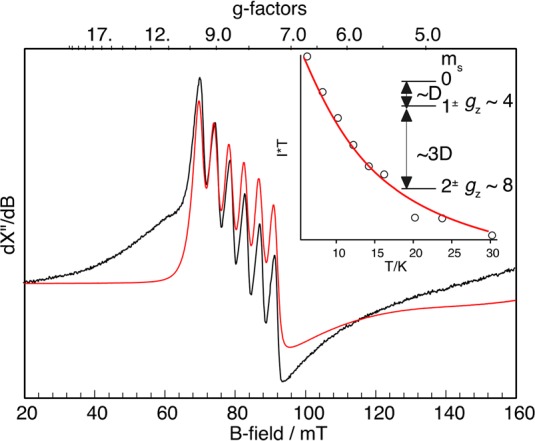
Parallel mode X-band EPR spectrum of 5′ (7.5 mM) recoded at 10 K (black) and the simulation (red). The inset shows signal intensity times temperature versus temperature of g ∼ 8 signal (dots) and a fit with the corresponding Boltzmann function (red line). Frequency 9.396 GHz, power 0.2 mW, and modulation 100 kHz/0.75 mT.

Remarkably, the D and A_z values measured for complex 5′ are nearly identical to the intrinsic values of the Mn^III center found for 2′ (D_Mn = −3.7 cm^–1 and A_Mn,z = 118 MHz), thereby suggesting that the Mn^III centers in both complexes feature a similar electronic structure and are ligated in an analogous coordination environment. All these observations confirm that 5 and 5′ are indeed high-spin Mn^III–hydroperoxo species. Unlike 5 and 5′, 6 and 6′ were found to be EPR-silent in both normal and parallel modes (Figure S10). This finding likely reflects a considerable change in the electronic structure induced by replacing an anionic hydroperoxo ligand with H₂O.

DFT Calculations of 2′ and 5′

In order to better understand the nature of 2′ and 5′, detailed computational studies on 2′ and 5′ were undertaken. Complex 2′ was predicted to have a quartet ground state, and the lowest-energy sextet state in which the high-spin Mn^III center is ferromagnetically coupled to the superoxo ligand is situated at ∼1300 cm^–1 higher in energy. The optimized quartet structure of 2′ features elongated octahedral coordination geometry. The two Mn–N_pyrrolidine bonds along the z direction are substantially longer than all of the metal–ligand bond distances in the equatorial plane (Figure 7). The different metal–ligand bond lengths simply reflect the fact that the equatorial plane consists of three negatively charged O donors and a rigidly chelated N_pyridine atom, whereas there are two neutral N_pyrrolidine donors in the axial direction. In keeping with this reasoning, the Mn^III center features an electron configuration of (d_yz)¹(d_xz)¹(d_xy)¹(d_z²)¹(d_x²–y²)⁰, in which the Mn^III d_x²–y² based molecular orbital is vacant. The calculated O–O distance (1.294 Å) of the O₂ moiety agrees with those found in structurally characterized metal–superoxo complexes (Table S2). Furthermore, one of the two O₂ π* orbitals is doubly occupied, and the other is resided by a β-electron. Such an orbital occupation pattern defines a high-spin Mn^III ion (S_Mn = 2) that is antiferromagnetically coupled to a superoxo radical (S_OO• = 1/2).

Figure 7.

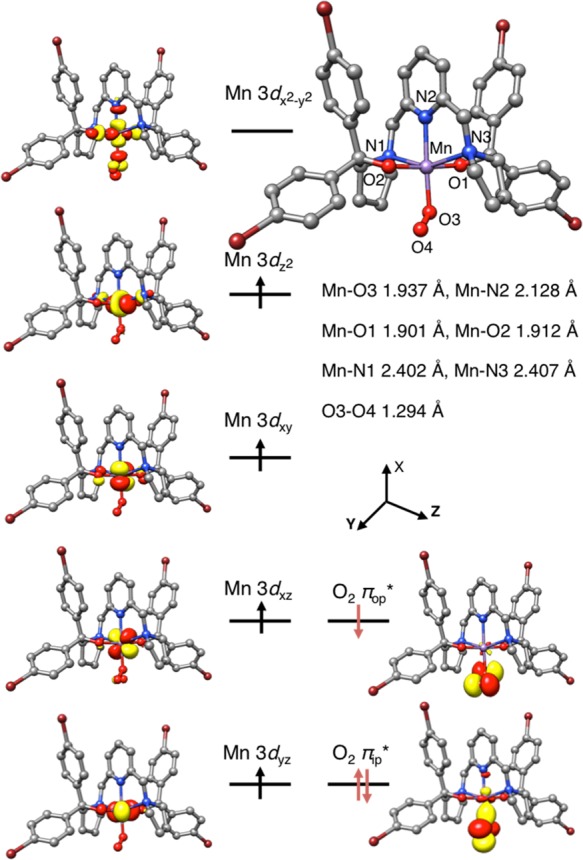
Computed structure of 2′ with key geometric parameters and its schematic molecular orbital diagram.

Complex 5′ also features an elongated octahedral coordination arrangement with the two considerably longer Mn–N_pyrrolidine bonds, similar to that of 2′ (Figure 8). Consequently, the Mn^III centers in both complexes possess the same electron configuration. Relative to 2′, the estimated O–O distance of the OOH unit in 5′ is significantly lengthened to 1.449 Å, a typical O–O bond length observed for metal–hydroperoxo species.¹⁶ Furthermore, the hydroperoxo ligand forms a hydrogen bond with one of the O atom of BDP^BrP, analogous to hydrogen bonding observed in the crystal structure of Co(BDPP)(OOH). Our theoretical results revealed that such interaction stabilizes 5′ by 5.3 kcal/mol relative to another isomer, in which the H atom in the OOH ligand points out of the O2 atom of BDP^BrP. Moreover, the computed spectroscopic parameters for 2′ and 5′ and the O–O stretching frequency for 2′ (1162 cm^–1) match the experimental data within the uncertainty range of the calculations, which further lends credence to the proposed geometric and electronic structures for them (Table S3).

Figure 8.

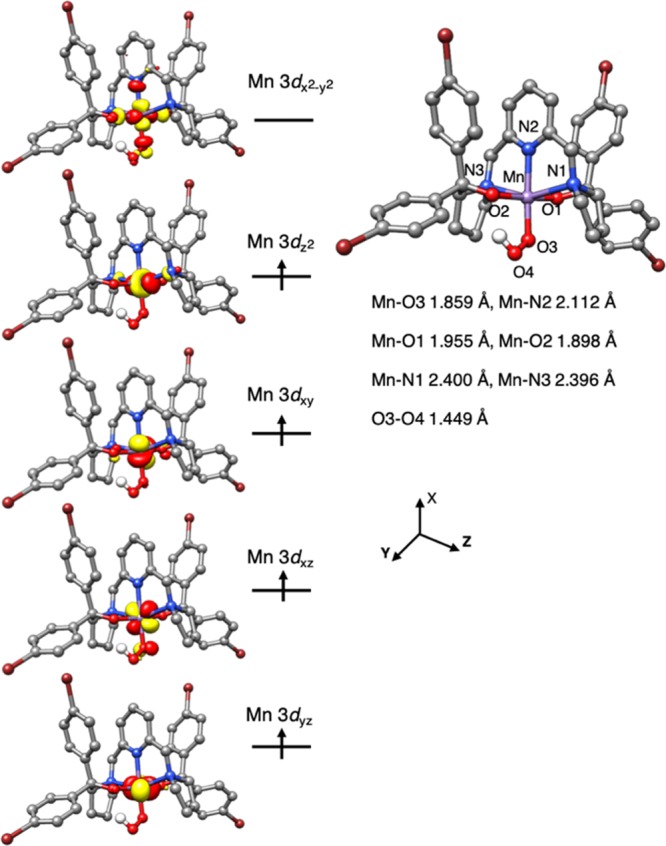
Computed structure of 5′ with key geometric parameters and its schematic molecular orbital diagram.

The weak axial coordination found for the Mn^III centers in complexes 2′ and 5′ is consistent with the observed negative D values and the relative magnitude of the three A components (|A_x| ≈ |A_y| < |A_z|) (for details, see the Supporting Information). In fact, [Mn^III(O₂)(OH₂)L]²⁺ features the same coordination geometry as that of 2′, but the distortion was found along the O₂–Mn–OH₂ axis,¹⁹ because the bowl-shaped calix[4]arene ligand with four phenolate groups predefines an equatorial plane and forces the superoxo ligand to coordinate the Mn^III center in the axial position.

Reactivity Comparisons of O₂ Activations by Mn, Fe, and Co Counterparts

Our findings reveal that 2 and 2′ can be prepared by using the same synthetic route as that for their Fe and Co counterparts, 3 and 4.^14,16 However, under the same experimental conditions, formation of 4 (∼0.26 min^–1 in THF, even slower rate in CH₂Cl₂) is at least 10-fold slower than that of 2′ and 3, a situation similar to that observed for O₂ binding to Co- and Fe-HPCD.⁹ Unexpectedly, the relative formation rates of 2′, 3, and 4 do not follow the trend of the redox potentials of their divalent precursors ([Mn^II(BDPP)]^0/+, −0.555 V; [Fe^II(BDPP)]^0/+, −0.328 V; [Co^II(BDPP)]^0/+, −0.476 V vs Fc/Fc⁺). Thus, we reason that the difference mainly results from the unavoidable spin transition from a high-spin Co^II in Co(BDPP) to a low-spin Co^III in 4, whereas such processes are not required for the generation of 2, 2′, and 3. Bubbling N₂ into a THF solution of 3 at −80 °C leads to O₂ dissociation,¹⁴ whereas analogous interconversion processes have not been found for 2, 2′ (Figure S5), and 4. This observation suggests that the metal–superoxo bonding is weaker in 3 than that in 2, 2′, and 4, consistent with the Fe–O₂^•– distance computed for 3 being considerably longer than those for 2, 2′, and 4 (Table S4).

Complex 3 is capable of performing HAA toward dihydroanthracene¹⁴ (DHA, D_C–H 78 kcal/mol²⁹), whereas no reaction was observed when mixing 2, 2′, and 4 with DHA. Instead, 4 was shown to convert 2,2,6,6-tetramethyl-1-hydroxypiperidine (TEMPO-H), a more potent H atom donor (D_O–H 69.7 kcal/mol²⁹), to TEMPO radical via HAA.¹⁶ Relative to 4, superior HAA efficacy is found for 2′, which breaks the O–H bond at least 500-fold faster. Owing to the rapid reaction rate of 2′ with a large excess of TEMPO-H, where pseudo-first-order reaction kinetics was beyond the temporal resolution of our apparatus, we then performed a kinetic titration experiment with n equiv of TEMPO-H (n ∼ 0.8–2.0). Second-order reaction kinetics was confirmed by the excellent agreement of experimental data and the model below, as shown in Figure 9:

where [A]₀ and [A]_t represent the concentrations of 2′ before and at a given time t after the addition of TEMPO-H, respectively. The ratio [A]_t/[A]₀ was obtained from the normalized transient absorption signal of 2′. An initial concentration of 2′ ([A]₀ = 1.86 × 10^–4 M, 93% yield from the EPR data) was applied in the nonlinear least-squared fitting, and the exact n value (for details, see the Supporting Information) and the rate constant, k, were obtained. The second-order rate constant of this reaction, k₂ = 500 ± 60 M^–1 s^–1, was deduced from the average of 4 independent measurements. Deuterated TEMPO-D was examined similarly. Linear plots (inset of Figure 9) were derived according to the following kinetic equation for both TEMPO-H and TEMPO-D at the concentration around 1.2 equiv to 2′.

A KIE value of 1.5 was obtained, suggesting that the homolytic O–H bond cleavage does not make the major contribution to the reaction coordinate of the rate-determining step for the conversion of Mn^III-superoxo 2′ to Mn^III-hydroperoxo 5′.

Figure 9.

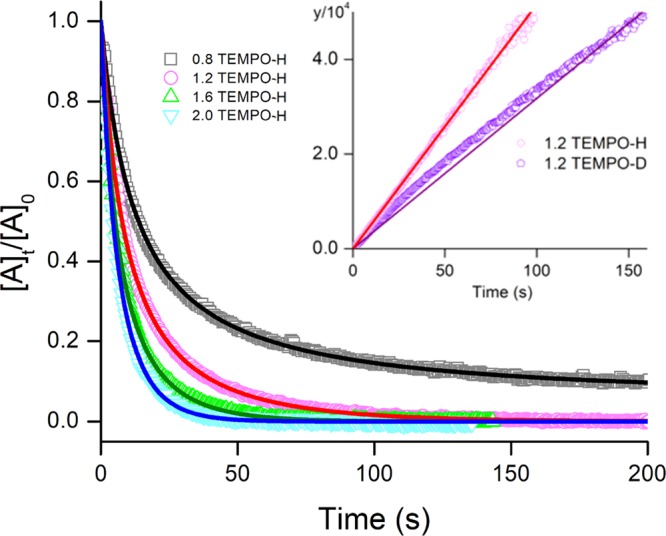
Nonlinear least-squared fitting for the reaction traces of 2′ in THF with various equiv of TEMPO-H monitored by UV–vis spectroscopy. The inset shows the linear plots of TEMPO-H and TEMPO-D following kinetic equation at the concentration around 1.2 equiv to 2′.

Obviously, complexes 2′, 3, and 4 exhibit differential HAA activity due to the nature of the individual metal center. After adjustment for differences in temperature and substrate D_C–H values, it appears that 2′ has a rate for HAA toward TEMPO-H much faster than those of Co(BDPP)(O₂^•–) (4, k₂ = 0.97 M^–1 s^–1 at −90 °C), [L¹Cu^II(O₂^•–)]PF₆ (L¹ = 1-(2-phenethyl)-5-[2-(2-pyridyl)ethyl]-1,5-diazacyclooctane, k₂ = 2.4 M^–1 s^–1 at −85 °C),³⁰ [L²Cu^II(μ-1,2-O₂^•–)]BPh₄ (L² = tacn/pyrazolate hybrid ligand, k₂ = 0.254 M^–1 s^–1 at −10 °C),³¹ and [K(Krypt)][L³Cu(O₂^•–)] (L² = a bis(arylcarboxamido)pyridine ligand, k₂ = 34.9 M^–1 s^–1 at −80 °C).³²

Conclusion

Mononuclear Mn^III–superoxo complexes 2 and 2′ were synthesized by reacting O₂ with precursors 1 and 1′ at −80 °C. Our combined spectroscopic and computational study reveals that 2 and 2′ are best formulated as a high-spin Mn^III center antiferromagnetically coupled to a superoxo ligand yielding an overall quartet ground state. Complexes 2 and 2′ were shown to activate a weak O–H bond of TEMPO-H to generate Mn^III–hydroperoxo complexes 5 and 5′. Notably, complex 2′ cleaves the O–H bond in TEMPO-H much faster than the reported Co- and Cu–superoxo complexes.³⁰⁻³² Acidification of 5 and 5′ produces nearly quantitative H₂O₂ and Mn^III-aqua complexes 6 and 6′. Conversely, complexes 5 and 5′ can be directly prepared from the reactions of 6 and 6′ with an excess amount of a 2:1 mixture of H₂O₂ and NEt₃ in THF at −90 °C.

Our earlier work showed that similar to 2 and 2′ their Fe^III and Co^III congeners (3 and 4) can be prepared in the same way and that the resulting trivalent metal–superoxo complexes can initiate HAA reactions and produce trivalent metal–hydroperoxo complexes. All these findings provide direct experimental support for the proposed mechanism for O₂ activation by distinct transition metals. Despite this, the three metal centers display different O₂ bonding rates, and O₂ adducts 2′, 3, and 4 exhibit distinct metal–superoxo bonding strengths and HAA activities. The observations warrant further systematic investigations devoting to pinpoint key features responsible for the metal specificity.

Experimental Section

Materials and Methods

All manipulations are performed under N₂ conditions using glovebox or Schlenk techniques. Acetonitrile was purified by the MBraun Solvent Purification System (MB-SPS). Diethyl ether, THF, and pentane were dried by sodium/benzophenone and distilled prior to use. Dichloromethane were dried by CaH₂ and distilled prior to use. 2,6-Bis(((S)-2-diphenylhydroxymethyl-1-pyrolidinyl)methyl)pyridine (H₂BDPP), 2,6-bis(((S)-2(bis(4-bromophenyl)hydroxyl-methyl-1-pyrolidinyl)methyl)pyridine (H₂BDP^BrP), and 2,2,6,6-tetramethyl-1-hydroxypiperidine (TEMPO-H) were synthesized according to the literature methods.³³ All the other chemical reagents were obtained from commercial sources and used without purification. UV–vis spectra were recorded with Agilent 8453 spectrophotometer equipped with cryostat from Unisoku Scientific Instruments, Osaka, Japan. Elemental analyses for C, H, and N were performed on an elementar Vario EL cube analyzer at the Instrumentation Center in National Taiwan University.

X-ray Data Collection and Structure Determination

X-ray diffraction data of crystals of 1, 1′, and 6′ were collected on a Bruker Kappa APEX II CCD diffractometer employing Mo Kα radiation (λ = 0.7107 Å) at 200 K and with a θ–2θ scan mode. The space groups for 1, 1′, and 6′ were determined on the basis of systematic absences and intensity statistics. Their structures were solved by direct methods using SIR92 or SIR97, and refined using SHELXL-97 with anisotropic displacement factors for all non-hydrogen atoms. For X-ray structures of 1′ and 6′, half or one CH₂Cl₂ solvent molecule in 1 and one Et₂O solvent molecule in 6′ per unit cell are squeezed by PLATON program. The detailed crystallographic data of 1, 1′, and 6′ were provided in their crystallographic information files.

EPR Measurements

X-band cw-EPR measurements were performed on a Bruker E500 ELEXSYS spectrometer equipped with the Bruker dual-mode cavity (ER4116DM) and an Oxford Instruments helium flow cryostat (ESR 900). The microwave bridge was the high-sensitivity bridge Super-X from Bruker (ER-049X) with integrated microwave frequency counter. The magnetic field controller (ER032T) was externally calibrated with a Bruker NMR field probe (ER035M). Spectral analysis and simulations were handled by using the EasySpin program.³⁴

Resonance Raman Collections

Resonance Raman spectra were recorded on a TriVista 555 triple monochromator equipped with a liquid-nitrogen-cooled Roper Scientific 400BR Excelon CCD camera. An excitation wavelength of 457 nm and 10 mW from a cobalt solid-state laser was used. The solution of a sample was packed into a quartz EPR tube and measured in an EPR quartz finger Dewar which was cooled with liquid nitrogen. The Raman signal was collected in a 180° backscattering geometry with a Thorlabs MPD249H–P01 off-axis parabolic mirror and focused onto the entrance slit of a spectrograph with a 100 mm diameter f/4 lens. The scattered light was dispersed with a grating of 1800 mm^–1 and further with two filter prestages of 900 mm^–1. The slit widths at the first and third stages amounted to 100 μm, thus providing a spectral resolution at the CCD camera of about 0.8 cm^–1. Spectra were collected for about 30 min for a given wavelength and spectral window. Calibration of the Raman shifts has been achieved to an accuracy of 1 cm^–1 by using Na₂SO₄ as well as the solvent signals as references.

Synthesis of Mn(BDPP) (1) and Mn(BDP^BrP) (1′)

Mn(BDPP) (1) was synthesized by reacting Mn(OTf)₂ (141.2 mg, 0.4 mmol) with H₂BDPP (244.0 mg, 0.4 mmol) and NaH (24.0 mg, 1.0 mmol) in 15 mL of CH₃CN in a 50 mL Schlenk flask. The solution was stirred for 3 h at ambient temperature and then vacuumed. The pale yellow residue was dissolved in CH₂Cl₂ (20.0 mL) and filtered. The filtrate was concentrated under vacuum and recrystallized by slow diffusion of Et₂O into the concentrated CH₂Cl₂ filtrate at ambient temperature. Yellow crystals of 1 were obtained in 55% yield over 1 day. The structure of 1 features a distorted square pyramidal geometry (τ₅ = 0.45). UV–vis (THF): 338 nm (450 M^–1 cm^–1). Anal. Calcd for C₄₁H₄₁MnN₃O₂ (F.W. = 662.71): C, 69.35; H, 5.92; N, 5.82. Found: C, 69.509; H, 6.176; N, 6.121. The synthesis of Mn(BDP^BrP) (1′) is similar to the procedures for that of 1 (Mn(OTf)₂: 0.1412 g, 0.4 mmol; H₂BDP^BrP: 0.3770 g, 0.4 mmol; NaH: 0.024 g, 1.0 mmol). Slow diffusion of pentane into the THF solution of 1′ at ambient temperature was performed for recrystallization. Yellow crystals of 1′ were obtained in 50% yield over 1 day. The structure of 1′ features a distorted square pyramidal geometry (τ₅ = 0.34). UV–vis (THF): 350 nm (322 M^–1 cm^–1). Anal. Calcd for C₄₁H₃₇Br₄MnN₃O₂·THF (F.W. = 1050.43): C, 51.45; H, 4.32; N, 4.00. Found: C, 51.587; H, 4.463; N, 3.801.

Formation of Mn(BDPP)(O₂^•–) (2) and Mn(BDP^BrP)(O₂^•–) (2′)

Complexes 2 and 2′ were generated by bubbling O₂ into THF or CH₂Cl₂ solutions of 1 and 1′ at −80 °C from an oxygen balloon for 2 min. Formation of 2 and 2′ was monitored by UV–vis spectroscopy on characteristic absorption bands at 370, 450, and 740 nm. We found that the volume of O₂ in the balloon and the elasticity of the balloon have a large influence on the formation rate of 2 and 2′, a situation similar to that encountered for Fe(BDPP)(O₂^•) (3), indicating that the formation of 2 and 2′ is rapid and close to the diffusion rate of O₂ in the working solutions.

Production of Mn^III(BDPP)(H₂O)(OTf) (6) and Mn^III(BDP^BrP)(H₂O)(OTf) (6′) from Protonation of 5 and 5′

Complex 6 was produced from the reaction of 5 (0.2 mmol) with 1 equiv of HOTf at −90 °C then warming up to room temperature. After 3 h, the resulting green solution was evaporated. The crude powder was redissolved in mixed THF/CH₃CN (10:1). Pentane was then added to the mixing THF/CH₃CN solution to obtain a green precipitate of 6 which was isolated in a yield of 116.2 mg (70%). Complex 6′ was prepared with the same procedure. Crystallization of 6′ gave a yield of 169.5 mg (74%). Anal. Calcd for C₄₂ H₃₉ Br₄ F₃ Mn N₃ O₆ S·0.5C₄H₈O (F.W. = 1182.46): C, 44.69; H, 3.75; N, 3.55; S, 2.71. Found: C, 44.50; H, 3.91; N, 3.47; S, 2.52.

Preparation of Mn(BDPP)(OOH) (5) and Mn(BDP^BrP)(OOH) (5′) from Reactions of 6 and 6′ with a Mixture of H₂O₂/NEt₃

A solution of basic hydrogen peroxide (10 equiv of H₂O₂ with 5 equiv of NEt₃, 100 μL) was added to a THF solution of 6 (1.0 mM, 3.0 mL) at −90 °C. The color of the reaction solution changed from green to pale purple exhibiting the formation of 5. Meanwhile, the absorption bands of 6 at 460 and 600 nm declined, and the bands of 5 at 510 and 720 nm grew as monitored by the UV–vis spectroscopy. Complex 5′ was prepared by the same procedure.

Kinetic Study of 2′ toward TEMPO-H

TEMPO-H (1.0, 1.5, 2.0, and 2.5 equiv) was added to a THF solution of 2′ at −90 °C. The reacting solution was monitored by UV–vis spectroscopy, and a rapid decline of the absorption band at 450 nm was recorded. Each condition was examined three times. Reaction of 2′ with 1.5 equiv of TEMPO-D was also performed, and the rate was obtained to derive the kinetic isotope effect (KIE) value.

Computational Details

Geometry optimizations and frequency calculations were carried out with the B3LYP density functional.³⁵ The triple-ζ quality basis set, def2-TZVP,³⁶ was used for Mn and the atoms in the first coordination sphere, while the remaining atoms were treated with def2-SVP³⁷ basis set. The calculations were accelerated by using RI (resolution of the identity) approximation,^38,39 for which the auxiliary coulomb-fitting basis set def2-TZVP/J³⁸ was used. All geometry optimizations were performed incorporating solvation effect through conductor-like polarizable continuum model (CPCM)⁴⁰ with the solvent THF (ε = 7.25). The noncovalent interactions were accounted for through atom-pairwise dispersion corrections with Becke–Johnson (D3BJ)⁴¹ damping.

Spectroscopic parameters were computed by using the TPSSh density functional⁴² in combination with the CP(PPP) basis set for Mn,⁴³ the def2-TZVP basis set for the atoms in the first coordination sphere, and the def2-SVP for the remaining atoms. The magnetic hyperfine coupling matrix, A, of the ⁵⁵Mn center was calculated by taking the isotropic Fermi contact term, the first-order traceless dipolar contribution, and the second-order nontraceless spin–orbit contribution into account. The Fermi-contact contributions were scaled by a factor of 1.49.⁴⁴ Spin–orbit contributions to the hyperfine tensors were calculated as second order properties employing the coupled perturbed (CP) Kohn–Sham theory.⁴⁵ The Mn magnetic hyperfine coupling constants of the “genuine” antiferromagnetic state A_i^AF were calculated from the magnetic hyperfine coupling constants of the corresponding broken symmetry state A_i by conversion into “site values” and multiplication with the spin projection coefficients C_i:⁴⁶

The contributions of spin orbit coupling (SOC) to the zero-field splitting (ZFS)²⁴ were calculated by linear response theory.⁴⁷

The spin–spin coupling contributions to ZFSs are calculated from the equation of McWeeny and Mizuno.⁴⁸

in which spin density matrix P^α–β was obtained on the basis of the spin-unrestricted natural orbital (UNO) determinant.⁴⁹ All calculations were performed by using the ORCA quantum chemical program package.⁵⁰

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.inorgchem.9b00767.

• UV–vis, NMR and HRMS spectra of 1–3, EPR spectra of 1–2, and computational result of 1 (PDF)

Accession Codes

CCDC 1898662–1898664 contain the supplementary crystallographic data for this paper. These data can be obtained free of charge via www.ccdc.cam.ac.uk/data_request/cif, or by emailing data_request@ccdc.cam.ac.uk, or by contacting The Cambridge Crystallographic Data Centre, 12 Union Road, Cambridge CB2 1EZ, UK; fax: +44 1223 336033.

The authors declare no competing financial interest.