Ultrafast Optical Pulse Shaping using Dielectric Metasurfaces

Abstract

Remarkable advances in ultrafast lasers, chirped pulse amplifiers and frequency comb technology require fundamentally new pulse modulation strategies capable of supporting unprecedentedly large bandwidth and high peak power while maintaining high spectral resolution. Here, we demonstrate of optical pulse shaping using a dielectric metasurface able to simultaneously control the amplitude, phase and polarization of the various frequency components of an ultrafast pulse. Dielectric metasurfaces offer a low cost, high resolution, high diffraction efficiency, high damage threshold and integration-friendly alternative to commercial spatial-light-modulators used for controlling ultrafast pulses. By offering the potential for complete spatio-temporal control of optical fields, metasurface based pulse-shapers are expected to have significant impact in the field of ultrafast science and technology.

One Sentence Summary:

Simultaneous amplitude, phase and polarization modulation of ultrafast optical pulses is achieved using a dielectric metasurface.

Development of ultrafast lasers that produce a train of optical pulses in the time-domain, or equivalently a comb of closely spaced spectral lines in the frequency-domain, have led to revolutionary advances in areas such as high-field physics (1), quantum optics (2, 3) and frequency metrology (4). These advances have been enabled by the development of techniques that began with dispersion compensation (5, 6) and eventually achieved customizable shaping of pulses with approaches in both the time (7, 8) and frequency domains (9-13). Because of the broadband nature of ultrafast pulses, the most common embodiment of pulse shaping involves some form of dispersion engineering – this includes both dispersion compensation to achieve transform-limited pulses for applications in long-distance communications (14) or nonlinear microscopy (15, 16), and pulse stretching that makes techniques such as chirped pulse amplification possible (17). Furthermore, arbitrary control over the phase and amplitude of individual comb lines enables optical arbitrary waveform generation (18, 19), which promises to have tremendous impact in applications such as coherent manipulation of quantum-mechanical processes (20-23), frequency-comb spectroscopy (24, 25), and ultrafast communications (26). Among the various pulse shaping techniques, Fourier-transform pulse shaping, which synthesizes optical pulses through parallel manipulation of spatially separated spectral components, has been the most widely adopted (10-12). This form of pulse shaping typically employs a liquid-crystal based spatial light modulator (SLM), which offers dynamic control over the optical amplitude and phase. However, SLMs are often bulky, costly, and limited in spectral resolution due to the finite pixel size and pixel density (27, 28).

Recently, dielectric metasurfaces – ultrathin, planar optical elements composed of an array of deep-subwavelength nanostructures – have emerged as a powerful technology for arbitrary control over the amplitude, phase and polarization of light for spatial-domain wavefront manipulation in a compact platform (29-33). Here, we implement and demonstrate a metasurface that can control the temporal profile of light through coherent control of its constituent frequency components. This control is demonstrated by using a metasurface made of deep-subwavelength dielectric pillars, patterned and positioned with nanometer precision, to simultaneously control the spectral amplitude, phase and polarization of the various frequency components that constitute an ultrafast pulse, leading to temporal shaping of the pulse with arbitrary flexibility. Two classes of pulse-shaping metasurfaces with increasingly complex functionality are explored. The first class is a set of phase-manipulating metasurfaces that impart, through phase shift that are quadratic or higher order functions of frequency, the equivalent of anomalous dispersion enabling pulse compression or stretching. The second class simultaneously manipulates both phase an amplitude to achieve precise control over the temporal profile of a pulse, for example to split one pulse into two.

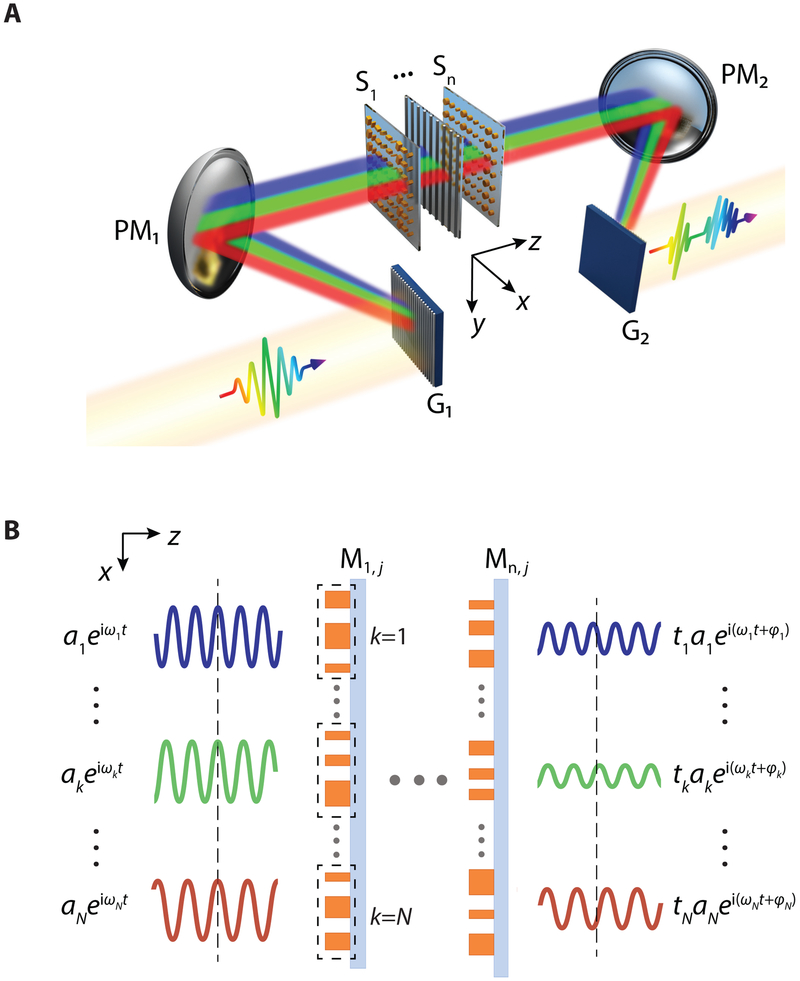
A Fourier transform setup (Fig. 1A), in which an optical pulse is first angularly dispersed by a grating and then focused by an off-axis metallic parabolic mirror (see Methods and Supplementary Figure S1), is used to spatially map the spectral components of the optical pulse onto the full length of one or more cascaded metasurface matrices (S_i=1 to S_i=n, schematically illustrated in Fig. 1A) each consisting of m different metasurfaces (M_i,j=1 to M_i,j=m). A given metasurface (M_i,j) is designed to treat in parallel the broad range of frequencies (ω_k for k = 1 to N) constituting the pulse by implementing a spatially dependent, one-dimensional custom masking function m_i(x) (discretized to N individual sectors, one for each ω_k, Fig. 1B). This function operates on either phase alone or both phase and amplitude, where each wavelength λ is mapped to a specific lateral position x (Fig. 1A). This mapping follows a quasi-linear function λ(x) (see Supplementary Figure S2). A polarizing metasurface element can also be inserted in the beam path to help achieve the required net masking function. After passing through the metasurfaces and undergoing local phase, amplitude and polarization transformations, the spectral components of the beam are recombined using a second parabolic mirror and grating pair, yielding a shape-modified pulse with the desired temporal characteristics. The metasurfaces are illuminated using a Ti: Sapphire oscillator generating ≲10 fs pulses, centered at 800 nm (FWHM bandwidth of ≈ 60 THz), with a repetition rate of 75 MHz and pulse energy of 6.5 nJ. The characteristics of the recombined pulse exiting the system, i.e. spectral amplitude and phase, are measured using the technique of spectral phase interferometry for direct electric-field reconstruction (SPIDER) (34).

Fig. 1. Optical pulse shaping using cascaded metasurfaces.

(A) Schematic diagram of a Fourier transform pulse shaping setup, consisting of a pair of diffraction gratings (G₁ and G₂), a pair of parabolic mirrors (PM₁ and PM₂), and a cascaded sequence of metasurfaces matrices S_i (i = 1, 2, … n). Each matrix S_i consists of m different metasurfaces (M_i,j=1 to M_i,j=m). An input optical pulse upon propagation through this setup is transformed into a shape-modified output pulse of tailored temporal characteristics. (B) Pulse shaping at the Fourier plane of the setup. A given metasurface M_i,j is discretized to N individual sectors to treat in parallel the broad range of frequencies (ω_k for k = 1 to N), imparting a complex transfer function t_i,ke^iφ_i,k for each ω_k. The spectral components of the input pulse are treated in parallel through a location specific effective masking function of complex amplitude t_ke^iφ_k, where $t_k={\prod }_{i=1}^n{t}_{i,k}$ and ${\phi }_k={\sum }_{i=1}^n{\phi }_{i,k}$.

The metasurface consists of nanopillars of polycrystalline silicon arrayed on a fused-silica substrate. The nanopillars are fabricated by patterning the silicon, which was deposited on the substrate by low-pressure chemical vapor deposition (LPCVD), using electron-beam lithography followed by reactive ion etching (see Methods). The nanopillars have a height H = 660 nm and a rectangular cross-section, where length L_x and width L_y range from 70 nm to 250 nm, and have a subwavelength spacing p ranging from 280 nm to 615 nm. Polycrystalline silicon was selected for its high damage threshold (35), large refractive index and low optical absorption in the near-infrared spectral range (Supplementary Figure S3) whereas fused-silica was selected for its low refractive index, low optical dispersion, and isotropy. The total length of any metasurface in this work along the x-axis, 3 cm, was chosen to match the spectral dispersion length in the Fourier plane to the full bandwidth of the pulse as set by grating pitch, off-axis parabolic mirror curvature and grating-mirror distance (accommodating the quasi-linear mapping λ(x) of slope 8.78 nm/mm). The number of individual metasurface elements in one row along the x-direction is approximately 10⁵, resulting in about 8 comb-lines per element for a pulse dispersed over its full bandwidth and corresponding to a theoretically achievable lower limit on the spectral resolution of ≈ 600 MHz. However, optical aberrations and the diffraction caused by the finite size of the optics in our case limits the spectral resolution to ≈ 150 GHz (corresponding to the number of independently controllable spectral features N ≈ 600). The metasurface width along the y-axis of 300 μm is chosen to contain the vertical spread of the loosely-focused (NA ≈ 0.026) spectrally dispersed beam at the Fourier plane (see Methods). The spectrally-averaged transmission power varies between 50-98 % per metasurface, with an average of approximately 80%. A typical 4 %-per-substrate-surface loss is also present due to reflections.

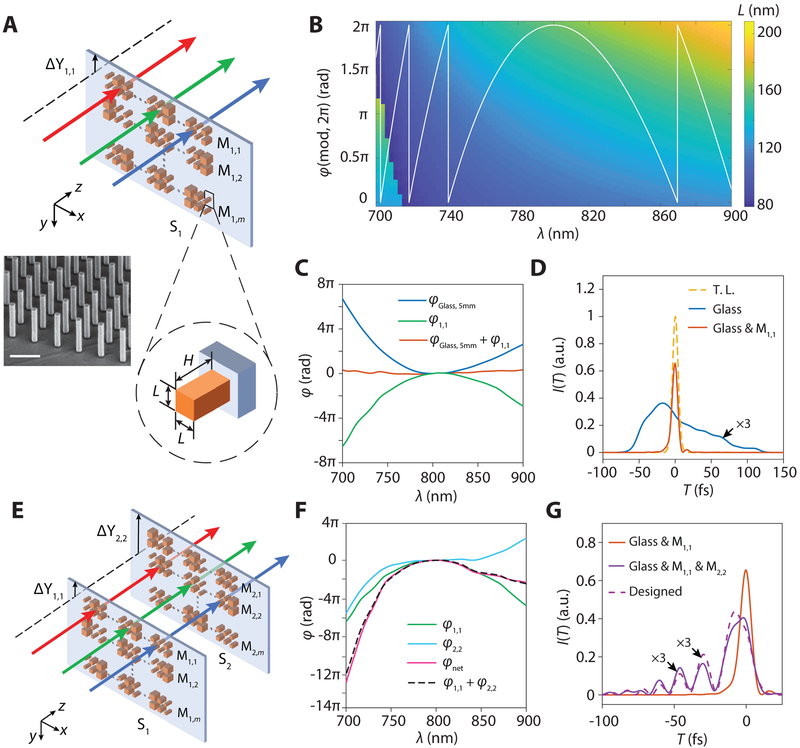
A metasurface can be designed to control the dispersion of an ultrafast pulse through manipulation of its spectral phase alone. Here we implement a metasurface matrix, S_i=1, bearing a discrete number j of different metasurfaces stacked in the y-direction, each with a masking function m_1,j(x) and accessed by a mechanical translation ΔY_1,j of the upper edge of the sample relative to the plane of the beam (Fig. 2A). By giving each metasurface pillar a square cross-section (L_x = L_y = L), and setting L(x) to a specific value in the interval [75 nm, 210 nm], a phase of any modulus between 0 and 2π can be imparted within the spectral bandwidth of the pulse with high transmittance (Fig. 2B and Supplementary Figure S4), as calculated by rigorous coupled wave analysis (RCWA) (36). We first demonstrate how such a phase-control metasurface can convert a positively chirped optical pulse into a transform limited pulse, by conferring a quadratic spectral phase-shift φ_1,j = −A_1,j(ν – ν₀)² to the pulse, where ν₀ = 375 THz is the center frequency of the pulse and A_1,j is a weighting factor (defined to be positive) that is intended to enable compensation of various degrees of dispersion. The spectral phase shift as a function of wavelength enabling compensation of lowest order dispersion for propagation through 5 mm of glass, φ_1,1(ν) = −A_1,1(ν – ν₀)² where A_1,1 = 6 × 10⁻³ rad/THz² is depicted by the white line of Fig. 2B; the locus of this line yields a specific design value of L for each wavelength (also see Supplementary Figure S5). The metasurface pillar dimensions at each location x are then set using the look-up function, L(ν(x)). Upon inserting the metasurface matrix S₁ into the Fourier transform setup, and translating the matrix to access metasurface M_1,1, the relative spectral phase shift conferred by the fabricated metasurface displays anomalous dispersion and closely replicates the designed phase profile (Fig. 2C). Providing this Fourier transform setup with an input of a positively chirped Gaussian optical pulse (of pulse length ≈ 100 fs, chirped by a ≈ 5 mm-thick glass slab) yields an output of a compressed, transform limited pulse (of length ≈ 10 fs, Fig. 2D). This demonstrates the ability of a single phase-only metasurface to compensate for normal dispersion via a tailored anomalous dispersion transformation. Additional higher order spectral shifts, for example cubic shifts, can be achieved by inserting, within the focal volume about the Fourier plane, an additional metasurface matrix S_i=2 composed of metasurfaces M_2,j’ characterized by φ_2,j′ = −A_2,j′(ν – ν₀)³. By translating metasurface M_2,2 to coincide with the plane of the beam via a shift ΔY_2,2 of S₂ (Fig. 2E) yields A_2,2 = 9 × 10⁻⁵ rad/THz³ resulting in a net designed spectral phase shift for the system of φ_net, displayed in Fig. 2F along with individual quadratic and cubic components, respectively. The close approximate between φ_net and (φ_1,1 + φ_2,2) indicates the linearity of the system. Propagating the transform-limited pulse through this additional cubic-phase masking function (m_2,2) results in a temporal pulse profile that is consistent with that expected for a pulse possessing a negatively chirped, linear group delay dispersion (Fig. 2G). The range of second- and third-order dispersion compensation made available by combining S₁ and S₂ is displayed in Supplementary Fig. S6. Nonlinear spectral phase distortions characteristic of high-energy pulse propagation through a dispersive medium could similarly be corrected using this cascaded metasurface approach in a dynamic manner.

Fig. 2. Femtosecond pulse shaping using phase modulating metasurfaces.

(A) Schematic diagram of a spectrally dispersed pulse propagating through a specific metasurface M_1,1 of a metasurface matrix S₁, including a magnified schematic of a unit-cell consisting of a Si nanopillar on glass. The nanopillars have a square cross-section with a position dependent side-length L(x) and constant height H. Inset: A representative scanning electron microscope (SEM) image of the metasurface. Scale bar represents 500 nm. (B) A color-map depicting the values of L required to achieve an arbitrary phase φ(mod, 2π) at any wavelength λ, calculated using the RCWA method. The overlaid white line represents a spectral phase function M_1,1 targeted to compensate the lowest order dispersion upon pulse-propagation through 5 mm of glass, yielding a quadratic function in frequency with anomalous spectral dependence φ_1,1(ν) = −A_1,1(ν – ν₀)², where A_1,1 = 6 × 10⁻³ rad/THz², and ν₀ = 375 THz is the center frequency. (C, D) Experimental pulse shaping using fabricated metasurface M_1,1 that implements masking function m_1,1(x) = e^{iφ_1,1(ν(x))}, where C represents the measured spectral phase conferred by the metasurface (solid green) and a 5 mm-thick glass (solid blue), and D represents metasurface-induced pulse compression (solid red) of a positively chirped Gaussian optical pulse (solid blue) to its transform limit (T.L., dashed yellow). (E) Schematic diagram of a spectrally dispersed pulse propagating through two cascaded metasurfaces M_1,1 and M_2,2 located on separate metasurface matrices S₁ and S₂ respectively, where the top edge of each matrix is shifted from the plane of the beam by distances ΔY_1,1 and ΔY_2,2 respectively. (F) Experimental pulse shaping using cascaded metasurfaces M_1,1 and M_2,2 where M_1,1 is the quadratic metasurface of C, and M_2,2 implements a cubic masking function m_2,2(x) = e^{iφ_2,2(ν(x))}, where φ_2,2(ν) = −A_2,2(ν – ν₀)³ and A_2,2 = 9 × 10⁻⁵ rad/THz³. The measured spectral phases conferred by the metasurfaces individually (M_1,1 as solid green, M_2,2 as solid cyan, and the numerical summation of the two as dashed black) and in cascade (solid magenta) are shown. (G) The measured (solid purple) and designed (dashed purple) temporal profile of the output pulse resulting from transformation of the chirped input pulse of C (solid red) by the cascaded quadratic and cubic metasurfaces. The temporal pulse profile is consistent with that expected for a pulse possessing a cubic spectral phase function (dashed purple). The random error in measuring the spectral phase using SPIDER is within the linewidth of the plots.

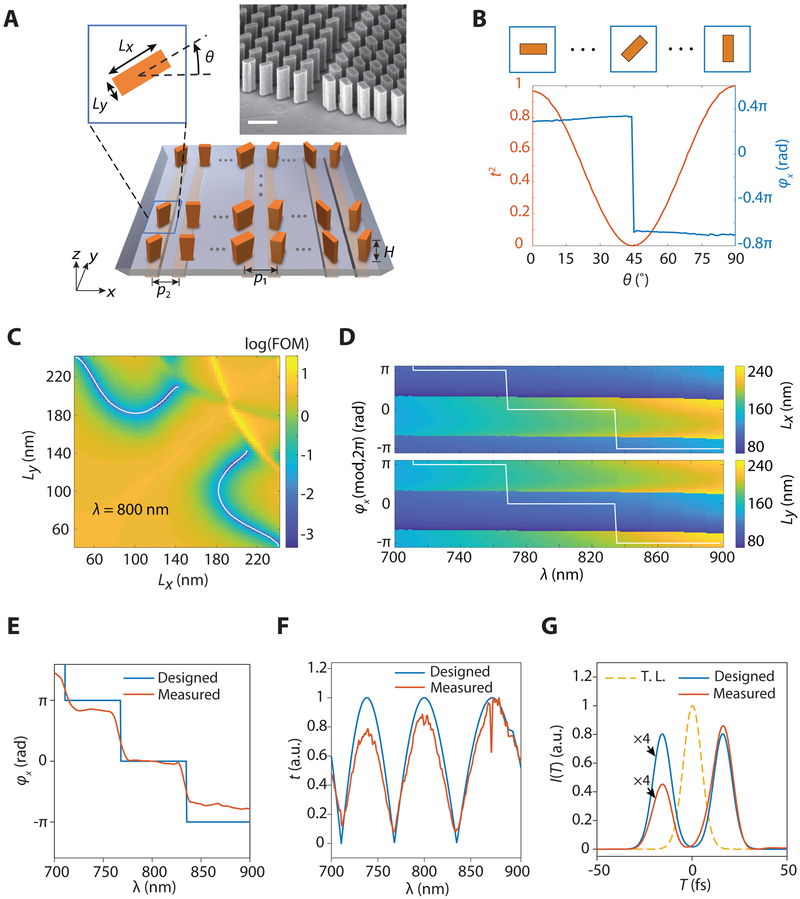
A more general embodiment of a pulse shaper requires the ability to control simultaneously, and independently, both phase and amplitude of the spectral components of an ultrafast pulse (27, 37). We achieve this by implementing metasurfaces based on nanopillars of rectangular cross-section that can control the local phase (through the respective length L_x and width L_y of a given rectangle, as calculated by RCWA) and local polarization (through the rotation θ of the rectangle with respect to the x-axis – each pillar acting as a nanoscale half-wave plate) of a linearly polarized pulse (electric-field parallel to the x-axis). The combination of half-wave plates with a wire-grid linear polarizer (Supplementary Figure S7), here custom-fabricated on the exit side of the metasurface-bearing substrate (Fig. 3A), yields amplitude modulation set by θ (Fig. 3B). In general, the polarization state of any frequency component exiting the polarizer after passage through a given metasurface pillar rotated to angle θ can be expressed by the Jones vector (see Supplementary Text):

$$J=\left[\begin{array}{c}\hfill e^{i{\phi }_x}{\mathit{cos}}^2\theta +e^{i{\phi }_y}{\mathit{sin}}^2\theta \hfill \\ \hfill 0\hfill \end{array}\right],$$ (1)

where φ_x and φ_y are the respective phase-shifts for θ = 0° and 90°, respectively. Enforcing the half-waveplate condition, φ_x – φ_y = ±π, then leads to a Jones vector for the final polarization state given by:

$$J=\left[\begin{array}{c}\hfill e^{i{\phi }_x}\mathit{cos}(2\theta )\hfill \\ \hfill 0\hfill \end{array}\right],$$ (2)

yielding an x-polarized wave of amplitude and phase determined by independent variables, θ and φ_x, respectively. The exit phase through the half-waveplate stays constant as the pillar is rotated, as further confirmed by RCWA simulations of a three-dimensional unit cell incorporating the pillar (Fig. 3B and Methods).

Fig. 3. Femtosecond pulse shaping using simultaneous phase and amplitude modulating metasurfaces.

(A) Schematic diagram of an integrated device consisting of (i) a metasurface composed of rectangular Si nanopillars (of position dependent length L_x, width L_y, and rotation angle θ, and uniform height H= 660 nm) on glass acting as nanoscale half-wave plates, and (ii) a wire-grid linear polarizer (pitch p₂) on the opposite side of the glass substrate – able to control simultaneously the phase and amplitude of the spectral components of a linearly polarized input pulse. Inset: A representative SEM image of the metasurface. Scale bar represents 500 nm. (B) RCWA calculated amplitude and phase of the conferred transmission factor for a pillar (L_x = 182 nm and L_y = 98 nm) at λ = 800 nm as a function of θ. (C) Color plot: an example of the figure-of-merit (FOM) quantifying the half-wave plate performance of the nanopillars as a function of L_x and L_y, displayed here for λ = 800 nm. The overlaid solid white lines depict the parametric curves f (L_x, L_y) representing the local minima in FOM. (D) Color-maps depicting the values of L_x and L_y respectively, required to achieve an arbitrary phase φ_x(mod, 2π) at any wavelength λ. The overlaid solid white lines represents the spectral phase function required to split an optical pulse into two time-separated replicas with separation ΔT =30 fs. (E, F, G) Experimental demonstration of pulse splitting, for an input Gaussian pulse of length 15 fs. E and F display respectively the measured spectral phase φ_x and transmission amplitude t conferred by the metasurface/polarizer combination along with the targeted design curves. G represents the measured temporal profile of the split pulse (solid red), along with the targeted profile (solid blue) for a Gaussian input pulse (dashed yellow). The random error in measuring the spectral phase and amplitude using SPIDER is within the linewidth of the plots.

Optimal half-waveplate performance is defined by maximum transmission amplitude and a relative phase ∣φ_x – φ_y∣ as close as possible to π. This occurs for pillar lateral dimension pairs (L_x, L_y) which minimize the following figure-of-merit (FOM) function:

$$\mathit{FOM}={\mid \frac{t_x{e}^{i{\phi }_x}}{t_y{e}^{i{\phi }_y}}-e^{i\pi }\mid }^2,$$ (3)

where t_x and t_y represent the transmission amplitude of a given pillar at θ = 0° and 90° respectively. The parametric curves f(L_x, L_y) representing the local minimum in the FOM can be numerically derived at each wavelength λ; the representative curves at λ = 800 nm are indicated by the solid white lines of Fig. 3C. The range of permissible (L_x, L_y) combinations given by f at a given wavelength yields a set of available phase shifts φ_x spanning the full range [0, 2π], This information is compiled into two look-up plots: L_x(φ_x, λ) and L_y (φ_x, λ) (Fig. 3D and Supplementary Figure S8) that, in combination with appropriate amplitude modulation set by pillar angle θ, can be used to design each metasurface element to achieve the desired masking function for pulse shaping via simultaneous control of spectral phase and amplitude. For example, a complex masking function characterized by a periodic spectral modulation via Fourier transformation translates into a time-shift convolution operation. An example pulse shaping operation enabled by such a complex masking function is to split a single optical pulse into two replicas time-separated by an interval ΔT. This operation requires simultaneous modulation of amplitude and phase over the entire spectral range of the pulse, with amplitude t(ν) = ∣g(ν)∣, where g(ν) = cos{π(ν – ν₀)/Δν} and Δν = 1/ΔT is the spectral period for t. The corresponding phase φ_x oscillates between 0 and π with dependence φ_x(λ) = π(sgn(g(ν)) + 1)/2. The performance of a metasurface designed according to this strategy (Supplementary Figure S9) to achieve pulse doubling with target ΔT = 30 fs, is illustrated in Fig. 3E-G, for a Gaussian input pulse of length 10 fs. The asymmetry in the pulse is due to the deviation between the applied and designed phases. In its most general embodiment, a pulse shaper is required to control simultaneously, and independently, the phase, amplitude and polarization of the spectral components of an ultrafast pulse, ideally using a single optical element. In our case, this can simply be achieved by utilizing the additional degree-of-freedom provided by the multiple metasurface matrix elements arrayed in the y-direction.

In summary, we have demonstrated the ability to arbitrarily control the temporal profile of large bandwidth optical pulses using an integration-friendly, lithographically-patterned, ultrathin-dielectric metasurface platform, offering promise for numerous applications in the areas of high-energy physics, frequency-combs, quantum-optics and lightwave-communications. We expect that metasurface techniques can be extended into the full spatiotemporal domain wherein masking functions will concurrently modulate both the temporal and spatial characteristics of a pulse. Such an extension would allow for the creation of custom space-time fields that enable precise control over ultrafast pulse propagation through complex scattering media. By extending the metasurface configuration to accommodate two-dimensional spectral dispersion, we expect that the number of individually controllable spectral features can be increased by several orders of magnitude, thereby allowing line-by-line shaping with record bandwidth and resolution (13). Additionally, we expect that the inherent nonlinearity of the metasurface constituent dielectric materials will allow for direct line-by-line frequency conversion in the Fourier domain (38, 39). Expanding metasurfaces into the realm of time-domain manipulation will amplify the already significant impact of their application as two-dimensional wavefront shapers, and open new vistas in the field of ultrafast science and technology.