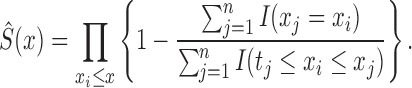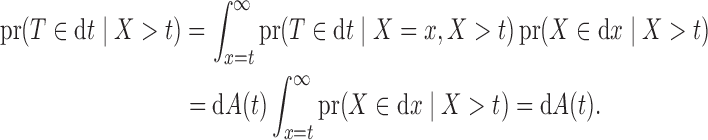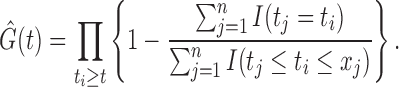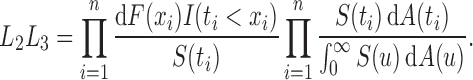Summary
A time to event, 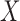 , is left-truncated by
, is left-truncated by 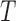 if
if  can be observed only if
can be observed only if 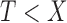 . This often results in oversampling of large values of
. This often results in oversampling of large values of 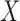 , and necessitates adjustment of estimation procedures to avoid bias. Simple risk-set adjustments can be made to standard risk-set-based estimators to accommodate left truncation when
, and necessitates adjustment of estimation procedures to avoid bias. Simple risk-set adjustments can be made to standard risk-set-based estimators to accommodate left truncation when 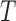 and
and 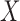 are quasi-independent. We derive a weaker factorization condition for the conditional distribution of
are quasi-independent. We derive a weaker factorization condition for the conditional distribution of 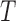 given
given 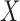 in the observable region that permits risk-set adjustment for estimation of the distribution of
in the observable region that permits risk-set adjustment for estimation of the distribution of 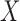 , but not of the distribution of
, but not of the distribution of 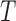 . Quasi-independence results when the analogous factorization condition for
. Quasi-independence results when the analogous factorization condition for 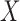 given
given 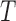 holds also, in which case the distributions of
holds also, in which case the distributions of 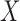 and
and 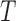 are easily estimated. While we can test for factorization, if the test does not reject, we cannot identify which factorization condition holds, or whether quasi-independence holds. Hence we require an unverifiable assumption in order to estimate the distribution of
are easily estimated. While we can test for factorization, if the test does not reject, we cannot identify which factorization condition holds, or whether quasi-independence holds. Hence we require an unverifiable assumption in order to estimate the distribution of 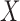 or
or 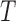 based on truncated data. This contrasts with the common understanding that truncation is different from censoring in requiring no unverifiable assumptions for estimation. We illustrate these concepts through a simulation of left-truncated and right-censored data.
based on truncated data. This contrasts with the common understanding that truncation is different from censoring in requiring no unverifiable assumptions for estimation. We illustrate these concepts through a simulation of left-truncated and right-censored data.
Keywords: Constant-sum condition, Kendall’s tau, Left truncation, Right censoring, Survival data
1. Introduction
Truncated survival data arise when observation of the time to event, 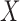 , occurs only when it falls within a subject-specific interval. Left truncation occurs when
, occurs only when it falls within a subject-specific interval. Left truncation occurs when 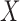 is observed only if
is observed only if 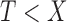 , where
, where 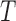 is the time to sampling, i.e., the truncation variable. It often arises in longitudinal cohort studies in which a subcohort is sampled on the basis of having had a post-baseline assessment prior to the event of interest. Another example is when the time origin of interest, such as onset of cognitive impairment, may occur prior to entry into the cohort, and the endpoint of interest is time from onset of cognitive impairment to death. Estimation must account for the truncation to avoid bias due to the selection based on the magnitude of
is the time to sampling, i.e., the truncation variable. It often arises in longitudinal cohort studies in which a subcohort is sampled on the basis of having had a post-baseline assessment prior to the event of interest. Another example is when the time origin of interest, such as onset of cognitive impairment, may occur prior to entry into the cohort, and the endpoint of interest is time from onset of cognitive impairment to death. Estimation must account for the truncation to avoid bias due to the selection based on the magnitude of 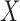 . A critical condition that enables simple risk-set adjustment to standard risk-set-based estimators (Lynden-Bell, 1971; Woodroofe, 1985; Wang et al., 1986) was described by Tsai (1990) as quasi-independence, or independence in the observed region, i.e.,
. A critical condition that enables simple risk-set adjustment to standard risk-set-based estimators (Lynden-Bell, 1971; Woodroofe, 1985; Wang et al., 1986) was described by Tsai (1990) as quasi-independence, or independence in the observed region, i.e., 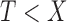 . In particular, this means that
. In particular, this means that 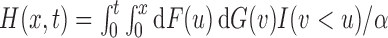 , where
, where 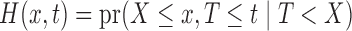 ,
, 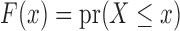 ,
, 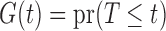 ,
, 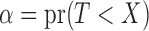 , and
, and 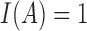 if the event
if the event 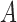 holds and 0 otherwise. For simplicity of presentation, we assume that
holds and 0 otherwise. For simplicity of presentation, we assume that 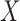 and
and 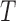 are continuous random variables and that
are continuous random variables and that 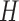 ,
, 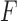 and
and 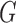 have densities
have densities 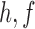 and
and 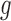 with respect to Lebesgue measure. Nonetheless, all of our results apply also to discrete random variables, as they are based on nonparametric maximum likelihoods (Vardi, 1989). The quasi-independence assumption expressed in terms of densities is
with respect to Lebesgue measure. Nonetheless, all of our results apply also to discrete random variables, as they are based on nonparametric maximum likelihoods (Vardi, 1989). The quasi-independence assumption expressed in terms of densities is
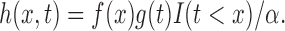 |
(1) |
This does not imply that the sampled random variables are conditionally independent given 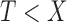 ; it is not equivalent to
; it is not equivalent to 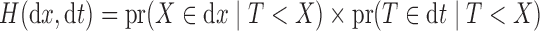 for
for 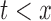 , where we use the notation
, where we use the notation  as a shorthand for
as a shorthand for 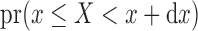 .
.
Examination of the likelihood based on left-truncated data elucidates the simplification in estimation that arises from quasi-independence, and reveals that weaker conditions also admit this simplification for estimation of the distribution of 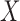 or
or 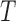 , but not of both. The factorization condition that enables estimation of the distribution of
, but not of both. The factorization condition that enables estimation of the distribution of 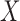 is
is
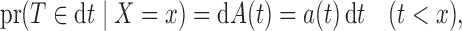 |
(2) |
where 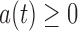 need not equal
need not equal  and is defined on the support of
and is defined on the support of  in the observable region
in the observable region 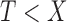 . In the unobservable region, we define
. In the unobservable region, we define 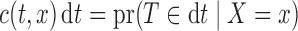 for
for 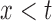 . For
. For 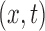 in the support of
in the support of 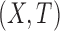 ,
, 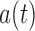 and
and 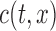 are constrained by
are constrained by
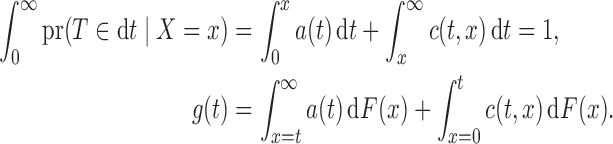 |
In the Supplementary Material we derive an explicit expression for 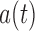 as a function of
as a function of  ,
, 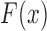 and
and 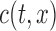 , under the factorization condition (2). We also discuss the special cases of overall independence and quasi-independence. The factorization condition is similar to the condition of Keiding (1992) that
, under the factorization condition (2). We also discuss the special cases of overall independence and quasi-independence. The factorization condition is similar to the condition of Keiding (1992) that 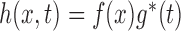 , upon identifying
, upon identifying 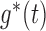 as
as 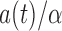 . The factorization condition is reminiscent of the constant-sum condition for right-censored data (Williams & Lagakos, 1977; Betensky, 2000), under which dependent censoring can be ignored and the Kaplan–Meier estimator is valid.
. The factorization condition is reminiscent of the constant-sum condition for right-censored data (Williams & Lagakos, 1977; Betensky, 2000), under which dependent censoring can be ignored and the Kaplan–Meier estimator is valid.
Proposition 4 shows that the distribution of 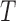 is not identifiable under (2) alone; it also requires a complementary factorization condition. The two factorization conditions together constitute quasi-independence (1), under which both distributions can be estimated. We explain in § 3 that the observed data can be used to test whether neither factorization condition holds, but cannot be used to identify which condition holds if either does. Therefore, we require unverifiable assumptions in order to estimate the distribution of
is not identifiable under (2) alone; it also requires a complementary factorization condition. The two factorization conditions together constitute quasi-independence (1), under which both distributions can be estimated. We explain in § 3 that the observed data can be used to test whether neither factorization condition holds, but cannot be used to identify which condition holds if either does. Therefore, we require unverifiable assumptions in order to estimate the distribution of 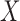 or
or 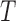 based on truncated data. This contrasts with the common understanding that truncation is distinct from censoring and requires no unverifiable assumptions for estimation.
based on truncated data. This contrasts with the common understanding that truncation is distinct from censoring and requires no unverifiable assumptions for estimation.
2. Nonparametric likelihood estimation
2.1. Estimation in the absence of censoring
First we consider estimation in the absence of right censoring. The likelihood of the observed data 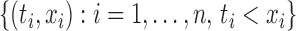 under left truncation and no censoring is
under left truncation and no censoring is
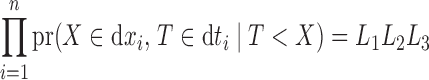 |
(3) |
where
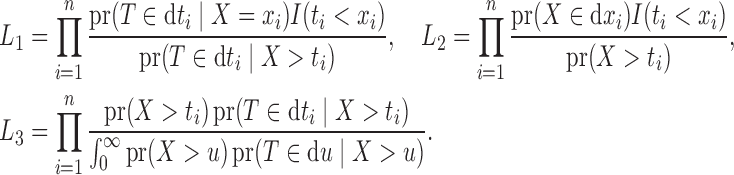 |
Proposition 1.
Under the factorization condition (2), the nonparametric maximum likelihood estimator of
is the risk-set-adjusted Kaplan–Meier estimator
(4)
Proof.
Under (2),
is equal to 1 since its denominator is equal to its numerator,
:
Thus,
effectively constitutes the full likelihood, with unknown parameters
and
. The standard risk-set-adjusted Kaplan–Meier estimator given by (4) is the maximum likelihood estimator of
based on
, and also equals that based on
(Wang, 1991). This is because, in the absence of parametric assumptions on
,
is a multinomial likelihood with maximum value
if there are no ties in
, which is attained when each factor in its product is set to the corresponding sample proportion. A similar argument holds in the presence of ties. □
Since (4) is the maximizer of 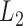 , if it also maximizes the full likelihood (3), then
, if it also maximizes the full likelihood (3), then 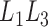 must be constant with respect to
must be constant with respect to  . If this latter condition implies factorization (2), then it would follow that (2) is a necessary condition for (4) to be the nonparametric maximum likelihood estimator of
. If this latter condition implies factorization (2), then it would follow that (2) is a necessary condition for (4) to be the nonparametric maximum likelihood estimator of 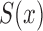 . We conjecture that this is false.
. We conjecture that this is false.
Under complete independence between 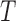 and
and 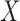 , (4) was shown to be uniformly consistent by Woodroofe (1985). Since the likelihoods that contribute to estimation of
, (4) was shown to be uniformly consistent by Woodroofe (1985). Since the likelihoods that contribute to estimation of 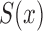 are identical and equal to
are identical and equal to  under any of the three conditions of complete independence between
under any of the three conditions of complete independence between 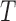 and
and 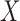 , quasi-independence (1), or factorization (2), the uniform consistency of (4) under (1) or (2) can be proved in the same way as under complete independence between
, quasi-independence (1), or factorization (2), the uniform consistency of (4) under (1) or (2) can be proved in the same way as under complete independence between 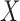 and
and 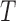 .
.
The likelihood (3) can also be expressed as 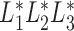 where
where
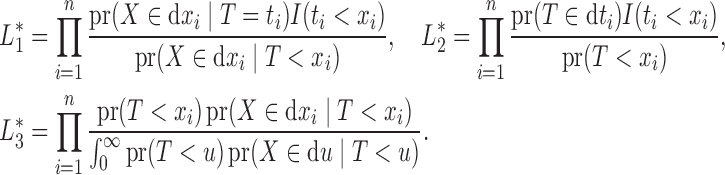 |
A complementary factorization condition to (2) for 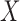 given
given 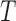 is
is
 |
(5) |
where  need not equal
need not equal 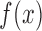 . Conditions (2) and (5) together are equivalent to quasi-independence, as stated in the following proposition.
. Conditions (2) and (5) together are equivalent to quasi-independence, as stated in the following proposition.
Proposition 2.
Under conditions (2) and (5),
and
, which implies quasi-independence (1). Conversely, quasi-independence (1) implies both (2) and (5).
Proof.
Under (2) and (5),
, implying
and
, i.e., quasi-independence. Under (1),
, implying (2) and (5) with
and
. □
Under (5), the likelihood for estimation of 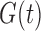 effectively reduces to
effectively reduces to 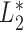 , and its estimation is dual to that of
, and its estimation is dual to that of 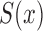 (Wang, 1991). This is summarized in the following proposition.
(Wang, 1991). This is summarized in the following proposition.
Proposition 3.
Under (5), the nonparametric maximum likelihood estimator of
is
Proof.
This follows from Proposition 1 via reversal of time, by treating
as left-truncated by
. □
Propositions 1–3 lead to the following corollary.
Corollary 1.
Quasi-independence yields the standard risk-set-adjusted estimators of the distributions of both
and
as the nonparametric maximum likelihood estimators.
Assumptions (1), (2) and (5) are indistinguishable given the observed data. We formalize this conclusion in Propositions 4 and 5 and Corollary 2. Proposition 4 shows that the likelihood under (2) is equivalent to that under (1), implying that these conditions cannot be distinguished. Proposition 5 shows that (5) and (1) cannot be distinguished.
Proposition 4.
Assuming factorization (2), quasi-independence (1) cannot be determined from the observed data. As a consequence, while
is identifiable under (2),
is not.
Proof.
This follows from the equivalence of the likelihood functions under quasi-independence (1) and factorization (2). Under the latter, the likelihood (3) is
Under quasi-independence (1), the likelihood (3) is
Since
is defined only on the observable region, it is unique only up to a constant factor. Assuming that
and
have positive mass at the observed times
only, but not assuming their functional forms, the contributions to the likelihood from
are identical under (1) and (2). Hence
is nonidentifiable from the data.
Proposition 5.
Assuming factorization (5), quasi-independence (1) cannot be determined from the observed data. Thus, while
is identifiable under (5),
is not.
Corollary 2.
Quasi-independence (1) cannot be distinguished from the factorization condition (2) only, or from the factorization condition (5) only, based on the observed data.
2.2. Estimation under right censoring
The nonidentifiability problem persists in the presence of right censoring. There are two practical models for right censoring in the presence of left truncation (Qian & Betensky, 2014): one is on the residual time scale, i.e., censoring of 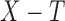 , and the other is on the original time scale, i.e., censoring of
, and the other is on the original time scale, i.e., censoring of 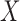 . We extend the likelihood decomposition (3) to accommodate these models.
. We extend the likelihood decomposition (3) to accommodate these models.
We first consider the independent residual censoring assumption. Suppose that 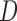 is a residual censoring time such that
is a residual censoring time such that 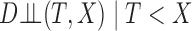 , where
, where 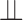 denotes independence, and that censoring of
denotes independence, and that censoring of 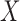 occurs at
occurs at 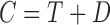 , the total censoring time starting from the time origin. The observed data then comprise
, the total censoring time starting from the time origin. The observed data then comprise 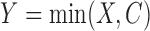 ,
, 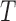 and
and 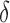 , where
, where 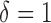 if
if 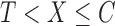 and
and 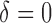 if
if 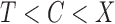 . This model is appropriate when censoring occurs only after entry into the study. The likelihood contribution for an uncensored observation is the same as that in (3):
. This model is appropriate when censoring occurs only after entry into the study. The likelihood contribution for an uncensored observation is the same as that in (3):
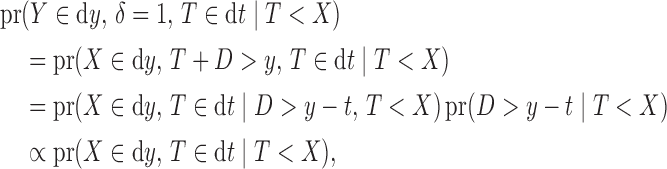 |
where the final relation follows from 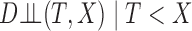 and the noninformativeness of the distribution of
and the noninformativeness of the distribution of 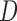 for that of
for that of 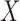 . The contribution for a censored observation is
. The contribution for a censored observation is
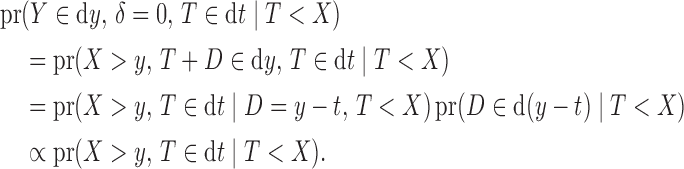 |
The probability 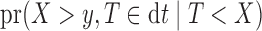 can be expressed as
can be expressed as
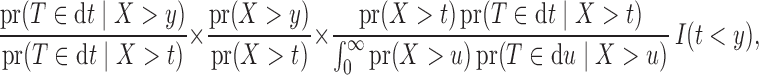 |
where the first term is unity under the factorization condition (2).
We next derive the likelihood decomposition under the censoring scheme on the original time scale, where  is measured from the time origin, with
is measured from the time origin, with  assumed, and
assumed, and 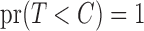 as in Tsai (1990). The condition
as in Tsai (1990). The condition 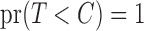 ensures that censoring can occur only for the sampled individuals. The overall likelihood under this censoring scheme equals that under the residual censoring model, given the assumed noninformativeness of
ensures that censoring can occur only for the sampled individuals. The overall likelihood under this censoring scheme equals that under the residual censoring model, given the assumed noninformativeness of  given
given 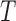 for
for 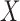 and that of
and that of 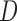 given
given 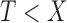 . Thus, under both models for censoring, the overall likelihood for left-truncated and right-censored data is
. Thus, under both models for censoring, the overall likelihood for left-truncated and right-censored data is
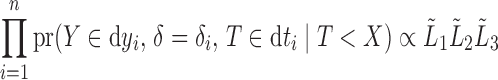 |
where
 |
Under (2), 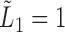 . As in the uncensored case,
. As in the uncensored case,  is the only component of the likelihood that contributes to estimation of
is the only component of the likelihood that contributes to estimation of 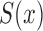 by the risk-set-adjusted Kaplan–Meier estimator (Wang, 1991)
by the risk-set-adjusted Kaplan–Meier estimator (Wang, 1991)
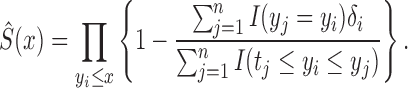 |
(6) |
As in Proposition 4, under (2) the data cannot inform whether 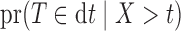 equals
equals  or
or 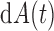 . Nonetheless, the nonparametric maximum likelihood estimator of
. Nonetheless, the nonparametric maximum likelihood estimator of 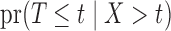 , assuming that it is a distribution function, is
, assuming that it is a distribution function, is
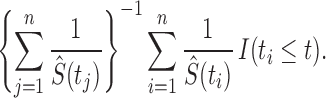 |
(7) |
In the setting of independent 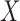 and
and 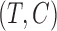 with
with 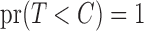 , (7) estimates
, (7) estimates 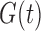 (Wang, 1991). Under factorization (2) without quasi-independence, (7) maximizes the likelihood
(Wang, 1991). Under factorization (2) without quasi-independence, (7) maximizes the likelihood 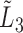 given
given  and estimates a normalized version of
and estimates a normalized version of 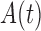 and not
and not 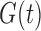 . Under factorization (5) without quasi-independence, an alternative decomposition of the likelihood with similar arguments yields the analogous result for estimation of
. Under factorization (5) without quasi-independence, an alternative decomposition of the likelihood with similar arguments yields the analogous result for estimation of 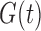 and
and 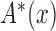 , as shown in the Supplementary Material.
, as shown in the Supplementary Material.
3. Testing for the factorization condition
A statistic commonly used to test for quasi-independence is the conditional Kendall’s tau (Tsai, 1990; Martin & Betensky, 2005). In the presence of censoring, this is defined as 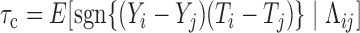 , where
, where  and
and 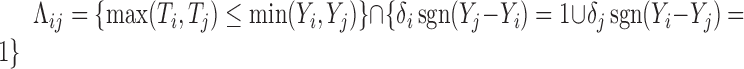 denotes the event that the pair
denotes the event that the pair 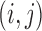 is comparable and orderable. A consistent estimator of
is comparable and orderable. A consistent estimator of 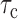 is the basis of a test for the null hypothesis of (2) or (5), versus the alternative of neither (2) nor (5). This is justified by
is the basis of a test for the null hypothesis of (2) or (5), versus the alternative of neither (2) nor (5). This is justified by 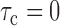 under (2) or (5). We derive this for (2); the calculations are similar under (5):
under (2) or (5). We derive this for (2); the calculations are similar under (5):
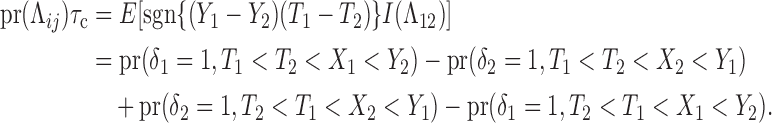 |
(8) |
Under the residual censoring model and factorization condition (2), and upon defining 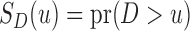 as the survival function of
as the survival function of 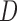 , we can express
, we can express  as
as
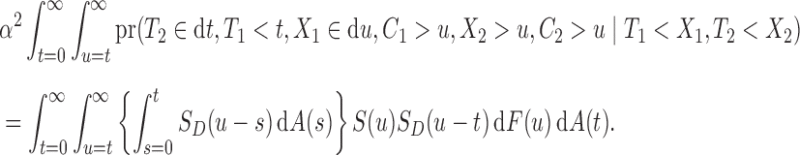 |
The second term of (8) can be expressed similarly, and the remaining two terms are trivially equivalent to the first two terms upon relabelling the indices. A similar result applies under the original-scale censoring model. This demonstrates that 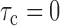 under either factorization condition, and the conditional Kendall’s tau provides a valid test for the null of either (2) or (5). If the test does not reject the null hypothesis, then under (2), Proposition 4 states that
under either factorization condition, and the conditional Kendall’s tau provides a valid test for the null of either (2) or (5). If the test does not reject the null hypothesis, then under (2), Proposition 4 states that 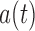 cannot be distinguished from
cannot be distinguished from  in the observable region, and so quasi-independence cannot be distinguished from factorization. This holds for any test of factorization in the absence of external information.
in the observable region, and so quasi-independence cannot be distinguished from factorization. This holds for any test of factorization in the absence of external information.
4. Simulation
We conducted a simulation study to illustrate empirically that the factorization condition (2) alone, without quasi-independence (1), is sufficient for the validity of the risk-set-adjusted Kaplan–Meier estimator for the distribution of 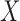 , as stated in Proposition 1. We also demonstrate that Kendall’s tau yields a valid test of the factorization condition even in the absence of quasi-independence. Finally, we illustrate Proposition 4, that under (2) without the complementary condition (5), we may not be able to estimate the truncation distribution
, as stated in Proposition 1. We also demonstrate that Kendall’s tau yields a valid test of the factorization condition even in the absence of quasi-independence. Finally, we illustrate Proposition 4, that under (2) without the complementary condition (5), we may not be able to estimate the truncation distribution 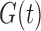 . Let
. Let
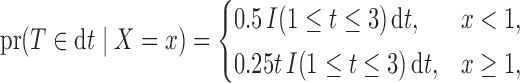 |
where 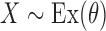 and we set
and we set  . It follows that
. It follows that 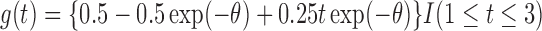 ,
, 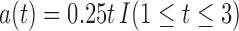 , and
, and 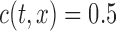 if
if 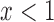 and
and 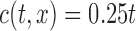 if
if  . Since
. Since 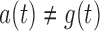 , quasi-independence does not hold. We generated right censoring through an independent residual censoring time
, quasi-independence does not hold. We generated right censoring through an independent residual censoring time 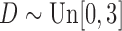 . Each sample consisted of
. Each sample consisted of  triples
triples 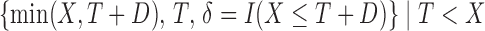 . This yielded 88% truncation and 30% censoring based on 1000 replications.
. This yielded 88% truncation and 30% censoring based on 1000 replications.
Our first aim is to check the validity of the risk-set-adjusted Kaplan–Meier estimator of the conditional distribution,  . The full marginal
. The full marginal 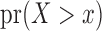 is not estimable because there is no information for
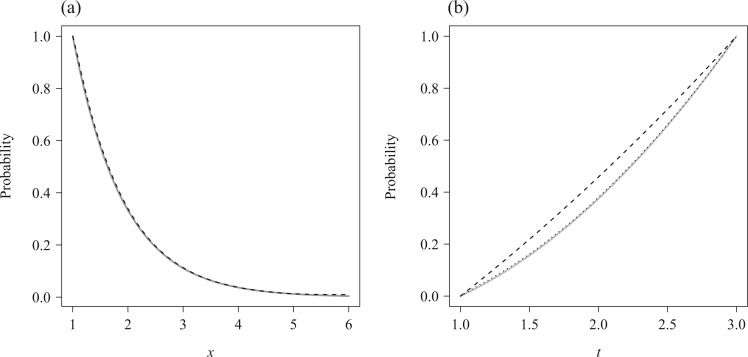
is not estimable because there is no information for  . Figure 1(a) displays the averaged adjusted Kaplan–Meier estimate, which is indistinguishable from its target, confirming that the adjusted Kaplan–Meier estimator is valid under condition (2) and does not require the stronger condition (1). We also applied the conditional Kendall’s tau test of Martin & Betensky (2005) and obtained an estimated Type I error of 0.041, which supports the validity of the test for either factorization condition even in the absence of quasi-independence. Figure 1(b) shows that the estimator (7) estimates
. Figure 1(a) displays the averaged adjusted Kaplan–Meier estimate, which is indistinguishable from its target, confirming that the adjusted Kaplan–Meier estimator is valid under condition (2) and does not require the stronger condition (1). We also applied the conditional Kendall’s tau test of Martin & Betensky (2005) and obtained an estimated Type I error of 0.041, which supports the validity of the test for either factorization condition even in the absence of quasi-independence. Figure 1(b) shows that the estimator (7) estimates 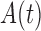 and not
and not  , as expected from Proposition 4.
, as expected from Proposition 4.
Fig. 1.
Simulation results for the estimation of: (a) 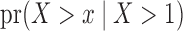 , with a grey solid line depicting the true curve and a black dashed line depicting the average of Kaplan–Meier estimates; (b)
, with a grey solid line depicting the true curve and a black dashed line depicting the average of Kaplan–Meier estimates; (b) 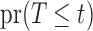 , with a grey solid line depicting the true
, with a grey solid line depicting the true  , a black dotted line depicting the average of the estimates of Wang (1991), and a black dashed line depicting
, a black dotted line depicting the average of the estimates of Wang (1991), and a black dashed line depicting  .
.
5. Discussion
We have shown that the commonly accepted requirement of quasi-independence of 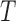 and
and 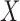 is stronger than the factorization condition (2) that is actually needed for nonparametric estimation of the distribution of
is stronger than the factorization condition (2) that is actually needed for nonparametric estimation of the distribution of 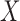 . While we can test for factorization, the observed data do not allow us to distinguish between quasi-independence (1) and the two factorization conditions (2) and (5). This highlights an identification problem that has not been recognized in the literature; an unverifiable assumption is therefore required in order to estimate the distribution of
. While we can test for factorization, the observed data do not allow us to distinguish between quasi-independence (1) and the two factorization conditions (2) and (5). This highlights an identification problem that has not been recognized in the literature; an unverifiable assumption is therefore required in order to estimate the distribution of 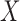 based on truncated data. In some observational studies, the origin may be observed for all subjects and the delayed study entry time may be externally determined, such as by calendar date. In this case,
based on truncated data. In some observational studies, the origin may be observed for all subjects and the delayed study entry time may be externally determined, such as by calendar date. In this case, 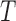 is known for the whole population and so
is known for the whole population and so  is known. If factorization is not rejected via Kendall’s tau test, knowledge of
is known. If factorization is not rejected via Kendall’s tau test, knowledge of 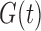 enables the factorization condition (2) to be distinguished from quasi-independence (1) and the factorization condition (5). In particular, if factorization holds and
enables the factorization condition (2) to be distinguished from quasi-independence (1) and the factorization condition (5). In particular, if factorization holds and 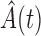 does not estimate
does not estimate 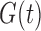 , it follows from Proposition 3 that condition (5) does not hold, which means that (2) must hold and, importantly, we can estimate
, it follows from Proposition 3 that condition (5) does not hold, which means that (2) must hold and, importantly, we can estimate  .
.
Supplementary Material
Acknowledgement
The first two authors contributed equally. We thank Micha Mandel and Richard Cook for helpful comments. We acknowledge funding from the U.S. National Institutes of Health.
Supplementary material
Supplementary material available at Biometrika online includes the derivation of an explicit expression for 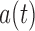 given
given 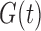 ,
, 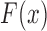 and
and 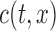 under factorization condition (2); it also contains a proof that under (5) and for both censoring models, although
under factorization condition (2); it also contains a proof that under (5) and for both censoring models, although 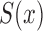 is nonidentifiable,
is nonidentifiable, 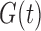 is identifiable and its nonparametric maximum likelihood estimator is similar to the estimator (7).
is identifiable and its nonparametric maximum likelihood estimator is similar to the estimator (7).
References
- Betensky, R. A. (2000). On nonidentifiability and noninformative censoring for current status data. Biometrika 87, 218–21. [Google Scholar]
- Keiding, N. (1992). Independent delayed entry In Survival Analysis: State of the Art, Klein J. P. & Goel P. K., eds. Dordrecht: Springer, pp. 309–26. [Google Scholar]
- Lynden-Bell, D. (1971). A method of allowing for known observational selection in small samples applied to 3CR quasars. Mon. Not. R. Astron. Soc. 155, 95–118. [Google Scholar]
- Martin, E. C. & Betensky, R. A. (2005). Testing quasi-independence of failure and truncation times via conditional Kendall’s tau. J. Am. Statist. Assoc. 100, 484–92. [Google Scholar]
- Qian, J. & Betensky, R. A. (2014). Assumptions regarding right censoring in the presence of left truncation. Statist. Prob. Lett. 87, 12–7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tsai, W.-Y. (1990). Testing the assumption of independence of truncation time and failure time. Biometrika 77, 169–77. [Google Scholar]
- Vardi, Y. (1989). Multiplicative censoring, renewal processes, deconvolution and decreasing density: Nonparametric estimation. Biometrika 76, 751–61. [Google Scholar]
- Wang, M.-C. (1991). Nonparametric estimation from cross-sectional data. J. Am. Statist. Assoc. 86, 130–43. [Google Scholar]
- Wang, M.-C., Jewell, N. P. & Tsai, W.-Y. (1986). Asymptotic properties of the product limit estimate under random truncation. Ann. Statist. 14, 1597–605. [Google Scholar]
- Williams, J. S. & Lagakos, S. W. (1977). Models for censored survival analysis: Constant-sum and variable-sum models. Biometrika 64, 215–24. [Google Scholar]
- Woodroofe, M. (1985). Estimating a distribution function with truncated data. Ann. Statist. 13, 163–77. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.