Abstract
Design of pharmacological trials for management of substance use disorders is shifting toward outcomes of successful individual-level behavior (abstinence or no heavy use). While binary success/failure analyses are common, McCann and Li (CNS Neurosci Ther 2012; 18: 414–418) introduced “number of beyond-threshold weeks of success” (NOBWOS) scores to avoid dichotomized outcomes. NOBWOS scoring employs an efficacy “hurdle” with values reflecting duration of success. Here we evaluate NOBWOS scores rigorously. Formal analysis of mathematical structure of NOBWOS scores is followed by simulation studies spanning diverse conditions to assess operating characteristics of five linear-rank tests on NOBWOS scores. Simulations include assessment of Fisher’s exact test applied to hurdle component. On average, statistical power was approximately equal for five linear-rank tests. Under none of conditions examined did Fisher’s exact test exhibit greater statistical power than any of the linear-rank tests. These linear-rank tests provide good Type I and Type II error control for comparing distributions of NOBWOS scores between groups (e.g., active vs. placebo). All methods were applied to re-analyses of data from four clinical trials of differing lengths and substances of abuse. These linear-rank tests agreed across all trials in rejecting (or not) their null (equality of distributions) at p ≤ 0.05.
Keywords: linear-rank tests, pharmacotherapy development, randomized clinical trial, statistical power, substance use disorders, Type I error
1. Introduction
Currently no official U.S. Food and Drug Administration (FDA) guidelines exist that specifically address the development of medications to treat substance use disorders; however, a recent commentary by FDA staff1 recommends the use of responder analyses in related clinical trials. This recommendation is consonant with FDA reviewers’ comments in drug approval packages. For example, in the approval package for naltrexone XR injection for alcohol use disorder,2 the applicant’s pre-defined primary efficacy endpoint (event rate of heavy drinking) was judged to be “inadequate” by FDA reviewers, who commented that “the endpoint is a result of group mean analysis and does not provide information on the effects of treatment on an individual level.” Naltrexone XR injection received regulatory approval after the FDA conducted a responder-based re-analysis of efficacy data, with treatment success defined as an absence of heavy drinking days (an absence of five or more drinks/day for men and an absence of four or more drinks/day for women). The reviewers stated that an absence of heavy drinking is the “optimal definition of treatment success in alcoholism trials,” citing data on the health consequences of heavy drinking in comparison with no heavy drinking. For other substances of abuse (e.g., tobacco, cocaine and methamphetamine), data on the relative health consequences of “heavy” vs. “light” use are lacking and, therefore, FDA staff have stated that abstinence is the only pattern of use with generally accepted clinical benefit.1 The application of abstinence as an efficacy endpoint is exemplified in the drug approval package for varenicline in smoking cessation.3 FDA reviewers allowed a grace period for onset of efficacy at the beginning of efficacy trials; and they defined success as “complete abstinence, suitably biochemically verified over multiple visits, from the end of the grace period to the end of the ascertainment period.” A grace period to allow time for onset of efficacy may also be used in alcohol medication trials with a primary endpoint of no heavy drinking.4
Whether the therapeutic goal is decreased alcohol use (no heavy drinking) or complete abstinence from other substances of abuse, the FDA-guided evolution of medication efficacy trials presents the field with two related problems. First, the period of time required for onset of efficacy may be unclear for a new medication, leading to the specification of an inappropriate grace period. This problem occurred during the development of varenicline for smoking cessation.3 The FDA initially advised the company (Pfizer) that a “last four weeks of treatment” window would be most suitable for efficacy evaluations. This resulted in specification of an 8-week grace period in the company’s 12-week trials. During their review of the varenicline new drug application, FDA staff reanalyzed the data using different grace periods and concluded that the 8-week grace period was “not fully justified.” The reviewers noted that the efficacy of varenicline was apparent even with a 2-week grace period; however, they also noted that “there were quite a few individuals who required several weeks to initiate abstinence.” Thus, even at the time of New Drug Application review, with data from eight completed Phase II/III studies in hand, no single, fixed grace period could be defined that was appropriate for all individuals. Given that similar individual-to-individual variation in time to onset of efficacy may be seen with any new medication, a second and related problem is posed by the dichotomization of data into treatment success and failure; it is well-established that the dichotomization of data may lead to a loss of statistical power5–9, and decreased statistical power necessitates larger, more expensive trials.
McCann and Li9 have attempted to address these problems by developing a non-binary method of efficacy scoring (and hypothesis testing) that allows researchers to define a minimum criterion for treatment success and then quantify the level of success in each individual. This method is best explained through example; and the above-mentioned 12-week varenicline trials will be used to describe its potential application. The first step is to define a minimum level of success that is clinically important. For the 12-week varenicline trials, abstinence during weeks 9 through 12 appears to be an adequate definition of minimum success because the FDA initially specified that abstinence during the last four weeks of treatment was the most suitable endpoint for varenicline. (It is assumed this reflects an FDA opinion on clinical importance). To implement McCann and Li’s9 method, 1) 3 weeks of abstinence lasting through the end of treatment (3 weeks of “end-of-study abstinence”) would serve as a threshold that must be exceeded to achieve success; 2) the duration of end-of-study abstinence would be determined from the data for each individual; and 3) the number of beyond-threshold weeks of success (NOBWOS) would be determined. For example, an individual who smoked during week 8 but did not smoke during weeks 9 through 12 would have exhibited four weeks of end-of-study abstinence (minimum success), and would receive a NOBWOS score of one. In contrast, an individual who did not smoke for the entire duration of the 12-week trial would have achieved 12 weeks of end-of-study abstinence and would receive a NOBWOS score of nine (12 minus the 3-week threshold). Any individuals failing to exceed the 3-week threshold (treatment failures) would be assigned NOBWOS scores of zero. NOBWOS scores in the placebo and varenicline groups would then be compared. With a similar focus on end-of-study abstinence, use of this method (hereafter referred to as “NOBWOS method”) has previously been illustrated in the re-analysis of data from a trial of bupropion in methamphetamine use disorder.9 However, it is important to note that the NOBWOS method does not require a focus on abstinence; by focusing on the number of weeks with no heavy drinking, the method can also be applied to medication trials in alcohol use disorder. As such, our development below is generalized to outcomes of “successful behavior” rather than abstinence only.
McCann and Li9 introduced the novel concept of the NOBWOS method and provided one example of its application to data from a clinical trial. The study detailed below in section 2 through section 4 goes much further, providing a thorough assessment of the statistical properties of the NOBWOS method, thereby providing a complete resource for practitioners who wish to apply NOBWOS scores in a fully informed way as a more powerful alternative to the current standard in the field—binary success/failure analysis. In particular, our study adds the following.
We explicitly recognize and define NOBWOS scores as a bivariate interval (“regional”) censoring that produces a two-component-mixture data-generating process of hurdle structure. McCann and Li9 did not recognize the presence of censoring at all.
We assess if any improvements in operating characteristics, especially statistical power, could be obtained by applying some alternatives to the only testing procedure advocated by McCann and Li9—van der Waerden testing.
We perform an extensive series of simulation studies and under a wide range of conditions to assess the operating characteristics of their original procedure, some alternative linear rank tests and, importantly, binary success/failure analysis. McCann and Li9 did not assess operating characteristics at all.
In contrast to McCann and Li9, we detail and emphasize throughout what specific hypothesis test their procedure is assessing (difference in distribution).
We demonstrate that the NOBWOS method can be applied to clinical trials of clinically divergent substances (methamphetamine, alcohol and nicotine). McCann and Li9 only examined application to methamphetamine.
Such an extensive and practitioner-oriented statistical assessment of the NOBWOS method is essential to 1) address concerns of those who are currently satisfied with application of binary success/failure analysis and thereby 2) allow substance-use disorder research to move forward through application of the statistically more powerful technique of linear-rank testing of NOBWOS scores. To further ease application by practitioners, we restrict attention to linear-rank testing because these are a class of distribution-free testing procedures and thereby do not require that practitioners assess any assumptions regarding parametric distributions.
2. Methods
2.1. Conceptual Model
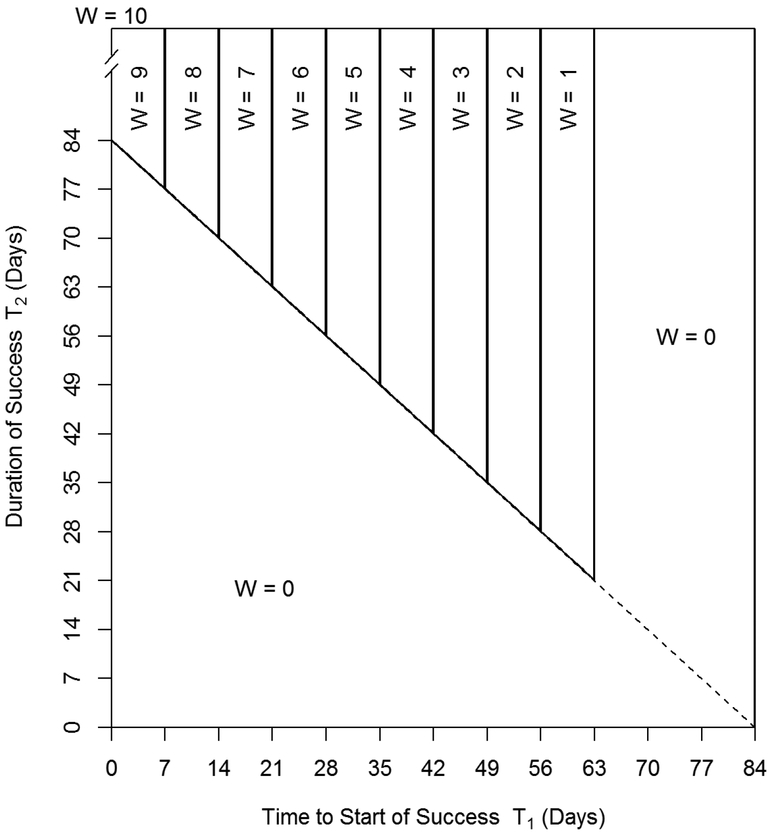
Suppose the active-intervention period of a randomized clinical trial has duration 0 < τ. Partition this duration into r intervals (e.g., weeks), [0,τ/r), [τ/r, 2 τ/r), …, [(r – 1)τ/r, τ], with r finite. Let the threshold period constitute the last s < r of these intervals, [(r – s)τ/r, τ]. An individual’s period of success begins at time T1, which defines the period of time required for onset of efficacy, and ends at a time given by the sum T1+T2, where T2 is the duration of efficacy. Denote the joint distribution of random variables T1 and T2 by , parameterized by θ, where the case convention is used throughout that lowercase x denotes a particular fixed instance of random variable X. T1 is measured from the time of randomization so that has support restricted to the upper right real quadrant {0 ≤ T1} ∪ {0 ≤ T2} (as in figure 1). An individual may experience multiple, discontinuous periods of success during the active-intervention period. Denote the jth such interval by Ij= [Tj1, Tj1 + Tj2]. Let the , be the set of all such intervals for the individual. Of interest here only is that Ij that extends from prior to and through (or to the end of) the threshold period.
Figure 1.
Mapping of the NOBWOS score W on the joint distribution of time to start of success T1 and duration of success T2 for an example where the total duration of τ = 84 days is partitioned into r =12 (i.e., weekly) intervals of which the last s = 2 weeks comprise the end-of-study threshold period. The vertical axis extends, in theory, to infinity. The nine quadrilaterals designate where the joint distribution of T1 and T2 map to the integer sequence of W for which 0 < W ≤ 9. A score of W = 10 only obtains at T1 = 0 and is confined to the vertical line segment extending toward infinity from {0, τ}. The six-sided concave polygon defines the continuous region wherein the joint distribution of T1 and T2 maps to W = 0, which represents individuals without any continuous periods of success that fully include the end-of-study threshold period (and individuals without a period of success). For example, consider an individual whose success begins on day 64. Even though this start is prior to threshold period, the full tenth week is not a success; so the individual receives W = 0. This explains why the vertical line on the right side of the W = 1 region is T1 = τ(r – s −1)/r. The region above the diagonal line (T2 = τ – T1, upper right triangle) is after the end of the active-intervention period (lower left triangle). If success is only defined during the active intervention period (Winsorization), NOBWOS scores greater than zero are mapped to the solid diagonal line.
The NOBWOS score W is an interval censoring10 or, more properly, a “regional” censoring in that each NOBWOS score defines a region of the joint distribution of T1 and T2 (figure 1). Denote this mapping by ∇(T1, T2) → W, with ∇(T1, T2) defined as
| E1 |
where ⌈r(T1/τ)⌉ is the ceiling operator, rounding r(T1/τ) up to the nearest integer. Note that a NOBWOS score W of zero results if either of two conditions obtains. The condition (r – s)τ/r < T1 signifies that success began too late, on or after start of the threshold period; while T1 + T2 < τ arises when success ends too early, before conclusion of the threshold period. If the threshold period is brief, a concentration of NOBWOS scores at zero can result. This is an example of a “hurdle” model.11 In this case the “hurdle” is that individuals must at least be successful during the threshold period. The full distribution of W can be written as follows:
| E2 |
where z = 1 for any W = 0 and z = 0 for any 0 < W, with convention 00 = 1. This mass function has two components. The first (hurdle) component m1(w|θ, r, s, τ) = 1 for W = 0. The second component has positive mass for 0 < W ≤ r − s and for W = 0. In the notation above, θ* is augmented with the design-parameter vector {r, s, τ} plus the mixing parameter ϖ, θ* = {θ, r, s, τ, ϖ}. Because is degenerate in that it is a point mass, can be written more compactly as
| E3 |
Thus far we have implicitly assumed full follow-up past τ into the post-intervention period. However, because pharmacotherapy trials are designed to assess if the assigned intervention causes successful behavior, some investigators may wish to limit assessment of success to the period of potential treatment exposure (i.e., active-intervention period). Effectively, this Winsorizes the distribution of the sum T1 + T2 at τ. That is, any value of T1 + T2 beyond τ is mapped back to τ. Denote the Winsorized joint distribution as . An interesting property of is that nearly all nonzero NOBWOS scores are confined to intervals along the upper boundary of its domain, represented, for example, by the partitions of the solid and dashed diagonal line of figure 1, running from coordinates {0, 84} to {84, 0} and subtending the various regions for W ∈ {1, 2, …, 9}. (These intervals are open at top left end and closed at bottom right end so that, for instance, the point (56, 28) maps to W = 2.) Two exceptions are the maximal score, W = 10 in this example, which is reduced to a point {0, τ} and the minimum score of W = 0 given by the lower left triangular region that includes the dashed line.
While the specific formulation of the joint continuous distribution differs among full follow-up and Winsorized conditions, the mass function of the NOBWOS scores does not, due to the interval censoring ∇(T1, T2) → W. Whether full follow-up or Winsorized, the mass assigned to any particular NOBWOS score is the result of a double integral over a planar region bounded below in the direction of T2 by an interval along the line segment from {0, τ} to {τ, 0} (e.g., figure 1). The distinction being that Winsorization concentrates mass in the direction of T2 along the line segment from {0, τ} to {τ, 0} for W ∈ {1, 2, …, 9}.
2.2. Hypothesis Testing
2.2.1. Linear-Rank Tests
For hypothesis tests comparing two different treatment conditions (e.g., placebo versus active compound) based on NOBWOS scores, McCann and Li9 suggested the van der Waerden test. (We are deliberately being vague here about the specific hypotheses being tested because this will be detailed later in this section.) This is a linear-rank test and, because McCann and Li9 focused on a linear-rank test, that is also our focus here. Also, we confine analysis to linear-rank testing because distribution-free procedures do not require that practitioners assess any assumptions regarding parametric distributions.
In the two-sample case, the general form of a linear-rank statistic is
| E4 |
where is a rank-score function of sample rank of the ith individual, i ∈ {1, …, n}, on the outcome of interest12 in the qth group q ∈ {1, 2}. For instance, sample ranks could be formed from the NOBWOS scores. The vqi are regression constants.13 For a two-sample comparison, the vqi are indicator variables for group membership (e.g., v1i = 0 and v2i = 1) so that is the sum within one of the two groups. The van der Waerden scores are obtained from the standard (expectation = 0, variance = 1) Gaussian inverse cumulative distribution function (ICDF), . For comparison, in sections 2.2.2 and 2.3 we also examine rank score functions using two contrasting ICDFs: the standard (expectation = 0, variance = 1) Laplace, which is more leptokurtic (“peaked”) than the normal distribution, and the central Student’s t on three degrees of freedom, which is more platykurtic (“fatter tailed”) than the normal distribution, where we denote the latter by t(3). We take this one step further with a beta distribution of parameters a = b = 1/2 which has a “bathtub” shape with equal modes at each end of the support. Finally, due to its widespread use, and simplicity of formulation, we also examine Wilcoxon scores that are , which yield the Mann-Whitney-Wilcoxon rank sum test.14
Tests based on linear-rank statistics employed for the purpose of testing two-sample hypotheses about location may detect other differences in populations’ distributions, namely differences in shape,15 because, at least traditionally, this is what they have been designed to do.16 However, in many settings, comparisons of efficacy or effectiveness between treatment conditions are intended to test hypotheses of location (e.g., differences in means). To illustrate, consider the following seven simulation studies (table 1). A random sample of 75 observations was drawn from each of two gamma distributions of common expectation (1), an asymptotic approximation of the van der Waerden test was applied, and the p-value was recorded. Gamma distributions were employed because these are often employed to model durations and NOBWOS scores are built upon observed durations. This process was repeated 7 500 times and Type I error was estimated as the proportion of tests yielding p < 0.05. In the second through fourth studies, variances are equal to near equal and Type I error is close to nominal (~5%). However, as differences between variances become larger, Type I error inflates considerably. One can perform linear-rank tests by making the (strong) assumption that the two distributions differ only with regard to location, as is often prescribed,14 what we can call the “shift hypothesis.” That assumption would need to evaluated for each application of NOBWOS scores because these scores are bounded on the closed interval [0, r − s]; and a bounded support coerces relationship between mean and variance.17 Practically speaking, situations where the shift hypothesis holds fully (change in mean only between populations) may be the exception.i
Table 1.
Seven simulation studies to estimate Type I error rates for the asymptotic approximation of the van der Waerden test applied to samples of 75 observations drawn from each of two gamma distributions. Null hypothesis is no difference in location between populations. Each estimate is based on 7 500 samplings from each population. In each study (except third), populations have the same mean (expectation) but different variances.
| Study | Population 1 | Population 2 | Estimated Type I Error |
||
|---|---|---|---|---|---|
| Expectation | Variance | Expectation | Variance | ||
| 1 | 1 | 1 | 1 | 4/3 | 0.098 |
| 2 | 1 | 1 | 1 | 10/9 | 0.055 |
| 3 | 1 | 1 | 1 | 1 | 0.045 |
| 4 | 1 | 1 | 1 | 9/10 | 0.052 |
| 5 | 1 | 1 | 1 | 3/4 | 0.085 |
| 6 | 1 | 1 | 1 | 1/2 | 0.207 |
| 7 | 1 | 2 | 1 | 1 | 0.356 |
Traditionally, tests based on linear rank statistics were derived assuming that ranking is performed on random variables drawn from continuous distributions.16 However, NOBWOS scores are discrete (integer-valued) and typically restricted to a narrow range of possible values because r is measured in weeks (e.g., zero to ten). Even if finer-grained units are employed (e.g., days), ties, perhaps many, occur at NOBWOS scores of zero. Here we adopt the convention of averaging sample rank values for tied observations, which has been shown to have identical asymptotic efficiencies to the mid-rank method and randomized-ranks method for handling ties.13 Throughout, asymptotic approximations were employed for calculating attained significance levels (p-values), which was done because these approximations would normally be used in practice in the larger samples examined here and also to keep run times manageable for the simulation studies.
2.2.2. Simulation Studies
2.2.2.1. Testing Procedures
Forty-two Monte Carlo simulation studies (sensu Dodge18) were conducted to assess the operating characteristics (Type I error and Type II error) of the five linear-rank tests (van der Waerden, Laplace, t(3), beta, and Mann-Whitney-Wilcoxon) and t-test performed on sample values of NOBWOS scores, with rationale for choice of tests given in section 2.2.1. Large-sample approximations were employed for all five linear-rank tests.19, ii We included a t-test because, in larger samples such as those simulated here, the tail probabilities of the t distribution are robust to even strong skewness in the sampled population.20 Also of interest is that parametric tests may not always demonstrate greater statistical power than corresponding nonparametric tests (e.g., two-sample comparisons), as mentioned in section 2.2.1; although correspondence is often imperfect because, for example, t-tests and linear rank-test are assessing different null hypotheses (equivalence of means vs. equivalence of distributions), unless further constraints are placed on the linear rank-test. For t-testing, Welch’s approximation was employed to accommodate possibly unequal variances.21 Comparisons also include Fisher’s exact testing of ϖ, the probability of success throughout the end-of-study threshold period plus at least one contiguous additional week during the active-intervention period (i.e., minimum success or the “hurdle” component). Compared to this binary outcome, NOBWOS scores are based on more and narrower censoring intervals, which should enhance statistical power for two-sample tests of location if the populations primarily differ in their distributions above W = 0 (i.e., the right tail).22 We employed Fisher’s exact testing 1) because sampling variation arises from random assignment of participants to conditions23, and 2) to allow for the fact that cell expectations for successes can be quite small.iii
2.2.2.2. Design of 42 Simulation Conditions
Simulations were designed to have realistic temporal patterns of usage of the target substance of abuse and of missing data. Pooled data were used from seven, separate NIDA-sponsored randomized clinical trials of candidate pharmacotherapies for cocaine use disorder: baclofen24, cabergoline, modafinil25, ondansetron26, reserpine27, selegiline28, and tiagabine.29 We did have data available to us from clinical trials for other substances of abuse (alcohol and tobacco). For some of these, the sample size per trial was sizable; however, the quantity of trials was small, limited to one or two. In contrast, the data from the cocaine studies was drawn from seven clinical trials and thus provided us with the largest quantity of independent samplings and as such represented the greatest opportunity to have data spanning the diversity of a treatment-seeking substance use disorder population. Data for simulations were restricted to the placebo arm to employ temporal usage patterns as similar as possible to untreated (on to which simulations artificially imposed a treatment effect of known size). For each iteration of the simulation, 150 individuals were randomly selected without replacement and half (75) of these were randomly assigned to the active arm. The quantity 150 was selected because this approximates sample sizes employed in NIDA-sponsored trials of pharmacotherapies for substance use disorders (e.g., bupropion, section 2.3). The data for each individual consisted of a matrix, the first column containing the times at which urine samples were provided and the second column containing the respective cocaine urine-metabolite results (positive or negative). By protocol for all seven studies, urine results were to be obtained three times per week. Per standard practice for NIDA-sponsored clinical trials, each column was censored at the date of the last dose of the assigned agent (here placebo) taken by the individual. Columns were also administratively censored at the trial length designated for the simulation study (either 8 or 12 weeks). An effect of active treatment was artificially introduced by randomly assigning a value for time to start of success T1 and duration of success T2 drawn from a bivariate exponential distribution formulated from a Gaussian copula with correlation ρ = 1/2 between T1 and T2. From T1 to T1 + T2, by definition, any usage was set to zero. Use of exponential distributions assumes a temporally constant “risk” of initiating successful behavior and, after successful behavior has initiated, a temporally constant risk of success ending. Clearly this is the simplest model and alternatives are possible (section 4). Simulations used an end-of-study threshold period with durations of 1, 3, and 5 weeks (table 2). Mean durations to onset of efficacy E[T1] were 1, 3, 5 and 7 weeks. Mean durations of success E[T2] were 12 and 14 weeks. These durations were selected to be on the same scale as the active intervention period in many trials of pharmacotherapies for substance use disorders (e.g., 8 to 12 weeks). Note that T1 and T2 create a period of success for the individual in addition to any such periods already present in the data for the individual from a placebo arm. Six additional simulations were conducted without artificial introduction of any success in order to characterize Type I error. One-thousand iterations were run for each of the 42 simulation studies.
Table 2.
Statistical power of forty-two simulation studies based on pooled placebo data from NIDA-sponsored trials of pharmacotherapies for cocaine use disorder. The duration of the end-of-study threshold period was either 1, 3 or 5 weeks in length. One-thousand iterations were run for each condition. The sample size for each iteration was 150 individuals, with 75 randomly assigned to placebo and 75 randomly assigned to active. Those randomly assigned to active were assigned a time until the start of a period of success T1.T1 is measured from randomization and T2 is measured from the end of T1. T1 and T2 were randomly drawn from a bivariate exponential distribution, with means for T1 as given in the third column. Mean for T2 was 12 weeks or 14 weeks, as indicated. Six conditions include no artificial introduction of a period of success to permit estimation of Type I error. The van der Waerden, t(3) linear-rank, Laplace linear-rank, beta linear-rank, Wilcoxon and t-tests are all performed on NOBWOS scores. t-tests allowed for unequal variances (Welch’s approximation). Fisher’s exact test is performed on presence or absence of success during the end-of-study threshold period plus one contiguous week during the active-intervention period. Weeks = wks and not applicable = NA.
| Duration of End-of-study Threshold Period |
Duration of Active-Intervention Period |
Mean Time to Onset of Efficacy T1 |
Mean Duration of Efficacy T2 | Error Type |
van der Waerden | t(3) | Laplace | Beta | Mann-Whitney-Wilcoxon | t-test | Fisher’s Exact |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 8 | 3 | 12 | I | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 | 0.02 |
| 1 | 8 | 1 | 12 | II | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 0.99 |
| 1 | 8 | 3 | 12 | II | 0.96 | 0.93 | 0.94 | 0.97 | 0.97 | 0.92 | 0.95 |
| 1 | 8 | 5 | 12 | II | 0.82 | 0.76 | 0.79 | 0.83 | 0.83 | 0.74 | 0.77 |
| 1 | 8 | 5 | 14 | II | 0.88 | 0.83 | 0.85 | 0.90 | 0.90 | 0.81 | 0.85 |
| 1 | 8 | 7 | 12 | II | 0.78 | 0.70 | 0.73 | 0.82 | 0.82 | 0.66 | 0.75 |
| 1 | 8 | 7 | 14 | II | 0.82 | 0.75 | 0.77 | 0.86 | 0.86 | 0.71 | 0.80 |
| 1 | 12 | 7 | 14 | I | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 | 0.04 | 0.02 |
| 1 | 12 | 1 | 12 | II | 0.88 | 0.91 | 0.91 | 0.82 | 0.85 | 0.93 | 0.74 |
| 1 | 12 | 3 | 12 | II | 0.89 | 0.91 | 0.90 | 0.83 | 0.86 | 0.92 | 0.76 |
| 1 | 12 | 5 | 12 | II | 0.77 | 0.80 | 0.80 | 0.74 | 0.77 | 0.80 | 0.66 |
| 1 | 12 | 5 | 14 | II | 0.88 | 0.89 | 0.89 | 0.85 | 0.86 | 0.89 | 0.79 |
| 1 | 12 | 7 | 12 | II | 0.72 | 0.69 | 0.71 | 0.69 | 0.70 | 0.63 | 0.61 |
| 1 | 12 | 7 | 14 | II | 0.81 | 0.80 | 0.81 | 0.80 | 0.81 | 0.76 | 0.72 |
| 3 | 8 | 5 | 12 | I | 0.06 | 0.06 | 0.06 | 0.05 | 0.05 | 0.04 | 0.02 |
| 3 | 8 | 1 | 12 | II | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 0.99 |
| 3 | 8 | 3 | 12 | II | 0.86 | 0.83 | 0.84 | 0.87 | 0.88 | 0.80 | 0.81 |
| 3 | 8 | 5 | 12 | II | 0.68 | 0.61 | 0.64 | 0.72 | 0.71 | 0.55 | 0.62 |
| 3 | 8 | 5 | 14 | II | 0.79 | 0.72 | 0.75 | 0.83 | 0.82 | 0.67 | 0.75 |
| 3 | 8 | 7 | 12 | II | 0.54 | 0.47 | 0.49 | 0.57 | 0.57 | 0.42 | 0.47 |
| 3 | 8 | 7 | 14 | II | 0.61 | 0.54 | 0.57 | 0.66 | 0.65 | 0.50 | 0.56 |
| 3 | 12 | 7 | 12 | I | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 | 0.01 | 0.00 |
| 3 | 12 | 1 | 12 | II | 0.89 | 0.90 | 0.90 | 0.88 | 0.88 | 0.90 | 0.81 |
| 3 | 12 | 3 | 12 | II | 0.88 | 0.88 | 0.88 | 0.87 | 0.88 | 0.87 | 0.78 |
| 3 | 12 | 5 | 12 | II | 0.75 | 0.74 | 0.75 | 0.75 | 0.76 | 0.68 | 0.63 |
| 3 | 12 | 5 | 14 | II | 0.84 | 0.83 | 0.84 | 0.84 | 0.85 | 0.76 | 0.75 |
| 3 | 12 | 7 | 12 | II | 0.52 | 0.50 | 0.51 | 0.51 | 0.52 | 0.43 | 0.37 |
| 3 | 12 | 7 | 14 | II | 0.69 | 0.66 | 0.67 | 0.69 | 0.70 | 0.57 | 0.58 |
| 5 | 8 | 5 | 12 | I | 0.04 | 0.04 | 0.04 | 0.04 | 0.04 | 0.01 | 0.00 |
| 5 | 8 | 1 | 12 | II | 0.97 | 0.96 | 0.97 | 0.97 | 0.97 | 0.96 | 0.96 |
| 5 | 8 | 3 | 12 | II | 0.64 | 0.58 | 0.61 | 0.64 | 0.65 | 0.54 | 0.53 |
| 5 | 8 | 5 | 12 | II | 0.35 | 0.33 | 0.33 | 0.34 | 0.35 | 0.27 | 0.23 |
| 5 | 8 | 5 | 14 | II | 0.47 | 0.43 | 0.45 | 0.46 | 0.47 | 0.37 | 0.32 |
| 5 | 8 | 7 | 12 | II | 0.29 | 0.28 | 0.29 | 0.27 | 0.28 | 0.21 | 0.16 |
| 5 | 8 | 7 | 14 | II | 0.33 | 0.29 | 0.31 | 0.31 | 0.32 | 0.22 | 0.18 |
| 5 | 12 | 3 | 12 | I | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 5 | 12 | 1 | 12 | II | 0.90 | 0.90 | 0.90 | 0.89 | 0.89 | 0.88 | 0.80 |
| 5 | 12 | 3 | 12 | II | 0.87 | 0.86 | 0.87 | 0.85 | 0.86 | 0.81 | 0.74 |
| 5 | 12 | 5 | 12 | II | 0.59 | 0.59 | 0.60 | 0.57 | 0.58 | 0.48 | 0.39 |
| 5 | 12 | 5 | 14 | II | 0.69 | 0.69 | 0.70 | 0.66 | 0.67 | 0.59 | 0.51 |
| 5 | 12 | 7 | 12 | II | 0.41 | 0.40 | 0.41 | 0.41 | 0.41 | 0.28 | 0.21 |
| 5 | 12 | 7 | 14 | II | 0.53 | 0.53 | 0.54 | 0.52 | 0.52 | 0.39 | 0.33 |
2.3. Examples
Example applications are provided of two-sample testing of NOBWOS scores (van der Waerden linear-rank, t(3) linear-rank, Laplace linear-rank, beta linear-rank, Mann-Whitney-Wilcoxon rank sum, and Welch’s approximate t-test), and Fisher’s exact test of binary end-of-study success scores. Data are drawn from four contrasting randomized clinical trials of varying length and substances of abuse: bupropion for the treatment of methamphetamine use disorder30, the COMBINE trial for the treatment of alcohol use disorder31, and varenicline for the treatment of tobacco use disorder.32, 33 The bupropion trial was 12 weeks in length, with urine assessments scheduled for three times per week. Seventy-nine individuals were randomized to bupropion and 77 were randomized to placebo. A week was considered to be a success if the individual abstained from methamphetamine use, per available urine results. The COMBINE trial was longer in duration, with a 16-week active-intervention period. A total of 1 383 individuals were randomized to nine different conditions. Rather than abstinence from all drinking, a week without heavy drinking was defined as a success.4 The original published analysis indicated that naltrexone without cognitive behavioral therapy resulted in the greatest improvement in duration of success from heavy drinking days, compared to placebo;31 so we restricted our analysis here to the arms for placebo and for naltrexone without cognitive behavioral therapy. Finally, data from two phase-3 varenicline trials were combined. Across the two trials, 696 participants were randomized to varenicline, 671 were randomized to bupropion, and 685 were randomized to placebo. Analyses here are limited to the varenicline and placebo arms. The active-intervention period for each trial was 12 weeks in length with carbon dioxide exhalation measured once per week.
For the bupropion trial, NOBWOS analysis examined four different end-of-study threshold periods of lengths 1, 3, 5, and 7 weeks; analysis of the COMBINE trial examined end-of-study threshold periods of lengths 1, 3, 7, and 11 weeks; and analysis of the varenicline trial examined end-of-study threshold periods of lengths 1, 3, 5, and 7 weeks. Together these extend the work of McCann and Li9 who examined a threshold period of 1 week in the bupropion study. The Research Compliance Office of Stanford University determined that the Institutional Review Board would not consider this work to involve human subjects because identifying information was removed from all analysis datasets such that it was not possible to readily identify individual participants.
3. Results
3.1. Simulations
Results of the 42 Monte Carlo simulation studies are summarized in table 2. Of these, 36 conditions examined Type II error and 6 examined Type I error. See section 2.2.2.2 for details of simulation studies’ design. In interpreting these results, it is important to remember that the linear-rank tests (van der Waerden, Laplace, t(3), beta, and Mann-Whitney-Wilcoxon), Welch’s approximate t-test, and Fisher’s exact test are each testing a different null hypothesis. The null for the linear-rank tests is equality of distributions between the two groups (as discussed in section 2.2.1); the null for the t-test is the equality of means between the two groups; and the null for Fisher’s exact test is the equality of the proportion successful between the two groups.
Across the various tests examined, all else equal, statistical power declines as mean time to onset of efficacy E[T1] increases. A later onset of efficacy permits less time for any differences in efficacy to diverge between conditions. In contrast, a longer duration of efficacy permits more time for divergence in efficacy between conditions. As such, all else equal, statistical power increases as mean duration of efficacy E[T2] increases. Statistical power is lowest when the trial is short, E[T1] is long, E[T2] is short, and the duration of the end-of-study success threshold period is long.
Averaged across all 36 conditions examined, statistical power was approximately equal for the five linear-rank tests, being slightly higher at 73% for van der Waerden, beta and Mann-Whitney-Wilcoxon compared to Laplace at 72% and t(3) at 71%. Average statistical power is lower on average for t tests (66%) and for Fisher’s exact test (64%). Under none of the 36 conditions examined did Fisher’s exact test exhibit greater statistical power than any of the linear-rank tests. All linear-rank tests exhibited good Type I error control, with estimated rates typically at or very near the nominal rate of 5%. In contrast, Type I error control for t tests and for Fisher’s exact test tended to be conservative with achieved error rates often below nominal, especially for Fisher’s exact test.
The 36 simulation studies that assessed Type II error also reveal specific conditions for which statistical power differs markedly among the five linear-rank tests. In particular, statistical power is lower for 1) the t(3) and Laplace linear-rank tests compared to 2) the van der Waerden, beta and Mann-Whitney-Wilcoxon linear-rank tests when the end-of-study threshold period is short to medium in duration (1–3 weeks), the active-intervention period is short in duration (8 weeks), and mean time to onset of efficacy is medium to long in duration (5–7 weeks).
3.2. Examples
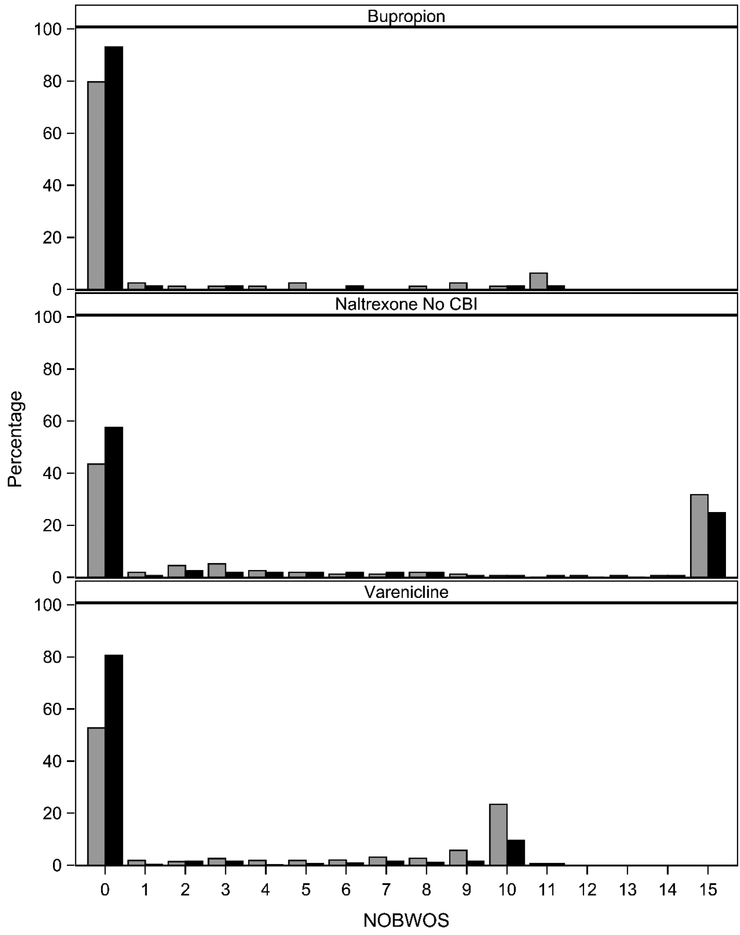
Figure 2 provides the distribution of NOBWOS scores for an end-of-study threshold of 1 week, by study arm, for each of the three clinical trials. For the Bupropion trial, the distribution is strongly peaked at zero with a long, thin right tail. In contrast, the distributions for COMBINE and varenicline trials are markedly bimodal. The distribution for COMBINE trials has a large secondary peak at the highest NOBWOS score. This resulted because a large number of participants in the COMBINE trial reported no heavy-drinking days―42 for placebo and 56 for naltrexone without cognitive behavioral therapy. Eleven of these 98 participants failed to complete the 16-week active intervention period and received NOBWOS scores of zero. The major peak in the distribution for the varenicline trials is at zero with a large secondary peak at the second largest NOBWOS score.
Figure 2.
Frequency of NOBWOS scores by condition for bupropion for the treatment of methamphetamine use disorder,30 the COMBINE trial for the treatment of alcohol use disorder,31 and the varenicline trials for treatment of tobacco use disorder.32,33 Tabulations are for an end-of-study threshold duration of 1 week. Placebo condition is black bar and active condition is gray bar. Cognitive behavioral intervention = CBI.
Table 3 provides estimates of various distributional shape parameters by study arm for each trial. Differences in shapes of distributions between study arms appear to be mild for the COMBINE trial and strong for the bupropion trial and varenicline trials. As such, linear-rank tests are, as tests of differences in distribution, potentially more sensitive to differences between arms for the bupropion and varenicline trials (section 2.2.1).
Table 3.
Sample estimates of shape parameters (variance, skewness and kurtosis) for each duration of end-of-study threshold period by condition for each of the four clinical trials of section 2.3. An estimated measure of location (sample mean) is provided.
| Trial | Duration of End-of-Study Threshold Period in Weeks |
Condition | Mean | Variance | Skewness | Kurtosis |
|---|---|---|---|---|---|---|
| Bupropion | 1 | Active | 1.42 | 10.94 | 2.26 | 3.44 |
| Control | 0.43 | 3.57 | 4.81 | 23.14 | ||
| 3 | Active | 1.04 | 6.93 | 2.41 | 4.28 | |
| Control | 0.31 | 2.19 | 5.20 | 27.01 | ||
| 5 | Active | 0.72 | 3.95 | 2.60 | 5.19 | |
| Control | 0.21 | 1.21 | 5.58 | 31.06 | ||
| 7 | Active | 0.47 | 1.89 | 2.77 | 6.23 | |
| Control | 0.13 | 0.56 | 5.99 | 35.27 | ||
| COMBINE | 1 | Active | 6.00 | 44.81 | 0.47 | −1.63 |
| Control | 4.72 | 41.15 | 0.84 | −1.12 | ||
| 3 | Active | 4.89 | 35.08 | 0.55 | −1.61 | |
| Control | 3.88 | 31.15 | 0.93 | −1.01 | ||
| 7 | Active | 3.12 | 17.45 | 0.66 | −1.53 | |
| Control | 2.42 | 15.18 | 1.07 | −0.81 | ||
| 11 | Active | 1.65 | 5.46 | 0.73 | −1.47 | |
| Control | 1.27 | 4.73 | 1.14 | −0.71 | ||
| Varenicline | 1 | Active | 3.78 | 19.6 | 0.48 | −1.62 |
| Control | 1.53 | 11.5 | 1.91 | 1.85 | ||
| 3 | Active | 2.85 | 12.5 | 0.58 | −1.53 | |
| Control | 1.15 | 7.12 | 2.02 | 2.26 | ||
| 5 | Active | 2.00 | 7.00 | 0.69 | −1.39 | |
| Control | 0.81 | 3.86 | 2.13 | 2.76 | ||
| 7 | Active | 1.22 | 3.05 | 0.84 | −1.16 | |
| Control | 0.50 | 1.65 | 2.31 | 3.55 |
Table 4 summarizes hypothesis testing for the linear-rank tests of NOBWOS scores, Welch’s approximate t-test of NOBWOS scores, and Fisher’s exact test of the binary success outcome. NOBWOS and binary-success outcomes’ results are shown for four different values for the end-of-study threshold durations, where some thresholds are longer for the longer trial (COMBINE). Recall that the null for the linear-rank tests, t-test, and Fisher’s exact test are equality of distributions, means, and proportion successful between the two groups, respectively. The five linear-rank tests are in agreement across all twelve cases examined (three trials × four end-of-study threshold durations) in rejecting (or not) their common null (equality of distributions) at attained significance levels of p ≤ 0.05. In contrast, the t-test failed to detect a difference in location between study arms at an end-of-study threshold of 7 weeks for the bupropion trial and at an end-of-study threshold of 1 week for the COMBINE trial. Fisher’s exact test detected a difference in proportions between study arms for the three lowest end-of-study thresholds for the bupropion trial and the end-of-study threshold of 1 week for the COMBINE trial but not for the end-of-study threshold of 7 weeks for the bupropion trial. Just as we saw in the simulation studies, the linear-rank tests are detecting more differences in study arms than the t-test; and this may be due, in part, to the fact that they are testing the more general null of equality of distributions, and those distributions do appear to differ in various ways (table 3).
Table 4.
Example analyses for the four clinical trials of section 2.3 for all seven hypothesis testing procedures of table 2. Attained significance levels (p-values) are shown.
| NOBWOS | ||||||||
|---|---|---|---|---|---|---|---|---|
| Trial | Duration of End-of-Study Threshold Period in Weeks |
Van der Waerden | t(3) | Laplace | Beta | Mann-Whitney-Wilcoxon | t-test | Fisher’s Exact |
| Bupropion | 1 | 0.018 | 0.019 | 0.019 | 0.018 | 0.018 | 0.025 | 0.020 |
| 3 | 0.032 | 0.034 | 0.033 | 0.034 | 0.033 | 0.035 | 0.041 | |
| 5 | 0.040 | 0.042 | 0.042 | 0.040 | 0.040 | 0.049 | 0.050 | |
| 7 | 0.046 | 0.049 | 0.048 | 0.043 | 0.044 | 0.055 | 0.059 | |
| COMBINE | 1 | 0.038 | 0.040 | 0.043 | 0.032 | 0.035 | 0.088 | 0.017 |
| 3 | 0.079 | 0.081 | 0.084 | 0.073 | 0.076 | 0.124 | 0.066 | |
| 7 | 0.150 | 0.150 | 0.150 | 0.152 | 0.150 | 0.134 | 0.189 | |
| 11 | 0.152 | 0.153 | 0.154 | 0.149 | 0.150 | 0.147 | 0.171 | |
| Varenicline | 1 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 |
| 3 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | |
| 5 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | |
| 7 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | |
4. Discussion
Linear-rank tests appear to be a good choice for comparing distributions of NOBWOS scores between groups (e.g., active vs. placebo). Because estimates of Type I error and Type II error are each so similar across linear-rank tests (table 2), any could be used in application to clinical trials, with Mann-Whitney-Wilcoxon perhaps being slightly preferred for its widespread availability in statistical software packages. Use of t-tests for comparing location between groups is not recommended nor is Fisher’s exact test for use with the binary success (“hurdle”) outcomes due to inferior Type I error control and Type II error control. That said, some gains in statistical power may be possible for binary success outcomes through application of tests that, unlike Fisher’s, do not condition on the observed marginal counts.34 We recommend the use of linear-rank tests on NOBWOS scores over Fisher’s exact test on binary hurdle scores based on the superior operating characteristics (Type I and Type II error) of the former. This recommendation comes with the important caveat that linear-rank tests on NOBWOS scores may detect differences between groups other than differences in location (section 2.2.1 and table 1), which would need to be assessed in each application.
While it may be tempting to draw conclusions about statistical power from the three example applications of section 3.2, statistical power is, of course, a probability statement; and the results from a single clinical trial only represent a single instance of the underlying generative probabilistic process. A much fuller understanding can be obtained by accumulating many observations on the same probabilistic process (in frequentist’s parlance, “the long run”). Results of simulation studies, especially those based on datasets from real clinical trials—as was done here—that summarize many instances of the same probabilistic process governing statistical power are much more useful in this regard than particularly individual example applications. Put another way, table 4 summarizes results based on real data from four clinical trials under three different conditions whereas table 2 summarizes the results based on real data of 42 000 trials spanning 36 conditions. The greatest benefits of particular example applications is just that—as demonstration of how to apply the proposed method to data from particular clinical trials.
That said, simulation studies do have limitations, often in terms of scope. A broad range of conditions were examined by the simulation studies presented here; although other conditions could be examined as well. For instance, additional work could examine bivariate distributions for simulating time to start of success T1 and duration of success T2 other than a bivariate exponential distribution. Perhaps these should encompass finite mixtures of distributions, including those in which a fraction of the population never starts successful behavior (T1 → ∞) or a fraction of the population that responds immediately with sustained efficacy, as seen in the COMBINE trial (figure 2). Here we based simulations on data obtained from clinical trials for treatment of cocaine use disorder; additionally, other substances of abuse (e.g., opioids) could be used for this purpose. Also, simulations were conducted at moderate sample sizes (75 participants per arm) so that recommendations provided at the outset of this section apply strictly to trials of moderate size. Of interest would be to examine the small-sample (≤ 75participants per arm) operating characteristics of the seven test procedures of table 2 in application to NOBWOS scores. That said, the sample size reported in table 2 did yield a breadth of statistical power.
Testing procedures presented here do not incorporate covariates even though covariate adjustment, especially adjustment for covariates that define randomization strata, is becoming increasingly standard in the analysis of clinical trials. To that end, one may be able to apply linear-rank hypothesis tests to residuals resulting from an ordinary least-squares fit of NOBWOS scores regressed on covariates.35
We examined a closely-related set of linear-rank tests, each based on a rank score derived from a symmetric density function; but other scoring functions could be devised and examined, including those based on asymmetric densities (e.g., exponential score function). The beta family of distributions may be especially useful in this regard. The particular symmetric beta distribution that we assessed here (a = b = 1/2) performed well in terms of statistical power and Type I error (table 2); and this family encompasses distributions that range widely in shape from symmetric to asymmetric and unimodal to bimodal. The Mann-Whitney-Wilcoxon rank sum test employs a beta distribution to construct with a = b =1, the uniform distribution. Of interest would be analyses that identify those values of a and b that optimize the asymptotic (section 2.2.1) relative efficiency of the beta distribution compared to a standard comparator, such as Fisher’s exact test. Each assessment would need to assume a particular joint distribution (or family of joint distributions) for T1 and T2 and is thereby beyond the scope of the present study. Of course, if the analyst is willing to make fully parametric assumptions about the joint distribution, even more powerful likelihood ratio tests become available that recognize NOBWOS scores as a censoring applied to that joint distribution (section 2.1). We deliberately focused here on a class of distribution-free testing procedures for their ease of use for practitioners.
Although the present paper has focused exclusively on applications of the NOBWOS method in clinical trials of medications to treat substance abuse disorders, the method may have utility in other indications, such as depression. In fact, the NOBWOS method may prove useful for any disease state that is amenable to a success/failure analysis and for which a delayed onset of pharmacological action may be observed. Within the context of the limitations described above, the current findings may have broad implications.
Supplementary Material
5. Acknowledgements
The authors acknowledge that the reported results are, in part, based on analyses of the COMBINE Data Set. These data were collected as part of a multisite clinical trial of alcoholism treatments supported by a series of grants from the National Institute on Alcohol Abuse and Alcoholism (NIAAA), National Institutes of Health, Department of Health and Human Services. This paper has not been reviewed by NIAAA or the COMBINE Research Group and does not necessarily represent the opinions of its members or NIAAA, who are not responsible for the contents. Data from the varenicline smoking cessation trials were generously provided by Pfizer. We wish to thank Dr. Kellie Takagi and Dr. Joseph Collins for their thoughtful reviews of the draft manuscript. The authors are grateful to Dr. Clete Kushida for the general support that he and his administrative staff provided to this study.
7. Funding
THH was supported in this work by the National Institute on Drug Abuse, National Institutes of Health, United States Department of Health and Human Services [Interagency Agreement 1 Y01 DA 40032].
Footnotes
Conflict of Interest
The Authors declare that there is no conflict of interest.
Trial registry, ClinicalTrials.gov (https://clinicaltrials.gov):
Baclofen (), Cabergoline (), Modafinil (), Ondansetron (), Reserpine (), Selegiline (), Tiagabine (), Naltrexone (), Varenicline (, ).
8. References
- 1.Winchell C, Rappaport BA, Roca R et al. Reanalysis of methamphetamine dependence treatment trial. CNS Neurosci Ther 2012; 18: 367–368. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.U. S. Food and Drug Administration, Center for Drug Evaluation and Research. Medical Review of Vivitrol NDA 21–897, http://www.accessdata.fda.gov/drugsatfda_docs/nda/2006/021897_toc_Vivitrol.cfm (2006a, accessed 27 Nov 2012).
- 3.U. S. Food and Drug Administration, Center for Drug Evaluation and Research. Medical Review of Varenicline NDA 21–928, http://www.accessdata.fda.gov/drugsatfda_docs/nda/2006/021928_s000_ChantixTOC.cfm (2006b, accessed 27 Nov 2012).
- 4.Falk D, Wang XQ, Liu L, et al. Percentage of individuals with no heavy drinking days: evaluation as an efficacy endpoint for alcohol clinical trials. Alcohol Clin Exp Res 2010; 34: 2022–2034. [DOI] [PubMed] [Google Scholar]
- 5.Deyi BA, Kosinski AS and Snapinn SM. Power considerations when a continuous outcome variable is dichotomized. J Biopharm Stat 1998; 8: 337–352. [DOI] [PubMed] [Google Scholar]
- 6.Altman DG and Royston P. The cost of dichotomising continuous variables. Br Med J 2006; 332: 1080. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Snapinn SM and Jiang Q. Responder analyses and the assessment of a clinically relevant treatment effect. Trials 2007; 8: 31. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Senn S and Julious S. Measurement in clinical trials: a neglected issue for statisticians? Stat Med 2009; 28: 3189–3209. [DOI] [PubMed] [Google Scholar]
- 9.McCann DJ and Li S-.A novel, nonbinary evaluation of success and failure reveals bupropion efficacy versus methamphetamine dependence: reanalysis of a multisite trial. CNS Neurosci Ther 2012; 18: 414–418. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Lawless JF. Statistical models and methods for lifetime data. 2nd ed Hoboken: John Wiley & Sons, Inc., 2003, pp.63–66. [Google Scholar]
- 11.Dalrymple ML, Hudson IL and Ford RPK. Finite mixture, zero-inflated Poisson and hurdle models with application to SIDS. Comput Stat Data Anal 2003; 41: 491–504. [Google Scholar]
- 12.Hajek J Asymptotic normality of simple linear rank statistics under alternatives. Ann Math Stat 1968; 39: 325–346. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Conover WJ. Rank tests for one sample, two samples, and k samples without the assumption of a continuous distribution function. Ann Stat 1973; 1: 1105–1125. [Google Scholar]
- 14.Daniel WW. Applied nonparametric statistics. 2nd ed Boston: PWS-KENT Publishing Company, 1990, p.90. [Google Scholar]
- 15.Pratt JW. Robustness of some procedures for the two-sample location problem. J Amer Stat Assoc 1964; 59: 665–680. [Google Scholar]
- 16.Mann HB and Whitney DR. On a test of whether one of two random variables is stochastically larger than the other. Ann Math Stat 1947; 18: 50–60. [Google Scholar]
- 17.Marshall AW and Olkin I. Distributions with bounded support: In: Bickel P, Diggle P, Feinberg S, et al. (eds) Life distributions. New York: Springer, 2007, pp.473–495. [Google Scholar]
- 18.Dodge Y The Oxford dictionary of statistical terms. Oxford: Oxford Press, 2003. p.266. [Google Scholar]
- 19.Randles RH and Wolfe DA. Introduction to the theory of nonparametric statistics. New York: John Wiley & Sons, 1979. [Google Scholar]
- 20.Ratcliffe JF. The effect on the t distribution of non-normality in the sampled population. Appl Stat 1968; 17: 42–48. [Google Scholar]
- 21.Welch BL. The significance of the difference between two means when the population variances are unequal. Biometrika 1938; 29: 350–362. [Google Scholar]
- 22.Permutt T and Berger VW. A new look at rank tests in ordered-2 × k contingency tables. Commun Stat Theory Methods 2000; 29: 989–1003. [Google Scholar]
- 23.Edgington ES. Randomization tests. 3rd ed. New York: Marcel Dekker, Inc., 1995, p. 88. [Google Scholar]
- 24.Kahn R, Biswas K, Childress A, et al. Multi-center trial of baclofen for abstinence initiation in severe cocaine-dependent individuals. Drug Alcohol Depend 2009; 103: 59–64. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Anderson AL, Reid MS, Li S-, et al. Modafinil for the treatment of cocaine dependence. Drug Alcohol Depend 2009; 104: 133–139. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Johnson BA, Roache JD, Ait-Daoud N, et al. A preliminary randomized, double-blind, placebo-controlled study of the safety and efficacy of ondansetron in the treatment of cocaine dependence. Drug Alcohol Depend 2006; 84: 256–263. [DOI] [PubMed] [Google Scholar]
- 27.Winhusen T, Somoza E, Ciraulo DA, et al. A double-blind, placebo-controlled trial of tiagabine for the treatment of cocaine dependence. Drug Alcohol Depend 2007a; 91: 141–148. [DOI] [PubMed] [Google Scholar]
- 28.Elkashef A, Fudala PJ, Gorgon L, et al. Double-blind, placebo-controlled trial of selegiline transdermal system (STS) for the treatment of cocaine dependence. Drug Alcohol Depend 2006; 85: 191–197. [DOI] [PubMed] [Google Scholar]
- 29.Winhusen T, Somoza E, Sarid-Segal O, et al. A double-blind, placebo-controlled trial of reserpine for the treatment of cocaine dependence. Drug Alcohol Depend 2007b; 91: 205–212. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Elkashef AM, Rawson RA, Anderson AL, et al. Bupropion for the treatment of methamphetamine dependence. Neuropsychopharmacol 2008; 33: 1162–1170. [DOI] [PubMed] [Google Scholar]
- 31.Anton RF, O’Malley SS, Ciraulo DA, et al. Combined pharmacotherapies and behavioral interventions for alcohol dependence: the COMBINE study: a randomized controlled trial. J Amer Med Assoc 2006; 295: 2003–2017. [DOI] [PubMed] [Google Scholar]
- 32.Gonzales D, Rennard SI, Nides M, et al. Varenicline, an α4β2 nicotinic acetylcholine receptor partial agonist, vs sustained-release bupropion and placebo for smoking cessation: A randomized controlled trial. J Amer Med Assoc 2006; 296: 47–55. [DOI] [PubMed] [Google Scholar]
- 33.Jorenby DE, Hays JT, Rigotti NA, et al. Efficacy of varenicline, an α4β2 nicotinic acetylcholine receptor partial agonist, vs placebo or sustained-release bupropion for smoking cessation: A randomized controlled trial. J Amer Med Assoc 2006; 296: 56–63. [DOI] [PubMed] [Google Scholar]
- 34.Mehrotra DV, Chan ISF and Berger RL. A cautionary note on exact unconditional inference for a difference between two independent binomial proportions. Biometrics 2003; 59: 441–450. [DOI] [PubMed] [Google Scholar]
- 35.Yuan A, Xu J, Yue Q, et al. Detecting case–control expression quantitative trait loci using locally most powerful or maximin robust rank tests. Stat Med 2012; 31: 887–900. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.