The role of mentorship in protégé performance

Abstract

The role of mentorship in protégé performance is a matter of importance to academic, business and governmental organizations. Although the benefits of mentorship for protégés, mentors and their organizations are apparent^1–9, the extent to which protégés mimic their mentors’ career choices and acquire their mentorship skills is unclear^10–16. The importance of a science, technology, engineering and mathematics workforce to economic growth and the role of effective mentorship in maintaining a ‘healthy’ such workforce demand the study of the role of mentorship in academia. Here we investigate one aspect of mentor emulation by studying mentorship fecundity—the number of protégés a mentor trains—using data from the Mathematics Genealogy Project¹⁷, which tracks the mentorship record of thousands of mathematicians over several centuries. We demonstrate that fecundity among academic mathematicians is correlated with other measures of academic success. We also find that the average fecundity of mentors remains stable over 60 years of recorded mentorship. We further discover three significant correlations in mentorship fecundity. First, mentors with low mentorship fecundities train protégés that go on to have mentorship fecundities 37% higher than expected. Second, in the first third of their careers, mentors with high fecundities train protégés that go on to have fecundities 29% higher than expected. Finally, in the last third of their careers, mentors with high fecundities train protégés that go on to have fecundities 31% lower than expected.

A large literature supports the hypothesis that protégés and mentors benefit from the mentoring relationship^1,2. Protégés that receive career coaching and social support, for instance, are reportedly more likely to have high performance ratings, a higher salary and receive promotions^1,3. In return, mentors receive fulfilment not only by altruistically improving the welfare of their protégés, but also by improving their own welfare^4,5,10. Organizations benefit as well, because protégés are more likely to be committed to their organization^6,7 and to exhibit organizational citizenship behaviour⁶. These benefits are not obtained only through the traditional dyadic mentor–protégé relationship, but also through peer relationships that supplement protégé development^8,9.

The benefits of mentorship underscore the importance of under-standing how mentors were in turn trained to foster the development of outstanding mentors. It might be suspected that protégés learn managerial approaches and motivational techniques from their mentors and, as a result, emulate their mentorship methodologies; this suggests that outstanding mentors are trained by other outstanding mentors. This possibility is sometimes formalized as the rising-star hypothesis^11,12; it postulates that mentors select up-and-coming protégés on the basic of their perceived ability and potential and past performance^10,13,14, including promotion history and proactive career behaviours¹². Rising-star protégés are reportedly more likely to intend to mentor, resulting in a ‘perpetual cycle’ of rising-star protégés that emulate their mentors by seeking other rising stars as their protégés¹⁵.

However, there is conflicting evidence concerning the rising-star hypothesis¹⁶, so the extent to which protégés mimic their mentors remains an open question. Indeed, we are unaware of any studies that systematically track mentorship success over the entire career of a mentor, so the validity of the rising-star hypothesis has yet to be fully explored. Here we investigate whether protégés acquire the mentorship skills of their mentors, by studying mentorship fecundity, that is, the number of protégés that a mentor trains over the course of their career. This measure is advantageous as it directly measures an outcome of the mentorship process that is relevant to sustained mentorship, allowing us to quantify the degree to which mentor fecundity determines protégé fecundity.

Scientific mentorship offers a unique opportunity to study this question because there is a structured mentorship environment between advisor and student that is, in principle, readily accessible^18,19. We study a prototypical mentorship network collected from the Mathematics Genealogy Project¹⁷, which aggregates the graduation date, mentor and protégés of 114,666 mathematicians from as early as 1637. This database is unique in its scope and coverage, tracking the career-long mentorship record of a large population of mentors in a single discipline (see the MPACT Project (http://ils.unc.edu/mpact/) for a smaller database of theses on information and library sciences and references therein). From this information, we construct a network in which links are formed from a mentor to each of his k protégés, where k denotes mentorship fecundity. We focus here on the 7,259 mathematicians who graduated between 1900 and 1960,because their mentorship record is the most reliable (Methods).

Although the mentorship records gathered from the Mathematics Genealogy Project provide the most comprehensive data source available for the study of academic performance throughout a mathematician’s career, there are obviously other plausible metrics for evaluating academic performance^20–22. We have also compared the mentorship data against a list of publications for 4,447 mathematicians and a list of 269 inductees into the US National Academy of Sciences (NAS; Methods). We find that mentorship fecundity is much larger for NAS members than for non-NAS members (Fig. 1a). We further find that the number of publications is strongly correlated with fecundity, regardless of whether or not a mathematician is an NAS member (Fig. 1b). These results demonstrate that although fecundity is not a typical measure of academic performance, it is closely related to other measures of academic success. Thus, even though our investigation concerns how fecundity is correlated between mentor and protégé, our results also address questions in the academic evaluation literature concerning the success of a mathematician.

Figure 1 |. Relationship between mentorship fecundity and other performance metrics.

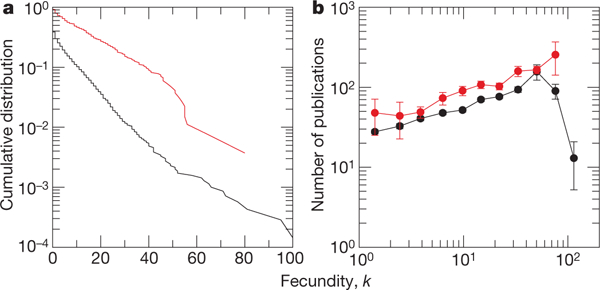
a, Cumulative distribution of the mentorship fecundity for NAS members (red) and non-NAS members (black). NAS members have an average fecundity of ${\langle k\rangle }_{\text{NAS}}=14$, which is far greater than the average fecundity of non-NAS members, ${\langle k\rangle }_{\text{non-NAS}}=3.1$, indicating that fecundity is closely related to academic recognition. Not all mathematicians in the non-NAS group were eligible for NAS membership, owing to citizenship and other circumstances. This fact makes the result in the figure all the more striking. b, Average number of publications as a function of the mentorship fecundity, for NAS members (red) and non-NAS members (black). NAS members have nearly twice as many publications on average as non-NAS members for all fecundity levels. Error bars, 1 s.e.

We first investigate whether it is possible to predict the fecundity of a mathematician by modelling the empirical fecundity distribution, p(k|t), as a function of graduation year, t. Considering that some mathematicians remain in academia throughout their careers whereas others spend only a portion of their careers in academia, it might be expected that there are two types of individual when it comes to academic mentorship fecundity—’haves’ and ‘have-nots’—in the sense that mathematicians from these types respectively have or have not had the opportunity to mentor students throughout their career.

If each mentor chooses to train a new academic protégé with probability ξ_h or ξ_hn, and stops training academic protégés otherwise, depending on whether they are a ‘have’ or, respectively, a ‘have-not’, then we would expect that the resulting fecundity distribution is a mixture of two discrete exponential distributions

$$p(k|\Theta )={\pi }_{\text{h}}p\left(k|{\kappa }_{\text{h}}\right)+\left(1-{\pi }_{\text{h}}\right)p\left(k|{\kappa }_{\text{hn}}\right)$$ (1)

where π_his the probability that a mathematician is a ‘have’ and p(k|κ_h) and p(k|κ_hn) are discrete exponential distributions $p(k|\kappa )={\text{e}}^{-k/\kappa }\left(1-{\text{e}}^{-1/k}\right)$ with respective average fecundities ${\kappa }_{\text{h}}=1/\ln \left({\xi }_{\text{h}}{}^{-1}\right)$ and ${\kappa }_{\text{hn}}=1/\ln \left({\xi }_{\text{hn}}{}^{-1}\right)$ for ‘haves’ and ‘have-nots’. We estimate the parameters $\Theta =\left\{{\pi }_{\text{h}},{\kappa }_{\text{h}},{\kappa }_{\text{hn}}\right\}$ of this distribution from the empirical data using expectation maximization²³. Using Monte Carlo hypothesis testing (Methods), we have found that equation (1) cannot be rejected as a candidate description of the fecundity distribution p(k|t) (Fig. 2a–c). For an alternative description of p(k|t), see Supplementary Discussion and Supplementary Fig. 1.

Figure 2 |. Evolution of the fecundity distribution.

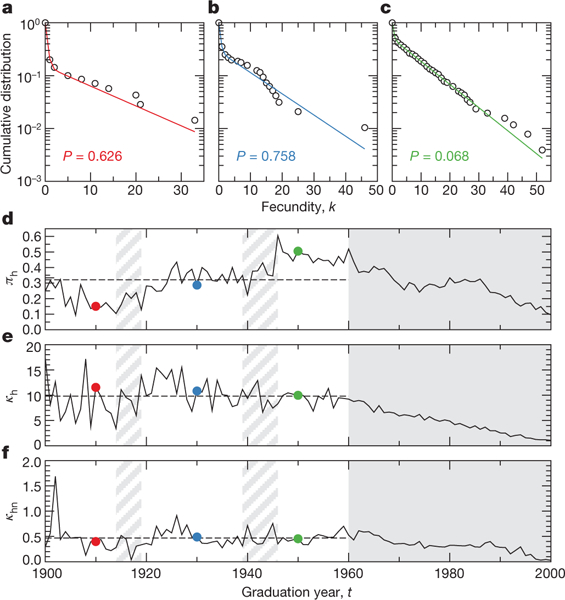
A–c, Cumulative distribution of the fecundity of mathematicians that graduated during 1910 (a), 1930 (b) and 1950 (c) (symbols), compared with the best-estimate predictions of a mixture of two discrete exponentials (lines). Monte Carlo hypothesis testing confirms that this model can not be rejected as a model of the fecundity distribution during every year from 1900–1960, as denoted by the P values above the α = 0.05 significance level (Methods). d–f, Best-estimate parameters as functions of time, calculated by maximum likelihood for a mixture of two discrete exponentials. Dashed lines denote average parameter values between 1900 and 1960 and coloured circles indicate the years displayed in panels a–c. The probability, π_h, of being a ‘have’ changes over time, generally in relation to historic events (hashed grey shading indicates the First and Second World Wars). In contrast, the average fecundities remain stable, with time-average values of ${\overline{\kappa }}_{\text{h}}=9.8\pm 0.4$ and ${\overline{\kappa }}_{\text{hn}}=0.47\pm 0.03$, until 1960, the time at which mentorship records become incomplete (Methods), and then steadily decrease (grey shaded region).

As might be expected, the probability, π_h, that an individual is a ‘have’ experiences drastic changes over time as a result of historical events, such as the First and Second World Wars, the beginning of the Cold War and considerable increases in academic funding (Fig. 2d). In contrast, the average fecundities of ‘haves’ and ‘have-nots’ do not exhibit systematic historical changes, suggesting that these quantities offer fundamental insight into the mentorship process among mathematicians (Fig. 2e, f). For the sixty year period considered, we find that ${\overline{\kappa }}_{\text{h}}=9.8\pm 0.4$ and ${\overline{\kappa }}_{\text{hn}}=0.47\pm 0.03$, where the overbar indicates a time average of the respective average fecundity.

The stationarity of κ_h and κ_hn also provides a simple heuristic for classifying an individual as a ‘have’ or a ‘have-not’; by maximum likelihood, an individual is a ‘have’ if k ≥ 2 and is a ‘have-not’ other-wise. These results raise the possibility that similar features, perhaps with different characteristic scales of fecundity, may be present in other mentorship domains.

Although our description of the fecundity distribution has high-lighted a fundamental property of mentorship among mathematicians, it is not predictive of the behaviour of individual mathematicians in the sense that fecundity, according to this model, is a random variable drawn from the distribution in equation (1). We next test whether protégés mimic the mentorship fecundity of their mentors, by comparing protégé fecundity with a suitable null model that does not introduce correlations in fecundity. As in the study of genealogical trees, we perform comparisons of the empirical data with networks generated from uncorrelated branching processes in our investigation of the mathematician genealogy network. Here graduation date is equivalent to birth date and mentors and protégés are equivalent to parents and children, respectively.

In a branching process²⁴, a parent p, born at time t_p, has k_p children. Child c of parent p is born at time t_c and subsequently has k_c children. The fecundity, k, of each individual is drawn from the conditional fecundity distribution p(k|t) for an individual born at time t. Networks generated from this type of branching process are therefore defined by the birth date of each individual, t, the fecundity distribution p(k|t), and the chronology of child births, {t_c}, for each parent (Fig. 3a).

Figure 3 |. Branching process null models.

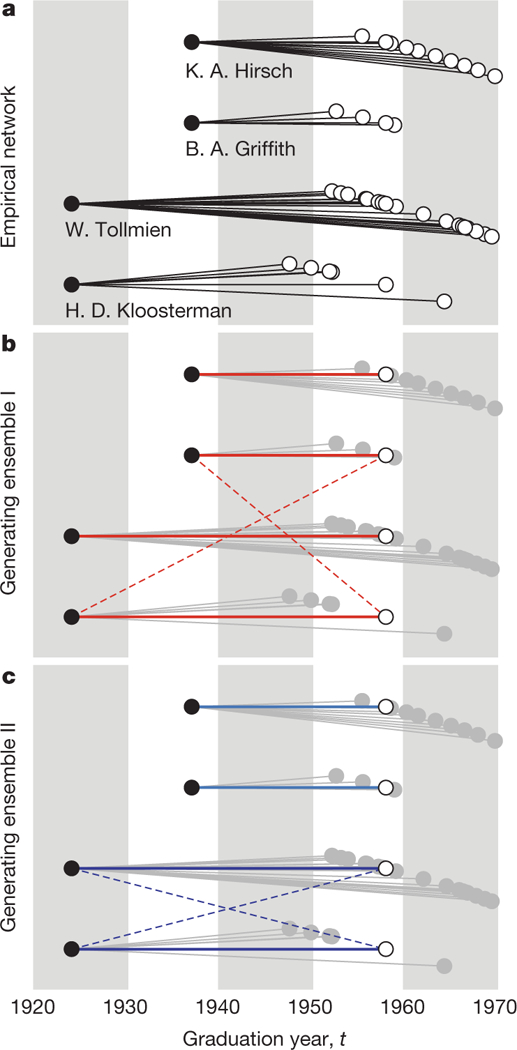
a, Subset of the mathematician genealogy network. Mentors/parents (black circles) are connected to each of their protégés/children (white circles). The horizontal positions of mathematicians represent their graduation/birth dates, t. The bottom two parents were born in 1924, the top two parents were born in 1937, and all four parents have a child born in 1958. From a parent’s perspective, three essential features of the empirical network must be preserved in random networks generated from the two branching process null models: the birth date, t_p, the fecundity, k_p, and the chronology of child births, {t_c}. b, Random networks from ensemble I preserve these three essential features. Solid red lines highlight the links in the empirical network whose end points can be randomized. Dashed red lines illustrate one of the possible randomization moves after switching the corresponding pair of links. We note that the age difference between parent and child is not preserved. c, Random networks from ensemble II preserve the three essential features as well as the age difference between parent and child. Solid blue lines of the same colour highlight the links in the empirical network whose end points can be randomized. Dashed blue lines illustrate one of the possible randomization moves after switching the corresponding pair of links. Random networks for each ensemble are generated by attempting 100 switches per link (Methods).

We compare the mathematician genealogy network with two ensembles of randomized genealogies from the branching process family. Random networks from ensemble I retain the birth date of each individual, the fecundity of each individual and the chronology of child births for each parent (Fig. 3b), as above. Random networks from ensemble II additionally restrict parent–child pairs to have the same age difference, t_c − t_p, as parent–child pairs in the empirical network (Fig. 3c). All other attributes of these networks are randomized using a link-switching algorithm^25,26 (Methods), so neither of these random-network ensembles introduces correlations between parent fecundity and child fecundity or temporal correlations in fecundity. They therefore provide a suitable basis for comparison with the mathematician genealogy network.

To explore the influence of mentor fecundity and age difference on protégé fecundity, we partition protégés according to the fecundity of their mentors and the age difference between mentor and protégé, t_c − t_p. Given our findings (Supplementary Discussion and Supplementary Figs 2 and 3), it is clear that age differences affect fecundity in a nonrandom manner for protégés whose mentors have k_p < 3. We partition the remaining protégés, whose mentors have k_p ≥ 3, into two groups: protégés whose mentors are below-average ‘haves’ (3 ≤ k_p < 10) and protégés whose mentors are above-average ‘haves’ (k_p ≥ 10).We then partition these three groups of protégés according to when they graduated during their mentors’ careers. Specifically, we split each group of protégés into terciles, the most fine-grained grouping that still gives us sufficient power to examine the statistical significance of any differences between the empirical data and the null models.

We use the partitioning of children into classes to examine the relationship between the average child fecundity, $\langle K_c\rangle$, and the age difference, t_c − t_p, between parent and child (Fig 4a, b and Supplementary Fig. 4a, b). If the data were consistent with a branching process, then we would expect $\langle K_c\rangle$ to have no temporal dependence. However, the regressions between the $\langle K_c\rangle$ z-score (Methods) and t_c − t_p deviate significantly (Fig. 4c and Supplementary Fig. 4c) from this expectation for both random ensembles, to reveal three distinct features. First, mentors with k_p < 3 train protégés that go on to have mentorship fecundities 37% higher than expected throughout their careers. Second, in the first third of their careers, mentors with k_p ≥ 10 train protégés that go on to have fecundities 29% higher than expected. Finally, in the last third of their careers, mentors with k_p ≥ 10 train protégés that go on to have fecundities 31% lower than expected.

Figure 4 |. Effect of age difference between mentor and protégé, t_c − t_p, on protégé fecundity.

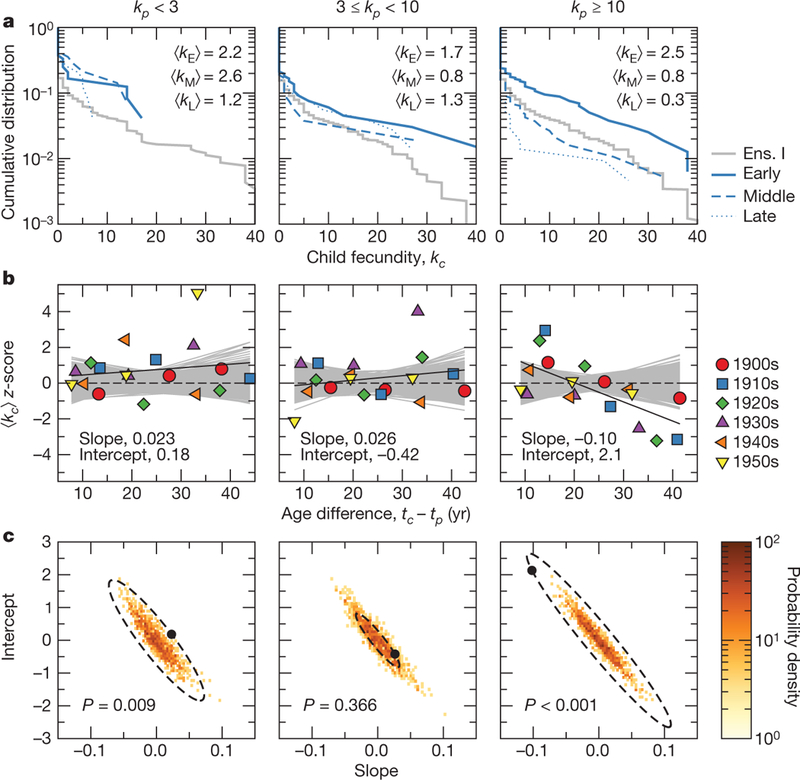
a, Fecundity distribution of children born during the 1910s (for which the average fecundity was 1.4) to parents with k_p < 3, 3 ≤ k_p < 10 and k_p ≥ 10, compared with the expectation from ensemble I (grey line). We separate children into terciles (early, middle, late) according to t_c − t_p, and denote the average fecundities of the children born early, middle and late in their parents’ lives as $\langle k_{\text{E}}\rangle$, $\langle k_{\text{M}}\rangle$ and $\langle k_{\text{L}}\rangle$, respectively. The average fecundity of children born to parents with k_p < 3 is higher than expected, regardless of whether they were born during the early, middle or later part of their parents’ lives. We also note that the average fecundity of children born to parents with k_p ≥ 10 decreases throughout their parents’ lives. b, We quantify the significance of these trends during each decade (coloured symbols) by computing the z-score of the average child fecundity, $\langle k_c\rangle$, compared with the average child fecundity in networks from ensemble I. This information is summarized by identifying the linear regression (solid black line; slope and intercept as shown). The regression lines for networks from our null model (grey lines) vary around the expectation of our null model (dashed black line). c, Significance of linear regressions in b. We compare the slope and intercept of the empirical regression (black circle) with the distribution of the slope and intercept of the same quantities computed from the null model. Because these quantities are approximately distributed as a multivariate Gaussian, we compute the equivalent of a two-tailed P value by finding the fraction of synthetically generated slope–intercept pairs that lie outside the equiprobability surface of the multivariate Gaussian (dashed ellipse). The slopes and intercepts of the regressions for children of parents with low (P = 0.009) and high (P < 0.001) fecundities are significantly different from the expectations for the null model, consistent with the data displayed in a. Comparisons with expectations from random networks from ensemble II yield the same conclusions (Supplementary Fig. 4).

The fact that mentors with k < 3 train protégés with higher-than-expected fecundities throughout their careers is somewhat counterintuitive. From the rising-star hypothesis^11,12, it might be expected that protégés trained by mentors with k < 3 are likely to mimic their mentors and therefore have lower-than-expected fecundities. Our results demonstrate that this is not the case. One possible explanation is that mentors with k < 3 are more aware of the resources they must allocate for effective mentorship, leading to a more enriching mentorship experience for their protégés. An alternative hypothesis is that mentors with k < 3 select for, or are selected by, protégés that have a greater aptitude for mentorship.

The striking temporal correlations for mentors with k_p ≥ 10 are also intriguing. Because mentors with k_p ≥ 10 represent the upper echelon of mentors in mathematics, these mentors were probably ‘rising stars’ early in their academic careers. The fact that these mentors train protégés with high fecundities early in their careers supports the rising-star hypothesis.

By the end of these mentors’ careers, however, their protégés have lower-than-expected fecundities. Perhaps mentors, who ultimately have high fecundities, spend fewer and fewer resources training each of their protégés as their careers progress. Alternatively, protégés with high mentorship fecundity aspirations might court prolific mentors early in their mentors’ careers whereas protégés with low fecundity aspirations might court prolific mentors later in their mentors’ careers. Our findings therefore reveal interesting nuances to the rising-star hypothesis.

It is unclear whether the temporal correlations we discover in mentorship fecundity generalize beyond mathematicians in academia. Anecdotally, mathematicians are thought to perform their best work at a young age²⁷, a perception that may influence how mentors and protégés choose each other. Perceptions in other domains, however, may differ and subsequently influence mentor and protégé selection in different ways. As data for other academic disciplines^18,19, business and the government becomes available, it will be important to determine whether temporal correlations in fecundity are a general consequence of mentorship or are a particular consequence of mentorship for mathematicians in academia.

Regardless, our results offer another means of judging academic impact in science as well as the impact of managers on their employees, both of which are notoriously complicated and risky affairs. These assessments are multidimensional, metrics and expectations are domain dependent, and placement of creative output, timescales of impact and recognition vary significantly from field to field. Ultimately, the assessment of individuals for awards and promotion is based on painstaking individual analysis by selection committees and peers. Although these committees may have varying goals and incentives, it is important that collective arguments—the kind of arguments we are making here—be based on sound quantitative analysis. Although the extent to which our findings extrapolate to other domains may vary, we are confident that the kind of analysis presented here will serve to elevate the discourse on scientific and managerial impact.

METHODS SUMMARY

Data acquisition.

We use data from the Mathematics Genealogy Project¹⁷ to identify the 7,259 protégé mathematicians that are in the giant component²⁸ and graduated between 1900 and 1960, of which 4,447 have linked publication records through the American Mathematical Society’s research database MathSciNet. We use a text-matching algorithm²⁹ to semi-automatically match members of the NAS with mathematicians from the Mathematics Genealogy Project.

Monte Carlo hypothesis testing for p(k|t).

We use Monte Carlo hypothesis testing³⁰ to determine whether equation (1) with maximum-likelihood²³ parameters Θ can be rejected as a candidate model for p(k|t) at the α = 0.05 significance level.

Random-network generation.

We use a variation of the Markov chain Monte Carlo algorithm^25,26 to construct each of the 1,000 random networks in ensembles I and II. Specifically, we restrict the switching of end points of links p→c that belong to the same link class L, where the link classes are defined as $L_{\text{I}}(t)=\left\{p\to c|t_c=t\right\}$ and $L_{\text{II}}(s,t)=\left\{p\to c|t_p=s,t_c=t\right\}$ for networks from ensembles I and II, respectively. Each link class can be thought of as a subgraph, which can then be randomized in the usual way by attempting 100 switches per link in the class^25,26.

Average-fecundity z-score.

By the central limit theorem, the average of variates drawn from p(k_c|t_c) is normally distributed because p(k_c|t_c) is well described by a mixture of discrete exponential distributions that has finite variance. Given a set of child fecundities, K_c = {k_c}, we quantify how significantly a subset of these child fecundities, $K_c^{*}\subset K_c$, deviates from K_c by measuring the z-score of $\langle k_c\rangle$, the average child fecundity of all nodes within the subset K_c*, compared with ${\langle k_c\rangle }_s$, the average child fecundity computed for children within a subset equivalent to K_c* in the synthetic networks. That is, we compute $z=\left(\langle k_c\rangle -\mu \right)/\sigma$, where μ is the ensemble average of $\left\{{\langle k_c\rangle }_s\right\}$ and σ is the standard deviation of the ensemble $\left\{{\langle k_c\rangle }_s\right\}$ over the 1,000 realizations generated for our null models.

METHODS

Mathematics Genealogy Project data.

We study a prototypical mentorship network collected from the Mathematics Genealogy Project¹⁷, which aggregates the graduation dates, mentors and advisees of 114,666 mathematicians from as early as 1637. From this information, we construct a mathematician genealogy network in which links are formed from a mentor to each of his or her k protégés.

The data collected by the Mathematics Genealogy Project are self-reported, so there is no guarantee that the observed genealogy network is a complete description of the mentorship network. In fact, 16,147 mathematicians do not have a recorded mentor and, of these, 8,336 do not have any recorded protégés. To avoid having these mathematicians distort our analysis, we restrict our analysis to the 90,211 mathematicians that comprise the giant component²⁸ of the network; that is, we restrict our analysis to the largest set of connected mathematicians in the mathematician genealogy network.

Although the Mathematics Genealogy Project contains information on mathematicians from as early as 1637, this does not necessarily indicate that all of these records are representative of the evolution of the network. For example, before 1900 the Project records fewer than 52 new graduates per year worldwide. Furthermore, because mathematicians often have mentorship careers lasting 50 years or more, we are not guaranteed to have complete mentorship records for mathematicians who graduated after 1960. We therefore restrict our analysis to the 7,259 protégé mathematicians who graduated between 1900 and 1960, for whom we believe that the graduation and mentorship record is the most reliable.

MathSciNet data.

Of the 7,259 protégé mathematicians that graduated between 1900 and 1960, 4,447 of them have linked MathSciNet publication records, which are used in our analysis.

US National Academy of Science data.

The US National Academy of Science maintains two databases of its membership. The first database consists of all deceased members elected to the NAS from as early as 1863. This database records the name of the inductee, their election year, their date of death and a link to a biographical sketch. The second database consists of all active members of the NAS. This database records the name of the inductee, their institution, their academic field and their election year.

The challenge to matching this data with the Mathematics Genealogy Project data is that there is no direct link between a member of the NAS and the Mathematics Genealogy Project, and vice versa. This is further confounded by the fact that some members of the NAS have the same name. To circumvent these problems, we use a text-matching algorithm²⁹ to semi-automatically detect whether a member of the NAS matches a name in the Mathematics Genealogy Project database. We use this procedure to curate the 269 members of the NAS that definitively match mathematicians in the Mathematics Genealogy Project database.

Monte Carlo hypothesis testing for p(k|t).

Given a model, M, with parameters Θ_t for the empirically observed fecundity distribution, p(k|t), we use Monte Carlo hypothesis testing to determine whether it can be rejected as a candidate model for p(k|t) (ref. 30). The Monte Carlo hypothesis testing procedure is as follows. First, we calculate the best-estimate parameters, θ_t, for model M at time t using maximum-likelihood estimation²³. Second, we compute the test statistic, S (detailed below), between the model M(Θ_t) and the empirical fecundity distribution, p(k|t). Next, we generate a synthetic fecundity distribution, p_s(k), from model M(Θ_t) using the best-estimate parameters, θ_t and we treat the synthetic data exactly the same as we treated the empirical data: first, we calculate the best-estimate parameters, Θ_s, for model M from maximum-likelihood estimation; second, we compute the test statistic, S_s, between the model M(Θ_s) and the synthetic fecundity distribution, p_s(k). We generate synthetic fecundity distributions and their corresponding synthetic test statistics until we accumulate an ensemble of 1,000 Monte Carlo test statistics, {S_s}. Finally, we calculate a two-tailed P value with a precision of 0.001.Asis customary in hypothesis testing, we reject the model M at time t if the P value is less than a threshold value. We select a P-value threshold of 0.05; that is, if less than 5% of the synthetic data sets exhibit deviations in the test statistic that are larger than those observed empirically, the model is rejected at time t.

Because we are conducting hypothesis tests with the fecundity distribution p(k|t), which is a distribution with a discrete support, it is important to use a test statistic S that is appropriate for testing discrete distributions. We use the χ² test statistic whereby we bin p(k|t) such that each bin has at least one expected observation according to the model M(Θ_t). This binning prevents observations that are exceptionally rare from dominating our statistical test and skewing our results.

Random-network generation.

We use the Markov chain Monte Carlo algorithm^25,26 to build random networks from the mathematician genealogy network. The standard version of this algorithm inherently preserves the fecundity of each individual, but it does not preserve the chronology of child births, {t_c}, for each parent. To obtain random networks belonging to ensemble I or ensemble II, we restrict the switching of end points of links p that belong to the same link class L, where the link classes are defined as $L_{\text{I}}(t)=\left\{p\to c|t_c=t\right\}$ and $L_{\text{II}}(s,t)=\left\{p\to c|t_p=s,t_c=t\right\}$ for networks from ensembles I and II, respectively. Each link class can be thought of as a subgraph, which can then be randomized using the Markov chain Monte Carlo algorithm. Here, we attempt 100 switches per link in each link class, which sufficiently alters random networks away from the original empirical network^25,26. We repeat this procedure 1,000 times to generate a set of 1,000 random networks for each ensemble.

Average-fecundity z-score.

The average of variates drawn from p(k_c|t_c) is normally distributed because p(k_c|t_c) is well described by a mixture of discrete exponential distributions—a distribution with finite variance—and, thus, the central limit theorem applies. Given a set of child fecundities, K_c = {k_c}, we quantify how significantly a subset, K_c*, of these child fecundities deviates from K_c, by measuring the z-score of $\langle K_c\rangle$, the average child fecundity of all nodes within the subset K_c*, compared with $\langle k_c\rangle$, the average child fecundity computed for children within a subset equivalent to K_c* in the synthetic networks. That is, we compute $z=\left(\langle k_c\rangle -\mu \right)/\sigma$, where μ is the ensemble average of $\left\{{\langle k_c\rangle }_s\right\}$ and σ is the standard deviation of the ensemble $\left\{{\langle k_c\rangle }_s\right\}$ over the 1,000 realizations generated for our null models.