Summary:
Analyzing the spatial organization of molecules in cells and tissues is a cornerstone of biological research and clinical practice. However, despite enormous progress in molecular profiling of cellular constituents, spatially mapping them remains a disjointed and specialized machinery-intensive process, relying on either light microscopy or direct physical registration. Here, we demonstrate DNA microscopy, a distinct imaging modality for scalable, optics-free mapping of relative biomolecule positions. In DNA microscopy of transcripts, transcript molecules are tagged in situ with randomized nucleotides, labeling each molecule uniquely. A second in situ reaction then amplifies the tagged molecules, concatenates the resulting copies, and adds new randomized nucleotides to uniquely label each concatenation event. An algorithm decodes molecular proximities from these concatenated sequences, and infers physical images of the original transcripts at cellular resolution with precise sequence information. Because its imaging power derives entirely from diffusive molecular dynamics, DNA microscopy constitutes a chemically encoded microscopy system.
Keywords: microscopy, machine learning, inverse problems, spatial transcriptomics
In Brief
DNA microscopy is an optics-free imaging method based on chemical reactions and a computational algorithm to infer spatial organization of transcripts while simultaneously preserving full sequence information.
Graphical Abstract
Introduction
The spatial organization of cells with unique gene expression patterns within tissues is essential to their function and is at the foundation of differentiation, specialization, and physiology in higher organisms. For example, neurons of the central nervous system express protocadherins and neurexins in highly diverse spatial patterns across neural tissue that govern cells’ intrinsic states, morphology, and synaptic connectivity (Lefebvre et al., 2012; Schreiner et al., 2014). Spatial co-localization of B- and T-lymphocytes in the immune system that express diverse immune receptors – genetically distinct due to somatic mutations – permits signaling feedback critical for immune clonal selection (Victora and Nussenzweig, 2012). In the gut, epithelial, immune, endocrine, and neural cells are spatially distributed in specific ways that impact how we sense and respond to the environment, with implications for autoimmune disease, food allergies, and cancer. And in the tissue context of disease, cell microenvironments may be critical for tumorigenesis (Herishanu et al., 2011; Joyce and Fearon, 2015), immune surveillance and dysfunction, invasion, and metastasis. In tumors in particular, genes with different mutations are expressed in distinct cells, impacting tumorigenesis and leading to neoantigens presented to the immune system (Schumacher and Schreiber, 2015).
Although imaging of cells and tissues has been a cornerstone of biology ever since cells were discovered under the light microscope centuries ago, advances in microscopy have to date largely not incorporated the growing capability to make precise measurements of genomic sequences. While microscopy illuminates spatial detail, it does not capture genetic information unless it is performed in tandem with separate genetic assays. Conversely, genomic and transcriptomic sequencing do not inherently capture spatial details.
One strategy to bridge this gap by spatially quantifying genes of known sequence are hybridization methods (Lubeck et al., 2014; Chen et al., 2015; Moffitt et al., 2016). However, somatic mutation, stochastic gene splicing, and other forms of single-nucleotide variation that is not known a priori play a central role in the function and pathology of spatially complex systems (such as the nervous, immune, gastrointestinal and tumor examples above). As a result, single-nucleotide sequencing and microscopy must be fully integrated to ultimately understand these systems. Recent approaches to do so rely on optical readouts that require elaborate experimental systems (Lee et al., 2014), physical registration and capture of molecules on grids (Junker et al., 2014; Ståhl et al., 2016), or an assumption of similarity among multiple samples so that distinct experiments performed on distinct specimens may be correlated (Satija et al., 2015; Achim et al., 2015). These approaches closely mirror the two ways in which microscopic images have been acquired to date: either (1) detecting electromagnetic radiation (e.g., photons or electrons) that has interacted with or been emitted by a sample, or (2) interrogating known locations by physical contact or ablation (e.g., dissection).
Here, we propose a distinct third modality for microscopy, which requires neither optics nor physical capture from known coordinates, but rather relies on image reconstruction from the relative physical proximity of individual molecules (Figure 1) and focuses on obtaining precise genetic information at high spatial resolution. This principle, of determining coordinates not in relation to an absolute coordinate system but instead in relation to one another, has previously been used in other contexts. For example, in the theory of sensor localization distances between points are explicitly measured and then their relative positions are estimated from these distances (Aspnes et al., 2006). Numerical work has further shown that such estimates can be made using sparse and noisy measurements (Singer, 2008). Here, we build on and adapt the same theoretical concept of “point-to-point communication” through biochemistry to allow position reconstruction from co-localization data of biomolecules to demonstrate a novel form of microscopy, called DNA microscopy. DNA microscopy reconstructs the positions of molecules from the stochastic output of a stand-alone chemical reaction. We confirm that DNA microscopy is able to resolve the 2D physical dimensionality of a specimen, and then demonstrate that it is able to accurately reconstruct a multicellular ensemble de novo without optics or any prior knowledge of how biological specimens are organized. Finally, we demonstrate the ability of DNA microscopy to resolve and segment individual cells for transcriptional analysis.
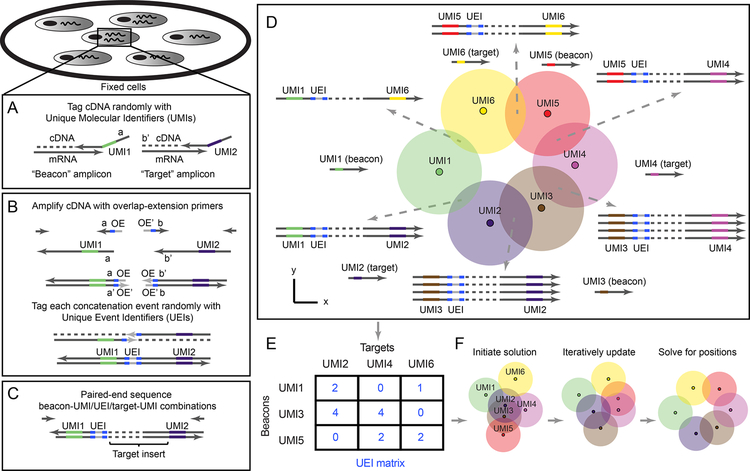
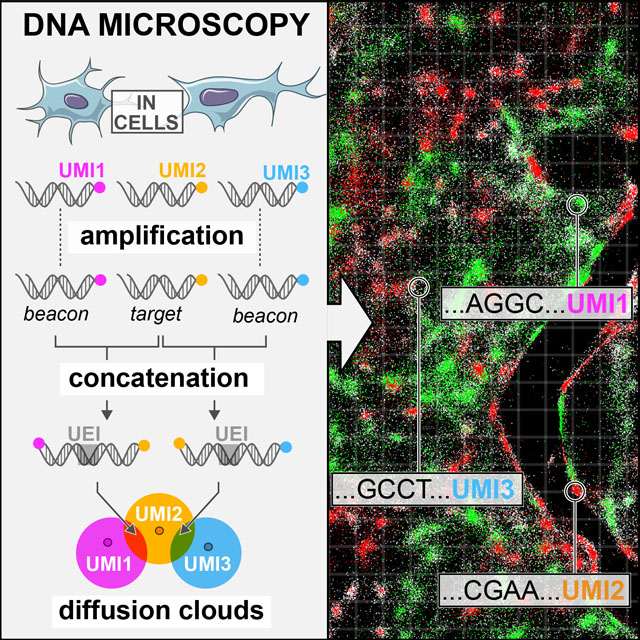
Figure 1. DNA microscopy.
(A–B) Method steps. Cells are fixed and cDNA is synthesized for beacon and target transcripts with randomized nucleotides (UMIs), labeling each molecule uniquely (A). In situ amplification of UMI-tagged cDNA directs the formation of concatemer products between beacon and target copies (B). The overhang-primers responsible for concatenation further label each concatenation event uniquely with randomized nucleotides, generating unique event identifiers (UEIs). Paired-end sequencing generates read-outs including a beacon-UMI, a target-UMI, the UEI that associates them, and the target gene insert (C). A bird’s-eye view of the experiment (D) shows the manner in which the DNA microscopy reaction encodes spatial location. Diffusing and amplifying clouds of UMI-tagged DNA overlap to extents that are determined by the proximity of their centers. UEIs between pairs of UMIs occur at frequencies determined by the degree of diffusion cloud overlap. These frequencies are read out by DNA sequencing, and inserted into a UEI matrix (E) that is then used to infer original UMI positions (F).
Results
Principle of DNA microscopy for spatio-genetic imaging
DNA microscopy generates images by first randomly tagging individual DNA or RNA molecules with DNA-molecular identifiers. Each deposited DNA-molecular identifier then “communicates” with its neighbors through two parallel processes. The first process broadcasts amplifying copies of DNA-molecular identifiers to neighbors in its vicinity via diffusion. The second process encodes the proximity between the centers of overlapping molecular diffusion clouds: DNA-molecular identifiers undergo concatenation if they belong to diffusion clouds that overlap. Finally, an algorithm infers from these association rates the relative positions of all original molecules.
DNA microscopy is premised on the notion that DNA can function as an imaging medium in a manner equivalent to light. In the same way that light microscopy images molecules that interact with photons (either due to diffraction or scattering or because these molecules emit photons themselves) and encodes these images in the wavelengths and directions of these photons, DNA microscopy images molecules that interact with DNA (including DNA, RNA, or molecules that have been tagged with either DNA or RNA) and encodes these images in the DNA sequence products of a chemical reaction.
With this analogy in mind, we can imagine superposing two distinct physical processes: a fluorophore radially emitting photons at a specific fluorescence wavelength, and a DNA molecule with a specific sequence undergoing PCR amplification, and its copies diffusing radially. Optical microscopes use lenses to ensure that photons hitting a detector or the human eye will retain some information regarding their point of origin, based on where they hit. However, the “soup” of DNA molecules generated in a DNA microscopy reaction does not afford this luxury. We therefore need a different way to distinguish the identities of point sources so that all data is encoded into the DNA itself.
To molecularly distinguish point sources we rely on Unique Molecular Identifiers, or UMIs (Kinde et al., 2011), consisting of randomized bases that tag a molecule before any copy of it has been made (Figure 1A). Because the diversity of UMIs scales exponentially with their length, we have high confidence that when one long UMI tags a molecule, no other molecule in the rest of that sample has been tagged with that same long UMI. We can now use overlap extension PCR to concatenate the diffusing and amplifying copies of these UMIs (with any biological DNA sequences they tag simply carried along). The rate at which they concatenate will reflect the distance between their points of origin.
However, once we sequence the final DNA products, we are still left with the problem of how to quantitatively read out these concatenation rates from DNA sequence alone. Using read-abundances belonging to concatenated DNA products carries serious drawbacks. For example, trace cross-contamination between samples could easily introduce artifactual UMI-UMI associations, and biases in downstream DNA library preparation could heavily distort association frequencies. Most serious, however, is PCR chimerization: any ex situ amplification of the DNA library would necessarily introduce template-switching at some rate that would corrupt the data.
We reasoned that if the overlap extension primers contained randomized bases that did not participate in priming themselves, then although each priming event would result in replacement of this randomized sequence, each overlap extension event would fix the new bases in between the now-concatenated sequences (Figure 1B). The concatenated sequences would then carry these randomized bases forward, intact, as they amplified. These bases would from then on be a unique record of that individual concatenation event. We called these new concatenated randomized sequences Unique Event Identifiers, or UEIs, and used them to encode molecular positions into the DNA microscopy reaction.
Experimental assay for DNA microscopy to encode relative positions of molecules in cells
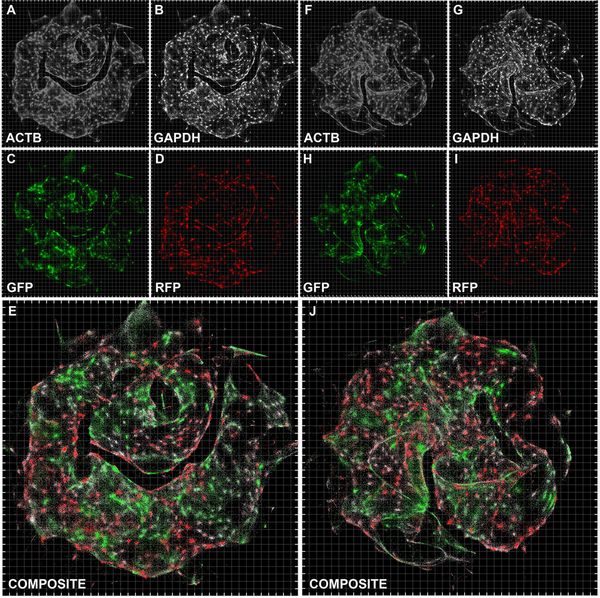
To demonstrate DNA microscopy, we aimed to image transcripts belonging to a mixed population of two co-cultured human cell lines, GFP-expressing MDA-MB-231 cells and RFP-expressing BT-549 cells. As an initial proof of concept we aimed to recover images that appear cell-like and where GFP and RFP transcripts are positioned in mutually-exclusive cells, whereas GAPDH and ACTB, expressed in both cell lines, are ubiquitous.
In the first step of the experiment, we tag with Unique Molecular Identifiers (UMIs) cDNA synthesized in situ. We designed reaction chambers to both grow cells and perform all reactions (Figure S1A–C, STAR Methods). We cultured the cells, and, following fixation and permeabilization, synthesized cDNA by reverse transcription from GFP, RFP, GAPDH, and ACTB gene transcripts (Tables S1–S2), with primers tagged with 29nt long UMIs (Figure 1A, Figure S1D). Notably, we designed the reaction to distinguish two types of UMI-tagged cDNA molecules: “beacons”, synthesized from ACTB (chosen as a universally expressed gene whose sequence would not be analyzed in later stages), and “targets” (everything else). We achieved this distinction between beacon and target amplicons by the artificial sequence-adapters assigned to the primers annealing to each.
In the second step of the experiment, we allow beacon-cDNA and target-cDNA molecules, along with the UMIs that tag them, to amplify, diffuse, and concatenate in situ in a manner that generates a new UEI distinct for each concatenation event (Figure 1B and S1D) through overlap-extension PCR (Turchaninova et al., 2013). By design, target amplicon-products will only concatenate to beacon amplicon-products, thereby preventing self-reaction. The middle of each overlap-extension primer includes 10 randomized nucleotides, such that each new concatenation event generates a new 20-nucleotide UEI. Paired-end sequencing of the final concatenated products generates reads each containing a beacon UMI, a target UMI, and a UEI associating them (Figure 1C).
The key to DNA microscopy is that because UEI formation is a second order reaction involving two UMI-tagged PCR amplicons, UEI counts are driven by the co-localization of UMI concentrations, and thus contain information on the proximity between the physical points at which each UMI began to amplify (Figure 1D). In particular, as UMI-tagged cDNA amplifies and diffuses in the form of clouds of clonal sequences that overlap to varying extents, the degree of overlap (Figure 1D, circle intersection) – and thus the probability of concatenation and UEI formation – depends on the proximity of the original (un-amplified) cDNA molecules (Figure 1D, small dark circles). UMI-diffusion clouds with greater overlap generate more UEIs/concatemers, whereas those clouds with less overlap generate fewer UEIs/concatemers. Although individual diffusion clouds may differ in form, their collective statistical properties will nevertheless allow for original UMI coordinates to be inferred by consensus, given the constraint that positions must occupy the low (two- or three-) dimensionality of physical space.
To obtain reliable estimates of UEIs between every pair of UMIs, we must address sources of noise, such as sequencing error. We cluster beacon-UMIs, target-UMIs, and UEIs by separately identifying “peaks” in read-abundances using a log-linear time clustering algorithm (STAR Methods, Figure S2A) in a manner analogous to watershed image segmentation, but in the space of sequences. For target UMIs, this allows us to aggregate biological gene sequences originating from single target molecules and achieve low error rates (0.1%−0.3%/bp across ~100 bp) by taking a consensus of the associated reads (Figure S2B). We then assign each identified UEI a single consensus beacon-UMI/target-UMI pair based on read-number plurality, and prune the data (by eliminating UMIs associating with only one UEI) to form a sparse matrix whose elements contain integer counts of UEIs pairing each beacon-UMI (matrix rows) and each target-UMI (matrix columns) (Figure 1E, STAR Methods). The resulting UEI matrices, containing on the order of 105 −106 total UMIs among which we estimate <1/1000 false-positives, have on average ~10 UEIs per UMI (Tables S3, S4, Figure S3), and form the data sets upon which we built an engine for image inference.
A two-part computational strategy to infer DNA microscopy images
Next, we developed an algorithmic approach to use UEI prevalence to infer UMI proximity and reconstruct an image of the original sample and its transcripts (Figure 1F). We follow a two-step approach. We first partitioned the data into smaller subsets to gauge how well local information between UMIs had been encoded into the UEI matrix. This entailed applying spectral graph theory (in a manner agnostic to the physics of the experiment) to the problem of cutting the data matrix into highly connected sub-matrices, allowing us to both analyze and visualize local structure and dimensionality. We then devise a more general solution to achieve DNA microscopy inference over large length scales. To do this, we constructed a physical model that used our preliminary linear analysis of the data matrix to constrain a non-linear maximization of the probability of observing the DNA microscopy data given underlying molecular coordinates.
A “zoom” function infers local spatial encodings from UEI matrices
We first appreciate that if the UEI matrix had successfully encoded relative UMI coordinates, these coordinates would be reflected in the rows and columns of the matrix. The matrix rows and columns would span a space having a dimensionality scaling with the total number of UMIs. However, if they encoded UMI coordinates within a sample, they would collectively sweep out a curve of far smaller dimensionality, only equal to the physical dimensionality of the sample.
As a toy example, consider a comparison between three systems in which a single target UMI (“2”) is in each of three positions in one dimension relative to two beacon UMIs (“1” and “3”) with which it forms UEIs (Figure 2A). The target UMI begins closest to one of the two beacon UMIs, and as a result, its diffusion cloud overlaps most with that beacon UMI’s diffusion cloud. Thus, its reaction rate with that beacon UMI is relatively higher (Figure 2B) and results in a correspondingly larger number of UEIs (Figure 2C). If the target UMI is further away, the balance of overlaps between diffusion clouds changes. Indeed, plotting expected UEI matrix elements for the target UMI on two axes, we see that its trajectory remains one-dimensional (Figure 2D).
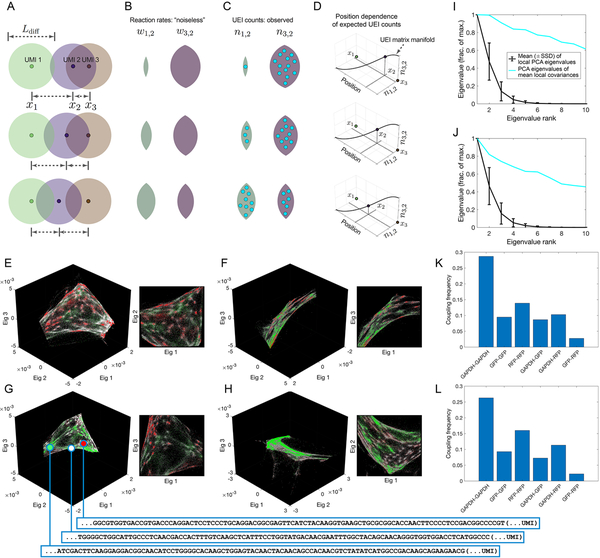
Figure 2. Encoding and decoding molecular localization with DNA microscopy.
(A-D) Expected behavior of UEI counts. Diffusion profiles with length scale Ldiff· belonging to different amplifying UMIs overlap to degrees that depend on the distance between their points of origin (A). Greater overlaps between diffusion profiles result in larger reaction rates (B), which in turn result in higher UEI formation frequencies (C). Because UEI counts are therefore proper functions of position, as a UMI relocates, it sweeps out a curve along the UEI count axes equal to the dimensionality of space it occupies (D). (E–H) Data segmentation permits individual sets of 104 strongly interacting UMIs to be visualized independently. The top three non-trivial eigenvectors for the largest data segments of samples 1 (E–F) and 2 (G–H) are shown, along with a different, magnified view of the same plot. Transcripts are colored by sequence identity: grey = ACTB (beacons), white = GAPDH, green = GFP, red = RFP. (I–J) Quantitative assessment of manifold dimensionality. PCA spectra from local (black) or averaged-local (cyan) covariance matrices formed from the global UEI matrix eigenvector-coordinates of UMIs in samples 1 (I) and 2 (J). Covariance matrices were constructed for each UMI forming UEIs with at least 100 other UMIs, using the first 100 eigenvector coordinates belonging to these associating UMIs alone. (K–L) Average coupling frequencies for each beacon with different target amplicons in samples 1 (K) and 2 (L). A coupling frequency between amplicon types k and l is defined as the average across all beacon UMIs i of the product PikPil, where . Here, nij is the number of UEIs associating beacon UMI i with target UMI j, and Sik is the set of all target UMIs of amplicon type k associating with beacon UMI i.
Extending to a large population of target UMIs across many positions, these new target UMIs, just like the target UMI in the toy example, also interact with the same two beacon UMIs. Therefore, we can also plot them on the same two axes, and wherever they land, we could expect them to scatter around the same one-dimensional manifold followed by the target UMI of the original example. It is important to note that although the variation of points across these axes may in fact all be equivalent, inspection of their axial projections allows visualization of their underlying dimensionality.
In any real data set, UEI count is affected not only by position but also by additional variables (such as amplification biases and diffusion rates), each potentially adding to the data’s total dimensionality. However, these sources of variation would be suppressed along the principal dimensions of a UEI matrix so long as their effect on neighboring UMIs is not systematically correlated.
To identify the principal dimensions of the UEI matrix, we can analyze the graph of UMI vertices and weighted UEI count edges by constructing a Graph Laplacian matrix from the raw UEI matrix (with its diagonal elements set so that each row sums to zero). The Graph Laplacian eigenvectors with the smallest-magnitude eigenvalues would visualize the most systematic forms of variation in the DNA microscopy data (STAR Methods) and illuminate the low-dimensional manifold, if any, it occupied. However, even a low-dimensional manifold could be folded in complex ways in the high-dimensional space formed by a full UEI matrix, making it difficult to analyze the manifold’s shape over large distances, especially in areas of the manifold that are sparsely populated. Analyzing the UEI matrix manifold therefore first requires analyzing UMI subsets corresponding to local regions of the original sample. We return to global relations in subsequent sections.
To perform this local investigation, we developed a “zoom” function for DNA microscopy data by applying a recursive graph-cut algorithm, identifying putative cuts by using the spectral approximation to the cut of minimum-conductance (Shi and Malik, 2000) (STAR Methods). This criterion separates sub-sets of UMIs exhibiting small UEI-flux relative to the number of UMIs they comprised. The algorithm first finds the sparsest cut to the entire data set, then the sparsest cuts to the resulting halves, and so on until a further sparse cut cannot be made (STAR Methods). We then visualize each of these sub-regions by the eigenvectors corresponding to the smallest-magnitude eigenvalues of their UEI-Graph Laplacian sub-matrix.
Successful inference of local structure identifies cell-like structures with specific marker expression
Strikingly, and consistent with our theoretical reasoning, although the UMIs in these sub-sets fully spanned at least all three eigenvector dimensions, the manifolds swept out by the UMIs appeared only two-dimensional when represented in three-dimensional scatter plots (Figure 2E–H). We further quantified the UEI data manifold’s local dimensionality by performing principal component analysis (PCA) on the spread of UMIs forming UEIs with each individual UMI (Figure 2I,J, STAR Methods). When highly connected UMIs (associating with at least 100 other UMIs) were analyzed individually over the first 100 eigenvectors of the UEI-Graph Laplacian matrix, their covariance matrix eigenvalues decayed quickly. However, when their covariance matrices were averaged, the eigenvalues of the resulting matrix decayed slowly. These observations confirmed a low dimensionality of the UEI data manifold, consistent with neighborhoods of UMIs with low spatial dimensionality having been successfully encoded into the UEI data matrix.
The two-dimensional manifolds exhibited clusters of UMIs with indications of cellular resolution, by recapitulating the genetic composition of the cell lines used in the experiment: a pervasive distribution of the constitutively expressed ACTB and GAPDH sequences, but a mutual exclusion between GFP and RFP (Figure 2E–H). Even on average across the data set, UEIs formed 3 to 5 times more frequently via an intermediary beacon UMI between two GFP or RFP target UMIs and GAPDH target UMIs than between GFP and RFP (Figure 2K,L). Thus, an observer unaware of the spatial dimensionality of the specimen or that cells even existed could discover both by analyzing the DNA microscopy sequencing data alone. Together, these two observations confirmed both cellular and local supra-cellular resolution in DNA microscopy.
Inference of global molecular positions from DNA microscopy data
Next, we expanded our inference beyond the local scope of a few thousands of proximal transcript molecules, by developing a framework for evaluating the likelihood of a global position-estimate solution.
We reasoned that each UEI’s occurrence is analogous to a “coin-toss” experiment performed on every UMI-pair, with each pair’s “occurrence” probability proportional to the corresponding reaction rate (Figure 3A, STAR Methods). We modeled the reaction rate between a beacon UMI and a target UMI as an isotropic Gaussian function of the distance separating them. Because, like in a coin-toss experiment, the probability of observing a given data set is contingent on the probabilities of all possible outcomes together, our diffusion model of a Gaussian “point-spread function” imposed constraints on the probabilities of UMIs in aggregate, not on each UMI individually.
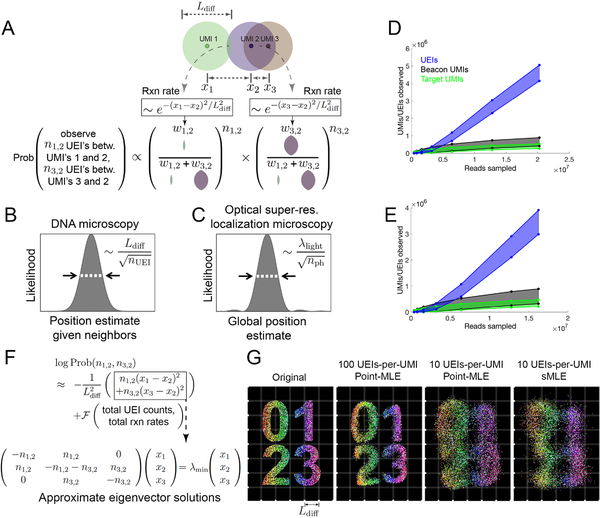
Figure 3. Image inference from DNA microscopy data.
(A) Modeling diffusion of amplifying UMIs as isotropic across length scale Ldiff allows the likelihood of a UMI-position solution to be evaluated given observed UEI counts. (B,C) Uncertainty in DNA vs. super-resolution microscopy. Given its reacting partners’ positions, DNA microscopy (left) defines a UMI’s uncertainty as a physical length scale (DNA diffusion distance, Ldiff) divided by the square-root of the number of individual quanta measured (UEIs) in a manner analogous to quanta (photons) in super-resolution microscopy (right). (D,E) Rarefaction of UMI and UEI data. Shown are curves with an upper-bound, indicating total UMI/UEI counts, and a lower-bound, indicating those from the final pruned UEI matrix, for samples 1 (D) and 2 (E). (F) The sMLE algorithm uses eigenvector solutions to part of the position-probability function to identify a linear basis for the solution to the full likelihood function. (G) sMLE enhances performance in free-diffusion simulation tests. From left: original image, results from point-MLE on simulated images with 100 or 10 UEIs/UMI, and from sMLE with 10 UEIs/UMI.
In this probability function, UEIs in DNA microscopy act in the same manner as photons do in optical super-resolution localization microscopy (Hell, 2009): both narrow a point-spread function governed by a physical length scale (wavelength in the case of light, diffusion distance in the case of DNA) as they accrue by dividing that length scale by the square-root of their total number (Figure 3B,C, STAR Methods). In real data sets, UEIs increase progressively with increasing read depth, whereas UMIs saturate more quickly (Figure 3D,E). In this way, read depth in DNA microscopy constitutes a dial to increase the number of UEIs per UMI, enhancing an image’s resolution.
Unlike its optical counterpart, however, DNA microscopy resolves a molecule’s position by orienting it relative to other molecules, and its uncertainty is therefore a function of these relationships. A relationship between two UMIs may come in two forms: those that are direct and involve UEIs linking them, and indirect relationships that occur via intermediaries. The latter emerges in the structure of the data, but will not strongly influence UMI positions if these positions are optimized independently. This may be seen in the logarithm of the UEI-count probability function (Figure 3F). This log-probability is the sum of two components (Figure 3F, top): (1) a sum of squared-differences between positions, weighted by individual UEI counts; and (2) a function of total UEI counts and total expected reaction rates (which are themselves functions of UMI positions) across the entire data set. In order to still calculate the log-probability as a whole in a way that scales linearly with data size, we implemented the Fast Gauss Transform (Greengard and Strain, 1991) (Figure S4A,B).
If each UMI’s position is updated independently to maximize this log-probability function, it will experience two forces, corresponding to the function’s two added components: the first pulls together UMIs that have directly formed UEIs between them, and the second repels all UMIs from all other UMIs. The likelihood of the position-solution is maximized when these two forces balance. During the maximization’s update-process, the only way in which an indirect relationship between UMIs will influence their position-solution is if intermediary UMIs that directly form UEIs with them separately have already changed position.
To ensure that large length scale optimization captures these indirect UMI relationships encoded in the data, we developed a new maximum likelihood framework, which we called spectral maximum likelihood estimation or sMLE, to generate global representations of the DNA microscopy data. First, we note that because maximizing the first component of the log-probability entails minimizing the magnitude of the sum of squared-differences, it can be individually solved by identifying the smallest-magnitude eigenvalue/eigenvector pairs of the UEI Graph Laplacian introduced earlier (Figure 3F, bottom, STAR Methods). Each eigenvector represents a distinct way in which UMIs can be globally rearranged to suit orientation requirements expressed by the sum of squared-differences between local points. The eigenvector with the smallest-magnitude eigenvalue represents the best arrangement, the second smallest-magnitude eigenvalue the second best, and so on. Critically, these eigenvectors are not themselves solutions to the global maximum likelihood problem for a DNA microscopy data set: they are local and linear solutions, and will individually exhibit all of the distortions observed in Figure 2E–H.
However, we reasoned that because sums of eigenvector solutions to the local linear problem would produce solutions that would also satisfy local constraints, sum-coefficients of these eigenvectors could act as variables in a larger-scale non-linear likelihood maximization. By seeding a solution with the two eigenvectors corresponding to the smallest-magnitude eigenvalues, optimizing their coefficients, then incorporating successive eigenvectors and repeating, we could find global solutions that were also well-constrained locally. These sMLE solutions showed strong advantages in simple simulations over maximizing the likelihood while treating every UMI independently, especially when UEI counts were limiting (Figure 3G). This effect remained present even when the simulated the form of the diffusion profiles deviated from our Gaussian model (Figure S4C).
DNA microscopy correctly recapitulates optical microscopy data
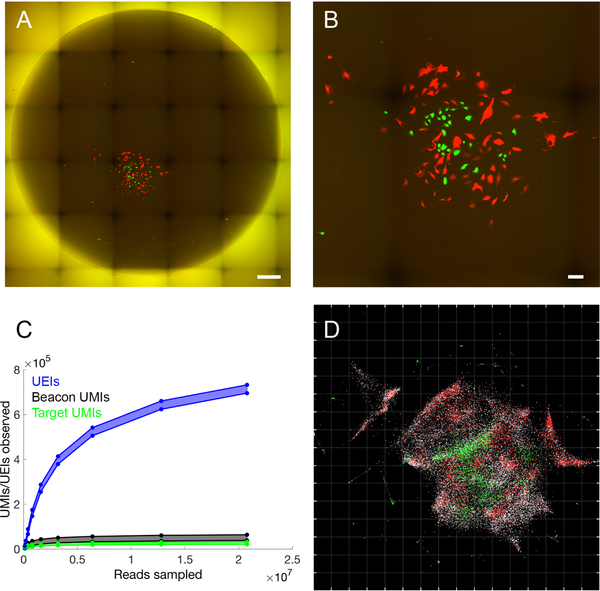
We next sought to apply the sMLE inference framework to determine whether DNA microscopy could resolve supra-cellular coordinates compared to optical microscopy. To this end, we constructed reaction chambers with glass slides (Figure S1B,C) and plated GFP- and RFP-expressing cells in a highly localized pattern within the chamber (Figure S1C). We then imaged GFP- and RFP-expression in cells across the entire area of the reaction chamber using an epifluorescence microscope before the DNA microscopy reaction (Figure 4A,B), sequenced the resulting DNA library to saturation (Figure 4C), and applied the sMLE inference algorithm.
Figure 4. Accurate reconstruction by DNA microscopy of fluorescence microscopy data.
(A,B) Optical imaging of co-cultured cells. (A) Full reaction chamber view of co-cultured GFP- and RFP-expressing cells (scale bar = 500 um). (B) Zoomed view of the same cell population (scale bar = 100 um). (C,D) DNA microscopy of co-cultured cells. (C) Rarefaction of UMIs and UEIs with increasing read-sampling depth. (D) sMLE inference applied to DNA microscopy data, reflected/rotated and rescaled for visual comparison with photograph. Transcripts, sequenced to 98 bp, are colored by sequence identity: grey = ACTB (beacons), white = GAPDH, green = GFP, red = RFP. Grid-line spacings: diffusion length scales (Ldiff), emerging directly from the optimization (STAR Methods).
Strikingly, the resulting image recapitulates optical microscopy data without systematic distortion (Figure 4D), and recapitulates both the shape of the cell population boundary as well as the distribution of GFP- and RFP-expressing cells within it. Importantly, the inferred image preserves the correct aspect ratio: the individual axes only needed to be rotated and reflected, but did not need to be independently re-scaled. This demonstrated that DNA microscopy is capable of generating accurate physical images of cell populations.
Large length scale optimization and the folded manifold problem
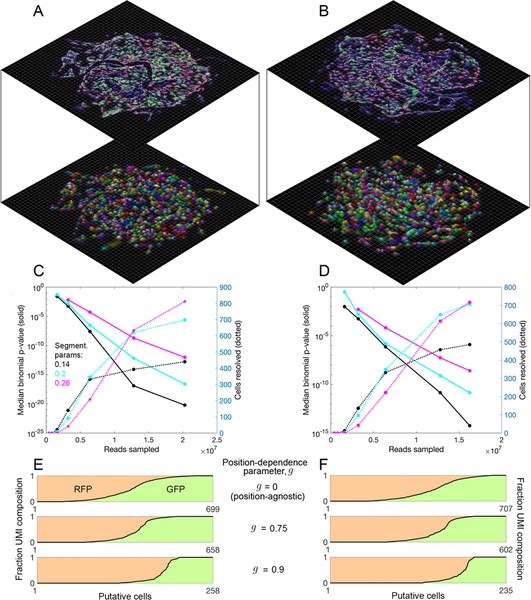
We applied DNA microscopy to optimization at larger length scales. Applying sMLE inference to the original data from several hundred cells used to generate the original eigenvector representations (Figure 2) gave images that reproduced the individual cell compositions of the earlier visualizations (Figure 5). These large-scale optimizations were also robust to data down-sampling (Figure S5).
Figure 5. Inferred large scale DNA microscopy images preserve cellular resolution.
Inference using the sMLE global inference approach for sample 1 (A–E) and sample 2 (F–J), with each transcript type shown separately (A–D, F–I) or together (E and J) (although inferences are performed on all transcripts simultaneously and are blinded to transcript identity). Grid-line spacings: diffusion length scales (Ldiff), emerging directly from the optimization (STAR Methods).
However, the reconstructed images exhibited “folding” that indicated how the process of projecting large and curved high-dimensional manifolds onto two-dimensional planes was vulnerable to distortions. The causes for this “manifold folding” problem are illustrated by how low-dimensional manifolds come into being within a high-dimensional UEI data matrix (Figure 2A–D). The eigenvector calculation (Figure 3F) involves identifying hyperplanes that can be drawn through these low-dimensional manifolds that maximally account for variation in the UEI data. It does this in a manner similar to linear regression, balancing the advantage of fitting certain parts of the data with the costs of not fitting other parts of the data.
This balancing can yield errors in several ways. If a large number of UMIs in one part of the data set rotate the top calculated eigenvectors (with the smallest-magnitude eigenvalues) away from UMIs in a different part of the data set, then projecting the global data set onto these eigenvectors will cause these neglected UMIs to fold on top of one another. This will produce the type of “folding” artifact observed for large scale optimization (Figure 5). If we avoid eigenvector calculation entirely and optimize each UMI’s position independently (Figure S6A,B) we avoid such defects, but obtain close-packed images, as predicted by simulation (Figure 3G), that do not preserve empty space. This highlights the distinct nature of DNA microscopy’s imaging capabilities compared to light microscopy’s: while in light microscopy density is the key challenge, in DNA microscopy it is sparsity that can be challenging.
Cell segmentation can be performed on the UEI matrix based on diffusion distance
We next analyzed the degree to which the UEI matrix could be used to segment cells and analyze single cell gene expression. Importantly, up to this point, no step in the process – experimental or computational – had knowledge that cells even exist. To perform segmentation, we applied the same recursive graph cut algorithm as used earlier (Figure 2E–H) to generate local eigenvector visualizations of the data. By increasing the conductance-threshold dictating whether segments of the data should be left intact, we assigned transcripts to putative cells (Figure 6A,B, S6C,D), again without regard to transcript identity (i.e., GFP vs. RFP). To quantify segmentation quality, we calculated the probability that, within each putative cell, the minority fluorescent gene transcript would occur at or lower than its current value, given its prevalence in the data set. We found the median p-value decayed rapidly, over a range of conductance thresholds, to <10−10, with increased numbers of reads and of resolved cells analyzed (Figure 6C,D).
Figure 6. Segmentation of DNA microscopy data recovers cells de novo.
(A,B) Data segmentation recovers putative cells without a priori knowledge. Cell segmentation for samples 1 (A) and 2 (B) by recursive graph-cutting of the UEI matrix is shown with a random color assigned to each inferred cell, qualifying if it contained at least 50 UMIs and had at least one transcript each of ACTB and GAPDH. The minimum conductance threshold was set to 0.2. Surface height and color opacity scale with likelihood density, normalized to the maximum value within each putative cell. (C,D) Segmentation performance. The effects of cell segmentation for samples 1 (C) and 2 (D) with minimum conductance thresholds 0.14 (black), 0.2 (cyan), and 0.26 (magenta) are shown on binomial p-values quantifying segmentation fidelity (solid lines) and putative cell count (dotted lines). (E,F) Inclusion of position information from sMLE inferences improves performance. Shown is the separation of fluorescent protein transgenes among decreasing numbers of identifiable cells for samples 1 (E) and 2 (F), with GFP UMI fraction and RFP UMI fraction shown in green and red shades, respectively.
This analysis remained agnostic to inferred molecular positions, and demonstrated that modularity within the raw UEI data matrix was sufficient to perform rough segmentation of individual cells. In order to observe the degree to which inferred molecular positions could help improve cell segmentation, we quantified, for each UEI-connected UMI pair belonging to the same spectrally-segmented cell, the fraction of their respective position uncertainties that overlapped (STAR Methods). We assigned this UMI overlap-fraction the symbol g, which could vary between 0 and 1. We then separated sub-sets of UMIs into distinct cells if no pair of UMIs connecting these sets had a value of g of at least a specified threshold. We analyzed GFP and RFP sequestration across cells with either the initial position-independent segmentation (g=0), or with fraction-overlap threshold g=0.75 or 0.9 (Figure 6E,F) using sMLE-inferred UMI coordinates. Increasing the threshold g enhanced the sequestration between GFP and RFP transcripts among cells, demonstrating the usefulness of applying inferred positions to the task of de novo cell segmentation.
Imaging large numbers of different transcripts in DNA microscopy
To demonstrate that DNA microscopy and its associated cell segmentation could be extended to larger numbers of genes, we synthesized cDNA by reverse transcription from up to 20 additional genes that have been previously shown to be differentially enriched (although not exclusively expressed) in MDA-MB-231 and BT-549 cell lines (Klijn et al., 2015) (Tables S5, S6, STAR Methods). We performed global image inference (Figure S6E,F) and applied our recursive graph-cutting cell segmentation algorithm (Figure S6G,H). Rarefaction analysis demonstrated rapid saturation of UMI and UEI counts (Figure S6I,J). Pearson correlations between the GFP-fraction per spectrally-segmented cell (out of total transgene transcripts per cell) and fraction of endogenous genes expected to be enriched in the GFP cell line (out of total endogenous gene transcripts enriched in either cell line) gave r = 0.29–0.41 (n=764 and 265) for two experiments, respectively (p-value<10−6, permutation test). This demonstrated that the transgenes labeling these cell types retained information about cell type-specific endogenous expression, and that this information could be read out from DNA microscopy data. Moreover, because DNA microscopy measure of full amplicon sequences, it can readily distinguish transcript variants for example from two different alleles, such that each localized transcript is assigned to a specific allele, without the need for any a priori known allele-specific primers (Figure S6K,L).
To more directly compare between the DNA microscopy data and bulk RNA profiling data for these genes, we classified each putative cell in our data set as MDA-MB-231 if it had more GFP UMIs than RFP UMIs, and as BT-549 otherwise, and then compared these cell’s profiles to previously measured ones. We found a good correlation between UMI counts and read counts among endogenous genes for each putative cell type individually (Spearman rs=0.54–0.64, Figure S6M,N), further matching DNA microscopy quantitation with bulk RNA-seq data. The data further provided the opportunity to analyze the contribution of gene insert size to average UEI formation distance. In the context of the DNA microscopy experiment and over the range of gene insert sizes measured (200–300 bp), we observed this effect to be minimal (Figure S6O–R).
Discussion
The fundamental advance of DNA microscopy is to physically image biological specimens using an unstructured and stand-alone chemical reaction without optical information, making it a distinct microscopic imaging modality. We have drawn a close technological analogy between DNA microscopy and optical super-resolution microscopy: both take advantage of stochastic physics to reduce measurement uncertainty beyond what may seem superficially to be a physically imposed limit.
However, the two differ in several fundamental ways and as a result are highly complementary. Optical super-resolution microscopy relies on the quantum mechanics of fluorescent energy decay. DNA microscopy, however, relies entirely on thermodynamic entropy. The moment we tag biomolecules with UMIs in the DNA microscopy protocol, the sample gains spatially stratified and chemically distinguishable DNA point sources. This tagging process thereby introduces a spatial chemical gradient across the sample that did not previously exist. Once these point sources begin to amplify by PCR and diffuse, this spatial gradient begins to disappear. This entropic homogenization of the sample is what enables different UMI diffusion clouds to interact and UEIs to form. It is therefore this increase in the system’s entropy that most directly drives the DNA microscopy reaction to record meaningful information about a specimen, including both the UMI coordinates and differences in spatial impedances that each UMI diffusion cloud experiences as it evolves.
Detection of these spatial barriers, achieved by comparing UEI formation rates at different length scales, is central to cell segmentation in DNA microscopy and offers an important distinct tool for analyzing biological morphology. The use of a low-pass spectral filter to perform cellular segmentation from UEI data matrices further clarifies the parallels between DNA microscopy and light microscopy, in which low-pass filters permit morphology to be inferred from high-variance pixel intensities.
However, one key weakness of DNA microscopy remains the resolution of empty space, and future work will be needed to eliminate this obstacle to produce high-quality reconstructions of samples over large lengths where there are gaps in molecular density. There are two potential solutions to this problem: an experimental one and an analytical one. First, a “landmark”-based experimental approach, in which specific DNA sequences are deposited at known physical locations to assist in the image reconstruction process, may ultimately prove the most cost-effective way to achieve this. Second, better analytical techniques to correct for large length scale distortions may prove equally effective, without complicating the experiment itself.
DNA microscopy offers a distinct form of optics-free imaging that leverages the large economies of scale in DNA sequencing. The technology does not require sacrificing spatial resolution for sequence accuracy, since it benefits, rather than suffers, from high signal density and it does not hinge on optical resolution of diffraction-limited “spots” in situ. By using chemistry itself as its means of image acquisition, DNA microscopy decouples spatial resolution from specimen penetration depth (otherwise linked by the properties of electromagnetic radiation) and thereby sidesteps a tradeoff imposed by the physics of wave propagation. Furthermore, by virtue of capturing an image of a sample through a volumetric chemical reaction, DNA microscopy may provide an ideal avenue for three-dimensional imaging of intact whole mount specimens.
Because DNA microscopy does not rely on specialized equipment and can be performed in a multi-well format with normal lab pipettes, it is highly scalable, such that a large number of samples can be processed in parallel. It is fully multiplex-compatible (imaging any PCR template) and uses sequencing-depth as a dial to enhance genetic detail, through the accrual of UMIs (including those belonging to low-abundance transcripts, in a manner equivalent to any traditional sequencing assay) and spatial detail through the accrual of UEIs.
Moreover, because DNA microscopy reads out single-nucleotide variation in the biological DNA or RNA sequences it targets, it spatially resolves the astronomically large potential variation that exists in somatic mutations, stochastic RNA splicing, RNA editing, and similar forms of genetic diversity in cell populations. We demonstrated that DNA microscopy achieves this at high sequencing accuracy (99.7–99.9%/bp) over long read lengths (~100 bp) (Figures S2 and S6), such that transcripts from different alleles are uniquely positioned, without the need to know a priori the extent of genetic diversity. In this way, DNA microscopy is a compelling approach to study the tissue organization of cells such as lymphocytes, neurons, or mutated cancer cells, where somatic mutation, recombined gene segments, and other sources of nucleotide-level variation endow unique molecular identities with important physical consequences.
Our development of a chemically encoded microscopy system lays the foundation for new theoretical and experimental applications and extensions of the technology. Future experimental and computational enhancements should better resolve large length scales that include large spatial gaps between groups of molecules. Furthermore, the UEI, by effectively functioning in these experiments as a DNA analog of the photon, has illuminated a wider potential role for DNA as a medium for artificial precise biological recordings of chemical kinetics. Most directly, the principle of DNA microscopy can be applied beyond the transcriptome, for example directly to DNA sequences or to proteins detected with DNA-labeled antibodies. Looking to the future, a full exploration of individual and idiosyncratic biological spatial structures by encoding them into DNA bases, instead of pixels, as demonstrated here, may complement existing grid-capture and wave-based imaging methods and reveal new and previously inaccessible layers of information.
STAR METHODS
CONTACT FOR REAGENT AND RESOURCE SHARING
Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Joshua A. Weinstein (jwein@broadinstitute.org).
EXPERIMENTAL MODEL AND SUBJECT DETAILS
All experiments were performed on female human cell lines BT-549-RFP (Cell Biolabs AKR-255) and MDA-MB-231-GFP (Cell Biolabs AKR-201). All sub-culturing was performed at 37 C under 5% CO2 in growth medium containing 10% FBS (Seradigm 1500), 1% NEAA (Thermo Fisher 11140), 1% pen-strep (Thermo Fisher 15140) in DMEM (Thermo Fisher 10569).
METHOD DETAILS
Bead-plate reaction chambers
Reaction chambers for large cell populations in samples 1–2 and 4–5 (Figure S1A) were designed in order to maximally adhere cells while providing a thermally robust container for PCR thermo-cycling. 3 mm glass beads (Sigma Z265926) were acid washed in 1 M HCl at 50–60 C for 4–5 hours in a glass beaker with occasional agitation and then kept sealed in 90% ethanol at room temperature until further use. After an initial rinse in acetone, beads were treated for 60 seconds in a 2% solution of (3-aminopropyl)triethoxysilane/APTES (Sigma 440140) in acetone. Beads were then rinsed 4 times in ddH2O, rinsed in isopropanol, and allowed to dry in a laminar flow hood 1 hour in a polystyrene petri dish. Dried beads were kept sealed at room temperature until further use.
PDMS (R.S. Hughes RTV615) was mixed at a ratio of 1:10 w/w cross-linker:potting reagent, and mixed/degassed 3 minutes at 2000 rpm. Uncured PDMS was immediately dispensed into PCR plate wells (Axygen PCR-96-HS-C) at ~ 20 ul in volume. Plates were then spun down at 500 xg for 1 minute. Volumes were carefully equalized across wells, and the plate was spun down again. APTES-treated glass beads were then placed into each PDMS-filled well of the PCR plate using plastic tweezers. The PCR plate was then spun down again at 500 ×g for 5 minutes, and beads were checked to ensure a small amount of surface was exposed above the PDMS. Bead-plates (illustrated in Figure S1A) were then cured at 80 C for 2 hours, and stored sealed at room temperature until further use.
Glass-slide reaction chambers
Reaction chambers for imaged cells in sample 3 are shown in Figure S1B–C. PDMS was mixed at a ratio of 1:10 w/w cross-linker:potting reagent as before, and mixed/degassed 3 minutes at 2000 rpm. Uncured PDMS of mass 33–35 g was immediately dispensed into 10 cm petri dishes and degassed under vacuum for 1 hour. PDMS was then cured at 80 C for 150 minutes, and holes were punched using Integra biopsy punches with diameter 6 mm in the pattern indicated (Figure S1B). Cut PDMS blocks were then bonded with oxygen plasma to plain glass slides (VWR 16004–422) and cured at 80 C for 3 hours. 100–120 ul of mineral oil (Sigma M5904) was then added to all wells and degassed 45 minutes. Slides were then baked at 80 C for 5 hours, then allowed to cool, and mineral oil was aspirated. Slides were washed heavily with acetone and isopropanol to get rid of residual mineral oil and allowed to dry. 2% APTES solution was prepared in acetone as above, and the bottom of the wells were immersed with 35 ul of this solution for 60 seconds. Wells were immediately rinsed 5 times with 120 ul water, 2 times with isopropanol, allowed to dry, and stored sealed at room temperature until further use.
Cell seeding
Before cell seeding, bead-plates were rinsed twice with 70% EtOH and allowed to dry 45 minutes under UV in a cell culture hood. All wells were then washed once with 100 ul DPBS (Sigma D8537). A fibronectin solution (Sigma F1141) was then prepared at a 1:100 dilution in DPBS and used to cover wells, which were left at room temperature for 1 hour. BT-549-RFP (Cell Biolabs AKR-255) and MDA-MB-231 -GFP (Cell Biolabs AKR-201) cell lines were then resuspended at 5000 cells/ml and 2500 cells/ml, respectively, in medium containing 10% FBS (Seradigm 1500), 1% NEAA (Thermo Fisher 11140), 1% pen-strep (Thermo Fisher 15140) in DMEM (Thermo Fisher 10569). After aspirating fibronectin, 50 ul of this cell suspension (totaling ~250 and 125 cells of the two cell lines, respectively, because the latter had a higher growth rate) was then added to the bottom of each beat-plate well.
For glass-slide reaction chambers, 85 ul of growth medium (without cells) was added, and parafilm was used to cover the top of the reaction chamber assemblage. Holes were cut in the middle of cell culture wells (the four interior wells in Fig S1B). 10 ul pipette tips were then cut (Fig S1C) and cell suspension was added from the wide end so that it traveled to the narrow end, and was held in place by capillary action. Parafilm was then added to wide end to create suction that would hold the cell suspension in place after the pipette tip was placed into growth medium. Pipette tips containing cell suspension and covered by parafilm were then placed vertically into the slide reaction chambers, and cells were allowed to settle. Cells in all reaction chambers were then cultured 36–48 hours.
In situ preparation
After culturing, growth medium was removed and cells were washed once with 1x PBS (prepared from Thermo Fisher AM9625). Cells were fixed in 4% formaldehyde (prepared from Thermo Fisher 28906) in 1×PBS for 15 minutes at room temperature. Formaldehyde solution was aspirated and replaced by 3 ×PBS, and left for 10 minutes. Samples were washed twice for 10 minutes in 1× PBS, and then permeabilized with a solution of 0.25% Triton X-100 (Sigma 93443) in 1 × PBS for 10 minutes. Samples were then washed twice in 1 × PBS, treated with 0.1 N HCl (VWR BJ318965) for 2–3 minutes and then washed an additional three times in 1 × PBS. Samples were then kept at 4 C during preparation of the reverse transcription reaction.
Immediately before reverse transcription, samples were rinsed once in ddH2O. After aspiration, reverse transcription mixes were added containing 400 uM dNTP (Qiagen N2050L), Superase-In (Thermo Fisher AM2696) at 1 U/ul, Superscript III (Thermo Fisher 18080) at 10 U/ul, 1× Superscript III buffer, and 4 uM DTT. RT ultramers containing UMI’s (Table S1 for 4- plex, Table S5 for 24-plex) were included at 850 nM (for Samples 1–2) or 100 nM (for all others) each. These reactions were then incubated 60 C for the 3 minutes, followed by 42 C for 1 hour, and then held at 4 C. After aspiration, samples were washed three times in 1 ×PBS, and kept at 4 C in the final wash overnight. Samples were rinsed with ddH2O, and after aspiration, 40 ul of an enzymatic digestion mix was added including 1× exonuclease-I buffer (NEB B0293S) and 1.4 U/ul exonuclease I (NEB M0293). Reactions were incubated at 37 C for 40 minutes, and then washed three times in 1 ×PBS.
Amplification mixes were prepared that included 400 nM each of primers OE1a and OE4b, 300 nM each of primers psbs12s (Lbs12s for 24-plex samples, Table S6) and s8B, 30 nM each of LF-primers (Table S2, or for 24-plex amplification, 10 nM each of the sF-primers in Table S6), 1.6 mM MgCl2, 200 uM dNTP, 0.5 mg/ml BSA (NEB B9000S), 8% v/v glycerol (Thermo Fisher 15514011), Platinum Taq DNA polymerase (Thermo Fisher 10966018), 1×Platinum Taq PCR buffer, a 4-arm acrylate PEG (Laysan Bio 4ARM-PEG-ACRL-10K) at 64 ug/ul, and a 2-arm thiol PEG (Laysan Bio SH-PEG-SH-3400) at 44 ug/ul. Solutions were prepared in two parts, one containing the 2-arm thiol PEG, BSA, and glycerol, and one containing all other components. Following an additional sample rinse with ddH2O and aspiration, these two distinct components were mixed by pipetting and immediately added in 20 ul volumes (as a combined mixture) to the sample to allow for a 10.8% w/v hydrogel to polymerize for 1 hour at room temperature. This hydrogel would slow diffusion during the amplification reaction (Xu et al., 2016).
Samples were then thermo-cycled at 95 C 2 min, 10×(95 C 30 s, 68 C 1 min), 2× (95 C 30 s, 55 C 30 s, 68 C 1 min), 16× (95 C 30 s, 60 C 30 s, 68 C 1 min), 68 C 1 min, 4 C. For 24-plex samples, samples were instead thermo-cycled 95 C 2 min, 1 × (95 C 30 s, 55 C 30 s, 68 C 1 min), 10 ×(95 C 30 s, 68 C 1 min), 1 × (95 C 30 s, 55 C 30 s, 68 C 1 min), 16 × (95 C 30 s, 60 C 30 s, 68 C 1 min), 68 C 1 min, 4 C. The initial sets of 10 cycles at high temperature in these programs were designed to prime only one end of the cDNA amplicon. This would thereby confine initial amplification to increasing molecule copy numbers linearly with time, rather than exponentially. It would thereby minimize the effect of potentially stochastic amplification start-times. Following in situ amplification, samples were stored at −20 C until further use.
Library preparation
Frozen amplified samples were allowed to thaw on ice. A PEG-dissolution mix containing 460 mM potassium hydroxide (VWR BJ319376), 100 mM EDTA (Sigma 03690), and 40 mM DTT (Thermo Fisher P2325) was added directly on top of the hydrogel at 4 ul per sample while the sample was still on ice, and left for 2 hours at that temperature. Samples were then heated to 72 C 5 minutes, and mixed by pipetting 10 times. 4 ul of a neutralization solution made by combining 400 ul 1N HCl (Sigma H9892) and 600 ul 1M Tris-HCl pH 7.5 (TekNova T5075), adding this to the samples, and immediately mixing the solution again by pipetting. 11.1 ul of a proteinase mix was then added that contained 0.35% v/v Tween 20 (Sigma P9416) and 0.35 mg/ml proteinase K (NEB P8107) in 10 mM Tris-HCl pH 8 (TekNova T1173). After mixing the samples by pipetting, incubation was performed at 50 C for 25 minutes.
55 ul of 10 mM Tris-HCl pH 8 was then added to each sample, and mixed by pipetting. 85 ul of the mixture was transferred to a new PCR plate, and 0.65 × volumes of Ampure XP beads (Beckman Coulter A63881) were added, mixed by pipetting, and left to incubate at room temperature 10 minutes. After twice washing with 70% ethanol, DNA was eluted into 35 ul 10 mM Tris-HCl pH 8. Product was then diluted 1:2 into a PCR reaction containing final concentrations of 300 nM SBS3LC primer, 300 nM rev-ill-214 primer, 3.3 uM each of 10T-0E-P and 10T-OEc-P interference primers (following on the strategy employed in Turchaninova et al 2013 to prevent new concatemers from forming), 0.02 U/ul Platinum Taq HiFi DNA polymerase (Thermo Fisher 11304029), 1× Platinum HiFi Buffer, 1.5 mM MgS04, and 200 uM dNTP. Reactions were thermo-cycled 95 C 2 min, 20× (95 C 30 s, 68 C 2 min), 4 C.
Reaction products were Ampure XP-purified just as before, with 0.65 × volumes of Ampure XP beads added, and eluted into 40 ul 10 mM Tris-HCl pH 8. As part of a final sequence-barcoding step, 10 ul of sample eluent was added to a reaction containing 300 nM forill-sbs3, 300 nM rev-ill-X (with a sample-specific barcode where indicated on the sequence),0.02 U/ul Platinum Taq HiFi DNA polymerase, 1 × Platinum HiFi Buffer, 2 mM MgS04, and 200 uM dNTP. Reactions were then thermo-cycled 95 C 2 min, 5× (95 C 30 s, 58 C 30 s, 68 C 2 min), and 1–5 × (95 C 30 s, 68 C 2 min), 4 C in order to obtain sufficient DNA library for sequencing.
Sequencing
Following a final Ampure XP purification as above, with 0.7 × volumes of Ampure XP beads added, NGS libraries were sequenced on an Illumina NextSeq 550 instrument using manufacturer- standardized protocols for paired-end sequencing. Sequenced reads were demultiplexed using the Illumina bcl2fastq pipeline using the 8nt sequence-barcode included 5’- adjacent to the SBS12 adapter 5 ‘ -GT GACTGGAGTTCAGACGT GT GCT CTTCCGATCT-3 ‘ (Figure S1, Table S2). Paired-end reads were sequenced from the SBS3 sequencing primer 5 ‘ -ACACT CTTTCCCT ACACGACGCT CTT CCGAT CT-3 ‘ to 103 bp, and from the SBS12 sequencing primer to either 57 bp or 151 bp, as indicated in Tables S1 and S5, depending on whether full amplicon sequences were intended to be captured (instead of simply a minimum number of identifying bases).
UMI/UEI design
The number of N’s to use in a UMI/UEI will depend on the expected diversity of molecules and/or events being tagged. Assuming an upper-bound for this diversity is known, the question reduces to the so-called “birthday-problem”. Given a UMI/UEI length ℓ (with each of ℓ bases having all 4 base possibilities), the probability that two randomly-drawn UMIs/UEIs will match (assuming uniform base-distributions) is P0(ℓ) = 4−ℓ. Similarly, the probability that there will be another UMI/UEI within 1 bp is
| (1) |
because there is 1 way for a randomly drawn sequence to be precisely the sequence of a previously drawn sequence, and 3ℓ ways for it to be the same except for exactly 1 mismatch.
The probability that no two UMIs/UEIs out of N will overlap in this way is
Define Ncrit(ℓ) through the relation
Then Ncrit(ℓ) is the maximum diversity of templates beyond which it becomes likely that at least 1 pair of UMI/UEI sequences will be within 1 bp of one another. For UMI/UEI sequences in which there are ℓ4 bases that are randomly selected across all 4 nucleotides and ℓ2 bases that are randomly selected across 2, we can re-write our original expression for P≤1(ℓ):
Since the UMIs used in our experiments (Table S1, Table S5) have ℓ4 = 20 and ℓ2 = 9, this gives us Ncrit = 3.3 × 106 for each beacon- and target-UMI data set presented here.
Note that for UEIs, the picture is far simpler. Because a UEI brings together exactly two UMIs, two UEIs that are grouped together will get one vote (assigned via plurality). Therefore, the less abundant indistinguishable UEI will simply be ignored. From here we can see that we can bring UEI diversity far closer to the upper limit of that which is physically possible (4ℓ, or in our case ~1012) without substantial problems.
Note furthermore that even for UMIs, things get easier if the target sequences are used to separate out UMIs (this is not done for any data-set presented here). For a set of target sequence frequencies (p1;p2,…,ps}(normalized to sum to one) of S distinct sequence-types labeled by UMIs, the probability that two randomly selected sequences will be the same is . This measure, also known as Simpson’s diversity index, affects the calculation above by multiplying P≤1. The more diverse and distributed the population of sequences, the smaller the product λP≤1 and the larger the value of Ncrit(ℓ).
Remark on reagent quality control
Although reagent quality control is crucial for every protocol, PEG reagents used for the in situ PCR step are especially sensitive to variation. Basic precautions that must be taken include desiccation with Drierite (Sigma 238961) or a similar agent in a sealed bag at −20 C. Lot- to-lot variation must be controlled by keeping a careful log of the lots used for each experiment. We found that in general this variation could be pre-checked by performing routine bulk PCR’s within the hydrogel, and comparing the results on a gel. UV/Vis comparison may also be used as a way to compare inorganic salt content that may have carried over from manufacture.
QUANTIFICATION AND STATISTICAL ANALYSIS
Read parsing
Reads were parsed by first gating out those with a mean quality score of less than 30 on either the forward or reverse read. Forward and reverse reads were then checked for inclusion of primer and stagger sequences, depending on the primers used and indicated in Tables S1 and S5. Capitalized bases were used to indicate those base positions intolerant of a single mismatch, whereas consecutive stretches of lower-case bases were used to indicate pieces of sequence that were permitted to contain mismatches up to the indicated maximum of 0.06 as a fraction of total. For 4-plex data, 5 bases after gene-specific primer sequences were used to gate reads in order to remove unrecognized gene inserts. Read counts and fractions retained for each data set are shown in Table S3.
UMI/UEI clustering
In order to identify UEI and UMI sequences in a way that would make efficient use of the data available and in a manner specifically accommodating to long-tailed distributions of PCR error, we developed a simple clustering algorithm, which we here on refer to as EASL, or Extended Abundance Single-Linkage. EASL relies on single-mismatch alignments alone to identify clouds of erroneous sequences that decay in density the further in sequence-space they exist from an abundant, putatively correct, original sequence.
EASL clustering (Figure S2A) initiates by grouping every UMI/UEI (from each read location separately, so that it disregards the rest of that read) within a data set by perfect identity. The abundance (by read-count) is assigned to each UMI/UEI sequence. Each pair of UMIs/UEIs is compared by un-gapped alignment. This may be performed by local similarity hashing in a way that permits full pairwise comparison in O(NL2) time, where N is the number of unique UMIs/UEIs, and L is the length of the UMI/UEI sequence. In brief, this may be achieved by generating L hash-tables/dictionaries of UMI/UEI sequences, where each of these dictionaries has a specific sequence-position removed. For each dictionary, the full collection of L — 1 length UMI/UEI sequences generated by removing that corresponding position are added to the dictionary. Those found grouped together will be those sets related by a single base mismatch.
EASL clustering then proceeds as follows (Figure S2A). UMI/UEI i directionally links to UMI/UEI j if and only if the read-abundance of UMI/UEI i is greater than or equal to the read- abundance of UMI/UEI j. Read number densities (RNDs) are calculated for each UMI/UEI sequence by summing read-abundances belonging both to the sequence itself and to all sequences (of equal or lower abundance) it links to. Each UMI/UEI data set is then independently sorted by decreasing RND, and accordingly clustered independently, as follows.
The UMI/UEI with the largest RND initiates clustering as the first cluster-seed. All UMIs/UEIs to which this seed links by the aforementioned criterion are accepted into its cluster. The algorithm then proceeds to the UMI/UEI with the next largest RND that has not already been assigned a cluster. This UMI/UEI becomes a new cluster seed and all UMIs/UEIs not yet assigned to a prior cluster are accepted to that belonging to the new seed. This process proceeds among all un-assigned UMIs/UEIs down the RND-sorted list. When no un-assigned UMIs/UEIs remain, the algorithm terminates.
UEI-UMI pairing
After clustering, UMIs were accepted to further analysis if they associated with at least two reads (UMIs and UEIs remaining after this preliminary filtering step are represented by the upper-curves in the rarefaction plots in Figures 3–4 and 5). UEI clusters were then matched with the beacon UMI/target UMI cluster-pair to which they were found to associate with the most reads in the original data. This filtering was intended to remove incorrect associations between beacon UMIs and target UMIs caused by, among other things, PCR chimera formation during downstream library preparation steps (we reasoned that the original UMI-UEI-UMI pairings would have a head-start before late-stage amplification - once a new and incorrect UMI-UEI- UMI pairing would form, it would begin amplifying from a quantity of 1 molecule later in downstream amplification).
The resulting “consensus” UMI-UEI-UMI pairings were then iteratively filtered by eliminating UMIs associating with fewer than 2 UEIs. After the initial set of UMIs were removed on account of having too few UEIs, the UEIs they associated with were removed, the matrix was re-filtered to exclude UMIs that no longer had at least 2 UEIs, and so on, until no remaining UMIs could be found associated with fewer than 2 UEIs. The resulting pruned data set is shown in the lower-curves of the rarefaction plots in Figures 3–4 and 5.
The target sequences grouped by UMI-clustering further allowed errors owing to PCR and sequencing to be suppressed. Aggregating the votes at every position for the reads grouped under a particular target UMI gave quality scores (−10 log10 Prob(incorrect)) that mostly stuck to Q=30 until 60–70 bp after the end of the primer, after which Q hovered between 25–30 until it ended nearly 100 bp into the transcript (Figure S2B).
Estimating a false positive rate
The EASL algorithm ensures that all UMI sequences within 1 bp will be grouped, unless there is a dip in read-abundances that would indicate a disjoint cluster of sequences has been encountered. DNA microscopy sequence analysis also removes UMIs associating with fewer than 2 UEIs. Taken together, we can estimate the rate at which “false positive” UMIs arise. The probability that a UMI is included in the final image inference that does not truly exist can be written
| (2) |
| (3) |
where
with μk being the average number of UMI-variants per EASL-clustered UMI found at k nucleotides away from the most abundant UMI-variant and
where μR,k is the average number of reads associated with a UMI variant at k nucleotides away from the most abundant UMI-variant. The final probability in the summand (that r reads belonging to UMI will consist of ≥2 UEIs of ≥2 reads each) is an empirically determined quantity, which in Table S4 is measured through 10 random draws for each UMI in each data set (sample-standard deviations from these random draws are also shown). Plugging these quantities into to equation 3 gives a false-positive rate ranging between 10−3 – 10−4 as a fraction of UMIs that we can expect to be duplicates of other UMIs. It is meanwhile worth noting that this quantity will be an upper bound in the sense that it does not account for the likely outcome that even if an erroneous UMI with at least 2 UEIs does make it to the final analysis, that it will not form a contiguous data set with the main body of the data.
Image inference
Formalization
Consider the evolving concentration distribution of products of a single UMI with index i, centered at position , during a DNA microscopy reaction. This can be modeled as isotropic diffusion using the Gaussian profile for concentration at position at time t:
| (4) |
where d is the dimensionality (of physical space), D is the diffusion constant, and A = log 2 /Δt where Δt is the time-scale of a PCR cycle. The rate of UEI/concatemer formation between UMIs i and j with the same diffusion constant will then be the volume-integral
| (5) |
| (6) |
| (7) |
Note that although the UEI formation rate is time-dependent - and that therefore the total observed reaction rate is in fact a sum of functions above from each PCR cycle — provided amplification happens quickly, prior time-dependence to some final reaction time τ will be swamped out by the reaction rate at that time τ. Therefore, for the sake of simplicity, we will drop the time dependence from our probability model, and say that UMIs i and j located at t = 0 at positions and , respectively, will have an expected cumulative reaction rate of
| (8) |
where Ai and Aj, are amplification “biases”, ie the cumulative effective amplitudes of the UMIs’ diffusion profiles. The length scale above is denoted
in the main text.
The probability of observing UEI counts {nij} for each UMI-pair <i,j> is then the multinomial expression
| (9) |
where dots “·” represent index summation (so that w.. = ∑ijwij). From this, we can write the log-likelihood
and, relying on the functional form from equation 8, we can write its gradient with respect to UMI position as consisting of two added sums:
| (10) |
The first sum (“sum #1”) is linear and sparse, in the sense that most values of nkj are zero. The second sum (“sum #2”), however, is non-linear and dense, in the sense that no value of wkj is exactly zero. A solution to the above occurs when the gradient is zero for every , and where contributions from equation 10 sums #1 and #2 balance. These two sums differ in several important ways.
The first difference is the role they play: sum #1 dictates how to center each UMI relative to one another, and attracts all UEI-associated UMIs together, whereas sum #2 regulates how to separate them, by repelling all UMIs from all other UMIs at the strengths dictated by the intrinsic length scale of the function wij. Second is the ease of calculation: sum #1 involves summing only the UEIs observed in the experiment, the summation is sparse in the same way our observations are sparse; sum #2 meanwhile makes no distinction between UEIs that are observed and UEIs that are not, and requires the summation over all UEIs that are possible. Finally, the two sums differ in the length scales over which they operate. Optimization over small length scales containing minimal point density variation will make sum #2 in equation 10 approach zero, since it involves the summation of repulsive forces pointed in all directions. In these circumstances, sum #1 will dominate. However, over long distances in which large-scale point densities may vary, sum #2 will contribute heavily.
Local linearization of the image inference problem
We can write sum #1 of equation 10 as , where x is now a solution to all UMI positions simultaneously, and where we’ve defined the zero row-sum UEI matrix, or what in the main text is referred to as the UEI Graph Laplacian:
Note that N is a sparse square matrix (all UMIs × all UMIs), re-written from the rectangular form in Figure 1E, which has exclusively beacon UMIs as rows and exclusively target UMIs as columns. N will always have a “trivial” eigenvector of all 1’s (with eigenvalue 0) that solves the equation by making all positions equal. Solving equation 10 part #1, by obtaining the non-trivial solution nearest to 0 means setting , and amounts to maximizing the numerator of the multinomial probability in equation 9. We will write the solution to this eigenvalue problem in a row-normalized form
| (11) |
where we use the diagonal matrix
to equalize contributions to the gradient by each UMI.
Because the solution to the maximum likelihood problem is only linear locally, we need a way to zoom in on local portions of the data in order to use it. We can do this by applying simple and approximate graph cut/spectral partitioning algorithms previously described (Shi and Malik, 2000). Specifically, we take the symmetric normalized form of the UEI Graph Laplacian, Λ−1/2NΛ−1/2, and find its second smallest-in-magnitude (after the trivial solution) eigen- value/eigenvector pair. We then perform a sweep of possible cuts within that eigenvector to minimize the conductance between the resulting UMI sub-sets A and B: N(A,B)/ min(N(A),N(B)), where N(A,B) is the number of UEIs associating UMI sub-sets A and B, and N(A) and N(B) are the total number of UEIs belonging to those two UMI sub-sets, respectively.
Minimizing this conductance value allows for the “sparse cut” described in the main text. By iteratively cutting the matrix, re-forming the matrix Λ−1/2NΛ−1/2, and continuing until the minimum available conductance-cut is above a threshold, we can obtain local linear data subsets depicted in Figure 2E–H.
Setting the threshold higher provides for more extensive cutting, and results in the cell segmentation shown in Figure 6A–B. The accompanying binomial p-values in Figure 6C–D present, for putative cells with ≥50 UMIs and at least one ACTB and one GAPDH transcript:
where k′ is the number of UMIs belonging to the minority transgene (GFP or RFP) within that putative cell, m is the total number of transgene UMIs observed, and q is the frequency of the minority transcript within the entire data set. It therefore describes the probability of observing the cell as-is under a random partitioning hypothesis.
Curating spectral segmentation using inferred UMI positions
We say that a UEI connecting UMIs i and j satisfies a spatial overlap threshold g (in Figure 6E–F) if given their respective positions and :
where d = 2 (the dimensionality of physical space in this manuscript), is the sum of position likelihood variances derived under the section Resolution and UEI count, ni. and n.j are the total UEIs belonging to UMIs i and j , respectively. Note that it will always be true that 0 ≤ g ≤ 1 by the Cauchy- Schwarz Inequality. We may then apply this criterion to the problem of cell segmentation by asserting that all sub-sets of UMIs that are part of the same putative cell must be connected, via UEIs, by some chain of sufficiently overlapping UMI-UMI pairs.
Global likelihood maximization
Moving to larger length scales means dealing with sum #2 of equation 10. In order to handle the large-scale summation of every pair of UMIs (otherwise prohibitive due to its quadratic scaling), we adapted the Fast Gauss Transform (Greengard and Strain, 1991) that allowed calculation of this sum with bounded error in linear time. Error bounds were parametrized as the maximum possible fraction of the calculation of the weight-sum wk for each UMI. This was set to 30%, which sufficed to constrain actual error levels to orders of magnitude smaller (Figure S4).
Point-MLE solution
The most straightforward way solve equation 10 is to randomly initialize the global solution with an “educated guess” of what the global solution might look like and perform a gradient ascent of the global likelihood function using each UMI position as an independent variable. Since the eigenvector solutions to equation 11 satisfy local constraints, they provide a logical starting-point to initialize this solution. To this end, we let the top 100 eigenvectors of the full data-set’s row-normalized UEI matrix Λ−1N be columns in the matrix Z. The d-dimensional (with all samples here having d = 2) initial UMI positions were then defined through the linear combination
where was a d-column matrix, with each row corresponding to a different eigenvector, and its elements being linear coefficients used to sum the columns of eigenvectors in Z. The elements of were normally distributed coefficients generated from ,. Amplitudes Ai were set to log ni (an approximation asserting that, on average, UMI density was uniform at the length scale of diffusion) and gradient ascent proceeded using the calculation from equation 10 (and applying the L-BFGS optimization method from the SciPy library). This point-MLE approach was applied in Figure 5A–H.
These global solutions illustrate, however, the difficulty in capturing information on empty space when each point is being optimized independently. Clusters of points are unable to separate by more than the length scale Ldiff indicated by grid-lines (which is defined as the unit-less value of 1.0 in the physical model of equation 8).
Spectral MLE (sMLE) solution
In order to capture more information on empty space than the point-MLE solution allows, we can expand on the local linear solutions previously described, and require our global solutions to remain linear combinations of the top eigenvectors of the full data-set’s row-normalized UEI matrix Λ_1N. Again assembling these top eigenvectors as columns in the matrix Z, the global d- dimensional (with all samples here having d = 2) solution of size M × d for all M UMIs was then defined as the linear combination
| (12) |
where, as before, y was a d-column matrix, with each row corresponding to a different eigenvector, and its elements being the linear coefficients used to sum the columns of eigenvectors in Z. Using equation 12 made a low-dimensional variable set that we could optimize directly. The coefficients in y therefore dictated the UMI positions and the gradients of each UMI in were then calculated using equation 10. These individual UMI gradients were then projected back onto the linear eigenspace defined by Z, allowing y to be updated accordingly. Because eigenvectors in Z were not orthogonal, the back-projection of high-dimensional gradient Δx to low-dimensional gradient Δy was defined (through equation 12) by .
We approached this low-dimensional optimization within the eigenspace Z in as incremental a way as possible. We called this incremental approach “spectral maximum likelihood estimation”, or sMLE. On iteration 1 of sMLE, the first 2 eigenvectors of matrix Z were taken in isolation (corresponding to the non-trivial eigenvalues with smallest magnitude), and performing a gradient-ascent optimization of equation 10 with their coefficients alone gave optimal coefficients for generating a solution from a linear combination of these two eigenvectors alone. On iteration 2, the eigenvector with the next smallest-magnitude eigenvalue/eigenvector pair in Z was added to those allowed to contribute to the solution , thereby adding to the number of optimizable coefficients in . This larger vector was then optimized for the now 3 eigenvectors. This was repeated until all top eigenvectors (numbering 100 in the presented data sets) were integrated into the linear combination defining solution .
The outputs are plotted in Figures 4–6 and - for down-sampled read counts - in Figure S5A–F. It should be noted that the two parameters that need to be fixed for this algorithm are the scaling factor that multiplies the initial 2 eigenvectors that seed the solution and the choice of total eigenvectors after which the algorithm terminates (Figure S5G–J). Although alterations in the initial scaling factor result in isomorphic images (due to their using a common set of eigenvectors to construct a solution), certain manifold folding-defects can be mitigated by scaling factor choice. A comparison is made between initializing y in equation 12 to the identity matrix I (applied to solutions in the main text and Figures S5A and S5D) versus initializing to , where n.. is the total UEI count (applied to Figures 4, S5G, and S5I). The total number of eigenvectors at which the sMLE algorithm terminates (shown at 50 in Figures S5H and S5J, compared to 100 everywhere else) similarly alters manifold folding by freezing out certain degrees of freedom the solution can use to maximize the position likelihood function.
Resolution and UEI count
The relationship between the uncertainty of a UMI’s position given its neighbors’ can be understood as the equivalent of the standard-error in a statistical average (namely, the standard- deviation divided by the square-root of the number of independent measurements). However, we sketch it out explicitly here in the context of the solution-likelihood function in equation 9. If we assert that in regions where the local linear conditions previously discussed apply (gradients in point density at the diffusion length scale Ldiff are small), a solely varying UMI k has solution-likelihood at position about some maximal likelihood
then we can simply calculate
Since under the local linear conditions, the multinomial probability in equation 9 becomes a simple product of Gaussians, we get
where we’ve retained the physical length Ldiff in equation 8. From this we can finally write
| (13) |
meaning a UMI’s positional uncertainty will shrink with the square root of the total number of UEIs with which it associates. This relationship is highlighted in Figure 3B–C.
Simulation
The efficacy of the sMLE algorithm was evaluated in a more controlled setting using simulated data exhibited in Figure 3G.
Simulations proceeded as follows. For each UMI i, molecular-copy numbers mi(t) at amplification cycle t was initiated at mi(t = 0) = 1. For discrete linear amplification cycles t = 1,2, …,τlin, with τlin being the total linear-amplification cycle number, the total molecular- copy numbers were updated as
where 0 < pdup ≤ 1 was the efficiency at which each template (UMI-tagged cDNA) molecule was copied. As in the experimental protocol, linear amplification was followed by exponential PCR amplification, in which molecular-copy numbers were updated as
for t = τlin + 1, τlin + 2,…, τlin + τexp. Meanwhile, during exponential PCR cycles t = τlin + 1, τlin + 2,…, τlin + τexp. the expected rate of UEI formation wij(t) between every beacon i and target j was calculated according to the previously derived equation 7
where the expectation values of the total molecular abundance of beacon UMI i and target UMI j are here explicit - mi(t) and mj(t), respectively. For a given total final UEI count N, we then calculated an expected UEI count for time t
The number of actual UEI formation events for every triplet (i,j,t) were then assigned randomly using Poisson statistics
The kth UEI forming event generated by UMI-UMI pair (i, j), would then come into existence at its time-of-creation t ׳ with a molecular count aijk(t = t′) = 1. That abundance would evolve in time until the end of the reaction t = τlin + τexp according to the iteration relation
Each UEI’s final read-abundance, given an expected total read depth Ω, was then assigned
Image inference algorithms were then applied to this simulated data set in Figure 3G. Here, freely diffusing products from 5000 beacons and 5000 targets, incorporating amplification stochasticity and sparse UEI sampling (50000 UEIs). “Original” coordinates are ground truth. UEIs in simulation are generated from an amplification reaction the same as in the experiment (see section In situ preparation), with 10 linear amplification cycles and 16 exponential amplification cycles. Amplification stochasticity was introduced by making each molecular duplication event 5% likely to not occur at all (pdup = 0.95). Each cycle taking place over Δt = 1 with a D = 1 diffusion constant: both of these are in arbitrary units, with ground-truth positions normalized to the length scale (the length scale from equation 7), since D = 1, d = 3, and τ = τlin + τexp = 26 (note that diffusion is still simulated in 3 dimensions, even if molecules are initiated on a 2-dimensional surface). Image inferences from simulations are re-scaled and registered (rotation/reflection) relative to ground-truth.
DATA AND SOFTWARE AVAILABILITY
Python code developed for this work is available for download at https://github.com/jaweinst/dnamic. Raw data is available for download from the short-reads archive (https://www.ncbi.nlm.nih.gov/sra) under SRA project number PRJNA487001.
Supplementary Material
Highlights.
DNA microscopy is a distinct imaging modality that encodes physical images into DNA
A stand-alone reaction first writes inter-molecular proximities into DNA
An algorithm then reconstructs a supra-molecular image from this DNA-recording
DNA microscopy thereby constitutes a chemically encoded microscopy system
Acknowledgments:
We thank Andrew Piacitelli for his help sustaining experimental progress while this paper was being written. We thank Paul Blainey and his lab for their generosity and provision of their clean room for PDMS work, and for particularly helpful discussions with David Feldman and Lily Xu.
Funding:
This work was supported by an NIH R01HG009276, the Simons Foundation LSRF Fellowship (J.A.W.), and the Klarman Cell Observatory. F.Z. is a New York Stem Cell Foundation–Robertson Investigator. F.Z. is supported by NIH grants (1R01- HG009761, 1R01-MH110049, and 1DP1-HL141201); the New York Stem Cell and G. Harold and Leila Mathers Foundations; the Poitras Center for Affective Disorders Research at MIT; the Hock E. Tan and K. Lisa Yang Center for Autism Research at MIT; and J. and P. Poitras, and R. Metcalfe. AR and FZ are Howard Hughes Medical Institute Investigators.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Declaration of interests: The authors are co-inventors on patent applications filed by The Broad Institute related to this work. F.Z. is a scientific founder of and advisor to Arbor Biotechnologies, Beam Therapeutics, Editas Medicine, and Pairwise Plants. A.R. is a founder and equity holder of Celsius Therapeutics and an SAB member of ThermoFisher Scientific and Syros Pharmaceuticals.
References
- Achim K, Pettit JB, Saraiva LR, Gavriouchkina D, Larsson T, Arendt D, Marioni JC (2015). High-throughput spatial mapping of single-cell RNA-seq data to tissue of origin. Nat Biotechnol, 33, 503–9. [DOI] [PubMed] [Google Scholar]
- Aspnes J, Goldenberg DK, Whiteley W, Anderson BDO (2006). A theory of network localization. IEEE Trans Mobile Comput, 5, 1663–78. [Google Scholar]
- Chen KH, Boettiger AN, Moffitt JR, Wang S, Zhuang X (2015). Spatially resolved, highly multiplexed RNA profiling in single cells. Science, 348. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Greengard L, Strain J (1991). The fast gauss transform. SIAM J Sci Stat Comput. 12, 79–94. [Google Scholar]
- Hell SW (2009). Microscopy and its focal switch. Nat Methods. 6, 24–32. [DOI] [PubMed] [Google Scholar]
- Herishanu Y, Pérez-Galán P, Liu D, Biancotto A, Pittaluga S, Vire B, Gibellini F, Njuguna N, Lee E, Stennett L, et al. (2011). The lymph node microenvironment promotes B-cell receptor signaling, NF-kappaB activation, and tumor proliferation in chronic lymphocytic leukemia. Blood 117, 563–574. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Joyce JA, Fearon DT (2015). T cell exclusion, immune privilege, and the tumor microenvironment. Science, 348, 74–80. [DOI] [PubMed] [Google Scholar]
- Junker JP, Noël ES, Guryev V, Peterson KA, Shah G, Huisken J, McMahon AP, Berezikov E, Bakkers J, van Oudenaarden A (2014). Genome-wide RNA Tomography in the zebrafish embryo. Cell, 159, 662–75. [DOI] [PubMed] [Google Scholar]
- Kinde I, Wu J, Papadopoulos N, Kinzler KW, Vogelstein B (2011). Detection and quantification of rare mutations with massively parallel sequencing. Proc Natl Acad Sci USA, 108, 9530–35. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klijn C, Durinck S, Stawiski EW, Haverty PM, Jiang Z, Liu H, Degenhardt J, Mayba O, Gnad F, Liu J, et al. (2015). A comprehensive transcriptional portrait of human cancer cell lines. Nat Biotechnol. 33, 306–12. [DOI] [PubMed] [Google Scholar]
- Lee JH, Daugharthy ER, Scheiman J, Kalhor R, Yang JL, Ferrante TC, Terry R, Jeanty SS, Li C, Amamoto R, et al. (2014). Highly multiplexed subcellular RNA sequencing in situ. Science, 343, 1360–3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lefebvre JL, Kostadinov D, Chen WV, Maniatis T, Sanes JR (2012). Protocadherins mediate dendritic self-avoidance in the mammalian nervous system. Nature, 488, 517–521. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lubeck E, Coskun AF, Zhiyentayev T, Ahmad M, Cai L (2014). Single-cell in situ RNA profiling by sequential hybridization. Nat Methods, 11, 360–1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moffitt JR, Hao J, Wang G, Chen KH, Babcock HP, Zhuang X (2016). High-throughput single-cell gene-expression profiling with multiplexed error-robust fluorescence in situ hybridization. Proc Natl Acad Sci USA, 113, 14456–61. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Satija R, Farrell JA, Gennert D, Schier AF, Regev A (2015). Spatial reconstruction of single-cell gene expression data. Nat Biotechnol, 33, 495–502. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schreiner D, Nguyen TM, Russo G, Heber S, Patrignani A, Ahrné E, Scheiffele P (2014). Targeted combinatorial alternative splicing generates brain region-specific repertoires of neurexins. Neuron, 84, 386–398. [DOI] [PubMed] [Google Scholar]
- Schumacher TN, Schreiber RD (2015). Neoantigens in cancer immunotherapy, 348, 69–74. [DOI] [PubMed] [Google Scholar]
- Shi J, Malik J (2000). Normalized cuts and image segmentation. IEEE Trans Pattern Anal Mach Intell. 22, 888–905. [Google Scholar]
- Singer A (2008). A remark on global positioning from local distances. Proc Natl Acad Sci USA, 105, 9507–11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ståhl PL, Salmén F, Vickovic S, Lundmark A, Navarro JF, Magnusson J, Giacomello S, Asp M, Westholm JO, Huss M, et al. (2016). Visualization and analysis of gene expression in tissue sections by spatial transcriptomics. Science, 353, 78–82. [DOI] [PubMed] [Google Scholar]
- Turchaninova MA, Britanova OV, Bolotin DA, Shugay M, Putintseva EV, Staroverov DB, Sharonov G, Shcherbo D, Zvyagin IV, Mamedov IZ, et al. (2013). Pairing of T-cell receptor chains via emulsion PCR. Eur J Immunol, 43, 2507–15. [DOI] [PubMed] [Google Scholar]
- Victora GD, Nussenzweig MC (2012). Germinal centers. Annu Rev Immunol, 30, 429–57. [DOI] [PubMed] [Google Scholar]
- Xu L, Brito IL, Alm EJ, Blainey PC (2016). Virtual microfluidics for digital quantification and single-cell sequencing. Nat Methods, 13, 759–62. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Python code developed for this work is available for download at https://github.com/jaweinst/dnamic. Raw data is available for download from the short-reads archive (https://www.ncbi.nlm.nih.gov/sra) under SRA project number PRJNA487001.