Abstract
Importance:
The use of existing data (real world data or prior trials) to design and analyze clinical studies has the potential to accelerate drug development processes and can contribute to rigorous examination of new treatments.
Objective:
We discuss designs and interpretable metrics of bias and statistical efficiency of “externally controlled” trials (ECTs) and compare ECTs performance to randomized and single arm designs.
Setting:
We specify an ECT design that leverages information from real world data (RWD) and prior clinical trials, to reduce bias associated with inter-study variations of the enrolled populations. We then used a collection of clinical studies in glioblastoma (GBM) and RWD from patients treated with the current standard of care to evaluate ECTs. Validation is based on a “leave one out” scheme, with iterative selection of a single arm from one of the studies, for which we estimate treatment effects using the remaining studies as external control. This produces interpretable and robust estimates on ECTs bias and type I errors.
Results:
We developed a model-free approach to evaluate ECTs based on collections of clinical trials and RWD. For GBM we verified that inflated false positive error rates of standard single-arm trials can be considerably reduced (up to 30%) by using external control data.
Conclusions:
The use of ECT designs in GBM, with adjustments for the clinical profiles of the enrolled patients, should be preferred to single arm studies with fixed efficacy thresholds extracted from published results on the current standard of care.
Introduction
Randomized controlled trials (RCTs) have been the gold standard for clinical experimentation since the Medical Research Council trial of streptomycin for tuberculosis in 19481. Randomization is the foundation for many statistical analyses and provides a method for limiting systematic bias related to patient selection and treatment assignment2. Indeed, many failures in phase III drug development may be attributed to overestimating treatment effects from previous early-stage uncontrolled trials3. Although RCTs reduce the risk of bias compared to single arm trials, they tend to require larger sample sizes to achieve the targeted power4, take longer to complete enrollment, and patients have typically a lower propensity to enroll into a RCT than a single arm trial5–7.
Many methods have been suggested as a compromise between uncontrolled trials and RCTs8–11. Recently, availability of data collected from electronic health records (EHR) at scale has increased the interest in using real-world data (RWD)12 as a “synthetic” or “external” control12–14. Additionally, data from prior clinical trials can be integrated in the design and analysis of single arm trials15 rather than using a single published estimate of the standard of care primary outcome distribution to specify a benchmark. Leveraging RWD and prior clinical trials has the potential for controlling for known prognostic factors that cause inter-trial variability of outcome distributions. This can reduce bias in single arms studies, and ultimately could lead to better decision making by sponsors and regulators.
In this manuscript, we illustrate the design and validation of an externally controlled trial (ECT) design to test for therapeutic impact on overall survival (OS) using both RWD and data from prior clinical trials for patients with newly diagnosed glioblastoma (GBM). We compare the ECT design to single arm trial designs and RCTs and show the benefits and limitations of the ECT approach.
Methods
General approach to design and evaluate ECTs
To design an ECT, estimate the sample size for a targeted power, and evaluate relevant operating characteristics, our approach was the following. First, define the patient population for the ECT (in our case GBM). Next, identify a set of prognostic factors associated with the outcome of interest. Finally, specify the control therapy and identify available datasets (trials and RWD) for the control treatment and extract relevant outcomes and patients’ characteristics.
As described below, to evaluate the ECT design, the control arm of each study is compared (using adjustment methods) to an external control, which is defined by the remaining available data for patients that received the same control treatment. In these comparisons the treatment effect is zero by construction, which facilitates interpretability and produces bias and variability summaries for ECT’s treatment effect estimates, and type I error rates estimates.
If the ECT design maintains (approximately) the targeted type I error rate, we can then determine the sample size required for ECT, single arm trial and RCT designs for a targeted probability of treatment discovery at a pre-defined treatment effect.
The binary variable A indicates the assignment of a patient to the experimental treatment, A = 1, or to the control arm, A = 0, and Y denotes the outcome. We focus on binary endpoints, such as survival at 12 months from enrollment (OS12) and expand the discussion to time-to-event outcomes in the Supplementary Material. The vector X indicates a set of pre-treatment patient characteristics. We evaluate whether characteristics X are sufficient to obtain (nearly) unbiased treatment effect estimates or not.
Externally Controlled Trial (ECT) design
The ECT is a single-arm clinical study that uses the trial data (experimental treatment) and external data (control) to conduct inference on treatment effects. More specifically, for a hypothetical randomized study, we estimate the unknown average treatment effect
| (1) |
which is a weighted average of the conditional outcome probabilities weighted with respect to a distribution PrX(x) of patients characteristics X. Possible definitions for PrX(x) used by existing adjustment methods are the distribution of patient characteristics X in the single arm study, PrSAT(x), or the distribution of X in the external (historical) control, PrHC(x). The unknown probabilities Pr(Y = 1|A, x) do not referee to a particulate parametric statistical model but are unknown model-free quantifies. We considered four adjustment methods, all based on the usual hypothesis of no unmeasured confounders16 to estimate the unknown average treatment effect TE (1), direct standardization, matching, inverse probability weighting and marginal structural methods16,17 (Supplementary Material).
Datasets
To develop an ECT design for newly diagnosed GBM, we used data from patients receiving standard temozolomide in combination with radiation (TMZ+RT) from both prior clinical trials and RWD (Table 1). Clinical trial data was from the Phase III AVAglio18 () trial and two phase II trials (PMID: 22120301 and )19,20. RWD was abstracted from patients undergoing treatment for newly diagnosed GBM at the Dana-Farber and UCLA, and a previously published RWD dataset21.
Table 1:
Distribution of pre-treatment patient characteristics for the TMZ+RT arm of three clinical studies and three RWE studies.
| Study | DFCI-cohort | UCLA-cohort | AVAglio | |||
|---|---|---|---|---|---|---|
| NCT ID | --- | |||||
| PubMed ID | PM21135282 | PM25910950 | PM22120301 | PM24552318 | ||
| Datatype | RWE | RWE | RWE | Phase II | Phase II | Phase III |
| Arm | TMZ+RT | TMZ+RT | TMZ+RT | TMZ+RT | TMZ+RT | TMZ+RT |
| Enrollment period | 8/06–11/08 | 2/09–6/11 | 8/05–2/11 | 6/09–3/11 | ||
| Enrollments to SOC | 378 | 305 | 110 | 29 | 16 | 460 |
| OS Events | 269 | 265 | 89 | 24 | 15 | 344 |
| Age | ||||||
| Median | 58 | 57 | 59 | 58 | 59 | 57 |
| Range | 18–91 | 20–84 | 20–90 | 26–73 | 36–69 | 18–79 |
| SD | 13 | 13 | 14 | 11 | 11 | 10 |
| Sex (%) | ||||||
| Females | 0.43 | 0.36 | 0.36 | 0.45 | 0.5 | 0.36 |
| Males | 0.57 | 0.64 | 0.64 | 0.55 | 0.5 | 0.64 |
| KPS (%) | ||||||
| <=80 | 0.55 | 0.39 | 0.32 | 0.24 | 0.44 | 0.31 |
| >80 | 0.45 | 0.61 | 0.68 | 0.76 | 0.56 | 0.69 |
| Data missing (n) | 27 | 17 | 0 | 0 | 0 | 0 |
| RPA (%) | ||||||
| 3 | NA | 0.22 | 0.25 | NA | 0.12 | 0.16 |
| 4 | NA | 0.42 | 0.41 | NA | 0.75 | 0.61 |
| 5 | NA | 0.34 | 0.33 | NA | 0.13 | 0.23 |
| 6 | NA | 0.02 | 0.01 | NA | 0 | 0 |
| Data missing (n) | 378 | 0 | 0 | 29 | 1 | 0 |
| Resection (%) | ||||||
| Biopsy | 0.14 | 0.22 | 0.21 | 0.21 | 0 | 0.09 |
| Sub Total | 0.47 | 0.47 | 0.36 | 0.48 | 0.31 | 0.49 |
| Gross Total | 0.39 | 0.31 | 0.43 | 0.31 | 0.69 | 0.42 |
| Data missing (n) | 12 | 15 | 0 | 0 | 0 | 0 |
| MGMT (%) | ||||||
| Unmethylated | 0.43 | 0.71 | 0.60 | 0.86 | 0.43 | 0.67 |
| Methylated | 0.57 | 0.29 | 0.40 | 0.14 | 0.56 | 0.32 |
| Data missing (n) | 194 | 128 | 40 | 7 | 0 | 0.23 |
| IDH1 (%) | ||||||
| Wildtype | 0.91 | 0.91 | 0.98 | 0.83 | NA | NA |
| Mutant | 0.09 | 0.09 | 0.02 | 0.17 | NA | NA |
| Data missing (n) | 188 | 0.46 | 52 | 6 | 16 | 344 |
Abbreviations: KPS, Karnofsky performance status; MGMT, O6-methylguanine-DNA methyltransferase; RPA, recursive partitioning analysis; IDH1, isocitrate dehydrogenase 1.
Model-free evaluation
We evaluated the ECT design by mimicking the comparison of an ineffective experimental arm to an external control. Hypothetical ECT experimental arms were generated from data of the TMZ+RT arm of one of the studies in Table 1 using the following model-free procedure. For each study, we iterated the following steps:
We randomly selected n patients (without replacement) from the TMZ+RT arm of the study and use the clinical profiles X and outcomes Y of these patients as experimental arm of the ECT. Here n is the number of enrolled patients.
The TMZ+RT arms of the remaining 5 studies (Table 1) were used as external control.
We estimated the treatment effect TE comparing the experimental arm (step a) and the external control (step b) using one of the adjustment methods (Supplementary Material), and tested the null hypothesis of no-benefit, H0: TE ≤ 0, at a targeted type I error rate of 10%.
We repeated steps (a-c) with different sets of n randomly selected patients. Here n is less or equal to the size of the TMZ+RT arm of each GBM study.
A similar model-free procedure allows one to evaluate the operating characteristics of ECTs in presence of positive treatment effects, by reclassifying in step (a) -randomly and with fixed probability-negative individual outcomes Y into positive outcomes. Section S1 of the supplementary material presents a detailed description of this procedure.
Comparison, ECT, single-arm and RCT designs
We compared the ECT to single-arm and RCT designs. We used the following criteria:
bias and variability of treatment effect estimates,
deviations of Type I error rates from targeted control of false positive results, and
the sample size to achieve a targeted power.
In a single arm trial, an estimate of the proportion πE of patients surviving, at a specific time point, say 12 months (OS-12), is compared to a historical estimate for the standard of care πHC, typically the result of a prior trial. Here πHC can be expressed as a weighted average of the OS-12 probability for a patient with profile X, which is averaged over the study-specific distribution PHC(X) of patient characteristics,
| (2) |
Similarly, the parameter πE can be written as a weighted average of the probability Pr(Y = 1|A = 1, x) over the distribution PSAT(X) of X in the single arm trial. If the distributions PrSAT(X) and PrHC(X) differs substantially, then πHC and πE are not comparable, treatment effect estimates can be biased, and type I error rates can deviate from the targeted value. If the patient’s prognostic profiles in the single arm study are favorable compared to the study used as benchmark, then the type I error probability tends to be above the targeted α-level, and vice versa. In the latter case the power decreases.
In an RCT, patients are randomized to the control and experimental arm, with patient characteristics -on average- equally distributed between arms, reducing the risk of bias compared to single arm trial designs.
Results
Limitations of the single arm design
We illustrate the bias and type I error deviation associated with single arm trials using an example for a hypothetical ineffective experimental treatment in a disease with one known prognostic biomarker X. We assume, for each patient, identical outcome probabilities under the experimental and control treatment. Panel (A) of Figure 1 shows the difference (πE − πHC) when the prevalence of the biomarker varies between PSAT(X = 1) = 0.1 and 0.9 for different correlation levels between the outcome Y and the biomarker X. Even with a moderate association between the biomarker and the outcome, the differences between the distributions (PHC, PSAT) result in bias and departures from the intended 10% type I error rate (Panel (B) of Figure 1).
Figure 1:
Bias (πSAT − πHC)and deviations from a targeted type I error rate of 10%. Bias is due to different patient populations in the single arm trial (SAT) and in the historical study. A single binary characteristic (X=1 or X=0) correlates with the binary outcome Y, and the experimental treatment has no therapeutic effect Pr(Y|X, A = 1) = Pr(Y|X, A = 0). The characteristic X=1 was present in 50% of the patients in the historical control arm, PHC(X = 1) = 0.5. Panel (A) shows the difference (πSAT − πHC) for a range of probabilities PSAT(X = 1). We consider four levels of association between X and Y; (Pr(Y|X = 1, A = a) and P(Y|X = 0, A = a) equal either to (0.3, 0.9), (0.4, 0.8), (0.5, 0.7) or (0.6, 0.6). Panel (B) indicates, for a SAT (with standard z-test for proportions, H0: πSAT ≤ πHC) how the false positive rate (y-axis) of the design deviates without adjustments from the targeted type I error rate of 10% when the prevalence PSAT(X = 1) = 0.3, 0.5, 0.6 or 0.8. We consider different sample sizes (x-axis) of the SAT. In panel (B) we assume to know the parameter πHC.
RT+TMZ in newly diagnosed GBM
The standard of care of RT+TMZ for newly diagnosed GBM was established in 2004 based on results from the EORTC-NCIC CE.322. Subsequently, nine additional trials enrolled patients on RT+TMZ control arms between 2005 and 2013 (Supplementary Table 1). The majority of single-arm studies used the reported results of EORTC-NCIC CE.3 as historical benchmark (Supplementary Table 1). Sample sizes of the RT+TMZ control arms in the RCTs varied between 1619 patients and 46318 patients. Supplementary Figure 1 shows reported Kaplan-Maier estimates, median OS, and OS-12 for the RT+TMZ arms. Point estimates for OS-12 varied between 0.56 and 0.81 across studies, and between 13.2 to 21.2 months for median OS.
Prognostic variables
Through a literature review, we identified prognostic factors associated with survival in newly diagnosed GBM23–26. A Cox regression analysis, stratified by trial and treatment arm, was used to quantify association of covariates with OS (Table 2). On multi-variable analyses, age (HR 1.03, p<0.001), male gender (HR 1.15, p=0.012), KPS >80 (HR 0.78, p<0.001), gross total resection vs biopsy (HR 0.62, p<0.001), sub-total resection vs biopsy (HR 0.82, p=0.028), MGMT promoter methylation (HR 0.46, p<0.001) and IDH1 (HR=0.52, p=0.01) showed association with OS.
Table 2:
Pre-treatment patient characteristics associated with OS. Estimated hazard-ratios in univariable and multivariable stratified Cox regression models. The baseline hazard rate was stratified by study and treatment arm.
| Multivariable | ||
|---|---|---|
| Variables | p-value | p-value |
| Age | ||
| Linear | <0.001 | <0.001 |
| Sex (Ref. Female) | ||
| Male | 0.004 | 0.012 |
| KPS (Ref. <= 80) | ||
| >80 | <0.001 | <0.001 |
| RPA (Ref. Class 3) | ||
| Class 4 | <0.001 | 0.327 |
| Class 5 | <0.001 | 0.734 |
| Class 6 | <0.001 | 0.059 |
| Resection (Ref. Biopsy) | ||
| Sub Total | 0.001 | 0.028 |
| Gross Total | <0.001 | <0.001 |
| MGMT (Ref. Unmethylated) | ||
| Methylated | <0.001 | <0.001 |
| IDH1 (Ref. Wilde-Type) | ||
| Mutant | <0.001 | 0.010 |
The prevalence of these factors varied across studies, from 0.5 to 0.64 for male gender, from 0.45 to 0.76 for KPS >80, and 0.14 to 0.57 for MGMT methylated status. Minimum (maximum) age varied between 18 and 36 (68 and 91) years across trials, and also resection showed noticeable variation across trials. We selected all five variables (age, gender, KPS, MGMT, extent of resection) for adjustments in the ECT design.
ECT and inconsistent definitions of outcomes and pre-treatment characteristics
We initially generated for each study j=1,2,…,6 in Table 1, a ECT by selecting all patients on the RT+TMZ arm. This produces a hypothetical experimental arm which is compared to all RT+TMZ patients in the remaining studies with adjustments for differences in patients’ characteristics X (Supplementary Figure S2). Treatment effects estimates appeared biased for the dataset (, 90%-CI 0.01 to 0.18). Upon further inspection of the definitions of patient characteristics and outcome, we noticed that OS in was defined as time from diagnosis to death. In contrast, the clinical trials (and DFCI, UCLA cohorts) used time of randomization (beginning of therapy) to death. Unsurprisingly, different definitions of the outcome or prognostic variables can be important sources of bias.
Evaluation of the ECT design
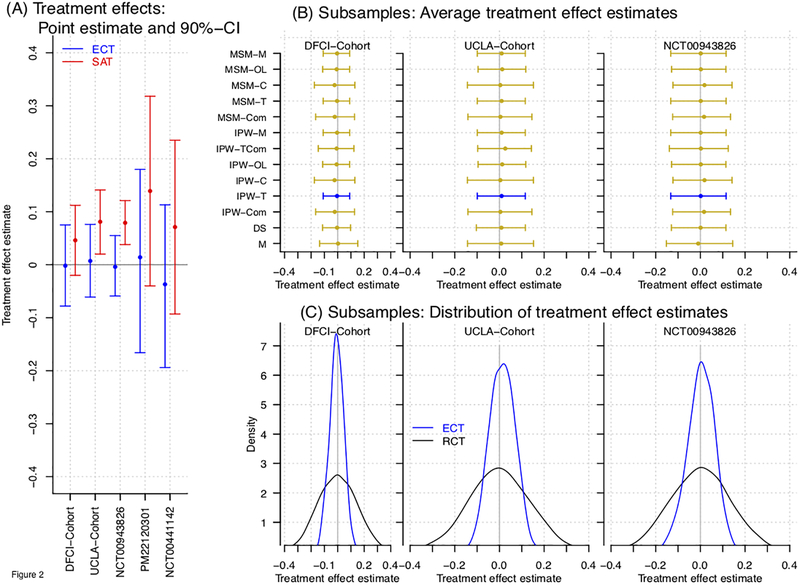
In consideration of the described definitions of the outcome Y across studies, we removed the dataset (Figures 2 and 3).
Figure 2:
Treatment effect estimates of the ECT design. For each studies the RT+TZM arm was used as ECT’s experimental arm and (after adjustment for patents characteristics) compared to the RT+TZM arms of the remaining four studies. Panel (A) shows, for each of the study, covariate adjusted treatment effect estimates (point estimates and 90% confidence interval, n equals to the arm-specific size). Panel (B) shows treatment effect estimates (average value, 5th and 95th percentile) across 10,000 subsamples of n=46 patients using different adjustment methods. We consider direct standardization, matching, inverse-probability weighting and marginal structural models (DSM, PS-M, IPW, MSM). For IPW and MSM we use different reference distributions PrX(x) (see expression 1) of pre-treatment characteristics X. Panel (C) shows the distribution of treatment effect estimates of the ECT (blue line) and RCT (black line) across subsamples of n=46 patients.
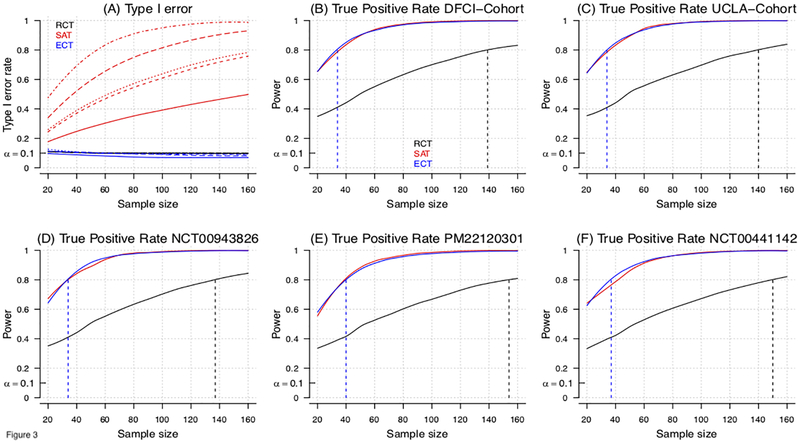
Figure 3:
Model-based evaluation of the type I error and power for RCT, ECT and single-arm trial (SAT) designs for an overall study sample size of n=20, …, 160 patients. In the model-based approach (Supplementary-Material) we sampled baseline characteristics X from the five studies in Table 1, and generated outcomes Y from models Pr(Y|X, A). Panel (A) shows for all studies the type I error rates of RCT, ECT and SAT designs at different overall sample sizes. Different line types (solid, dashed, dotted, etc.) indicate different studies (Table 1). Panels (B-F) show for each study, the power of RCT, SAT and ECT designs, and sample size to achieve 80% power (dotted vertical lines). In panel A, the single arm trial experimental outcomes have been generated as in the ECT simulations, but outcomes Y are directly compared to the EORTC-NCIC CE.3 study estimates, without adjustments for different distributions of patients’ characteristics. For RCTs, half of the randomly selected profiles X are used to define the experimental arm and the remaining half defines the control arm. Two-group (RCT) and single-group (single arm trial) z-tests for proportions were used for testing. To compute the power in Panels B-F of the SAT, we assumed that the historical control benchmark πHC was correctly specified.
Model-free ECT evaluation.
Figure 2A shows ECT treatment effect estimates for each of the remaining 5 studies. Treatment effect estimates, in all cases, were close to zero. In comparison, a single arm trial design, with the EORTC-NCIC CE.3 used as historical benchmark (Supplementary Table 1), would lead to overestimation of treatment efficacy.
Next, we generated ECTs for a fixed sample size of n=46. The sample size was selected for a targeted power of 80%, and 10% Type I error rate, for a single arm trial (one-sided binomial test) with OS-12 improvement from = 61% to 76%, with from the EORTC-NCIC CE.322 study. Since the RT+TMZ arm of PM22120301 and had only 16 patients and 29 patients, we could not use these studies to generate ECTs with size n=46. Figures 2B and 2C show the results of nearly identical analyses as Figure 2A across 10,000 subsamples of n=46 randomly selected patients using four adjustment methods – direct standardization (DSM), matching (M), inverse probability weighting (IPW, and marginal structural model (MSM). For IPW and MSM we used multiple reference distribution PX(x) (see expression 1)27–29. We used IPW-T in the analyses for Figure 2A and 2C. Supplementary Figure S3 shows ECT treatment effect estimates obtained by adjustment using different sets of prognostic characteristics.
Figure 2C shows the distribution of treatment effect estimates across the generated trials for ECT (in blue) and RCT (in black). The RCT data was obtained by randomly dividing the simulated single arm trial dataset into two parts of 23 patients which are labeled as control and experimental arms. With identical sample size (n=46) the assignment of all patients in ECT to the experimental arm results in lower variability of the treatment effect estimates compared to the RCT. The empirical type I error rate (targeted value 10%) across generated ECTs (model-free analysis with n=46) was 9.1%, 6.1% and 8.6% for the RT+TMZ arm of the AVAglio, the DFCI cohort and the UCLA cohort, compared to 40.7%, 21.9% and 40.5% for the single arm trial design (historical benchmark: 0.611 reported in EORTC-NCIC CE.322) and a targeted value of 10%, respectively. The latter estimates, well above the 10% target, are consistent with different outcome distributions under RT+TMZ observed in these three studies compared to the EORTC-NCIC-CE.3 study. Indeed, underestimation of RT+TMZ’s efficacy in SAT translates into inflated type I error rates.
Model-based ECT evaluation.
Figure 3A and 3B–F report model-based type I error rates and power for hypothetical RCTs, single arm trials and ECTs with sample size ranging between 20 and 160. We used the pre-treatment characteristics X from the five studies to evaluate designs using a model-based approach (Supplementary-Material) which consists in sampling baseline characteristics X from the studies and generating outcomes Y from models P(Y|X, A). We specify P(Y|X, A) with a logistic model, obtained by fitting the RT+TMZ data from all five studies combined, with or without the addition of a positive treatment effect.
Both the RCT and ECT have false positive rates, across simulated trials, close to the targeted value of 10% for all five studies (Figure 3A). The single arm trial design (historical benchmark: EORTC-NCIC CE.3) overestimates treatment effects, and presents inflated Type I error rates, 21–59% for n=30 and 30–83% for n=60 patients (Figure 3A).
The reported power in Figures 3B–3D corresponds to a scenario with improvement in OS-12 equal to an odds ratio of 2.6. For example, with X corresponding to a male patient, age 59 (median age in the studies RT+TMZ arms) with biopsy, KPS<=80 and negative MGMT status, Pr(Y = 1|A = 0, X) = Pr(Y = 1|A = 0, X) = 0.15. The RCT requires more than 139 patients (139, 140, 137 154, 150 patients, X-distributions of DFCI, UCLA cohorts, AVAglio, PM22120301 and ) to achieve a power of 80% at 10% type I error rate. In contrast, the ECT requires between 34 and 40 patients (34, 34, 34, 40 and 37 patients) to achieve the 80% power.
Discussion
Clinical researchers have discussed and debated the relative merits of single-arm versus randomized trial design4,30–36. Single arm trials have obvious attraction for patients, could potentially be smaller, and are logistically easier to employ as pragmatic trials. The associated increased risk for bias, however, could lead to poor therapeutic development and regulatory decision-making. Overly optimistic analysis and interpretation can result in large negative phase III trials. Negatively biased results can cause discontinuation in the development of therapies with positive effects. This potential for bias is less pronounced for endpoints with minimal variation under the control. For example, single arm designs for monotherapies using tumor response as an endpoint have low risk for inflated type I error37. Evaluation of therapeutic combinations and use of endpoints such as PFS and OS are more complicated with increased risk for biased results, however. Randomization is the best way to limit this bias. But alternative methodologies could improve on single arm designs without the limitations of setting up a randomized control.
Historic benchmarks in single arm trial designs have two major problems. The first problem is ignoring discrepancies of the estimated survival functions across trials due to population differences. Controlling for known prognostic factors has been shown to mitigate this issue somewhat15. Additionally, single arm trials by design compare a single point of a PFS or OS curve, for example OS-12, to a benchmark. Such approaches do not leverage the power of statistical analyses that incorporate all time to event data, including censoring. The use of external control arms can address both these limitations.
Clearly, ECTs can increase power compared with RCTs by leveraging additional information from outside of the trial rather than committing resources to an internal control. In our analysis in GBM the ECT reached nearly the same power as a single arm trial that specifies the correct historical response rate (zero bias) of the standard of care. This efficacy gain of ECTs will not necessarily be the same in other disease settings, and will depend on the size of the external control, the number of patient characteristics X that are required to control for confounding and the variability of these patient characteristics across and within studies. By standard statistical arguments38–40, in settings that are favorable to the ECT design (large external control cohort, a few relevant covariates, and no unmeasured confounders), the sample size for an RCT to match uncertainty summaries of ECTs such as the variance of a treatment effect estimate or the length of a confidence interval for TE is approximately four times larger than the sample size of an ECT. The major question is whether this comes with the downside of increasing Type I errors. In our analysis in newly diagnosed GBM, the ECT’s Type I error rates were comparable to RCTs, whereas SATs showed significantly inflated type I error rates. These results are in concordance with previous findings of a meta-analysis in GBM of Vanderbeek et al., 201841, which associate single arm Phase II trial in GBM during a 10 years period with under-estimation of the RT+TMZ efficacy. The majority of single arm studies used the EORTC-NCIC CE.3 trial as historical benchmark. Under-estimation of the control efficacy translates into inflated type I error rates.
Another key question is whether our results were limited to newly diagnosed GBM or generalizable. We can consider three questions when evaluating the use of an ECT for a given experimental treatment: 1) are there time trends in the outcome under the control; 2) are the available prognostic factors sufficient to explain most of the variation in the outcome distributions across trials; and 3) is there evidence of significant latent unobserved confounding after controlling for known prognostic factors. Our evaluation of ECTs in GBM required use of an entire collection of datasets, to address these questions, and there isn’t a simple strategy to determine how other diseases or indications might compare.
The first step of our validation analyses was the selection of potential confounders. Based on previous recommendations, see for example Greenland, 200842- before data collection and analyses - we identified a list of potential confounders through a review of the GBM literature. In selecting the set of patient characteristics, we tried to be as comprehensive as possible, since the exclusion of confounders can compromise the ECT performance. Sensitivity summaries of the validation analysis, similar to supplementary Figure S2, can then be computed to illustrate variations of the estimated ECT performances when smaller sets of variables are used for adjustments.
A strength of our evaluation was the use of both data from prior clinical trials and RWD. Most discussions of external controls tend to focus on one or the other, but each has strengths and weaknesses. Clinical trial data is more meticulously collected, resulting in more standardized definitions and entry. This was evident in our dataset where several covariates from RWD datasets were characterized by missing data. This problem can be mitigated through the use of RWD datasets at scale rather than from a single institution. Furthermore, we initially found erroneous treatment effects due to differences in the definitions of the time to event variables (index dates) in our RWD compared to the remaining RCTs. While this is easily correctable in our example, care must be taken to define endpoints in RWD43. Conversely, RWD has the advantage of being generated during routine clinical care which is less costly, potentially available at larger scale, and more contemporary. Since each kind of data has benefits and limitations, leveraging both has value for ECT generation.
A limitation of our study is the relatively small number of datasets that we used to evaluate the ECT design. The higher the number of available trials and cohorts, the more precise the estimation of ECT type I error rates and other key operating characteristics can be. The extension of our results in the future for GBM and the generation of ECTs for other diseases will undoubtedly be aided by clinical trial data sharing efforts like Project Data Sphere44, Vivli45, YODA46 and the availability of RWD at scale from groups like Flatiron Health, Tempus, and ASCO through CancerLinQ47.
The validation procedure that we used builds on clinical studies that included the same control (in our case TMZ+RT) with the aim to evaluate the use of ECT for future trials. A limitation of the procedure is the identical use of all the available studies. Potentially relevant differences, such as the year when each study started the enrollment, are not considered. Nonetheless, a simple and interpretable scheme for validation has the advantage of being robust to selection-bias. We included all studies for which we could access patient-level data. However, after the utility of the ECT design has been rigorously evaluated for a specific disease setting based on interpretable and robust procedures, it becomes appropriate to refine the set of studies used as external control. This could be done for example by multi-study analyses to identify studies with a risk of inducing bias in the ECT results if used as external control. Moreover, Bayesian models that incorporate differences across studies48,49 could be used to compute treatment effects estimates and credible intervals for ECTs.
An extension of our validation framework could include the evaluation of procedures to use external control data in the analysis and interpretation of RCTs. In some cases, external data may contribute to more accurate treatment effects estimates in RCTs. Statistical methods for the use of external control data in RCTs, for example early stopping rules, will require, similar to ECT designs, validation studies before their implementation in clinical trials.
Summary
ECT designs have the potential to improve the evaluation of novel experimental agents in clinical trial and accelerate the drug development process by leveraging external data. Challenges in the use external data compared to standard RCTs include
the identification of a comprehensive list of potential confounders X for adjustments,
access to a large set of RWD datasets or completed RCT’s to create a library of studies for robust validation analyses,
availability of patient level data and possible missing data problems,
coherent definitions and consistent measurements of patient characteristics and outcomes across datasets,
possible trends in calendar time in the distributions of the outcomes under the control treatment due to improved clinical practice and
the use of robust statistical procedures to evaluate ECT designs in comparison to traditional single arm and RCT designs.
Here we introduced a simple algorithm to evaluated operating characteristics such as bias, variability of treatment effect estimates and type I error rates of ECT designs. We considered different ECT designs that use distinct adjustment-methods. Our results indicate that the ECTs constitute a useful alternative to standard single arms trials and RCTs in GBM, which could significantly reduce the current false positive rates41 of single arm Phase II GBM trials.
Supplementary Material
Funding:
This work was supported by the Burroughs Wellcome Innovations in Regulatory Science Award.
Conflicts of interest: AL reports grants from Millennium/Takeda and Genentech/Roche; personal fees from Genentech, Novocure, Abbvie, and Merck., PYW reports grants, personal fees and non-financial support from Agios and Novartis, non-financial support from Angiochem, GlaxoSmithKline, ImmunoCellular Therapeutics, VBI Vaccines, and Karyopharm and, personal fees and non-financial support from AstraZeneca, Genentech/Roche, and Vascular Biogenics, grants and non-financial support from Merck, and non-financial support from Oncoceutics, Sanofi Aventis, personal fees from Cavion, INSYS Therapeutics, Monteris, from Novogen, Regeneron Pharmaceuticals, and Tocagen. TFC reports consulting fees from: Roche/Genentech, VBL, Merck, BMS, Pfizer, Agios, Novogen, Boston Biomedical, MedQIA, Tocagen, Cortice Biosciences, Novocure, NewGen, Oxigene, Wellcome Trust, Sunovion Pharmaceuticals, Abbvie, Celgene, Lilly; and reports equity in Notable Labs. BMA reports employment at Foundation Medicine, Inc.
Footnotes
Presentations: This study has not been previously presented.
References
- 1.Marshall G, Blacklock JW, Cameron C, et al. Streptomycin Treatment of Pulmonary Tuberculosis: A Medical Research Council Investigation. Bmj. 1948. doi: 10.1136/bmj.2.4582.769 [DOI] [Google Scholar]
- 2.Armitage P. Fisher, Bradford Hill, and randomization. Int J Epidemiol. 2003;32(6):925–928. doi: 10.1093/ije/dyg286 [DOI] [PubMed] [Google Scholar]
- 3.Seruga B, Ocana A, Amir E, Tannock IF. Failures in Phase III: Causes and consequences. Clin Cancer Res. 2015;21(20):4552–4560. doi: 10.1158/1078-0432.CCR-15-0124 [DOI] [PubMed] [Google Scholar]
- 4.Gan HK, Grothey A, Pond GR, Moore MJ, Siu LL, Sargent D. Randomized phase II trials: Inevitable or inadvisable? J Clin Oncol. 2010;28(15):2641–2647. doi: 10.1200/JCO.2009.26.3343 [DOI] [PubMed] [Google Scholar]
- 5.Eborall HC, Stewart MCW, Cunningham-Burley S, Price JF, Fowkes FGR. Accrual and drop out in a primary prevention randomised controlled trial: Qualitative study. Trials. 2011;12(1):7. doi: 10.1186/1745-6215-12-7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Donovan J, Mills N, Smith M, et al. Quality improvement reportImproving design and conduct of randomised trials by embedding them in qualitative research: ProtecT (prostate testing for cancer and treatment) studyCommentary: presenting unbiased information to patients can be difficult. Bmj. 2002;325:766. doi: 10.1136/bmj.325.7367.766 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Featherstone K, Donovan JL. “Why don’t they just tell me straight, why allocate it?” The struggle to make sense of participating in a randomised controlled trial. Soc Sci Med. 2002;55(5):709–719. doi: 10.1016/S0277-9536(01)00197-6 [DOI] [PubMed] [Google Scholar]
- 8.Berry DA. The Brave New World of clinical cancer research: Adaptive biomarker-driven trials integrating clinical practice with clinical research. Mol Oncol. 2015;9(5):951–959. doi: 10.1016/j.molonc.2015.02.011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Pocock SJ. The combination of randomized and historical controls in clinical trials. J Chronic Dis. 1976;29(3):175–188. doi: 10.1016/0021-9681(76)90044-8 [DOI] [PubMed] [Google Scholar]
- 10.Viele K, Berry S, Neuenschwander B, et al. Use of historical control data for assessing treatment effects in clinical trials. Pharm Stat. 2014;13(1):41–54. doi: 10.1002/pst.1589 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Thall PF, Simon R. Incorporating historical control data in planning phase II clinical trials. Stat Med. 1990;9(3):215–228. doi: 10.1002/sim.4780090304 [DOI] [PubMed] [Google Scholar]
- 12.Corrigan-Curay J, Sacks L, Woodcock J. Real-world evidence and real-world data for evaluating drug safety and effectiveness. JAMA. 2018;320(9):867–868. doi: 10.1001/jama.2018.10136 [DOI] [PubMed] [Google Scholar]
- 13.Agarwala V, Khozin S, Singal G, et al. Real-world evidence in support of precision medicine: Clinico-genomic cancer data as a case study. Health Aff. 2018;37(5):765–772. doi: 10.1377/hlthaff.2017.1579 [DOI] [PubMed] [Google Scholar]
- 14.Khozin S, Blumenthal GM, Pazdur R. Real-world Data for Clinical Evidence Generation in Oncology. J Natl Cancer Inst. 2017;109(11):1–5. doi: 10.1093/jnci/djx187 [DOI] [PubMed] [Google Scholar]
- 15.Korn EL, Liu PY, Lee SJ, et al. Meta-analysis of phase II cooperative group trials in metastatic stage IV melanoma to determine progression-free and overall survival benchmarks for future phase II trials. J Clin Oncol. 2008;26(4):527–534. doi: 10.1200/JCO.2007.12.7837 [DOI] [PubMed] [Google Scholar]
- 16.Imbens GW, Rubin DB. Causal Inference: For Statistics, Social, and Biomedical Sciences an Introduction. Cambridge University Press; 2015. doi: 10.1017/CBO9781139025751 [DOI] [Google Scholar]
- 17.Robins JM, Hernán MÁ, Brumback B. Marginal structural models and causal inference in epidemiology. Epidemiology. 2000;11(5):550–560. doi: 10.1097/00001648-200009000-00011 [DOI] [PubMed] [Google Scholar]
- 18.Chinot OL, Wick W, Mason W, et al. Bevacizumab plus Radiotherapy–Temozolomide for Newly Diagnosed Glioblastoma. N Engl J Med. 2014;370(8):709–722. doi: 10.1056/NEJMoa1308345 [DOI] [PubMed] [Google Scholar]
- 19.Cho DY, Yang WK, Lee HC, et al. Adjuvant immunotherapy with whole-cell lysate dendritic cells vaccine for glioblastoma multiforme: A phase II clinical trial. World Neurosurg. 2012;77(5–6):736–744. doi: 10.1016/j.wneu.2011.08.020 [DOI] [PubMed] [Google Scholar]
- 20.Lee EQ, Kaley TJ, Duda DG, et al. A multicenter, phase II, randomized, noncomparative clinical trial of radiation and temozolomide with or without vandetanib in newly diagnosed glioblastoma patients. Clin Cancer Res. 2015;21(16):3610–3618. doi: 10.1158/1078-0432.CCR-14-3220 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Lai A, Tran A, Nghiemphu PL, et al. Phase II study of bevacizumab plus temozolomide during and after radiation therapy for patients with newly diagnosed glioblastoma multiforme. J Clin Oncol. 2011;29(2):142–148. doi: 10.1200/JCO.2010.30.2729 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Stupp R, Mason WP, van den Bent MJ, et al. Radiotherapy plus Concomitant and Adjuvant Temozolomide for Glioblastoma. N Engl J Med. 2005;352(10):987–996. doi: 10.1056/NEJMoa043330 [DOI] [PubMed] [Google Scholar]
- 23.Thakkar JP, Dolecek TA, Horbinski C, et al. Epidemiologic and molecular prognostic review of glioblastoma. Cancer Epidemiol Biomarkers Prev. 2014;23(10):1985–1996. doi: 10.1158/1055-9965.EPI-14-0275 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Lamborn KR. Prognostic factors for survival of patients with glioblastoma: Recursive partitioning analysis. Neuro Oncol. 2004;6(3):227–235. doi: 10.1215/S1152851703000620 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Curran WJ, Scott CB, Horton J, et al. Recursive partitioning analysis of prognostic factors in three Radiation Therapy Oncology Group malignant glioma trials. J Natl Cancer Inst. 1993;85(9):704–710. doi: 10.1093/jnci/85.9.704 [DOI] [PubMed] [Google Scholar]
- 26.Franceschi E, Tosoni A, Minichillo S, et al. The Prognostic Roles of Gender and O6-Methylguanine-DNA Methyltransferase Methylation Status in Glioblastoma Patients: The Female Power. World Neurosurg. 2018;112:e342–e347. doi: 10.1016/j.wneu.2018.01.045 [DOI] [PubMed] [Google Scholar]
- 27.Hirano K, Imbens GW. Estimation of causal effects using propensity score weighting: An application to data on right heart catheterization. Heal Serv Outcomes Res Methodol. 2001;2(3–4):259–278. doi: 10.1023/A:1020371312283 [DOI] [Google Scholar]
- 28.Li L, Greene T. A weighting analogue to pair matching in propensity score analysis. Int J Biostat. 2013;9(2):215–234. doi: 10.1515/ijb-2012-0030 [DOI] [PubMed] [Google Scholar]
- 29.Li F, Morgan KL, Zaslavsky AM. Balancing Covariates via Propensity Score Weighting. J Am Stat Assoc. 2018;113(521):390–400. doi: 10.1080/01621459.2016.1260466 [DOI] [Google Scholar]
- 30.Grayling MJ, Mander AP. Do single-arm trials have a role in drug development plans incorporating randomised trials? Pharm Stat. 2016;15(2):143–151. doi: 10.1002/pst.1726 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Grossman SA, Schreck KC, Ballman K, Alexander B. Point/counterpoint: Randomized versus single-arm phase II clinical trials for patients with newly diagnosed glioblastoma. Neuro Oncol. 2017;19(4):469–474. doi: 10.1093/neuonc/nox030 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Pond GR, Abbasi S. Quantitative evaluation of single-arm versus randomized phase II cancer clinical trials. Clin Trials. 2011;8(3):260–269. doi: 10.1177/1740774511401764 [DOI] [PubMed] [Google Scholar]
- 33.Ratain MJ, Sargent DJ. Optimising the design of phase II oncology trials: The importance of randomisation. Eur J Cancer. 2009;45(2):275–280. doi: 10.1016/j.ejca.2008.10.029 [DOI] [PubMed] [Google Scholar]
- 34.Rubinstein L, Leblanc M, Smith MA. More randomization in phase II Trials: Necessary but not sufficient. J Natl Cancer Inst. 2011;103(14):1075–1077. doi: 10.1093/jnci/djr238 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Sambucini V Comparison of single-arm vs. Randomized phase II clinical trials: A bayesian approach. J Biopharm Stat. 2015;25(3):474–489. doi: 10.1080/10543406.2014.920856 [DOI] [PubMed] [Google Scholar]
- 36.Sharma MR, Stadler WM, Ratain MJ. Randomized phase II Trials: A long-term investment with promising returns. J Natl Cancer Inst. 2011;103(14):1093–1100. doi: 10.1093/jnci/djr218 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Seymour L, Ivy SP, Sargent D, et al. The design of phase II clinical trials testing cancer therapeutics: Consensus recommendations from the Clinical Trial Design Task Force of the National Cancer Institute Investigational Drug Steering Committee. Clin Cancer Res. 2010;16(6):1764–1769. doi: 10.1158/1078-0432.CCR-09-3287 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Hirano K, Imbens GW, Ridder G. Efficient estimation of average treatment effects using the estimated propensity score. Econometrica. 2003;71(4):1161–1189. doi: 10.1111/1468-0262.00442 [DOI] [Google Scholar]
- 39.Abadie A, Imbens GW. Large sample properties of matching estimators for average treatment effects. Econometrica. 2006;74(1):235–267. doi: 10.1111/j.1468-0262.2006.00655.x [DOI] [Google Scholar]
- 40.Crump RK, Hotz VJ, Imbens GW, Mitnik OA. Dealing with limited overlap in estimation of average treatment effects. Biometrika. 2009;96(1):187–199. doi: 10.1093/biomet/asn055 [DOI] [Google Scholar]
- 41.Vanderbeek AM, Rahman R, Fell G, et al. The clinical trials landscape for glioblastoma: Is it adequate to develop new treatments? Neuro Oncol. 2018;20(8):1034–1043. doi: 10.1093/neuonc/noy027 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Greenland S Invited commentary: Variable selection versus shrinkage in the control of multiple confounders. Am J Epidemiol. 2008;167(5):523–529. doi: 10.1093/aje/kwm355 [DOI] [PubMed] [Google Scholar]
- 43.Curtis MD, Griffith SD, Tucker M, et al. Development and Validation of a High-Quality Composite Real-World Mortality Endpoint. Health Serv Res. 2018;53(6):4460–4476. doi: 10.1111/1475-6773.12872 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Bertagnolli MM, Sartor O, Chabner BA, et al. Advantages of a Truly Open-Access Data-Sharing Model. N Engl J Med. 2017;376(12):1178–1181. doi: 10.1056/NEJMsb1702054 [DOI] [PubMed] [Google Scholar]
- 45.Bierer BE, Li R, Barnes M, Sim I. A Global, Neutral Platform for Sharing Trial Data. N Engl J Med. 2016;374(25):2411–2413. doi: 10.1056/NEJMp1605348 [DOI] [PubMed] [Google Scholar]
- 46.Krumholz HM, Waldstreicher J. The Yale Open Data Access (YODA) Project — A Mechanism for Data Sharing. N Engl J Med. 2016;375(5):403–405. doi: 10.1056/NEJMp1607342 [DOI] [PubMed] [Google Scholar]
- 47.Miller RS, Wong JL. Using oncology real-world evidence for quality improvement and discovery: The case for ASCO’s CancerLinQ. Futur Oncol. 2018;14(1):5–8. doi: 10.2217/fon-2017-0521 [DOI] [PubMed] [Google Scholar]
- 48.Kaizer AM, Koopmeiners JS, Hobbs BP. Bayesian hierarchical modeling based on multisource exchangeability. Biostatistics. 2018;19(2):169–184. doi: 10.1093/biostatistics/kxx031 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Hobbs BP, Carlin BP, Mandrekar SJ, Sargent DJ. Hierarchical Commensurate and Power Prior Models for Adaptive Incorporation of Historical Information in Clinical Trials. Biometrics. 2011;67(3):1047–1056. doi: 10.1111/j.1541-0420.2011.01564.x [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.