TIGAR: An Improved Bayesian Tool for Transcriptomic Data Imputation Enhances Gene Mapping of Complex Traits

Abstract

The transcriptome-wide association studies (TWASs) that test for association between the study trait and the imputed gene expression levels from cis-acting expression quantitative trait loci (cis-eQTL) genotypes have successfully enhanced the discovery of genetic risk loci for complex traits. By using the gene expression imputation models fitted from reference datasets that have both genetic and transcriptomic data, TWASs facilitate gene-based tests with GWAS data while accounting for the reference transcriptomic data. The existing TWAS tools like PrediXcan and FUSION use parametric imputation models that have limitations for modeling the complex genetic architecture of transcriptomic data. Therefore, to improve on this, we employ a nonparametric Bayesian method that was originally proposed for genetic prediction of complex traits, which assumes a data-driven nonparametric prior for cis-eQTL effect sizes. The nonparametric Bayesian method is flexible and general because it includes both of the parametric imputation models used by PrediXcan and FUSION as special cases. Our simulation studies showed that the nonparametric Bayesian model improved both imputation R² for transcriptomic data and the TWAS power over PrediXcan when ≥1% cis-SNPs co-regulate gene expression and gene expression heritability ≤0.2. In real applications, the nonparametric Bayesian method fitted transcriptomic imputation models for 57.8% more genes over PrediXcan, thus improving the power of follow-up TWASs. We implement both parametric PrediXcan and nonparametric Bayesian methods in a convenient software tool “TIGAR” (Transcriptome-Integrated Genetic Association Resource), which imputes transcriptomic data and performs subsequent TWASs using individual-level or summary-level GWAS data.

Introduction

Genome-wide association studies (GWASs) have successfully identified thousands of genetic risk loci for complex traits. However, the majority of these loci are located within noncoding regions whose molecular mechanisms remain unknown.^{1, 2, 3} Recent studies have shown that these associated regions were enriched for regulatory elements such as enhancers (H3K27ac marks)^{4, 5} and expression of quantitative trait loci (eQTL),^{6, 7} suggesting that the genetically regulated gene expression might play a key role in explaining the etiology of complex traits. Multiple studies have recently generated rich transcriptomic datasets for diverse tissues of the human body (besides genotype data), e.g., the Genotype-Tissue Expression (GTEx) project for >44 human tissues,⁶ Genetic European Variation in Health and Disease (GEUVADIS) for lymphoblastoid cell lines,⁸ Depression Genes and Networks (DGN) for whole-blood samples,⁹ and the North American Brain Expression Consortium (NABEC) for cortex tissues.¹⁰ Previous studies^{11, 12, 13, 14, 15, 16} have also shown that integrating transcriptomic data in GWASs can help identify functional loci.

The majority of GWAS projects do not profile transcriptomic data and thus cannot enable direct integrative analysis. However, existing studies^{11, 12} have shown that one can impute the genetically regulated gene expression (GReX) within such GWAS projects by using reference datasets like GTEx⁶ and GEUVADIS⁸ to train gene expression imputation models, and then test for the association between imputed GReX for GWAS samples and the trait of interest—referred to as transcriptome-wide association studies (TWASs).^{11, 12} Specifically, the gene expression imputation models are fitted by regressing assayed gene-expression levels on cis-eQTL genotypes with reference dataset. For examples, the PrediXcan¹¹ method uses an Elastic-Net¹⁷ variable selection model and the FUSION¹² tool implements a Bayesian sparse linear mixed model (BSLMM)¹⁸ to estimate the cis-eQTL effect sizes with reference dataset. The estimated cis-eQTL effect sizes are then used to impute the GReX for GWAS samples.

In short, the Elastic-Net¹⁷ model used by PrediXcan¹¹ assumes a combination of LASSO¹⁹ (L₁) and Ridge²⁰ (L₂) penalties on the cis-eQTL effect sizes, which is equivalent to a Bayesian model with a mixture Gaussian and Laplace prior.²¹ In contrast, the BSLMM¹⁸ used by FUSION¹² is a combination of Bayesian variable selection model (BVSR)²² and linear mixed model (LMM)²³ by assuming a normal mixture prior. Since a parametric prior is assumed for the cis-eQTL effect sizes by both Elastic-Net and BSLMM, it restricts the capability of PrediXcan and FUSION for handling the underlying complex genetic architecture of transcriptomes. Existing studies^{11, 12} have also shown that both PrediXcan¹¹ and FUSION¹² estimated the average regression R² (i.e., the percentage of gene expression variation that can be explained by cis-genotypes) as ∼5% for human whole-blood transcriptome, while the average genome-wide heritability of gene expression in human whole-blood transcriptome is estimated to be more than double that quantity.^{24, 25}

Therefore, to flexibly model cis-eQTL distributions, we use a nonparametric Bayesian method that was originally proposed for genetic prediction of complex traits,²⁶ where the prior for effect sizes is nonparametric and can be estimated from the data by assuming a Dirichlet process prior on effect-size variance. This Bayesian model is also known as latent Dirichlet process regression (DPR) model,²⁶ which can flexibly model the underlying complex genetic architecture of transcriptomes. Thus, DPR is a more generalized model that includes Elastic-Net (implemented in PrediXcan¹¹) and BSLMM (implemented in FUSION¹²) as special cases. Consequently, DPR can robustly estimate cis-eQTLs and then improve imputation R² (the squared Pearson correlation between the observed and imputed values on test samples). Moreover, a variational Bayesian algorithm^{26, 27, 28} can be employed as an alternative of Monte Carlo Markov Chain (MCMC)²⁹ to efficiently fit the Bayesian model.

Similar to PrediXcan¹¹ and FUSION¹² methods, we employ DPR to estimate cis-eQTLs effect sizes from a reference dataset, which can then be used for downstream TWASs using either individual-level or summary-level GWAS data. In subsequent sections, we first describe the DPR²⁶ approach for estimating cis-eQTL effect sizes from a reference dataset and how we can then use these effect sizes for a downstream TWAS. We then compare the performance of DPR with PrediXcan using both simulated data and real GWAS and transcriptomic data from the Religious Orders Study and Rush Memory Aging Project (ROS/MAP)^{30, 31, 32, 33} for studying Alzheimer disease (AD).

Our in-depth simulation studies demonstrated that the DPR method obtained higher imputation R² on test samples, when ≥1% cis-SNPs are true causal and the true expression heritability is ≤0.2. Consequently, better imputation R² resulted in improved power for follow-up association studies. Meanwhile, application of DPR to the ROS/MAP study imputed GReX for 57.8% more genes than PrediXcan. Using DPR, we also found a potentially associated gene TRAPPC6A for AD pathology indices, which was missed by PrediXcan. Further, by using the transcriptomic imputation models fitted from ROS/MAP data and summary-level GWAS data generated from the International Genomics of Alzheimer’s Project (IGAP),³⁴ we identified three known AD loci^{34, 35, 36, 37, 38} that potentially affect the late-onsite AD risk through transcript abundance. We conclude with a discussion of future topics and further describe our software tool TIGAR (Transcriptome-Integrated Genetic Association Resource) implementing both parametric Elastic-Net and nonparametric Bayesian DPR methods for public use.

Material and Methods

Here, we briefly describe the underlying statistical model of gene-expression imputation. Consider the following linear regression model for estimating the cis-eQTL effect sizes from a reference study that has both genetic and transcriptomic data available,

$${\mathbf{E}}_{\mathbf{g}}=\mathbf{X}\mathbf{w}+\mathbf{\epsilon },\mathbf{\epsilon }\sim \mathbf{N}\left(0,{\mathbf{\sigma }}_{\mathbf{\epsilon }}^2\mathbf{I}\right)$$ (Equation 1)

where E_g denotes the gene expression levels (after corrections for confounding covariates such as age, sex, and principal components) for gene g, X denotes the genotype matrix for all cis-genotypes (encoded as the number of minor alleles or genotype dosages), w denotes the corresponding cis-eQTL effect-size vector, and $\mathrm{\epsilon }$ denotes the error term. The intercept term is dropped in Equation 1 for assuming both E_g and X are centered at 0. Generally, SNPs within 1 Mb of the flanking 5′ and 3′ ends (cis-SNPs) are included in this regression model and non-zero $\hat{\mathit{w}}$ will be used for follow-up analysis. The GReX will be imputed by

$$\widehat{\mathit{GReX}}={\mathit{X}}_{\mathit{new}}\hat{\mathit{w}},$$

with cis-SNP data X_new for GWAS samples.

Nonparametric Bayesian Method

Following the nonparametric Bayesian DPR model proposed in previous studies for genetic prediction of complex traits,²⁶ a normal prior $N\left(0,{\sigma }_w^2\right)$ is assumed for the cis-eQTL effect sizes (w_i, i = 1,…, p) and a Dirichlet process (DP) prior³⁹ is assumed for the effect-size variance ${\text{σ}}_{\text{w}}^2$ (as in Equation 1):

$${\mathbf{w}}_{\mathbf{i}}\sim \mathbf{N}\left(0,{\mathbf{\sigma }}_{\mathbf{w}}^2\right),{\mathbf{\sigma }}_{\mathbf{w}}^2\sim \mathbf{D},\mathbf{D}\sim \mathbf{D}\mathbf{P}\left(\mathbf{I}\mathbf{G}\left(\mathbf{a},\mathbf{b}\right),\mathbf{\xi }\right).$$ (Equation 2)

The prior distribution D deviates from the DP with base distribution as an inverse gamma (IG) distribution and concentration parameter $\xi$. Note that ${\sigma }_w^2$ can be viewed as a latent variable and integrating out ${\sigma }_w^2$ will induce a nonparametric prior distribution for w_i, which is equivalent to a DP normal mixture model,^{26, 27, 28}

$${\mathbf{w}}_{\mathbf{i}}\sim \sum _{\mathbf{k}=0}^{+\infty }{\mathbf{\pi }}_{\mathbf{k}}\mathbf{N}\left(0,{\mathbf{\sigma }}_{\mathbf{k}}^2\right),{\mathbf{\sigma }}_{\mathbf{k}}^2\sim \mathbf{I}\mathbf{G}\left({\mathbf{a}}_{\mathbf{k}},{\mathbf{b}}_{\mathbf{k}}\right),{\mathbf{\pi }}_{\mathbf{k}}={\mathbf{\nu }}_{\mathbf{k}}\prod _{\mathbf{l}=0}^{\mathbf{k}-1}\left(1-{\mathbf{\nu }}_{\mathbf{l}}\right),{\mathbf{\nu }}_{\mathbf{k}}\sim \mathbf{B}\mathbf{e}\mathbf{t}\mathbf{a}\left(1,\mathbf{\xi }\right).$$ (Equation 3)

Here, the nonparametric prior distribution on w_i is equivalently represented by a mixture normal prior that is a weighted sum of an infinitely number of normal distributions $\left(\text{N}\left(0,{\text{σ}}_{\text{k}}^2\right),k=0,\dots ,+\infty \right)$, corresponding weight ${\pi }_k$ is determined by (v_l, l = 0,…, k) with a Beta prior, and $\xi$ in the Beta prior (the same concentration parameter as in Equation 2) determines the number of components with non-zero weights in the mixture normal prior. Conjugate hyper priors $\xi \sim Gamma\left(a_{\xi },b_{\xi }\right)$ and ${\sigma }_{\mathit{\epsilon }}^2\sim IG\left(a_{\mathit{\epsilon }},b_{\mathit{\epsilon }}\right)$ are assumed.

Generally, the hyper parameters $a_k,b_k,a_{\mathit{\epsilon }},b_{\mathit{\epsilon }}$ in the inverse gamma distributions can be set as 0.1 and $\left(a_{\xi },b_{\xi }\right)$ in the gamma distribution can be set as (1, 0.1) to induce non-informative priors for $\left({\sigma }_k^2,{\sigma }_{\mathit{\epsilon }}^2,\xi \right)$. That is, the parameters $\left({\sigma }_k^2,{\sigma }_{\mathit{\epsilon }}^2,\xi \right)$ will be adaptively estimated from the data and the nonparametric prior on w_i will be data driven. The posterior estimates for w can be obtained by the MCMC²⁹ or variational Bayesian algorithm,^{28, 40} from the following joint conditional posterior distribution

$$P\left(\mathit{w},\mathit{\pi },\mathit{\nu },\text{ξ},{\sigma }_{\mathit{\epsilon }}^2|{\mathit{E}}_{\mathit{g}},\mathit{X}\right)\propto$$

$$P\left({\mathit{E}}_{\mathit{g}}|\mathit{w},\mathit{X},{\sigma }_{\mathit{\epsilon }}^2\right)P\left(\mathit{w}|\mathit{\pi },{\sigma }_1^2,\dots ,{\sigma }_k^2,\dots \right)\left(\prod _{k=0}^{+\infty }P\left({\sigma }_k^2|a_k,b_k\right)\right)P\left(\mathit{\pi }|\mathit{\nu }\right)P\left(\mathit{\nu }|\text{ξ}\right)P\left(\text{ξ}|a_{\text{ξ}},b_{\text{ξ}}\right)P\left({\sigma }_{\mathit{\epsilon }}^2|a_{\mathit{\epsilon }},b_{\mathit{\epsilon }}\right).$$

Particularly, the variational Bayesian algorithm^{28, 40} is an approximation for the MCMC²⁹ with greatly improved computational efficiency, which is also used in our tool. Please refer to the Supplemental Material and Methods for technical details of both MCMC sampling and variational inference algorithms for obtaining the Bayesian posterior estimates for the cis-eQTL effect sizes.

Elastic-Net and BSLMM Methods

The Elastic-Net model¹⁷ (used by PrediXcan¹¹) estimates the cis-eQTL effect sizes $\hat{\mathit{w}}$ in Equation 1 with a combination of L₁ (LASSO)¹⁹ and L₂ (Ridge)²⁰ penalties by

$$\hat{\mathit{w}}=\underset{\mathit{w}}{\text{argmin}}\left(\Vert {\mathit{E}}_{\mathit{g}}-\mathit{X}\mathit{w}{\Vert }_2^2+\lambda \left(\alpha \Vert \mathit{w}{\Vert }_1+\frac{1}{2}\left(1-\alpha \right)\Vert \mathit{w}{\Vert }_2^2\right)\right),$$

where ${\Vert ·\Vert }_2$ denotes L₂ norm, ${\Vert ·\Vert }_1$ denotes L₁ norm, $\alpha \in \left[\mathrm{0,1}\right]$ denotes the proportion of L₁ penalty, and $\lambda$ denotes the penalty parameter. Particularly, PrediXcan¹¹ takes $\alpha =0.5$ and tunes the penalty parameter $\lambda$ by a 5-fold cross validation.

As pointed out by previous studies,^{17, 21} the Elastic-Net model is equivalent to a Bayesian model with a mixture Gaussian and Laplace (mixture normal) prior for $\mathit{w}$, that is, $p\left(\mathit{w}\right)\propto \text{exp}\left(-\lambda \left(\alpha \Vert \mathit{w}{\Vert }_1+\frac{1}{2}\left(1-\alpha \right)\Vert \mathit{w}{\Vert }_2^2\right)\right)$. In contrast, the BSLMM¹⁸ assumes a mixture of two normal as the prior for cis-eQTL effect sizes, $w_i\sim \pi N\left(0,\left({\sigma }_1^2+{\sigma }_2^2\right)\right)+\left(1-\pi \right)N\left(0,{\sigma }_2^2\right)$. That is, the BSLMM¹⁸ assumes all cis-SNPs have at least a small effect, which are normally distributed with variance ${\sigma }_2^2$, and some proportion $\left(\pi \right)$ of cis-SNPs have an additional effect, normally distributed with variance ${\sigma }_1^2$. Particularly, with ${\sigma }_2^2=0$, BSLMM becomes BVSR,²² and with $\pi =0$, the BSLMM becomes the LMM.²³ Therefore, the DP normal mixture^{26, 27, 28} as assumed by the DPR method includes the parametric (mixture normal) priors used by Bayesian Elastic-Net²¹ and BSLMM¹⁸ as special cases, which is the main reason why DPR is a more generalized model including Elastic-Net and BSLMM as special cases. This is also why the DPR method can robustly model complex genetic architecture and improve the imputation R².

Association Study with Univariate Phenotype

Given individual-level GWAS data (genotype data X_new, phenotype Y, covariant matrix C) and cis-eQTL effect size estimates $\hat{\mathit{w}}$, the follow-up TWAS (using a burden type gene-based test⁴¹) is to test the association between $\widehat{\mathit{GReX}}={\mathit{X}}_{\mathit{new}}\hat{\mathit{w}}$ and Y based on the following generalized linear regression model

$$\mathbf{f}\left(\mathbf{E}\left[\mathbf{Y}|\mathbf{X},\mathbf{C}\right]\right)=\mathbf{\eta }\mathbf{C}+\mathbf{\beta }\widehat{\mathbf{G}\mathbf{R}\mathbf{e}\mathbf{X}}.$$ (Equation 4)

Here, $f(·)$ is a pre-specified link function, which can be set as identity function for quantitative phenotype or set as logit function for dichotomous phenotype. The gene-based association test is equivalent to test $H_0:\beta =0$ in Equation 4.

If only summary-level GWAS data are available, we can take the same approach as implemented by the FUSION¹² method. Let Z denote the vector of Z-scores generated by single variant tests (Wald, likelihood ratio, score tests, etc.) for all cis-SNPs. The burden Z-score for gene-based association test is defined as

$$\tilde{\mathbf{Z}}=\frac{\mathbf{Z}\hat{\mathbf{w}}}{\sqrt{\mathbf{Z}\hat{\mathbf{w}}}}=\frac{\mathbf{Z}\hat{\mathbf{w}}}{\sqrt{{\hat{\mathbf{w}}}^{\text{'}}\mathbf{V}\hat{\mathbf{w}}}},$$ (Equation 5)

where V denotes the covariance matrix of analyzed SNPs that can be estimated from training data or reference panels such as 1000 Genomes Project⁴² (of the same ethnicity).

Association Study with Multivariate Phenotype

To test the association between multivariate phenotypes and imputed GReX of the focal gene, we take a similar approach as the MultiPhen method.⁴³ For example, consider two phenotypes (Y₁,Y₂) and a covariate matrix C, we first adjust for the covariates by taking the residuals $\left(\widetilde{{\mathit{Y}}_1},\widetilde{{\mathit{Y}}_2}\right)$ respectively from the linear regression models ${\mathit{Y}}_{\mathit{j}}=\mathit{\eta C}+\mathrm{\epsilon },j=\mathrm{1,2}$. Then we test whether the regression R² is significantly greater than zero $\left(H_0:R^2=0\right)$ for the following regression model

$$\widehat{\mathbf{G}\mathbf{R}\mathbf{e}{\mathbf{X}}_{\mathbf{g}}}={\mathbf{\beta }}_1\widetilde{{\mathbf{Y}}_1}+{\mathbf{\beta }}_2\widetilde{{\mathbf{Y}}_2}+\mathbf{\epsilon }.$$ (Equation 6)

That is, we test whether the multivariate phenotypes can jointly explain a non-zero percentage of variance in the imputed GReX. The p value can be calculated by using the F-statistic for the regression R² in Equation 6.

Even when only summary-level GWAS data are available, we can first obtain a burden Z-score per phenotype from Equation 5, i.e., $\tilde{\mathit{Z}}=\left(\widetilde{Z_1},\widetilde{Z_2}\right)$ with two phenotypes. Then, a similar burden approach can be used to obtain a joint Z-score for multi-phenotype test,

$${\tilde{\mathit{Z}}}_{\text{joint}}=\frac{\tilde{Z}\mathit{J}}{\sqrt{\tilde{Z}\mathit{J}}}=\frac{\tilde{Z}\mathit{J}}{\sqrt{\mathit{J}\text{'}{\mathit{V}}_{\mathit{Y}}\mathit{J}}},\mathit{J}={\left(1,\dots ,1\right)}^{\text{'}},$$

where ${\mathit{V}}_{\mathit{Y}}$ is the covariance matrix among multiple traits.

Simulation Study Design

We conducted in-depth simulation studies to compare the performance of both PrediXcan and DPR methods with respect to imputation R² in the test data and the power of TWASs. Specifically, we used data from 499 ROS/MAP participants⁴⁴ which contains both RNA-sequencing and genotype data as training data, and genotype data from an additional 1,200 ROS/MAP participants⁴⁴ as test data. The test sample size (1,200) was chosen arbitrarily (randomly selected from the ROS/MAP study) to be comparable with the sample size (1,164) in the real association study of AD pathology indices. The genotyped and imputed genetic data for 2,799 cis-SNPs (with minor allele frequency (MAF) > 5% and Hardy-Weinberg p value > 10⁻⁵) of the arbitrarily chosen gene ABCA7 (see Figure S1 for the LD block structure) were used to simulate gene expression levels.

We performed comprehensive scenarios that varied the proportion of causal SNPs (out of 2,799 SNPs, influenced gene expression) among values in the vector p_causal = (0.001, 0.01, 0.1, 0.2). We varied the proportion of gene expression variance explained by causal SNPs (i.e., expression heritability), along with the proportion of phenotypic variance explained by simulated gene expression levels (i.e., phenotypic heritability), among values in the vector $\left(h_e^2,h_p^2\right)=\left(\left(0.05,0.8\right),\left(0.1,0.5\right),\left(0.2,0.25\right),\left(0.5,0.1\right)\right)$. The phenotypic heritability was selected arbitrarily with respect to expression heritability such that the follow-up association study power fell within the range of (25%, 85%). We also considered various training sample sizes (100, 300, 499) for simulation scenario with p_causal = 0.2 and $\left(h_e^2,h_p^2\right)=\left(0.2,0.25\right)$.

With genotype matrix X_g of the randomly selected causal SNPs (according to p_causal), we generated effect sizes w_i from N(0,1) and then re-scaled the effect sizes to ensure the targeted $h_e^2$. Gene expression levels were generated by ${\mathit{E}}_{\mathit{g}}={\mathit{X}}_{\mathit{g}}\mathit{w}+\mathit{\epsilon }$, with $\mathit{\epsilon }\sim N\left(0,\left(1-h_e^2\right)\right)$. Then the phenotype values were generated by $\mathit{Y}=\beta {\mathit{E}}_{\mathit{g}}+\mathit{\epsilon }$, where $\beta$ was selected with respect to $h_p^2$ and $\mathit{\epsilon }\sim N\left(0,\left(1-h_p^2\right)\right)$.

For each scenario, we repeated simulations for 1,000 times, where we applied both PrediXcan¹¹ and DPR methods to obtain imputation models with training samples, impute the GReX for test samples, and then conduct follow-up association studies using the imputed GReX. We did not compare with FUSION¹² using BSLMM because of the computational burden of estimating cis-eQTL effect sizes by MCMC (∼2 h per gene). The association study power was calculated as the proportion of 1,000 repeated simulations with p value < 2.5 × 10⁻⁶ (genome-wide significance threshold adjusting for testing 20K independent genes).

ROS/MAP Data

Samples in the ROS/MAP data were collected from participants of the Religious Orders Study (ROS) and the Rush Memory and Aging Project (MAP), which are prospective cohort studies of studying aging and dementia.^{30, 31, 33} The ROS/MAP study recruited senior adults without known dementia at enrollment who underwent annual clinical evaluation. Brain autopsy was done at the time of death for each participant. All participants signed an informed consent and Anatomic Gift Act, and the studies were approved by the Institutional Review Board of Rush University Medical Center, Chicago, IL. Specifically, microarray genotype data generated for 2,093 European-decent participants⁴⁴ were further imputed to the 1000 Genomes Project Phase 3⁴² in our analysis. The post-mortem brain samples (gray matter of the dorsolateral prefrontal cortex) from ∼30% these participants were profiled for transcriptomic data by next-generation RNA seqencing.⁴⁵ In this paper, we conducted TWASs for two important indices of AD pathology that were quantified with $\beta$-antibody specific immunostains:^{30, 31, 33} neurofibrillary tangle density (tangles) with stereology and $\beta$-amyloid load (amyloid) with image analysis. The neurofibrillary tangle density quantifies the average Tau tangle density within two or more 20 μm sections from eight brain regions—hippocampus, entorhinal cortex, midfrontal cortex, inferior temporal, angular gyrus, calcarine cortex, anterior cingulate cortex, and superior frontal cortex. The $\beta$-amyloid load quantifies the average percent area of cortex occupied by $\beta$-amyloid protein in adjacent sections from the same eight brain regions.

Results

Simulation Studies

In the simulation studies, we observed that the DPR method performed robustly with respect to different causal proportions and gene expression heritability. Specifically, when p_causal > 0.01 DPR outperformed PrediXcan across all expression heritability values, giving higher imputation R² in test data (Figure 1A). For example, when p_causal = 0.2, the average imputation R² of 1,000 simulations was estimated as 4.55% by using DPR versus 2.64% by using PrediXcan with $h_e^2=0.1$, while the average imputation R² was estimated as 12.02% by using DPR versus 9.13% by using PrediXcan with $h_e^2=0.2$ (Table 1). When p_causal = 0.01, DPR performed slightly out-performed PrediXcan with $h_e^2=\left(0.05,0.1,0.2\right)$ and PrediXcan outperformed DPR with $h_e^2=$ 0.5 (Table 1, Figure 1). On the other hand, under a sparse cis-eQTL causality model with p_causal = 0.001 (i.e., with 3 true causal cis-eQTL), the Elastic-Net method resulted in higher imputation R² and TWAS power on test data (Figure 1).

Figure 1.

Performance Comparison of DPR versus PrediXcan

Plots of average imputation R² (A) and TWAS power (B) in test samples by DPR and PrediXcan, with various proportions of true causal SNPs p_causal = (0.001, 0.01, 0.1, 0.2) and true expression heritability ${\text{h}}_{\text{e}}^2=\left(0.05,0.1,0.2,0.5\right)$. TWAS power was evaluated with paired expression and phenotype heritability $\left({\text{h}}_{\text{e}}^2,{\text{h}}_{\text{p}}^2\right)=\left(\left(0.05,0.8\right),\left(0.1,0.5\right),\left(0.2,0.25\right),\left(0.5,0.1\right)\right)$.

Table 1.

Simulation Prediction R² Comparison

$h_e^2$	Causal Proportion 0.01		Causal Proportion 0.2
	DPR	PrediXcan	DPR	PrediXcan
0.05	1.60%∗	1.12%	1.54%∗	0.76%
0.1	4.54%∗	4.13%	4.55%∗	2.64%
0.2	12.54%∗	12.29%	12.02%∗	9.13%
0.5	39.31%	42.05%∗	38.78%∗	36.04%

Various simulation scenarios were considered, with the proportion of true causal SNPs p_causal = (0.01, 0.2) and expression heritability ${\text{h}}_{\text{e}}^2=\left(0.05,0.1,0.2,0.5\right)$. The best prediction R² per scenario is indicated with asterisk (^∗).

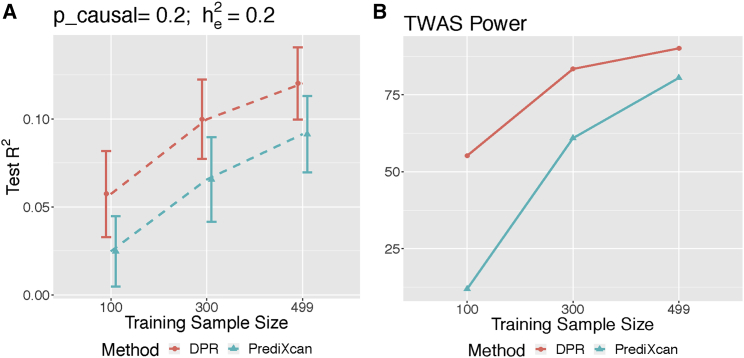
Consequently, when pcausal ≥ 0.01 and $h_e^2\le 0.2$, the power of association studies was higher by using DPR than using PrediXcan imputation models (Figure 1B). When $h_e^2=0.5$, using both imputation models led to comparable power for association studies (Figure 1B). Even though both methods had similar over-estimated training R² (Figure S2), the DPR method resulted in higher imputation R² for test data (Table 1; Figures 1A) and higher power for association studies under cis-eQTL causality models with p_causal ≥ 0.01 and $h_e^2\le 0.2$ (Figure 1B). In addition, from the simulation studies with various training sample sizes (100, 300, 499), p_causal = 0.2, and $\left(h_e^2,h_p^2\right)=\left(0.2,0.25\right)$, the imputation R² and TWAS power increases as sample size increases while the DPR method consistently outperforms PrediXcan (Figure 2). Overall, these results demonstrated the advantages of the DPR method for modeling the complex genetic architecture of transcriptomes, especially when the causal proportions ≥0.01 and the expression heritability ≤0.2.

Figure 2.

Performance of DPR and PrediXcan with Respect to Various Training Sample Sizes

Test R² (A) and TWAS power (B) from simulation studies with causal proportion p_causal = 0.2, expression heritability and phenotype heritability $\left({\text{h}}_{\text{e}}^2,{\text{h}}_{\text{p}}^2\right)=\left(0.2,0.25\right),$ and various training sample sizes (100, 300, 499).

Real Applications to ROS/MAP Data

To illustrate the performance of the DPR method in real studies, we applied both DPR and PrediXcan on the ROS/MAP data (see Material and Methods). We trained the gene expression imputation models using 499 samples that have both transcriptomic data for prefrontal cortex tissues and genotype data (imputed to 1000 Genomes Phase 3, with MAF > 5%, Hardy-Weinberg p value > 10⁻⁵, and genotype imputation R² > 0.3). A total of 15,583 genes had gene expression levels after standard RNA-sequencing quality control. The gene expression levels were first adjusted for age at death, sex, postmortem interval, study (ROS or MAP), batch effects, RNA integrity number scores, and cell type proportions (with respect to oligodendrocytes, astrocytes, microglia, neurons) by linear regression models. For each gene, cis-SNPs within the 1 Mb of the flanking 5′ and 3′ ends were used in the imputation models as predictors.

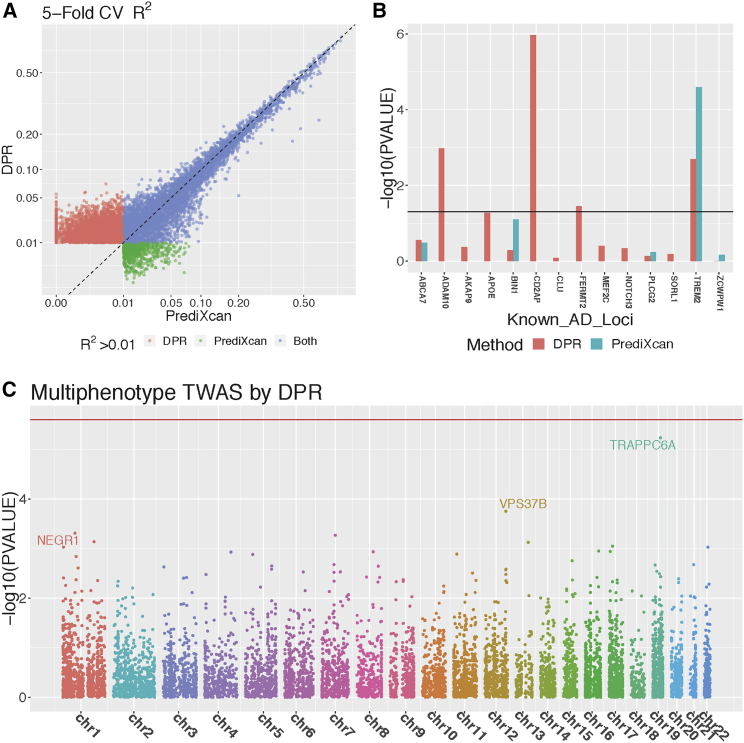
First, we compared transcriptome-wide 5-fold cross validation (CV) regression R² estimated by using both DPR and PrediXcan methods. Specifically, we randomly split 499 training samples into 5 folds, where the imputation R² of each fold was calculated using the model trained with the other 4-fold samples. If the training model is null, we take the imputation R² as 0 and take the average imputation R² across all 5-fold test samples as 5-fold CV R². The transcriptome-wide median of 5-fold CV R² is 0.013 by DPR versus 0.005 by PrediXcan. The 5-fold CV R² was used as the criterion for selecting significant imputation models (R² > 0.01 as used by previous studies^{11, 46}). From Figure 3A, we can see that the DPR method obtained more imputation models and higher imputation R² when 5-fold CV R² is in the range of (0.01, 0.05), which is also consistent with our simulation studies. Overall, the DPR method obtained significant imputation models for 8,752 genes versus 5,547 genes by PrediXcan (with 57.8% increases). Thus, the DPR method featuring data-driven nonparametric prior for the cis-eQTL is preferred in real studies for identifying more genes with imputable expression levels.

Figure 3.

TWAS Results of Studying Alzheimer's Disease

Transcriptome-wide 5-fold cross validation R² (A) by PrediXcan and DPR with 499 ROS/MAP training samples, with different colors denoting whether the imputation R² > 0.01 by DPR, PrediXcan, or both methods (genes with R² > 0.01 by both DPR and PrediXcan were excluded from the plot). TWAS results (B) at known AD loci using GWAS summary-level statistics from IGAP and imputation models fitted from ROS/MAP data, where missing values are due to NULL imputation models by PrediXcan. Manhattan plot (C) for the multiphenotype TWAS (with neurofibrillary tangle density and $\text{β}$-amyloid load), using individual-level ROS/MAP data.

Second, to investigate how both DPR and PrediXcan methods perform in real studies with independent prediction cohort, we used the ROS cohort (256 samples) to train gene expression imputation models and then used the MAP cohort (243 samples) as a test dataset. Specifically, we compared the median prediction R² by both DPR and PrediXcan with MAP test cohort. As shown in Table 2, the DPR method obtained higher median prediction R² than PrediXcan among 8,752 genes that have 5-fold CV R² > 0.01 by DPR (0.011 versus 0.003), performed similarly as PrediXcan among 5,547 genes that have 5-fold CV R² > 0.01 by PrediXcan (0.026 versus 0.026), obtained slightly lower median predication R² among 4,819 genes that have 5-fold CV R² > 0.01 by both DPR and PrediXcan (0.033 versus 0.036). These results are also consistent with our simulation results and 5-fold cross validation results with ROS/MAP data. That is, PrediXcan method is preferred for genes with sparse causal eQTL that have relatively large effect sizes, whereas DPR is preferred for genes with less sparse causal eQTL that have minor effect sizes due to low expression heritability.

Table 2.

Real Study Prediction R² Comparison

Number of Genes	DPR	PrediXcan
8,752a	0.011	0.003
5,547b	0.026	0.026
4,819c	0.033	0.036

Median prediction R² in MAP test cohort by using imputation models trained with ROS cohort with both DPR and PrediXcan methods.

^aGenes that have 5-fold CV R² > 0.01 by DPR.

^bGenes that have 5-fold CV R² > 0.01 by PrediXcan.

^cGenes that have 5-fold CV R² > 0.01 by both DPR and PrediXcan.

Third, we used all 499 training samples to fit imputation models for genes with respective 5-fold CV R² > 0.01 by both DPR and PrediXcan, and then used these models to impute the GReX for all GWAS samples. We conducted univariate phenotype association studies (Material and Methods) using all GWAS samples (n = 1,164) that have the AD pathology indices (neurofibrillary tangle density and $\beta$-amyloid load, with Pearson correlation 0.48) quantified. Possible confounding covariates including age at death, sex, study (ROS or MAP), smoking, education, and first three genotype principle components were adjusted in the association studies. Interestingly, the association studies for both AD pathology indices using the DPR imputation models identified the same top significant gene TRAPPC6A (within the 2 Mb region from the major risk gene APOE, encoding apolipoprotein E, but independent of APOE) with p values 1.64 × 10⁻⁵ and 5.35 × 10⁻⁵ (Figures S3A and S4A). Moreover, the multivariate phenotype association studies (Material and Methods) for both AD pathology indices identified TRAPPC6A as the most significant gene with p value 5.81 × 10⁻⁶ and FDR 0.08 (Figure 3C). On the other hand, the PrediXcan failed to obtain a transcriptomic imputation model for TRAPPC6A (Figures S3B, S4B, and S6). Quantile-quantile plots for these TWAS p values were presented in Figure S5.

In addition, for 14 known common and rare loci of late-onset AD^{34, 35, 36, 37, 38} with significant imputation models, we conducted association studies using transcriptomic imputation models (DPR and PrediXcan) fitted from ROS/MAP data and summary-level GWAS data from IGAP.³⁴ Using the imputation models fit by DPR, we identified three significant loci with FDR < 0.05 (Figure 3B)—ADAM10, CD2AP, and TREM2—that potentially affect late-onset AD risk through transcriptomic changes. Here, TREM2 was also identified by using the PrediXcan imputation model (Figure 3B). Particularly, the PrediXcan method imputed GReX for only 5 out of these 14 loci. In summary, these results show that the DPR method has superior power for follow-up TWASs.

Discussion

In this paper, by both in-depth simulations and real applications using individual-level ROS/MAP^{30, 31, 32, 33} and summary-level IGAP³⁴ GWAS data, we demonstrated that the nonparametric Bayesian DPR method is preferred for imputing gene expression when the proportion of causal cis-eQTL ≥ 0.01 and the true gene expression heritability ≤ 0.2. The advantage of DPR model is due to the flexible nonparametric modeling of cis-eQTL effect sizes that results in improved imputation R² for gene expression levels and higher power for TWASs. Here, we provide an integrated tool (freely available on GITHUB), referred as Transcriptome-Integrated Genetic Association Resource (TIGAR), which integrates both parametric Elastic-Net and nonparametric Bayesian DPR models as two options for transcriptomic data imputation, along with TWAS options using individual-level and summary-level GWAS data for univariate and multi-variate phenotypes. TIGAR also conducts 5-fold cross validation by default and output significant imputation models with CV R² > 0.01.

With respect to user-friendly interface and computational efficiency, TIGAR can (1) take standard input files such as genotype files in VCF and dosage formats, phenotype files in PED format, and a combined text file for gene annotations and expression levels; (2) load input data per gene by TABIX for memory efficiency; (3) filter SNPs based on input thresholds of MAF and Hardy-Weinberg p value; (4) provide options of training both Elastic-Net (use Python3 scripts) and DPR (generate input files and call the executable tool developed with C++²⁶) imputation models with unified output format; and (5) implement multi-threaded computation to take full advantage of multi-core clusters. These features make TIGAR a preferred tool for saving tedious data preparation and computation time for users. For example, TIGAR can complete training imputation models for ∼20K genes and ∼1K samples within ∼20 h and TWAS within ∼1 h with a 2.4 GHz 16-core CPU.

It is important to notice that imputing GReX with cis-eQTL effect sizes estimated from a training dataset is analogous to the idea of estimating polygenic risk scores (PRSs).⁴⁷ Even though studies of population heterogeneity are lacked for imputing GReX, the same philosophy of estimating PRSs still applies because of the same underlying statistical models. That is, given both genetic and transcriptomic heterogeneities across different populations, one needs to be cautious not using training dataset of a different ethnicity for a TWAS.⁴⁷

As observed in the real ROS/MAP studies, there remains a large gap between the 5-fold CV R² using cis-eQTL predictors (∼5%) and the average genome-wide heritability of gene expression levels (21.8% estimated by GCTA⁴⁸ based on a LMM). This is likely due to the large trans-acting contribution to transcript abundance documented for most genes. Thus, we hypothesize that it is promising to further improve the imputation R² by fitting transcriptomic imputation models with genome-wide variants as predictors. Scalable Bayesian inference techniques such as the Expectation Maximization MCMC (EM-MCMC) algorithm⁴⁹ are required for incorporating genome-wide variants.

Another limitation of existing TWAS methods is that the uncertainty of cis-eQTL effect-size estimates has not been taken into accounted in the association studies. A Bayesian framework can also be derived by taking the standard errors of these cis-eQTL effect-size estimates as prior standard deviations, which is part of our continuing research.

Besides the follow-up gene-based association studies (i.e., TWASs) described in this paper, the transcriptomic imputation models can be further extended by incorporating environmental contributions. The imputed transcript abundance levels can then be used for gene network analysis, differential gene expression analysis, and transcriptome mediation analysis with GWAS data. Validation of transcriptomic prediction accuracy in independent datasets will be critical in this regard, but unfortunately multiple large and similar datasets are not yet generally available for tissues other than peripheral blood.

In conclusion, we expect our work will provide a convenient and improved tool for transcriptomic imputation using the currently available rich reference datasets, as well as enhanced gene mapping for better understanding the genetic etiology of complex traits.

Declaration of Interests

The authors declare no competing interests.

Published: June 20, 2019

Web Resources

• FUSION, http://gusevlab.org/projects/fusion/

• IGAP data, http://web.pasteur-lille.fr/en/recherche/u744/igap/igap_download.php

• PrediXcan, https://github.com/hakyim/PrediXcan

• RADC Research Resource Sharing Hub, http://www.radc.rush.edu/

• ROS/MAP data, https://www.synapse.org/#!Synapse:syn3219045

• TIGAR, https://github.com/yanglab-emory/TIGAR