Tuning and predicting mesh size and protein release from step growth hydrogels

Abstract

Hydrogel-based depots are of growing interest for release of biopharmaceuticals; however, a priori selection of hydrogel compositions that will retain proteins of interest and provide desired release profiles remains elusive. Toward addressing this, in this work, we have established a new tool for the facile assessment of protein release from hydrogels and applied it to evaluate the effectiveness of mesh size estimations on predicting protein retention or release. Poly(ethylene glycol) (PEG)-based hydrogel depots were formed by photo-initiated step growth polymerization of four-arm PEG functionalized with norbornene (PEG-norbornene, 4% w/w to 20% w/w, M_n ~ 5 to 20 kDa) and different dithiol crosslinkers (PEG M_n ~ 1.5 kDa or enzymatically-degradable peptide), creating well-defined, robust materials with a range of mesh sizes estimated with Flory-Rehner or rubber elasticity theory (~ 5 to 15 nm). A cocktail of different model proteins was released from compositions of interest and SDS-PAGE was used to facilely and quantitatively analyze temporal release profiles. Mesh size was predictive of retention of relatively large proteins and release of relatively small proteins. Proteins with diameters comparable to the mesh size, which is often the case for growth factors, were released by hindered diffusion and required experimental assessment of retention and release. With this knowledge, hydrogels were designed for the controlled release of a therapeutically-relevant growth factor, PDGF-BB.

Graphical Abstract

1. Introduction

Biopharmaceuticals, or pharmaceuticals produced by biological organisms (e.g., antibodies, growth factors), continue to grow in importance and market share.¹ Controlled drug delivery devices, such as hydrogels,² liposomes,³ and protein nanocapsules,⁴ are being designed to alter the pharmacokinetics of biopharmaceuticals and attain appropriate localized concentrations over extended periods of time toward improved efficacy and reduced side effects and cost. Hydrogel-based carriers in particular allow loading of high concentrations of hydrophilic, bioactive proteins with tunable release profiles.⁵ These include well-defined materials based on synthetic macromers (e.g., multifunctional poly(ethylene glycol) (PEG)) and formed by step growth polymerization, such as thiol–maleimide⁶ and thiol–vinyl sulfone⁷ Michael type reactions, azide–alkyne⁸ and Diels–Alder⁹ cycloaddition reactions, and photointiated thiol–norbornene reactions.^10-12 The modular nature of hydrogels formed by step-growth polymerization allows facile incorporation of degradable linkages and tuning of crosslink density to control drug release.^13,14 For example, hyaluronic acid-based hydrogels formed by thiol–maleimide chemistry were designed for the release of bone morphogenetic protein 2 (BMP-2), where initial crosslink density and matrix metalloproteinase (MMP)-driven degradation controlled the rate of release for modulating bone regeneration.¹⁵ Despite their utility and promise, developing hydrogels for widespread use in protein delivery for commercial applications remains challenging, as optimizing hydrogel formulations for controlling network mesh size and therapeutic release remains cumbersome.¹⁶

Mesh size (correlation length or ξ) is defined as the linear distance between two adjacent crosslinks¹⁷ and is a key structural parameter for hydrogel-based drug carriers, roughly dictating retention of cargo molecules that are greater than it in size.¹⁸ Consequently, understanding the relationship between precursor solution composition and mesh size is critical for the design of carriers for controlled release of therapeutics. Most frequently, hydrogel mesh size is measured using equilibrium swelling theory (i.e., Flory-Rehner)^19–23 or rubber elasticity theory^24–26, although the Mackintosh theory,²⁷ the blob model,²⁸ NMR,²⁹ small angle X-ray scattering,³⁰ small angle neutron scattering,³¹ and correlations based on dextran diffusion³² also have been used with success. While both equilibrium swelling theory and rubber elasticity theory have been successfully applied to hydrogels, few studies compare the results of the two theories. Typically, one of the two theories is selected and used throughout the particular study without justification. However, greater accuracy is needed for a priori prediction of whether cargo molecules, such as biopharmaceuticals, will be released or retained in a hydrogel network, since many bioactive proteins of interest are on the size scale of 1 to 10 nm,³³ similar to the mesh sizes of these networks.^19,34

Another complication in predicting protein release from hydrogel networks is the presence and contribution of network defects and statistical mesh size distributions. Calculated mesh size is an average property that typically does not account for the effects of larger pores in the mesh on the rate of protein release, where these larger pores may provide a pivotal route for protein escape.^35,36 For example, in PEG-based thiol–acrylate networks, lower crosslinker functionalities (f = 3 or 4 compared with f = 8) or lower PEG-acrylate precursor concentrations (10 wt% compared with 60 wt%) led to the formation of more primary cycles that caused deviations in PEG hydrogel behavior from that predicted by equilibrium swelling theory.³⁷ Additionally, for a thiol-norbornene system (linear PEG-norbornene and a small tetrafunctional thiol), crosslinking was efficient but observed to decrease with increasing molecular weight of PEG-Nb (up to M_n ~ 35 kDa).³¹ Further, structural heterogeneities were observed at larger length scales (> 180 nm), whereas phase separation was hypothesized to occur with low PEG molecular weights (M_n ~ 4 and 8 kDa). Defects and large mesh size distributions such as these may have a significant effect on controlling the release of biopharmaceuticals, potentially resulting in significant deviations from theoretical predictions and the need for experimental approaches for efficient and inexpensive assessments of protein retention and release.

Herein, we aim to i) provide insight into controlling the release of biopharmaceuticals from step growth hydrogels with an in-depth comparison of theory and measurements of hydrogel properties and, more broadly, ii) establish a method for rapidly assessing the release of a variety of proteins from different hydrogel designs (Figure 1). The moduli and swelling ratios for a range of step growth PEG hydrogel compositions were measured and used in estimating mesh size, with equilibrium swelling theory and rubber elasticity theory, for an in-depth comparison of accuracy and evaluation as predictors of protein retention or release. Further, we established a new strategy using a cocktail of inexpensive model proteins followed by analysis with SDS-PAGE to simultaneously assess release of multiple proteins from the same hydrogel, rather than individual proteins each from a different sample, saving time and conserving material. Finally, to demonstrate utility of this approach, we examined the release of a growth factor of interest for wound healing and regenerative medicine,³⁸ platelet-derived growth factor-BB (PDGF-BB), a potent mitogen, chemokine, and mediator of stem cell differentiation.³⁹ We anticipate that the approach established here could be applied to a number of different model and therapeutically-relevant proteins and may prove useful for the rapid and cost-effective screening of a variety of hydrogel designs for the release of biopharmaceuticals of interest.

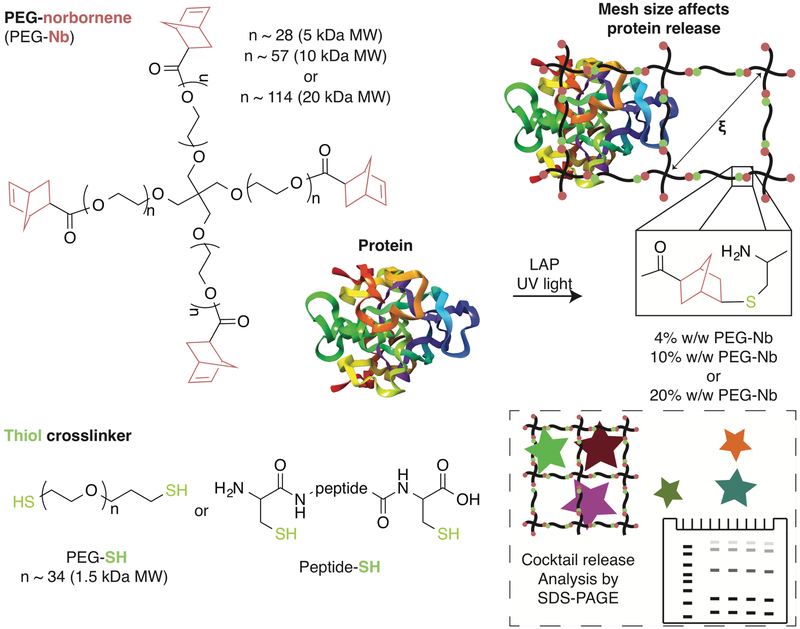
Figure 1. Designing hydrogels for protein release.

For in-depth analysis of material compositions for controlling protein release, PEG-4Nb of a range of molecular weights (5 kDa, 10 kDa, or 20 kDa; left) was reacted with dithiol crosslinkers (PEG-2SH or cysteine-containing peptides; bottom) in the presence of the photoinitiator LAP and light to form well-defined hydrogels by thiol–ene step growth polymerization (right). The resulting mesh sizes (ξ) of these hydrogels were characterized. Uniquely, release of proteins with different hydrodynamic diameters from specific hydrogel compositions of interest was rapidly assessed using a new approach based on a model protein cocktail (box; bottom right) and SDS-PAGE, providing insight into the release of bioactive proteins of moderate molecular weight such as PDGF.

2. Materials and Methods

2.1. Materials for hydrogel formation

Hydroxyl-terminated, 4-arm PEG of various molecular weights (PEG-4OH; Jenkem; 5 kDa, 10 kDa, and 20 kDa) were reacted to form 4-arm PEG-norbornene (PEG-4Nb) following modifications of previously published protocols.^10,40,41 All molar excess values for this synthesis were calculated relative to PEG hydroxyl groups. Diisopropylcarbodiimide (DIC; Sigma-Aldrich; 5x molar excess) or dicyclohexylcarbodiimide (DCC; Alfa Aesar; 5x molar excess) and 5-norbornene-2-carboxylic acid (Sigma-Aldrich; 10x molar excess) were dissolved in DCM (Acros Organics; ~ 40 mL) and purged with inert gas (argon) for 15 min. In a separate flask, PEG-4OH, 4-dimethylaminopyridine (DMAP; Alfa Aesar; 0.5x molar excess), and pyridine (Sigma-Aldrich; 5x molar excess) were also dissolved in DCM (~ 40 mL) and purged with argon. After both argon purges were complete, the contents of the two flasks were mixed and allowed to react overnight.

After overnight reaction, one of two purification procedures was used. Initially, purification was performed following the procedure outlined by Singh et al. and described briefly below;⁴⁰ however, this procedure led to lower yields (< 30%) for the 5 kDa PEG-4Nb. The second purification procedure utilizing a series of precipitations, described briefly below and in greater detail in our previous publication,⁴¹ led to improved yields for 5 kDa PEG-4Nb (> 60%).

For the first purification procedure (adapted from Singh et al.⁴⁰), the reaction mixture was concentrated by rotary evaporation, precipitated at 4°C in 9x volume diethyl ether (Fisher Scientific), recovered by centrifugation for several hours (4400 x g), and re-dissolved in chloroform (Fisher Scientific). The chloroform-PEG mixture was extracted twice with glycine buffer [0.05 M glycine (Alfa Aesar); 0.05 M sodium chloride (Alfa Aesar); 0.05 M sodium hydroxide (Fisher Scientific)] and then once with brine (300 g/L sodium chloride); in all extraction steps, the PEG-4Nb remained in the chloroform phase. After the extractions, the product was again precipitated in 9x ice-cold diethyl ether and recovered by centrifugation. The PEG pellet was dissolved in deionized water (Milli-Q Advantage A10, EMD Millipore, Billerica, MA), dialyzed for 48 hours (MWCO 1000 g/mol, Spectrum Laboratories), and then recovered by freeze-drying.

For the second purification procedure, the reaction mixture was concentrated by rotary evaporation, precipitated in 9x volume ice-cold diethyl ether, recovered by centrifugation at 4400 x g, re-dissolved in DCM, precipitated again in 9x volume ice-cold diethyl ether, and recovered by centrifugation. The PEG pellet was dissolved in deionized water, dialyzed for 48 hours (MWCO 2000 g/mol, Spectrum Laboratories), and then recovered by freeze-drying.

Product purity in all cases was confirmed by ¹H-NMR in DMSO-d6: 400 mHz δ 6.20 to 5.86 (m, 2H), δ 3.65 to 3.40 (m, 114H, 227H, or 454H; PEG backbone peak for 5, 10, or 20 kDa) and disappearance of the -OH peak at δ 4.60 to 4.50 (t, 1H). Both purification procedures led to comparable product purities (< 5% residual PEG-4OH, greater than 88% modification by integration of the norbornene peaks, and no detectible contamination by other reagents used in the synthesis, all verified by ¹H-NMR; Figures S1 - S3).

PEG-dithiol (PEG-2SH; 1.5 kDa) was obtained from Nanocs. The dithiol crosslinking peptides CGGRDYGC (NondegXlink) and GCRDVPMS↓MRGGDRCG (DegXlink) were obtained from Genscript or synthesized on a Tribute (Protein Technologies, Inc., Tucson, AZ). Synthesis was performed using standard Fmoc-based solid phase peptide synthesis techniques on Rink Amide MBHA resin (Novabiochem). Fmoc-protected amino acids were obtained from Chem-Impex International, AAPPTec, ChemPep, or Protein Technologies, and solvents were obtained from Fisher Scientific. Peptides were purified by reverse-phase high-pressure liquid chromatography (HPLC; XBridge BEH C18 OBD 5 μm column; Waters, Milford, MA) with a linear water-acetonitrile (ACN) gradient. Peptide molecular weight was verified with electrospray ionization mass spectrometry (ESI-MS; LCQ Advantage, Thermo Finnigan, Waltham, MA or Waters Acquity H-Class UPLC/SQD2, Waters, Milford, MA; Figure S4 and Figure S5).

The lithium phenyl-2,4,6-trimethylbenzoylphosphinate (LAP) photoinitiator was synthesized following previously published procedures.^42,43 Briefly, equimolar amounts of dimethyl phenylphosphonite (Sigma-Aldrich) and 2,4,6-trimethylbenzoyl chloride (Sigma-Aldrich) were reacted overnight under argon. The following day, lithium bromide (Sigma-Aldrich; 4x molar excess) was dissolved in 2-butanone (Sigma-Aldrich; ~100 mL) and added dropwise to the reaction mixture. After the addition of lithium bromide and butanone, the reaction was heated to 50°C for 10 minutes, forming a solid precipitate. The resulting solid/liquid mixture was allowed to sit at room temperature for 4 hours and then filtered. The final powder product was dried in a desiccator. Product purity was confirmed by ¹H-NMR in D₂O: 400 mHz δ 7.59 (m, 2H), 7.44 (m, 1H), 7.36 (m, 2H), 6.78 (s, 2H), 2.12 (s, 3H), and 1.90 (s, 6H).

2.2. Hydrogel formation

Stock solutions were prepared by dissolving each monomer in Dulbecco's phosphate buffered saline (PBS; Gibco; pH 7.0 - 7.3; no calcium or magnesium). Stock solutions varied in concentration depending on the particular gel composition; these were typically 10 - 30% w/w for PEG-4Nb, 100 - 200 mM for the dithiol crosslinkers (PEG-2SH, NondegXlink, and DegXlink), and 0.5 - 3% w/w LAP. The free-thiol functionality of the peptides, which can vary from batch to batch, was determined for each stock solution using Ellman's assay.

Hydrogel precursor solutions were prepared by diluting each stock solution to the appropriate concentration in PBS with 50 U/mL penicillin, 50 μg/mL streptomycin (Gibco), and 0.2% Fungizone (Gibco). Norbornene concentration and thiol concentration were kept equal. LAP was maintained at 0.05% w/w for all hydrogel preparations.

Hydrogels were formed by irradiating precursor solutions in a cylindrical mold (a 0.04” thick gasket (McMaster-Carr) containing 8-mm diameter cylindrical voids cut with a biopsy punch). The mold was placed between glass slides treated with an anti-adhesive (i.e., Rain-X used following the manufacturer’s instructions) (Figure S6). Hydrogels were formed by irradiating with low doses of long wavelength UV light (10 mW/cm² at 365 nm for 1 minute, Omnicure S2000). The irradiation time was selected from modulus measurements: Irradiation times of 30 seconds or longer led to a relatively constant modulus (Figure S7), and conservatively, irradiation for 1 minute was selected to ensure complete polymerization for all conditions.

Hydrogels were removed from the mold by submerging the mold in deionized water and gently opening the mold with a single edge razor blade. A plastic spatula was then used to place the hydrogel discs immediately in PBS, and the hydrogels were allowed to equilibrium swell until the time of the desired measurement. All of the incubation steps in this manuscript were conducted on a rocker to ensure good mixing.

2.3. Measurement of swelling ratios

The volumetric swelling ratio, Q, was measured with Eq. 1:

$$Q=\frac{V_{\mathit{swollen}}}{V_{\mathit{dry}}}=\frac{\rho V_{\mathit{swollen}}}{m_{\mathit{dry}}}$$ Eq.1

where V_swollen is the volume of the swollen network, V_dry and m_dry are the volume and mass, respectively, of the dry network, and ϱ is the density of the polymer (here, 1.07 g/mL for PEG). V_swollen was measured using calipers; the initial volume was measured immediately after polymerization, and the equilibrium-swollen volume was measured after 48 hours of incubation in PBS at room temperature. m_dry was measured by briefly washing the equilibrium swollen hydrogels in deionized water to remove salts, freezing at −80°C, lyophilizing the frozen hydrogels, and then measuring the mass of the dry polymer after lyophilization.

2.4. Measurement of shear modulus

Rheometry measurements were taken on an AR-G2 rheometer (TA Instruments, New Castle, DE) using a UV-visible light attachment connected to an Omnicure S2000 light source with 365 nm bandpass filter (Excelitas, Waltham, MA). Hydrogel precursor solutions were irradiated (10 mW/cm² at 365 nm). The shear modulus was measured after irradiation at a strain of 1% and a frequency of 2 Hz, which was in the linear viscoelastic regime for these hydrogels.

2.5. Rubber elasticity theory

The mesh size was calculated from rubber elasticity theory using equations summarized by Metrailler.⁴⁴ The shear stress on a polymer sample, τ, is given by Eq. 2, from Peppas et al.¹⁷:

$$\tau =\frac{\rho \mathit{RT}}{\overline{M_c}}\left(1-\frac{2\overline{M_c}}{\overline{M_n}}\right)\left(\alpha -\frac{1}{{\alpha }^2}\right){\left(\frac{{\nu }_{2,s}}{{\nu }_{2,r}}\right)}^{{}^1∕_3}$$ Eq.2

where ϱ is the density of the polymer; R is the universal gas constant; T is the absolute temperature; $\overline{M_c}$ is the molecular weight between crosslinks; $\overline{M_n}$ is the average molecular weight of the monomers; α is the elongation ratio; v_2,s is the polymer volume fraction in the equilibrium swollen state; and v_2,r, is the polymer volume fraction in the relaxed state (i.e., after crosslinking but before swelling). The polymer volume fractions are given by the reciprocal of the swelling ratio, as calculated by Eq. 3.

$${\nu }_{2,s}=\frac{1}{Q_s};{\nu }_{2,r}=\frac{1}{Q_r}$$ Eq.3

where Q_s is the equilibrium swelling ratio, and Q_r is the relaxed-state swelling ratio. The shear modulus, G, is related to the shear stress, τ, using Eq. 4 from Anseth et al.⁴⁵:

$$\tau =G\left(\alpha -\frac{1}{{\alpha }^2}\right)$$ Eq.4

Combining Eq. 2 and Eq. 4 yields Eq. 5:

$$G=\frac{\rho \mathit{RT}}{\overline{M_c}}\left(1-\frac{2\overline{M_c}}{\overline{M_n}}\right){\left(\frac{{\nu }_{2,s}}{{\nu }_{2,r}}\right)}^{{}^1∕_3}$$ Eq.5

The modulus measurements in this study were obtained immediately after formation, using the AR-G2 rheometer as discussed above. The equilibrium-swollen modulus thus was obtained by Eq. 6:

$$\frac{G_s}{G_r}=\frac{\mathit{RT}{\rho }_x{Q}_s^{{}^{-1}∕_3}}{\mathit{RT}{\rho }_x{Q}_r^{{}^{-1}∕_3}}=\frac{Q_s^{{}^{-1}∕_3}}{Q_r^{{}^{-1}∕_3}}$$ Eq.6

where G_s is the equilibrium swollen modulus; G_r is the relaxed-state modulus (i.e., the value measured on the rheometer in situ); and ϱ_x is the hydrogel crosslink density. The molecular weight between crosslinks subsequently is obtained with Eq. 5 using the equilibrium-swollen modulus (measured and adjusted for swelling with Eq. 6) and measured equilibrium swelling ratio. Finally, the mesh size, ξ, is obtained with Eq. 7, from Peppas et al.:^17,46

$$\xi ={\nu }_{2,s}^{{}^{-1}∕_3}l\sqrt{\frac{2C_n\overline{M_c}}{M_r}}$$ Eq.7

where l is the bond length along the polymer backbone (~ 0.15 nm⁴⁷); C_n is the Flory characteristic ratio (taken as 4 for PEG⁴⁸); and M_r is the molecular weight of the repeat unit (44 g/mol). Following the approach of Schwartz et al.,²⁴ the contributions of the peptide crosslinkers to C_n and M_r were neglected; this is a reasonable assumption as the hydrogel networks are predominantly PEG, but determining appropriate parameters for peptides in these networks may improve the accuracy of the mesh size predictions.

2.6. Equilibrium swelling theory

The mesh size was calculated from equilibrium swelling theory using the procedure outlined by Peppas et al.¹⁷ First, the average molecular weight between crosslinks, $\overline{M_c}$, is calculated from Eq. 8:

$$\frac{1}{{\overline{M}}_c}=\frac{2}{{\overline{M}}_n}-\left[\frac{\overline{\nu }\left[\text{ln}\right(1-{\nu }_{2,s})+{\nu }_{2,s}+{\chi }_1{\nu }_{2,s}^2]}{V_1{\nu }_{2,r}}\right]{\left[{\left(\frac{{\nu }_{2,s}}{{\nu }_{2,r}}\right)}^{{}^1∕_3}-\left(\frac{{\nu }_{2,s}}{2{\nu }_{2,r}}\right)\right]}^{-1}$$ Eq.8

where $\overline{\nu }$ is the specific volume of the polymer (taken to be 0.93 mL/g for PEG⁴⁹); V₁ is the molar volume of water (18 mL/mol²³); and χ₁ is the polymer-solvent interaction parameter (taken to be 0.426 for PEG in water⁴⁷). The mesh size subsequently was obtained with Eq. 7 and the calculated $\overline{M_c}$. Again, the contributions of the peptide to the constants required by this theory were neglected.

2.7. Protein release, SDS-PAGE, and ELISA

Model proteins were dissolved in PBS and frozen in aliquots at −80°C for up to 1 year until use. Concentrations of the stock solutions of model proteins were determined by absorbance measurements on a NanoDrop 2000c Spectrophotometer (Thermo Scientific, Waltham, MA). Extinction coefficients for each protein at 280 nm are summarized in Table S1. Concentrations of the protein stock solutions were calculated using the Beer-Lambert Law (Eq. 9):

$$c=\frac{A}{\epsilon L}$$ Eq.9

where c is the protein concentration; A is the absorbance (here, at 280 nm); ε is the extinction coefficient (at 280 nm); and L is the path length.

The final concentrations of the model proteins in PEG hydrogels were selected to give bands of approximately equal intensity in SDS-PAGE gels if they were completely released into the buffer solution. Bovine aprotinin (Sigma-Aldrich; 7 kDa) was loaded into hydrogels at 0.35 mg/mL; myoglobin from bovine skeletal muscle (Worthington Biochemical; 17 kDa) was loaded at 0.60 mg/mL; human lactoferrin (Sigma-Aldrich; 77 kDa) was loaded at 0.07 mg/mL; bovine serum albumin (BSA; Sigma-Aldrich; 66 kDa) was loaded at 0.06 mg/mL; and bovine thyroglobulin (Sigma-Aldrich; 670 kDa) was loaded at 0.09 mg/mL. Linear calibration curves were obtained for each of the proteins of interest (aprotinin, myoglobin, lactoferrin, bovine serum albumin, and thyroglobulin) using 4 different concentrations for each protein. The calibration curves were verified to be linear over the ranges studied in this experiment (R² = 0.95 for aprotinin, R² = 0.92 for myoglobin, R² = 0.97 for BSA, R² > 0.99 for lactoferrin, and R² = 0.95 for thyroglobulin).

Hydrogels for protein release were synthesized as described in Hydrogel Formation (above), but with the addition of the model protein cocktail or PDGF-BB and immediate placement of hydrogels into PBS sink solution after their formation. All of the protein release experiments were conducted at room temperature; based on thermodynamics and transport theories, we expect that the release rate would be slightly greater at physiological temperatures. Release of the model proteins was monitored by incubating hydrogels at room temperature in PBS (1.7 mL) while rocking until the desired timepoint, when the buffer was removed and replaced with fresh buffer. Protein/buffer samples were frozen at −80°C until analysis by SDS-PAGE. When all of the desired timepoints were collected, samples were thawed and concentrated using 0.5 mL, 3 kDa molecular weight Amicon centrifugal filters (MilliporeSigma) following the manufacturer’s instructions. The concentration factor was calculated by measuring the volume loaded into the device initially and measuring the volume after centrifugation with a micropipette. The concentrated protein samples were then diluted in 4x Laemmli buffer (Bio-Rad) with 10% 2-mercaptoethanol (Sigma-Aldrich) and heated at 85°C for 3 minutes. Finally, the samples were loaded into 4-20% gradient SDS-PAGE gels (Mini-PROTEAN TGX, Bio-Rad) and run for approximately 1 hour at 125 V in a Mini-PROTEAN Tetra Vertical Electrophoresis Cell (Bio-Rad).

After running, SDS-PAGE gels were stained with SYPRO Ruby (1x; Bio-Rad) for 3 hours at room temperature with gentle rocking. Gels subsequently were washed three times in destain solution (83% v/v deionized water, 10% v/v methanol, 7% v/v acetic acid) for 1 hour each. After destaining, the gels were washed twice with deionized water for 5 minutes and imaged on a Typhoon 9400 Imager (Amersham Biosciences, Piscataway, NJ). Images were analyzed with the Gels submenu in ImageJ software (National Institutes of Health, Bethesda, MD). Two standards from the linear calibration curves were run on each gel to ensure consistency between gels, which can vary in background signal and maximum staining intensity:⁵⁰ i) a negative control consisting of only PBS in Laemmli buffer and ii) a protein release control consisting of the concentration of proteins that would be present if 100% of all proteins were released. With this, the intensities of the protein bands were converted to percent released. For studies measuring PDGF-BB release, PDGF-BB (Peprotech) was dissolved in PBS with 0.8 mg/mL BSA and frozen at −80°C in aliquots; these aliquots were used within up to 1 year of freezing. Detection of PDGF-BB by ELISA was particularly affected by freeze-thaw cycles; thus, all samples, including standards, were subjected to the same number of freeze-thaw cycles (1 freeze-thaw cycle before loading into the hydrogel, and 1 additional freeze-thaw cycle between release and detection). PDGF-BB was loaded at the same concentration in hydrogels (2.5 ng/μL) as previously used by Holloway et al. for bone morphogenic proteins.¹⁵ Hydrogels containing PDGF-BB (~ 50 μl) were immersed in 2 mL PBS at room temperature with rocking, and, at the desired timepoints, the PBS was removed, frozen, and replaced with fresh PBS until analysis.

For the studies where collagenase was used to tune the rate of protein release, hydrogels were formed using the DegXlink peptide and incubated in PBS with or without 5 U/mL collagenase (Type II collagenase from Clostridium histolyticum; Gibco; 293 units/mg). At every timepoint, the PBS with collagenase was removed, frozen, and replaced with freshly dissolved collagenase. After 6 days, at the end of the experiment, all remaining hydrogels (i.e., those hydrogels incubated with 0 U/mL collagenase) were changed to 500 U/mL collagenase until complete hydrogel dissolution to recover any remaining PDGF-BB before analysis.

PDGF-BB concentrations were analyzed using a commercial ELISA kit (Abcam). The detection limits of the recombinant PDGF-BB used here were slightly different from the detection limits for physiological PDGF-BB listed in the manufacturer’s instructions; to account for this, a standard curve between 0 - 4000 pg/mL (rather than 0 - 400 pg/mL) was used. The remaining steps in the ELISA protocol were followed according to the manufacturer’s instructions. For data analysis, the standard curve was fit with a 4-parameter logistic curve as recommended by the manufacturer (Origin 2016, OriginLab, Northampton, MA).

Release studies were designed for achieving roughly one-dimensional (1-D) Fickian diffusion. Hydrogels were fabricated with a diameter approximately ten times greater than their thickness and kept floating in sink solution throughout protein release. Assuming axial 1-D Fickian diffusion, an effective diffusivity (D_eff) was fit to the release profile for each replicate with a numerical algorithm in MATLAB. Diffusivity in water (D_H2O) was estimated using the Stokes Einstein equation (Eq. 10):

$$D=\frac{k_{B}T}{6\pi \eta r}$$ Eq.10

where k_B is Boltzmann’s constant; T is temperature; η is dynamic viscosity of the solution (i.e., for water); and r is the hydrated radius of the protein.

2.8. Statistics

Each experiment was conducted in at least triplicate (n ≥ 3). All values are represented as mean ± standard error. All error bars in graphs represent standard error.

3. Results and Discussion

Hydrogels produced by step growth polymerization are of growing interest for protein release owing to a number of advantageous properties. Step growth polymerizations, such as those formed with multifunctional PEGs, often result in networks with high functional group conversion and defined network structure, producing materials with robust properties for protein release.^31,51,52 In these systems, PEG concentration and molecular weight can be tuned to modulate mesh size and the rate of protein release. For example, Tong et al. tuned the release of BSA from 8-arm PEG-Nb/PEG-2SH hydrogels and from 8-arm PEG-Nb/8-arm PEG-2SH hydrogels by varying PEG concentration,¹⁹ and Zustiak and Leach tuned the release of BSA from 4-arm PEG-vinyl sulfone/PEG-2SH hydrogels by varying PEG molecular weight.⁷ Thiol–norbornene systems are of particular interest as their photopolymerization properties allow for the creation of defined geometries, on the nano and micro scales, that can influence cellular uptake and other properties relevant for drug delivery.⁵³,⁵⁴ Here, we use them as a model step growth hydrogel system for examining the effectiveness of theoretical mesh size estimations in predicting protein release and establishing hydrogel compositions relevant for controlling the release of a variety of proteins.

3.1. PEG concentration and molecular weight modulate hydrogel mesh size

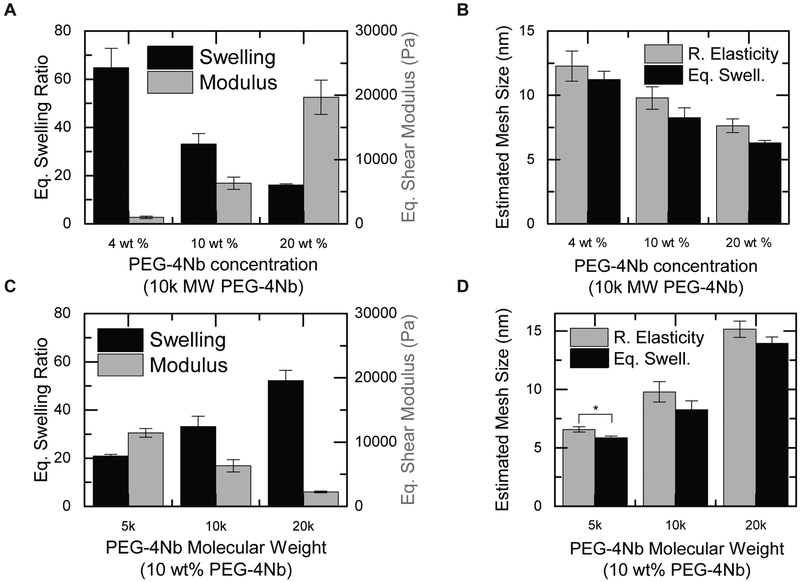
First, to evaluate the effects of PEG concentration on hydrogel mesh size, we used different concentrations of PEG-10k-4Nb (4% w/w, 10% w/w, and 20% w/w) and sufficient PEG-1.5k-2SH to give equimolar norbornene and thiol groups. This range of PEG-4Nb concentrations was selected to approach the limits of concentrations which produced gels with consistent polymerization, appropriate solubility, and easy handling. We then measured the equilibrium swelling ratios and shear moduli after preparation of the resulting hydrogels and predicted their mesh size using the equations associated with each theory (Eqs. 2-8). Increasing the concentration of PEG monomers increased the shear modulus and decreased the equilibrium volumetric swelling ratio (Figure 2A). These trends were consistent with those observed by Toepke et al,¹⁴ and the orders of magnitude for the values were also consistent, despite the fact that Toepke used different molecular weights and methods of measurement from those described here. We then calculated the mesh sizes by equilibrium swelling theory and rubber elasticity theory (Figure 2B and Table S2). Increasing PEG-4Nb concentration from 4% w/w to 20% w/w resulted in a 43% decrease in mesh size by equilibrium swelling theory (from 11.2 ± 0.6 nm to 6.3 ± 0.2 nm) and a 38% decrease by rubber elasticity theory (from 12.3 ± 1.2 nm to 7.6 ± 0.5 nm).

Figure 2. PEG concentration and molecular weight modulate hydrogel mesh size.

The effects of PEG-4Nb concentration (listed here as weight (wt) %) on (A) equilibrium swelling ratio (black) and equilibrium shear modulus (grey) were assessed. (B) Mesh size was calculated using rubber elasticity theory (grey) and equilibrium swelling theory (black). Increasing PEG-4Nb concentration decreased the equilibrium swelling ratio and increased the shear modulus of the hydrogel, leading to significant decreases in mesh size as calculated by both rubber elasticity theory and equilibrium swelling theory. The effects of PEG-4Nb molecular weight on (C) equilibrium swelling ratio (black) and shear modulus after preparation (grey) were also probed and (D) used to calculate mesh size using rubber elasticity theory (grey) and equilibrium swelling theory (black). Increasing PEG-4Nb molecular weight increased the equilibrium swelling ratio and decreased the shear modulus of the resulting hydrogel, leading to statistically significant increases in mesh size between all compositions by both rubber elasticity theory and equilibrium swelling theory. The change in mesh size with molecular weight (C, D) is more significant than the change with polymer concentration (A, B). Slightly lower mesh sizes were predicted by equilibrium swelling theory than by rubber elasticity theory for all compositions; the difference between the two theories was statistically significant only for the 5 kDa PEG-4Nb sample. * p < 0.05 by t-test.

To evaluate the effects of PEG molecular weight on hydrogel mesh size, we reacted different molecular weights of PEG-4Nb (5 kDa, 10 kDa, and 20 kDa) with PEG-1.5k-SH (1:1 Nb:SH). Molecular weight has been shown to increase the modulus of hydrogels, which rubber elasticity theory uses to determine mesh size;¹⁴ these particular molecular weights were chosen to represent the molecular weights of interest in other biopharmacuetical retention studies.⁷,⁵⁵ For these studies, the concentration of PEG-4Nb monomers was fixed at 10% w/w PEG-4Nb. Although not investigated here, similar trends would be expected with changes in the PEG-2SH molecular weight, as, for both monomers, changing the molecular weight changes the molecular weight between crosslinks in the hydrogel network. As expected, increasing the molecular weight of the PEG-4Nb monomer increased the equilibrium volumetric swelling ratio and decreased the initial shear modulus (Figure 2C). As shown in Figure 2D and Table S2, decreasing the PEG-4Nb molecular weight from 20 kDa to 5 kDa resulted in a 58% decrease in mesh size by equilibrium swelling theory (from 13.9 ± 0.5 nm to 5.9 ± 0.1 nm) and a 57% decrease by rubber elasticity theory (from 15.2 ± 0.7 nm to 6.6 ± 0.2 nm).

Rubber elasticity theory predicted a slightly larger mesh size than equilibrium swelling theory for all five PEG-PEG compositions, although the differences were only statistically significant for the 10% w/w, 5 kDa PEG-4Nb case. While both the monomer molecular weight and the polymer concentration had significant effects on the mesh size, the monomer molecular weight had a stronger effect, at least in the ranges considered here, which are typical ranges for step-growth PEG-based hydrogel systems. Consequently, in designing hydrogel-based delivery vehicles for release of biopharmaceuticals of different sizes, varying polymer molecular weight may be more effective than changing polymer concentration. These mesh sizes are smaller than those reported in a similar study on the PEG-vinyl sulfone/PEG-thiol system.⁵⁶ This may be a result of the crosslinker molecular weight; Zustiak and Leach used a 3.4 kDa molecular weight PEG-2SH compared to the 1.5 kDa molecular weight PEG-2SH used here. However, it may also highlight the high crosslinking efficiency of the thiol–norbornene system.⁵⁷ Notably, all of these mesh sizes are on the same order of magnitude as the size of most proteins³³ (e.g., IgG,⁵⁸ acidic fibroblast growth factor,⁵⁹ PDGF-BB⁶⁰), highlighting the importance of accurately and precisely characterizing mesh size and the need for complementary empirical techniques for the study of controlled protein release.

3.2. Crosslinker identity impacts hydrogel properties

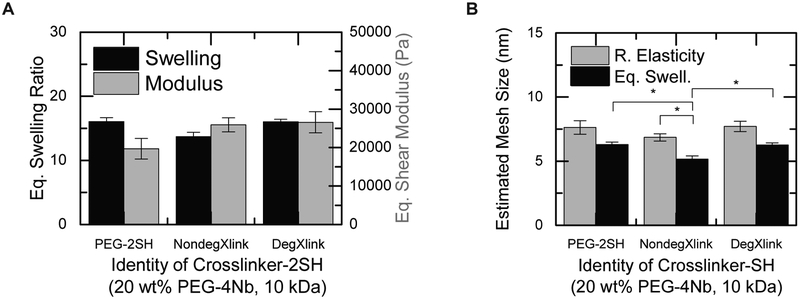
One major advantage of PEG-based systems is their modular nature, allowing for straightforward incorporation of groups that degrade or respond to external stimuli to change material properties over time.⁶¹ Incorporation of cleavable or stimulus-responsive functionality can be used advantageously in protein release applications, as materials can be designed to release proteins in specific environments, such as environments with high concentrations of glutathione⁶ or proteases.⁶² Frequently, this dynamic behavior is introduced into hydrogels by crosslinking the hydrogels with matrix metalloproteinase (MMP)-cleavable peptides.^10,63,64 Thus, we also characterized the relationships between crosslinker identity and mesh size for a PEG-2SH crosslinker, an inert peptide crosslinker (CGGRDYGC; NondegXlink), and an MMP-degradable peptide crosslinker⁶⁵ (GCRDVPMS↓MRGGDRCG; DegXlink). Here, we used 20% w/w PEG-10k-Nb and sufficient crosslinker to give equimolar norbornene and thiol groups.

Changing the identity of the crosslinker did not have a significant effect on the hydrogel modulus (Figure 3A). A significant decrease in the equilibrium swelling ratio was observed with NondegXlink crosslinker, likely due to the smaller size of this crosslinker (MW = 829 Da) when compared to the PEG (MW = 1500 Da) or DegXlink crosslinker (MW = 1696 Da). However, there were no significant differences between the swelling ratios for the PEG-PEG or the PEG-DegXlink systems. Interestingly, equilibrium swelling theory indicated that the crosslinker identity was a significant factor for determining mesh size (Figure 3B and Table S3; One-way ANOVA p < 0.05), but there were no significant differences observed in the mesh sizes calculated with rubber elasticity theory (Figure 3B and Table S3; One-way ANOVA p = 0.41). Tukey’s post-hoc test on the equilibrium swelling theory data indicated that the PEG-NondegXlink networks had significantly smaller mesh sizes (p < 0.05) than either the PEG-PEG networks or the PEG-DegXlink networks. Tukey’s post-hoc test found no significant difference between the calculated mesh sizes of the PEG-PEG and the PEG-DegXlink networks (p = 0.87).

Figure 3. Crosslinker identity impacts hydrogel properties.

The effects of the chemical identity of the dithiol crosslinker on (A) equilibrium swelling ratio (black) and shear modulus after preparation (grey) were assessed. (B) Mesh size calculated using rubber elasticity theory (black) and equilibrium swelling theory (grey). The identity of the crosslinker generally does have a measurable impact on mesh size; however, its effect was less than that of monomer molecular weight or concentration. Differences in hydrogel mesh size were detected between the NondegXlink peptide and the DegXlinkpeptide or PEG-2SH when equilibrium swelling theory is used to calculate the mesh size, which may be a result of the increased precision observed with equilibrium swelling measurements. Notably, differences between DegXlinkpeptide and PEG-2SH were not observed, suggesting PEG-2SH as a relatively inexpensive surrogate for this peptide crosslinker when performing initial mesh size and release measurements. Statistically significant differences between rubber elasticity theory and equilibrium swelling theory were observed for PEG-NondegXlink hydrogels. * p < 0.05 by Tukey’s post-hoc test (comparing NondegXlink to PEG-2SH or DegXlink) or p < 0.05 by t-test (comparing rubber elasticity theory to equilibrium swelling theory for NondegXlink).

Notably, the moduli measured here are significantly higher than PEG-vinyl sulfone/peptide-SH gels formed under similar conditions.⁶⁶ For example, the 20% w/w, 10 kDa PEG-4Nb/NondegXink gels formed here had a shear modulus of 32200 ± 2100 Pa; 20% w/w, whereas 10 kDa PEG-vinyl sulfone/peptide-SH gels have a reported elastic modulus (typically higher than the shear modulus for these systems⁶⁷) of 4900 Pa.⁶⁶ This difference may reflect the high reaction efficiency of the thiol–norbornene system.⁵⁷

Regardless of the theory used, the mesh sizes of these PEG step-growth networks do not seem to be drastically altered by the identity of the crosslinker, as long as the crosslinkers are of comparable molecular weight. This may be advantageous for studying protein release from these networks, as PEG-based crosslinkers are often less expensive and easier to synthesize than peptide-based crosslinkers. We postulate that PEG-based crosslinkers can be used for initial characterization and screening of PEG hydrogel-based drug carriers, as long as a PEG crosslinker of comparable size to the final crosslinker is used. Further, equilibrium swelling theory led to detection of statistically significant differences in mesh size based on crosslinker identity. This analysis suggests, that with the types of gels and number of replicates used here, equilibrium swelling theory may be a more sensitive method for assessing differences in how composition influences mesh size. We speculate that this is because rubber elasticity incorporates experimental error from both modulus and swelling measurements, whereas equilibrium swelling only incorporates error from swelling measurements, making it more precise (but not necessarily more accurate) with the number of replicates we have here (n between 8 to 12 for each composition).

3.3. Protein cocktail approach was established for assessment of initial burst and long-term release of proteins of different sizes

The mesh size predictions for these step growth hydrogels are similar in magnitude to the sizes of many bioactive proteins of interest, presenting a challenge for utilizing theory alone in gel design for biopharmaceutical release. Here, we set out to establish an empirical method for rapidly evaluating protein release from hydrogel-based drug delivery vehicles. Our goal was to provide a technique that is complementary to existing theoretical and experimental analyses and also provides both specificity and insight into hydrogel design for achieving the release of a variety of proteins over desired timescales. Studies to measure protein release from hydrogels have been previously conducted with fluorescently-labeled model molecules, such as dextrans^68–70 or BSA.^6,71 While relevant, these macromolecules lack diversity in representing the range of different protein geometries and chemistries present in biopharmaceuticals. Likewise, fluorescently-labeled versions of therapeutically-relevant proteins are often not commercially available, and fluorescent modification of proteins without compromising their structure can be challenging.⁷²,⁷³ Release profiles of single proteins loaded into hydrogels have been measured by total protein assays such as the Bradford assay,⁷⁴ the Bio-Rad protein assay,⁷ or UV-Vis spectroscopy.⁷⁵ SDS-PAGE is commonly used to verify protein integrity after release from hydrogels (i.e., verify that the protein molecular weight is unchanged by the hydrogel crosslinking and release process).⁶,²⁸,⁷⁶ However, SDS-PAGE is typically complemented by individual-protein analysis techniques such as fluorescence,⁷⁶ absorbance,⁷⁷ or ELISA⁷⁸ to determine release rate. While valuable, these assays generally require one hydrogel per macromolecule and substantial analysis time.

One of the goals of the current work was to demonstrate the value of a protein mixture-based approach. Multiple proteins were loaded into the same hydrogel and their release was analyzed by SDS-PAGE, a tool available in many labs for protein characterization but underutilized for studies of therapeutic delivery (Figure 4A). Indeed, quantification of SDS-PAGE gel bands and subsequent staining with SYPRO Ruby has a linear dynamic range of 3-4 orders of magnitude for protein quantification,⁷⁹ and the SYPRO Ruby stain can be used to detect proteins at amounts as low as ~ 0.5 ng, making SDS-PAGE a reliable and sensitive method for protein quantification over a wide range of concentrations.^50,80 The proteins discussed here were selected to cover a wide range of protein sizes (Table 1) while remaining inexpensive to obtain in large amounts (compared to, e.g., growth factors). To the best of our knowledge, this is the first time such an approach has been used to quantify the extent of protein release from hydrogel-based delivery systems. This strategy increases throughput when screening for drug release carriers, decreasing the amount of material, time, and the screening cost.

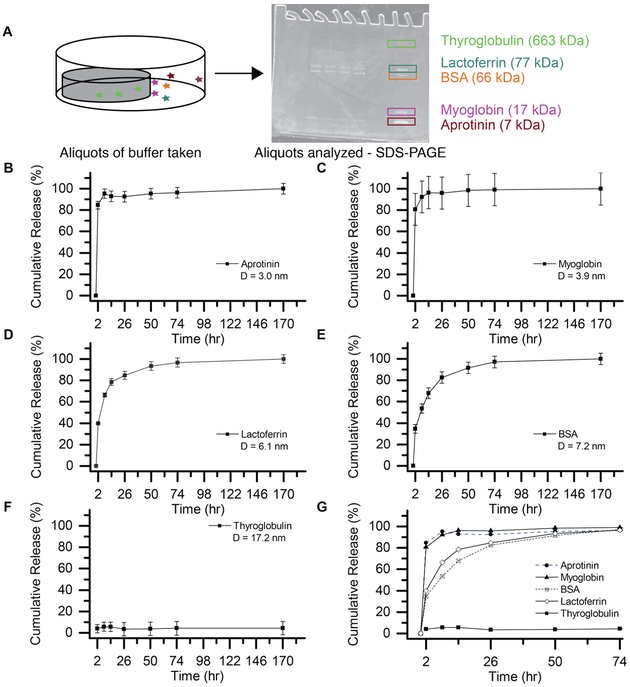
Figure 4. Model protein cocktail enables rapid assessment of release profiles from a single gel composition.

(A) A mixture of model proteins was loaded into each hydrogel replicate, here 10% w/w, 5 kDa PEG-4Nb/PEG-2SH hydrogels, to assess gel retention of mid-size proteins similar in diameter to the measured gel mesh size. (B-F) The release profile of each individual protein is plotted separately, even though each profile was obtained from the same hydrogel samples (n=3). (B-C) Aprotinin and myoglobin were rapidly released from the network, achieving greater than 90% release within 8 hours. (D-E) Lactoferrin and BSA were released more slowly from the network, reaching greater than 90% release after approximately 50 hours of incubation. (F) Thyroglobulin is not released from the network to any significant degree. (G) The release profiles are overlaid to demonstrate the size-dependence of the release rate. The smallest proteins (aprotinin and myoglobin) were released significantly faster than the proteins with diameters comparable to the hydrogel mesh size (lactoferrin and BSA). This technique provides greater throughput and conservation of material than the more typical analysis of a separate hydrogel for each protein. Error bars were removed from (G) for ease of viewing.

Table 1.

Molecular weights, hydrodynamic diameters, and calculated diffusivities for proteins used in the cocktail approach.

Protein	Molecular Weight	Hydrodynamic Diameter	Diffusivity in Water (x10−8 cm2/s)	Diffusivity in Hydrogel (x10−8 cm2/s)
Aprotinin	7 kDa	3.0 nm81	161	24.1 ± 3.8
Myoglobin	17 kDa	3.9 nm75	124	9.4*
Lactoferrin	77 kDa	6.1 nm75	79	2.8 ± 0.1
BSA	66 kDa	7.2 nm75	67	1.9 ± 0.5
Thyroglobulin	670 kDa	17.2 nm (Manufacturer)	28	< 0.1**

^*Represents an average effective diffusivity (D_e) for n=2; variability in the release profile for one sample led to a poor fit assuming 1-D Fickian diffusion, and a D_e for that sample could not be appropriately determined and was excluded from the average.

^**Diffusion out of the hydrogel is limited and negligible over the time scale of the experiment.

To conduct these studies, we first selected five proteins of various sizes (Table 1). We loaded these five proteins in PEG-5k-Nb/PEG-1.5k-SH hydrogels at 10% w/w PEG-4Nb, which have a mesh size of 5.9 ± 0.1 nm by equilibrium swelling theory and 6.6 ± 0.2 nm by rubber elasticity theory. We hypothesized that aprotinin and myoglobin would be released (i.e., mesh size > diameter) and bovine serum albumin (BSA) and thyroglobulin retained (i.e., mesh size < diameter). The final protein, lactoferrin, was intended to provide information to compare the two theories: according to rubber elasticity theory, lactoferrin would be released, but according to equilibrium swelling theory, lactoferrin would be retained in the network.

To test our hypothesis, the hydrogels were immersed in PBS buffer after polymerization, and release of the protein cocktail was measured by removing the PBS at desired timepoints and replacing with fresh buffer. The samples were then concentrated using a Millipore Amicon centrifugal filter and analyzed with SDS-PAGE. Interestingly, significant release of aprotinin (Figure 4B), myoglobin (Figure 4C), lactoferrin (Figure 4D), and BSA (Figure 4E) were observed; the release profiles are presented in Figure 4 normalized to the total protein released after one week. The release of thyroglobulin from these networks was negligible; the release profile is presented in Figure 4F normalized to the total protein loaded in the hydrogel. Figure 4G shows the size dependence of the release profile; note, error bars have been removed from this combined graph for ease of viewing. The smallest proteins, aprotinin and myoglobin, are released rapidly, with over 90% of the observed release occurring within 8 hours of when the hydrogels were placed in buffer. This result is consistent with our hypothesis based on the theoretical predictions of mesh size. Lactoferrin and BSA, which have hydrodynamic diameters comparable to the mesh size of the PEG-5k-Nb network, were released more slowly, reaching 90% release after the hydrogels had been in buffer for 50 hours. Notably, the inclusion of the full protein cocktail or BSA alone did not significantly affect the hydrogel swelling ratio (Figure S8) or the hydrogel mesh size (Figure S9), when compared to the unloaded hydrogel.

To further demonstrate the size dependence of release, each release profile was fit with a 1-D Fickian diffusion curve to calculate the effective diffusivity for each protein for release from these hydrogels (Table 1). Aprotinin, myoglobin, lactoferrin, and BSA exhibit hindered diffusion, with diffusivities approximately one order of magnitude less than the estimated diffusivities of these proteins in water. In contrast, the largest protein, thyroglobulin, has a diffusivity that approaches 0 in these hydrogels, indicating entrapment of the protein within the polymer network over the time scale of the experiment.

Importantly, BSA was not retained in the network, despite having a larger hydrodynamic diameter than the mesh size of the network according to both theories studied here. While BSA has a hydrodynamic diameter of 7.2 nm, it is actually an ellipsoid with dimensions 14 × 4 nm (Figure S10).^82,83 We speculate, based on its geometry, that it can diffuse through the network in a hindered fashion as it can fit through pores depending on its spatial orientation. This finding is of particular relevance for studying and predicting the release of bioactive proteins of similar hydrodynamic diameter, which often are composed of subunits that lead to different shapes and geometries in solution. Alternatively, while the average mesh size was smaller than the diameter of BSA, the most common mesh size (i.e., mesh size mode rather than mean) might actually be larger than the diameter of BSA. In a similar system (step growth PEG hydrogels formed by Diels-Alder polymerization), Kirchhof et al. characterized the mesh size distributions by low-field NMR and observed that the most abundant mesh size was ~ 70% larger than the average mesh size.³⁶ A similar phenomenon might be occurring in the thiol–norbornene hydrogels in this work.

Taken together, while theories provide insight into gel structure and a means of estimating mesh size, experimental measurements, such as the approach presented here, remain critical in the design of hydrogels for the controlled release of proteins. The combinatorial cocktail-based approach established here may prove broadly useful as a first screen in material design for the release of biopharmaceuticals of a specific size such as PDGF, which we investigate further here, or other growth factors or chemokines.

3.4. The rate of PDGF release is comparable to the rate of BSA release

In wound treatment and other applications, a large initial burst of cargo followed by a slower, but consistent, release to sustain cargo levels at appropriate concentrations is desirable to stimulate the healing cascade and promote gradual healing;⁸⁴ however, the initial burst release is difficult to predict and to control.⁸⁴ Thus, one goal of the present work was to use a combination of theory and experiments to predict release of a therapeutically-relevant protein, PDGF. PDGF is a dimer of A and B chains which associate to form PDGF-AA, PDGF-AB, and PDGF-BB.⁸⁵ PDGF-BB in particular is a potent mitogen for many cells⁸⁵ and is effective at stimulating human mesenchymal stem cell migration,³⁸ a topic of therapeutic interest to our group and many others.

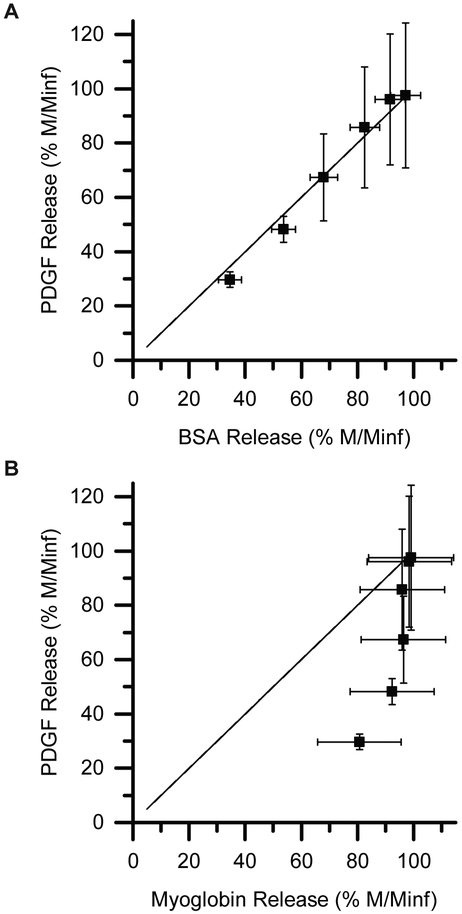
In the systems studied here, release is largely mediated by hindered diffusion. Thus, we wanted to determine if we could predict release of PDGF by comparing the release of PDGF with the release of a protein that has a similar hydrodynamic diameter (the diameter of a hard sphere that diffuses at the same rate as the protein). The hydrodynamic diameter of PDGF-BB is approximately 7.0 nm,⁶⁰ so it should diffuse at approximately the same rate as BSA, which has a hydrodynamic diameter of 7.2 nm.⁷⁵ We plotted the release rate of PDGF-BB against the release rate of BSA (Figure 5A) and myoglobin, a poor match in hydrodynamic diameter (Figure 5B). As shown in Figure 5A, the rate of BSA release matches the rate of PDGF release very well, as the data points fall very close to the x = y line. If a model protein with a poor size match is selected, such as myoglobin, the release data does not match well with the x = y line (Figure 5B). Thus, the best predictor of PDGF-BB release was the release of BSA, a protein with a similar hydrodynamic diameter.

Figure 5. Comparison of release rates of bioactive PDGF-BB with model proteins.

The release rate of PDGF-BB (hydrodynamic diameter = 7.0 nm) is similar to (A) the release rate of BSA (hydrodynamic diameter = 7.2 nm), falling on the x=y line, but not (B) that of myoglobin (hydrodynamic diameter = 3.9 nm). BSA, which has a comparable hydrodynamic diameter to PDGF, thus provides a relatively inexpensive, reasonable surrogate for studying the release of PDGF.

A number of cell types have been observed to migrate in response to gradients of PDGF: for example, mesenchymal fibroblasts respond to increases in PDGF concentration by increasing their migration speed, reaching a steady state (i.e., maximum migration speed) approximately 4 hours after exposure to PDGF.⁸⁶ We hypothesize that roughly matching that timescale (i.e., having PDGF release occur on the timescale of hours) could be beneficial for promoting cell migration in regenerative medicine applications (e.g., fibroblast migration or hMSC homing in wound healing). For example, releasing growth factor faster than the cells are able to respond would potentially lead to greater than required doses at the injury site; this could result in premature protein degradation, due to the instability of many growth factors in vivo, or off-target effects due to protein diffusion.⁸⁷ Releasing growth factor slower than the cells are able to respond (i.e. on the timescale of days to weeks) would unnecessarily delay the migration response. Importantly, PDGF (Figure S11) and other proteins¹² retain bioactivity after exposure to the polymerization conditions that form PEG-based thiol–norbornene networks, highlighting their potential for use in MSC migration.

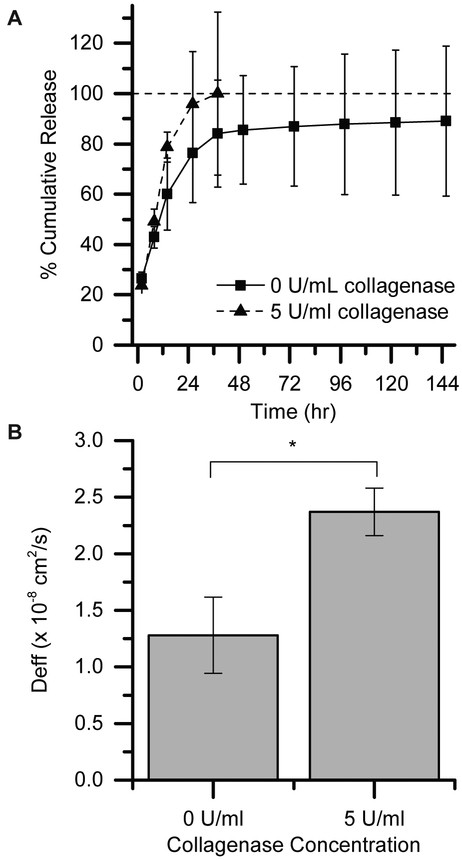
PDGF was released from networks containing 10% w/w PEG-5k-Nb and equimolar DegXlink peptide. At short times, PDGF is rapidly released from this network (Figure 6A), with greater than 70% of PDGF released within 24 hours. At long times, PDGF release levels out and the rate is greatly decreased, but a non-zero release rate is observed for at least 6 days. Although not verified in this study, Tong et al. have observed non-zero release of bFGF from PEG-based, thiol–norbornene networks for at least 35 days.¹⁹ The networks described by Tong et al. were formed by reacting PEG-8-Nb (10 kDa) with PEG-8-SH (10 kDa) with ester bonds between the crosslinks to promote hydrolytic degradation. Comparing our work to theirs, it is likely that increasing our PEG-Nb functionality from 4 to 8 and increasing our thiol crosslinker functionality from 2 to 8 (or 2 to 4) would provide additional handles with which the release rate of PDGF-BB could be slowed, if longer-term release was desired.

Figure 6: Controlling the release of PDGF over hours to days toward wound healing applications.

(A) PDGF was released from from 10% w/w, 5 kDa PEG-4Nb/DegXlink hydrogels over several days, with greater than 70% of PDGF released within 24 hours. (B) The release profiles were fit to a model to estimate the effective diffusivity. Applying collagenase increased the rate of release until 36 hours, when the hydrogels were completely degraded in the presence of 5 U/mL collagenase (*p ≤ 0.05 by t-test).

A secondary goal of this work was to explore the ability to tune the rate of PDGF delivery from PEG-based, thiol–norbornene hydrogels. Enzymatically-degradable networks have been used with success in other hydrogel drug delivery systems, typically where the protein is entrapped and only released after application of exogenous enzyme.¹⁵,⁸⁸,⁸⁹ We demonstrate that this strategy also can be used in diffusion-based release to modulate release profiles for applications of interest, such as wound healing where initial burst followed by continuous release is often desirable.⁸⁴ We used an MMP-responsive system, the PEG-DegXlink network, in the presence of different levels of collagenase to demonstrate the ability to tune the burst release of PDGF. The peptide, GCRDVPMS↓MRGGDRCG, degrades in response to a number of MMPs upregulated in wound-healing environments, including MMP-1, MMP-2, and MMP-9.⁶⁵ Here, we used collagenase to degrade the network and tune PDGF release due to its relatively low cost compared with other MMPs. Higher diffusivity values were observed in the presence of 5 U/mL collagenase (Figure 6B). Although we presented one case study here, this approach and these techniques could be used to design a wide variety of drug carriers for a number of therapeutic proteins. While our goal was to demonstrate release of a bioactive protein over days, the mesh size of the hydrogel could be further decreased for entrapment and degradation-based release. For example, Aimetti et al. have demonstrated the ability to release BSA and carbonic anhydrase from a less highly-swollen PEG-based thiol-norbornene hydrogel (i.e. a network with a smaller mesh size) in response to human neutrophil elastase, where release was dictated by degradation of the hydrogel and not by diffusion.⁶²

It is important to note that PEG has anti-fouling properties and limited protein adsorption.⁹⁰ If a different hydrogel system were used for protein release (e.g., charged networks²⁷), interactions between the hydrogel and the protein would be expected to influence the release rate. In these cases, the chemistry of both the hydrogel and the model proteins should be selected to match the system of interest as closely as possible for evaluation of release profiles. If the interaction is relatively strong, using model proteins may not yield useful rate-based information; in these cases, the approach discussed in this paper could be used to directly characterize the release rate of the desired therapeutics from the hydrogel system of interest, as the approach relies on protein analysis methods (i.e., SDS-PAGE and SYPRO Ruby stain) that will stain most or all protein-based therapeutics. In addition, after the initial screen with model proteins, the release rate of the desired therapeutic from the identified hydrogel composition of interest should be performed, as done here with PDGF, ensuring accuracy in the absence of different protein-protein interactions that may be present with the cocktail of model proteins.

A main advantage of the screening method presented in this manuscript is its flexibility: it can be used for diffusion-based release and degradation-based release, with particular insight into the rate of initial burst in these systems which has historically been challenging to predict. Thus, we postulate this approach may prove further useful for the design of similar gel systems for erosion-mediated release of different biopharmaceuticals.

4. Conclusions

Mesh size is a critically important parameter for predicting the retention or release of a therapeutic protein from hydrogels. Here, we calculated the mesh size by two commonly used theories (equilibrium swelling theory and rubber elasticity theory) for a number of different well-defined hydrogel formulations, where monomer molecular weight, concentration, and chemical identity are varied. Equilibrium swelling theory and rubber elasticity theory give relatively consistent results, with slightly higher mesh sizes predicted by rubber elasticity theory in the compositions studied here. While each theory proved consistent in predicting mesh size trends, when a protein of interest has a similar hydrodynamic diameter to the mesh size of its hydrogel delivery vehicle, empirical assessment of protein release is warranted. To accomplish the latter, our novel model protein cocktail technique can be employed to rapidly identify appropriate conditions to obtain optimal protein release kinetics. The value of this approach was highlighted here by its ability to predict the rate of PDGF release by comparing it to the release of model protein BSA, which is similarly-sized and less expensive. Thus, we predict that this approach will hold utility in the design of hydrogel-based protein carriers for a wide variety of applications, especially those that need controlled initial burst and diffusion-mediated release of biotherapeutics.