Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2019 Jul 1;19(8):4934–4940. doi: 10.1021/acs.nanolett.9b00986

Multiflat Bands and Strong Correlations in Twisted Bilayer Boron Nitride: Doping-Induced Correlated Insulator and Superconductor

Lede Xian †, Dante M Kennes ‡, Nicolas Tancogne-Dejean †, Massimo Altarelli †, Angel Rubio †,§,∥,*
PMCID: PMC6699729  PMID: 31260633

Abstract

graphic file with name nl-2019-00986r_0004.jpg

Two-dimensional materials, obtained by van der Waals stacking of layers, are fascinating objects of contemporary condensed matter research, exhibiting a variety of new physics. Inspired by the breakthroughs of twisted bilayer graphene (TBG), we demonstrate that twisted bilayer boron nitride (TBBN) is an even more exciting novel system that turns out to be an excellent platform to realize new correlated phases and phenomena; exploration of its electronic properties shows that in contrast to TBG in TBBN multiple families of 2,4, and 6-fold degenerate flat bands emerge without the need to fine tune close to a “magic angle”, resulting in dramatic and tunable changes in optical properties and exciton physics, and providing an additional platform to study strong correlations. Upon doping, unforeseen new correlated phases of matter (insulating and superconducting) emerge. TBBN could thus provide a promising experimental platform, insensitive to small deviations in the twist angle, to study novel exciton condensate and spatial confinement physics, and correlations in two dimensions.

Keywords: Twisted bilayer, multiflat bands, strong correlations, Mott insulator, topological superconductor, ab initio calculation

The consequences of strongly correlated physics such as, for example, high-Tc superconductivity in cuprates, are as highly relevant to technologies as they are complicated to describe because of the complex compositions of the materials where they are typically found. This complex composition hinders theoretical descriptions which struggle to incorporate the many competing effects arising, for example, from electronic and lattice degree of freedoms. Although it is now believed that, for example, the cuprates behave quasi-two-dimensional, it is still difficult to disentangle the role of the aforementioned degrees of freedom in this material. The recent experimental discovery of features reminiscent of those found in high-Tc cuprates, such as Mott insulating behavior and superconductivity, but in a simple system of doped twisted bilayer graphene1−4 has thus caused widely spread excitement. This discovery could pave the way to new inroads to understanding the mechanism(s) of high-Tc superconductivity by studying a much simpler system in which two graphene layer are stacked with a small twist angle. However, the reported correlation effects seem to be very sensitive and appear only at twist angles very close to the “magic angles” of twisted bilayer graphene (TBG), where the Fermi velocity of the system vanishes, the bandwidth achieves its minimum, and it becomes ultraflat. Away from the magic angles, the bandwidth increases again and the Tc decreases dramatically.1 Although there are multiple magic angles predicted in tight-binding model calculations,5 most of them are below 1° twist angle, where atomic reconstruction significantly alters the underlying electronic structure.6 It is unclear whether ultraflat bands can survive strong reconstructions. Of the magic angles, only the first one is slightly larger than 1°. At these small angles, the synthesis of a large area sample without incurring significant strain is still a particular experimental challenge.4 Avoiding reconstruction and strain therefore renders finding another two-dimensional (2D) system to study such correlation physics (and beyond) without the constraint of magic angles highly desirable.

Among 2D materials, hexagonal boron nitride (hBN) has similar hexagonal structure as graphene7,8 and therefore it is also commonly referred to as “white graphene”. Although graphene has two identical carbon atoms in the unit cell, they are replaced by one nitrogen and one boron atom in hBN. This difference gives rise to a large band gap and finite effective mass for the low-energy electrons in hBN. As a consequence, hBN is widely used as an ideal insulator in 2D electronic devices (and to enhance the properties of graphene and 2D transition metal dichalcogenides (TMDs) by isolating them from their environment). Interestingly, our density functional theory (DFT) calculations reveal that flat bands develop at both the top of the valence band and bottom of the conduction band in twisted bilayer hBN with a small twist angle. In marked contrast to the TBG systems, the bandwidth of these flat bands decrease monotonically with twist angle and there is no occurrence of “magic angles”.5 The presence of flat bands at the edges of the gap is expected to strongly modify the optical properties (direct versus indirect nature of the bulk hBN material) and the structure of excitons and because the charge densities associated with the flat bands are not uniformly distributed in the Moiré supercell with spatial separation of electrons and holes at the edges of the band gap. In the case in which doping or photodoping could locate the Fermi level in the top valence band manifold, turning twisted bilayer boron nitride (TBBN) into a metallic system, we expect to encounter a situation in which the very narrow bandwidth can lead to strong electronic correlation effects for realistic values of the Coulomb interaction parameter. In TBG at the magic angles, the electron–electron pairing is among the strongest in nature (relative to the small carrier density). We expect similar strong pairing to be realized in TBBN at small twist angles (no magic angles needed). To further explore this situation, we evaluate the Coulomb interaction among the states in the flat bands, using a self-consistent ab initio DFT+U,9 and make use of the functional renormalization group (FRG)10 method to show that the flat band at the top of the valence bands can host exotic strongly correlated physics, such as the appearance of a Mott insulator phase and unconventional superconductivity. Those results provide strong evidence that TBBN could be a highly tunable platform to study unconventional superconductors, much like TBG, but without the constraint of magic angles. Although some other 2D bilayer systems besides graphene have been proposed, such as twisted TMD homo- and heterobilayers,11,12 those studies are based on DFT band structure analysis or simple model calculations only. Our comprehensive study clearly suggests that the gaplessness and masslessness of graphene is not essential in the observed exotic strongly correlated phenomena, motivating studies of many more two-dimensional materials stacked with a small twist angle. Moreover, instead of having only one pair of flat bands as in TBG, or one flat band as in twisted TMDs, multiflat bands appear at the band edges of TBBN with different characters, significantly enriching the physics that can be explored.

Ab Initio Characterization

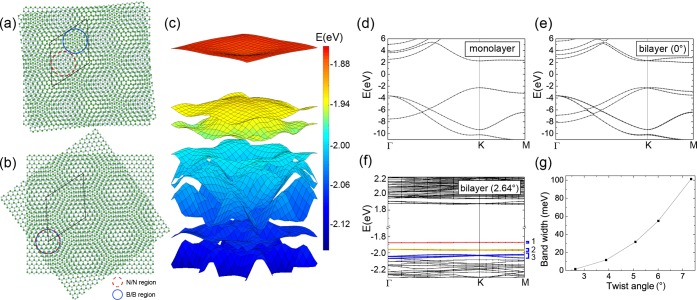
Starting from a regular bilayer hBN with stacking as in the bulk, TBBN can be formed by twisting the top or the bottom layer with angle θ. As shown in Figure 1a,b, there are two possible distinct configurations of TBBN, called α and β, that lead to the same supercell. Their twist angles differ by 60°. In TBBN, there are regions where nitrogen atoms on the top layer are approximately on top of those of the bottom layer (the N/N region, as highlighted by dash red circles) and regions where the same holds for the boron atoms (the B/B region, as highlighted by solid blue circles). In configuration α, the two regions are located at different sites of the supercell, whereas in configuration β they are located at the same sites (see Figure 1a,b). The total energy of two configurations is almost identical with that of the configuration β slightly lower. For TBBN with twist angle 2.64° after relaxation, the total energy difference is less than 2 meV/atom in both DFT and DFT+U calculations.

Figure 1.

Figure 1

Open in a new tab

Atomic and electronic structures of TBBN. (a,b) Schematic illustration of the two possible configurations in twisted bilayer hBN that have the same Moiré pattern. The B/B regions (highlighted with solid blue circle) and the N/N regions (highlighted with dash red circle) are located in different sites in the supercell in configuration α (a), whereas they share the same sites in configuration β (b). (c) Calculated DFT band structure of unrelaxed twisted bilayer hBN at 2.64° in a region of 0.11 × 0.11 1/Å2 around the Γ-point in the supercell Brillouin zone. (d–f) DFT band structures of monolayer (d), normal bilayer without twist (e), and unrelaxed twisted bilayer hBN (f). (g) Band width of the first set of flat bands at the top of the valence bands of unrelaxed TBBN for different twist angles.

To study the effect of twisted stacking, we first investigate the band structures of TBBN with fixed interlayer separation d, which is set to be the optimized interlayer distance of bilayer hBN without twist (3.23 Å, that is very close to the experimental value). As shown in Figure 1c,f, similar to the case of TBG, flat bands appear at the top of the valence band in TBBN at small twist angles. These flat band structures are significantly different from those of monolayer and normal bilayer hBN shown in Figure 1d,e, respectively. In contrast to the case of graphene, the flat bands are isolated from the other bands with a relatively large energy difference of over 100 meV, and intriguingly more than one set of them develop as twist angle decreases. For the smallest twist angle we studied in Figure 1f, three sets of flat bands can be clearly identified (see the labels on the right side of Figure 1f) and the number of bands in each set is 2, 4, and 6. The bandwidth of these flat bands decreases significantly with the twist angle. As shown in Figure 1g, the bandwidth of the top of the valence bands (the first set of flat bands) decreases from 101.4 meV at 7.34° to 1.6 meV at 2.64°. Modeling the top of the valence bands of hBN by a massive Dirac Hamiltonian suggests that indeed the bandwidth of these flat bands will decrease monotonically with twist angles without the existence of any magic angles (see Supporting Information). Similarly, flat bands also appear at the bottom of the conduction bands as the twist angle decreases (see Figure 1f at around 1.87–1.90 eV).

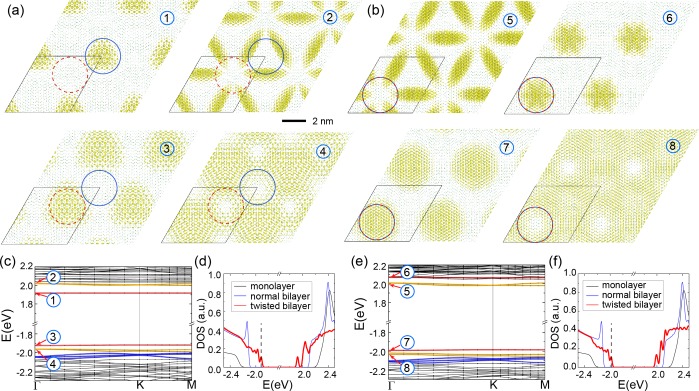
The calculated DFT band structures for the two configurations α and β of TBBN with fixed interlayer separation are almost identical, showing only subtle differences, whereas they are noticeably different after a complete structural relaxation. To further understand the effect of the structural relaxation in the two configurations and the nature of the flat bands, we plot the charge density distribution for the low-energy states in the two configurations of TBBN in Figure 2. Consistent with their narrow bandwidth, those low-energy states are well localized in real space, with different characters in different flat bands. The low-energy states at the top of the valence bands are dominated by nitrogen pz orbital and those at the bottom of the conduction bands are dominated by boron pz orbital. Therefore, the flat-band states of the top valence bands are indeed localized around the N/N region, while those of the bottom conduction bands are localized around the B/B region. The relaxation slightly increases the interlayer separation (∼0.14 Å) in the N/N region for both configurations and the valence bands of the two configurations remain very similar. However, remarkably we found that the response to the relaxation in the B/B regions is different for the two configurations, because of their different relative positions with respect to the N/N regions. This difference leads to different energy ordering of these flat band states in the conduction bands for the two configurations. Along with the different response to the relaxation, the band gaps of the two configurations are also different. In the total density of states, shown in Figure 2d,f, the low energy flat bands manifest as a few sharp peaks near the band edges, which are significantly different from those of the monolayer and untwisted bilayer hBN.

Figure 2.

Figure 2

Open in a new tab

Localization of electronic states in the flat bands of TBBN at 2.64°. (a,b) Top view of the charge density plot for the electronic states highlighted in the band structures shown in (c,e) for configurations α and β after relaxation, respectively. (d,f) The corresponding density of states of twisted bilayer hBN in the two configurations in comparison to those of monolayer and bilayer hBN without twist. The vertical dash lines in (d,f) indicate the zero of the chemical potential μ used in Figure 3c.

The optical properties of bulk and few-layer hBN systems have been investigated experimentally and theoretically (see, for example, refs (7 and 13−18)). For the (untwisted!) bilayer, estimates of exciton binding energy range up to 1.6 eV.17 The effect of twisting at the LDA level, however, is to reduce the band gap, therefore to increase the dielectric screening and reduce the exciton binding energy. Nonetheless, as one can see in Figure 2c,e the separation of the flat bands closest to the maximum (minimum) of the valence (conduction) bands of order ≃100 meV is smaller or comparable to the exciton binding energies, so that the formation of the exciton states shall involve more than one valence (conduction) bands, and the optical matrix elements shall strongly reflect the geometry of the charge densities of electrons and holes with marked differences between the two types of stacking configurations of TBBN. (Note that this energy is also close to the phonons of hBN that are responsible for the strong hyperbolic response of hBN.19 We expect that interesting nesting behavior would be obtained in the case of doped TBBN.) Considering the stronger interlayer interaction with localization in both conduction and valence band edges and the multiflat bands character, we expect even richer Moiré exciton behaviors in TBBN than those observed in twisted TMDs recently.20−24

DFT+U Analysis

Next, in order to characterize the electronic correlations in those flat bands (that tend to be beyond the capabilities of standard local and semilocal XC functionals) we investigate TBBN by means of self-consistent DFT+U (see Supporting Information Methods). We aim at extracting the most ab initio information possible concerning the electron–electron correlations in TBBN that afterward will be used to motivate the functional renormalization group (FRG) treatment (see below). We focus on the bands labeled 3 in Figure 2 hereafter. These are 2-fold degenerated bands, well described by a two-band Hubbard model. Concentrating on local interactions in such a model, one needs to determine an on-site Hubbard U in addition to the Hunds-coupling J. Assessing how important J is from ab initio calculations is crucial to our model building of TBBN.

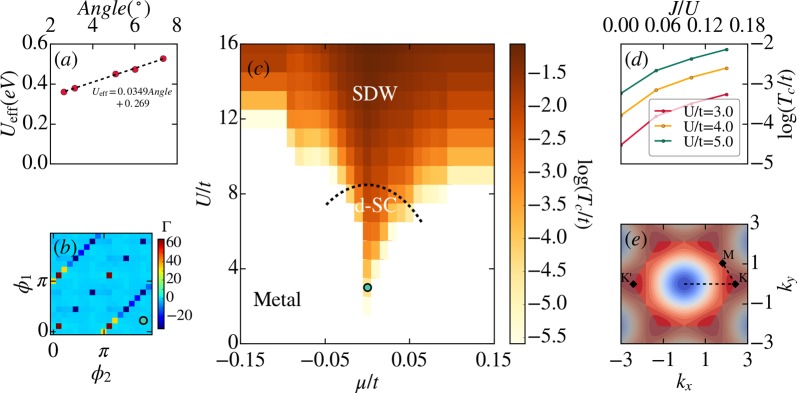
DFT+U is routinely used to describe transition metal oxides. A study of TBBN is quite different, as the localization occurs at a much larger spatial scale, and the effective electronic parameters are expected to be much smaller. Extracting quantitative parameters at finite doping is currently numerically not feasible and we consider without loss of generality just the undoped scenario. Notwithstanding, in order to address the role of J and U at least in this simpler case, we use the recently proposed ACBN0 functional,25 which allows for a DFT-based consistent ab initio calculation of the value of U and J (see Supporting Information Methods). For each system, from 7.34° to 2.64° we constructed the “single shot” Wannier states corresponding to the flat bands and then computed the effective Ueff = U – J. As shown in Figure 3a, we obtained a Ueff that scales linearly with the twist angle, similar to what was proposed for TBG.2 The calculated scaling of Ueff is 34.9 meV/degree. Compared with the value of about 5 to 26 meV/degree proposed for TBG,2 this relatively large value suggests a quite strong electron–electron correlation effect in TBBN, probably due to the smaller dielectric constant in hBN.

Figure 3.

Figure 3

Open in a new tab

Correlations in twisted bilayer boron nitride. (a) Interaction parameter as obtained by DFT+U without doping. (b) Structure of the effective two-particle interaction Γ (k1, k2, k3) at the end of the FRG flow for fixed ϕ3 (angle of momentum k3) dependent on the remaining two angles ϕ1 and ϕ2 (of momenta k1 and k2) for U = 3t as well as μ/t = 0 and J = 0. Dominant features along the diagonal (incoming momenta sum to zero) as well as the alternating sign (negative (red) to positive (blue)) signal a d-wave pairing instability. (c) Phase diagram dependent on U/t and μ/t for J = 0 (values of J in the single digit percent regime as found by DFT+U do not affect the phase diagram qualitatively). We distinguish metallic, d-wave and spin density wave behavior. The false color plot indicates the estimated transition temperature. (d) Influence of the Hund’s coupling J on the transition temperature for different values of U/t. DFT+U puts J/U in the single digit percent regime where its influence does not to alter the found phases but can increase the transition temperature. (e) False color plot of the dispersion relation in the full Brillouin zone (nonshaded area). The paths plotted for the dispersion relation in Figures 1 and 2 are shown as dashed lines.

In order to asses the role of J, we also computed the so-called Hubbard–Kanamori parameters U, U′, and J, using the bare Coulomb interaction (see Supporting Information Methods). Our results yield two important results: (i) we found that (U – U′)/2 is always very close to J (which is a relation strictly motivated only for the case of cubic symmetry for d orbitals26); (ii) the ratio of J/U is found to be small (between 0.03 to 0.05 for the various angles). These results are consistent with previous assumptions made for TBG but are here confirmed using ab initio simulations. At finite doping, screening will decrease the values of the interaction parameters, reduce the quasiparticle band gap, and increase the bandwidth, which unfortunately is beyond an ab initio analysis at present. We thus next consider the effect of correlations, keeping U and J as free parameters but assuming J = (U–U′)/2.

Correlation Effects

We now turn to the construction of an effective low-energy model to deal with the inclusion of correlations, which can drive the system into different phases of matter. We find that the dispersion relation of the bands labeled by 3 and 7 in Figure 2 are fitted well by a two-band nearest neighbor hopping t tight binding model on a triangular lattice (in agreement with the corresponding charge density plots in Figure 2). In particular, this fit works well irrespective of the twist angle. This implies that the twist angle only appears as an indirect parameter of our model, via U, J, and the hopping t (which is directly taken as one-ninth of the DFT bandwidth). Therefore, analyzing the results in terms of U/t, J/t, and band-filling covers all the twist angles at once.

The role of Coulomb interaction versus phonons in TBBN is unclear at the moment. If phonons dominate we would expect an instability to emerge in the paring channel driving the system into a (BCS-type) s-wave superconducting phase, similar to what has been proposed for TBG.27−29 If on the other hand Coulomb repulsion is dominant, the fragile balance of competing orders gives rise to a zoo of different possible phases dependent on interaction strength and filling.30−36 Because there is some evidence that electronic correlation effects are dominant,4 we explore the latter scenario employing an FRG approach (see Supporting Information Methods), which can be viewed as a renormalization group enhanced random phase approximation treatment of the interacting system. To this end, we include an onsite Hubbard-type U as well as a weak Hund’s coupling37 term J (in agreement with the above DFT+U analysis). The dispersion relation in the full Brillouin zone is illustrated in a false color plot in Figure 3e. We define the chemical potential μ with respect to the van Hove filling (meaning that at μ = 0 the density of states exhibits a van Hove singularity cf. Figure 2d,f). At this filling, the Fermi surface also exhibits nesting giving rise to a competition between a tendency for d ± id superconductivity and a spin density wave as the interaction is turned on. This competition can be studied in an unbiased fashion using the FRG for small to intermediate U/t by considering the so-called effective two-particle interaction Γ. During the renormalization group flow this effective two-particle interaction flows to strong coupling (diverges), which can be seen as the onset of ordering in the system. The energy scale at which this divergence occurs can be identified roughly with the critical temperature scale Tc of the corresponding order. The momentum structure of the effective two-particle interaction indicates the type of ordering. We here parametrize the three independent momenta of the effective two-particle interaction Γ (k1, k2, k3) by their projection on the Fermi surface as well the angles ϕi of this projection. The calculated FRG phase diagram is summarized in Figure 3c for zero Hund’s coupling J/t = 0. Turning on small Hund’s couplings of up to 18% changes Tc as shown in Figure 3d but does not influence the phase-diagram qualitatively, reinforcing the idea that the Hund’s coupling J does not play a major role here. Close to van Hove filling (μ = 0)4 we find topological d ± id superconductivity in this model for not too large U/t whereas it turns into a spin-density wave (SDW) for larger values of U/t.38 Further away from μ = 0, we also find metallic behavior which means that up to the point in energy space where the flow was stopped no divergence was encountered in the effective two-particle interaction. Figure 3b illustrates the momentum structure of the effective two-particle interaction in the phase of d ± id superconductivity. The dominant diagonal features with sign change (blue to red) indicate that d ± id superconductivity is the dominant ordering tendency in doped TBBN.

Finally, we note that our ab initio results show a linear dependence of U in the twist angle, and a polynomial (order 2) variation of the bandwidth (and hence of hopping t) in the twist angle for angle >2° (see Figure S3 in the Supporting Information). These two results imply that the ratio U/t decreases as the twist angle increases and the system can be mechanically tuned through a controlled transition from the SDW to the d-wave superconducting phase by tuning the twist angle.

A condition to observe strong correlation effects is that the Fermi level should be inside the flat bands, which may pose challenges for the experimental realization as hBN is a large-gap insulator. Nonetheless, recent progress on liquid ionic gating (or electric double layer (EDL) gating)39 has shown that this technique can be used to generate extremely high carrier density up to 1015 cm–240 with a relatively small bias and to induce insulator-to-metal transition in wide band gap semiconductors and insulators.41,42 Similar methods may be applied to gate TBBN to the desired filling condition, considering only very low density of charge carriers is required when the twist angle is small (see Figure S4 in SI). Alternatively, free carriers may be induced in TBBN by doping before further gating. It has been reported in the literature43−45 that Be, Mg, and Zn impurities introduced in hBN films induce shallow acceptor levels (with binding energy as low as 31 meV for Mg) and result in p-type semiconducting behavior. These results for multilayer films need not be easily reproduced in twisted bilayers, however they are encouraging in that semiconducting behavior with different dopants is consistently observed in thicker films. Also ab initio theoretical calculations for doped hBN support the possibility of semiconducting behavior.46 Furthermore, suitable substrates and overlayers might facilitate the emergence of degenerate semiconductor properties. Photodoping may be another interesting approach to realize exotic correlated phases in TBBN. Hot charge carriers may be excited from in gap defect states47 or band edges by photoexcitation. Transient photoinduced correlated insulating or superconducting behaviors could emerge before the formation of excitons and the recombination of the electron–holes pairs.

In conclusion, here we demonstrate that twisted bilayer boron nitride is a fascinating material in which a zoo of different electronic phenomena are expected. If the twist angle between the layers is small, groups of two-, four- and six-fold nearly degenerate and energetically separated flat-bands show up. These do not rely crucially on how close the chosen angle is to a “magic” angle as in the recently studied twisted bilayer graphene. The formation of these flat band manifolds is expected to affect the optical spectra and the formation of excitons as a function of the twist angle, with localization of carriers in distinct regions of the Moiré supercell. Furthermore, at small angles the flat bands are truly separated from the valence and conduction bands, rendering twisted bilayer boron nitride as an ideal candidate to study the physics of strong correlations in these materials. A combined DFT+U and FRG ansatz reveals that the physics of the group of bands that are 2-fold degenerate should be very similar to that of twisted bilayer graphene, possibly supporting topological d-wave superconductivity upon hole (or electron) doping. The existence of multiple flat bands significantly enriches the physics that can be probed. For example, the separation of the flat bands found is in the 100 meV regime. Coupling the present findings with the excitation of hyperbolic phonons19 opens the possibility of having a strong phonon-mediated coupling between the flat bands as the distance between them is in quasi-resonance with these phonon modes (strong phonon nesting mediated by hyperbolic phonons in hole-doped TBBN). Doping the system to obtain a degenerate semiconductor, and/or use ionic gating to tune the Fermi energy in one of the narrow bands appears possible, given the experience on thicker samples, and photodoping the system is another particularly intriguing avenue of future research. We predict that using acceptor doping or photodoping the identified correlated phases (insulator and superconducting ones) can be induced in an equilibrium or in a transient, nonequilibrium manner, strongly motivating experimental advances along these lines. Our study also opens the door to similar theoretical work in other 2D materials.

Acknowledgments

The authors thank Martin Claassen and Mei-Yin Chou for useful discussions. This work was supported by the European Research Council (ERC-2015-AdG694097). The Flatiron Institute is a division of the Simons Foundation. L.X. acknowledges the European Unions Horizon 2020 research and innovation programme under the Marie Sklodowska-Curie Grant Agreement number 709382 (MODHET). D.M.K. acknowledges funding from the Deutsche Forschungsgemeinschaft through the Emmy Noether program (KA 3360/2-1). FRG calculations were performed with computing resources granted by RWTH Aachen University under projects prep0010. We acknowledge computing resources from the Garching supercomputing center of the Max Planck Society as well as Columbia University’s Shared Research Computing Facility project, which is supported by NIH Research Facility Improvement Grant 1G20RR030893-01, and associated funds from the New York State Empire State Development, Division of Science Technology and Innovation (NYSTAR) Contract C090171, both awarded April 15, 2010.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.nanolett.9b00986.

  • Calculational details, model analysis of general twist bilayer systems with massive Dirac Hamiltonian, twist angle dependency of the doping density required to achieve half-filling in TBBN, DFT band structures of unrelaxed TBBN with different twist angles, and polynomial fitting of the bandwidth of the top of valence bands in unrelax TBBN (PDF)

Author Contributions

⊥ L.X. and D.M.K. contributed equally.

The authors declare no competing financial interest.

Supplementary Material

nl9b00986_si_001.pdf (719.4KB, pdf)

References

  1. Cao Y.; Fatemi V.; Fang S.; Watanabe K.; Taniguchi T.; Kaxiras E.; Jarillo-Herrero P. Unconventional superconductivity in magic-angle graphene superlattices. Nature 2018, 556, 43. 10.1038/nature26160. [DOI] [PubMed] [Google Scholar]
  2. Cao Y.; Fatemi V.; Demir A.; Fang S.; Tomarken S. L.; Luo J. Y.; Sanchez-Yamagishi J. D.; Watanabe K.; Taniguchi T.; Kaxiras E.; Ashoori R. C.; Jarillo-Herrero P. Correlated insulator behaviour at half-filling in magic-angle graphene superlattices. Nature 2018, 556, 80. 10.1038/nature26154. [DOI] [PubMed] [Google Scholar]
  3. Yankowitz M.; Chen S.; Polshyn H.; Zhang Y.; Watanabe K.; Taniguchi T.; Graf D.; Young A. F.; Dean C. R. Tuning superconductivity in twisted bilayer graphene. Science 2019, 363, 1059–1064. 10.1126/science.aav1910. [DOI] [PubMed] [Google Scholar]
  4. Kerelsky A.; McGilly L.; Kennes D. M.; Xian L.; Yankowitz M.; Chen S.; Watanabe K.; Taniguchi T.; Hone J.; Dean C.; Rubio A.; Pasupathy A. N.. Magic Angle Spectroscopy. arXiv:1812.08776, 2018. (accessed Decemeber 20, 2018). [Google Scholar]
  5. Bistritzer R.; MacDonald A. H. Moiré bands in twisted double-layer graphene. Proc. Natl. Acad. Sci. U. S. A. 2011, 108, 12233–12237. 10.1073/pnas.1108174108. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Yoo H.; et al. Atomic and electronic reconstruction at the van der Waals interface in twisted bilayer graphene. Nat. Mater. 2019, 18, 448. 10.1038/s41563-019-0346-z. [DOI] [PubMed] [Google Scholar]
  7. Wirtz L.; Marini A.; Rubio A. Excitons in Boron Nitride Nanotubes: Dimensionality Effects. Phys. Rev. Lett. 2006, 96, 126104. 10.1103/PhysRevLett.96.126104. [DOI] [PubMed] [Google Scholar]
  8. Blase X.; Rubio A.; Louie S. G.; Cohen M. L. Quasiparticle band structure of bulk hexagonal boron nitride and related systems. Phys. Rev. B: Condens. Matter Mater. Phys. 1995, 51, 6868–6875. 10.1103/PhysRevB.51.6868. [DOI] [PubMed] [Google Scholar]
  9. Tancogne-Dejean N.; Oliveira M. J. T.; Rubio A. Self-consistent DFT+Umethod for real-space time-dependent density functional theory calculations. Phys. Rev. B: Condens. Matter Mater. Phys. 2017, 96, 245133. 10.1103/PhysRevB.96.245133. [DOI] [Google Scholar]
  10. Metzner W.; Salmhofer M.; Honerkamp C.; Meden V.; Schönhammer K. Functional renormalization group approach to correlated fermion systems. Rev. Mod. Phys. 2012, 84, 299–352. 10.1103/RevModPhys.84.299. [DOI] [Google Scholar]
  11. Naik M. H.; Jain M. Ultraflatbands and Shear Solitons in Moiré Patterns of Twisted Bilayer Transition Metal Dichalcogenides. Phys. Rev. Lett. 2018, 121, 266401. 10.1103/PhysRevLett.121.266401. [DOI] [PubMed] [Google Scholar]
  12. Wu F.; Lovorn T.; Tutuc E.; MacDonald A. H. Hubbard Model Physics in Transition Metal Dichalcogenide Moiré Bands. Phys. Rev. Lett. 2018, 121, 026402. 10.1103/PhysRevLett.121.026402. [DOI] [PubMed] [Google Scholar]
  13. Watanabe K.; Taniguchi T.; Kanda H. Direct-bandgap properties and evidence for ultraviolet lasing of hexagonal boron nitride single crystal. Nat. Mater. 2004, 3, 404. 10.1038/nmat1134. [DOI] [PubMed] [Google Scholar]
  14. Wirtz L.; Marini A.; Grüning M.; Attaccalite C.; Kresse G.; Rubio A. Comment on ”huge excitonic effects in layered hexagonal boron nitride. Phys. Rev. Lett. 2008, 100, 189701. 10.1103/PhysRevLett.100.189701. [DOI] [PubMed] [Google Scholar]
  15. Attaccalite C.; Bockstedte M.; Marini A.; Rubio A.; Wirtz L. Coupling of excitons and defect states in boron-nitride nanostructures. Phys. Rev. B: Condens. Matter Mater. Phys. 2011, 83, 144115. 10.1103/PhysRevB.83.144115. [DOI] [Google Scholar]
  16. Attaccalite C.; Wirtz L.; Marini A.; Rubio A. Efficient Gate-tunable light-emitting device made of defective boron nitride nanotubes: from ultraviolet to the visible. Sci. Rep. 2013, 3, 2698. 10.1038/srep02698. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Paleari F.; Galvani T.; Amara H.; Ducastelle F.; Molina-Sánchez A.; Wirtz L. Excitons in few-layer hexagonal boron nitride: Davydov splitting and surface localization. 2D Mater. 2018, 5, 045017. 10.1088/2053-1583/aad586. [DOI] [Google Scholar]
  18. Ferreira F.; Chaves A.; Peres N.; Ribeiro R. Excitons in hexagonal boron nitride single-layer: a new platform for polaritonics in the ultraviolet. J. Opt. Soc. Am. B 2019, 36, 674–683. 10.1364/JOSAB.36.000674. [DOI] [Google Scholar]
  19. Dai S.; et al. Tunable Phonon Polaritons in Atomically Thin van der Waals Crystals of Boron Nitride. Science 2014, 343, 1125–1129. 10.1126/science.1246833. [DOI] [PubMed] [Google Scholar]
  20. Wu F.; Lovorn T.; MacDonald A. H. Topological Exciton Bands in Moiré Heterojunctions. Phys. Rev. Lett. 2017, 118, 147401. 10.1103/PhysRevLett.118.147401. [DOI] [PubMed] [Google Scholar]
  21. Tran K.; et al. Evidence for moiré excitons in van der Waals heterostructures. Nature 2019, 567, 71. 10.1038/s41586-019-0975-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Jin C.; Regan E. C.; Yan A.; Utama M. I. B.; Wang D.; Zhao S.; Qin Y.; Yang S.; Zheng Z.; Shi S.; Watanabe K.; Taniguchi T.; Tongay S.; Zettl A.; Wang F. Observation of moiré excitons in WSe 2/WS 2 heterostructure superlattices. Nature 2019, 567, 76. 10.1038/s41586-019-0976-y. [DOI] [PubMed] [Google Scholar]
  23. Seyler K. L.; Rivera P.; Yu H.; Wilson N. P.; Ray E. L.; Mandrus D. G.; Yan J.; Yao W.; Xu X. Signatures of moiré-trapped valley excitons in MoSe 2/WSe 2 heterobilayers. Nature 2019, 567, 66. 10.1038/s41586-019-0957-1. [DOI] [PubMed] [Google Scholar]
  24. Alexeev E. M.; et al. Resonantly hybridized excitons in moiré superlattices in van der Waals heterostructures. Nature 2019, 567, 81. 10.1038/s41586-019-0986-9. [DOI] [PubMed] [Google Scholar]
  25. Agapito L. A.; Curtarolo S.; Buongiorno Nardelli M. Reformulation of DFT+Uas a Pseudohybrid Hubbard Density Functional for Accelerated Materials Discovery. Phys. Rev. X 2015, 5, 011006. 10.1103/PhysRevX.5.011006. [DOI] [Google Scholar]
  26. Werner P.; Millis A. J. High-Spin to Low-Spin and Orbital Polarization Transitions in Multiorbital Mott Systems. Phys. Rev. Lett. 2007, 99, 126405. 10.1103/PhysRevLett.99.126405. [DOI] [PubMed] [Google Scholar]
  27. Lian B.; Wang Z.; Bernevig B. A. Twisted Bilayer Graphene: A Phonon Driven Superconductor. Phys. Rev. Lett. 2019, 257002. 10.1103/PhysRevLett.122.257002. [DOI] [PubMed] [Google Scholar]
  28. Choi Y. W.; Choi H. J. Strong electron-phonon coupling, electron-hole asymmetry, and nonadiabaticity in magic-angle twisted bilayer graphene. Phys. Rev. B: Condens. Matter Mater. Phys. 2018, 98, 241412. 10.1103/PhysRevB.98.241412. [DOI] [Google Scholar]
  29. Wu F.; Hwang E.; Das Sarma S. Phonon-induced giant linear-in-T resistivity in magic angle twisted bilayer graphene: Ordinary strangeness and exotic superconductivity. Phys. Rev. B: Condens. Matter Mater. Phys. 2019, 99, 165112. 10.1103/PhysRevB.99.165112. [DOI] [Google Scholar]
  30. Kennes D. M.; Lischner J.; Karrasch C. Strong correlations and d + id superconductivity in twisted bilayer graphene. Phys. Rev. B: Condens. Matter Mater. Phys. 2018, 98, 241407. 10.1103/PhysRevB.98.241407. [DOI] [Google Scholar]
  31. Kang J.; Vafek O. Strong Coupling Phases of Partially Filled Twisted Bilayer Graphene Narrow Bands. Phys. Rev. Lett. 2019, 122, 246401. 10.1103/PhysRevLett.122.246401. [DOI] [PubMed] [Google Scholar]
  32. Yuan N. F. Q.; Fu L. Model for the metal-insulator transition in graphene superlattices and beyond. Phys. Rev. B: Condens. Matter Mater. Phys. 2018, 98, 045103. 10.1103/PhysRevB.98.045103. [DOI] [Google Scholar]
  33. Koshino M.; Yuan N. F. Q.; Koretsune T.; Ochi M.; Kuroki K.; Fu L. Maximally Localized Wannier Orbitals and the Extended Hubbard Model for Twisted Bilayer Graphene. Phys. Rev. X 2018, 8, 031087. 10.1103/PhysRevX.8.031087. [DOI] [Google Scholar]
  34. Su Y.; Lin S.-Z. Pairing symmetry and spontaneous vortex-antivortex lattice in superconducting twisted-bilayer graphene: Bogoliubov-de Gennes approach. Phys. Rev. B: Condens. Matter Mater. Phys. 2018, 98, 195101. 10.1103/PhysRevB.98.195101. [DOI] [Google Scholar]
  35. Ochi M.; Koshino M.; Kuroki K. Possible correlated insulating states in magic-angle twisted bilayer graphene under strongly competing interactions. Phys. Rev. B: Condens. Matter Mater. Phys. 2018, 98, 081102. 10.1103/PhysRevB.98.081102. [DOI] [Google Scholar]
  36. Chittari B. L.; Leconte N.; Javvaji S.; Jung J. Pressure induced compression of flatbands in twisted bilayer graphene. Electronic Structure 2019, 1, 015001. 10.1088/2516-1075/aaead3. [DOI] [Google Scholar]
  37. Xu C.; Balents L. Topological Superconductivity in Twisted Multilayer Graphene. Phys. Rev. Lett. 2018, 121, 087001. 10.1103/PhysRevLett.121.087001. [DOI] [PubMed] [Google Scholar]
  38. Thomson A.; Chatterjee S.; Sachdev S.; Scheurer M. S. Triangular antiferromagnetism on the honeycomb lattice of twisted bilayer graphene. Phys. Rev. B: Condens. Matter Mater. Phys. 2018, 98, 075109. 10.1103/PhysRevB.98.075109. [DOI] [Google Scholar]
  39. Kötz R.; Carlen M. Principles and applications of electrochemical capacitors. Electrochim. Acta 2000, 45, 2483–2498. 10.1016/S0013-4686(00)00354-6. [DOI] [Google Scholar]
  40. Dhoot A. S.; Yuen J. D.; Heeney M.; McCulloch I.; Moses D.; Heeger A. J. Beyond the metal-insulator transition in polymer electrolyte gated polymer field-effect transistors. Proc. Natl. Acad. Sci. U. S. A. 2006, 103, 11834–11837. 10.1073/pnas.0605033103. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Shimotani H.; Asanuma H.; Tsukazaki A.; Ohtomo A.; Kawasaki M.; Iwasa Y. Insulator-to-metal transition in ZnO by electric double layer gating. Appl. Phys. Lett. 2007, 91, 082106. 10.1063/1.2772781. [DOI] [Google Scholar]
  42. Ueno K.; Nakamura S.; Shimotani H.; Ohtomo A.; Kimura N.; Nojima T.; Aoki H.; Iwasa Y.; Kawasaki M. Electric-field-induced superconductivity in an insulator. Nat. Mater. 2008, 7, 855. 10.1038/nmat2298. [DOI] [PubMed] [Google Scholar]
  43. He B.; Zhang W. J.; Yao Z.; Chong Y.; Yang Y.; Ye Q.; Pan X.; Zapien J.; Bello I.; Lee S.; Gerhards I.; Zutz H.; et al. Hofsäss, p-type conduction in beryllium-implanted hexagonal boron nitride films. Appl. Phys. Lett. 2009, 95, 252106. 10.1063/1.3276065. [DOI] [Google Scholar]
  44. Dahal R.; Li J.; Majety S.; Pantha B.; Cao X.; Lin J.; Jiang H. Epitaxially grown semiconducting hexagonal boron nitride as a deep ultraviolet photonic material. Appl. Phys. Lett. 2011, 98, 211110. 10.1063/1.3593958. [DOI] [Google Scholar]
  45. Nose K.; Oba H.; Yoshida T. Electrical conductivity of boron nitride thin films enhanced by in situ doping of zinc. Appl. Phys. Lett. 2006, 89, 112124. 10.1063/1.2354009. [DOI] [Google Scholar]
  46. Oba F.; Togo A.; Tanaka I.; Watanabe K.; Taniguchi T. Doping of hexagonal boron nitride via intercalation: A theoretical prediction. Phys. Rev. B: Condens. Matter Mater. Phys. 2010, 81, 075125. 10.1103/PhysRevB.81.075125. [DOI] [Google Scholar]
  47. Ju L.; Velasco J. Jr; Huang E.; Kahn S.; Nosiglia C.; Tsai H.-Z.; Yang W.; Taniguchi T.; Watanabe K.; Zhang Y.; G Z.; Crommie M.; Zettl A.; Wang F. Photoinduced doping in heterostructures of graphene and boron nitride. Nat. Nanotechnol. 2014, 9, 348. 10.1038/nnano.2014.60. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

nl9b00986_si_001.pdf (719.4KB, pdf)

Articles from Nano Letters are provided here courtesy of American Chemical Society

RESOURCES