Abstract
Many computational models for analyzing and predicting cell physiology rely on in vitro data collected in dilute and controlled buffer solutions. However, this can mislead models because up to 40% of the intracellular volume—depending on the organism, the physiology, and the cellular compartment—is occupied by a dense mixture of proteins, lipids, polysaccharides, RNA, and DNA. These intracellular macromolecules interfere with the interactions of enzymes and their reactants and thus affect the kinetics of biochemical reactions, making in vivo reactions considerably more complex than the in vitro data indicates. In this work, we present a new, to our knowledge, type of kinetics that captures and quantifies the effect of volume exclusion and other spatial phenomena on the kinetics of elementary reactions. We further developed a framework that allows for the efficient parameterization of these kinetics using particle simulations. Our formulation, entitled generalized elementary kinetics, can be used to analyze and predict the effect of intracellular crowding on enzymatic reactions and was herein applied to investigate the influence of crowding on phosphoglycerate mutase in Escherichia coli, which exhibits prototypical reversible Michaelis-Menten kinetics. Current research indicates that many enzymes are reaction limited and not diffusion limited, and our results suggest that the influence of fractal diffusion is minimal for these reaction-limited enzymes. Instead, increased association rates and decreased dissociation rates lead to a strong decrease in the effective maximal velocities Vmax and the effective Michaelis-Menten constants KM under physiologically relevant volume occupancies. Finally, the effects of crowding were explored in the context of a linear pathway, with the finding that crowding can have a redistributing effect on the effective flux responses in the case of twofold enzyme overexpression. We suggest that this framework, in combination with detailed kinetics models, will improve our understanding of enzyme reaction networks under nonideal conditions.
Significance
Kinetic models are essential for understanding and designing biochemical and biophysical processes in living organisms. Currently, kinetic models rely on the in vitro characterization of biochemical reactions, although intracellular reactions are taking place in crowded, nonideal conditions. The interactions of the enzymes and their reactants with other macromolecules in a cell alter the enzyme kinetics significantly, but little has been done to model and quantify the impact of these interactions on the in vivo reaction rates. We present a computational framework that allows us for the first time, to our knowledge, to estimate the in vivo apparent kinetic parameters of an enzyme that follows Michaelis-Menten kinetics. Interestingly, crowding conditions similar to those in Escherichia coli can reduce the maximal enzyme activity 10-fold.
Introduction
The intracellular environment is a crowded place, with ∼20–40% of the interior volume of living cells occupied by a variety of macromolecules, including proteins, RNA, DNA, and lipids (1, 2). The composition of this mixture depends considerably on the organism, the cell type, and its environment, but even within the cell, the local density and size distribution of the macromolecules varies between and within compartments (3, 4, 5). Because the presence of these macromolecules can impact diffusion rates, protein conformation, folding and aggregation, catalytic rates, and enzyme-substrate affinities (6, 7, 8), an alteration in the elementary properties governing the spatiotemporal dynamics of cells can affect all cellular functions, such as expression, translation signaling, and metabolism. Because many of these cellular functions depend on specific reactions catalyzed by cellular enzymes, it is necessary to study the effect of macromolecular crowding on the function of enzyme-catalyzed reaction systems, and to do this, it is necessary to characterize the kinetics of these systems under the altered conditions.
Computational models are used to analyze and predict cell physiology, though computational studies are limited in their frequent reliance on in vitro characteristics to directly parameterize their models (9, 10), reduce uncertainty (11, 12), or to evaluate predicted parameters (13). This results in the actual enzyme in vivo characteristics not being captured such that the model predictions from these studies might deviate significantly from the ones measured in vitro. This is especially true considering that in vitro characterizations are usually performed in dilute, homogenous conditions, whereas reactions in the cytoplasm occur in an inhomogeneous and densely packed environment (14).
The relevance of environmental impact on enzyme kinetics is therefore an important topic of study, especially in terms of crowding in the densely packed intracellular space. In early studies of crowded enzyme catalysis, it was believed that the main effect of diffusion-limited Michaelis-Menten kinetics was caused by altered, anomalous diffusion accompanied by increased effective concentrations. These studies were limited, however, in that volume exclusion effects caused by the reactive partners themselves were often neglected, which results in the change in activity due to interaction with macromolecules not being captured (15, 16, 17, 18). A more recent work on the subject was presented by Mourao et al., in which fractal behavior, indicating that the diffusion and the apparent order of the elementary reactions is altered, was studied using a lattice-based model for an irreversible Michaelis-Menten mechanism. They showed that fractal kinetics only occur under very restrictive conditions, suggesting that it might be less common than previously assumed (19).
Further recent work has shown that the effective rate constant for bimolecular reactions changes under crowded conditions (20, 21). Berezhkovskii and Szabo demonstrated that it is possible to express the effective rate for bimolecular reactions as a function of a crowding-induced interaction potential between two reaction partners, which results from an interaction with the surrounding particles when two reactants are in contact. Repulsive interactions between the reactants and particles would, therefore, result in an attractive effective potential between the reactants and vice versa. Relatedly, it has been shown that for rate-limited reactions, the influence of diffusion is minimal, indicating that the effective crowding-induced interaction potential might be more dominant for some enzymatic reactions (22).
Because of its importance in modeling in vivo systems, the effects of crowding on biochemical reactions have been extensively studied by various computational and experimental methods, as seen in several reviews (1, 2, 23). Most of the effort in these studies has been directed toward investigating the impact of diffusion in fractal media on the reaction kinetics (22), with little focus on characterizing the effect of crowding on the mean effective enzyme kinetics. However, because it has now been shown that in vitro, some enzymes might not be limited by their translational diffusion but by their apparent association rate constants (24, 25, 26, 27, 28), the reevaluation of crowding in these reactions is important. In this work, therefore, we introduced computational methods for studying spatial effects of any kind, applying our work to the effects of crowding on reaction-limited enzymes with the goal of bridging the discrepancy between the in vitro measurement of kinetic parameters and the actual in vivo conditions. The proposed method will also allow for studying the differences in the impact of spatial effects for single reactions and for integrated reaction networks. Although the scope of this work is the study of a reaction-limited system, we further evaluated the performance of the proposed method for a simple system under diffusion-limited conditions.
In contrast to the previous studies on the Michaelis-Menten kinetics, which used a diffusion-limited irreversible reaction scheme, we studied the effect of crowding on enzyme kinetics by employing a fully reversible reaction scheme and present herein an example with a representative catalytic activity and affinities that result in a reaction-limited enzyme. Additionally, our molecular particle model accounts for volume exclusion and the diffusion of all species, including reactants and crowding agents, and this was used to study the effect of different size distributions of crowding agents on reaction kinetics.
Previous studies on crowding conditions were often limited by their computational cost and lack of global insight into the sensitivity of the reaction kinetics or are missing a direct connection to the first physical principles. They often use spatial simulation techniques to simulate multiple realizations of reaction trajectories to determine the influence on the effective kinetics under very specific conditions, meaning that these studies only gain insight into the local sensitivity of the kinetics with respect to the crowding conditions. Furthermore, it is computationally very expensive to resolve the reaction trajectories from particle simulations for reaction-limited reactions because the timescale to resolve the diffusion of the particle is up to seven orders of magnitude faster than the reaction timescale. This requires billions of time steps to be solved for tens of thousands of particles, resulting in a month of simulation time for a single trajectory (29). An effective approach to reduce the computational complexity of the Brownian is the crowder-free formulation of the Cichocki-Hinsen algorithm (30), which has been validated for homogenous and locally homogenous crowding conditions (31). Whether the validity of the homogenous or local homogenous crowding assumption holds for inert molecules with a diverse size distribution remains to be examined and shall be discussed elsewhere. Another way to overcome the computational challenges is mesoscopic formulations based on the reaction-diffusion master equation (32, 33). These formulations require additional models to capture the microscopic effect of obstacles on the macroscopic rate constant, meaning that they can capture the effect of obstacles on the apparent transport coefficient but need additional models to capture how the microscopic collision dynamics are altered.
In the work presented here, we resolve these challenges with a new, to our knowledge, formulation entitled generalized elementary kinetics (GEEK). The formulation allows us to characterize kinetic mechanisms that are influenced by various spatial effects, including volume exclusion, confinement (one-dimensional/two-dimensional diffusion), strong and weak interaction forces, localization, or any combination of similar phenomena. In this work, we use a coarse-grained particle model based on HSRB to parameterize this formulation, which can be used in a straightforward way to build ordinary differential equation (ODE) models that use power-law approximations to capture the characteristics of spatial effects and to directly quantify the impact of fractal diffusion. The formulation presented here is achieved by a regression model that is trained from data governed by simulating the microscopic diffusion and collisions from the first physical principle. For the workflow, any kind of simulation algorithm with single molecule detail can be used. Possible alternatives are, for example, the Cichocki-Hinsen algorithm (30), the reaction Brownian dynamic algorithm (34), the Green’s function reaction dynamics algorithm (35), smoldyn (36), or Readdy (37). In this work, we used an algorithm that combines hard-sphere Brownian dynamics (38) and Brownian reaction dynamics (39, 40, 41, 42).
We applied our method to the investigation of macromolecular crowding on the function of phosphoglycerate mutase (PGM) in Escherichia coli. Our example clearly demonstrates that accounting solely for an increased local concentration and anomalous diffusion is not sufficient to properly describe crowding effects. We show that a mechanism-dependent effect emerges upon crowding that is facilitated by an increase in both product and substrate association activity and a decrease in the dissociation activity. For reversible Michaelis-Menten kinetics, these effects result in an increase in the binding affinity for the product and substrate as well as a decrease in the maximal reaction rate. Finally, we investigated the effects of crowding on a linear pathway, in which we show that crowding can significantly redistribute the relative flux responses with respect to enzyme overexpression, indicating that the impact of altered kinetics is also propagated on a network level.
Methods
Reversible Michaelis-Menten kinetics
In this study, we primarily investigated a reversible Michaelis-Menten reaction mechanism, in which a substrate S binds to an enzyme E to form a complex ES via a reversible reaction, which can reversibly transform the substrate and reversibly dissociate the product P. The overall reaction scheme is given by
| (1) |
where k1,f, k1,b, k2,f, and k2,b denote the rate constants of the elementary reactions. The typical form of the reaction rate v as a function of substrate and product concentrations (see Eq. 2) is derived from the assumption that all enzymes are conserved such that [ES] + [E] = [ET], where [ET] denotes the total enzyme concentration and the enzyme-substrate complex concentration [ES] is in a quasi-steady state, i.e., d[ES]/dt ≈ 0 (43):
| (2) |
where the parameters , , KM,S, and KM,P are related to the elementary rate constants k1/2,f/b given an [ET]:
| (3a) |
| (3b) |
| (4a) |
| (4b) |
The equilibrium constant of the system is then
| (5) |
Geek
By introducing inert molecules, we observe an alteration of the effective rate constants due to a change in the diffusion and the collision dynamics. In the most general case, this can, compared to mass-action kinetics, result in a change of the effective order and effective rate constant. Berezhkovskii and Szabo showed that the effective (Collins-Kimball) reaction rate constant kCK for a diffusion-influenced, bimolecular reaction under crowded conditions can be expressed in terms of an altered diffusion constant D1 and an external crowding-induced interaction potential ΔU between the two reacting species. This potential is an implicit representation of the interaction of the individual reactant species with the molecules in their environment and whether these interactions keep the reactants in contact or if they are tearing them apart. The expression for the Collins-Kimball rate constant was found to follow that described by Berezhkovskii and Szabo (20):
| (6) |
where k0 is the reaction rate upon collision. For the reaction-limited case , this expression simplifies to an exponential relation, kCK ≈ k0exp(ΔU/kBT). In general, the induced interaction potential ΔU and the diffusion constant D1 are a function of the global state of the system, which includes concentrations and intermolecular interactions.
To approximate this deviation of the effective elementary rate constants—indicated by kj,eff, where j ∈ [(1, f), (1, b), (2, f), (2, b)]—from the free rate constants in ideal conditions, kj,0 in a general form, the logarithmic deviation ζj was introduced:
| (7) |
To quantify this deviation as a function of the species’ concentrations, a linear function of the scaled logarithmic concentrations log([Xi]/[Xi]0) was introduced and tested for ζj:
| (8) |
where αi,j are the coefficients quantifying the effect of one of the N reactants Xi on reaction j and βj is an offset attributed to the effect of different occupied volume fractions.
The effective reaction rate is thus given by
| (9) |
From this expression, a generalized mass-action rate law is defined for the elementary reactions:
| (10) |
where ni,j denotes the stoichiometric coefficient of the substrate Xi in reaction j. The generalized elementary mass-action rate law (10) can be directly used to create a system of ODEs that can approximate the time evolution of the system under nonideal conditions.
Generalized elementary Michaelis-Menten kinetics
Given the generalized elementary rate laws, the quasi-steady-state approximation for the Michaelis-Menten reaction rate with GEEK can be defined. Therefore, it can be assumed that the enzyme is conserved, [ES] + [E] = [ET], and the enzyme complex is in a quasi-steady state, i.e.,
| (11) |
where each flux vj is given by a generalized rate law as given in Eq. 10. For the case of and , it is not possible to obtain an explicit expression for the reaction rate vnet,qss. To calculate the amount of enzyme-substrate complex in the quasi-steady state for a given [ET], [S], and [P], the conservation relation [E] = [ET] − [ES] is introduced, and the resulting nonlinear equation Eq. 11 is solved numerically for the steady-state enzyme concentration [ES]qss using nsolve from the Python package sympy. The numerical solution is obtained using the reference concentration [ES]0 as an initial guess for the nonlinear solver. The reaction rate of the enzymatic reaction at steady state, for a set of constant [S] and [P], is then given by the net reaction rate of product formation at steady state:
| (12) |
where [ES]qss is the enzyme-complex concentration at the quasi-steady state. The average apparent Michaelis-Menten parameters are then extracted using a linear approximation of v([X]) with v([X])/[X] for either [S] = 0 or [P] = 0, i.e., the Eadie-Hofstee form of Michaelis-Menten kinetics (44, 45). The slope of these linear regressions yields the respective KM, and the y axis intercept yields the respective Vmax:
| (13) |
To express the thermodynamic driving forces, the elementary rate model was considered as M reversible reactions ρ ∈ [1, 2], with the forward flux vρ,f and the backward flux vρ,b. Using the principle of detailed balance, the free energy of the reaction can be expressed as a function of the displacement from equilibrium Γ = vb/vf (46):
| (14) |
where R is the general gas constant and T is the absolute temperature. With the fluxes expressed in terms of the generalized elementary rate law (10), the free energy reads
| (15) |
In general, the overall free energy consists of ideal and nonideal contributions. The ideal contribution consists of the standard free energy of the reaction and the concentration contributions, and the nonideal contribution contains terms emerging from molecular interactions, such as by steric repulsion, van der Waals forces, electrostatic interactions, or nonspecific attractions.
| (16) |
In this work, only the nonideal contributions due to steric repulsion were modeled by means of a hard-sphere potential, though in the most general case, the formulation presented in this work allows for the inclusion of any kind of nonideal contribution. The presented approach shows that a power-law approximation suffices to describe the effect of steric repulsion. The approximation of the effect of nonspecific attractions and other interactions in terms of kinetic parameters and free energies will probably require alternative functional forms in these approximations in addition to this power-law formulation. A functional to account for the approximation of nonspecific attractions could be based on the derivations of Kim and Mittal (47).
By comparing the free energy of the generalized elementary rate model to the free energy of the dilute mass-action equivalent, the ideal contribution can be identified as
| (17) |
The remaining contributions can be identified as the nonideal contribution:
| (18) |
can be further partitioned into a reactant-independent and a reactant-dependent contribution:
| (19) |
The free energy of the generalized elementary Michaelis-Menten kinetics is given by the sum of all reversible-reaction free-energy contributions :
| (20) |
With [Xi] = [[S], [E], [ES], [P]], the free energy of the reaction can be simplified to the well-known ideal contribution containing only the chemically modified species [S] and [P] as well as a nonideal contribution, wherein the nonideal contribution is a phenomenological description of free-energy change based on the GEEK.
| (21) |
The formulation of the reversible Michaelis-Menten rate law in terms of GEEK allows for the phenomenological capture of nonlinear effects on the collision level.
Hard-sphere Brownian reaction dynamics
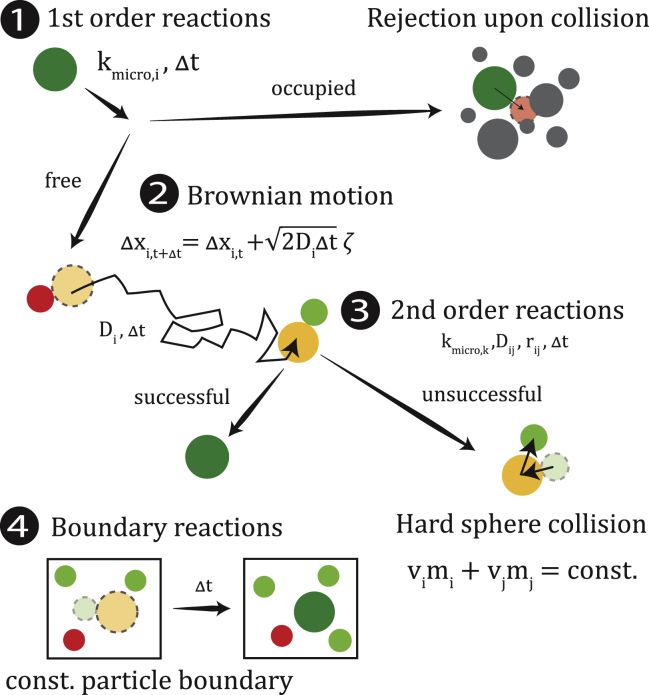
To incorporate the spatial effects into the enzymatic reaction system, hard-sphere Brownian reaction dynamics (HSBRD) were used. This method is using the elastic hard-sphere Brownian dynamics algorithm (38) to compute the transport and the collisions dynamics of the particles and implement reactions according to the Brownian dynamics algorithm (39, 40), see Fig. 1. Similar methods combining these two approaches have been presented by Wilson et al. (41) and Kim et al. (42).
Figure 1.
Individual algorithm steps of the molecular particle model. 1) First-order reactions are determined by a probabilistic success rate depending on the microscopic reaction rate per molecule kmicro,i and the time step Δt. 2) The Brownian motion for every molecule is determined by its individual diffusion coefficient Di. 3) For second-order reactions, success is determined upon collision given the microscopic reaction, the sum of the diffusion coefficient Dij = Di + Dj, the sum of the radii of the colliding particles rij = ri + rj, and the time step (24). 4) Boundary reactions are given as constant particle boundaries, wherein the removal or insertion of particles is done if the number of particles deviates from the given boundary condition.
The method describes the movement of independent particles as a random walk of point particles diffusing in a viscous medium. Thereby, HSBRD neglects the hydrodynamic interactions between the particles. The equations of motion are given in terms of the overdamped Langevin equation. Using the Einstein-Smoluchwoski relation, its velocity is given by Wang and Uhlenbeck (48):
| (22) |
where is a force acting on the particle, kB is the Boltzmann constant, T is the absolute temperature of the surrounding fluid, and is the result of a three-dimensional Wiener process. An explicit Euler formulation was used to update the positions at every time step, Δt, as follows:
| (23) |
where ηt is a random vector drawn from a normal distribution.
When two reactants collided, i.e., their radii overlapped after the positions were updated, a uniform distributed random number r was compared to the reaction with a probability p to determine if the reaction occurred within this time step Δt. The probability p was determined by the microscopic reaction rate kj,micro (34):
| (24) |
where I(D, R, Δt) is a normalization factor for the effective collision volume in Brownian reaction dynamics simulations to account for all possible diffusion path within Δt, as derived by Morelli and ten Wolde (34). Using the relation derived by Collins and Kimball, the observed steady-state reaction rate kj,0 for a bimolecular reaction, j ∈ [(1, f), (2, b)] with educts A and B, in homogenous, dilute conditions is related to its microscopic or transition rate constant kj,micro and the diffusion-limited reaction rate constant γj = 4π(DA + DB)(rA + rB) (49). Assuming that the Collins-Kimball rate constant corresponds to the observed rate constant in the experimental in vitro system and the dilute particle simulation, the corresponding microscopic rate constant can be expressed as a function of the rate constant observed in vitro kj,0 and the diffusion-limited rate constant γj, calculated based on the molecular properties of the collision radii rA, rB and self-diffusion constants DA, DB:
| (25) |
In the case of a particle collision without a subsequent reaction, an elastic hard-sphere collision was assumed to take place. The new particle position was computed from the momentum conservation using the average velocity of the move that led to the particle overlap (38).
First-order reactions, j ∈ [(1, b), (2, f)], are modeled similarly to bimolecular reactions by comparing a uniformly distributed random variable to the probability that the reaction took place in the time interval Δt, with the reaction probability of p = 1 − exp(−kj,microΔt). The reaction products are placed in contact around the original position of the educt using a random orientation. If the products were to collide with any other particles, the move would be rejected, and the educt would remain at its original position. Otherwise, the educt would be removed, and the products would be placed instead.
Furthermore, constant particle boundary conditions were applied at every time step through the random insertion or removal of particles of a given species to match the specified particle count of the species. The HSBRD particle simulation was implemented in C++ using the OPENFPM framework (50).
Measuring effective rate constants
Because it is necessary to resolve the particle movement on the nanosecond timescale as opposed to the timescales of the reaction dynamics, which are found to be on the order of seconds to hours, a separated timescale approach was proposed to efficiently bridge these differences. The effective elementary reaction rates at constant concentrations and crowding conditions in particle simulation were therefore measured. To measure the effective rate constants from a particle simulation, two separate schemes for monomolecular and bimolecular rate constants were proposed.
For monomolecular rate constants, j ∈ [(1, b), (2, f)], the effective reaction rates were extracted by probing the space around the enzyme-substrate complexes. Therefore, for every valid educt molecule k of a monomolecular reaction j, L dissociation reactions were attempted with a random orientation. For each molecule k and reaction j, the success of the l-th attempt ωjkl is determined. If the dissociation were to be successful, meaning that the dissociated particles would not collide, ωjkl = 1. If the dissociation were to yield a collision, ωjkl = 0. Averaging over the results of all dissociation attempts ωjkl of the probed molecule k, a local success probability of was obtained. To describe the equivalent homogenous system, the reaction success probability was computed as the mean of the local average success rate over all N probed particles:. In the limit of continuous concentrations, the effective rate constant, keff,j, is given by the rate constant k0,j scaled by the reaction success probability ωj:
| (26) |
The effective bimolecular rate constants, j ∈ [(1, f), (2, b)], can be extracted from the effective collision frequency zA,B between the two educts A and B of reaction j. This collision frequency is estimated as the number of collisions between A and B in an integration time interval cA,B(t, t + Δt) per time step Δt:
| (27) |
Given the probability of a reactive collision (Eq. 24), the effective bimolecular rate constant can be measured as the mean collision frequency per number of possible interactions pairs, i.e., NANB, scaled by the fraction of successful collisions within a measurement time interval Δt:
| (28) |
Modeling framework
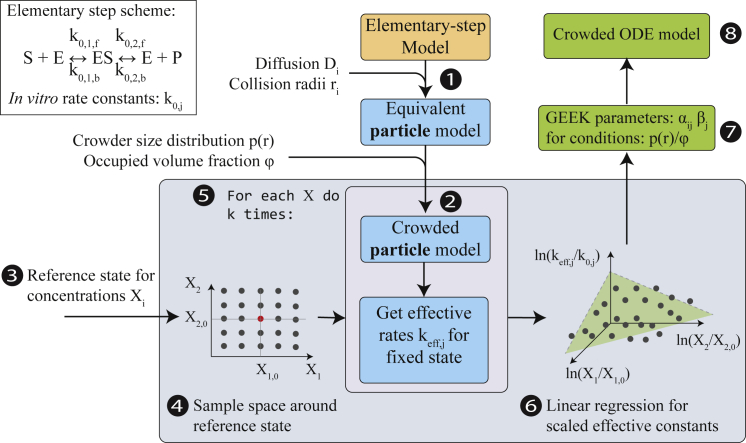
In this work, we propose a new, to our knowledge, simulation framework using the above-described concept of GEEK. In our simulation framework, an equivalent particle model is first created from an elementary step mechanism (Fig. 2, part 1). To create an equivalent particle model, only the elementary reactions of the enzyme mechanism are required. If only phenomenological constants, e.g., parameters for the quasi-steady-state approximation, are given for the enzymatic reaction, it is necessary to map these to the elementary reaction rate constants. Furthermore, all species involved in the elementary reaction properties need to be assigned to describe their molecular movement, i.e., a diffusion coefficient, a collision radius, and a mass. Given the molecular data, the rate constants of the particle model are matched with the rate constants of the elementary step model with the assumption that the measured or calculated rate constants were measured in homogenous, dilute conditions. In the case of monomolecular reactions, the observed rate constants are then equivalent to the microscopic transition rates. For bimolecular reactions j ∈ [(1, b), (2, f)], the diffusion-limited rate constant γj is first computed based on the diffusion coefficients and collision radii and then matched to the effective reaction rate of the dilute, homogenous particle system with the rate constant in the elementary step model by adapting the corresponding microscopic rate constant kj,micro using Eq. 25. A volume that is large enough to capture the local bulk properties of a locally well-mixed enzyme-substrate system is then chosen such that the number of particles of each species in the system is large enough to discretize the concentration space of interest.
Figure 2.
Modeling framework for crowded generalized elementary kinetics (GEEK). The input for the modeling framework is an arbitrary elementary step model containing in vitro data for the enzyme kinetics. 1) This model is then translated into an equivalent in vitro particle model of the enzymatic reaction. 2) The space is filled with inert molecules that are drawn from a size distribution p(r) until the fraction ϕ of the simulation space is occupied. 3) A reference concentration state is then chosen for the GEEK model, and 4) the space around the concentration space is sampled. 5) The k particle model realizations are then simulated for each concentration sample, i.e., repeat step 2 and simulate. 6) From the resulting particle traces, the effective rate constants are measured from the particle collision frequencies and the locally available volume. 7) These effective reaction rate constants are log transformed, and a linear regression is performed with respect to the scaled logarithmic concentrations. The output of the linear regression directly links to the GEEK parameters; see Eqs. 7 and 8. 8) Finally, the GEEK model can approximate the crowded kinetics using ODEs. To see this figure in color, go online.
In the second step, the system is perturbed on the microscopic level to investigate the influence of crowding (Fig. 2, part 2). Therefore, inert particles are introduced into the system that therefore alter effective particle interactions between the reactive species (20). To model a realistic crowding environment, a size distribution function p(r) is estimated from the mass distribution p(Mw) and an empirical mass size relation,, with Mw in [Da], as reported for proteins in E. coli by Kalwarczyk et al. (51). The simulation volume is then populated with inert molecules by randomly drawing collision radii from the size distribution until the specified inert volume fraction ϕ is reached. The diffusion constant of the individual species is then calculated using the Stokes-Einstein relation, assuming that the hydrodynamic radius is equal to the collision radius:
| (29) |
where rhyd is the hydrodynamic radius and η is the dynamic viscosity.
Next, the model is sampled around a chosen reference state (Fig. 2, parts 3 and 4). In this work, we chose to generate our sample with a full-factorial design. For each concentration sample, a particle simulation is performed where the effective rate constants keff,j are measured for every elementary reaction as described in the previous section (Fig. 2, part 5).
Subsequently, multivariate linear regression is used to estimate the mean GEEK parameters αij and βj for the specified crowding conditions (Fig. 2, part 6). Finally, the GEEK, as described above, is used to analyze the response behavior of an equivalent crowded ODE-enzyme model (Fig. 2, part 7).
Weighted linear regressions
To estimate the GEEK parameters using multivariate regression, a multivariate regression was performed. Because the variance of the reaction rate would be expected to be dependent on the regression variables, a weighted linear regression was performed to avoid fitting data with large heteroscedasticity (see Supporting Materials and Methods). The conditional variance of the residuals was therefore extracted, and a weighted linear regression was performed in which each observation was weighted by the inverse of the conditional variance of the residual. To perform these calculations, the Python package statsmodels was used (52).
Computational details
The Brownian reaction dynamics simulations were performed with a time step Δt of 0.25 ns. The dynamics viscosity of the liquid between the particles was assumed to be water with 0.7 Pa s at T = 310.15 K. The system is considered to be isothermal (T = constant). At each time step, all possible first-order reactions are attempted L = 100 times. For the regression input space, all combinations of substrate and product concentrations that were n-fold increased and decreased with respect to the reference concentration of [S]0 = [P]0 = 49 μM were used, with n ∈ [1, 2, 3, 4, 5], in combination with all free-enzyme and enzyme-complex concentrations that yielded saturations of σ = [ES]/[ET] = [0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9] given a total amount of enzyme [Etot] = [ES] + [E] = 64 μM. Each sampled concentration state is simulated 1 μs, where the first 0.1 μs are discarded. Furthermore, 10 independent realizations of the crowding population were used for every concentration sample to capture the variability that comes from differently sized crowding agents drawn from the size distribution.
Results and Discussion
To address the pitfalls currently associated with computational studies of enzymatic reactions in the intracellular space, this work presents GEEK, a novel, to our knowledge, approach to capture spatial effects, such as crowding, in ODE models. The framework is available in the form of two Python packages: a package to implement GEEK expressions into ODE (https://github.com/EPFL-LCSB/geek) and a package to perform openfpm-based HSBRD simulations (https://github.com/EPFL-LCSB/openbread). The GEEK formulation directly quantifies the deviation from dilute mass-action behavior in a systematic and efficient procedure, and we have focused our studies on the impact of crowding due to the influence of densely packed biomolecules on enzyme reaction rates in vivo.
We validate the GEEK framework by comparing 1) an HSBRD-based GEEK model with the exact solutions obtained by HSBRD and 2) a GEEK model based on the crowder-free Cichocki-Hinsen algorithm with the respective solution of the full simulation (see Supporting Materials and Methods). We therefore used the initial rate experiment of a simple association-dissociation system. We simulated this system in dilute conditions and with single-sized inert molecules, r = 2.1 nm, for volume fractions between ϕ = 0.0 andϕ = 0.4. We show that for this reaction system, the GEEK models are able to capture the dynamics and the impact of crowding on the dynamics as predicted by the respective full simulation of the system (see Figs. S4–S7). We further discuss the results of 1 and 2 with respect to their modeling assumptions (see Fig. S8; Supporting Materials and Methods).
We then applied the described modeling framework to investigate the effects of macromolecular crowding on the enzymatic activity of PGM in E. coli. PGM is part of the lower glycolysis pathway and functions by reversibly transforming 3-phospho-D-glycerate (g3p) into 2-phospho-D-glycerate (g2p). We use PGM for our investigation because it exhibits a prototypical reversible Michaelis-Menten kinetics and its in vitro kinetics are well-known (53).
Impact of crowding on the elementary reaction level
For our reference elementary step mass-action model, which will serve as a basis for constructing the GEEK model, we calculated the elementary rate constants by the relations given in Eqs. 3, a and b and 4, a and b from the in vitro Michaelis-Menten parameters measured by Fraser et al. (Table 1; (53)). Based on this in vitro elementary step model, we built an equivalent in vitro particle model that required additional information on the molecular parameters, including mass, diffusion, and collision radius, of all the species involved in a reaction, meaning the substrates, products, free enzymes, and enzyme complexes. To estimate the collision radius of the enzyme and the enzyme-substrate complex, we followed the suggestions of Gameiro et al. and used the empirical relation between mass and size to estimate the inert molecule size from the enzyme mass (51, 54). In the same way, we applied the Stokes-Einstein relation to calculate the diffusion constants from the collision radius. We additionally assumed that the enzyme-substrate complex entirely enclosed the substrate with its binding pocket, thus rendering the collision radius of the complex and enzyme equal. To estimate the collision radius of g3p and g2p, we also followed the suggestions of Gameiro et al. and used the method developed by Zhao et al. to estimate their van der Waals volume and to calculate the equivalent sphere radius (54, 55). The diffusion constants of g2p and g3p were obtained from the literature (56). All molecular properties are summarized in Table 2.
Table 1.
In Vitro Michaelis-Menten Parameters and Calculated Elementary Rate Constants for PGM in E. coli
Table 2.
Molecular Properties of the Reacting Particles
Given the effective elementary rate constants and the molecular properties of the species, we calculated the effective microscopic rate constants using the relation given in Eq. 25 (Table 3). Comparing the microscopic rate constants in Table 3 with the diffusion-limited rate constants, it can be seen that the diffusion-limited constants γ1,f = γ2,b = 3.88 × 1010 M−1 s−1 are about five orders of magnitude higher than the microscopic reaction constants. This indicates that the microscopic binding process is much slower than the diffusion process and that the kinetics are reaction limited and not diffusion limited. Thus, the mean time until the first collision between two reactants, i.e., the mean first passage time, is orders of magnitudes shorter than the mean time to the first reaction. For a reaction to be successful, tens of thousands of collisions are occurring; hence, the impact of any increase in high-frequency first passage events due to fractal diffusion is limited (22).
Table 3.
Microscopic Reaction Rates per Reacting Particle, per Collision, and Diffusion-Limited Rate Constants of the Bimolecular Reactions
| Microscopic Rate Constants | |
|---|---|
| k1,f (c) | 1.57 × 105 s−1 M−1 |
| k1,b (p) | 10 s−1 |
| k2,f (p) | 22 s−1 |
| k2,b (c) | 3.40 × 105 s−1 M−1 |
p, particle; c, collision.
To build a GEEK model that allows us to characterize the enzyme kinetics in a crowded environment, we sampled the concentration space. This was done using a full-factorial design, allowing us to study the effect of several variables on the response output, as well as interactions between those variables, that sampled both the product and substrate concentrations as well as different enzyme saturation levels, indicating the percentage of bound enzyme with respect to the total enzyme concentration. The computational details of the simulation procedure are summarized in the respective method subsection above.
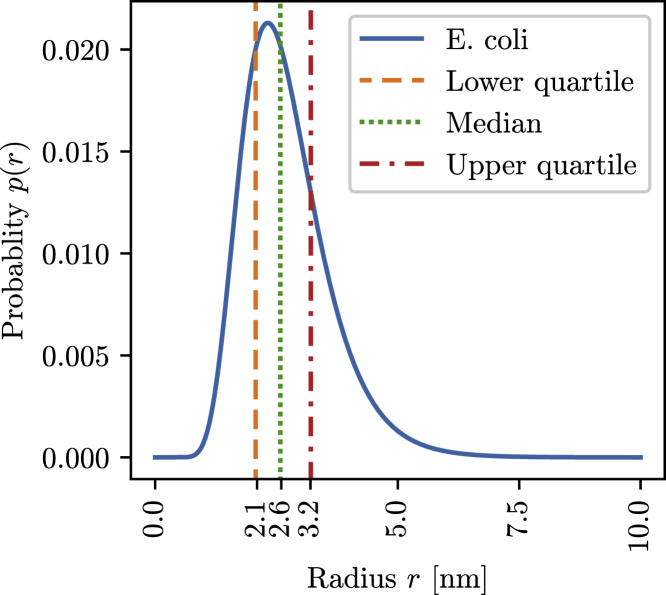
In total, we generated 21 generalized elementary kinetic models for five different inert volume fractions ϕk and four different size distributions pk(r), plus one without any crowding. This allowed for a detailed comparison of the effects of the volume fraction and size distribution of the crowding agents on enzyme kinetics. For the size distributions, we used 1) the E. coli distribution derived from Kalwarczyk et al., 2) a population containing only particles of the median size of the E. coli distribution, 3) a population the size of the upper quartile of the E. coli size distribution, and 4) a population the size of the lower quartile (Fig. 3; (51)). These crowding populations were each investigated for inert volume fractions of ϕ ∈ [0.0, 0.1, 0.2, 0.3, 0.4, 0.5].
Figure 3.
Size distribution function of the inert particles, numerically calculated from the mass distribution and empirical mass size relation as reported for proteins in E. coli by Kalwarczyk et al. (51). To see this figure in color, go online.
For each crowding condition, we estimated the mean GEEK parameters αij and βij using multivariate weighted linear regression, which indicate conditions that likely influenced the enzyme kinetics. To further quantify the uncertainty of the mean GEEK parameters, the 95% confidence intervals of the regression results are given in Table 4. For parameter estimates with a p-value ≥ 0.05, it was assumed that no significant correlation existed, and these parameters were not accounted for in the GEEK model. A closer analysis shows that the offset βj could always be determined with statistical significance; only some of the coupling parameters αij were not be able to be determined with the required significance level. Excluding a coupling relation from Eq. 9 corresponds to αij = 0. Note that this mean GEEK parameter model assumes that the crowding composition of an average cell is given by the average effect of a crowding configuration on the rate constant, which should accurately reflect the mean behavior of cell populations. Further, it should be taken into account that the calculations leading to the effective rate constants are based on the assumption of the microscopic model, considering that effective association rate constants are proportional to the collision frequency of their educts and that effective dissociation reaction constants are proportional to the surface accessible to the products. The validity of the GEEK approximation is therefore always dependent on the validity of the underlying microscopic model used to compute the effective rate constants. As mentioned in the Introduction, the workflow within the GEEK framework will remain valid even if a more detailed microscopic model is used for the estimation of the rate constant.
Table 4.
Parameters of the GEEK, i.e., αij and βj, for All Elementary Reactions at Different Inert Volume Fractions
| Elementary Reaction | Crowding Conditions | ||||||
|---|---|---|---|---|---|---|---|
| Formula | Parameters | 0% | 10% | 20% | 30% | 40% | 50% |
| β1,f | 7.31 × 10−2 | 2.61 × 10−1 | 4.57 × 10−1 | 6.87 × 10−1 | 9.57 × 10−1 | 1.25 | |
| αS,1,f | 4.74 × 10−3 | ∗ | 3.22 × 10−3 | 7.22 × 10−3 | 6.95 × 10−3 | 3.23 × 10−3 | |
| αE,1,f | 1.07 × 10−2 | 1.89 × 10−2 | 9.67 × 10−3 | 8.07 × 10−3 | 1.23 × 10−2 | ∗ | |
| αES,1,f | ∗ | 1.34 × 10−2 | ∗ | ∗ | ∗ | ∗ | |
| αP,1,f | ∗ | 2.51 × 10−3 | −3.47 × 10−3 | ∗ | ∗ | 2.42 × 10−3 | |
| β1,b | −1.48 × 10−2 | −1.17 × 10−1 | −2.80 × 10−1 | −5.46 × 10−1 | −1.03 | −2.26 | |
| αS,1,b | −2.94 × 10−3 | −3.56 × 10−3 | −4.53 × 10−3 | −6.09 × 10−3 | −8.33 × 10−3 | −9.58 × 10−3 | |
| αE,1,b | −1.90 × 10−4 | 1.71 × 10−3 | 6.47 × 10−4 | 3.32 × 10−3 | ∗ | 3.16 × 10−3 | |
| αE,1,b | ∗ | 3.46 × 10−3 | ∗ | 2.03 × 10−3 | −1.22 × 10−3 | ∗ | |
| αP,1,b | −2.94 × 10−3 | −3.58 × 10−3 | −4.52 × 10−3 | −6.09 × 10−3 | −8.33 × 10−3 | −9.58 × 10−3 | |
| β2,f | −1.48 × 10−2 | −1.17 × 10−1 | −2.80 × 10−1 | −5.46 × 10−1 | −1.03 | −2.26 | |
| αS,2,f | −2.94 × 10−3 | −3.56 × 10−3 | −4.53 × 10−3 | −6.09 × 10−3 | −8.34 × 10−3 | −9.58 × 10−3 | |
| αE,2,f | −1.90 × 10−4 | 1.71 × 10−3 | 6.53 × 10−4 | 3.31 × 10−3 | ∗ | 3.13 × 10−3 | |
| αES,2,f | ∗ | 3.46 × 10−3 | ∗ | 2.01 × 10−3 | 1.20 × 10−3 | ∗ | |
| αP,2,f | −2.94 × 10−3 | −3.58 × 10−3 | −4.52 × 10−3 | −6.10 × 10−3 | −8.34 × 10−3 | −9.57 × 10−3 | |
| β2,b | 6.88 × 10−2 | 2.54 × 10−1 | 4.58 × 10−1 | 6.85 × 10−1 | 9.52 × 10−1 | 1.25 | |
| αS,2,b | ∗ | ∗ | 2.29 × 10−3 | ∗ | 3.09 × 10−3 | ∗ | |
| αE,2,b | ∗ | ∗ | 1.05 × 10−2 | ∗ | ∗ | ∗ | |
| αES,2,b | ∗ | ∗ | ∗ | −7.78 × 10−3 | ∗ | ∗ | |
| αP,2,b | 6.59 × 10−3 | 2.76 × 10−3 | 4.70 × 10−3 | 6.85 × 10−3 | 8.45 × 10−3 | 3.74 × 10−3 | |
The asterisks denote GEEK parameters with a significance of p ≤ 0.05.
Comparing the parameters αi,j and βj of each elementary reaction j (Table 4), it can generally be observed that the direct effect βj is about one to two orders of magnitude larger than each corresponding coupling coefficient, αi,j. Therefore, the direct effect is on the order of ±10−2 to ±100, whereas the coupling coefficients are on the order of ±10−4 to ±10−2. Assuming a twofold increase in a concentration, the change in the coupling is smaller than 1%, whereas the direct effect varies between one and 1000%. This suggests that the effect of the reduced dimensionality only plays a small role compared to the effective interaction potential and the diffusion inhibition.
Effects of crowding on the reversible Michalis-Menten kinetics
We used the results of the linear regression to parameterize GEEK models to compare the ODE simulations of the classical Michaelis-Menten experiment with the mass-action model. The basis of this experiment involved an initial substrate concentration [S]init that was added to a volume with a fixed enzyme concentration [E]init = [E]tot. When the substrate was added, the enzyme started to convert the substrate into a product. If the enzyme was operating reversibly, part of the product would also be converted back to a substrate, and the reaction would become indistinguishable as it approached equilibrium. In this equilibrium state, the overall free energy of the reaction was close to zero. Therefore, the ratio between the product and substrate concentrations could be used to estimate the apparent equilibrium constant Keq.
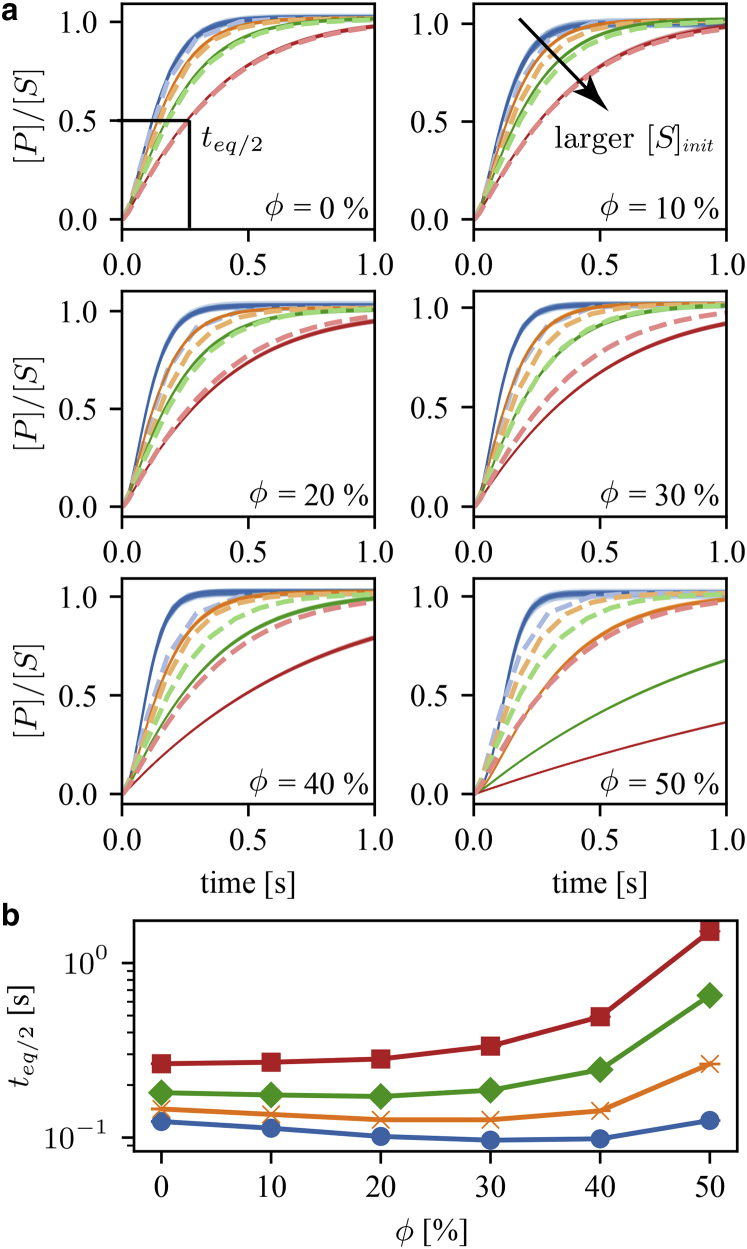
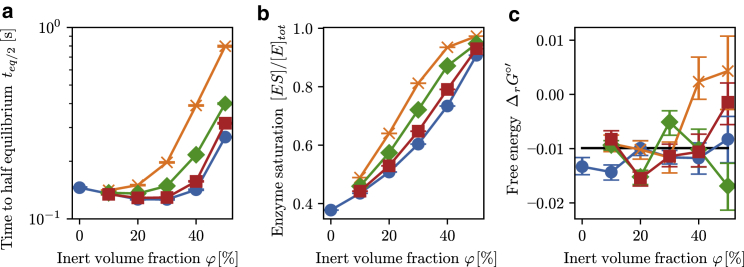
To characterize the dynamics of this system, the time to half-equilibrium teq/2 was measured, which indicates the time needed for the ratio between the product and substrate concentrations to equal Keq/2 (Fig. 4 a). In general, an increase in the teq/2 was seen with an increasing substrate concentration (Fig. 4 a). The time to half-equilibrium for the interconversion between g3p to g2p was reduced for small substrate concentrations and inert molecule fractions, up to ϕ = 30–40%. In the case of [S]init = [S]ref/4, the time to half-equilibrium was reduced to a minimal value for an inert volume fraction of ϕ = 40% (Fig. 4 a). For [S]init = [S]ref and [S]init = 2[S]ref, this decrease in half-life time persists, though the overall half-life times are larger than for [S]init = [S]ref/4, and the minimal point occurs at lower inert volume fractions. Finally, in the [S]init = 4[S]ref case, this decrease in teq/2 is no longer visible. It follows from this that the average initial rate increases with substrate concentration and decreases with an increasing volume occupancy. This suggest that the same substrate concentrations yield higher enzyme saturations, meaning that the ratio of enzyme-substrate complex/total amount of enzyme increases and that the dissociation of the enzyme-substrate complex is inhibited.
Figure 4.
(a) [P]/[S] dynamics determined for mass-action and GEEK models for different initial substrate concentrations [S]init and different occupied volume fractions (ϕ) for the E. coli molecular weight distributions. The light dashed lines represent the dilute mass-action model, whereas the thin solid lines represent a population of 100 resampled GEEK models. (b) Time to half-equilibrium teq/2 as a function of the occupied volume fraction for different initial substrate concentrations [S]init is shown. The colors of the lines denote the different initial concentrations: blue corresponds to [S]init = [S]ref/4, yellow to [S]init = [S]ref, green to [S]init = 2[S]ref, and red to [S]init = 4[S]ref.
For a closer analysis of these findings, the Michaelis-Menten parameters were estimated using Eadie-Hofstee diagrams, solving for the steady-state flux of the substrate and product concentrations between 4.9 and 490 μM (Eq. 11). The Eadie-Hofstee diagrams (Fig. S9) reveal that for both high- and low-occupancy volume fractions, a slight nonlinearity with respect to the linear Eadie-Hofstee form of the reversible Michaelis-Menten is introduced with the GEEK. This indicates that the effective maximal flux and effective Michealis-Menten constant KM,X,eff are actually functions of the reactant concentrations [S] and [P]. For the case of ϕ = 0%, this nonlinearity is only pronounced at small reactant concentrations, whereas for higher volume occupancy conditions, the nonlinearity is visible over the entire measurement range. Nevertheless, we used linear regression to estimate the effective average parameters to compare the steady-state GEEK model to the traditional Michaelis-Menten kinetics (Fig. S3).
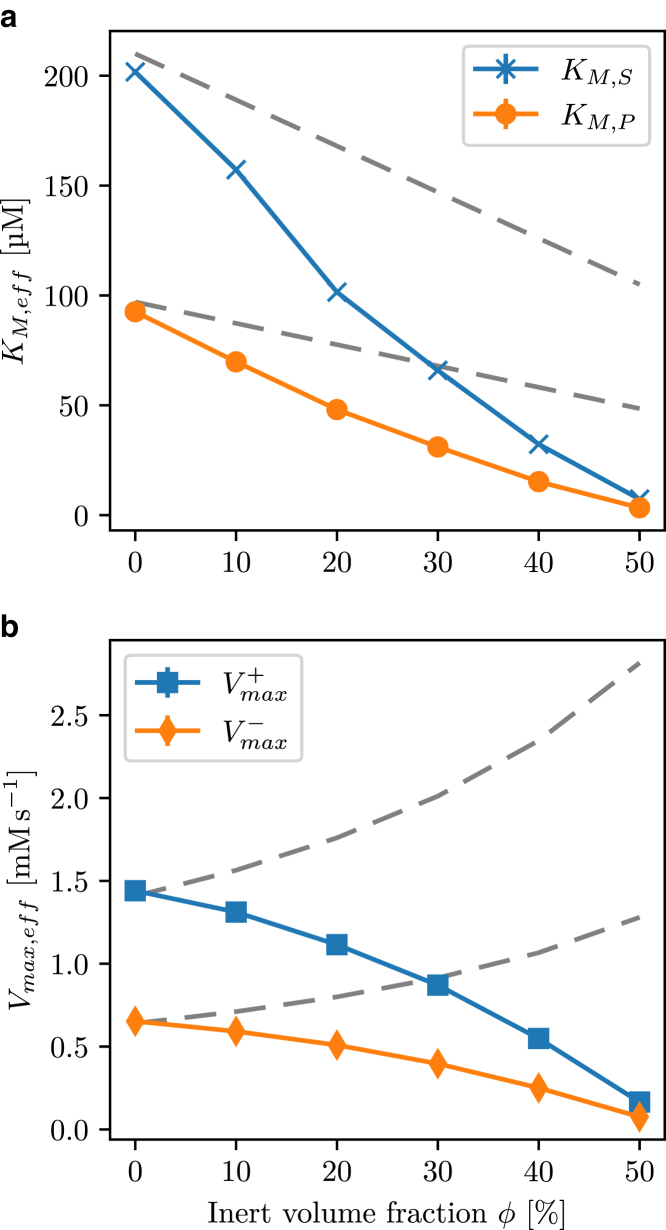
Interestingly, the steady-state analysis revealed that all the effective Michaelis-Menten parameters , KM,X,eff decreased as a function of the inert occupied volume ϕ, shown in Fig. 5, a and b respectively. These results complement our primary analysis because the maximal flux of the enzyme directly relates to the ability of the enzyme-substrate complex to dissociate, and the Michaelis-Menten constant is a measure of the affinity of the reactant binding to the enzyme. The lower the Michaelis-Menten constant, the higher the binding affinity to the enzyme. Consequently, a decreasing Michaelis-Menten constant indicates more enzyme bound at the same reactant concentration, or in other words, an increased enzyme saturation. For the effective flux through the enzyme, this results in two counteracting effects: a potential increase in flux due to an increase in saturation or a decrease in flux due to the reduced dissociation. From the analysis of teq/2 and the effective Michaelis-Menten parameters, it is evident that the flux-increasing effect is dominating if enough free enzyme is available to increase the saturation. If the enzyme capacity does not allow more substrate to associate, the flux-decreasing effect dominates.
Figure 5.
Effective Michaelis-Menten parameters (a) KM,S and KM,P and (b) and as a function of volume fraction. The gray dashed lines represent the effective parameters when all concentrations are scaled to an effective volume Veff = V(1 − ϕ) that excludes the volume occupied by inert molecules. The errors in the values calculated from uniformly resampling the GEEK parameters are smaller than 2% of the mean.
Influence of crowder size on the Michaelis-Menten kinetics
We further investigated the influence of the size of the inert molecules on the enzyme kinetics by comparing crowding with different inert molecule sizes obtained using the results for the E. coli size distribution. When comparing the teq/2 as a function of the volume occupancy obtained from crowding using the E. coli distribution to the population consisting of a single inert molecule size, a general flux-decreasing effect was observed for crowding in the single-sized population, shown in Fig. 6 a. Furthermore, smaller inert molecule sizes showed a stronger flux-decreasing effect that was alleviated as the size of the inert molecules increased. When we compared the enzyme saturation at equilibrium for the different inert molecule sizes, the single-sized crowding showed an increased saturation, and smaller crowding sizes had a stronger effect, illustrated in Fig. 6 b. This shows that the overall substrate affinity is increased more if the inert molecules are smaller than the enzyme-substrate collision radius.
Figure 6.
Effects of the particle size distribution. (a) Time to half-equilibrium teq/2, (b) enzyme saturation [ES]/[E]tot for [S]ref = 49 μM, and (c) apparent standard free energy of the reaction measured as RTlog([P]eq/[S]eq) under different crowding conditions are shown. The circles represents the apparent equilibrium measured from the E. coli size distribution; crosses, diamonds, and squares are obtained using a single size of inert molecules corresponding to the lower quartile, the median quartile, and the upper quartile of the E. coli size distribution, respectively. The error bars denote the upper and lower quartile of the resulting population that was obtained by resampling the GEEK model parameters within their confidence bounds. The horizontal black line denotes the equilibrium constant calculated from the in vitro kinetic parameters. To see this figure in color, go online.
Finally, we determined the effective standard free energy of the reaction from the effective equilibrium constant where the effective equilibrium constant was determined from the reactant concentrations at equilibrium Keq = [P]eq/[S]eq, seen in Fig. 6 c. This showed that the overall apparent standard free energy of reaction does not vary significantly with crowding size or volume fraction. Because the nonideal contributions, which contain the terms emerging from molecular interactions, from steric interaction for the substrates and products are exactly equal, we would expect the overall nonideal contribution to the free energy of the enzymatic reaction to be zero. The deviation in the effective standard energy using GEEK can be attributed to the approximation over the state space at points far from equilibrium (see Fig. S10).
Consequences of the crowded kinetics on the pathway level
We further investigated the effects of crowding at a system level using an example linear pathway with three enzymes. We considered a linear pathway where a compound Xn was reversibly converted into a compound Xn + 1. All reactions were considered to follow reversible Michaelis-Menten kinetics. The concentration of the first compound [X1] was considered to be 250 μM and the concentration of the last compound [X4] to be 50 μM. These boundary concentrations were considered to be constant. The last reaction catalyzed by enzyme 3 was parameterized using the results found for PGM. We further choose the parameters of enzyme 1 and 2 by scaling the product-specific Michaelis-Menten constant KM,P by factors of 2 and 3, respectively, as well as the maximal backward flux by factors of 0.5 and 0.33, respectively (Table 5). We further considered that all enzymes and reactants were of the same size and that, therefore, their GEEK parameters αij and βj were assumed to be the same. This models a short pathway in which only minor modifications occur on the molecule, for example, the reallocation of a phosphate group or a double bond.
Table 5.
Enzyme Parameterizations Used for the Linear Pathway Example
| Parameters | Enzyme 1 | Enzyme 2 | Enzyme 3 |
|---|---|---|---|
| KM,S | 200 μM | 200 μM | 200 μM |
| KM,P | 300 μM | 200 μM | 100 μM |
| 1.5 mM/s | 1.5 mM/s | 1.5 mM/s | |
| 0.15 mM/s | 0.25 mM/s | 0.5 mM/s |
To characterize the influence of crowding on our pathway, we calculated the relative responses of the flux with respect to a twofold increase in each of the enzyme concentrations, modeling an overexpression of the respective enzyme. We then compared the results obtained for the traditional mass-action model with the GEEK models representing the E. coli size distribution at different occupied volume fractions (Fig. 7). Comparing the GEEK model without any inert molecules with the results from the mass-action model, only minor differences were observed. On the other hand, a redistribution of the flux control was clearly seen for increasing volume fractions, wherein the initially largest flux response decreased and the lower flux responses increased as a function of the volume fraction. Considering the typical volume occupancy in cells of 20–40%, the relative order between the flux responses was still the same as under dilute conditions, though the magnitude of the largest flux response is significantly reduced. In this case, it is the relative sensitivity of the flux that is reduced. This could act as an additional stabilization mechanism with respect to fluctuations in the enzyme levels, though it should be noted that this effect does depend on many factors, such as relative KM values, Vmax, and reaction ΔrG values. How these factors impact the response of the pathway fluxes with respect to the change in enzyme levels will require an extensive analysis, considering different pathway structures and different types of enzyme kinetics. Given the extent of such a study, it will beneficial to first understand the impact for different types of enzyme kinetics before moving to the network level.
Figure 7.
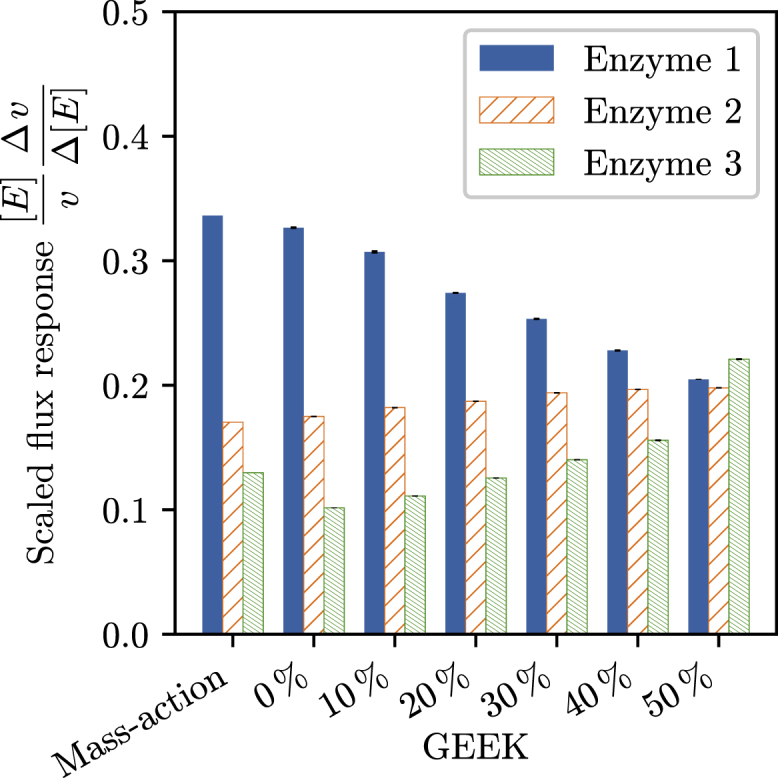
Flux responses corresponding to a twofold increase in the respective enzyme concentration for the basic mass-action model and the GEEK models derived from the E. coli distributions as well as the different volume fractions of the inert molecules. The error bars denote the upper and lower quartile of the resulting population that was obtained by resampling the GEEK model parameters within their confidence bounds. To see this figure in color, go online.
Conclusions
This research presents a method for characterizing spatial effects of any nature on biochemical reactions based on the mapping of average effects to ODEs. We therefore supplement recent work on the transport properties of macromolecule in heterogeneous environments (57, 58) and improvements on Brownian reaction dynamics in crowded media (31), as well as efforts to integrate models for altered diffusion and rate constants into macroscopic transport equations (32, 59), with a framework that allows for efficiently characterizing the observable rate constant from Brownian reaction dynamics simulations. In addition, we consider the reaction-diffusion dynamics in a diverse, heterogeneous environment represented by a size distribution. Besides studying the effects of intracellular crowding as we have done, this framework can influence the study of membrane-confined biochemical reactions, enzyme channeling, and DNA- or actin-bound reaction systems, which are all current topics in biochemistry that lack dedicated study tools.
Using a representative example, we confirm the hypothesis of recent research in the field that for reaction-limited enzyme kinetics, the diffusion effects in fractal spaces are negligible and are most likely not dominating in reaction networks. Instead, we confirm earlier research by Grima that observed a strong direct effect of crowding on the effective rates, for which a decrease in dissociation rates and an increase in association rates was observed when increasing occupied volume fraction (59). Both effects can be sufficiently explained by an effective increase of the crowding-induced potential with the volume fraction, confirming that this is a better predictor of intracellular enzyme kinetics than the diffusion. Furthermore, we show that the effective Michaelis-Menten parameters strongly depended on the volume occupancy and the size distribution of inert molecules, indicating that the kinetics is likely to vary dramatically in different cellular compartments. We finally show that crowding at a simplified network level can lead to a redistribution of the effective control on the flux response, suggesting that crowding can have a stabilizing effect with respect to fluctuation in enzyme levels, potentially indicating why enzymatic systems in vivo systems show higher robustness compared to in vitro.
In future work, this framework will be used to analyze the impact of crowding on other kinetic mechanisms and on an expanded network level. The results will illuminate the strength of the overall impact of crowding on the regulation of metabolism.
Authors Contributions
D.R.W. designed the model and performed the simulations. V.H. conceived the original idea and supervised the project. Both D.R.W. and V.H. contributed to the final version of the manuscript.
Acknowledgments
The authors thank the MOSAIK Group (Center for Systems Biology Dresden), in particular Pietro Incardona, for technical support on OPENFPM.
This project has received funding from the European Union’s Horizon 2020 research and innovation program under grant agreement no. 686070.
Editor: Alexander Berezhkovskii.
Footnotes
Supporting Material can be found online at https://doi.org/10.1016/j.bpj.2019.06.017.
Supporting Material
References
- 1.Ellis R.J. Macromolecular crowding: obvious but underappreciated. Trends Biochem. Sci. 2001;26:597–604. doi: 10.1016/s0968-0004(01)01938-7. [DOI] [PubMed] [Google Scholar]
- 2.Minton A.P. The influence of macromolecular crowding and macromolecular confinement on biochemical reactions in physiological media. J. Biol. Chem. 2001;276:10577–10580. doi: 10.1074/jbc.R100005200. [DOI] [PubMed] [Google Scholar]
- 3.Zhou H.X., Qin S. Simulation and modeling of crowding effects on the thermodynamic and kinetic properties of proteins with atomic details. Biophys. Rev. 2013;5:207–215. doi: 10.1007/s12551-013-0101-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Aon M.A., Cortassa S. Function of metabolic and organelle networks in crowded and organized media. Front. Physiol. 2015;5:523. doi: 10.3389/fphys.2014.00523. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Hancock R. Internal organisation of the nucleus: assembly of compartments by macromolecular crowding and the nuclear matrix model. Biol. Cell. 2004;96:595–601. doi: 10.1016/j.biolcel.2004.05.003. [DOI] [PubMed] [Google Scholar]
- 6.Poggi C.G., Slade K.M. Macromolecular crowding and the steady-state kinetics of malate dehydrogenase. Biochemistry. 2015;54:260–267. doi: 10.1021/bi5011255. [DOI] [PubMed] [Google Scholar]
- 7.Yadav J.K. Macromolecular crowding enhances catalytic efficiency and stability of α-amylase. ISRN Biotechnol. 2012;2013:737805. doi: 10.5402/2013/737805. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.van den Berg B., Ellis R.J., Dobson C.M. Effects of macromolecular crowding on protein folding and aggregation. EMBO J. 1999;18:6927–6933. doi: 10.1093/emboj/18.24.6927. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Emiola A., George J., Andrews S.S. A complete pathway model for lipid a biosynthesis in Escherichia coli. PLoS One. 2015;10:e0121216. doi: 10.1371/journal.pone.0121216. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Watterson S., Guerriero M.L., Ghazal P. A model of flux regulation in the cholesterol biosynthesis pathway: immune mediated graduated flux reduction versus statin-like led stepped flux reduction. Biochimie. 2013;95:613–621. doi: 10.1016/j.biochi.2012.05.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Andreozzi S., Chakrabarti A., Hatzimanikatis V. Identification of metabolic engineering targets for the enhancement of 1,4-butanediol production in recombinant E. coli using large-scale kinetic models. Metab. Eng. 2016;35:148–159. doi: 10.1016/j.ymben.2016.01.009. [DOI] [PubMed] [Google Scholar]
- 12.Andreozzi S., Miskovic L., Hatzimanikatis V. iSCHRUNK--In silico approach to characterization and reduction of uncertainty in the kinetic models of genome-scale metabolic networks. Metab. Eng. 2016;33:158–168. doi: 10.1016/j.ymben.2015.10.002. [DOI] [PubMed] [Google Scholar]
- 13.Khodayari A., Zomorrodi A.R., Maranas C.D. A kinetic model of Escherichia coli core metabolism satisfying multiple sets of mutant flux data. Metab. Eng. 2014;25:50–62. doi: 10.1016/j.ymben.2014.05.014. [DOI] [PubMed] [Google Scholar]
- 14.Brooks H.B., Geeganage S., Weidner J.R. Basics of enzymatic assays for HTS. In: Sittampalam G.S., Coussens N.P., Xu X., editors. Assay Guidance Manual. Eli Lilly & Company and the National Center for Advancing Translational Sciences; 2004. [PubMed] [Google Scholar]
- 15.Zimmerman S.B., Trach S.O. Estimation of macromolecule concentrations and excluded volume effects for the cytoplasm of Escherichia coli. J. Mol. Biol. 1991;222:599–620. doi: 10.1016/0022-2836(91)90499-v. [DOI] [PubMed] [Google Scholar]
- 16.Schnell S., Turner T.E. Reaction kinetics in intracellular environments with macromolecular crowding: simulations and rate laws. Prog. Biophys. Mol. Biol. 2004;85:235–260. doi: 10.1016/j.pbiomolbio.2004.01.012. [DOI] [PubMed] [Google Scholar]
- 17.Grima R., Schnell S. A systematic investigation of the rate laws valid in intracellular environments. Biophys. Chem. 2006;124:1–10. doi: 10.1016/j.bpc.2006.04.019. [DOI] [PubMed] [Google Scholar]
- 18.Klann M.T., Lapin A., Reuss M. Agent-based simulation of reactions in the crowded and structured intracellular environment: influence of mobility and location of the reactants. BMC Syst. Biol. 2011;5:71. doi: 10.1186/1752-0509-5-71. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Mourão M., Kreitman D., Schnell S. Unravelling the impact of obstacles in diffusion and kinetics of an enzyme catalysed reaction. Phys. Chem. Chem. Phys. 2014;16:4492–4503. doi: 10.1039/c3cp52417e. [DOI] [PubMed] [Google Scholar]
- 20.Berezhkovskii A.M., Szabo A. Theory of crowding effects on bimolecular reaction rates. J. Phys. Chem. B. 2016;120:5998–6002. doi: 10.1021/acs.jpcb.6b01892. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Galanti M., Fanelli D., Piazza F. Theory of diffusion-influenced reactions in complex geometries. Phys. Chem. Chem. Phys. 2016;18:15950–15954. doi: 10.1039/c6cp01147k. [DOI] [PubMed] [Google Scholar]
- 22.Bénichou O., Chevalier C., Voituriez R. Geometry-controlled kinetics. Nat. Chem. 2010;2:472–477. doi: 10.1038/nchem.622. [DOI] [PubMed] [Google Scholar]
- 23.Shim A.R., Almassalha L., Szleifer I. Dynamic modeling shows long-term gene expression is highly dependent on macromolecular crowding. FASEB J. 2017;31:575.3. [Google Scholar]
- 24.Bar-Even A., Noor E., Milo R. The moderately efficient enzyme: evolutionary and physicochemical trends shaping enzyme parameters. Biochemistry. 2011;50:4402–4410. doi: 10.1021/bi2002289. [DOI] [PubMed] [Google Scholar]
- 25.Vijaykumar A., Ten Wolde P.R., Bolhuis P.G. The magnitude of the intrinsic rate constant: how deep can association reactions be in the diffusion limited regime? J. Chem. Phys. 2017;147:184108. doi: 10.1063/1.5009547. [DOI] [PubMed] [Google Scholar]
- 26.Ivancic V.A., Krasinski C.A., Lazo N.D. Enzyme kinetics from circular dichroism of insulin reveals mechanistic insights into the regulation of insulin-degrading enzyme. Biosci. Rep. 2018;38 doi: 10.1042/BSR20181416. BSR20181416. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Cross M., Biberacher S., Hofmann A. Trehalose 6-phosphate phosphatases of Pseudomonas aeruginosa. FASEB J. 2018;32:5470–5482. doi: 10.1096/fj.201800500R. [DOI] [PubMed] [Google Scholar]
- 28.Westerhoff H.V., Welch G.R. Enzyme organization and the direction of metabolic flow: physicochemical considerations. Curr. Top. Cell. Regul. 1992;33:361–390. doi: 10.1016/b978-0-12-152833-1.50026-5. [DOI] [PubMed] [Google Scholar]
- 29.Feig M., Sugita Y. Reaching new levels of realism in modeling biological macromolecules in cellular environments. J. Mol. Graph. Model. 2013;45:144–156. doi: 10.1016/j.jmgm.2013.08.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Cichocki B., Hinsen K. Dynamic computer-simulation of concentrated hard-sphere suspensions. 1. Simulation technique and mean-square displacement data. Phys. Stat. Mech. Appl. 1990;166:473–491. [Google Scholar]
- 31.Smith S., Grima R. Fast simulation of Brownian dynamics in a crowded environment. J. Chem. Phys. 2017;146:024105. doi: 10.1063/1.4973606. [DOI] [PubMed] [Google Scholar]
- 32.Grima R., Schnell S. A mesoscopic simulation approach for modeling intracellular reactions. J. Stat. Phys. 2007;128:139–164. [Google Scholar]
- 33.Hattne J., Fange D., Elf J. Stochastic reaction-diffusion simulation with MesoRD. Bioinformatics. 2005;21:2923–2924. doi: 10.1093/bioinformatics/bti431. [DOI] [PubMed] [Google Scholar]
- 34.Morelli M.J., ten Wolde P.R. Reaction Brownian dynamics and the effect of spatial fluctuations on the gain of a push-pull network. J. Chem. Phys. 2008;129:054112. doi: 10.1063/1.2958287. [DOI] [PubMed] [Google Scholar]
- 35.van Zon J.S., ten Wolde P.R. Green’s-function reaction dynamics: a particle-based approach for simulating biochemical networks in time and space. J. Chem. Phys. 2005;123:234910. doi: 10.1063/1.2137716. [DOI] [PubMed] [Google Scholar]
- 36.Andrews S.S., Addy N.J., Arkin A.P. Detailed simulations of cell biology with Smoldyn 2.1. PLoS Comput. Biol. 2010;6:e1000705. doi: 10.1371/journal.pcbi.1000705. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Schöneberg J., Noé F. ReaDDy--a software for particle-based reaction-diffusion dynamics in crowded cellular environments. PLoS One. 2013;8:e74261. doi: 10.1371/journal.pone.0074261. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Strating P. Brownian dynamics simulation of a hard-sphere suspension. Phys. Rev. E Stat. Phys. Plasmas Fluids Relat. Interdiscip. Topics. 1999;59:2175–2187. [Google Scholar]
- 39.Allen M.P. Brownian dynamics simulation of a chemical-reaction in solution. Mol. Phys. 1980;40:1073–1087. [Google Scholar]
- 40.Northrup S.H., Allison S.A., Mccammon J.A. Brownian dynamics simulation of diffusion-influenced bimolecular reactions. J. Chem. Phys. 1984;80:1517–1526. [Google Scholar]
- 41.Wilson D.B., Byrne H., Bruna M. Reactions, diffusion, and volume exclusion in a conserved system of interacting particles. Phys. Rev. E. 2018;97:062137. doi: 10.1103/PhysRevE.97.062137. [DOI] [PubMed] [Google Scholar]
- 42.Kim M., Lee S., Kim J.H. Concentration effects on the rates of irreversible diffusion-influenced reactions. J. Chem. Phys. 2014;141:084101. doi: 10.1063/1.4893340. [DOI] [PubMed] [Google Scholar]
- 43.Heinrich R., Schuster S. Chapman & Hall; New York: 1996. The Regulation of Cellular Systems. [Google Scholar]
- 44.Eadie G.S. The inhibition of cholinesterase by physostigmine and prostigmine. J. Biol. Chem. 1942;146:85–93. [Google Scholar]
- 45.Hofstee B.H. Non-inverted versus inverted plots in enzyme kinetics. Nature. 1959;184:1296–1298. doi: 10.1038/1841296b0. [DOI] [PubMed] [Google Scholar]
- 46.Demirel Y. Elsevier; Amsterdam: 2014. Nonequilibrium Thermodynamics: Transport and Rate Processes in Physical, Chemical and Biological Systems. [Google Scholar]
- 47.Kim Y.C., Mittal J. Crowding induced entropy-enthalpy compensation in protein association equilibria. Phys. Rev. Lett. 2013;110:208102. doi: 10.1103/PhysRevLett.110.208102. [DOI] [PubMed] [Google Scholar]
- 48.Wang M.C., Uhlenbeck G.E. On the theory of the Brownian motion II. Rev. Mod. Phys. 1945;17:323–342. [Google Scholar]
- 49.Collins F.C., Kimball G.E. Diffusion-controlled reactions in liquid solutions. Ind. Eng. Chem. 1949;41:2551–2553. [Google Scholar]
- 50.Incardona P., Leo A., Sbalzarini I.F. OpenFPM: a scalable open framework for particle and particle-mesh codes on parallel computers. Comput. Phys. Commun. 2019;241:155–177. [Google Scholar]
- 51.Kalwarczyk T., Tabaka M., Holyst R. Biologistics--diffusion coefficients for complete proteome of Escherichia coli. Bioinformatics. 2012;28:2971–2978. doi: 10.1093/bioinformatics/bts537. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Seabold S.P., Perktold J. Statsmodels: econometric and statistical modeling with Python. In: van der Walt S., Millman J., editors. Proceedings of the 9th Python in Science Conference. 2010. pp. 57–61. [Google Scholar]
- 53.Fraser H.I., Kvaratskhelia M., White M.F. The two analogous phosphoglycerate mutases of Escherichia coli. FEBS Lett. 1999;455:344–348. doi: 10.1016/s0014-5793(99)00910-2. [DOI] [PubMed] [Google Scholar]
- 54.Gameiro D., Pérez-Pérez M., Lourenço A. Computational resources and strategies to construct single-molecule metabolic models of microbial cells. Brief. Bioinform. 2016;17:863–876. doi: 10.1093/bib/bbv096. [DOI] [PubMed] [Google Scholar]
- 55.Zhao Y.H., Abraham M.H., Zissimos A.M. Fast calculation of van der Waals volume as a sum of atomic and bond contributions and its application to drug compounds. J. Org. Chem. 2003;68:7368–7373. doi: 10.1021/jo034808o. [DOI] [PubMed] [Google Scholar]
- 56.Perry R.H. McGraw-Hill; New York: 1973. Perry’s Chemical Engineers’ Handbook. [Google Scholar]
- 57.Grima R., Yaliraki S.N., Barahona M. Crowding-induced anisotropic transport modulates reaction kinetics in nanoscale porous media. J. Phys. Chem. B. 2010;114:5380–5385. doi: 10.1021/jp9025865. [DOI] [PubMed] [Google Scholar]
- 58.Smith S., Cianci C., Grima R. Macromolecular crowding directs the motion of small molecules inside cells. J. R. Soc. Interface. 2017;14:20170047. doi: 10.1098/rsif.2017.0047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Grima R. Intrinsic biochemical noise in crowded intracellular conditions. J. Chem. Phys. 2010;132:185102. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.