Computational models advance the development of drug therapies for sickle cell disease.
Abstract
Sickle cell disease is induced by a mutation that converts normal adult hemoglobin to sickle hemoglobin (HbS) and engenders intracellular polymerization of deoxy-HbS and erythrocyte sickling. Development of anti-sickling therapies requires quantitative understanding of HbS polymerization kinetics under organ-specific conditions, which are difficult to assess with existing experimental techniques. Thus, we developed a kinetic model based on the classical nucleation theory to examine the effectiveness of potential anti-sickling drug candidates. We validated this model by comparing its predictability against prior in vivo and in vitro experimental results. We used the model to quantify the efficacy of sickling inhibitors and obtain results consistent with recent screening assays. Global sensitivity analysis on the kinetic parameters in the model revealed that the solubility, nucleation rate prefactor, and oxygen affinity are quantities that dictate HbS polymerization. This finding provides quantitative guidelines for the discovery of intracellular processes to be targeted by sickling inhibitors.
INTRODUCTION
Sickle cell disease (SCD), a genetic blood disorder, originates from the mutation of a single nucleotide in the gene for hemoglobin, a group of oxygen-binding proteins residing in the red blood cells (RBCs; erythrocytes) (1). This mutation enables polymerization of HbS molecules into polymers under hypoxia. Polymerization of HbS molecules is initiated by deoxygenation and the associated conformational change in hemoglobin from R (relaxed) state and the T (tense) state (2). HbS molecules rapidly aggregate once a nucleus forms, leading to the growth of fibers. The subsequent branching of fibers has been cast as double nucleation mechanism (3). The growing HbS fibers distort RBCs and impair cell deformability, potentially contributing to the initiation and propagation of vaso-occlusion (VOC), a hallmark of SCD. Recurrent and unpredictable episodes of VOC lead to stroke, frequent painful crisis, and other serious complications, including acute chest syndrome, splenic sequestration, and aplastic crises (4).
Therapeutic treatments have been developed on the basis of increased understanding of the pathophysiology of SCD (5). Transplantation of stem cells from a matched sibling donor has been used to cure SCD patients with high severity. Other curative treatments, such as gene replacement and gene editing, are at the stage of clinical trials. These approaches require advanced medical facilities associated with high costs, which render them impractical for most of the SCD patients. Drug therapy, therefore, is still the most feasible way to treat SCD patients. However, hydroxyurea was the only available SCD drug in the past 60 years before Endari was approved in July 2017. Hydroxyurea inhibits RBC sickling by diluting intracellular HbS through boosting the content of fetal hemoglobin (HbF), a type of hemoglobin that does not assemble into fibers (6). Endari is thought to reduce the oxidative stress in RBCs, but the underlying mechanism is still not well understood (7). Currently, most of the new drugs in clinical trials target either the adhesion of blood cells (RBCs, leukocytes, neutrophils, and platelets) to endothelium or vascular inflammation, which are downstream consequences of HbS polymerization (8). Few drug candidates aim at inhibiting HbS polymerization and sickling of RBCs, the root cause of SCD.
Substantial progress has been made in elucidating the kinetics of HbS polymerization and RBC sickling (3, 9–11), which provided insights into the development of anti-sickling drugs. However, few of the prior studies focus on testing the efficacy of the SCD drugs. In this work, we connect fundamental physical principles of HbS polymerization at the molecular level with clinical data of RBC sickling by integrating a kinetic model and a mechanistic model, aiming to build a detailed framework that could be used to assess potential SCD drugs and individualized pathology. To the best of our knowledge, this framework uses nucleation theory to explicitly describe the kinetics of homogeneous and heterogeneous nucleation of HbS monomers and chemical rate laws to model the growth dynamics of HbS fibers to capture the complexity of SCD. These quantities are not considered explicitly in a previous model (11), which was developed on the basis of numerical fitting of the correlation between RBC sickling delay time and supersaturation. In addition, the proposed kinetic model can predict the fraction of sickled RBCs under organ-specific conditions, which are difficult to assess through in vivo studies of animal models or in vitro microfluidic experiments. An important feature of this proposed framework is that each of its components can be refined by future experimental or analytical studies to improve the accuracy and capability of the model predictions. We also perform sensitivity analysis of the kinetic variables implemented in the model, through which we identify the quantities that can be considered as potential druggable targets. Specifically, the new model, as shown in Fig. 1, can predict the fraction of sickled RBCs according to patient-specific inputs and organ-specific environmental conditions and examine the therapeutic efficacy of anti-sickling agents. Furthermore, it can quantify the impact of multiple polymerization factors in the process of HbS polymerization and identify the key governing parameters that can be targeted by drugs to efficiently prevent RBC sickling.
Fig. 1. A kinetic model is developed to provide quantitative prediction of RBC sickling with or without the effects of anti-sickling drugs.
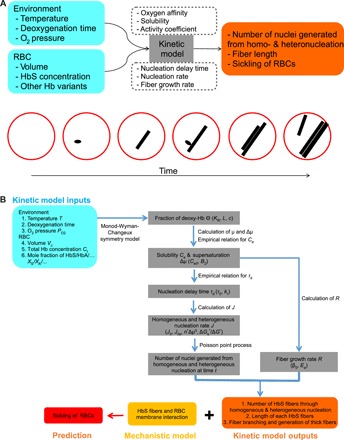
(A) Schematic of the inputs and outputs of the kinetic model (top), which describes the nucleation, growth, and branching of HbS fibers and RBC sickling (bottom). (B) Concise flow chart of prediction of RBC sickling through the kinetic model. The model inputs are temperature T, oxygen tension PO2, deoxygenation rate, HbS/HbA/… mole fraction Xs/XA/…, total hemoglobin concentration Ct, and RBC volume Vc. The kinetic model computes the following key quantities: the fraction of oxyhemoglobin Θ, hemoglobin solubility Ce and supersaturation Δμ, the nucleation delay time τd, homogeneous and heterogeneous nucleation rates J and Js, fiber growth rate R, fiber length, and the RBC sickling time. The theories or empirical relations used to compute these kinetic quantities are given between each step. The parameters in the kinetic model are highlighted in the parentheses at each step.
RESULTS
We propose a predictive model of RBC sickling by integrating a stochastic kinetic model, which describes the homogeneous and heterogeneous nucleation of HbS polymer fibers and their growth, with a mechanistic model, which considers the interaction between HbS fibers and the RBC membrane. The driving force for HbS fiber nucleation and their growth is the supersaturation (12), i.e., the excess of deoxy-HbS chemical potential in the cytosol over that of HbS in the polymer. Prior studies have introduced an all-encompassing delay time between the setting of supersaturation and sickling of RBCs and used an empirical scaling relation to evaluate this time (3, 11). Here, we use a fundamentally different strategy. We represent the nucleation and growth of HbS fibers with established biophysical kinetic laws (9, 13), which allows for a detailed analysis of initiation of RBC sickling. As shown in Fig. 1A, the inputs of the kinetic model include environmental variables, such as temperature, deoxygenation time, and oxygen tension (the partial pressure of oxygen in blood), and patient-specific variables of RBCs, such as mean corpuscular volume (MCV; the average volume of RBCs), hemoglobin distribution, and concentration of other hemoglobin variants. The outputs are numbers of nuclei generated through homogeneous and heterogeneous pathways, respectively, the lengths of HbS fibers, the configuration of fiber domains, and the sickling of RBCs. Detailed information of the new stochastic kinetic model can be found in Materials and Methods.
Mechanics of RBC sickling in SCD
Sickling of RBCs is induced by the growth of intracellular HbS fibers, which distort RBCs into a variety of shapes, including elongated, granular, oval, holly leaf, and crescent (classic sickle) shapes (14). However, a quantitative correlation between the mechanical properties of HbS fibers and the resulting morphological changes of RBCs has not been investigated in sufficient detail. Here, we combine a coarse-grained molecular dynamics (CGMD) HbS fiber model (15) with a CGMD RBC model (16) to simulate the interaction between an RBC and HbS fibers, through which we clarify the relation between the stiffness of HbS fibers and the deformations of RBCs.
The RBC model simulates the lipid bilayer and the cytoskeleton as well as transmembrane proteins explicitly by coarse-grained (CG) particles (Fig. 2A). The HbS fiber model is an intracellular fiber bundle with a chain of CG particles. The diameter of the fiber chain can be tuned to mimic HbS fiber bundles that contain various numbers of single HbS fibers. The bending stiffness of the fiber bundle with an increased number of constituent fibers (blue curve in Fig. 2B) is tuned such that it follows the experimental data reported in (17) (black curve in Fig. 2B).
Fig. 2. Simulations of RBC sickling with a mechanistic model.

(A) Configuration of an HbS fiber bundle in a stretched RBC. Green particles, actin junctions; purple particles, spectrin filaments; black particles, glycophorin proteins; yellow particles, band-3 proteins; red particles, lipid bilayer. Yellow bar inside the RBC represents a chain of CG HbS particles with varying thickness, mimicking an HbS fiber bundle. (B) Bending stiffness of fiber bundles plotted as a function of the number of constituent fibers. Bending stiffness of fiber bundle dictates the variations in the ensuing fiber bundle and RBC shapes, as illustrated in the plot: (I) fiber buckled, (II) fiber buckled with one protrusion on the RBC, (III) fiber buckled with two protrusions on the RBC, (IV) nonbuckled with two protrusions on RBC. Fibers are plotted with an exaggerated thickness for clarity. In the insets, a part of the RBC membrane is not shown such that the HbS fiber configuration inside the RBC can be viewed.
To probe the correlation between the mechanical properties of HbS fibers and the resulting morphological changes of RBCs, we initially placed a fiber bundle with a length of 15 μm in a prestretched RBC (Fig. 2A), following the strategy used in (18). Once the simulation begins, the RBC attempts to recover the biconcave shape and interacts with the fiber bundle. The final configurations of the RBC and fiber bundle are dictated by the bending stiffness of the fiber bundle. Figure 2B illustrates that when the fiber bundle contains equal to or less than 13 single HbS fibers, the fiber bundle becomes convoluted after interacting with the RBC membrane. When the number of fibers increases to 14, the fiber bundle still becomes buckled, but it creates one protrusion on the cell surface. As the number of fibers in the bundle increases, the fiber bundle becomes less buckled due to the increased bending stiffness. Meanwhile, two growing protrusions are observed on the surface of the RBC. Notably, these simulation results are consistent with an analytical study, which demonstrated that an intracellular fiber bundle, consisting of 10 or more tightly bonded single HbS fibers, sickles an RBC (19). Therefore, in the kinetic model, RBCs are considered to be “sickled” when an intracellular bundle, consisting of 10 or more HbS fibers, reaches the width of an erythrocyte (6 μm or longer). A parametric study for these criteria is shown in the Supplementary Materials.
Sickling of RBCs in the hepatic vein
The hepatic veins are the location with the lowest oxygen saturation of 51% in the venous circulation, corresponding to PO2 = 28.1 mmHg (20). To validate the model prediction of RBC sickling in hepatic vein, we compare the simulation results with experimental measurements conducted in (20). Since the distribution of hemoglobin concentration and composition was not reported in the original work, we assume that hemoglobin distribution follows a Gaussian distribution with a mean of 32.7 g/dl and an SD of 2.3 g/dl (Fig. 3B) (21, 22). We also assume that the examined RBCs contain only one hemoglobin variant, HbS. In addition, PO2 is assumed to decrease linearly from 100 to 28.1 mmHg. The deoxygenation time is selected to be 1 s, comparable to the average capillary transit time of RBCs (23). Other model inputs can be found in table S3 (condition I).
Fig. 3. Deoxygenation and fraction of sickled RBCs in hepatic vein.
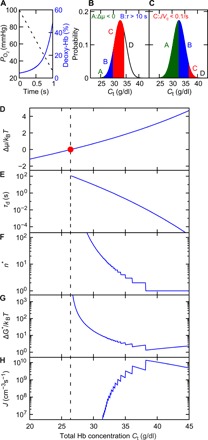
(A) The linear decrease of PO2 from 100 to 28.1 mmHg in 1 s (dashed line) enforces deoxygenation of hemoglobin from 4.3 to 49% correspondingly (blue curve). Fractions of RBCs classified according their sickling propensities in the hepatic vein of (B) SCD patients and (C) SCT individuals correspondingly. Areas A, B, C, and D denote fractions of RBCs with distinct polymerization propensities at PO2 = 28.1 mmHg. Area A: Deoxy HbS is undersaturated. Area B: The nucleation delay time is longer than 10 s. Area C: Less than 1 polymer is generated via homogeneous nucleation within 10 s. Area D: RBCs are likely to become sickled within 10 s. (D to H) Variation of supersaturation Δμ/kBT (D), delay time τd (E), homogeneous nucleus size n* (F), homogeneous nucleation barrier ΔG* (G), and homogeneous nucleation rate J (H) with respect to the total hemoglobin concentration Ct at the end of deoxygenation. Vertical dash line highlights the beginning of supersaturation.
As shown in Fig. 3A, the concentration of fully deoxygenated hemoglobin in T-state conformation, which is determined by the total hemoglobin concentration Ct and oxygen tension PO2, increases to 0.49Ct at the end of deoxygenation period. The propensity of the deoxy-HbS to polymerize and induce RBC sickling is dictated by the value of Ct, e.g., RBCs with higher Ct are more likely to sickle. Figure 3 (D to H) present the dependence of the supersaturation, nucleation delay time, nucleus size, nucleation barrier, and nucleation rate on the hemoglobin concentration in RBCs during their passage through hepatic vein. On the basis of these results, the RBCs are divided into fractions with different sickling probabilities, as shown in Fig. 3B. When Ct is less than a threshold value of 26.4 g/dl (area A in Fig. 3B), the red cell cytosol is undersaturated after deoxygenation (Δμ/kBT < 0) (see Fig. 3D), and polymerization is thermodynamically prohibited. For RBCs with Ct larger than 26.4 g/dl, the intracellular hemoglobin becomes supersaturated, and nucleation proceeds after a delay time of τd, a fundamental characteristic of nucleation, defined as the length of the transition from a stable homogeneous solution to the moment when nucleation proceeds at a steady rate (9, 13). As shown in Fig. 3E, this delay time could range from hundreds of seconds to 0 s, depending on Ct. RBCs with Ct less than 30.0 g/dl (area B in Fig. 3B) are likely to return to the lungs without sickling, due to the long delay time (>10 s) (see Fig. 3D). When Ct is larger than 30.0 g/dl, the delay time is shortened to several seconds, comparable to RBC capillary transit time (23). However, the probability of sickling is small for RBCs with Ct < 34.3 g/dl (area C in Fig. 3B) because the corresponding homogeneous nucleation rate J is smaller than 1.07 × 109 cm−3 s−1, under which fewer than one nucleus is generated in 10 s (see Fig. 3H). Hence, sickling of RBCs is more likely to occur for those RBCs with Ct > 34.3 g/dl (area D in Fig. 3B), which accounts for ~24.3% of RBCs. This result is close to the fraction of sickled RBCs (22%) observed in the hepatic vein of the SCD patients examined in (20), demonstrating the power of the kinetic model to predict the fraction of sickled RBCs in vivo.
To demonstrate the robustness of the model, we also computed the fraction of sickled RBCs in hepatic vein of sickle cell trait (SCT) individuals. Unlike SCD patients who have two mutated genes that cause the production of HbS, SCT individuals carry only one mutated gene, and thus have a lower percentage of HbS in RBCs compared to SCD patients. People with SCT typically live a normal life and only experience symptoms of SCD under extreme conditions such as severe dehydration and high-intensity physical activities. In our simulation, the distribution of hemoglobin in SCT RBCs is selected to be identical to that of SCD patients, but the hemoglobin composition is 38% HbS and 62% Hemoglobin A (HbA), consistent with the data reported in (22). The reduced HbS percentage increases the solubility of hemoglobin and thus reduces the propensity for polymerization. As shown in Fig. 3C, the threshold values of Ct for Δμ/kBT < 0, τd > 10 s, and JVc < 0.1 s−1 increased. Note that the population of RBCs with the largest propensity to sickle (area D in Fig. 3C) only accounts for less than 0.03% of the RBCs. This finding provides a rationale for the clinical observation that, under normal conditions, individuals with SCT do not experience symptoms or complications similar to those of SCD patients.
Patient-specific studies of RBC sickling under hypoxia in microfluidic channel
In this section, we compute the fractions of sickled RBCs from seven SCD patients under the experimental conditions of Du et al. (24). In this in vitro study, PO2 in the microfluidic channel was reduced from 160 mmHg (O2 concentration of 21%) to 15.2 to 38 mmHg (O2 concentration of 2 to 5%) in 15 s. The compositions of hemoglobin, MCV, mean corpuscular hemoglobin concentration (MCHC) for the seven SCD patients are listed in table S1. In our simulations, we assume that the distribution of Ct in the examined RBCs follows a Gaussian distribution with a mean of MCHC (listed in table S1) and a universal variance of 2.3 g/dl, as the actual variances for each patient were not provided in the original work (24). Other model inputs can be found in table S3 (condition II).
First, we compute the fractions of sickled RBCs, assuming that PO2 is reduced to 15.2 mmHg (2%) after deoxygenation, the lower bound of O2 concentration range reported in the microfluidic experiments (24). The fractions of sickled RBCs are recorded in the subsequent 240 s after deoxygenation begins. As shown in Fig. 4, significant discrepancies are observed between our simulation results (red dashed curve) and experiential data (black curve) (24) for patient VII, which probably results from the underestimated PO2 and application of the universal variance for hemoglobin distribution. To confirm our hypothesis, we vary O2 concentration within 2 to 5%, the range reported in the original experiments (24). Meanwhile, we tune the variance of hemoglobin distribution such that our simulation results gradually approach the experimental results (black curve in Fig. 4). These tests indicate that when O2 concentration is 3.75% and the variance is 0.7 g/dl, our simulation results (blue dashed curve in Fig. 4) are in agreement with the experimental data. Similar computations are performed for the other six SCD patients, and the results can be found in fig. S5.
Fig. 4. Evolution of fraction of sickled RBCs under hypoxia.
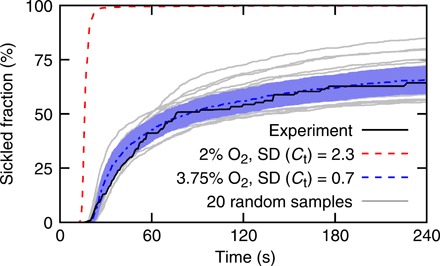
Deoxygenation completes in 15 s after the simulations begin. Black line represents the experimental results reported in (24). Red dashed line denotes model prediction with O2 concentration of 2% and variance of HbS distribution of 2.3 g/dl. Blue dashed curve denotes model prediction with O2 concentration of 3.75% and variance of HbS distribution of 0.7 g/dl. Gray lines represent 20 of 5000 sensitivity tests with O2 concentration varying at 3.75 ± 0.01% and the variance of hemoglobin distribution varying between 0.7 ± 0.35 g/dl. Blue area represents SD.
An additional 5000 simulations for each SCD patient (20 of 5000 sensitivity tests for patient VII are plotted as gray lines in Fig. 4) are performed to examine the sensitivity of the model prediction to O2 concentration and the variance of hemoglobin distribution. We find that a fraction of sickled RBCs is more sensitive to variation of O2 concentration. However, we note that the agreement between the simulation and experimental results cannot be achieved by varying the PO2 alone, suggesting that patient-specific hemoglobin distribution is an essential determinant of the transient sickling of RBCs. The above findings demonstrate the capability of the kinetic model to predict the RBC sickling based on patient-specific inputs.
Examination of sickling inhibitors
Although the molecular basis of SCD was discovered about 70 years ago (1), only a single drug, hydroxyurea, was available to SCD patients until Endari was approved in 2017. Hydroxyurea inhibits HbS polymerization by reducing the fraction of HbS in the red cell cytosol through inducing the synthesis of HbF (6). However, clinical evidence indicates that hydroxyurea exhibits heterogeneous outcomes and that the causes of these findings are still under investigation (25). An alternative approach to inhibit RBC sickling is to increase cell volume using compounds that interact with the cell membrane. Two compounds of this class, monensin A and gramicidin A, have demonstrated strong therapeutic effects in recent screening assays (22). In this section, we apply our model to test the suggested mechanism of action of sickling inhibitors.
First, we use the kinetic model to evaluate the sickled fraction of SCT cells before application of a drug. We select a hemoglobin composition of 38% HbS and 62% HbA, comparable to the composition of the SCT subjects (38% HbS, 58% HbA, 3.7% HbA2, and 0.3% HbF) reported in (22). We use the hemoglobin concentration distribution for normal RBCs reported in (21). Following the original experiments in (22), the initial PO2 is set to 0 mmHg. Other model inputs can be found in table S3 (condition III). Our simulation predicts a wide distribution of nucleation delay times primarily due to variation in MCHC. As illustrated in Fig. 5A (blue dashed curve), this wide distribution of nucleation delay time leads to a gradually increased fraction of sickled RBCs with time. Notably, the prediction from our kinetic model is consistent with experimental data reported in (black curve in (22) (black curve in Fig. 5A). Moreover, when the deoxygenation time is shorter than 20 s, our model (blue dashed curve) provides a more accurate prediction of the fraction of sickled RBCs than a prior model (red dashed curve) based on the universal curve of delay time versus supersaturation (11). This discrepancy is likely attributed to the fact that the present model considers the number of HbS molecules in the nucleus n* as discrete integer numbers, whereas the model applied in (22) represents n* as a continuous variable. Continuous representation of n* leads to infinitely high HbS polymerization rates when the delay time is zero, and thus causes an overestimation of the fraction of sickled RBCs at the early stage of measurements (see red dashed curve in Fig. 5A).
Fig. 5. Predictions of the efficacy of sickling inhibitors with the kinetic model.
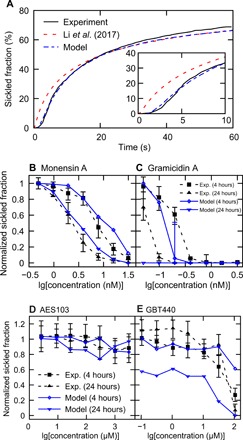
(A) Evolution of the fraction of sickled RBCs in the absence of sickling inhibitors. Black line, experimental results reported in (22); red dashed line, the prediction based on the universal curve of delay time versus supersaturation in (22); blue dashed line, prediction of the kinetic model. (B and C) The fraction of sickled RBCs decreases with increased MCV at 60 s after photolysis. The swelling of RBCs is induced by (B) monensin A and (C) gramicidin A. Blue curves represent our simulation results, and black dashed curves denote the experimental results reported in (22). Squares and diamonds denote 4-hour incubations. Triangles denote 24-hour incubations. (D and E) Sickled fractions at 60 after photolysis of SCT RBCs treated with (D) AES103 and (E) GBT440 at a variety of concentrations. Blue curves represent our simulation results, and black curves denote the experimental results reported in (22). Square and diamond symbols denote 4-hour incubations. Triangle symbols denote 24-hour incubations. logarithm bas 10, Log10.
Next, we examined the efficacy of two anti-sickling agents, monensin A and gramicidin A, both of which operate by reducing the concentration of HbS through increasing the cell volume. To evaluate the increased RBC volume with various dosages of these two drugs, we followed the Coulter counter measurements performed in (22). As shown in Fig. 5B, the kinetic model predicts that as the concentration of the monensin A increases, the sickled fraction decreases in the same pattern as the results of the screening assay for 4- and 24-hour incubations, respectively. This finding demonstrates the capability of the kinetic model in predicting the efficacy of SCD drugs. For gramicidin A, our predictions for 4-hour incubation are close to the results of the screening assay (Fig. 5C). However, the simulation results for 24-hour incubation correspond to a stronger efficacy than the experimental results at the lower end of the examined concentration range (Fig. 5C). This discrepancy suggests that the correlation between the increased cell volume and decreased sickled fraction for gramicidin A–treated RBCs is nonmonotonic (22). Apparently, besides inhibiting RBC sickling through increasing RBC volume, gramicidin A has additional mechanisms of promoting RBC sickling, which is overwhelmed by the effect of increased cell volume as the concentration of gramicidin A increases.
Last, we examine the efficacy of another two SCD drugs, AES103 and GBT440, both of which are proposed to inhibit RBC sickling by increasing the oxygen affinity. Following the screening assay in (22), the efficacy of these two drugs is tested in the absence of oxygen. We use condition III in table S3 for model inputs. Since the quantitative correlations between the concentrations of these two drugs and their effects on the oxygen binding parameters, such as c, KR, and L, are not available, we only consider their effects on changing the cell volume, as reported in (22). As shown in Fig. 5D, AES103 exhibits no anti-sickling effect in the absence of oxygen because it does not increase cell volume, consistent with the finding of the screening assay (22). For GBT440, our simulations in Fig. 5E show that after a 4-hour incubation, no considerable anti-sickling effect is observed at a low concentration, but the effect becomes significant at a high concentration, in agreement with the screening assay (22). However, in the case of 24-hour incubation, our simulation predicts notable sickling inhibition by GBT440 at low concentration due to the cell volume change, which was not observed from the screening assay (22). This discrepancy implies that there are the additional mechanisms of GBT440 that cancel out the effect of cell volume changes on inhibiting RBC sickling at low concentration. As the concentration of GBT440 is increased, both our simulation and the screening assay predict a therapeutic inhibition due to the increased cell volume.
Identification of targets for sickling inhibitors
The kinetics of HbS polymerization involves the release of oxygen from HbS, hemoglobin supersaturation, formation of HbS nuclei after a delay time, and growth of HbS fibers. To accurately describe each step of this process, the kinetic model uses multiple parameters. A comprehensive understanding of the dependence of RBC sickling on each of these parameters and their interaction can facilitate the determination of potential druggable targets and thus provide guidance on the development of new drugs. The default values of the model parameters are selected according to prior experimental and clinical studies. Detailed information can be found in Materials and Methods. However, many of these parameters are patient specific and thus may vary from patient to patient. Therefore, a quantitative evaluation of the impact of varying these parameters within their physiological ranges on the predictions of RBC sickling is necessary.
In this section, we analyze the global sensitivity of sickled fractions to the model parameters and identify the key quantities that dictate RBC sickling. To perform sensitivity analysis, we use the analysis of variance functional decomposition (26), where we vary 13 model parameters simultaneously. The examined parameters include oxygen affinity constants (c, KR, and L), hemoglobin solubility at 0°C and full deoxygenation (Ce0), the second virial coefficient (B2), which determines the HbS activity coefficient, delay time factors (τ0 and kτ), the number of HbS molecules in the nucleus n*, prefactor in the homogeneous nucleation rate law (J0), the acceleration due to heterogeneous nucleation (J0s/J0), the decrease of the heterogeneous nucleation barrier from homogeneous nucleation barrier (/ΔG*), and the factors for fiber growth (β0 and Eα). The definitions of these parameters can be found in Materials and Methods, and their varying ranges can be found in table S2. To illustrate the results of sensitivity analysis, we placed the examined model parameters in a ring, as shown in Fig. 6 (A and B). The sensitivity of a single parameter is plotted as a circle, whose diameter reflects the sensitivity of the polymerization kinetics to that parameter. The connecting lines indicate the interaction of two parameters, which describes how the fraction of sickled RBCs changes when two parameters are varied synchronously. The line thickness corresponds to the sensitivity of the pair.
Fig. 6. Global sensitivity analysis illustrates the key model parameters that determine the sickling of RBCs.
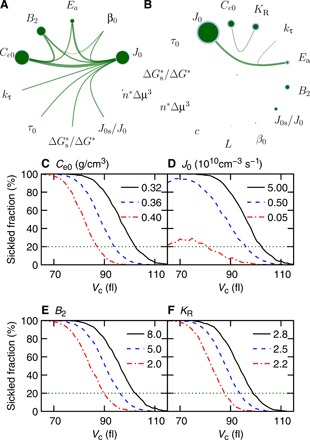
(A and B) Global parametric sensitivity analysis on the model parameters with model inputs following an in vitro study (22) (A) and an in vivo study (20) (B). The diameter of green circles is the sensitivity index of each parameter (first-order sensitivity index). The blue ring outside the green circle is the 95% confidence interval of the sensitivity index. The thickness of lines between two parameters is the sensitivity index of this two parameter pair (second-order sensitivity index). Sensitivity smaller than 0.01 is not plotted. (C to F) Sensitivity of the correlation between the fraction of sickled RBCs and cell volume Vc at 60 s after deoxygenation to four kinetic parameters: (C) Ce0, (D) J0, (E) B2, and (F) KR: The tested values of each parameter are listed in the plots. Black lines denote the default model parameters. Horizontal green dashed lines mark the threshold value of sickled fractions that define the therapeutic effects in (22).
First, we examined the sensitivity of the model parameters by using model inputs for the screening assay in (22) (condition III in table S3). Our analysis indicates that the fraction of sickled RBCs is most sensitive to Ce0, followed by J0 and B2 (see Fig. 6A). The sensitivity of the interaction pairs between these 13 parameters is similar and much weaker than the sensitivity of single parameters of Ce0, J0, and B2. This finding provides a therapeutic rationale for inhibiting the HbS polymerization through increasing HbS solubility (27). Furthermore, our results suggest that suppressing the activity of HbS and nucleation rate law prefactor can be potential druggable targets to efficiently inhibit HbS polymerization. Notably, the screening assay in (22) was performed in the absence of oxygen, and thus, the above results do not take the effects of the oxygen affinity parameters, such as c, KR, and L, into consideration. To fill this gap, we analyzed the sensitivity by using the model inputs following the conditions in the hepatic vein (condition I in table S3) (20). As illustrated in Fig. 6B, our results show that the fraction of sickled RBCs is most sensitive to J0, followed by Ce0 and KR. It is noted that the effect of KR overwhelms that of B2 when the effect of oxygen binding is considered. This result implies that enhancing the binding affinity of hemoglobin could be a more effective approach than suppressing the thermodynamic activity of hemoglobin. Moreover, we quantitatively illustrate the effects of changing Ce0, J0, B2, and KR on reducing the fraction of sickled RBCs. As shown in Fig. 6 (C to F), the correlation between fractions of sickled RBCs and their cell volume at three values of Ce0, J0, B2, and KR demonstrate that therapeutic efficacy can be achieved by modulating these four kinetic parameters with anti-sickling agents.
DISCUSSION
The clinical manifestations of SCD are heterogeneous. A possible cause of this heterogeneity is the variations in patient-specific RBC variables, such as hemoglobin distribution, hemoglobin compositions, and MCV, which determine the morphology and biomechanical properties of sickle RBCs (28). Organ-specific environmental variables, such as temperature, deoxygenation time, initial and final oxygen pressure, etc., also contribute to the clinical heterogeneity of SCD. Recent developments in quantitative microfluidic assays improve the understanding of RBC sickling dynamics under hypoxia with or without the influence of drugs (22, 24). However, these in vitro investigations cannot accurately reproduce the organ-specific conditions. The stochastic kinetic model we present here is able to simulate the kinetics of HbS polymerization and predict the fraction of sickled RBCs based on patient-specific inputs and organ-specific conditions, thereby complementing the in vitro microfluidic assays. The validity of the model is verified by comparing the model predictions with prior in vivo (20) and two independent in vitro studies (22, 24). It is noted that our kinetic model can reproduce different experimental results (20, 22, 24) without tuning the model parameters, indicating the capability of our model to confirm and analyze the laboratory and clinical findings. In particular, we demonstrate that our model can capture the transient sickling of RBCs from blood samples of individual SCD patients, and the results are consistent with in vitro experiments (24). By using temperature, deoxygenation time, and oxygen pressure as model inputs, this kinetic model is able to provide predictions of RBC sickling under organ-specific conditions that cannot be assessed by existing in vivo and in vitro experimental techniques.
New SCD drugs in the clinical trial pipeline target multiple pathways, including sickling, adhesion, inflammation, and anticoagulation, among which inhibition of adhesion molecules and their downstream targets has been the focus of many ongoing investigations (5). However, the underlying mechanisms causing various complications in SCD could be different. For example, a possible cause of acute splenic sequestration crisis, a life-threatening complication of SCD, is the retention of less deformable sickled RBCs by the narrow interendothelial slits in the spleen (29). In this context, anti-adhesion drugs alone may not be able to provide desirable therapeutic effects. Therefore, development of new SCD drugs targeting an anti-sickling pathway should not be discounted. In this work, we demonstrate that the kinetic model can be used to examine the efficacy of anti-sickling agents and identify their additional mechanisms. Our prediction on the efficacy of monensin A, which inhibits RBC sickling by increasing cell volume (22), agrees well with the screening assay, whereas our results somewhat overestimate the efficacy of gramicidin A, which prevents RBC sickling through a similar mechanism to monensin A. The discrepancy between our simulation results and the screening assay suggests that, besides increasing cell volume, gramicidin A has additional effects that compromise its anti-sickling activity, which is evidenced by the nonuniform correlation between the increased cell volume and decreased sickled fraction reported in screening assay (22). These results demonstrate the capability of the present model to predict the efficacy of sickling inhibitors and identify additional effects of existing and future drugs.
Although both screening assay (22) and our simulations suggest that increasing the cell volume can be an efficient approach to inhibit RBC sickling, new drugs that delay RBC sickling through other pathways such as altering the kinetics of HbS polymerization should also be considered (8). Our global sensitivity analysis identifies that RBC sickling is sensitive to the hemoglobin solubility, nucleation rate factor (related to intermolecular contacts), oxygen binding affinity, and hemoglobin activity. These findings provide therapeutic rationales for anti-sickling targets found in the past four decades [see a recent review by Eaton and Bunn (8)]. Our results further predict that modulating each of these four kinetic parameters can achieve anti-sickling efficacy that is comparable to increasing the cell volume. However, because of a lack of quantitative correlations between concentrations of anti-sickling agents and these parameters, whether this predicted anti-sickling efficiency can be achieved requires further experimental investigations.
There are discrepancies between our model predictions and prior experimental data, which likely result from several limitations of the proposed model and uncertainties in the experiments. We assume that the hemoglobin in the examined RBCs follows a Gaussian distribution with a mean of 32.7 g/dl and an SD of 2.3 g/dl (21), and MCV is selected to be 93.05 (fl) when these quantities were not reported in the original work. Since the response of sickle RBCs under hypoxia depends on patient-specific hemoglobin distribution, hemoglobin compositions, and MCV, these assumptions could cause discrepancies between our model prediction and experimental results. With the increased information of these patient-specific quantities and further extensive testing, the accuracy of the model prediction can be improved. As shown in Fig. 4, with a refined patient-specific quantities as inputs, our model can capture the transient sickling fraction of RBCs from blood samples of individual SCD patients (24). In addition, the oxygen tension in our simulation is assumed to be uniform for all simulated RBCs, while oxygen distribution could be heterogeneous in the chambers of microfluidic experiments, which could lead to the variations when evaluating the fraction of sickled RBCs. It is worth mentioning that we only vary the model inputs (table S3), while all the model parameters (table S2), which are verified or informed by prior studies (see “Kinetic model of HbS polymerization” section in Materials and Methods), remain constant for different predictions. These model parameters can be varied to incorporate the effect of anti-sickling agents once the correlations between the dosages of anti-sickling agents and the model parameters are tested. Each component of the proposed model and the corresponding parameters can also be replaced or refined by future experimental or theoretical studies to improve the accuracy and capability of the model predictions. In this work, we show that the proposed model is capable of predicting the polymerization of HbS at physiological concentrations within the volume of an RBC. To cover the large dataset summarized in (11), which contains a wide range of HbS concentrations, solution volumes, and temperatures, the description of nucleation rate in the current model needs to be further refined.
Together, the proposed kinetic model is capable of predicting RBC sickling based on patient- and organ-specific data and thus can be used to guide the prognosis for SCD patients with various degrees of severity. This kinetic model can also be used to examine the efficacy of anti-sickling drugs and accelerate years of laboratory experiments in animals and human cells before new drugs enter the stages of clinical trials. Furthermore, this kinetic model can be potentially used to provide guidance for the drug dosage based on patient-specific data, thereby facilitating the development of precision medicine to eliminate the side effects of SCD drugs.
MATERIALS AND METHODS
Kinetic model of HbS polymerization
The kinetic model, which is developed on the basis of classical nucleation theory, is capable of simulating the polymerization kinetics of HbS and predicting the sickling of RBCs in SCD. As shown in Fig. 1B, the model inputs patient- and organ-specific conditions, including temperature, oxygen tension, MCV, MCHC, and mole fraction of different Hb variants, and predicts the number of nuclei through homogeneous and heterogeneous nucleation, fiber growth, and RBC sickling time. In this section, we go over each step of the flow chart in Fig. 1B and introduce each component of the kinetic model.
Deoxygenation of hemoglobin
We assumed that the kinetics of HbS polymerization commences with deoxygenation of cytosol in RBCs. At t = 0, RBCs were fully oxygenated, and the oxygen tension Pa,O2 in the cytosol was 100 mmHg. When t = τc, where τc is the duration of the deoxygenation process, oxygen tension was reduced to Pv,O2, which varies at different vascular sites in the human body (20).
We assumed that the oxygen tension decreases linearly during the deoxygenation process. We also assumed that the deoxygenation occurs through quasiequilibrium processes, considering the fast diffusion of oxygen (diffusion coefficient of oxygen is ~10−9 m2/s) and the effect of facilitated oxygen diffusion (30). Therefore, each PO2 corresponds to a unique concentration of deoxyhemoglobin, denoted by C. The fraction of deoxyhemoglobin is
| (1) |
where Θ is the oxygen saturation (the fraction of oxyhemoglobin), and Ct is the total hemoglobin concentration. We used the Monod-Wyman-Changeux (MWC) symmetry model (2) to describe the dependence of Θ on PO2, which is expressed as
| (2) |
where n denotes the number of binding sites per molecule, i.e., n = 4 for hemoglobin, and α = PO2/KR is a normalized ligand concentration. Monod et al. (2) reported a parameter set of the affinity of the R state KR = 2.8, the allosteric constant L = 9054, and the ratio of the affinities of R and T states for the ligand, c = 0.014, which give the best fit to the experimental oxygen binding data. By using Eqs. 1 and 2, the concentration of deoxyhemoglobin, C(t), at a given time can be computed.
In this work, we examined different Hb compositions, including polymerization of pure HbS, HbS/HbF mixture, and HbS/HbA mixture under fully and partially deoxygenated conditions, respectively. In the case of partially deoxygenated HbS, we computed the nucleation-competent species through Eq. 2, where Θ accounts for both fully and partially oxygenated HbS. Partially oxygenated HbS is the product of O2 binding independently to the four heme groups of HbS, which is suppressed, but not fully eliminated, by the cooperativity of oxygen binding enforced by a conformational change from T to R states (31). Thus, 1 − Θ is the fraction of fully deoxygenated HbS in the T state. Careful experiments have established an approximate linear correlation with slope one between 1 − Θ and the fraction of HbS associating to polymers (32). In the cases of HbS/HbF and HbS/HbA mixtures, we used total deoxygenated Hb to calculate C in Eq. 5, following the work by Li et al. (22). In addition, we used copolymerization theoretical equation to calculate the solubility (Eqs. 7 to 10) (22).
Activity coefficient, solubility, and supersaturation
The kinetics of HbS polymerization begins with the formation of a nucleus, followed by the growth of HbS fibers. We used the chemical potential μ to describe the tendency of deoxyhemoglobin to polymerize. The chemical potential μ of hemoglobin was calculated by (9)
| (3) |
where a = γC is the activity of deoxyhemoglobin with concentration C, γ is the activity coefficient accounting for the nonideality of a solution (33), μ0 is the standard μ value at a = 1, kB is the Boltzmann constant, and T is the temperature of the solution. The main source of nonideality in hemoglobin solutions is the excluded volume effect. Hence, γ depends on the total hemoglobin concentration Ct,
| (4) |
where the coefficients {Bi=2,…,7} are selected to be {8,15,24.48,35.30,47.4,65.9}, respectively, following prior studies in (11, 33). ϕ = VCt, where V = 0.79 ml/g is the specific volume of hemoglobin.
The driving force for HbS nucleation and polymerization is the supersaturation (12), , and
| (5) |
where Ce is the solubility, and ae = γeCe is the equilibrium activity, which is determined in fully deoxygenated hemoglobin solutions (9). The solubility of pure HbS, Ce,S, is a function of temperature and fractional hemoglobin O2 saturation. Eaton and Hofrichter (34) proposed an empirical relation for the solubility
| (6) |
where Ce0 = 0.321 g/cm3, T is the temperature in °C, and Θ is the fraction of oxy-HbS. When the HbS/HbA mixture is considered, the solubility Ce can be calculated from a relation accounting for copolymerization (22)
| (7) |
| (8) |
| (9) |
| (10) |
where XS and XA are the mole fraction of HbS and HbA respectively, cp= 0.69 g/ml is the concentration of hemoglobin in the fiber phase, γe and γe, S are the activity coefficients for the mixture (with concentration Ce) and for pure HbS (with concentration Ce, S), respectively, and e2 = 0.4 is the probability of the hybrid tetramer HbAS incorporating into the fiber relative to HbS. HbC has the same effect on fiber formation as HbA, and hence, it has the same effect on solubility. Considering the fact that the hybrid tetramer HbFS is not incorporated into the fiber, e2 = 0 was used to calculate the solubility of HbS/HbF mixture. Similar to HbF, e2 = 0 was used for HbA2.
Nucleation delay time
The nucleation delay time τd is defined as the length of the transition from a stable homogeneous solution to the moment when nucleation proceeds at a steady rate (13). It is determined from the dependency of the number of nuclei on time after supersaturation is imposed. We note that τd is characteristic of homogeneous nucleation only and is unaffected by the kinetics of growth and branching (9, 13). Here, τd defined in Eq. 11 and J defined in Eq. 12 characterize two distinct stages of the nucleation process: the transition of the supersaturated solution to steady-state nucleation and the formation of the first nucleus after steady state is reached. This delay time is distinct from both the 1/10th time, introduced in (3), and the expectancy time of the first polymer, which represents the sum of three characteristic time scales: τd + (JV)−1 + l/R, where J is the nucleation rate at steady state, V is the observed volume, l is the resolution limit of the method used for new phase detection, and R is the growth rate of the new phase domains. Prior experimental data showed that τd obeys an empirical relation (10)
| (11) |
By fitting the experimental data reported in (9), which were obtained at four HbS concentrations and in the temperature ranging from 19° to 37°C, we obtained τ0 ≈ 113.6 and kτ ≈ 3.446. During the deoxygenation period, τd is time dependent, and it decreases as the deoxygenation proceeds and reaches a steady value once the deoxygenation is completed.
Nucleation rate
After the delay time elapses, the homogeneous nucleation proceeds at steady rate J. To evaluate the probability of nucleation, we calculated J using
| (12) |
where ΔG* is the nucleation barrier (35). The nucleation barrier ΔG* is largely determined by the nucleus structure: the arrangement of the molecules in the nucleus core, possible distinct structures of the interface between the nucleus and the solution, possible compositional inhomogeneity, possible transient effects during nucleus evolution, and others. Unfortunately, nuclei have been imaged only in systems with spherical or near-spherical symmetry (36), and the data for these simple compounds only partially address the open questions on nucleus structure. No experimental evidence exists for the nucleus structure of HbS. Thus, we used a shortcut provided by the classical nucleation theory (37), which posits that the excess free energy of the nucleus ΔG*, i.e., the kinetic barrier for nucleation, can be evaluated from the number of molecules in the nucleus n* as
| (13) |
This relation is based on the capillary approximation, a fundamental tenet of the classical nucleation theory, which implies that the structure and composition of the nucleus are steady and identical to those of a large domain of the new phase and the interface thickness is negligible. Because of the difficulty in modeling or imaging the nucleus structure, we represented n* by a weak and discrete function of Δμ. The thermodynamic part of the classical nucleation theory shows that (35)
| (14) |
By fitting the experimental data reported in (8, 9), we obtained
| (15) |
In many protein polymerization processes, primary nucleation is nonclassical and proceeds via metastable prenucleation clusters. The properties of the mesoscopic clusters and their responses to environmental parameters have been documented. A rate law that accounts for the two-step nucleation mechanism has been developed (13). As demonstrated in these works, the functional form of the nucleation rate dependence on the supersaturation is not modified from that predicted by classical nucleation theory and is introduced as Eq. 12. The precursor clusters affect the value of the pre-exponential factor in the expression J0. The properties of the clusters are a sensitive function of the solution composition. We accounted for this sensitivity by defining relatively broad ranges of variation of the J0 and its equivalent for secondary nucleation J0s. J0 is estimated as 5.1 × 1010 cm−3 s−1 by fitting Eq. 12 with J = 4 × 107 cm−3 s−1 at Δμ/kBT = 1.1 (10).
Homogeneous (primary) nucleation: Homogeneous Poisson point process
Formation of homogeneous nuclei is a stochastic process, which satisfies the conditions of homogeneous Poisson point process with the constant intensity λ = JVc, where Vc ≈ 10−10cm3 is the volume of an RBC. Therefore, the number of homogeneous nuclei N(t) that exists in an RBC satisfies the following equations
| (16) |
| (17) |
where τc + τd ≤ t1 ≤ t2 and P{N(t1, t2] = n} is the probability of generating n nuclei during time interval (t1, t2]. According to the law of large numbers, we can further obtain
| (18) |
| (19) |
where denotes the expectation operator. An acceptance-rejection procedure was used to generate the independent and identically distributed samples of Poisson point process.
Growth rate of HbS fibers
Once a nucleus is generated in the solution, HbS monomers start to associate to the two opposing ends, forming a linear HbS fiber. HbS fibers grow with a rate proportional to the activity a of deoxy-HbS (3, 38)
| (20) |
where β is a temperature-dependent kinetic coefficient and it can be computed by
| (21) |
where β0 ≈ 4.21 × 108mM−1s−1 ≈ 29368.6 μm(g/dl)−1s−1 and Ea = 9.14 kcal/mol is the activation energy (38). Note that 1 μm of HbS fiber contains approximately 2222 molecules, due to the 63-Å molecular spacing and the presence of 14 molecules in the fiber cross section.
Heterogeneous (secondary) nucleation: Inhomogeneous Poisson point process
We assumed that the nucleation of new HbS fibers on the top of existing ones can be described by the same set of equations that describe the homogeneous nucleation of fibers except that the nucleation barrier is reduced by two-thirds (39), equivalent to assuming that . As a result, the heterogeneous nucleation rate was calculated by . Since the potential contacts on the surface of the fiber with incoming molecules are similar to those within the fiber, we assumed that J0s is much larger than J0; we chose J0s = 5000J0. A parametric study of the ratio J0s/J0 indicated that the fraction of sickled RBCs is insensitive to this ratio when J0s > 1000J0.
Similar to homogeneous nucleation, generation of heterogeneous nuclei on top of each existing fiber is a Poisson point process. However, the intensity λs(t) is a function of time as it is proportional to the fiber length
| (22) |
where l(t) is the fiber length at time t, and As is the area near the primary fiber where a heterogeneous nucleation may occur. We assumed that the width of this area is equal to the diameter of a fiber, i.e., 22, and thus, .
The number of heterogeneous nuclei Ns(t) on top of each existing fiber satisfies the relation
| (23) |
| (24) |
where t1 ≤ t2 are moments after the primary fiber nucleate and start growth. On the basis of the law of large numbers, we have
| (25) |
Notably, heterogeneous nucleation also occurs on top of fibers originated from previous heterogeneous nuclei, resulting in the exponential growth of polymerized HbS (3). A detailed flow chart summarizing all the quantities and parameters in the kinetic model is illustrated in fig. S1.
Supplementary Material
Acknowledgments
We would like to thank W. A. Eaton of NIH for providing valuable suggestions during the preparation of this work. We would also like to thank F. Ferrone of Drexel University for helpful discussion. We want to thank E. Du for providing the experimental data. Funding: This work was supported by National Heart, Lung, and Blood Institute grant no. U01HL114476. Author contributions: P.G.V. conceived the model. P.G.V. and L.L. developed the model. L.L. implemented the computer code. L.L., Z.L., and H.L. performed computations. L.L., Z.L., H.L., X.L., P.G.V., and G.E.K. analyzed data. L.L., Z.L., H.L., X.L., P.G.V., and G.E.K. wrote the paper. G.E.K. supervised the project. Competing interests: The authors declare that they have no competing interests. Data and materials availability: All data needed to evaluate the conclusions in the paper are present in the paper and/or the Supplementary Materials. Additional data related to this paper may be requested from the authors.
SUPPLEMENTARY MATERIALS
Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/5/8/eaax3905/DC1
Section S1. Depletion, diffusion, and concentration of hemoglobin near a growing fiber
Section S2. Polymerization of deoxygenated HbS
Section S3. Sensitivity analysis of RBC sickling criterion
Section S4. Sickling of patient-specific RBCs in microfluidic channel under hypoxia
Section S5. Determinants of RBC sickling time in the kinetic model
Section S6. Model parameters
Section S7. Model inputs
Fig. S1. Detailed flow chart of the kinetic model.
Fig. S2. Predicted nucleation barriers near a growing fiber.
Fig. S3. Simulation of HbS polymerization in purified HbS solution.
Fig. S4. Sensitivity of model predictions.
Fig. S5. Evolution of fractions of sickled RBCs under hypoxia for seven SCD patients.
Fig. S6. Cumulative contributions to the RBC sickling time factors 1 to 5.
Table S1. Patient-specific RBC variables for seven SCD patients examined in (24).
Table S2. The default values of model parameters and their varying ranges in the sensitivity analysis.
Table S3. Three sets of model inputs following the in vivo study (20) (condition I), in vitro study (24) (condition II), and the screening assay (22) (condition III).
REFERENCES AND NOTES
- 1.Pauling L., Itano H. A., Singer S. J., Wells I. C., Sickle cell anemia, a molecular disease. Science 110, 543–548 (1949). [DOI] [PubMed] [Google Scholar]
- 2.Monod J., Wyman J., Changeux J.-P., On the nature of allosteric transitions: A plausible model. J. Mol. Biol. 12, 88–118 (1965). [DOI] [PubMed] [Google Scholar]
- 3.Ferrone F. A., Hofrichter J., Eaton W. A., Kinetics of sickle hemoglobin polymerization: II. A double nucleation mechanism. J. Mol. Biol. 183, 611–631 (1985). [DOI] [PubMed] [Google Scholar]
- 4.Piel F. B., Steinberg M. H., Rees D. C., Sickle cell disease. N. Engl. J. Med. 376, 1561–1573 (2017). [DOI] [PubMed] [Google Scholar]
- 5.Kato G. J., Piel F. B., Reid C. D., Gaston M. H., Ohene-Frempong K., Krishnamurti L., Smith W. R., Panepinto J. A., Weatherall D. J., Costa F. F., Vichinsky E. P., Sickle cell disease. Nat. Rev. Dis. Primers. 4, 18010 (2018). [DOI] [PubMed] [Google Scholar]
- 6.Eaton W. A., Hofrichter J., The biophysics of sickle cell hydroxyurea therapy. Science 268, 1142–1143 (1995). [DOI] [PubMed] [Google Scholar]
- 7.Quinn C. T., L-glutamine for sickle cell anemia: More questions than answers. Blood 132, 689–693 (2018). [DOI] [PubMed] [Google Scholar]
- 8.Eaton W. A., Bunn H. F., Treating sickle cell disease by targeting HbS polymerization. Blood 129, 2719–2726 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Galkin O., Vekilov P. G., Mechanisms of homogeneous nucleation of polymers of sickle cell anemia hemoglobin in deoxy state. J. Mol. Biol. 336, 43–59 (2004). [DOI] [PubMed] [Google Scholar]
- 10.Galkin O., Nagel R. L., Vekilov P. G., The kinetics of nucleation and growth of sickle cell hemoglobin fibers. J. Mol. Biol. 365, 425–439 (2007). [DOI] [PubMed] [Google Scholar]
- 11.Cellmer T., Ferrone F. A., Eaton W. A., Universality of supersaturation in protein-fiber formation. Nat. Struct. Mol. Biol. 23, 459–461 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Hofrichter J., Ross P. D., Eaton W. A., Supersaturation in sickle cell hemoglobin solutions. Proc. Natl. Acad. Sci. U.S.A. 73, 3035–3039 (1976). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Kashchiev D., Vekilov P. G., Kolomeisky A. B., Kinetics of two-step nucleation of crystals. J. Chem. Phys. 122, 244706 (2005). [DOI] [PubMed] [Google Scholar]
- 14.Christoph G. W., Hofrichter J., Eaton W. A., Understanding the shape of sickled red cells. Biophys. J. 88, 1371–1376 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Lu L., Li H., Bian X., Li X., Karniadakis G. E., Mesoscopic adaptive resolution scheme toward understanding of interactions between sickle cell fibers. Biophys. J. 113, 48–59 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Tang Y.-H., Lu L., Li H., Evangelinos C., Grinberg L., Sachdeva V., Karniadakis G. E., OpenRBC: A fast simulator of red blood cells at protein resolution. Biophys. J. 112, 2030–2037 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Wang J. C., Turner M. S., Agarwal G., Kwong S., Josephs R., Ferrone F. A., Briehl R. W., Micromechanics of isolated sickle cell hemoglobin fibers: Bending moduli and persistence lengths. J. Mol. Biol. 315, 601–612 (2002). [DOI] [PubMed] [Google Scholar]
- 18.Zhu W., von dem Bussche A., Yi X., Qiu Y., Wang Z., Weston P., Hurt R. H., Kane A. B., Gao H., Nanomechanical mechanism for lipid bilayer damage induced by carbon nanotubes confined in intracellular vesicles. Proc. Natl. Acad. Sci. U.S.A. 113, 12374–12379 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Cohen A. E., Mahadevan L., Kinks, rings, and rackets in filamentous structures. Proc. Natl. Acad. Sci. U.S.A. 100, 12141–12146 (2003). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Serjeant G. R., Petch M. C., Serjeant B. E., The in vivo sickle phenomenon: A reappraisal. J. Lab. Clin. Med. 81, 850–856 (1973). [PubMed] [Google Scholar]
- 21.Lew V. L., Raftos J., Sorette M., Bookchin R. M., Mohandas N., Generation of normal human red cell volume, hemoglobin content, and membrane area distributions by “birth” or regulation? Blood 86, 334–341 (1995). [PubMed] [Google Scholar]
- 22.Li Q., Henry E. R., Hofrichter J., Smith J. F., Cellmer T., Dunkelberger E. B., Metaferia B. B., Jones-Straehle S., Boutom S., Christoph G. W., Wakefield T. H., Link M. E., Staton D., Vass E. R., Miller J. L., Hsieh M. M., Tisdale J. F., Eaton W. A., Kinetic assay shows that increasing red cell volume could be a treatment for sickle cell disease. Proc. Natl. Acad. Sci. U.S.A. 114, E689–E696 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Hogg J. C., Coxson H. O., Brumwell M. L., Beyers N., Doerschuk C. M., MacNee W., Wiggs B. R., Erythrocyte and polymorphonuclear cell transit time and concentration in human pulmonary capillaries. J. Appl. Physiol. 77, 1795–1800 (1994). [DOI] [PubMed] [Google Scholar]
- 24.Du E., Diez-Silva M., Kato G. J., Dao M., Suresh S., Kinetics of sickle cell biorheology and implications for painful vasoocclusive crisis. Proc. Natl. Acad. Sci. U.S.A. 112, 1422–1427 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Ware R. E., Optimizing hydroxyurea therapy for sickle cell anemia. ASH Educ. Progr. Book 2015, 436–443 (2015). [DOI] [PubMed] [Google Scholar]
- 26.Sobol I. M., Global sensitivity indices for nonlinear mathematical models and their monte carlo estimates. Math. Comput. Simul. 55, 271–280 (2001). [Google Scholar]
- 27.Poillon W. N., Kim B. C., 2, 3-diphosphoglycerate and intracellular pH as interdependent determinants of the physiologic solubility of deoxyhemoglobin S. Blood 76, 1028–1036 (1990). [PubMed] [Google Scholar]
- 28.Kaul D. K., Fabry M. E., Windisch P., Baez S., Nagel R. L., Erythrocytes in sickle cell anemia are heterogeneous in their rheological and hemodynamic characteristics. J. Clin. Investig. 72, 22–31 (1983). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Brousse V., Buffet P., Rees D., The spleen and sickle cell disease: The sick (led) spleen. Br. J. Haematol. 166, 165–176 (2014). [DOI] [PubMed] [Google Scholar]
- 30.Bouwer S. T., Hoofd L., Kreuzer F., Diffusion coefficients of oxygen and hemoglobin measured by facilitated oxygen diffusion through hemoglobin solutions. Biochim. Biophys. Acta 1338, 127–136 (1997). [DOI] [PubMed] [Google Scholar]
- 31.Perutz M. F., Wilkinson A., Paoli M., Dodson G. G., The stereochemical mechanism of the cooperative effects in hemoglobin revisited. Annu. Rev. Biophys. Biomol. Struct. 27, 1–34 (1998). [DOI] [PubMed] [Google Scholar]
- 32.Yosmanovich D., Rotter M., Aprelev A., Ferrone F. A., Calibrating sickle cell disease. J. Mol. Biol. 428, 1506–1514 (2016). [DOI] [PubMed] [Google Scholar]
- 33.Minton A. P., Excluded volume as a determinant of macromolecular structure and reactivity. Biopolymers 20, 2093–2120 (1981). [Google Scholar]
- 34.Eaton W. A., Hofrichter J., Sickle cell hemoglobin polymerization. Adv. Protein Chem. 40, 63–279 (1990). [DOI] [PubMed] [Google Scholar]
- 35.Vekilov P. G., Nucleation. Cryst. Growth Des. 10, 5007–5019 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Yau S.-T., Vekilov P. G., Quasi-planar nucleus structure in apoferritin crystallization. Nature 406, 494–497 (2000). [DOI] [PubMed] [Google Scholar]
- 37.Gibbs J. W., On the equilibrium of heterogeneous substances. Trans. Connecticut Acad. Arts Sci. 3, 108–248 (1876). [Google Scholar]
- 38.Aprelev A., Liu Z., Ferrone F. A., The growth of sickle hemoglobin polymers. Biophys. J. 101, 885–891 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.D. Kashchiev, Nucleation (Butterworth-Heinemann, 2000). [Google Scholar]
- 40.Keller K. H., Canales E. R., Yum S. I., Tracer and mutual diffusion coefficients of proteins. J. Phys. Chem. 75, 379–387 (1971). [DOI] [PubMed] [Google Scholar]
- 41.Briehl R. W., Nucleation, fiber growth and melting, and domain formation and structure in sickle cell hemoglobin gels. J. Mol. Biol. 245, 710–723 (1995). [DOI] [PubMed] [Google Scholar]
- 42.Ferrone F. A., Hofrichter J., Eaton W. A., Kinetics of sickle hemoglobin polymerization: I. Studies using temperature-jump and laser photolysis techniques. J. Mol. Biol. 183, 591–610 (1985). [DOI] [PubMed] [Google Scholar]
- 43.Bishop M. F., Ferrone F. A., Kinetics of nucleation-controlled polymerization. A perturbation treatment for use with a secondary pathway. Biophys. J. 46, 631–644 (1984). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Cohen S. I. A., Vendruscolo M., Welland M. E., Dobson C. M., Terentjev E. M., Knowles T. P. J., Nucleated polymerization with secondary pathways. I. Time evolution of the principal moments. J. Chem. Phys. 135, 065105 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Michaels T. C. T., Cohen S. I. A., Vendruscolo M., Dobson C. M., Knowles T. P. J., Hamiltonian dynamics of protein filament formation. Phys. Rev. Lett. 116, 038101 (2016). [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/5/8/eaax3905/DC1
Section S1. Depletion, diffusion, and concentration of hemoglobin near a growing fiber
Section S2. Polymerization of deoxygenated HbS
Section S3. Sensitivity analysis of RBC sickling criterion
Section S4. Sickling of patient-specific RBCs in microfluidic channel under hypoxia
Section S5. Determinants of RBC sickling time in the kinetic model
Section S6. Model parameters
Section S7. Model inputs
Fig. S1. Detailed flow chart of the kinetic model.
Fig. S2. Predicted nucleation barriers near a growing fiber.
Fig. S3. Simulation of HbS polymerization in purified HbS solution.
Fig. S4. Sensitivity of model predictions.
Fig. S5. Evolution of fractions of sickled RBCs under hypoxia for seven SCD patients.
Fig. S6. Cumulative contributions to the RBC sickling time factors 1 to 5.
Table S1. Patient-specific RBC variables for seven SCD patients examined in (24).
Table S2. The default values of model parameters and their varying ranges in the sensitivity analysis.
Table S3. Three sets of model inputs following the in vivo study (20) (condition I), in vitro study (24) (condition II), and the screening assay (22) (condition III).


