Robustifying Trial-Derived Optimal Treatment Rules for A Target Population

Abstract

Treatment rules based on individual patient characteristics that are easy to interpret and disseminate are important in clinical practice. Properly planned and conducted randomized clinical trials are used to construct individualized treatment rules. However, it is often a concern that trial participants lack representativeness, so it limits the applicability of the derived rules to a target population. In this work, we use data from a single trial study to propose a two-stage procedure to derive a robust and parsimonious rule to maximize the benefit in the target population. The procedure allows a wide range of possible covariate distributions in the target population, with minimal assumptions on the first two moments of the covariate distribution. The practical utility and favorable performance of the methodology are demonstrated using extensive simulations and a real data application.

1. Introduction

In the new era of personalized medicine, it has been advocated that treatments should be recommended according to individual patient characteristics to account for considerable heterogeneity among patients’ responses to different treatments (Hayes et al., 2007; Hamburg and Collins, 2010). Randomized clinical trials (RCTs) are ideal for constructing such rules, since they provide internal validity by ensuring consistency, positivity and no unmeasured confounders (Greenland, 1990; Hernán and Robins, 2006) that may be violated in observational studies.

Sophisticated statistical methods have been developed to estimate optimal individualized treatment rules using data from randomized trials. Regression-based methods estimate outcome as a function of patient covariates and treatment, and then select the treatment that maximizes the predicted outcome for each individual (Brinkley et al., 2010; Qian and Murphy, 2011; Kang et al., 2014). Some recent developments directly search for the individualized treatment rules that maximize the benefit for future patients (Zhang et al., 2012; Zhao et al., 2012). When the primary outcome of interest is survival time subject to right censoring, some methods have been proposed in this regard using either regression-based methods Goldberg and Kosorok (2012); Huang et al. (2014) or direct search methods Zhao et al. (2015).

The derived optimal rules sometimes are complex and nonlinear, so they are highly variable and may not be practically useful. To better inform clinical practice, it is more desirable that a recommended treatment rule be easy to interpret and disseminate. As suggested in Orellana et al. (2010), the class of practically enforceable candidate regimes is significantly smaller than the class of arbitrary functions of covariates. Usually these regimes are comprised of functions that only depend on a small set of covariates, and are indexed by a set of finite dimensional parameters. Statistically, Qian and Murphy (2011) used a rich linear basis for better modeling the outcome, with a sparsity penalty imposed to preserve the parsimoniousness of the resulting rule, while most works considered and recommended rules from a linear functional class.

Unfortunately, it has been well known that the RCT may have limited generalizability when the distribution of treatment effect modifiers in trial participants differs from the one in a target population (Buchanan et al., 2016). A parsimonious treatment rule constructed from trial data using current methods cannot be directly carried over to a target population, when the population characteristics are different between the two. Some attempts have been made to adjust population difference using inverse probability-of-selection weight method (Cole and Stuart, 2010). This, however, requires complete knowledge of population selection mechanism, and it is yet to be extended to the context of developing optimal treatment rules.

In this paper, we aim to robustify the treatment rule from a trial so that the robustified rule is (1) parsimonious (linear in patient features in particular); (2) still maximizes a general benefit criterion when applied to the target population. We provide a new framework, called minimax linear decision (MiLD), to robustify the treatment rule. MiLD enables the construction of a linear rule that optimizes the general benefit function in the target population, allowing differences between the target and the trial populations in the means and covariances in treatment effect modifiers. It can be further extended to construct nonlinear rules using the ‘kernel trick’, which avoids the explicit feature mapping but only relies on a kernel function to learn a nonlinear decision boundary. Regardless, MiLD requires no further assumptions beyond the first two moments of the covariate distributions. Moreover, our developed framework is applicable to all types of outcomes.

The remainder of the paper is organized as follows. In Section 2, we formulate the problem of finding a robust and parsimonious treatment rule using data from a clinical trial. The proposed method, MiLD, is then developed to optimize a general benefit function in the target population, allowing the covariate distribution to be different between the two populations. Consistency and convergence rate results are established for the proposed method. We present simulation studies to evaluate performances of the proposed method in Section 4. We further illustrate the method using a data example from a US NIH funded SWOG trial on castration-resistant prostate cancer patients in Section 5. The proofs of theoretical results are given in the Appendix.

2. Methodology

2.1. Background and the optimal treatment rule

Let T denote the outcome of interest, A ∈ {−1, 1} denote a binary treatment, and X = (X₁, …,X_m)^T ∈ ℝ^m denote patient covariates. We assume the dimension is small to moderate, and fixed. The outcome could be a continuous, discrete, or time-to-event outcome subject to censoring. A treatment regime $d\in \mathcal{D}$ is a function mapping from the space of X to the space of treatments. A future patient with X = x is then assigned with treatment d(x). Let T(a) denote the potential outcome under treatment a ∈ {−1, 1} (Rubin, 1978), and T(d) = T{d(X)} be the potential outcome under the rule d for the given covariate X. The quality of d can be measured by the marginal mean outcome E{T(d)}, which represents the trial population mean outcome were all patients in the trial population to receive treatment according to d. We denote this quantity as $\mathcal{V}(d)$, which is also called the value function of d. The optimal treatment regime d* maximizes $\mathcal{V}(d)$ over all possible d. We assume that in the trial,

• (A1)P(A = a|X) > 0 with probability one for a ∈ {−1, 1};
• (A2){T(−1),T(1)} are independent of A conditional X;
• (A3)consistency so that $T(a)={\sum }_{a}I(A=a)T$.

Since $\mathcal{V}(d)=E\{T(d)\}=E_X(E[T\{d(X)\}|X\}])$, where the outer expectation E_X(·) is taken with respect to the marginal distribution of X in the trial population, the optimal treatment for any patient with characteristics x is d*(x) = argmax_a∈{−1,1}E{T(a)|X = x} when there is no restriction of the functional form of the rule. These assumptions are typically standard and satisfied in randomized clinical trials (Robins et al., 2000), because application of the intervention to any individual is under the control of the investigator. This is however, not guaranteed in observational studies. For example, consistency assumption can be violated given that there could be variations of treatment, and each of them may have a different causal effect on the outcome. In addition, noncompliance can be severe in observational studies, where some subjects may never take what they are asked to take. If (A1)-(A3) are satisfied, the optimal treatment rule is

$$d*(x)=\mathrm{sign}\left\{f*(x)\right\},\text{where}f*(x)=E(T|X=x,A=1)-E(T|X=x,A=-1).$$

To assess the overall benefit of the obtained rule when applied to the target population, we let p_X(x) denote the distribution of X in the trial population, and q_X(x) denote the distribution of X in the target population, which is not necessarily the same as p_X(x). Furthermore, we assume

• (A4)the support of q_X(x) is contained in the support of p_X(x), i.e., there is no under-coverage in the trial study;
• (A5)the potential outcome mean given X is the same between the trial population and the target population. Thus, the treatment works the same in both populations.

Thus, the only difference between the two populations is due to the covariate distributions. Let P^q denote the distribution of X in the target population and P^p denote the distribution of X in the trial population. Let $\tilde{E}$ denote the expectation is taken with respect to the distribution of X in the target population. Under (A4) and (A5), it is easy to observe that the expected outcome of rule d(X) for the target population is

$$\begin{gathered} \tilde{\mathcal{V}}(d)=\tilde{E}[T\{d(X)\}]=\int E[T\{d(X)\left\}\right|X]d{P}^q \\ =\int E[T\{d(X)\}|X]\frac{d{P}^q}{d{P}^p}d{P}^p=E_X\left(E[T\{d(X)\left\}\right|X]\frac{q_X(X)}{p_X(X)}\right), \end{gathered}$$

where E_X[·] denotes the expectation under X ~ p_X(x). Consequently, the optimal rule obtained from the trial population, d*, is also the optimal for the target population if there is not any restriction to the formulation in d*.

2.2. A General Quality Value of Treatment Rules for the Target Population

We propose a general criterion assessing the quality of a decision rule for the target population, which includes both the value function and the correct allocation rate to the optimal rule as special cases. For a given rule d(X), the proposed quality assessment in the target population is defined as

$$\tilde{\mathcal{B}}(d)=\tilde{E}\left[W(X)I\left\{d(X)=d*(X)\right\}\right],$$

where W(X) is a non-negative function, essentially a reward if the treatment rule d(x) is the optimal.

The quality value in the definition has a different interpretation depending on the choice of W(x). For example, let W(x) = W₁(x) = E{T|A = d*(x),X = x}−E{T|A ≠ d*(x),X = x} = |f*(x)|. That is, for subject with covariate X = x, W(x) is the gain if he/she follows treatment rule d*. $\tilde{\mathcal{B}}(d)$ achieves optimal if d = d*. This is because $\tilde{\mathcal{B}}(d)=\tilde{\mathcal{V}}(d)+\tilde{E}\left\{T\left(-d*\right)\right\}$. Hence, maximizing $\tilde{\mathcal{B}}(d)$ is equivalent to maximizing the value function in the target population. If we set W(X) = W₂(X) ≡ 1, then $\tilde{\mathcal{B}}(d)=\tilde{P}\left\{d\left(X\right)=d*\left(X\right)\right\}$ and the criterion corresponds to the correct allocation rate of the optimal treatment. Additionally, in practice, W(X) could allow more general trade off between the benefit of optimal treatment and the relative cost of giving optimal treatment to patients instead of standard care. In this paper, we will focus on the choice of W = W₁ and W₂.

2.3. Learning Robust Linear Rules for the Target Population

In many practices, since the set of enforceable treatment rules are usually restrictive and cannot be arbitrary, a parsimonious and interpretable decision rule is preferred. In particular, we focus on a linear decision rule, i.e., d(x) = sign{f(x)} where f(x) = x^Tβ₁ +β₀. A patient x is assigned to treatment 1 if x^Tβ₁ + β₀ ≥ 0 and treatment −1 otherwise. For example, let the potential outcome model be $E[\log \{\tilde{T}(a)\}|X]=\left(2I\left[{\{3X/4+\sin (X)/4-2\}}^2-1\right]-1\right)a$. The optimal rule d*(x) = 1 if 3x/4 + sin(x)/4 − 1 ≤ 0 or 3x/4 + sin(x)/4 − 3 > 0, and d*(x) = −1 otherwise. Consider the space of linear decision rules with ${\mathcal{D}}_L=\{d(X)=\mathrm{sign}\left({\beta }_0+{\beta }_{1}X\right),{\beta }_0,{\beta }_1\in ℝ\}.$ Therefore d*(x) is highly nonlinear, and $d^{*}(x)\notin {\mathcal{D}}_L.$ Assume that X ~ N(2, 1) and X ~ N(4, 1) in the trial and target population, respectively. Then the optimal linear rule is $d_L^{*}(X)=\mathrm{sign}(X-0.9)$ using the trial data. However, sign(−X +0.28) should be the optimal linear rule in the target population, which lead to a benefit of 0.997, versus a benefit of −0.387 using the optimal rule derived from the trial data. Hence, the optimal linear rules could be substantially different between the two populations.

We should note that unless the true optimal rule is linear itself, once restricted to such a class of linear rules, the optimal rule within this class may no longer be the optimal for the target population, since both p_X(x) and q_X(x) can be very different. It is thus desirable to guarantee that $\tilde{\mathcal{B}}(d)$ is not small, regardless of X and which treatment is optimal; and ideally, the larger the better. To this end, we propose the following method, namely, Minimax Linear Decisions (MiLD). Note that

$$\begin{gathered} \tilde{\mathcal{B}}(d)=\tilde{E}\left[W(X)I\{d(X)=1\}|d*(X)=1\right]\tilde{P}\left\{d*(X)=1\right\} \\ +\tilde{E}\left[W(X)I\{d(X)=-1\}|d*(X)=-1\right]\tilde{P}\left\{d*(X)=-1\right\}. \end{gathered}$$

We introduce a lower bound α on $\tilde{E}\{W(X)I\left\{\mathrm{sign}\left(X^T{\beta }_1+{\beta }_0\right)=j|d*(X)=j\right\},j=\pm 1$, which represents the expected benefit that would have been obtained if the patients were to receive treatment j, whose optimal treatments would indeed be j in the target population. Hence, α controls the worst case overall benefits for each group, and we set the same lower bound for both quantities for simplicity. We then consider the following optimization problem:

$$\begin{gathered} \underset{{}_{\alpha ,{\beta }_1,{\beta }_0}}{\max }\alpha \text{subject}\text{to}\underset{X~f_1}{\inf }\tilde{E}\left\{W(X)I\left(X^{\top }{\beta }_1+{\beta }_0\ge 0\right)|d*(X)=1\right\}\ge \alpha , \\ \underset{X~f_{-1}}{\inf }\tilde{E}\left\{W(X)I\left(X^{\top }{\beta }_1+{\beta }_0<0\right)|d*(X)=-1\right\}\ge \alpha , \end{gathered}$$ (1)

where f₁ and f₋₁ are the density of X in patients whose optimal treatment are 1 or −1 respectively. That is, we want to guarantee the quality of being given optimal treatment as large as possible among those who should indeed be treated with the same treatment.

Let ${\tilde{q}}_j(x)$ denote the density of X for patients with d*(X) = j, j = ±1 in the target population. Then

$$\begin{gathered} \tilde{E}\left\{W(X)I\left(X^{\top }{\beta }_1+{\beta }_0\ge 0\right)|d*(X)=j\right\}=\int W(x)I\left(x^{\top }{\beta }_1+{\beta }_0\ge 0\right)q_j(x)dx \\ \propto \check{P}\left(X^{†\top }{\beta }_1+{\beta }_0\ge 0\right), \end{gathered}$$

where the density of X^† is proportional to ${\tilde{q}}_j\left(x^{†}\right)W\left(x^{†}\right).$ Hence, (1) is equivalent to

$$\begin{gathered} \underset{{}_{\alpha ,{\beta }_1,{\beta }_0}}{\max }\alpha \text{subject}\text{to}\underset{X^{†}~f_1^{†}}{\inf }\check{P}\left(X^{†\top }{\beta }_1+{\beta }_0\ge 0\right)\ge \alpha , \\ \underset{X^{†}~f_{-1}^{†}}{\inf }\check{P}\left(X^{{†}^{\top }}{\beta }_1+{\beta }_0<0\right)\ge \alpha , \end{gathered}$$ (2)

where $f_1^{†}$ and $f_{-1}^{†}$ are the density of X^† in patients with optimal treatment being 1 or −1 respectively.

However, $f_1^{†}$ and $f_{-1}^{†}$ could be very different, and difficult to characterize based on the trial data. We propose to quantify the difference between the target population and the trial population in terms of the first two moment conditions, without making any specific distributional assumptions for the two populations. In other words, the covariate moments of X^† in patients with d*(x) = j, j = ±1 in the target population could be different from that of the trial population to some degree.

Suppose that the means of covariate X^† are ${\tilde{\mu }}_j^{†}$, and intraclass covariance matrices are ${\tilde{\mathrm{\Sigma }}}_j$ for patients with d*(X) = j in the target population, and ${\mu }_j^{†}$ and ${\mathrm{\Sigma }}_j^{†}$, j = ±1 respectively, in the trial population under the new density. We assume that the quantities in the target population belong to

$${\mathcal{U}}_j^{†}=\left\{\left({\tilde{\mu }}_j^{†},{\tilde{\mathrm{\Sigma }}}_j^{†}\right):{\left({\tilde{\mu }}_j^{†}-{\mu }_j^{†}\right)}^{\top }{\tilde{\mathrm{\Sigma }}}_j^{†}\left({\tilde{\mu }}_j^{†}-{\mu }_j^{†}\right)\le {\nu }^2,{\Vert {\tilde{\mathrm{\Sigma }}}_j^{†}-{\mathrm{\Sigma }}_j^{†}\Vert }_F\le {\rho }_j\right\},j=\pm 1.$$ (3)

Here, ν ≥ 0 and ρ_j ≥ 0 are known constants, and ∥ · ∥_F is the Frobenius norm defined as $\Vert M{\Vert }_F^2=\mathrm{Tr}\left(M^{\top }M\right)$. Such conditions define the closeness of the target population to the trial population. ${\mathcal{U}}_j^{†}$ suggests that the mean ${\tilde{\mu }}_j^{†}$ in the target population belongs to an elliptical region around ${\mu }_j^{†}$ with shape determined by the covariance ${\tilde{\mathrm{\Sigma }}}_j^{†}$, j = ±1. The covariance matrix ${\tilde{\mathrm{\Sigma }}}_j^{†}$, centered around ${\mathrm{\Sigma }}_j^{†}$, can also vary to certain degrees. Clearly, the larger ν or ρ_j, the more different the two populations are. (2) is consequently written as

$$\begin{gathered} \underset{{}_{\alpha ,{\beta }_1,{\beta }_0}}{\max }\alpha \text{subject}\text{to}\underset{X^{†}~\left({\tilde{\mu }}_1^{†},{\tilde{\mathrm{\Sigma }}}_1^{†}\right)\in {\mathcal{U}}_1^{†}}{\inf }\check{P}\left(X^{{†}^{\top }}{\beta }_1+{\beta }_0\ge 0\right)\ge \alpha , \\ \underset{X^{†}~\left({\tilde{\mu }}_{-1}^{†},{\tilde{\mathrm{\Sigma }}}_{-1}^{†}\right)\in {\mathcal{U}}_{-1}^{†}}{\inf }\check{P}\left(X^{†\top }{\beta }_1+{\beta }_0<0\right)\ge \alpha . \end{gathered}$$ (4)

This yields a linear decision rule that safeguards against the possible difference of the distribution of X between the trial and the target populations. Such robustness of the treatment regime estimation is mainly due to the minimum requirements on the means and covariances. The above objective function has a similar form to the minimax probability machine techniques developed in Lanckriet et al. (2003), and their techniques for deriving the optimal linear rule can be employed if $\left({\tilde{\mu }}_j^{†},{\tilde{\mathrm{\Sigma }}}_j^{†}\right),j=\pm 1$, were known. The key step is to recognize that the condition ${\inf }_{X^{†}~\left({\tilde{\mu }}_j^{†},{\tilde{\mathrm{\Sigma }}}_j^{†}\right)}P\left(X^{†\top }{\beta }_1+{\beta }_0\ge 0\right)\ge \alpha$ holds if and only if

$${\beta }_0+{\tilde{\mu }}_j^{†\top }{\beta }_1\ge \kappa (\alpha )\sqrt{{\beta }_1^{\top }{\tilde{\mathrm{\Sigma }}}_j^{†}{\beta }_1},j=\pm 1,$$ (5)

by applying the generalized Chebychev inequality (Marshall and Olkin, 1960), where $\kappa (\alpha )=\sqrt{\alpha /(1-\alpha )}$ (Lemma 1, Lanckriet and others (2003)). The constraint (5) is imposed on the distance with respect to the mean of the covariates within the class, taking into account the effect of the covariance matrices, which could be representable of the class. In other words, we search a line such that the normalized margin between the means of classes is as large as possible. Consequently, (4) is equivalent to

$$\begin{gathered} \underset{\alpha ,{\beta }_1,{\beta }_0}{\max }\alpha \text{subject}\text{to}{\beta }_0+{\tilde{\mu }}_1^{†\top }{\beta }_1\ge \kappa (\alpha )\sqrt{{\beta }_1^{\top }{\tilde{\mathrm{\Sigma }}}_1^{†}{\beta }_1} \\ {\beta }_0+{\tilde{\mu }}_{-1}^{†\top }{\beta }_1\ge \kappa (\alpha )\sqrt{{\beta }_1^{\top }{\tilde{\mathrm{\Sigma }}}_{-1}^{†}{\beta }_1}. \end{gathered}$$

As shown in the Appendix, a further simplified objective function can be obtained as

$$\underset{{}_{{\beta }_1}}{\min }\sqrt{{\beta }_1^{\top }\left({\mathrm{\Sigma }}_1^{†}+{\rho }_1{I}_p\right){\beta }_1}+\sqrt{{\beta }_1^{\top }\left({\mathrm{\Sigma }}_{-1}^{†}+{\rho }_{-1}{I}_p\right){\beta }_1},$$ (6)

subject to ${\beta }_1^{\top }\left({\mu }_1^{†}-{\mu }_{-1}^{†}\right)=1$. We can eliminate the equality constraint in (6) by letting β₁ = β₁₀ + Fu, where u ∈ ℝ^p−1, ${\beta }_{10}=\left({\mu }_1^{†}-{\mu }_{-1}^{†}\right)/{\Vert {\mu }_1^{†}-{\mu }_{-1}^{†}\Vert }_2^2$ is a p × (p − 1) matrix. Let h denote the position of the maximum element in ${\mu }_1^{†}-{\mu }_{-1}^{†}$. F is constructed from a (p − 1) × (p − 1) identity matrix, with $-\left({\mu }_1^{†}-{\mu }_{-1}^{†}\right)/\max \left({\mu }_1^{†}-{\mu }_{-1}^{†}\right)$ inserted into the h^th row. We can see that F is an orthogonal matrix whose columns span the subspace of vectors orthogonal to ${\mu }_1^{†}-{\mu }_{-1}^{†}$. Hence, the optimization problem can be written as

$$\underset{{\beta }_1}{\min }\sqrt{{\left({\beta }_{10}+Fu\right)}^{\top }\left({\mathrm{\Sigma }}_1^{†}+{\rho }_1{I}_p\right)\left({\beta }_{10}+Fu\right)}+\sqrt{{\left({\beta }_{10}+Fu\right)}^{\top }\left({\mathrm{\Sigma }}_{-1}^{†}+{\rho }_{-1}{I}_p\right)({\beta }_{10}+Fu}.$$

The lower bound on the worst case allocation rate α* = (κ* − ν)²/{1 + (κ* − ν)²}, and ν should not exceed κ*. Here, $\kappa *={\left\{\sqrt{{\beta }_1^{*\top }\left({\tilde{\mathrm{\Sigma }}}_{-1}^{†}+{\rho }_{-1}{I}_p\right){\beta }_1^{*}}+\sqrt{{\beta }_1^{*\top }\left({\tilde{\mathrm{\Sigma }}}_1^{†}+{\rho }_1{I}_p\right){\beta }_1^{*}}\right\}}^{-1}$ and ν is defined in (3). More details can be found in the Appendix.

Remark 1 Although the MiLD is proposed to identify a robust linear rule, it can be easily generalized using nonlinear kernel functions. We seek a decision rule in the form of f(x) = φ(x)^Tβ₁ + β₀, where φ(x) is a set of basis functions. The kernelization of the proposed approach is possible because the objective function (6) can be expressed in terms of inner products between different X′s. Hence, the objective and constraint can be expressed in terms of inner products of φ(X). Subsequently, we can compute the robust nonlinear rule by slightly modifying the algorithm.

2.4. Estimating robust rules using empirical data

To solve for the minimax linear decisions given the observed data from a clinical trial, we first need to estimate $\left({\mu }_j^{†},{\mathrm{\Sigma }}_j^{†}\right),j=\pm 1$, which depends on both the optimal treatment rule d*(x) and the weight W(X). A three-step procedure is outlined below.

Step 1. Estimate d*(x) using a nonparametric method with the trial data, denoted by $\widehat{d}(x)$.

Step 2. Estimate $\left({\tilde{\mu }}_j^{†};{\tilde{\mathrm{\Sigma }}}_j^{†}\right)$ using the initial estimate $\widehat{d}(x)$, denoted by $\left({\widehat{\mu }}_j^{†},{\widehat{\mathrm{\Sigma }}}_j^{†}\right)$.

Step 3. Implement MiLD based on the estimated $\left({\widehat{\mu }}_j^{†},{\widehat{\mathrm{\Sigma }}}_j^{†}\right)$.

In Step 1, there are several ways to estimate d*. Indirect estimation methods model the response as a function of X and A, and select treatment, which maximizes the predicted mean outcome (Qian and Murphy, 2011). Since a consistent estimator $\widehat{d}(x)$ is required to guarantee the performance, a flexible nonparametric method in Step 1 is preferred. For example, support vector machine and support vector regression can be used to estimate E(T|X,A) for binary and continuous outcomes respectively. Alternatively, outcome weighted learning proposed in Zhao et al. (2012) circumvents the two-step procedure by directly optimizing the value function. We can employ a kernel function to induce nonlinearity in obtaining the initial estimator $\widehat{d}$.

In a cancer clinical trial, it is common that the primary endpoint is survival time that subjects to censoring. Given that d*(x) is invariant over the covariate distribution, we suggest utilizing flexible nonparametric machine learning methods. In particular, we will use the random forest survival tree method (Ishwaran et al., 2008) to estimate E(T|X,A), an ensemble tree method that extended random forest method (Breiman, 2001) for analysis of right-censored survival data. It uses independent bootstrap samples to grow trees by randomly selecting a subset of variables at each node and splitting the node using a survival criterion adjusting for censoring status. The ensemble estimated cumulative hazard function is the average of the Nelson-Aalen estimator for each case’s terminal node. Easy-to-use software is available on R CRAN (https://cran.r-project.org). We can estimate E(T|X,A) correspondingly via $\mathrm{via}E(T|X,A)={\int }_0^{\tau }P(T>t|X,A)dt$. Then $\widehat{d}(x)=\mathrm{sign}\{\widehat{f}(x)\}$, where $\widehat{f}(x)=\widehat{E}(T|X=x,A=1)-\widehat{E}(T|X=x,A=-1)$.

To estimate $\left({\mu }_j^{†},{\mathrm{\Sigma }}_j^{†}\right)$ with a general weight W(x), we treat it as a multiplicative adjustment to X where we now sample from a density proportional to p_X(x)W(x) instead of p_X(x). This motivates us to employ techniques from importance sampling to estimate $\left({\mu }_j^{†},{\mathrm{\Sigma }}_j^{†}\right),j=\pm 1$. In particular, ${\mu }_j^{†}$ can be estimated by

$${\widehat{\mu }}_j^{†}=\frac{{\sum }_{i=1}^n{X}_{i}W\left(X_i\right)I\left\{\widehat{d}\left(X_i\right)=j\right\}}{{\sum }_{i=1}^{n}W\left(X_i\right)I\left\{\widehat{d}\left(X_i\right)=j\right\}};$$

and ${\mathrm{\Sigma }}_j^{†}$ can be estimated by

$${\widehat{\mathrm{\Sigma }}}_j^{†}=\sum _{i=1}^n{\left[\frac{W\left(X_i\right)I\left\{\widehat{d}\left(X_i\right)=j\right\}}{{\sum }_{i=1}^{n}W\left(X_i\right)I\left\{\widehat{d}\left(X_i\right)=j\right\}}\right]}^2{\left(X_i-{\widehat{\mu }}_j^{†}\right)}^{\top }\left(X_i-{\widehat{\mu }}_j^{†}\right).$$

In our case, we choose

$$\begin{gathered} W(x)={\widehat{W}}_1(x)=\widehat{E}\left\{T|A=d*(x),X=x\right\}-\widehat{E}\left\{T|A\ne d*(x),X=x\right\} \\ =\left|\widehat{E}\right\{T|A=1,X=x\}-\widehat{E}\left\{T\right|A=-1,X=x\left\}\right| \\ =|\widehat{f}(X)| \end{gathered}$$

or W(X) = W₂(X) ≡ 1.

Provided with the estimated $\left({\widehat{\mu }}_j^{†},{\widehat{\mathrm{\Sigma }}}_j^{†}\right),j=\pm 1$, we solve for the robust linear treatment regimes in Step 3 using the procedure outlined in Section 2.3. In particular, estimates will be plugged in for ${\mu }_j^{†}$ and ${\mathrm{\Sigma }}_j^{†},j=\pm 1$ and related quantities. We obtain ${\widehat{\beta }}_1$ and ${\widehat{\beta }}_0$ accordingly.

2.5. Choices of (ν, ρ_j)

Sometimes pilot data from the target population or the general patient population data are available. We can use this information to choose ρ_j and ν. First we obtain $\widehat{d}(x)$ as an initial estimate of d*(x) using the trial data. Based on this preliminary decision boundary $\widehat{d}(x)$, we can estimate ${\tilde{\mu }}_j^{†}$ and ${\tilde{\mathrm{\Sigma }}}_j^{†},j=\pm 1$, denoted as ${\widehat{\mu }}_j$ and ${\tilde{\mathrm{\Sigma }}}_j$, for a target population using the pilot data. Then we can set ${\rho }_j=b{\Vert {\widehat{\mathrm{\Sigma }}}_j\Vert }_F$, and $\nu ={\sum }_j\left(b{\widehat{\mu }}_j^{\top }\right){\widehat{\mathrm{\Sigma }}}_j^{\top -1}\left(b{\widehat{\mu }}_j\right)/2$, where b is a constant characterizing the potential differences between two population means, as well as the norm of the covariance matrix. If relevant data is not available, we can conduct sensitivity analyses on different combinations of (ν, ρ_j), and assess how the changes in (ν, ρ_j) will influence the resulting decision rules and the worst-case allocation rates.

3. Theoretical results

In this section, we will establish some theoretical properties of the proposed MiLD method. Assume that (X_i,A_i, T_i), i = 1, …, n, are i.i.d observations from the trial. Additionally, we assume that

Assumption 1

All covariates are bounded such that |X| ≤ M.

Assumption 2

Let ${\beta }_1^{*}$ be the unique solution to (1). ${\beta }_1^{*}$ lies in the interior of a compact set B.

We assume the following condition on f*(x) = E(T|X = x,A = 1) − E(T|X = x,A = −1):

Assumption 3

Margin condition: there exist K₁, γ > 0 such that for all t > 0

$$\tilde{P}\left(\left|f*(X)\right|\le t\right)\le K_1{t}^{\gamma }.$$

Assumption 4

$\widehat{f}$ converges to f^m, which could be different from f*. The convergence rate of estimated $\widehat{f}$ to f^m satisfies ${\Vert \widehat{f}-f*\Vert }_2=O_p\left(r_n\right)$, where ∥f∥₂ = E{f(X)²}^1/2 and the expectation is taken with respect to the distribution in the trial data.

Assumption 5

The difference of the covariates is uniformly bounded

$$\underset{{}_{i,i^{\prime }\le n}}{\max }\left|X_i-X_i^{\prime }\right|\le C_X,$$

for some constant C_X > 0.

Assumption 6

Let ${\check{f}}_i(x)$ be the estimate of f*(x) using the Step 1 data except that the i^th observation (x_i, a_i, t_i) is replaced by an independent observation $\left({\check{x}}_i,{\check{a}}_i,{\check{t}}_i\right)$. We assume that

$$\underset{X}{\sup }\left|{\check{f}}_i(X)-\widehat{f}(X)\right|\le \rho /n$$

for some constant ρ.

Assumption 3 is an analogue of the well-known margin condition (Tsybakov, 2004), which is commonly used to characterize the noise around the decision boundary in a binary classification problem. Here, the assumption describes the distribution of f*(X) when X is near the boundary {x : f*(x) = 0} in the target population, which usually contains more noise, and γ controls the size of these regions. Particularly, larger values of γ mean that the two treatment effects are less likely to be similar, and it is easier to distinguish patients who would have benefited from one treatment from those who would have benefited from the other. Usually, γ ∈ [0,m] for a smooth contrast function f*(x), unless f*(x) does not cross 0 at any point, i.e., all the patients benefit from one treatment (Audibert et al., 2007). For example, if X ~ Uniform[−1, 1], P(A = 1|X = P(A = −1|X) = 1/2) and E(T|X,A) = XA, then γ = 1. The bounded covariate assumption, Assumption 5, is satisfied in most real applications. Assumption 6 indicates that small changes in the data will only lead to small changes in the estimates. For example, if we use Cox regression with nonlinear basis functions, or nonparametric kernel estimators, this condition will be satisfied (Devroye et al., 2013). The following results are proved in the supplementary materials.

Theorem 1

Under the Assumptions 1-6, it holds that $\left|{\widehat{\beta }}_1-{\beta }_1^{*}\right|=O_p({\Vert f*-f^m\Vert }_2^{\min }{}^{\left(1,\frac{2\gamma }{\gamma +2}\right)}+r_n^{\min }{}^{\left(1,\frac{2\gamma }{\gamma +2}\right)}+n^{-1/2})$.

The first term reflects the approximation error due to the initial estimator $\widehat{f}$. If $\widehat{f}$ is a consistent estimator of f*, where f* = f^m, then the first term will disappear. The other terms bound the stochastic error, which arises from the variability inherent in a finite sample size, which captures the efficiency loss due to the first stage estimation. As an example, if we use random forest to estimate the required quantities, r_n = n^−θ with $\theta =\frac{0.75}{2\{S\log (2)+0.75\}}$ under some mild assumptions, where S denotes the number of strong features used in the estimating process (Biau, 2012). The theorem indicates that the convergence rate of the estimated linear treatment rules depends on the the initial treatment rule, and the behavior of f*(x) in the neighborhood of the boundary. For example, if a kernel estimator is used, the optimal rate of r_n would be n^−2/(m+4), and the conclusion rate is n^{−4γ/(m+4)(γ+2)}.

4. Simulation Studies

We conduct extensive simulations to evaluate the proposed methods. In all scenarios, the dimension of the covariate space is 10. Binary treatments A are generated from {−1, 1} with equal probability. Three different scenarios are presented, with outcomes generated as follows.

Scenario 1. We simulate the first half of patients from X₁,X₂ ~ N(1, 1),X₃, …, X₁₀ ~ N(0, 1) and the second half of patients with X₁, …, X₁₀ from N(0, 1). The survival time is the minimum of τ = 0.5 and $\tilde{T}$, where $\tilde{T}$ is generated with

$$\log \tilde{T}=\exp \left\{0.6*X_1-0.8*X_2+A*c(X)\right\}+\log ϵ.$$

Here, c(X) = 1 for the first half of patients and c(X) = −1 for the other half, and is generated from an exponential distribution with mean 1. Censoring time C is generated from Uniform[0,1]. The censoring percentage is around 24%. The optimal decision boundary is d*(X) = sign(X₁ + X₂ − 1).

Scenario 2. X₁, …, X₁₀ are generated from N(0, 1). The survival time is the minimum of τ = 4 and $\tilde{T}$, where $\tilde{T}$ is generated with the hazard rate function

$${\lambda }_{\tilde{T}}(t|X,A)=\exp \left[0.6X_1+0.8X_2-1+\left\{2X_1+3{\left(X_2+1\right)}^2-2\right\}A\right].$$

Censoring time C is generated from Uniform[0, 5]. The censoring percentage is around 42%. The optimal decision boundary is d*(X) = −sign{2X₁ + 3(X₂ + 1)² − 2}.

Scenario 3. X₁, …, X₁₀ are generated from N(0, 1). The survival time is the minimum of τ = 4 and $\tilde{T}$, which is generated with

$$\log (\tilde{T})=X_1+X_2+1+A\left(2X_1^3+2X_2+0.5\right)+N(0,1).$$

Censoring time C is generated from

$$\log (C)~X_1+X_2+X_3+N(0,1).$$

The censoring percentage is around 51%. The optimal decision boundary is $d*(X)=\mathrm{sign}\left(2X_1^3+2X_2+0.5\right)$.

We also consider settings where there is a mismatch between the trial participants and the target population, and we will denote these mismatch scenarios as Scenarios 1’, 2’, and 3’ respectively. In Scenario 1, half of the patients will gain benefits from treatment 1 in both populations. We modify it in Scenario 1’ such that the proportion of patients with d*(x) = 1 is 1/3 in the trial population, and 1/2 in the target population. In Scenario 2’, we let the covariate distribution in the trial data with X₁ ~ N(−0.25, 1.5) and other covariates following N(0, 1.5), which are different from the distribution in the target population with all covariates generated from N(0, 1). Eligibility criteria are usually applied for the trial recruitment, and thus trials might selectively enroll patients from the target population. Instead of randomly choosing patients for participation in the trial, patients are selectively enrolled with certain probability, denoted by π(X), into the trial data. In Scenario 3’, the model for the enrollment is $\mathrm{logit}\{\pi (X)\}=-2X_1^3-1$, where logit(t) = log{t/(1−t)}. Hence, covariates predictive of participation in the trial could be predictive of treatment effects, where patients with d*(x) = 1 are less likely to participate in the trial. Subsequently, the covariate distributions in trial data and the target population are not the same.

We hope to discover a simple linear decision rule of high quality even if the true treatment effect might be nonlinear. MiLD will be evaluated for this purpose. In this paper, we utilize random survival forest to obtain the initial estimate of d*(x), but other methods can also be applied. Then we apply both ${\widehat{W}}_1(x)$ and W₂(x) ≡ 1 in MiLD, targeted to optimize the value and the allocation rate to the optimal rule, respectively. We denote them as MiLD-V and MiLD-P. The results might be affected with possible deviations between the target and the trial populations. When we do not have prior information on the target population, we can vary (ν, ρ_j) to evaluate the resulting changes. As suggested in Section 2.5, we set ${\rho }_j=b{\Vert {\widehat{\mathrm{\Sigma }}}_j\Vert }_F$, $\nu =\left\{\sum _j{\left(b{\widehat{\mu }}_j\right)}^{\top }\left({\widehat{\mathrm{\Sigma }}}_j+b{\Vert {\widehat{\mathrm{\Sigma }}}_j\Vert }_F{I}_p\right)\left(b{\widehat{\mu }}_j\right)\right\}/2,j=\pm 1$. Here, ${\Vert {\widehat{\mathrm{\Sigma }}}_j\Vert }_F$ is the Frobenius norm of ${\widehat{\mathrm{\Sigma }}}_j,$ and b is a constant that reflects the deviations relative to the covariance matrix norms and the means, in the trial populations. We consider two cases with b = 0 and b = 0.1 for both MiLD-V and MiLD-P.

We compare the proposed methods to the following two approaches.

1. OWL (outcome weighted learning): we find the best linear decision rule by directly targeting maximizing the overall expected outcome (Zhao et al., 2012).

2. COX: we find the linear decision rule based on a Cox regression model, where interactions between X and A are included.

All methods are performed by deriving the best linear treatment rules using trial data. We then calculate the misclassification rate under the estimated rules via Monte Carlo methods. Specifically, a large testing dataset of 10,000 from the target population is generated. Training datasets representing the trial population are repeatedly simulated, and each time the rules yielded by various methods are evaluated on this testing set. Different training data sample sizes n = 250,500 and 1000 are considered. We report the average misallocation to non-optimal treatments over 500 replicates. We also report the expected overall survival of the estimated rules using the derived treatment rules by different methods in the supplementary materials.

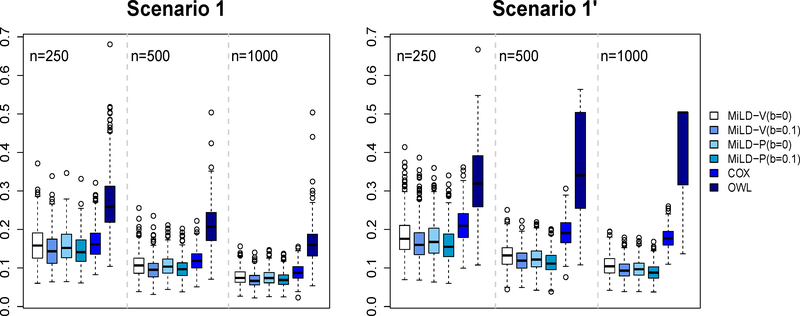
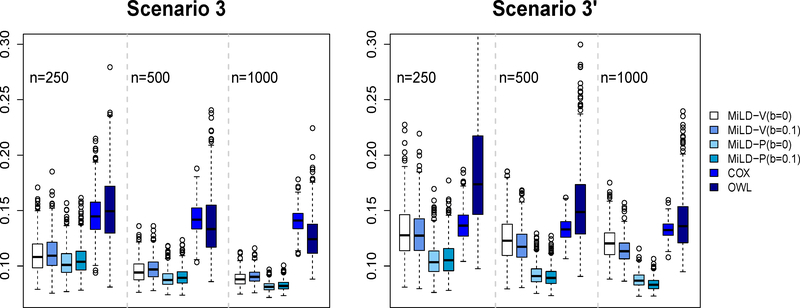
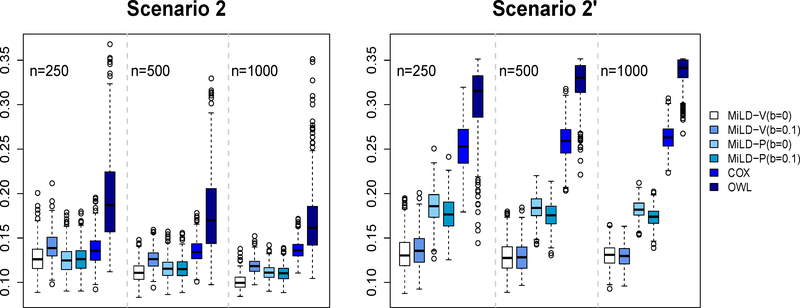
The results in Figures 1–3 present evidence that the proposed methods perform well compared with the other methods. The Cox regression method relies on model fitting, and thus many subjects are recommended the wrong treatments by the resulting linear decision rule, labeled as misallocation rates in Figures 1 - 3. Even in Scenarios 1 and 1’ where the optimal treatment rule is linear, the non-proportional hazards model negatively impacts the performance of Cox regression. The OWL method in general leads to a larger variability. On the other hand, both MiLD-V and MiLD-P perform well throughout, and the results are insensitive to the value of b. The limits of misallocation rates that MiLD-V and MiLD-P converge to are the lowest among all competitors. It can be seen that when the trial population is not representative as illustrated in Scenarios 1’, 2’ and 3’, MiLD-V and MiLD-P are robust to the bias, and they yield favorable results. We note that the results in MiLD with b = 0.1, which allows a larger deviation between the trial and the target population, give a slightly better result most of the time in these cases. We also illustrate the efficiency loss due to the first stage estimation of f*(x) numerically. Details can be found in supplementary material.

Figure 1:

Misallocation rates in Scenarios 1 and 1’ using trial data with sample sizes varying from 250 to 1000. The misallocation rate is evaluated by using 500 Monte Carlo repetitions.

Figure 3:

Misallocation rates in Scenarios 3 and 3’ using trial data with sample sizes varying from 250 to 1000. The misallocation rate is evaluated by using 500 Monte Carlo repetitions.

5. Data Analysis

Prior studies suggest that elevated markers of bone turnover are prognostic for poor survival in castration-resistant prostate cancer, but their predictive value for the bone-targeted therapy has not been fully investigated. We illustrate the proposed methods using data from SWOG 0421 study, a North American Intergroup phase III trial (participants: SWOG, Eastern Cooperative Oncology Group, Cancer and Leukemia Group B/Alliance) for men with metastatic castration-resistant prostate cancer. They were randomly assigned in a blinded fashion in a 1:1 ratio to docetaxel administered every 21 days at a dose of 75 mg/m² with or without the bone-targeted oral agent atrasentan taken daily for up to 12 cycles (Quinn et al., 2013; Lara et al., 2014). S0421 enrolled 1038 eligible patients; of these, 855 submitted serum for the bone biomarkers and 778 patients had usable specimens at baseline. After removing missing observations, the sample size for our analysis is 751, where 371 patients are in the docetaxel + atrasentan arm and 380 patients are in the docetaxel + placebo arm.

Co-primary endpoints in this study were progression-free survival and overall survival. In our analysis, we use overall survival as our outcome, which is truncated at the end of the study, and could be censored due to loss of follow-up. We use 10 baseline covariates to inform the optimal treatment rule, including age (range 40–92), serum prostate-specific antigen (PSA, range 0.1–10414.1), indicator of bisphosphonate usage (61%), indicator of metastatic disease beyond the bones (55%), indicator of pain at baseline (60%), indicator of performance status (2–3 versus 0–1, 56% 2–3), and bone marker levels. Four bone markers are measured, including Bone alkaline phosphatase (BAP, range 1.9–1761.0 u/L), C-terminal of type 1 collagen (CICP, range 1.4–273.6 ng/mL), N-telopeptides of type 1 collagen (NTx, range 1.4–480.0 nM) and pyridinoline (PYD, range 0.3–15.0 nmol/L). The distribution of bone marker concentrations and serum PSA were skewed with a wide range; therefore, we use log transformation for these variables. All covariates are then standardized for analysis. We intend to find the optimal linear treatment rule that is robust to a potential difference between the trial population and the future population.

We compare the proposed methods with Cox regression and OWL method. Practitioners often directly generalize the results from a clinical trial to the general patient population. However, It is not uncommon that the participants in clinical trials are in general more healthier than the patient population, due to the restrictions on patient eligibility. Hence, in our data analysis, we mimic this phenomenon by changing the distribution of healthier patients in the trial population and the target population. We categorize patients to healthier patients whose serum PSA is below the median level and sicker patients whose serum PSA is above the median level. We employ a cross-validated type analysis. At each run, we partition the whole data set into 5 pieces, where 2 parts of the data are used as training data to estimate the optimal rules, and the remaining part as the validation set for evaluating the estimated rules. Specifically, each training data set consists of 2/3 healthier patients and 1/3 sicker patients; on the other hand, each validation set contains 1/3 healthier patients and 2/3 sicker patients. Thus, there is a substantial discrepancy between the training set and the validation set, which represents the trial population and the target population, respectively. The cross-validated values are obtained by averaging the empirical value on all 3 validation subsets. To adjust for censoring when calculating the empirical values, we use inverse probability of censoring weighting techniques, where the empirical value for a treatment decision rule d is calculated by ${\mathbb{P}}_n[\tilde{Y}I\{A=d(X)\}]/{\mathbb{P}}_n[\tilde{I}\{A=d(X)\}],$ with $\tilde{Y}$ equaling to $\Delta Y/{\widehat{S}}_C(Y|A,X).$ We use a kernel estimator developed in Li et al. (1999) to obtain ${\widehat{S}}_C(t|A,X),$ which does not require a model assumption. The procedure is repeated 200 times. The averages and standard errors of these values are reported in Table 1, where a larger value corresponds to a longer expected survival time. The results show better performances of both MiLD-V and MiLD-P procedures compared to other methods. MiLD-V performs the best perhaps because it targets to optimize the value directly.

Table 1:

Mean (s.e.) cross-validated values (days)

COX	OWL	MiLD-V		MiLD-P
		b = 0	b = 0.1	b = 0	b = 0.1
749.2 (69.8)	711.1 (71.2)	764.6 (70.2)	765.0 (68.9)	753.5 (69.4)	753.7 (69.4)

“s.e.” denotes standard errors.

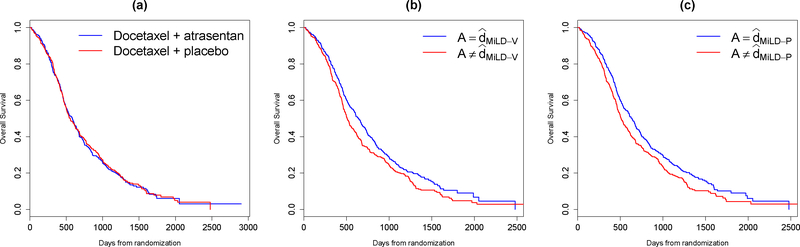
We then apply the proposed methods to the whole data set. The coefficients in the treatment decision rule recommended by MiLD-V and MiLD-P are presented in Table 2. The results yielded by MiLD-V and MiLD-P are close, where 80% of the patients receive the same treatment recommendation. In Figure 4(a), we compare the Kaplan–Meier curves for overall survival between two treatment arms. There does not appear to be separation. However, when comparing the group whose treatment assignments were in accordance with the treatments recommended by MiLD-V or MiLD-P with the other group, the Kaplan–Meier survival curves show a clear separation, as shown in Figures 4(b) and (c).

Table 2:

Coefficients for the estimated linear decision rules by MiLD-V and MiLD-P using the SWOG0421 data

	MiLD-V	MiLD-P
Intercept	0.021	0.037
Age	0.538	0.150
Baseline serum PSA	−0.510	−0.734
Bisphosphonate usage (YES = 1)	0.787	1.235
Metastatic disease beyond the bones (YES = 1)	−0.301	0.008
Pain (YES = 1)	−0.272	0.050
Performance Status (‘2–3’ = 1)	0.515	0.796
BAP	0.382	0.972
CICP	−0.023	0.302
NTx	0.137	0.657
PYD	−0.339	−0.326

Figure 4:

Kaplan–Meier survival curves of overall survival in castration-resistant prostate cancer patients: (a) by treatment received; (b) by accordance between treatment recommended by MiLD-V and treatment received; (c) by accordance between treatment recommended by MiLD-P and treatment received.

6. Discussion

In practice, it is preferable to use interpretable decision rules when communicating with clinical practitioners about treatment recommendation. A canonical example is linear decision rule, which is attractive because it can be easily understood, and thus can be used to guide future research. Our present work shows that it is possible to identify high-quality linear decision rule that leads to a greater overall benefit, even if the truth may be nonlinear. Furthermore, the proposed method is robust across future populations, taking into account the fact that the study sample may not be representative.

We consider survival time outcomes in this paper. Such endpoints are critical in many settings especially in oncology. However, MiLD can be readily applied for binary or continuous outcomes, provided that we can use existing nonparametric methods to obtain preliminary estimates of the decision boundaries. Popular methods for binary outcomes include support vector machine and boosting (Hastie et al., 2009), and for continuous outcomes, we can apply random forest (Breiman, 2001) and support vector regression (Vapnik et al., 1997). Our current proposal suggests an L₂ penalty for handling high-dimensional covariates. However, this does not provide sparse solutions. In certain circumstances, several important variables characterize the optimal treatment rules, where the means and covariance matrices of those unimportant variables do not matter. It would be interesting to develop robust methods that conduct variable selection simultaneously, which would eliminate the unimportant variables and further improve the ease of interpretation. Another interesting extension of the current work is to consider settings involving more than two treatments. While it is straightforward to conduct a series of pairwise comparisons, further development is required to identify the best rule among all treatments. It will also be interesting to investigate extensions to Boolean combination of linear rules, i.e., rules of the form {X₁β₁₁ + β₀₁ ≥ 0} ∩ {X₂β₂₁ + β₀₂ ≥ 0}.

Figure 2:

Misallocation rates in Scenarios 2 and 2’ using trial data with sample sizes varying from 250 to 1000. The misallocation rate is evaluated by using 500 Monte Carlo repetitions.

7. Appendix

Solving minimax linear decisions

It follows from the generalized Chebychev inequality (Marshall and Olkin, 1960) that (2) is equivalent to

$$\begin{gathered} \underset{{}_{\alpha ,{\beta }_1,{\beta }_0}}{\max }\alpha s.t.\underset{X^{†}~\left({\tilde{\mu }}_1^{†},{\tilde{\mathrm{\Sigma }}}_1^{†}\right)\in {\mathcal{U}}_1^{†}}{\inf }{\beta }_0+{\tilde{\mu }}_1^{†\top }{\beta }_1\ge \kappa (\alpha )\sqrt{{\beta }_1^{\top }{\tilde{\mathrm{\Sigma }}}_1^{†}{\beta }_1} \\ \underset{X^{†}~\left({\tilde{\mu }}_{-1}^{†},{\tilde{\mathrm{\Sigma }}}_{-1}^{†}\right)\in {\mathcal{U}}_{-1}^{†}}{\inf }-{\beta }_0-{\tilde{\mu }}_1^{†\top }{\beta }_1\ge \kappa (\alpha )\sqrt{{\beta }_1^{\top }{\tilde{\mathrm{\Sigma }}}_{-1}^{†}{\beta }_1}, \end{gathered}$$

where $\kappa (\alpha )=\sqrt{\alpha /(1-\alpha )}.$ As shown in Lanckriet et al. (2003), ${\min }_{{\mu }_j:{\left({\tilde{\mu }}_j^{†}-{\mu }_j^{†}\right)}^{\top }{\tilde{\mathrm{\Sigma }}}_j^{†}-1}{{}_{\left({\tilde{\mu }}_j^{†}-{\mu }_j^{†}\right)}}_{\le {\nu }^2}{\beta }_1^{\top }{\tilde{\mu }}_j^{†}={\beta }_1^{\top }{\mu }_j^{†}-\nu \sqrt{{\beta }_1^{\top }{\mathrm{\Sigma }}_j^{†}{\beta }_1},$ and ${\max }_{{\tilde{\mathrm{\Sigma }}}^{†}:{\Vert {\tilde{\mathrm{\Sigma }}}^{†}-{\mathrm{\Sigma }}^{†}\Vert }_F\le \rho }{\beta }_1^T{\tilde{\mathrm{\Sigma }}}^{†}{\beta }_1={\beta }_1^T\left({\mathrm{\Sigma }}^{†}+\rho I_p\right){\beta }_1,$ where I_p is the identified matrix. Recall that ${\mathcal{U}}_j^{†}=\left\{\left({\tilde{\mu }}_j^{†},{\tilde{\mathrm{\Sigma }}}_j^{†}\right):{\left({\tilde{\mu }}_j^{†}-{\mu }_j^{†}\right)}^{\top }{\tilde{\mathrm{\Sigma }}}_j^{†}\left({\tilde{\mu }}_j^{†}-{\mu }_j^{†}\right)\le {\nu }^2,{\Vert {\tilde{\mathrm{\Sigma }}}_j^{†}-{\mathrm{\Sigma }}_j^{†}\Vert }_F\le {\rho }_j\right\},j=\pm 1$, We have ${\beta }_0+{\beta }_1^{\top }{\tilde{\mu }}_j^{†}={\beta }_0+{\beta }_1^{\top }{\mu }_j^{†}-\nu \sqrt{{\beta }_1^{\top }{\mathrm{\Sigma }}_j^{†}{\beta }_1}$, and ${\beta }_1^{\top }{\tilde{\mathrm{\Sigma }}}_j^{†}{\beta }_1={\beta }_1^{\top }\left({\mathrm{\Sigma }}_j^{†}+{\rho }_j{I}_p\right){\beta }_1.$ We thus further rewrite the optimization problem to

$$\begin{gathered} \underset{\alpha ,{\beta }_1,{\beta }_0}{\max }\alpha s.t.{\beta }_0+{\beta }_1^{\top }{\mu }_1^{†}\ge \kappa (\alpha )\sqrt{{\beta }_1^{\top }\left({\mathrm{\Sigma }}_1^{†}+{\rho }_1{I}_p\right){\beta }_1} \\ -{\beta }_0-{\beta }_1^{\top }{\mu }_{-1}^{†}\ge \kappa (\alpha )\sqrt{{\beta }_1^{\top }\left({\mathrm{\Sigma }}_{-1}^{†}+{\rho }_{-1}{I}_p\right){\beta }_1}. \end{gathered}$$

We will assume that ${\mu }_1^{†}\ne {\mu }_{-1}^{†};$ otherwise, the above problem is not identifiable. We also assume that ${\mathrm{\Sigma }}_j^{†},j=\pm 1$ are both positive definite. Since κ(α) is a monotone increasing function of α, we can rewrite our problem as

$$\underset{\kappa }{\max }\kappa s.t.,{\beta }_1^{\top }{\mu }_{-1}^{†}+\kappa \sqrt{{\beta }_1^{\top }\left({\mathrm{\Sigma }}_{-1}^{†}+{\rho }_{-1}{I}_p\right){\beta }_1}\le {\beta }_0\le {\beta }_1^{\top }{\mu }_1^{†}-\kappa \sqrt{{\beta }_1^{\top }\left({\mathrm{\Sigma }}_1^{†}+{\rho }_1{I}_p\right){\beta }_1},$$

and these inequalities will become equalities at the optimum. We can eliminate the equality constraint by letting β₁ = β₁₀ + Fu, where u ∈ ℝ^p−1, ${\beta }_{10}=\left({\mu }_1^{†}-{\mu }_{-1}^{†}\right)/{\Vert {\mu }_1^{†}-{\mu }_{-1}^{†}\Vert }_2^2,$ and F ∈ ℝ^p×(p−1) is an orthogonal matrix whose columns span the subspace of vectors orthogonal to ${\mu }_1^{†}-{\mu }_{-1}^{†}.$ Hence, the optimization problem can be written as in (2). The optimal

$${\beta }_0^{*}={\beta }_1^{*\top }{\tilde{\mu }}_1^{†}-{\kappa }^{*}\sqrt{{\beta }_1^{*\top }\left({\tilde{\mathrm{\Sigma }}}_1^{†}+{\rho }_1{I}_p\right){\beta }_1^{*}}={\beta }_1^{*\top }{\tilde{\mu }}_{-1}^{†}+{\kappa }^{*}\sqrt{{\beta }_1^{*\top }\left({\tilde{\mathrm{\Sigma }}}_{-1}^{†}+{\rho }_{-1}{I}_p\right){\beta }_1^{*}},$$

where κ* is the optimal value of κ with ${\kappa }^{*}={\left\{\sqrt{{\beta }_1^{*\top }\left({\tilde{\mathrm{\Sigma }}}_{-1}^{†}+{\rho }_{-1}{I}_p\right){\beta }_1^{*}}+\sqrt{{\beta }_1^{*\top }\left({\tilde{\mathrm{\Sigma }}}_1^{†}+{\rho }_1{I}_p\right){\beta }_1^{*}}\right\}}^{-1}.$ The lower bound on the worst case allocation rate α* = (κ* − ν)²/{1 + (κ* − ν)²}, and ν should not exceed κ*.

Proof of Theorem 1

We first show that $\left|{\widehat{\mu }}_j^{†}-{\mu }_j^{†}\right|=O_p\left(r_n^{\frac{2\gamma }{\gamma +2}}+n^{-1/2}\right)$ and $\Vert {\widehat{\mathrm{\Sigma }}}_j^{†}-{\mathrm{\Sigma }}_j^{†}\Vert =O_p\left(r_n^{\frac{2\gamma }{\gamma +2}}+n^{-1/2}\right),j=\pm 1,$ where $W(X)={\widehat{W}}_1(X)=|\widehat{f}(X)|$ and $\Vert A\Vert ={\sup }_{x\in \mathcal{X}}\Vert Ax{\Vert }_2.$ For the convergence rate in means,

$$\begin{gathered} \left|{\widehat{\mu }}_j^{†}-{\mu }_j^{†}\right|=\left|{\mathbb{P}}_{n}X\widehat{f}(X)I\{\widehat{d}(X)=j\}-\mathbb{P}Xf*(X)I\left\{d*(X)=j\right\}\right| \\ \le \left|{\mathbb{P}}_{n}X\widehat{f}(X)I\{\widehat{d}(X)=j\}-\mathbb{P}X\widehat{f}(X)I\{\widehat{d}(X)=j\}\right| \\ +\left|\mathbb{P}X\widehat{f}(X)I\{\widehat{d}(X)=j\}-\mathbb{P}X{f}^m(X)I\{\widehat{d}(X)=j\}\right| \\ +\left|\mathbb{P}X{f}^m(X)I\{\widehat{d}(X)=j\}-\mathbb{P}Xf*(X)I\{\widehat{d}(X)=j\}\right| \\ +\left|\mathbb{P}Xf*(X)I\{\widehat{d}(X)=j\}-\mathbb{P}Xf*(X)I\left\{d*(X)=j\right\}\right| \\ =(I)+(II)+(III)+(IV). \end{gathered}$$

We will use McDiarmid’s inequality to bound (I).

$$\begin{gathered} |\frac{1}{n}\sum _{k=1}^n{x}_k\widehat{f}\left(x_k\right)I\left\{\widehat{d}\left(x_k\right)=j\right\}-\frac{1}{n}\sum _{k=1,k\ne i}^n{x}_k{\check{f}}_i\left(x_k\right)I\left\{\check{d}\left(x_k\right)=j\right\}-\frac{1}{n}{\check{x}}_i{\check{f}}_i\left({\check{x}}_i\right)I\left\{\check{d}\left({\check{x}}_i\right)=j\right\}| \\ \le \left|\frac{1}{n}\sum _{k=1}^n{x}_k\left\{\widehat{f}\left(x_k\right)-{\check{f}}_i\left(x_k\right)\right\}I\left\{\widehat{d}\left(x_k\right)=j\right\}\right|+|\frac{1}{n}\sum _{k=1}^n{x}_k{\check{f}}_i\left(x_k\right)\left[I\left\{\widehat{d}\left(x_k\right)=j\right\}-I\left\{\check{d}\left(x_k\right)=j\right\}\right]| \\ +\frac{1}{n}|\left(x_i-{\check{x}}_i\right)\widehat{f}\left(x_i\right)I\left\{\widehat{d}\left(x_i\right)=j\right\}+{\check{x}}_i\left\{\widehat{f}\left(x_i\right)-{\check{f}}_i\left({\check{x}}_i\right)\right\}I\left\{\widehat{d}\left(x_i\right)=j\right\} \\ +{\check{x}}_i{\check{f}}_i\left({\check{x}}_i\right)\left[I\left\{\widehat{d}\left(x_i\right)=j\right\}-I\left\{\check{d}\left({\check{x}}_i\right)=j\right\}\right]|\le M_{\rho }/n, \end{gathered}$$

where M_ρ depends on M,C_X and ρ. The last inequality follows from Assumptions 1, 5 and 6.

By McDiarmid’s inequality,

$$P\left(\left|{\mathbb{P}}_{n}X\widehat{f}(X)I\{\widehat{d}(X)=j\}-\mathbb{P}X\widehat{f}(X)I\{\widehat{d}(X)=j\}\right|\ge ϵ\right)\le e^{-2n{ϵ}^2/M_{\rho }^2}.$$

Then with probability ≥ 1 − δ,

$$\left|{\mathbb{P}}_{n}X\widehat{f}(X)I\{\widehat{d}(X)=j\}-\mathbb{P}X\widehat{f}(X)I\{\widehat{d}(X)=j\}\right|\le c_M\sqrt{\frac{\log (1/\delta )}{n}}.$$ (7)

For (II), by Cauchy-Schwaz inequality and the boundedness of X,

$$\begin{gathered} \left|\mathbb{P}X\widehat{f}(X)I\{\widehat{d}(X)=j\}-\mathbb{P}X{f}^m(X)I\{\widehat{d}(X)=j\}\right| \\ \le \sqrt{\mathbb{P}{\left\{\widehat{f}(X)-f^m(X)\right\}}^2}\sqrt{\mathbb{P}\left(X^2\right)} \\ =O_p\left(r_n\right), \end{gathered}$$

where the last step follows from Assumption 4. For (III),

$$\begin{gathered} \left|\mathbb{P}X{f}^m(X)I\{\widehat{d}(X)=j\}-\mathbb{P}Xf*(X)I\{\widehat{d}(X)=j\}\right| \\ \le \sqrt{\mathbb{P}{\left\{f^m(X)-f*(X)\right\}}^2}\sqrt{\mathbb{P}\left(X^2\right)} \\ \le M{\Vert f*-f^m\Vert }_2. \end{gathered}$$

For (IV),

$$\begin{gathered} \left|\mathbb{P}X{f}^{*}(X)I\{\widehat{d}(X)=j\}-\mathbb{P}Xf*(X)I\left\{d*(X)=j\right\}\right| \\ =\left|\mathbb{P}Xf*(X)I\left\{d*(X)=j,\widehat{d}(X)\ne d*(X)\right\}\right| \\ \le \left|\mathbb{P}Xf*(X)I\left\{d*(X)=j\right\}I\left\{0<\left|f*(X)\right|\le \left|f*(X)-\widehat{f}(X)\right|\right\}\right| \\ \le \left|\mathbb{P}\left[Xf*(X)I\left\{d*(X)=j\right\}\right]\mathbb{P}\left\{0<\left|f*(X)\right|\le \left|f*(X)-\widehat{f}(X)\right|\right\}\right| \\ \le \left|\mathbb{P}\left[Xf*(X)I\left\{d*(X)=j\right\}\right]\mathbb{P}\left\{0<\left|f*(X)\right|\le \left|f*(X)-\widehat{f}(X)\right|\right\}\right|\le ϵ\} \\ \le |\mathbb{P}\left[Xf*(X)I\left\{d*(X)=j\right\}\right]\mathbb{P}\left\{I\left\{0<\left|f*(X)\right|\le ϵ\right\}I\left\{\left|f*(X)-\widehat{f}(X)\right|\le ϵ\right\}\right\} \\ +I\left\{\left|f*(X)-\widehat{f}(X)\right|>ϵ\right\}]| \\ \le {\mu }_j^{†}\left(\frac{{\Vert f*-\widehat{f}\Vert }_2^2}{{ϵ}^2}+{ϵ}^{\gamma }\right), \end{gathered}$$

where ∥f∥₂ = E{f(x)²}^1/2. Choosing the optimal $ϵ\text{as}{\Vert f^{*}-\widehat{f}\Vert }_2^{\frac{2}{\gamma +2}},$ we have that

$$\left|\mathbb{P}Xf*(X)I\{\widehat{d}(X)=j\}-\mathbb{P}Xf*(X)I\left\{d*(X)=j\right\}\right|\le {\mu }_j^{†}{\Vert f*-\widehat{f}\Vert }_2^{\frac{2\gamma }{\gamma +2}}\le M\left(r_n^{\frac{2\gamma }{\gamma +2}}+{\Vert f*-f^m\Vert }_2^{\frac{2\gamma }{\gamma +2}}\right).$$ (8)

Combining the above results, we obtain that with probability ≥ 1 − δ,

$$\left|{\widehat{\mu }}_j^{†}-{\mu }_j^{†}\right|\le M\left\{{\Vert f*-f^m\Vert }_2^{\min \left(1,\frac{2\gamma }{\gamma +2}\right)}+r_n^{\min \left(1,\frac{2\gamma }{\gamma +2}\right)}\right\}+c_M\sqrt{\frac{\log (1/\delta )}{n}}.$$

Therefore, $\left|{\widehat{\mu }}_j^{†}-{\mu }_j^{†}\right|$ is $O_p\left({\Vert f^{*}-f^m\Vert }_2^{\min \left(1,\frac{2\gamma }{\gamma +2}\right)}+r_n^{\min \left(1,\frac{2\gamma }{\gamma +2}\right)}+n^{-1/2}\right)$.

We then consider the bound on $\Vert {\widehat{\mathrm{\Sigma }}}_j^{†}-{\mathrm{\Sigma }}_j^{†}\Vert ,j=\pm 1$. Let $\widehat{F}(X)={\sum }_{i=1}^n\widehat{f}\left(X_i\right)I\{\widehat{d}\left(X_i\right)=j\}$ and $F^m(X)={\sum }_{i=1}^n{f}^m\left(X_i\right)I\{\widehat{d}\left(X_i\right)=j\}$ and $F*(X)={\sum }_{i=1}^{n}f*\left(X_i\right)I\{\widehat{d}\left(X_i\right)=j\}$. With probability ≥ 1 − δ,

$${\widehat{\mathrm{\Sigma }}}_j^{†}=\sum _{i=1}^n{\left[\frac{W\left(X_i\right)I\left\{\widehat{d}\left(X_i\right)=j\right\}}{{\sum }_{i=1}^{n}W\left(X_i\right)I\left\{\widehat{d}\left(X_i\right)=j\right\}}\right]}^2{\left(X_i-{\widehat{\mu }}_j^{†}\right)}^{\top }\left(X_i-{\widehat{\mu }}_j^{†}\right).$$

$$\begin{gathered} \Vert {\widehat{\mathrm{\Sigma }}}_j^{†}-{\mathrm{\Sigma }}_j^{†}\Vert \le \Vert \left({\mathbb{P}}_n-\mathbb{P}\right)\left[{\left\{\frac{\widehat{f}(X)}{\tilde{F}(X)}\right\}}^2{\left(X-{\widehat{\mu }}_j^{†}\right)}^{\top }\left(X-{\widehat{\mu }}_j^{†}\right)I\{\widehat{d}(X)=j\}\right]\Vert \\ +\Vert \mathbb{P}\left[{\left\{\frac{\widehat{f}(X)}{\tilde{F}(X)}\right\}}^2{\left(X-{\widehat{\mu }}_j^{†}\right)}^{\top }\left(X-{\widehat{\mu }}_j^{†}\right)I\{\widehat{d}(X)=j\}\right] \\ -\mathbb{P}\left[{\left\{\frac{f*(X)}{F*(X)}\right\}}^2{\left(X-{\widehat{\mu }}_j^{†}\right)}^{\top }\left(X-{\mu }_j^{†}\right)I\{d*(X)=j\}\right]\Vert \\ \le c_{\delta }\sqrt{\frac{\log (1/\delta )}{n}}+\Vert \mathbb{P}\left[{\left\{\frac{\widehat{f}(X)}{\widehat{F}(X)}\right\}}^2{\left(X-{\widehat{\mu }}_j^{†}\right)}^{\top }\left(X-{\widehat{\mu }}_j^{†}\right)I\{\widehat{d}(X)=j\}\right] \\ -\mathbb{P}\left[{\left\{\frac{\widehat{f}(X)}{\widehat{F}(X)}\right\}}^2{\left(X-{\mu }_j^{†}\right)}^{\top }\left(X-{\mu }_j^{†}\right)I\{\widehat{d}(X)=j\}\right]\Vert \\ +\Vert \mathbb{P}\left[{\left\{\frac{\widehat{f}(X)}{\widehat{F}(X)}\right\}}^2{\left(X-{\mu }_j^{†}\right)}^{\top }\left(X-{\mu }_j^{†}\right)I\{\widehat{d}(X)=j\}\right] \\ -\mathbb{P}\left[{\left\{\frac{\widehat{f}(X)}{\widehat{F}(X)}\right\}}^2{\left(X-{\mu }_j^{†}\right)}^{\top }\left(X-{\mu }_j^{†}\right)I\{\widehat{d}(X)=j\}\right]\Vert \\ +\Vert \mathbb{P}\left(\left[\left\{\frac{\widehat{f}(X)}{\widehat{F}(X)}\right\}-{\left\{\frac{f*(X)}{F*(X)}\right\}}^2\right]{\left(X-{\mu }_j^{†}\right)}^{\top }\left(X-{\mu }_j^{†}\right)I\{\widehat{d}(X)=j\}\right)\Vert \\ \le c_{\delta }\sqrt{\frac{\log (1/\delta )}{n}}+2\Vert \mathbb{P}\left[{\left\{\frac{\widehat{f}(X)}{\widehat{F}(X)}\right\}}^2{\left(X-{\mu }_j^{†}\right)}^{\top }\left({\widehat{\mu }}_j^{†}-{\mu }_j^{†}\right)I\{d(X)=j\}\right]\Vert \\ +\Vert \mathbb{P}\left[{\left\{\frac{\widehat{f}(X)}{\widehat{F}(X)}\right\}}^2{\left({\widehat{\mu }}_j^{†}-{\mu }_j^{†}\right)}^{\top }\left({\widehat{\mu }}_j^{†}-{\mu }_j^{†}\right)I\{d(X)=j\}\right]\Vert \\ +\Vert \mathbb{P}\left[{\left\{\frac{\widehat{f}(X)}{\widehat{F}(X)}\right\}}^2{\left(X-{\mu }_j^{†}\right)}^{\top }\left(X-{\mu }_j^{†}\right)\left\{d*(X)=j,\widehat{d}(X)\ne d*(X)\right\}\right]\Vert \\ +\Vert \mathbb{P}\left(\left[{\left\{\frac{\widehat{f}(X)}{\widehat{F}(X)}\right\}}^2-{\left\{\frac{f^m(X)}{F^m(X)}\right\}}^2\right]{\left(X-{\mu }_j^{†}\right)}^{\top }\left(X-{\mu }_j^{†}\right)I\left\{d^{*}(X)=j\right\}\right)\Vert \\ +\Vert \mathbb{P}\left(\left[{\left\{\frac{f^m(X)}{F^m(X)}\right\}}^2-{\left\{\frac{f*(X)}{F*(X)}\right\}}^2\right]{\left(X-{\mu }_j^{†}\right)}^{\top }\left(X-{\mu }_j^{†}\right)I\left\{d*(X)=j\right\}\right)\Vert \\ \le O_p\left({\Vert f*-f^m\Vert }_2^{\min \left(1,\frac{2\gamma }{\gamma +2}\right)}+r_n^{\min \left(1,\frac{2\gamma }{\gamma +2}\right)}+n^{-1/2}\right). \end{gathered}$$

Now we prove Theorem 1’s result. Define

$$M(u)=\sqrt{{\left({\beta }_{10}+Fu\right)}^{\top }\left({\mathrm{\Sigma }}_1^{†}+{\rho }_1{I}_p\right)\left({\beta }_{10}+Fu\right)}+\sqrt{{\left({\beta }_{10}+Fu\right)}^{\top }\left({\mathrm{\Sigma }}_{-1}^{†}+{\rho }_{-1}{I}_p\right)\left({\beta }_{10}+Fu\right)},$$

and

$$M_n(u)=\sqrt{{\left({\widehat{\beta }}_{10}+\widehat{F}u\right)}^{\top }\left({\widehat{\mathrm{\Sigma }}}_1^{†}+{\rho }_1{I}_p\right)\left({\widehat{\beta }}_{10}+\widehat{F}u\right)}+\sqrt{{\left({\widehat{\beta }}_{10}+Fu\right)}^{\top }\left({\widehat{\mathrm{\Sigma }}}_{-1}^{†}+{\rho }_{-1}{I}_p\right)\left({\widehat{\beta }}_{10}+\widehat{F}u\right)},$$

where we use the estimated ${\widehat{\mathrm{\Sigma }}}_{\pm 1},\widehat{F}$ and ${\widehat{\beta }}_{10}$ in M(u). Since u belongs to a compact set, ${\widehat{\beta }}_{10}\to {\beta }_{10},{\widehat{\mathrm{\Sigma }}}_j\to {\mathrm{\Sigma }}_j$ and $\widehat{F}\to F,$ ${\sup }_u\left|M_n(u)-M(u)\right|\to 0$ in probability. Given that M(u) has a unique maximizer and u is in a compact set, we have ${\sup }_{\Vert u-u^{*}\Vert \ge ϵ}M(u)<M\left(u^{*}\right).$ Hence the conditions of Theorem 5.7 of van der Vaart (1998) are satisfied, and it follows that $\widehat{u}\to u^{*}$ in probability, and subsequently ${\widehat{\beta }}_1\to {\beta }_1^{*}$ in probability.

We now show the convergence rate of ${\widehat{\beta }}_1\text{to}{\beta }_1^{*}.$ Given that u ↦ M(u) is twice differentiable at u*, we have M(u) − M(u*) ≲ −c∥u − u*∥² for all u in the neighborhood of u* and some c > 0, where u* is the unique maximizer of M(u). Since $\left|{\widehat{\mu }}_j-{\mu }_j\right|=O_p(O_p\left({\Vert f^{*}-f^m\Vert }_2^{\min \left(1,\frac{2\gamma }{\gamma +2}\right)}+r_n^{\min }{}^{\left(1,\frac{2\gamma }{\gamma +2}\right)}+n^{-1/2}\right)$ and $\Vert {\widehat{\mathrm{\Sigma }}}_j-{\mathrm{\Sigma }}_j\Vert =O_p({\Vert f^{*}-f^m\Vert }_2^{\min \left(1,\frac{2\gamma }{\gamma +2}\right)}+r_n^{\min }{}^{\left(1,\frac{2\gamma }{\gamma +2}\right)}+n^{-1/2})$,

$$\begin{gathered} \left|\left(M_n-M\right)(u)-\left(M_n-M\right)\left(u^{*}\right)\right| \\ =\left|\left\{M_n(u)-M_n\left(u^{*}\right)\right\}-\left\{M(u)-M\left(u^{*}\right)\right\}\right|\lesssim {\left|\frac{\partial M_n(u)}{\partial u}-\frac{\partial M(u)}{\partial u}\right|}_{u=u^{*}}\Vert u-u^{*}\Vert \approx \left({\Vert f^{*}-f^m\Vert }_2^{\min \left(1,\frac{2\gamma }{\gamma +2}\right)}+r_n^{\min \left(1,\frac{2\gamma }{\gamma +2}\right)}+n^{-1/2}\right)\Vert u-u^{*}\Vert . \end{gathered}$$

Thus,

$$E^{*}\underset{\Vert u-u^{\prime }\Vert <\delta }{\sup }\left|\left(M_n-M\right)(u)-\left(M_n-M\right)\left(u^{*}\right)\right|\lesssim \left({\Vert f^{*}-f^m\Vert }_2^{\min \left(1,\frac{2\gamma }{\gamma +2}\right)}+r_n^{\min \left(1,\frac{2\gamma }{\gamma +2}\right)}+n^{-1/2}\right)\delta .$$

When $\delta \mapsto \varphi (\delta )=\sqrt{n}\left({\Vert f^{*}-f^m\Vert }_2^{\min \left(1,\frac{2\gamma }{\gamma +2}\right)}+r_n^{\min \left(1,\frac{2\gamma }{\gamma +2}\right)}+n^{-1/2}\right)\delta ,\varphi (\delta )/{\delta }^{\eta }$ is decreasing for any η ∈ (1, 2). In addition, $\widehat{u}\to u^{*}$ in probability, and $\widehat{u}$ maximize M_n(u). The conditions of Theorem 14.4 in Kosorok (2008) are satisfied with $\varphi (\delta )=\sqrt{n}({\Vert f^{*}-f^m\Vert }_2^{\min \left(1,\frac{2\gamma }{\gamma +2}\right)}+{\gamma }_n^{\min \left(1,\frac{2\gamma }{\gamma +2}\right)}+n^{-1/2})\delta .$ Hence, $\Vert u-u^{*}\Vert =O_p\left({\Vert f^{*}-f^m\Vert }_2^{\min \left(1,\frac{2\gamma }{\gamma +2}\right)}+r_n^{\min \left(1,\frac{2\gamma }{\gamma +2}\right)}+n^{-1/2}\right),$ and the desired result follows.