Selection, Linkage, and Population Structure Interact To Shape Genetic Variation Among Threespine Stickleback Genomes

Genome-wide patterns of heterogeneous genetic diversity are now well documented across organisms. How these patterns arise is, however, still not clear. Nelson et al. combine population genomics and genetic mapping of threespine...

Abstract

The outcome of selection on genetic variation depends on the geographic organization of individuals and populations as well as the organization of loci within the genome. Spatially variable selection between marine and freshwater habitats has had a significant and heterogeneous impact on patterns of genetic variation across the genome of threespine stickleback fish. When marine stickleback invade freshwater habitats, more than a quarter of the genome can respond to divergent selection, even in as little as 50 years. This process largely uses standing genetic variation that can be found ubiquitously at low frequency in marine populations, can be millions of years old, and is likely maintained by significant bidirectional gene flow. Here, we combine population genomic data of marine and freshwater stickleback from Cook Inlet, Alaska, with genetic maps of stickleback fish derived from those same populations to examine how linkage to loci under selection affects genetic variation across the stickleback genome. Divergent selection has had opposing effects on linked genetic variation on chromosomes from marine and freshwater stickleback populations: near loci under selection, marine chromosomes are depauperate of variation, while these same regions among freshwater genomes are the most genetically diverse. Forward genetic simulations recapitulate this pattern when different selective environments also differ in population structure. Lastly, dense genetic maps demonstrate that the interaction between selection and population structure may impact large stretches of the stickleback genome. These findings advance our understanding of how the structuring of populations across geography influences the outcomes of selection, and how the recombination landscape broadens the genomic reach of selection.

BIOLOGISTS have long known that natural populations harbor abundant genetic variation that is distributed heterogeneously across geography (Dobzhansky and Queal 1938; Hubby and Lewontin 1966; Lewontin and Hubby 1966). A recent wave of discoveries reveals that genetic variation is distributed heterogeneously across genomes as well (Turner et al. 2005; Begun et al. 2007; Hohenlohe et al. 2010; Ellegren et al. 2012). Are these patterns related? For example, does the manner in which evolutionary processes play out across the geography of organisms influence heterogeneous genomic patterns of genetic diversity? With ever-increasing access to DNA sequence data, evolutionary biologists have come to recognize that selection strongly influences patterns of linked neutral variation (Charlesworth et al. 1993; Hahn 2008; Langley et al. 2012; Schrider and Kern 2017). Linked positive or purifying selection can affect genetic variation far beyond the causal mutations in the surrounding genomic neighborhood (Elyashiv et al. 2016; Schrider and Kern 2017). Indeed, persistent and pervasive linked selection can structure genetic variation during speciation (Burri et al. 2015) and lead to predictable genome-wide genetic divergence across multiple speciation events (Stankowski et al. 2018). Consequently, any process that can influence linkage across the genome, such as variation in recombination, will affect the outcome of linked selection on patterns of genetic variation (Begun and Aquadro 1992; Charlesworth et al. 1993; Gillespie 2000).

Interacting with the genomic context of physical linkage is the geographic context over which evolutionary processes play out (Charlesworth et al. 1997; Lenormand 2002; Stankowski et al. 2017). A single selective sweep in one population can eliminate genetic variation at a selected locus and at linked sites (Maynard Smith and Haigh 1974; Fay and Wu 2000; Hermisson and Pennings 2005; Nielsen et al. 2005; Cutter and Payseur 2013). However, in nature, selective pressures tend to vary across time and space in ways that can maintain variation (Clausen et al. 1941; Endler 1977; Lenormand et al. 1999). Temporally fluctuating selection can maintain alleles at intermediate frequencies, as has been observed in Drosophila melanogaster (Bergland et al. 2014) and the yellow monkeyflower, Mimulus guttatus (Troth et al. 2018). Local adaptation in a geographically structured species can lead to the partitioning of variation among populations and the maintenance of alternatively adaptive alleles (Charlesworth et al. 2003; Wallbank et al. 2016; Nelson and Cresko 2018) as has been observed in insects (Mettler et al. 1977; Nosil and Crespi 2006; Van Belleghem et al. 2018), plants (Clausen et al. 1941; Angert et al. 2018; Tavares et al. 2018), and vertebrates (Hoekstra et al. 2004; Jones et al. 2018). Consequently, gene flow can strongly influence the geographic distribution of genetic variation among populations (Wright 1931; Slatkin 1985, 1991) and across species boundaries (Pardo-Diaz et al. 2012; Fontaine et al. 2015). Although genetic introgression from one species to another may impede neutral divergence, it is now recognized as an important source of adaptive variation (Lewontin and Birch 1966; Stankowski and Streisfeld 2015; Wallbank et al. 2016; Meier et al. 2017; Jones et al. 2018).

Even in the absence of selection, population subdivision alone may affect the overall abundance of neutral genetic variation within a species. Theoretical models provide useful—but at times contradictory—predictions on this matter, with subdivision either increasing or decreasing expected coalescence times depending on model specifications and assumptions. For example, Slatkin (1991) generalized the island model to demonstrate that population structure increases coalescence times (T_T) in a structured population by:

$$T_T=T_0+ \frac{{\left(d-1\right)}^2}{2dm},$$ (1)

where d is the number of demes, m is the migration rate, and T₀ is the expected coalescence time with no population structure (using the nomenclature of Charlesworth et al. 2003). However, Whitlock and Barton (1997) used a similar model, but allowed deme extinction and variable contributions of each deme to the total population. The result was a decrease in effective population size (N_e) with increasing subdivision, and, thus, a decrease in expected levels of genetic variation.

Despite this growing understanding of the general importance of genomic organization of selected loci and geographic context of organisms in the wild on the structuring of genetic variation, precise understanding of how they interact to produce heterogeneous patterns of genetic variation across the genome is still lacking. Therefore, empirical and simulation studies that examine the joint effects of selection regime, geographic context, and recombination are necessary to fully understand the effects of these biological factors on genomic patterns of genetic variation in the wild.

Here, we investigate how multiple evolutionary forces interact to shape the genomic and geographic distribution of genetic variation in the threespine stickleback fish, Gasterosteus aculeatus. The threespine stickleback is distributed holarctically in coastal marine, brackish, and freshwater habitats. The large marine population has repeatedly given rise to derived freshwater populations, resulting in phenotypic divergence and parallel evolution throughout the species range (Bell and Foster 1994; Cresko et al. 2004; Jones et al. 2012). When marine stickleback invade freshwater habitats, more than a quarter of the genome can rapidly respond to the action of divergent selection (Hohenlohe et al. 2010; Terekhanova et al. 2014; Bassham et al. 2018). This process largely uses standing genetic variation (Colosimo et al. 2005; Schluter and Conte 2009; Roesti et al. 2015; Samuk et al. 2017) that can be found ubiquitously at low frequency in marine populations (Bassham et al. 2018), much of which has likely been maintained for millions of years by significant bidirectional gene flow (Caldera and Bolnick 2008; Kitano et al. 2008; Berner et al. 2009; Nelson and Cresko 2018).

While previous work has often focused on the genomic targets of selection, we focus here on the processes that maintain and structure variation in regions of the genome physically linked to those targets. We use a combination of population genomics of wild stickleback, forward-time simulations using SLiM (Haller and Messer 2017), and dense genetic maps to support a model whereby differences in population structure between marine and freshwater habitats has led to divergent outcomes of molecular evolution at loci linked to adaptive variants. Our results provide new links between theoretical and empirical evolutionary genetics, new tools for future work in the stickleback system, and new perspectives on the maintenance of genetic variation.

Materials and Methods

Study populations and natural genetic variation

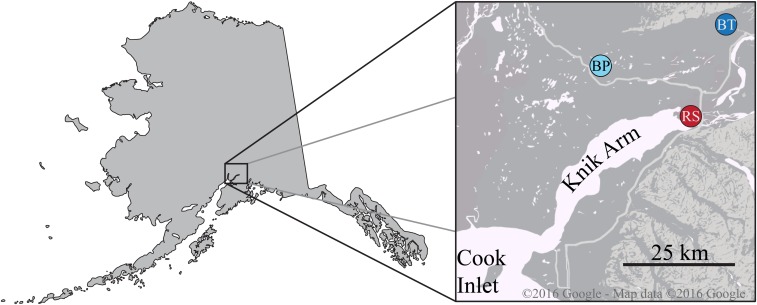
Wild threespine stickleback were collected from Rabbit Slough (RS; N 61.5595, W 149.2583), Boot Lake (BT; N 61.7167, W 149.1167), and Bear Paw Lake (BP; N 61.6139, W 149.7539). RS is an offshoot of the Knik Arm of Cook Inlet, and is known to be populated by anadromous populations of stickleback that are stereotypically marine in phenotype and genotype (Figure 1; Cresko et al. 2004). BT and BP are both shallow lakes formed during the end-Pleistocene glacial retreat ∼12,000 years ago. Fish were collected in the summers of 2009 (RS), 2010 (BP), and 2014 (BT) using wire minnow traps and killed in situ with Tricaine solution. Killed fish were immediately fixed in 95% ethanol and shipped to the Cresko Laboratory at the University of Oregon (Eugene, OR).

Figure 1.

Sampling locations of marine and freshwater stickleback populations from southcentral Alaska. Inset: Geography of Cook Inlet near Anchorage, AK. Marine stickleback were sampled from Rabbit Slough (RS, red). Freshwater stickleback were sampled from Boot Lake (BT, dark blue) and Bear Paw Lake (BP, light blue). All areas in the inset were glaciated during the Late Wisconsin glaciation until ∼10,000 years ago.

We generated restriction site-associated DNA (RAD) libraries of five fish each from RS and BT, and four fish from BP. Genomic DNA was isolated from ethanol-preserved fin clips by proteinase K digestion followed by DNA extraction with solid phase reversible immobilization (SPRI) beads. We created RAD libraries using the single digest and shearing method of Baird et al. (2008), with the modifications of Nelson and Cresko (2018). Genomic DNA from each fish was digested with PstI-HF (New England Biolabs) and ligated to Illumina P1 adaptors with 6-bp inline barcodes. All barcodes differed by at least two positions, allowing for recovery of sequence reads with single errors in the barcode sequence. Ligated samples were then multiplexed at approximately equimolar concentrations, and mechanically sheared via sonication to a fragment range of ∼200–800 bp. Sheared DNA was size selected by extraction from a 1.25% agarose gel to generate a narrow insert size range of 425–475 bp. This size range allowed consistent overlap of paired-end Illumina reads for the construction of local contigs surrounding restriction enzyme cut sites. We then ligated Illumina P2 adaptors to the size-selected libraries and amplified P1/P2-adapted fragments with 12 cycles of PCR using Phusion-HF polymerase (New England Biolabs). RAD libraries were then sequenced in a single lane on an Illumina HiSeq 2500 to generate paired-end 250 bp sequence reads. All libraries generated for this study were sequenced at the University of Oregon’s Genomics and Cell Characterization Core Facility (GC3F: http://gc3f.uoregon.edu).

We used the Stacks analysis pipeline to process RAD sequence read pairs and call SNPs (Catchen et al. 2011, 2013b). Raw reads were first demultiplexed without quality filtering using process_radtags, and then quality filtered using process_shortreads. This allowed for read trimming, rather than strict removal, if quality decreased toward the end of the first-end read. Overlapping read pairs were then merged using fastq-join (Aronesty 2011), allowing for up to 25% of bases in the overlapping region to mismatch, and the resulting contigs were trimmed to 350 bp. Any read pairs that failed to merge, or were less than 350 bp, were removed from further analysis. This step was required for processing reads through the Stacks pipeline. Below, a “locus” refers to the combined sequence assembled from a single restriction site in the stickleback genome.

All polymorphisms were called relative to the threespine stickleback reference genome v1.0 (Jones et al. 2012), using the updated scaffolding of Glazer et al. (2015). Trimmed contigs were aligned to the reference using bbmap with the most sensitive settings (“vslow = t”; http://jgi.doe.gov/data-and-tools/bbtools/). We then used the Stacks core pipeline to identify read stacks, call SNPs, and identify alleles and haplotypes based on genomic alignment (pstacks and cstacks); find homologous RAD tags across individuals (sstacks); and catalog biologically plausible haplotypes based on within- and among-individual haplotype variation (populations). We required that a RAD tag be present in all three populations, and in at least four fish in each population.

We used the program PHASE (Stephens et al. 2001; Scheet and Stephens 2006) to combine sequence information from both RAD tags at a PstI cut site, and generate phased haplotypes at each RAD locus. We wrote custom Python scripts to identify all unique haplotypes at each pair of RAD tags and code them as alleles at a single, multiallelic locus (Nelson and Cresko 2018; available at www.github.com/thomnelson/ancient-divergence). We required that each individual included in this analysis was genotyped at both RAD tags. Loci containing individuals genotyped only at a single RAD tag were removed from further analysis. RAD haplotypes at each locus represent 696 bp of contiguous genomic sequence, giving us high-quality estimates of sequence diversity and divergence even with our relatively small population-level sample sizes (Nei 1987, chapter 13; Cruickshank and Hahn 2014; Nelson and Cresko 2018). Sequencing of wild stickleback resulted in 57,992 RAD loci distributed across all 21 threespine stickleback chromosomes, averaging 7514 bp between adjacent RAD loci.

Population genetic statistics

The scripting language R version 3.5 (R Core Team 2016) was used for all downstream data analysis. We estimated differentiation among threespine stickleback populations (all pairwise combinations) and among ecotypes (combined freshwater ponds vs. RS) using a haplotype-based F_ST (equation 3 in Hudson et al. 1992) implemented in the R package “PopGenome” (Pfeifer et al. 2014). We calculated π per site within and among populations and absolute sequence divergence (d_XY) at each RAD locus by calculating pairwise distances between all RAD haplotypes with the R package “ape” (Paradis et al. 2004; Popescu et al. 2012).

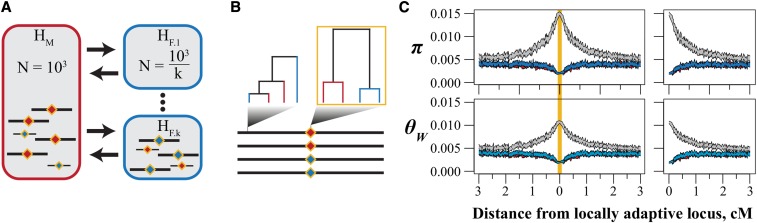
Previously, we detected patterns of reciprocal monophyly between marine and freshwater haplotypes using maximum clade credibility trees generated in BEAST v1.7 (Drummond and Rambaut 2007; Drummond et al. 2012; Nelson and Cresko 2018; Suchard et al. 2018). Tree topologies for all RAD loci were inferred from MCMC runs of 10⁶ states with 10% burn-in periods. We used blanket priors and parameters across all RAD loci, including a coalescent tree prior and the GTR+Γ substitution model. Monophyly of haplotypes from each population (RS, BT, BP) and each habitat (marine, freshwater) was assessed using the is.monophyletic() function of the R package “ape.” Here, we use topological classifications that we inferred previously, and designate gene trees with reciprocally monophyletic marine and freshwater haplogroups (1129 of 57,992 RAD loci) as “divergent” loci (Figure 2B, see also Nelson and Cresko 2018).

Figure 2.

The structure of simulations to test the effects of population structure on genetic variation in a model of local adaptation. (A) Habitat H_M (red) consists of a single deme while habitat H_F (blue) consists of k demes. We adjust the size of each deme in H_F so that the total census size of each habitat is constant across simulations. Diamonds represent a single locus with locally adaptive alleles. (B) We assessed genetic diversity at the locally adaptive locus and in nonoverlapping windows. We used the pattern of reciprocal monophyly (outlined in gold) to classify RAD loci as divergent in the threespine stickleback population genomic dataset. [See Materials and Methods and Nelson and Cresko (2018)]. (C) Genetic diversity within (red and blue) and among (gray) allelic classes in a simulation where k = 1. Shown are 95% confidence intervals of nucleotide diversity (π) and Watterson’s θ after 10N generations of selection. Because patterns of variation are symmetrical about the locus under selection, we present “folded” curves [(C) right] throughout this work.

Forward simulations using SLiM

We used forward simulations implemented in SLiM (Haller and Messer 2017) to model the effects of selection, linkage, and population structure in a manner that reflects the stickleback metapopulation structure (Figure 2). We simulated a metapopulation of 2000 diploid individuals in two habitats, H_M and H_F, to model the marine and freshwater stickleback populations, respectively. The genome consisted of a single chromosome with a genetic length of 10 cM, containing 50 kbp of freely recombining sequence (recombination rate 1 × 10⁻⁶ per bp) on either side of a 2 kbp nonrecombining “core,” which contained the locally adaptive locus. Per-base mutation rate was kept constant at 5 × 10⁻⁷, resulting in a population-scaled mutation rate (4Nμ = 0.004) aligned with genome-wide estimates of genetic diversity in stickleback (Hohenlohe et al. 2010; Nelson and Cresko 2018). The general form of the simulations was as follows:

1. Initialize population H_M.

   1. N = 1000 diploids.

   2. Evolve for 10,000 generations.

2. Create k new populations, collectively “H_F.”

   1. Each of size N/k.

   2. Set migration rate m to H_M.

   3. Evolve for 10,000 generations.

3. Introduce mutation as single copy into H_F.

   1. Deleterious in H_M, advantageous in H_F.

   2. Run selection for [4,10,20]N generations.

   3. (If locally adaptive mutation is lost, go to [3]).

4. End simulation.

Simulations included three phases: (1) a burn-in without population structure, (2) a burn-in after creating population structure, and (3) a selection phase contingent on establishment of a locally adaptive allele. The first burn-in began with a single panmictic population of size N = 1000 and no sequence variation. We evolved this population for 10N (10,000) generations. The second burn-in of 10N generations began by creating k new populations, each of size N/k, by sampling variation from the existing population (Figure 2). k ranged from 1 to 25. We set bidirectional migration rates equivalent to one migrant per generation between the existing population, now designated habitat H_M, and each new population, now collectively referred to as habitat H_F. We chose this migration structure to reflect the stickleback metapopulation, where freshwater stickleback populations are thought to be derived most often from marine ancestors, and because gene flow among freshwater populations occurs primarily through the marine population, especially across broader geographic scales.

To start the selection phase, we introduced a mutation at the center of the core of a single chromosome in habitat H_F that is advantageous in H_F and deleterious in H_M. Progression through the selection phase was conditional on establishment of the locally adaptive mutation: if the mutation was lost from the metapopulation, the simulation restarted at the end of the second burn-in.

Genetic diversity among chromosomes carrying H_M- and H_F-adaptive alleles was assessed at the end of the selection phase. We sampled 10 chromosomes of each allelic state and calculated nucleotide diversity (π) and Watterson’s θ (θ_W) within and among chromosomes of the two allelic states in nonoverlapping 250 bp (0.025 cM) bins. We include results from θ_W because this statistic is based on the number of segregating sites, and is therefore more reflective of the abundance of sequence variation and less affected by shifts in allele frequencies. We fold the calculations of genetic diversity about the locally adaptive locus to emphasize the effects of evolutionary forces on variation at a given distance from the locus (Figure 2C). These summaries mirror our estimates of genetic variation on stickleback chromosomes and results from theoretical work on the effects of local adaptation on linked variation (Charlesworth et al. 1997).

Laboratory crosses and genetic mapping

To compare how heterogenous genomic divergence on the physical map is distributed across the genetic map, we generated mapping families from laboratory lines of fish derived from BT and an F₁ hybrid female (hereafter F₁) produced from a cross between a BT female and a RS male. These crosses allowed us to examine variation in the recombinational landscape within and among chromosomes in distinct, evolutionarily relevant genetic backgrounds. We also generated a genetic map of a RS-derived male (Supplemental Material, Figure S1), but, because ecotype was confounded with sex (Sardell et al. 2018), we limit our discussion to the BT and F₁ maps.

All maps were constructed using a pseudotestcross design, which takes advantage of existing heterozygosity in outbred individuals without the need to generate inbred lines or F₁ mapping parents. To generate the BT mapping family, we manually crossed unrelated laboratory-reared individuals. We mapped the F₁ female by backcrossing it to a BT male. All progeny were raised to 14 days postfertilization, euthanized with MS-222 (Sigma Aldrich, St. Louis, MO), and fixed in 95% ethanol. We extracted genomic DNA from whole progeny, and from pectoral and caudal fins from all parents using proteinase K digestion (Qiagen, Germantown, MD) followed by DNA purification with SPRI beads.

RAD genotyping of progeny and parents was used to identify segregating haplotypes using a RAD-seq protocol similar to that described previously but using the restriction enzyme SbfI. RAD-seq data from all mapping crosses were processed with the Stacks analysis pipeline (Catchen et al. 2013b). We demultiplexed and quality filtered sequences with process_shortreads and aligned them to the stickleback reference genome with GSNAP (Wu and Nacu 2010). We used ref_map.pl to identify RAD tags and call genotypes. The Stacks component program genotypes was used to identify segregating markers for export to genetic mapping software. We specified a minimum coverage of 3× to call individual genotypes and required that a marker be genotyped in at least 50% of progeny. Below, we use the term “RAD marker” to refer to a RAD tag with segregating haplotypes.

Below, we present genetic maps for the female parent from each cross (Table 1 and Table S1). By conducting pseudotestcrosses, we identified polymorphic RAD markers segregating in all mapping parents. However, to investigate the genome-wide recombination landscape, as well as relationships between recombination rate and natural levels of polymorphism and divergence, we restricted our analysis to parents of the same sex for which we observed segregating markers on all 21 chromosomes with no gaps greater than 1 Mbp between adjacent markers.

Table 1. Genetic map statistics for the three maps used in this study.

Family	Progeny	Markers	Map lengtha	Genomic coverageb	cM/Mbp
Boot Lake (BT)	189	6041	2255	0.993	5.20
BT subset	94	6169	2396	0.993	5.52
F1 hybrid	102	6669	1878	0.995	4.33
F1 subset	94	7678	1958	0.995	4.51

^aMap length given in centiMorgans (cM).

^bGenomic coverage is a percentage of the reference genome assembled onto chromosomes (436.6 Mbp)

We estimated genome-wide recombination rates between RAD markers under the assumption of collinearity between all genetic maps and the stickleback reference genome (Glazer et al. 2015) (with some exceptions, see below). We used the mapping software Lep-MAP2 (Rastas et al. 2015) to estimate map positions of RAD markers with the marker order fixed to the aligned positions on the reference genome. Known marker orders increased throughput of mapping iterations and reduced the impact of genotyping errors on recombination rate estimation.

While fixed marker orders do not explicitly allow the detection of structural variation among genomes—such as chromosomal inversions that are known to exist among stickleback populations—discrepancies in the estimated map do provide indirect, and correctable, evidence of changes to map order (Figure S2). For example, inversions in genetic map order relative to the reference order spuriously inflate recombination rates between markers closely flanking inversion breakpoints when inverted segments are forced into the wrong orientation. This is because genetic map distances are estimated independently while the physical distance between markers is drastically underestimated. The observed jumps in map distance on either side of the inversion are equal to each other and to the total map length of the inversion. Reversing the marker order within the inversion removes these artifacts and reduces the overall map length of the region. We observed and corrected this artifact for a single previously known inversion on chromosome 21 (Figure S1, Figure S2, Jones et al. 2012). Two other known inversions on chromosomes 1 and 11 were too small to create artifacts in our data.

Recombination rate correlations

We employed three methods to investigate the relationships between the recombinational landscape and patterns of polymorphism within and among natural populations. To compare our results to other studies in stickleback (Samuk et al. 2017), we quantified genome-wide correlations among recombination rate and population genetic statistics. We divided the stickleback genome into nonoverlapping windows, and calculated average recombination rates (in cM/Mbp), sequence diversity (π_BT, π_RS, and π), and genetic divergence (F_ST, d_XY) in each window. We calculated F_ST between RS and BT as a measure of recent genetic differentiation, and d_XY between RS and the combined freshwater populations as a measure of long-term genetic divergence (Nelson and Cresko 2018). We additionally measured the distance between each window and the centromere based on known centromeric repeats (Urton et al. 2011; Cech and Peichel 2015; Sardell et al. 2018). RAD marker density made estimates of local recombination rates less reliable and more variable when using small window sizes (e.g., 100 kbp windows; Figures S3 and S4). As a result, we show results from 1-Mbp genomic windows. We used nonparametric correlations to test for correlations between variables because the distributions of most variables lacked normality even using standard data transformations. Below we present Spearman’s rank order correlations. Kendall’s tau and parametric linear models gave qualitatively similar results (Table S2).

Genomic heterogeneity exists not only in the proportion of the genome affected by divergent selection, but also in how genetic variation and divergence are clustered within the genome. Marine-freshwater genomic divergence in stickleback is clustered into few, large regions that can encompass most of the length of a chromosome. We sought to directly compare the genomic distributions of population genetic statistics along the physical genome and on the genetic maps we constructed. We used a windowing approach that allowed direct comparisons across maps despite differing numbers and distributions of markers among genetic maps. Using the R package “ksmooth,” we binned each chromosome into equally sized intervals, the number of which we set equal to the number of segregating RAD markers on the genetic map with fewest markers. For each interval, we calculated genetic position from each laboratory cross and F_ST between RS and BT populations (Hohenlohe et al. 2010; Nelson and Cresko 2018) within a 250 kbp normally distributed kernel. We also imputed the genetic positions of all divergent loci using the lm() function in R: we found the nearest flanking RAD markers in each mapping cross and predicted the genetic position of the divergent locus assuming a constant recombination rate between the flanking markers. With these approaches, we were able to make direct comparisons between recombination within and among genetic maps from different genetic backgrounds and patterns of polymorphism in the populations from which the laboratory lines were derived.

Data availability

Raw sequence data are available on NCBI under BioProjects PRJNA429207 and PRJNA507799. RAD sequences for mapping families are available on the Sequence Read Archive, BioSamples SAMN10498162-10498548. Supplemental material, including scripts and processed data, are available on GitHub at https://github.com/thomnelson/linkedvariation and at FigShare: https://doi.org/10.25386/genetics.8061755.

Animal care and compliance

Treatment of animals followed protocols approved by the University of Oregon Institutional Animal Care and Use Committee (IACUC).

Results

Chromosomes from freshwater but not marine stickleback contain abundant variation linked to loci under divergent selection

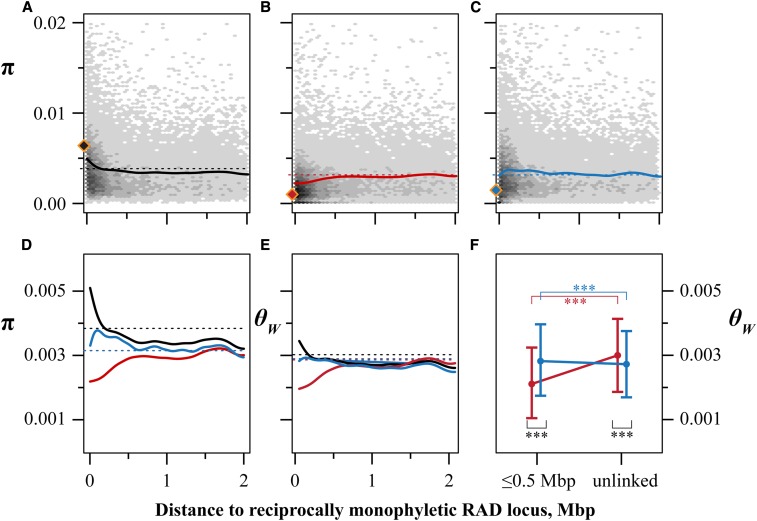
To examine patterns of variation linked to loci under selection, we first partitioned RAD loci from the population genomics dataset into those with evidence of complete marine-freshwater lineage sorting (“divergent,” with allelic states “marine” and “freshwater,” see Figure 2B), those on the same chromosome as a divergent locus (“linked”), and those on chromosomes without divergent loci (“unlinked”). At divergent loci, average sequence diversity was partitioned almost entirely among chromosomes carrying marine and freshwater alleles; overall π averaged 0.0067 per site (Figure 3A, black-filled diamond, genome-wide mean = 0.0042); average d_XY between marine and freshwater alleles was 0.0124, nearly threefold higher than the genome-wide average (0.0044). In contrast, and as expected at locally adaptive loci (Figure 2C), π was substantially reduced within allelic states; π among marine alleles averaged 0.0012 per site (Figure 3B, red-filled diamond) while average π among freshwater alleles at divergent loci was 0.0015 per site (Figure 3C, blue-filled diamond).

Figure 3.

Patterns of sequence variation differ on marine and freshwater stickleback chromosomes. (A–C) Genome-wide sequence diversity (π) as a function of the distance from a RAD locus with reciprocal monophyly of marine and freshwater haplotypes. Diamonds show average sequence diversity among reciprocally monophyletic RAD loci. Density of RAD loci at x distance from the nearest reciprocally monophyletic locus with y level of diversity is shown in shades of gray. Bold lines are smoothed splines, dashed lines are genome-wide means. (A) Sequence diversity in the combined dataset [marine (RS) + freshwater (BT and BP)]. (B) Sequence diversity on chromosomes carrying marine haplotypes. (C) Sequence diversity on chromosomes carrying freshwater haplotypes. (D) Smoothed splines as in (A–C). (E) Splines as in (A–D) of Watterson’s θ. (F) θ_W of RAD loci within 0.5 Mbp of a reciprocally monophyletic RAD locus and on chromosomes not carrying a reciprocally monophyletic locus (“unlinked”). Data are means ± 1 SD ***P < 0.001.

Patterns of linked variation among habitats and on marine chromosomes followed the expectations from simulated local adaptation (Figure 2C and Figure 3, A and B). Sequence diversity at linked loci was highly correlated with proximity to a divergent locus (Figure 3, A–C, Spearman’s ρ: all P-values ≤ 10⁻¹⁰). When all populations were combined, π at linked loci decreased sharply in the first ∼250 kbp from a divergent locus (Figure 3, A and D), and linked loci in closest proximity to divergent loci were nearly as polymorphic as those directly impacted by divergent selection. As expected under local adaptation, π among chromosomes sampled from marine RS stickleback was lowest in close proximity to divergent loci (Figure 3B), and a substantial fraction (12%) of RAD loci within 250 kbp of a divergent locus showed no variation at all on these chromosomes (π_RS = 0; 1651/13762 loci).

In stark contrast, diversity among freshwater chromosomes showed a proximity effect that was distinct from either RS or the combined populations (Figure 3, C–E). Rather than being lowest near divergent loci, diversity actually increased with proximity to a divergent locus, peaking ∼200 kbp away on average before reversing direction. This pattern persisted using either π or Watterson’s theta (θ_W), indicating that the density of segregating sites on freshwater chromosomes is highest near divergent loci and that the signal we observe is not simply due to a greater abundance of intermediate frequency alleles. We also note that this increase in diversity qualitatively persisted within both freshwater populations individually (Figure S5).

Linkage to divergent loci, therefore, was associated with opposing effects on genetic variation in stickleback: decreasing it among marine chromosomes while increasing variation among freshwater chromosomes (Figure 3E). Chromosomes with no evidence of divergent selection had a slightly higher density of segregating sites in RS than the combined freshwater populations (Figure 3E and Table 2), though π was indistinguishable (Figure S6). However, within 500 kbp of a divergent locus, genetic diversity (π and θ_W) was greater among freshwater populations than in RS (Figure 3E, Figure S6, and Table 2; population*proximity interaction P ≤ 10⁻¹⁰).

Table 2. ANOVA results for proximity-by-ecotype analyses.

	F1,34068			Tukey’s HSD vs. RSunlinked
	Ecotype	Linkage	Ecotype*linkage	RSlinked	FWlinked	FWunlinked
π	858.8***	62.5***	382.8***	—	+	=
θW	343.4***	149.6***	358.9***	—	—	—

F statistics are from ANOVAs on untransformed values, ***P ≤ 10⁻¹⁰. For Tukey’s Honest Significant Difference (HSD), “+” and “−” indicate an increase or decrease in diversity, respectively, compared to variation at unlinked loci on marine (RS) chromosomes. “linked” indicates loci ≤500 kbp from a divergent locus, as in Figure 3

Population structure maintains linked variation on simulated chromosomes

To determine how population structure within the freshwater habitat influences patterns of linked variation in stickleback, we conducted forward simulations of chromosomes under a model of local adaptation with migration using SLiM v2.6 (Haller and Messer 2017, Figure 2). In simulations with two habitat types, each composed of a single, panmictic population (Figure 4, column 1), total genetic diversity was highest at, and adjacent to, the locally adaptive locus (Figure 2C). Within allelic classes diversity was lowest in proximity to the locally adaptive locus and recovered equally within both allelic classes with increasing recombinational distance from the selected locus (Figure 2C and Figure 4). This scenario is essentially the same as that presented by Charlesworth et al. (1997), and the results are qualitatively the same.

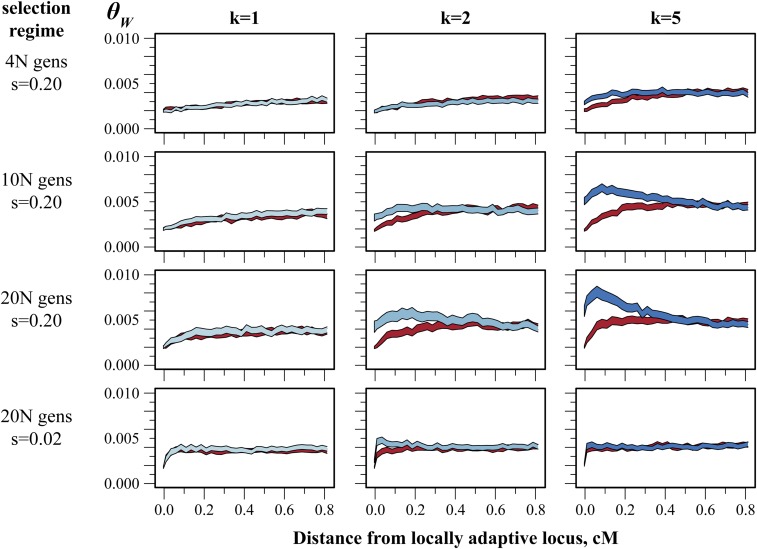
Figure 4.

Asymmetric population structure generates asymmetric patterns of linked variation on simulated chromosomes. Simulations were performed as described in Materials and Methods and Figure 2. Bands are 95% confidence intervals of Watterson’s θ at a given distance from a locally adaptive locus (red: θ_W on chromosomes carrying the H_M-adaptive allele, blue: θ_W on chromosomes carrying the H_F-adaptive allele). Columns show the effect of increasing population structure (k) in habitat H_F. Rows show the effect of increasing the length of the selection phase of the simulations. Rows 1–3 show results under strong selection (s = 0.20). Row 4 shows results for simulations identical to row 3 but with moderate selection (s = 0.02). All simulations were performed using a migration rate, m, of one migrant per generation between habitat H_M and each population of habitat H_F. Total diversity (see Figure 2) is excluded to highlight variation within each allelic class.

The addition of population structure to these simulations led to habitat-specific effects on genetic variation. When the second habitat (H_F)—representing the freshwater stickleback habitat—consisted of two or more demes (Figure 2A and Figure 4, columns 2 and 3) the additional structure maintained greater variation exclusively on H_F-adaptive (H_F⁺) chromosomes—an effect dependent on the duration and strength of selection and the number of demes. Under strong selection (s = 0.20), population structure had a barely noticeable effect on variation until the length of the selection phase was on the order of the neutral coalescence time (∼9N generations, Slatkin 1991; Charlesworth et al. 2003; Equation 1). Beyond this point, any amount of population structure resulted in higher levels of variation on H_F⁺ than H_M⁺ chromosomes within ∼0.2 cM from the selected locus. Moderate selection (s = 0.02) was generally ineffective at altering among-habitat levels of variation, though we did observe a modest effect on H_F⁺ chromosomes immediately adjacent to the selected locus.

Increasing population structure in H_F led to substantial levels of variation near the selected locus (Figure S6, column 3; Figure S7). When H_F consisted of five demes, genetic variation on H_F⁺ chromosomes was greatest ∼0.1 cM from the selected locus even though levels of variation among allelic states remained indistinguishable in distal regions of the chromosome. Greater subdivision of H_F first accentuated the accumulation of variation (5 ≤ k ≤ 15, Figure S7) but eventually attenuated it when k ≥ 20. While we did not fully explore this attenuation, we note that we held both N and m (the average number of migrants per generation) constant across simulations; higher values of k were therefore accompanied by greater total migration between habitats and stronger within-deme drift in H_F.

The interaction we observed between selection and geographic structure in simulated populations closely mimicked the patterns found in stickleback, but the extent of this effect seemed limited. Even in the case of strong selection (s = 0.20) and substantial population structure, increases in genetic diversity extended <0.5 cM away from the locus under selection; maximal levels of variation required even tighter linkage. We therefore examined how recombination rate varies across stickleback genomes to better understand the extent to which selection may influence linked genetic variation.

The recombination landscape varies among individuals

RAD sequencing of both the BT and F₁ Hybrid (F₁) mapping crosses resulted in over 6000 segregating markers, with markers averaging 70 kbp apart on the BT map, and 56 kbp apart on the F₁ map (Table 1). Mean per-locus sequencing depth was 35 and 23× for the BT and F₁ families, respectively (range: BT = (28×, 57×), F₁ = (10×, 90×); Table S1]. RAD markers were consistently genotyped in over 90% of progeny [BT: mean = 98%, range = (95%, 99%); F₁: mean = 91%, range = (57%,99%)].

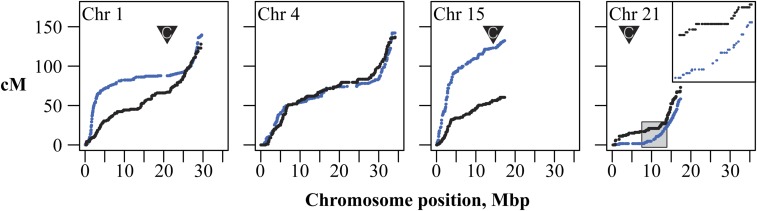
Patterns of recombination were generally consistent between the genetic maps (Figure 5 and Figure S1). As has been described previously (Roesti et al. 2013; Glazer et al. 2015), recombination on the larger metacentric chromosomes in the stickleback genome (e.g., chromosomes 4 and 7) was biased toward chromosome ends, with little recombination occurring across central, presumably centromeric, regions. Recombination rates across a number of the smaller chromosomes, in contrast, was typically highest toward one end (Figure 5, chromosome 15; Figure S1).

Figure 5.

The recombination landscape varies within and among genetic maps of BT and F₁ hybrid threespine stickleback. Each point represents a RADseq-based marker segregating within a mapping family. Blue: BT, black: F₁. Inverted triangles represent the locations of centromeric repeats, where known, from Sardell et al. (2018). The inset on chromosome 21 shows suppression of recombination due to inversion heterozygosity in the F₁. Genetic maps for all chromosomes and for the marine (RS) map are given in Figure S1.

We also observed stark differences between genetic maps. As expected, recombination in the hybrid map was completely suppressed within, and immediately surrounding, an inversion on chromosome 21, but this region recombined freely in the collinear BT map (length 4.3 cM, Figure 5). Conversely, on chromosome 1, the BT map showed the expected bias in recombination away from the centromere (Spearman’s ρ = 0.43, P < 0.05). This bias was almost entirely absent in the hybrid map (Spearman’s ρ = 0.14, P > 0.47), with recombination occurring steadily throughout the chromosome. In both cases, the total map lengths of each chromosome were similar (chromosome 1: BT = 129 cM, F₁ = 137.5 cM; chromosome 21: BT = 61.0 cM; F₁ = 75.7 cM), indicating that these differences were due to differences in the distribution but not the number of crossovers.

Much of the genome is tightly linked to loci under divergent selection

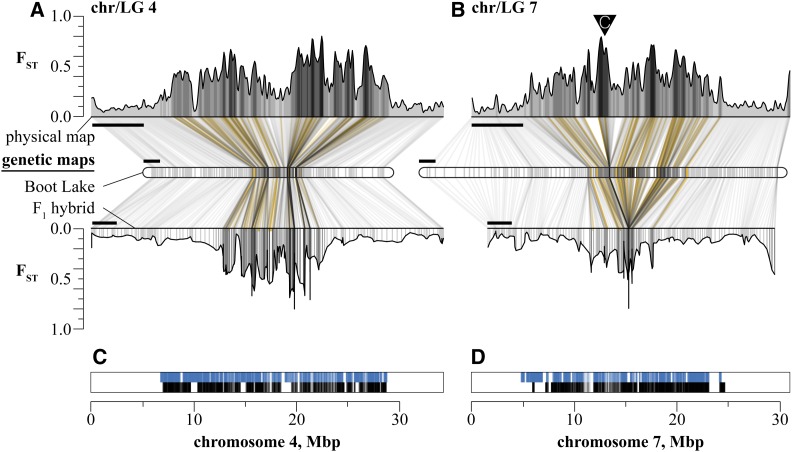
Genomic regions of greatest differentiation were compressed into proportionally smaller regions of the genetic maps (Figure 6, Table S2, and Appendix 1). Some of the largest regions of differentiation we observed—including those surrounding eda, the major effect locus for lateral plate number (Colosimo et al. 2005), and the chromosome 21 inversion—had average F_ST values > 0.4. Regions above this threshold spanned 8.1% of the physical genome (35.3 Mbp) but only 3.7% of the BT genetic map and 3.3% of the F₁ hybrid genetic map (Figure S8). On chromosome 4, the large central regions of differentiation are similarly compressed on both genetic maps, but this was not always the case. On chromosome 21, recombination was suppressed—and genomic differentiation compressed—only on the heterokaryotypic F₁ map (Figure S1). A similar effect was seen across a large region of differentiation on chromosome 7 (Figure 6B), despite this chromosome being collinear between marine and freshwater stickleback genomes (Figure S1). On the physical map, chromosome 7 contained three peaks of strong differentiation between BT and RS spanning over 9 Mbp. All three peaks were clearly separated on the BT map—though they comprise a relatively smaller region than on the physical map—but collapsed to a single locus on the hybrid map (span: 0 cM, position 57.7 cM on the map).

Figure 6.

The recombination landscape extends the genomic reach of divergent selection. (A and B) RS-BT F_ST scans were performed on the physical map (top, Bar, 5 Mbp) and imputed onto the freshwater and F₁ hybrid genetic maps (middle and bottom, Bar, 10 cM) for chromosomes 4 and 7. Lines connect evenly spaced windows on the physical map to the imputed positions on each genetic map and are shaded by the kernel-averaged F_ST for that window. Positions of divergent RAD loci are shown in gold. The inverted triangle represents the position of centromeric repeats (Sardell et al. 2018). (C and D) physical positions of all RAD loci within 0.2 cM from a divergent locus on the freshwater map (blue lines) and the F₁ hybrid map (black lines).

Because our simulations suggested that population structure could interact with selection to maintain variation, but only with tight linkage (≤0.2 cM), we imputed the positions of RAD loci from the population genomic dataset onto the BT and hybrid genetic maps. Based on average genome-wide recombination rates, 0.2 cM equates to less than 50 kbp of sequence space (BT map: 36 kbp; F₁ map: 44 kbp) and includes ∼6% of sequenced loci. However, the clustering of divergent loci in regions of low recombination resulted in ∼20% of all loci in the dataset fitting this linkage criterion (BT map: 19.5%; F₁ map: 20.4%; Figure 6, C and D and Figure S9). These tightly linked loci averaged over 200 kbp away from a divergent locus (BT map: 219 kbp; F₁ map: 256 kbp) and included loci greater than 2 Mbp away (max, BT map: 2.3 Mbp; max, F₁ map: 2.9 Mbp).

Discussion

Asymmetric population structure maintains asymmetries in patterns of linked genetic variation

The patterns of linked variation that we document here highlight not only the importance of selection, but also the structure of the threespine stickleback metapopulation in maintaining genetic variation. Throughout the species range, the marine population is remarkably uniform phenotypically, which we now know is reflected genetically by minimal isolation-by-distance over thousands of kilometers (Bell and Foster 1994; Catchen et al. 2013a; Defaveri et al. 2013). This large population with few barriers to migration is contiguous with thousands of freshwater lake and stream populations that are more clearly isolated by geography. While the influence of freshwater populations on the evolution of the species was once unclear (Bell and Foster 1994), it is now evident that gene flow between freshwater and marine stickleback populations is common, and may facilitate adaptation through the indirect sharing of alleles among freshwater populations (Schluter and Conte 2009).

Our findings suggest that the structuring of the freshwater habitat acts as a reservoir of genetic variation in the species, and that this effect is particularly potent in regions of the genome experiencing divergent selection. In genomic regions that are recombinationally distant to targets of divergent selection, gene flow among habitats homogenizes variation such that levels of genetic variation are similar (Figure 3) and differentiation is low (Figure 6) across habitats. At divergent loci themselves, selection has maintained a small number of haplotypes in each habitat, and variation is partitioned almost entirely among habitats (Figure 2 and Figure 3, Nelson and Cresko 2018). However, in the substantial fraction of the genome that is tightly linked to divergent loci, we hypothesize that selection has reduced the effective migration rate between alternative habitats such that the geographic structuring of the freshwater habitat becomes a significant factor affecting levels of genetic variation. Because migration among freshwater populations occurs primarily through the marine environment, divergent selection accentuates the effect of population structure in the freshwater habitat.

Forward simulations support this hypothesis. We found that under realistic migration rates (Caldera and Bolnick 2008; Berner et al. 2009) and selection coefficients (Barrett et al. 2008; Kitano et al. 2008), such asymmetric population subdivision by itself provides a simple explanation for the counterintuitive observation that smaller, isolated populations contain abundant linked variation (Figure 3 and Figure 4). The degree to which population structure increased levels of diversity depended both on the amount of substructure and the length of time over which selection acted. While even minimal substructure eventually resulted in patterns of diversity mirroring those we observed in stickleback, this effect required a selection phase on the order of the expected coalescence time of the metapopulation. This follows from the fact that selection and population structure protect variants from fixation or loss at adaptive and linked loci, respectively. Our findings generally agree with expectations from Slatkin’s (1991) model, where limited migration among demes increases the expected coalescence times of chromosomes sampled from a metapopulation (Equation 1). Near an alternatively adaptive locus, selection accentuates this effect by reducing effective migration rates among demes of alternative habitats.

Our empirical and simulated results, in combination with previous findings in threespine stickleback (Reimchen 1994; Kaeuffer et al. 2012; Roesti et al. 2014), have important implications for the long-term evolution of the species. Freshwater populations are ecologically diverse (Bell and Foster 1994; McKinnon and Rundle 2002; Kaeuffer et al. 2012; Leaver and Reimchen 2012; Reimchen et al. 2013), and the relative impacts of parallel vs. nonparallel selection pressures among freshwater populations is actively debated (Kaeuffer et al. 2012; Stuart et al. 2017). While it is possible that multifarious selection pressures also contribute to the maintenance of more genetic diversity on chromosomes from freshwater fish, our model does not require additional selection to maintain linked variation. Furthermore, the freshwater pond populations studied here are ecologically similar and geographically proximal (Cresko et al. 2004), so it is likely that parallel selection on a common pool of variation is largely responsible for the patterns of variation we observe. Put another way, we find no need to invoke more complex selection regimes in order to explain the patterns of variation we observe. Also studying ecologically similar freshwater populations, Roesti et al. (2014) found that parallel adaptation led to increases in F_ST among freshwater populations near peaks of marine-freshwater divergence, and inferred that sweeps of common SNPs on different genetic backgrounds led to this pattern. We have shown these linked genomic regions to be not only the most heavily partitioned but also the most diverse in the genome (Figure 3F and Figure S6). We find it likely that selection and gene flow happening over shorter evolutionary timescales (tens to thousands of years), like those investigated by Roesti et al. (2014), have occurred throughout the evolutionary history of this species and have long-lasting, collective effects on patterns of genomic variation over the course of millions of years.

A variable recombination landscape increases the genomic reach of selection and simplifies the architecture of divergence

In addition to the consequences of asymmetric population structure in maintaining genetic variation unevenly across geography, the recombination landscape also can have profound effects on heterogenous genome-wide patterns of genetic variation. Linkage to or among selected sites is now thought to affect many, if not most, variable sites in the genome (Schrider and Kern 2017; Kern and Hahn 2018), and suppression of recombination among the genomes of diverging populations and species appears in large part to determine patterns of genetic differentiation and divergence (Burri et al. 2015; Samuk et al. 2017; Vijay et al. 2017; Stankowski et al. 2018). In the threespine stickleback, genetic differentiation among phenotypically divergent populations is known to accumulate in regions of low recombination (Roesti et al. 2013; Marques et al. 2016; Samuk et al. 2017). Our work adds an important outcome of this phenomenon: low recombination adjacent to targets of divergent selection extends selection’s reach into linked regions, maintaining genetic variation, and structuring it among chromosomes with divergent evolutionary histories.

The accumulation of genetic diversity adjacent to targets of selection required tight linkage in our simulations, potentially limiting the relevance of this model in explaining patterns of genetic variation. However, because adaptive divergence has occurred principally in regions of low recombination, a substantial fraction of the genome is likely near enough (∼0.2 cM) to divergent loci for our model to explain the accumulation of variation on freshwater chromosomes. The absolute genetic distance through which divergent selection can influence linked variation is proportional to the strength of selection (e.g., Figure 4) and inversely proportional to the migration rate (e.g., Figure S10, Charlesworth et al. 1997). While we did not fully explore either parameter space, our chosen values are congruent with empirical estimates from stickleback. Estimates of migration rates vary widely across studies of stickleback, from nearly zero to rates that could swamp divergent selection (Caldera and Bolnick 2008; Berner et al. 2009). Estimated selection coefficients on lateral plate armor are consistently > 0.2 (Barrett et al. 2008; Kitano et al. 2008), and the total effect of selection on a locus depends on the total number of nearby selected sites (i.e., the “selection density”: Aeschbacher et al. 2017). Given the rate of adaptation observed in recently colonized freshwater habitats (Lescak et al. 2015; Bassham et al. 2018) combined with generally low recombination rates, the effect of selection may at times extend across entire chromosomes.

Our results also provide general insight into the variability and evolution of the recombination landscape. First, genomic divergence that occurs in the centers of the largest chromosomes (Hohenlohe et al. 2010; Jones et al. 2012; Bassham et al. 2018; Nelson and Cresko 2018) occurs within regions of consistently low recombination across maps from different genetic backgrounds (Hohenlohe et al. 2012; Roesti et al. 2013; Samuk et al. 2017). The negative association between divergence and recombination rate is a common finding across systems (Nachman 2002; Carneiro et al. 2009; Geraldes et al. 2011; Cutter and Payseur 2013; Burri et al. 2015; Aeschbacher et al. 2017), and can result from both negative (Burri et al. 2015; Stankowski et al. 2018) and positive (Aeschbacher et al. 2017; Samuk et al. 2017) selection between allopatric populations (Burri et al. 2015) and those currently exchanging genes (Carneiro et al. 2009; Aeschbacher et al. 2017). Our results agree that stickleback are no exception to this rule, and that divergent selection in the face of (historical) gene flow has generated this relationship both at the local (i.e., specific genomic regions, Figure 6) and genome-wide (Figure S8 and Table S2) scales. Second, although these results generally hold using both intra- and interpopulation genetic maps, we find that recombination rates in regions of divergence were often lowest in the F₁ map (Figure 5, Figure 6B, and Figure S8). This was expected within chromosomal inversions, where the alternative homozygotes demonstrated steady recombination throughout the inverted region, but also occurred on chromosome 7 despite the apparent lack of any large scale, simple structural variation (Figure 2 and Figure 4) although clusters of smaller structural variants that could not be detected in our maps could also reduce recombination. On the hybrid map, this entire physical region collapsed to a genetic region inherited essentially as a single Mendelian locus.

The specific reductions in recombination on the hybrid map are suggestive of the evolution of the recombination landscape itself, and, if true, could have profound implications for adaptation and genomic divergence in stickleback. For example, inversions are advantageous when recombination between multiple linked alleles that contribute to fitness (either in an additive or epistatic fashion) is maladaptive (Kirkpatrick and Barton 2006). The three previously identified inversions on chromosomes 1, 11, and 21 (Jones et al. 2012) are associated with divergence between the freshwater and marine habitats and occur in regions of the genome that readily recombine in chromosomal homozygotes (Figure 4, Figure S1, and Figure S2). Had inversions not evolved, gene flow and recombination among marine and freshwater populations may have been strong enough to prevent adaptive divergence in these genomic regions (Lenormand 2002; Yeaman and Whitlock 2011; Aeschbacher et al. 2017).

In contrast, our work and that of others (Roesti et al. 2013; Glazer et al. 2015) has shown that megabase pair-scale inversions have not evolved across the largest regions of divergence in the genome. In these regions, low recombination rates—which may themselves have evolved adaptively or been ancestral platforms for adaptive divergence—combined with strong selection has been effective at maintaining allelic combinations across megabase pairs of genomic space. These are also regions of exceptional sequence divergence between marine and freshwater chromosomes (Table S2; Samuk et al. 2017; Nelson and Cresko 2018). Sequence divergence alone may limit double-strand break resolution as crossovers in these regions (Modrich and Lahue 1996; Opperman et al. 2004; Li et al. 2006), biasing crossovers toward regions of lower sequence divergence. Explicit tests of this hypothesis, for example with F₃ mapping families where the effects of marine-freshwater hetero- and homozygosity in specific genomic regions can be directly assessed, will be a productive avenue of research.

The coincidence of reduced recombination and genomic divergence may help explain the repeatable and rapid adaptive divergence in stickleback (Bell and Foster 1994; Lescak et al. 2015) that is largely the result of the reuse of standing genetic variation (Colosimo et al. 2005; Schluter and Conte 2009; Deagle et al. 2012; Jones et al. 2012; Terekhanova et al. 2014; Roesti et al. 2015; Marques et al. 2016; Bassham et al. 2018). Because freshwater populations are typically founded by marine stickleback, the sources of standing genetic variation are low frequency variants in the marine population that nearly always exist in a heterozygous state with a marine genome (Bassham et al. 2018). Our results suggest that the recombination landscape may therefore facilitate the maintenance of freshwater haplotypes during their transit through the marine environment by reducing recombination even in collinear genomic regions. Multi-megabase haplotypes—potentially containing many alleles contributing to local adaptation—then have a higher probability of being selected in concert when a new freshwater population is established.

Conclusions

Divergent natural selection is a powerful force for the maintenance of genetic variation in nature. When local adaptation plays out on variable geographic and recombinational landscapes, we find that the effect of selection on genetic variation are amplified and shape patterns of linked variation in unexpected ways. Here, using empirical and simulation studies, we documented that asymmetric population subdivision among habitats in stickleback leads to an overall greater maintenance of diversity in freshwater as compared to the larger ancestral marine population. Furthermore, we hypothesized that the stickleback recombinational landscape is the product of repeated adaptive evolution that transforms a large genomic architecture of marine-freshwater divergence into a much more simplified genetic architecture. If true, two consequences are the efficient maintenance of adaptive divergence in the face of gene flow, including larger freshwater-adapted haplotypes at low frequency in the marine populations, and widespread linked selection that eliminates genetic variation in the panmictic marine population while maintaining genetic diversity in the freshwater habitat. The interaction of selection, recombination, and population structure has turned small, isolated freshwater stickleback populations into primary reservoirs of standing genetic variation that may potentiate future evolutionary change.