Significance
An ecological community is a dynamic complex system with a myriad of interacting species, which are controlled by various scale-dependent deterministic and stochastic forces. With rapid advances in genomics technologies, categorizing biological diversity, particularly microbial diversity, becomes relatively easy, but the great challenge is to disentangle the mechanisms controlling biological diversity. The general null model-based framework developed in this study provides an effective and robust tool to ecologists for quantitatively assessing ecological stochasticity. By highlighting the caveats such as model selection, similarity metrics, and spatial scales, this study provides guidance for appropriate use of null model-based approaches for examining community assembly processes. Although this framework was tested with microbial data, it should also be applicable to plant and animal ecology.
Keywords: stochasticity, community assembly, microbial ecology
Abstract
Understanding the community assembly mechanisms controlling biodiversity patterns is a central issue in ecology. Although it is generally accepted that both deterministic and stochastic processes play important roles in community assembly, quantifying their relative importance is challenging. Here we propose a general mathematical framework to quantify ecological stochasticity under different situations in which deterministic factors drive the communities more similar or dissimilar than null expectation. An index, normalized stochasticity ratio (NST), was developed with 50% as the boundary point between more deterministic (<50%) and more stochastic (>50%) assembly. NST was tested with simulated communities by considering abiotic filtering, competition, environmental noise, and spatial scales. All tested approaches showed limited performance at large spatial scales or under very high environmental noise. However, in all of the other simulated scenarios, NST showed high accuracy (0.90 to 1.00) and precision (0.91 to 0.99), with averages of 0.37 higher accuracy (0.1 to 0.7) and 0.33 higher precision (0.0 to 1.8) than previous approaches. NST was also applied to estimate stochasticity in the succession of a groundwater microbial community in response to organic carbon (vegetable oil) injection. Our results showed that community assembly was shifted from more deterministic (NST = 21%) to more stochastic (NST = 70%) right after organic carbon input. As the vegetable oil was consumed, the community gradually returned to be more deterministic (NST = 27%). In addition, our results demonstrated that null model algorithms and community similarity metrics had strong effects on quantifying ecological stochasticity.
One of the major goals in community ecology is to understand the processes and mechanisms underlying the biodiversity patterns across space and time (1–5). There are 2 types of processes controlling community assembly: deterministic and stochastic. The former is generally referred to as any ecological process that involves nonrandom, niche-based mechanisms, including environmental filtering (e.g., pH, temperature, moisture, and salinity) and various biological interactions (e.g., competition, facilitation, mutualisms, predation, and tradeoffs) (3, 5–7). In contrast, the latter signifies ecological processes generating community diversity patterns indistinguishable from random chance alone, which typically include random birth–death events, probabilistic dispersal (e.g., random chance for colonization), and ecological drift (random changes in organism abundances) (2, 3, 5, 7, 8). After over a decade’s debate, now it is generally believed that both deterministic and stochastic processes work together simultaneously in structuring ecological communities (9–11). However, determining their relative importance in governing community diversity, especially in microbial ecology, is still challenging (3, 5, 12, 13). Quantifying their relative importance is even more difficult (14).
Several different types of approaches have been used to infer the importance of deterministic and stochastic processes in determining ecological communities (4), including multivariate analysis (15–17), null modeling (18–20), and theory-based approaches (2, 21). Null model-based methods are most widely used (5–7, 13, 19, 20, 22–27). However, most null model-based inferences on community assembly mechanisms are qualitative rather than quantitative (6, 7, 13, 19, 22, 25). Previously, we proposed selection strength (SS) to quantify the relative importance of determinism and stochasticity in a fluidic groundwater ecosystem in response to a carbon source addition, in this case emulsified vegetable oil (EVO) to stimulate bioremediation (5). EVO has low solubility and provides diverse organic carbon sources for longer-term stimulation of the microbial community. The selection strength for a pairwise comparison is defined as the proportion of the difference between the observed similarity and the null expected similarity divided by the observed similarity, and their average across all pairwise comparisons is used as a quantitative index for measuring the importance of determinism vs. stochasticity (5). Since its publication, many readers have expressed interest in using this approach in their studies. This approach, however, is not general enough and sometimes gave values exceeding expected maximum (>100%) because it only considers the situation when deterministic forces drive communities more similar than random patterns. Thus, in this study, we refined the model to suit more general situations in quantifying ecological stochasticity underlying community assembly. We first developed a general mathematical framework with a normalized index, followed by testing it with different simulated communities by considering environmental noise, biotic interactions, and spatial scales. We then used it to reassess the importance of determinism and stochasticity in mediating the succession of groundwater microbial communities in response to organic carbon injection (5). In addition, we evaluated the effects of different null model algorithms and similarity metrics on quantitative assessment of stochasticity in governing the groundwater microbial community assembly in response to the carbon amendment. To avoid confusion, in this paper, we refer to the random changes in community structure with respect to species identities and/or functional traits due to stochastic processes of birth, death, immigration and emigration, spatiotemporal variation, and/or historical contingency as “ecological stochasticity” (or stochasticity if not specified) (4) and the random fluctuations of deterministic environmental factors (e.g., temperature, moisture, and salinity) over space and time as “environmental noise,” which is also commonly called “environmental stochasticity” (28, 29). In addition, “community similarity” (or “dissimilarity”) here serves as a general term to describe any measure used to quantify the resemblance (or difference) between 2 local communities.
Mathematical Framework.
Theoretically, deterministic processes can drive ecological communities more similar or more dissimilar than null expectation (12, 30, 31). For instance, since phylogenetically closely related species are ecologically more similar, they could cooccur more than expected upon abiotic environmental selection (32). Thus, this type of deterministic process (e.g., environmental filtering) is expected to drive the community to be more similar under homogeneous environmental conditions or more dissimilar if the environment is heterogeneous. In contrast, some other deterministic factors (e.g., competition and trophic interactions) generally drive the communities to be more dissimilar because closely related species should cooccur less than randomly expected due to competitive exclusion (31, 33). However, competition could also cause communities to be more similar if competitive exclusion could eliminate more different and less related species which lack certain competitive traits (30, 31). We provide quantitative assessment of community assembly mechanisms by considering both situations below.
Assume that there is a metacommunity consisting of m communities. Let Cij represent the observed similarity (ranging from 0 to 1) between the ith community and the jth community . If a similarity metric does not range from 0 to 1, it can be standardized (SI Appendix, Supplementary Text A). Dij is the dissimilarity between the ith community and the jth community, that is, . Let Eij represent the randomly expected similarity between the ith community and the jth community after randomization of the metacommunity, which is repeated for 1,000 times to generate a set of null expected communities. Then, we will have as the average of the null expected similarity between the ith and jth communities. is the average of the null expected dissimilarity between the ith and jth communities. The SD of the null expected similarity is Vij.
If communities are structured by the deterministic factors leading to communities more similar, the actual similarity values (Cij) between the ith and the jth communities will be greater than the null expectation . Thus, the difference between the observed and average null expectation can be used to assess the strength of determinism acting against otherwise stochastic forces with respect to the ith and jth communities (18), which is referred to as selection strength between the ith and jth communities (5), ranging from 0 to 1. In this case,
| [1] |
so-called type A selection strength. Correspondingly, the type A stochasticity ratio is
| [2] |
If communities are structured by the deterministic factors which produce communities more dissimilar, the actual similarity values (Cij) between the ith and the jth communities should be less than the null expectation between with a SD Vij (i.e., ). In other words, the actual dissimilarity, will be larger than the randomly expected dissimilarity, . The larger the differences between the actual dissimilarity and the null expected dissimilarity, the greater the roles of this type of deterministic factors. Thus, in this case, we should use dissimilarity to measure the selection strength , that is,
| [3] |
so-called type B selection strength. Correspondingly, the type B stochasticity ratio is
| [4] |
Let and be the numbers of the pairwise similarities which are larger or less than null expectations, respectively; then the total number of pairwise comparisons (n) is the sum of and . The average of the selection strength of type A, type B, and total are
| [5] |
| [6] |
| [7] |
The average strength of stochasticity (ST) is
| [8] |
| [9] |
| [10] |
Ideally, if the community assembly is extremely deterministic without any stochasticity, the selection strength index should be 100%, and the stochasticity index should be 0%. Similarly, when the community assembly is completely stochastic without any determinism, the selection strength index should be 0%, and the stochasticity index should be 100%. However, the SS and ST described above do not necessarily vary from 0 to 100% because always have substantial deviations from 0 and 1. We applied the following formula to obtain normalized selection strength (NSS) and normalized stochasticity ratio (NST), which range from 0 to 100%, and hence, they could be better measures than SS and ST for assessing determinism and stochasticity (see SI Appendix, Supplementary Text B, for mathematical details).
| [11] |
| [12] |
| [13] |
| [14] |
| [15] |
where and are the extreme values of under completely deterministic and stochastic assembly, respectively. The superscript A and B indicate type A and type B pairwise comparisons. is the similarity between community i and j under extremely deterministic assembly. is one of the null expected values of similarity between community i and j under stochastic assembly. is a generalized function for SSij under observed, extremely deterministic, or stochastic assembly.
Results
Validation with Simulated Communities.
Since there is not yet a gold-standard experimental dataset for assessing the relative importance of determinism and stochasticity, simulated communities with known levels of stochasticity are needed. In the simulated communities, the ground truth of assembly processes is known, and hence, the performances with different approaches can be systematically evaluated. In this study, we used a spatially implicit model which simply considers the communities under the scenario of type A selection. The communities consist of a combination of 2 types of species: one is under completely deterministic assembly (so-called deterministic species), and the other is under completely stochastic assembly (so-called stochastic species). The levels of stochasticity were predetermined by assigning different ratios of stochastic species. We simulated 21 datasets with different levels of expected stochasticity ranging from 0 to 100% (see SI Appendix, Supplementary Text C, Table S1, and Fig. S1A, for details). The synthetic datasets were used to evaluate the performance of ST, NST, and the neutral species percentage (NP) calculated from Sloan’s neutral model (34, 35), based on the accuracy and precision coefficients derived from concordance correlations (36, 37).
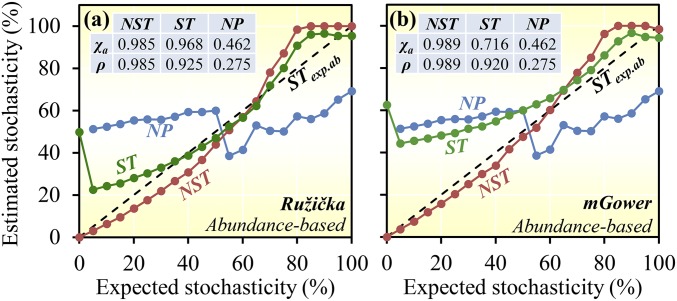
NST had considerably higher accuracy and precision than ST, which was in turn better than NP for the majority of similarity metrics examined (Fig. 1 and SI Appendix, Table S2). Also, the performance of NST varied substantially with similarity metrics. The 13 incidence-based metrics tested can be classified into 3 major categories based on relative ratio of unique taxa (e.g., Jaccard), the number of unique taxa (e.g., Manhattan), or the squared root of the number of unique taxa (Euclidean and modified Euclidean) (SI Appendix, Supplementary Text A). NST had high accuracy and precision (>0.99) with all incidence-based metrics (SI Appendix, Table S2). About 2 to 3 times of differences in accuracy and precision were observed for NST with various abundance-based similarity metrics (SI Appendix, Table S2). The 15 abundance-based metrics tested can be categorized into 4 major groups based on relative difference (e.g., Ružička), average relative difference (e.g., Canberra), absolute difference (e.g., Manhattan), and squared sum of difference (e.g., Euclidean) (SI Appendix, Supplementary Text A). Abundance-based NST showed very high accuracy and precision (>0.95) with all relative difference metrics (Ružička, Bray–Curtis, Kulczynski, and Chao), some average relative difference (modified Gower), and some absolute difference metrics (Manhattan and modified Manhattan) but always worse using squared-sum metrics (SI Appendix, Table S2). In addition, it seems that the performance of NST and ST indexes varied with stochasticity levels. For instance, at lower stochasticity levels (0 to 5%), NST performed much better than ST (22 to 50% improvement) (Fig. 1). At the high stochasticity levels, ST showed similar or slightly higher accuracy than NST (Fig. 1). By considering their overall performance, characteristics, and popularity, NST based on Jaccard/Ružička similarity metrics is recommended for estimating the magnitude of stochasticity in community assembly.
Fig. 1.
Consistency between the estimated and expected stochasticity with different methods based on the simulated communities with various levels of expected stochasticity. The simulation model was spatially implicit. Red indicates NST, green indicates ST, and blue indicates NP. STexp.ab (black), expected abundance-based stochasticity in the simulated communities. NST and ST were calculated based on (A) Ružička and (B) modified Gower. The inner tables show accuracy coefficient (χa) and precision coefficient (ρ), which are derived from concordance correlation coefficient (SI Appendix, Eqs. S21 and S22). See SI Appendix, Supplementary Text C, Table S1, and Fig. S1A, for more details about the simulation model; SI Appendix, Table S2, for the results of other similarity metrics; and SI Appendix, Table S3, for the definition of each metric.
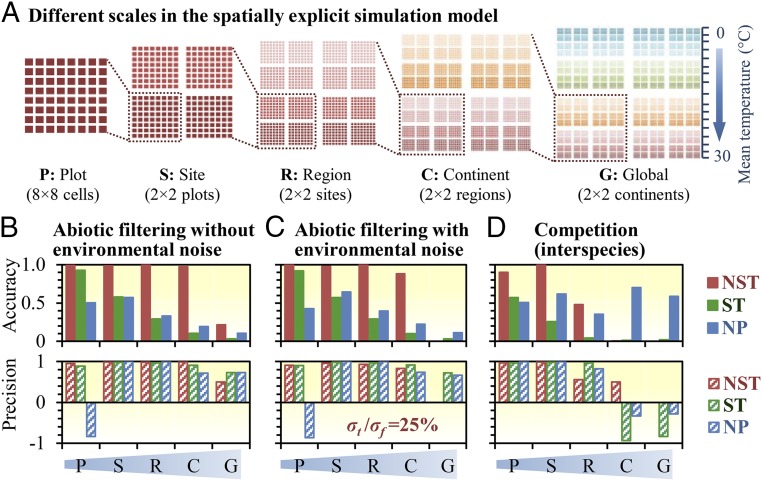
Since community diversity patterns and the underlying assembly mechanisms are scale dependent (38), we also evaluated the accuracy and precision of different stochasticity indexes using spatially explicit models by considering scales, environmental noise, and biotic competitive interactions (Fig. 2 and SI Appendix, Supplementary Text C, Figs. S1B and S2, and Table S1). Communities and metacommunities were constructed in a hierarchical way to simulate different spatial scales, including cells (local communities), plots, sites, regions, continents, and global (Fig. 2A and SI Appendix, Fig. S1B). These scale levels used are to facilitate description of multilevel scales but do not mean the corresponding real spatial scales. Scale dependence was examined by estimating stochasticity in pairwise comparisons among all samples within individual spatial scales, and the main results were summarized as below (Fig. 2 and SI Appendix, Fig. S2). First, in contrast to ST and NP, NST showed high accuracy and precision (both coefficients >0.9) at local scale (i.e., plot and site levels) in all scenarios (Fig. 2 and SI Appendix, Fig. S1B) except that with very high environmental noise (σt/σf = 200%, where σt is temperature deviation and σf is fitness deviation as defined in SI Appendix, Supplementary Text C and Fig. S2C). Second, all of the approaches examined (NST, ST, and NP) showed scale dependence. The accuracy and/or precision of stochasticity estimation dramatically decreased at larger spatial scales (e.g., global scale in all scenarios; Fig. 2 and SI Appendix, Fig. S2 B and C), suggesting that it might be better to apply NST and other null/neutral model-based approaches to study community assembly at local scale (e.g., within plot or site). Under the scenario of competition without noise (Fig. 2D), NST had high accuracy and precision below site scales but not above regional scales, suggesting the influence of competition on diversity patterns could be very sensitive to spatial scale. Third, NST precision considerably decreased if sample size was very small (≤6 samples in our simulation; SI Appendix, Fig. S2A), although accuracy did not. Fourth, none of the tested indexes showed sufficient accuracy when environmental noise was very high (σt/σf = 200%; SI Appendix, Fig. S2C). Interestingly, ST still had high precision (>0.95) across all spatial scales with high environmental noise (SI Appendix, Fig. S2C), implying that the variation of ST could be still useful in examining the relative change of ecological stochasticity even with high environmental noise. In addition, when the simulated communities were purely controlled by deterministic forces (i.e., expected stochasticity to be 0), the observed similarity can still be close to random pattern if environmental filtering and competition simultaneously affect the communities and/or the spatial scale is too large, leading to overestimation of stochasticity. In this case, NST generally performed better than other approaches (SI Appendix, Fig. S2 D–F), with relatively low overestimation (NST < 20%) within small scales (plot and site) when 1 deterministic process is predominant (filtering or competition > 80%; SI Appendix, Fig. S2G). However, even NST still obviously overestimated stochasticity when filtering and competition were comparable (NST > 50%) and/or spatial scale is too large (NST up to 100% at regional to global scale; SI Appendix, Fig. S2G), indicating pure but complex deterministic forces can lead to random diversity pattern which is more obvious at larger spatial scales.
Fig. 2.
Accuracy and precision of stochasticity estimation of different methods across various spatial scales under different simulated scenarios. (A) Spatial configurations of the spatially explicit simulation models across different spatial scales (plot [P], site [S], region [R], continent [C], and global [G]). Deterministic species were simulated in 3 different scenarios as below: (B) abiotic filtering without environmental noise (SI Appendix, Table S1, scenario B), (C) abiotic filtering with medium-level environmental noise (σt/σf =25%, where σt is the temperature deviation and σf is the fitness deviation defined in SI Appendix, Supplementary Text C; scenario D in SI Appendix, Table S1), and (D) competition among a total of 256 competitors (SI Appendix, Table S1, scenario F). Three indexes were used to estimate stochasticity at different spatial scales, including NST (red bars), ST (green bars), and NP (blue bars). NST and ST were calculated based on Ružička similarity index and the null model PF (SI Appendix, Table S3). Accuracy (solid bars) and precision (crossed bars) were evaluated by the coefficients derived from concordance correlation coefficient (SI Appendix, Eqs. S21 and S22). See SI Appendix, Supplementary Text C, Table S1, and Fig. S1B, for more details about the simulation model and SI Appendix, Fig. S2, for the results of other scenarios.
Applications to the Microbial Community Succession in a Fluidic Ecosystem.
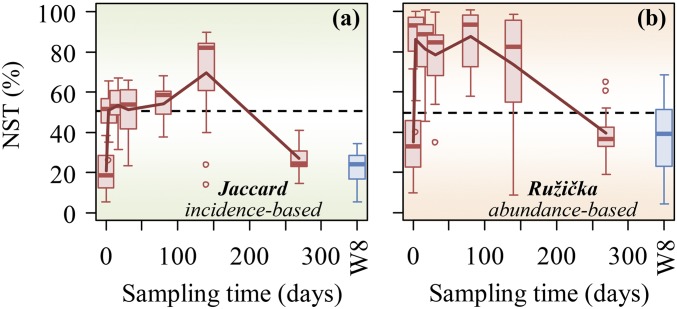
Previously, SS was used to quantify the degree of determinism in controlling the succession of the groundwater microbial communities in response to organic carbon injection (5) by focusing only on the situation in which deterministic forces drive the communities to be more similar. However, it seems that both situations (more similar or more dissimilar than null expectation) exist at day 140, although the latter occur for a relatively small portion of the pairwise comparisons (19.0% more dissimilar than null expectation). We reanalyzed the experimental data using the above framework. By considering different situations, the estimated stochasticity at day 140 (ST = 79 ± 15%; NST = 70 ± 23%; Fig. 3A) is lower than previously reported (previous ST = 92 ± 12%) (5). Also, as shown previously (5), the estimated stochasticity varied substantially with time (Fig. 3). In addition, the estimated NST at the beginning and end (21% at day 0 and 27% at day 269 on average; Fig. 3A) were similar to the control well (22% on average), which is considerably below the 50% boundary point (Wilcoxon test P < 0.0001). In contrast, the estimated NST during the middle phase of the succession were 70% on average with Jaccard (Fig. 3A) and 74% on average with Ružička (Fig. 3B), which are considerably above the 50% boundary (Wilcoxon test P < 0.003). All of these results indicate that stochastic processes could play more important roles in controlling community succession in its middle phase, while deterministic processes could be more important in its early (before injection) and late phases, which are consistent with theoretical expectations and site geochemistry (5). The result in the middle phase seems counter to intuition that adding fresh carbon should drive selection and hence leads to a more deterministic outcome. However, since the groundwater is highly contaminated and carbon poor (39, 40), the existing communities are under strong selection pressure. Consequently, adding fresh complex carbon would relieve the selection pressure and drive the communities more stochastic (5).
Fig. 3.
Dynamic changes of the estimated NST during the succession of the groundwater microbial communities in response to emulsified vegetable oil injection. NST was calculated based on (A) Jaccard and (B) Ružička metrics using null model algorithm PF. In null model PF, the probabilities of taxa occurrence are proportional to the observed occurrence frequencies, and taxon richness in each sample is fixed as observed (19). When using abundance-based metric, Ružička, null taxa abundances in each sample are calculated as random draw of the observed number of individuals with probability proportional to regional relative abundances of null taxa in the sample (26). W8 is the control well on which the vegetable oil had no or minimal impact. See SI Appendix, Figs. S3–S5, for results of other null model algorithms and similarity metrics.
Since the results from null model analyses are very sensitive to the model algorithms and similarity metrics (41), further analyses were performed to understand how the choice of model algorithms and similarity metrics affects the estimation of stochasticity based on NST. For the incidence (presence–absence) data, there are basically 9 null model algorithms (also referred to as null models), differing in whether rows (representing different taxa) and columns (representing sites, samples, or communities) are treated as fixed sums, equiprobable, or proportional (41) (SI Appendix, Supplementary Text D and Table S4). Equiprobable means every taxon has equal probability to be present in a sample, or every sample has equal probability to hold a taxon; proportional means the probability is proportional to observed occurrence frequency or taxon richness; and fixed means the occurrence frequency of each taxon or taxon richness in each sample is the same as observed. Among all 9 null model algorithms tested, the 4 null models with fixed or proportional taxa richness and equiprobable or proportional taxa occurrence frequency (SI Appendix, Fig. S3) gave obvious trends which are very similar to what we previously reported (5). However, no clear or less consistent patterns were observed for the other 5 null models (SI Appendix, Fig. S3), suggesting that the estimated stochasticity is null model dependent. In general, a more constrained null model (fixed > proportional > equiprobable) restricts the null results closer to observed values and thus leads to higher estimated stochasticity. For example, considerably higher stochasticity was obtained with proportional taxa occurrence frequency (NST up to 69 to 70%; e.g., SI Appendix, Fig. S3) than with equiprobable taxa occurrence frequency (NST < 38%; e.g., SI Appendix, Fig. S3; Wilcoxon test P < 0.0001) for the samples from different time points.
The null model analysis is also dependent on the community similarity metrics used (41). To understand whether and how community similarity metrics affect the estimation of stochasticity, 13 different incidence-based community similarity metrics were tested (SI Appendix, Fig. S4). Since the algorithm PF (proportional taxa occurrence frequency, fixed richness) has been used more often (19, 26), we examined different metrics based on this null model. With respect to the 3 types of incidence-based metrics, only squared-root metrics showed relatively stochastic (NST > 50%; SI Appendix, Fig. S4) assembly before the organic carbon input, which is not expected under such a highly stressful environment. All other incidence-based metrics showed very similar trends in the changes of stochasticity with time (SI Appendix, Fig. S4). However, the magnitude of NST could be different. For example, higher (Wilcoxon test P < 0.008) stochasticity was obtained with Grower (NST up to 79%; SI Appendix, Fig. S4) than with Jaccard (NST less than 70%; Fig. 3A) similarity metrics. We also tested different abundance-based similarity metrics (Fig. 3B and SI Appendix, Fig. S4). Compared to other types of metrics, the absolute difference and squared-sum metrics showed obviously higher stochasticity before organic carbon input (NST > 45%) or large variation (interquartile range up to 50%, Morisita and Morisita–Horn; SI Appendix, Fig. S4), which appear less preferred. All other abundance-based metrics revealed a trend of stochasticity similar to the incidence-based metrics. However, the magnitude of NST is generally higher (around 20% higher on average in NST; Fig. 3B and SI Appendix, Fig. S4) than those based on their corresponding incidence-based metrics, suggesting higher stochasticity in terms of quantitative change than qualitative change. In addition, compared to ST, NST showed much less variations or even no significant difference when using different metrics (e.g., Jaccard vs. Sørensen, incidence-based mGower, or Ružička vs. Bray–Curtis, abundance-based mGower; SI Appendix, Fig. S5), suggesting higher robustness of NST to metrics variations. Altogether, these results suggest that appropriate selections of community similarity indexes are also important in quantitative estimation of stochasticity underlying community assembly.
Discussion
Quantifying stochasticity in governing community assembly is important but difficult, and even more so in microbial ecology. To address this challenge, we developed a general mathematical framework to provide quantitative assessment of ecological stochasticity under both situations in which deterministic factors drive the communities more similar or dissimilar than null expectations. When tested with simulated communities, NST showed higher accuracy and precision than ST and NP, and Jaccard/Ružička metrics is the most recommended among various metrics. Applying this framework to the succession of groundwater microbial communities in response to carbon injection indicated that null model algorithms and community similarity metrics had strong effects on quantitatively estimating ecological stochasticity. Since the rationale and mathematical derivation are universal, NST should be applicable to other biological systems (e.g., plants and animals) or at least other highly diverse communities than microbial ones.
NST is different from other indexes based on null model analysis. In null model-based indexes, the modified Raup–Crick metrics (RC, e.g., RCJaccard and RCBray) (19, 26) and standardized effect size (SES, e.g., βNTI based on phylogenetic dissimilarity) (7, 20, 25) have been widely applied to infer ecological stochasticity (4). RC is calculated from the percentage of null dissimilarity values lower than or equal to the observed value, and SES is the difference between observed value and null expectation divided by SD of null results. RC and SES reflect the significance of the difference between observed and null dissimilarity and usually serve as qualitative identification of deterministic patterns (i.e., |RC| > 0.95, |SES| > 2). ST is calculated from relative difference between observed and null similarity (or dissimilarity), and NST derived from ST is to measure the relative position of observed value between the extremes under pure deterministic and pure stochastic assembly. Thus, NST reflects the contribution of stochastic assembly relative to deterministic assembly, based on magnitude rather than significance of the difference between observed and null expectation, and therefore can serve as a better quantitative measure of stochasticity (SI Appendix, Fig. S6).
There are several limitations for null model-based stochasticity estimation. First, special attention is needed for selection of null model algorithms and similarity metrics for randomization, which could lead to quite different results of stochasticity estimation. Based on the results presented here, the null models of fixed taxa richness and proportional taxa occurrence frequency (PF) in coupling with Jaccard/Ružička similarity metrics appear to be more preferred. Nevertheless, it is anticipated that the performances of different null models and similarity metrics are also community dependent. Therefore, depending on ecological questions, multiple null models and metrics (both incidence- and abundance-based) should be explored in quantifying community assembly mechanisms.
Second, deterministic forces are generally compounded by multiple intricate abiotic and biotic processes (4, 28, 33, 42). It is generally believed that competitive exclusion drives communities to be more dissimilar by excluding closely related ecologically similar species, but the impacts of competition on community structure appear to be much more complicated. Recent studies indicate that competitive exclusion could also drive a community to be more similar by eliminating competitively inferior, more distantly related taxa (30). Trophic interactions could also promote community divergence (33). However, it is difficult to differentiate such types of biotic interactions using the null model-based statistical approach from those of environmental filtering, which leads community diversity to be more similar (30, 32). More interestingly, about 3 decades ago, it was argued that competition may not be of primary importance in shaping community structure because it is less likely that niche differentiation of competitors has come about by coevolution (43), due to low probability of consistent coexistence of a particular pair of competing species, especially under the situations of high community diversity and high spatial and temporal heterogeneity. If this is true, we expected that the type A situation is much more common than type B. This is supported by this study with >90% type A even though competition appears to be very intensive based on network analysis (44). However, it seems that this argument is not supported by some recent studies on animals (e.g., refs. 45 and 46) and plants (e.g., ref. 47), in which competition was regarded as predominant force in structuring community composition. Nevertheless, given the extremely high diversity of microbial communities, we hypothesize that compared to plant and animal communities, competition could be less important in structuring microbial community as commonly assumed (48). Alternatively, each type of deterministic force (e.g., competition, facilitation, or environmental filtering) can predominate under certain conditions of stress and resources as found in plants and animals (49–51). If neither is true and different deterministic forces are equivalent to one another, deterministic assembly can lead to random patterns, and hence, null model analysis could overestimate stochasticity (SI Appendix, Fig. S2G).
Third, community diversity patterns and the underlying assembly mechanisms could vary across differential scales of space, time, environmental gradients, and/or taxonomic and ecological organizations (38, 52, 53). For examples, it was observed that strong competition at local scales resulted in weak competition at broader scales (54), and bird competition is important from plot to country scale but becomes unimportant at continental scale (53). However, the challenge is how to define appropriate scales that are relevant to the organisms or processes being examined (38) because the characteristics and behaviors of natural ecosystems are quite different across different spatial, temporal, and/or organizational scales. According to our simulation, NST can maintain good performance and robustness when the spatial scale is where dispersal rates within the metacommunity (i.e., randomization range in null model) are the same or comparable (e.g., simulated plot and site level; Fig. 2 and SI Appendix, Fig. S2).
Fourth, since different assembly mechanisms could generate similar diversity patterns, using the null model-based statistical approach to infer assembly mechanisms from empirical diversity patterns is only an introductory point (4, 38). Although NST was evaluated with taxonomic β-diversity metrics in this study, it is applicable to phylogenetic β-diversity metrics (SI Appendix, Table S3) as we did for ST recently (55), and integration of multiple dimensions of diversity (taxonomic, phylogenetic, functional, etc.) will facilitate further disentanglement of complicated assembly processes (4, 26). As a next step, process-based modeling approaches by considering various ecological processes such as dispersal limitation, life history traits (e.g., growth, reproduction, and dormancy), conspecific density dependence, and/or ecological drift (e.g., ref. 56) should allow us to further assess the relative importance of various assembly mechanisms, design possible experiments for validation, differentiate the possible consequences of individual biotic and abiotic factors which are not easily separated via experimentation, and evaluate the scale the observed phenomena from local to regional and global (38, 56).
In addition, the operational distinction of stochasticity and determinism can appear somewhat arbitrary (28, 57), and it is difficult to distinguish ecological stochasticity from the noise caused by deterministic environmental factors, as shown in our simulation (SI Appendix, Fig. S2C). More importantly, because of the measurement noise associated with high-throughput technologies in terms of reproducibility, sensitivity and/or quantification, and uncertainties in data processing and analyses (58–60), it is very challenging to obtain measurements close to the true values of stochasticity and determinism for particular communities. Thus, the ecological stochasticity and determinism estimated using the framework described above should be viewed as statistical proximate rather than ultimate forces in shaping community diversity and structure (4). Thus, as statistical proximate, the estimation requires sufficient biological replicates (e.g., >6) to ensure enough statistical power as our simulation showed (SI Appendix, Fig. S2A). Finally, because of the inherent uncertainty in selecting appropriate null model algorithms, similarity metrics, spatial scales for comparisons, and regional species pool for a particular study, the estimated degree of stochasticity should be best used for relative comparison across different conditions or treatments, rather than used as absolute values.
Materials and Methods
Details for all methods are provided in SI Appendix, Supplementary Text. Briefly, 21 datasets were simulated by a spatially implicit model, and 11 datasets under each of 5 scenarios were simulated by a spatially explicit model, with the defined stochasticity ranging from 0 to 100% (SI Appendix, Table S1). Each local community is a combination of deterministic and stochastic species with a ratio fitting the defined stochasticity. The stochastic species are assembled according to neutral theory models (2, 34, 61) in a spatially implicit model, while spatially explicit stochastic assembly is neutral theory-based assembly across 4-level metacommunities from 1 global metacommunity down to 16,384 local communities. Deterministic species can only live in their preferred environment due to strong abiotic filtering in the scenarios of abiotic filtering without noise in spatially implicit and explicit models (scenarios A and B in SI Appendix, Table S1). If environmental noise is considered (scenarios C through E in SI Appendix, Table S1), the abundances of deterministic species are determined by temperature in each local community, which has a normal-distributed random deviation from plot mean temperature. If competition is considered (scenario F in SI Appendix, Table S1), deterministic species consist of 256 competitors randomly occupying local communities, where the first-arrived competitor excludes other competitor(s) and stops them passing through. To investigate complex deterministic forces, simulated species controlled by abiotic filtering are combined with those controlled by competition to generate deterministic part of each simulated community (scenario G in SI Appendix, Table S1). For each simulated dataset, stochasticity was estimated with NP (35), ST (5), and NST, of which the quantitative performance was evaluated by accuracy (χa; SI Appendix, Eq. S21) and precision (ρ; SI Appendix, Eq. S22) coefficients derived from concordance correlation coefficient (36). The empirical data were obtained from the previous publication (5). Then, stochasticity was estimated by NST and ST based on different null model algorithms and different similarity metrics for comparison. NST analysis can be performed using a package NST written with the R language (62), which can be downloaded or installed from CRAN (https://cran.r-project.org/package=NST), or a web-based pipeline (http://ieg3.rccc.ou.edu:8080) built on Galaxy platform (63).
Supplementary Material
Acknowledgments
We thank John Quensen for early comments that helped stimulate this additional work. This work was conducted as part of Ecosystems and Networks Integrated with Genes and Molecular Assemblies, a Scientific Focus Area Program at Lawrence Berkeley National Laboratory, under Contract DE-AC02-05CH11231 through the Office of Science, Office of Biological and Environmental Research, of the US Department of Energy. This work is also partially supported by the US Department of Energy Office of Science, Office of Biological and Environmental Research Genomic Science program under Awards DE-SC0014079, DE-SC0016247, and DE-SC0010715.
Footnotes
The authors declare no conflict of interest.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1904623116/-/DCSupplemental.
References
- 1.MacArthur R. H., Wilson E. O., The Theory of Island Biogeography (Princeton University Press, Princeton, NJ, 1967). [Google Scholar]
- 2.Hubbell S. P., The Unified Neutral Theory of Biodiversity and Biogeography (Princeton University Press, Princeton, NJ, 2001), pp. 375. [Google Scholar]
- 3.Chase J. M., Myers J. A., Disentangling the importance of ecological niches from stochastic processes across scales. Philos. Trans. R. Soc. Lond. B Biol. Sci. 366, 2351–2363 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Zhou J., Ning D., Stochastic community assembly: Does it matter in microbial ecology? Microbiol. Mol. Biol. Rev. 81, e00002-17 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Zhou J., et al. , Stochasticity, succession, and environmental perturbations in a fluidic ecosystem. Proc. Natl. Acad. Sci. U.S.A. 111, E836–E845 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Chase J. M., Stochastic community assembly causes higher biodiversity in more productive environments. Science 328, 1388–1391 (2010). [DOI] [PubMed] [Google Scholar]
- 7.Stegen J. C., Lin X., Konopka A. E., Fredrickson J. K., Stochastic and deterministic assembly processes in subsurface microbial communities. ISME J. 6, 1653–1664 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Nemergut D. R., et al. , Patterns and processes of microbial community assembly. Microbiol. Mol. Biol. Rev. 77, 342–356 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Adler P. B., Hillerislambers J., Levine J. M., A niche for neutrality. Ecol. Lett. 10, 95–104 (2007). [DOI] [PubMed] [Google Scholar]
- 10.Gewin V., Beyond neutrality—Ecology finds its niche. PLoS Biol. 4, e278 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Gravel D., Canham C. D., Beaudet M., Messier C., Reconciling niche and neutrality: The continuum hypothesis. Ecol. Lett. 9, 399–409 (2006). [DOI] [PubMed] [Google Scholar]
- 12.Dini-Andreote F., Stegen J. C., van Elsas J. D., Salles J. F., Disentangling mechanisms that mediate the balance between stochastic and deterministic processes in microbial succession. Proc. Natl. Acad. Sci. U.S.A. 112, E1326–E1332 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Zhou J., et al. , Stochastic assembly leads to alternative communities with distinct functions in a bioreactor microbial community. MBio 4, e00584-12 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Hanson C. A., Fuhrman J. A., Horner-Devine M. C., Martiny J. B. H., Beyond biogeographic patterns: Processes shaping the microbial landscape. Nat. Rev. Microbiol. 10, 497–506 (2012). [DOI] [PubMed] [Google Scholar]
- 15.Legendre P., Borcard D., Peres-Neto P. R., Analyzing or explaining beta diversity? Comment. Ecology 89, 3238–3244 (2008). [DOI] [PubMed] [Google Scholar]
- 16.Peres-Neto P. R., Leibold M. A., Dray S., Assessing the effects of spatial contingency and environmental filtering on metacommunity phylogenetics. Ecology 93 (suppl. sp8), S14–S30 (2012). [Google Scholar]
- 17.Borcard D., Legendre P., All-scale spatial analysis of ecological data by means of principal coordinates of neighbour matrices. Ecol. Modell. 153, 51–68 (2002). [Google Scholar]
- 18.Chase J. M., Biro E. G., Ryberg W. A., Smith K. G., Predators temper the relative importance of stochastic processes in the assembly of prey metacommunities. Ecol. Lett. 12, 1210–1218 (2009). [DOI] [PubMed] [Google Scholar]
- 19.Chase J. M., Kraft N. J. B., Smith K. G., Vellend M., Inouye B. D., Using null models to disentangle variation in community dissimilarity from variation in α-diversity. Ecosphere 2, art24 (2011). [Google Scholar]
- 20.Webb C. O., Ackerly D. D., McPeek M. A., Donoghue M. J., Phylogenies and community ecology. Annu. Rev. Ecol. Syst. 33, 475–505 (2002). [Google Scholar]
- 21.Tilman D., Isbell F., Cowles J. M., Biodiversity and ecosystem functioning. Annu. Rev. Ecol. Evol. Syst. 45, 471–493 (2014). [Google Scholar]
- 22.Chase J. M., Drought mediates the importance of stochastic community assembly. Proc. Natl. Acad. Sci. U.S.A. 104, 17430–17434 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Stegen J. C., et al. , Stochastic and deterministic drivers of spatial and temporal turnover in breeding bird communities. Glob. Ecol. Biogeogr. 22, 202–212 (2013). [Google Scholar]
- 24.Stegen J. C., Lin X., Fredrickson J. K., Konopka A. E., Estimating and mapping ecological processes influencing microbial community assembly. Front. Microbiol. 6, 370 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Kraft N. J. B., et al. , Disentangling the drivers of β diversity along latitudinal and elevational gradients. Science 333, 1755–1758 (2011). [DOI] [PubMed] [Google Scholar]
- 26.Stegen J. C., et al. , Quantifying community assembly processes and identifying features that impose them. ISME J. 7, 2069–2079 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Webb C. O., Exploring the phylogenetic structure of ecological communities: An example for rain forest trees. Am. Nat. 156, 145–155 (2000). [DOI] [PubMed] [Google Scholar]
- 28.Vellend M., et al. , Assessing the relative importance of neutral stochasticity in ecological communities. Oikos 123, 1420–1430 (2014). [Google Scholar]
- 29.Fujiwara M., Takada T., “Environmental stochasticity” in eLS - Ecology, Baxter R., Ed. (John Wiley & Sons, Ltd., Chichester, UK, 2017). [Google Scholar]
- 30.Mayfield M. M., Levine J. M., Opposing effects of competitive exclusion on the phylogenetic structure of communities. Ecol. Lett. 13, 1085–1093 (2010). [DOI] [PubMed] [Google Scholar]
- 31.HilleRisLambers J., Adler P. B., Harpole W. S., Levine J. M., Mayfield M. M., Rethinking community assembly through the lens of coexistence theory. Annu. Rev. Ecol. Evol. Syst. 43, 227–248 (2012). [Google Scholar]
- 32.Goberna M., Navarro-Cano J. A., Valiente-Banuet A., García C., Verdú M., Abiotic stress tolerance and competition-related traits underlie phylogenetic clustering in soil bacterial communities. Ecol. Lett. 17, 1191–1201 (2014). [DOI] [PubMed] [Google Scholar]
- 33.Pontarp M., Petchey O. L., Community trait overdispersion due to trophic interactions: Concerns for assembly process inference. Proc. R Soc. Lond. B Biol. Sci. 283, 20161729 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Sloan W. T., et al. , Quantifying the roles of immigration and chance in shaping prokaryote community structure. Environ. Microbiol. 8, 732–740 (2006). [DOI] [PubMed] [Google Scholar]
- 35.Burns A. R., et al. , Contribution of neutral processes to the assembly of gut microbial communities in the zebrafish over host development. ISME J. 10, 655–664 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Lin L., Hedayat A. S., Sinha B., Yang M., Statistical methods in assessing agreement: Models, issues, and tools. J. Am. Stat. Assoc. 97, 257–270 (2002). [Google Scholar]
- 37.Lin L. I., A concordance correlation coefficient to evaluate reproducibility. Biometrics 45, 255–268 (1989). [PubMed] [Google Scholar]
- 38.Levin S. A., The problem of pattern and scale in ecology: The Robert H. MacArthur Award Lecture. Ecology 73, 1943–1967 (1992). [Google Scholar]
- 39.He Z., et al. , Microbial functional gene diversity predicts groundwater contamination and ecosystem functioning. MBio 9, e02435-17 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Zhang P., et al. , Dynamic succession of groundwater sulfate-reducing communities during prolonged reduction of uranium in a contaminated aquifer. Environ. Sci. Technol. 51, 3609–3620 (2017). [DOI] [PubMed] [Google Scholar]
- 41.Gotelli N. J., Null model analysis of species co-occurrence patterns. Ecology 81, 2606–2621 (2000). [Google Scholar]
- 42.Vellend M., Conceptual synthesis in community ecology. Q. Rev. Biol. 85, 183–206 (2010). [DOI] [PubMed] [Google Scholar]
- 43.Connell J. H., Diversity and the coevolution of competitors, or the ghost of competition past. Oikos 35, 131–138 (1980). [Google Scholar]
- 44.Deng Y., et al. , Network succession reveals the importance of competition in response to emulsified vegetable oil amendment for uranium bioremediation. Environ. Microbiol. 18, 205–218 (2016). [DOI] [PubMed] [Google Scholar]
- 45.Calsbeek R., Cox R. M., Experimentally assessing the relative importance of predation and competition as agents of selection. Nature 465, 613–616 (2010). [DOI] [PubMed] [Google Scholar]
- 46.Cerdá X., Arnan X., Retana J., Is competition a significant hallmark of ant (Hymenoptera: Formicidae) ecology? Myrmecol. News 18, 131–147 (2013). [Google Scholar]
- 47.Zhang J., Huang S., He F., Half-century evidence from western Canada shows forest dynamics are primarily driven by competition followed by climate. Proc. Natl. Acad. Sci. U.S.A. 112, 4009–4014 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Ghoul M., Mitri S., The ecology and evolution of microbial competition. Trends Microbiol. 24, 833–845 (2016). [DOI] [PubMed] [Google Scholar]
- 49.Menge B. A., Sutherland J. P., Community regulation: Variation in disturbance, competition, and predation in relation to environmental stress and recruitment. Am. Nat. 130, 730–757 (1987). [Google Scholar]
- 50.Maestre F. T., Callaway R. M., Valladares F., Lortie C. J., Refining the stress-gradient hypothesis for competition and facilitation in plant communities. J. Ecol. 97, 199–205 (2009). [Google Scholar]
- 51.Lhotsky B., et al. , Changes in assembly rules along a stress gradient from open dry grasslands to wetlands. J. Ecol. 104, 507–517 (2016). [Google Scholar]
- 52.Kennedy P., Ectomycorrhizal fungi and interspecific competition: Species interactions, community structure, coexistence mechanisms, and future research directions. New Phytol. 187, 895–910 (2010). [DOI] [PubMed] [Google Scholar]
- 53.McGill B. J., Ecology. Matters of scale. Science 328, 575–576 (2010). [DOI] [PubMed] [Google Scholar]
- 54.Pacala S. W., Levin S. A., “Biologically generated spatial pattern and the coexistence of competing species” in Spatial Ecology: The Role of Space in Population Dynamics and Interspecific Interactions, Tilman D., Kareiva P. M., Eds. (Princeton University Press, Princeton, NJ, 1997), pp. 204–232. [Google Scholar]
- 55.Guo X., et al. , Climate warming leads to divergent succession of grassland microbial communities. Nat. Clim. Chang. 8, 813–818 (2018). [Google Scholar]
- 56.Chave J., Muller-Landau H. C., Levin S. A., Comparing classical community models: Theoretical consequences for patterns of diversity. Am. Nat. 159, 1–23 (2002). [DOI] [PubMed] [Google Scholar]
- 57.Denny M., Gaines S., Chance in Biology: Using Probability to Explore Nature (Princeton University Press, Princeton, 2002). [Google Scholar]
- 58.Zhou J., et al. , High-throughput metagenomic technologies for complex microbial community analysis: Open and closed formats. MBio 6, e02288-14 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Zhou J., et al. , Random sampling process leads to overestimation of β-diversity of microbial communities. MBio 4, e00324-13 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Zhou J., et al. , Reproducibility and quantitation of amplicon sequencing-based detection. ISME J. 5, 1303–1313 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Alonso D., McKane A. J., Sampling Hubbell’s neutral theory of biodiversity. Ecol. Lett. 7, 901–910 (2004). [Google Scholar]
- 62.R Core Team , R: A Language and Environment for Statistical Computing (R Foundation for Statistical Computing, Vienna, Austria, 2019).
- 63.Afgan E., et al. , The Galaxy platform for accessible, reproducible and collaborative biomedical analyses: 2018 update. Nucleic Acids Res. 46, W537–W544 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.