Towards better prediction of Mycobacterium tuberculosis lineages from MIRU-VNTR data

Abstract

The determination of lineages from strain-based molecular genotyping information is an important problem in tuberculosis. Mycobacterial interspersed repetitive unit-variable number tandem repeat (MIRU-VNTR) typing is a commonly used molecular genotyping approach that uses counts of the number of times pre-specified loci repeat in a strain. There are three main approaches for determining lineage based on MIRU-VNTR data - one based on a direct comparison to the strains in a curated database, and two others, on machine learning algorithms trained on a large collection of labeled data.

All existing methods have limitations. The direct approach imposes an arbitrary threshold on how much a database strain can differ from a given one to be informative. On the other hand, the machine learning-based approaches require a substantial amount of labeled data. Notably, all three methods exhibit suboptimal classification accuracy without additional data.

We explore several computational approaches to address these limitations. First, we show that eliminating the arbitrary threshold improves the performance of the direct approach. Second, we introduce RuleTB, an alternative direct method that proposes a concise set of rules for determining lineages. Lastly, we propose StackTB, a machine learning approach that requires only a fraction of the training data to outperform the accuracy of both existing machine learning methods.

Our approaches demonstrate superior performance on a training dataset collected in New York City over 10 years, and the improvement in performance translates to a held-out testing set. We conclude that our methods provide opportunities for improving the determination of pathogenic lineages based on MIRU-VNTR data.

1. Introduction

The genetic diversity of the infectious pathogen Mycobacterium tuberculosis has played an important role in its adaptation to its diverse host species, including humans [1, 2, 3]. This diversity is commonly organized into groups of related strains, called lineages, that are correlated with the strain’s geographical origin [4]. Lineage information can help inform us of the phylogeographic provenance of the strain [5], and has been shown to influence mutation rates and likelihood of drug resistance [6], as well as transmissibility and virulence [7, 8]. The aggregated information obtained by combining lineage classification with epidemiological or clinical data can provide the basis for a molecular surveillance program [9].

Several different molecular genotyping methods have been used to assign lineages to M. tuberculosis, including restriction fragment length polymorphism (RFLP), spacer oligonucleotide typing (spoligotyping), large sequence polymorphisms (LSPs), single nucleotide polymorphisms (SNPs), and mycobacterial interspersed repetitive unit-variable number tandem repeats (MIRU-VNTR). These and other molecular genetic approaches for tuberculosis genotyping are reviewed in Mathema et al [14] as well as Kato-Maeda et al [15]. The typing of MIRU-VNTR is a commonly used approach for genotyping tuberculosis strains due to its reproducibility [10] and discriminatory power for identifying potential transmission clusters [11], a process in which it is often used in combination with spoligotyping.

MIRU-VNTR is a mini-satellite typing system that has been proposed as a tool to analyze the diversity of tuberculosis isolates [12, 13]. It consists in performing a PCR amplification step with primers designed for the regions before and after the tandem repeats, and determining the sizes of the amplicons. This produces a readout containing the number of copies of a repeated region at several pre-selected loci, each of the repeats being between 50 and 150 base pairs long. These copy number variants (CNVs) are then used to compare the M. tuberculosis strain to other similarly typed strains. The prevalence of MIRU-VNTR as the genotyping method of choice for tuberculosis naturally gives rise to the problem of determining lineages based only on information obtained with this technique.

One commonly used method for solving this problem is based on a reference database called MIRU-VNTRplus, which contains a collection of 186 strains with their 24 MIRU-VNTR loci and lineage assignments [16] - we note that another widely used genotypic marker database for M. tuberculosis, SITVIT [20], primarily contains spoligotypes. The method consists in assigning to a strain of interest the lineage of the strain in the database that differs from it in the smallest number of loci, provided that this number does not exceed 4 out of 24 loci. Another widely used method, called TB-Insight [21], uses a machine learning method called Conformal Bayesian Networks for the classification problem. It only provides major lineages, rather than the more specialized minor lineages like MIRU-VNTRplus. One final method, called TBminer [22], uses several popular machine learning techniques to learn lineage assignments based on either MIRU-VNTR loci, spoligotypes, or both, and outputs the majority-vote prediction. TBminer can provide both major and lineages, as well as its own “consensus” classification.

Since TB-Insight only predicts major lineages, we focus our comparison to existing methods on this level of granularity. However, both our approaches can be adapted to determine minor lineages, at the cost of only a slight decrease in accuracy due to the smaller number of strains in our training data that belong to each lineage, as we describe in Sections 2.1 and 4.

We address the limitations of existing methods with several proposed improvements, described in detail below. First, we suggest that removing the arbitrary threshold of 4 out of 24 loci recommended by the authors of the MIRU-VNTRplus database retains the accuracy of the method based on it while increasing the number of strains that can be classified. Second, we develop a state-of-the-art interpretable lineage classifier by using an optimization framework to extract a set of rules suitable for classification; each of these rules considers only a small number of MIRU-VNTR loci. Finally, we also consider an approach that uses the ensembling technique from machine learning, which captures the strengths of different machine learning classifiers within a single model in a principled way.

We test all our proposed improvements on a dataset collected in New York City over a period of 10 years, and representative of the substantial diversity found among M. tuberculosis strains and the M. tuberculosis complex. We separate it into a training set, which we use to develop our methods, and a testing set, which we use to evaluate their performance.

2. Materials and Methods

2.1. Dataset preparation

There are two sources of data that we use to develop our algorithms. The first is the publicly available database MIRU-VNTRplus [16], which contains 186 strains (including 2 strains with a locus containing two different copy numbers, which we consider as representing two different MIRU patterns). These MIRU patterns are assigned to 22 different narrow lineages. We eliminate the 9 lineages that do not contain sufficient data, and coarsen the remaining 13 into 6 broad lineages, according to the transformation described in Table 1. This leaves us with 155 strains that are used in the analysis.

Table 1:

Correspondence between the narrow lineages used in MIRU-VNTRplus database, together with their frequencies there, and the broad lineages in TB-Insight as well as the broad and refined ones in our study.

Narrow lineage	Broad lineage	Refined lineage	# (unique)
Beijing	East-Asian	East-Asian	10 (8)
Bovis	M. bovis	M. bovis	11 (11)
Cameroon	Euro-American	Euro-American	10 (10)
Canettii	not used due to sparsity	not used	2 (2)
Caprae	not used due to sparsity	M. caprae	11 (11)
Delhi/CAS	East-African Indian	East-African Indian	10 (8)
EAI	Indo-Oceanic	Indo-Oceanic	12 (2)
Ghana	Euro-American	Euro-American	10 (6)
Haarlem	Euro-American	Euro-American	13 (12)
H37Rv	not used due to sparsity	not used	1 (1)
LAM	Euro-American	Euro-American	11 (11)
llama	not used due to sparsity	not used	4 (4)
NEW-1	not used due to sparsity	not used	3 (3)
S	Euro-American	Euro-American	12 (11)
Seal	not used due to sparsity	not used	2 (1)
TUR	not used due to sparsity	not used	4 (2)
Uganda*	Euro-American	Euro-American	20 (17)
Ural	not used due to sparsity	not used	4 (4)
vole	not used due to sparsity	not used	2 (2)
West African 1	M. africanum†	M. africanum 1	22 (21)
West African 2	M. africanum†	M. africanum 2	11 (11)
X	Euro-American	Euro-American	3 (2)

^*- includes Uganda I and II;

^†- includes West African 1 and 2.

We also perform a second analysis, with what we refer to as “refined lineages”, in which we keep the 11 strains belonging to the Mycobacterium caprae lineage, for a total of 166 strains from the MIRU-VNTRplus database. For this analysis we also subdivide the Mycobacterium africanum lineage into sub-lineages 1 and 2, as is commonly done in the field [17].

The second source of data is a collection of strains collected by the New York City Department of Health and Mental Hygiene (NYCDOHMH) Bureau of TB Control from tuberculosis (TB) patients counted in New York City over a period of 10 years (2001-2010). There are a total of 1860 strains with no missing values that are assigned to 6 different broad lineages based on the SNP analysis described previously [14, 18]. After the two datasets are combined, we are left with 2015 strains containing 1978 unique MIRU patterns, which we split into a training and a testing set in a 4:1 ratio in a manner that preserves the lineage distribution. For the second analysis we proceed analogously with a total of 2026 strains falling into 8 refined lineages.

In order to test our methods’ robustness to the number of categories, and to demonstrate their ability to identify known substructure within the Euro-American lineage, we also perform a third analysis in which the NYC strains are categorized into 12 SNP clusters, 9 of which contain M. tuberculosis sensu stricto and a further 6 of which are a subdivision of the Euro-American lineage [19]. We refer to this as the “SNP cluster” analysis. To the 1834 strains classified in this way we add the 44 MTBC strains belonging to M. bovis and M. africanum from the MIRU-VNTRplus database, since the NYC dataset contains very few of those. In summary, our third analysis contains 1878 strains assigned to 12 SNP clusters.

2.2. Removing the arbitrary threshold

One straightforward performance improvement can be obtained by removing arbitrary thresholds. Namely, the MIRU-VNTRplus method contains the requirement that the strain of interest have no more than 4 out of 24 loci with values different from those of a strain in the database. One would expect that having a more conservative threshold would lead to more accurate lineage predictions, at the cost of not being able to classify certain strains. We test this assumption to understand the influence that this threshold has both on the fraction of the lineages to which the method is able to assign a strain, as well as on the accuracy of this assignment.

2.3. Producing interpretable rules: RuleTB

In order to produce an accurate yet interpretable classifier for lineages, we use the methodology of Malioutov and Varshney [23] to come up with a small set of rules for predicting each lineage that has the lowest possible error on the training dataset. We define a simple rule by an inequality of the form either s_l ≤ b or s_l ≥ b for some MIRU-VNTR locus l and integer b. A strain s satisfies this rule if the inequality is valid for it, and fails it otherwise. A strain s satisfies a complex rule (defined as a collection of rules) if it satisfies each one, otherwise it fails the complex rule. The goal is to find the smallest set of such complex rules that correctly predict the lineage for the largest number of strains.

As we describe in the Supplementary Materials, Malioutov and Varshney [23] propose an approach based on linear programming (LP) to the NP-hard problem [24] of identifying the smallest set of complex rules of this form. This approach is guaranteed to work correctly under certain specific conditions, and provides a useful heuristic otherwise. We modify their approach in two ways. First, instead of solving the linear programming relaxation of the rule inference problem that they propose, we directly solve its integer linear programming (ILP) formulation, including a penalty term for violated constraints, using the CPLEX software [25]. Second, to generalize to the case where multiple lineages need to be classified at the same time, we propose a greedy iterative approach which produces complex rules for one lineage at a time, as we describe in the Supplementary Materials.

2.4. Designing a machine learning method: StackTB

StackTB is an algorithm which combines a number of machine learning modelling methodologies using a technique called stacking. In this section, we describe how the different models are stacked together, and then provide descriptions of the individual methodologies in the Supplementary Materials.

Ensembling is a technique for aggregating the results of multiple machine learning models to improve their collective performance. For each instance to be classified, some aggregator function is used to aggregate the classifications of all of the constituent algorithms to get the ensemble classification. The simplest aggregator function is the majority vote, which is used, for instance, in the TBminer method [22]. However, it is usually possible to do better with more advanced ensembling methods, by using aggregator functions which enhance the signal from constituent classifiers which do well on the instances to be classified, and dampen the signal from those that do not.

The specific ensembling technique we use is called stacking, and it uses another machine learning algorithm to perform the aggregation. Each of the stacked algorithms is trained on some resampling of the training data. The outputs of each of these models are concatenated and fed as the input to the combining model. These inputs are then used to optimize the parameters of the combining model. Any new data points that the model is to predict go through a similar process, first being transformed by the stacked models, and then having the final prediction be determined by the combining model. See Figure 1 for a visualization of how the models we use for StackTB get stacked.

Figure 1:

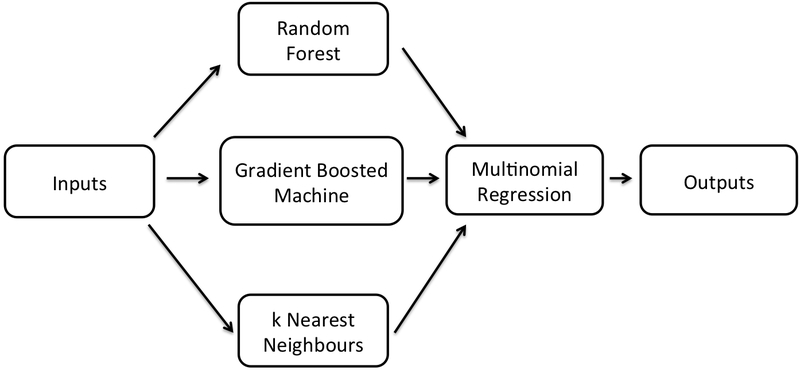
A schematic illustration of the StackTB classifier.

3. Implementation

RuleTB and StackTB are implemented in the R programming language [26]. The implementation took place in five phases, as described below.

3.1. Data Cleaning

In this phase we cleaned and combined both datasets described in Section 2.1. This involved mapping the loci names and lineage names to be consistent across the datasets and translating all string-encoded hexadecimal numbers to their numerical equivalents. We also removed any samples with missing MIRU-VNTR values for at least one locus.

3.2. Train-Test Split

We then randomly split this combined dataset into a training and test set. The training set consisted of 1613 samples of labeled MIRU-VNTR data, which is eighty percent of our combined data set. Twenty percent of the data, or 402 samples, was held out as a test set from which we determined our out of sample accuracy. The remaining data was used as a training set to develop the rules in RuleTB and train the machine learning algorithms in StackTB. We performed the same fractional splits (80% for training, 20% for testing) on the data used in our second and third analyses.

3.3. Model Training

Using the training data, we constructed the rule for each lineage. We also trained each of the individual models that are needed for stacking in StackTB: random forest, two gradient boosted machines, and k-nearest neighbors. We used five-fold cross-validation on this training data to select hyper-parameters and train the stacking multinomial regression model.

3.4. Performance Analysis

We evaluated the quality of the constructed rules and models on the test set, by analyzing the confusion matrix and looking at the overall accuracy for each classifier. We compared this accuracy to that of the state of the art MIRU-VNTRplus, TB-Insight and TBminer algorithms on our test set. Our results are discussed in Section 4.

3.5. Sensitivity Analysis

To ensure that our results do not depend on the particular random partition of the data into a training and a testing set that we used, we repeated the process on 100 additional random partitions of the data, each time with 80% used for training and the remaining 20% used for testing. As the results presented in Table 1 in the Supplementary Materials show, our results held for all partitions of the data.

The final RuleTB rules are listed in Table 3. The final StackTB model can be used through a user-friendly Web interface¹, which also includes a sample file based on the strains contained in the MIRU-VNTRplus database.

Table 3:

Rules used by RuleTB for each broad lineage, in order.

Rule	M. bovis	M. africanum	Indo-Oceanic	EAI	East-Asian	Euro-American
Rule 1	MIRU10 ≤ 2	MIRU24 ≥ 2	MIRU26 ≤ 3	MIRU16 ≥ 2	MIRU10 ≤ 4	MIRU31 ≤ 4
Rule 2	Mtub29 ≤ 3	3 ≤ MIRU26 ≤ 4	Mtub29 ≤ 3	MIRU31 ≥ 4	MIRU31 ≥ 4	MIRU39 ≤ 2
Rule 3	Mtub30 ≥ 3	Mtub 21 ≤ 6	Mtub30 ≤ 3	ETRC ≤ 2	MIRU40 ≤ 5
Rule 4	QUB4156 ≤ 1	ETRA ≤ 7		ETRA ≥ 3	QUB11b ≥ 2
Rule 5		QUB26 ≤ 7			Mtub30 ≥ 3

4. Results

4.1. Performance of our methods on broad lineages

Tables 2 and 4 show the confusion matrices of RuleTB and StackTB with broad lineages, respectively. In both methods, very few errors were made on the testing set, and StackTB consistently performed better than or as well as RuleTB on every lineage at the cost of being less transparent.

Table 2:

Confusion Matrix of RuleTB with broad lineages.

Sensitivity	Predicted Lineage						Overall accuracy: 95.0%
	EAI	East-Asian	Euro-American	Indo-Oceanic	M. africanum	M. bovis
88.2%	30	0	3	1	0	0	EAI	Actual Lineage
95.9%	2	70	0	0	1	0	East-Asian
96.0%	0	3	217	3	3	0	Euro-American
94.4%	0	0	3	51	0	0	Indo-Oceanic
90.0%	0	0	0	1	9	0	M. africanum
100%	0	0	0	0	0	5	M. bovis
	93.8%	95.9%	97.3%	91.0%	69.2%	100%	Specificity

Table 4:

Confusion Matrix of StackTB with broad lineages.

Sensitivity	Predicted Lineage						Overall accuracy: 97.0%
	EAI	East-Asian	Euro-American	Indo-Oceanic	M. africanum	M. bovis
88.2%	30	0	3	1	0	0	EAI	Actual Lineage
98.6%	1	72	0	0	0	0	East-Asian
98.2%	0	1	222	3	0	0	Euro-American
96.3%	0	0	2	52	0	0	Indo-Oceanic
90.0%	0	0	0	1	9	0	M. africanum
100%	0	0	0	0	0	5	M. bovis
	96.8%	98.6%	97.8%	91.2%	100%	100%	Specificity

Table 3 shows the rules extracted by RuleTB for broad lineages. The number of rules needed for each lineage varied between 2 and 6, with an average of 4 (the Mycobacterium africanum lineage is shown with 5 rules since two of the rules affect the same locus, MIRU26, and can be combined into one). Interestingly, only 15 out of 24 MIRU-VNTR loci participated in at least one rule, suggesting that a smaller subset of the loci might be sufficient for lineage assignment when a sufficiently large training set is available. We note that only 12 out of these 15 loci are also on the list of the 15 most highly discriminatory MIRU-VNTR loci [13], which suggests that the task of predicting lineages is different from, albeit similar to, the task of discriminating strains into as many clusters as possible.

To verify this hypothesis in an additional experiment, we tested whether our rules could correctly predict the lineage of those 253 strains that were excluded during preprocessing due to missing information about one or more loci (all of these come from the NYC dataset). We applied the rules extracted by RuleTB to these incompletely specified strains, in the same order. We obtained an overall accuracy of 85% on this subset. This result suggests that, even in the presence of missing information, lineages can often be reliably inferred by a robust set of rules such as the one extracted by RuleTB.

4.2. Performance of our methods on a refined classification

To ensure that our methods generalize well to situations with more refined labels, we tested our methods on the two additional sets of labels. We obtained a comparable overall accuracy of 98.0% (94.0%) with StackTB (RuleTB), respectively, in the second analysis (with a refinement of M. africanum and some additional M. caprae strains), and a slightly lower accuracy of 92.7% (78.8%), respectively, in the third analysis (with a refinement of the Euro-American lineage into 6 SNP clusters). We also test the rules derived from RuleTB on the incompletely specified strains in the dataset and obtain a slightly lower accuracy of 82.6 in the second analysis, and a much lower accuracy of 62.8% in the third analysis. For both of these analyses, the rules extracted by RuleTB involve 19 out of the 24 loci, and only 10 of those are highly variable ones.

These results suggest that our methods are robust to the presence of multiple lineages, although they do suffer from a loss of accuracy when their number increases too much. Remarkably, however, a lot of the mistakes made by StackTB are “reasonable” ones, insofar as they consist of assigning a strain from a lineage to a closely related lineage. For instance, a lot of the errors made by StackTB on the refined lineages involve the two sublineages of M. africanum (Table 8), while most of the errors made on the SNP clusters involve different clusters within the Euro-American lineage (see Table 12, where most non-zero off-diagonal elements are in rows and columns corresponding to LIII through LVIII).

Table 8:

Confusion Matrix of StackTB with refined lineages.

Sensitivity	Predicted Lineage								Overall accuracy: 98.0%
	EAI	East-Asian	Euro-American	Indo-Oceanic	M. africanum 1	M. africanum 2	M. bovis	M. caprae
91.2%	31	0	3	0	0	0	0	0	EAI	Actual Lineage
100%	0	73	0	0	0	0	0	0	East-Asian
100%	0	0	226	0	0	0	0	0	Euro-American
100%	0	0	0	54	0	0	0	0	Indo-Oceanic
50.0%	0	0	1	2	4	1	0	0	M. africanum 1
50.0%	0	0	0	0	1	1	0	0	M. africanum 2
100%	0	0	0	0	0	0	5	0	M. bovis
100%	0	0	0	0	0	0	0	2	M. caprae
	100%	100%	98.3%	96.4%	80.0%	50.0%	100%	100 %	Specificity

Table 12:

Confusion Matrix of StackTB with SNP clusters.

Sensitivity	Predicted Lineage												Overall accuracy: 92.7%
	LI	LII	LIIa	LIII	LIV	LV	LVI	LVII	LVIII	M. afri 1	M. afri 2	M. bovis
100%	51	0	0	0	0	0	0	0	0	0	0	0	LI	Actual Lineage
100%	0	71	0	0	0	0	0	0	0	0	0	0	LII
90.9%	1	0	30	1	0	0	0	1	0	0	0	0	LIIa
94.6%	0	0	0	53	1	0	0	2	0	0	0	0	LIII
87.0%	1	0	0	1	20	0	0	1	0	0	0	0	LIV
75.0%	0	0	0	0	1	6	1	0	0	0	0	0	LV
87.7%	0	1	0	2	1	1	64	4	0	0	0	0	LVI
84.2%	0	0	0	3	2	0	1	32	0	0	0	0	LVII
100%	0	0	0	0	0	0	0	0	4	0	0	0	LVIII
87.5%	0	0	0	0	0	0	0	0	0	7	1	0	M. afri 1
100%	0	0	0	0	0	0	0	0	0	0	2	0	M. afri 2
100%	0	0	0	0	0	0	0	0	0	0	0	5	M. bovis
	98.1%	98.6%	100%	88.3%	80.0%	85.7%	97.0%	80.0%	100%	100%	66.7%	100%	Specificity

4.3. Comparison to existing methods

In order to compare our results to those obtained with existing methods, we first need to establish a correspondence between the lineage assignments produced by those methods and those in our datasets. These are summarized in Table 1 above. We make several observations:

Both MIRU-VNTRplus and TBminer are able to produce finer classifications than our method (our training data does not extend to sublineages since it was labeled using SNP analysis rather than spoligotyping). Since those methods (especially TBminer) were trained on finer classifications, they might appear to perform worse than they do. On the other hand, we reason that obtaining a correct fine classification should only come after obtaining a correct coarse one, and if these methods make mistakes in the latter they will inevitably make mistakes in the former as well. Therefore, we believe that our comparison is fair overall.

We test MIRU-VNTRplus and TBminer in up to four modes each. For MIRU-VNTRplus, we can train the method only on the MIRU-VNTRplus database or on the entire training dataset (in the latter case we can learn an arbitrary classification of strains into lineages), and we can also use the recommended threshold of d = 4 loci having differences or not use any threshold (as we recommend in this paper). If a threshold is used, some strains do not get assigned to any lineage, and we report both the accuracy of the assignments made as well as that of the overall assignment (which count no assignment as an incorrect assignment). For TBminer, the returned lineages can be based on either the MIRU-VNTR classification or the expert classification developed by the authors [22], and it can consider all 24 loci or only the 15 most variable ones.

For the refined lineages (second analysis), we do not test TB-Insight because it does not distinguish between M. africanum 1 and M. africanum 2, and is also unable to detect M. caprae. To evaluate the results of TBminer, we count assignments to the L0 lineage (animal strains) as correct for M. bovis, but incorrect for M. caprae; this guarantees the best possible outcome for TBminer since there are roughly 2.5 times more M. bovis strains than M. caprae ones in the dataset.

Lastly, for the SNP clusters (third analysis) we do not test any of the other methods except the MIRU-VNTRplus method trained on the entire training part of the data. This is because the classification into SNP clusters is not directly comparable with those produced by the other methods.

We see that, despite other methods sometimes coming close, StackTB is the most accurate method on all three classifications (Tables 5, 9 and 13). Our sensitivity analysis results (in the Supplementary Materials) further corroborates this as being a robust and systematic performance advantage, rather than the artifact of a “lucky” split of the data into training and testing sets. We discuss possible reasons for this performance advantage in the next section.

Table 5:

Accuracy of algorithms by broad lineage.

Algorithm	Overall	EAI	East-Asian	Euro-American	Indo-Oceanic	M. africanum	M. bovis
MIRU-VNTRplus (*)	44.5 [97.8]	44.1	69.9	31.9	53.7	70.0	100
Same, no threshold (*)	96.9	88.2	99.8	98.1	94.4	90.0	100
MIRU-VNTRplus (†)	91.8 [97.1]	88.0	97.3	93.8	77.2	93.3	100
Same, no threshold (†)	96.3	88.0	98.6	98.2	90.1	93.3	100
TB-Insight	96.3	82.4	97.3	98.2	96.3	90.0	100
TBminer - MIRU-VNTRplus	96.3	79.4	98.6	98.2	96.3	90.0	100
TBminer - Expert	95.8	82.3	98.6	98.2	92.6	80.0	100
TBminer - MIRU-VNTRplus (‡)	95.8	82.4	94.5	98.2	96.3	90.0	100
TBminer - Expert (‡)	95.0	79.4	94.5	97.8	94.4	90.0	100
RuleTB	95.0	88.2	95.9	96.0	94.4	90.0	100
StackTB	97.0	88.2	98.6	98.2	96.3	90.0	100

^(*)= the MIRU-VTNRplus database is used for training;

^(†)= the training subset of the entire data is used for training;

^‡= only the 15 most discriminative VNTR loci are used for the prediction. The numbers in square brackets indicate the accuracy of only the assignments actually made (excluding NAs).

Table 9:

Accuracy of algorithms by refined lineage.

Algorithm	Overall	EAI	East-Asian	Euro-American	Indo-Oceanic	M. africanum 1	M. africanum 2	M. bovis	M. caprae
MIRU-VNTRplus (*)	49.8 [98.5]	44.1	72.6	39.4	61.1	25.0	100	100	100
Same, no threshold (*)	97.4	91.2	99.1	99.7	100	25.0	100	100	100
MIRU-VNTRplus (†)	91.9 [97.0]	93.4	99.7	95.5	75.2	45.3	40.0	100	50.0
Same, no threshold (†)	96.5	96.3	99.7	99.8	87.8	45.3	40.0	100	100
TBminer - MIRU-VNTRplus	97.0	88.2	100	100	100	25.0	100	100	0
TBminer - Expert	96.8	91.2	100	100	96.3	25.0	100	100	0
TBminer - MIRU-VNTRplus (‡)	97.0	88.2	100	100	100	25.0	100	100	0
TBminer - Expert (‡)	96.8	88.2	98.6	100	100	25.0	100	100	0
RuleTB	94.0	88.2	93.1	96.0	98.1	50.0	50.0	100	100
StackTB	98.0	91.2	100	100	100	50.0	50.0	100	100

^(*)= the MIRU-VTNRplus database is used for training;

^(†)= the training subset of the entire data is used for training;

^‡= only the 15 most discriminative VNTR loci are used for the prediction. The numbers in square brackets indicate the accuracy of only the assignments actually made (excluding NAs). Note that TB-Insight is omitted because it does not identify lineages at this level of re nement.

Table 13:

Accuracy of algorithms by SNP cluster.

Algorithm	Overall	LI	LII	LIII	LIV	LV	LVI	LVII	LVIII	M. afri 1	M. afri 2	M. bovis	M. caprae
MIRU-VNTRplus (†)	83.7 [91.3]	76.5	97.2	91.7	86.0	73.9	74.9	80.5	81.3	41.2	90.0	77.5	40.0
Same, no threshold (†)	89.4	90.8	100	91.7	86.8	77.4	74.9	87.1	85.7	66.2	90.0	77.5	100
RuleTB	78.8	96.1	85.9	84.8	83.9	26.1	50.0	69.9	86.8	25.0	87.5	100	80.0
StackTB	92.7	100	100	90.9	94.6	87.0	75.0	87.7	84.2	100	87.5	100	100

^(†)= the training subset of the entire data is used for training. The numbers in square brackets indicate the accuracy of only the assignments actually made (excluding NAs). Note that MIRU-VNTRplus (with the database as training set), TB-Insight and TBminer do not produce this classification, and are therefore omitted.

5. Discussion

In this work we have explored a number of possible improvements to the standard methods of predicting lineage from MIRU-VNTR data, based on a curated database of strains with known lineages. One of the biggest improvements at no computational cost came from simply removing the threshold from the direct method, suggesting that requiring a limit on how close two strains needed to be was unnecessarily limiting for the lineage assignment problem. Designing different interpretable rules for different lineages has provided some additional improvement, although it was a small incremental one relative to the removal of the threshold. The use of a machine learning-based classifier further improved classification accuracy, leading to the best currently existing predictor. Interestingly, the two methods appear to share a lot of their errors, which suggests that some of the strains have MIRU-VNTR patterns atypical for their lineage and get misclassified by even the most sophisticated methods.

One of the key advantages of our approach is that it can rapidly provide lineage assignment on large datasets that already exist, while being flexible enough to accommodate information from additional strains labeled with their lineage by independent methods. In addition, the ideas behind our approach - systematic rule extraction for RuleTB and aggregation of machine learning methods via stacking for StackTB - can also be used for other pathogens for which data are available on both lineages and VNTR copy numbers, or other classification systems such as multi-locus sequence typing.

One specific advantage of our machine learning method, StackTB, over both TB-Insight as well as TBminer, is the use of a more sophisticated aggregator function of the individual predictors. TB-Insight uses a conformal Bayesian network, which aggregates data by postulating a number of conditional independence assumptions, which may not hold for the VNTR data. On the other hand, TBminer uses a simple voting procedure, which may be leaving some information on the table compared to the stacking approach used by StackTB.

One of the limitations of our method is that our training dataset was more limited in size than the one used in some of the previous work - TB-Insight used over 35,000 labeled strains [21], while TBminer used over 3,000 [22]; in comparison, we used around 2,000. While this was advantageous in restricting us to algorithms that learn from even small amounts of data, this also meant that we are unable to produce predictions for any lineages that were either not present at all in the dataset we used (such as Lineage 7 [27]) or that were not present in a sufficient quantity (such as M. canettii [28], of which we only had 2 strains). It seems that our methods are able to learn lineages correctly with as few as 11 example strains, as they did with M. caprae, but not fewer than that.

We believe that a more rigorous investigation of currently accepted methods is needed, and we hope that this work paves the way for such an investigation. One open problem that remains unsolved is the systematic incorporation of information from lineages that may be present in only a few samples in some datasets, and not at all in others. A principled solution to this problem would add substantial value to existing databases.

Table 6:

Confusion Matrix of RuleTB with refined lineages.

Sensitivity	Predicted Lineage								Overall accuracy: 94.0%
	EAI	East-Asian	Euro-American	Indo-Oceanic	M. africanum 1	M. africanum 2	M. bovis	M. caprae
88.2%	30	1	3	0	0	0	0	0	EAI	Actual Lineage
93.1%	5	68	0	0	0	0	0	0	East-Asian
96.0%	3	5	217	1	0	0	0	0	Euro-American
98.1%	1	0	0	53	0	0	0	0	Indo-Oceanic
50.0%	0	0	1	2	4	1	0	0	M. africanum 1
50.0%	0	0	0	0	1	1	0	0	M. africanum 2
100%	0	0	0	0	0	0	5	0	M. bovis
100%	0	0	0	0	0	0	0	2	M. caprae
	76.9%	91.9%	98.2%	94.6%	80.0%	50.0%	100%	100 %	Specificity

Table 7:

Rules used by RuleTB for each refined lineage, in order.

Rule	M. caprae	M. bovis	M. africanum 2	M. africanum 1	Indo-Oceanic	EAI	East-Asian	Euro-American
Rule 1	MIRU24 ≥ 2	MIRU10 ≤ 2	MIRU16 ≥ 3	MIRU23 ≤ 5	MIRU26 ≤ 4	MIRU10 ≥ 4	MIRU10 ≤ 3	MIRU31 ≤ 4
Rule 2	Mtub34 ≤ 2	Mtub29 ≤ 3	ETRA ≥ 6	MIRU24 ≥ 2	Mtub29 ≤ 3	MIRU16 ≥ 2	MIRU31 ≥ 4	MIRU39 ≤ 2
Rule 3	Mtub39 ≤ 1	Mtub30 ≥ 3	Mtub30 ≥ 4	MIRU40 ≤ 2	Mtub30 ≤ 3	MIRU31 ≥ 4	MIRU40 ≤ 5
Rule 4		QUB4156 ≤ 1	Mtub39 ≥ 4	QUB11b ≤ 6		Mtub04 ≥ 3	Mtub04 ≥ 2
Rule 5			QUB26 ≥ 6	QUB26 ≤ 6		Mtub21 ≥ 2	Mtub21 ≥ 3
Rule 6						ETRA ≥ 2	Mtub30 ≥ 2
Rule 7						Mtub29 ≥ 3	ETRB ≥ 2

Table 10:

Confusion Matrix of RuleTB with SNP clusters.

Sensitivity	Predicted Lineage												Overall accuracy: 78.8%
	LI	LII	LIIa	LIII	LIV	LV	LVI	LVII	LVIII	M. afri 1	M. afri 2	M. bovis
96.1%	49	0	1	0	0	0	0	0	0	1	0	0	LI	Actual Lineage
85.9%	0	61	0	1	8	0	1	0	0	0	0	0	LII
84.8%	1	0	28	3	0	1	0	0	0	0	0	0	LIIa
83.9%	0	0	1	47	0	0	0	8	0	0	0	0	LIII
26.1%	1	0	0	14	6	0	0	0	1	1	0	0	LIV
50.0%	0	0	0	2	1	4	0	1	0	0	0	0	LV
69.9%	0	5	1	2	0	1	51	12	0	1	0	0	LVI
86.8%	0	0	1	1	0	0	1	33	1	1	0	0	LVII
25.0%	0	0	0	0	0	0	0	3	1	0	0	0	LVIII
87.5%	0	0	0	0	0	0	0	0	0	7	1	0	M. afri 1
100%	0	0	0	0	0	0	0	0	0	0	2	0	M. afri 2
80.0%	0	0	0	1	0	0	0	0	0	0	0	4	M. bovis
	96.1%	92.4%	87.5%	66.2%	40.0%	66.7%	96.2%	57.9%	33.3%	63.6%	66.7%	100%	Specificity

Table 11:

Rules used by RuleTB for each SNP cluster, in order.

	M. bovis	M. africanum 2	LVIII	M. africanum 1	LI	LV
Rule 1	MIRU04 ≥ 3	ETRC ≥ 5	MIRU40 ≤ 1	MIRU04 ≤ 3	MIRU24 ≥ 2	MIRU23 ≤ 5
Rule 2	Mtub30 ≥ 3	ETRA = 6	Mtub04 ≤ 3	MIRU23 ≤ 6	MIRU26 ≤ 4	MIRU40 ≤ 3
Rule 3	QUB4156 ≤ 1	Mtub30 ≥ 4	Mtub21 ≤ 2	MIRU24 ≥ 2		Mtub04 ≥ 3
Rule 4		QUB26 ≥ 6	QUB11b ≥ 3	MIRU26 ≤ 4		ETRC = 3
Rule 5			Mtub30 = 2	QUB11b ≤ 6		Mtub21 ≥ 3
Rule 6				ETRA ≤ 7		2 ≤ QUB11b ≤ 4
Rule 7				QUB26 ≤ 6		Mtub34 ≥ 3
	LII	LIIa	LIV	LIII	LVII	LVI
Rule 1	MIRU04 ≤ 3	MIRU10 ≥ 4	MIRU10 ≤ 5	Mtub30 ≥ 3	MIRU40 ≥ 1	MIRU04 ≤ 3
Rule 2	MIRU10 ≤ 5	MIRU24 ≤ 1	ETRC ≥ 4	QUB26 ≤ 10	ETRA ≤ 3	MIRU26 ≥ 2
Rule 3	MIRU39 ≥ 3	MIRU31 ≥ 4	Mtub30 ≥ 3		Mtub30 ≥ 2	Mtub04 ≥ 3
Rule 4	MIRU40 ≤ 5	Mtub21 ≥ 2			Mtub34 ≥ 2
Rule 5	ETRC ≥ 3	Mtub29 ≥ 3			QUB26 ≥ 2
Rule 6		Mtub30 ≥ 2
Rule 7		Mtub39 ≤ 6