Confidence regions for spatial excursion sets from repeated random field observations, with an application to climate

Abstract

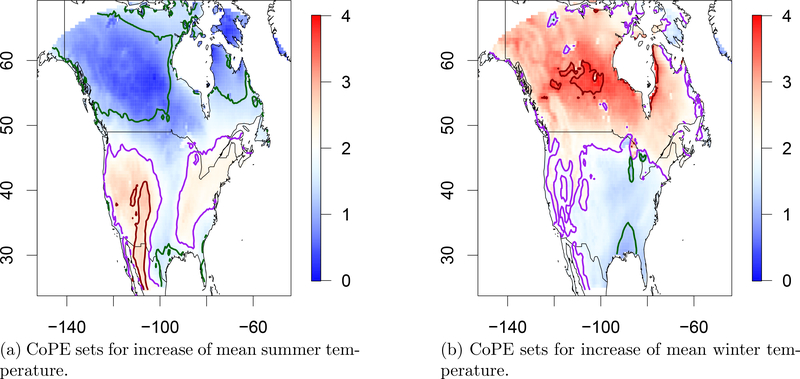
The goal of this paper is to give confidence regions for the excursion set of a spatial function above a given threshold from repeated noisy observations on a fine grid of fixed locations. Given an asymptotically Gaussian estimator of the target function, a pair of data-dependent nested excursion sets are constructed that are sub- and super-sets of the true excursion set, respectively, with a desired confidence. Asymptotic coverage probabilities are determined via a multiplier bootstrap method, not requiring Gaussianity of the original data nor stationarity or smoothness of the limiting Gaussian field. The method is used to determine regions in North America where the mean summer and winter temperatures are expected to increase by mid 21st century by more than 2 degrees Celsius.

1. Introduction

Our motivation comes from the following problem. Faced with a global change in temperature within the next century, it is important to assess which geographical regions are particularly at risk of extreme temperature change. The data used here, obtained from the North American Regional Climate Change Assessment Program (NARCCAP) project (Mearns et al., 2009, 2012, 2013), consists of two sets of 29 spatially registered arrays of mean seasonal temperatures for summer (June-August) and winter (December-February) evaluated at a fine grid of fixed locations 0.5 degrees apart in geographic longitude and latitude over North America over two time periods: late 20th century (1971–1999) and mid 21st century (2041–2069). Specifically, the data was produced by the WRFG climate model (Michalakes et al., 2004) using boundary conditions from the CGCM3 global model (Flato, 2005). We would like to determine the regions whose difference in mean summer or winter temperature between the two periods is greater than the 2^◦C benchmark (Rogelj et al., 2009, Anderson and Bows, 2011). However, the observed differences may be confounded by the natural year-to-year temperature variability. Can we set confidence bounds on such regions that reflect the year-to-year variability in the data?

In mathematical terms, suppose that for some unknown target function μ : S → ℝ on a spatial domain S ⊂ ℝ^d (in our case the difference in mean temperature between the two time periods), we are interested in the excursion set of μ(s) above a fixed threshold c, defined as A_c := A_c(μ) := {s ϵ S : μ(s) ≥ c}. More specifically, based on an estimate ${\widehat{\mu }}_n(\mathbf{s})$ of μ(s) we wish to obtain confidence regions ${\widehat{A}}_c^{\pm }$ for which the probability that

$${\widehat{A}}_c^{+}\subset A_c\subset {\widehat{A}}_c^{-}$$ (1)

holds is asymptotically above a desired level, say 90%.

We obtain such sets ${\widehat{A}}_c^{\pm }$ as excursion sets of the estimate ${\widehat{\mu }}_n(\mathbf{s})$ and we call them Coverage Probability Excursion (CoPE) sets. Assuming that μ(s) is continuous in the proximity of the level set ∂A_c = {s ∈ S: μ(s) = c}and that the estimator ${\widehat{\mu }}_n(\mathbf{s})$ satisfies a functional central limit theorem (CLT), we show that the probability that the inclusions (1) hold is given asymptotically by the distribution of the supremum of the limiting Gaussian random field on the level set ∂A_c.

To apply this general framework to our data, we model the yearly average temperature fields Y_i(s), i = 1,...,n, as realizations of a general linear model indexed by s ∈ S

$$\mathbf{Y}(\mathbf{s})=\mathbf{X}\mathbf{b}(\mathbf{s})+\mathit{ϵ}(\mathbf{s}),$$ (2)

with X indicating the two time periods. Setting a simple contrast vector w, the target function μ(s) = w^T b(s) represents the difference of means to be estimated. For the general model (2) with arbitrary X and w, we show that under proper conditions on design and error fields ϵ(s) a least-squares fit at each location s will produce a consistent and asymptotically Gaussian estimator ${\widehat{\mu }}_n(\mathbf{s})={\mathit{w}}^T\widehat{\mathbf{b}}(\mathbf{s})$ thereby allowing the construction of CoPE sets, as described above.

For illustration, Figure 1 shows CoPE sets for the temperature data. We target the region where the mean temperature in the future period (2041–2069) exceeds the mean temperature in the past (1971–1999) by 2^◦C or more. With simultaneous approximate probability of 90% this region is no smaller than the region given by the red boundary $({\widehat{A}}_c^{+})$ and no larger than indicated by the green boundary $({\widehat{A}}_c^{-})$.

Figure 1:

Output of our method for the increase of the mean summer (June-August) and winter (December-February) temperatures. Shown are heat maps of the estimate of the difference. The uncertainty in the excursion set estimate ${\widehat{A}}_c$ (purple boundary) for c = 2^◦C is captured by the CoPE sets ${\widehat{A}}_c^{+}$ (red boundary) and ${\widehat{A}}_c^{-}$ (green boundary). The threshold was obtained according to Theorem 1 to guarantee inclusion ${\widehat{A}}_c^{+}\subset A_c\subset {\widehat{A}}_c^{-}$ with confidence 1−α = 0.9. The horizontal and vertical axes are indexed in degrees longitude and latitude, respectively.

Climate model output is a new high-dimensional type of geostatistical data. With the increasing interest in climate modeling, there is a large amount of data of this type, e.g. from NARCCAP and its European counterpart ENSEMBLES (van der Linden and Mitchell, 2009). Unlike the traditional data setup of spatial statistics, climate model output data is produced at all locations (in practice, on a fine grid) without measurement error (Bukovsky, 2012). In this sense, our setup is more similar to that of population studies in brain imaging, where a difference map between two conditions is estimated from repeated co-located image observations at a fine spatial grid under those conditions (see e.g. Worsley et al. (1996), Genovese et al. (2002), Taylor and Worsley (2007), Schwartzman et al. (2010)). In the discussion we suggest an approach to apply our ideas in the setting of dense discrete observed locations and in the presence of measurement error, inspired by functional data analysis.

The problem of finding the threshold for our CoPE sets involves computation of the quantiles of the supremum of a limiting Gaussian random field. While the general theory is valid whenever a functional CLT can be established for the estimator ${\widehat{\mu }}_n(\mathbf{s})$, we offer a practical procedure in the case of a linear model. In French (2014) a similar task was performed by Monte Carlo simulation assuming a parametric class for the covariance structure of the field. More generally for unknown and typically non-stationary covariance function, as we attempt here, we propose a simple and efficient multiplier bootstrap procedure (Wu, 1986, Hardle and Mammen, 1993, Mammen, 1992, 1993), that does not require estimating the unknown correlation function. The validity of this procedure for very high-dimensional data has been shown by Chernozhukov et al. (2013).

This problem has also been addressed and elegantly solved by Taylor and Worsley (2007) using the Gaussian kinematic formula. However, this method requires that the observations themselves be Gaussian and requires the field to be differentiable. The multiplier bootstrap allows us to avoid both these assumptions while being extremely fast to compute. We compare the finite sample performance of the Gaussian kinematic formula method and the multiplier bootstrap in a simulation.

Related Work

The problem of finding confidence regions for spatial excursion sets (exceedance regions) or level sets (contours), has been studied in other contexts. In the geostatistics literature, the target function is itself a Gaussian field, partially observed at relatively few spatial locations. The limited amount of information available is typically compensated by assuming that the field is stationary, which we do not. The uncertainty on the estimation of the random level contours and excursion sets has been addressed from a frequentist perspective for the former (Lindgren and Rychlik, 1995, Wameling, 2003, French and Sain, 2013) and the latter (French and Sain, 2013), as well as from a Bayesian perspective for both (Bolin and Lindgren, 2014). Incidentally, our techniques share some similarities with French (2014), although we will show that distinguishing between level contours and excursion sets is important.

In non-parametric density estimation and regression the target function is a probability density or regression function, estimated from realizations random vector or observations at a discrete set of locations, respectively. While the estimation of both level sets and contours have been well studied (Tsybakov, 1997, Cavalier, 1997, Cuevas et al., 2006, Willett and Nowak, 2007, Singh et al., 2009, Rigollet and Vert, 2009), there is less literature on confidence statements. Mason and Polonik (2009) showed asymptotic normality of plug-in level set estimates with respect to the measure of symmetric set difference. Mammen and Polonik (2013) proposed a bootstrapping scheme to obtain confidence regions analogous to our CoPE sets from vector-valued samples.

Other settings involving excursions over thresholds (albeit not necessarily excursion sets in our sense) include the following. Extreme value theory studies the occurence and size of exceedances over high thresholds (Davison and Smith, 1990). The spatial cumulative distribution function (SCDF) of a random field measures measures the proportion of the area where the field takes values below a certain threshold (Majure et al., 1995, Lahiri et al., 1999, Zhu et al., 2002). In a Bayesian framework, special loss functions have been proposed to obtain estimates of maxima or near-maxima or exceedance regions from the posterior (Wright et al., 2003, Zhang et al., 2008). A related approach is Bayesian hotspot detection (De Oliveira and Ecker, 2002). Scan statistics are widely used to detect hotspots or clusters (Patil and Taillie, 2004, Tango and Takahashi, 2005, Duczmal et al., 2006).

Software

All required functions for computation and visualization of CoPE sets developed in this paper are available in the R-package cope (Sommerfeld, 2015) in R (R Core Team, 2015).

2. Error control for excursion sets - CoPE sets

2.1. Setup

The domain S ⊂ ℝ^Non which all our functions and processes are defined, is assumed to be a compact (but not necessarily connected) subset of Euclidean space.

Assumption 1. We assume that

• (a)every open ball around a point in the contour or level set ∂A_c = {s ∈ S : μ(s) = c} has non-empty intersection with {s : μ(s) > c} and with {s : μ(s) < c}. Further, there exists η₀ > 0 such that the target function μ(s) is continuous on the set U = {s ∈ S : |μ(s) − c| ≤ η₀}.
• (b)
  the estimators ${\widehat{\mu }}_n(\mathbf{s})$ are continuous on U for all n ∈ ℕ large enough and there exist a sequence of numbers τ_n → 0 and a continuous function σ : U → ℝ⁺ bounded from above and below such that

  $${\left\{\frac{{\widehat{\mu }}_n(\mathbf{s})-\mu (\mathbf{s})}{{\tau }_n\sigma (\mathbf{s})}\right\}}_{\mathbf{s}\in U}\to {\{G(\mathbf{s})\}}_{\mathbf{s}\in U},$$ (3)

  weakly in C(U) as n → ∞. Here, G is a Gaussian field on U with mean zero, unit variance and continuous sample paths with probability one.
• (c)
  there is a constant C > 0 such that for every s ∉ U we have

  $$\left({\widehat{\mu }}_n(\mathbf{s})-c\right)\cdot \mathrm{sgn}(\mu (\mathbf{s})-c)\ge C+\sigma (s)Z_n(\mathbf{s}),a.s.,$$ (4)

  with Z_n(s) a sequence of stochastic processes on S such that ${\sup }_{\mathbf{s}\in S}|Z(\mathbf{s})|={\mathcal{O}}_P\left({\tau }_n\right)$.

Remark 1. The above assumptions need some explanation.

• (a)The first part of Assumptions 1 (a) ensures that μ(s) is not flat at the level c such that ∂A_c is in fact of lower dimension than N and excludes pathological cases where c is an isolated point in the image of μ(s) such that U = ∂A_c for positive η₀. The second part guarantees that μ(s) is continuous whenever it has values close to c.
• (b)Part (b) says that ${\widehat{\mu }}_n(\mathbf{s})$ needs to be a good estimator of μ(s) around the level c in the sense that it satisfies a funtional central limit theorem.
• (c)The last assumption concerns the quality of ${\widehat{\mu }}_n(\mathbf{s})$ away from the level c. It need not be a good estimator there, not even consistent. We merely require that whenever μ(s) is smaller/larger than c that also ${\widehat{\mu }}_n(\mathbf{s})$ is (eventually with high probability) smaller/larger than c. This flexibility can be useful when the target function μ(s) is not continuous outside of U since in this case it might not be possible to find an estimator that is consistent everywhere.

Remark 2.

• (a)The Assumptions 1 reflect the properties of the temperature data motivating the theory. Notably, we have disconnectedness of the domain in question (cf. Figure 1) due to islands and discontinuities can appear on the boundaries of large lakes.
• (b)While we require continuity of the target function around the level of interest c for our theory, simulations suggest (see the supplement) that this assumption is not essential to attain the desired coverage.
• (c)In general, Assumptions 1 may include estimators based on an increasing number of repeated observations (like in our data example) or an increasing number of sampling spatial points (like in the spatial statistics and nonparametric regression problems).

Finite Locations

In practice, we might check inclusion only on a subset of locations D_n, e.g. a grid of points, which may change with n. That is, we may want to control the probability that $({\widehat{A}}_c^{+}\cap D_n)\subset (A_c\cap D_n)\subset ({\widehat{A}}_c^{-}\cap D_n).$ The following quantities of the set D_n will be relevant. Define for every s ∈ S the projections

$${\mathfrak{p}}_n^{\pm }(\mathbf{s})={\mathrm{argmin}}_{{\mathbf{s}}^{\prime }\in D_n\cap \{s^{\prime }:\pm (\mu (s^{\prime })-c)>0\}}\left|\mathbf{s}-{\mathbf{s}}^{\prime }\right|.$$

Note that ${\mathfrak{p}}_n^{\pm }(\mathbf{s})$ are functions of the point s. Further, let

$${\mathrm{\Delta }}_n^{\pm }=\underset{\mathbf{s}\in \partial A_c}{\sup }\left|{\mathfrak{p}}_n^{\pm }(\mathbf{s})-\mathbf{s}\right|,{\nabla }_n^{\pm }=\underset{\mathbf{s}\in \partial A_c}{\sup }\left|\frac{\mu \left({\mathfrak{p}}_n^{\pm }(\mathbf{s})\right)-c}{\sigma \left({\mathfrak{p}}_n^{\pm }(\mathbf{s})\right)}\right|.$$

Assumption 2. We assume that the sequence of sets D_n ⊂ S is such that ${\mathrm{\Delta }}_n^{\pm }\to 0$ and ${\nabla }_n^{\pm }/{\tau }_n\to 0$ as $n\to \infty$.

Remark 3.

• (a)The quantity ${\mathrm{\Delta }}_n^{\pm }$ controls how dense D_n is around the contour ∂A_c. For example, if D_n is a regular grid with spacing δ_n, then ${\mathrm{\Delta }}_n^{\pm }\le {\delta }_n$.
• (b)On the other hand, ${\nabla }_n^{\pm }$ describes the regularity of the function μ around ∂A_c. If μ(s) is Lipschitz continuous with Lipschitz constant L in a neighborhood of ∂A_c then ${\nabla }_n^{\pm }\le L{\sup }_{\mathbf{s}\in \partial A_c}\left|{\sigma }^{-1}(\mathbf{s})\right|{\mathrm{\Delta }}_n^{\pm }$. Hence, in this case, Assumption 2 is satisfied if ${\mathrm{\Delta }}_n^{\pm }=o\left({\tau }_n^{-1}\right)$.

Combining both observations, Assumption 2 holds, for example, if μ(s) is continuously differentiable in a neighborhood of the contour and D_n is a regular grid with spacing $o\left({\tau }_n^{-1}\right)$.

2.2. CoPE Sets

We will obtain nested estimates by thresholding the surface ${\widehat{\mu }}_n(\mathbf{s})$ as follows:

$${\widehat{A}}_c^{+}≔{\widehat{A}}_c(+a)≔\left\{\mathbf{s}:\frac{{\widehat{\mu }}_n(\mathbf{s})-c}{{\tau }_n\sigma (\mathbf{s})}\ge +a\right\},{\widehat{A}}_c^{-}≔{\widehat{A}}_c(-a)≔\left\{\mathbf{s}:\frac{{\widehat{\mu }}_n(\mathbf{s})-c}{{\tau }_n\sigma (\mathbf{s})}\ge -a\right\},$$ (5)

where a is an appropriate non-negative constant to be determined. Note that ${\widehat{A}}_c={\widehat{A}}_c\left(0\right)$ and ${\widehat{A}}^{\pm }$ are themselves excursion sets. Moreover, for any choice of a ≥ 0 we have the inclusions ${\widehat{A}}_c^{+}\subset {\widehat{A}}_c\subset {\widehat{A}}_c^{-}$, and hence the estimates obtained via (5) are nested. We refer to ${\widehat{A}}_c^{+}$ and ${\widehat{A}}_c^{-}$ as inner and outer confidence region, respectively. The function used to define the excursion sets is similar to the test statistic used in French and Sain (2013).

The following main result shows how the constant a in (5) can be chosen such that the desired inclusions hold with a predefined probability.

Theorem 1. If the Assumptions 1 hold, then

• (a)
  $$\underset{n\to \infty }{\lim }P\left[{\widehat{A}}_c^{+}\subset A_c\subset {\widehat{A}}_c^{-}\right]=P\left[\underset{\mathbf{s}\in \partial A_c}{\sup }|G(\mathbf{s})|\le a\right].$$
• (b)
  for any subset D ⊂ S,

  $$\underset{n\to \infty }{\lim \inf }P\left[(D\cap {\widehat{A}}_c^{+})\subset (D\cap A_c)\subset (D\cap {\widehat{A}}_c^{-})\right]\ge P\left[\underset{\mathbf{s}\in \partial A_c}{\sup }|G(\mathbf{s})|\le a\right].$$
• (c)
  for a sequence of sets D_n that additionally satisfy Assumption 2,

  $$\underset{n\to \infty }{\lim }P\left[(D_n\cap {\widehat{A}}_c^{+})\subset (D_n\cap A_c)\subset (D_n\cap {\widehat{A}}_c^{-})\right]=P\left[\underset{\mathbf{s}\in \partial A_c}{\sup }|G(\mathbf{s})|\le a\right].$$

A direct consequence of Theorem 1 is that ${\widehat{A}}_c^{+}\subset A_c\subset {\widehat{A}}_c^{-}$ with asymptotic probability at least 1−α if we choose a such that $P\left[{\sup }_{\mathbf{s}\in \partial A_c}|G(\mathbf{s})|\ge a\right]\le \alpha .$ The determination of a poses a computational challenge since the distribution of the supremum of $|G(\mathbf{s})|$ and the set ∂A_c are unknown. In Section 3.2 we propose an easy and fast way to approximate this distribution by a multiplier bootstrap.

The second and third part of Theorem 1 address situations in which the fields are only observed on a, usually finite, set of locations D, e.g. a finite grid. In this case, the theorem asserts that, independent of the set D, the desired inclusions hold at all observed locations D asymptotically with probability at least 1 − α. This is in agreement with the intuition that the desired inclusion is easier to obtain if one only considers a small set of locations. The third part of the Theorem asserts that for a sequence of sets D_n that become dense around the contour sufficiently fast, the inclusion even holds with probability equal to 1−α. We address this issue further in the simulations section and in the discussion.

Confidence regions for the excursion set A_c yield confidence sets for the contour ∂A_c.

Corollary 1. Under the assumptions of Theorem 1, we have

$$\underset{n\to \infty }{\lim }P\left[\partial A_c\subset \mathrm{cl}\left({\widehat{A}}_c^{-}\backslash {\widehat{A}}_c^{+}\right)\right]=P\left[\underset{\mathbf{s}\in \partial A_c}{\sup }|G(\mathbf{s})|\le a\right],$$

where cl denotes the topological closure.

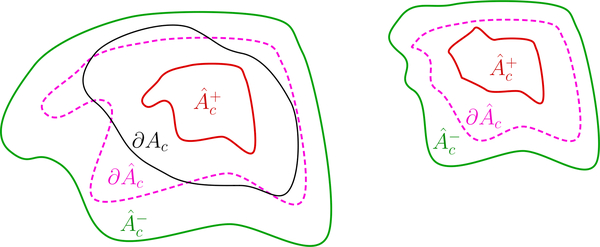
Note that, conversely, confidence sets for the contour do not automatically give confidence regions for the excursion set. In Figure 2 we show a simple schematic example of a pair of nested sets ${\widehat{A}}_c^{\pm }$ for which $\partial A_c\subset {\widehat{A}}_c^{-}\backslash {\widehat{A}}_c$ holds but ${\widehat{A}}_c^{+}\subset A_c\subset {\widehat{A}}_c^{-}$ does not. In fact, excluding these cases is the more laborious part of the proof of Theorem 1. The key is to divide the region S into a close-range zone where μ(s) is close to c, given by the inflated boundary $A_c^{\eta }=\{\mathbf{s}\in S:c-\eta \sigma (\mathbf{s})\le \mu (\mathbf{s})\le c+\eta \sigma (\mathbf{s})\}$ and a long-range zone. Then, the strategy of the proof is to let the parameter η go to zero at an appropriate rate as n → ∞ such that, eventually, the probability of a part of ${\widehat{A}}_c^{+}$ falsely appearing in the long-range zone $S\backslash A_c^{\eta }$ (as shown in Figure 2) vanishes. The probability of making an error remains in the close-range zone, and is asymptotically given by $P\left[{\sup }_{\partial A_c}|G(s)|>a\right].$

Figure 2:

A simple example of nested sets ${\widehat{A}}_c^{\pm }$ that bound the contour ∂A_c but do not satisfy the inclusion ${\widehat{A}}_c^{+}\subset A_c\subset {\widehat{A}}_c^{-}$

3. CoPE sets for general linear models

For concreteness and later application to the climate data, we here present how CoPE sets are obtained, in theory and in practice, when the target function is a parameter function in a general linear model and n is the number of repeated observations.

3.1. Asymptotic coverage probabilities

We consider the model

$$\mathbf{Y}(\mathbf{s})=\mathbf{X}\mathbf{b}(\mathbf{s})+\mathit{ϵ}(\mathbf{s}),\mathbf{s}\in S\subset {ℝ}^N,$$ (6)

where Y(s) is an n × 1 vector of observations, X is a known n × p design matrix, b(s) = (b₁(s),...,b_p(s)) is an unknown p × 1 vector of parameters and ϵ(s) = (ϵ ₁(s),..., ϵ _n(s)) an unknown stochastic process. CLTs of the kind presented here are known in the case of independent errors (see e.g. Eicker (1963)). We show and prove versions tailored to our specific purpose for coherence and convenience. Specifically, for the noise ϵ, we assume that there exists a positive definite function $\mathfrak{c}:S\times S\to (-1,1)$ with $\mathfrak{c}$(s,s) = 1 for all s ∈ S, and a spatially varying positive definite matrix Ω(s) ∈ ℝ^n×n such that

$$\mathrm{cov}\left[\mathit{ϵ}({\mathbf{s}}_k),\mathit{ϵ}({\mathbf{s}}_l)\right]=\mathfrak{c}({\mathbf{s}}_k,{\mathbf{s}}_l){\mathbf{\Omega }}^{1/2}({\mathbf{s}}_k){\mathbf{\Omega }}^{1/2}({\mathbf{s}}_l).$$

The correlation function $\mathfrak{c}$(·,·) describes the (non-stationary) spatial correlation structure of the error field, while Ω(s) describes the dependence structure between errors in different observations at each location. Note that it will not be necessary to estimate this function.

To estimate b(s) we use the generalized least squares estimator (GLS) (Rao and Touten- burg, 1995)

$$\widehat{\mathbf{b}}(\mathbf{s})={({\mathbf{X}}^T{\mathbf{\Omega }}^{-1}(\mathbf{s})\mathbf{X})}^{-1}{\mathbf{X}}^T{\mathbf{\Omega }}^{-1}(\mathbf{s})\mathbf{Y}(\mathbf{s}).$$

The matrix Ω(s) is unknown in general but can be replaced by a consistent estimate when a sufficiently simple model is assumed. We will use an autoregressive model for our data application in Section 5.

In the notation of Section (2), the target function μ(s) is now a linear combination w^T b(s) for some vector of coefficients w ∈ ℝ^p. Naturally, ${\mathit{w}}^T\widehat{\mathbf{b}}(\mathbf{s})$ now plays the role of the estimator ${\widehat{\mu }}_n(\mathbf{s})$.

Next, we establish a CLT for the parameter estimators in our setting, generalizing well-known CLTs in the case of independent errors (see e.g. Eicker (1963)).

Additional notation

Recall that for 1 ≤ p ≤ ∞, the p-norm ||A||_p of a matrix A is defined to be ||A||_p = sup_||x||p=1 ||Ax||_p. Hence, by definition ||Ax||_p ≤ ||A||_p||x||_p for all x. When p = ∞ the matrix norm ||A||_∞ is the maximum absolute row sum of A, i.e.

$${\Vert A={(a_{ij})}_{1\le i\le m,1\le j\le n}\Vert }_{\infty }=\underset{{}_{1\le i\le m}}{\max }{\displaystyle \sum _{j=1}^n\left|a_{ij}\right|}.$$

Definition 1. We denote the Lebesgue measure of a set A ⊂ S by |A|.For vectors s,t ∈ ℝ^N define the block (s, t] = (s₁,t₁]×···×(s_N,t_N] ⊂ℝ^N and for a stochastic process (s) with index set containing (s,t] define the increment of (s) around (s, t] (cf. Bickel and Wichura (1971)) as

$$ϵ((\mathbf{s},\mathbf{t}])={\displaystyle \sum _{{\kappa }_1=0,1}\cdots }{\displaystyle \sum _{{\kappa }_N=0,1}{(-1)}^{N-{\displaystyle {\sum }_j{\kappa }_j}}}ϵ(s_1+{\kappa }_1(t_1-s_1),\cdots ,s_N+{\kappa }_N(t_N-s_N)).$$

In dimension N = 1 the definition of an increment yields ϵ((s₁,t₁] = ϵ (t₁)− ϵ(s₁), while in dimension N = 2, ϵ((s, t]) = ϵ(t₁, t₂) − ϵ(s₁, t₂) − ϵ(t₁, s₂) + ϵ(s₁, s₂).

Assumption 3. Write Z(s) = Ω^−1/2(s)X(X^T Ω⁻¹(s)X)^−1/2 for brevity. Assume that

• (a)the noise field (s) has continuous sample paths with probability one. Moreover, a centered unit variance Gaussian field with the same correlation function c(s₁,s₂) as the noise field (s) also has continuous sample paths with probability one.
• (b)the map s 7↦ Ω(s) is continuous as a function S → ℝ^n×n.
• (c)the de-correlated error field $\widetilde{\mathit{ϵ}}(\mathbf{s})={\mathbf{\Omega }}^{-1/2}(\mathbf{s})\mathit{ϵ}(\mathbf{s})$ has independent components.
• (d)there exists δ > 0 and a constant K_δ > 0 such that ${\sup }_{\mathbf{s}\in S}E{\left|{\widetilde{ϵ}}_j(\mathbf{s})\right|}^{2+\delta }\le K_{\delta },$ independent of j and n and such that ${\sup }_{\mathbf{s}\in S}n\Vert \mathit{Z}(\mathbf{s}){\Vert }_{\infty }^{2+\delta }\to 0$ as n → ∞.
• (e)there exist γ ≥ 0 and β > 0 such that for a constant K_{(β γ,)} > 0 independent of n and s we have $E\Vert [\mathit{Z}(\cdot )\mathit{ϵ}(\cdot )](B){\Vert }_1^{2+\gamma }\le K_{(\beta ,\gamma )}|B{|}^{1+\beta }$.
• (f)the function ${\mathbf{v}}_n(\mathbf{s})={\mathit{w}}^T{(X^T{\mathbf{\Omega }}^{-1}(\mathbf{s})X)}^{-\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}$ satisfies v_n(s)/‖v_n(s)‖₂ → v₀(s) uniformly in s as n → ∞ for some continuous function v₀ : S → ℝ.

Remark 4. These assumptions will ensure that w^T b(s) enjoys a functional CLT as required in Assumptions 1. Let us give some explanation.

• (a)Conditions (a) and (b) ensure the continuity of the relevant fields, such that conver-gence can be considered in the space of continuous functions on S.
• (b)Condition (c) is, for example, satisfied for autoregressive moving average (ARMA) models, which we will employ in our data application. However, we note that condition (c) could be replaced by an appropriate mixing condition.
• (c)Conditions (d) and (e) are assumptions on the moments and increments of the error field, coupled with conditions on the design matrix X and the correlation structure Ω(s). In the simple case of independent noise and a first order linear model with equally spaced design points these conditions decouple and reduce to standard conditions on moments and increments of the noise field (see Remark 6).

Theorem 2 (CLT for general linear model). Under Assumption 3 (a)- (d) the weak con-vergence

$$\sqrt{{\mathbf{X}}^T{\mathbf{\Omega }}^{-1}(\mathbf{s})\mathbf{X}}(\widehat{\mathbf{b}}(\mathbf{s})-\mathbf{b}(\mathbf{s}))\to G^{\otimes p}(\mathbf{s}),$$

holds as n → ∞, where G^⊗p is an ℝ^p-valued mean zero, unit variance Gaussian random field with correlation function $\left[G^{\otimes p}({\mathbf{s}}_1),G^{\otimes p}({\mathbf{s}}_2)\right]=\mathfrak{c}({\mathbf{s}}_1,{\mathbf{s}}_2){\mathbf{I}}_p$.

If additionally part (e) of Assumptions 3 holds, then we have

$${\Vert {\mathbf{v}}_n(\mathbf{s})\Vert }_2^{-1}\left({\mathit{w}}^T\widehat{\mathbf{b}}(\mathbf{s})-{\mathit{w}}^T\mathbf{b}(\mathbf{s})\right)\to G(\mathbf{s}),$$

weakly as n → ∞, where G is a mean zero, unit variance Gaussian field on S with correlation function cov $\left[G({\mathbf{s}}_1),G({\mathbf{s}}_2)\right]=\mathfrak{c}({\mathbf{s}}_1,{\mathbf{s}}_2)$.

The statement of Theorem 2 guarantees that parts (b) and (c) of Assumptions 1 hold. Therefore, we can obtain CoPE sets for w^T b(s) as follows.

Corollary 2 (CoPE sets for general linear model). If the function μ(s) = w^T b(s) satisfies part (a) of Assumptions 1 and if Assumptions 2 and 3 hold, then

$${\widehat{A}}_c^{\pm }=\{\mathbf{s}:\frac{{\mathit{w}}^T\widehat{\mathbf{b}}(\mathbf{s})-c}{{\Vert {\mathbf{v}}_n(\mathbf{s})\Vert }_2}\ge \pm a\}$$ (7)

are CoPE sets for A_c ={s ∈ S : w^T b(s) ≥ c}, that is,

$$\underset{n\to \infty }{\lim }P\left[(D_n\cap {\widehat{A}}_c^{+})\subset (D_n\cap A_c)\subset (D_n\cap {\widehat{A}}_c^{-})\right]=P\left[\underset{\mathbf{s}\in \partial A_c}{\sup }|G(\mathbf{s})|\le a\right].$$

Remark 5. Note that Theorem 2 and hence also Corollary 2 will (by Slutzky’s Theorem) continue to hold if Ω(s) is replaced by a consistent estimate $\widehat{\mathbf{\Omega }}(\mathbf{s})$. This is what one will typically obtain from a GLS estimate with a fixed correlation structure, e.g. an ARMA process with fixed orders but unknown coefficients.

3.2. Approximating the tail probabilities of G

3.2.1. Multiplier bootstrap

In practice, the distribution of G in Corollary 2 is unknown, because it depends on the unknown (non-stationary) covariance function. In our motivating application the only information we have about G is contained in the de-correlated residuals

$$(R_1(\mathbf{s}),\dots ,R_n(\mathbf{s}))=\mathbf{R}(\mathbf{s})={\mathbf{\Omega }}^{-1/2}(\mathbf{s})(\mathbf{Y}(s)-\mathbf{X}\widehat{\mathbf{b}}(\mathbf{s}))$$

of the linear regression.

A way of approximating the distribution of the limiting Gaussian field G is given by the multiplier or wild bootstrap first introduced by Wu (1986) and later studied by Mammen (1992, 1993), Hardle and Mammen (1993). Let g₁,...,g_n be i.i.d standard Gaussian random variables independent of the data. Then, conditional on the residuals ${\left\{R_j(\mathbf{s})\right\}}_{j=1}^n$, the field $\tilde{G}(\mathbf{s})=n^{-\frac{1}{2}}{\displaystyle {\sum }_{j=1}^n{g}_j}{R}_j(\mathbf{s})$ is Gaussian and has covariance

$$\mathrm{cov}\left[\tilde{G}({\mathbf{s}}_1),\tilde{G}({\mathbf{s}}_2)|\mathbf{R}(\mathbf{s})\right]=\frac{1}{n}{\displaystyle \sum _{i,j=1}^n{R}_i}({\mathbf{s}}_1)R_j({\mathbf{s}}_2)\mathrm{cov}\left[g_i,g_j\right]=\frac{1}{n}{\displaystyle \sum _{j=1}^n{R}_j}({\mathbf{s}}_1)R_j({\mathbf{s}}_2),$$ (8)

the sample covariance. The idea is to approximate $P\left[{\sup }_{\mathbf{s}\partial A_c}|G(\mathbf{s})|\le a\right]$, needed in Theorem 1 by $P\left[{\sup }_{\mathbf{s}\in \partial A_c}|\tilde{G}(\mathbf{s})|\le a|{\left\{R_j(\mathbf{s})\right\}}_{j=1}^n\right]$. The latter can be efficiently computed by generating a large number M of i.i.d. copies ${\tilde{G}}_1(\mathbf{s}),\dots ,{\tilde{G}}_M(\mathbf{s})\mathrm{of}\tilde{G}(\mathbf{s})$, conditional on ${\left\{R_j(\mathbf{s})\right\}}_{j=1}^n$ and evaluating $M^{-1}{\displaystyle {\sum }_{j=1}^{M}1}\left[{\sup }_{\mathbf{s}\in \partial A_c}\left|{\tilde{G}}_j(\mathbf{s})\right|\le a\right].$

The sample covariance (8) itself is not a good estimator of the true covariance function in our high dimensional setting, where the number of locations is much higher than the sample size n (about ten thousand grid points vs. 58 field realizations in the climate data). However, the claim of the approximation is about the distribution of the supremum of the process instead. For a discrete set of locations, the supremum sup_s∈∂Ac |G(s)| has the distribution of the maximum of a high-dimensional Gaussian random vector. Extending the results of Mammen (1993) in the high dimensional setting, Chernozhukov et al. (2013) show that the distribution of the maximum can be well approximated by the Gaussian multiplier bootstrap using realizations of a not necessarily Gaussian random vector with the same covariance matrix. In this sense, the multiplier bootstrap is valid in our setting. This is confirmed by simulations in Section 4 below.

3.2.2. An alternative method for smooth Gaussian fields

If the limiting field is twice differentiable and the error field ∊(s) in (6) is Gaussian itself then the Gaussian Kinematic Formula (GKF) (e.g. Taylor (2006), Taylor et al. (2005), Taylor and Worsley (2007)) offers an elegant and accurate way of computing tail probabilities of Gaussian fields that does not require simulations.

The GKF is based on two properties of smooth Gaussian fields. First, for such fields the exceedance probability for high thresholds can be approximated by the expected Euler characteristic: for any set B ⊂ S with smooth boundary,

$$P\left[\underset{\mathbf{s}\in B}{\sup }G(\mathbf{s})\ge a\right]=E\left[\chi (A_a(G)\cap B)\right]+\mathcal{O}(\exp (-a^2/2)),$$ (9)

where χ is the Euler characteristic (see e.g. Adler and Taylor (2007)). Second, the expected Euler characteristic in (9) has the closed formula

$$E\left[\chi (A_a(G)\cap B)\right]={\displaystyle \sum _{d=0}^N{\mathcal{L}}_d}(B,\mathrm{\Lambda }){\rho }_d(a),$$ (10)

with ${\mathcal{L}}_d$ the d-th order Lipschitz-Killing curvature (LKC) (Taylor, 2006) dependent on the covariance Λ(s) of the partial derivatives of G and known functions ρ_d(a). The GKF shows that, at least for smooth fields, the tail probability of the supremum is intrinsically lowdimensional, as it depends only (up to an exponential error term) on N + 1 parameters. This gives an additional justification for the ability of the multiplier bootstrap method to estimate the tail probability despite the high dimensionality of the field.

We can also use the GKF to obtain CoPE sets: If the Assumptions (1) are satisfied then Theorem (1) implies in conjunction with (9) and(10) that

$$\underset{n\to \infty }{\lim }P\left[{\widehat{A}}_c^{+}\subset A_c\subset {\widehat{A}}_c^{-}\right]=1-{\displaystyle \sum _{d=0}^{N-1}{\mathcal{L}}_d}(\partial A_c,\mathrm{\Lambda }){\rho }_d(a)+\mathcal{O}(\exp (-a^2/2)).$$ (11)

To use (11), the problem amounts to estimating the LKCs of the boundary ∂A_c. Taylor and Worsley (2007) propose a method to estimate LKCs based on a finite number of realizations of the Gaussian field G and a triangulation of a plug-in estimate ∂Â_c of the boundary ∂A_c. In our application, however, we only have realizations of a generally non-Gaussian field (the residuals in of the linear model, cf. Section 5) with asymptotically the same covariance as G. For completeness, we compare this method to the multiplier bootstrap method in the simulations section below.

3.3. Algorithm

Combining the results of the previous sections we can give the exact procedure for obtaining CoPE sets for the parameters of the linear model Y(s) = Xb(s) + ∊(s).

Algorithm 1. Given a design matrix X and observations Y(s) following the linear model (6). If the assumptions of Corollary 2 hold, the following yields CoPE sets for w^T b(s).

• (a)Compute the estimate $\widehat{\mathbf{b}}(\mathbf{s})={({\mathbf{X}}^T{\widehat{\mathbf{\Omega }}}^{-1}(\mathbf{s})\mathbf{X})}^{-1}{\mathbf{X}}^T{\widehat{\mathbf{\Omega }}}^{-1}(\mathbf{s})\mathbf{Y}(\mathbf{s})$ and the corresponding de-correlated residuals $\mathbf{R}(\mathbf{s})={\widehat{\mathbf{\Omega }}}^{-1/2}(\mathbf{s})(\mathbf{Y}(\mathbf{s})-\mathbf{X}\widehat{\mathbf{b}}(\mathbf{s})),$ with the empirical covariance matrix $\widehat{\mathbf{\Omega }}(\mathbf{s})$ determined according to the model used for Ω(s).
• (b)Determine a such that approximately $P\left[{\sup }_{\mathbf{s}\in \partial A_c}|G(\mathbf{s})|\ge a\right]\le \alpha .$ For example, use the multiplier bootstrap procedure with the residuals ${\left\{R_j(\mathbf{s})\right\}}_{j=1}^n$ to generate i.i.d. copies of a Gaussian $\tilde{G}$ field with covariance structure given by the sample covariance. Then, use these and the plug-in estimate $\partial {\widehat{A}}_c=\left\{\mathbf{s}:{\mathit{w}}^T\widehat{\mathbf{b}}(\mathbf{s})=c\right\}$ for the boundary ∂A_c to determine a such that $P\left[{\sup }_{\mathbf{s}\in \partial {\widehat{A}}_c}|\tilde{G}(\mathbf{s})|\ge a\right]\le \alpha$.
• (c)
  Obtain the nested CoPE sets defined by

  $${\widehat{A}}_c^{\pm }=\left\{\mathbf{s}:\frac{{\mathit{w}}^T\widehat{\mathbf{b}}(\mathbf{s})-c}{{\Vert {\widehat{\mathbf{v}}}_n(\mathbf{s})\Vert }_2}\ge \pm a\right\},$$

  with ${\Vert {\widehat{\mathbf{v}}}_n(\mathbf{s})\Vert }_2=\sqrt{{\mathit{w}}^T{X}^T{\widehat{\mathbf{\Omega }}}^{-1}(\mathbf{s})X\mathit{w}}$.

3.4. Model for the climate data

In our application we have a total of n = n^(a) +n^(b) observations, the first n^(a) observations are the ’past’, the last n^(b) are the ’future’. Within each period we model the change in mean temperature linearly in time. Model (6) takes the form

$$\begin{gathered} Y_j(\mathbf{s})=T^{(a)}(\mathbf{s})+m^{(a)}(\mathbf{s})t_j^{(a)}+{ϵ}_j(\mathbf{s}),j=1,\dots ,n^{(a)} \\ {Y}_j(\mathbf{s})=T^{(b)}(\mathbf{s})+m^{(b)}(\mathbf{s})t_j^{(b)}+{ϵ}_j(\mathbf{s}),j=n^{(a)}+1,\dots ,n^{(a)}+n^{(b)}. \end{gathered}$$ (12)

Without loss of generality, we may assume that ${\displaystyle {\sum }_{j=1}^{n^{(a)}}{t}_j^{(a)}}=0$ and ${\displaystyle {\sum }_{j=n^{(a)}+1}^{n^{(a)}+n^{(b)}}{t}_j^{(b)}}=0.$ Our goal is to give CoPE sets for the excursion sets of the difference T^(b)(s)−T^(a)(s). Therefore, we define w = (−1,1,0,0)^T. The next statement is a direct application of Corollary 2.

Proposition 1. If the design and the noise field in model (12) satisfy Assumptions 3 then Algorithm 1 yields asymptotically valid CoPE sets for T^(b)(s) − T^(a)(s).

Remark 6. In the case of independent noise fields ₁(s),...,_n(s)~ ϵ(s) we can replace parts (d)-(f) of Assumptions 3 by the following simpler conditions. A proof is given in the appendix.

• There exist numbers δ, > 0 and γ ≥ 0 and constants K_δ > 0 and K_(𝛽,γ) > 0 such that sup_s∈S $E|ϵ(\mathbf{s}){|}^{1+\delta }\le K_{\delta }$ and $E\Vert ϵ(B){\Vert }_1^{2+\gamma }\le K_{(\beta ,\gamma )}|B{|}^{1+\beta }$ for every block B ℝ^D.

• n^(a) = n^(b) = $\raisebox{1ex}{$n$}\!\left/ \!\raisebox{-1ex}{$2$}\right.$ and both sets of design points $t_j^{(a)}$ and $t_j^{(b)}$ are equally spaced (possibly with different spacing for the periods (a) and (b)).

4. Simulations

The simulations in this section show that the proposed methods provide approximately the right coverage in practical non-asymptotic situations with non-smooth, non-stationary and non-Gaussian noise. Our objective in the design of the error fields with these properties is not to imitate the data but to introduce non-stationarity and non-Gaussianity in a transparent and reproducible way, showing the full potential of the method. In fact, the error field that we encounter in the data (cf. Section (5)) is better behaved as far as smoothness and stationarity are concerned than the artificial fields we investigate here.

4.1. Setup

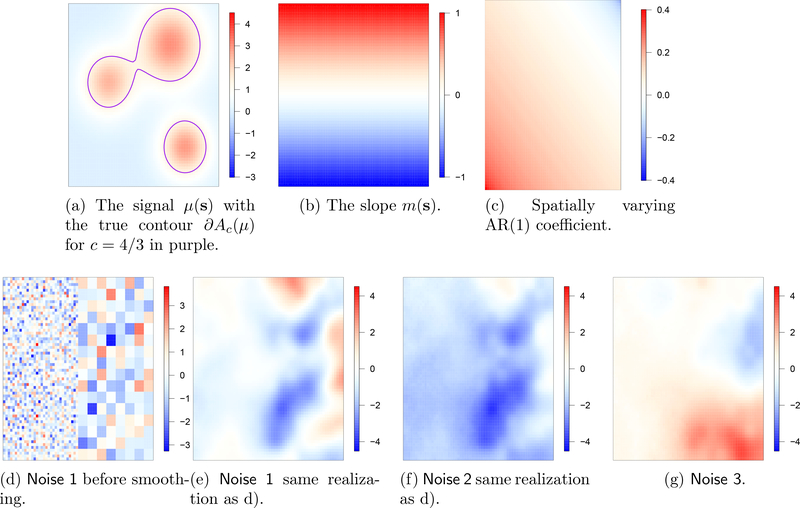
We consider a one-group version of model (12) (n = n^(a), n^(b) = 0) on t_j = 0,1/(n − 1),2/(n − 1)...,1, with non-stationary and non-Gaussian noise over a square region S = [0,1]² sampled at a uniform 64 × 64 grid. The signal μ = T^(a) is a linear combination of three Gaussians and the slope field m(s) is linear in the y-coordinate and constant in the x-coordinate (Figure 3a,3b). We consider IID and AR(1) processes (₁(s),...,_n(s)) (according to the spatial pattern in Figure 3c) for three different base fields:

Figure 3:

The spatial signal, temporal slope, temporal AR coefficient, and one realization of each of the noise fields in the toy example.

Noise 1

Independent standard normal random variables are assigned to each pixel in the left half of S and to blocks of 4-by-4 pixels in the right half (Figure 3d). The entire picture is convolved with a Gaussian kernel with bandwidth 0.1 and all values are multiplied by a scaling factor of 50 (Figure 3e).

Noise 2

Identical to Noise 1 except the image is smoothed by a Laplace kernel with bandwidth 0.1 instead of a Gaussian and the scaling factor is 100 (Figure 3f).

Noise 3

Each pixel in the upper half is assigned a Laplace random variable with mean zero and variance two. In the lower half, pixels are assigned independent Student t-distributed random variables with 10 degrees of freedom. The entire picture is convolved with a Gaussian kernel of bandwidth 0.1 and scaled with a factor of 25 (Figure 3g).

The noise fields Noise 1–3 are intentionally designed to have non-homogeneous variance and scaling factors are chosen ad-hoc such that all three fields can be conveniently displayed on a common scale (Figure 3 d-f).

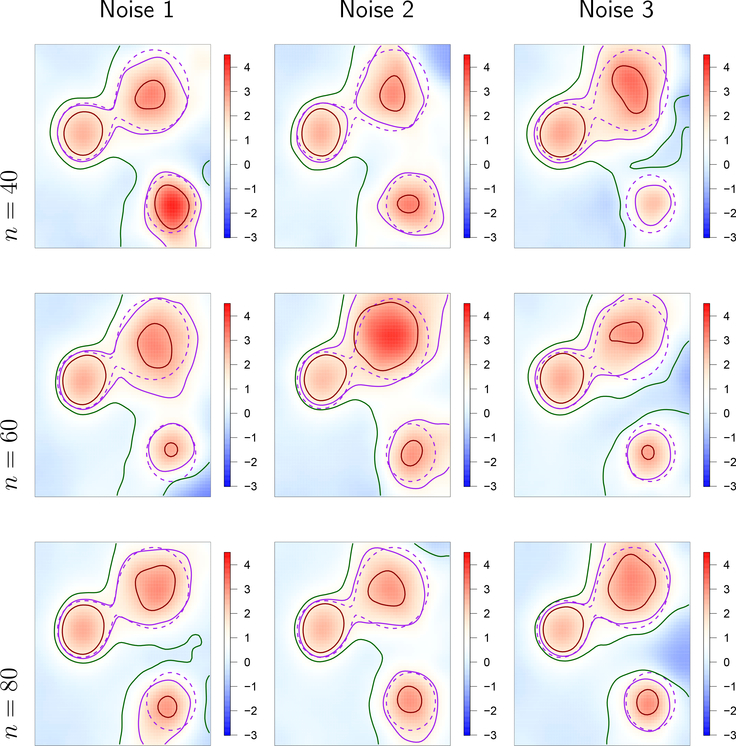
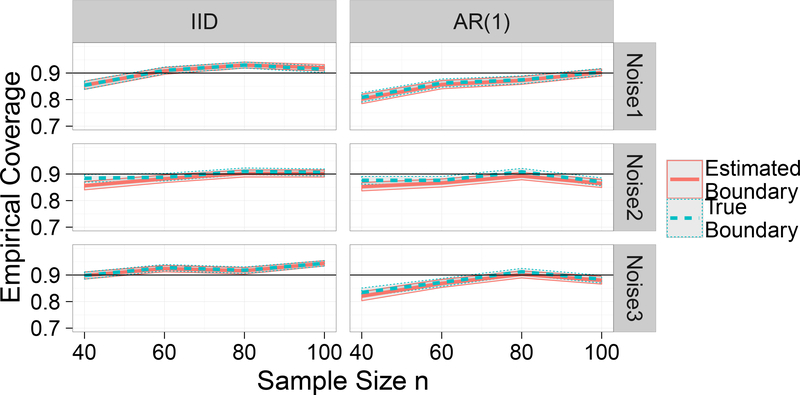
Our target is the excursion set of the mean function μ(s) at level c = 4/3. Note that the spatially varying AR parameter was not assumed to be known but was rather estimated in each trial from the data. We controlled the probability of coverage at the level 1 − α = 0.9 using Corollary 2. The threshold a was computed using the multiplier bootstrap procedure proposed in Section 3.2.1 using either the true boundary ∂A_c or the plug-in estimate ∂Â_c These boundaries were determined as piece-wise linear splines with the R-function contourLines where values of fields on non-grid locations are determined via linear interpolation. The results using ∂Â_c for each one run with the three noise fields and sample sizes n = 40,60,80 are shown in Figure 4.

Figure 4:

Single realizations of the output of our method at confidence level 90% for the three noise fields (rows) and for sample sizes n = 40,60,80 (columns) with the target function μ(s) from Figure 3a. In all pictures we show a heat map of the estimator ${\widehat{\mu }}_n(s)$, the boundary of A_c(μ) (solid purple) and $A_c(\widehat{\mu })$ (dashed purple) and the boundaries of ${\widehat{A}}_c^{+}$ (red) and ${\widehat{A}}_c^{-}$ (green). The threshold a was obtained using the multiplier bootstrap and the plug-in estimate of the boundary A_c.

4.2. Performance of CoPE sets

We analyzed the performance of our method on 5000 runs of the toy examples in Section 4.1. Figure 5 shows the percentage of trials in which coverage ${\widehat{A}}_c^{+}\subset A_c\subset {\widehat{A}}_c^{-}$ was achieved, if either the true boundary ∂A_c or the plug-in estimator ∂Â_c was used to determine the threshold. The empirical coverage is seen to approach the nominal level of 90% as the sample size increases, suggesting asymptotic unbiasedness. Comparing the coverage for the true and estimated boundaries, we see that the non-asymptotic bias is not caused by the lack of knowledge of the true boundary. It may be a consequence of the bootstrap procedure instead.

Figure 5:

Percentage of trials in which ${\widehat{A}}_c^{+}\subset A_c\subset {\widehat{A}}_c^{-}$. The nominal coverage probability is 90%.

We conducted several additional experiments with different choices of parameters for the noise fields and obtained results very similar to those reported here.

Computational performance

As already noted in Section 3.2.1, the multiplier bootstrap allows for a very fast computation of CoPE sets. In the simulations, the CoPE sets for a sample of size n = 120, each on a grid of 64×64 = 4096 locations could be computed in less than two minutes on a standard laptop for all noise models. We found that only a negligible fraction of the total runtime of the method is spent on the multiplier bootstrap - with the pointwise generalized least squares estimation taking far longer.

4.3. Estimation of exceedance probabilities

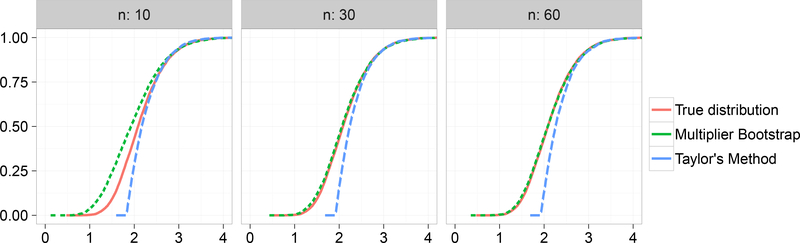
In this Section we compare the multiplier bootstrap with the method proposed by Taylor and Worsley (2007), as described in Section 3.2.2, where (s) is distributed according to Noise 1 (see Section 4.1 above), σ²(s) = var[(s)] and ∂A_c is the contour A_c(μ) of the function μ(s) shown in Figure 3a at level c = 4/3. The true cumulative density function for ${\sup }_{\mathbf{s}\in \partial A_c}|ϵ(\mathbf{s})/\sigma (\mathbf{s})|$ and its empirical approximations based on both methods are shown in Figure 6. The empirical cdfs are each based on a single i.i.d. sample ϵ₁(s),..., ϵ _n(s) for n = 10,30 and 60. For the multiplier bootstrap we generated 5,000 bootstrap realizations. The true cdf was calculated empirically using 10,000 i.i.d. samples of ϵ (s).

Figure 6:

The probability $P\left[{\sup }_{\mathbf{s}\in \partial A_c}|ϵ(\mathbf{s})/\sigma (\mathbf{s})|\le a\right]$ (the horizontal axis shows a) and approximations of it via the multiplier bootstrap or Taylor’s method based on a sample of size n. Here, the error field ϵ(s) has the distribution described in Noise 1 and A_c = A_c(μ) for the function μ shown in Figure 3a.

Both methods give a remarkably good approximation of the true distribution of the supremum, particularly for sample sizes of n = 30 and higher. However, while Taylor’s method only gives a valid approximation in the tail of the distribution, the multiplier bootstrap approximates all parts of the cdf.

4.4. Effect of Grid Coarseness

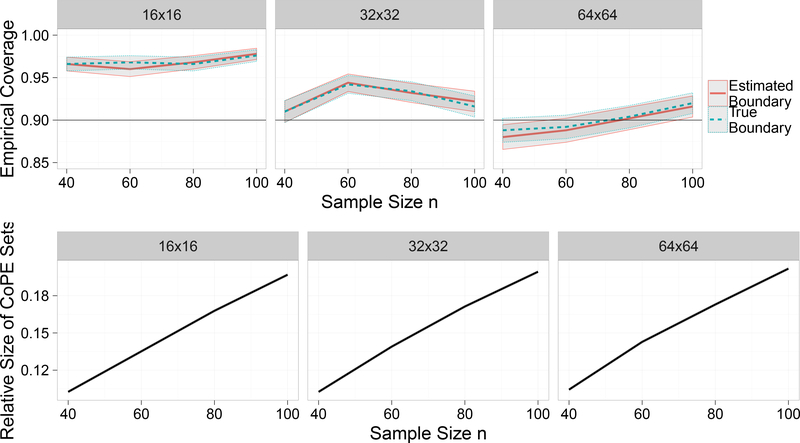
In order to assess the influence of the coarseness of the grid we repeated the experiment of Section 4.1 on grids of sizes 16×16, 32×32 and 64×64, in the same setting as in the top left panel of Figure 5, with 500 trials.

The results are shown in Figure 7 (top row). For the lower resolutions 16 × 16 and 32 × 32, coverage is above the nominal level of 90%, but it approaches the nominal level as the resolution increases. This is consistent with parts b) and c) of Theorem 1 stating that the procedure may produce over-coverage if D_n is small but coverage will approach the nominal level for increasing grid size.

Figure 7:

Empirical coverage for CoPE sets (top row) and relative size of inner and outer CoPE sets for different grid sizes (bottom row).

In order to check whether over-coverage for lower resolutions is due to the CoPE sets being overly conservative, Figure 7 (bottom row) shows the ratio $\#{\widehat{A}}_c^{+}/\#{\widehat{A}}_c^{-}$ of number of grid points contained in the inner CoPE set over the number of grid points contained in the outer CoPE set. We see that there is hardly any difference between the resolutions. We conclude that CoPE sets do not become more conservative as the resolutions decreases.

5. Application to the climate data

Data processing

Since the climate model used to generate the data does not give meaningful values over water we applied a mask to only include temperature over land. This also has the benefit that the data shows no apparent discontinuities over land, in agreement with Assumptions 1.

For step (a) of Algorithm 1 we used the R-package nlme to obtain estimates $\widehat{\beta }(\mathbf{s})$ and $\widehat{\mathbf{\Omega }}(\mathbf{s})$ assuming an AR(1) correlation within past and future time periods and no correlation between the two periods. For step (b) we used the multiplier bootstrap to obtain the threshold a. The entire analysis for either the summer or winter data including the pointwise GLS and the multiplier bootstrap to obtain the CoPE sets was performed in under seven minutes on a regular laptop.

Results

The results for the climate data, shown in Figure 1, correspond to CoPE sets for T^(b)(s) − T^(a)(s). The target level is c = 2^◦C and nominal coverage probability is fixed at 1 − α = 0.9.

For the mean summer temperature, it may be stated with 90% confidence that the Rocky Mountains and the Sierra Madre Occidental mountains of Mexico are at risk of exhibiting a warming of 2◦C or more in the given time period, while the Florida Peninsula, parts of the Mexican Gulf, large parts of the Canadian Northwest and the northern part of the Labrador Peninsula are not at risk.

For the mean winter temperature, some regions around the Hudson Bay and in the Canadian Shield are identified to be at a high risk while a comparatively small region north of the Mexican Gulf is considered not at risk for extreme warming.

In the supplement to this paper we show CoPE sets when the domain is restricted to the contiguous USA. These sets are only marginally different from the ones shown here.

6. Discussion

Discrete Locations and Measurement Errors

Consistent with our data, we have assumed that we have repeated observations of the entire fields contaminated with a continuous noise field and without nugget effect. Our theory for CoPE sets may be extended following Degras (2011) who considered a model of the form

$$Y_{ij}=\mu (x_j)+{ϵ}_i(x_j)+{\eta }_{ij},1\le i\le n;1\le j\le p$$ (13)

with locations x_j in the domain of interest, the ∊_i independent copies of an unknown random process and ∊ η_ij i.i.d. Gaussian noise (nugget effect). They show that (in dimension 1 or 2) under suitable assumptions on the target function and the model, a local linear estimate $\widehat{\mu }$ of μ, depending on a smoothing parameter, satisfies a functional CLT, that is $\sqrt{n}(\widehat{\mu }-\mu )$ converges weakly to a Gaussian random field with the same covariance as ϵ. The functional CLT gives the major part of our assumptions 1 needed to obtain CoPE sets. However, it still depends on the design locations x_j becoming dense quickly. It is an interesting question for further research how the threshold a may be obtained in this setting and how it may be affected by the choice of the smoothing parameter.

More Efficient Estimators

In view of techniques from geostatistics, it is natural to ask whether more efficient estimators than pixel-wise regression can be used to estimate the parameter functions in the model (6). There is a trade-off in the feasibility of such estimators. While local pooling may increase the accuracy, optimal bandwidth will vary spatially and depend on the unknown covariance structure of the field. Obtaining an estimator in this fashion is feasible if one makes strong parametric assumptions on the covariance structure, but not so if one only assumes non-stationarity and general moment and increment conditions (as we do here).

A Proofs

Proof of Theorem 1. In part I of the proof, we show that

$$\underset{n\to \infty }{\lim \inf }P\left[{\widehat{A}}_c^{+}\subset A_c\subset {\widehat{A}}_c^{-}\right]\ge P\left[\underset{\partial A_c}{\sup }|G(s)|\le a\right].$$ (14)

Note that (14) immediately gives the second part of the theorem since

$$P\left[D\cap {\widehat{A}}_c^{+}\subset D\cap A_c\subset D\cap {\widehat{A}}_c^{-}\right]\ge P\left[{\widehat{A}}_c^{+}\subset A_c\subset {\widehat{A}}_c^{-}\right].$$

In part II we show that for a sequence of sets D_n that satisfy Assumption 2 we have

$$\underset{n\to \infty }{\lim \sup }P\left[D_n\cap {\widehat{A}}_c^{+}\subset D_n\cap A_c\subset D_n\cap {\widehat{A}}_c^{-}\right]\le P\left[\underset{s\in \partial A_c}{\sup }|G(\mathbf{s})|\le a\right].$$ (15)

This and part b) of the Theorem immediately give part c). Part a) also follows from (14) and (15) since D_n ≡ S trivially satisfies Assumption 2.

Part I

For η > 0 define the inflated boundary $A_c^{\eta }=\{\mathbf{s}\in S:c-\eta \sigma (\mathbf{s})\le \mu (\mathbf{s})\le c+\eta \sigma (\mathbf{s})\}$. Points outside of $A_c^{\eta }$ become irrelevant in the limit n → ∞ since their values are far from c and, if η goes to zero at an appropriate rate, we finally end up with the boundary ∂A_c.

Assume η < η₀ and let C′ = inf_s∈U σ(s). We first show that

$$\underset{\mathbf{s}\in A_c^{\eta }}{\sup }\left|\frac{{\widehat{\mu }}_n(\mathbf{s})-\mu (\mathbf{s})}{{\tau }_n\sigma (\mathbf{s})}\right|\le a,\underset{\mathbf{s}\in U}{\sup }\left|\frac{{\widehat{\mu }}_n(\mathbf{s})-\mu (\mathbf{s})}{{\tau }_n\sigma (\mathbf{s})}\right|\le a+C^{\prime }\eta {\tau }_n^{-1}\mathrm{and}\underset{\mathbf{s}\in S}{\sup }\left|{\tau }_n^{-1}{Z}_n(\mathbf{s})\right|\le a+C{\tau }_n^{-1}$$

implies that ${\widehat{A}}_c^{+}\subset A_c\subset {\widehat{A}}_c^{-}$. To see this, assume the above conditions hold and considers ∊ A_c. If $\mathbf{s}\in A_c\cap A_c^{\eta }$ we have that

$$\frac{{\widehat{\mu }}_n(\mathbf{s})-c}{{\tau }_n\sigma (\mathbf{s})}\ge \frac{{\widehat{\mu }}_n(\mathbf{s})-\mu (\mathbf{s})}{{\tau }_n\sigma (\mathbf{s})}\ge -a$$

and hence $\mathbf{s}\in {\widehat{A}}_c^{-}$. If $\mathbf{s}\in A_c\cap (U\backslash A_c^{\eta })$ then

$$\frac{{\widehat{\mu }}_n(\mathbf{s})-c}{\sigma (\mathbf{s}){\tau }_n}\ge \frac{{\widehat{\mu }}_n(\mathbf{s})-\mu (\mathbf{s})}{\sigma (\mathbf{s}){\tau }_n}+C^{\prime }\eta {\tau }_n^{-1}\ge -a-C^{\prime }\eta {\tau }_n^{-1}+C^{\prime }\eta {\tau }_n^{-1}=-a$$

and therefore again $\mathbf{s}\in {\widehat{A}}_c^{-}$. If finally s ∈ A_c \ U we have

$$\frac{{\widehat{\mu }}_n(\mathbf{s})-c}{{\tau }_n\sigma (\mathbf{s})}\ge C{\tau }_n^{-1}+{\tau }_n^{-1}{Z}_n(\mathbf{s})\ge C{\tau }_n^{-1}-a-C{\tau }_n^{-1}=-a$$

and hence $\mathbf{s}\in {\widehat{A}}_c^{-}$ as well. Therefore we have shown that the above properties imply $A_c\subset {\widehat{A}}_c^{-}$. An analogous argument works for the inclusion ${\widehat{A}}_c^{+}\subset A_c$.

Now, let {η_n}_n∊ℕ be a sequence of positive numbers such that η_n → 0 and ${\eta }_n{\tau }_n^{-1}\to \infty$.

With what we showed above, we can write

$$\begin{gathered} P\left[{\widehat{A}}_c^{+}\subset A_c\subset {\widehat{A}}_c^{-}\right]\ge P\left[\underset{\mathbf{S}\in A_c^{{\eta }_n}}{\sup }\left|\frac{{\widehat{\mu }}_n(\mathbf{s})-\mu (\mathbf{s})}{{\tau }_n\sigma (\mathbf{s})}\right|<a\right] \\ +P[\underset{\mathbf{s}\in U}{\sup }\left|\frac{{\widehat{\mu }}_n(\mathbf{s})-\mu (\mathbf{s})}{{\tau }_n\sigma (\mathbf{s})}\right|\le a+C^{\prime }{\eta }_n{\tau }_n^{-1}]-1+P\left[\underset{\mathbf{s}\in S}{\sup }\left|{\tau }_n^{-1}{Z}_n(\mathbf{s})\right|<a+C{\tau }_n^{-1}\right]-1. \end{gathered}$$ (16)

First, note that the last two probabilities in this expression go to one since ${\sup }_{\mathbf{s}\in U}({\widehat{\mu }}_n(\mathbf{s})-\mu (\mathbf{s}))/({\tau }_n\sigma (\mathbf{s}))$ and ${\sup }_{\mathbf{s}\in S}\left|{\tau }_n^{-1}{Z}_n(\mathbf{s})\right|$ are tight and ${\eta }_n{\tau }_n^{-1}\to \infty$.

To prove convergence of the first term we need the following

Lemma 1. Under Assumptions 1 part (a) if η_n → 0 then the Hausdorff distance δ_n := d_H $(A_c^{{\eta }_n},\partial A_c)\to 0$.

Proof. Define the set (∂A_c)_ε := {s ∊ S : d(s, ∂A_c) < ε}. We prove the assertion by showing that for any ε > 0 there exists an η > 0 such that $A_c^{\eta }\subset {(\partial A_c)}_{\epsilon }$. To this end, assume the contrary. Then, there exists ε > 0 such that for any η > 0 we find ${\mathbf{S}}_{\eta }\in A_c^{\eta }$ with d(s_η,∂A_c) ≥ ε. The sequence (s_η)_η↓0 is contained in the compact set S and hence has a convergent subsequence with limit s^*, say. By construction and continuity of μ on $A_c^{\eta }$ for η small enough, we have s^* $\in {\cap }_{\eta >0}{A}_c^{\eta }=\partial A_c$. On the other hand, 0 = d(s^*, ∂A_c) =lim_η→0 d(s_η, ∂A_c) ≥ ε, a contradiction.

Recall that for a function f : S → ℝ and some number δ > 0 the modulus of continuity is defined as

$$w_U(f,\delta )=\underset{{\mathbf{s}}_1,{\mathbf{s}}_2\in U,\left|{\mathbf{s}}_1-{\mathbf{s}}_2\right|\le \delta }{\sup }\left|f({\mathbf{s}}_1)-f({\mathbf{s}}_2)\right|.$$ (17)

Since ${\left\{{\tau }_n^{-1}\sigma {(\mathbf{s})}^{-1}({\widehat{\mu }}_n(\mathbf{s})-\mu (\mathbf{s}))\right\}}_{\mathbf{s}\in U,n\in \mathbb{N}}$ is weakly convergent, we have

$$\underset{\delta \to 0}{\lim }\underset{n\to \infty }{\lim \sup }P\left[w_U\left(\frac{{\widehat{\mu }}_n(\mathbf{s})-\mu (\mathbf{s})}{{\tau }_n\sigma (\mathbf{s})},\delta \right)\ge \zeta \right]=0$$ (18)

for all positive ζ (Khoshnevisan, 2002, Prop. 2.4.1 and Exc. 3.3.1). Together with Lemma 1 this implies that for n large enough

$$|\underset{s\in A_c^{{\eta }_n}}{\sup }\left|\frac{{\widehat{\mu }}_n(\mathbf{s})-\mu (\mathbf{s})}{{\tau }_n\sigma (\mathbf{s})}\right|-\underset{\mathbf{s}\in \partial A_c}{\sup }\left|\frac{{\widehat{\mu }}_n(s)-\mu (s)}{{\tau }_n\sigma (s)}\right||\le w_U\left(\frac{{\widehat{\mu }}_n(\mathbf{s})-\mu (\mathbf{s})}{{\tau }_n\sigma (\mathbf{s})},{\delta }_n\right)\to 0,$$

in probability. Since ${\sup }_{\mathbf{s}\in \partial A_c}\left|({\widehat{\mu }}_n(\mathbf{s})-\mu (\mathbf{s}))/({\tau }_n\sigma (\mathbf{s}))\right|$ converges in distribution to ${\sup }_{\mathbf{s}\in \partial A_c}|G(\mathbf{s})|$ this yields

$$\underset{\mathbf{s}\in A_c^{{\eta }_n}}{\sup }\left|\frac{{\widehat{\mu }}_n(\mathbf{s})-\mu (\mathbf{s})}{{\tau }_n\sigma (\mathbf{s})}\right|\to \underset{\mathbf{s}\in \partial A_c}{\sup }|G(\mathbf{s})|$$

in distribution. In view of (16) this completes the proof of (14).

Part II

To show (15) we first prove that the inclusion $({\widehat{A}}_c^{+}\cap D_n)\subset (A_c\cap D_n)$ does not hold if for some δ > 0 we have ${\sup }_{\mathbf{s}\in \partial A_c}({\widehat{\mu }}_n(\mathbf{s})-c)/({\tau }_n\sigma (\mathbf{s}))\ge a+\delta$ and ${\nabla }_n^{-}/{\tau }_n+w_n^{-}\le \delta$.

To this end, assume the latter holds and let s₀ ∈ ∂A_c such that $({\widehat{\mu }}_n({\mathbf{s}}_0)-c)/({\tau }_n\sigma ({\mathbf{s}}_0))\ge a+\delta$. Then, with (17) and the abbreviation

$$w_n^{\pm }≔w_U\left(\frac{{\widehat{\mu }}_n(\mathbf{s})-\mu (\mathbf{s})}{{\tau }_n\sigma (\mathbf{s})},{\mathrm{\Delta }}_n^{\pm }\right),$$

we have for large enough n for the projection ${\mathfrak{p}}_n^{-}\left({\mathbf{s}}_0\right)$ of s₀ that

$$\begin{gathered} \frac{{\widehat{\mu }}_n({\mathfrak{p}}_n^{-}({\mathbf{s}}_0))-c}{{\tau }_n\sigma ({\mathfrak{p}}_n^{-}({\mathbf{s}}_0))}=\frac{\mu ({\mathfrak{p}}_n^{-}({\mathbf{s}}_0))-c}{{\tau }_n\sigma ({\mathfrak{p}}_n^{-}({\mathbf{s}}_0))}+\frac{{\widehat{\mu }}_n({\mathfrak{p}}_n^{-}({\mathbf{s}}_0))-\mu ({\mathfrak{p}}_n^{-}({\mathbf{s}}_0))}{{\tau }_n\sigma ({\mathfrak{p}}_n^{-}({\mathbf{s}}_0))} \\ \ge \frac{\mu ({\mathfrak{p}}_n^{-}({\mathbf{s}}_0))-c}{{\tau }_n\sigma ({\mathfrak{p}}_n^{-}({\mathbf{s}}_0))}+\frac{{\widehat{\mu }}_n({\mathbf{s}}_0)-\mu ({\mathbf{s}}_0)}{{\tau }_n\sigma ({\mathbf{s}}_0)}-w_n^{-} \\ \ge a+\delta -{\nabla }_n^{-}/{\tau }_n-w_n^{-}\ge a. \end{gathered}$$

This shows ${\mathfrak{p}}_n^{-}({\mathbf{s}}_0)\in {\widehat{A}}_c^{+}$. But ${\mathfrak{p}}_n^{-}({\mathbf{s}}_0)\in (S\backslash A_c)\cap D_n$ by definition and hence $({\widehat{A}}_c^{+}\cap D_n)\subset (A_c\cap D_n)$ does not hold.

Since an analogous calculation works for the inclusion $(A_c\cap D_n)\subset ({\widehat{A}}_c^{-}\cap D_n)$ we obtain the bound

$$P\left[D_n\cap {\widehat{A}}_c^{+}\subset D_n\cap A_c\subset D_n\cap {\widehat{A}}_c^{-}\right]\le P\left[\underset{S\in \partial A_c}{\sup }\left|\frac{{\widehat{\mu }}_n(\mathbf{s})-\mu (\mathbf{s})}{{\tau }_n\sigma (\mathbf{s})}\right|<a+\delta \right]+P\left[{\nabla }_n^{\pm }/{\tau }_n+w_n^{\pm }>\delta \right].$$

By assumptions 1 and because ${\nabla }_n^{\pm }\to 0$ and $w_n^{\pm }\to 0$ in probability by (18) the right hand side of this bound converges to $P[{\sup }_{\mathbf{s}\in \partial A_c}|G(\mathbf{s})|\le a+\delta ]$. Since δ > 0 was arbitrary and ${\sup }_{\mathbf{s}\in \partial A_c}|G(\mathbf{s})|$ has a continuous distribution the claim follows.

Proof of Corollary 1. For any pair of nested sets ${\widehat{A}}_c^{\pm }$. we have that ${\widehat{A}}_c^{+}\subset A_c\subset {\widehat{A}}_c^{-}$ implies $\partial A_c\subset \mathrm{cl}({\widehat{A}}_c^{-}\backslash {\widehat{A}}_c^{+})$. On the other hand, the latter will certainly fail to hold if ${\sup }_{\mathbf{s}\in \partial A_c}\left|{\widehat{\mu }}_n(\mathbf{s})-c\right|/\left|{\tau }_n\sigma (\mathbf{s})\right|>a$. Combining these two observations yields

$$P\left[{\widehat{A}}_c^{+}\subset A_c\subset {\widehat{A}}_c^{-}\right]\le P\left[\partial A_c\subset \mathrm{cl}({\widehat{A}}_c^{-}\backslash {\widehat{A}}_c^{+})\right]\le P[\underset{\mathbf{s}\in \partial A_c}{\sup }\left|\frac{{\widehat{\mu }}_n(s)-c}{{\tau }_n\sigma (\mathbf{s})}\right|\le a].$$

Taking the limit n → ∞ of this inequality and using Theorem 1 gives the assertion.

Proof of Theorem 2. Define A = X^T Ω⁻¹(s)X⁻¹ X^T Ω^−1/2(s), giving $\widehat{\mathbf{b}}(\mathbf{s})-\mathbf{b}(\mathbf{s})=\mathbf{A}\widetilde{ϵ}(\mathbf{s})$. To prove weak convergence of the process we first show convergence of the finite dimensional distributions and then tightness of the sequence (Khoshnevisan, 2002, Prop. 3.3.1).

For the former, let s₁,...,s_K ∈ S be arbitrary. We need to show that with

$$\begin{gathered} U=\left(\sqrt{{\mathbf{X}}^T{\mathbf{\Omega }}^{-1}(\mathbf{s})\mathbf{X}}\left(\widehat{\mathbf{b}}({\mathbf{s}}_1)-\mathbf{b}({\mathbf{s}}_1)\right),\dots ,\sqrt{{\mathbf{X}}^T{\mathbf{\Omega }}^{-1}(\mathbf{s})\mathbf{X}}\left(\widehat{\mathbf{b}}({\mathbf{s}}_K)-\mathbf{b}({\mathbf{s}}_K)\right)\right) \\ =\mathrm{diag}\left[\sqrt{{\mathbf{X}}^T{\mathbf{\Omega }}^{-1}({\mathbf{s}}_1)\mathbf{X}}\mathbf{A},\dots ,\sqrt{{\mathbf{X}}^T{\mathbf{\Omega }}^{-1}({\mathbf{s}}_K)\mathbf{X}}\mathbf{A}\right](\widetilde{ϵ}({\mathbf{s}}_1),\dots ,\widetilde{ϵ}({\mathbf{s}}_K)), \end{gathered}$$

(here, ‘⊗’ denotes the Kronecker product of two matrices) we have convergence U → $\mathcal{N}(0,{\left[\mathfrak{c}({\mathbf{s}}_i,{\mathbf{s}}_j)\right]}_{i,j=1}^K\otimes {\mathbf{I}}_p)$ in distribution. We readily see that E [U] = 0 and for the covariance we compute

$$\begin{gathered} \mathrm{cov}[U]=\mathrm{diag}[\sqrt{{\mathbf{X}}^T{\mathbf{\Omega }}^{-1}({\mathbf{S}}_1)\mathbf{X}}\mathbf{A},\dots ,\sqrt{{\mathbf{X}}^T{\mathbf{\Omega }}^{-1}({\mathbf{s}}_K)\mathbf{X}}\mathbf{A}]E\left\{(\widetilde{ϵ}({\mathbf{s}}_1),\dots ,\widetilde{ϵ}({\mathbf{s}}_K)){(\widetilde{ϵ}({\mathbf{s}}_1),\dots ,\widetilde{ϵ}({\mathbf{s}}_K))}^T\right\} \\ \times \mathrm{diag}\left[{\mathbf{A}}^T\sqrt{{\mathbf{X}}^T{\mathbf{\Omega }}^{-1}({\mathbf{s}}_1)\mathbf{X}},\dots ,{\mathbf{A}}^T\sqrt{{\mathbf{X}}^T{\mathbf{\Omega }}^{-1}({\mathbf{s}}_K)\mathbf{X}}\right] \\ =\left\{\mathrm{diag}\right[\sqrt{{\mathbf{X}}^T{\mathbf{\Omega }}^{-1}({\mathbf{s}}_1)\mathbf{X}}\mathbf{A}\dots ,\sqrt{{\mathbf{X}}^T{\mathbf{\Omega }}^{-1}({\mathbf{s}}_K)\mathbf{X}\mathbf{A}}\left]\right\}\left\{{\left[\mathfrak{c}({\mathbf{s}}_i,{\mathbf{s}}_j)\right]}_{i,j=1}^K\otimes {\mathbf{I}}_n\right\} \\ \times \left\{\mathrm{diag}\left[{\mathbf{A}}^T\sqrt{{\mathbf{X}}^T{\mathbf{\Omega }}^{-1}({\mathbf{s}}_1)\mathbf{X}},\dots ,{\mathbf{A}}^T\sqrt{{\mathbf{X}}^T{\mathbf{\Omega }}^{-1}({\mathbf{s}}_K)\mathbf{X}}\right]\right\}={\left[\mathfrak{c}({\mathbf{s}}_i,{\mathbf{s}}_j)\right]}_{i,j=1}^K\otimes {\mathbf{I}}_p. \end{gathered}$$

We employ the Cramér-Wold device to show convergence of U. Indeed, let and (α₁,...,α_K) ∈ ℝ^K×p be some fixed arbitrary vector and compute

$$\begin{gathered} ⟨U,\alpha ⟩=⟨(\widetilde{ϵ}({\mathbf{s}}_1),\dots ,\widetilde{ϵ}({\mathbf{s}}_K)),\mathrm{diag}\left[{\mathbf{A}}^T\sqrt{{\mathbf{X}}^T{\mathbf{\Omega }}^{-1}({\mathbf{s}}_1)\mathbf{X}},\dots ,{\mathbf{A}}^T\sqrt{{\mathbf{X}}^T{\mathbf{\Omega }}^{-1}({\mathbf{s}}_K)\mathbf{X}}\right]\alpha ⟩ \\ ={\displaystyle \sum _{i=1}^K⟨\widetilde{ϵ}({\mathbf{s}}_i),{\mathbf{A}}^T\sqrt{{\mathbf{X}}^T{\mathbf{\Omega }}^{-1}({\mathbf{s}}_i)\mathbf{X}}{\alpha }_i⟩}={\displaystyle \sum _{i=1}^K{\displaystyle \sum _{j=1}^n{\widetilde{ϵ}}_j}}({\mathbf{s}}_i){\left({\mathbf{A}}^T\sqrt{{\mathbf{X}}^T{\mathbf{\Omega }}^{-1}(\mathbf{s})\mathbf{X}}{\alpha }_i\right)}_j. \end{gathered}$$

By interchanging the sums and defining $W_j={\displaystyle {\sum }_{i=1}^K{\widetilde{ϵ}}_j}({\mathbf{s}}_i){\left(A^T\sqrt{{\mathbf{X}}^T{\mathbf{\Omega }}^{-1}({\mathbf{s}}_i)\mathbf{X}}{\alpha }_i\right)}_j,$ we have by Assumption 3 part (c) managed to write ⟨U, α⟩ as a sum of independent random variables ⟨U, α⟩ = Σ_j W_j. The goal is now to use the CLT in the form of Lyapunov for the random variables W_j. To this end compute var $\left[{\sum }_{j=1}^n{W}_j\right]=\mathrm{var}[⟨U,\alpha ⟩]={\alpha }^T$ cov [U]α and note that since we have already showed U to have the right covariance the claimed convergence will follow once we establish the Lyapunov condition. For this purpose let δ be as in Assumption 3 to give

$$\begin{gathered} {\displaystyle \sum _{j=1}^{n}E}{\left|W_j\right|}^{2+\delta }\le K^2{\displaystyle \sum _{j=1}^n}{\displaystyle \sum _{i=1}^K}E{\left|{\widetilde{ϵ}}_j({\mathbf{s}}_i)\right|}^{2+\delta }{\left|\right({\mathbf{A}}^T\sqrt{{\mathbf{X}}^T{\mathbf{\Omega }}^{-1}({\mathbf{s}}_i)\mathbf{X}}{\alpha }_i{)}_j|}^{2+\delta } \\ \le K^2{K}_{\delta }{\displaystyle \sum _{j=1}^n}{\displaystyle \sum _{i=1}^K}{\Vert \left({\mathbf{A}}^T\sqrt{{\mathbf{X}}^T{\mathbf{\Omega }}^{-1}({\mathbf{s}}_i)\mathbf{X}}{\alpha }_i\right)\Vert }_{\infty }^{2+\delta } \\ \le K^3{K}_{\delta }\Vert \alpha {\Vert }_{\infty }n{\Vert {\mathbf{A}}^T\sqrt{{\mathbf{X}}^T{\mathbf{\Omega }}^{-1}({\mathbf{s}}_i)\mathbf{X}}\Vert }_{\infty }^{2+\delta }\to 0, \end{gathered}$$

as n → ∞. This concludes the proof of convergence for the finite dimensional distributions.

Tightness of the sequnce $\left\{\sqrt{{\mathbf{X}}^T{\mathbf{\Omega }}^{-1}(\mathbf{s})\mathbf{X}}\mathbf{A}\widetilde{ϵ}(\mathbf{s})\right\}$ follows from Assumption 3 (e) and (Bickel and Wichura, 1971, Thm. 3).

The second statement follows from the fact that

$$\begin{gathered} {\Vert {\mathbf{v}}_n(\mathbf{s})\Vert }_2^{-1}\left({\mathit{w}}^T\widehat{\mathbf{b}}(\mathbf{s})-{\mathit{w}}^T\mathbf{b}(\mathbf{s})\right)={\Vert {\mathbf{v}}_n(\mathbf{s})\Vert }_2^{-1}{\mathit{w}}^T{\left({\mathbf{X}}^T{\mathbf{\Omega }}^{-1}(\mathbf{s})\mathbf{X}\right)}^{-\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\sqrt{{\mathbf{X}}^T{\mathbf{\Omega }}^{-1}(\mathbf{s})\mathbf{X}}(\widehat{\mathbf{b}}(\mathbf{s})-\mathbf{b}(\mathbf{s})) \\ \to {\mathbf{v}}_0{(\mathbf{s})}^T{G}^{\otimes p}(\mathbf{s})\stackrel{\mathcal{D}}{=}G(\mathbf{s}), \end{gathered}$$

where the weak convergence from the previous part is used.

Proof of Corollary 2. This is an application of Theorem 1. Part (a) of Assumption 3 is tantamount to part (a) of Assumption 1. Theorem 2 gives part (b) of Assumption 1. Part (c) of the Assumptions follows from

$${\mathit{w}}^T\widehat{\mathbf{b}}(\mathbf{s})-c=({\mathit{w}}^T\mathbf{b}(\mathbf{s})-c)+({\mathit{w}}^T\widehat{\mathbf{b}}(\mathbf{s})-{\mathit{w}}^T\mathbf{b}(\mathbf{s}))$$

where the supremum of the absolute value of the second summand is ${\mathcal{O}}_P({\Vert {\mathbf{v}}_0(\cdot )\Vert }_{\infty })$ by part (b) of the Theorem. To conclude the proof, note that ${\mathit{w}}^T\mathbf{b}(\mathbf{s})-c\ge \eta \mathrm{sgn}({\mathit{w}}^T\mathbf{b}(\mathbf{s})-c)$ for $\mathbf{s}\notin A_c^{\eta }({\mathit{w}}^T\mathbf{b})$.

Proof of Remark 6. We compute

$${\mathbf{X}}^T\mathbf{X}=\mathrm{diag}\left(n/2,n/2,{\omega }^{(a)},{\omega }^{(b)}\right),{\omega }^{(a)}={\displaystyle \sum _{j=1}^{n^{(a)}}{\left(t_j^{(a)}\right)}^2},{\omega }^{(b)}={\displaystyle \sum _{j=n^{(a)}+1}^{n^{(a)}+n^{(b)}}{\left(t_j^{(b)}\right)}^2}.$$

It follows that

$${({\mathbf{X}}^T\mathbf{X})}^{-1/2}=\mathrm{diag}\left(\sqrt{2/n},\sqrt{2/n},1/\sqrt{{\omega }^{(a)}},1/\sqrt{{\omega }^{(b)}}\right).$$

With this we obtain

$${\Vert \mathbf{X}{({\mathbf{X}}^T\mathbf{X})}^{-\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\Vert }_{\infty }\le \frac{2}{\sqrt{n}}+\frac{{\max }_{1\le j\le \raisebox{1ex}{$n$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\left|t_j^{(a)}\right|}{\sqrt{{\omega }^{(a)}}}+\frac{{\max }_{\raisebox{1ex}{$n$}\!\left/ \!\raisebox{-1ex}{$2$}\right.+1\le j\le n}\left|t_j^{(b)}\right|}{\sqrt{{\omega }^{(b)}}}.$$

Now we note that since the design points $t_j^{(a)}$ and $t_j^{(b)}$ are equally spaced by assumption we have ${\max }_{1\le j\le n}|t_j^{(a)}|=\mathcal{O}(n)$ and ${\omega }^{(a)}=\mathcal{O}(n^3)$, and the same is true for the (b)-counterparts. This shows that ${\Vert \mathbf{X}{({\mathbf{X}}^T\mathbf{X})}^{-\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\Vert }_{\infty }=\mathcal{O}(n^{-\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.})$ and therefore Assumptions 3 d) -f) are valid.

Moreover, in the notation of Theorem 2, we have ${\mathbf{v}}_n=\sqrt{\frac{2}{n}}(1,-1,0,0)$ so that ${\mathbf{v}}_n/{\Vert {\mathbf{v}}_n\Vert }_2^{-1}={(-1,1,0,0)}^T$. This finally gives $\frac{\sqrt{n}}{2}\sigma {(\mathbf{s})}^{-1}({\mathit{w}}^T\widehat{\mathbf{b}}(\mathbf{s})-{\mathit{w}}^T\mathbf{b}(\mathbf{s}))\to G(\mathbf{s})$.