Abstract
Pacemaker depolarization in interstitial cells of Cajal (ICCs) is believed to be induced by Ca2+ transients and activation of anoctamin-1 (Ano1) channels in the plasma membrane. However, block of store-operated calcium entry (SOCE) or the Na-K-2Cl cotransporter (NKCC1) terminates pacemaker activity in ICC, indicating these transporters are involved in the initiation or maintenance of pacemaker activity. We hypothesized that SOCE contributes to pacemaker depolarization by maintaining [Ca2+] in the endoplasmic reticulum, which is the underlying source of Ca2+ transients for activation of Ano1. NKCC1 maintains the Cl− gradient supporting the driving force for inward current mediated by Ano1. Currently mechanisms sustaining release of Ca2+ and activation of Ano1 channels during the plateau phase of slow waves are unknown, but the reverse mode of the Na+/Ca2+ exchange may contribute. We generated a mathematical model of pacemaker activity based on current empirical observations from ICC of mouse small intestine that incorporates functions of SOCE and NKCC1. This model reproduces experimental findings, suggesting roles for SOCE and Ano1 channels: blocking of either NKCC1 or SOCE in our model terminates pacemaker activity. Direct contribution of NKCC1 to pacemaker activity in a beat-to-beat manner is not predicted by our model. Instead, NKCC1 plays a maintenance role supporting the driving force for Cl− efflux. Incorporation of SOCE allows the model to drive pacemaker activity without a diastolic depolarization, as observed in cardiac pacemaking. Further biological experiments are necessary to validate and further refine the roles of NKCC1, Na+/Ca2+ exchange, and Ano1 in the pacemaker mechanism of ICC.
Introduction
Interstitial cells of Cajal (ICC) form an electrically coupled network in the region of the myenteric plexus (ICC-MY) between the circular and longitudinal muscle layers of the gastrointestinal (GI) tract (1). Other populations of these cells, with apparently different functions, are intermingled among smooth muscle cells (SMCs) in muscle bundles and are closely associated with the terminals of enteric motor neurons (e.g., intramuscular ICC [ ICC-IM and ICC in the deep muscular plexus region of the small intestine (ICC-DMP)]) (1). ICC-MY have a prominent nuclear region and multiple long and branching processes. Mitochondria and smooth endoplasmic reticulum (ER) are abundant in these cells (2, 3). Each class of ICC forms gap junctions with neighboring SMCs, and therefore pacemaker activity and neural responses transduced by ICC can be conducted to SMCs (4, 5, 6). Recently, a third type of cell was also found to contribute to the neural regulation of SMCs, platelet-derived growth factor receptor α-positive cells (7). These cells are innervated and provide responses to purinergic neurotransmitters (8). Together, SMCs, ICC, and platelet-derived growth factor receptor α-positive cells form a multicellular syncytial structure known as the SIP syncytium.
ICC-MY display intrinsic pacemaker activity and generate electrical slow waves that propagate in a regenerative manner through the ICC-MY network and conduct, passively, into electrically coupled SMCs (1). Slow waves depolarize SMCs and activate CaV1.2 (L-type Ca2+) channels. Ca2+ entry through these channels initiates contractions. Thus, slow waves elicit the patterns of contractile activity in GI muscles that result in stereotypic motor activities such as peristalsis and segmentation.
Release of Ca2+ from inositol 1,4,5-triphosphate [IP3]-sensitive Ca2+ stores was suggested as the key event underlying pacemaker activity in ICC (9). However, recent information has also suggested a fundamental role for ryanodine receptors, at least for the slow waves in the murine small intestine (10). It is quite possible that the basal nature, level of expression, and balance between IP3 and ryanodine receptors varies between different populations of ICC, so no single dominance of Ca2+ release channels should be assigned as the basis for ICC functions at this time. ICC of several species display robust expression of anoctamin-1 (Ano1), a Ca2+-activated Cl− channel, and Ano1 was identified as one of the most highly expressed genes in ICC (11, 12, 13). Ano1−/− mice display no slow-wave activity in the small bowels and stomachs of juvenile mice, whereas normal slow waves are omnipresent in wild-type and heterozygous litter mates (14). Ano1 channels in ICC are activated by Ca2+ release events (13, 15, 16). A challenge for a Cl− conductance in slow waves is sustaining a suitable driving force for Cl− efflux (i.e., which by electrophysiological convention constitutes inward current). One study reported ECl to be −52 mV in ICC, based on measurements of intracellular Cl− using the fluorescent indicator N-(6-methoxyquinolyl) acetoethyl ester (17). In such a case, the maximal depolarization obtainable during active events involving a Cl− conductance would be −52 mV, which is much more negative than the peak depolarization or plateau potential of slow waves in ICC. Lees-Green et al. proposed that a microdomain may exist where the Na-K-2Cl cotransporter (NKCC) increases [Cl−] to a level that would sustain greater Cl− efflux (18). NKCC1 is expressed at high levels in ICC, and an antagonist of this transporter inhibited pacemaker activity (19). These studies also suggested that ECl of ICC lies close to −10 mV (19). Because the activation of Ano1 channels results in efflux of Cl− during slow waves, it is imperative that a mechanism exists for the recovery of Cl− loss.
The first biophysically based model of ICC reproduced spontaneous generation of pacemaker potentials (20). Although the model was able to reproduce some of the characteristic features of pacemaker potentials in mouse intestinal ICC, Ano1 channels were not included in this model. Recently, a new model was developed in which store-operated calcium entry (SOCE) was included and coupled to Ano1 (18). As for plausible currents contributing to the plateau, voltage-gated Na+ channels, voltage-gated nonselective channels, Ca2+-activated nonselective channels, and voltage-gated Ca2+ channels were suggested and tested, but the identity of a specific plateau current was not clarified. Because the role of ECl and contributions from Ano1 channels to pacemaker activity appear significant, we built a model of pacemaker activity with the inclusion of Ano1, SOCE, and NKCC1. As for the role of SOCE in the pacemaker activity, we hypothesized that constant oscillatory ER Ca2+ depletion would activate formation of STIM-Orai complexes and induce SOCE to yield Ca2+ entry and maintenance of store Ca2+ levels. A role for NKCC1 was conceived for restoration of ECl and maintenance of the driving force for Cl− efflux. Because NKCC1 restores Cl− lost during each slow-wave cycle, concomitant entry of Na+ and the depolarization during the plateau phase of the slow waves favors reverse-mode operation of Na+/Ca2+ exchange (NCX). This may contribute to Ca2+ entry, sustain Ca2+ release events, and maintain increased [Ca2+] near the intracellular aspects of Ano1 channels. Sustained activation of Ano1 is thought to play a primary role in the plateau phase of slow waves. Here, we have developed and present a new, to our knowledge, slow-wave model and compare its output with experimental results.
Methods
Model features
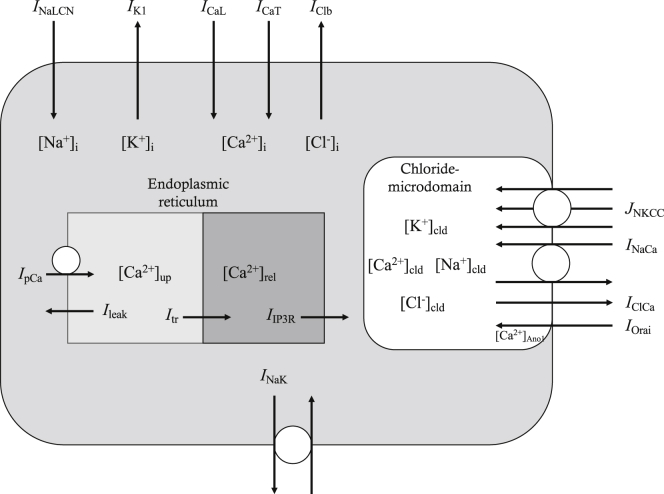
The model of ICC is based on a model published previously (20), with inclusion of new components such as NKCC1 and Ano1. The same numerical methods are employed to develop a new, to our knowledge, model of ICC. Fig. 1 shows a schematic diagram of the model described, consisting of 10 ion channels, two transporters, and two pumps, which are distributed on the membrane surrounding a chloride microdomain, the membrane surrounding the bulk cytosolic space, and the ER membrane. Movement of ions between the chloride microdomain and the bulk cytosolic space was assumed to occur by diffusion. Bulk cytosolic Ca2+ were assumed to be pumped into the uptake pool of ER and subsequently diffuse into the release pool. Ca2+ in the release pool ([Ca2+]rel) of ER move to cytosolic space by [IP3]-mediated Ca2+ release. Direct diffusion between ER and the chloride microdomain was not assumed in our model. There are altogether 62 time-dependent variables and 199 equations in the model. A glossary (Table S1), general model constants (Table S2), and initial values (Table S3) are provided in the Supporting Materials and Methods. Complete model equations are provided in the Supporting Materials and Methods. Simulation codes were written and compiled with Microsoft Visual Studio Community 2015. All the simulations were performed on a personal computer with Intel(R) Core(TM) i7-4790K CPU at 4.00 GHz.
Figure 1.
Schematic drawing of cell compartments, ion channels, transporters, and pumps in our model of ICC. The model of ICC is divided into three compartments: bulk cytosol, endoplasmic reticulum (ER), and chloride microdomain. 10 ion channels, two transporters, and two pumps are distributed along the membrane surrounding these three compartments. ICaL, L-type Ca2+ current; ICaT, T-type Ca2+ current; IK1, inward rectifier K+ current; INaLCN, Na+-leak current; IClCa, Ca2+-activated Cl− current; IClb, background Cl− current; IOrai, current carried by Orai (SOCE); INaCa, NCX current; INaK, Na+/K+ exchange current; JNKCC, flux by Na-K-2Cl cotransporter (NKCC1); IpCa, ER Ca2+ pump current; IIP3R, IP3-mediated Ca2+ release current from the ER; Ileak, Ca2+ leak from ER uptake pool; Itr, Ca2+ transfer between ER uptake and release pool; [X]i, internal or bulk cytosolic concentration of ion X; [X]up, [X] in uptake pool of ER; [X]rel, [X] in release pool of ER; [X]cld, [X] in chloride microdomain; [Ca2+]Ano1, local [Ca2+]i near Ano1.
Model of NKCC1
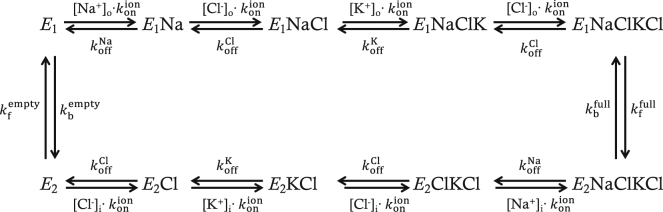
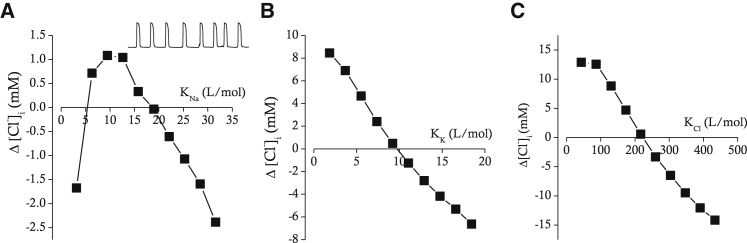
NKCC1 is known to be involved in the regulation of cell volume and maintenance of ion gradients (21). Lytle et al. suggested that only fully loaded or empty carriers are capable of undergoing the conformational change to opposite facing membrane (22), and the complete reaction cycle is demonstrated in Fig. 2. The first event is the Na+ binding to the transporter. Then sequential binding of the first Cl−, K+, and second Cl− occurs. If all the binding sites are occupied by the appropriate four ions, the transporter undergoes a conformational change that allows the transporter to be translocated. Then, the transporter releases Na+ first and three other ions sequentially. The empty transporter undergoes a conformational change and is translocated to the cell exterior to begin a new cycle. All the parameter values for NKCC1 (Table 1) were adopted from the work of Benjamin and Johnson (23). Among the parameters for renal epithelial cell lines, HeLa cells, and duck erythrocytes used by these authors, the parameters for HeLa cells were chosen for our simulations because ECl (= −10.05 mV) obtained for HeLa cells was closest to the experimentally obtained value (= −10.5 mV) for ICC (19). An optimum set of binding constants (KNa, KK, and KCl) in NKCC1 would allow the model of ICC to maintain [Cl−]i unchanged during several episodes of pacemaker activity. We sequentially varied those binding constants and monitored net changes in [Cl−]i (Δ[Cl−]i) after 100 s of pacemaker activity. KNa values (L/mol) between 3.16 and 31.6 were tested, and Δ[Cl−]i after 100 s of pacemaker activity were plotted against KNa as shown in Fig. 3 A. Δ[Cl−]i was minimal when KNa is 18.96 L/mol, which is slightly above the value obtained from HeLa cells (15.8 L/mol). KK values (L/mol) between 1.844 and 18.44 were tested, and Δ[Cl−]i after 100 s of pacemaker activity were plotted against KK as shown in Fig. 3 B. Δ[Cl−]i was minimal when KK is 9.7067 L/mol, which is similar to the value from HeLa cells (9.22 L/mol). KCl values (L/mol) between 43.38 and 433.8 were tested, and Δ[Cl−]i after 100 s of pacemaker activity were plotted against KCl as shown in Fig. 3 C. Δ[Cl−]i was minimal when KCl is 225.23 L/mol, which is again similar to the value from HeLa cells (216.9 L/mol). A detailed method and equations for calculating unidirectional ion fluxes are presented in Supporting Materials and Methods. The maximal rate of transport was adjusted to counterbalance the Cl− efflux by Ano1.
Figure 2.
Schematic drawing of reaction cycle for NKCC1 cotransporter. , association constant; , dissociation rate constants for ion X; , forward rate constants for the empty cotransporter; , backward rate constants for the empty cotransporter; , forward rate constants for the ion-filled cotransporter; , backward rate constants for the ion-filled cotransporter; [X]o, external concentration of ion X; [X]i, internal concentration of ion X.
Table 1.
Parametric Set for NKCC1
| Parameter | Value | Unit | Description |
|---|---|---|---|
| KNa | 15.80 | L/mol | equilibrium (binding) constant of Na+ |
| KK | 9.22 | L/mol | equilibrium (binding) constant of K+ |
| KCl | 216.90 | L/mol | equilibrium (binding) constant of Cl− |
| 1002.00 | s−1 | forward rate constant in ion-filled cotransporter | |
| 2255.00 | s−1 | backward rate constant in ion-filled cotransporter | |
| 37,760.00 | s−1 | forward rate constant in empty cotransporter | |
| 16,783.00 | s−1 | backward rate constant in empty cotransporter |
Figure 3.
Relations between KNa (A), KK (B), KCl (C), and net changes in [Cl−]i (Δ[Cl−]i) during 100 s of pacemaker activity. Initial [Cl−]i is 87.464 mM. The small trace in the upper right corner of (A) shows representative pacemaker activity during a time period corresponding to 30 s.
Cl− influx by NKCC1
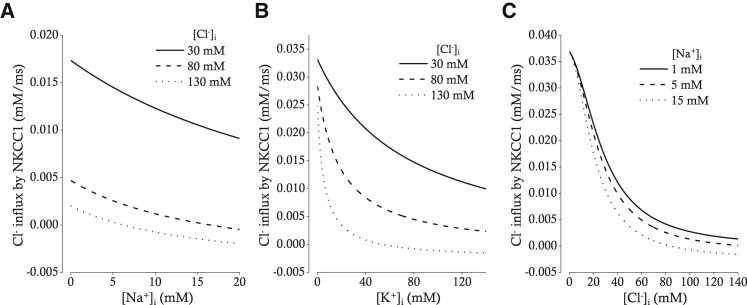
Cl− influx via NKCC1 was calculated based on the set of parameters (KNa, KCl, and KK) for HeLa cells chosen by Benjamin and Johnson (23). The relations between intracellular ion concentrations and Cl− influx in our model of NKCC1 are demonstrated in Fig. 4. As [Na+]i is increased, Cl− influx is decreased for three different [Cl−]i (Fig. 4 A). When [Cl−]i is 30 mM (solid line), the Cl− influx is positive along the whole range of [Na+]i between 0 and 20 mM. When [Cl−]i is 80 mM (broken line), the Cl− flux reverses where [Na+]i is 16.57 mM. When [Cl−]i is 130 mM (dotted line), the Cl− flux reverses at lower [Na+]i (6.26 mM). As [K+]i is increased, Cl− influx is decreased with a relatively steeper slope (Fig. 4 B). In other words, lowering the [K+]i below 40 mM greatly accelerates the rate of Cl− influx, especially if [Cl−]i is higher than 80 mM (dotted lines). Cl− influx is also in an inverse relation with [Cl−]i (Fig. 4 C), and the direction of Cl− flux is reversed under the condition in which [Cl−]i exceeds 80 mM and [Na+]i is over 15 mM (dotted line). In other words, the direction of Cl− flux is always inward under the condition of low [Na+]i (<5 mM) irrespective of [Cl−]i in the range of 0–130 mM.
Figure 4.
Relations between [Na+]i (A), [K+]i (B), [Cl−]i (C), and Cl− influx by NKCC1. (A) The relation between [Na+]i and Cl− influx by NKCC1 for three different [Cl−]i (30, 80, and 130 mM) is shown. [K+]i is fixed at 130 mM. (B) The relation between [K+]i and Cl− influx by NKCC1 for three different [Cl−]i (30, 80, and 130 mM) is shown. [Na+]i is fixed at 5 mM. (C) The relation between [Cl−]i and Cl− influx by NKCC1 for three different [Na+]i (1, 5, and 15 mM) is shown. [K+]i is fixed at 130 mM. Extracellular [Na+], [K+], and [Cl−] are fixed at 140, 5, and 140 mM, respectively (A–C).
Model of NCX
The model of NCX was similarly constructed to that of NKCC1 and was used to calculate fluxes of Na+ and Ca2+. Three binding sites for Na+ and one for Ca2+ were assumed to be present in the NCX. The half-saturation constants of Na+ and Ca2+ for NCX were adopted from the Kyoto model (24). The calculated fluxes were basically identical (less than 0.1% difference) to those calculated by the lumped two-state model of NCX (24).
Reverse-mode NCX
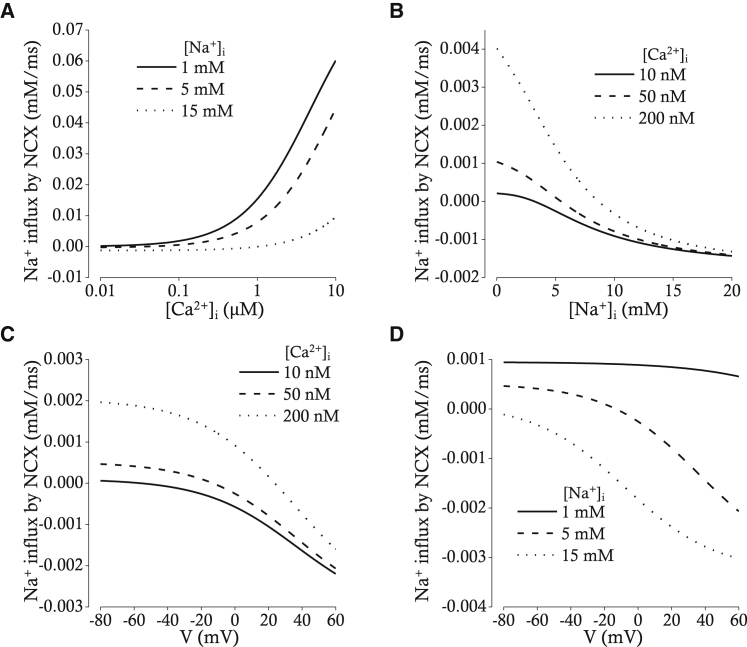
If NKCC1 recovers the Cl− loss during pacemaker depolarization evoked by activation of Ano1, the cell would take up Na+ and K+ in addition to Cl−. This raises the question, would Na+ loading by NKCC1 induce reverse-mode operation of NCX in our model? Under the condition in which extracellular [Na+] and [Ca2+] is 140 and 1.8 mM, respectively, and the membrane potential is −20 mV, [Na+]i around 15 mM induces a reverse-mode operation of NCX if [Ca2+]i is lower than 1 μM (Fig. 5 A). Under the same condition in which [Ca2+]i is lower than 100 nM, the [Na+]i higher than 7 mM results in a reverse-mode operation of NCX (Fig. 5 B). The direction of NCX operation is also reversed by membrane depolarization (Fig. 5 C). When the extracellular [Na+] is 140 mM, extracellular [Ca2+] is 1.8 mM, and [Ca2+]i is 50 nM, 15 mM [Na+]i reverses the direction of NCX operation at membrane potentials between −80 and +60 mV (Fig. 5 D). In short, under the condition in which [Na+]i increases, [Ca2+]i decreases, and the membrane depolarizes, NCX operates in the reverse mode, which subsequently results in a sustained increase of [Ca2+]i.
Figure 5.
Relations between [Ca2+]i (A), [Na+]i (B), V (C and D), and Na+ influx by Na+/Ca2+ exchange (NCX). (A) The [Ca2+]i-Na+ influx relation is shown for three different [Na+]i (1, 5, and 15 mM). The membrane potential was fixed at -20 mV. (B) The [Na+]i-Na+ influx relation is shown for three different [Ca2+]i (10, 50, and 200 nM). The membrane potential was also fixed at -20 mV. (C) The V-Na+ influx relation is shown for three different [Ca2+]i (10, 50, and 200 nM). (D) The V-Na+ influx relation is shown for three different [Na+]i (1, 5, and 15 mM).
Model of SOCE
Because the controversy on Cl− dynamics and the pacemaker mechanism still remains unresolved (18, 20), the model of SOCE was also incorporated. As for the role of SOCE and Ano1 in the pacemaker mechanism, we hypothesized that the oscillatory depletion of Ca2+ from the ER activates STIM-Orai complexes, and SOCE activates nearby Ano1 by elevating [Ca2+]i near Ano1. As for the role of NKCC1 and NCX in the plateau, we hypothesized that the Ano1 activation results in Cl− efflux, which subsequently activates NKCC1. As NKCC1 restores Cl− lost during slow-wave activity, the concerted actions of [Ca2+]i decrease, [Na+]i increase, and membrane depolarization favor a reverse-mode operation of NCX. This can sustain [Ca2+]i near Ano1 channels or evoke further Ca2+ release events. The sustained activation of Ano1 is thought to play a primary role during the plateau phase of slow waves. The model of SOCE was adopted from the work of Lees-Green et al. (18) and modified to generate the cyclic Ca2+ release in our model.
SOCE and Ano1 activation
Because the Ca2+-activated Cl− current (IClCa) carried by Ano1 is activated by Ca2+ near the mouth of channel pore (25, 26), [Ca2+] diffused from nearby Ca2+ sources, such as the STIM-Orai complex or bulk cytosol, should be first determined. The following equation derived from an analytical steady-state solution gives an answer for the level of [Ca2+] activating Ano1 (27).
| (1) |
| (2) |
| (3) |
| (4) |
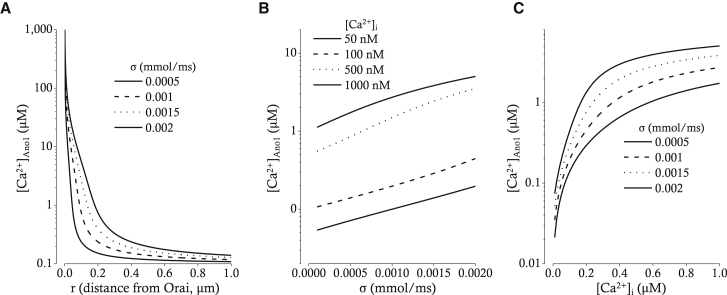
In these equations, Dc is the diffusion constant of the free cytosolic Ca2+, Km is the affinity of the mobile Ca2+ buffer, σ denotes the Ca2+ flux through a single Orai, r is the distance between Ano1 and nearby Orai, c∞ is the bulk cytosolic Ca2+ concentration far from the Ano1, Dm is the diffusion constant of one mobile Ca2+ buffer, Bm is the concentration of one mobile Ca2+ buffer, JOrai is the total flux through all Orais (see equation in Supporting Materials and Methods), nOrai is the number of Orais, and Volcyt is the volume of the cytosol. The relation between r and [Ca2+]Ano1 is demonstrated in Fig. 6 A. Dependencies of [Ca2+]Ano1 on Ca2+ flux through a single Orai (σ) and bulk cytosolic Ca2+ concentration (c∞) are also demonstrated in Fig. 6, B and C, respectively. Those relations demonstrate that the colocalization of Ano1 and Orai is essential for tight coupling of SOCE and Ano1 activation.
Figure 6.
Relations between distance from nearby Orai (A), Ca2+ flux through a single Orai (B), bulk [Ca2+] (C), and [Ca2+] at the mouth of Ano1 pore. (A) [Ca2+] at the mouth of Ano1 ([Ca2+]Ano1) along the diffusion pathway from Ca2+ source (Orai) was calculated at four different magnitudes of Ca2+ flux through Orai (σ; 0.0005, 0.001, 0.0015, and 0.002 mmol/ms). (B) [Ca2+]Ano1 was plotted against the magnitude of Ca2+ flux through Orai (σ) under the condition of four different bulk cytosolic [Ca2+] ([Ca2+]i; 50, 100, 500, and 1000 nM). (C) The relation between [Ca2+]Ano1 and [Ca2+]i was shown at four different magnitudes of Ca2+ flux through Orai (σ; 0.0005, 0.001, 0.0015, and 0.002 mmol/ms).
Model of IClCa
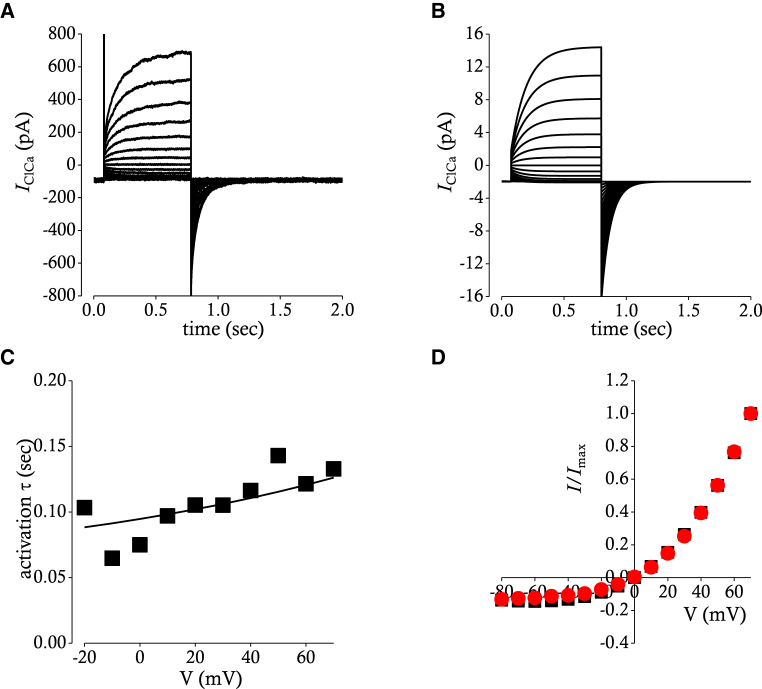
Gating of Ano1 is not only Ca2+-dependent but also voltage-dependent, and its current-voltage relationship is outwardly rectifying in the submicromolar concentration of [Ca2+]i (25, 26). Fig. 7 A shows a voltage-clamp recordings of CaCC (IClCa) carried by Ano1 activated by test potentials between −80 and +70 mV in the presence of 100 nM [Ca2+]i. Time courses of IClCa indicate that there is only activation process in the gating of Ano1. As for activation time constants and steady-state current-voltage relation, the Ca2+ dependency was adopted from the work of Lees-Green et al. (18), whereas the voltage dependency was derived from voltage-clamp data in the presence of 100 nM [Ca2+]i (26). The following equations were obtained to reproduce the voltage and Ca2+ dependency of activation time constants and steady-state current-voltage relation of IClCa.
| (5) |
| (6) |
Figure 7.
Simulation of Ca2+ activated Cl− currents carried by Ano1. (A) A representative current recording of depolarization-activated Ano1 is shown. Ca2+-activated Cl− currents (IClCa) were evoked by application of voltage steps from −80 to 70 mV in 10 mV increments from a holding potential of −80 mV. (B) Simulated currents evoked by the same pulse protocol used in (A) are shown. (C) Relations between membrane potential (mV) and time constants of activation (τ) are shown. Time constants obtained from experimental recording (▪) in (A) are superimposed with a red line plotted by mathematical function used in (B). (D) Current-voltage relationships from (A) (▪) and from (B) (●) are superimposed. Current amplitudes are measured at the end of test pulses and are normalized to the maximum. In this case, current amplitude measured at a test pulse of +70 mV is used as the maximum. To see this figure in color, go online.
In these equations, τ is the activation time constants of Ano1 (ms), V is the membrane potential (mV), OClCa∞ is the open probability of Ano1 at steady state, Vh is the half-activation potential (mV), k is the slope factor associated with the gating charge of Ano1 (mV−1), and EC50 is a voltage-dependent expression of the [Ca2+]Ano1 for half-activation of IClCa (mV). Then, IClCa could be calculated by the following equation,
| (7) |
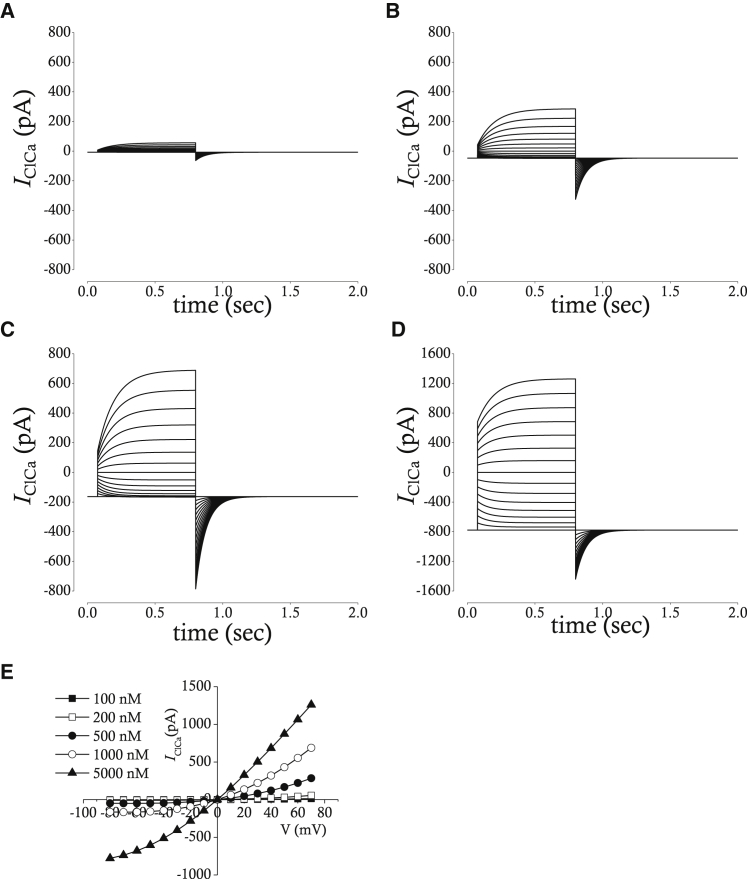
where IClCa is the current amplitude of Ano1 (pA), gClCa is the maximal whole-cell conductance of Ano1 (nS), and ECl is the equilibrium potential of Cl− (mV). Simulated IClCa is presented in Fig. 7 B. The activation time constants and steady-state current voltage relations are compared between experiment and simulation in Fig. 7, C and D. IClCa is simulated in the presence of different intracellular [Ca2+] near channel pore as shown in Fig. 8, A–D. The current-voltage relation (Fig. 8 E) loses outward rectification in the few micromolar range of [Ca2+]i, which is the same case as in experimental recordings (25).
Figure 8.
(A–D) Simulated whole-cell membrane currents with 200 nM (A), 500 nM (B), 1000 nM (C), and 5000 nM (D) of [Ca2+]Ano1. The pulse protocol is the same one used in Fig. 7 A. (E) Current-voltage relation at five-different [Ca2+]Ano1 is shown. Current amplitudes are measured at the end of test pulses and are plotted against voltages of test pulses.
Estimation of Cl− efflux and influx
Because the upstroke velocity of slow-wave depolarization is ∼7 V/s and membrane capacitance is around 25 pF (28), the amplitude of pacemaker current could be estimated to be about −175 pA. The current amplitude of pacemaker current could then be used to estimate change in [Cl−] in microdomain during pacemaker depolarization by using the following equation:
| (8) |
where [Cl−]cld is [Cl−] in Cl− microdomain (mM), t is time (ms), IClCa is the amplitude of Ca2+-activated Cl− current carried by Ano1 protein (pA), F is the Faraday constant (= 96.4867 C ⋅ mmol−1), and Volcld is the assumed volume of Cl− microdomain (= 0.05 × 0.715 pL). Because the maximal amplitude of IClCa is 140 pA and the maximal duration of IClCa is ∼50 ms, change in [Cl−] during one event of pacemaker depolarization cannot exceed 2.5 mM. Maximal conductance of IClCa and flux of NKCC1 were set to match the balance of Cl− dynamics.
Results
Inhibition of STICs by NKCC1 blocker
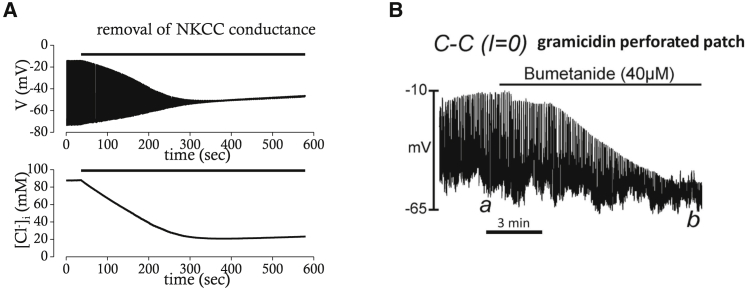
Spontaneous transient inward currents (STICs) are consistently observed in ICC at constant holding potentials between −80 and +20 mV under whole-cell voltage-clamp condition (29). It was suggested that STICs reflect periodic activation of Ano1. Cyclic ER Ca2+ release or ER Ca2+ depletion with subsequent activation of SOCE is believed to drive the periodic activation of Ano1. Bumetanide, a blocker of NKCC1, blocked STICs at a holding potential of −80 mV within a few minutes (19). The amplitude of STICs decreased in a time-dependent manner, whereas the frequency was not changed. The drug presumably affects the electrochemical gradient for Cl− across the membrane rather than the open probability of Ano1. Because continuous Cl− influx through the NKCC1 could counterbalance Cl− efflux by Ano1, inhibition of NKCC1 would eventually reduce the intracellular [Cl−] to a point at which the electrochemical gradient of Cl− is dissipated. The effect of blocking NKCC1 on STICs at a holding potential of −80 mV was reproduced by our mathematical model of ICC. When the conductance for NKCC1 was set to 0, the amplitude of STICs (Fig. 9 A, upper panel) gradually decreased with a time course similar to that seen empirically (Fig. 9 B). The time course of decrease in intracellular [Cl−] is also similar in both cases (Fig. 9 A, lower panel). The model supports the idea that the effect of NKCC1 block on STICs is mediated by loss of the electrochemical gradient for Cl− because STICs were unaffected by numerical removal of NKCC1 under the condition in which the equilibrium potential of Cl− was held at a constant value (data not shown). Measurement of intracellular [Cl−] during application of bumetanide should be performed to demonstrate how the inhibition of NKCC1 affects the amplitude of STICs.
Figure 9.
Effects of NKCC1 block on STICs in simulation (A) and experimental recording (B). (A) Simulated effects of NKCC1 block on STICs and [Cl−] at a holding potential of −80 mV are shown and compared for the same time period (∼200 s). (B) Effects of bumetanide (40 μM), a blocker of NKCC1, on STICs are examined in the murine small intestine at a holding potential of −80 mV (Zhu et al. (19), with permission). The expanded trace of STICs is presented below. To see this figure in color, go online.
Inhibition of pacemaker activity by NKCC1 blocker
If the inhibition of NKCC1 dissipates the electrochemical gradient for Cl−, the pacemaker activity of ICC should be disrupted because slow waves are thought to depend upon activation of Ano1, and its amplitude is dependent on the electrochemical gradient for Cl− as well as intracellular [Ca2+]. Indeed, application of bumetanide gradually decreased the amplitude of pacemaker potentials, whereas its frequency was unaffected (19). The mathematical model faithfully reproduced the effects of blocking NKCC1 on pacemaker activity (Fig. 10 A). The amplitude of pacemaker depolarization and intracellular [Cl−] are both slowly reduced with a similar time course to that of experimental results (Fig. 10 B), whereas the frequency of pacemaker potentials was unaffected. These results indicate again that the effect of blocking NKCC1 is primarily mediated by dysregulation of intracellular [Cl−].
Figure 10.
Effects of NKCC1 block on pacemaker activity in simulation (A) or experimental recording (B). (A) Simulated effects of NKCC1 block on pacemaker activity and [Cl−] are shown and compared for the same time period (∼600 s). (B) Effects of bumetanide (40 μM) on pacemaker activity are examined in the murine small intestine (Zhu et al. (19), with permission).
Inhibition of STICs by SOCE blocker
There is a growing body of evidence that SOCE is involved in pacemaker activity of ICC (10, 30, 31). Inhibitors of SOCE such as GSK7975A or SK&F96365 reduce the pacemaker activity of ICC (32, 33, 34). Lees-Green et al. proposed that periodic ER Ca2+ depletion induces SOCE through the STIM-Orai complex, which subsequently activates nearby Ano1 (18). Because the inhibitory effect of SOCE blockers on STICs or pacemaker activity is not mediated by change in the electrochemical gradient across the cell membrane, one could predict the effect would be rapid in comparison to that of NKCC1 blockers. GSK7975A, a specific blocker of SOCE, was found to inhibit STICs at a holding potential of −80 mV, but complete inhibition was not achieved until the drug had been perfused for ∼100 s (31). The slower effect of GSK7975A on the STIM-Orai complex was previously demonstrated in Orai1-transfected HEK cells where the t1/2 was in the range 75–100 s (35). It was speculated that the GSK7975A may interfere with the permeation of Ca2+ through the pore of the STIM-Orai complex by binding to a site near the selectivity filter. Alternatively, GSK7975A might cross the cell membrane by diffusion to reach its binding site given its moderate lipophilicity (35).
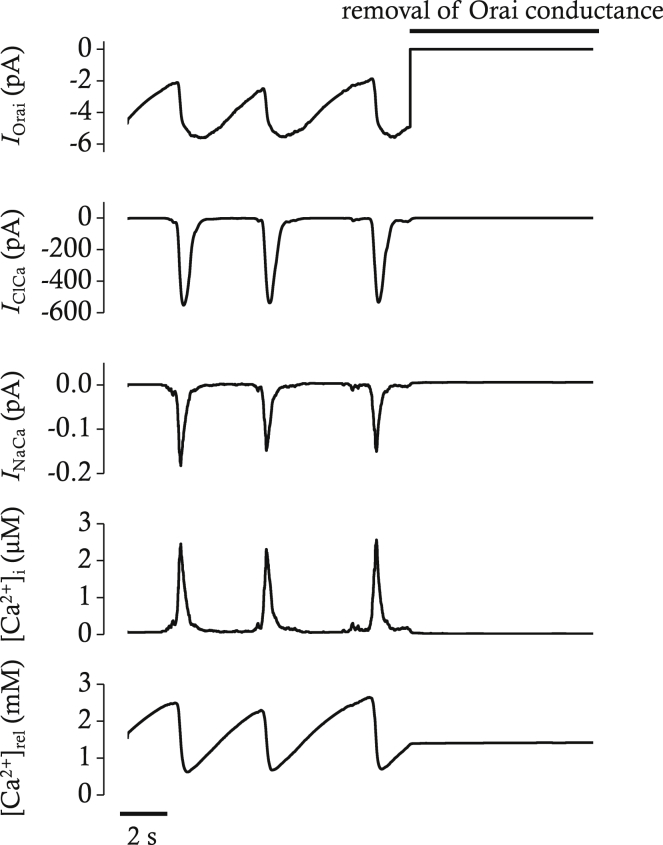
Our mathematical model reproduces the disappearance of STICs (Ano1) when the conductance of Orai is set to 0 (Fig. 11). The inhibitory effect on Ano1 caused by blocking Orai, however, is rapid compared to the effect of GSK7975A on STICs in experiments on ICC. The discrepancy may be due to the fact that our mathematical model does not consider the kinetics of the actions of GSK7975A on STIM-Orai complexes. Interestingly, Ca2+ transients were almost completely blocked by elimination of Orai, indicating SOCE might be a prerequisite for periodic Ca2+ release, another phenomenon also observed in ICC (31).
Figure 11.
Simulated effects of Orai block on IOrai, IClCa, INaCa, [Ca2+]i, and [Ca2+]rel in voltage-clamp mode. The voltage was clamped at −80 mV. The block of Orai conductance was simulated by removal of conductance after 12 s. IOrai represents the SOCE carried by Orai protein. IClCa is the Ca2+-activated Cl− current carried by Ano1 protein. INaCa is the NCX current. [Ca2+]rel represents free calcium concentration in ER release pool. Spontaneous transient inward currents (STICs) represented by IClCa disappear with simulated block of Orai.
Inhibition of pacemaker activity by SOCE blocker
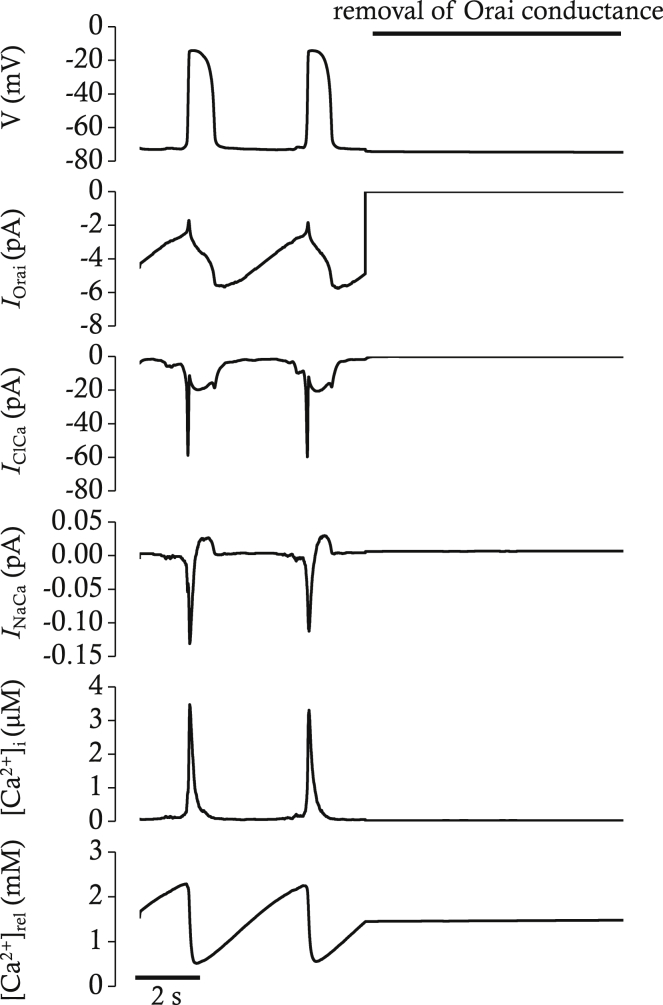
The inhibitory effect of GSK7975A on pacemaker activity was faster than the effect of GSK7579A on STICs (31). In contrast to the NKCC1 blocker, the main impact of GSK7579A on the pacemaker potential was not on the amplitude but on the frequency. Application of GSK7579A halted the pacemaker activity within 20 s. There was no transition period in which the amplitude of pacemaker potential gradually decreased while frequency remained unchanged. The inhibitory effect of blocking Orai on pacemaker activity was reproducible in our mathematical model. When the conductance of STIM-Orai complex was set to 0, pacemaker activity disappeared rapidly (Fig. 12).
Figure 12.
Simulated effects of Orai block on the pacemaker activity, IOrai, IClCa, INaCa, [Ca2+]i, and [Ca2+]rel in current-clamp mode. The block of Orai conductance was simulated by removal of conductance after 7 s. Resting membrane potential is slightly hyperpolarized by block of Orai. All the oscillatory activities are abolished.
Putative role of SOCE: Electrogenicity or Ca2+-mediated?
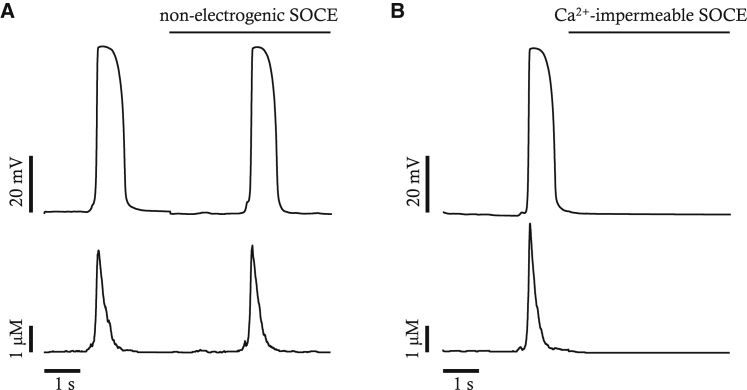
SOCE can directly depolarize cell membranes because it produces inward current. SOCE can also indirectly depolarize cell membranes by activating a pacemaker current such as Ano1 because it elevates local Ca2+ near Ano1. We separated those two effects of SOCE and tested which of them is more important for pacemaker activity using our mathematical model. First of all, we assumed that the SOCE is electroneutral but increases local Ca2+ near Ano1. Under this assumption, the mathematical model is still able to continue pacemaker activity as shown in Fig. 13. Then, we assumed that SOCE is electrogenic but could not change local Ca2+ near Ano1. Under this assumption, the pacemaker activity as well as Ca2+ transients disappear. These results suggest that the primary role of SOCE in pacemaker activity might be activation of Ano1 by increasing local Ca2+ rather than by its direct depolarizing effect. Studies on ICC should be conducted to confirm the role of SOCE on pacemaker activity, as suggested by our mathematical studies. In our model, it was calculated that SOCE contributes to [Ca2+] near Ano1 channels by as much as 39.1% during a pacemaker cycle.
Figure 13.
Impact of nonelectrogenic SOCE (A) or Ca2+-impermeable SOCE (B) on normal pacemaker activity and Ca2+ transients. Nonelectrogenic SOCE is a virtual SOCE that is permeable to Ca2+ but does not contribute to membrane depolarization. The Ca2+-impermeable SOCE is a virtual SOCE that contributes to membrane depolarization but is impermeable to Ca2+.
Discussion
This study describes a mathematical model of pacemaker activity in ICC that is based on current information obtained from voltage-clamp experiments performed on ICC of the murine small intestine and Ca2+ imaging experiments performed on the pacemaker class of ICC (ICC-MY) of the small intestine in situ. Several ion channels and ion transporters have been incorporated in the model that have been shown to impact electrical rhythmicity in intact GI muscles and spontaneous pacemaker currents in freshly isolated and identified ICCs.
Role of NKCC1
Measurement of ESTICs in ICC was made by Zhu et al. (19) using the gramicidin-permeabilized patch-clamp technique, which leaves intracellular [Cl−] undisturbed. ESTICs (which was thought to approximate ECl) was found to be −10.5 mV, which is close to peak depolarization and plateau phase of slow waves recorded in murine small intestinal ICC (36). Ano1 has been suggested as the current that depolarizes ICC during the plateau phase. Opening of Cl− channels during each slow-wave cycle is likely to cause net loss of cytosolic Cl−. Activation of Ano1 persists during the plateau phase because of the continued asynchronous release of Ca2+ during this period (10). The relatively long duration of the plateau phase (>1 s) might cause cells to lose a significant amount of Cl−. However, the plateau potential comes to a semistable level near ECl, so net Cl− current is likely to be minimal during most of the plateau phase. The major loss of Cl−, therefore, may be during the initial depolarization, shortly after Ca2+ entry and initiation of Ca2+-induced Ca2+ release, and perhaps to a lesser extent during repolarization of the slow wave, as Ca2+ release events decline in frequency and Ano1 channels begin to deactivate. Expression of Slc12a2 transcripts and NKCC1 protein was found in ICC in the myenteric region of the murine small intestine, and blocking of NKCC1 caused a rapid negative shift in ECl, inhibition of STICs in ICCs (19), and inhibition of slow waves in intact muscles (37).
NKCC1 is found on the basolateral membrane of epithelial cells for Cl− secretion as well as in many nonepithelial cells for volume regulation, whereas NKCC2 is found on the apical membrane of thick ascending limb in the loop of Henle for reabsorption of salts. There are two kinetic models for the operation of NKCC (21). One is the glide symmetry model, and the other is the alternative model with a reversed order of Na+ and Cl− binding. The glide symmetry model postulates that Na+ ion binding occurs first on the outside face of cotransporter, followed by Cl−, K+, and the second Cl−. In the alternative model, Cl− ion binding occurs first, followed by Na+, the second Cl−, and K+. Markadieu and Delpire (21) suggested that the alternative model is more appropriate for NKCC, based on their observations that a K+/K+ exchange can still occur in the alternative model when partially loaded carriers reverse their orientation and reload K+ ions. Those two kinetic models, however, do not make any difference in the calculation of net ionic flux.
Role of SOCE
Slow waves in ICC of the murine small intestine are mediated by activation of Ano1 and T-type Ca2+ channels. Activation of Ano1 is dependent on increased [Ca2+] near the intracellular aspect of the channel protein (12, 13). Increase in [Ca2+]i for activation of Ano1 is achieved in ICC by Ca2+ release from the ER (ryanodine- and IP3-receptor-gated) (9). Because Ca2+ release from the ER can be initiated by a local increase in Ca2+ near ryanodine and IP3 receptors, the first event might be Ca2+ entry through a Ca2+-influx pathway, such as T-type Ca2+, which induces release of Ca2+ from the ER (38, 39). The increase in localized Ca2+ from ER release activates Ano1 and depolarizes ICC. This is thought to be an important step in creating and maintaining the plateau phase of slow waves (10). Among the Ca2+-influx pathways, SOCE is particularly remarkable in that it is activated by depletion of ER Ca2+. SOCE is thought to replenish the ER in response to depletion of Ca2+ in stores (40, 41, 42). Although the Ca2+ ATPases (SERCA) is also able to replenish the Ca2+ store, it is more sensitive to cytosolic Ca2+ than store Ca2+. Therefore, the STIM-Orai complex, a molecular identity of SOCE, is an important contributor to replenishment of Ca2+ stores after Ca2+ release events occur (31). In our mathematical model, the rhythmic occurrence of pacemaker potentials and Ca2+ transients were abolished by removal of the SOCE conductance. Increasing the window region of T-type Ca2+ current by shifting the activation curve to the left about −20 mV, however, resulted in the reappearance of rhythmic pacemaker potentials and Ca2+ transients (simulation data not shown). T-type Ca2+ channels may contribute to the initial increase in cytosolic Ca2+ that triggers Ca2+-induced Ca2+ release and activation of Ano1, but SOCE might provide a more sustained source of Ca2+ because it is not constrained by a narrow window current region as with T-type Ca2+ currents. Furthermore, SOCE responds to ER Ca2+ depletion and supports periodic Ca2+ influx in our mathematical model. As for the mechanism of how the STIM-Orai can sense ER Ca2+ depletion, a general consensus is that emptying of stores causes oligomerization and translocation of STIM proteins within ER membrane (43, 44). Although we proposed that the depletion of ER Ca2+ store activates SOCE allowing Ca2+ entry, the oligomerization and translocation of STIM may not occur with every cycle of pacemaker activity because assembly of the STIM-Orai complex, as observed in nonexcitable cells, takes >10 s. However, there may be splice variants that accomplish assembly and disassembly of the STIM-Orai complex on a faster timescale (45) or the assembly of the complex may be sustained over slow-wave cycles, allowing recovery of Ca2+ through Orai channels that is not strictly dependent upon STIM-Orai assembly after each Ca2+ release event.
Plausible plateau currents contributing to slow waves
Lees-Green et al. considered four hypothetical plateau currents: 1) voltage-activated, non-inactivating Na+ currents; 2) voltage-dependent, nonselective currents; 3) Ca2+-dependent, nonselective currents; and 4) voltage-dependent Ca2+ currents (18). Among the four hypothetical plateau currents examined in their mathematical model, the voltage-dependent Na+ currents and voltage-dependent, nonselective currents reproduced more plateau-like waveforms than the other two types of current in their simulations. Voltage-dependent, non-inactivating Na+ currents are frequently mentioned in cardiac myocytes, and they can be important in pathologic situations (46, 47). However, there is no evidence that ICC express such long-lasting Na+ currents. Voltage-dependent nonselective currents have also not been identified in ICC of the murine small intestine. TRPM7 was suggested as one of the nonselective cationic channels, but it is not voltage-dependent (48, 49). Hyperpolarization-activated cyclic nucleotide channels have been suggested as pacemaker channels in colonic ICC (50, 51), but they are inactivated rather than activated in the range of the plateau potential. In cardiac myocytes, the NCX has the ability of reversing the direction of ion exchange. During diastole, NCX usually operates in the forward mode, pumping Ca2+ out of the cell in exchange for Na+ influx. This has a depolarizing effect on the membrane potential because the net current is inward. In cardiac muscle, the rapid upstroke phase of action potential is caused by Na+ influx through voltage-gated Na+ channels, and this can reverse the direction of NCX, pumping Na+ out and Ca2+ into the cell. However, the slower rise in intracellular [Ca2+] by L-type Ca2+ currents and ER Ca2+ release shifts NCX to forward mode, resulting in prolongation of action potential. NCX in forward mode indeed contributes to the plateau in our simulation, but only to a negligible degree. 50% reduction of NCX density reduced the length of the plateau (as measured by time the membrane is depolarized as high as at least 90% of maximal depolarization) from 520.86 to 519.75 ms (see Table 2). Reverse-mode NCX could have an indirect effect on plateau current. Ca2+ entry into microdomains via reverse-mode NCX could possibly evoke Ca2+-induced Ca2+ release that would activate a Ca2+-dependent inward current such as Ano1. Although Lees-Green et al. excluded the possibility that Ano1 channels contribute to the plateau, the Ca2+-activated Cl− current carried by Ano1 (IClCa) is a strong candidate for plateau currents considering their biophysical properties, such as Ca2+ dependency and kinetics (52). Indeed, the IClCa was the predominant current contributing to the length of the plateau in our simulations (see Table 2): 50% reduction in Ano1 density reduced the duration of plateau from 520.86 to 429.18 ms. For comparison, 50% reduction in T-type Ca2+ channel density minimally affected the duration of the plateau (i.e., from 520.86 to 520.11). Therefore, Ano1 may have two roles in slow waves: 1) it may be a key conductance in generating STICs and initiation of slow waves, and 2) it may be an important conductance in the formation and duration of the plateau phase of slow waves.
Table 2.
Contribution of INaCa, IClCa, and ICaT to Characteristics of Pacemaker Potential
| Condition | Maximal Diastolic Potential (mV) | Peak Potential (mV) | Length of Plateau (ms) |
|---|---|---|---|
| Control | −73.58 | −14.20 | 520.86 |
| 50% INaCa | −73.53 | −14.21 | 519.75 |
| 50% IClCa | −73.99 | −15.55 | 429.17 |
| 50% ICaT | −73.73 | −14.37 | 520.10 |
The question of how activation of Ano1 channels is sustained for up to several seconds during the plateau phase of slow waves in some GI muscles remains unanswered (1). However, recent studies have shown that Ca2+ release events persist for approximately the duration of slow waves in small intestinal ICC-MY (10). Ca2+ release, initiated by Ca2+ entry through T-Type Ca2+ channels, is organized into clusters of asynchronous events that occur at multiple discrete sites in ICC-MY. Summation of the clustered Ca2+ transients approximates the duration of the plateau phase in small intestinal muscles. Sustained, asynchronous Ca2+ transients appear to explain the sustained activation of Ano1 channels through the time course of the plateau. As discussed previously, asynchronous Ca2+ release events could result from localized Ca2+-induced Ca2+ release that might be stimulated by a Ca2+ influx mechanism, such as reverse-mode NCX or window current provided by a voltage-dependent Ca2+ conductance.
Conclusions
The model of ICC reproduces spontaneous transient depolarizations and inward currents that represent the activity of Ano1, biophysical properties of NKCC1 and Ano1, and pharmacologic actions of drugs on NKCC1 and Ano1. The modeling approach suggests that ER Ca2+ oscillations drives pacemaker activity. It also suggests that NKCC1 does not contribute primarily to the plateau phase in a beat-to-beat manner, but it provides a steady-state of cytosolic Cl− and maintains the driving force for Ano1 currents. NKCC1 can elongate the plateau phase by activation of reverse-mode NCX. The effect of SOCE on pacemaker depolarization is primarily mediated by Ca2+ entry rather than by a direct depolarizing effect.
Author Contributions
J.B.Y. conceived of the idea, wrote the model, wrote the manuscript, and revised. H.Z. collected data used in the model. S.D.K. and K.M.S. conceived of the idea, wrote the manuscript, and revised the final manuscript. All authors approved of the final submission.
Acknowledgments
This project was supported by a Program Project Grant: P01-DK41315-30 and R01- DK120759 from the National Institute of Diabetes and Digestive and Kidney Diseases (NIDDK). This work was also supported by the Inje Research and Scholarship Foundation in 2009 and by the EDISON Program through the National Research Foundation of Korea funded by the Ministry of Science and Information and Communications Technology (NRF-2016M3C1A6936606).
Editor: Meyer Jackson.
Footnotes
Supporting Material can be found online at https://doi.org/10.1016/j.bpj.2019.07.020.
Supporting Material
References
- 1.Sanders K.M., Ward S.M., Koh S.D. Interstitial cells: regulators of smooth muscle function. Physiol. Rev. 2014;94:859–907. doi: 10.1152/physrev.00037.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Rumessen J.J., Thuneberg L. Interstitial cells of Cajal in human small intestine. Ultrastructural identification and organization between the main smooth muscle layers. Gastroenterology. 1991;100:1417–1431. [PubMed] [Google Scholar]
- 3.Faussone Pellegrini M.S., Cortesini C., Romagnoli P. [Ultrastructure of the tunica muscularis of the cardial portion of the human esophagus and stomach, with special reference to the so-called Cajal’s interstitial cells] Arch. Ital. Anat. Embriol. 1977;82:157–177. [PubMed] [Google Scholar]
- 4.Daniel E.E., Wang Y.F., Cayabyab F.S. Role of gap junctions in structural arrangements of interstitial cells of Cajal and canine ileal smooth muscle. Am. J. Physiol. 1998;274:G1125–G1141. doi: 10.1152/ajpgi.1998.274.6.G1125. [DOI] [PubMed] [Google Scholar]
- 5.Horiguchi K., Komuro T. Ultrastructural characterization of interstitial cells of Cajal in the rat small intestine using control and Ws/Ws mutant rats. Cell Tissue Res. 1998;293:277–284. doi: 10.1007/s004410051119. [DOI] [PubMed] [Google Scholar]
- 6.Horiguchi K., Sanders K.M., Ward S.M. Enteric motor neurons form synaptic-like junctions with interstitial cells of Cajal in the canine gastric antrum. Cell Tissue Res. 2003;311:299–313. doi: 10.1007/s00441-002-0657-1. [DOI] [PubMed] [Google Scholar]
- 7.Iino S., Horiguchi K., Nojyo Y. c-Kit-negative fibroblast-like cells express platelet-derived growth factor receptor alpha in the murine gastrointestinal musculature. Histochem. Cell Biol. 2009;131:691–702. doi: 10.1007/s00418-009-0580-6. [DOI] [PubMed] [Google Scholar]
- 8.Kurahashi M., Zheng H., Sanders K.M. A functional role for the ‘fibroblast-like cells’ in gastrointestinal smooth muscles. J. Physiol. 2011;589:697–710. doi: 10.1113/jphysiol.2010.201129. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Zhu M.H., Sung T.S., Sanders K.M. Intracellular Ca(2+) release from endoplasmic reticulum regulates slow wave currents and pacemaker activity of interstitial cells of Cajal. Am. J. Physiol. Cell Physiol. 2015;308:C608–C620. doi: 10.1152/ajpcell.00360.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Drumm B.T., Hennig G.W., Baker S.A. Clustering of Ca2+ transients in interstitial cells of Cajal defines slow wave duration. J. Gen. Physiol. 2017;149:703–725. doi: 10.1085/jgp.201711771. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Huang F., Rock J.R., Jan L.Y. Studies on expression and function of the TMEM16A calcium-activated chloride channel. Proc. Natl. Acad. Sci. USA. 2009;106:21413–21418. doi: 10.1073/pnas.0911935106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Gomez-Pinilla P.J., Gibbons S.J., Farrugia G. Ano1 is a selective marker of interstitial cells of Cajal in the human and mouse gastrointestinal tract. Am. J. Physiol. Gastrointest. Liver Physiol. 2009;296:G1370–G1381. doi: 10.1152/ajpgi.00074.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Hwang S.J., Blair P.J., Ward S.M. Expression of anoctamin 1/TMEM16A by interstitial cells of Cajal is fundamental for slow wave activity in gastrointestinal muscles. J. Physiol. 2009;587:4887–4904. doi: 10.1113/jphysiol.2009.176198. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Rock J.R., Futtner C.R., Harfe B.D. The transmembrane protein TMEM16A is required for normal development of the murine trachea. Dev. Biol. 2008;321:141–149. doi: 10.1016/j.ydbio.2008.06.009. [DOI] [PubMed] [Google Scholar]
- 15.Sanders K.M., Zhu M.H., Ward S.M. Anoctamins and gastrointestinal smooth muscle excitability. Exp. Physiol. 2012;97:200–206. doi: 10.1113/expphysiol.2011.058248. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Malysz J., Gibbons S.J., Farrugia G. Conditional genetic deletion of Ano1 in interstitial cells of Cajal impairs Ca2+ transients and slow waves in adult mouse small intestine. Am. J. Physiol. Gastrointest. Liver Physiol. 2017;312:G228–G245. doi: 10.1152/ajpgi.00363.2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Zhu Y., Parsons S.P., Huizinga J.D. Measurement of intracellular chloride ion concentration in ICC in situ and in explant culture. Neurogastroenterol. Motil. 2010;22:704–709. doi: 10.1111/j.1365-2982.2010.01501.x. [DOI] [PubMed] [Google Scholar]
- 18.Lees-Green R., Gibbons S.J., Cheng L.K. Computational modeling of anoctamin 1 calcium-activated chloride channels as pacemaker channels in interstitial cells of Cajal. Am. J. Physiol. Gastrointest. Liver Physiol. 2014;306:G711–G727. doi: 10.1152/ajpgi.00449.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Zhu M.H., Sung T.S., Sanders K.M. Na+-K+-Cl- cotransporter (NKCC) maintains the chloride gradient to sustain pacemaker activity in interstitial cells of Cajal. Am. J. Physiol. Gastrointest. Liver Physiol. 2016;311:G1037–G1046. doi: 10.1152/ajpgi.00277.2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Youm J.B., Leem C.H., Han J. Modeling of stochastic behavior of pacemaker potential in interstitial cells of Cajal. Prog. Biophys. Mol. Biol. 2014;116:56–69. doi: 10.1016/j.pbiomolbio.2014.09.002. [DOI] [PubMed] [Google Scholar]
- 21.Markadieu N., Delpire E. Physiology and pathophysiology of SLC12A1/2 transporters. Pflugers Arch. 2014;466:91–105. doi: 10.1007/s00424-013-1370-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Lytle C., McManus T.J., Haas M. A model of Na-K-2Cl cotransport based on ordered ion binding and glide symmetry. Am. J. Physiol. 1998;274:C299–C309. doi: 10.1152/ajpcell.1998.274.2.C299. [DOI] [PubMed] [Google Scholar]
- 23.Benjamin B.A., Johnson E.A. A quantitative description of the Na-K-2Cl cotransporter and its conformity to experimental data. Am. J. Physiol. 1997;273:F473–F482. doi: 10.1152/ajprenal.1997.273.3.F473. [DOI] [PubMed] [Google Scholar]
- 24.Kuzumoto M., Takeuchi A., Matsuoka S. Simulation analysis of intracellular Na+ and Cl- homeostasis during beta 1-adrenergic stimulation of cardiac myocyte. Prog. Biophys. Mol. Biol. 2008;96:171–186. doi: 10.1016/j.pbiomolbio.2007.07.005. [DOI] [PubMed] [Google Scholar]
- 25.Ferrera L., Caputo A., Galietta L.J. Regulation of TMEM16A chloride channel properties by alternative splicing. J. Biol. Chem. 2009;284:33360–33368. doi: 10.1074/jbc.M109.046607. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Sung T.S., O’Driscoll K., Sanders K.M. Influence of intracellular Ca2+ and alternative splicing on the pharmacological profile of ANO1 channels. Am. J. Physiol. Cell Physiol. 2016;311:C437–C451. doi: 10.1152/ajpcell.00070.2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Smith G.D. Analytical steady-state solution to the rapid buffering approximation near an open Ca2+ channel. Biophys. J. 1996;71:3064–3072. doi: 10.1016/S0006-3495(96)79500-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Goto K., Matsuoka S., Noma A. Two types of spontaneous depolarizations in the interstitial cells freshly prepared from the murine small intestine. J. Physiol. 2004;559:411–422. doi: 10.1113/jphysiol.2004.063875. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Zhu M.H., Sung I.K., Sanders K.M. Muscarinic activation of Ca2+-activated Cl- current in interstitial cells of Cajal. J. Physiol. 2011;589:4565–4582. doi: 10.1113/jphysiol.2011.211094. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Park C.G., Wu M.J., Choi S. Regulation of intracellular calcium by endoplasmic reticulum proteins in small intestinal interstitial cells of cajal. J. Neurogastroenterol. Motil. 2018;24:128–137. doi: 10.5056/jnm16212. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Zheng H., Drumm B.T., Sanders K.M. SOCE mediated by STIM and Orai is essential for pacemaker activity in the interstitial cells of Cajal in the gastrointestinal tract. Sci. Signal. 2018;11:eaaq0918. doi: 10.1126/scisignal.aaq0918. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Jiang N., Zhang Z.M., Zhang Z.C. Effects of Ca2+ channel blockers on store-operated Ca2+ channel currents of Kupffer cells after hepatic ischemia/reperfusion injury in rats. World J. Gastroenterol. 2006;12:4694–4698. doi: 10.3748/wjg.v12.i29.4694. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Lo K.J., Luk H.N., Chueh S.H. Store depletion-induced calcium influx in rat cerebellar astrocytes. Br. J. Pharmacol. 2002;135:1383–1392. doi: 10.1038/sj.bjp.0704594. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Yoshida M., Ishikawa M., Morisawa M. Store-operated calcium channel regulates the chemotactic behavior of ascidian sperm. Proc. Natl. Acad. Sci. USA. 2003;100:149–154. doi: 10.1073/pnas.0135565100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Derler I., Schindl R., Romanin C. The action of selective CRAC channel blockers is affected by the Orai pore geometry. Cell Calcium. 2013;53:139–151. doi: 10.1016/j.ceca.2012.11.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Kito Y., Ward S.M., Sanders K.M. Pacemaker potentials generated by interstitial cells of Cajal in the murine intestine. Am. J. Physiol. Cell Physiol. 2005;288:C710–C720. doi: 10.1152/ajpcell.00361.2004. [DOI] [PubMed] [Google Scholar]
- 37.Wouters M., De Laet A., Vanderwinden J.M. Subtractive hybridization unravels a role for the ion cotransporter NKCC1 in the murine intestinal pacemaker. Am. J. Physiol. Gastrointest. Liver Physiol. 2006;290:G1219–G1227. doi: 10.1152/ajpgi.00032.2005. [DOI] [PubMed] [Google Scholar]
- 38.Faville R.A., Pullan A.J., Smith N.P. Biophysically based mathematical modeling of interstitial cells of Cajal slow wave activity generated from a discrete unitary potential basis. Biophys. J. 2009;96:4834–4852. doi: 10.1016/j.bpj.2009.03.058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Dixon R.E., Britton F.C., Ward S.M. Electrical slow waves in the mouse oviduct are dependent on extracellular and intracellular calcium sources. Am. J. Physiol. Cell Physiol. 2011;301:C1458–C1469. doi: 10.1152/ajpcell.00293.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Alswied A., Parekh A.B. Ca2+ influx through store-operated calcium channels replenishes the functional phosphatidylinositol 4,5-bisphosphate pool used by cysteinyl leukotriene type I receptors. J. Biol. Chem. 2015;290:29555–29566. doi: 10.1074/jbc.M115.678292. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Putney J.W. The physiological function of store-operated calcium entry. Neurochem. Res. 2011;36:1157–1165. doi: 10.1007/s11064-010-0383-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Trebak M., Zhang W., Zhang X. What role for store-operated Ca2+ entry in muscle? Microcirculation. 2013;20:330–336. doi: 10.1111/micc.12042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.McNally B.A., Somasundaram A., Prakriya M. Gated regulation of CRAC channel ion selectivity by STIM1. Nature. 2012;482:241–245. doi: 10.1038/nature10752. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Vig M., Peinelt C., Kinet J.P. CRACM1 is a plasma membrane protein essential for store-operated Ca2+ entry. Science. 2006;312:1220–1223. doi: 10.1126/science.1127883. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Stiber J.A., Rosenberg P.B. The role of store-operated calcium influx in skeletal muscle signaling. Cell Calcium. 2011;49:341–349. doi: 10.1016/j.ceca.2010.11.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Dumaine R., Wang Q., Kirsch G.E. Multiple mechanisms of Na+ channel--linked long-QT syndrome. Circ. Res. 1996;78:916–924. doi: 10.1161/01.res.78.5.916. [DOI] [PubMed] [Google Scholar]
- 47.Sicouri S., Antzelevitch D., Antzelevitch C. Effects of sodium channel block with mexiletine to reverse action potential prolongation in in vitro models of the long term QT syndrome. J. Cardiovasc. Electrophysiol. 1997;8:1280–1290. doi: 10.1111/j.1540-8167.1997.tb01019.x. [DOI] [PubMed] [Google Scholar]
- 48.Kim B.J., Lim H.H., Kim K.W. Melastatin-type transient receptor potential channel 7 is required for intestinal pacemaking activity. Gastroenterology. 2005;129:1504–1517. doi: 10.1053/j.gastro.2005.08.016. [DOI] [PubMed] [Google Scholar]
- 49.Kim B.J., Park K.J., Kim S.J. Identification of TRPM7 channels in human intestinal interstitial cells of Cajal. World J. Gastroenterol. 2009;15:5799–5804. doi: 10.3748/wjg.15.5799. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Shahi P.K., Choi S., Jun J.Y. The possible roles of hyperpolarization-activated cyclic nucleotide channels in regulating pacemaker activity in colonic interstitial cells of Cajal. J. Gastroenterol. 2014;49:1001–1010. doi: 10.1007/s00535-013-0849-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Shin D.H., Kim M.W., Jun J.Y. Regulation of the pacemaker activity of colonic interstitial cells of cajal by protease-activated receptors: involvement of hyperpolarization-activated cyclic nucleotide channels. Pharmacology. 2016;98:171–182. doi: 10.1159/000446990. [DOI] [PubMed] [Google Scholar]
- 52.Zhu M.H., Kim T.W., Sanders K.M. A Ca(2+)-activated Cl(-) conductance in interstitial cells of Cajal linked to slow wave currents and pacemaker activity. J. Physiol. 2009;587:4905–4918. doi: 10.1113/jphysiol.2009.176206. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.