Centering in Multiple Regression Does Not Always Reduce Multicollinearity: How to Tell When Your Estimates Will Not Benefit From Centering

Abstract

Within the context of moderated multiple regression, mean centering is recommended both to simplify the interpretation of the coefficients and to reduce the problem of multicollinearity. For almost 30 years, theoreticians and applied researchers have advocated for centering as an effective way to reduce the correlation between variables and thus produce more stable estimates of regression coefficients. By reviewing the theory on which this recommendation is based, this article presents three new findings. First, that the original assumption of expectation-independence among predictors on which this recommendation is based can be expanded to encompass many other joint distributions. Second, that for many jointly distributed random variables, even some that enjoy considerable symmetry, the correlation between the centered main effects and their respective interaction can increase when compared with the correlation of the uncentered effects. Third, that the higher order moments of the joint distribution play as much of a role as lower order moments such that the symmetry of lower dimensional marginals is a necessary but not sufficient condition for a decrease in correlation between centered main effects and their interaction. Theoretical and simulation results are presented to help conceptualize the issues.

Introduction

Within the social, behavioral, and health sciences, the product-interaction term in a multiple linear regression context is perhaps the most prevalent and popular approach researchers are familiar with when attempting to account for nonlinear influences in their statistical models (Baron & Kenny, 1986; Dawson, 2014; Wu & Zumbo, 2008). Although its origins can be traced to the early 20th century in Court (1930), the use of product-interactions was popularized by Cohen (1968) when advocating for the use of multiple regression as a “general” data-analytic strategy and took its final form in the seminal work of Aiken and West (1991) on simple slope analysis. The term moderation became synonymous with multiplicative interaction and, today, it is an essential tool in the methodologist’s repertoire and a staple of any introductory course to linear regression and the general linear model (Chaplin, 1991; Irwin & McClelland, 2001).

Using Aiken and West’s (1991) notation, the classical product-interaction approach in linear regression follows a model of the form:

$$Y={\beta }_0+{\beta }_{1}X+{\beta }_{2}Z+{\beta }_{3}XZ+ϵ$$ (1)

for continuous, nondegenerate random variables $Y$, $X$, and $Z$ and where all the assumptions of ordinary least square linear regression are satisfied, as described in Cohen, Cohen, West, and Aiken (2002). A recommended preliminary step before running model (1) is to subtract the mean from $X$ and $Z$ so that the predictors in the equation are

$$Y={\beta }_0+{\beta }_1(X-E(X))+{\beta }_2(Z-E(Z))+{\beta }_3(X-E(X))(Z-E(Z))+ϵ$$

This process is known as “centering” and is usually advocated both on conceptual and statistical grounds. The conceptual reasoning is mostly due to the interpretation of the coefficients in the presence of the multiplicative interaction term, and a thorough discussion of this issue can be found in Bedeian and Mossholder (1994), Iacobucci, Schneider, Popovich, and Bakamitsos (2016), and Kraemer and Blasey (2004). The statistical reasoning, however, is the main focus of this article, which we expect to clarify by revisiting some old assumptions made by Aiken and West (1991).

The main statistical concern behind centering in regression models is the issue of multicollinearity. Product-interaction terms are generally highly correlated with their main effects and subtracting the mean of the predictors has been recommended to alleviate the issue (Cohen et al., 2002). Indeed, Cohen et al. (2002, p. 264) advise,

• If $X$ and $Z$ are each completely symmetrical as, in our numerical example, then the covariance between $X$ and $\mathrm{XZ}$ is

  $$\mathrm{Cov}(X,\mathrm{XZ})=\mathrm{Var}(X)E(Z)+\mathrm{Cov}(X,Z)E(X)$$

• If $X$ and $Z$ are centered then $E\left(X\right)$ and $E\left(Z\right)$ are both zero and the covariance between $X$ and $\mathrm{XZ}$ is zero as well. The same holds for the covariance between $Z$ and $\mathrm{XZ}$. The amount of correlation that is produced between $X$ and $\mathrm{XZ}$ by the nonzero means of $X$ and $Z$ is referred to as nonessential multicollinearity. This nonessential multicollinearity is due purely to scaling when variables are centered, it disappears. The amount of correlation between $X$ and $\mathrm{XZ}$ that is due to skew in $X$ cannot be removed by centering. This source of correlation between $X$ and $\mathrm{XZ}$ is termed essential multicollinearity.

We will see, however, that there are three mistakes with this typical advice. First, we provide an explicit example when $X$ and $Z$ are both completely symmetrical, yet the covariance identity given by Cohen et al. (2002) does not hold (see Figure 3 and accompanying text). Second, what Cohen et al. (2002) refer to as “nonessential multicollinearity” does not automatically disappear when variables are centered. And third, the implication that centering always reduces multicollinearity (by reducing or removing “nonessential multicollinearity”) is incorrect; in fact, in many cases, centering will greatly increase the multicollinearity problem.

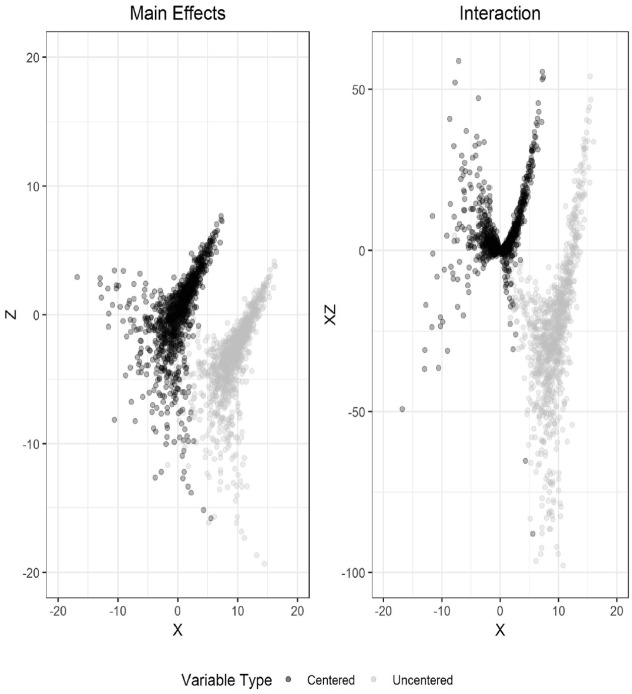
Figure 3.

Centered and uncentered X and Z from a Joe copula distribution.

The covariance between the product term and any of its constituent terms was derived by Bohrnstedt and Goldberger (1969) and reproduced in Aiken and West (1991) as

$$\mathrm{Cov}(\mathrm{XZ},X)=E(X_c^2{Z}_c)+\mathrm{Var}(X)E(Z)+\mathrm{Cov}(X,Z)E(X)$$

where $X_c=X-E(X)$ and $Z_c=Z-E(Z)$. If the predictors in multiple regression are centered, then $E(X_c)=E(Z_c)=0$ and the covariance between the main effects and their interaction is exclusively a function of $E(X_c^2{Z}_c)$, a central third-order moment of the joint distribution. Aiken and West (1991), Osborne and Waters (2002), Tabachnick and Fidell (2007), and others further assume that the variables in the model are jointly normally distributed so that $E(X^{2}Z)$ is in fact equal to 0. Note that this fact takes advantage of special properties of a bivariate normal distribution; it has nothing to do with the idea that odd moments of even functions are always zero. Indeed, such a statement only makes sense in a purely univariate setting as the concept of distributional symmetry is not uniquely defined in higher dimensions. We will explore this subtlety in greater detail in the section “Symmetry and Expectation-Independence.”

Within the social sciences, most of what is known with regard to the properties of the covariance of the interaction term and its main effects comes indirectly from reinterpretations of the work of Bohrnstedt and Goldberger (1969). As such, understanding the assumptions made in the original source and how they were translated into data analytic practice are crucialto better characterize the instances where they hold, where they are suspect, and how the overall process of analyzing multiplicative interactions would change if different assumptions were set in place. The main purpose of this article is, therefore, to highlight the original framework of Bohrnstedt and Goldberger (1969), with particular emphasis on the assumption they label “expectation-independence.” By adjusting this assumption, we present a class of bivariate random variables that exhibit a rotational form of expectation-independence to expand the class of described bivariate distributions where centering decreases the covariance between the product terms and their interaction. Moreover, we identify some prototypical cases where the opposite holds; that is, where centering increases (rather than decreases) the covariance between the product terms and their interaction. We derive a set of general conditions for this increase in covariance to take place. We will define a type of symmetry relevant to bivariate distributions and connect it to the concept of expectation-independence to show that this symmetry implies expectation-independence in the sense of Bohrnstedt and Goldberger (1969), so that the vanishing correlation between main effects and their multiplicative interaction is a consequence of it. We also present a graphical representation of these conditions and discuss their impact on the analysis of three-way interaction terms.

Results

Centered Versus Uncentered Covariance Products

Consider the jointly distributed, nondegenerate, continuous random variables $(X,Z)$ with $Z$ expectation-independent of $X$; that is, $\mathbb{E}(Z|X)=\mathbb{E}(Z)$. This condition states that the average value of $Z$ does not depend on the value of $X$. Geometrically then, the joint distribution of $X$ and $Z$ should enjoy reflectional symmetry about the $X$ axis. Bohrnstedt and Goldberger (1969) show that $Z$ expectation-independent of $X$ yields $\mathbb{E}[(X-\mathbb{E}(X){)}^2(Z-\mathbb{E}(Z))]=0$, which implies that

$$\mathbb{E}(X^{2}Z)=2\mathbb{E}(\mathrm{XZ})-\mathbb{E}(X{)}^2\mathbb{E}(Z)+\mathbb{E}(X^2)\mathbb{E}(Z)$$ (2)

Using the definition of the covariance between random variables and substituting the expression derived in (1), the Aiken and West (1991) identity A.14 can be obtained as

$$\begin{array}{c}\multicolumn{1}{c}{\mathrm{Cov}(X,\mathrm{XZ})=\mathbb{E}(X^{2}Z)-\mathbb{E}(\mathrm{XZ})\mathbb{E}(X)}\\ \multicolumn{1}{c}{=\mathbb{E}(\mathrm{XZ})\mathbb{E}(X)-2\mathbb{E}{(X)}^2\mathbb{E}(Z)+\mathbb{E}(X^2)\mathbb{E}(Z)}\\ \multicolumn{1}{c}{=\mathbb{E}(X)\mathrm{Cov}(X,Z)+\mathbb{E}(Z)\mathrm{Var}(X)}\end{array}$$

As before, set $X_c=X-\mathbb{E}(X)$ and $Z_c=Z-\mathbb{E}(Z)$. It then follows from the previous definitions that $\mathrm{Cov}(X_c,X_c{Z}_c)=\mathbb{E}(X_c^2{Z}_c)$ and, by expectation independence, if $\mathbb{E}(Z|X)=\mathbb{E}(Z)$ then $\mathbb{E}(Z_c|X)=\mathbb{E}(Z_c)=0$, in which case $\mathbb{E}(X_c^2{Z}_c)=\mathrm{Cov}(X_c,X_c{Z}_c)=0$ and

$$|\mathrm{Cov}(X_c,X_c{Z}_c)|\le |\mathrm{Cov}(X,\mathrm{XZ})|$$ (3)

which is the standard result presented in introductory textbooks in regression analysis. Note that we could derive the analogous result

$$|\mathrm{Cov}(Z_c,Z_c{X}_c)|\le |\mathrm{Cov}(Z,\mathrm{ZX})|$$

by simply assuming that $X$ is expectation-independent of $Z$.

If no kind of expectation-independence is assumed, however, the following expression can be derived for $\mathrm{Cov}(X_c,X_c{Z}_c)$. The proof of this identity can be found in the appendix:

$$\mathrm{Cov}(X_c,X_c{Z}_c)=\mathrm{Cov}(X,\mathrm{XZ})-\mathbb{E}(Z)\mathrm{Var}(X)-\mathbb{E}(X)\mathrm{Cov}(X,Z)$$ (4)

From this identity, one can obtain four different conditions under which the covariance of the centered terms is larger than the covariance of the uncentered terms. $|\mathrm{Cov}(X,\mathrm{XZ})|\le |\mathrm{Cov}(X_c,X_c{Z}_c)|$ if:

$$\begin{array}{c}\multicolumn{1}{c}{0\le \mathrm{Cov}(X,\mathrm{XZ})\le \mathrm{Cov}(X_c,X_c{Z}_c)\iff }\\ \multicolumn{1}{c}{\mathbb{E}(Z)\mathrm{Var}(X)\le -\mathbb{E}(X)\mathrm{Cov}(X,Z)}\end{array}$$ (5)

$$\begin{array}{c}0\le \mathrm{Cov}(X,\mathrm{XZ})\le -\mathrm{Cov}(X_c,X_c{Z}_c)\iff \hfill \\ \multicolumn{1}{c}{-\mathbb{E}(Z)\mathrm{Var}(X)\le -2\mathrm{Cov}(X,\mathrm{XZ})+\mathbb{E}(X)\mathrm{Cov}(X,Z)}\end{array}$$ (6)

$$\begin{array}{c}0\le -\mathrm{Cov}(X,\mathrm{XZ})\le -\mathrm{Cov}(X_c,X_c{Z}_c)\iff \hfill \\ \multicolumn{1}{c}{-\mathbb{E}(Z)\mathrm{Var}(X)\le \mathbb{E}(X)\mathrm{Cov}(X,Z)}\end{array}$$ (7)

$$\begin{array}{c}0\le -\mathrm{Cov}(X,\mathrm{XZ})\le \mathrm{Cov}(X_c,X_c{Z}_c)\iff \hfill \\ \multicolumn{1}{c}{\mathbb{E}(Z)\mathrm{Var}(X)\le 2\mathrm{Cov}(X,\mathrm{XZ})-\mathbb{E}(X)\mathrm{Cov}(X,Z)}\end{array}$$ (8)

Note that there are really only two distinct conditions here, as replacing $X$ by $-X$ and $Z$ by $-Z$ will transform Conditions (5) and (6) into Conditions (7) and (8), respectively.

To apply these conditions in practice, one must first estimate $\mathrm{Cov}(X,\mathrm{XZ})$. If we have $\mathrm{Cov}(X,\mathrm{XZ})>0$, and if exactly one of Conditions (5) or (6) hold, then centering will not reduce the correlation between $X$ and $\mathrm{XZ}$. On the other hand, if both or none of Conditions (5) and (6) hold, while $\mathrm{Cov}(X,\mathrm{XZ})>0$, then centering must reduce the correlation between $X$ and $\mathrm{XZ}$. If $\mathrm{Cov}(X,\mathrm{XZ})<0$, then simply replacing $X$ by $-X$ and $Z$ by $-Z$, one can apply the same diagnostics to determine if centering will reduce correlation.

Symmetry and Expectation-Independence

We have already remarked that the concept of a symmetric distribution is not uniquely defined in a multivariate setting. In a single variable, we often use a density function’s evenness to facilitate analytical arguments; that is, the property $f_X(x)=f_X(-x)$ enjoyed by the normal distribution, for example. In a bivariate setting, one natural generalization of this property is to suppose that the joint density function of $X$ and $Z$ satisfies the following two conditions:

$$f_{X,Z}(x,z)=f_{X,Z}(-x,z)=f_{X,Z}(x,-z).$$ (9)

Notice that these two conditions imply the final component-wise symmetry condition $f_{X,Z}(x,z)=f_{X,Z}(-x,-z)$ and that these conditions taken together force the density function to be symmetric in each quadrant of the plane, with respect to the origin.

From this definition of an “even” bivariate density function, we have the following result:

• Proposition 1: Suppose $X$ and $Z$ are jointly distributed such that their joint density function is symmetric in the sense of condition (9). Then $X$ is expectation-independent of $Z$ and $Z$ is expectation-independent of $X$.

• Proof. We first show that $\mathbb{E}(X|Z)=\mathbb{E}(Z|X)=0$, proceeding as follows:

$$\begin{array}{c}\mathbb{E}(X|Z)={\int }_{\mathbb{R}}x{f}_{X|Z}(x|z)\mathrm{dx}\hfill \\ \multicolumn{1}{c}{={\int }_{\mathbb{R}}x\frac{f_{X,Z}(x,z)}{f_Z(z)}\mathrm{dx}}\\ \multicolumn{1}{c}{=\frac{1}{f_Z(z)}({\int }_{-\infty }^{0}x{f}_{X,Z}(x,z)\mathrm{dx}+{\int }_0^{\infty }x{f}_{X,Z}(x,z)\mathrm{dx})}\\ \multicolumn{1}{c}{=\frac{1}{f_Z(z)}({\int }_{\infty }^{0}x{f}_{X,Z}(-x,z)\mathrm{dx}+{\int }_0^{\infty }x{f}_{X,Z}(x,z)\mathrm{dx})}\\ \multicolumn{1}{c}{=\frac{1}{f_Z(z)}(-{\int }_0^{\infty }x{f}_{X,Z}(x,z)\mathrm{dx}+{\int }_0^{\infty }x{f}_{X,Z}(x,z)\mathrm{dx})=0,}\end{array}$$

where the final step follows from the definition of “even” presented before. The same argument shows that $\mathbb{E}(Z|X)=0$. Now applying double expectaction (Casella & Berger, 2002), we find $\mathbb{E}(X)=\mathbb{E}(Z)=0$. □

Because expectation-independence guarantees that centering will reduce the covariance between the interaction and first-order terms in regression model (1), Proposition 1 shows that symmetric joint distributions in the sense of (9) also satisfy the covariance condition in (3). It turns out that we can characterize another class of bivariate distributions where (3) holds that are neither symmetric in the sense of (9) nor expectation-independent in terms of the original variables $X$ and $Z$. For this class of distributions, we can find a new system of coordinates $(\tilde{X},\tilde{Z})$ where the kind of symmetry given by (9), and thus expectation-independence, holds with respect to these transformed coordinates. As a special case, this class includes all bivariate normal random variables.

• Proposition 2: Suppose that there exists an invertible linear transformation of the plane $A$ such that for $(\tilde{X},\tilde{Z}{)}^T:=A·(X_c,Z_c{)}^T$ the following conditions hold: (i) $\tilde{X}$ is expectation-independent of $\tilde{Z}$, (ii) $\tilde{Z}$ is expectation-independent of $\tilde{X}$, (iii) $\mathbb{E}({\tilde{X}}^3)=\mathbb{E}({\tilde{Z}}^3)=0$. Then, $\mathbb{E}(X_c^2{Z}_c)=\mathbb{E}(Z_c^2{X}_c)=0$ and thus the covariance condition (3) must hold for $X$ and $\mathrm{XZ}$ and for $Z$ and $\mathrm{XZ}$.

To prove Proposition 2, we will need the following technical lemma.

• Lemma 1: If $\mathbb{E}(X_1)=\mathbb{E}(X_2)=0$, and if $({\tilde{X}}_1,{\tilde{X}}_2{)}^T:=A·(X_1,X_2{)}^T$ for some rotation of the plane $A$, then $\mathbb{E}({\tilde{X}}_1)=\mathbb{E}({\tilde{X}}_2)=0$.

• Proof. Let ${\pi }_j$ denote the $j$th coordinate projection operator; that is, ${\pi }_j:{\mathbb{R}}^2\to \mathbb{R}$ via ${\pi }_j(\mathbf{x})=x_j$. Then,

$$\mathbb{E}({\tilde{X}}_1)=\mathbb{E}({\pi }_1(A·(X_1,X_2{)}^T)).$$

Now, $A$ is a $2\times 2$ matrix of real numbers, so ${\pi }_1(A·(X_1,X_2{)}^T)$ is a linear combination of $X_1$ and $X_2$. Consequently, we may write,

$$\mathbb{E}({\tilde{X}}_1)=\mathbb{E}(c_1{X}_1+c_2{X}_2),$$

for some real numbers $c_1$ and $c_2$. But since $\mathbb{E}(X_1)=\mathbb{E}(X_2)=0$, we must have that $\mathbb{E}({\tilde{X}}_1)=0$. A similar argument shows that $\mathbb{E}({\tilde{X}}_2)=0$ as well. □

• Proof of Proposition 2: We imitate the method in the proof of Lemma 1 and write,

$$\mathbb{E}(X^{2}Z)=\mathbb{E}[{({\pi }_1(A^{-1}·{(\tilde{X},\tilde{Z})}^T))}^2({\pi }_2(A^{-1}·{(\tilde{X},\tilde{Z})}^T))].$$

Recall that $A^{-1}$ exists as a $2\times 2$ matrix of real numbers since $A$ is assumed to be invertible. Now, ${\pi }_2(A^{-1}·(\tilde{X},\tilde{Z}{)}^T)$ is a linear combination of $X$ and $Z$; thus, we may write,

$$\mathbb{E}(X^{2}Z)=\mathbb{E}[{(c_1\tilde{X}+c_2\tilde{Z})}^2(c_3\tilde{X}+c_4\tilde{Z})],$$

for some real numbers $c_j$, $1\le j\le 4$. Expanding the product and distributing the expectation yields,

$$\mathbb{E}(X^{2}Z)=\mathbb{E}(d_1{\tilde{X}}^3)+\mathbb{E}(d_2{\tilde{X}}^2\tilde{Z})+\mathbb{E}(d_3\tilde{X}{\tilde{Z}}^2)+\mathbb{E}(d_4{\tilde{Z}}^3),$$

for some other real numbers $d_j$, $1\le j\le 4$. By conditions (i) and (ii) of our Proposition, the two cross terms must equal zero, while condition (iii) ensures that the third moments are zero. Thus, $\mathbb{E}(X^{2}Z)=0$. A similar argument will show that $\mathbb{E}(Z^{2}X)=0$. □

Recall that all invertible linear transformations of the plane are at most combinations of reflections, rotations, expansions or compressions, and shears. Geometrically then, what Proposition 2 tells us is that centering will reduce the correlation between $X$ and $\mathrm{XZ}$ whenever there exists a pair of perpendicular lines through the joint distribution of $X$ and $Z$, each marginally unskewed, such that the joint distribution has the same shape in each of the quadrants defined by those lines. In other words, whenever we can define a new set of coordinate axes so that the joint distribution is symmetric in the sense of (9) and unskewed with respect to the transformed variables $\tilde{X}$ and $\tilde{Z}$ defined by the new coordinate axes. Figure 1 in the following section illustrates a typical case.

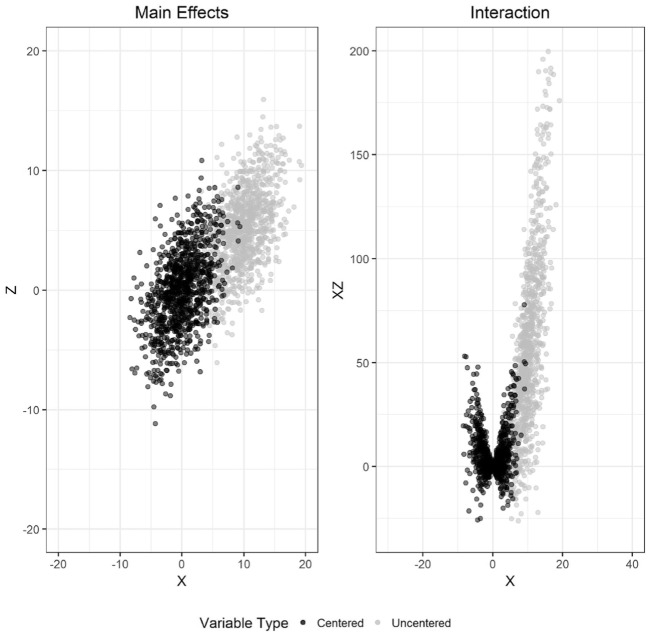
Figure 1.

Centered and uncentered X and Z from a bivariate normal distribution.

Empirical Simulation

To further develop the theory elucidated in the previous section, a series of simulated examples are presented here to further explore the cases where the correlation between centered terms and their interaction is larger than between the latter and its uncentered main effects. Notice the differences in the scaling of the axes in the pairs of plots throughout this section.

Figure 1 presents the “benchmark” case alluded to in Aiken and West (1991) and Cohen et al. (2002) where $(X,Z)$ are jointly normally distributed. For this example, ${\mu }_x=10;{\mu }_z=5;{\sigma }_x^2={\sigma }_z^2=10;{\sigma }_{\mathrm{xz}}=5$ so that $\rho =0.5$ and $N=1,000$.

Notice that neither is $X$ expectation-independent of $Z$ nor is $Z$ expectation-independent of $X$ in this example. However, their joint distribution does satisfy the criterion of Proposition 2; that is, there exists a line through the centered joint distribution of $(X_c,Z_c)$ such that if we rotate this line atop the $Z$-axis, say, then the transformed joint distribution is expectation-independent in the transformed variables $(\tilde{X},\tilde{Z})$. Moreover, the corresponding marginal distributions will not be skewed.

The left panel presents the scatter plot of the marginal distributions and the right panel shows the relationship between one of the marginal distributions, $X$, and the product term $\mathrm{XZ}$. As it is commonly known, the leftmost plot of one-dimensional marginals shows the classical elliptical shape that characterizes the multivariate normal distribution (among others). The rightmost one depicts the quadratic effect of the product-interaction term so that a saddle-like point can be observed along the origin, which further expands as one move along the horizontal axis. For this particular example, $\mathrm{Cor}(X,\mathrm{XZ})=0.918$ and $\mathrm{Cor}(X_c,X_c{Z}_c)=0.033$, showing the expected reduction in correlation when one centers the main effects.

Now consider the following bivariate normal mixture:

$$(0.9)\times {\mathcal{N}}_1\left(\begin{array}{cc}\left[\begin{array}{c}4\hfill \\ \multicolumn{1}{c}{4}\end{array}\right],\hfill & \left[\begin{array}{cc}1\hfill & 0.6\hfill \\ \multicolumn{1}{c}{0.6}& 1\hfill \end{array}\right]\hfill \end{array}\right)+(0.1)\times {\mathcal{N}}_2\left(\begin{array}{cc}\left[\begin{array}{c}7\hfill \\ \multicolumn{1}{c}{-1}\end{array}\right],\hfill & \left[\begin{array}{cc}1\hfill & 0.1\hfill \\ \multicolumn{1}{c}{0.1}& 1\hfill \end{array}\right]\hfill \end{array}\right)$$

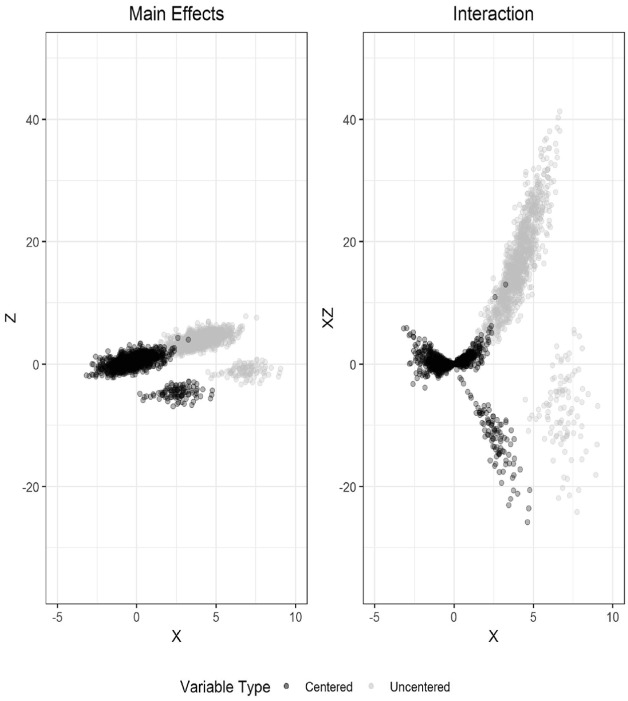
Figure 2 shows the scatter plot of the main effects and interaction of 1,000 units sampled from this distribution. Notice that, whether one looks at the centered or uncentered clouds of points, two distinct clusters can be observed as a function of the mixture proportions. Once $X$ and $Z$ are centered and the multiplicative interaction term is formed, the smaller cluster for the centered case rotates, creating a downward-sloping line that connects the origin to the mean of this smaller group of points, forcing a correlation between the main effect $X$ and its interaction. Although the cloud of points for the uncentered terms still remains and is also present, the points are too far apart to induce a slope connecting the new center of the interaction term with the smaller cloud of points. For this particular example $\mathrm{Cor}(X,\mathrm{XZ})=-0.033$ and $\mathrm{Cor}(X_c,X_c{Z}_c)=-0.585$.

Figure 2.

Centered and uncentered X and Z from a bivariate normal mixture.

Figure 3 presents a third example, a bivariate distribution generated through the copula-based method outlined in Mair, Satorra, and Bentler (2012). For this particular case, normal distributions are chosen for the marginals with parameters ${\mu }_X=15,{\mu }_Z=5;{\sigma }_X={\sigma }_Z=10$ and ${\sigma }_{X,Z}=5$ to obtain a correlation coefficient of $\rho =0.5$. A Joe copula function with parameter $\theta =19$ was used (see Joe, 2014, p. 170) and 1,000 datapoints were sampled. The scenario presented here highlights the fact that even though lower order (i.e. marginal) symmetry can be present (such as with the normal distribution), lack of symmetry in higher dimensions can still make centered interaction terms exhibit higher correlation than their uncentered counterparts. The left panel of Figure 3 suggests a jointly skewed distribution with its longer tail in the positive quadrant and the rest of the mass moving toward the negative quadrant, becoming more dispersed as it does. When the multiplicative interaction is formed, the points of the shorter tail among the centered distributions are mostly reflected upward with a smaller group of them creating a subset close to the origin so that an upward-sloping line can be traced from the origin to these points. For the uncentered case, it is possible to again see the horizontal reflection that induces a $U$-shape, but the spread of points below their mean centroid is not as strongly defined as in the centered case to induce an upward-sloping line. For this particular case, $\mathrm{Cor}(X,\mathrm{XZ})=0.190$ and $\mathrm{Cor}(X_c,X_c{Z}_c)=0.273$.

Table 1 offers a summary of the increase or decrease in correlation between $X$ or $Z$ and the $\mathrm{XZ}$ term as well as which conditions from section “Centered Versus Uncentered Covariance Products” hold for each of the three cases just described. The “symmetric” case (which encompasses the bivariate normal distribution) shows the classic reduction in correlation for the centered main effects. As expected, neither Condition (5) nor Condition (6) hold true. The mixture of normal distributions shows the greatest increase (in absolute value) of the correlation between the centered terms and their interaction. Condition (5) holds in this case, after replacing $X$ by $-X$ and $Z$ by $-Z$. Finally, the Joe copula with standard normal marginals does not show an increase in the absolute value of the correlation as dramatic as the normal mixture case, but it still demonstrates the fact that under nonsymmetric conditions, the correlation between uncentered terms can be lower than that for centered terms. Condition (5) is also true in this scenario.

Table 1.

Correlation for Centered and Uncentered Main Effects With Interactions.

Distribution	Uncentered correlation	Centered correlation	Condition (5)	Condition (6)
Symmetric	0.918	0.033	False	False
Mixture	−0.033	−0.585	True*	False
Copula	0.190	0.273	True	False

^*Refers to the need to switch signs for X and Z before testing the conditions.

Conclusion

As the theory and examples we have explored show, centering will not always reduce the multicollinearity problem of multiple regression, even when a pair of predictors $X$ and $Z$ have marginally symmetric distribution functions. This fact runs counter to some common wisdom on the centering issue, presented, for example, in Cohen et al. (2002). Making use of careful mathematical definitions like expectation-independence and bivariate symmetry, as in (9), can greatly help correct and clarify our understanding of these issues.

In practice, centering can still be considered a viable tool for the applied researcher when multicollinearity is a concern, but only in certain cases. This article describes what to watch for, but we can summarize our general advice as follows. If centering is being considered:

1. Plot the $(X,Z)$ and $(X,\mathrm{XZ})$ data.

2. Visually assess if there could exist a pair of perpendicular lines one could place on the $(X,Z)$ plane so that the distribution of points in the scatterplot are symmetric with respect to the transformed origin created by the intersection of these perpendicular lines. If yes, then centering will reduce the problem of multicollinearity.

3. On the other hand, if the $(X,Z)$ data appear in clusters, centering is unlikely to reduce the problem of multicollinearity.

We have included the R code used to generate our example figures in the Supplementary Material (available in the online version of the article) as a teaching resource for introductory regression courses.

Finally, we remark that our investigations in this article apply only to the bivariate setting of Model (1). In higher dimensional settings, the issue of multicollinearity becomes considerably more complicated. Indeed, centering will actually change the least squares estimators and standard errors of the pairwise interaction term coefficients when third-order (or higher) interactions are present in a linear regression model. Thus, a researcher’s ability to detect pairwise interaction effects can be greatly altered by choosing to center variables when three or more predictors (and their interactions) are under consideration.

Appendix

To show that $\mathrm{Cov}(X_c,X_c{Z}_c)=\mathrm{Cov}(X,\mathrm{XZ})-\mathbb{E}(Z)\mathrm{Var}(X)-\mathbb{E}(X)\mathrm{Cov}(X,Z)$ one merely needs to rely on the definition of covariance $\mathrm{Cov}(X,Z)=\mathbb{E}[(X-\mathbb{E}(X))(Z-\mathbb{E}(Z))]$ and expand the terms as necessary. Please notice that, by definition, $\mathbb{E}(X_c)=\mathbb{E}(Z_c)=0$.

$$\begin{array}{c}\mathrm{Cov}(X_c,X_c{Z}_c)=\mathbb{E}(X_c^2{Z}_c)=\mathbb{E}[(X-\mathbb{E}(X){)}^2(Z-\mathbb{E}(Z))]\hfill \\ =\mathbb{E}(X^{2}Z)-2\mathbb{E}(X)\mathbb{E}(\mathrm{XZ})+\mathbb{E}(X{)}^2\mathbb{E}(Z)-\mathbb{E}(X^2)\mathbb{E}(Z)+2\mathbb{E}(X{)}^2\mathbb{E}(Z)-\mathbb{E}(X{)}^2\mathbb{E}(Z)\hfill \\ =\mathbb{E}(X^{2}Z)-2\mathbb{E}(X)\mathbb{E}(\mathrm{XZ})-\mathbb{E}(Z)[(X^2)-2\mathbb{E}(X{)}^2]\hfill \\ =\mathbb{E}(X^{2}Z)-2\mathbb{E}(X)\mathbb{E}(\mathrm{XZ})-\mathbb{E}(Z)\mathrm{Var}(X)+\mathbb{E}(Z)\mathbb{E}(X{)}^2\hfill \\ =\mathbb{E}(X^{2}Z)-\mathbb{E}(Z)\mathrm{Var}(X)-\mathbb{E}(X)[\mathbb{E}(\mathrm{XZ})+\mathbb{E}(\mathrm{XZ})-\mathbb{E}(X)\mathbb{E}(Z)]\hfill \\ =\mathbb{E}(X^{2}Z)-\mathbb{E}(Z)\mathrm{Var}(X)-\mathbb{E}(X)\mathbb{E}(\mathrm{XZ})-\mathbb{E}(X)\mathrm{Cov}(X,Z)\hfill \\ =\mathrm{Cov}(X,\mathrm{XZ})+\mathbb{E}(\mathrm{XZ})\mathbb{E}(X)-\mathbb{E}(Z)\mathrm{Var}(X)-\mathbb{E}(X)\mathbb{E}(\mathrm{XZ})-\mathbb{E}(X)\mathrm{Cov}(X,Z)\hfill \\ =\mathrm{Cov}(X,\mathrm{XZ})-\mathbb{E}(Z)\mathrm{Var}(X)-\mathbb{E}(X)\mathrm{Cov}(X,Z).\hfill \end{array}$$