Landmark Linear Transformation Model for Dynamic Prediction with Application to a Longitudinal Cohort Study of Chronic Disease

Summary.

Dynamic prediction of the risk of a clinical event using longitudinally measured biomarkers or other prognostic information is important in clinical practice. We propose a new class of landmark survival models. The model takes the form of a linear transformation model, but allows all the model parameters to vary with the landmark time. This model includes many published landmark prediction models as special cases. We propose a unified local linear estimation framework to estimate time-varying model parameters. Simulation studies are conducted to evaluate the finite sample performance of the proposed method. We apply the methodology to a dataset from the African American Study of Kidney Disease and Hypertension and predict individual patient’s risk of an adverse clinical event.

1. Introduction

Precision or personalized medicine is widely viewed as the future of healthcare. It promotes the development of prognostic models based on time-fixed and time-varying individual characteristics related to genetics, lifestyle, environment, and clinical history. In medical studies with long-term follow-up, especially for the management of chronic diseases, biomarkers and other prognostic information are often collected longitudinally. However, most prognostic models in the literature are still based on static prediction, i.e., predicting the subsequent risk of a clinical event with predictors at a pre-specified earlier time point, such as the baseline. The static prediction model approach is suboptimal for prediction in the longitudinal context: much of the longitudinal data are ignored in model estimation; the prediction may be biased due to not adapting to the changing at-risk population; and the ever-increasing duration of clinical history is not incorporated into the prediction (van Houwelingen and Putter, 2011; Li et al., 2016b). In this paper, we propose novel methodological development for dynamic prediction, a field pioneered by the work of Taylor et al. (2005); Zheng and Heagerty (2005); van Houwelingen (2007); van Houwelingen and Putter (2011); Rizopoulos (2011), among others. In contrast to static prediction, dynamic prediction forecasts the time to clinical events in the longitudinal context, where the prediction can be made at any time during follow-up, while adapting to the changing at-risk population and incorporating the cumulating clinical history. We apply the proposed methodology to a cohort of patients with chronic kidney disease (CKD) and predict their personalized risk of adverse clinical events in real-time using longitudinal data collected during extended follow-up.

An estimated 23 million Americans (11.5% of the adult U.S. population) have CKD of various stages and are at increased risk of terminal adverse clinical events such as kidney failure and other morbidity such as adverse cardiovascular events (Coresh et al., 2007; Tangri et al., 2011). Patients with advanced CKD are often monitored through frequent clinical visits, where clinical assessments and lab tests are performed to evaluate disease progression and make personalized treatment decisions. Predicting the time to end-stage renal disease (ESRD), including dialysis and other kidney replacement therapy, at clinical visits is important for patient counselling as well as disease management. For example, procedures such as arteriovenous fistula placement and kidney transplantation are considered optimal when implemented before the initiation of dialysis, but there may be unnecessary expense and/or risk in performing these procedures too early in the course of declining kidney function (Grams et al., 2015). The possibility of nonlinear progression of renal function further complicates medical decision making (Li et al., 2012). The clinical practice guidelines published as Kidney Disease: Improving Global Outcomes recommend the use of risk prediction models to determine the appropriate time to prepare for renal replacement therapy (KDIGO, 2012). In this paper, we analyze a dataset from a cohort of 1,094 individuals enrolled in the African American Study of Kidney Disease and Hypertension (AASK) (Gassman et al., 2003). The participants of this study were followed up to 12 years. Lab and clinical data were scheduled to be collected every 6 months, though the actual measurement times varied substantially over time and across subjects, leading to irregularly spaced longitudinal time points. The estimated glomerular filtration rate (eGFR), a biomarker derived from blood creatinine that quantifies the renal function, ranges between 20 and 65 mL/min/1.73m² at baseline. Previous research has shown that though many CKD patients have relentless decline in renal function, nonlinear patterns, such as a sharp decline or improvement, can happen at any stage of CKD (Li et al., 2012, 2014; Hu et al., 2012). As a result, biomarkers associated with renal function, including eGFR and proteinuria, may also progress in nonlinear trajectories (Li et al., 2016b), which complicates modelling the prognostic relationship between longitudinal biomarkers and adverse clinical events.

There are two widely used approaches to dynamic prediction. One is based on joint models of the event time and longitudinal biomarker processes, e.g., Wulfsohn and Tsi-atis (1997); Tsiatis and Davidian (2004); Rizopoulos (2011); Rizopoulos et al. (2014), and the other is based on landmark models or partly conditional models, e.g., Anderson et al. (1983); Zheng and Heagerty (2005); van Houwelingen (2007); van Houwelingen and Putter (2008, 2011); Gong and Schaubel (2013, 2017). A typical joint model consists of sub-models for the longitudinal and survival processes, and their correlation is accounted for by shared random effects. The joint modelling approach can be efficient, provided that the distribution of the event times as well as the distribution of the longitudinal trajectories are correctly specified. However, a satisfactory model for trajectories is not easy to identify due to complex longitudinal patterns at the individual level. In addition, joint model fitting usually requires iteratively optimizing the log-likelihood with high-dimensional numerical integration over the random effects, which can be computationally intensive or even prohibitive in the presence of nonlinear trajectories or multiple longitudinal biomarkers. In our data application, a number of biomarkers, including GFR, proteinuria, and blood pressure (BP), are strongly predictive of the renal events and demonstrate nonlinearity in the extended follow-up. The landmark survival models, on the other hand, do not need to model the longitudinal trajectories and are particularly suitable for large problems with multiple, nonlinear biomarker trajectories. Furthermore, the landmark approach does not require integration over random effects, so the computational burden does not increase as the number of longitudinal biomarkers increases. A comprehensive discussion and comparison of landmark models and joint models can be found in Maziarz et al. (2017).

In this paper, we focus on the landmark model method for dynamic prediction. At the time of prediction, it specifies a survival model for the residual time to the event of interest that is associated with some longitudinal predictor variables observed up to that time. Predictor variables can be numeric summaries of the observed history of a longitudinal data process through the time of prediction (often known as a landmark time), in addition to the current value of it. However, they are treated as time-invariant covariates in the regression model for the residual time to the event in the framework of landmark prediction models. Landmark Cox proportional hazards (PH) models have been studied by Zheng and Heagerty (2005), van Houwelingen (2007), van Houwelingen and Putter (2011), and Li et al. (2016b), among others. However, as commented in van Houwelingen (2007), a landmark model is not a probability model in the strict sense because it implies that a certain model assumption is satisfied at any selected landmark time. For example, the assumption of PH at any or multiple pre-specified landmark times is a strong assumption. Although landmark models are often used as working models in applications, violation of model assumptions can result in incorrect characterization of covariate effects and biased prediction. In this article, we propose a broader and more flexible class of landmark models that relaxes model assumptions and includes many published landmark models as special cases. We develop a unified estimation approach that applies to all the models in this class. It offers alternative choices when the PH assumption does not hold or performs unsatisfactorily, as illustrated in our data application.

The remainder of the paper is organized as follows. Section 2 introduces the proposed model and its estimation method. Section 3 provides simulation results to examine the finite sample performance. Section 4 applies the methodology to the AASK data, and Section 5 provides some concluding remarks and discussion.

2. Model, Estimation, and Prediction

In dynamic prediction, interest lies in the estimation of the survival probability at a future time t given survival up to an earlier time s(< t) and the predictor information available up to s, i.e., S{t; s|Z(s)} = P{T > t|T > s, Z(s)}, where T denotes the event time under study and Z(s) denotes a vector of pre-specified functions of the history of prognostic variables observed prior to s. For example, Z(s) may include the biomarker measurement at the landmark time s or the average biomarker value for a fixed duration prior to time s. Landmark models reset the time origin at a selected time s and model the residual lifetime (T_s = T – s) conditional on the observed history up to s. At any s ≥ 0, we let u = t – s. Objective of dynamic prediction is to estimate P{T_s > u|Z(s)} for individuals who are at risk at s, where Z(s) are treated as time-invariant covariates, though they may vary with the landmark time s. In the following, we propose a class of landmark models that takes the form of linear transformation and describe the methodology for parameter estimation and risk prediction based on that.

2.1. Landmark Linear Transformation Model

Linear transformation models introduced by Dabrowska and Doksum (1988) have a general form of

$$g\{S(t)\}=H(t)+{\mathit{Z}}^{\prime }\beta .$$ (1)

Semiparametric estimation based on model (1) has been studied by Cheng et al. (1995, 1997); Chen et al. (2002); Zeng and Lin (2006, 2007), among others. Function g(·) in (1) is a known strictly decreasing link function; H(t) is a completely unspecified strictly increasing function that maps the positive half line onto the whole real line and satisfies H(0) = –∞; β is a q × 1 vector of unknown regression coefficients and Z is a q × 1 vector of time-invariant covariates. Model (1) can also be written as

$$H(T)=-Z^{\prime }\beta +ϵ,$$ (2)

where ϵ is a random error with distribution function F_ϵ = 1 – g⁻¹. It can be shown that g(x) = log{−log(x)} and g(x) = −logit(x) = log{(1 – x)/x} correspond to PH models and proportional odds (PO) models, respectively. For example, a Cox model can be written as log[−log{S(t)}] = log{Ʌ₀(t)} + Z′β, where Ʌ₀(t) denotes the cumulative baseline hazard function of failure time T. Additionally, an accelerated failure time model can be written as model (1) with a parametrically specified H(t). More generally, Dabrowska and Doksum (1988) and Chen et al. (2002) considered a transformation specified by the distribution of ϵ as

$${\lambda }_{ϵ}(t)=\text{exp}(t)/\{1+r\text{exp}(t)\},$$ (3)

where λ_ϵ(t) is the hazard function of ϵ in (2). Under this specification, PH models and PO models respectively correspond to r = 0 and r = 1.

To extend the linear transformation model for dynamic prediction, we use the landmark model framework and allow all the model parameters to vary along the landmark time s. That is, for individuals who are at risk at s, i.e., T_i > s, the landmark linear transformation model is defined by

$$g\left[P\left\{T_{is}>u|Z_i(s)\right\}\right]=H(u;s)+Z_i^{\prime }(s)\beta (s),$$ (4)

for any selected s ≥ 0 and u > 0, where H(u; s) is an unspecified strictly increasing function of u given s; g = g_s is a link function that is allowed to vary along s as well, so a certain model assumption does not necessarily need to be satisfied at multiple landmark times. Similarly, model (4) can be written in the form of a linear model as (2)

$$H\left(T_{is};s\right)=-Z_i^{\prime }(s)\beta (s)+{ϵ}_s,$$ (5)

where the error term ϵ_s has a distribution given by $F_{ϵ}=1-g_s^{-1}$.

Let C_i be the censoring time of subject i, X_i = min{T_i, C_i} be the observed time and δ_i = I(T_i ≤ C_i) be a failure/censoring indicator. We also define $0\le t_{i1}<\cdots <t_{i{m}_i}\le X_i$ as the m_i measurement times of Z_i(t) for subject i. Note that model (4) is defined for any s ≥ 0. Therefore, for subjects with visit time t_ij, prediction at t_ij can be performed by fitting the following model with residual event times $T_{i,t_{ij}}=T-t_{ij}$

$$g\left[P\left\{T_{i,t_{ij}}>u|Z_i\left(t_{ij}\right)\right\}\right]=H\left(u;t_{ij}\right)+Z_i^{\prime }\left(t_{ij}\right)\beta \left(t_{ij}\right).$$

In addition, it is assumed that (X_i,δ_i, {Z_i(t_ij) : j = 1,…,m_i}), i = 1,…,n, are independent and identically distributed random vectors with Z_i(t_ij) bounded. For simplicity, we also assume that the censoring time and the longitudinal measurement times are non–informative in the sense that C_i and t_ij are independent of failure time T_i and the biomarker process {Z_i(t) : t ≥ 0} for any subject i.

2.2. Estimation Methods with Regular and Irregular Trajectory Measurement Times

We describe the estimation procedures under two settings. The first one is that the longitudinal measurements of all subjects are made on a common set of pre–specified time points. This situation could arise in a prospective cohort study where every subject follows a pre–specified schedule of clinical visits (e.g., monthly measurements). Missing visits are allowed, as long as the data missingness is non–informative. The second setting is that the longitudinal measurement times are continuously distributed and irregularly spaced in time, and the measurement times of different subjects are not on a common set of discrete time points. This is a common situation in observational studies or electronic health records, where patients do not strictly follow their visit schedules.

In the first setting, it is supposed that Z_i(t) is measured at a finite set of common measurement times (regular or irregular), e.g., 0 ≤ t₁ < ⋯ < t_m. We define Y_i(u; s) = I(X_is ≥ u) and N_i(u; s) = δ_iI(X_is ≤ u), where X_is = X_i – s. Then H(u; s) and β(s) in model (4), for s = t_ℓ, ℓ = 1,…, m, are estimated by solving the martingale version of the estimating equations proposed by Chen et al. (2002) and using the data at landmark time t_ℓ

$$U_1\left({\beta }_{\ell },H_{\ell }\right)=\sum _{i=1}^n{\int }_0^{\infty }{Z}_i\left(t_{\ell }\right)\left[d{N}_i\left(u;t_{\ell }\right)-Y_i\left(u;t_{\ell }\right)d{\Lambda }_{ϵ}\left\{{\beta }^{\prime }\left(t_{\ell }\right)Z_i\left(t_{\ell }\right)+H\left(u;t_{\ell }\right)\right\}\right]=0,$$ (6)

$$U_2\left({\beta }_{\ell },H_{\ell }\right)=\sum _{i=1}^n\left[d{N}_i\left(u;t_{\ell }\right)-Y_i\left(u;t_{\ell }\right)d{\Lambda }_{ϵ}\left\{{\beta }^{\prime }\left(t_{\ell }\right)Z_i\left(t_{\ell }\right)+H\left(u;t_{\ell }\right)\right\}\right]=0\forall u\ge 0,$$ (7)

where Ʌ_ϵ(·) is the cumulative hazard function of ϵ in (5), e.g., Ʌ_ϵ(t) = exp(t) for Cox models. Because $M\left(t;t_{\ell }\right)=N\left(t;t_{\ell }\right)-{\int }_0^{t}Y\left(u;t_{\ell }\right)d{\Lambda }_{ϵ}\left\{{\beta }_0^{\prime }\left(t_{\ell }\right)Z_i\left(t_{\ell }\right)+H_0\left(u;t_{\ell }\right)\right\}$ is a martingale process, given that (β₀, H₀) are the true values of (β, H), it is easily seen that (6) and (7) are unbiased estimating equations and the resulting estimators are consistent. Solving these estimating equations is equivalent to fitting a separate linear transformation model at each measurement time t_ℓ. It can be implemented by following the algorithm introduced in Chen et al. (2002), which is available in the R function TransModel. Under suitable regularity conditions, $\widehat{\beta }\left(t_{\ell }\right)$ obtained by solving (6) and (7) has asymptotic normal distribution (Chen et al., 2002) and the estimated variance is also provided by TransModel.

We now discuss model estimation when the measurement times are randomly distributed and irregularly spaced in time. In long follow–up studies, deviation from the schedule of clinical visits suggested in the protocol is fairly common. For example, the AASK protocol suggests a visit every 6 months, but patients’ actual visit gap times have a median of 7 months and a standard deviation of 6.3 months. If a predictor is defined as the current value of eGFR, then the irregular measurement times of eGFR may cause the predictor variables of many individuals missing at the selected landmark time. The last–value–carried–forward (LVCF) method, i.e., imputing the missing predictor at the time of prediction with the most recent biomarker measurement prior to that time, can be applied, as in van Houwelingen (2007) and van Houwelingen and Putter (2011). However, as shown in the simulations, this method can result in biased estimates, particularly when the gap times between visits are wide or when biomarker processes have large short–term variabilities. In this article, we propose an alternative approach that is based on a local polynomial approximation to β(s) and H(u; s) in model (4); a kernel–weighted version of estimating equations (6) and (7) is defined such that β(s) and H(u; s) can be estimated for any given s. The details are described below.

First, for t_ij in the neighbourhood of s, by Taylor’s expression, we have

$${\beta }_l\left(t_{ij}\right)\approx {\beta }_l(s)+{\beta }_l^{(1)}(s)\left(t_{ij}-s\right)+\frac{{\beta }_l^{(2)}(s)}{2!}{\left(t_{ij}-s\right)}^2+\cdots +\frac{{\beta }_l^{(p)}(s)}{p!}{\left(t_{ij}-s\right)}^p,$$

where l = 1,…, q, and the function with superscript (p) denotes the pth derivative of it. We let ${\tilde{Z}}_i^p\left(t_{ij}-s\right)={\left(1,t_{ij}-s,{\left(t_{ij}-s\right)}^2/2!,\dots ,{\left(t_{ij}-s\right)}^p/p!\right)}^{\prime }\otimes Z_i\left(t_{ij}\right),$ Where ⊗ denotes the operator for Kronecker product, and θ(s) = (β′ (s), β⁽¹⁾′ (s),…, β^(p)′(s))′, where β(s) = (β₁(s),…, β_q(s))′. Then, me estimating equations ioi H (u; s) and θ(s) with the pth order local polynomial smoother are defined as

$$\sum _{i=1}^n\sum _{j=1}^{m_i}{K}_h\left(t_{ij}-s\right){\int }_0^{\infty }{\tilde{Z}}_i^p\left(t_{ij}-s\right)\left[d{N}_i\left(u;t_{ij}\right)-Y_i\left(u;t_{ij}\right)d{\Lambda }_{ϵ}\left\{{\theta }^{\prime }(s){\tilde{Z}}_i^p\left(t_{ij}-s\right)+H(u;s)\right\}\right]=0,$$ (8)

$$\sum _{i=1}^n\sum _{j=1}^{m_i}{K}_h\left(t_{ij}-s\right)\left[d{N}_i\left(u;t_{ij}\right)-Y_i\left(u;t_{ij}\right)d{\Lambda }_{ϵ}\left\{{\theta }^{\prime }(s){\tilde{Z}}_i^p\left(t_{ij}-s\right)+H(u;s)\right\}\right]=0\forall u\ge 0,$$ (9)

where K_h(·) = K(·/h)/h, K(·) is a symmetric kernel density function, and 0 < h ≜ h_n → 0⁺ (n → ∞) is a positive bandwidth sequence. Given a landmark time s, $\widehat{\theta }(s)$ and Ĥ(u; s) can be obtained by solving (8) and (9) using an iterative algorithm similar to that in Chen et al. (2002). Because there is no existing software available, we extend this algorithm and describe it in Web Appendix A in the web–based supporting materials.

When measurement times (t_ij) are irregular, we barely observe multiple measures from different subjects at one certain time point. Therefore, solving estimating equations (6) and (7) at each t_ij is impossible; whereas kernel smoothing can group t_ij within a local neighbourhood of the selected landmark time s and weight the observation at t_ij by its distance from s, making the estimation of H(u; s) and β(s) at any s ≥ 0 possible. There is a general trade–off in kernel smoothing methods: smaller bandwidths lead to less bias and larger variances, while larger bandwidths result in greater bias and smaller variances. Data–driven bandwidth selection is widely used in practice, e.g., we conduct Monte Carlo cross–validation to select bandwidths in the application to the AASK data in a later section. In addition, note that measurement times t_ij, which contribute to (8) and (9) for the estimation of H(u; s) and θ(s) at s, can include multiple measures from one subject. We consider the independent working correlation for multiple measurement times from one subject, which may lead to some loss of efficiency, but the loss is mild if measurement times are not closely spaced. We discuss this further in a subsequent section. In practice, local linear smoothing (p = 1) is widely used and has good asymptotic properties, as discussed in Fan (1993) and Fan and Gijbels (1996). In the subsequent sections, we thus consider a local linear smoother in the estimating equations (8) and (9).

Asymptotic variances of regression parameter estimators obtained from (8) and (9) are not derived. We propose to use bootstrapping to obtain inferences for coefficients $\widehat{\beta }(s)$, though prediction is of primary interest in this article. To generate bootstrap samples, we nonparametrically sample B times with replacement from the original set of all subjects (X_i, δ_i, {Z_i(t_ij) : j = 1,…, m_i}), i = 1,…, n. At a given landmark time s, we estimate H(u; s) and β(s) for each bootstrap sample by solving (8) and (9). As a result, we obtain B bootstrap estimates ${\widehat{\beta }}_b(s)$ and the variance $\sigma \{\widehat{\beta }(s)\}$ is estimated by the sample standard deviation of ${\widehat{\beta }}_b(s)$. Upon the normality is checked by the QQ–plot, pointwise confidence interval of β(s) can be estimated by $\widehat{\beta }(s)\pm Z_{1-\alpha /2}\widehat{\sigma }\{\widehat{\beta }(s)\}$ with Z_1–α/2 denoting the 1 – α/2 percentile of a standard normal distribution. We illustrate the variance estimation in Table 4 in Section 3.3 where we evaluate the estimation and prediction under correct and misspecified working models via simulation.

Table 4.

Bias, average estimated standard errors (ASEs), empirical standard errors (ESEs), coverage probabilities (CPs), and mean squared errors (MSEs) for the regression coefficient estimates by the proposed method under possibly misspecified working model. Number of simulation replicates is N = 100. Each simulation includes a training dataset with 200 subjects. Standard errors are estimated by bootstrapping and B = 200 bootstrap samples are generated.

			misspecified working model					correct working model
coef	s	TRUE	bias	ASE	ESE	MSE	CP	bias	ASE	ESE	MSE	CP
β1	2	0.383	−0.149	0.039	0.041	0.024	0.05	0.014	0.057	0.054	0.003	0.93
β2	2	−0.590	0.256	0.297	0.299	0.154	0.88	0.004	0.443	0.419	0.174	0.95
β3	2	0.420	−0.160	0.096	0.104	0.036	0.65	0.017	0.144	0.143	0.021	0.94
β4	2	−0.300	0.127	0.080	0.076	0.022	0.69	0.002	0.119	0.114	0.013	0.96
β1	4	0.500	−0.204	0.055	0.054	0.045	0.07	0.010	0.079	0.073	0.005	0.95
β2	4	−0.580	0.255	0.318	0.330	0.173	0.87	−0.048	0.472	0.431	0.186	0.96
β3	4	0.440	−0.177	0.104	0.104	0.042	0.55	0.014	0.150	0.138	0.019	0.97
β4	4	−0.300	0.117	0.085	0.085	0.021	0.72	−0.009	0.128	0.118	0.014	0.96
β1	6	0.590	−0.229	0.074	0.076	0.058	0.13	0.013	0.106	0.102	0.010	0.97
β2	6	−0.570	0.177	0.362	0.335	0.142	0.93	−0.080	0.537	0.448	0.205	0.97
β3	6	0.460	−0.188	0.118	0.117	0.049	0.60	−0.010	0.170	0.162	0.026	0.96
β4	6	−0.300	0.123	0.098	0.085	0.022	0.79	0.000	0.144	0.126	0.016	0.98

2.3. Dynamic Prediction

Suppose that there is a training dataset composed of n subjects and a test dataset composed of n* subjects, and both datasets have irregular biomarker trajectory measurement times. If we consider the measurement time $t_{ij}^{*}$ of subject i in the test dataset as the prediction time for this individual, the conditional survival probability $P\{T_{i,t_{ij}^{*}}>u|Z_i\left(t_{ij}^{*}\right)\}$ can be estimated by

$${\widehat{\pi }}_i\left(u;t_{ij}^{*}\right)\triangleq g^{-1}\left\{\widehat{H}\left(u;t_{ij}^{*}\right)+Z_i^{\prime }\left(t_{ij}^{*}\right)\widehat{\beta }\left(t_{ij}^{*}\right)\right\},$$ (10)

where u denotes a prediction horizon, $\widehat{H}\left(u;t_{ij}^{*}\right)$ and $\widehat{\beta }\left(t_{ij}^{*}\right)$ are obtained by solving (8) and (9) with $s=t_{ij}^{*}$ applied to the training dataset, $\widehat{\beta }\left(t_{ij}^{*}\right)$ represents the estimates of the first q elements of $\theta \left(t_{ij}^{*}\right)$ in (8) and (9), and g⁻¹ is the inverse function of link function g in model (4).

In practice, prediction of individual risk is usually pursued at clinical visit times, e.g., $t_{ij}^{*}$ of subject i in the test dataset. However, prediction at any $s\ge t_{ij}^{*}$ can also be obtained by using ${\widehat{\pi }}_i\left(u;t_{ij}^{*}\right)$, if it is desired, where $t_{ij}^{*}$ is the most recent visit time prior to s. For example, the conditional survival probability, $P\left\{T_i>s+u|T_i>s,Z_i\left(t_{ij}^{*}\right)\right\}$, can be obtained by

$$\begin{array}{ll}S\left\{u;s|Z_i\left(t_{ij}^{*}\right)\right\}\hfill & =\frac{P\left\{T_i>s+u|T_i>t_{ij}^{*},Z_i\left(t_{ij}^{*}\right)\right\}}{P\left\{T_i>s|T_i>t_{ij}^{*},Z_i\left(t_{ij}^{*}\right)\right\}}\hfill \\ \hfill & =\frac{P\left\{T_{i,t_{ij}^{*}}>s-t_{ij}^{*}+u|Z_i\left(t_{ij}^{*}\right)\right\}}{P\left\{T_{i,t_{ij}^{*}}>s-t_{ij}^{*}|Z_i\left(t_{ij}^{*}\right)\right\}}\hfill \\ \hfill & ={\pi }_i\left(s-t_{ij}^{*}+u;t_{ij}^{*}\right)/{\pi }_i\left(s-t_{ij}^{*};t_{ij}^{*}\right),\hfill \end{array}$$ (11)

where ${\pi }_i\left(\cdot ;t_{ij}^{*}\right)$ is estimated by (10). To facilitate evaluating and reporting the predictive performance at a few selected s, we use (11) to compute the conditional survival probabilities in the analysis of the AASK data in Section 4.

3. Simulation Studies

Data generation for landmark models is generally challenging, since landmark models are not strict probability models. Zheng and Heagerty (2005) and Maziarz et al. (2017) constructed a particular joint distribution where the derived event time distribution satisfies the PH assumption in their working model. We developed a more general procedure to simulate data from the landmark model framework directly (Zhu et al., 2018). Our procedure is applicable to all landmark linear transformation models, including the landmark Cox model as a special case. Therefore, it greatly facilitates the empirical studies of a more general class of landmark models in terms of parameter estimation and prediction under correct model specification. Details about data generation are provided in Web Appendix B. We only present and discuss the simulation results in this section.

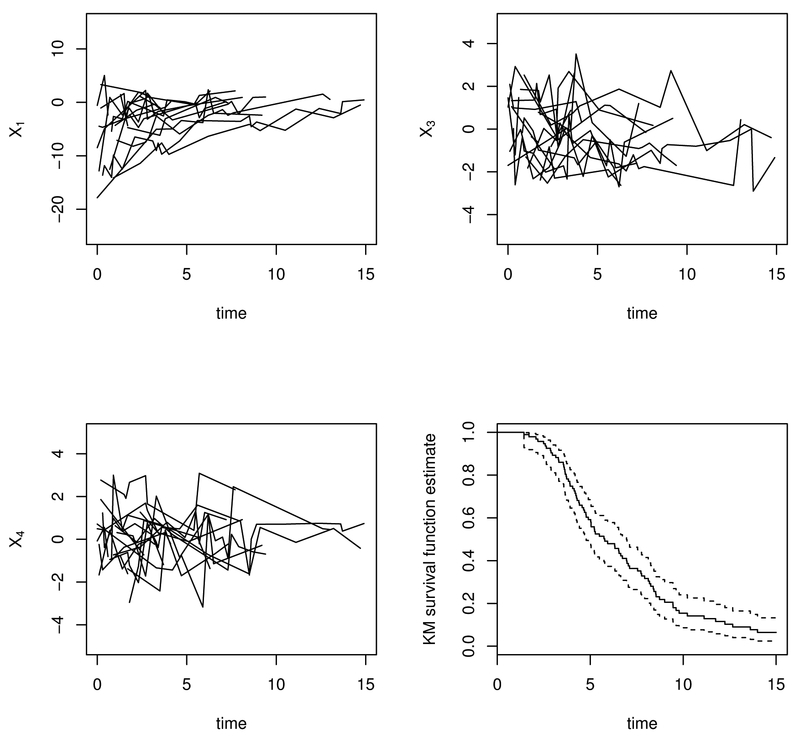
Two simulation studies based on a landmark PH model and a landmark PO model are conducted respectively. In each simulation study, a training dataset with sample size n = 200 or n = 500 is generated. There are about 20% of failure times subject to right censoring in the training dataset. Censoring is assumed to be independent. We also generate a test dataset of 200 subjects, while no censoring is imposed for simplicity. Regarding the visit process, for technical convenience, we discretize time from 0 to 15 by a grid of 10 per unit. In the training dataset, we simulate irregular but independent visit times t_ij with an intensity of 0.10 so that subjects have about 6 ~ 7 visits/per person on average. For convenience in presenting the prediction performance metrics in simulations, we generate regular measurement times in the test dataset, i.e., $t_{i1}^{*}=2$, $t_{i2}^{*}=4$, and $t_{i3}^{*}=6$ for i = 1,…, 200. Figure 1 displays the trajectories of X₁(t_ij), X₃(t_ij) and X₄(t_ij) for 20 randomly selected individuals and the Kaplan–Meier estimate of marginal survival function for the training dataset based on a landmark PH model.

Fig. 1.

Trajectories of X₁(t), X₃(t), and X₄(t) for 20 randomly selected subjects and the Kaplan–Meier (KM) estimate of marginal survival curve for the whole sample of training data based on a landmark PH model from one simulation.

We examine the finite sample performance of the proposed method and compare it with the LVCF method. Three landmark times (s = 2, 4, or 6) and two prediction horizons (u = 3 or 5) are selected for evaluation. Additionally, since landmark models are often used as working models in applications, we investigate the performance of our proposed method with correct and misspecified working models in Section 3.3. For example, using proportional hazards as the working model, yet data are generated from a landmark proportional odds model. In each simulation study, we use the Epanechnikov kernel with bandwidths between 0.4 and 0.6 for n = 200 and between 0.2 and 0.5 for n = 500. Generally the bandwidth should be smaller with a larger number of subjects in the risk set (i.e., smaller bandwidths are given at earlier landmark times when more subjects have not experienced the event yet).

3.1. Simulation for A Landmark Proportional Hazards Model

To evaluate the predictive performance in simulation, we use the mean squared error (MSE) and survival proportion difference (SPD) to assess the calibration of the prediction, and use the area under the receiver operating characteristic (ROC) curve, i.e., the AUC, to assess the discrimination of prediction. The MSE and SPD are defined by $E[{\{{\widehat{\pi }}_i(u;t_{ij}^{*})-{\pi }_i(u;t_{ij}^{*})\}}^2]$ and $E[I\{T_{i,t_{ij}^{*}}>u\}-{\widehat{\pi }}_i(u;t_{ij}^{*})]$, respectively, where ${\pi }_i\left(u;t_{ij}^{*}\right)$ denotes the true value of the conditional survival probability for subject i in the test dataset and is given in (10). These quantities can be estimated by taking the average over the sample of the test data. The AUC summarises the probabilities of true positive (sensitivity) and false positive (1–specificity) diagnoses. We consider the definitions of sensitivity and specificity by Heagerty et al. (2000) for time–to–event data as P(V > c|T ≤ u) and P(V ≤ c|T > u), respectively, where V denotes a continuous risk predictor. In our simulation, we use $1-{\widehat{\pi }}_i\left(u;t_{ij}^{*}\right)$ as the predictor V. Since there is no censoring in our test dataset in the simulation, the AUC can be computed by the auc function from R package pROC after calculating the binary indicator $I(T_{i,t_{ij}^{*}}>u)$ and predicted probability ${\widehat{\pi }}_i\left(u;t_{ij}^{*}\right)$. The averages of all these measures over 100 simulation replicates are summarised in Table 1.

Table 1.

Summary of the prediction performance evaluation of the proposed method and the LVCF method based on a landmark PH model. We consider mean squared error (MSE) and survival proportion difference (SPD) regarding the predicted survival probability ${\widehat{\pi }}_i\left(u;t_{ij}^{*}\right)$, and the area under an estimated ROC curve (AUC). The size of the training dataset is n = 200 or n = 500; that of the test dataset is 200. Means of the quantities over N = 100 simulation replicates are reported.

n=200		proposed metdod			LVCF metdod
s	u	SPD(×100)	MSE(×100)	AUC	SPD(×100)	MSE(×100)	AUC
2	3	0.024	0.479	0.810	1.520	0.652	0.806
2	5	−0.159	0.469	0.868	3.345	0.787	0.864
4	3	−0.250	0.554	0.843	4.379	0.632	0.843
4	5	−0.603	0.530	0.902	4.119	0.669	0.902
6	3	−1.263	1.109	0.852	5.212	1.217	0.854
6	5	−1.472	1.021	0.896	4.302	1.009	0.899
n=500		proposed method			LVCF method
s	u	SPD(×100)	MSE(×100)	AUC	SPD(×100)	MSE(×100)	AUC
2	3	−0.280	0.344	0.815	0.595	0.554	0.813
2	5	−0.843	0.386	0.873	3.014	0.687	0.872
4	3	−1.034	0.345	0.851	4.061	0.464	0.852
4	5	−0.377	0.298	0.902	4.614	0.533	0.903
6	3	−0.209	0.477	0.861	6.425	0.768	0.862
6	5	0.156	0.361	0.905	5.788	0.753	0.905

From Table 1, we see that the proposed method leads to much smaller MSEs and absolute values of SPDs than the LVCF method, though the resulting AUCs are close for these two methods. Specifically, in the current simulation setting, our proposed method mitigates up to 40% of the MSEs of the predicted survival probabilities and eliminates up to over 90% of the absolute SPDs from the LVCF method. The poor calibration by the LVCF method is mainly caused by the biased estimates of regression coefficients. We evaluate the point estimates of regression coefficients, i.e., ${\widehat{\beta }}_1(s),\dots ,{\widehat{\beta }}_4(s)$, and summarise the results in Tables A1–A2 in Web Appendix C, where we can see that the LVCF estimates are fairly biased (up to 29% of the true values). The LVCF method is widely used in practice due to its methodological and computational simplicity and it may perform satisfactorily, especially when consecutive measurement times are close and biomarkers do not have large short–term variation. However, we see from this simulation study that it could lead to biased estimates of regression parameters and inaccurate prediction which can cause misleading model interpretation and wrong prognostic decisions.

3.2. Simulation for A Landmark Proportional Odds Model

For a landmark PO model, simulated biomarker trajectories and Kaplan–Meier survival curve estimate for the training dataset from one simulation sample are plotted in Figure A1 in Web Appendix B. Prediction evaluation is summarised in Table 2. Compared to the LVCF method, it is seen that the proposed method results in comparable AUCs, but much smaller MSEs and absolute values of SPDs. Point estimates of regression coefficients are evaluated and summarised in Tables A3–A4 in Web Appendix C. We similarly see that the LVCF method leads to obviously biased estimates, while the proposed method yields negligible bias, especially for a large sample size (n = 500).

Table 2.

Summary of the prediction performance evaluation of the proposed method and the LVCF method based on a landmark PO model. We consider mean squared error (MSE) and survival proportion difference (SPD) regarding the predicted survival probability ${\widehat{\pi }}_i\left(u;t_{ij}^{*}\right)$, and the area under an estimated ROC curve (AUC). The size of the training dataset is n = 200 or n = 500; that of the test dataset is 200. Means of the quantities over N = 100 simulation replicates are reported.

n=200		proposed metdod			LVCF metdod
s	u	SPD(×100)	MSE(×100)	AUC	SPD(×100)	MSE(×100)	AUC
2	3	−1.291	0.565	0.847	−3.628	1.095	0.842
2	5	−0.635	0.657	0.854	−1.094	1.182	0.849
4	3	−0.289	0.726	0.851	1.152	0.823	0.850
4	5	−0.188	0.816	0.860	2.562	1.037	0.858
6	3	−0.536	0.906	0.855	2.393	1.079	0.851
6	5	−0.136	0.962	0.848	2.990	1.045	0.845
n=500		proposed method			LVCF method
s	u	SPD(×100)	MSE(×100)	AUC	SPD(×100)	MSE(×100)	AUC
2	3	−0.259	0.400	0.847	−2.208	0.884	0.844
2	5	−0.275	0.409	0.853	0.060	0.906	0.851
4	3	−0.315	0.326	0.850	1.237	0.442	0.850
4	5	0.288	0.333	0.860	2.761	0.624	0.859
6	3	0.111	0.408	0.858	3.138	0.536	0.858
6	5	−0.507	0.400	0.857	2.813	0.579	0.857

From Section 3.1 and Section 3.2, it is seen that the proposed method effectively eliminates the bias of parameter estimation and performs satisfactorily in terms of calibration and discrimination for prediction. Therefore, our proposed landmark models and the estimation method described in Section 2.2 overall do well and outperform the LVCF method.

3.3. Simulation under Model Misspecification

So far we have studied the performance of the proposed method under either a PH model or a PO model when the model is correctly specified. Landmark models are often used as working models for prediction in practice. Since the true distributions of longitudinal data and the correct models are generally unknown in practice, misspecified working models could happen. In this subsection, we investigate how the proposed method performs under model misspecification.

Data are generated based on a landmark PO model. Then, we use model (4) with g(x) = log{−log(x)}, i.e., a landmark PH model, for estimating the model components and conducting prediction. Performance of the misspecified working model is evaluated and compared with correct model. MSE, SPD and AUC are assessed and summarised in Table 3. Note that the true values of ${\widehat{\pi }}_i\left(u;t_{ij}^{*}\right)$ used for calculating the MSEs in Table 3 are based on a landmark PO model (4) with g(x) = log{(1 – x)/x}. From Table 3 we see that SPD and MSE obviously increase when working model is misspecified. However, AUC is found not sensitive to model specification. In addition, point estimates of regression coefficients are examined for bias, standard errors and mean squared errors. Standard errors of the estimates from each simulation are estimated by bootstrapping as described earlier and B = 200 bootstrap samples are generated. The results are summarised over N = 100 simulations and are represented in Table 4. It shows that misspecified working model could lead to larger bias, larger MSEs and lower coverage than the correct model. When working model is correctly specified, on the other hand, we see that the bias is negligible, bootstrap estimated standard errors agree with the empirical standard errors and coverage probabilities are close to the 95% nominal level.

Table 3.

Summary of the mean squared error (MSE) and survival proportion difference (SPD), and the area under an estimated ROC curve (AUC) for the proposed method. Data are generated based on a landmark PO model. Correct and misspecified working models are compared. The sizes of training dataset and test dataset are both 200. Means of the quantities over N = 100 simulation replicates are reported.

		misspecified working model			correct working model
s	u	SPD(×100)	MSE(×100)	AUC	SPD(×100)	MSE(×100)	AUC
2	3	−0.201	0.776	0.846	−1.291	0.565	0.847
2	5	1.152	0.871	0.852	−0.635	0.657	0.854
4	3	1.098	1.001	0.848	−0.289	0.726	0.851
4	5	1.436	1.023	0.858	−0.188	0.816	0.860
6	3	1.042	1.146	0.853	−0.536	0.906	0.855
6	5	0.931	0.992	0.847	−0.136	0.962	0.848

Our proposed landmark linear transformation model allows time–varying model specification with a link function g specified. This provides more flexibility adapting to complex real data situations and reduces the adverse effects that a wrong working model could cause. This is the biggest merit of the method proposed in this article, making it distinguished from the predecessors. Model specification parameters such as r in (3) can be considered as tuning parameters and chosen by cross–validation. We will further discuss this in the analysis of the AASK data.

4. Application to AASK Data

4.1. The Analytic Set and Prediction Models

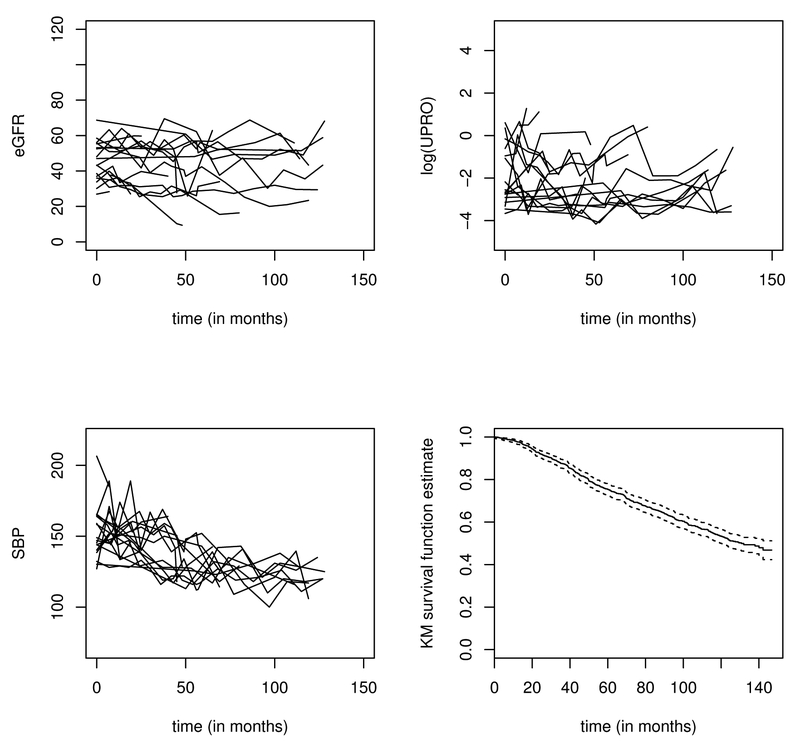
In this section, we apply the proposed methodology to an AASK dataset and predict the time to a terminal event of ESRD or death using longitudinal biomarkers. This composite outcome is often used in CKD epidemiology research (e.g. De Nicola et al. (2011); Chen et al. (2016); Mc Causland et al. (2016)) including the AASK data (Erickson et al., 2012). Our analytic set consists of 992 patients who have longitudinal measures of BP, eGFR, and proteinuria, out of the 1094 patients originally enrolled in this study. Among the 992 patients, 449 reached the terminal event before loss to follow–up. The length of follow–up is up to 12 years, with a median of 7 years (standard deviation, 3.8 years). On average, each patient has 9 follow–up visits and the median visit gap time is about 7 months (1st quartile = 6 months, 3rd quartile = 12 months, standard deviation = 6.3 months). We include in our prediction model three time–varying biomarkers, eGFR, logarithm of urine protein (UPRO), BP and one time–fixed variable, gender (female = 1, male = 0). Figure 2 shows the trajectories of eGFR, log(UPRO) and BP of 20 randomly selected patients and the Kaplan–Meier estimate of the marginal survival curve for the 992 patients. In addition to using the “current” value of these biomarkers, we also consider using the linear slope of eGFR in the past 3 years as a predictor variable. The eGFR is one of the most important measures of renal function. Its slope measures the “progression rate” of the decline in renal function. The individual slope of eGFR for each patient at a measurement time is calculated by fitting a random intercept–slope model to the eGFR data collected during the past 3 years. We also include the volatility of BP. Volatility is calculated as the mean of the absolute difference of two consecutive measures in the past three years. To our knowledge, there has been no published joint modeling methodology that can handle multiple longitudinal biomarkers with nonlinear longitudinal trajectories and volatility. Therefore, existing methods in literature cannot sufficiently address the analytical challenges in the AASK data.

Fig. 2.

Trajectories of eGFR, log(UPRO), and blood pressure for 20 randomly selected subjects and the Kaplan–Meier (KM) estimate of the marginal survival curve for 992 patients in the AASK data.

Since both the slope and volatility are defined over a period of three years, we use a reduced prediction model for prediction at times prior to the third year. For prediction times less than or equal to 3 years, we have the prediction model as (4) with Z_i(s) defined by eGFR(s), log(UPRO)(s), BP(s) and gender. For prediction times greater than 3 years, we let Z_i(s) be eGFR(s) and eGFR–slope(s), log(UPRO)(s), BP(s) and BP–volatility(s), and gender. We randomly select 300 patients from the 992 patients as a test dataset and use the rest as a training dataset. We present the results at the two landmark times, s = 48 and s = 72 months. Although prediction can be done at any measurement time $\left(t_{ij}^{*}\right)$ in the test dataset, to facilitate presenting the assessment of predictive performance at a fixed universal time point, e.g., s = 48 months, we use the most recent measurement time $t_{ij}^{*}$ of patient i in the test dataset prior to s as her/his prediction time. Following that, we estimate the conditional survival probability $S\left\{u;s|Z_i\left(t_{ij}^{*}\right)\right\}$ by (11) given in Section 2.3; we estimate $\beta \left(t_{ij}^{*}\right)$ and $H\left(u;t_{ij}^{*}\right)$ needed in (10) by the method introduced in Section 2.2 using the training dataset. We set the prediction horizon u starting from landmark time s at 3 years. We employ the areas under the time–dependent ROC curve to assess the predictive performance for censored failure times. The time–dependent ROC can be estimated following the method introduced by Li et al. (2016a), and has been implemented in R package tdROC. In the following subsections, we use the AUC corresponding to the time–dependent ROC computed by tdROC as the metric to evaluate predictive performance.

4.2. Bandwidth and Model Selection

To select bandwidths, we use Monte Carlo cross–validation (Picard and Cook, 1984), also known as repeated random sub–sampling validation, based on a landmark PH working model. We consider bandwidths h = 2.5, 3.0,…,5.0 and h = 5.5, 6.0,…,8.0 months for s = 48 and s = 72 months, respectively. The candidate bandwidths are larger at later landmark times because the sample sizes in the corresponding at–risk sets are smaller. Specifically, each time we randomly select 300 patients to compose a test dataset and treat the rest as a training dataset and then implement prediction for individuals in the test dataset at landmark times s = 48 and s = 72, with a prediction horizon u = 36 months. We repeat this random split 100 times and calculate the AUC each time. We use the average AUC from 100 replicates to select the best bandwidth for each landmark time. As a result, we select h = 3 months (AUC=0.8018) for s = 48 months and h = 7 months (AUC=0.8410) for s = 72 months, which is understandable since smaller bandwidths are suitable for earlier landmark times when the risk sets are relatively larger.

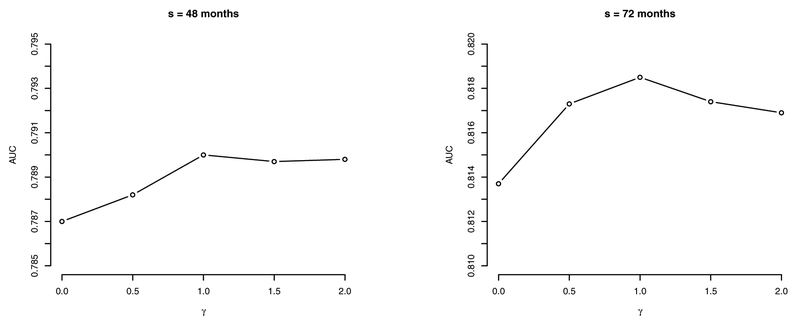
At each landmark time s, we consider a transformation studied by Dabrowska and Doksum (1988); Chen et al. (2002); Zeng and Lin (2006), i.e., ${\lambda }_{{ϵ}_s}(t)=\text{exp}(t)/\{1+r_s\text{exp}(t)\}$, where ${\lambda }_{{ϵ}_s}(t)$ denotes the hazard function of ϵ_s in model (5). We consider r_s = 0,0.5,1,1.5,2, as in Chen et al. (2002), where r_s = 0 and 1 corresponds to a PH model and a PO model, respectively. Note that r_s is allowed to vary with landmark time s. Prediction based on the method introduced in Section 2.2 & Section 2.3 with the selected bandwidths is performed at s = 48 and s = 72 months. The resulting AUCs of prediction with horizon u = 36 months are exhibited in Figure 3, where the PO model (i.e., r_s = 1) turns out to be the best working model with the highest AUC estimates. Moreover, we see that at a latter landmark time (e.g., s = 72 months), predictive performance is more affected by different values of r_s than at an earlier landmark time (e.g., s = 48 months).

Fig. 3.

AUC measures from landmark times of 48 months and 72 months at prediction horizon u = 36 months, for r_s = 0, 0.5, 1, 1.5, 2.0 in the AASK data.

4.3. Prediction and Performance Evaluation

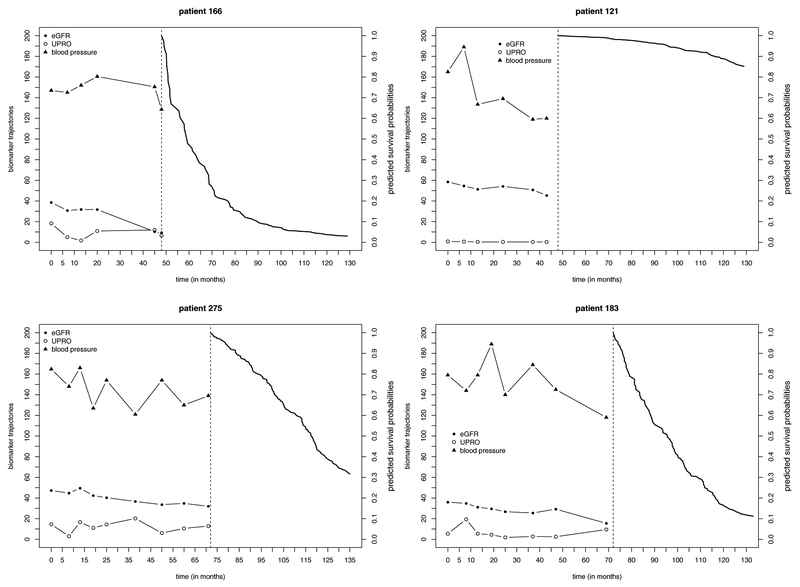
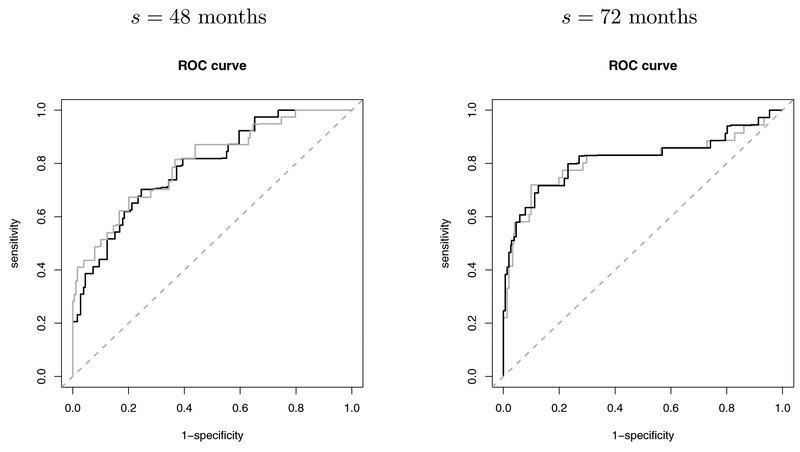
Based on the selected model and bandwidth, we predict the time to ESRD or death in the test dataset of 300 individuals who are randomly selected from the original AASK dataset. Figure 4 illustrates the trajectories of three longitudinal biomarkers (eGFR, UPRO, BP) and the predicted conditional survival probabilities $\widehat{S}\left\{u;s|Z_i\left(t_{ij}^{*}\right)\right\}$ for two patients (one has failed and one is alive at the end of follow–up) at each of the landmark times (s = 48 months and s = 72 months). We compare the proposed method with the LVCF method based on a PO model. For the LVCF method, regression parameters are estimated by solving (6) and (7) with t_ℓ = s and the most recent measurement at t_ij ≤ s in the training dataset carried forward to s. Predictive performance is evaluated by time–dependent ROC curves calculated by the R package tdROC. The resulting ROC curves are presented in Figure 5. At s = 48 months, AUCs yielded by the proposed method and the LVCF method are respectively 0.7900 and 0.8028; at s = 72 months, AUCs of the proposed method and the LVCF method are respectively 0.8185 and 0.8126.

Fig. 4.

Trajectories of biomarkers and predicted conditional survival curves for patient 166 (failed at 52:83 months), patient 121 (censored at 128:92 months), patient 183 (failed at 91:79 months), and patient 275 (censored at 107:99 months) in the AASK data. Measures of UPRO are multiplied by 10; eGFR and blood pressure are plotted on their original scales. Landmark times s = 48 and s = 72 months are denoted by vertical dashed lines.

Fig. 5.

ROC curves calculated by the LVCF method (grey solid curve) and by the proposed method (black solid curve).

To validate this result, we conduct the Monte Carlo cross–validation similarly as we did for bandwidth selection. The AUCs averaged over the 100 cross–validation splits are found to be 0.8025 (s = 48) and 0.8405 (s = 72) by the proposed method, and 0.8023 (s = 48) and 0.8341 (s = 72) by the LVCF method, respectively. Overall, we see that the proposed method shows satisfactory discrimination ability with high AUCs around 0.80. Because the AASK includes a trial phase followed by a cohort phase, biomarker measurement times are nearly regular especially at early follow–up times. Furthermore, in the studies on chronic diseases such as CKD, patient’s longitudinal biomarker measurements usually do not have instant or rapid changes over time at the individual level; see Figure 2. The overall levels of biomarkers are rather more powerful for discrimination. Therefore, the LVCF method produces very close AUCs to the proposed method as expected. In addition, the proposed method that involves kernel smoothing and uses visits within the neighbourhood of a selected landmark time could yield some bias when visit times are nearly regular (e.g. at s = 48). However, when patients’ visit times are more irregular (e.g. at s = 72), we see that the proposed method leads to a relatively higher AUC.

5. Discussion

Dynamic prediction of a clinical event with longitudinally measured biomarkers or other prognostic information is important in clinical practice for early prevention, treatment planning, and medical cost estimation. Multiple longitudinal biomarkers with highly complex and diverse trajectories at the individual level are commonly seen in clinical and biomedical applications. Joint models need specific model assumptions for each longitudinal biomarker and such assumptions are usually untestable in practice. The method of landmarking is particularly suitable for problems with multiple longitudinal biomarkers and nonlinear trajectories, for which it is difficult to identify the distribution and specify an appropriate model for each longitudinal variable. The method we propose in this article uses local polynomial smoothing to nonparametrically estimate the model components at any selected landmark times so that minimum model assumptions are imposed and the estimation is robust. Furthermore, most joint model literature or software consider only univariate cases and assume linear mixed–effects model for longitudinal data, e.g. Rizopoulos (2010, 2011). This is because multiple longitudinal biomarkers or nonlinear trajectories necessitate numerical integrations over high–dimensional random effects in the joint likelihood. Then, computation is very intensive and convergence can even be poor. Our proposed method readily handles multiple longitudinal biomarkers without notable increase in computational complexity when the number of biomarkers increases. We consider the LVCF method for comparison in simulation and real data example, because this method is often considered attractive in real data analysis due to its simplicity. However, it could lead to biased estimation and inaccurate prediction especially when measurement times are sparse and longitudinal data have large short–term variation. It is shown in our simulation studies that the predicted survival probabilities by the LVCF have large MSEs and the resulting coefficient estimates have non–negligible bias, which could lead to misleading interpretation and ill decisions.

In the existing literature about landmark models for dynamic prediction, a variety of formulations based on Cox models have been developed and studied. However, model assumption regarding the failure time process calls for attention. The assumption that the PH hold at any landmark time is a strong assumption that can be violated in many applications. Misspecified models also can lead to biased estimation and invalid prediction. We made an attempt to relax this assumption by proposing a class of landmark transformation models. It is more flexible and includes many predecessors based on proportional hazards as special cases. The proposed method is applied to the AASK data to predict the risk of ESRD or death. The AASK data illustrate a situation in which the Cox model is not the best fitting model. In fact, the landmark Cox model performed worse than all the other model candidates according to the AUC results in Figure 3. This finding suggests that by relaxing the model assumptions, we may improve the model fit and predictive performance.

With further pursuit of flexibility, we can incorporate time–varying coefficients in model (3) so that covariate effect β(s) depends not only on the landmark time s but also on the elapsed time since s, denoted by u. Zheng and Heagerty (2005) discussed this extension based on the partly conditional proportional hazards model and incorporated local linear kernel smoother to estimate time–varying model parameters. We can extend Zheng and Heagerty (2005)’s model to our landmark linear transformation framework and consider time–varying coefficients β(u; s) as a smooth bivariate function of u and s, i.e.

$$g\left[P\left\{T_{is}>u|Z_i(s)\right\}\right]=H(u;s)+Z_i^{\prime }(s)\beta (u;s),$$

varying coefficients β_k(u; s), k = 1,…, q, can be modeled with expansions of a set of smooth basis functions such as B–splines or regression splines, e.g. ${\beta }_k(u;s)=B_d^{\prime }(u;s){\gamma }_k(s)$, where B_d(u; s) denotes a B–spline basis function of u given s with d degrees of freedom and γ_k(s) is a d×1 vector of unknown regression parameters corresponding to the kth predictor Z_ik(s). Then, with replacement of β′(s)Z_i(s) with $B_d^{\prime }(u;s)\left({\gamma }_1(s),\dots ,{\gamma }_q(s)\right)Z_i(s)$ the estimation methods that are introduced in Section 2.2 can be straightforwardly extended to estimate H(u; s) and γ_k(s).

There are a few limitations to the proposed methodology. Estimating equations (8) and (9) given in Section (2.2) treat the residual lifetimes at multiple visit times of one subject independently. This “working independence” approach has been widely used in the analysis of multivariate survival data (Lin, 1994; Spiekerman and Lin, 1998). However, this may cause the estimators to be less efficient than a full–likelihood approach, especially for cases where people have very close follow–up visit times. In addition, we currently assume that visit times are randomly distributed and are independent of the time–to–event outcomes. In practice, the frequency and timing of visits can depend on disease progression, which in turn may be related to the biomarkers or the risk of the failure event. Dynamic prediction using longitudinal data measured at informative visit times is being studied as an extension. In Section 4, we studied a composite endpoint in the AASK data as an illustration of the proposed methodology. Competing risks models would be considered in the future to predict the risk of dialysis or transplantation with considering death occurring before that as a competing risk. Furthermore, although the proposed linear transformation models relax the model assumption of a landmark Cox model, further improvements can be sought by considering non–linear models. Future work to address these problems will be valuable.