Energy metabolism controls phenotypes by protein efficiency and allocation

Significance

Organisms use the central carbon metabolism for both breakdown of substrate into biomass precursors and extraction of energy, making the pathways overlapping. We present a modeling concept that can decompose the overlapping pathways and hence account for protein cost for each of them. This enables comparisons between pathways within an organism or between organisms. Using this concept, we model energy metabolism for Escherichia coli and Saccharomyces cerevisiae, and accurately predict metabolic switches. Besides, we find that the total mass of the proteins involved in energy metabolism is conserved across conditions, which is simulated to correlate with ATP production rate in cells growing at unlimited conditions.

Abstract

Cells require energy for growth and maintenance and have evolved to have multiple pathways to produce energy in response to varying conditions. A basic question in this context is how cells organize energy metabolism, which is, however, challenging to elucidate due to its complexity, i.e., the energy-producing pathways overlap with each other and even intertwine with biomass formation pathways. Here, we propose a modeling concept that decomposes energy metabolism into biomass formation and ATP-producing pathways. The latter can be further decomposed into a high-yield and a low-yield pathway. This enables independent estimation of protein efficiency for each pathway. With this concept, we modeled energy metabolism for Escherichia coli and Saccharomyces cerevisiae and found that the high-yield pathway shows lower protein efficiency than the low-yield pathway. Taken together with a fixed protein constraint, we predict overflow metabolism in E. coli and the Crabtree effect in S. cerevisiae, meaning that energy metabolism is sufficient to explain the metabolic switches. The static protein constraint is supported by the findings that protein mass of energy metabolism is conserved across conditions based on absolute proteomics data. This also suggests that enzymes may have decreased saturation or activity at low glucose uptake rates. Finally, our analyses point out three ways to improve growth, i.e., increasing protein allocation to energy metabolism, decreasing ATP demand, or increasing activity for key enzymes.

ATP is the energy currency in living cells and the key to drive energy-consuming processes such as growth, motility, and stress-related functions. The energy utilized for growth, e.g., macromolecular synthesis and growth-associated maintenance, can be defined as growth-associated energy costs (GAEC), while the energetic cost of other processes is referred to as non–growth-associated maintenance (NGAM). Accordingly, at steady state the total energy generated in cells should be allocated between GAEC and NGAM. Cells seem to have an upper bound of ATP production capacity as higher level of stress usually results in slower growth (1, 2), indicating a competition between GAEC and NGAM for the limited energy that can be provided by metabolism. Therefore, an interesting question is how to increase the maximal ATP production capacity. This is expected to improve fitness of cells, and thereby important in industrial processes and biotechnological applications.

ATP is mostly produced by a few pathways in the central carbon metabolism (CCM), which, in heterotrophs, e.g., Escherichia coli and Saccharomyces cerevisiae, includes glycolysis, by-product formation pathways, the tricarboxylic acid (TCA) cycle, and oxidative phosphorylation. These pathways together are defined as energy metabolism in this study, which is typically divided into 2 different strategies. One is glycolysis followed by the TCA cycle and oxidative phosphorylation, namely respiration, and the other is glycolysis followed by by-product formation pathways, namely fermentation. Moreover, the CCM acts as not only energy producer to extract ATP from substrate but also biomass producer to break down the substrate into biomass precursors, meaning that ATP-producing and biomass formation pathways are heavily overlapping and intertwined within the CCM. Another 2 questions accordingly arise, why cells select a particular ATP-producing mode for a given condition and how cells allocate resource between energy generation and biomass formation?

It has been proposed that there is a tradeoff between yield and rate of ATP production by the different metabolic modes (3). For example, cells prefer to use respiration when a high ATP yield is favorable, while they activate fermentation when a high rate is favorable. This hypothesis is, however, not sufficient to explain the concurrent use of both respiration and fermentation observed in glucose-limited chemostats (4–10). This may be explained by another tradeoff, which is between ATP yield and protein required for carrying the fluxes (11). The hypothesis that a higher yield pathway requires more protein than a lower yield pathway for the same glucose uptake rate has been predicted by computational analysis based on thermodynamics (12) or enzyme kinetics data (13), and experimentally confirmed by proteomics measurement (14). Furthermore, genome-scale metabolic models (GEMs) with the integration of protein constraints have shown improved predictions of metabolic switches (15–18).

Here, inspired by these efforts, we propose a modeling concept to investigate energy metabolism for E. coli and S. cerevisiae, the best-studied prokaryal and eukaryal microorganisms, respectively. We firstly decomposed energy metabolism into biomass formation and ATP-producing pathways, allowing for independent estimation of ATP yield and protein efficiency for each pathway. With the models we accurately predicted metabolic switches observed in experiments by fixing the protein constraint, which is in good agreement with the finding that protein allocation to energy metabolism is conserved. On the other hand, model simulations showed that increasing protein mass of energy metabolism or fraction of flux through low-yield ATP-producing pathway can improve ATP production rate. The former seems to be common in reality as we found in cells growing at unlimited conditions a strong correlation between protein mass of energy metabolism and the ATP production rate. Besides, we found that improved growth rate of evolved strains is caused by increased protein allocation and/or decreased ATP demand. Finally, we predicted that increasing the activity of some key enzymes in energy metabolism is an effective strategy for improving the specific growth rate.

Results

A Modeling Concept to Investigate Energy Metabolism.

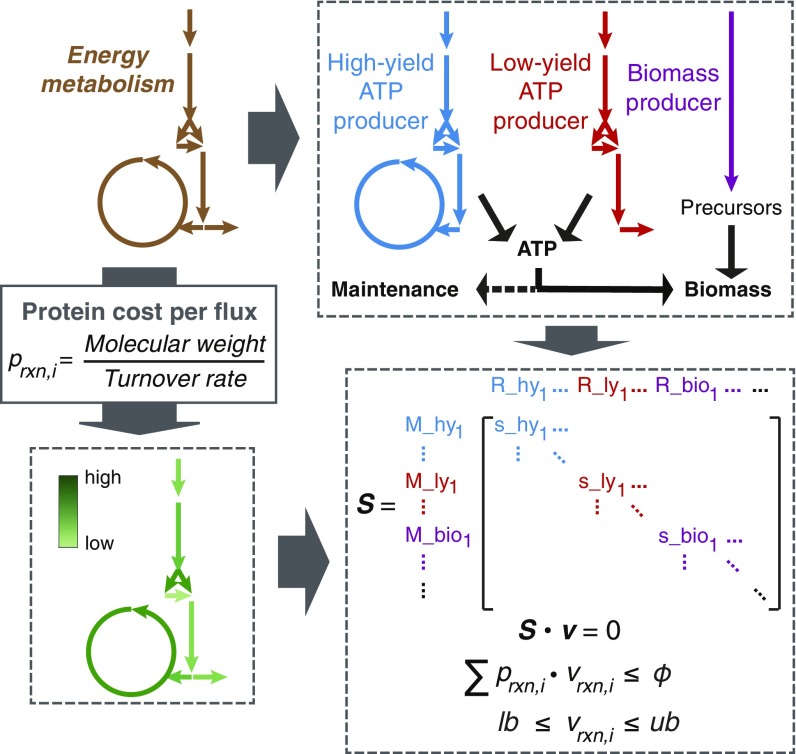
We propose a modeling concept (Fig. 1) that includes 2 parts, i.e., decomposing an entire metabolic network into independent pathways and integrating protein cost as an additional constraint. Firstly, the entire network of energy metabolism is extracted from a GEM, which consists of uptake of glucose, glycolysis, by-product formation, the TCA cycle, and oxidative phosphorylation. Subsequently, the network is decomposed into three pathways (Materials and Methods). Two of them are ATP-producing pathways and the other one relates to biomass formation. The ATP-producing pathways are divided into a high-yield (HY) and a low-yield (LY) pathway depending on the ATP yield per glucose. On the other hand, protein required for carrying 1 unit of flux is estimated for each enzymatic reaction, which is defined as “protein cost” in this study and equal to the molecular weight of the enzyme over its turnover rate. Accordingly, an additional constraint can be imposed using constraint-based simulations, i.e., the total protein content of energy metabolism. We applied the concept to model the energy metabolism of E. coli and S. cerevisiae, resulting in 2 models for describing aerobic growth on minimal media with glucose as the sole carbon source.

Fig. 1.

Overview of modeling energy metabolism. The modeling process includes 2 parts. One is to decompose energy metabolism into 3 independent pathways, i.e., HY ATP producer, LY ATP producer, and biomass producer. The ATP producers generate ATP, which is used for biomass formation and maintenance. The other is to estimate protein cost per flux for each reaction in the network, which is calculated using molecular weight and turnover rate of the enzyme that catalyzes the reaction. By doing so, constraint-based simulations can be performed, which can take into account the constraints of not only mass balance and bounds, but also total protein allocation to energy metabolism.

Modeling Energy Metabolism for E. coli and S. cerevisiae.

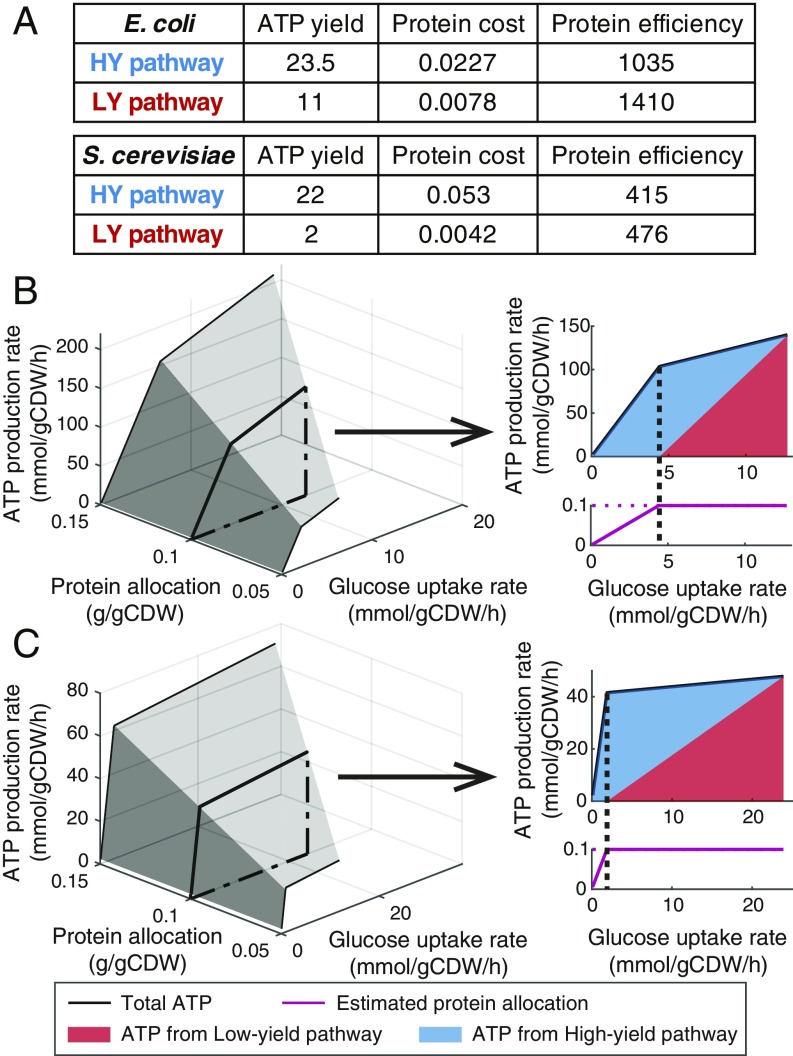
The energy metabolism in E. coli consists of the Embden–Meyerhof–Parnas (EMP) pathway, acetate fermentation, the TCA cycle, and oxidative phosphorylation (SI Appendix, Fig. S1), extracted from the latest E. coli GEM iML1515 (19). The EMP pathway followed by the TCA cycle and oxidative phosphorylation is defined as the HY pathway since it yields 23.5 ATP per glucose, higher than the LY pathway (11 ATP per glucose) that consists of the EMP pathway, acetate fermentation, and oxidative phosphorylation (Fig. 2A and SI Appendix, Fig. S1). Based on the protein cost information (SI Appendix, Fig. S1 and Datasets S1 and S2) and flux distribution (SI Appendix, Fig. S1), the total protein cost per flux of glucose can be calculated for both ATP-producing pathways. As a result, the HY pathway needs more protein mass than the LY pathway for consuming glucose at the same rate (Fig. 2A). Using ATP yield and total protein cost, we can calculate protein efficiency for producing ATP. The result shows that the LY pathway is more proteome-efficient than the HY pathway (Fig. 2A).

Fig. 2.

Model properties and simulations. (A) Model-inferred properties of energy metabolism in E. coli and S. cerevisiae. ATP yield: ATP produced per glucose consumed (Unit: molATP per molGlucose); Protein cost: protein mass required per flux (mmol/gCDW/h) of glucose (Unit: g/gCDW); Protein efficiency: ATP produced per protein mass per time (Unit: mmolATP/gProtein/h). (B) Simulations using E. coli model. (C) Simulations using S. cerevisiae model.

In S. cerevisiae, the energy metabolism consists of the EMP pathway, ethanol fermentation, the TCA cycle, and oxidative phosphorylation (SI Appendix, Fig. S1), extracted from iMM904 (20) and the consensus model Yeast7.6 (21). The HY pathway including the EMP pathway, TCA cycle, and oxidative phosphorylation yields 22 ATP per glucose, while the LY pathway including the EMP pathway and ethanol fermentation only yields 2 ATP per glucose (Fig. 2A and SI Appendix, Fig. S1). Likewise, the LY pathway shows higher protein efficiency than the HY pathway (Fig. 2A).

Subsequently, we used the models to investigate how to increase the ATP production rate. We changed the glucose uptake rate and protein allocation constraint, and then maximized the ATP production rate. The simulations show several similar trends in E. coli (Fig. 2B) and S. cerevisiae (Fig. 2C). For a given protein allocation constraint, the ATP production rate increases with glucose uptake rate but eventually reaches a maximum due to the limitation of protein allocation (Fig. 2 B and C). By increasing the protein allocation constraint, we can see an increase in not only ATP production rate for a given glucose uptake rate but also the maximal ATP production rate (Fig. 2 B and C). Interestingly, the 3D plots both have 2 distinct regions (Fig. 2 B and C), indicating 2 different metabolic modes. Next, we selected the simulations of protein allocation constraint at 0.1 gram per gram of cell dry weight (gCDW) to estimate ATP distribution and protein allocation. The 2D plots also both show a similar trend (Fig. 2 B and C), i.e., ATP is exclusively produced by the HY pathway at low glucose uptake rates while the LY pathway is activated when the glucose uptake rate exceeds a critical value. The switch of ATP production is consistent with the switch of the estimated protein allocation, i.e., above the critical glucose uptake rate the protein mass is limited. Besides, higher fraction of flux through the LY pathway leads to higher ATP production rate when the protein mass is limited (Fig. 2 B and C). Accordingly, there are 2 model-guided solutions to improve the ATP production rate: 1) increasing protein allocation to energy metabolism, and 2) increasing the fraction of flux through the LY pathway, which is accompanied by an increase in the glucose uptake rate.

Predictions of Metabolic Switches.

Given that the model is able to predict the switch of ATP production, it is expected to capture overflow metabolism (14) in E. coli and the Crabtree effect (10) in S. cerevisiae, which refer to the activation of the LY pathway in the presence of oxygen for fast-growing cells.

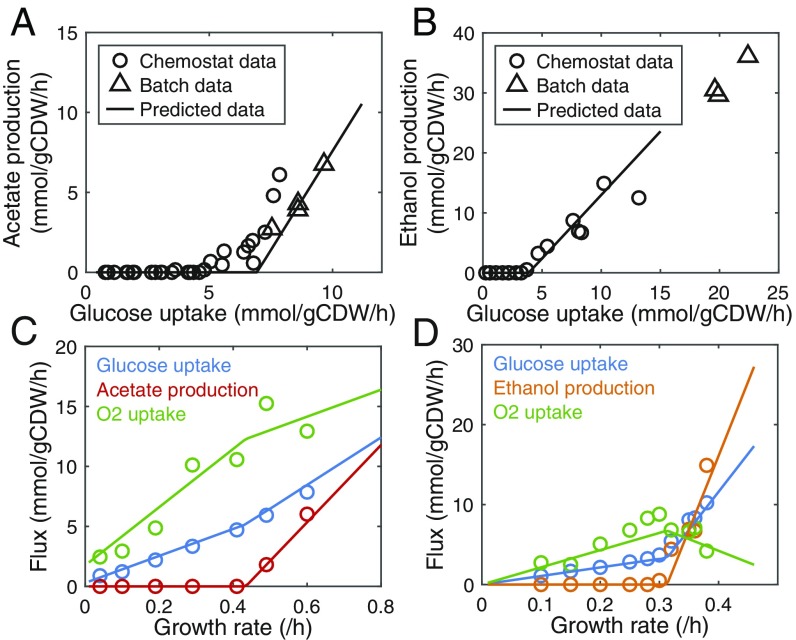
It seems that the protein allocation constraint determines the critical glucose uptake rate where the metabolic switch occurs (Fig. 2 B and C); we should therefore determine a reasonable protein allocation constraint. In order to obtain it, we minimized protein allocation for cells grown at unlimited conditions with constraining the models using experimentally measured exchange rates. The calculated protein allocation can be used as the constraint as it appears to be a protein-limited state when the LY pathway becomes active (Fig. 2 B and C). With the identified protein allocation constraint, we next minimized the glucose uptake rate for a range of growth rates, and found that the models predicted acetate production of E. coli (Fig. 3A) and ethanol of S. cerevisiae (Fig. 3B) as observed in glucose-limited chemostat and glucose batch cultures.

Fig. 3.

Model predictions of metabolic switches compared with experimental data. Circle represents data from chemostats, triangle represents data from batch cultures, and line represents predicted data. (A) Comparison between predicted and measured acetate production rate in E. coli. Chemostat data were obtained from figure 5 of ref. 22, which were originally reported in refs. 4–7 and 23; batch data were from refs. 24–27. (B) Comparison between predicted and measured ethanol production rate in S. cerevisiae. Chemostat data were obtained from figure 3 of ref. 22, which were originally reported in refs. 8 and 9; batch data were from refs. 28–30. (C) Comparison between predicted and measured exchange rates in E. coli. Data were from chemostats (4). (D) Comparison between predicted and measured exchange rates in S. cerevisiae. Data were from chemostats (9).

Despite capturing the overall changes in metabolites the simulations do not fit perfectly experiments (Fig. 3 A and B), e.g., the simulated critical points are not the same as experimental observations, neither are the slopes of product flux versus glucose flux. This could be explained by the fact that the in vivo turnover rates are not completely identical to those used in the models, which were mostly measured in vitro under various conditions. This is one of the shortcomings of turnover-rate–based modeling methods (15, 16, 18), which could be overcome by using an enzyme saturation factor (13, 18). Here we used overall enzyme saturation factors to adjust the protein efficiencies for the HY and LY pathways, respectively, rather than for individual enzymes, in the enzymatic reaction rate equation:

$$v_i=\overline{k_{cat,i}}\cdot {\displaystyle \sum E_i\cdot {\rho }_i},$$ [1]

where $\overline{k_{cat,i}}$ is the average turnover rate for each of the 2 pathways, ${\displaystyle \sum E_i}$ the protein allocation, and ${\rho }_i$ the overall saturation factor, which is not greater than 1. By changing ${\rho }_i$, we can adjust the protein efficiency for each pathway. We found that this alters the critical point and the slope. More specifically, as ${\rho }_{\text{LY}}/{\rho }_{\text{HY}}$ increases, i.e., the ratio of protein efficiencies between the LY and HY pathways increases, both the critical glucose uptake rate and slope of product flux versus glucose flux decrease (SI Appendix, Fig. S2). Only by increasing ${\rho }_{\text{LY}}/{\rho }_{\text{HY}}$ can we obtain best-fitted simulations (Fig. 3 C and D), meaning that the enzyme saturation should be higher for the LY pathway than for the HY pathway. As a result, we estimated the protein efficiency ratio between the LY and HY pathways in S. cerevisiae being 1.66 and in E. coli being 2.31, which is consistent with a reported value for E. coli of 1.92 (14). The slightly higher estimated value by our model may be due to 2 factors. One is a different phosphate/oxygen ratio used in our model, and the other is the fact that absolute protein mass was used in this study while the fraction of total protein in the previous one (14). Our analysis is an effort to estimate the ratio in S. cerevisiae, enabling comparison between these 2 model microorganisms.

Protein Allocation to Energy Metabolism Is Conserved.

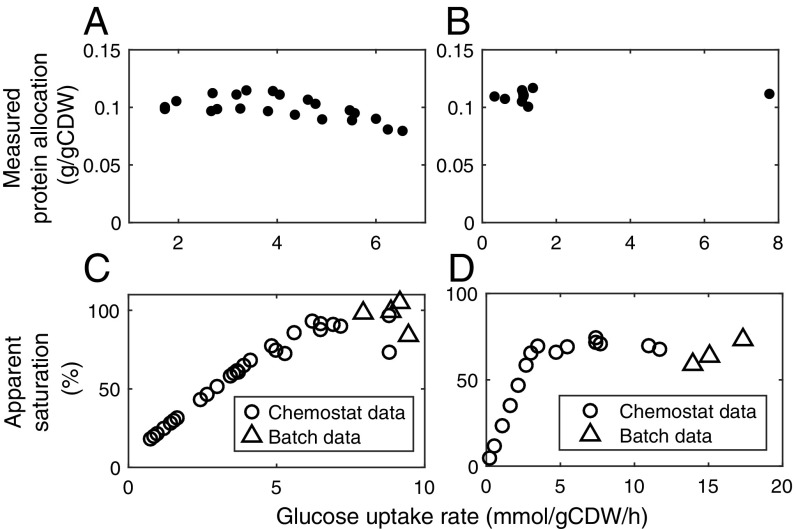
The protein allocation constraint plays a key role in predicting the metabolic switches, which is implemented as a fixed upper bound in the model. Given that not only the total protein content (31, 32) but also individual proteins within the CCM (7, 33–35) can vary greatly in diverse conditions, it is essential to investigate how the protein mass of energy metabolism responds to different environmental conditions. We collected absolute proteomics data of E. coli (7) and S. cerevisiae (36), and found that protein allocation to energy metabolism is almost conserved across a wide range of glucose uptake rates (Fig. 4 A and B) even though there are a great deal of individual proteins having considerably varying levels (SI Appendix, Fig. S3 and Dataset S3). This supports the workability of utilizing a fixed protein allocation for energy metabolism as a constraint in the model.

Fig. 4.

Analyses of protein allocation and saturation in energy metabolism. (A) Total protein mass of energy metabolism in E. coli. Data were from ref. 7. (B) Total protein mass of energy metabolism in S. cerevisiae. Data were from ref. 36. (C) Apparent saturation in E. coli. (D) Apparent saturation in S. cerevisiae.

As protein cost data are integrated, our models are capable of estimating the minimal protein allocation required for energy metabolism for a certain phenotype. The results show that the minimal protein allocation increases and then hits the upper constraint with increasing glucose uptake rates (SI Appendix, Fig. S4), and the switch point is at the critical point where the metabolic switch occurs. When the glucose uptake rate is lower than the critical value, there is clearly no need for the amount of protein actually allocated for energy metabolism. This discrepancy can be explained by a decrease in the apparent catalytic rate at low glucose uptake rates due to, for example, incomplete saturation with substrates (37) and/or decreased enzyme activity caused by posttranslational modification (38). Using the measured proteome levels assigned to energy metabolism (around 0.1 g/gCDW), we estimated the apparent saturation levels for different glucose uptake rates (see SI Appendix for details). The results show that the apparent saturation increases and then approaches an upper value with increasing glucose uptake rates (Fig. 4 C and D). This is equivalently consistent with the finding that the average in vivo catalytic rate tends to increase with growth rate (39).

Maximal Growth Rate Is Controlled by ATP Demand and Protein Allocation.

To investigate how energy metabolism controls the maximal growth rate, we applied the models to various E. coli and S. cerevisiae strains. The E. coli strains include 1 wild-type strain K-12 MG1655 (25), 2 knock-in mutant strains (rpoBE546V and rpoBE672K) (40), and 9 strains with increased growth rates through adaptive laboratory evolution (ALE) (25). The physiological data were obtained under exponential growth with excess glucose, where cells grow at the maximal rates. The S. cerevisiae strains include 1 wild-type strain CEN.PK113-7D (41) and 5 ALE strains with increased growth rates at 40 °C (2, 41). The physiological data were obtained under exponential growth with excess glucose at 40 °C, and the data of the wild-type strain at 30 °C were also included.

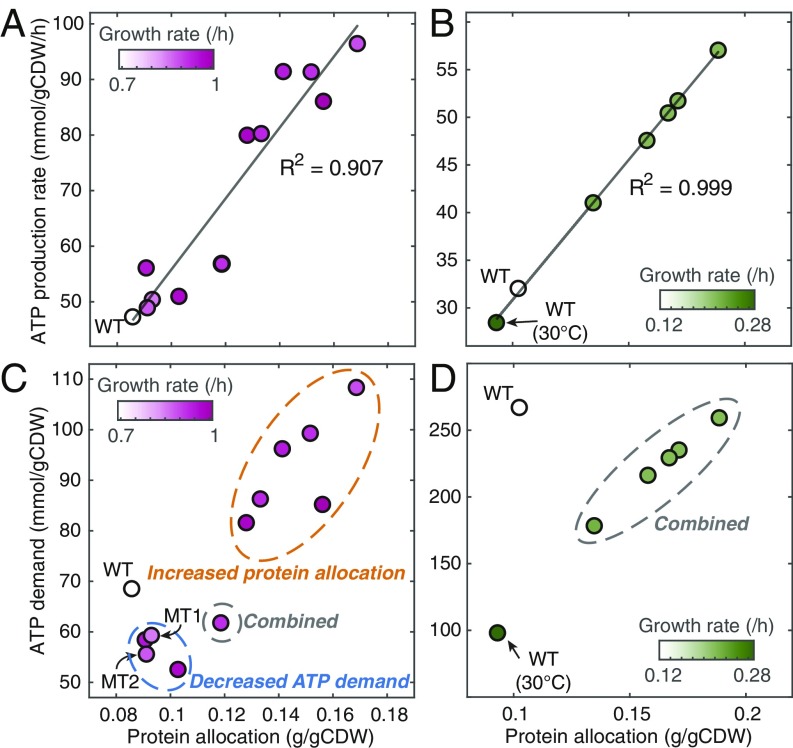
Generally, higher growth rate relies on higher ATP production rate, and as mentioned earlier there are 2 ways to increase the ATP production rate, with 1 being to increase the fraction of flux through the LY pathway. However, we found that all of the strains exhibit a mixed ATP-producing strategy at maximal growth, and there is no clear trend between the fraction of flux through LY pathway and growth rate (SI Appendix, Fig. S5). Accordingly, changing the fraction of flux through the LY pathway appears not to be a strategy for increasing growth rate. This is consistent with the previous finding that down-regulation of the HY pathway in E. coli resulted in only a small improvement of growth rate on glucose (42). The alternative is to increase protein allocation to energy metabolism. With the models, we estimated the protein content for each strain by assuming that all of the turnover rates in the models are conserved across strains as few mutations was detected involved in energy metabolism in the evolved strains (2, 25). We found that the correlation between the protein allocation to energy metabolism and growth rate is quite poor (SI Appendix, Fig. S5). We therefore questioned the correlation between the ATP production rate and growth rate, and found that it is also weak (SI Appendix, Fig. S5), which is against our original expectation. However, when plotting estimated protein allocation and the ATP production rate, we obtained strong correlations between them in both E. coli and S. cerevisiae (Fig. 5 A and B). This is consistent with our previous finding that protein allocation increases the maximal ATP production rate (Fig. 2 B and C).

Fig. 5.

Simulations of exponential growth. (A) Correlation between ATP production rate and protein allocation to energy metabolism in E. coli. (B) Correlation between ATP production rate and protein allocation to energy metabolism in S. cerevisiae. (C) Plot of ATP demand for biomass formation versus protein allocation to energy metabolism for E. coli strains. MT1 and MT2 are knock-in mutant strains, rpoBE546V and rpoBE672K, respectively from the study (25). (D) Plot of ATP demand for biomass formation versus protein allocation to energy metabolism for S. cerevisiae strains.

When we compared protein allocation with the ATP demand for producing biomass (Fig. 5 C and D), which is calculated as the ATP use per gram of CDW, i.e., a yield rather than a flux, we obtained 2 distinct ways by which cells can achieve higher growth rate, i.e., increasing protein allocation to energy metabolism and/or decreasing ATP demand for biomass production. In the E. coli cases, the strains with increased growth rates can be divided into 3 groups (Fig. 5C). One group (orange circle in Fig. 5C) shows increased protein allocation to energy metabolism and also increased ATP demand, suggesting that the increase in protein allocation cannot only compensate increased ATP demand caused by other negative mutations but also support higher ATP supply for increased growth. Another group (blue circle in Fig. 5C) shows a similar protein content of energy metabolism with the wild type but much lower ATP demand. In this group, there are 2 knock-in mutant strains, i.e., rpoBE546V and rpoBE672K, and the mutations in rpoB have been reported to decrease energy demand (40). The last group (gray circle in Fig. 5C) shows a combined strategy. For the S. cerevisiae cases, we see that increased temperature increases ATP demand (Fig. 5D), which is due to higher maintenance (43). Therefore, the decreased growth of the wild type at 40 °C compared to 30 °C can be explained by the fact that the ATP production rate is limited by the constant protein allocation to energy metabolism, and the increased ATP allocation to maintenance thereby decreases growth. For the ALE strains, we found that they all show increased protein allocation and decreased ATP demand (Fig. 5D), with the latter possibly contributed by the change in sterol composition (2).

Improving Enzyme Activity Is Predicted to Elevate Growth Rate.

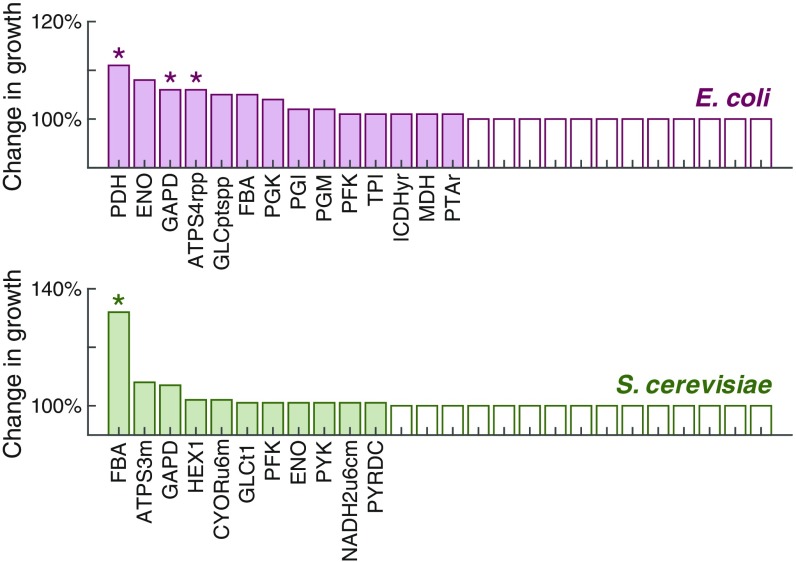
Besides the ALE approach, directed modification of enzymes by protein engineering is promising to obtain enhanced strains. While overexpression of glycolytic enzymes has been shown to result in no flux increase and even cause growth defects (44), improving protein efficiency for individual enzymes could be an effective strategy. To evaluate this we therefore doubled the turnover rate for each enzyme in the models, which corresponds to increasing the catalytic efficiency of the enzyme, and then normalized the predicted maximal growth rate to the reference which was obtained without changing any turnover rates. Hereby we identified several targets for improving the growth rate (Fig. 6). Several of these have been supported by the evidence that higher enzyme activity, rather than expression level, of an individual enzyme leads to higher growth or glycolytic rate (45–48). All of the predicted targets show very high protein cost for carrying fluxes according to the protein cost analysis (SI Appendix, Fig. S1). Accordingly, the models present an angle to aid rational design of strains for enhancing growth and metabolic fluxes.

Fig. 6.

Predicted change in growth rate after doubling turnover rate of each reaction in the models. The x axis only presents the reactions that can affect growth rate. Reaction ID is consistent with that in Datasets S1 and S2. The asterisk represents experimental evidence for the reaction: PDH (45), DAPD (46), ATPS4rpp (47), and FBA (48).

Discussion

In this study we propose a modeling method to decompose energy metabolism. This enables independent analysis of each pathway, e.g., estimation of protein efficiency, and comparison between pathways. With the concept, we modeled energy metabolism for E. coli and S. cerevisiae, allowing for the comparison between the 2 widely used model microorganisms. We found that the protein efficiencies of the LY and HY pathways in E. coli are much higher than those in S. cerevisiae (Fig. 2A), although most individual enzymes in E. coli show lower protein efficiencies than those in S. cerevisiae (SI Appendix, Fig. S6). For the LY pathway, higher protein efficiency in E. coli compared to S. cerevisiae is caused by higher ATP yield (5.5-fold) due to the utilization of oxidative phosphorylation even though accompanied by higher protein costs (around 2-fold) (Fig. 2A). For the HY pathway, we found that lower capacity of ATP synthase in S. cerevisiae compared to E. coli is a dominant factor to lower protein efficiency of the HY pathway (SI Appendix, Fig. S6), which is consistent with the previous finding that the ATP synthase has flux control over respiration (13). Therefore, considering the finding that E. coli and S. cerevisiae allocate considerable protein contents to energy metabolism (Fig. 4 A and B), higher protein efficiencies of the LY and HY pathways in E. coli could explain its faster growth compared to S. cerevisiae. Another interesting parameter is the ratio of protein efficiencies between the LY and HY pathways. We found that the ratio is higher in E. coli (2.31) than that in S. cerevisiae (1.66), meaning that E. coli shows a larger difference in the protein efficiencies between the LY and HY pathways. This enables E. coli to switch easier from the HY to LY mode, i.e., the ATP production rate at the critical point over the maximal ATP production rate is lower in E. coli than that in S. cerevisiae (SI Appendix, Fig. S7).

By imposing protein constraint, our models successfully predicted overflow metabolism in E. coli and the Crabtree effect in S. cerevisiae (Fig. 3 C and D). This is as expected since some other models using protein allocation constraints can also capture metabolic switches (13, 16–18). Differing from these previous modeling efforts, our models, however, only focus on energy metabolism, which is smaller in terms of the scope. This suggests that energy metabolism is sufficient to explain the metabolic switches in both E. coli and S. cerevisiae, which is consistent with the finding in E. coli based on a coarse-graining approach (14). Furthermore, we used a fixed upper bound for protein constraint in the model, which is consistent with the experimental finding that protein allocation to energy metabolism is conserved (Fig. 4 A and B). This static constraint can be adopted in our model but would not work for large-scale models as the total mass allocation to the proteins involved in those models may change greatly across conditions (18). The conserved protein content of energy metabolism suggests that cells tend to reallocate protein resource within energy metabolism rather than exchanging with other processes. On the other hand, it suggests that below the critical point cells still keep the constant mass of protein in energy metabolism but operate with decreased saturation or activity as described by the apparent saturation (Fig. 4 C and D). However, there is still a limitation of our method, i.e., the lack of regulation beyond translation, which is also a common problem in other turnover-rate–based models (16, 18). A potential solution is to integrate already-known regulation into the model by adjusting the saturation factor ${\rho }_i$ in Eq. 1 for specific enzymes. For example, given that the activity of phosphotransferase system (PTS) in E. coli changes proportionally with growth rate (16), one could set a linear growth-rate–dependent ${\rho }_i$ for PTS to implement this regulation. This is expected to expand the applicability of the model in future studies.

With the models, we investigated the maximal growth rate and found that ALE strains having increased growth rate exhibit either or both of the following changes, i.e., increase in protein allocation to energy metabolism and decrease in ATP demand (Fig. 5 C and D). The link between protein mass of energy metabolism and growth rate is established in this study by the strong correlation between protein allocation to energy metabolism and ATP production rate in cells exponentially growing at unlimited conditions (Fig. 5 A and B). Our models predict that most of the ALE strains have evolved to allocate greater protein mass to energy metabolism compared to the wild-type strains (Fig. 5 C and D). Considering that the maximum growth rate of the wild-type strain E. coli NCM3722 is higher than that of MG1655 at the same condition (17), we estimated the protein mass of energy metabolism for each. It has been shown by proteomics data that NCM3722 allocates around 13% of the total proteome to energy metabolism (14), while it is around 9% (Dataset S3) in MG1655 according to the PaxDb database (49). Therefore, higher growth rate of the strain E. coli NCM3722 could be contributed by its higher protein content in energy metabolism. Besides, it has been shown that the overexpression of LacZ, which is able to reduce the proteome of energy metabolism (50), decreases growth rate of E. coli (14, 50). Taken together, it appears to be validated that increased protein allocation to energy metabolism may improve growth rate.

Overall, by modeling energy metabolism for E. coli and S. cerevisiae, we showed 3 potential strategies to improve growth rate: 1) decrease ATP demand for growth, 2) increase the proteome allocation for energy metabolism, or 3) increase activity for key enzymes. The first 2 strategies can be achieved through ALE approach, and using our modeling approach we could clearly calculate which strategy a given strain has chosen. Besides, the model is able to predict the key enzymes that could limit growth due to low protein efficiency, and modification of the enzymes would be an effective strategy to improve growth rate. In conclusion, we therefore believe that our simple model is very useful for analysis of energy metabolism in engineered or evolved strains, which will find wide use in both the field of synthetic biology and basic biology.

Materials and Methods

All of the materials and methods are detailed in SI Appendix: modeling energy metabolism for E. coli and S. cerevisiae; protein cost analysis; model simulations; adjustment of protein efficiency; proteomics data analysis; calculating apparent saturation. All of the simulations were performed in MATLAB with the COBRA toolbox (51). Codes and models are available at https://github.com/SysBioChalmers/Energy_metabolism_model.