Important role of forest disturbances in the global biomass turnover and carbon sinks

Abstract

Forest disturbances leading to replacement of whole tree stands are a cornerstone of forest dynamics, with drivers including fire, wind-throw, biotic outbreaks and harvest. The frequency of disturbances may change over the next century, impacting the age, composition and biomass of forests. However, the variation in disturbance return time, i.e. the mean interval between disturbance events, across the world’s forested biomes remains poorly characterised, hindering quantification of their role in the global carbon cycle. Here we present the global distribution of stand-replacing disturbance return time inferred from satellite-based observations of forest loss. Prescribing this distribution within a vegetation model with a detailed representation of stand structure, we quantify the importance of stand-replacing disturbances for biomass carbon turnover globally over 2001-2014. Return time varied from less than 50 years in heavily-managed temperate ecosystems to over 1000 years in tropical evergreen forests. Stand-replacing disturbances accounted for 12.3% (95% confidence interval, 11.4-13.7%) of annual biomass carbon turnover due to tree mortality globally, and in 44% of forested area biomass stocks are strongly sensitive to changes in disturbance return time. Relatively small shifts in disturbance regimes in these areas would substantially influence the forest carbon sink, that currently limits climate change by offsetting emissions.

The amount of carbon stored in global forest biomass is similar to that in the atmosphere¹, and, excluding the effects of land-use change, has been estimated to have grown at ca. 1.5 PgC a^-1 over recent decades². This uptake has significantly slowed the atmospheric growth rate of carbon dioxide and thus the rate of climate change³. The accumulation of carbon in the stems of growing trees results from the balance between the growth rates of vegetation and the average length of time carbon remains in live biomass (hereafter, “biomass”), the turnover time, calculated as the carbon stock divided by the flux of carbon loss through plant and tissue death⁴. Quantification of this turnover time is crucial because it governs the size of biomass stocks for a given growth rate and it is one of the most significant uncertainties affecting projections of the terrestrial carbon cycle^5,6. Large-scale estimates of carbon turnover times for whole ecosystems and for biomass have been recently developed^7,8, but offer limited insight into the processes governing biomass stocks because the turnover flux could only be approximated by estimates of net primary productivity (NPP). This conflates turnover of soft tissues, such as leaves and roots, with that of the woody carbon pools that dominate biomass carbon stocks¹. To understand forest biomass turnover times globally, large-scale tree mortality rates must be quantified.

Tree death is often the culmination of a prolonged period of physiological stress related to a shortage of essential resources required for the synthesis of basic metabolites, for instance, due to shading by other plants, low water availability, or a shortage of soil nutrients such as N and P in plant-available forms^9,10. Alternatively, disturbances such as wind-throw, fire, insect and disease outbreaks, or anthropogenic activities such as wood harvest may constitute the cause of death^11–16. Disturbances act on scales ranging from a single tree to whole forest stands or landscapes. Here we investigate stand-replacing disturbances, defined operationally as discrete events resulting in the death of all, or almost all, living tree biomass at a scale of 0.1 ha or larger. Such events affect the average tree age as well as the stature, density and composition of forest stands^11,17, in turn impacting carbon storage¹⁸. There is evidence that the frequency of disturbances may be changing globally, with continued change likely in the future^{8,13–15,19,20}. Yet, to understand the consequences of future changes, it is first necessary to provide a baseline of current conditions. Such a baseline is lacking for stand-replacing disturbances across global forests.

The frequency of stand-replacing disturbances

We estimated the frequency of stand-replacing disturbances across all global forests at 1° spatial resolution. Drawing on a Landsat-based (2000-2014) forest-loss product²¹, we performed a space-for-time substitution, calculating the disturbance rotation period, τ, defined as the mean time period for the area disturbed to equal the area of the grid cell¹¹,

$${\tau }_i=\frac{A_{T,i}}{\overline{A_{L,l}}-\overline{A_{C,l}}}$$ (1)

where i is a grid-cell index, A_T is total forest area in that 1° x 1° grid cell, $\overline{A_L}$ the annual mean total forest loss over 2000-2014 calculated based on all Landsat-pixels within the grid cell and $\overline{A_C}$ the annual mean forest loss due to conversion to a non-forest land-use type (Methods). This observation-based τ is referred to as τ_o. While rare disturbances may be undersampled for individual grid cells, this is less of an issue across a neighbourhood of many grid cells, and the global-scale pattern is expected to be robust (Suppl. Note 1). We take τ as indicative of the typical or average disturbance return time from all causes at any location in a grid cell, reflecting causes such as wood harvest, as well as natural disturbances such as fires, large-scale wind-throws and biotic outbreaks. Whilst the drivers of each of these disturbance agents differ markedly, their consequences for carbon turnover in live biomass are assumed to be similar at large scales. Disturbances associated with the conversion of forests to other land-uses were explicitly excluded (Methods), allowing us to focus on dynamics within closed-canopy forests.

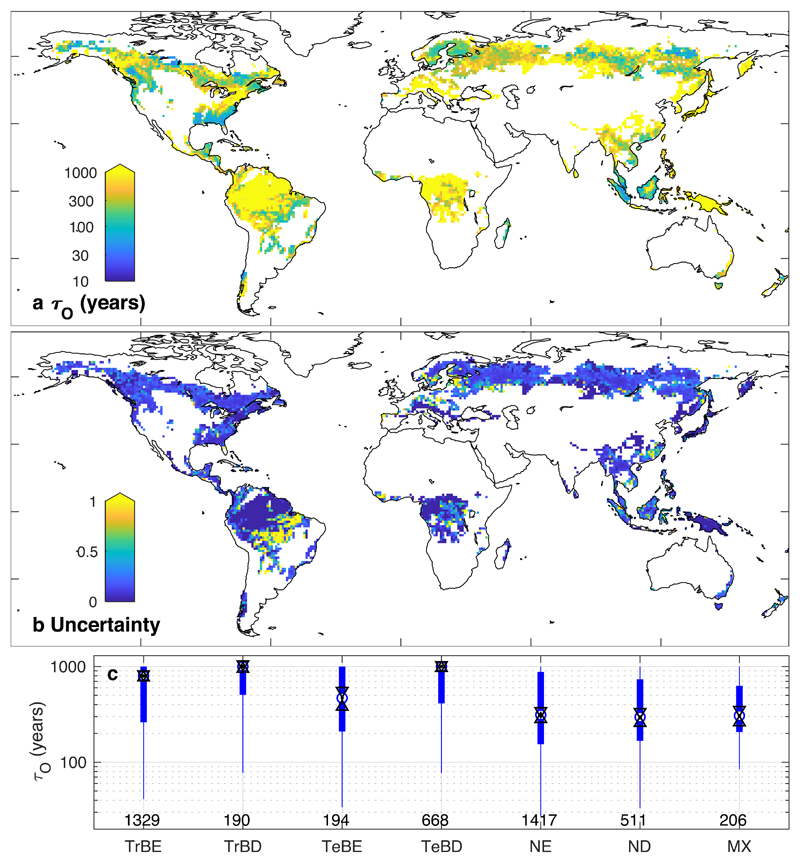
Disturbance return time varies substantially across the global forest area (Fig. 1a). The stand-replacing disturbances quantified here are more common in needleleaf and mixed forests (median τ_o of ca. 300 years) than they are in temperate or tropical broadleaf forests (median τ_o of 830 to more than 1000 years), however forest type emerges as a poor predictor of the spatial distribution of τ_o (Fig. 1c). In large areas of forest, stand-replacing disturbances are actually very rare events; 35% of forest area experienced stand-replacing disturbances with an average frequency equivalent to less than once every thousand years. In these forests the vast majority of tree mortality must thus be non-stand-replacing. The 95% confidence intervals for τ_o typically span a range less than one third of the absolute value of τ_o, except in areas of substantial land-use change (Fig. 1b, Suppl. Fig. 7).

Figure 1. Forest disturbance rotation periods.

a, τ_o calculated over 2000-2014. b, Uncertainty in τ_o, displayed as the difference between the 95% confidence intervals divided by the central estimate. Uncertainty values of zero reflect 95% confidence that τ_o is over 1000 years. c, Boxplot of τ_o grouped by forest type (see Methods for codes). Circles show the median value, black triangles the 95% confidence limits of the median, thick lines the interquartile range and whiskers extend to a maximum of 1.5 times the interquartile range. Numbers indicate the number of grid cells for each forest type.

We compared our results against an inventory-based compilation of forest stand age (GFADv1.1²²). Despite the different scale and characteristics of inventory data we found qualitative consistency in tropical evergreen and boreal forests, as well as some regions under intensive forest management, but also suggestions of a substantial amount of disturbance in some temperate forests below the scale captured in the Landsat data and of legacies of past afforestation (Suppl. Note 2, Suppl. Fig. 1). We also found consistency between our results and previous studies of disturbance frequencies in the tropics^17,23,24 and Canada²⁵ (Suppl. Note 3; Suppl. Fig. 2), and biotic outbreak disturbances in the U.S.A.²⁶ (Suppl. Note 3; Suppl. Fig. 3).

Influence of stand-replacing disturbances on the carbon cycle

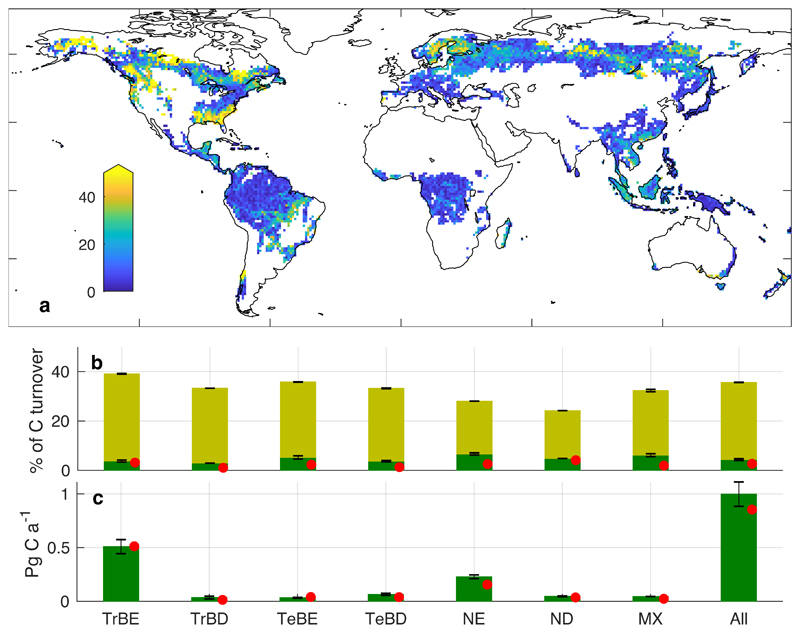
We apply the gridded estimates of τ_o within a dynamic global vegetation model (DGVM) with an explicit representation of forest stand structural development. τ was kept constant in each grid cell for the entire model simulation, calculating the pseudoequilibrium effect of τ_o on forest dynamics. Stand-replacing disturbances are simulated to dominate overall tree mortality, and associated carbon turnover, across large areas of the mid-latitude and boreal forests, accounting for over 60% in some locations, but are not the dominant cause of mortality in most tropical forests (Fig. 2a,b).

Figure 2. Carbon turnover fluxes from closed-canopy forest for 2001-2014.

a, Fraction of carbon turnover fluxes resulting from vegetation mortality due to stand-replacing disturbances (colour scale capped at 50%), calculated using τ_o to drive LPJ-GUESS. Breakdown by forest type of: b, fraction of carbon turnover fluxes resulting from vegetation mortality (whole bars) and from stand-replacing disturbances (darker shading); c, total turnover flux of vegetation carbon due to stand-replacing disturbance. Error bars show the range of simulations driven by the 95% confidence intervals of τ_o. Red dots show results from an observationally-based cross-check method (Methods). Forest types as in Fig. 1.

The total turnover of biomass carbon as a result of stand-replacing disturbances at pseudo-equilibrium in our simulations is 1.00 (95% confidence interval, 0.91-1.11) PgC a^-1, equivalent to 4.4 (4.0-4.9) % of total biomass carbon turnover in closed-canopy forests (i.e. including soft-tissue turnover) (Fig. 2b,c). These numbers are supported by an empirical cross-check based on satellite-derived NPP and biomass estimates which combined satellite LIDAR and radar observations with ground-based reference plots (red dots in Fig. 2b,c; Methods). The fraction of biomass carbon turnover due to mortality must be taken with caution, however, until biomass turnover rates from other forms of mortality can be fully constrained. Likewise the total turnover flux is dependent on accurate calculation of global biomass stocks, which remain uncertain¹.

The tropical broadleaved evergreen forest type provides the largest contribution to global biomass carbon turnover from stand-replacing disturbances, followed by needleleaved evergreen forest (Fig. 2c). Although stand-replacing disturbances are infrequent in tropical evergreen forest, the disturbance-related flux is significant, as the amount of biomass in these forests is very high compared to elsewhere^27–30. Conversely, low τ will tend to suppress biomass stocks, limiting the turnover flux generated in each disturbance event. Our estimates of biomass carbon losses for tropical evergreen forest will tend towards the upper limit of uncertainty because τ_o was capped at 1000 years for reasons of sampling (Methods); disturbance return times could in fact be even longer in some parts of the tropics³¹. However, as demonstrated below, the sensitivity of biomass to very high τ is low. Different disturbance agents cannot be distinguished in our data, but carbon emissions from wildfire taken from the GFED dataset³² summed over the same global forest area give a mean of 0.12 Pg C a^-1 over 2000-2014 (Methods), suggesting that fires are globally a relatively minor driver of stand-replacing disturbances in closed-canopy forests.

Sensitivity of forest biomass to disturbance return time

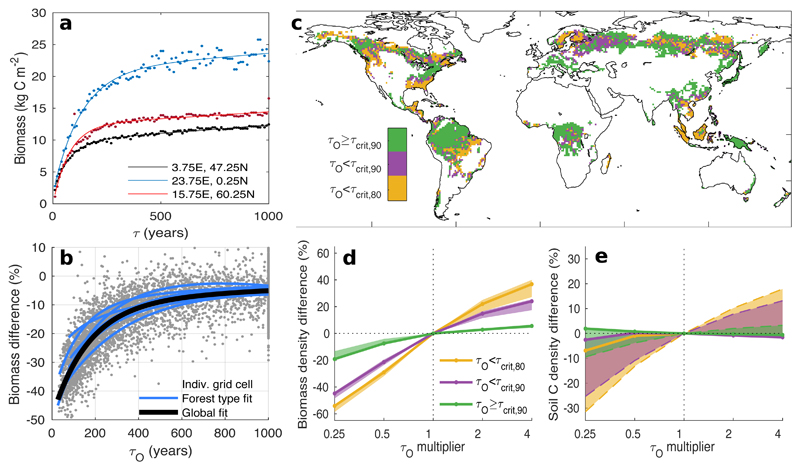
We ascertain the influence on ecosystem properties of possible changes in τ, or errors in its determination, for a randomly-selected grid cell from each of the tropical, temperate and boreal zones. For each grid cell we run 100 individual simulations varying τ sequentially within a plausible range of 10 to 1000 years. The resultant range in pseudo-equilibrium carbon stocks reflects variation in τ alone, independent of other environmental conditions or vegetation attributes (in particular that the resilience of vegetation to disturbance does not change with τ). The resulting curve of biomass carbon versus τ shows two distinct regimes (Fig. 3a); a regime of strong sensitivity of biomass to τ when τ is low, and a weak sensitivity regime when τ is high. These regimes result from shifts in the primary cause of dominant tree death. With low τ the majority of trees die from stand-replacing disturbance before they get old enough to die from another cause. Thus, τ emerges as the primary limit on simulated stand biomass across almost all stands. In contrast, when τ is large most canopy trees die from causes other than stand-replacing disturbances. In this case, τ is not a primary limit on simulated stand maximum biomass and changes in τ will only affect a subset of stands across the landscape at any time.

Figure 3. Sensitivity of biomass to changes in τ.

a, Simulated biomass versus τ for three random forested locations. Dots show individual simulations and lines a fitted exponential function. b, Sensitivity to τ_o of difference in simulated biomass between simulations with τ_o and 0.5τ_o. c, Sensitivity of biomass carbon stocks to changes in τ. Shading indicates the sensitivity regime. d, e, Effect of multiplicative perturbation in τ on vegetation and soil carbon density averaged across the different sensitivity classes. Shaded areas show range of sensitivity simulations testing assumptions on the type of disturbance assumed (solid lines for standard simulation) (Methods).

To map the sensitivity of forests to changes in τ globally we propose a new metric based on a fractional reduction of τ_o. Plotting τ_o against the difference in simulated biomass between global simulations run with τ_o and 0.5τ_o reveals a similar curve to the site-based simulations (Fig. 3b). We categorise global forests into two classes of sensitivity to disturbances: where the biomass under 0.5τ_o is less than 90% of that under τ_o, the forest is classified as having strong sensitivity to changes in τ (i.e. stand-replacing disturbance frequency is a strong control on biomass), with other areas having weak sensitivity (i.e. other forms of mortality control biomass). The τ0 at which this sensitivity threshold, τ_crit,90, is crossed varies with forest type, with a global average of 444 (429-457) years. This implies a mean recovery time of 222 years (i.e. 0.5τ_crit,90) to 90% of biomass stocks under τ_o. This is substantially longer than the 66 years reported for regain 90% of old-growth biomass in individual tropical forest stands³³ and follows because our simulations take account of succession and also scale one stage further to the net landscape change in biomass. I.e. individual stands may recover rapidly, but across the landscape more stands are in a recently-disturbed state. Overall, 44 (39-49) % of global forest falls into the strongly sensitive category, with 23 (20-27) % falling into a very strong sensitivity category in which halving τ_o leads to biomass dropping below 80% of that under τ_o (τ_crit,80). Forests in weak-sensitivity τ regimes are particularly located in tropical and temperate zones.(Fig. 3c).

The biomass content of weak-sensitivity forests would still be vulnerable to very large reductions in τ, for instance through a catastrophic shift to an entirely new disturbance regime³⁴ or introduction of a new disturbance type³⁵, but is robust to moderate changes in τ. This is demonstrated in additional simulations using τ_o adjusted up or down by a factor of up to 4; weak-sensitivity forests show large biomass changes only with substantial reductions in τ, whereas high-sensitivity forests show a steep relationship with τ (Fig. 3d). These results were robust to assumptions on the type of disturbance (shaded areas in Fig. 3d), although we note that selective effects of disturbance type on species composition^35,36, and thus potentially on biomass and turnover³⁷, could only be treated crudely within the plant functional type classes used for global simulation and there may be non-linear shifts not accounted for in the model³⁸. The time taken for forest biomass to approach a new pseudo-equilibrium state will depend on the new value of τ to which the ecosystem is subjected. In general, changes in τ will only be fully reflected in carbon fluxes over the next century if that new τ is of the order of 100 years or less.

Unlike the influence of τ on biomass (Fig. 3d), its influence on soil carbon stocks is strongly sensitive to the rate of decompostion of the resulting litter and soil organic matter, and also depends on biomass removals, for instance in conjunction with wood harvest (Fig. 3e). When disturbed biomass is transferred to the litter, disturbance only has notable negative consequences when τ becomes very low, reducing the fraction of longer-lived woody biomass entering the litter. However, harvest removals or burning of biomass substantially reduce the input rate of carbon to the soil, leading to a strong positive relationship between soil carbon density and τ. This strong sensitivity of soil carbon storage to the type, as well as the frequency, of disturbance, underlines the need for improved discrimination of different disturbance types at the global scale³⁹. Response times for soil will lag those for vegetation, and be influenced by the form of necromass left after disturbance⁴⁰, another area of high process uncertainty. Summing over both vegetation and soil, a widespread shift in disturbance regimes equivalent to a halving of τ_o across all closed-canopy forests would ultimately release 47-80 Pg C, depending on the form of that disturbance, while an increase in time between disturbances could promote carbon uptake (Suppl. Fig. 10).

Concluding remarks

The results of this study allow us to partition one important component of overall biomass turnover rates in global forests^1,8. Although stand-replacing disturbances constitute a relatively small portion of the overall global biomass turnover flux, small changes in τ would exert a strong influence on biomass stocks in almost half of the world's forests. DGVMs and land-surface models currently incorporating explicit representations of forest demography⁴¹ must properly account for stand-replacing disturbances to avoid biases in net carbon uptake or erroneous calibration of processes to account for these biases. Our study highlights the importance of accounting for variability in forest disturbance regimes, yet constitutes only a first step; 88% of global carbon turnover due to tree mortality is not explained by stand-replacing disturbances. It thus remains crucial to constrain other causes of mortality, including disturbances below stand-scale^23,42, drought⁴³, and demography. High-resolution data from satellites, along with forest inventories, will be key in this regard.

Our results provide a snapshot of a global stand-replacing disturbance pattern that may be undergoing rapid change^13–15. Drivers of such change, whether climate, management or otherwise are uncertain and likely highly region-specific^{13–16,19,20}. Future work must consider how carbon emissions through changes in τ are likely to interact with other aspects of environmental change, such as the fertilising effects of rising CO₂ concentrations, which may reduce vulnerability to disturbance⁴⁴, as well as seeking to close the feedback loops between disturbances, climate and vegetation properties. Changing disturbances could both augment and offset carbon loading of the atmosphere caused by anthropogenic carbon emissions³; better understanding the role of forest disturbances in the carbon cycle is therefore highly relevant to the assessment of emissions reductions necessary to meet climate targets.

Methods

Calculation of τ_o

τ_o was calculated as defined in Eq. 1. We first created a forest mask by aggregating year 2000 forest canopy cover data at 0.00025° (ca. 30 m) resolution²¹ to 0.01° resolution. Grid cells with at least 50% canopy cover at 0.01° resolution were assigned as closed-canopy forest. Further aggregation then provided the fractional coverage of closed-canopy forest at 1° resolution (A_T). Across each 1° grid cell we then summed up the total area of 0.00025° pixels which underwent forest loss during 2000-2014 and were located within the 0.01° grid cells assigned as closed-canopy forest. A grid cell could only be counted as lost once during the period. Dividing this sum by the length of the 14 year observation period provided $\overline{A_L}.$ A threshold of 25% forest cover at the 1° grid cell level was used throughout this study in order to provide sufficient statistical power for calculation of τ_o. The total forested area meeting these conditions is 2.71 × 10⁷ km². Fig. 1c was calculated from the gridded τ_o estimate using the “boxplot” function of Matlab® 2014b.

This above definition provides a calculation of τ as a function of forest area. An alternative definition of τ would be to define it relative to canopy area. In this case A_T would be the total canopy area within the 0.01° grid cells designated as closed canopy forest, making use of the fractional canopy cover metric provided by Hansen et al. ²¹, and $\overline{A_L}$ would be the sum of pixels undergoing forest loss multiplied by the fractional canopy cover of those pixels before disturbance. Using this canopy-area definition slightly reduces our estimates of τ_o in most locations (Suppl. Fig. 4), but the forest-area definition is preferred as it recognises that whilst disturbances reduce canopy cover, they do not reduce the area of forest unless associated with a land-use change.

Forest losses due to land-use change, $\overline{A_C},$ were calculated for the period 2000-2014 using the ESA CCI landcover product v2.0.7 (accessed 29^th June 2017). ESA CCI landcover classes were simplified into forested (classes 50, 60, 61, 62, 70, 71, 72, 80, 81, 82, 90, 100, 160, 170) and non-forested (classes 10, 11, 20, 30, 110, 130, 190) classes, the latter corresponding to cropland, grassland and urban land uses. Then the area of 0.0028° pixels which were classified as forested in 2000 but non-forested in 2014 was calculated. The forest loss due to land-use change calculated from this dataset shows excellent consistency with the total forest loss dataset based on Hansen et al. ²¹, with only very few locations where the loss due to land-use change is reported to be larger than the total (Suppl. Fig. 5).

Uncertainties in τ_o due to the sample sizes in the forest loss data were estimated through bootstrapping. In each 1° grid cell 1000 samples of $\overline{A_L}$ were created by resampling with replacement the 0.01° grid cells designated as closed-canopy forest. Uncertainties in $\overline{A_C}$ result from classification accuracy and scaling differences between the Hansen et al.²¹ and ESA CCI datasets. Producer’s accuracy for the forest and non-forest classification in ESA CCI v2.0.7 is 92% and 78% respectively, whilst the corresponding user’s accuracy is 78% and 85%⁴⁵. However, because we count the whole area of the pixel when an ESA CCI pixel changes from forest to non-forest, and the CCI pixel area is ca. 100 times that of Landsat, a scaling inaccuracy is induced, whereby the fraction of forest conversion within the grid cell may be enough to cause a land-cover classification switch, but substantially less than complete deforestation of the ESA pixel. To conservatively account for classification and scaling errors we thus assume a 95% confidence interval of +- 50% in the forest conversion area values. For each 1° grid cell, 1000 samples of $\overline{A_C}$ were taken from a normal distribution defined by this confidence interval. We crossed these 1000 samples of $\overline{A_C}$ with those from $\overline{A_L}$ to create a matrix of 1 x 10⁶ estimates of the denominator in Eq. 1. The 2.5^th and 97.5^th percentiles of this matrix were then used to estimate the 95% confidence limits of τ_o. This resampling of the forest loss areas within the 1° pixel addresses the uncertainty induced when the forest area in the pixel is relatively small, in which case confidence in the fidelity of the space-for-time swap would be reduced. It also accounts for classification errors if those errors are not correlated across the grid cell. Hansen et al. ²¹ report a tendency to underestimate forest loss by ca. 4% in the tropics and overestimate it by ca. 6% in the temperate and boreal regions. These classification biases are not captured in our uncertainty estimate, nor are potential biases from $\overline{A_T}$ for which global quantification was not available. Based on the available information, these biases are expected to be small and focused in regions where the uncertainty is already assessed as being large (Suppl. Note 4; Suppl. Fig. 8). Note that the capping of τ_o at 1000 years often leads to very low uncertainty for these grid cells, i.e. there is very high certainty that τ_o > 1000 years. Calculated τ_o is robust to subsampling of the 14 year observational period, especially when the data series exceeds 10 years (Suppl. Fig. 6).

The resolution of ESA CCI landcover means it will have limited sensitivity to very small-scale land-use conversions, such as have been recently reported in the Amazon⁴⁶. However, given that our τ_o values in the tropical evergreen forests are very high, even in absence of the land-use correction (Suppl. Fig. 7) we expect the influence on our results to be minimal.

The use of a 1° aggregation resolution represents a compromise between spatial detail and sufficient area to make an effective space-for-time substitution. Following the simplifying assumption that disturbance events are equally likely in all locations in the grid cell, the maximum τ that we can expect to reliably quantify, τ_m, for a given disturbance size, D, can be calculated as:

$${\tau }_m=\frac{A_T\times t}{D},$$ (2)

where t is the total number of years sampled. The largest disturbance events are generally fires, especially in the Canadian boreal region, for which the typical large fire size is 6000 ha⁴⁷. Assuming a grid-cell area of 628 000 ha (60° latitude), a forest coverage of 25% of grid-cell area (i.e. A_T = 157 000 ha) and a 14-year sampling period, τ_m is 350 years at this scale. For smaller disturbances much larger values of τ can be expected to be reliably captured. Substantial undersampling of large rare events at 1° resolution would be expected to induce scatter in our results, but Fig. 1 shows spatial coherence in variation of τ, suggesting any such under-sampling to have minimal effects. τ_o was capped at 1000 years to avoid spuriously large values in grid cells with very infrequent disturbance. The influence of this capping on simulated forest biomass is very small (e.g. Fig. 3b).

Forest type classification

Forest types were classified based on ESA CCI landcover v2.0.7. The mapping of landcover classes to the forest types used in this analysis in shown in Suppl. Table 2. A map of these forest types is shown in Suppl. Fig. 11. There is a small fraction of forest area that is not assigned to any of these major forest classes, but is included in the global totals. Note that open canopy forests (<50% canopy cover at 0.01° scale, see above) are not included in any of the calculations herein. Forest type codes are: Tropical broadleaved evergreen (TrBE), tropical broadleaved deciduous (TrBD), temperate broadleaved evergreen (TeBE), temperate broadleaved deciduous (TeBD), needleleaved evergreen (NE), needleleaved deciduous (ND), broadleaved-needleleaved mixed forest (MX).

Forest age dataset

For cross comparison of spatial patterns in our results, we used the Global Forest Age Dataset (GFAD v1.1)²², a forest stand age dataset developed as part of the EU FP7 GEOCARBON project. It provides a distribution of stand age and associated uncertainties in 10-year age bins up to an age of 140 years from a base year of 2010 on a 0.5° grid. The salient features are summarised here and described in more detail in Pugh et al.⁴⁸. It combines datasets of forest age distributions from the following forest inventories: United States Forest Inventory and Analysis (v 5.1, state summaries, representative for the 2000s), IIASA Russian Forests and Forestry Database (late 2000s), Canadian Forest Inventory (CanFI, state summaries, 2001-2006), EFISCEN (Europe, 32 countries, 2000s), 6th National Forest Inventory (China, 1999-2003), and the national forest inventories of Kazakhstan (2000s), New Zealand (2000s), Mongolia (2000s) and Japan (2005). GFAD estimates forest age in tropical regions, where widespread inventories are not available, by applying plant-functional-type-specific biomass-age curves⁴⁹ to a large-scale forest biomass dataset⁵⁰.

Forest modelling

The LPJ-GUESS DGVM v4.0⁵¹ was used to calculate the effects of τ on forest structure, dynamics and carbon cycling. LPJ-GUESS explicitly simulates forest stand development and canopy structure divided among age cohorts of trees co-occurring in patches representative of a wider landscape. Leaf area to sapwood area ratio and maximum crown area for tropical evergreen tree types were set to 10 000 and 130 m² respectively, in accordance with estimates for tropical forests^52,53. Mortality and establishment are stochastic, with replicate 1000 m² patches simulated to capture the distribution of stands of different time-since-last-disturbance across each grid cell. Stand-replacing disturbances are simulated by clearing all trees in a patch and transferring their biomass stocks to litter or out of the ecosystem (see below). We introduced a spatially-varying stochastic disturbance frequency with an annual probability defined by 1/τ. In order to allow LPJ-GUESS to simulate the closed-canopy forest area unrestricted by the 25% cover threshold used to calculate τ_o, the nearest-neighbour rule was used to assign τ values to grid cells with less than 25% forest coverage. All forest-type-level and global numbers are presented based on a 5% minimum forest coverage mask at the grid-cell level to avoid overextrapolation of τ_o to regions with very low forest cover. The map in Fig. 2 is presented with a 25% closed-canopy forest cover map for consistency with Fig. 1. Inclusion of τ_o in LPJ-GUESS improves the simulation of biomass compared to the disturbance settings in the standard version of the model (Suppl. Fig. 12).

In the standard simulation setting, all cleared biomass is transferred to the litter pools. For sensitivity simulations underlying ranges in Fig. 3d,e and Suppl. Fig. 10 two further setting types were employed to test the effect of the fate of disturbed material. In the harvest sensitivity simulations fine root and leaf biomass, along with 34% of woody biomass, are transferred to the litter, with the remaining woody biomass being removed from the ecosystem, emulating product extraction. The fire sensitivity simulations employ the interactive fire sub-model^51,54 with a local probability of fire occurrence (burnt area fraction) set to 1/τ, resulting in most biomass carbon and some litter carbon being transferred to the atmosphere. Stochastic processes use the same seed to ensure replication between simulations. Simulations covered 1901-2014 using climate, atmospheric CO₂ mixing ratio and N deposition as described in Le Quéré et al.⁵⁵. All model outputs shown are means for 2001-2014. The standard simulations with τ_o and 0.5τ_o used 100 replicate patches per grid cell. Simulations testing additional multiplicative perturbations of τ (0.25, 2, 4) and using the confidence intervals of τ_o used 10 replicate patches. Differences at forest-type level were negligible between simulations with 10 and 100 patches.

Simulations used to create Fig. 3a used the standard model setup described above, but the model was only run for the specified three grid cells. 100 simulations were carried out for each grid cell using levels of τ from 10 years to 1000 years. A second-order exponential equation of the form B = ae^bτ + ce^dτ was fitted to these simulations using the “fit” function of Matlab® 2014b.

Sensitivity metric

The metric is based upon differencing biomass between the τ_o and 0.5τ_o simulations. The choice of a halving of τ_o for the sensitivity metric was informed by recent disturbance trends in Europe¹⁴, and is also similar to changes in background mortality rates in the western U.S.A.⁵⁶. It thus represents a reasonable sensitivity test. The sensitivity threshold τ_crit (Suppl. Table 1) was estimated by first plotting against τ_o the difference between biomass simulated with τ = τ_o and that simulated with τ = 0.5τ_o, (Fig. 3b, Suppl. Fig. 13). A second-order exponential function was fitted to the data as for Fig. 3a. These fits were carried out both globally and for individual forest types. 95% confidence intervals for the fits were calculated using 1000 bootstrapped samples of the modelled grid cells. τ _crit,90 and τ _crit,80 were taken as the intersection of the fitted line with a difference of -10% and -20% biomass respectively (Suppl. Fig. 13), with confidence intervals for τ _crit estimated using the confidence intervals of the fitted lines. Scatter in the results is caused by the stochastic nature of the LPJ-GUESS model, as well as variation in climate across the domain. The 90% biomass threshold is consistent with recent work on the recovery of forest biomass³³ and with the character of the curve in Fig. 3b.

The area of forest in each sensitivity regime (Fig. 3c) was created by comparing τ_o for each grid cell with the τ_crit for the forest type to which that grid cell was assigned. Uncertainty in the areas of the regimes (Main text) was calculated based on the 95% confidence intervals of τ _O. For forest grid cells not classified by one of the seven forest types, not enough data points existed to make a reliable fit to calculate τ _crit. Therefore the global mean τ_crit was used to determine the sensitivity regime. Fig. 3d,e shows the difference in biomass and soil carbon density between model sensitivity simulations with different multiplicative factors of τ (see above) averaged across the area of forest allocated to each sensitivity class. Variation in response across the vulnerability classes is much less than that between them (Suppl. Fig. 9).

Empirical cross-checks

For cross-checking of biomass carbon turnover flux due to disturbance (F_d) we used the GEOCARBON global biomass dataset^27–29, in which biomass values are based on linking satellite-based LIDAR and radar observations with ground-based forest plot data. We replaced values for northern forests with those of Thurner et al.³⁰ due to the latter’s more sophisticated approach to linking satellite-based radar observations with above- and below-ground biomass in these regions. Below-ground biomass for the GEOCARBON dataset was estimated following Saatchi et al.⁵⁰ and a biomass to carbon conversion factor of 0.5 was assumed. We then multiplied the carbon content of this observationally-based total biomass dataset by 1/τ_o to calculate F_d. Cross-checking the fraction of total turnover due to disturbance (T_frac) involved making the assumption that NPP and turnover fluxes are not drastically out of equilibrium, and therefore NPP must be broadly equal to the turnover flux of biomass carbon in the multi-annual mean. Annual mean NPP over the period 2001-2010 was calculated from Zhao and Running⁵⁷. T_frac was then approximated as F_d/NPP. Fire emissions from the GFED dataset³² were calculated by summing the boreal, temperate and tropical forest wildfire emissions, excluding the savannah category, which does not fit our definition of closed-canopy forest. The mask of at least 5% forest cover per grid cell was applied to all these cross-check calculations as above.

Data availability

Calculations of τ_o, data from the model simulations and the forest mask used are available from https://dataguru.lu.se/app#PughDisturbance2019 (dois: 10.18161/disturbance_tauo.201905, 10.18161/disturbance_lpj-guess.201905, 10.18161/disturbance_forestmask.201905). GFAD v1.1 was obtained from PANGAEA²², and the Global Forest Change 2000-2014 v1.2 forest loss product from https://earthenginepartners.appspot.com/science-2013-global-forest/download_v1.2.html. The ESA CCI Landcover v2.0.7 was obtained from http://maps.elie.ucl.ac.be/CCI/viewer/.

Code availability

Matlab code for the data analysis herein is available from GitHub, https://github.com/pughtam/GlobalDist. Source code for LPJ-GUESS v4.0 can be obtained on request through Lund University, see web.nateko.lu.se/lpj-guess.