Empowering statistical methods for cellular and molecular biologists

Abstract

We provide guidelines for using statistical methods to analyze the types of experiments reported in cellular and molecular biology journals such as Molecular Biology of the Cell. Our aim is to help experimentalists use these methods skillfully, avoid mistakes, and extract the maximum amount of information from their laboratory work. We focus on comparing the average values of control and experimental samples. A Supplemental Tutorial provides examples of how to analyze experimental data using R software.

PERSPECTIVE

Our purpose is to help experimental biologists use statistical methods to extract useful information from their data, draw valid conclusions, and avoid common errors. Unfortunately, statistical analysis often comes last in the lab, leading to the observation by the famous 20th century statistician R. A. Fisher (Fisher, 1938):

“To consult [statistics] after an experiment is finished is often merely to […] conduct a post mortem examination. [You] can perhaps say what the experiment died of.”

To promote a more proactive approach to statistical analysis, we consider seven steps in the process. We offer advice on experimental design, assumptions for certain types of data, and decisions about when statistical tests are required. The article concludes with suggestions about how to present data, including the use of confidence intervals. We focus on comparisons of control and experimental samples, the most common application of statistics in cellular and molecular biology. The concepts are applicable to a wide variety of data, including measurements by any type of microscopic or biochemical assay. Following our guidelines will avoid the types of data handling mistakes that are troubling the research community (Vaux, 2012). Readers interested in more detail might consult a biostatistics book such as The Analysis of Biological Data, Second Edition (Whitlock and Schluter, 2014).

SEVEN STEPS

1. Decide what you aim to estimate from your experimental data

Experimentalists typically make measurements to estimate a property or “parameter” of a population from which the data were drawn, such as a mean, rate, proportion, or correlation. One should be aware that the actual parameter has a fixed, unknown value in the population. Take the example of a population of cells, each dividing at their own rate. At a given point in time, the population has a true mean and variance of the cell division rate. Neither of these parameters is knowable. When one measures the rate in a sample of cells from this population, the sample mean and variance are estimates of the true population mean and variance (Box 1). Such estimates differ from the true parameter values for two reasons. First, systematic biases in the measurement methods can lead to inaccurate estimates. Such measurements may be precise but not accurate. Making measurements by independent methods can verify accurate methods and help identify biased methods. Second, the sample may not be representative of the population, either by chance or due to systematic bias in the sampling procedure. Estimates tend to be closer to the true values if more cells are measured, and they vary as the experiment is repeated. By accounting for this variability in the sample mean and variance, one can test a hypothesis about the true mean in the population or estimate its confidence interval.

Box 1: Statistics describing normal distributions

The sample mean (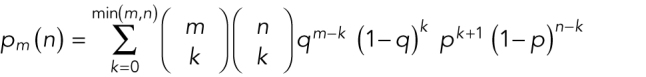) is the average value of the measurements: 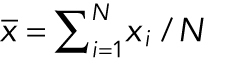, where 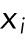is a measurement and N is the number of measurements. The sample mean is an estimate of the true population mean (µ). The median is the middle number in a ranked list of measurements, and the mode is the peak value. The peak of a normal distribution is equal to the mean, median, and mode. This is generally not true for asymmetrical distributions.

The sample standard deviation (SD) is the square root of the variance of the measurements in a sample and describes the distribution of values around the mean:

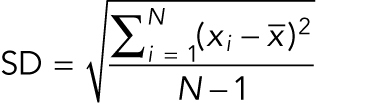where 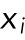is a measurement, 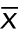is the sample mean, and N is the number of measurements. SD is an estimate of the true population SD(σ). Note (Figure 1A) that for a normal distribution ±1σ around the mean includes 68% of the values and ±2σ around the mean includes ∼95% of the values. Use the SD in the figures to show the variability of the measurements.

The standard error of the mean, SEM, is the SD divided by the square root of the number of measurements: 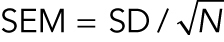. Therefore, N must always be reported along with SEM. SEM is an estimate of how closely the sample mean matches the actual population mean. The agreement increases with the number of measurements. SEM is used in the t test. SD shows transparently the variability of the data, whereas SEM will approach zero for large numbers of measurements. Mistaking SEM for SD gives a false impression of low variability. Using SEM reduces the size of error bars on graphs but obscures the variability. Using confidence intervals (see Box 2) is preferred to using SEM.

2. Frame your biological and statistical hypotheses

A critical step in designing a successful experiment is translating a biological hypothesis into null and alternative statistical hypotheses. Hypotheses in cellular and molecular biology are often framed as qualitative statements about the effect of a treatment (i.e., genotype or condition) relative to a control or prediction. For example, a biological hypothesis might be that the rate of contractile ring constriction depends on the concentration of myosin-II. Statistical hypothesis testing requires the articulation of a null hypothesis, which is typically framed as a concrete statement about no effect of a treatment or no deviation from a prediction. For example, a null hypothesis could be that the mean rate of contractile ring constriction is the same for cells depleted of myosin-II by RNA interference (RNAi) and for cells treated with a control RNAi molecule. Likewise, the alternative hypothesis is all outcomes other than the null hypothesis. For example, the mean rates of constriction are different under the two conditions. Most hypothesis testing allows for the effect of each treatment to be in either direction relative to a control or other treatments. These are referred to as two-sided hypotheses. Occasionally, the biological circumstances are such that the effect of a treatment could never be in one of the two possible directions, and therefore a one-sided hypothesis is used. The null hypothesis then is that the treatment either has no effect or an effect in the direction that is never expected. The section on hypothesis testing illustrates how this framework enables scientists to assess quantitatively whether their data support or refute the biological hypothesis.

3. Design your experiment

As indicated by Fisher’s admonition, one should build statistical analysis into the design of an experiment including the number of measurements, nature and number of variables measured, methods of data acquisition, biological and technical replication, and selection of an appropriate statistical test.

Nature and number of variables.

All variables that could influence responses and are measurable should be recorded and considered in statistical analyses. In addition to intentional treatments such as genotype or drug concentration, so-called nuisance variables (e.g., date of data collection, lot number of a reagent) can influence responses and if not included can obscure the effects of the treatments of interest.

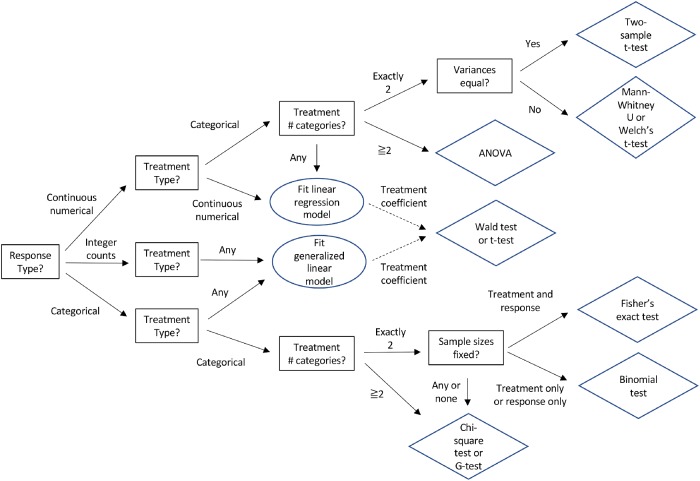
Treatments and measured responses can either be numerical or categorical. Different statistical tools are required to evaluate numerical and categorical treatments and responses (Table 1 and Figure 2). Failing to make these distinctions may be the most common error in the analysis of data from experiments in cellular and molecular biology.

TABLE 1:

Matching types of data appropriately with commonly used statistical tests (Crawley, 2013; Whitlock and Schluter, 2014).

Response type	Treatment type	Statistical tests	Typical null ­hypothesis	Assumptions	Functions in Excel and R	Examples
Continuous numerical (e.g., reaction rate)	Binary (e.g., wild type vs. mutant)	t test	Means equal for two treatments	Randomized treatment; normally distributed response; equal variance of response for two treatment groups	Excel: TTEST(controlrate, ­genotype, tails = 2, type = 2) R: t.test(rate∼genotype, var.equal = TRUE)	Zhuravlev et al., 2017; Figure 1C
Continuous numerical (e.g., reaction rate)	Categorial (e.g. wild type vs mutant 1 vs mutant 2)	ANOVA followed by Tukey-Kramer post-hoc test	Means equal across treatments	Randomized treatment; normally distributed response; equal variance of response between treatment groups	Excel: Analysis ToolPak add-in for single factor ANOVA required if treatment has more than two levels R: aov(rate∼genotype) TukeyHSD()	Plooster et al., 2017; Figure 1D
Continuous numerical (e.g., reaction rate)	Continuous numerical (e.g., drug concentrations)	Linear regression followed by t test on regression coefficients or ­correlation test	Coefficients equal to zero; correlation ­coefficient equal to zero	Randomized treatment; linear relationship between treatment and response; treatment and response bivariate normally distributed; normally distributed residuals	Excel: LINEST(rate, drug, const = TRUE, stats = TRUE) R: lm(rate∼drug) summary()	Spencer et al., 2017; Figure 4
Continuous numerical (e.g., reaction rate)	More than one treatment: Continuous numerical (e.g., drug concentrations) plus categorical (e.g., wild type vs. mutant 1 vs. mutant 2)	Analysis of ­covariance (­ANCOVA)	Coefficients equal to zero	Randomized treatment; numerical treatment and response bivariate normally distributed; equal variance of response between treatment groups; linear relationship between numerical treatment and response; normally distributed residuals	Excel: LINEST(rate, treatments, const = TRUE, stats = TRUE) R: lm(rate∼drug + genotype) summary()	Nowotarski et al., 2014; Figures 3 and 4
Categorical (e.g., cell cycle stage)	Categorical (e.g., wild type vs. mutant 1 genotype vs. mutant 2 genotype)	Chi-square or G contingency test; binomial test; Fisher’s exact test	Proportions ­between ­response ­categories are equal between treatments	Randomized treatment; all expected counts are one or more and no more than 20% of expected counts less than five; binomial: response or treatment sample sizes fixed; Fisher’s: response and treatment sample sizes fixed	Excel: CHISQ.TEST(actual_range,expected_range) R: chisq.test(stage, genotype)	Bartolini et al., 2016; Figures 2F and 5B
Binary categorical (e.g., alive or dead)	Continuous numerical (e.g., drug concentrations)	Logistic regression; generalized linear model	Slope or ­intercept equal to zero	Randomized treatment; linear relationship between treatment and log odds of one response	Excel: Not available R: glm(alive∼drug, family = binomial) summary()	Atay and Skotheim, 2014; Figure 2
Binary categorical (e.g., alive or dead)	More than one treatment: Categorical (e.g., wild type vs. mutant 1 vs. mutant 2) plus categorical (e.g., day 1 vs. day 2 vs. day 3)	Logistic regression; generalized linear model	Slope or ­intercept equal to zero	Randomized treatment	Excel: Not available R: glm(alive∼genotype + day, family = binomial) summary()	Kumfer et al., 2010; Table 1

FIGURE 2:

Decision tree to select an appropriate statistical test for association between a response and one or more treatments. Multiple treatments or a treatment and potential confounders can be tested using linear models (also known as ANCOVA) or generalized linear models (e.g., logistic regression for binary responses). Multiple treatments with repeated measurements on the same specimens, such as time courses, can be tested using mixed model regression. Questions in squares; answers on solid arrows; actions in ovals; tests in diamonds.

A range of inhibitor concentrations or time after adding a drug are examples of numerical treatments. Examples of categorical treatments are comparing wild-type versus mutant cells or control cells versus cells depleted of a mRNA.

Continuous numerical responses are measured as precisely as possible, so every data point may have a unique value. Examples include concentrations, rates, lengths, and fluorescence intensities. Categorical responses are typically recorded as counts of observations for each category such as stages of the cell cycle (e.g., 42 interphase cells and eight mitotic cells). Proportions (e.g., 0.84 interphase cells and 0.16 mitotic cells) and percentages (e.g., 84% interphase cells and 16% mitotic cells) are also categorical responses but are often inappropriately treated as numerical responses in statistical tests. For example, many authors make the mistake of using a t test to compare proportions. They may think that proportions are numerical responses, because they are numbers, but they are not numerical responses. The decision tree in Figure 2 guides the experimentalist to the appropriate statistical test and Table 1 lists the assumptions for widely used statistical tests.

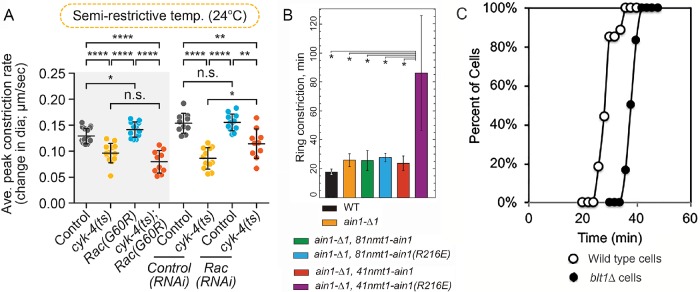
Often researchers must make choices with regard to the number and nature of the variables in their experiment to address their biological question. For example, color can be measured as a categorical variable or as a continuous numerical variable of wavelengths. Recording variables as continuous numerical variables is best, because they contain more information and subsequently can be converted into categorical variables, if the data appear to be strongly categorical. Furthermore, the choice of variable may be less clear with complicated experiments. For example, in the time-course experiments described in Figure 3, one study measured rates as a response variable (Figure 3A) and two others used time until an event (Figure 3, B and C). All could have treated the event as a categorical variable and used time as a treatment variable. It is often best to record the most direct observations (e.g., counts of cells with and without the event) and then subsequently to consider using response variables that involve calculations (e.g., rate of event or time until event).

FIGURE 3:

Comparison of data presentation for three experiments on the constriction of cytokinetic contractile rings with several perturbations. (A) Rate of ring constriction in Caenorhabditis elegans embryos from Zhuravlev et al. (2017). Error bars represent SD; p values were obtained by an unpaired, two-tailed Student’s t test; n.s., p ≥ 0.05; *, p < 0.05; **, p < 0.01; ****, p < 0.0001. Sample sizes 10–12. (B) Time to complete ring constriction in Schizosaccharomyces pombe from Li et al. (2016). Error bars, SD; n ≥ 10 cells. *, p < 0.05 obtained with one-tailed t tests for two samples with unequal variance. (C) Kaplan-Meier outcomes plots comparing the times (relative to spindle pole body separation) of the onset of contractile ring constriction in populations of (○) wild-type and (⬤) blt1∆ fission yeast cells from Goss et al. (2014). A log-rank test determined that the curves differed with p < 0.0001.

Methods of data acquisition.

Common statistical tests (Table 1) assume randomization and exchangeability, meaning that all experimental units (e.g., cells) are equally likely to get each treatment and the data for one experimental unit is the same as that of any other receiving the same treatment. The challenge is to understand your experiment well enough to randomize treatments effectively across potential confounding variables. For example, it is unwise to image all mutant cells one week and all control cells the next week, because differences in the conditions during the experiment could have confounding effects difficult to separate from any differences between mutant and control cells. Randomly assigning mutants and controls to specific dates allows for date effects to be separated from the genotype effects that are of interest if both genotype and date are included in the statistical test as treatments. Many possible experimental designs effectively control for the effects of confounding variables such as randomized block designs and factorial designs. Planning ahead allows one to avoid the common mistake of failing to randomize batches of data acquisition across experimental conditions.

Many statistical tests further assume that observations are independent. When this is not the case, as with paired or repeated measurements on the same specimen, one should use methods that account for correlated observations, such as paired t tests or mixed model regression analysis with random effects (Whitlock and Schluter, 2014). Time-course studies are a common example of repeated measurements in molecular cell biology that require special handling of nonindependence with approaches such as mixed models.

Statistical test.

Having decided on the experimental variables and the method to collect the data, the next step is to select the appropriate statistical test. Statistical tests are available to evaluate the effect of treatments on responses for every type and combination of treatment and response variables (Figure 2 and Table 1). All statistical tests are based on certain assumptions (Table 1) that must be met to maintain their accuracy. Start by selecting a test appropriate for the experimental design under ideal circumstances. If the actual data collected do not meet these assumptions, one option is to change to an appropriate statistical test as discussed in Step 4 and illustrated in Example 1 of the Supplemental Tutorial. In addition to matching variables with types of tests, it is also important to make sure that the null and alternative hypotheses for a test will address your biological hypothesis.

Most common statistical tests require predetermining an acceptable rate of false positives. For an individual test this is referred to as the type I error rate (α) and is typically set at α = 0.05, which means that a true null hypothesis will be mistakenly rejected at most five times out of 100 repetitions of the experiment. The type I error rate is adjusted to a lower value when multiple tests are being performed to address a common biological question (Dudoit and van der Laan, 2008). Otherwise, lowering the type I error rate is not recommended, because it decreases the power of the test to detect small effects of treatments (see below).

Biological and technical replication.

Biological replicates (measurements on separate samples) are used for parameter estimates and statistical tests, because they allow one to describe variation in the population. Technical replicates (multiple measurements on the same sample) are used to improve estimation of the measurement for each biological replicate. Treating technical replicates as biological replicates is called pseudoreplication and often produces low estimates of variance and erroneous test results. The difference between technical and biological replicates depends on how one defines the population of interest. For example, measurements on cells within one culture flask are considered to be technical replicates, and each culture flask to be a biological replicate, if the population is all cells of this type and variability between flasks is biologically important. But in another study, cell to cell variability might be of primary interest, and measurements on separate cells within a flask could be considered biological replicates as long as one is cautious about making inferences beyond the population in that flask. Typically, one considers biological replicates to be the most independent samples.

The design should be balanced in the sense of collecting equal numbers of replicates for each treatment. Balanced designs are more robust to deviations from hypothesis test assumptions, such as equal variances in responses between treatments (Table 1).

Number of measurements.

Extensive replication of experiments (large numbers of observations) has bountiful virtues, including higher precision of parameter estimates, more power of statistical tests to detect small effects, and ability to verify the assumptions of statistical tests. However, time and reagents can be expensive in cellular and molecular biology experiments, so the numbers of measurements tend to be relatively small (<20). Fortunately, statistical analysis in experimental biology has two major advantages over observational biology. First, experimental conditions are often well controlled, for example using genetically identical organisms under laboratory conditions or administering a precise amount of a drug. This reduces the variation between samples and compensates to some extent for small sample sizes. Second, experimentalists can randomize the assignment of treatments to their specimens and therefore minimize the influence of confounding variables. Nonetheless, small numbers of observations make it difficult to verify important assumptions and can compromise the interpretation of an experiment.

Statistical power.

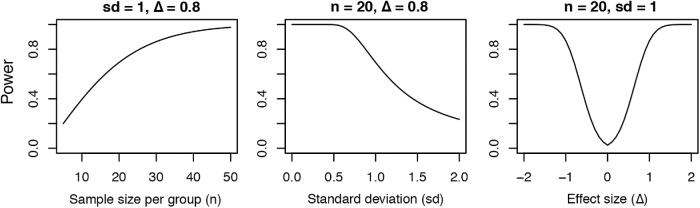
One can estimate the appropriate number of measurements required by calculating statistical power when designing each experiment. Statistical power is the probability of rejecting a truly false null hypothesis. A common target is 0.80 power (Cohen, 1992). Three variables contribute to statistical power: number of measurements, variability of those measurements (SD), and effect size (mean difference in response between the control and the treated populations). A simple rule of thumb is that power decreases with the variability and increases with sample size and effect size as shown in Figure 4. One can increase the power of an experiment by reducing measurement error (variance) or increasing the sample size. For the statistical tests in Table 1, simple formulas are available in most statistical software packages (e.g., R [www.r-project.org], Stata [www.stata.com], SAS [www.sas.com], SPSS [www.ibm.com/SPSS/Software]) to compute power as a function of these three variables.

FIGURE 4:

Three graphs show factors affecting the statistical power, the probability of rejecting a truly false null hypothesis in a two-sample t test. The statistical power depends on three factors: (A) increases with the number of measurements (n); (B) decreases with the size of the SD (sd); and (C) increases with effect size (Δ), the difference between the control and the test samples on both sides of minimum at zero effect size. Two variables are held constant in each example.

Of course, one does not know the outcome of an experiment before it is done, but one may know the expected variability in the measurements from previous experiments, or one can run a pilot experiment on the control sample to estimate the variability in the measurements in a new system. Then one can design the experiment knowing roughly how many measurements will be required to detect a certain difference between the control and experimental samples. Alternatively, if the sample size is fixed, one can rearrange the power formula to compute the effect size one could detect at a given power and variability. If this effect size is not meaningful, proceeding is not advised. This strategy avoids performing a statistical “autopsy” after the experiment has failed to detect a significant difference.

4. Examine your data and finalize your analysis plan

Experimental data should not deviate strongly from the assumptions of the chosen statistical test (Table 1), and the sample sizes should be large enough to evaluate if this is the case. Strong deviations from expectations will result in inaccurate test results. Even a very well-designed experiment may require adjustments to the data analysis plan, if the data do not conform to expectations and assumptions. See Examples 1, 2, and 4 in the Supplemental Tutorial.

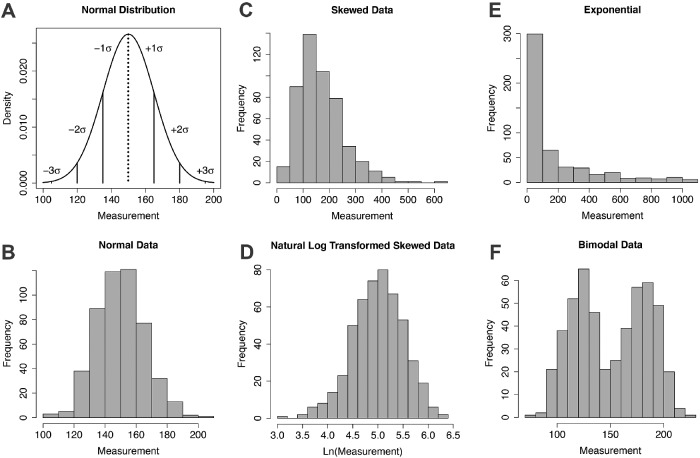
For example, a t test calls for continuous numerical data and assumes that the responses have a normal distribution (Figure 1, A and B) with equal variances for both treatments. Samples from a population are never precisely normally distributed and rarely have identical variances. How can one tell whether the data are meeting or failing to meet the assumptions?

FIGURE 1:

Examples of distributions of measurements. (A) Normal distribution with vertical lines showing the mean = median = mode (dotted) and ±1, 2, and 3 standard deviations (SD or σ). The fractions of the distribution are ∼0.67 within ±1 SD and ∼0.95 within ±2 SD. (B) Histogram of approximately normally distributed data. (C) Histogram of a skewed distribution of data. (D) Histogram of the natural log transformation of the skewed data in C. (D) Histogram of exponentially distributed data. (F) Histogram of a bimodal distribution of data.

Find out whether the measurements are distributed normally by visualizing the unprocessed data. For numerical data this is best done by making a histogram with the range of values on the horizontal axis and frequency (count) of the value on the vertical-axis (Figure 1B). Most statistical tests are robust to small deviations from a perfect bell-shaped curve, so a visual inspection of the histogram is sufficient, and formal tests of normality are usually unnecessary. The main problem encountered at this point in experimental biology is that the number of measurements is too small to determine whether they are distributed normally.

Not all data are distributed normally. A common deviation is a skewed distribution where the distribution of values around the peak value is asymmetrical (Figure 1C). In many cases asymmetric distributions can be made symmetric by a transformation such as taking the log, square root, or reciprocal of the measurements for right-skewed data, and the exponential or square of the measurements for left-skewed data. For example, an experiment measuring cell division rates might result in many values symmetrically distributed around the mean rate but a long tail of much lower rates from cells that rarely or never divide. A log transformation (Figure 1D) would bring the histogram of this data closer to a normal distribution and allow for more statistical tests. See Example 2 in the Supplemental Tutorial for an example of a log transformation. Exponential (Figure 1E) and bimodal (Figure 1F) distributions are also common.

One can evaluate whether variances differ between treatments by visual inspection of histograms of the data or calculating the variance and SD for each treatment. If the sample sizes are equal between treatments (i.e., balanced design), tests like the t test and analysis of variance (ANOVA) are robust to variances severalfold different from each other.

To determine whether the assumption of linearity in regression has been met, one can look at a plot of residuals (i.e., the differences between observed responses and responses predicted from the linear model) versus fitted values. Residuals should be roughly uniform across fitted values, and deviations from uniform fitted values suggest nonlinearity. When nonlinearity is observed, one can consider more complicated parametric models of the relationship of responses and treatments.

If the data do not meet the assumptions or sample sizes are too small to verify that assumptions have been met, alternative tests are available. If the responses are not normally distributed (such as a bimodal distribution, Figure 1F), the Mann-Whitney U test can replace the t test, and the Kruskal-Wallis test can replace ANOVA with the assumption of consistently distributed responses across treatments. However, relaxing the assumptions in such nonparametric tests reduces the power to detect the effects of treatments. If the data are not normally distributed but sample sizes are large (N > 20), a permutation test is an alternative that can have better power than nonparametric tests. If the variances are not equal, one can use Welch’s unequal variance t test. See Supplemental Tutorial Example 1 for an example.

Categorical tests typically only assume sample sizes are large enough to avoid low expected numbers of observations in each category. It is important to confirm that these assumptions have been met, so larger samples can be collected, if they have not been met.

5. Perform a hypothesis test

A hypothesis test is done to determine the probability of observing the experimental data, if the null hypothesis is true. Such tests compare the properties of the experimental data with a theoretical distribution of outcomes expected when the null hypothesis is true. Note that different tests are required depending on whether the treatments and responses are categorical or numerical (Table 1).

One example is the t test used for continuous numerical responses. In this case the properties of the data are summarized by a t statistic and compared with a t distribution (Figure 5). The t distribution gives the probability of obtaining a given t statistic upon taking many random samples from a population where the null hypothesis is true. The shape of the distribution depends on the sample sizes.

FIGURE 5:

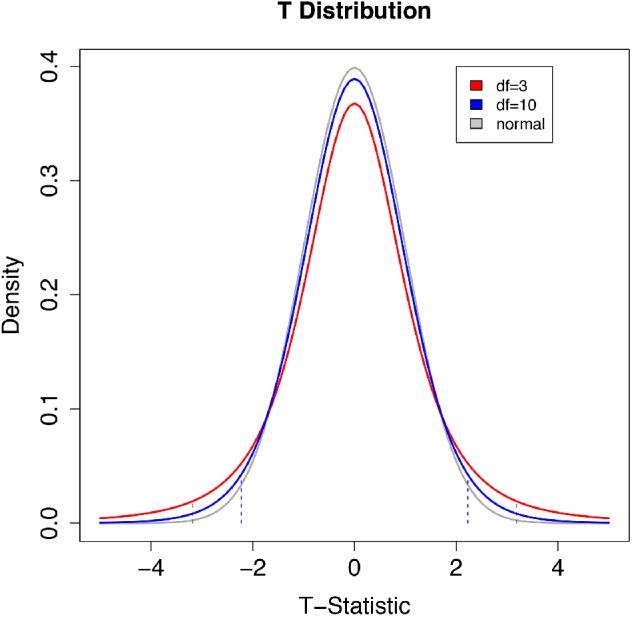
Comparison of two t distributions with degrees of freedom of 3 (sample size 4) and 10 (sample size 11) with a normal distribution with a mean value of 0 and SD = 1. The vertical dashed lines are 2.5th and 97.5th quantiles of the corresponding (same color) t distribution. The area below the left dashed line and above the right dashed line totals 5% of the total area under the curve. The t distribution is the theoretical probability of obtaining a given t statistic with many random samples from a population where the null hypothesis is true. The shape of the distribution depends on the sample size. The distribution is symmetric, centered on 0. The tails are thicker than a standard normal distribution, reflecting the higher chance of values away from the mean when both the mean and the variance are being estimated from a sample. The t distribution is a probability density function so the total area under the curve is equal to 1. The area under the curve between two x-axis (t statistic) values can be calculated using integration. With large sample sizes the accuracy of estimates of the true variance in an experiment increase and the t distribution converges on a standard normal distribution. To determine the probability of the observed statistic if the null hypothesis were true, one compares the t statistic from an experiment with the theoretical t distribution. For a one-sided test in the greater-than direction, the area above the observed t statistic is the p value. The 97.5th quantile has p = 0.025. For a one-sided test in the less-than direction, the area below the observed t statistic is the p value. The 2.5th quantile has p = 0.025 in this case. For a two-sided test, the p value is the sum of the area beyond the observed statistic and the area beyond the negative of the observed statistic. If this probability value (p value) is low, the data are not likely under the null hypothesis.

If the null hypothesis for a t test is true (i.e., the means of the control and treated populations are the same), the most likely outcome is no difference (t = 0). However, depending on the sample sizes and variances, other outcomes occur by chance. Comparing the t statistic from an experiment with the theoretical t distribution gives the probability that the experimental outcome occurred by chance. If the probability value (p value) is low, the null hypothesis is unlikely to be true.

One-sample t test.

To start with a simple example, one tests the null hypothesis that the true mean is equal to a null value µ₀ with the one-sample t statistic:

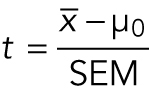A useful way to think about this equation is that the numerator is the signal (the difference between the sample mean and µ₀) and the denominator is the noise (SEM or the variability of the samples). If the sample mean and µ₀ are the same, then t = 0. If the SEM is large relative to the difference in the numerator, t is also small. Small t statistic values are consistent with the null hypothesis of no difference between the true mean and the null value, while large t statistic values are less consistent with the null hypothesis. To see the signal over the noise, the variability must be small relative to the deviation of the sample mean from the null value.

Two-sample t test.

If an experiment comparing two categorial treatments (wild-type vs. mutant cells) produces continuous numerical data and the responses are normal distributions with equal variances (Figure 2, top series of decisions), then the appropriate test is a two-sample t test, also known as Student’s t test. This test compares the difference in means of the samples (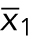 and 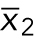) divided by an estimate of the variability of this difference, which is conceptually similar to SEM but with a more complex formula:

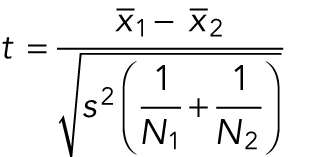where N₁ and N₂ are the numbers of measurements in each sample, and the pooled sample variance is

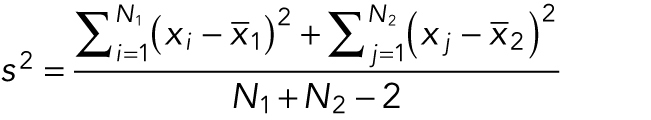Again, if the data are noisy, the large denominator weighs down any difference in the means and the t statistic is small.

Conversion of a t statistic to a p value.

One converts the test statistic (such as t from a two-sample t test) into the corresponding p value with conversion tables or the software noted in Table 1. The p value is the probability of observing a test statistic at least as extreme as the measured t statistic if the null hypothesis is true. One assumes the null hypothesis is true and calculates the p value from the expected distribution of test statistic values.

In the case of a two-sample t test, under the null hypothesis, the t distribution is completely determined by the number of replicates for the two treatments (i.e., degrees of freedom). For two-sided null hypotheses, values near 0 are very likely under the null hypothesis while values far out in the positive and negative tails are unlikely. If one chooses a p value cutoff (α) of 0.05 (a false-positive outcome in five out of 100 random trials), the area under the curve in the extreme tails (i.e., where t statistic values result in rejecting the null hypothesis) is 0.025 in the left tail and 0.025 in the right tail. An observed test statistic that falls in one tail at exactly the threshold between failing to reject and rejecting the null hypothesis has a p value of 0.05 and any test statistics farther out in the tails has smaller p values. The p value is calculated by integrating between the measured t statistic and the infinite value in the nearest tail of the distribution and then multiplying that probability by 2 to account for both tails (Minitab Blog, 2019).

If the p value is less than or equal to α, the null hypothesis is rejected because the data are improbable under the null hypothesis. Else the null hypothesis is not rejected. The following section discusses the interpretation of p values.

Note that t tests come with assumptions about the nature of the data, so one must choose an appropriate test (Table 1). Beware that statistical software will default to certain t tests that may or may not be appropriate. For example, when “t.test” is selected, the R package defaults to Welch’s t test, but the user can also specify Student’s or Mann-Whitney t tests where they are more appropriate for the data (Table 1). Furthermore, the software may not alert the user with an error message if categorical response data are incorrectly entered for a test that assumes continuous numerical response data.

Confidence intervals (Box 2) are a second, equivalent way to summarize evidence for the null versus alternative hypothesis.

Box 2: Confidence intervals

A confidence interval is a range of values for a population parameter that has a high probability of containing the true value based on a sample of measurements. For example, the 95% confidence interval for a normally distributed cell division rate is the range of values 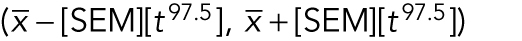, where t^97.5 is the 97.5th percentile of the t distribution with N − 1 degrees of freedom and N is the sample size (i.e., t statistics are greater than t or less than −t 5% of the time). This interval is expected to contain the true rate in approximately 95 out of 100 repetitions of the experiment. If a 95% confidence interval does not contain a hypothesized value µ₀, this is equivalent to rejecting the null hypothesis that the true rate is equal to µ₀ using p value <0.05. Just as hypothesis tests can be conducted with error rates α other than 0.05, the value can be replaced with a different percentile of the t distribution to give a confidence other than 95%. See the Supplemental Tutorial for examples of calculating confidence intervals and including confidence intervals in figures.

Comparing the outcomes of multiple treatments.

A common misconception is that a series of pairwise tests (e.g., t tests) comparing each of several treatments and a control is equivalent to a single integrated statistical analysis (e.g., ANOVA followed by a Tukey-Kramer post-hoc test). The key distinction between these approaches is that the series of pairwise tests is much more vulnerable to false positives, because the type I error rate is added across tests, while the integrated statistical analysis keeps the type I error rate at α = 0.05. For example, in an experiment with three treatments and a control the total type I error across the tests rises up to 0.3 with six pairwise t tests each with α = 0.05. On the other hand, an ANOVA analysis on the three treatments and control tests the null hypothesis that all treatments and control have the same response with α = 0.05. If the test rejects that null, then one can run a Tukey-Kramer post-hoc analysis to determine which pairs differed significantly, all while keeping the overall type I error rate for the analysis at or below α = 0.05. A series of pairwise tests and a single integrated analysis typically gives the same kind of information, but the integrated approach does so without exposure to high levels of false positives. See Figure 3A for an example where an integrated statistical analysis would have been helpful and Example 5 in the Supplemental Tutorial for how to perform the analysis.

6. Frame appropriate conclusions based on your statistical test

Assuming that one has chosen an appropriate statistical test and the data conform to the assumptions of that test, the statistical test will reject the null hypothesis that the control and treatments have the same responses, if the p value is less than α.

Still, one must use judgment before concluding that two treatments are different or that any detected difference is meaningful in the biological context. One should be skeptical about small but statistically significant differences that are unlikely to impact function. Some statisticians believe that the widespread use of α = 0.05 has resulted in an excess of false positives in biology and the social sciences and recommend smaller cutoffs (Benjamin et al., 2018). Others have advocated for abandoning tests of statistical significance altogether (McShane et al., 2018; Amrhein et al., 2019) in favor of a more nuanced approach that takes into account the collective knowledge about the system including statistical tests.

Likewise, a biologically interesting trend that is not statistically significant may warrant collecting more samples and further investigation, particularly when the statistical test is not well powered. Fortunately, rigorous methods exist to determine whether low statistical power (see Step 3) is the issue. Then a decision can be made about whether to repeat the experiment or accept the result and avoid wasting effort and reagents.

7. Choose the best way to illustrate your results for publication or presentation

The nature of the experiment and statistical test should guide the selection of an appropriate presentation. Some types of data are well displayed in a table rather than a figure, such as counts for a categorical treatment and categorical response (see Example 4 in the Supplemental Tutorial). Other types of data may require more sophisticated figures, such as the Kaplan-Meier plot of the cumulative probability of an event through time in Figure 3C.

The type of statistical test, and any transformations applied, must be specified when reporting results. Unfortunately, researchers often fail to provide sufficient detail (e.g., software options, test assumptions) for others to repeat the analysis. Many papers report p values that appear improbable based on simple inspection of the data and without specifying the statistical test used. Some report SEM without the number of measurements, so the actual variability is not revealed.

It is helpful to show raw data along with the results of a statistical test. Some formats used to present data provide much more information than others (Figure 3). These figures display both the mean and the SD for each treatment as well as the p value from comparing treatments. Figure 3A includes the individual measurements so that the number and distribution of data points are available to show whether the assumptions of a test are met and to help with the interpretation of the experiment. Bar graphs (Figure 3B) do not include such raw data, but strip plots (see Figure 3A and Examples 1, 2, and 5 in the Supplemental Tutorial), histograms, and scatter plots do.

An alternative to indicating p values on a figure is to display 95% confidence intervals as error bars about the mean for each treatment (see Supplemental Tutorial Examples 1, 2, 3, and 5 for examples). When the 95% confidence intervals of two treatments do not overlap, we know that a t test would produce a significant result, and when the confidence interval for one treatment overlaps the mean of another treatment we know that a t test would produce a nonsignificant result. We do not recommend using SEM as error bars, because SEM fails to convey either true variation or statistical significance. Unfortunately, authors commonly use SEM for error bars without appreciating that it is not a measure of true variation and, at best, is difficult to interpret as a description of the significance of the differences of group means. Many (Figure 3, A and C) but not all (Figure 3B) papers explain their statistical methods clearly. Unfortunately, a substantial number of papers in Molecular Biology of the Cell and other journals include error bars without explaining what was measured.

CONCLUSION

Cellular and molecular biologists can use statistics effectively when analyzing and presenting their data, if they follow the seven steps described here. This will avoid making common mistakes (Box 3). The Molecular Biology of the Cell website has advice about experimental design and statistical tests aligned with this perspective (Box 4). Many institutions also have consultants available to offer advice about these basic matters or more advanced topics.

Box 3: Common mistakes to avoid

Not publishing raw data so analyses can be replicated.

Using proportions or percentages of categorical variables as continuous numerical variables in a t test or ANOVA.

Combining biological and technical replicates (pseudoreplication).

Ignoring nuisance treatment variables such as date of experiment.

Performing a hypothesis test without providing evidence that the data meet the assumptions of the test.

Performing multiple pairwise tests (e.g., t tests) instead of a single integrated test (e.g., ANOVA to Tukey-Kramer).

Not reporting the details of the hypothesis test (name of test, test statistic, parameters, and p value).

Figures lacking interpretable information about the spread of the responses for each treatment.

Figures lacking interpretable information about the outcomes of the hypothesis tests.

Box 4: Molecular Biology of the Cell statistical checklist

Where appropriate, the following information is included in the Materials and Methods section:

1. How the sample size was chosen to ensure adequate power to detect a prespecified effect size.

2. Inclusion/exclusion criteria if samples or animals were excluded from the analysis.

3. Description of a method of randomization to determine how samples/animals were allocated to experimental groups and processed.

4. The extent of blinding if the investigator was blinded to the group allocation during the experiment and/or when assessing the outcome.

5. Justification for statistical tests that address the following questions (as appropriate):

   • a. Do the data meet the assumptions of the tests (e.g., normal distribution)?
   • b. Is there an estimate of variation within each group of data?
   • c. Is the variance similar between the groups that are being statistically compared?

Source: www.ascb.org/files/mboc-checklist.pdf

STATISTICS TUTORIAL

The Supplemental Materials online provide a tutorial as both a pdf file and a Jupyter.ipynb file to practice analyzing data. The Supplemental Tutorial uses free R statistical software (www.r-project.org/) to analyze five data sets (provided as Excel files). Each example uses a different statistical test: Welch’s t test for unequal variances; Student’s t test on log transformed responses; logistic regression for categorical response and two treatment variables; chi-square contingency test on combined response and combined treatment groups; and ANOVA with Tukey-Kramer post-hoc analysis.