Reliability of Signal Transfer at a Tonically Transmitting, Graded Potential Synapse of the Locust Ocellar Pathway

Abstract

We assessed the performance of a synapse that transmits small, sustained, graded potentials between two classes of second-order ocellar “L-neurons” of the locust. We characterized the transmission of both fixed levels of membrane potential and fluctuating signals by recording postsynaptic responses to changes in presynaptic potential. To ensure repeatability between stimuli, we controlled presynaptic signals with a voltage clamp. We found that the synapse introduces noise above the level of background activity in the postsynaptic neuron. By driving the presynaptic neuron with slow-ramp changes in potential, we found that the number of discrete signal levels the synapse transmits is ∼20. It can also transmit ∼20 discrete levels when the presynaptic signal is a graded rebound spike. Synaptic noise level is constant over the operating range of the synapse, which would not be expected if presynaptic potential set the probability for the release of individual quanta of neurotransmitter according to Poisson statistics. Responses to individual quanta of neurotransmission could not be resolved, which is consistent with a synapse that operates with large numbers of vesicles evoking small responses. When challenged with white noise stimuli, the synapse can transmit information at rates up to 450 bits/s, a performance that is sufficient to transmit natural signals about changes in illumination.

Introduction

For a chemical synapse, the rate of information transmission is constrained by variability in vesicle release and a signal band-width that is limited by membrane time constants. Although variability in transmission at synapses where the presynaptic neuron produces impulses is well documented (Redman, 1990; Wadiche and Jahr, 2001), little quantitative data exists on the performance of synapses that convey graded changes in potential. Communication with graded potentials should allow information to be transmitted at greater rates than communication with spike trains, because it avoids the process of converting between an analog and a frequency code, and there is some support for this from estimates, using tools first developed by Shannon and Weaver (1949). For example, lamina monopolar cells (LMCs) in the blowfly compound eye can carry information at rates three to five times greater than axons that convey impulse trains (de Ruyter van Steveninck and Laughlin, 1996a), and in a spider mechanoreceptor, axonal impulse trains may carry information at a rate several-fold lower than the receptor potential (Juusola and French, 1997). The only quantitative estimate so far of the rate at which information can be conveyed from one neuron to another is in the fly eye, in which the synaptic ensemble connecting a single photoreceptor and an LMC can carry ∼1250 bits per second (de Ruyter van Steveninck and Laughlin, 1996a).

In the locust ocellar pathway, transmission across different types of synapses can be studied routinely (Simmons, 2002a). Seven “L-neurons” connect each lateral ocellus with the brain (Goodman, 1974), and they signal changes in light with graded potentials. L-neurons L1-3 make output synapses with contrasting dynamic properties: one at which transmission depresses extremely rapidly (Simmons, 2002b) and a second that shows no depression and can transmit potential changes of both polarities (Simmons, 1981, 1993). Here, we describe the reliability of transmission at the second type of synapse. It is made from L1-3 to third-order “DN neurons” (Griss and Rowell, 1986) that are involved in flight control (Simmons, 1980) and also to neurons L4 and L5 (Simmons, 1982). We studied the synapses with L4-5, because DN neurons experience much background synaptic activity from wind-sensitive and other sensory pathways (Simmons, 1980), and their postsynaptic sites are relatively small. We used a voltage clamp to control changes in presynaptic potential in a precise and repeatable manner. First, we determined the resolution with which the synapse can convey graded changes in potential by assessing variations in postsynaptic potential when the presynaptic neuron was at different membrane potentials. Second, we established that, at this synapse, there were no fundamental differences between transmission mediated by gradually changing or sustained presynaptic signals compared with transmission mediated by rebound spikes. Finally, we estimated the rate at which the synapse can transmit information by driving the presynaptic neuron with a repeated, white noise waveform and comparing the power spectra of the mean postsynaptic response with the power spectrum of postsynaptic noise (de Ruyter van Steveninck and Laughlin, 1996a).

Materials and Methods

Experiments were performed on 40 adult Schistocerca gregaria, taken from a laboratory culture. To collect data on responses to light stimuli, a locust was fixed onto a block of modeling clay, and the brain and ocellar nerves were exposed to permit an electrode to be inserted into an L-neuron axon in the ocellar tract or nerve (Simmons, 1993). In experiments to study transmission from L1-3 to L4-5, the brain was prepared for electrophysiology and placed within the dissected head capsule in a small Perspex chamber (Simmons, 1999). In most experiments, a two-electrode voltage clamp was used to control changes in presynaptic potential while a third electrode recorded postsynaptic potential, as described previously (Simmons, 2002b). The three microelectrodes were inserted into the axons of L-neurons within 250 μm of the junction of a lateral ocellar nerve with the brain, either within the nerve or the ocellar tract. A digital-to-analog (D-to-A) converter on a microcomputer graphics card, controlled by software written using Borland Turbo Pascal, produced the electrical signals used to drive the voltage clamp. White noise stimuli were generated as a series of 2048 pseudorandom voltage levels using routines written in MatLab (MathWorks, Natick, MA). The series was played out repeatedly with a repetition period of T_repeat = 2.4 s. Electrical coupling between the current-injecting electrode of the voltage clamp and the postsynaptic recording electrode contaminated recording badly in more than one-half of the experiments we performed. The coupling is frequency dependent. To reduce it, we smoothed the steps in adjacent voltage levels generated by the MatLab routine by interposing a quarter sine wave cycle of appropriate phase between them. Approximately 40% of our experiments yielded recordings in which we could detect no coupling artifacts at frequencies <100 Hz, and these were the experiments that we analyzed. Noise introduced by the electrode and instruments, measured as the SD in voltage over 10 s with an electrode in saline, was 0.02 mV, with a power spectrum flat to ≥2 kHz. Noise contributions from adjacent L-neurons were likely to be negligible, because a rebound spike in one L-neuron generated no simultaneous signal in other L-neurons. In experiments with light stimuli, the output of the D-to-A card controlled the current flow through the light-emitting diode (LED). Light stimuli were delivered from a bright green light-emitting diode (peak wavelength, 525 nm; maximum intensity, 17,000 millicondela; Yoldal, Taipei, Taiwan) held 50 mm from the ocellus by a centering device that allowed the light to be directed at the ocellar lens. The stimulus waveform was not smoothed in these experiments. The LED was calibrated using a radiometer (Ealing, Holliston, MA). Recordings were acquired using a Micro1401 acquisition system controlled by Spike2 for Windows software (Cambridge Electronic Design, Cambridge, UK) and were later analyzed using MatLab and SigmaPlot (SPSS, Chicago, IL).

To find the signal power spectral density for a cell, we first averaged the individual response traces across all trials. This average response trace was Fourier transformed, and the magnitude squared of the Fourier components, with appropriate normalization, gave the signal power density, S(f), as plotted in Figure 6A (open circles; postsynaptic signal) and Figure 7B (filled circles; average response power) [for details on the procedure, see de Ruyter van Steveninck and Laughlin (1996b) and Rieke et al. (1997)]. The noise power spectral density, N(f), was calculated by first subtracting the average waveform, as defined above, from all of the individual experimental traces. This defined a set of fluctuation waveforms. Taking the power spectrum of each of these waveforms and then averaging these spectra provided the noise power spectral densities, as plotted in Figure 6A (triangles) and Figure 7B (open circles).

Figure 6.

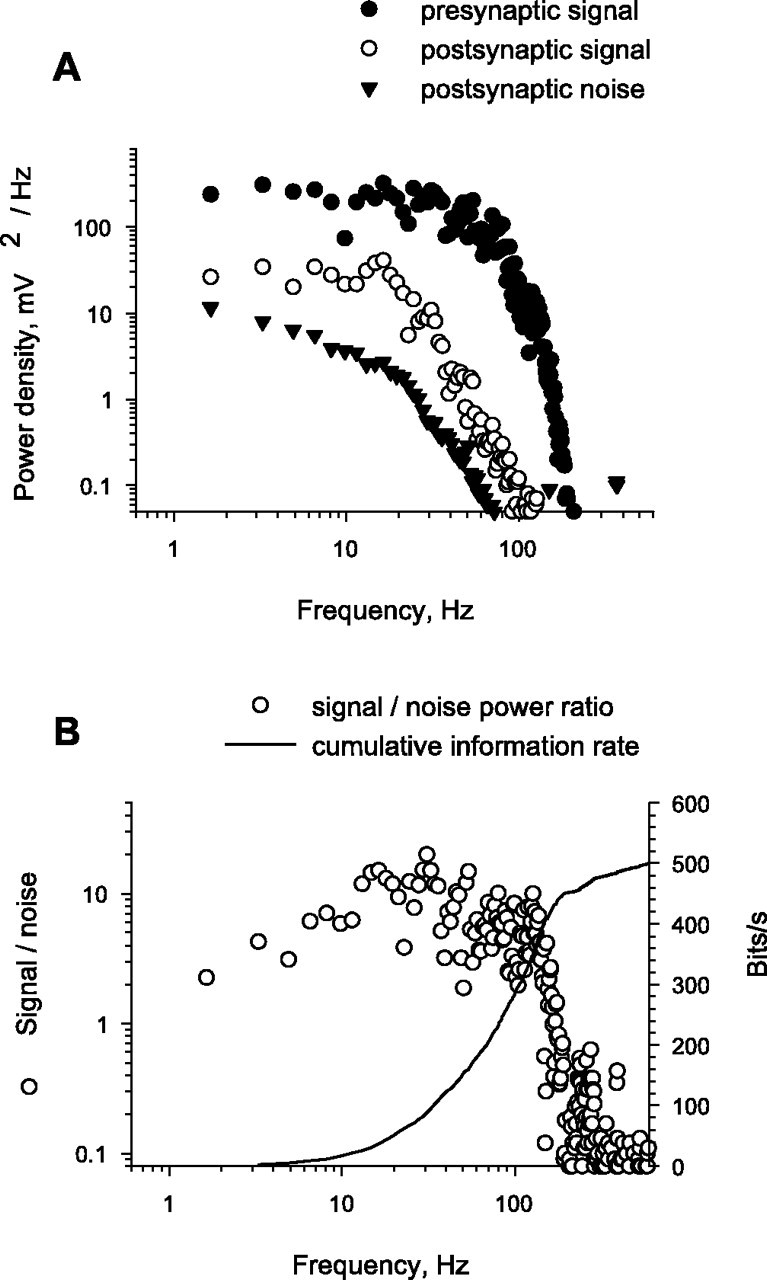
Estimate of the information-carrying capacity of the synapse. A, Frequency plots for presynaptic signal, postsynaptic mean signal, and mean frequency plot for postsynaptic noise from recordings shown in Figure 5. B, Postsynaptic signal-to-noise ratio and of estimated cumulative information rate transmitted across the synapse plotted against frequency.

Figure 7.

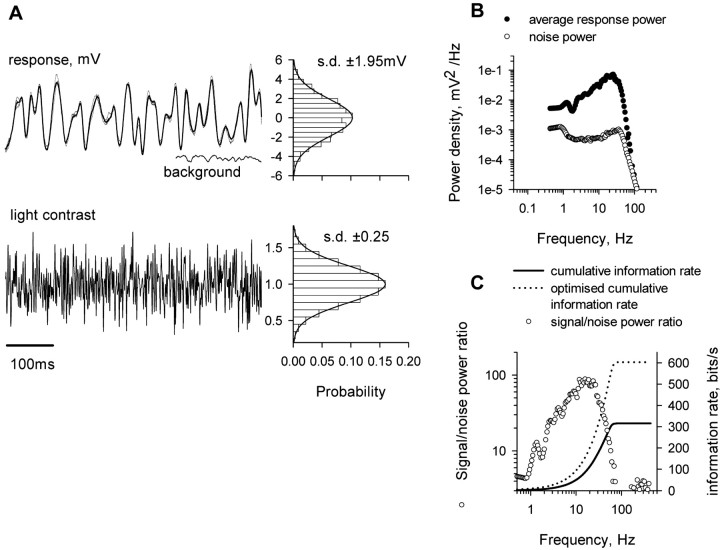
Estimation of the information carried by an L-neuron when stimulated with white noise light stimuli. A, Excerpt of a fluctuating light stimulus (bottom), of the mean L-neuron response (dark line; top), and of three individual responses (lighter lines). A recording of the background response by the L-neuron to steady illumination at the mean stimulus intensity is also shown. To the right are probability distributions for the light contrasts and for mean L-neuron responses for the entire 2.4 s stimulus waveform. B, Frequency plot for power of average L-neuron response and mean of the power spectra of deviations from the mean response. C, Plots of signal-to-noise power ratio and of cumulative information rate against frequency from this experiment. The dotted line plots the cumulative information rate that would be obtained under optimal conditions, as described in Results.

Information transmission rates were estimated based on the previous result (Shannon and Weaver, 1949) for Gaussian channels as follows:

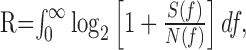(1)

where R is the information transmitted (in bits per second), and f is the frequency (in hertz). The Gaussian approximation is reasonable, as indicated by the amplitude distributions in Figures 5, D and E, and 7A. There were subtle deviations from Gaussianness, however, as indicated by running a Kolmogorov-Smirnov test. These deviations were too small to affect the result significantly. We tested this by a direct information estimation method (Strong et al., 1998) developed by Juusola and de Polavieja (2003) for the case of graded potential signals. We can also calculate information transmitted over a limited frequency band, and in Figures 6 B and 7C, we plotted the information rate, R(f₀), as the discrete approximation to Equation 1 over the frequency interval (0,f₀) as follows:

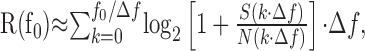(2)

Figure 5.

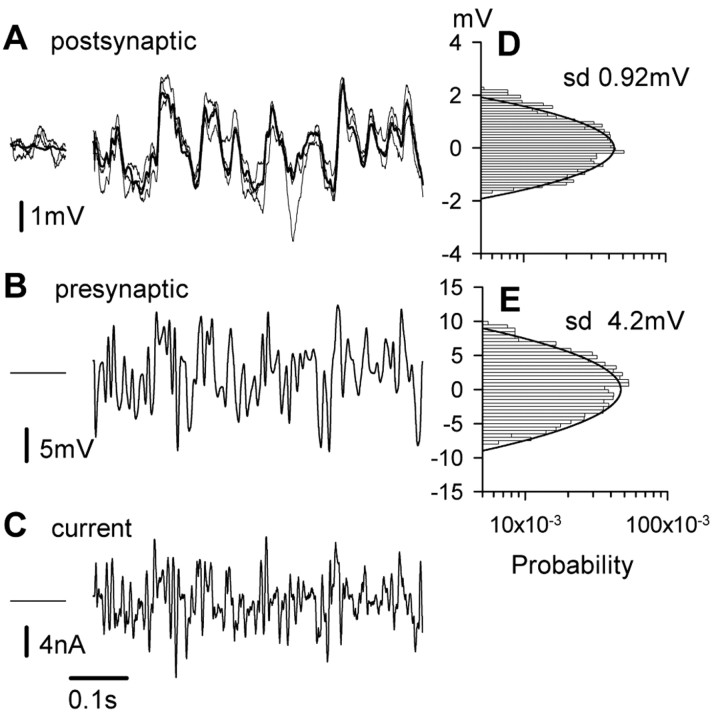
Recordings used to estimate the information-carrying capacity of the synapse. A, Mean (bold line) and three individual responses (light lines) from the postsynaptic neuron responding to an excerpt of the presynaptic wave form. B shows the excerpt from the presynaptic waveform. The voltage clamp ensured that the 2.4-s-long pseudorandom waveform was exactly replicated in each of 20 repetitions. C, Presynaptic current injected during one stimulus. To the left of A-C are brief periods when the presynaptic neuron was held clamped at dark resting potential. D, E, Probability distributions for mean postsynaptic response to 20 stimulus repetitions and for presynaptic potential during a 2.4 s stimulus waveform.

where the frequency resolution, Δf, is the inverse of the stimulus repetition period: Δf = 1/T_repeat ≈ 0.42 Hz. The maximum value of f₀ in these calculations was the Nyquist frequency: f₀ = 1/(2 × t_s) ≈ 427 Hz. The signal and noise spectra in these equations are those obtained directly from the experiments.

As motivated in the text, for experiments with light stimuli, we can optimize the signal spectrum to maximize I, given that we use a certain total amount of contrast variance. Dividing S(f) by the stimulus contrast power spectrum, C(f), we obtained the power transfer function, T(f). T(f) represents the square of the frequency-dependent gain of the system in transducing contrast into voltage; its units are Volt²/(contrast unit)². To maximize I, we modified the shape of the contrast signal spectrum, which we denote C_opt(f), keeping the total contrast variance, σ²_c, equal to 0.1 as follows:

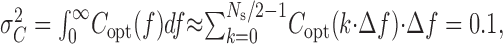(3)

with N_s = 2048, the number of samples in the stimulus waveform. We chose the shape of C_opt(f) such that the sum of the noise spectrum and the contrast induced signal spectrum:

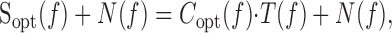(4)

was constant over as large a frequency range as possible. The optimal spectrum can be found easily by iteration. Details of this procedure can be found in the studies by de Ruyter van Steveninck and Laughlin (1996a) and Rieke et al. (1997).

Results

General features of transmission between L1-3 and L4-5

Each L-neuron has an axon 10-20 μm wide that travels from a lateral ocellus into the protocerebrum of the brain, with L4 and L5 extending more posteriorly than L1, L2, and L3 (Goodman, 1974). The connections at which L1-3 excite L4-5 occur approximately midway along a lateral ocellar tract in the brain, and each consists of an ensemble of several hundred discrete synaptic contacts made between the axons of L1-3 and about five 50-μm-long branches of L4-5 (Fig. 1A) (Littlewood and Simmons, 1992).

Figure 1.

General features of the excitatory synapse between L-neurons. A, Summary of the morphologies of an L1-3 neuron and an L4-5 neuron. Each neuron has an axon with one arbor in the lateral ocellus and another in the brain. Discrete anatomical contacts of the excitatory synapses are made in the ocellar tract from the axon of L1-3 onto fine, stubby processes that project from the axon of L4-5. One process is represented near the bend in the ocellar tract. B, Graded transmission across the synapse, demonstrated by using one electrode to inject current pulses into the presynaptic neuron while separate electrodes recorded the membrane potentials of the presynaptic and postsynaptic neurons. At dark resting potential, the synapse releases neurotransmitter tonically so that both depolarizing and hyperpolarizing changes in potential are conveyed (left). Sudden depolarizing potentials in both neurons are enhanced by rebound spikes, which are graded in amplitude (details are shown in the right panels). C, A two-electrode voltage clamp allows good control of membrane potential over a range of voltages. The current-injecting and voltage-clamp electrodes were placed 200 μm apart in the axon of an L-neuron in the ocellar tract, while an independent recording electrode was placed in the same axon in the ocellar tact, ∼200 μm from the origin of the nerve. Recordings are shown from two 50 Hz sine waves, the first oscillating about dark resting potential and the second depolarized by 15 mV. D, E, Frequency-dependent transmission across the synapse. A voltage clamp-controlled presynaptic potential, which was held at a mean 15 mV depolarized from dark resting potential and driven with sine waves of various frequencies. Averages of postsynaptic potential over 10 cycles are shown for three different frequencies, with different time scales, so that the recordings of presynaptic potential superimpose. E, Plots of synaptic gain (averages of 10 cycles; peak-to-trough postsynaptic/presynaptic) against frequency. pre-, Presynaptic; post-, postsynaptic; vc, voltage command.

General operating characteristics of the L1-3 to L4-5 synapse are demonstrated by responses to pulses of current injected into a presynaptic neuron (Fig. 1B). In darkness, the presynaptic neuron releases transmitter tonically, so that both hyperpolarizing and depolarizing potentials are conveyed across the synapse. Responses to rapid depolarizations are enhanced by regenerative responses that give rise to rebound spikes, which are graded in amplitude and depolarize an L-neuron briefly by up to 30 mV from dark resting potential (Wilson, 1978b; Simmons, 1999). Evidence that the neurons were healthy was gained by observing continual fluctuations in potential in darkness (probably resulting from spontaneous release of neurotransmitter from photoreceptors) (Wilson, 1978c; Simmons, 1999) and by responses to brief light pulses ≥30 mV in amplitude. Here, we made measurements only from synapses in which a 10 mV change in presynaptic neuron caused a change of ≥5 mV in a postsynaptic neuron and in which stable recordings from both were held for several minutes. Each experiment described in this study was repeated successfully at least four times, with similar results. All experiments were conducted in darkness, because illumination causes a relatively large increase in L-neuron conductance. Measurements were made relative to dark resting potential, which is approximately -30 mV.

In most experiments, a two-electrode voltage clamp was used to control presynaptic potential. This was done to ensure that the presynaptic signal could be exactly duplicated in successive stimulus presentations by eliminating background fluctuations in presynaptic potential. The voltage clamp can control the presynaptic zone of an L-neuron axon adequately for a range of speeds of change of signal, including step changes in potential (Simmons, 2002b). In Figure 1C, we show that the clamp is effective for potentials up to ∼30 mV depolarized from dark resting potential. It is important that the clamp works effectively in this regime, because the input resistance of an L-neuron, and therefore its length constant, decreases markedly when it is depolarized (Wilson, 1978b).

The frequency response of the excitatory synapse was examined by recording postsynaptic responses when the presynaptic neuron was driven with sine waves of different frequencies, using the voltage clamp (Fig. 1D). For signals up to 1 Hz, synaptic gain is level. At higher frequencies, gain decreases sharply (Fig. 1E).

Variability in transmission of sustained or slowly changing potentials

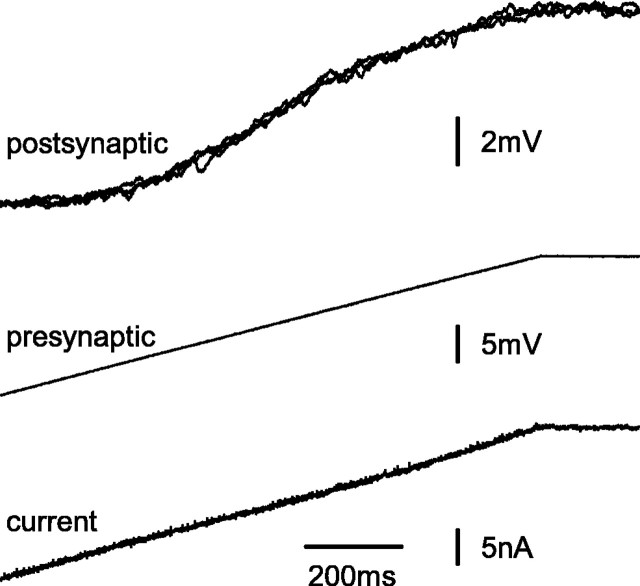
To characterize variability in postsynaptic potentials mediated by different levels of presynaptic potential, the voltage clamp was used to drive presynaptic L-neurons with slow, depolarizing ramp changes in potential (Figs. 2, 3). Each ramp altered the presynaptic potential from -10 to +10 mV relative to dark resting potential over 1 s. The postsynaptic neuron gradually began to depolarize as the presynaptic neuron was driven positive from approximately -8 mV. The slope of the transfer curve increased gradually until the presynaptic neuron was at approximately -4 mV (Fig. 3A). Then, for presynaptic potentials between -4 and +4 mV, there was a linear change in postsynaptic potential of 0.7 mV for each 1 mV change in presynaptic potential (Fig. 3A). Finally, as the presynaptic neuron depolarized further, the slope of the transfer curve declined. This decline was apparent in all six successful experiments of this type. Although it might indicate a reduction in the relationship between presynaptic potential and rate of increase in transmitter release, other features that could contribute are a decrease in input resistance of the postsynaptic neuron (Wilson, 1978b) and a reduction in driving force for the postsynaptic potential.

Figure 2.

Transmission of slow-ramp changes in presynaptic potential. The presynaptic neuron was driven under control of the voltage clamp with gradual ramp depolarizations, changing between -10 and +10 mV relative to dark resting potential. Three separate records of postsynaptic potential are superimposed (top), whereas single recordings of presynaptic potential (middle) and of current injected (bottom) are shown.

Figure 3.

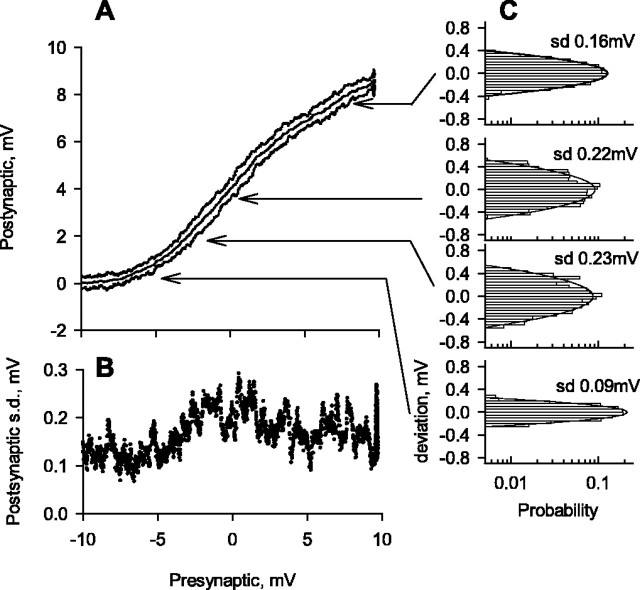
Transfer curve for the synapse, determined by driving the presynaptic neuron with ramp changes in potential shown in Figure 2. A, Mean postsynaptic potential and two SDs from the mean on either side for 31 identical presynaptic ramp stimuli. B, Plot of SD in postsynaptic potential against presynaptic potential. C, Frequency distributions of deviations in postsynaptic potential from the mean at four different locations on the transfer curve.

The three individual records of postsynaptic potential superimposed in Figure 2 indicate the variability in postsynaptic responses to repetitions of an identical presynaptic signal. Quantitative data shown in Figure 3 are from 31 repetitions of the ramp presynaptic stimulus. Figure 3A plots the transfer curve, including the mean relationship between presynaptic and postsynaptic potentials and two SDs either side of the mean. The SD is plotted against the presynaptic potential in Figure 3B, and distributions of postsynaptic potentials at four different locations on the transfer curve are plotted in Figure 3C. Each histogram in Figure 3C is plotted from three measurements within 0.02 mV of the same presynaptic potential made for each of the 31 repetitions and is fitted with a normal curve with the same mean value and SD as the measured data.

Figure 3 illustrates two important points. First, the synapse adds noise during transmission. We can see this by comparing the SD of postsynaptic potential when the synapse was active with the SD in the subthreshold region of the transfer curve, where variability of postsynaptic potential was entirely caused by background activity of other synapses impinging on the neuron, including from photoreceptors (Wilson, 1978c; Simmons, 1999). Second, synaptic noise does not rise continuously throughout the linear part of the operating range of the synapse. It peaks when the presynaptic potential is about dark resting potential and declines slightly to a steady level for more positive presynaptic potentials (Fig. 3B). The same conclusions were reached from measurements of postsynaptic potential variation in response to holding the presynaptic neuron at different steady potentials for several seconds.

To separate the intrinsic synaptic contribution to the total postsynaptic noise from other sources, we assumed that these sources add linearly and independently, which implies that their variances should add. We therefore calculated the variance of intrinsic noise for the synapse illustrated in Figures 2 and 3 as 0.042 mV² (SD = 0.20 mV) by subtracting the variance of background noise from the variance in postsynaptic potential measured over the linear part of the transfer function. As an approximate estimate, using a criterion for difference for signals to be distinguishable as two SDs, or 0.41 mV (Snyder et al., 1977) and a range for the postsynaptic potential of 8.3 mV, we estimate that ∼20 different signal levels can be distinguished based on instantaneous measurement.

Transmission mediated by rebound spikes

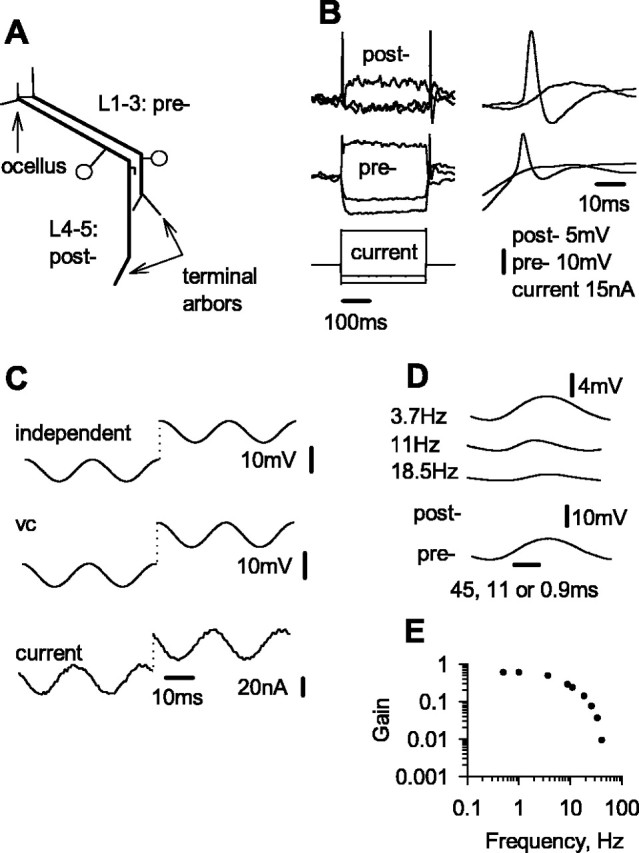
Rebound spikes in L1 invariably trigger rebound spikes in L4, which boost the postsynaptic potential. Consequently, to measure variability in postsynaptic responses mediated by presynaptic spikes, it was necessary to measure postsynaptic currents rather than postsynaptic potentials. In these experiments (Fig. 4), the two-electrode voltage clamp recorded postsynaptic currents. A single electrode with the amplifier in bridge balance mode was used to trigger and record rebound spikes in the presynaptic neuron, and altering the strength of 0.2-s-long negative current pulses injected presynaptically produced a series of presynaptic spikes of different amplitudes. A pulse was injected every 1.2 s, and a steady current of -5 nA was injected between pulses so that the synapse was subthreshold in the periods between spikes. Figure 4A shows two amplitudes of presynaptic spike together with postsynaptic currents and the corresponding postsynaptic potentials (the postsynaptic potentials were recorded later with the voltage clamp switched off). Superimposing the postsynaptic currents produced in response to two different spike amplitudes shows that the time to reach peak depends on spike amplitude (Fig. 4B), in contrast to the IPSPs that L1-3 mediate in each other (Simmons, 2002b).

Figure 4.

Transmission of discrete postsynaptic responses mediated by presynaptic spikes. A, Recordings of postsynaptic current (psc) and of postsynaptic potential (psp) mediated by presynaptic spikes (pre-) of two different amplitudes. B, The two postsynaptic currents from A are shown superimposed and with each scaled relative to its maximum amplitude to emphasize that the time to peak varies with amplitude. C, Plots of presynaptic spike amplitude against postsynaptic current amplitude and background noise, measured as described in Results. D, Probability distribution of residuals from the regression line for presynaptic spike amplitude against postsynaptic current amplitude in C. E, Probability distribution for background noise in postsynaptic current.

There was a linear relationship between postsynaptic current amplitude and the peak of a presynaptic spike over the range of 4-14 mV (Fig. 4C). The scatter of individual postsynaptic currents from the regression line was similar for all amplitudes of presynaptic spike. Residuals of postsynaptic current were normally distributed about the regression line, with SD = 0.20 nA (Fig. 4D). The SD of background noise, measured at 0.5 s after each presynaptic spike as the change in postsynaptic current during a time equal to the rise time of the postsynaptic current, was 0.13 nA (Fig. 4E). Using the same method as for slowly changing or static presynaptic potential, we calculated that noise intrinsic to the synapse itself had an SD of 0.15 nA (Fig. 4D, dotted line). The range of postsynaptic currents in this experiment is 6-7 nA. Using the same criterion for signal discriminability as for the case of graded potentials (that is, 2 SDs; equivalent here to 0.30 nA in postsynaptic current), the number of distinct signal levels is ∼20, the same as that found for transmission of slowly changing or sustained presynaptic potentials.

Postsynaptic responses to white noise presynaptic stimuli

To characterize the performance of the synapse in conveying fluctuating signals, we used the voltage clamp to drive presynaptic neurons with repeated 2.4-s-long white noise stimuli (Figs. 5, 6). We then calculated the signal-to-noise ratio in the postsynaptic response by dividing the power spectrum of the mean response by the mean of the power spectra of deviations from mean response. From this, we obtained an estimate for information transmission as described in Materials and Methods.

Figure 5A shows the mean postsynaptic response (bold trace) and three individual responses (lighter traces) to 20 repetitions of part of a stimulus waveform shown in Figure 5B. Figure 5C shows a single record of current injected presynaptically. Both the presynaptic and postsynaptic voltage waveforms had amplitude distributions that were nearly Gaussian (Fig. 5D,E). The power spectrum of the presynaptic waveform was flat up to 100 Hz and dropped by a factor of 1000 by 200 Hz (Fig. 6A, filled circles). The power spectrum of the mean postsynaptic response (Fig. 6A, open circles) lay well within the stimulus spectrum. Dividing the power spectrum of the mean postsynaptic response (Fig. 6A, open circles) by the mean power spectrum of postsynaptic noise (Fig. 6A, triangles) allowed us to compute signal-to-noise ratios (Fig. 6B, open circles). Figure 6B also shows that the synapse accumulated information up to a frequency of ∼150 Hz and allows us to estimate that the synapse transmitted information at a rate of ∼450 bits/s. Beyond 150 Hz, the signal-to-noise ratio quickly decreases. Note that 450 bits/s is not necessarily the maximum rate that the synapse is able to transmit, which is hard to calculate because the synapse is likely to be limited by a finite voltage range rather than a total power constraint. The optimum distribution of presynaptic signals is probably non-Gaussian, which is much harder to analyze.

Responses by L-neurons to fluctuating light signals

Under normal conditions, the presynaptic signal would be the responses mediated by photoreceptors to a fluctuating light stimulus in an L1-3 neuron. The presynaptic signal will therefore be limited by the dynamics and noise introduced during the processes of phototransduction and of synaptic transfer from photoreceptors to L3. To characterize how variations in illumination contribute to a natural signal in an L-neuron, we quantified the information capacity of the L-neuron in response to fluctuating light stimuli (Fig. 7). The ocellus was stimulated by a bright green LED modulated by a white noise contrast waveform. The modulation trace contained 2048 sample values (Fig. 7A, bottom trace) played out over 2.4 s and presented repeatedly. The mean illumination at the ocellar lens was 0.58 mW/cm², and the SD of the light contrast trace was 0.25. This was chosen as slightly lower than that used in previous experiments on fly photoreceptors (de Ruyter van Steveninck and Laughlin, 1996a) to allow for the enormous fields of view that locust L-neurons have (Wilson, 1978a). A 0.6 s section of the light stimulus is shown in Figure 7A, together with the mean response to 104 stimulus repetitions (bold trace) and three individual responses (lighter traces). Responses fall within a range of 5.5 mV either side of the mean, with an SD of 1.95 mV. The power spectra for the mean response and the mean spectrum of noise power are plotted in Figure 7B. There is a gradual increase in mean signal power as frequency increases up to 20 Hz (Fig. 7C) and then the signal power falls rapidly. Its overall shape is reminiscent of that of the blowfly LMC, except that the point of high-frequency roll-off lies at a lower frequency (Juusola et al., 1995).

We calculated the signal-to-noise ratio and estimated information transmission rate as before. The signal-to-noise ratio and cumulative information rate are plotted against frequency in Figure 7C. The plot of cumulative information rate indicates that information is accumulated for frequencies up to 100 Hz, and that the maximum rate transmitted during this experiment was 312 bits/s. In general, a white noise stimulus under a total power constraint does not maximize information transmission. Therefore, to enable comparison between different experiments and different animals, it is useful to calculate the optimized value of information transmission by distributing contrast power in such a way that the sum of contrast noise and stimulus power is constant over a frequency that is as wide an interval as possible. The optimal rate of information transmission calculated as described in Materials and Methods is almost twice the measured value (Fig. 7C, dotted line). Locust ocellar L-neurons have a slower frequency response than the equivalent neurons of the fly compound eye, and we estimate that, for this reason, their information carrying capacity is three to four times lower.

This estimate is comparable with the estimate made above for the rate of information that the excitatory synapse between two L-neurons can carry. The SD of presynaptic potential changes in the experiment in which the presynaptic neuron was driven with a white-noise, voltage-clamp stimulus (4.2 mV) was greater than the SD of potential changes in an L-neuron stimulated with white noise light stimuli (Fig. 7), and the power spectrum of the presynaptic voltage fluctuations in response to electrical stimuli (Fig. 6A) encompassed a greater frequency range than the power spectrum of responses to light stimuli (Fig. 7B). If we had used, as a presynaptic stimulus, the waveform that an L-neuron would produce in response to a light stimulus that maximized information transmission rate, we calculated that the rate of information transfer would have saturated at ∼315 bit/s or approximately half the maximum that we estimated the presynaptic neuron did convey in our experiment.

Discussion

Synaptic reliability and information transmission

Our experiments with slow-ramp stimuli show that ∼20 discrete signal levels can be distinguished in the postsynaptic neuron within an operating range of ∼8.5 mV. Data are available for two other synapses, both in insect visual pathways and showing depression in transmission, and these have a similar level of resolution. The inhibitory synapse between partner L1-3 locust ocellar neurons operates with just <10 distinct signal levels (Simmons, 1999). A blowfly LMC can resolve 2% modulations in light contrast (Laughlin, 1989), and accounting for the improvement in signal-to-noise by convergence of photoreceptors (Laughlin et al., 1987), a single photoreceptor-LMC connection operates with ∼20 distinct levels.

A more useful measure of performance takes into account the ability of a synapse to convey fluctuating signals. We obtained a direct estimate of 450 bit/s by challenging the synapse with white noise fluctuations in presynaptic membrane potential. Data on the rate of information transmission has been published only for one other synaptic connection: the fly photoreceptor to LMC synapse. In response to fluctuating light stimuli, the information capacity of a blowfly LMC is 1650 bits/s, and a connection between one photoreceptor and an LMC can be estimated reliably at 1250 bits/s (de Ruyter van Steveninck and Laughlin, 1996a). Our measurements of information transmission rate between L1-3 and L4-5 are more direct, because only a single presynaptic neuron was stimulated. They indicate that an L1-3 neuron transmits information to an L4-5 neuron at slightly under half the rate estimated for the connection between a blowfly photoreceptor and an LMC, a rate that primarily reflects the slower frequency response of locust L-neurons. At the fly photoreceptor to LMC synapse, the remarkable constancy in the lengths of individual anatomical synaptic contacts in the ensemble of the 200 contacts between a single photoreceptor and LMC (Fröhlich, 1985; Meinertzhagen and Hu, 1996) has allowed the information-carrying capacity of a single, discrete anatomical contact to be estimated as 55 bits/s (de Ruyter van Steveninck and Laughlin, 1996a). We cannot be confident of making a reliable estimate for each discrete anatomical contact between L1-3 and L4-5 in the locust, because there is considerable variation in the lengths of individual anatomical contacts in this ensemble (Littlewood and Simmons, 1992; Leitinger and Simmons, 2002).

The control of transmitter release

The ability of a graded potential synapse to convey small changes in signal level will be enhanced if it operates with large numbers of quanta, each evoking a small postsynaptic response. Tonically releasing output synapses from L1-3 are ensembles of hundreds of discrete contacts, each associated with large numbers of vesicles (Leitinger and Simmons, 2002). Postsynaptic responses to individual quanta are probably too small to be resolved in intracellular recordings. Similarly, synapses between fly photoreceptors and LMCs probably operate with a few hundred small quanta released each second (Laughlin et al., 1987, 1998), a similar release rate to that at vertebrate synapses with ribbon-shaped presynaptic specializations (von Gersdorff and Matthews, 1999; Moser and Beutner, 2000; von Gersdorff, 2001). In general, connections between neurons in the insect nervous system consist of hundreds of discrete synaptic contacts (Watson and Burrows, 1981, 1985; Nicol and Meinertzhagen, 1982; Peters et al., 1985; Simmons and Littlewood, 1989), which is consistent with the notion that they operate with large numbers of small quanta. However, for impulse-evoked transmission in insects, two physiological studies suggest that postsynaptic responses contain a handful of 0.2-0.3 mV quantal responses (Laurent and Sivaramakrishnan, 1992; Sosa and Blagburn, 1995), but another suggests postsynaptic events contain many small-amplitude quantal responses (Simmons, 2001).

A synapse that transmits graded potentials must be able to regulate the release of vesicles in a manner that depends on presynaptic voltage. Although our experiments do not shed light on the way the intracellular machinery works, they invite speculation on the design of the system. For instance, it is plausible that the production of vesicles is a limiting process. If so, information transmission could be maximized by regulating vesicle release tightly, analogous to the way that an integrate and fire model neuron can produce a regular spike train in response to steady input current (Dayan and Abbott, 2001). This is consistent with our observation that the noise level in synaptic transmission does not rise strongly as input level increases. Our data do not directly support a Poisson model for synaptic release, which would predict a monotonic rise in noise as the average rate of vesicle discharge increases. The same finding has been made for the inhibitory synapses made between L1 and L3 (Simmons, 1999). Similarly, at an output synapse made by vertebrate hair cells, the scatter in postsynaptic current amplitudes does not vary with different levels of presynaptic potential (Glowatzki and Fuchs, 2002), and in some retinal bipolar cells, there is evidence that vesicles are released cooperatively rather than independently of each other from a single active zone (Singer et al., 2004).

For the vertebrate hair cell synapse, it has been suggested that a presynaptic signal controls the release of vesicles in sets rather than by affecting the probability for individual vesicle release (Glowatzki and Fuchs, 2002). Sets of discrete synapses within the ensemble between L1-3 and L4-5 might differ in their noise characteristics, which could explain why synaptic noise has a slight peak near the dark resting potential before declining at more depolarized potentials. It is tempting to propose that variability in presynaptic length between different individual contacts at synapses made by L1-3 (Leitinger and Simmons, 2002) is related to variability in physiological characteristics. Our data do support the idea that individual synaptic contacts at output synapses made by L1-3 can differ markedly in their physiological characteristics. At the synapses that L1-3 make among each other, transmission depresses so rapidly that the rate of change of presynaptic potential rather than its amplitude determines the amplitude of the postsynaptic response (Simmons, 2002b). In contrast, at the synapses with L4-5, we found that a graded rebound spike in the presynaptic neuron evokes a postsynaptic current with a rise time that varies with its amplitude. Consequently, here, the amplitude of the presynaptic potential regulates the rate of neurotransmitter release, whether the presynaptic signal is a slow change in potential or a rebound spike.

The ocellar pathway

How do the operating characteristics of the synapse relate to its function? Our estimate that the L1-3 to L4-5 synapse can transmit 450 bits/s lies between the measured (312 bit/s) and the optimized (600 bit/s) rates at which an L-neuron transmits information in response to random fluctuations in light intensity, and so the performance synapse seems well matched to transmit signals about fluctuating light levels. But it must be kept in mind that our experiments were performed with a light source that had a narrower field and lower intensity than a locust ocellus would experience outside in daylight. The tonically transmitting output synapse an L1-3 neuron makes with L4-5, or with a DN-neuron, would be able to match an information rate of 500-600 bits/s.

However, these synapses do not simply transfer a copy of the signal in an L-neuron. Two significant transformations occur. First, moderate increases in light hyperpolarize a presynaptic L-neuron beyond the threshold for release (Simmons, 1981, 1993), so that signals for increases in light are severely clipped. Second, rebound spikes in postsynaptic L4-5 or DN neurons enhance rapid depolarizing signals. Consequently, although the synapses are well able to convey signals caused by small fluctuations in light, rapid decreases in illumination cause the largest postsynaptic potentials. This may be related to the function of ocelli in the flight autopilot mechanism of the locust.

The functional organization of ocelli and manner in which ocellar DN neurons contact flight motor neurons and premotor interneurons are both consistent with the proposal that ocelli mediate adjustments in flight attitude by monitoring shifts in the visual horizon (Wilson, 1978a; Simmons, 1980). Particularly, large decreases in illumination would be triggered if a locust pitched downwards or else rolled sharply to one side, either of which might require urgent corrective changes in flight attitude. The frequency response of the synapse shows that it rolls off steeply for frequencies >20 Hz. The response to light signals by an L-neuron peaks slightly at 20 Hz (Simmons, 1993) and then declines for higher frequencies. The tonically transmitting output synapses made by L1-3 therefore act as low-pass filters. The frequency responses of third-order neurons to light stimuli have not been measured, but multiplying L-neuron responses to light by synaptic gain at different frequencies indicates that the maximum response to light stimuli would occur at 4 Hz, with an amplitude two to four times greater than the response to light stimuli at 20 Hz. Wingbeat frequency is ∼20 Hz for a free-flying locust (Weis-Fogh, 1956). The relatively low-frequency response of the synapse, therefore, would reduce responses in third-order neurons to nodding movements of the head caused by individual wingbeats, whereas changes in flight attitude that occurred over a time span of four to five wingbeats would be enhanced.