Few Ca_V1.3 Channels Regulate the Exocytosis of a Synaptic Vesicle at the Hair Cell Ribbon Synapse

Abstract

Hearing relies on faithful sound coding at hair cell ribbon synapses, which use Ca²⁺-triggered glutamate release to signal with submillisecond precision. Here, we investigated stimulus–secretion coupling at mammalian inner hair cell (IHC) synapses to explore the mechanisms underlying this high temporal fidelity. Using nonstationary fluctuation analysis on Ca²⁺ tail currents, we estimate that IHCs contain ∼1700 Ca²⁺ channels, mainly of Ca_V1.3 type. We show by immunohistochemistry that the Ca_V1.3 Ca²⁺ channels are localized preferentially at the ribbon-type active zones of IHCs. We argue that each active zone holds ∼80 Ca²⁺ channels, of which probably <10 open simultaneously during physiological stimulation. We then manipulated the Ca²⁺ current by primarily changing single-channel current or open-channel number. Effects on exocytosis of the readily releasable vesicle pool (RRP) were monitored by membrane capacitance recordings. Consistent with the high intrinsic Ca²⁺ cooperativity of exocytosis, RRP exocytosis changed nonlinearly with the Ca²⁺ current when varying the single-channel current. In contrast, the apparent Ca²⁺ cooperativity of RRP exocytosis was close to unity when primarily manipulating the number of open channels. Our findings suggest a Ca²⁺ channel–release site coupling in which few nearby Ca_V1.3 channels impose high nanodomain [Ca²⁺] on release sites in IHCs during physiological stimulation. We postulate that the IHC ribbon synapse uses this Ca²⁺ nanodomain control of exocytosis to signal with high temporal precision already at low sound intensities.

Introduction

The auditory system enables us to discriminate and recognize complex acoustical signals (Hudspeth, 1997). This requires high temporal precision and wide dynamic range coding at the hair cell ribbon synapse (Kiang et al., 1965) (for review, see Fuchs et al., 2003; Fuchs, 2005).

Inner hair cell (IHC) exocytosis is mediated by Ca²⁺ influx through Ca_V1.3 Ca²⁺ channels (Brandt et al., 2003), whereas transmitter release at conventional synapses is preferentially linked to P/Q-, N-, and/or R-type Ca²⁺ channels (for review, see Stanley, 1997; Augustine et al., 2003; Reid et al., 2003). Hair cell Ca²⁺ channels are thought to cluster at active zones (Lewis and Hudspeth, 1983; Art and Fettiplace, 1987; Roberts et al., 1990; Zenisek et al., 2003). Tens of Ca²⁺ channels were suggested to cooperate in imposing a “[Ca²⁺] microdomain” on synaptic vesicle release sites at each active zone (Roberts et al., 1990; Roberts, 1994; Tucker and Fettiplace, 1995). Single Ca²⁺ channel gating averages out in these population-based Ca²⁺ microdomains, such that changes in open-channel number or single-channel current would have indistinguishable effects on exocytosis (Augustine et al., 1991; Mintz et al., 1995; Wu et al., 1999).

However, some features of auditory signaling seem incompatible with a Ca²⁺ microdomain control of hair cell synaptic transmission. For instance, phase-locking of auditory nerve fiber spiking with near-threshold tones (Rose et al., 1967) indicates temporally precise synaptic coding even for weak stimuli. However, release kinetics controlled by Ca²⁺ microdomains would be sluggish for weak stimuli, because of the high intrinsic Ca²⁺ cooperativity of hair cell exocytosis in the low micromolar range (Beutner et al., 2001). Furthermore, the time course of synaptic depression, suggested to reflect depletion of readily releasable vesicles (Furukawa et al., 1978; Moser and Beutner, 2000; Spassova et al., 2004), shows little dependence on the stimulus intensity (Furukawa et al., 1978; Westerman and Smith, 1984). This, too, is not compatible with a Ca²⁺ microdomain control, in which varying stimulus intensities should result in very different readily releasable vesicle pool (RRP)-depletion kinetics.

These findings seem more consistent with exocytosis of a synaptic vesicle being predominantly controlled by one or few Ca²⁺ channels located in nanometer proximity from the release site of a vesicle. There, high “nanodomain [Ca²⁺]” triggers rapid vesicle fusion and “slow” Ca²⁺ chelators fail to inhibit exocytosis (Neher, 1998). Different from the microdomain regimen, the apparent Ca²⁺ cooperativity of exocytosis during manipulations of Ca²⁺ current would depend on whether single-channel current or open-channel number is changed (Augustine et al., 1991; Mintz et al., 1995). It would be high only when small single-channel currents were changed, thereby varying the [Ca²⁺]ofthe release site in the low micromolar range. Changing the number of open channels would cause nearly linear changes of RRP exocytosis (Augustine et al., 1991).

We used patch-clamp recordings of Ca²⁺ current and membrane capacitance (C_m) changes to study how manipulations of single-channel current and/or the number of open channels affect RRP exocytosis in IHCs. A Ca²⁺ nanodomain control is suggested to underlie the high temporal precision of sound coding at the hair cell ribbon synapse.

Materials and Methods

Electrophysiology. IHCs from the apical coil of freshly dissected organs of Corti from Naval Medical Research Institute mice [postnatal day 13 (P13) to P20] were patch clamped at their basolateral face at room temperature (20–25°C) [for details, see Moser and Beutner (2000)]. The pipette solution contained the following (in mm): 140 Cs-gluconate, 13 tetraethylammonium-Cl (TEA-Cl), 10 CsOH-HEPES, 1 MgCl₂, 2 MgATP, 0.3 NaGTP, and 5 EGTA (see Fig. 5) or 10 BAPTA (see Fig. 1). For perforated-patch experiments, amphotericin B (250 μg/ml) was added. The extracellular solution contained the following (in mm): 105 NaCl, 35 TEA-Cl, 2.8 KCl, 1 MgCl₂, 10 NaOH-HEPES, and 10 d-glucose, pH 7.2. Ca²⁺ and Ba²⁺ were added as chloride salts as specified in the figure legends; the standard extracellular Ca²⁺ concentration ([Ca²⁺]_e) was 10 mm. Dihydropyridines (DHPs) (isradipine, Novartis, Summit, NJ; nifedipine and BayK8644, Sigma, St. Louis, MO) were dissolved in DMSO at a concentration of 10 mm. They were diluted to their final concentration (see figure legends; DMSO not exceeding 0.1%) in extracellular solution immediately before the experiments and protected from light. Solution changes were achieved by slow bath exchange or by local perfusion using a large-tip-diameter superfusion pipette.

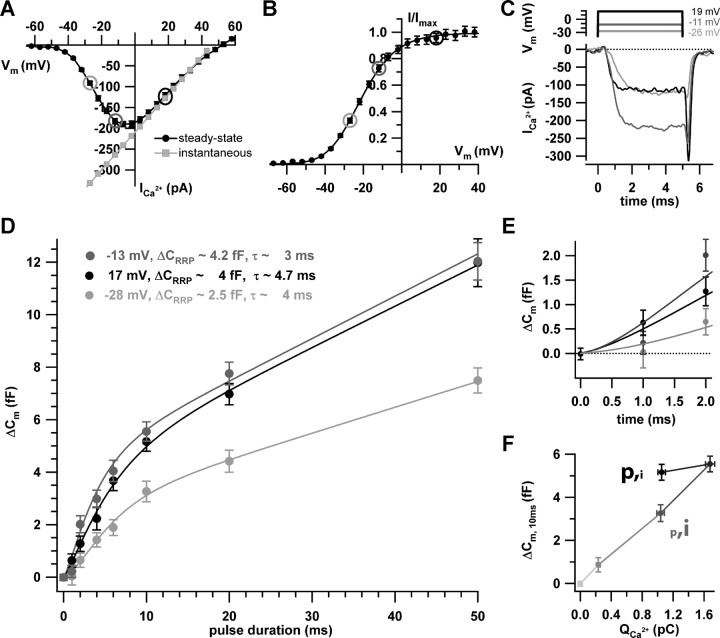
Figure 5.

Effects of depolarization strength on RRP exocytosis. A, B, The steady-state IV (black symbols) of the experiments used to study the voltage dependence of RRP exocytosis (10 mm [Ca²⁺]_e). The circles indicate the potentials for which the kinetics of exocytosis was studied. The instantaneous IV (A; gray symbols) was approximated as the ratio of the steady-state IV (A; black symbols) and the channel activation curve (B) in the range of 5–50 mV and then linearly extrapolated toward hyperpolarized potentials. C, Example currents for depolarization to –26, –11, and 19 mV, using the color coding of A and B. D, Summary of the exocytic ΔC_m achieved for the three depolarization levels and different pulse durations. Pulses were applied to 33 IHCs in random order with an interval of at least 30 s and 1073 sweeps were used for analysis. Of those, a smaller number of sweeps was acquired at –41 mV (n = 158; data not shown), which did not provide a sufficiently resolved kinetics plot. E, The first 2 ms of exocytosis kinetics in better resolution. F, The exocytic responses (ΔC_{m, 10 ms}) to 10-ms-long depolarizations to four potentials (–41, –28, –13, and 17 mV) versus the corresponding Ca²⁺ current integrals. The first point corresponds to a 20 ms blank (–86 mV). The gray scale codes for depolarization strength as in the other panels: from light gray (–86 mV) to black (17 mV). Note the different amounts of exocytosis despite similar Ca²⁺ current integrals for –28 mV [larger single-channel current (see A) but lower open probability (see B)] and 17 mV [smaller i (see A) but larger p (see B)]. Error bars represent SEM.

Figure 1.

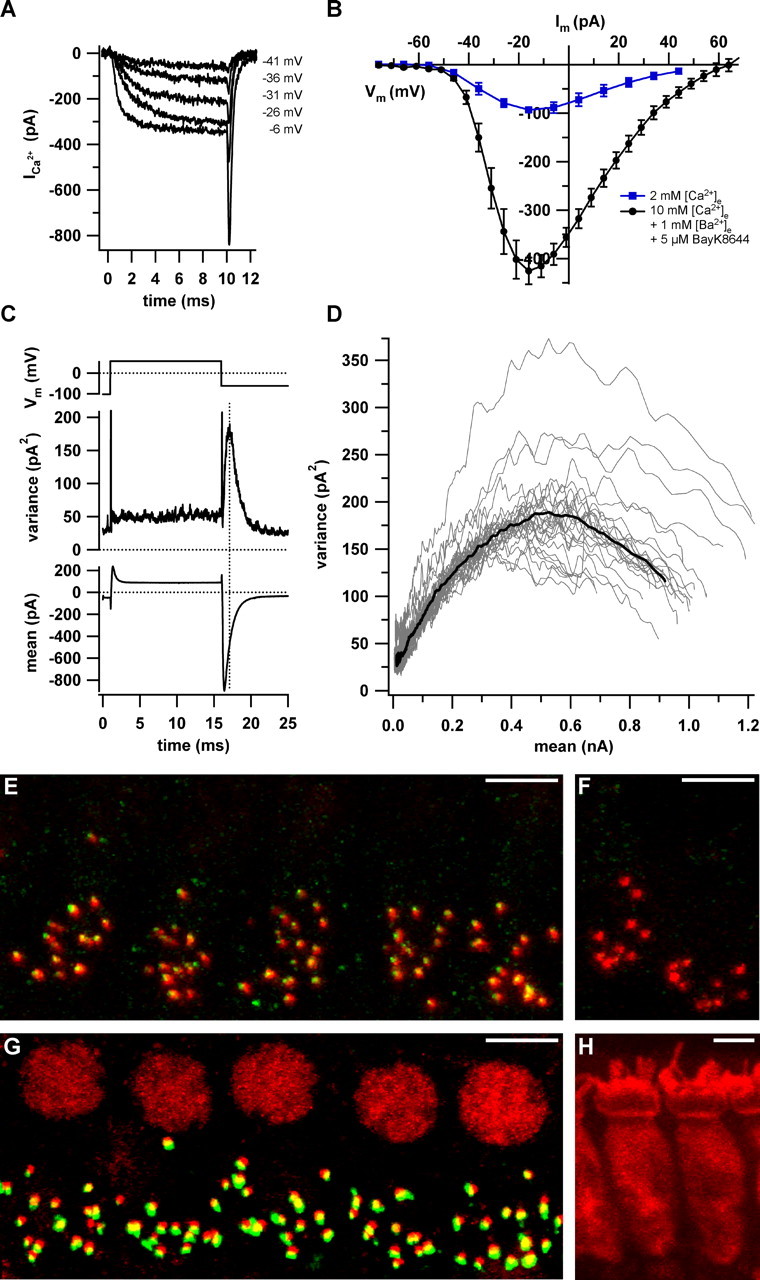
Counting Ca²⁺ channels and ribbon synapses in apical IHCs. A, Example Ca²⁺ currents evoked by 10 ms step depolarizations from –86 mV to the specified levels in the presence of 5μm BayK8644, 10 mm Ca²⁺, and 1 mm Ba²⁺. B, Average steady-state IV relationships in augmenting conditions (black circles; solutions as in A) and at close to physiological [Ca²⁺]_e (2 mm; blue squares). C, Voltage-clamp protocol (top), variance (middle), and mean (bottom) calculated from a P/n-corrected ensemble of 500 sweeps (interval, 80 ms). D, Variance versus mean parabolas obtained from 27 ensembles of nine cells (gray traces) and the grand average calculated from parabolas of the individual cells (black trace). E, A typical 3D reconstruction of a wild-type organ of Corti after staining for Ca_V1.3 (green) and RIBEYE/CtBP2 (red). F, Identical processing of an organ of Corti from a Ca_V1.3 knock-out mouse. G, A typical double staining for RIBEYE/CtBP2 (red) and GluR2/3 glutamate receptors (green). Juxtaposed spots of red and green fluorescence represent intact ribbon synapses. IHCs were counted by means of their nuclear CtBP2 signal. H, The cytosolic staining using an antibody to calbindin (red). Scale bars, 5 μm.

EPC-9 amplifiers (HEKA Elektronik, Lambrecht, Germany) controlled by Pulse software (HEKA Elektronik) were used for measurements. All voltages were corrected for liquid junction potentials [16 mV, except Fig. 1 B, C (17 mV)]. C_m was measured using the Lindau-Neher technique (Lindau and Neher, 1988), as described previously (Moser and Beutner, 2000). ΔC_m was estimated as the difference of the mean C_m over 60–400 ms after the end of the depolarization (the initial 40 ms was skipped) and the mean prepulse capacitance (400 ms). Ca²⁺ current integrals were calculated from the total depolarization-evoked inward current, including Ca²⁺ tail currents after leak subtraction. Note that the tail current is low-pass filtered because of the limited clamp speed of the perforated-patch configuration (e.g., ∼180 μs time constant for a 20 MΩ access resistance and a typical 9 pF cell) (Khimich et al., 2005) and hence spreads out in time, which, however, does not affect the Ca²⁺ current integral estimation. Leak subtraction was done either by using P/n protocols or by subtracting a linear function calculated from the leak current at holding potential and the approximated reversal potential of the leak current. Cells that displayed a membrane current exceeding –50 pA at our standard holding potential of –86 mV were discarded from the analysis. Several responses were collected for each cell with an interstimulus interval of at least 30 s to ensure sufficient pool recovery (Moser and Beutner, 2000). Data analysis was performed using Igor Pro software (WaveMetrics, Lake Oswego, OR). Variance (var) of Ca²⁺ tail currents recorded at –62 mV was estimated as average of the squared differences between pairs of consecutive responses, as described previously by Roberts et al. (1990), rather than as the average squared difference from the mean to minimize effects of Ca²⁺ current rundown and variable capacitative currents that were not fully eliminated by capacitance cancellation and P/n correction (P/100 before the ensemble of 500 sweeps). Least-squares fitting (Levenberg-Marquardt algorithm implemented in Igor Pro software) of the variance versus mean parabolas according to the equation var = iI_mean – I_mean²/N + offset was used to estimate N_Ca (the total number of Ca²⁺ channels) and i (the single-channel current). Means are expressed ± SEM and compared by Student's t test.

Immunohistochemistry. Immunostaining of whole mounts of apical cochlear turns was performed as described by Khimich et al. (2005) for Figure 1, G and H. For the Ca_V1.3 staining in Figure 1, E and F, fixation was performed for 20 min in 99.9% ethanol (Merck, Darmstadt, Germany) at –20°C, because no specific staining was obtained with other fixation protocols. The following antibodies were used: mouse IgG1 anti-C-terminal binding protein 2 (anti-CtBP2; 1:150; BD Biosciences, Franklin Lakes, NJ), rabbit anti-Ca_V1.3 (1:75; Alomone Labs, Jerusalem, Israel), rabbit anti-glutamate receptor 2/3 (anti-GluR2/3; 1:200; Chemicon, Temecula, CA), rabbit anti-calbindin (1:400; Swant, Bellinzona, Switzerland), and secondary AlexaFluor488- and AlexaFluor568-labeled antibodies (1:200; Invitrogen, San Diego, CA). Confocal images were collected using an LSM 510 microscope (Carl Zeiss, Jena, Germany) and analyzed using LSM 5 Image Browser, ImageJ, and Adobe Photoshop (Adobe Systems, San Jose, CA). Three-dimensional (3D) reconstructions of CtBP2- and GluR2/3-stained organs of Corti were animated, and juxtaposed pairs of CtBP2 and GluR2/3 spots were counted as ribbon-containing synapse if no discernible space was found between the presynaptic and postsynaptic signals (Khimich et al., 2005). We approximated the basolateral circumference of the cell using ImageJ and assumed the soma of the hair cell to represent a symmetric rotational solid to estimate its basolateral surface.

Results

Number of active-zone Ca²⁺ channels in inner hair cells

How many L-type channels open simultaneously at an IHC active zone during physiological stimulation? We first set out to count the total number of L-type Ca²⁺ channels in apical IHCs by nonstationary fluctuation analysis on Ca²⁺ tail currents. The experiments were performed in presence of the dihydropyridine agonist BayK8644 (5 μm). BayK8644 raises the mean open time of L-type Ca²⁺ channels (Brown et al., 1984; Hess et al., 1984), enabling faithful assessment of the binomial channel statistics in whole-cell recordings (Roberts et al., 1990). Figure 1A shows representative Ca²⁺ currents evoked in augmenting conditions (BayK8644; 10 mm Ca²⁺ and 1 mm Ba²⁺) as used for constructing the average steady-state current–voltage (IV) relationship of Figure 1B (black circles). Under these conditions, the maximal Ca²⁺ current was about fourfold larger than under more physiological conditions (2 mm [Ca²⁺]_e; absence of BayK8644; blue squares). For fluctuation analysis, we repetitively depolarized IHCs to 58 mV in augmenting conditions to maximally activate L-type Ca²⁺ channels. From these ensembles of tail currents recorded at –62 mV, we calculated variances and means (Fig. 1C, Table 1) (see Materials and Methods for details). As expected, the variance reached its maximum (dotted line) during the decay of the tail current. Figure 1D plots the variance versus mean parabolas, which were fitted by the equation in Materials and Methods to estimate total channel number (N_Ca) and single channel current (i). Table 1 summarizes the findings obtained in nine IHCs. The average N_Ca of apical cochlear IHCs amounted to ∼1700 channels with an i of 0.63 pA (at –62 mV, in the presence of 10 mm Ca²⁺ and 1 m Ba²⁺ m) and a maximal open probability of 0.82 (p_max in the presence of BayK8644).

Table 1.

Ensemble-fluctuation analysis of IHC Ca²⁺ currents

Cell	NCa [mean ± SEM (n)]	iCa [mean ± SEM (n)]	pmax [mean ± SEM (n)]
1	1776 ± 157 (n = 2)	0.53 ± 0.03 (n = 3)	0.87 ± 0.04 (n = 2)
2	1635 ± 133 (n = 2)	0.63 ± 0.02 (n = 4)	0.89 ± 0.01 (n = 2)
3	1894 ± 177 (n = 3)	0.59 ± 0.01 (n = 10)	0.86 ± 0.02 (n = 3)
4	2030 (n = 1)	0.57 ± 0.02 (n = 6)	0.81 (n = 1)
5	1909 ± 77 (n = 4)	0.60 ± 0.01 (n = 2)	0.76 ± 0.01 (n = 4)
6	1449 ± 213 (n = 3)	0.87 ± 0.01 (n = 3)	0.82 ± 0.02 (n = 3)
7	1262 ± 67 (n = 5)	0.62 ± 0.03 (n = 5)	0.72 ± 0.01 (n = 5)
8	1580 ± 59 (n = 6)	0.63 ± 0.01 (n = 6)	0.79 ± 0.01 (n = 6)
9	1867 (n = 1)	0.60 (n = 1)	0.84 (n = 1)
All	1711 ± 83 (n = 9)	0.63 ± 0.03 (n = 9)	0.82 ± 0.02 (n = 9)

Fluctuation analysis of Ca²⁺ channels quantifies N_Ca, single-channel current (i_Ca), and p_max, determined by nonstationary fluctuation analysis in nine apical IHCs as described in Figure 1. In seven IHCs, we acquired at least two ensembles of 500 current sweeps and obtained average estimates of the channel parameters. The maximal open probability could be slightly underestimated because we had to limit tail current analysis to start only 100 μs after the repolarization as a result of contaminating capacitative currents. The grand averages represent equally weighted means of the results of the individual cells.

Next, we investigated the distribution of Ca²⁺ channels by immunostaining for Ca_V1.3 and confocal analysis. As shown in Figure 1E, we observed Ca_V1.3-specific fluorescent spots, which were strictly juxtaposed to the hair cell ribbons (identified by staining for the major ribbon component RIBEYE) (Khimich et al., 2005) and absent from Ca_V1.3-deficient hair cells (Platzer et al., 2000) (Fig. 1F). In addition, a ring-like unspecific fluorescence was detected close to the cuticular plate in both wild-type and Ca_V1.3-deficient hair cells [as described previously by Sidi et al. (2004); data not shown]. Hence, we did not detect any significant extrasynaptic Ca_V1.3-specific immunofluorescence preventing a semiquantitative comparison of synaptic and extrasynaptic Ca_V1.3 channel densities based on fluorescence intensity.

To approximate the number of Ca_V1.3 channels per active zone, we first estimated the number of ribbon synapses per IHC (Khimich et al., 2005) by counting juxtaposed pairs of RIBEYE-labeled ribbons and postsynaptic glutamate receptor-immunoreactive spots in 3D reconstructions from confocal sections (Fig. 1G). We found an average of 13.7 ± 0.6 (n = 75 apical IHCs of four ears; age, P16) ribbon synapses in the apical range of the 3-week-old cochlea used for our cell-physiological experiments.

For an approximation of the number of extrasynaptic Ca²⁺ channels, we estimated the average basolateral membrane surface of apical IHCs by membrane capacitance measurements and by confocal microscopy. The average membrane capacitance was 7.8 ± 0.26 pF (n = 28 IHCs) translating into 780 μm² (specific capacitance of 10 fF/μm²) (Breckenridge and Almers, 1987). According to Roberts et al. (1990), the apical hair cell pole, which is likely devoid of voltage-gated Ca²⁺ channels, accounts for ∼30% of the total surface, leaving ∼550 μm² for basolateral membrane surface. This value agrees reasonably well with a geometric estimate of basolateral surface of ∼512 ± 44 μm² obtained from 3D reconstructions of confocal images of calbindin-stained IHCs (n = 12 IHCs) (Fig. 1G) (see Materials and Methods). From our previous EM analysis (Khimich et al., 2005), we obtained an upper estimate of the IHC active zone area of ∼0.44 μm² (assuming a round active zone with the diameter of the postsynaptic density). The total synaptic area (∼6.2 μm²) would then amount to ∼1% of the basolateral membrane.

Apparent Ca²⁺ cooperativity of RRP exocytosis: manipulation of Ca²⁺ channel domain

Next, we investigated how changes of Ca²⁺ channel domain amplitude affect RRP exocytosis to test whether the apparent Ca²⁺ cooperativity during Ca²⁺ influx mimics the intrinsic Ca²⁺ cooperativity of vesicle fusion. RRP exocytosis was monitored in perforated-patch recordings as C_m change in response to 20-ms-long depolarizations to the peak Ca²⁺ current potential (Brandt et al., 2003).

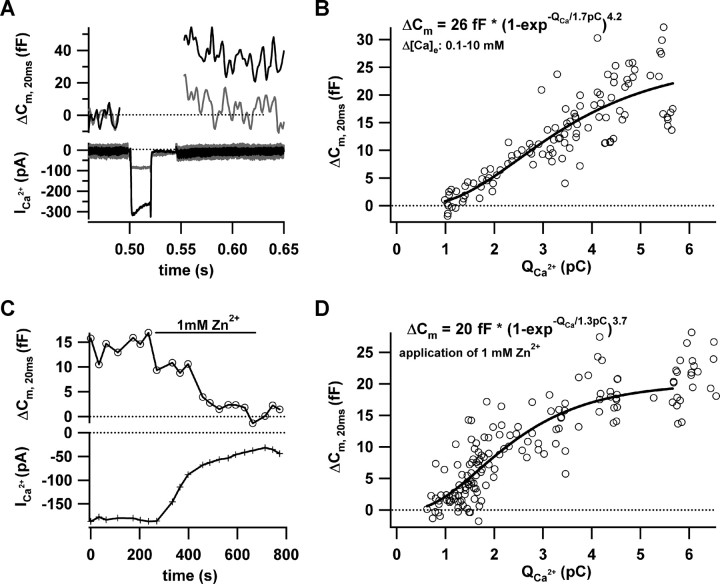
First, we varied the Ca²⁺ channel domain amplitude by changing [Ca²⁺]_e between 10 and 0.25 mm by local perfusion (10, 4, 2, 1, 0.5, 0.25 mm). The [Ca²⁺]_e changes shifted the peak Ca²⁺ current potential as a result of surface charge screening effects. The stimuli were adjusted accordingly to minimize these effects and keep the number of open channels comparable. The representative examples (Fig. 2A) demonstrate that RRP exocytosis is lost before the Ca²⁺ current vanishes, indicating a nonlinear dependence. The relationship of RRP exocytosis and the Ca²⁺ current integral takes an approximately sigmoidal shape that was approximated by a power of exponent function (Fig. 2B). The initial rise is supralinear (apparent cooperativity, 4.2), nearly approaching the steep intrinsic Ca²⁺ dependence in the low micromolar [Ca²⁺] range (Beutner et al., 2001). For larger Ca²⁺ currents, we observed saturation of exocytosis. This probably indicated that [Ca²⁺] at the release sites had already driven exocytosis to the maximum rate, such that further Ca²⁺ increases did not cause a major change of exocytosis. In addition, or alternatively, it might reflect RRP depletion.

Figure 2.

Effects of changes in (apparent) single channel Ca²⁺ domain amplitude. A, Representative Ca²⁺ currents (bottom) and exocytic capacitance changes (ΔC_{m, 20 ms}; top) in response to 20 ms depolarization to the peak Ca²⁺ current potential. The Ca²⁺ current was large and the ΔC_m sizable in the presence of 10 mm [Ca²⁺]_e, but the reduced Ca²⁺ current at 0.25 mm [Ca²⁺]_e failed to elicit an obvious ΔC_m. B, Scatter plot of ΔC_{m, 20 ms} versus the corresponding Ca²⁺ current integrals (Q_Ca) for three experiments in which [Ca²⁺]_e was gradually changed (10, 4, 2, 1, 0.5, and 0.25 mm). The solid line is a least-squares fit of a power of exponent function to the data approximating the plateau of RRP exocytosis, the specific Q_Ca, and the apparent cooperativity. C, The time course of ΔC_{m, 20 ms} (top trace) and the Ca²⁺ current (bottom trace; 10 mm [Ca²⁺]_e) for a typical perforated-patch experiment, in which Zn²⁺ (1 mm) was applied after a control steady state had been established. An obvious ΔC_{m, 20 ms} drop occurred only after the Ca²⁺ current had already substantially declined. D, ΔC_{m, 20 ms} and Q_Ca of five such experiments (circles). The solid line presents a power of exponent fit (as in B).

To avoid potential differences in open-channel number, unstable leaks at low [Ca²⁺], or differences in synaptic vesicle priming, we next varied the Ca²⁺ current at a constant [Ca²⁺]_e by the inorganic Ca²⁺ channel blocker Zn²⁺.Zn²⁺ causes a rapid flicker block of L-type channels (Winegar and Lansman, 1990), which does not result in a true change of single-channel current amplitude as is the case when varying [Ca²⁺]_e (see above). However, we argue for an apparent amplitude reduction of the Ca²⁺ domain “seen by the vesicle” in the presence of Zn²⁺, because the limited kinetics of Ca²⁺ binding to the exocytic machinery cannot follow the rapid Ca²⁺ domain changes during the microsecond current flickering. As illustrated in Figure 2C, Zn²⁺ (1 mm) was slowly washed in and out again to study RRP exocytosis during a graded decrease or increase of apparent single Ca²⁺ channel domain. Figure 2D pools the RRP exocytosis estimates as a function of Ca²⁺ current integral for five Zn²⁺ experiments and presents a power of exponent fit to the pooled data. Comparable with the true Ca²⁺ channel domain change demonstrated above, we also observed a high apparent Ca²⁺ cooperativity (3.7) of RRP exocytosis during the Zn²⁺ flicker block. Fitting the power of exponent function (Fig. 2) to the individual cells yielded a mean cooperativity of 3.5 ± 0.1 (n = 4; no convergence of fit in one of five cells). Line fitting to exocytosis during the first 2 pC of Ca²⁺ influx (including the steepest part of the relationship) revealed a y-axis crossing at –7.2 ± 1.2 fF (n = 5), supporting the notion of a nonlinear relationship.

Apparent Ca²⁺ cooperativity of RRP exocytosis: primary manipulation of the number of open Ca²⁺ channels

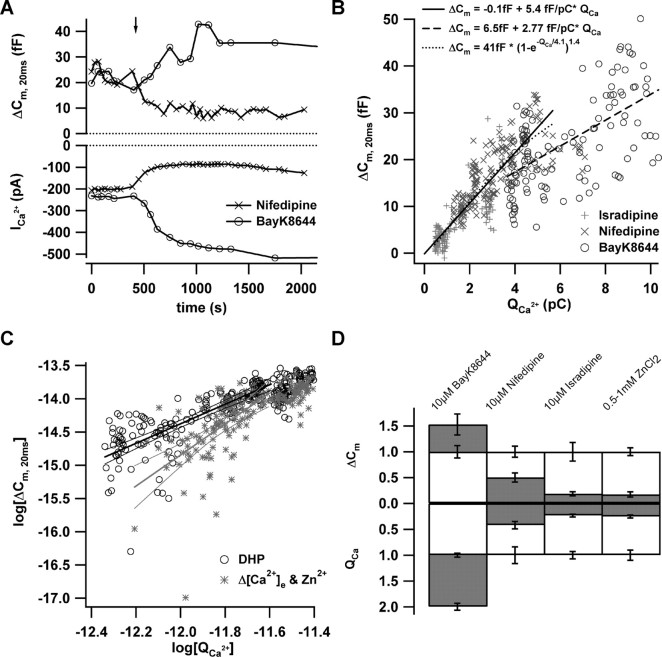
Next, we tested the effects of DHP inhibition or augmentation of Ca²⁺ influx on RRP exocytosis. L-type Ca²⁺ channels are thought to be shifted to the long-lasting nonconducting “mode zero” after binding to inhibitory DHP (Hess et al., 1984). Augmenting DHP such as BayK8644, on the other hand, are thought to push the channel to the high open probability “mode two,” which is characterized by long bursts of openings (Hess et al., 1984). Fortunately, from the point of view of our experiments, DHP do not affect the single-channel current amplitude (Hess et al., 1984). Therefore, and to a first approximation, we consider the number of Ca_V1.3 channels that open during the 20 ms depolarization to be decreased by inhibitory DHP and increased by augmenting DHP. We used slow drug application to study RRP exocytosis during a graded decrease or increase of open Ca²⁺ channel number (Fig. 3A). Distinct from the delayed and nonlinear reduction of exocytosis during the Zn²⁺ flicker block, RRP fusion declined immediately and linearly when the Ca²⁺ current was reduced by the DHP antagonist nifedipine. The augmentation of Ca²⁺ current by slow wash-in of BayK8644 caused a graded increase of exocytosis. Figure 3B relates RRP exocytosis to Ca²⁺ current integrals obtained in control conditions and after application of isradipine (10 μm; n = 5 IHCs) or nifedipine (10 μm; n = 5 IHCs). During DHP inhibition, an apparent cooperativity of 1.4 was observed (Fig. 3B), compared with 3–4 obtained with the same power of exponent fit for the data of Figure 2. Line fitting to exocytosis during the first 2 pC of Ca²⁺ influx of the isradipine data revealed a y-axis crossing at –2.0 ± 0.7 fF, which is significantly less negative than the value obtained during Zn²⁺ block (–7.2; p < 0.005).

Figure 3.

Effects of primary changes in open Ca²⁺ channel number. A, The time course of exocytic ΔC_{m, 20 ms} (top) and Q_Ca (bottom) in response to repetitive depolarization (20 ms; to the peak Ca²⁺ current potential; 10 mm [Ca²⁺]_e). In these representative perforated-patch experiments, nifedipine (10μm; ×) or BayK8644 (10μm; ○) were applied by slow bath perfusion as indicated by the arrow. B, ΔC_{m, 20 ms} and Q_Ca for a total of 15 such experiments (10μm isradipine, +; 10 μm nifedipine, ×; and 5 μm BayK8644, ○; n = 5 for each condition). DHP were washed in after achieving a control steady state as illustrated in A. The lines correspond to the fit functions provided in the graph. Solid and dotted lines, Line and power of exponent fits to the data acquired with inhibitory DHP (the fit interval from lowest integral up to 5 pC was chosen as in Fig. 2 for better comparison); dashed line, line fit to BayK8644 data. C, The logarithms of exocytic ΔC_{m, 20 ms} (in farads) and Q_Ca (in coulombs) for both manipulations (DHP, black circles; Zn²⁺ and Δ[Ca²⁺]_e, gray asterisks). The lines represent line fits to both data sets (along with 99% confidence intervals) yielding Ca²⁺ cooperativities of 1.4 and 2.3 for DHP and Zn²⁺/Δ[Ca²⁺]_e, respectively. D, Steady-state effects of 10 μm BayK8644, 10 μm nifedipine, 10 μm isradipine, or 0.5–1 mm Zn²⁺ (n = 5 for each condition) on ΔC_{m, 20 ms} (top) and Q_Ca (bottom). The gray filling indicates the average ΔC_{m, 20 ms} and Q_Ca estimates after drug application after normalization to the grand averages obtained before drug. Error bars represent SEM. Q_Ca, Ca²⁺ current integrals.

Figure 3C displays the exocytosis–Ca²⁺ charge relationships obtained for DHP inhibition as well as for Zn²⁺ flicker block and reduction of [Ca²⁺]_e in the traditional double-log plot. The lowest current integrals were chosen as the range of linear fitting, because saturation of exocytosis sets in for larger integrals (Fig. 2). Linear fitting to the exocytosis evoked in the low Ca²⁺ charge range yielded apparent cooperativities of 1.4 and 2.3 for DHP and Zn²⁺/reduction of [Ca²⁺]_e data sets, respectively. This estimate of the apparent Ca²⁺ cooperativity during Zn²⁺ flicker block is smaller than the one reported above by the power of exponent fitting (3.7) (Fig. 2D). Potential reasons for this discrepancy include the limited signal-to-noise ratio in our measurements of exocytosis in the low range of Ca²⁺ current integrals. This is of less impact on the power of exponent fitting, which relies on exocytosis estimates over a larger range of Ca²⁺ current integrals.

The near linear relationship observed during DHP block was extended to larger Ca²⁺ currents and exocytic responses by BayK8644 (n = 5 IHCs; circles; 5 μm), albeit with a shallower slope (Fig. 3B). This finding is surprising in the view of a finite RRP (Moser and Beutner, 2000) and raises the possibility that the number of available fusion-competent vesicles is functionally regulated by the number of open channels. A linear dependence of RRP exocytosis on the Ca²⁺ current was also observed during DHP block in the presence of 2 mm [Ca²⁺]_e (n = 5 IHCs; data not shown). Figure 3D summarizes the steady-state effects of DHP and Zn²⁺ on RRP exocytosis and Ca²⁺ current (at 10 mm [Ca²⁺]_e).

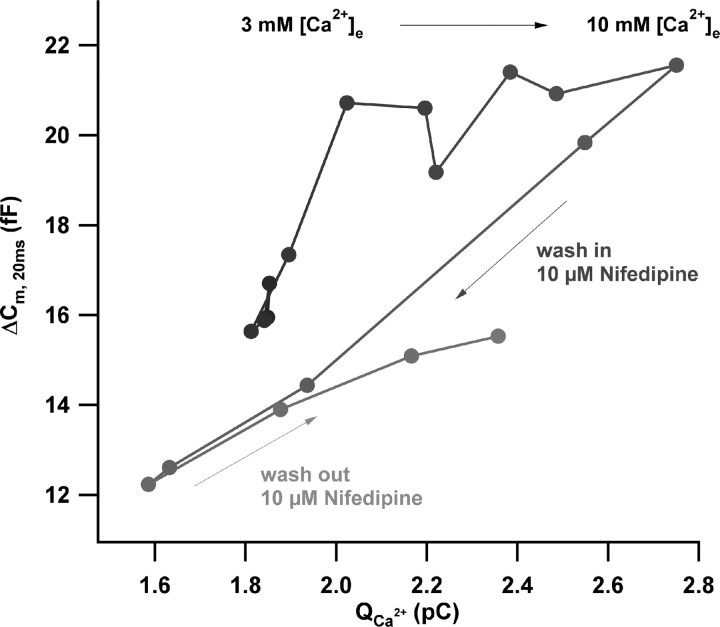
Figure 4 shows data from a representative experiment in which both single-channel current and number of open channels were manipulated subsequently (performed in nine IHCs). The change of [Ca²⁺]_e from 3 to 10 mm initially caused a steep rise of RRP exocytosis. In a later phase, exocytosis saturated despite the continued increase of Ca²⁺ current. These findings are in line with the results of Figure 2B. However, the subsequent wash-in of nifedipine (10 μm) resulted in an immediate and linear reduction of exocytosis with the Ca²⁺ current (Fig. 3A). The partial recovery after wash out of nifedipine confirms that rundown of exocytosis did not strongly bias this experiment.

Figure 4.

Direct comparison of the effects of changes in single-channel current and open-channel number on RRP exocytosis. Scatter plot of ΔC_{m, 20 ms} versus the corresponding Ca²⁺ current integrals of a representative perforated-patch experiment during (1) slow change of [Ca²⁺]_e from 3 to 10 mm, (2) application of 10 μm nifedipine at 10 mm [Ca²⁺]_e, and (3) wash out of nifedipine in the continued presence of 10 mm [Ca²⁺]_e are shown. Data were smoothed by nonoverlapping two-point box car averaging. The time course of the experiment is indicated by the black-to-gray gradient.

Graded potential control of RRP exocytosis

Ribbon-containing neurons use graded potentials rather than action potentials to control transmitter release. The hair cell potential controls presynaptic Ca²⁺ influx by both recruiting active channels and setting the single-channel current. We anticipate larger single-channel current but weaker channel activation for the hyperpolarized limb of the IV relationship and stronger channel activation but smaller single-channel current for the depolarized limb. If under nanodomain control, exocytosis should be primarily determined by the number of open channels and, hence, be larger for more depolarized potentials for the same whole-cell Ca²⁺ influx (Llinas et al., 1981; Smith et al., 1985; Zucker and Fogelson, 1986). In the case of a Ca²⁺ microdomain control, the same Ca²⁺ influx should be equally potent at both potentials.

To further distinguish between Ca²⁺ microdomain and nanodomain control of exocytosis, we investigated the voltage dependence of RRP exocytosis by recording ΔC_m in response to short stimuli of varying depolarization strength. To improve the reliability of our RRP analysis, we suppressed sustained exocytosis by intracellular dialysis with 5 mm EGTA (Moser and Beutner, 2000). Figure 5A shows the steady-state IV relationship and indicates the potentials used to study exocytosis (circles). These were set to the peak-current potential (–13 mV) and to higher and lower potentials (17 and –28 mV) with comparable steady-state currents. The level of channel activation increased (Fig. 5B) (reflecting the number of open channels) and the single-channel current (proportional to the calculated instantaneous IV relationship of Fig. 5A) decreased with the strength of depolarization. As expected, channel activation was faster at the more depolarized potentials (Fig. 5C). We stimulated each of the 33 IHCs with a random order of depolarizations of varying strength and length. Figure 5D summarizes the kinetics of RRP exocytosis evoked by the three different depolarization levels. The RRP size was reduced when compared with perforated-patch measurements, probably because of stronger rundown in whole-cell experiments. The kinetics of exocytosis at a given potential was approximated using the following equation: ΔC_m (t) = ΔC_RRP× (1 – exp^–t/τ)^y + (rate of sustained exocytosis) × t, yielding RRP size estimates and depletion time constants for the three depolarization levels as provided in Figure 5D. Comparing exocytosis at –28 and –13 mV, the twofold increase of Ca²⁺ channel activation caused a 1.5-fold increase in RRP size, as if the additional opening of channels recruited additional release sites. In addition, we observed more RRP exocytosis for comparable Ca²⁺ current at the more depolarized potential (17 mV compared with at –28 mV).

This finding is demonstrated by Figure 5F, which relates exocytic responses evoked by 10-ms-long depolarizations to the four selected potentials (–41, –28, –13, and 17 mV) versus the corresponding Ca²⁺ current integrals. Figure 5F also indicates a linear relationship of RRP exocytosis and Ca²⁺ influx for depolarizations between –41 and –13 mV. We corroborated the finding in a set of perforated-patch experiments (sole presence of endogenous Ca²⁺ buffers; data not shown) to assure that this low apparent Ca²⁺ cooperativity is not caused by a selection of Ca²⁺ nanodomain control by the high concentration of EGTA.

Discussion

In this study, we investigated Ca²⁺ influx–secretion coupling in IHCs. A high apparent Ca²⁺ cooperativity of RRP exocytosis was observed during changes of single-channel current and rapid flicker block, reporting the intrinsic Ca²⁺ dependence of hair cell exocytosis. In contrast, we found near-linear changes of RRP exocytosis with the Ca²⁺ current during DHP or voltage modulation of the Ca²⁺ current, which probably affected exocytosis mainly by changing the number of active channel-release site units. Together, our data argue that sound coding at the IHC ribbon synapse involves Ca²⁺ nanodomain control of synaptic vesicle release by few nearby Ca_V1.3 Ca²⁺ channels.

Ca²⁺ channel number and distribution in IHCs

Our estimate of ∼1700 L-type Ca²⁺ channels per apical inner hair cell of the mouse cochlea agrees very well with previous results obtained on amphibian hair cells [e.g., ∼1800 in frog saccular hair cells (Roberts et al., 1990)]. The relationship of channel count (∼1700) and active zone area (∼0.62 μm²) is comparable with amphibian and chicken hair cells (Martinez-Dunst et al., 1997). Our immunostaining revealed a clustering of Ca_V1.3 channels at the active zones (Fig. 1E), which is in line with previous studies showing a preferential Ca²⁺ influx at the ribbon synapses of amphibian hair cells (Roberts et al., 1990; Issa and Hudspeth, 1994; Tucker and Fettiplace, 1995; Rodriguez-Contreras and Yamoah, 2001; Zenisek et al., 2003; Sidi et al., 2004). However, cell-attached investigation of Ca²⁺ channel distribution in frog saccular hair cell revealed a lower but still substantial abundance of L-type Ca²⁺ channels also outside the observed dense clusters (Rodriguez-Contreras and Yamoah, 2001). This is consistent with the finding that synaptic vesicles can dock and fuse also outside ribbon-type active zones in hair cells (Lenzi et al., 2002) and retinal bipolar nerve terminals (Zenisek et al., 2000). Extrasynaptic fusion is likely to occur also in mouse IHCs during prolonged depolarization (Moser and Beutner, 2000; Beutner et al., 2001), arguing for at least some extrasynaptic Ca²⁺ influx. Here, we considered a lower bound of 500 extrasynaptic Ca²⁺ channels for IHCs based on our estimate of basolateral surface (>500 μm²) and assuming an extrasynaptic density of one channel per μm². This assumption relies on an estimate of the extrasynaptic channel density at the calyceal presynaptic terminal of chick ciliary ganglion neurons [one or two Ca²⁺ channels per square micrometer, estimated by atomic force microscopy of gold-labeled N-type Ca²⁺ channels (E. Stanley, personal communication)].

The other ∼1200 channels would distribute among the ∼14 synapses (Fig. 1C), such that each active zone would hold a total of ∼80 channels. What would be an upper bound for the number of simultaneously open channels per active zone? Our fluctuation analysis tells that an open probability of 0.82 can be achieved with saturating depolarizations in the presence of BayK8644 (Table 1). Relating the maximal Ca²⁺ currents before and after wash-in of BayK8644 indicated a maximum open probability of ∼0.4 in the absence of BayK8644 [a value of 0.2 was obtained for frog saccular hair cells by single-channel recordings under comparable ionic conditions by Rodriguez-Contreras and Yamoah (2001)]. Relying on our estimate, we would expect that maximally ∼30 channels open simultaneously at an inner hair cell active zone. Dividing the Ca²⁺ current at –20 mV (130 pA) (Fig. 5A) by the single-channel current reported for L-type channels (0.3 pA at –20 mV, 10 mm [Ca²⁺]_e) (Church and Stanley, 1996) and assuming the same fraction of extrasynaptic channels (∼30%) yielded an estimate of 20 open channels at the synapse. These estimates set upper bounds for the number of open channels, which will probably never be met in physiology, despite the fact that the higher temperature will increase the open probability (Nobile et al., 1990; Johnson et al., 2005).

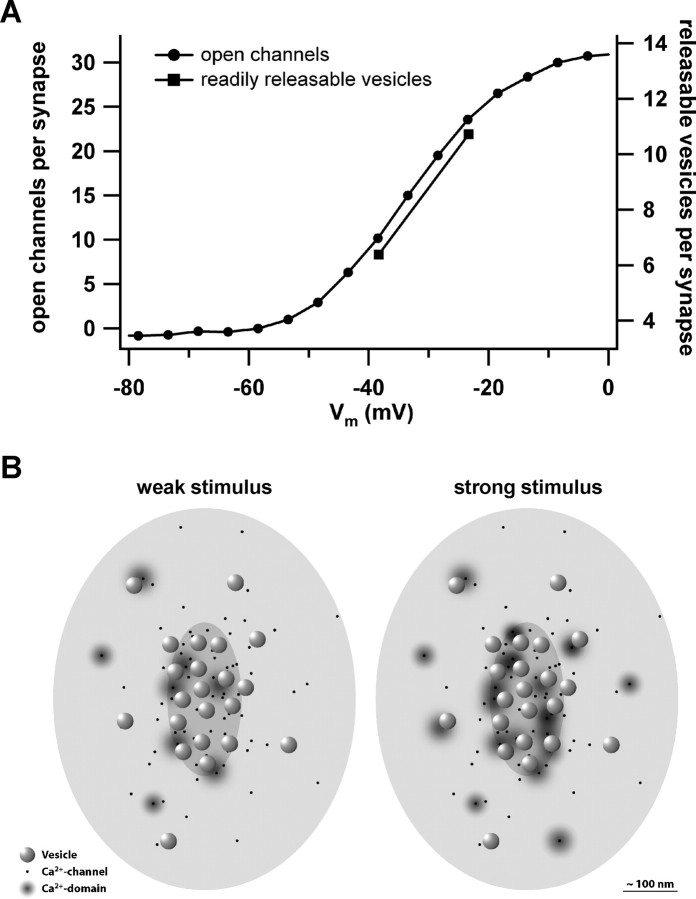
Figure 6A replots Ca²⁺ channel activation (Fig. 5B) after scaling it to the maximal number of simultaneously open Ca²⁺ channels at a synapse and shifting it in voltage to the physiological activation range (according to Fig. 1B). In conclusion, very few channels would open at an active zone for physiological depolarizations.

Figure 6.

Putative relationship of open Ca²⁺ channels and active release sites at the IHC synapses during depolarization. A, The putative Ca²⁺ channel activation at the average IHC ribbon synapse as function of depolarization (circles). The squares represent the numbers of readily releasable vesicles estimated at –28 and –13 mV [analysis of Fig. 5D; conversion factor 28 aF (Khimich et al., 2005)]. B, A diagram sketching the IHC active zone seen from hair cell cytosolic site with the ribbon removed. We pseudo-randomly scattered 80 Ca²⁺ channels (black dots) at the active zone with a higher density underneath the ribbon (medium gray ellipsoid) than for the rest of the active zone (postsynaptic density indicated as light gray ellipsoid). Synaptic vesicles (spheres) preferentially dock to the plasma membrane opposite to the postsynaptic density and were placed in a more regular array according to our electron microscopy findings (data not shown). Domains of elevated [Ca²⁺] are indicated by gray gradients. Whereas in the case of weak stimulation, only few channels open and drive exocytosis of their vesicles, overlap of Ca²⁺ domains is expected for saturating stimulation.

Mechanism of stimulus–secretion coupling

The 80 Ca_V1.3 channels face a pool of ∼50–60 release ready synaptic vesicles that is probably dominated by docked vesicles (16–30) (Khimich et al., 2005) at an IHC synapse. Each docked vesicle would be surrounded by three to five Ca²⁺ channels when simply distributing the channels among sufficiently separated docked vesicles. These numbers are comparable with estimates for the ribbon synapse of goldfish bipolar nerve terminals (five to seven) (von Gersdorff et al., 1998).

The actual Ca²⁺ channel–release site topography remains unknown for the inner hair cell ribbon synapse. Roberts et al. (1990) inferred a specific topography of Ca²⁺ and K⁺ channels at the synapses of frog saccular hair cells based on the freeze-fracture electron microscopy finding of clusters of intramembrane particles and the numerical correspondence of particle count and electrophysiologically estimated Ca²⁺ and K⁺ channel numbers. Whether release is controlled by the Ca²⁺ nanodomain shaped by the stochastic gating of one or few Ca²⁺ channels (as indicated here) or by a Ca²⁺ microdomain produced by many channels (Roberts, 1994; Tucker and Fettiplace, 1995) (in which the single channel properties are averaged) is not trivial to predict from morphology, even if the actual Ca²⁺ channel–release site topography was known. This is because the functional stimulus–secretion coupling further depends on the channel open probability (set by the stimulus and the maximal open probability), the width of the single-channel Ca²⁺ domain (set by the single-channel current and the cytosolic Ca²⁺ buffers), and the intrinsic Ca²⁺ sensitivity of exocytosis.

We suggest that IHC transmitter release is under Ca²⁺ nanodomain control during physiological sound coding. This is consistent with the expected low open probability of Ca_V1.3 channels during physiological receptor potentials (Russell and Sellick, 1978) and the low Ca²⁺ sensitivity of exocytosis (k_D, ∼78 μm) (Beutner et al., 2001) and supported by our recent functional results. First, RRP exocytosis of IHCs depended almost linearly on the amount of Ca²⁺ influx when titrating the number of open Ca²⁺ channels by varying membrane depolarization (Fig. 5E), DHP treatment, or genetic means (Brandt et al., 2003). A linear relationship of Ca²⁺ influx to fast exocytosis during graded changes of IHC depolarizations has been reported previously at room temperature (Moser and Beutner, 2000) and physiological temperature (Johnson et al., 2005). The different effects of the mechanistically distinct pharmacological Ca²⁺ influx manipulations offer a strong argument against a microdomain control of exocytosis (Augustine et al., 1991; Mintz et al., 1995). Second, we observed more exocytosis for the same Ca²⁺ influx at stronger depolarization (Fig. 5E) (more open channels, smaller single-channel current). This “hysteresis” of ascending and descending limbs of the exocytosis–Ca²⁺ current is usually interpreted as result of higher Ca²⁺ channel open probability and overlap of single-channel Ca²⁺ domains for strong depolarizations (Zucker and Fogelson, 1986; Augustine et al., 1991). Finally, the rapidly binding Ca²⁺ chelator BAPTA interfered much more efficiently with RRP exocytosis in IHCs than the slower chelator EGTA (Moser and Beutner, 2000), which further argues against a microdomain control (Augustine et al., 2003).

Figure 6 sketches our current view of stimulus–secretion coupling at the IHC ribbon synapse for two different stimulus intensities. Opening of a nearby channel would raise the [Ca²⁺]ofthe release site high enough to drive Ca²⁺ binding and exocytosis at high speed even at low depolarization levels, in which few Ca²⁺ channels are open at the active zone.

Implications of nanodomain control of transmitter release at the hair cell active zone for hearing

The Ca²⁺ nanodomain control hypothesis fits nicely with other mechanisms thought to enable the precise timing of hair cell synaptic transmission [e.g., fast vesicle fusion at saturating release site [Ca²⁺](τ, ∼1 ms) (Beutner et al., 2001)] and cooperation of synchronously released vesicles in driving a precisely timed postsynaptic response (Glowatzki and Fuchs, 2002; Khimich et al., 2005). A Ca²⁺ nanodomain control of exocytosis can also explain the classical finding in fish saccular hair cells that large changes of stimulus intensity leave the kinetics of synaptic depression essentially unaffected (Furukawa and Matsuura, 1978). Analyzing the statistics of hair cell synaptic transmission, Furukawa and colleagues concluded that stimulus intensity varies the number of release sites rather than the probability of release for a given synaptic vesicle (Furukawa et al., 1978, 1982). Our data now suggest that stimulus intensity mainly varies the number of active Ca²⁺ channel–release site units. Such a stimulus–secretion coupling would have the advantage of precise timing at low-intensity stimulation and enable phase-locking of the synaptic output also to weak sounds (Rose et al., 1967). Temporal precision of synaptic transmission and hence the quality of phase-locking improves at higher intensities (Rose et al., 1967), probably because more synaptic vesicles are released in synchrony (Khimich et al., 2005).